Chapter 5

THE POWER OF COMPLEX NUMBERS

Imagine a person with a gift of ridicule. [He might say] First that a negative quantity has no logarithm; secondly that a negative quantity has no square root; thirdly that the first nonexistent is to the second as the circumference of a circle is to the diameter.

Augustus De Morgan

Strange Happenings

Apart from admiration for the committed effort and ingenuity displayed in a note to the American Mathematical Monthly by H. S. Uhler, the casual reader might be surprised by the approximate value

0.207 879 576 350 761 908 546 955 619 834 978 770 033 877 841 631 769 614

the author gives to a real number.¹ The purpose of the note was to give high-order decimal approximations to eight numbers, each of which is a power of e; two of those numbers were e^π, the Gelfond constant, which we will mention later, and e^−π/2, which was written alternatively as iⁱ. The remarkable fact that together with a look at De Morgan’s quotation above and some material underlying them will occupy us over the next few pages.

Throughout their history, complex numbers have caused conceptual and philosophical difficulty, and their logarithms grave confusion. For example, in the mathematical ferment of the eighteenth century it was of natural and considerable importance to reconcile the two different answers to the integral (omitting the arbitrary constant)

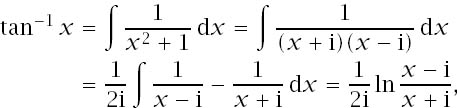
which meant giving a sensible meaning to the logarithm of complex numbers, and, in particular, to ln i. Johann Bernoulli argued that, since (−x)² = x², ln(−x)² = lnx² and so 2 ln(−x) = 2 lnx, which means that ln (−x) = ln x, and in particular ln (−1) = ln 1 = 0; this of course would mean that ln (−1) = ln i = 0. The great Leibniz disagreed, arguing that, if y = lnx, then

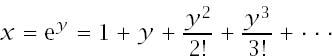
and putting x = −1 and y = 0 would result in −1 = 1. It was Leibniz’s belief that ln (−1) had to be an imaginary number and it was the genius Leonard Euler’s arguments that were to find in his favour and also resolve the seeming contradiction. In a 1728 letter to Bernoulli he provided arguments that easily led to the expression and in his 1749 article (published in 1751), ‘Recherches sur les racines imaginaries des equations’ (Memoires de l’Academy de Science de Berlin 5(1749):222–88), in attempting to prove that the complex numbers were complete, and as a special case of a general formula, he evaluated as 0.207 879 576 350 7, remarking

Qui est d’autant plus remarquable, qu’elle est réelle, et qu’elle renferme même une infinite de valeurs réelles différentes.
(What is all the more remarkable is that it is real, and it has an infinity of different actual values.)

It was the multivalued nature of the logarithm of complex numbers that was the key to resolving the Bernoulli–Leibniz conundrum.

Chapter 7 of Nonplussed! referred to the distinguished eighteenth-century British mathematician Augustus De Morgan (actually born in India) and the paradoxers who plagued him. This chapter’s opening quotation might suggest that paradoxers had been at work, but De Morgan knew better and offered his observation as an amusing example of the subtlety which is inherent in the study of complex numbers.

Complex numbers are, perhaps, well named, although subtle numbers might be a better alternative: at least the phrase would sidestep the suggestion of frightening difficulty and hint at the inherent beauty of this ‘ultimate’ extension of the number system. (The use of the quoted adjective must be tentative, with the existence of Hamilton’s quaternions, Conway’s surreal numbers and Cantor’s transfinite numbers, etc.

The ‘Ultimate’ Extension

The fundamental need to solve equations has brought with it successive, natural extensions of the natural number system = {1, 2, 3, . . . }.

For a simple equation like x + 2 = 5, where all of the coefficients belong to , there is no difficulty; its solution is x = 3, and an equation which exists in has its solution in .

Now consider the following alternatives, each of which is an equation framed in N, but in order to find solutions(s) we need to move to an extended number system:

• x + 5 = 2: to solve this we need to extend to the set of all integers = {. . . , −3, −2, −1, 0, 1, 2, 3, . . . }, or Zahlen, the German word for number;

Figure 5.1.

• 5x = 2 requires a further extension to = {Fractions}, or quotients, for its solution;

• x² = 2 requires the extension to the real numbers , and so include the irrationals like ± , and we have captured its two solutions.

These extensions are represented by the schema shown in figure 5.1. Each progressively fills up the number line, which we can picture as the x-axis, and once has been rigorously defined (and that is not at all a simple matter), it can be shown that the number line is full: there is no more room for more extensions to solve more equations.

So, what about the equation x² = −1?

The long, tortuous and mathematically painful story of the extension to the complex number system cannot occupy us here, but the inclusion of a single new number i = brings about the more general numbers x + iy, for x, y , and extends figure 5.1 by one final, enclosing circle. It proves to be the final extension that is necessary to solve all polynomial equations. To be precise, any polynomial of degree n with coefficients in has all of its n solutions in ; a result of such importance that it is universally known as the Fundamental Theorem of Algebra, first proved in 1799 by the inimitable Gauss.

Early Problems

As the number system is progressively extended—natural numbers, integers, rationals and reals—nothing very surprising happens. This is not to say that the rigorous definitions of some of these extensions are not themselves challenging, but more that the new numbers behave themselves ‘properly’. The ‘final’ extension to the complex numbers, , brings with it beauty, great utility and the genesis of counterintuitivity. We will mention two early problems.

First, the concept of order is lost; that is, it is no longer possible to ask the seemingly reasonable question, ‘which of two numbers is the greater?’ To see this, since i ≠ 0, we can ask the question, is i > 0 or is i < 0? If i > 0 we can multiply both sides of the inequality by i and preserve it to give i² > 0i, this means that −1 > 0. Alternatively, it must be that i < 0 and this time multiplying both sides by i it must therefore reverse the inequality to give i² > 0i once more and again −1 > 0. The assumption of order brings with it an irreconcilable contradiction and so must be abandoned.

To approach the second difficulty, we need to consider the Fundamental Theorem of Arithmetic: any natural number can be factorized in a unique way into the product of primes. For example, 504 can be decomposed into the product 2³ × 3² × 7 and no other combination of primes can be chosen. Notice that it is a theorem—and so needs proof. To be exact, it is two theorems:

(1) Any natural number can be factorized into primes.

(2) The factorization is unique (which denies 1 being considered as a prime).

The equivalent result appears in Book VII of Euclid’s Elements as a combination of three propositions:

Proposition 30. If two numbers multiplied by one another make some number, and any prime number measures the product, then it also measures one of the original numbers.

Proposition 31. Any composite number is measured by some prime number.

Proposition 32. Any number is either prime or is measured by some prime number.

Whatever the provenance of the result, it is important and often taken for granted—but its veracity is entirely dependent on the nature of the natural numbers and its associated set of prime numbers. We can easily change matters. Take as an example the set S of natural numbers of the form 3n + 1, n = 0, 1, 2, . . . ; that is, S = {1, 4, 7, 10, . . . }. This set is closed under multiplication; that is, the product of two such numbers is itself such a number. It also has its set of prime numbers: for example, 4, 10 and 25 have no factors within the system and so must be considered as prime; yet 100 = 4 × 25 = 10 × 10.

Now consider the set of complex numbers where a and b are real numbers, and the associated set of (what are called algebraic) integers for a and b ordinary integers. It is the case (and it is not at all obvious) that and are all primes in the system, yet

Unique factorization by primes is no longer valid.

Now that we have complex numbers properly placed and our mind receptive to lurking difficulty, we will consider what should be a simple computation for a calculator.

A Calculator’s Dilemma

Calculators are becoming ever more sophisticated and for very little money we can buy one which is capable of giving many answers in exact form, and of dealing with expressions which are complex in both senses of the word. Such sophisticates should have no difficulty in dealing with (−1)^2/3 or (−1)^3/2 but even they might not tell the whole story—and as we write there are plenty of calculators in circulation which would simply announce ‘Math Error’ as their answer.

Using the standard laws of indices, we can achieve the evaluations with ease:

and

Of course, we could have evaluated the expressions by splitting them in the alternative way with the first becoming

The symbol (−1)^2/3 really does seem to have the value 1. But now look at the result of doing this to the second expression:

In a way we can provide a sort of explanation of this second phenomenon: for sure, but −1 has two square roots, ±i. Interpreting the symbols one way round seems to choose one of the roots and the other way round the other root. But why? And what, if anything, has the evaluation of (−1)^2/3 to do with complex numbers?

What Is a^b?

If we wish to evaluate, for example, 3⁴, we can write it as 3 × 3 × 3 × 3 and evaluate the expression to 81 (even without a calculator!). The likes of 273¹⁴ would have us reach for electronic help but there would be no surprise that the help was effective and that we have been saved the drudgery of performing thirteen long multiplications. But what about, for example, Since we cannot write the number 2 down times we reach for our calculator, press the buttons and magically it seems to be able to as it comes up with the answer to the degree of accuracy of which it is capable: 2.665 144 142 690 225 188 650 297 249 87. . . .

In fact, this particular number has a famous history and a name to convince one of its importance: it is the Gelfond–Schneider constant and its nature was the subject matter of the seventh of the great David Hilbert’s famous 1900 list of unsolved problems. It took until 1934 before Aleksandr Gelfond and Theodor Schneider independently proved that

If α (≠ 0, 1) and β are algebraic numbers and if β is not a real rational, then any value of α^β is transcendental.

The calculator has done its best but is doomed to give a mere approximation to the actual value of the expression.

Of course, is simply an example of an awkward power; we could ask the value of any other difficult expression: uninterestingly, 3.827^4.916, or, very much more interestingly, e^π or π^e. In fact, the nature of π^e remains an unsolved problem, yet the Gelfond–Schneider theorem establishes the transcendence of e^π, even though e itself is transcendental—for reasons we shall see.

In fact, all exponential expressions, whether simple or complicated, are evaluated in the same manner, using the identity a^b = e^{b In a}, where both the exponential and logarithmic functions are evaluated using numerical methods based on the standard Taylor Series. A somewhat heavy approach for the likes of 3⁴, one might think, but it does allow the standard calculator to cope with the formidable : what it might not cope with is (−1)^2/3 or (−1)^3/2 and the reason for this failure is exposed by the rewrites (−1)^2/3 = e^{(2/3) In (−1)} and (−1)^3/2 = e^{(3/2) In (−1)}. We are forced to confront the same dilemma as those eighteenth-century luminaries: ascribing a value to ln (−1). Recall De Morgan’s quip: ‘a negative quantity, (which) has no logarithm’.

The Calculator Problem Solved

The standard representation of a complex number in rectangular and polar forms has us write z = x + iy = r cos θ + ir sin θ = r (cos θ + i sin θ) = re^iθ. If we are to give a meaning to w = In z, then it must be that e^w = z, and choosing the rectangular form for w and the polar form for z we have e^u+iv = re^iθ and so e^ue^iv = re^iθ, which means that e^u = r and v = θ. All of this results in the observation that u = In r = In |z| and v = θ = arg z and the fact that In z = In |z| + i arg z. Evidently, z = −1 is a complex number with |−1| = 1 and arg (−1) = π and using the above we have that

In (−1) = In |−1| + i arg (−1) = 0 + i π = i π.

This means that

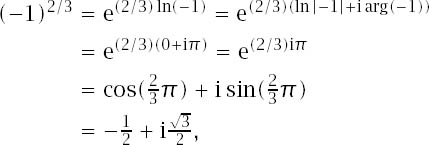
which is great, but it is not the 1 it evidently should be.

One way of achieving reconciliation is to look at the equation z = (−1)^2/3 and its equivalent form z³ = (−1)² = 1. In asking for the value of (−1)^2/3 we are asking for a cube root of 1, and Gauss’s Fundamental Theorem tells us that there are precisely three of them. Factorizing the cubic results in the equation

z³ −1 = (z −1) (z² + z + 1) = 0,

which generates our long-desired z = 1 as well as

Another (more useful) approach is to realize that the polar form of a complex number is many valued. For example, 1 = e^2πi = e^4πi = e^6πi = . . . ; in each case the modulus is 1 but the arguments differ by multiples of 2π. In our example above, we are dealing with the complex number −1, which has the polar forms −1 = e^iπ = e^3iπ = e^5iπ = . . .  and, taking the general case, we have that

for any integral k = 0, 1, 2, . . . . If we start to enumerate the possibilities, we have that

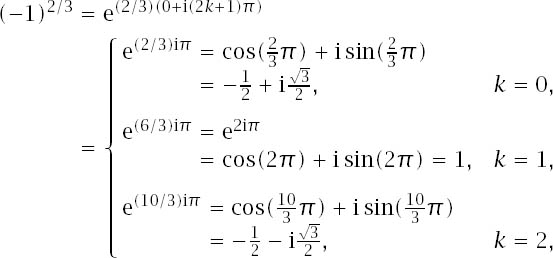
with the natural value appearing in the second row and two alternatives either side of it. Of course, there are an infinite number of choices for arg (−1) but that Fundamental Theorem holds sway since moving to the next value of k = 4,

starts to repeat the values.

A Remarkable Result

Now that the evaluation of powers has been discussed and an anomaly explained, we move to the meaning of iⁱ.

Since |i| = 1 and the fundamental value of arg (i) = π, we have that

and we have that striking result:

That said, we know that the full story has not been told, since arg (i) = (π + 2kπ).

The complete form of the expression is

So, the exotic has an infinite number of values, each of which is real and each of which involves the ubiquitous e and π.

Now, perhaps, the reader can cope with the puzzling

And we should conclude by addressing the De Morgan quotation with which the chapter began. His words translate into symbols as

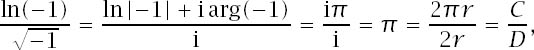
at least as a principal value!

¹H. S. Uhler, 1921, On the numerical value of iⁱ, American Mathematical Monthly 28(3):114–16.