As is usually the case, you can take several approaches to solve this problem. For example, you could write the equation for one of the circles, solve for x and y, and plug those values into the equation for the second circle. Then, you would solve the new equation for x and y.

Unfortunately, as you saw in the preceding solution, the equation for a circle centered at the point (cx, cy) is fairly complicated, so solving that equation for x and y isn't trivial. When you plug those values into the equation for the other circle, things really get complicated.

Instead of using that method, I'm going to use a geometric approach. Take a look at the circles shown in the following diagram. Our goal is to find the points of intersection between the two circles with the centers C0 and C1 and radii R0 and R1:

Let D be the distance between the circles' centers. There are several possible scenarios:

• If D > R₀ + R₁, then the circles are so far apart that they do not intersect
• If D < | R₀ – R₁|, then one circle lies inside the other so, again, the circles do not intersect
• If D = 0 and R₀ = R₁, then the circles are the same
• If D = R₀ + R₁, then the circles touch at a single point
• Otherwise, the circles intersect at two points

If you look at the triangle ΔC₀ P₂ P₃, the Pythagorean theorem gives us the equation H² = R₀² – A². Similarly, if you look at the triangle ΔC₁ P₂ P₃, the Pythagorean theorem gives us H² = R₁² – B². Setting these equations as equal gives the following:

We know that D = A + B. If we solve for A, that gives us A = D – B. If we substitute this value into the preceding equation, we get the following:

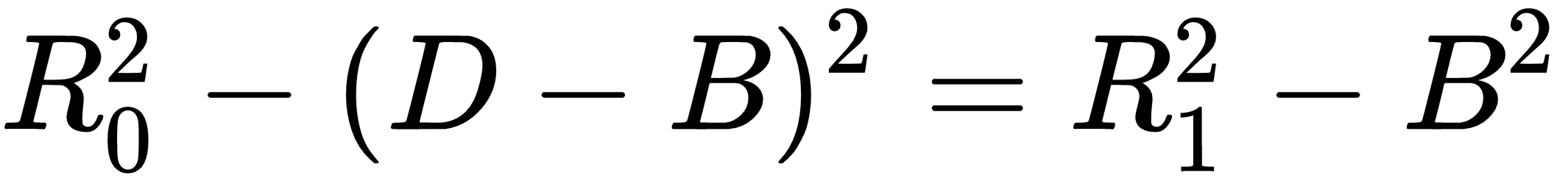
Multiplying this out gives the following:

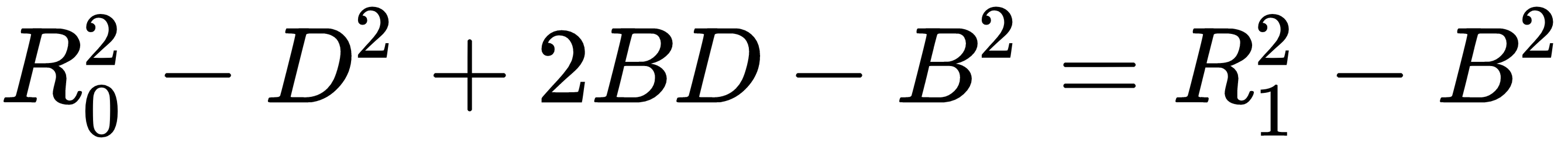
If you cancel the –B² terms on both sides and solve for B, you get the following:

Now, if you go back to the equations given by the Pythagorean theorem and solve for A instead of B, you get the following:

The only difference between these two equations is that the roles of R₀ and R₁ are switched.

We know all of these values, so we can use these equations to find A and B. All that remains is to use those values to find the points of intersection P₃ and P₄.

Let the vector <vx, vy> be the vector between the two circles' centers. Then, the vectors
<vy, -vx> and <-vy, vx> are perpendicular to that vector. We can add multiples of those perpendicular vectors to the point P₂ to find the points P₃ and P₄.

To reach the points P₃ and P₄, we need the perpendicular vectors to have the lengths H. We can achieve that by dividing the vectors by their current lengths and then multiplying them by H. We add those vectors to P₂ and we have the points of intersection.

FindCircleCircleIntersections uses this method to find the points where two circles intersect:

// Find the points of intersection between the circles defined
// by points p00, p01, p02 and p10, p11, p12.
private List<PointF> FindCircleCircleIntersections(
    Point p00, Point p01, Point p02,
    Point p10, Point p11, Point p12)
{
    const float tiny = 0.0001f;

    List<PointF> results = new List<PointF>();

    // Find the two circles, their centers, and their radii.
    Circle0 = FindCircle(p00, p01, p02);
    float R0 = Circle0.Width / 2;
    PointF C0 = new PointF(
        Circle0.X + R0,
        Circle0.Y + R0);

    Circle1 = FindCircle(p10, p11, p12);
    float R1 = Circle1.Width / 2;
    PointF C1 = new PointF(
        Circle1.X + R1,
        Circle1.Y + R1);

    // Find the distance between the centers.
    double D = Distance(C0, C1);

    // See how many solutions there are.
    if (D > R0 + R1)
    {
        Console.WriteLine(
            "No intersections, the circles are too far apart");
    }
    else if (D < Math.Abs(R0 - R1))
    {
        Console.WriteLine(
            "No intersections, one circle contains the other");
    }
    else if ((Math.Abs(D) < tiny) && (Math.Abs(R0 - R1) < tiny))
    {
        Console.WriteLine(
            "No intersections, the circles are the same");
    }
    else
    {
        // Find A and H.
        double A = (R0 * R0 - R1 * R1 + D * D) / (2 * D);
        double H = Math.Sqrt(R0 * R0 - A * A);

        // Find P2.
        double P2x = C0.X + A * (C1.X - C0.X) / D;
        double P2y = C0.Y + A * (C1.Y - C0.Y) / D;

        // Get the point P3.
        results.Add(new PointF(
            (float)(P2x + H * (C1.Y - C0.Y) / D),
            (float)(P2y - H * (C1.X - C0.X) / D)));

        // See if we a second solution.
        if (Math.Abs(D - (R0 + R1)) >= tiny)
        {
            // Add the second solution with the +/- signs switched.
            results.Add(new PointF(
                (float)(P2x - H * (C1.Y - C0.Y) / D),
                (float)(P2y + H * (C1.X - C0.X) / D)));
        }

        Console.WriteLine(results.Count.ToString() + " intersections");
    }

    // Return whatever results we found.
    return results;
}

The method starts by using the points that define the circles to find their centers and radii. It then uses the Distance helper method to find the distance between the two centers.

The code then uses a sequence of if statements to determine the correct number of intersections. If there are any intersections, the code calculates A and H, as described earlier and uses them to find the point P₂.

Next, the code uses P₂ to find the first point of intersection, P₃, and adds it to the results list.

The method then checks whether D equals R₀ + R₁. If the two values are equal, then P₃ is the only point of intersection. If D does not equal R₀ + R₁, then the code finds the other point of intersection, P₄ and adds it to the results list.

The method finishes by returning any points of intersection that it found.

Download the CircleCircleintersection example solution to see additional details.