Chapter 1
Integers and Permutations
God made the integers, and all the rest is the work of man.
—Leopold Kronecker
The use of arithmetic is a basic aspect of human culture. Anthropologists tell us that even the most primitive societies, because of their desire to count objects, have developed some sort of terminology for the numbers 1, 2, and 3, although many go no further. As a culture develops, it needs more sophisticated counting to deal with commerce, warfare, the calendar, and so on. This leads to methods of recording numbers often (but by no means always) based on groups of 10, presumably from counting on the fingers. Then the recording of numbers by making marks or notches becomes important (in bookkeeping, for example), and a variety of systems have been constructed for doing so. Many of these systems were not very useful for adding or multiplying (try multiplying with Roman numerals), and the development of our positional system, originating with the Babylonians using base 60 rather than 10, was a great advance.
In this chapter we assume the validity of the elementary arithmetic properties of the integers and use them to derive some more subtle facts related to divisibility and primes. Then two fundamental algebraic systems are described: the integers modulo n and the permutations of the set {1, 2, . . ., n}. These are, respectively, excellent examples of rings and groups, two of the basic algebraic structures presented in detail in Chapters 2 and 3.
Great fleas have little fleas upon their backs to bite ’em, And little fleas have lesser fleas, and so ad infinitum.
—Augustus De Morgan
Consider the sequence of equations:

It is clear there is a pattern. The right sides are the squares 12, 22, 32, 42, . . ., and, when the right side is n2, the left side is the sum of the first n odd integers. As the nth odd integer is 2n − 1, the following expression is true for n = 1, 2, 3, and 4:
(Pn)![]()
Now it is almost irresistible to ask whether the statement (pn) is true for every n ≥ 1. There is no hope of separately verifying all these statements, because there are infinitely many of them. A more subtle approach is required.
The idea is to prove that pk ⇒ pk+1 for every k ≥ 1. Then the fact that p1 is true implies that p2 is true, which in turn implies that p3 is true, then p4, and so on. This is one of the most important axioms for the integers.
Principle of Mathematical Induction6 Let pn be a statement for each integer n ≥ 1. Suppose that the following conditions are satisfied:
(1) p1is true.
(2) pk ⇒ pk+1 for every k ≥ 1.
Then pn is true for every n ≥ 1.
In the proof that pk ⇒ pk+1, we assume that pk is true and use it to prove that pk+1 is also true. The assumption that pk is true is called the induction hypothesis.
For a graphic illustration, consider an infinite row of dominoes labeled 1, 2, 3, . . . standing so that if one is knocked over, it will knock the next one over. If pk is the statement that domino k falls over, this means that pk ⇒ pk+1 for each k ≥ 1. The principle of induction asserts that knocking domino 1 over causes them all to fall.
As another illustration, let pn be the statement 1 + 3 + 5 + ![]() + (2n − 1) = n2 mentioned above. Then p1 has already been verified. To prove that pk ⇒ pk+1 for each k ≥ 1, we assume that pk is true (the induction hypothesis) and use it to simplify the left side of the sum pk+1:
+ (2n − 1) = n2 mentioned above. Then p1 has already been verified. To prove that pk ⇒ pk+1 for each k ≥ 1, we assume that pk is true (the induction hypothesis) and use it to simplify the left side of the sum pk+1:
![]()
This expression shows that pk+1 is true and hence, by the induction principle, that pn is true for all n ≥ 1.
Example 1. Prove Gauss' Formula7 : ![]() for all n ≥ 1.
for all n ≥ 1.
Solution. Let pn denote the statement ![]() Then p1 is true because
Then p1 is true because ![]() If we assume that pk is true for some k ≥ 1, we get
If we assume that pk is true for some k ≥ 1, we get
![]() ,
,
which shows that pk+1 is true. Hence, pn is true for all n ≥ 1 by the principle of mathematical induction.
Example 2 gives an inductive proof of a useful formula for the sum of a geometric series 1 + x + ![]() + xn. We use the convention that x0 = 1 for all numbers x.
+ xn. We use the convention that x0 = 1 for all numbers x.
Example 2. If x is any real number, show that
![]()
Solution. Let pn be the given statement. Then p1 is (1 − x)1 = 1 − x1, which is true. If we assume that pk is true for some k ≥ 1, then the left side of pk+1 becomes

This proves that pk+1 is true and so completes the induction.
Example 3. Let ![]() denote the number of n -letter words that can be formed using only the letters a and b. Show that
denote the number of n -letter words that can be formed using only the letters a and b. Show that ![]() for all n ≥ 1.
for all n ≥ 1.
Solution. Clearly, a and b are the only such words with one letter, so ![]() If k ≥ 1, we obtain each such word of k + 1 letters by adjoining an a or a b to a word of k letters, and there are
If k ≥ 1, we obtain each such word of k + 1 letters by adjoining an a or a b to a word of k letters, and there are ![]() of each type. Hence,
of each type. Hence, ![]() for each k ≥ 1 so, if we assume inductively that
for each k ≥ 1 so, if we assume inductively that ![]() we get
we get ![]() as required.
as required.
The principle of induction starts at 1 in the sense that if p1 is true and pk ⇒ pk+1 for all k ≥ 1, then pk is true for all k ≥ 1. There is nothing special about 1.
Theorem 1. If m is any integer, let pm, pm+1, pm+2, . . . be statements such that
(1) pm is true.
(2) pk ⇒ pk+1 for every k ≥ m.
Then pn is true for each n ≥ m.
Proof. Let tn = pm+n−1 for each n ≥ 1. Then t1 = pm is true, and tk ⇒ tk+1 because pm+k−1 ⇒ pm+k. Hence, tn is true for all n ≥ 1 by induction; that is, pn is true for all n ≥ m.
Example 4. If n ≥ 8, show that any postage of n cents can be made exactly using only 3-and 5 cent stamps.
Solution. The assertion clearly holds if n = 8. If it holds for some k ≥ 8, we consider two cases:
Case 1. One or more 5 cent stamps are used to make up k cents postage.
Then replace one of them with two 3 cent stamps.
Case 2. Three or more 3 cent stamps are used to make up k cents postage.
Then replace three of them with two 5 cent stamps.
Because one of these cases must occur (as k ≥ 8), the assertion holds for k + 1 cents in both cases and the induction goes through.
If n ≥ 1 is an integer, the integer n ! (read n-factorial) is defined to be the product
![]()
of all the integers from n to 1. Thus, 1 ! = 1, 2 ! = 2, 3 ! = 6, and so on. Clearly,
![]()
which we extend to n = 0 by defining
![]()
Example 5. Show that 2n < n ! for all n ≥ 4.
Solution. If pk is the statement 2k < k !, note that p1, p2, and p3 are actually false, but p4 is true because 24 = 16 < 24 = 4 !. If pk is true where k ≥ 4, then 2k < k ! so
![]()
Hence, pk+1 is true and the induction is complete.
Let n and r be integers with 0 < r ≤ n. The binomial coefficient nr is defined as follows:
![]()
As ![]() , we have
, we have ![]() and
and ![]() . It is easy to verify that
. It is easy to verify that
![]()
We leave the proof of the following formula (the Pascal identity) as Exercise 13.
![]()
The name honors Blaise Pascal. The identity leads to a way of displaying the binomial coefficients known as Pascal's triangle:
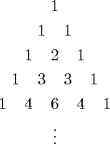
The nth row of the triangle is ![]() , starting at n = 0. The Pascal identity shows that each entry in a given row (except at the ends) can be found by adding the two entries adjacent to it in the row above. Hence, Pascal's triangle is easy to write down row by row.8
, starting at n = 0. The Pascal identity shows that each entry in a given row (except at the ends) can be found by adding the two entries adjacent to it in the row above. Hence, Pascal's triangle is easy to write down row by row.8
The entries in each row also arise in another way. The formulas
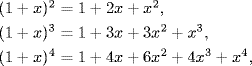
are easily verified, and the coefficients on the right side in each case are the integers in rows 2, 3, and 4 of Pascal's triangle. The general result follows by induction, and will be used several times in this book.
Example 6. Prove the Binomial Theorem:
![]()
Solution. The theorem holds if n = 0 because ![]() and (1 + x)0 = 1. If it holds for some k ≥ 0 then, using the Pascal identity, we obtain
and (1 + x)0 = 1. If it holds for some k ≥ 0 then, using the Pascal identity, we obtain
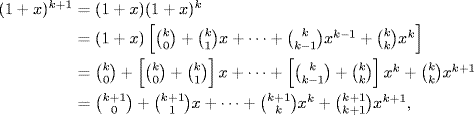
which completes the induction.
When proving inductively that statements pm, pm+1, . . ., pk are true, the most difficult part is usually showing that pk ⇒ pk+1 for each k ≥ m. Clearly, this task would be easier if we could assume the truth of pm, . . ., pk−1 in addition to the truth of pk when deducing pk+1. This assumption leads to a useful variant of the principle of induction (in fact, it is equivalent to it).
Theorem 2. Principle of Strong Induction. Let m be an integer and, for each n ≥ m, let pn be a statement. Suppose the following conditions are satisfied.
(1) pm is true.
(2) If k ≥ m and all of pm, pm+1, . . ., pk are true, then pk+1 is also true.
Then pn is true for every n ≥ m.
Proof. For each n ≥ m, let tn be the statement that pm, pm+1, . . ., pn are all true. Then, tm is true by (1). If tk is true for some k ≥ m, then (2) implies that pk+1 is true, so tk+1 is also true. Hence, tn is true for all n ≥ m by Theorem 1, so certainly pn is true for all n ≥ m.
In the next example, we use strong induction to prove an important fact about primes that would be more difficult to deduce using (ordinary) induction. Recall that a prime number (or prime) is an integer p ≥ 2 that cannot be factored as a product of two smaller positive integers.
Example 7. Show that every integer n ≥ 2 is a product of (one or more) primes.
Solution. This assertion is true if n = 2 because 2 is a prime. If k ≥ 2, we assume inductively that 2, 3, . . ., k are all products of primes. To apply strong induction, we must show that k + 1 is a product of primes. This is clear if k + 1 is itself prime; otherwise, let k + 1 = ab, where 2 ≤ a ≤ k and 2 ≤ b ≤ k. Then both a and b are products of primes by the (strong) induction hypothesis, so k + 1 = ab is also a product of primes.
We conclude with an intuitively clear property of ![]() that is equivalent to the principle of induction, and which is usually taken as an axiom.
that is equivalent to the principle of induction, and which is usually taken as an axiom.
Well-Ordering Principle. Every nonempty set of nonnegative integers has a smallest member.
Proof. If the principle is false, let X ⊆ {0, 1, 2, . . . } be a nonempty set that has no smallest member. For each n ≥ 0, let pn be the statement “n ∉ X.” It suffices to show that pn is true for all n ≥ 0—since then X is empty, contrary to our assumption. We prove this by strong induction. First, p0 is true because if 0 ![]() X, then it is the smallest member of X (because X ⊆ {0, 1, 2, . . . }). Now assume inductively that p0, p1, . . ., pk are all true, so that none of 0, 1, . . ., k is in X. This implies that k + 1 ∉ X since otherwise it would be the smallest member of X. This means pk+1 is true, and so completes the induction.
X, then it is the smallest member of X (because X ⊆ {0, 1, 2, . . . }). Now assume inductively that p0, p1, . . ., pk are all true, so that none of 0, 1, . . ., k is in X. This implies that k + 1 ∉ X since otherwise it would be the smallest member of X. This means pk+1 is true, and so completes the induction.
The way the well-ordering principle is used can be illustrated by the following frivolous example: Suppose that we want to show that every positive integer is interesting. If this assertion were false, the set of uninteresting positive integers would be nonempty and so would contain a smallest member by the axiom. But the smallest uninteresting integer would surely be interesting—a contradiction! This technique can also be applied to serious situations.
For example, the well-ordering principle implies the induction principle. Indeed, let p1, p2, p3, . . . be statements such that p1 is true and pk ⇒ pk+1 for every k ≥ 1. If X = {n ≥ 1 ![]() pn is false}, we must show that X is empty. But if not, then X has a smallest member, which leads to a contradiction. The details are in Exercise 15.
pn is false}, we must show that X is empty. But if not, then X has a smallest member, which leads to a contradiction. The details are in Exercise 15.
We have proved the following implications (the first is Theorem 2):
Induction ⇒ Strong Induction ⇒ Well Ordering.
Moreover, well ordering implies induction (see above), so the three principles are logically equivalent. The validity of these principles is one of the basic Peano axioms9 for the integers.
Inductive Definition
Many arguments in algebra (in fact, in mathematics generally) refer to sequences a0, a1, a2, a3, ![]() , an,
, an, ![]() from a set A where each ai is an element of A called the ith term of the sequence. Hence 1, 2, 4, 8, 16, . . . are the first five terms of the sequence an = 2n from
from a set A where each ai is an element of A called the ith term of the sequence. Hence 1, 2, 4, 8, 16, . . . are the first five terms of the sequence an = 2n from ![]() This sequence can be compactly described as follows:
This sequence can be compactly described as follows:
(*)![]()
These conditions uniquely describe the sequence (the formula an = 2n for n ≥ 0 can be proved by induction), and for this reason (*) is called an inductive definition of the sequence. More generally, a sequence is said to be defined inductively if the first term is specified and each later term is uniquely determined by the earlier terms (often by a formula). It is usually very difficult to give an explicit formula for the nth term an in terms of the earlier terms; nevertheless, the following theorem shows that such a sequence always exists and is uniquely determined.
Theorem 3. Recursion Theorem. Given a set A and a ![]() A, there is exactly one sequence a0, a1, a2, a3, . . ., an, . . . from A that satisfies the following requirements:
A, there is exactly one sequence a0, a1, a2, a3, . . ., an, . . . from A that satisfies the following requirements:
(1) a0 = a.
2. For each n ≥ 1, the term an is uniquely determined by the preceding terms a0, a1, a2, . . ., an−1.
Proof. The existence of such a sequence is given in Appendix D; we prove uniqueness by strong induction on n ≥ 0. Clearly, a0 is uniquely determined by (1). If each of a0, a1, a2, . . . an−1 has been uniquely specified, then an is uniquely determined by (2). Hence, the sequence is uniquely determined by (1) and (2).
1. Prove each equation by induction on n.
(a) 1 + 5 + 9 + ![]() + (4n − 3) = n(2n − 1) for all n ≥ 1.
+ (4n − 3) = n(2n − 1) for all n ≥ 1.
(b) ![]() for all n ≥ 1.
for all n ≥ 1.
(c) ![]() for all n ≥ 1.
for all n ≥ 1.
(d) ![]() for all n ≥ 1.
for all n ≥ 1.
(e) ![]() for all n ≥ 1.
for all n ≥ 1.
(f) ![]() for all n ≥ 1.
for all n ≥ 1.
(g) ![]() for all n ≥ 1.
for all n ≥ 1.
(h) ![]() for all n ≥ 1.
for all n ≥ 1.
(i) ![]() for all n ≥ 1.
for all n ≥ 1.
2. Prove each inequality by induction on n.
(a) n < 2n for all n ≥ 0.
(b) n2 ≤ 2n for all n ≥ 4.
(c) ![]() for all n ≥ 4 (compare with Example 5).
for all n ≥ 4 (compare with Example 5).
(d) ![]() for all n ≥ 1.
for all n ≥ 1.
(e) ![]() for all n ≥ 1.
for all n ≥ 1.
(f) ![]() for all n ≥ 1.
for all n ≥ 1.
3. Prove each statement by induction on n.
(a) n3 + (n + 1)3 + (n + 2)3 is a multiple of 9 for all n ≥ 1.
(b) n3 − n is a multiple of 3 for all n ≥ 1.
(c) 32n+1 + 2n+2 is a multiple of 7 for all n ≥ 0.
4. Show that ![]() for all n > 2.
for all n > 2.
5. Show that 33n + 1 is a multiple of 7 for all odd n ≥ 1.
6. Suppose that n straight lines in the plane are positioned so that no two are parallel and no three pass through the same point. Show that they divide the plane into ![]() distinct regions.
distinct regions.
7. Show that there are 3n positive integers with n digits, where each digit must be 4, 5, or 6.
8. A polygon in the plane is called convex if every line joining two vertices is either an edge or lies entirely within the polygon. If n ≥ 3, show that the sum of the interior angles of an n-sided convex polygon equals (n − 2) · 180![]() .
.
9. A straight line segment joining two distinct points on a circle is called a secant. For n ≥ 1, draw n secants with no two identical. Show that the resulting regions can be unambiguously colored black and white (where unambiguously means that no two regions sharing a straight line boundary are of the same color).
10.
(a) Show that any postage of n ≥ 2 cents can be made of 2 and 3 cent stamps.
(b) Show that any postage of n ≥ 12 cents can be made of 3 and 7 cent stamps.
(c) Show that any postage of n ≥ 18 cents can be made of 4 and 7 cent stamps.
(d) Can you generalize from the results in (a)–(c)?
11. Let an = 23n − 1 for n ≥ 0. Guess a common divisor of each an and prove your assertion.
12.
(a) Try to prove the statement “13 + 23 + ![]() + n3 is a perfect square” by induction. Now look at Exercise 1(c).
+ n3 is a perfect square” by induction. Now look at Exercise 1(c).
(b) Try to prove that ![]() by induction. Now formulate a stronger equality for the sum on the left, prove it by induction, and use it to deduce the inequality.
by induction. Now formulate a stronger equality for the sum on the left, prove it by induction, and use it to deduce the inequality.
13. Prove the Pascal identity: ![]() for 1 ≤ r ≤ n.
for 1 ≤ r ≤ n.
14.
(a) Show that ![]() for all n ≥ 0.
for all n ≥ 0.
(b) Show that ![]() if n > 0.
if n > 0.
15. Use the well-ordering principle to prove the principle of induction. [Hint: See the discussion following the well-ordering principle.]
16. Let X be a nonempty set of integers. Then X is said to be bounded below(bounded above) if an integer m exists such that m ≤ x for all x ![]() X (respectively m ≥ x for all x
X (respectively m ≥ x for all x ![]() X).
X).
(a) If X is bounded below, show that it has a smallest member.
(b) If X is bounded above, show that it has a largest member.
17. Use strong induction to prove that every integer n ≥ 2 has a prime factor.
18. In each case, conjecture a formula for an and prove it by induction.
(a) a0 = 2, an+1 = − an, n ≥ 0.
(b) a0 = 1, a1 = − 2, an+2 = 2an − an+1, n ≥ 0.
(c) a0 = 1, an+1 = 1 − an, n ≥ 0.
(d) a0 = 3, an+1 = (an)2, n ≥ 0.
19. Let n lines in the plane be such that no two are parallel and no three are concurrent. Find the number an of regions into which the plane is divided by first showing that an+1 = an + (n + 1).
20. Prove the following induction principle. Let m be an integer and let pn be a statement for all n ≥ m. Assume that (1) pm and pm+1 are true. (2) If k ≥ m and both pk and pk+1 are true, then pk+2 is true. Then pn is true for all n ≥ m.
21. Let an denote a number for each integer n ≥ 0 and assume that an+2 = an+1 + 2an holds for every n ≥ 0. Use the principle in Exercise 20 to prove each assertion.
(a) If a0 = 1 and a1 = − 1, then an = (− 1)n for each n ≥ 0.
(b) If a0 = 1 and a1 = 2, then an = 2n for each n ≥ 0.
(c) If a0 = p and a1 = q, then ![]() for each n ≥ 0.
for each n ≥ 0.
22. Let pn denote the statement: “3n + 2 is a multiple of 3.” Show that pk ⇒ pk+1 for all k ≥ 1. What does this say about Theorem 1?
23. Let pn denote the statement: “In any class of n algebra students, every student obtains the same grade.” Then p1 is clearly true. If pn is satisfied for n > 1, suppose that x1, x2, . . ., xn+1 denotes a class of n + 1 students. Then x1, x2, . . ., xn all have the same grade (by induction) as do x2, x3, . . ., xn+1. Thus x1, x2, . . ., xn+1 all have the same grade (the same as xn), so pn+1 is true. Hence, pn is true for all n. What is wrong with this argument?
24. Suppose that pn is a statement about n for each n ≥ 1. In each case what must be done to prove that pn is true for all n ≥ 1?
(a) pn ⇒ pn+2 for each n ≥ 1.
(b) pn ⇒ pn+8 for each n ≥ 1.
(c) pn ⇒ pn+1 for each n ≥ 10.
25. If pn is a statement about n for each n ≥ 1, argue that pn is true for all n ≥ 1 if pn ⇒ pn−1 for each n ≥ 2 and pn is true for infinitely many values of n.
26. For a sequence a1, a2, . . ., suppose that a1 + a2 + ![]() + an is to be evaluated.
+ an is to be evaluated.
(a) If a sequence b1, b2, . . . can be found such that an = bn+1 − bn for all n > 1, prove by induction that a1 + a2 + ![]() + an = bn+1 − b1.
+ an = bn+1 − b1.
(b) Use the technique in (a) to evaluate 1 · 2 · 3 + 2 · 3 · 4 + ![]() + n(n + 1)(n + 2). [Hint: Try bn = (n − 1)n(n + 1)(n + 2).]
+ n(n + 1)(n + 2). [Hint: Try bn = (n − 1)n(n + 1)(n + 2).]
27. Suppose that a sequence a0, a1, . . . is given.
(a) Show that the sequence s0, s1, . . . exists where s0 = a0 and sn is the sum of the first n + 1 of ai.
(b) Show that the sequence p0, p1, . . . exists where p0 = a0 and pn is the product of the first n + 1 of the ai.
1.2 Divisors and Prime Factorization
Mathematics is the queen of the sciences and number theory is the queen of mathematics.
—Carl Friedrich Gauss
The set ![]() of integers will be used in several ways throughout this book: as a major source of examples of algebraic systems; to state definitions and prove theorems (often by induction); and as a prototype for results about more general systems. For the most part, the properties of
of integers will be used in several ways throughout this book: as a major source of examples of algebraic systems; to state definitions and prove theorems (often by induction); and as a prototype for results about more general systems. For the most part, the properties of ![]() that we need are familiar facts about addition, multiplication, and ordering of the integers, although we present a more detailed look at these properties in Section 3.2. However, we also utilize several less familiar properties of divisibility and primes in
that we need are familiar facts about addition, multiplication, and ordering of the integers, although we present a more detailed look at these properties in Section 3.2. However, we also utilize several less familiar properties of divisibility and primes in ![]() and so devote this section to them.
and so devote this section to them.
The Greatest Common Divisor
When we write 22/7 in the form ![]() we are using the fact that 22 = 3· 7 + 1; that is, 22 leaves a remainder of 1 when divided by 7. The general result is a consequence of the well-ordering axiom.
we are using the fact that 22 = 3· 7 + 1; that is, 22 leaves a remainder of 1 when divided by 7. The general result is a consequence of the well-ordering axiom.
Theorem 1. Division Algorithm. Let n and d ≥ 1 be integers. There exist uniquely determined integers q and r such that
![]()
Proof. Let ![]() n − td ≥ 0}. Then X is nonempty. In fact, if n ≥ 0, then n = n − 0d is in X; if n < 0, then n − nd = n(1 − d) is in X. Hence, by the well-ordering principle, let r be the smallest member of X. Then r = n − qd for some q and r ≥ 0, so it remains to show that r < d. But if r ≥ d, then 0 ≤ r − d = n − (q + 1)d. This means that r − d is in X, contradicting the minimality of r. This result proves the existence of q and r.
n − td ≥ 0}. Then X is nonempty. In fact, if n ≥ 0, then n = n − 0d is in X; if n < 0, then n − nd = n(1 − d) is in X. Hence, by the well-ordering principle, let r be the smallest member of X. Then r = n − qd for some q and r ≥ 0, so it remains to show that r < d. But if r ≥ d, then 0 ≤ r − d = n − (q + 1)d. This means that r − d is in X, contradicting the minimality of r. This result proves the existence of q and r.
To prove uniqueness, suppose also that n = q′d + r′ with 0 ≤ r′ < d. Assume r ≤ r′ (the case r′ ≤ r is similar). Then (q − q′)d = r′ − r is a nonnegative, integral multiple of d that is less than d (because r′ − r ≤ r′ < d). This can occur only if r = r′, which implies that q = q′ and so proves uniqueness.
For n and d ≥ 1, the integers q and r in Theorem 1 are called the quotient and remainder, respectively. Thus, for example, if we divide n = − 17 by d = 5, the result is −17 = (− 4) · 5 + 3, so the quotient is −4 and the remainder is 3.
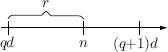
The division algorithm can also be seen geometrically. If the real line is marked off in multiples of d, n clearly falls either on a multiple qd of d or between qd and (q + 1)d
(see the diagram). Hence, qd ≤ n < (q + 1)d, so 0 ≤ n − qd < d, and we take r = n − qd.
If both n and d are positive and a calculator is available, the quotient q and the remainder r can be easily found as follows: Calculate ![]() and let q denote the largest integer that is less than or equal to
and let q denote the largest integer that is less than or equal to ![]() Hence,
Hence,
![]()
If we multiply through by d, we get 0 ≤ n − qd < d, so take r = n − qd.
Example 1. Find the quotient and remainder if n = 4187 and d = 129.
Solution. We have ![]() approximately, so q = 32. Then r = n − dq = 59, and so 4187 = 32 · 129 + 59, as desired.
approximately, so q = 32. Then r = n − dq = 59, and so 4187 = 32 · 129 + 59, as desired.
If n and d are integers, d is called a divisor of n if n = qd for some integer q. When this is the case, we write d|n. If d|n is not true, we write d![]() n. Thus, 7|84 but 7
n. Thus, 7|84 but 7![]() 85. Note that 1|n and n|0 for all integers n. The following properties of divisors will be used frequently.
85. Note that 1|n and n|0 for all integers n. The following properties of divisors will be used frequently.
Theorem 2. Let m, n and d denote integers.
(1) n|n for all n.
(2) If d|m and m|n, then d|n.
(3) If d|n and n|d, then d = ± n.
(4) If d|n and d|m, then d|(xn + ym) for all integers x and y.
Proof. The proofs of (1) and (2) are left to the reader. In (3), let n = qd and d = pn for integers p and q. If d = 0, then n = qd = 0 = d. If d ≠ 0, then d = pn = pqd, which implies that 1 = pq. As p and q are integers, this means that p = q = 1 or p = q = − 1, and so d = n or d = − n, which proves (3). As to (4), if n = ad and m = bd in (4), then xn + ym = (xa + yb)d, so d|(xn + ym), as required.
Expressions of the form xn + ym, where x and y are integers, are called linear combinations of n and m.
Example 2. If d ≥ 1 is such that d|(3k + 5) and d ![]() (7k + 2) for some k, show that d = 1 or d = 29.
(7k + 2) for some k, show that d = 1 or d = 29.
Solution. The hypotheses and (4) of Theorem 2 imply that d divides the linear combination 7(3k + 5) − 3(7k + 2) = 35 − 6 = 29. Hence, d is a positive divisor of 29, so d = 1 or d = 29.
An integer d is called a common divisor of two integers m and n if d|m and d|n. To motivate the next theorem, consider the positive divisors of 36 and 84:
- Positive divisors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Positive divisors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
- Common divisors: 1, 2, 3, 4, 6, 12
We wish to focus attention on the fact that the largest common divisor 12 is actually a multiple of all the other positive common divisors. This idea is built into the following definition. Let m and n be integers.
An integer d is called a greatest common divisor of m and n if:
(1) d ≥ 1
(2) d|m and d|n
(3) If k|m and k|n, then k|d.
When it exists we write d = gcd (m, n).
For example, gcd (18, 30) = 6, gcd (6, 7) = 1, and gcd (− 9, 15) = 3.
Conditions (2) and (3) can be stated as follows: gcd (m, n) is a common divisor of m and n by (2), which is a multiple of every common divisor by (3). If it exists, d = gcd (m, n) is unique. In fact, if d′ is another integer satisfying (1), (2), and (3), then d′|d by (3). Similarly, d|d′ so d = ± d′ by Theorem 2. But then d′ = d because we insist that greatest common divisors are positive.
The following fundamental theorem shows that, if m and n are not both zero, then d = gcd (m, n) does indeed exist and, surprisingly, that d is actually a linear combination of m and n.
Theorem 3. Let m and n be integers, not both zero. Then d = gcd (m, n) exists and d = xm + yn for some integers x and y.
Proof. Let ![]() xm + yn ≥ 1}. Then X is not empty because m2 + n2
xm + yn ≥ 1}. Then X is not empty because m2 + n2 ![]() X, so let d be the smallest member of X (by the well-ordering principle). Since d
X, so let d be the smallest member of X (by the well-ordering principle). Since d ![]() X, we have d ≥ 1 and d = xm + yn for integers x and y. Also, if k|m and k|n, then k|(xm + yn) = d by Theorem 2. So it remains to show that d|m and d|n.
X, we have d ≥ 1 and d = xm + yn for integers x and y. Also, if k|m and k|n, then k|(xm + yn) = d by Theorem 2. So it remains to show that d|m and d|n.
To show that d|m, write m = qd + r where 0 ≤ r ≤ d − 1. Then,
r = m − qd = m − q(xm + yn) = (1 − qx)m + (− qy)n.
Hence, if r ≥ 1, then r ![]() X and r < d, contradicting the choice of d. So r = 0, that is, m = qd. Thus, d|m, and d|n is proved similarly.
X and r < d, contradicting the choice of d. So r = 0, that is, m = qd. Thus, d|m, and d|n is proved similarly.
Note that gcd (m, n) does not exist if m = 0 = n (verify), which explains the requirement in Theorem 3 that m and n are not both zero. Also, the greatest common divisor of m and n can be a linear combination of m and n in more than one way. For example, gcd (2, 3) = 1 and we have 1 = 2 · 1 − 3and 1 = 3 − 2.
Example 3. If p and q are distinct primes, show that gcd (p, q) = 1.
Solution. Write d = gcd (m, n). Then d|p, so d = 1 or p. Similarly, d = 1 or q, so d = 1 because, otherwise, p = d = q is contrary to the assumption that p ≠ q.
The next example (which is needed later) illustrates how the definition of the greatest common divisor is used.
Example 4. If m = qn + r, show that gcd (m, n) = gcd (n, r).
Solution. Write d = gcd (m, n) and k = gcd (n, r). Then k divides both n and r and so divides m = qn + r. Thus, k is a common divisor of m and n, so k|d because d = gcd (m, n). A similar argument (using r = − qn + m) shows that d|k, so d = ± k by (3) of Theorem 2. Hence, d = k, because both d and k are positive.
How do we compute d = gcd (m, n) in general? There is an efficient procedure for doing so, which also shows how to express d as a linear combination of m and n. To illustrate how it works, consider the numbers 78 and 30. The idea is to use the division algorithm repeatedly. First divide 78 by 30:

At each stage (after the first) we divide the divisor at the previous stage by the remainder at that stage. The last nonzero remainder is 6, and this equals gcd (78, 30). This is no coincidence as we shall see. To express 6 as a linear combination of 78 and 30, eliminate the remainders from the second last lineup:

This procedure is called the euclidean algorithm, and it works in general. For positive integers m and n, not both zero, we use the division algorithm repeatedly:

At each stage we divide the divisor at the previous stage by the remainder, so the remainders form a decreasing sequence of nonnegative integers:
![]()
Clearly, we must encounter a remainder of 0 (in at most n steps). If rt denotes the last nonzero remainder, the last two equations are
![]()
Now, repeated application of the result in Example 4 gives
![]()
Hence, gcd (m, n) really is the last nonzero remainder.
Example 5. Find gcd (41, 12) and express it as a linear combination of 41 and 12.
Solution. The algorithm is not needed to find gcd (41, 12). In fact, 1 and 41 are the only positive divisors of 41, so gcd (41, 12) = 1 because 41 does not divide 12. However, guessing a linear combination 1 = x · 41 + y · 12 is not easy. The euclidean algorithm gives

Hence, gcd (41, 12) = 1 as expected. Elimination of remainders gives

which is the required linear combination.
The following definition will be used frequently throughout this book.
Two integers m and n are called relatively prime if gcd (m, n) = 1.
For example, 2 and 3 are relatively prime, as are 20 and 9. Note that 1 is relatively prime to every integer n. The condition in Theorem 4 is useful.
Theorem 4. Let m and n be integers, not both zero. Then m and n are relatively prime if and only if 1 = xm + yn for some integers x and y .
Proof. If gcd (m, n) = 1, then 1 = xm + yn by Theorem 3. Conversely, if 1 = xm + yn, then any common divisor of m and n must divide 1. In particular, gcd (m, n) = 1.
For example, any two consecutive integers k and k + 1 are relatively prime because (k + 1) − k = 1. Similarly, 5(6k + 5) − 6(5k + 4) = 1 shows that 6k + 5 and 5k + 4 are relatively prime for any integer k.
Corollary. If d = gcd (m, n), ![]() then
then ![]() and
and ![]() are relatively prime.
are relatively prime.
Proof. If ![]() dividing by d gives
dividing by d gives ![]()
The following theorem contains two very useful properties of relatively prime integers, and will be referred to several times below.
Theorem 5. Let m and n be relatively prime integers.
1. If m|k and n|k for some integer k, then mn|k.
2. If m|kn for some integer k, then m|k.
Proof. We first prove (1). By Theorem 4, let 1 = xm + yn, where x and y are integers. If k = qm and k = pn where p and q are integers, then
k = 1 · k = xmk + ynk = xm(pn) + yn(qm) = (xp + yq)mn.
Hence, mn|k, proving (1). As to (2), let nk = qm where q is an integer. Then,
k = 1 · k = xmk + ynk = xmk + y(qm) = (xk + yq)m.
This shows that m|k, and so proves (2).
Prime Factorization
Clearly, every integer n ≥ 2 has at least two positive divisors: 1 and n. The integers for which these are the only positive divisors are important. An integer p is called a prime if it satisfies the following conditions:
1. p ≥ 2.
2. If d|p and d > 0, then either d = 1 or d = p.
Thus, the first few primes are 2, 3, 5, 7, 11, 13, . . . . We know (Example 7 §1.1) that every integer greater than 1 is a product of primes; the reason for not regarding 1 as a prime is to ensure that this factorization is unique (see Theorem 7).
If the product of two integers is even, one of these integers must be even (because the product of two odd integers is odd). We can rephrase this statement as follows: If 2|mn, where m and n are integers, then 2|m or 2|n. This statement holds for any prime in place of 2.
Theorem 6. Euclid's Lemma. Let p denote a prime.
1. If p|mn where m and n are integers, then p|m or p|n.
2. If p|m1m2 ![]() mr where each mi is an integer, then p|mi for some i.
mr where each mi is an integer, then p|mi for some i.
Proof. (1) Write d = gcd (m, p). Then d|p, so d = 1 or d = p because p is a prime. If d = p, then p|m because d|m; if d = 1, then p|n by (2) of Theorem 5.
(2) This assertion follows by induction on r. If r = 1, it is obvious. If (2) holds for some r ≥ 1, let p|m1m2 ![]() mrmr+1. Then (1) shows that either p|m1
mrmr+1. Then (1) shows that either p|m1 ![]() mr or p|mr+1. In the first case, p|mi for some i = 1, 2, . . ., r by the induction hypothesis. Hence, in any case, p|mi for some i = 1, 2, . . ., r + 1, completing the induction.
mr or p|mr+1. In the first case, p|mi for some i = 1, 2, . . ., r by the induction hypothesis. Hence, in any case, p|mi for some i = 1, 2, . . ., r + 1, completing the induction.
Note that Euclid's lemma fails for nonprimes. For example, 6 is a divisor of 3 · 4, but 6 does not divide 3 or 4.
It is not too difficult to convince yourself that every integer n ≥ 2 is either a prime itself or can be factored as a product of primes—just keep factoring as long as possible. For example, 12 = 22 · 3, 25 = 52, and 360 = 23 · 32 · 5. In fact, every integer greater than 1 is a product of primes, and this factorization is unique up to the order of the factors.
Theorem 7. Prime Factorization Theorem.
1. Every integer n ≥ 2 is a product of (one or more) primes.
2. This factorization is unique up to the order of the factors. That is, if
n = p1p2 ![]() pr and n = q1q2
pr and n = q1q2 ![]() qs,
qs,
where pi and qj are primes, then r = s and qj can be relabeled
so that pi = qi for all i = 1, 2, . . ., r.
Proof. We proved (1) in Example 7 §1.1. If (2) fails, let (by the well-ordering principle) m ≥ 2 be the smallest integer with two distinct factorizations into primes:
m = p1p2 ![]() pr = q1q2
pr = q1q2 ![]() qs.
qs.
Then m is not a prime (verify), so r ≥ 2 and s ≥ 2. We have p1|q1q2 ![]() qs, so p1|qj for some j by Euclid's lemma. By relabeling qj, we may assume that p1|q1. Then p1 = q1 because both are primes, so
qs, so p1|qj for some j by Euclid's lemma. By relabeling qj, we may assume that p1|q1. Then p1 = q1 because both are primes, so
![]()
is an integer—smaller than m—that admits two distinct factorizations into primes. This result contradicts the choice of m, and so proves (2).
Corollary. Two integers m ≥ 2 and n ≥ 2 are relatively prime if and only if no prime divides both m and n.
Proof. Write d = gcd (m, n). If d = 1, then any common prime divisor would have to divide 1, so no such common divisor exists. Conversely, suppose no prime divides both m and n. If d > 1 and p|d where p is a prime, then p|m and p|n, contrary to our assumption. So d = 1, that is m and n are relatively prime.
If n ≥ 2 is an integer and p1, p2, . . ., pr are the distinct prime divisors of n, the prime factorization theorem asserts that n can be written uniquely in the form
![]() ,
,
where ni ≥ 1 for each i. This means that the primes pi and the integers ni are uniquely determined by n. For example, 60 = 22 · 3 · 5 and 882 = 2 · 32 · 72.
If n has only one prime divisor, we call it a prime power, examples being 7 = 71, 9 = 32, and 32 = 25. At the other extreme, we say that n is square free if all the exponents ni = 1. Hence, any prime is square free as are 6 = 2 · 3 and 70 = 2 · 5 · 7.
If n is not prime, it must have a prime divisor ![]() (it cannot have two prime divisors greater than
(it cannot have two prime divisors greater than ![]() ). So to test whether n is prime, it suffices to verify that it has no prime divisor
). So to test whether n is prime, it suffices to verify that it has no prime divisor ![]() (which is impractical if n is very large).
(which is impractical if n is very large).
Example 6. Factor 1591 into primes.
Solution. We start dividing 1591 by the successive primes, 2, 3, 5, 7, . . . . Since ![]() (because 402 = 1600), we need go only as high as 37; in fact, the first prime that divides 1591 is 37. As 1591 = 37 · 43 and 43 is a prime, we have the required prime factorization.
(because 402 = 1600), we need go only as high as 37; in fact, the first prime that divides 1591 is 37. As 1591 = 37 · 43 and 43 is a prime, we have the required prime factorization.
Obviously, the method in Example 6 requires that we have a list of the primes. Although large tables of primes are available, the method clearly fails for very large numbers. Finding the prime factorization of large integers is very difficult. Even so, on December 15, 2005 it was announced that 230,402,457 − 1 is a prime with 9,152,052 digits, the largest prime known to that date. Such a result requires a very large amount of computer time.10
The prime factorization theorem gives a systematic way of listing all the positive divisors of an integer n when the prime factorization of n is known. For example, if n = 12 = 23 · 3, these divisors are 1, 2, 3, 4, 6, and 12, and they can be written as
![]()
Thus, they can all be expressed as 2r3s, where 0 ≤ r ≤ 2 and 0 ≤ s ≤ 1 (where p0 = 1 for any prime p). The general situation is as follows:
Theorem 8. Let n be an integer with prime factorization
![]() ,
,
where pi are distinct primes and ni ≥ 1 for each i. Then the positive divisors of n are precisely the integers d of the form:
![]() ,
,
where 0 ≤ di ≤ ni holds for each i.
Proof. The prime divisors of d are contained in {p1, . . ., pr} by Euclid's lemma, and d cannot contain a higher power of pi than ![]() by Theorem 7.
by Theorem 7.
In much the same way, the prime factorization theorem provides a simple way to compute the greatest common divisor of any finite set of positive integers (rather than just two). It also provides the “dual” notion, the least common multiple. The definitions are as follows. Let n1, n2, . . ., nr be positive integers.
1. The greatest common divisor gcd (n1, n2, . . ., nr) of these integers is the positive common divisor that is a multiple of every common divisor.
2. The least common multiple lcm(n1, n2, . . ., nr) of these integers is the positive common multiple that is a divisor of every common multiple.
Thus, gcd (4, 6, 10) = 2 and lcm(4, 6, 10) = 60 by inspection. Theorem 9 below shows that the gcd and lcm always exist. They are uniquely determined in the same way as the gcd of two integers (see the discussion preceding Theorem 3). The next example illustrates a systematic method for finding the gcd and lcm.
Example 7. Find d = gcd (12, 20, 18) and m = lcm(12, 20, 18).
Solution. We might find d = 2 by experiment, but m = 180 is not clear. A systematic method involves writing the prime factorizations as follows:
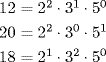
We have d = 2a · 3b · 5c for some a, b, and c by Theorem 8. We have a ≤ 1 because d|18, and b = c = 0 because d|20 and d|12. Thus, d = 2 is the largest possibility. Similarly, write the prime factorization of m as m = 2p · 3q · 5r · k, where k ≥ 1 is the factor involving primes (if any) other than 2, 3, or 5. Then p ≥ 2 because 12|m (or because 20|m), q ≥ 2 because 18|m, and r ≥ 1 because 20|m. The smallest possibility is thus m = 22 · 32 · 51 = 180.
In Example 7, the power of 2 in d = gcd (12, 20, 18) is thesmallest of the powers of 2 occurring in 12, 20, and 18; the same is true for the powers of 3 and 5 in d. Similarly, the power of 2 in m = lcm(12, 20, 18) is the largest of the powers of 2 in 12, 20, and 18, with similar statements for the primes 3 and 5. This method works in general. For finitely many integers a, b, c, . . ., let
max (a, b, c, . . .) and min (a, b, c, . . .)
denote the largest and the smallest of these integers, respectively. For example, we have max (3, 1, − 5, 3) = 3 and min (1, 0, 5) = 0.
Using Theorem 8, the solution to Example 7 extends to a proof of Theorem 9.
Theorem 9. Let {a, b, c, . . . } be a finite set of positive integers, and write
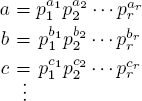
where pi are primes dividing at least one of a, b, c, . . ., and where an exponent is zero if the prime in question does not occur in that number. Then,
![]()
where ki = min (ai, bi, ci, . . .)and mi = max (ai, bi, ci, . . .) for each i.
Example 8. Find gcd (63, 60, 105) and lcm(63, 60, 105).
Solution. The prime factorizations are
63 = 20325071, 60 = 22315170, and 105 = 20315171.
Hence, gcd (63, 60, 105) = 20315070 = 3 and lcm(63, 60, 105) = 22325171 = 1260.
Of course we can use Theorem 9 to find lcm(a, b) and gcd (a, b) for two integers a and b. However, the euclidean algorithm is also available to compute gcd (a, b), so the next result is useful for finding lcm(a, b).
Corollary. If a and b are positive integers, then lcm(a, b) · gcd (a, b) = ab.
Proof. The assertion follows from Theorem 9 and the fact that, for integers m and n, max (m, n) + min (m, n) = m + n.
Note that lcm(a, b, c) · gcd (a, b, c) ≠ abc can occur (consider Example 8).
We conclude with one last application of the prime factorization theorem.
Theorem 10. Euclid's Theorem. There are infinitely many primes.
Proof. Suppose, on the contrary, that there are only n primes, denoted p1, p2, . . ., pn. Then consider the integer m = 1 + p1p2 ![]() pn. Since m ≥ 2, some prime divides m by Theorem 7. But if pi|m, then pi divides m − p1p2
pn. Since m ≥ 2, some prime divides m by Theorem 7. But if pi|m, then pi divides m − p1p2 ![]() pm = 1, a contradiction. Hence the assumption that there are only finitely many primes is untenable.
pm = 1, a contradiction. Hence the assumption that there are only finitely many primes is untenable.
Euclid's theorem certainly implies that there are infinitely many odd primes, that is, primes of the form 2k + 1, k = 0, 1, . . ., and a natural question is whether there are infinitely many primes of the form mk + n for any positive integers m and n. This clearly cannot happen unless m and n are relatively prime. However, in this case it is valid, a result first proved by P.G.L. Dirichlet. One instance of Dirichlet's theorem is treated in Exercise 39.
However, there are many unanswered questions about primes, among them the celebrated Goldbach conjecture, which asserts that every even integer greater than 2 is the sum of two primes. The conjecture dates from 1742 and originated in some correspondence between C. Goldbach and L. Euler. It is not known whether this assertion is true; the question appears to be extremely difficult to answer. The best result known is that every sufficiently large even number is the sum of a prime and a number that is the product of at most two primes.
1. In each case find the quotient and remainder when n is divided by d;.
| (a) n = 391, d = 17 | (b) n = 401, d = 19 |
| (c) n = − 116, d = 13 | (d) n = − 162, d = 17 |
2. In each case write r = n − qd, as in Example 1.
| (a) n = 51837, d = 386 | (b) n = 39214, d = 871 |
3. If n and d ≠ 0 are integers, show that integers q and r exist such that n = qd + r and 0 ≤ r < |d|.
4. Show that the negative divisors of an integer n are just the negatives of the positive divisors.
5. If m and n are odd integers, show that m2 − n2 is divisible by 8.
6. Given three consecutive integers, show that one must be a multiple of 3.
7. (a) If d > 0, d|(11k + 4), and d|(10k + 3) for some integer k, show that d = 1 or d = 7. (b) If d > 0, d|(35k + 26), and d|(7k + 3) for some integer k, show that d = 1 or d = 11.
8. Explain why gcd (0, 0) does not exist. If n > 0, what is gcd (0, n)?
9. In each case, compute gcd (m, n) and express it as a linear combination of m and n.
| (a) m = 72, n = 42 | (b) m = 41, n = 25 |
| (c) m = 327, n = 54 | (d) m = 198, n = 241 |
| (e) m = 377, n = 29 | (f) m = 527, n = 31 |
| (g) m = 72, n = − 175 | (h) m = − 231, n = 150 |
10. If m ≥ 1, show that m|n if and only if gcd (m, n) = m.
11. Let d = gcd (m, n). If k|d, k ≥ 1, show that ![]()
12. If m and n are relatively prime and k|m, show that k and n are relatively prime.
13. Is n2 + n + 11 prime for all n ≥ 1? Support your answer.
14. Show that gcd (m + n, m) = gcd (m, n).
15. If m|m1 and n|n1, show that gcd (m, n)| gcd (m1, n1).
16. If n|k(n + 1), show that n|k.
17. If gcd (m, n) = 1 and gcd (k, n) = 1, show that gcd (mk, n) = 1.
18. If gcd (m, n) = 1, let d = gcd (m + n, m − n). Show that d = 1 or d = 2.
19. Show that gcd (km, kn) = k gcd (m, n) if k ≥ 1.
20. Show that m and n are relatively prime if and only if no prime divides both.
21. Suppose that p ≥ 2 is an integer with the following property: If m and n are integers and p|mn, either p|m or p|n. Show that p must be a prime.
22. If d1, . . ., dr are all divisors of n and if gcd (di, dj) = 1 whenever i ≠ j, show that d1d2 ![]() dr divides n.
dr divides n.
23. If d = gcd (a, n), must ![]() and n be relatively prime? Prove or disprove.
and n be relatively prime? Prove or disprove.
24. Show that any two consecutive odd integers are relatively prime.
25. Show that 3, 5, and 7 is the only prime triple (that is, three consecutive odd integers, each of which is prime). It is not known if there are infinitely many prime pairs.
26. Let p be a prime. If n is any integer, show that either p|n or gcd (p, n) = 1.
27. If gcd (m, p) = 1 and p is a prime, show that gcd (m, pk) = 1 for all k ≥ 1.
28. Show that none of n ! + 2, n ! + 3, . . ., n ! + n are primes for any n ≥ 2. Hence, show that there are arbitrarily long gaps in the primes.
29. Let ab = a1b1, where a, b, a1, and b1 are positive integers. If gcd (a, b1) = 1 and gcd (a1, b) = 1, show that a = a1 and b = b1.
30. Find the prime factorizations of the following integers:
| (a) 27783 | (b) 1331 | (c) 2431 |
| (d) 18900 | (e) 241 | (f) 1457 |
31. Find the gcd and the lcm of the following pairs of numbers:
| (a) 735, 110 | (b) 101, 113 | (c) 139, 278 | (d) 221, 187 |
32. If d = gcd (a, b) and m = ab/d, show that m = lcm(a, b) using only Theorem 3.
33. Let n be a positive integer with prime factorization ![]() where the pi are distinct primes and ni ≥ 1 for each i. (a) Show that n has (n1 + 1)(n2 + 1) . . . (nr + 1) distinct positive divisors. (b) Write down all the positive divisors of 340, 108, pn, p2q, where p and q are distinct primes. (c) How many positive divisors does n have if n = 25200; n = 41472?
where the pi are distinct primes and ni ≥ 1 for each i. (a) Show that n has (n1 + 1)(n2 + 1) . . . (nr + 1) distinct positive divisors. (b) Write down all the positive divisors of 340, 108, pn, p2q, where p and q are distinct primes. (c) How many positive divisors does n have if n = 25200; n = 41472?
34. If m ≥ 1 and n ≥ 1 are relatively prime integers and nm is the square of an integer, show that both m and n are squares. Is this result true if m and n are not relatively prime?
35. If gcd (m, n) = 1, where m ≥ 1 and n ≥ 1, and if d|mn, show that d = m1n1 for some m1|m and n1|n. [Hint: Theorem 7.]
36. Do Exercise 35 without assuming that gcd (m, n) = 1. [Hint: If 0 ≤ e ≤ f + g, where f ≥ 0 and g ≥ 0 are integers, show that e can be written e = f1 + g1, where 0 ≤ f1 ≤ f and 0 ≤ g1 ≤ g. Use Theorem 8.]
37. Let a ≥ 1 and b ≥ 1 be integers. Show that there exist integers u ≥ 1 and ![]() such that
such that ![]() and
and ![]() [Hint: Theorem 9.]
[Hint: Theorem 9.]
38. If q is a rational number such that q2 is an integer, show that q is an integer. [Hint: If m2|n2, show that m|n using Theorem 7.]
39. (a) Show that every prime p > 2 has the form p = 4k + 1 or p = 4k + 3. (b) Modify the proof of Theorem 10 to show that there are infinitely many primes of the form 4k + 3.
40. A school has n lockers in a row along one side of a hall. The n students run down the hall one after the other. The first student closes all the lockers; then the second opens doors 2, 4, 6, . . . ; the third changes doors 3, 6, 9, . . . (that is, opens a door if it is closed and closes it if it is open); the fourth student changes doors 4, 8, 12, . . ., and so on. When all n students have gone through, which locker doors remain closed? Prove your answer. [Hint: Exercise 33(a).]
41. Compute the following: (a) gcd (28665, 22869) and lcm(28665, 22869) (b) gcd (231, 273, 429) and lcm(231, 273, 429) (c) gcd (1365, 1911, 1155, 1925) and lcm(1365, 1911, 1155, 1925)
42. Show that gcd (a, b, c) = gcd [a, gcd (b, c)].
43. Let d = gcd (a1, a2, a3, . . ., ak), where the ai are positive integers. Show that in-tegers x1, x2, . . ., xk exist such that d = x1a1 + ![]() + xkak. [Hint: Let m be the smallest member of
+ xkak. [Hint: Let m be the smallest member of ![]() and show that m = d. See the proof of Theorem 3.]
and show that m = d. See the proof of Theorem 3.]
44. Let b ≥ 2 be a fixed integer. If n ≥ 0 is any integer, show that n can be written in the form n = rtbt + rt−1bt−1 + ![]() + r1b + r0, where t ≥ 0 and 0 ≤ ri < b for all i. Show further that these integers ri and t are uniquely determined by n. This expression is called the base b representation of n.
+ r1b + r0, where t ≥ 0 and 0 ≤ ri < b for all i. Show further that these integers ri and t are uniquely determined by n. This expression is called the base b representation of n.
45. Let m ≥ 1 and n ≥ 1 be integers. (a) If ![]() show that 2m − 1 = x(2n − 1) + (2r − 1) for some
show that 2m − 1 = x(2n − 1) + (2r − 1) for some ![]() where 0 ≤ (2r − 1) < 2n − 1. (b) If d = gcd (m, n), show that gcd (2m − 1, 2n − 1) = 2d − 1. [Hint: Get d by the euclidean algorithm and use (a).]
where 0 ≤ (2r − 1) < 2n − 1. (b) If d = gcd (m, n), show that gcd (2m − 1, 2n − 1) = 2d − 1. [Hint: Get d by the euclidean algorithm and use (a).]
Two integers a and b are said to have the same parity if both are even or both are odd, that is, if 2|(a − b). The following definition extends this idea and introduces an important equivalence on the set ![]() of integers. Let n ≥ 2 be an integer.
of integers. Let n ≥ 2 be an integer.
Then integers a and b are said to be congruentmodulo n n |(a -b) In this case we write a≡b (mod n) and referto nas the modulus
Thus, we have 2 ≡ 5 (mod3), 21 ≡ 16 (mod5), and −4 ≡ 2 (mod6). The expression 21832 ≡ 32 (mod100) explains why we can test whether an integer is divisible by 100 by looking at the last two digits. Note that a ≡ 0 (modn) if and only if n ![]() a. We assume that n ≥ 2 because congruence modulo 0 or 1 is of no interest (verify).
a. We assume that n ≥ 2 because congruence modulo 0 or 1 is of no interest (verify).
As the notation ≡ suggests, congruence modulo n is an equivalence relation on ![]() .11 The notation is justified in Theorem 1 and the proof is left as Exercise 6(a).
.11 The notation is justified in Theorem 1 and the proof is left as Exercise 6(a).
Theorem 1. Congruence modulo n is an equivalence on ![]() ; that is:
; that is:
1. a ≡ a (modn) for every integer a.
2. If a ≡ b (modn), then b ≡ a (modn).
3. If a ≡ b (modn) and b ≡ c (modn), then a ≡ c (modn).
If a is an integer, its equivalence class [a] with respect to congruence modulo n is called its residue class modulo n, and we write ![]() for convenience:
for convenience:
![]()
The following result will be used frequently below.
Theorem 2. Given n ≥ 2, ![]() if and only if a ≡ b (modn).
if and only if a ≡ b (modn).
Proof. Suppose ![]() Since
Since ![]() , we have
, we have ![]() , so a ≡ b. Conversely, let a ≡ b. Since
, so a ≡ b. Conversely, let a ≡ b. Since ![]() and
and ![]() are sets, we must show that
are sets, we must show that ![]() and
and ![]() If
If ![]() , then x ≡ a; so, as a ≡ b, we have x ≡ b by (3) of Theorem 1. This proves that
, then x ≡ a; so, as a ≡ b, we have x ≡ b by (3) of Theorem 1. This proves that ![]() Since b ≡ a by (2) of Theorem 1, a similar proof shows that
Since b ≡ a by (2) of Theorem 1, a similar proof shows that ![]()
Residue classes are easy to describe. For example, if n = 2,
![]()
In general, if a is an integer, the division algorithm gives a = qn + r, where 0 ≤ r ≤ n − 1, so a ≡ r (modn). Thus every residue class modulo n appears in the list ![]() In fact it appears exactly once.
In fact it appears exactly once.
Theorem 3. Let n ≥ 2 be an integer.
1. If ![]() , then
, then ![]() for some r where 0 ≤ r ≤ n − 1.
for some r where 0 ≤ r ≤ n − 1.
2. The residue classes ![]() modulo n are distinct.
modulo n are distinct.
Proof. It remains to verify (2). Suppose ![]() where 0 ≤ r ≤ n − 1 and 0 ≤ s ≤ n − 1. We may assume that r ≤ s. Then
where 0 ≤ r ≤ n − 1 and 0 ≤ s ≤ n − 1. We may assume that r ≤ s. Then ![]() means that r ≡ s (modn), so s − r is an integral multiple of n such that 0 ≤ s − r ≤ n − 1. This implies that r = s.
means that r ≡ s (modn), so s − r is an integral multiple of n such that 0 ≤ s − r ≤ n − 1. This implies that r = s.
The set of all residue classes modulo n is denoted
![]()
and is called the set of integers modulo n. Thus, (2) of Theorem 3 is the assertion that ![]() In particular,
In particular, ![]() and so on.12
and so on.12
Example 1. Locate ![]() and
and ![]() in
in ![]()
Solution. It seems that ![]() does not appear. However, 48 ≡ 6 (mod7) means that
does not appear. However, 48 ≡ 6 (mod7) means that ![]() does indeed occur. Similarly, −16 ≡ 5 (mod7), so
does indeed occur. Similarly, −16 ≡ 5 (mod7), so ![]() also appears.
also appears.
Example 2. If a is an odd integer, show that ![]() or
or ![]() in
in ![]()
Solution. We know that ![]() is one of
is one of ![]() or
or ![]() in
in ![]() If
If ![]() then a ≡ 2 (mod4), so a − 2 = 4q for some integer q. This means that a is even, contrary to assumption. So
then a ≡ 2 (mod4), so a − 2 = 4q for some integer q. This means that a is even, contrary to assumption. So ![]() and, similarly,
and, similarly, ![]() The only other possibilities are
The only other possibilities are ![]() and
and ![]()
Example 3. In ![]() show that
show that ![]() if and only if n|a.
if and only if n|a.
Solution. By Theorem 2, ![]() means that a ≡ 0 (modn), that is, n|a.
means that a ≡ 0 (modn), that is, n|a.
Congruence modulo n is compatible with addition and multiplication of integers in the following sense. Let a, a1, b, and b1 denote integers.
If ![]() then
then ![]() (*)
(*)
In fact, let a − a1 = pn and b − b1 = qn, where p and q are integers. Adding these equations gives (a + b) − (a1 + b1) = (p + q)n, and this implies that a + b ≡ a1 + b1 (modn). Similarly, multiplying the equations a = a1 + pn and b = b1 + qn gives ab ≡ a1b1 (modn).
Condition (*) means that the arithmetic of ![]() extends naturally to
extends naturally to ![]() as follows: We define addition and multiplication of residue classes
as follows: We define addition and multiplication of residue classes ![]() and
and ![]() in
in ![]() by
by
![]() and
and ![]() (**)
(**)
Of course, we must verify that these operations are well defined, that is, we must check that they do not depend on which generators are used for the residue classes ![]() and
and ![]() More precisely, suppose that
More precisely, suppose that
![]() and
and ![]() ,
,
where a ≠ a1 and b ≠ b1 are possible. If we add these classes as ![]() and
and ![]() (**) gives their sum as
(**) gives their sum as ![]() but if we represent the classes as
but if we represent the classes as ![]() and
and ![]() their sum is
their sum is ![]() Clearly, the definition of addition makes no sense unless
Clearly, the definition of addition makes no sense unless ![]() But a ≡ a1 and b ≡ b1 by Theorem 2, so a + a1 ≡ b + b1 by (*), so
But a ≡ a1 and b ≡ b1 by Theorem 2, so a + a1 ≡ b + b1 by (*), so ![]() as required. Similarly, (*) shows that
as required. Similarly, (*) shows that ![]() , so the definition of multiplication also makes sense. In other words, addition and multiplication of residue classes are well defined by (**).
, so the definition of multiplication also makes sense. In other words, addition and multiplication of residue classes are well defined by (**).
Example 4. In ![]() compute
compute ![]() and
and ![]()
Solution. The definition gives ![]() because 8 ≡ 2 (mod6). Similarly,
because 8 ≡ 2 (mod6). Similarly, ![]()
Theorem 4 collects several properties of these operations in ![]() each of which is the analogue of the corresponding property for
each of which is the analogue of the corresponding property for ![]()
Theorem 4. Let n ≥ 2 be a fixed modulus and let a, b, and c denote arbitrary integers. Then the following hold in ![]()
1. ![]() and
and ![]()
2. ![]() and
and ![]()
3. ![]() and
and ![]()
4. ![]()
5. ![]()
Proof. We prove (5) and leave the rest as Exercise 6(b). Thus,

which proves (5).
These properties enable us to do arithmetic in ![]() in much the same way as in
in much the same way as in ![]() In particular, (3) shows that
In particular, (3) shows that ![]() and
and ![]() play roles in
play roles in ![]() analogous to those of 0 and 1 in
analogous to those of 0 and 1 in ![]() For this reason,
For this reason, ![]() and
and ![]() are called the zero of
are called the zero of ![]() and the unity of
and the unity of ![]() respectively. Similarly, because of (4),
respectively. Similarly, because of (4), ![]() is called the negative of
is called the negative of ![]() in
in ![]() and is denoted
and is denoted ![]() Then subtraction in
Then subtraction in ![]() is defined by
is defined by
![]()
an operation used much as it is in ![]()
Now consider the addition and multiplication tables for ![]() :
:
![]()
These tables reveal many differences between the arithmetic of ![]() and that of
and that of ![]() For example, while 0 and 1 are the only integers k in
For example, while 0 and 1 are the only integers k in ![]() with the property that k2 = k, each of
with the property that k2 = k, each of ![]() , and
, and ![]() enjoy this property in
enjoy this property in ![]() Another difference is that if ab = ac in
Another difference is that if ab = ac in ![]() and a ≠ 0, then b = c. But
and a ≠ 0, then b = c. But ![]() in
in ![]() and
and ![]() but
but ![]() Hence, we must be careful about “cancellation” in
Hence, we must be careful about “cancellation” in ![]() In fact, this concern is related to another difference between
In fact, this concern is related to another difference between ![]() and
and ![]() If ab = 0 in
If ab = 0 in ![]() then a = 0 or b = 0. However, this need not hold in
then a = 0 or b = 0. However, this need not hold in ![]() For example,
For example, ![]() in
in ![]() , but
, but ![]() and
and ![]()
In Examples 5–7, we use the arithmetic of ![]() to deduce facts about
to deduce facts about ![]() The connection is the fact (in Theorem 2) that
The connection is the fact (in Theorem 2) that ![]() in
in ![]() means that a ≡ b (modn).
means that a ≡ b (modn).
Example 5. Show that a5 ≡ a (mod5) holds for all integers a.
Solution. For an integer a, it suffices by Theorem 2 to show that ![]() in
in ![]() Because
Because ![]() equals
equals ![]() or
or ![]() we examine each case separately.
we examine each case separately.
- If
 then
then 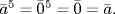
- If
 then
then 
- If
 then
then 
- If
 then
then 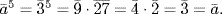
- If
 then
then 
Hence, ![]() in every case, so a5 ≡ a (mod5) for all integers a.
in every case, so a5 ≡ a (mod5) for all integers a.
Example 5 is a special case of Fermat's theorem, which, for any prime p, asserts that ap ≡ a (modp) for all integers a. We return to it later (Theorem 8).
Example 6. What is the remainder when 4119 is divided by 7?
Solution. If we can show that 4119 ≡ r (mod7), where 0 ≤ r ≤ 6, then r is the desired remainder. We do the computation in ![]() Note that, as
Note that, as ![]() in
in ![]() we have
we have ![]() With this in mind, divide the exponent 119 by 3 to get 119 = 3 · 39 + 2. Then,
With this in mind, divide the exponent 119 by 3 to get 119 = 3 · 39 + 2. Then,
![]()
Hence, 4119 ≡ 2 (mod7), so the required remainder is 2.
If a is an integer in decimal notation, it is common knowledge that a is divisible by 2 or 5 if and only if the same is true of its unit digit. Example 7 gives a similar test for divisibility by 9.
Example 7. Casting Out Nines. Show that a positive integer is divisible by 9 if and only if the sum of its digits is divisible by 9.
Solution. If a = drdr−1 . . . d1d0 in decimal notation, where d0, d1, ![]() , dr are the digits, then a = d0 + 10d1 + 102d2 +
, dr are the digits, then a = d0 + 10d1 + 102d2 + ![]() + 10rdr. Now
+ 10rdr. Now ![]() in
in ![]() so
so ![]() for each k. Hence, in
for each k. Hence, in ![]()
![]()
Thus, a ≡ d0 + d1 + ![]() + dr (mod9), and the result follows from Example 3.
+ dr (mod9), and the result follows from Example 3.
These three examples show that the properties in Theorem 4 allow many of the operations of ordinary arithmetic to be carried out in ![]() However, these properties tell us nothing about how to solve an equation such as
However, these properties tell us nothing about how to solve an equation such as ![]() in
in ![]() For example, consider
For example, consider
![]()
in ![]() The desired solution (if there is one) is a residue class x in
The desired solution (if there is one) is a residue class x in ![]() so x is one of
so x is one of ![]() Hence, one method is simply to try all these classes! If we do so, we find that
Hence, one method is simply to try all these classes! If we do so, we find that ![]() is the only solution. However, this method is impractical if the modulus is large.
is the only solution. However, this method is impractical if the modulus is large.
A better approach is as follows. Suppose that a residue class ![]() can be found such that
can be found such that ![]() Then if we multiply both sides of the equation
Then if we multiply both sides of the equation ![]() by
by ![]() the result is
the result is ![]() that is,
that is, ![]() The class
The class ![]() (if it exists) can again be found by trial and error. In fact
(if it exists) can again be found by trial and error. In fact ![]() works, so
works, so ![]() as before.
as before.
Fortunately, there is a systematic way of finding ![]() in
in ![]() such that
such that ![]() Note that 5 and 17 are relatively prime, so the euclidean algorithm can be used to express gcd (5, 17) = 1 as a linear combination of 5 and 17. In fact, we have
Note that 5 and 17 are relatively prime, so the euclidean algorithm can be used to express gcd (5, 17) = 1 as a linear combination of 5 and 17. In fact, we have
17 = 3 · 5 + 2 and then 5 = 2 · 2 + 1;
so, eliminating remainders, 1 = 5 − 2(17 − 3 · 5) = 7 · 5 − 2 · 17. This implies that 7 · 5 ≡ 1 (mod17), and so ![]() in
in ![]() This gives
This gives ![]()
This method clearly generalizes. For a modulus n ≥ 2 and an integer a, a residue class ![]() in
in ![]() is called an inverse of
is called an inverse of ![]() if
if ![]() in
in ![]() If
If ![]() has an inverse, that inverse is unique (Exercise 23) and we say
has an inverse, that inverse is unique (Exercise 23) and we say ![]() is invertible. Theorem 5 characterizes when an inverse exists, and the proof shows that (as above) the euclidean algorithm can be used to find it.
is invertible. Theorem 5 characterizes when an inverse exists, and the proof shows that (as above) the euclidean algorithm can be used to find it.
Theorem 5. Let a and n be integers with n ≥ 2. Then ![]() has an inverse in
has an inverse in ![]() if and only if a and n are relatively prime.
if and only if a and n are relatively prime.
Proof. If a and n are relatively prime, then 1 = gcd (a, n) is a linear combination of a and n (by Theorem 4 §1.2), say 1 = ba + cn, where b and c are integers. Hence, ba ≡ 1 (modn), so ![]() by Theorem 2. Conversely, if b exists such that
by Theorem 2. Conversely, if b exists such that ![]() then ba ≡ 1 (modn). Thus, n|(1 − ba), say 1 − ba = qn for some integer q. But then 1 = ba + qn, so a and n are relatively prime (again by Theorem 4 §1.2).
then ba ≡ 1 (modn). Thus, n|(1 − ba), say 1 − ba = qn for some integer q. But then 1 = ba + qn, so a and n are relatively prime (again by Theorem 4 §1.2).
Example 8. Find the inverse of ![]() in
in ![]() and use it to solve
and use it to solve ![]() in
in ![]()
Solution. The inverse exists as gcd (35, 16) = 1. The euclidean algorithm gives
35 = 2 · 16 + 3 and then 16 = 5 · 3 + 1,
so 1 = 16 − 5(35 − 2 · 16) = 11 · 16 − 5 · 35. Thus, 11 · 16 ≡ 1 (mod35), and so ![]() is the inverse of
is the inverse of ![]() in
in ![]() Now multiply the equation
Now multiply the equation ![]() by
by ![]() to obtain
to obtain ![]() that is,
that is, ![]()
Example 9. Find the elements in ![]() that have inverses.
that have inverses.
Solution. The members of ![]() are of the form
are of the form ![]() where r = 0, 1, 2,
where r = 0, 1, 2, ![]() , 8. Since 9 = 32, r is relatively prime to 9 if and only if r is not a multiple of 3. Hence,
, 8. Since 9 = 32, r is relatively prime to 9 if and only if r is not a multiple of 3. Hence, ![]() and
and ![]() will all have inverses. Indeed,
will all have inverses. Indeed, ![]() and
and ![]() are both self-inverse, whereas
are both self-inverse, whereas ![]() and
and ![]() are inverses of each other as are
are inverses of each other as are ![]() and
and ![]()
Example 10. Solve the system ![]() of equations in
of equations in ![]()
Solution. The usual techniques apply. Since ![]() we eliminate y by first multiplying the second equation by
we eliminate y by first multiplying the second equation by ![]() to get
to get ![]() Subtract this from the first equation to get
Subtract this from the first equation to get ![]() Now
Now ![]() is the inverse of
is the inverse of ![]() in
in ![]() so multiplication by
so multiplication by ![]() gives
gives ![]() Then the last equation gives
Then the last equation gives ![]() Finally,
Finally, ![]() is the inverse of
is the inverse of ![]() so
so ![]()
If a is a real number, an expression x2 + ax becomes a square if ![]() is added:
is added: ![]() This process is called completing the square, and it works in
This process is called completing the square, and it works in ![]() provided
provided ![]() has an inverse in
has an inverse in ![]() (that is, if n is odd).
(that is, if n is odd).
Example 11. Solve the quadratic ![]() in
in ![]()
Solution. First subtract ![]() from both sides to obtain
from both sides to obtain ![]() The inverse of
The inverse of ![]() in
in ![]() is
is ![]() so we complete the square on the left by adding
so we complete the square on the left by adding ![]() to both sides. The result is
to both sides. The result is ![]() that is,
that is, ![]() Now
Now ![]() has 13 elements and, by inspection, only 2 of them square to
has 13 elements and, by inspection, only 2 of them square to ![]() namely,
namely, ![]() and
and ![]() Hence,
Hence, ![]() or
or ![]() and so
and so ![]() and
and ![]() are the solutions.
are the solutions.
Note that there are two solutions in Example 11. The reason is that ![]() has two “square roots” in
has two “square roots” in ![]() :
: ![]() and
and ![]() However, other situations are possible: In
However, other situations are possible: In ![]() has no square root, whereas in
has no square root, whereas in ![]() has six square roots,
has six square roots, ![]() and
and ![]() and
and ![]() and finally
and finally ![]() and
and ![]()
The following fact about congruences is useful in number theory and computer science, and was known to the Chinese in the fourth century.
Theorem 6. Chinese Remainder Theorem. Let m and n be relatively prime integers. If s and t are arbitrary integers, there exists a solution ![]() to the simultaneous congruences
to the simultaneous congruences
x ≡ s (mod m) and x ≡ t (mod n).
Proof. Since gcd (m, n) = 1, the euclidean algorithm gives p and q in ![]() such that 1 = mp + nq. Take
such that 1 = mp + nq. Take
x = (mp)t + (nq)s.
Then x − s = mpt + (nq − 1)s = mp(t − s), so x ≡ s (mod m). A similar argument gives x ≡ t (mod n).
The nice thing about Theorem 6 is that the proof gives an algorithm for finding the solution x: The euclidean algorithm gives p and q such that 1 = mp + nq, and the solution is x = mpt + nqs. Furthermore, this method can be iterated to solve a system of more than two congruences, provided that only the moduli are relatively prime in pairs. To illustrate, let m1, m2, and m3 be integers relatively prime in pairs. Given arbitrary integers s1, s2, and s3, we want to find an integer x such that
x ≡ si (modmi) for each i = 1, 2, 3.
The Chinese remainder theorem yields a such that a ≡ si (modmi) for i = 1, 2. Since m1m2 and m3 are relatively prime, apply the Chinese remainder theorem again to obtain x such that
x ≡ a (modm1m2) and x ≡ s3 (modm3).
But then x ≡ a (modm1), so since a ≡ s1 (modm1), we have x ≡ s1 (modm1). Similarly, x ≡ s2 (modm2).
In general, if m1, m2, . . ., mk are relatively prime in pairs, and if s1, s2, . . ., sk are arbitrary integers, then there exists ![]() such that
such that
x ≡ si (modmi) for each i = 1, 2, . . ., k.
These general systems of congruences are important in computer science because they provide a method for doing arithmetic with integers that exceed the word size of the computer (the largest integer that can be used in machine arithmetic).
The only elements of ![]() that have an inverse in
that have an inverse in ![]() are 1 and −1 (because
are 1 and −1 (because ![]() does not lie in
does not lie in ![]() if k ≠ 1, − 1). Thus,
if k ≠ 1, − 1). Thus, ![]() resembles
resembles ![]() in this respect (see the table following Theorem 4). At the other extreme, every nonzero real number x ≠ 0 has an inverse
in this respect (see the table following Theorem 4). At the other extreme, every nonzero real number x ≠ 0 has an inverse ![]() in
in ![]() Theorem 7 characterizes when this happens in
Theorem 7 characterizes when this happens in ![]()
Theorem 7. The following are equivalent for an integer n ≥ 2.
1. Every element ![]() in
in ![]() has an inverse.
has an inverse.
2. If ![]() in
in ![]() then either
then either ![]() or
or ![]()
3. n is a prime.
Proof. We prove that (1) ⇒ (2), (2) ⇒ (3), and (3) ⇒ (1).
(1) ⇒ (2). Assume (1) is true and let ![]() in
in ![]() If
If ![]() there is nothing to prove. Otherwise,
there is nothing to prove. Otherwise, ![]() has an inverse by (1), say
has an inverse by (1), say ![]() Then we multiply both sides of
Then we multiply both sides of ![]() by
by ![]() to get
to get ![]() that is,
that is, ![]()
(2) ⇒ (3). If n is not prime, let n = ab, where 2 ≤ a < n and 2 ≤ b < n. But then ![]() where
where ![]() and
and ![]() This contradicts (2), so the assumption that n is not prime cannot be valid.
This contradicts (2), so the assumption that n is not prime cannot be valid.
(3) ⇒ (1). If n is prime, let ![]() in
in ![]() Then gcd (a, n) = 1 (because otherwise gcd (a, n) = n, so n|a). But then 1 = ba + cn for integers b and c (by Theorem 4 §1.2), so ba ≡ 1 (modn). Thus,
Then gcd (a, n) = 1 (because otherwise gcd (a, n) = n, so n|a). But then 1 = ba + cn for integers b and c (by Theorem 4 §1.2), so ba ≡ 1 (modn). Thus, ![]() in
in ![]() proving (1).
proving (1).
Hence, if p is a prime, ![]() has the property that every nonzero element has an inverse. This is also true of the real numbers
has the property that every nonzero element has an inverse. This is also true of the real numbers ![]() and such systems are called fields.
and such systems are called fields.
The following consequence of Theorem 7 will be referred to later.
Corollary. Wilson's Theorem. If p is a prime, then (p − 1) ! ≡ − 1 (modp).
Proof. We write ![]() in
in ![]() for convenience. Since p is prime, each element 1, 2, 3, . . ., p − 1 in
for convenience. Since p is prime, each element 1, 2, 3, . . ., p − 1 in ![]() has an inverse by Theorem 7. Hence, pairs of inverses in the product (p − 1) ! = 123
has an inverse by Theorem 7. Hence, pairs of inverses in the product (p − 1) ! = 123 ![]() (p − 1) will cancel leaving only the self-inverse elements 1 and −1 (Exercise 26). Thus, (p − 1) ! = 1 (− 1) = − 1 in
(p − 1) will cancel leaving only the self-inverse elements 1 and −1 (Exercise 26). Thus, (p − 1) ! = 1 (− 1) = − 1 in ![]() as required.
as required.
Example 12. Write down the multiplication table of ![]() and illustrate Theorem 7.
and illustrate Theorem 7.
Solution. The first row and column of the table consist entirely of zeros (true for any modulus), but the fact that no other entry equals ![]() verifies (2) of Theorem 7. Similarly, the fact that every row (or column) except the first contains
verifies (2) of Theorem 7. Similarly, the fact that every row (or column) except the first contains ![]() verifies (1) of Theorem 7.
verifies (1) of Theorem 7.


The simplest situation in which Theorem 7 applies is when n = 2. In this case, ![]() and the addition and multiplication tables are as follows:
and the addition and multiplication tables are as follows:

This is binary arithmetic, which is important in the design of computers.
We conclude with a famous theorem of Pierre de Fermat. In Example 5, we showed that a5 ≡ a (mod5) holds for all integers a. In fact, it holds if we replace 5 by any prime.
Theorem 8. Fermat's Theorem. If p is a prime, then
![]() (mod p) for all integers a.
(mod p) for all integers a.
In fact, ![]() (modp) for all integers a that are relatively prime to p.
(modp) for all integers a that are relatively prime to p.
Proof. We must show that ![]() in
in ![]() Because this equation is true if
Because this equation is true if ![]() it suffices to show that
it suffices to show that ![]() in
in ![]() whenever
whenever ![]() But if
But if ![]() , then
, then ![]() has an inverse in
has an inverse in ![]() by Theorem 7, say
by Theorem 7, say ![]() Now multiply all the nonzero elements in
Now multiply all the nonzero elements in ![]() by
by ![]() to obtain
to obtain
![]()
These are all distinct (because ![]() yields
yields ![]() after multiplication by
after multiplication by ![]() ) and none equals
) and none equals ![]() so they must be the set of all nonzero elements
so they must be the set of all nonzero elements ![]() in some order. In particular, the products are the same, and we obtain
in some order. In particular, the products are the same, and we obtain
![]()
But the element ![]() is invertible in
is invertible in ![]() (Exercise 24). Hence, multiplication by its inverse gives
(Exercise 24). Hence, multiplication by its inverse gives ![]() which is what we wanted.
which is what we wanted.
![]()
Note that Fermat's theorem fails if p is not prime; for example, ![]() (mod4).
(mod4).
Fermat's theorem is important in number theory, and the following result will be referred to several times. To state it, we use the following useful observation (Exercise 36): If prime p > 2 is a prime, then p ≡ 1 (mod4) or p ≡ 3 (mod4).
Corollary. Let p > 2 be a prime.
(1) If ![]() , then
, then ![]() in
in ![]() , where
, where ![]()
(2) If ![]() , then the equation
, then the equation ![]() has no solution in
has no solution in ![]()
Proof. Write ![]() in
in ![]() for convenience.
for convenience.
(1) We have (p − 1) ! = − 1 by the Corollary to Theorem 7. Write
![]()
Then,
![]()
![]()
Thus, it suffices to show that q = x. Now observe that we can write q as follows:
![]()
Since ![]() , the integer
, the integer ![]() is even. Hence, q has an even number of factors, and it follows that q = x after all. This proves (1).
is even. Hence, q has an even number of factors, and it follows that q = x after all. This proves (1).
(2) Let p = 4n + 3 in ![]() Suppose
Suppose ![]() satisfies a2 = − 1 in
satisfies a2 = − 1 in ![]() we look for a contradiction. Since ap−1 = 1 by Fermat's theorem, we have
we look for a contradiction. Since ap−1 = 1 by Fermat's theorem, we have
![]()
a contradiction because p > 2. So x2 = − 1 has no solution in ![]() proving (2).
proving (2).
![]()
Clearly, a residue class ![]() is not the same thing as the integer a. However, because of the definitions
is not the same thing as the integer a. However, because of the definitions ![]() and
and ![]() in
in ![]() the arithmetic of
the arithmetic of ![]() closely resembles that of
closely resembles that of ![]() —so much so that in subsequent chapters we adopt the following convention (used above in the Corollaries to Theorems 7 and 8):
—so much so that in subsequent chapters we adopt the following convention (used above in the Corollaries to Theorems 7 and 8):
Notational Convention. When working in ![]() we frequently write the residue class
we frequently write the residue class ![]() simply as a.
simply as a.
Then ![]() and equations such as 3 · 4 = 2 and 2 + 3 = 0 appear. This notation is harmless, once everyone knows that we are using it, and it facilitates hand calculations (the reader as probably been using it already!). Of course, when the convention causes confusion, we revert to the more formal
and equations such as 3 · 4 = 2 and 2 + 3 = 0 appear. This notation is harmless, once everyone knows that we are using it, and it facilitates hand calculations (the reader as probably been using it already!). Of course, when the convention causes confusion, we revert to the more formal ![]() notation.
notation.
Pierre De Fermat (1601–1685) Fermat was a lawyer by profession and served in the parliament in Toulouse, France. His mathematical work was a pastime, and he has been called “the prince of amateurs.” This appellation should not be taken as diminishing his stature, because he did first-rate work in several areas. He invented analytic geometry prior to Descartes and made contributions to the development of calculus. Along with Pascal, he is credited with starting the theory of probability.
However, he is most remembered for his work in number theory. Theorem 8 first appeared in a letter in 1640, and a proof was first published much later by Euler. Fermat published virtually nothing, and his results became known through letters to his friends (many to Mersenne) and as notes jotted in the margin of his copy of Arithmetica by Diophantus, usually with no proof. The most famous of these notes is the assertion that, if n ≥ 3, positive integers x, y, and z do not exist such that xn + yn = zn. This assertion has become known as “Fermat's Last Theorem”, and he wrote that “I have found a truly remarkable proof but the margin was too small to contain it.” His intuition was so good that every other theorem that he claimed he could prove has been subsequently verified. However, despite the best efforts of the greatest mathematicians, the “Last Theorem” remained open for 300 years. But in 1997, in a spectacular display of mathematical virtuosity, Andrew Wiles of Princeton University finally proved the result. Wiles related Fermat's conjecture to a problem in geometry, which he solved.
1. In each case determine whether the statement is true or false.

2. In each case find all integers k making the statement true.
![]()
3. Find all integers k ≥ 2 such that
![]()
4. Find all integers k ≥ 2 such that k2 ≡ 5k (mod15).
5. (a) Show that congruence modulo 0 is equality.
(b) What can you say about congruence modulo 1?
6. (a) Prove Theorem 1.
(b) Prove (1)–(4) of Theorem 4.
7. If a ≡ b (modn) and m|n, show that a ≡ b (modm).
8. Find the remainder when
![]()
9. Find the unit decimal digit of
![]()
10. Show that the unit decimal digit of k4 must be 0, 1, 5, or 6 for all integers k.
11. If p ≠ 2, 3 is prime, show that ![]() or
or ![]() in
in ![]()
12. (a) If a is an integer, show that a2 ≡ 0 or a2 ≡ 1 (mod4).
(b) Show that none of 11, 111, 1111, 11111, . . ., is a perfect square.
13. Show that a5 is congruent to 0, 1, or −1 mod 11 for every integer a.
14. Show that ![]() in
in ![]() for every integer a using the method of Example 5.
for every integer a using the method of Example 5.
15. Show that ![]() in
in ![]() for every integer a.
for every integer a.
16. Show that a3 + 2 is not divisible by 7 for every integer a.
17. Show that ![]() in
in ![]() for every integer a.
for every integer a.
18. (a) Show that every integer a has a cube root in ![]() (
(![]() for some integer b).
for some integer b).
(b) If n ≥ 3, show that some integer has no square root in ![]()
19. (a) Show that no integer of the form k2 + 1 is a multiple of 7.
(b) Find all integers k such that k2 + 1 is a multiple of 17.
20. If a space mission takes exactly 175 hours and the craft blasts off at 8 a.m., at what hour of the day will it land?
21. Let n = dkdk−1 ![]() d2d1d0 be the decimal representation of n.
d2d1d0 be the decimal representation of n.
(a) Show that 3|n if and only if 3 divides (d0 + d1 + ![]() + dk).
+ dk).
(b) Show that 11|n if and only if 11 divides (d0 − d1 + d2 − d3 + ![]() ± dk).
± dk).
(c) Show that 6|n if and only if 6 divides [d0 + 4(d1 + d2 + ![]() + dk)].
+ dk)].
22. (a) In ![]() find the inverse of
find the inverse of ![]() and use it to solve
and use it to solve ![]()
(b) In ![]() find the inverse of
find the inverse of ![]() and use it to solve
and use it to solve ![]()
(c) In ![]() find the inverse of
find the inverse of ![]() and use it to solve
and use it to solve ![]()
(d) In ![]() find the inverse of
find the inverse of ![]() and use it to solve
and use it to solve ![]()
23. (a) If ![]() in
in ![]() and if
and if ![]() has an inverse in
has an inverse in ![]() show that
show that ![]()
(b). If ![]() has an inverse in
has an inverse in ![]() n, show that the inverse is unique.
n, show that the inverse is unique.
24. (a) If ![]() and
and ![]() both have inverses in
both have inverses in ![]() show that the same is true for
show that the same is true for ![]()
(b) If ![]() all have inverses in
all have inverses in ![]() show that the same is true of their product
show that the same is true of their product ![]()
25. Find all solutions in ![]() (as indicated) for each of the given equations.
(as indicated) for each of the given equations.
![]()
26. If p is a prime and ![]() in
in ![]() show that
show that ![]() or
or ![]()
27. (a) Find all x in ![]() such that
such that ![]()
(b) Find all x in ![]() such that
such that ![]()
(c) Find all x in ![]() such that
such that ![]()
(d) Find all x in ![]() such that
such that ![]()
(e) Let n be odd. Show that ![]() has an inverse
has an inverse ![]() in
in ![]() Show that
Show that ![]() has a solution in
has a solution in ![]() if and only if
if and only if ![]() is a square in
is a square in ![]()
28. Find ![]() such that x ≡ 8 (mod10), x ≡ 3 (mod9), and x ≡ 2 (mod7).
such that x ≡ 8 (mod10), x ≡ 3 (mod9), and x ≡ 2 (mod7).
29. (a) If ![]() in
in ![]() and gcd (a, n) = 1, show that
and gcd (a, n) = 1, show that ![]()
(b) Show that ![]() is invertible in
is invertible in ![]() if and only if
if and only if ![]() implies that
implies that ![]()
30. Show that the following conditions on an integer n ≥ 2 are equivalent.
(1) ![]() in
in ![]() implies that
implies that ![]()
(2) n is square free (that is, a product of distinct primes).
[Hint: Theorem 5 §1.2.]
31. Show that the following conditions on an integer n ≥ 2 are equivalent.
(1) If ![]() is in
is in ![]() then either
then either ![]() is invertible or
is invertible or ![]() for some k ≥ 1.
for some k ≥ 1.
(2) n is a power of a prime.
32. If p ≥ 3 is a prime, show that every element of ![]() has a (p − 2) th root. [Hint: Use Fermat's theorem to show that
has a (p − 2) th root. [Hint: Use Fermat's theorem to show that ![]() is one-to-one, where
is one-to-one, where ![]() Apply Theorem 2 §0.3.]
Apply Theorem 2 §0.3.]
33. Show that 237 − 1 is divisible by 223 and that 232 + 1 is divisible by 641. (Remarkably, ![]() is also prime.) Note: If p is a prime, numbers of the form 2p − 1 and
is also prime.) Note: If p is a prime, numbers of the form 2p − 1 and ![]() are called Mersenne numbers and Fermat numbers, respectively, and were once thought to be all primes.
are called Mersenne numbers and Fermat numbers, respectively, and were once thought to be all primes.
34. Let a and n denote integers with n ≥ 2, and write d = gcd (a, n).
(a) Show that ax ≡ b (modn) has a solution if and only if d|b.
(b) If d = ra + sn, r and s integers, show that x0 = r(b/d) is one solution.
(c) If x0 is any solution, show that there are exactly d solutions that are distinct modulo n: ![]() [Hint: If ax ≡ b (modn), show that a(x − x0) ≡ 0 (modn), so (a/d)(x − x0) ≡ 0 [mod(n/d)] by Exercise 11 §1.2. Conclude that x − x0 ≡ 0 [mod(n/d)].]
[Hint: If ax ≡ b (modn), show that a(x − x0) ≡ 0 (modn), so (a/d)(x − x0) ≡ 0 [mod(n/d)] by Exercise 11 §1.2. Conclude that x − x0 ≡ 0 [mod(n/d)].]
(d) Find all solutions to 15x ≡ 25 (mod35).
(e) Find all solutions to 21x ≡ 14 (mod35).
(f) Find all solutions to 21x ≡ 8 (mod33).
35. Let p be a prime. If ![]() in
in ![]() show that
show that ![]() or
or ![]()
36. Let p be a prime, show that either p ≡ 1 (mod4) or p ≡ 3 (mod4).
37. (a) Show that if an ≡ a (modn) holds for all integers a, the modulus n must be square free, that is, a product of distinct primes. (b) Show that a561 ≡ a (mod561) for all integers a. [Hint: Use Theorem 5 §1.2 to reduce the problem to showing that a561 ≡ a (modp), where p = 3, 11, or 17. In each case, use Fermat's theorem in the form ap−1 ≡ 1 (modp) whenever p does not divide a.]
A permutation of the numbers 1, 2, and 3 is a rearrangement of these numbers in a definite order. Thus, the six possibilities are
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
They can also be described as mappings {1, 2, 3} → {1, 2, 3}:

We use this terminology of mappings to describe permutations.
If X and Y are sets, recall that a mapping α: X → Y is a rule that assigns to every element x of X exactly one element α(x) of Y, called the image of x under α. Hence, the diagram
![]()
describes the mapping α: {1, 2, 3} → {1, 2, 3} given by the rule α(1) = 1, α(2) = 3, α(3) = 2.
Now consider a mapping α: {1, 2, . . ., n} → {1, 2, . . ., n}. Because such mappings occur frequently, we write α(k) = αk for simplicity. Our interest is in when the images α1, α2, . . ., αn are a permutation of the numbers 1, 2, . . ., n; that is, each element of {1, 2, . . ., n} occurs exactly once in the list α1, α2, . . ., αn. In other words, the function α is both one-to-one and onto (a bijection).13
Given an integer n ≥ 1, write Xn = {1, 2, . . ., n}.
A permutation of Xn is a bijection σ: Xn → Xn.
We call the set Snof all permutations of Xn the symmetric group of degree n. Two permutations σ and τ in Sn are equal if they are equal as functions, that is, if σk = τk for all k in Xn.
To simplify the manipulation of these permutations, a matrix-type notation is useful. For example, if the permutation σ: X4 → X4 is defined by σ1 = 3, σ2 = 1, σ3 = 4, and σ4 = 2, we write it as
![]()
Here the image of each element of X4 = {1, 2, 3, 4} is written below that element. In general, a permutation σ ![]() Sn is written in matrix form as
Sn is written in matrix form as
![]()
Hence, a typical member of Sn takes this form, where σ1, σ2, . . ., σn is the list of numbers 1, 2, . . ., n in a (possibly) different order.
Example 1. List the elements of S3 in matrix notation.
Solution. There are six different permutations:
![]()
In general, to construct a permutation
![]()
we must choose the numbers σ1, σ2, . . ., σn from Xn so that they are all distinct. Hence, we have n choices for σ1, then n − 1 choices for σ2, then n − 2 choices for σ3, and so on. Thus, σ can be chosen in n(n − 1)(n − 2) ![]() 3 · 2 · 1 = n ! ways, which proves the following theorem:
3 · 2 · 1 = n ! ways, which proves the following theorem:
Theorem 1. The set Sn of permutations of Xn has |Sn| = n ! elements .
Let σ and τ be permutations in Sn. Both are mappings from Xn to Xn, and we write them as follows:
![]()
We then define the composite ![]() by first applying τ and then σ:
by first applying τ and then σ:
![]() for all
for all ![]()
Because both σ and τ are one-to-one and onto, these properties hold for the composite στ (see Theorem 3 §0.3). Hence, στ is again a permutation in Sn.
Example 2. Compute στ if
![]() and
and ![]()
Solution. Consider the action of στ on 1: (στ)1 = σ2 = 4. We can compute it directly from the matrix forms:
![]()
It is important to remember that, in computing στ, we apply τ first and then σ. Thus, we read ![]() from the matrix for τ, then
from the matrix for τ, then ![]() from the matrix for σ. The result is
from the matrix for σ. The result is ![]() , as indicated. Similarly,
, as indicated. Similarly, ![]() leads to
leads to ![]() We can read the entire action of στ in this manner. The following diagrams illustrate what is happening:
We can read the entire action of στ in this manner. The following diagrams illustrate what is happening:
![]()
The action of στ is read from the first diagram by following the arrows. ![]()
Note that ![]() in general: If σ and τ are as in Example 2,
in general: If σ and τ are as in Example 2,
![]()
is not the same as στ (computed in Example 2). If it happens that στ = τσ, we say that σ and τ commute. Thus, two permutations need not commute (but see Theorem 3). On the other hand, if σ, τ, and μ are three permutations in Sn then we always have
(στ)μ = σ(τμ),
which we can easily verify directly (see Theorem 3 §0.3).
The identity permutation ε in Sn is defined as
![]()
In other words, εk = k holds for every k ![]() Xn. It is easy to verify that
Xn. It is easy to verify that
![]()
holds for all σ ![]() Sn, so ε plays the role in Sn that 1 plays for multiplication of numbers.
Sn, so ε plays the role in Sn that 1 plays for multiplication of numbers.
Consider the permutation
![]()
in S4. The action of σ is obtained by reading down: σ1 = 3, σ2 = 4, σ3 = 2, and σ4 = 1. There is clearly another permutation in S4 obtained by reading up 3 → 1, 4 → 2, 2 → 3, and 1 → 4. This new permutation is determined uniquely by σ; In fact, it is the inverse of σ (denoted σ−1 as in Section 0.3). Thus,
![]()
In general, if σ ![]() Sn, the fact that σ: Xn → Xn is one-to-one and onto implies (Theorem 6 §0.3) that a uniquely determined permutation σ−1: Xn → Xn exists (called the inverse of σ), which satisfies
Sn, the fact that σ: Xn → Xn is one-to-one and onto implies (Theorem 6 §0.3) that a uniquely determined permutation σ−1: Xn → Xn exists (called the inverse of σ), which satisfies
![]()
Equations (*) imply that each of σ and σ−1 reverses the action of the other and hence that we can indeed obtain the action of σ−1 from
![]()
by reading up.
Example 3. Find the inverse of ![]() in S8.
in S8.
Solution. Reversing the action of σ gives ![]()
![]()
If σ ![]() Sn, it is related to σ−1 by composition. Indeed, because the identity permutation ε in Sn satisfies εk = k for all k
Sn, it is related to σ−1 by composition. Indeed, because the identity permutation ε in Sn satisfies εk = k for all k ![]() Xn, we can write equations (*) as
Xn, we can write equations (*) as
σσ−1 = ε and σ−1σ = ε.
This and other properties of composition discussed earlier are recorded in the following theorem for reference.
Theorem 2. Let σ, τ, and μ denote permutations in Sn.
1. στ is in Sn.
2. σε = σ = εσ.
3. σ(τμ) = (στ)μ.
4. σσ−1 = ε = σ−1σ.
By virtue of this, Sn is said to be a group under composition that explains the name “symmetric group.” Groups in general are discussed in Chapter 2.
Example 4. Given
![]()
and
![]()
find χ in S5 such that χσ = τ.
Solution. Suppose that χ ![]() Sn exists such that τ = χσ. Multiply on the right by σ−1 to get τσ−1 = χσσ−1 = χε = χ. Thus,
Sn exists such that τ = χσ. Multiply on the right by σ−1 to get τσ−1 = χσσ−1 = χε = χ. Thus,
![]()
The reader should verify that χ actually works, that is, χσ = τ. ![]()
Let σ ![]() Sn so that σ: Xn → Xn is a bijection. We say that an element k
Sn so that σ: Xn → Xn is a bijection. We say that an element k ![]() Xn is fixed by σ if σk = k. If σk ≠ k, we say that k is moved by σ, and we write Mσ = {k
Xn is fixed by σ if σk = k. If σk ≠ k, we say that k is moved by σ, and we write Mσ = {k ![]() Xn
Xn ![]() k is moved by σ}. Two permutations σ and τ are called disjoint if no element of Xn is moved by both; that is, if Mσ ∩ Mτ = ∅.
k is moved by σ}. Two permutations σ and τ are called disjoint if no element of Xn is moved by both; that is, if Mσ ∩ Mτ = ∅.
Clearly, the identity permutation ε in Sn is the only permutation that fixes every element of Xn. By contrast,
![]()
moves every element of Xn, whereas
![]()
moves 1, 3, and 5 and fixes 2 and 4. The following result is needed in the proof of Theorem 3.
Lemma 114. If k ![]() Mσ then σk
Mσ then σk ![]() Mσ.
Mσ.
Proof. Otherwise, σk is fixed by σ; that is, σ(σk) = σk. But then the fact that σ is one-to-one gives σk = k, which is contrary to the hypothesis. ![]()
Theorem 3. If σ and τ in Sn are disjoint, then στ = τσ.
Proof. For k ![]() Xn, we must show that (τσ)k = (στ)k. Since Mσ ∩ Mτ = ∅ by hypothesis, there are three cases (see the diagram).
Xn, we must show that (τσ)k = (στ)k. Since Mσ ∩ Mτ = ∅ by hypothesis, there are three cases (see the diagram).
- Case 1: k
 Mσ. Then σk
Mσ. Then σk  Mσ too (by Lemma 1), so neither lies in Mτ. Hence, both are fixed by τ, so τk = k and τ(σk) = σk. Hence,
Mσ too (by Lemma 1), so neither lies in Mτ. Hence, both are fixed by τ, so τk = k and τ(σk) = σk. Hence,
(τσ)k = τ(σk) = σk = σ(τk) = (στ)k.

- Case 2: k
 Mτ. This case is analogous to Case 1, and is left to the reader.
Mτ. This case is analogous to Case 1, and is left to the reader. - Case 3: k ∉ Mσ and k ∉ Mτ. Then σk = k and τk = k, so

This completes the proof. ![]()
Note that the converse to Theorem 3 is not true. For example, σσ−1 = σ−1σ for any σ in Sn, but σ and σ−1 are certainly not disjoint. Theorem 3 is important because it leads to a proof of the fact (Theorem 5 below) that every permutation in Sn can be written as a product of pairwise disjoint (and commuting) factors. We now turn our attention to this topic.
Cycles
Consider the permutation
![]()
in S6. The action of σ is described graphically as

Thus, the elements σ moves are moved in a cycle, and σ is called a cycle for this reason. We write σ as σ = (1426). This notation lists only elements moved by σ, and each is moved to its neighbor to the right, except the last element, which “cycles around” to the first. We generalize this type of permutation as follows.
Let k1, k2, . . ., kr be distinct elements of Xn. Then, as shown in the diagram, the cycle
σ = (k1k2 ![]() kr)
kr)

is the permutation in Sn defined by

We say that σ has length r and refer to σ as an r-cycle. Note that the only cycle of length 1 is ε, that is (k) = ε for each k ![]() Xn.
Xn.
Example 5. Write
![]()
in cycle notation.
Solution. ![]() Note that τ fixes 5.
Note that τ fixes 5.
Example 6. ![]() from Example 1. Hence, S3 consists of cycles; however, the same is not true of Sn in general, as we show later.
from Example 1. Hence, S3 consists of cycles; however, the same is not true of Sn in general, as we show later.
Example 7. The only cycle of length 1 is the identity permutation ε.
To reverse the action of a cycle, we simply go around the cycle in the opposite direction. Thus we obtain
Theorem 4. If σ is an r-cycle, then σ−1 is also an r-cycle. More precisely, if ![]() then
then ![]()
Cycle notation is much simpler than two-row matrix notation. However, we must briefly discuss two ambiguous aspects of cycle notation. First, the same permutation can be written in several ways in cycle notation. For example, ![]() in S4 can be written as
in S4 can be written as ![]() This is harmless once we are aware of it.
This is harmless once we are aware of it.
The second ambiguity can be illustrated as follows: Given ![]() is it in S4 (fixing 3) or in S5 (fixing 3 and 5)? We introduce the following convention so that it does not matter.
is it in S4 (fixing 3) or in S5 (fixing 3 and 5)? We introduce the following convention so that it does not matter.
Convention. Every permutation in Sn is regarded as a permutation in Sn+1 that fixes n + 1. Thus,
S1 ⊆ S2 ⊆ S3 ⊆ ![]() .
.
We shall adhere to this convention throughout this book.
Of course, not every permutation is a cycle. For example, consider
![]()
in S10. If we represent the action of σ geometrically, we obtain

The four cycles are ![]() and (9) = ε. These are pairwise disjoint, so each commutes with the others by Theorem 3. Even more remarkable is the fact that σ is the product of these cycles (where we omit (9) = ε):
and (9) = ε. These are pairwise disjoint, so each commutes with the others by Theorem 3. Even more remarkable is the fact that σ is the product of these cycles (where we omit (9) = ε):
![]()
The reader should check this assertion. In fact, every permutation can be expressed as a product of disjoint cycles in this way. Here is another example.
Example 8. Factor
![]()
as a product of (pairwise) disjoint cycles.
Solution. Starting with 1, follow the action of σ: 1 → 5 → 9 → 7 → 4 → 1. Thus, it has cycled, and the first cycle is ![]() Now start with any member of X13 not already considered, say 2→ 12 → 8 → 3 → 2; so the next cycle is
Now start with any member of X13 not already considered, say 2→ 12 → 8 → 3 → 2; so the next cycle is ![]() However, 6 has still not been used. It provides the cycle
However, 6 has still not been used. It provides the cycle ![]() The remaining member of X13 is 10 that is fixed by σ, so the corresponding cycle is (10) = ε. Hence,
The remaining member of X13 is 10 that is fixed by σ, so the corresponding cycle is (10) = ε. Hence,
![]()
is the desired factorization (where we drop the 1-cycles as before). Of course, the action of σ can be sketched as shown previously.
The method of Example 8 will express every permutation as a product of disjoint cycles because each cycle agrees with σ on the elements it moves, and these elements are fixed by the other cycles. In addition, the factorization is unique up to the order of the disjoint cycles, and we give a formal inductive proof of the following theorem at the end of this section.
Theorem 5. Cycle Decomposition Theorem. If σ ≠ ε is a permutation in Sn, then σ is a product of (one or more) disjoint cycles of length at least 2. This factorization is unique up to the order of the factors.
Example 9. List all the elements of S4, each factored into disjoint cycles.
Solution. The 4 ! = 24 elements are as follows:

The permutations in Example 9 are classified according to the following notion: Two permutations in Sn have the same cycle structure if, when they are factored into disjoint cycles, they have the same number of cycles of each length. We refer to this notation again later.
The Alternating Group
A cycle of length 2 is called a transposition. Thus, each transposition δ has the form ![]() where m ≠ n. Hence,
where m ≠ n. Hence,
δ2 = ε and δ−1 = δ, for every transposition δ.
Note, however, that ![]() also satisfies σ2 = ε and σ−1 = σ, so these properties do not characterize the transpositions.
also satisfies σ2 = ε and σ−1 = σ, so these properties do not characterize the transpositions.
One reason for studying transpositions is that every permutation is a product of transpositions. For example, the cycle ![]() factors as follows:
factors as follows:
![]()
as is easily verified. This pattern works in general.
Theorem 6. Every cycle of length r > 1 is a product of r − 1 transpositions:
![]()
Hence, every permutation is a product of transpositions.
Proof. The verification of the cycle factorization is left to the reader. The rest follows because every permutation is a product of cycles by Theorem 5.
In contrast to the factorization into cycles, factorizations into transpositions are not unique. For example,
![]()
Indeed, any factorization into m transpositions gives rise to a factorization into m + 2 transpositions simply by inserting ![]() somewhere. This gives a glimpse (admittedly not convincing!) into why the next theorem is true. It asserts that if a permutation can be factored in one way as a product of an even (or odd) number of transpositions, then any factorization into transpositions must involve an even (respectively odd) number of factors.
somewhere. This gives a glimpse (admittedly not convincing!) into why the next theorem is true. It asserts that if a permutation can be factored in one way as a product of an even (or odd) number of transpositions, then any factorization into transpositions must involve an even (respectively odd) number of factors.
Two integers m and n are said to have the same parity if they are both even or both odd; equivalently, if m ≡ n (mod2).
Theorem 7. Parity Theorem. If a permutation σ has two factorizations
![]()
where each γi and μj is a transposition, then m and n have the same parity.
The proof of this astonishing fact is given at the end of this section.
A permutation σ is called even or odd accordingly as it can be written in some way as the product of an even or odd number of transpositions. The parity theorem ensures that this is unambiguous, that is no permutation is both even and odd.
The parity of a cycle γ is easy to determine: Theorem 6 shows that γ is even if its length is odd, and odd if its length is even. When combined with Theorem 5, this result provides a way to easily compute the parity of any permutation.
Example 10. Determine the parity of ![]() .
.
Solution. The factorization of σ into disjoint cycles is ![]() Then,
Then, ![]() is even and
is even and ![]() is odd by Theorem 6, so σ is odd (because the sum of an even and an odd integer is odd).
is odd by Theorem 6, so σ is odd (because the sum of an even and an odd integer is odd).
The set of all even permutations in Sn is denoted An. It is called the alternating group of degree n and plays an important role in the theory of groups (in Chapter 2). Theorem 8 collects several facts about An that will be needed later.
Theorem 8. If n ≥ 2, the set An has the following properties:
1. ε is in An and, if σ and τ are in An, then both σ−1 and στ are in An.
2. ![]()
Proof. (1) ![]() so it is even. If σ and τ are even, write σ = γ1γ2
so it is even. If σ and τ are even, write σ = γ1γ2 ![]() γn and τ = δ1δ2
γn and τ = δ1δ2 ![]() δm, where n and m are even and γi and δj are transpositions. Then στ = γ1γ2
δm, where n and m are even and γi and δj are transpositions. Then στ = γ1γ2 ![]() γnδ1δ2
γnδ1δ2 ![]() δm is a product of n + m transpositions, and so is even. Finally, write μ = γn
δm is a product of n + m transpositions, and so is even. Finally, write μ = γn ![]() γ2γ1. The fact that
γ2γ1. The fact that ![]() for each i implies that σμ = ε (verify). Hence, σ−1 = σ−1ε = σ−1σμ = εμ = μ. But μ is even because n is even, so σ−1 is even.
for each i implies that σμ = ε (verify). Hence, σ−1 = σ−1ε = σ−1σμ = εμ = μ. But μ is even because n is even, so σ−1 is even.
(2) Let On denote the set of odd permutations in Sn. Then Sn = An ∪ On and the parity theorem guarantees that An ∩ On = ∅. Since |Sn| = n !, it suffices to show that |An| = |On|. We do so by exhibiting a bijection f: An → On. Let ![]() and define f by f(σ) = γσ for all σ
and define f by f(σ) = γσ for all σ ![]() An. (Note that γσ is odd if σ is even.) The fact that γ2 = ε implies that f is a bijection. In fact, γσ = γσ1 gives σ = γ2σ = γ2σ1 = σ1 (so f is one-to-one); if τ
An. (Note that γσ is odd if σ is even.) The fact that γ2 = ε implies that f is a bijection. In fact, γσ = γσ1 gives σ = γ2σ = γ2σ1 = σ1 (so f is one-to-one); if τ ![]() On, then σ = γτ
On, then σ = γτ ![]() An and f(σ) = γσ = γ2τ = τ (so f is onto). Thus, |An| = |On|.
An and f(σ) = γσ = γ2τ = τ (so f is onto). Thus, |An| = |On|.
A set of permutations is called a group if it contains the identity permutation, the product of any two of its members, and the inverse of any member. Hence, Sn is a group, and the first part of Theorem 8 shows that An is a group. The general idea of a group is defined and discussed at length in Chapter 2.
Proof of the Cycle Decomposition Theorem
If σ ≠ ε is a permutation in Sn, we show it is a product of disjoint cycles by induction on n ≥ 2. This is clear if n = 2. If n > 2, assume that the result is true for Sn−1 and let σ ![]() Sn. If σn = n, then σ
Sn. If σn = n, then σ ![]() Sn−1 and we are done. So assume σn ≠ n and write m = σ−1n. Then σm = σ(σ−1n) = εn = n, and m ≠ n (because σn ≠ n). We write γ = (mn) and consider τ = σγ. Because γ2 = ε, we have τγ = σγ2 = σε = σ. Moreover, τn = σγn = σm = n, so τ
Sn−1 and we are done. So assume σn ≠ n and write m = σ−1n. Then σm = σ(σ−1n) = εn = n, and m ≠ n (because σn ≠ n). We write γ = (mn) and consider τ = σγ. Because γ2 = ε, we have τγ = σγ2 = σε = σ. Moreover, τn = σγn = σm = n, so τ ![]() Sn−1 and τ is a product of disjoint cycles by induction. There are two cases:
Sn−1 and τ is a product of disjoint cycles by induction. There are two cases:
- Case 1: τm = m. In this case, γ and τ are disjoint (as τn = n) and we are done because σ = γτ.
- Case 2: τm ≠ m. Then m is moved by (exactly one) cycle factor of τ. Hence we can write

where μ is a product of disjoint cycles fixing m, k1, k2, . . ., kr (and also fixing n because τn = n). Finally, it is easy to verify that
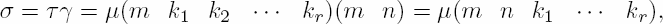
which gives σ as a product of disjoint cycles.
Turning to the uniqueness, suppose that σ = γa . . . γ2γ1 = δb ![]() δ2δ1 are two factorizations into disjoint cycles. We proceed by induction on max (a, b). If this is 1, then σ = γ1 = δ1. Otherwise, let σ move m. Then m occurs in exactly one γi and exactly one δj. By reordering the factors if necessary, assume that m occurs in γ1 and in δ1. Hence, we can write
δ2δ1 are two factorizations into disjoint cycles. We proceed by induction on max (a, b). If this is 1, then σ = γ1 = δ1. Otherwise, let σ move m. Then m occurs in exactly one γi and exactly one δj. By reordering the factors if necessary, assume that m occurs in γ1 and in δ1. Hence, we can write
γ1 = (k1k2 ![]() kr) and δ1 = (l1l2
kr) and δ1 = (l1l2 ![]() ls),
ls),
where k1 = m = l1. We may assume that r ≤ s. Then, because k1 = l1,

If r < s, the next step gives
l1 = k1 = σkr = σlr = lr+1,
a contradiction. Thus, r = s and γ1 = δ1. If we write λ = γ1 = δ1, we obtain σ = γa . . . γ2λ = δb ![]() δ2λ. It follows that σλ−1 = γa . . . γ2 = δb
δ2λ. It follows that σλ−1 = γa . . . γ2 = δb ![]() δ2 is a product of a − 1 (and b − 1) disjoint cycles. By induction, a = b and (after possible reordering) γi = δi for i = 2, 3,
δ2 is a product of a − 1 (and b − 1) disjoint cycles. By induction, a = b and (after possible reordering) γi = δi for i = 2, 3, ![]() , a, which completes the induction.
, a, which completes the induction.
Proof of the Parity Theorem
The proof depends on two preliminary results about transpositions.
Lemma 2. Let γ1 ≠ γ2 be transpositions. If γ1 moves k, transpositions δ1 and λ2 exist such that
γ2γ1 = λ2δ1, where δ1 fixes k and λ2 moves k.
Proof. Let ![]() Because γ1 ≠ γ2, the transposition γ2 has one of the forms
Because γ1 ≠ γ2, the transposition γ2 has one of the forms ![]() or
or ![]() where k, a, b, and c denote distinct integers. In these cases,
where k, a, b, and c denote distinct integers. In these cases,

Hence the conclusion of Lemma 2 holds in every case.
Lemma 3. If the identity permutation ε can be written as a product of n ≥ 3 transpositions, then it can be written as a product of n − 2 transpositions.
Proof. Let ε = γn ![]() γ4γ3γ2γ1, where n ≥ 3 and γi are transpositions. Suppose that γ1 moves k. If γ1 = γ2, then γ2γ1 = ε, so ε = γn
γ4γ3γ2γ1, where n ≥ 3 and γi are transpositions. Suppose that γ1 moves k. If γ1 = γ2, then γ2γ1 = ε, so ε = γn ![]() γ4γ3 and we are done. Otherwise, Lemma 2 gives γ1γ2 = λ2δ1, where δ1 fixes k and λ2 moves k. Thus,
γ4γ3 and we are done. Otherwise, Lemma 2 gives γ1γ2 = λ2δ1, where δ1 fixes k and λ2 moves k. Thus,
ε = γn ![]() γ4γ3λ2δ1.
γ4γ3λ2δ1.
Again, we are done if λ2 = γ3, so we let γ3λ2 = λ3δ2, where δ2 fixes k and λ3 moves k. Hence,
ε = γn ![]() γ5γ4λ3δ2δ1.
γ5γ4λ3δ2δ1.
Continue in this way. Either we are done at some stage or we finally arrive at a factorization
ε = λnδn−1 ![]() δ2δ1,
δ2δ1,
where each δi fixes k and λn moves k. But this cannot happen because, if it did,
k = εk = λnδn−1 ![]() δ2δ1k = λnk ≠ k,
δ2δ1k = λnk ≠ k,
a contradiction. This proves Lemma 3.
Proof of the parity theorem. Suppose a permutation σ has two factorizations into transpositions:
σ = γn . . . γ2γ1 = μm . . . μ2μ1.
We must show that n and m are both even or both odd. The fact that ![]() for all j gives ε = μ1μ2 . . . μmγn . . . γ2γ1. Hence, it suffices to show that ε cannot be written as the product of an odd number of transpositions. But if ε is a product of p transpositions, where p ≥ 3 is odd, then repeating Lemma 3 gives factorizations into p − 2, p − 4, . . ., transpositions. Ultimately we get a factorization of ε as one transposition, which is impossible.
for all j gives ε = μ1μ2 . . . μmγn . . . γ2γ1. Hence, it suffices to show that ε cannot be written as the product of an odd number of transpositions. But if ε is a product of p transpositions, where p ≥ 3 is odd, then repeating Lemma 3 gives factorizations into p − 2, p − 4, . . ., transpositions. Ultimately we get a factorization of ε as one transposition, which is impossible.
1. Let
![]() ,
, ![]() ,
, ![]()
be permutations. Compute:
![]()
2.
(a) Verify that any two of σ, τ, and μ commute:
![]() ,
, ![]() ,
, ![]() .
.
(b) Do (a) by first verifying that σ = τ2 and μ = τ3.
3. Let
![]()
and
![]() .
.
In each case solve for χ in S4.
![]()
4. Suppose that
![]()
and
![]()
in S5. If σ1 = 2, find σ and τ.
5. Show that
![]()
and
![]()
is impossible for σ and τ in S4.
6. If σ and τ fix k, show that στ and σ−1 both fix k.
7.
(a) How many permutations in S5 fix 1?
(b) How many fix both 1 and 2?
8.
(a) If στ = ε in Sn, show that σ = τ−1.
(b) If σ2 = σ in Sn, show that σ = ε.
9. In Sn, show that σ = τ if and only if στ−1 = ε.
10. If σ and τ are disjoint in Sn and στ = ε, what can you say about σ and τ? Support your answer.
11. Write the following in two-row matrix notation.
a. ![]()
b. ![]()
12. Let ![]() and
and ![]() in S3.
in S3.
(a) Show that S3 = {ε, σ, σ2, τ, τσ, τσ2} and that σ3 = ε = τ2 and στ = τσ2.
(b) Use (a) to fill in the multiplication table for S3.
13. Factor each of the following permutations into disjoint cycles, find its parity, and factor the inverse into disjoint cycles.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) ![]()
(f) ![]()
14. If στ = σμ or τσ = μσ in Sn, show that τ = μ. Does στ = μσ imply that τ = μ? Support your answer.
15. In each of (a) S5, and (b) S6, list one permutation of each possible cycle structure (see Example 9).
16. If ![]() show that σn = ε and that n is the smallest positive integer with this property.
show that σn = ε and that n is the smallest positive integer with this property.
17.
(a) If ![]() factor σ−1 into disjoint cycles.
factor σ−1 into disjoint cycles.
(b) If σ = γ1γ2 ![]() γn, where the γi are disjoint cycles, how is the factorization of σ−1 into disjoint cycles related to the γi? Support your answer.
γn, where the γi are disjoint cycles, how is the factorization of σ−1 into disjoint cycles related to the γi? Support your answer.
18. Find the parity of
![]() .
.
19. Find the parity of each permutation in Exercise 13.
20. Show that ![]() is not a product of 3-cycles.
is not a product of 3-cycles.
21.
(a) If γ1, γ2, ![]() , γm are transpositions, show that (γ1 γ2
, γm are transpositions, show that (γ1 γ2 ![]() γm)−1 = γmγm−1
γm)−1 = γmγm−1 ![]() γ2γ1.
γ2γ1.
(b) Show that σ and σ−1 have the same parity for all σ in Sn.
(c) Show that σ and τστ−1 have the same parity for all σ and τ in Sn.
22. Show that An+1 ∩ Sn = An for all n ≥ 3 (regard Sn ⊆ Sn+1 in the usual way).
23. Let σ ![]() Sn, σ ≠ ε. If n ≥ 3, show that γ
Sn, σ ≠ ε. If n ≥ 3, show that γ ![]() Sn exists such that σγ ≠ γσ. [Hint: If σk = l with k ≠ l, choose m ∉ {k, l} and take
Sn exists such that σγ ≠ γσ. [Hint: If σk = l with k ≠ l, choose m ∉ {k, l} and take ![]() ]
]
24. If σ ![]() Sn, show that σ2 = ε if and only if σ is a product of disjoint transpositions.
Sn, show that σ2 = ε if and only if σ is a product of disjoint transpositions.
25. If n ≥ 3, show that every even permutation in Sn is a product of 3 -cycles.
26. Let γ be any cycle of length r. If σ ![]() Sn, show that σγσ−1 is also a cycle of length r. More precisely, if
Sn, show that σγσ−1 is also a cycle of length r. More precisely, if ![]() show that
show that ![]()
27.
(a) Show that ![]()
(b) Show that each σ ![]() Sn is a product of the transpositions
Sn is a product of the transpositions ![]() [Hint: Each transposition is such a product by (a) and Exercise 26.]
[Hint: Each transposition is such a product by (a) and Exercise 26.]
(c) Repeat (b) for the transpositions ![]() [Hint: Use (a) and Exercise 26.]
[Hint: Use (a) and Exercise 26.]
(d) If ![]() show that each element of Sn is a product of the permutations
show that each element of Sn is a product of the permutations ![]() and σ−1. [Hint: Use (b) and Exercise 26.]
and σ−1. [Hint: Use (b) and Exercise 26.]
28. Let ![]() be a cycle of length n ≥ 2.
be a cycle of length n ≥ 2.
(a) If n = 2k, find the factorization of σ2 into disjoint cycles.
(b) If n = mq with m ≥ 3 and q ≥ 2, show that σm is a product of m disjoint cycles, each of length q.
(c) If 1 ≤ m ≤ n, show that σmk ≡ k + m (modn).
(d) If n = p is a prime, show that σm is a cycle of length p for each m = 1, 2, . . ., p − 1.
29. Define the sign of a permutation σ to be
 .
.
Prove that sgn(στ) = sgn σ sgn τ for all σ and τ in Sn.
30. Consider a puzzle made up of five numbered squares in a 2 × 3 frame. Assume that the squares slide vertically and horizontally so that rearrangements are possible. For example, arrangement (2) can be obtained from (1) (in four moves). Call an arrangement “nice” if the lower right position is vacant. Then, the “nice” arrangements correspond to permutations in S5. For example, arrangement (2) corresponds to ![]() .
.

Show that every “nice” arrangement corresponds to an even permutation.15
1.5 An Application to Cryptography
How often have I said to you that when you have eliminated the impossible, whatever remains, however improbable, must be the truth.
—Sir Arthur Conan Doyle
The ability to transmit messages in a way that cannot be recognized by adversaries has intrigued people for centuries. In this brief section, we outline a method that uses Fermat's theorem to encode information in a way that is very difficult to break. The idea is based on the following consequence of that theorem.
Theorem 1. Let n = pq, where p and q are distinct primes, write m = (p − 1)(q − 1), and let e > 2 be any integer such that e ≡ 1 (modm). Then
xe ≡ x (mod n) for all x such that gcd (x, n) = 1.
Proof. Because e ≡ 1 (modm), write e − 1 = ym, where y is an integer. Then xe = x · (xm)y, so it suffices to show that xm ≡ 1 (modn) whenever gcd (x, n) = 1. This condition certainly implies that p does not divide x. Hence, Fermat's theorem shows that xp−1 ≡ 1 (modp) and so xm = (xp−1)q−1 ≡ 1q−1 ≡ 1 (modp). Similarly, xm ≡ 1 (modq) and so, as p and q are relatively prime, Theorem 5 §1.2 shows that xm ≡ 1 (modpq). This is what we wanted.
The coding process can be described as follows. Two distinct primes p and q are chosen, each very large in practice. Then the words available for transmission (and punctuation symbols) are paired with distinct integers x ≥ 2. The integers x used may be assumed to be chosen relatively prime to p and q if these primes are large enough and, in practice, to be smaller than each of these primes. The idea is to use p and q to compute an integer r from x and then to transmit r rather than x. Clearly, r must be chosen in such a way that x (and hence the corresponding word) can be retrieved from r. The passage from x to r (called encoding) is carried out by the sender of a message, the integer r is transmitted, and the computation of x from r (decoding) is done by the receiver.
Here is how the process works. Given the distinct primes p and q, the cryptographer denotes
n = pq and m = (p − 1)(q − 1)
and then chooses any integer k ≥ 2 such that gcd (k, m) = 1. The sender is given only the numbers n and k. If the sender wants to transmit an integer x, he or she encodes it by reducing xk modulo n, say,
xk ≡ r (mod n), where 0 ≤ r < n.
Then the sender transmits r to the receiver of the message who must use it to retrieve x. If the receiver knows the inverse k′ of k in ![]() then k′k ≡ 1 (mod m). Hence, Theorem 1 (with e = k′k) gives
then k′k ≡ 1 (mod m). Hence, Theorem 1 (with e = k′k) gives ![]() (mod n) and
(mod n) and
![]()
modulo n. Knowing both r and k′, the receiver can compute x (and hence the corresponding word in the message).
Note that all the sender really has to know are n and k. A third party intercepting the message r cannot retrieve x without k′, and computing it requires p and q. Even if the third party can extract the integers n and k from the sender, factoring n = pq in practice is very time-consuming if the primes p and q are large, even with a computer. Hence, the code is extremely difficult to break. Example 1 illustrates how the process works, although the primes used are small.
Example 1. Let p = 11 and q = 13 so that n = 143 and m = 120. Then let k = 7, chosen so that gcd (k, m) = 1. Encode the number x = 9 and then decode the result.
Solution. The sender reduces xk = 97 modulo n = 143. Working modulo 143: 92 ≡ 81, 93 ≡ 14, 94 ≡ 126, 97 ≡ 48. Hence, r = 48 is transmitted. The receiver then finds k′, the inverse of k = 7 modulo m = 120. In fact, the euclidean algorithm gives 1 = 120 − 17 · 7, so k′ ≡ − 17 ≡ 103 (mod120) is the required inverse. Hence, x is retrieved (modulo n) by ![]() (mod143). One fairly efficient way to compute this is to note that 103 = 1100111 in binary, so 103 = 1 + 2 + 22 + 25 + 26. Then the receiver computes 48t, where t is a power of 2 by successive squaring of 48 modulo 143:
(mod143). One fairly efficient way to compute this is to note that 103 = 1100111 in binary, so 103 = 1 + 2 + 22 + 25 + 26. Then the receiver computes 48t, where t is a power of 2 by successive squaring of 48 modulo 143:
![]()
Again working modulo 143 gives
![]()
which retrieves the original 9.
This system is called the RSA system after its inventors.16 Other, more comprehensive coverage of cryptography is available,17 including overviews of the subject, methods, and bibliographies.
The RSA system works by finding two large primes p and q and computing the number n = pq. The code is difficult to break because it is difficult to find p and q given n. However, in 2002, Maninda Agrawal and two undergraduate students (Neeraj Kayal and Nitin Saxena) gave a simple algorithm that can decide whether a given integer n is prime or not. Moreover, the time taken is approximately a polynomial function of n. This is an important breakthrough in computer science, and certainly affects algorthms like the RSA system.
Cryptography, in general, refers to the transmission of messages where the primary aim is to disguise the message to make its interpretation by an unauthorized interceptor very difficult. Coding theory, in contrast, aims at fast and correct transmission of messages; we briefly discuss this topic in Sections 2.11 and 6.7.
Notes
6. One of the earliest uses of the principle is in the work of Francesco Maurolico in the 16th century. Augustus De Morgan coined the name mathematical induction in 1838.
7. This formula was probably known to the ancient Greeks. However, the great mathematician Carl Friedrich Gauss is said to have derived a special case of the formula (n = 100) at age 7 by writing the sum 1 + 2 + . . . + 100 in two parts:
![]()
and observing that each pair of terms, 1 + 100,2 + 99, . . ., 50 + 51, adds to 101. As there are 50 such pairs, the sum is 50 · 101 = 5050.
8. Note that this shows the binomial coefficients are all integers, a fact that is not clear from the definition.
9. Named after Giuseppe Peano, an Italian mathematician and logician who, in 1889, reduced the theory of the natural numbers ![]() to five simple axioms. For a discussion of this, see R.A. Beaumont and R.S. Pierce, The Algebraic Foundations of Mathematics, Addison-Wesley, 1963.
to five simple axioms. For a discussion of this, see R.A. Beaumont and R.S. Pierce, The Algebraic Foundations of Mathematics, Addison-Wesley, 1963.
10. On the other hand, in 2002, Maninda Agrawal and two undergraduate students (Neeraj Kayal and Nitin Saxena) gave a simple algorithm that can decide whether a given integer n is prime or not. Moreover, the time taken is approximately a polynomial function of n. This is an important breakthrough in computer science.
11. See Section 0.4 for a discussion on equivalence relations.
12. Note that ![]() means different things in
means different things in ![]() so to avoid ambiguity, perhaps we should denote residue classes
so to avoid ambiguity, perhaps we should denote residue classes ![]() in such a way that the modulus is apparent (say,
in such a way that the modulus is apparent (say, ![]() ). However, this is rarely done in practice as the modulus is usually clear from the context.
). However, this is rarely done in practice as the modulus is usually clear from the context.
13. A review of one-to-one and onto mappings can be found in Section 0.3.
14. The word “lemma” means a subsidiary proposition used in the proof of another proposition.
15. In fact, every even permutation arises in this way. (See Newman, J. R., World of Mathematics, New York: Simon & Schuster, 1956, p. 2431.)
16. Rivest, R. L., Shamir, A., and Adleman, L., A method for obtaining digital signatures and public-key cryptosystems, Communication of the ACM, 21 (1978), 120–126.
17. For example, see the section on Algebraic Cryptography in Lidl, R. and Pilz, G., Applied Abstract Algebra, New York: Springer-Verlag, 1983.
