Chapter 8
p-Groups and the Sylow Theorems
Mathematics is the tool specially suited for dealing with abstract concepts of any kind. There is no limit to its power in this field.
—Paul Adrien Maurice Dirac
Historically, the theory of groups was concerned only with groups of permutations of a set. This point of view is reinforced by Cayley's theorem, which shows that every abstract group can be viewed as a subgroup of a group of permutations. The concept of an abstract group became important because it focuses attention on those aspects of a group of permutations that do not depend on the underlying set. However, this abstract formulation of the theory loses sight of the combinatorial aspects that are more in evidence for groups of permutations. And these counting methods give important information about abstract groups. The best example is Lagrange's theorem, which is based on the fact that a subgroup partitions the group into cosets each having the same number of elements as the subgroup.
In Section 8.2, we derive another such counting theorem, the class equation, from a partition of a finite group and use it, among other things, to deduce many properties of groups of prime power order. Then, in Section 8.3, we present a far-reaching counting method that includes the proof of Lagrange's theorem and the class equation and which, in Section 8.4, we use to prove the Sylow theorems. These beautiful results guarantee the presence of subgroups of prime power order in every finite group and inform us about how many such subgroups there are. 351
An important goal of the theory of groups is to prove structure theorems, that is to describe all groups of a certain type in terms of particular constructions of well-known subgroups of that type. For example, in Section 7.2 we showed that every finite abelian group is a finite direct product of cyclic subgroups. We begin this section by describing when a group G is isomorphic to a finite direct product G1 × G2 × ![]() × Gn of subgroups of G. These direct factors Gi are also images of G, and we gain some insight as to how to describe these images in the second part of this section.
× Gn of subgroups of G. These direct factors Gi are also images of G, and we gain some insight as to how to describe these images in the second part of this section.
Products of Subgroups
If X and Y are nonempty subsets of a group, define their product as follows:
XY = {xy ![]() x
x ![]() X and y
X and y ![]() Y}.
Y}.
This is an associative multiplication; indeed if Z is another nonempty subset then
(XY)Z = {xyz ![]() x
x ![]() X, y
X, y ![]() Y and z
Y and z ![]() Z} = X(YZ).
Z} = X(YZ).
as the reader can verify. Moreover, {1}X = X = X{1} for all nonempty sets X, so the set of all nonempty subsets of G is a monoid with unity {1}. Moreover, the map a ![]() {a} is a group embedding (one-to-one homomorphism), so we identify G as a subgroup of this monoid by identifying a = {a} for all a
{a} is a group embedding (one-to-one homomorphism), so we identify G as a subgroup of this monoid by identifying a = {a} for all a ![]() G. Hence, we write X{a} = Xa and {a}X = aX, which agrees with our earlier usage for cosets Ha and conjugates a−1Ha of a subgroup H.
G. Hence, we write X{a} = Xa and {a}X = aX, which agrees with our earlier usage for cosets Ha and conjugates a−1Ha of a subgroup H.
These products are most useful for subgroups. If H and K are subgroups of some group, the product HK is again a subgroup if and only if HK = KH (Lemma 2 §2.8), and this holds if either H ![]() G or K
G or K ![]() G (where K
G (where K ![]() G means K is normal in G). The following result will be used several times in this chapter.
G means K is normal in G). The following result will be used several times in this chapter.
Lemma 1. Modular law. If H, K, and M are subgroups of a group and H ⊆ M then H(K ∩ M) = HK ∩ M.
Proof. The inclusion H(K ∩ M) ⊆ HK ∩ M is clear because H ⊆ M. If x ![]() HK ∩ M, say x = hk = m, then k = h−1m
HK ∩ M, say x = hk = m, then k = h−1m ![]() K ∩ M, so x = hk
K ∩ M, so x = hk![]() H(K ∩ M).
H(K ∩ M).
For reference, Theorem 6 §2.8 reads
(*) ![]()
The next theorem is an important extension of this which requires only that K ![]() G. Recall that the isomorphism theorem for groups asserts that, if α: G → H is a group homomorphism, then ker α
G. Recall that the isomorphism theorem for groups asserts that, if α: G → H is a group homomorphism, then ker α ![]() G and G/ker α ≅ Gα.
G and G/ker α ≅ Gα.
Theorem 1. Second Isomorphism Theorem. Let H and K be subgroups of a group G with K ![]() G. Then HK is a subgroup of G, K
G. Then HK is a subgroup of G, K ![]() HK, H ∩ K
HK, H ∩ K ![]() H, and
H, and
![]()
Proof. HK is a subgroup by Lemma 2 §2.8, and K ![]() HK because K ⊆ HK. Define α: H → HK/K by α(h) = Kh. (Note that Kh is in HK/K because H ⊆ HK.) Then α is a homomorphism, and it is onto because, if x
HK because K ⊆ HK. Define α: H → HK/K by α(h) = Kh. (Note that Kh is in HK/K because H ⊆ HK.) Then α is a homomorphism, and it is onto because, if x ![]() HK = KH, say x = kh, then Kx = K(kh) = (Kk)h = Kh = α(h). Now the theorem follows from the isomorphism theorem because ker (α) = {h
HK = KH, say x = kh, then Kx = K(kh) = (Kk)h = Kh = α(h). Now the theorem follows from the isomorphism theorem because ker (α) = {h ![]() H
H ![]() Kh = K} = H ∩ K.
Kh = K} = H ∩ K.
If H and K are both finite subgroups, we saw in Corollary 1 to Theorem 6 §2.8 that whenever H ∩ K = {1}. Here is a useful generalization.
Theorem 2. Let H and K be finite subgroups of a group. Then
![]()
Proof. Write N = H ∩ K for convenience. Let Nk1, . . ., Nkm be the distinct cosets of N in K, so that is the index of N in K.
Claim. HK = Hk1∪ Hk2 ∪ ![]() ∪Hkm, a disjoint union.
∪Hkm, a disjoint union.
Proof. If k ![]() K, then k = nki for some n
K, then k = nki for some n ![]() N. If h
N. If h ![]() H then hk = (hn)ki
H then hk = (hn)ki ![]() Hki, which proves that HK ⊆Hk1 ∪
Hki, which proves that HK ⊆Hk1 ∪ ![]() ∪ Hkn. Thus, HK = Hk1 ∪
∪ Hkn. Thus, HK = Hk1 ∪ ![]() ∪ Hkm. To see that this is a disjoint union, suppose that Hki ∩ Hkj is nonempty. Then Hki = Hkj, so
∪ Hkm. To see that this is a disjoint union, suppose that Hki ∩ Hkj is nonempty. Then Hki = Hkj, so ![]() Hence, Nki = Nkj, so i = j. This proves the Claim.
Hence, Nki = Nkj, so i = j. This proves the Claim.
Finally, the Claim gives ![]() , as required.
, as required.
We now give two generalizations of Theorem 6 §2.8—see (*) above; the first drops the condition that H ∩ K = {1}.
Theorem 3. If H ![]() G and K
G and K ![]() G then
G then ![]()
Proof. Write N = H ∩ K for convenience, and define
![]() by α(hk) = (Nh, Nk).
by α(hk) = (Nh, Nk).
Then α is well defined because hk = h1k1 means ![]() Hence, hN = h1N, so Nh = Nh1 because N
Hence, hN = h1N, so Nh = Nh1 because N ![]() G. Similarly, Nk = Nk1.
G. Similarly, Nk = Nk1.
Claim. α is a homomorphism.
Proof. Write x = hk and y = h1k1 in HK = KH, and write kh1 = h2k2 in HK. Then xy = hh2 k2k1 so α(xy) = (Nh Nh2, Nk2 Nk1). On the other hand, we have α(x)α(y) = (Nh Nh1, Nk Nk1), so we must prove that Nh Nh2 = Nh Nh1 and Nk2 Nk1 = Nk Nk1, equivalently (since G/N is a group) Nh2 = Nh1 and Nk2 = Nk. But we have kh1 = h2k2, so
![]() because K
because K ![]() G, and
G, and
![]() because H
because H ![]() G.
G.
Hence, Nh2 = Nh1 and Nk2 = Nk, which proves the Claim.
With the Claim, α is an onto homomorphism, so we are done by the isomorphism theorem because ker α = {hk ![]() Nh = N and Nk = N} = N.
Nh = N and Nk = N} = N.
Our second generalization of Theorem 6 §2.8—see (*) above; is to extend it to more than two factors. We require the following result, interesting in itself.
Lemma 2. The following are equivalent for subgroups G1, G2, . . ., Gn of a group:
1. (G1G2 . . . Gk−1) ∩ Gk = {1} for each k = 2, 3, . . ., n.
2. If g1g2 ![]() gn = 1, where gi
gn = 1, where gi ![]() Gi for each i, then gi = 1 for each i.
Gi for each i, then gi = 1 for each i.
Proof. Given (1), if g1g2 ![]() gn = 1 then gn
gn = 1 then gn ![]() (G1G2 . . . Gn−1) ∩ Gn = {1}, so gn = 1 and g1g2
(G1G2 . . . Gn−1) ∩ Gn = {1}, so gn = 1 and g1g2 ![]() gn−1 = 1. Now repeat the procedure to obtain gn−1 = 1. Continue to prove (1) ⇒ (2). The proof that (2) ⇒ (1) is left to the reader.
gn−1 = 1. Now repeat the procedure to obtain gn−1 = 1. Continue to prove (1) ⇒ (2). The proof that (2) ⇒ (1) is left to the reader.
Call subgroups G1, G2, . . ., Gn unconnected if the conditions in Lemma 2 are satisfied. Using this notion, we now give a useful characterization of when a group is isomorphic to a direct product of finitely many subgroups.
Theorem 4. Let G be a group and assume that G = G1G2 ![]() Gn where the Gi are subgroups. Then the following conditions are equivalent:
Gn where the Gi are subgroups. Then the following conditions are equivalent:
1. The Gi are unconnected and Gk ![]() G for each k.
G for each k.
2. The Gi are unconnected and gigj = gjgi when gi ![]() Gi, gj
Gi, gj ![]() Gj and i ≠ j.
Gj and i ≠ j.
3. (G1 . . . Gk−1Gk+1 . . . Gn) ∩ Gk = {1} and Gk ![]() G for each k.
G for each k.
4. (G1 . . . Gk−1Gk+1 . . . Gn) ∩ Gk = {1} for each k and gigj = gjgi whenever gi ![]() Gi, gj
Gi, gj ![]() Gj and i ≠ j.
Gj and i ≠ j.
In this case G ≅ G1 × G2 × ![]() × Gn, and each g
× Gn, and each g ![]() G is uniquely represented as a product g = g1g2
G is uniquely represented as a product g = g1g2 ![]() gn, where gi
gn, where gi ![]() Gi for each i.
Gi for each i.
Proof. (1) ⇒ (2). Given (1), let gi ![]() Gi, gj
Gi, gj ![]() Gj and i ≠ j. Assume i < j, so that Gi ∩ Gj ⊆ (G1G2 . . . Gj−1) ∩ Gj = {1}. If we write
Gj and i ≠ j. Assume i < j, so that Gi ∩ Gj ⊆ (G1G2 . . . Gj−1) ∩ Gj = {1}. If we write ![]() then a
then a ![]() Gi because
Gi because ![]() Similarly a
Similarly a ![]() Gj, so a
Gj, so a ![]() Gi ∩ Gj = {1}. Hence a = 1, so gigj = gjgi, as required.
Gi ∩ Gj = {1}. Hence a = 1, so gigj = gjgi, as required.
(2) ⇒ (1). Let b ![]() Gk, a
Gk, a![]() G; we want a−1ba
G; we want a−1ba ![]() Gk. If a = a1a2
Gk. If a = a1a2 ![]() an, ai
an, ai ![]() Gi then, since b commutes with each of
Gi then, since b commutes with each of ![]() by (2), we have
by (2), we have
![]()
But ![]() and so commutes with each of ak+1, . . ., an. It follows that
and so commutes with each of ak+1, . . ., an. It follows that ![]() , so Gk
, so Gk ![]() G. This proves (1).
G. This proves (1).
(3) ![]() (4) and (4) ⇒ (2). Both (3) and (4) imply that the Gi are unconnected.
(4) and (4) ⇒ (2). Both (3) and (4) imply that the Gi are unconnected.
(2) ⇒ (4). Choose bk ![]() Gk ∩ (G1
Gk ∩ (G1 ![]() Gk−1Gk+1
Gk−1Gk+1 ![]() Gn) and write bk = a1
Gn) and write bk = a1 ![]() ak−1 · ak+1
ak−1 · ak+1 ![]() an with ai
an with ai ![]() Gi for each i. Since bk commutes with these ai, this gives
Gi for each i. Since bk commutes with these ai, this gives ![]() , so bk = 1 by (2) and Lemma 2. This proves (4).
, so bk = 1 by (2) and Lemma 2. This proves (4).
Now define θ: G1 × G2 × ![]() × Gn → G by θ(g1, g2, . . ., gn) = g1g2
× Gn → G by θ(g1, g2, . . ., gn) = g1g2 ![]() gn. This is onto because G = G1G2
gn. This is onto because G = G1G2 ![]() Gn, and it is a homomorphism because the Gi commute elementwise. (Note, this does not require that the Gi are abelian.) As θ is one-to-one (because the Gi are unconnected), θ is an isomorphism, and so G ≅ G1 × G2 ×
Gn, and it is a homomorphism because the Gi commute elementwise. (Note, this does not require that the Gi are abelian.) As θ is one-to-one (because the Gi are unconnected), θ is an isomorphism, and so G ≅ G1 × G2 × ![]() × Gn. Finally, if g = a1a2
× Gn. Finally, if g = a1a2 ![]() an = b1b2
an = b1b2 ![]() bn, ai
bn, ai ![]() Gi, bi
Gi, bi![]() Gi; we must show ai = bi for all i. First
Gi; we must show ai = bi for all i. First ![]() . Since b2 commutes with
. Since b2 commutes with ![]() by (2), we get
by (2), we get ![]() . Continue to get
. Continue to get ![]() . Hence, each
. Hence, each ![]() by Lemma 2, proving the last sentence of the Theorem.
by Lemma 2, proving the last sentence of the Theorem.
The Correspondence Theorem
If α: G → H is an onto group homomorphism, the group H = α(G) is called a homomorphic image of G, or simply an image of G. Thus, the image α(G) enjoys any property of G that is preserved by homomorphisms, for example, being abelian or cyclic. The image is a simplified version of the group and so is easier to study. The idea is to learn about the group G by investigating its homomorphic images.
The isomorphism theorem (Theorem 4 §2.10) provides a fundamental tool for investigating a homomorphic image α(G) of a group G. It asserts that α(G) is isomorphic to a factor group of G, indeed that α(G) ≅ G/K, where K denotes the kernel of α. On the other hand, if K is any normal subgroup of G, the factor group G/K is a homomorphic image of G via the coset homomorphism G → G/K given by g ![]() Kg. Thus, studying the images α(G) of G is the same as studying the factors G/K of G. The factors of G are very closely connected to G itself and we now focus on these factors and how to use them to study the group G.
Kg. Thus, studying the images α(G) of G is the same as studying the factors G/K of G. The factors of G are very closely connected to G itself and we now focus on these factors and how to use them to study the group G.
Because many properties of G can be described in terms of the subgroups of G, we need to be able to obtain information about these subgroups from knowledge of the subgroups of a factor group G/K. The next theorem provides a method of doing this. It gives a very useful correspondence between the set of subgroups of G that contain K and the set of all subgroups of G/K. Moreover, the correspondence is such that, if we can determine all the subgroups in one of these sets, we can easily compute the subgroups in the other set.
To show how this correspondence works let K ![]() G, and consider the set of subgroups H of G such that K ⊆ H. For any such H, define
G, and consider the set of subgroups H of G such that K ⊆ H. For any such H, define
H/K = {Kh ![]() h
h ![]() H}.
H}.
Lemma 3. If K ⊆ H ⊆ G are groups and K ![]() G, then
G, then
1. H/K is a subgroup of G/K.
2. If K ⊆ H1 ⊆ G, then H ⊆ H1 if and only if H/K ⊆ H1/K.
Proof. (1) This is because H/K is the image of H under the coset map G → G/K.
(2) Clearly H ⊆ H1 implies H/K ⊆ H1/K. Conversely, assume H/K ⊆ H1/K, and let h ![]() H. Then Kh
H. Then Kh ![]() H/K = H1/K, say Kh = Kh1 for some h1
H/K = H1/K, say Kh = Kh1 for some h1 ![]() H1. As K ⊆ H1 this gives h
H1. As K ⊆ H1 this gives h ![]() Kh1 ⊆ H1h1 ⊆ H1, so H⊆ H1.
Kh1 ⊆ H1h1 ⊆ H1, so H⊆ H1.
Theorem 5. Correspondence Theorem. If K ![]() G are groups, define a map
G are groups, define a map
Θ: {H ![]() K ⊆ H ⊆ G, H is a subgroup
K ⊆ H ⊆ G, H is a subgroup![]() is a subgroup}
is a subgroup}
by Θ(H) = H/K. Let H, H1 and H2 be subgroups of G containing K. Then:
1. The map Θ is a bijection.
2. If ![]() is a subgroup, then
is a subgroup, then ![]() where
where ![]()
3. Θ preserves containment: H ⊆ H1 if and only if H/K ⊆ H1/K.
4. Θ preserves normality: H ![]() H1 if and only if H/K
H1 if and only if H/K ![]() H1/K.
H1/K.
5. Θ preserves intersections: (H1/K) ∩ (H2/K) = (H1 ∩ H2)/K.
6. Θ preserves products: (H1/K)(H2/K) = (H1H2)/K if H1H2 is a subgroup.
Proof. (1) The map Θ is one-to-one by Lemma 2, and it is onto by (2).
(2) Given a subgroup ![]() define
define ![]() as in (2). Then H is a subgroup of G and K ⊆ H. Moreover
as in (2). Then H is a subgroup of G and K ⊆ H. Moreover ![]() because
because ![]() implies that g
implies that g ![]() H, whence Kg
H, whence Kg ![]() H/K. Conversely, if Kg
H/K. Conversely, if Kg ![]() H/K then Kg = Kh for some h
H/K then Kg = Kh for some h ![]() H so, as K ⊆ H, g
H so, as K ⊆ H, g ![]() Kh ⊆ Hh ⊆ H. But then
Kh ⊆ Hh ⊆ H. But then ![]() by the definition of H, and we have shown that
by the definition of H, and we have shown that ![]() Hence
Hence ![]() as required.
as required.
(3) This restates Lemma 2.
(4) Assume H/K ![]() H1/K. To show H
H1/K. To show H ![]() H1, let h
H1, let h ![]() H and h1
H and h1 ![]() H1. Then
H1. Then
![]()
Hence ![]() for some h′
for some h′ ![]() H, so
H, so ![]() because K ⊆ H. As h
because K ⊆ H. As h ![]() H was arbitrary, this shows that H
H was arbitrary, this shows that H ![]() H1.
H1.
Conversely, let H ![]() H1. Then (Kh1)−1Kh
H1. Then (Kh1)−1Kh ![]() for all h1
for all h1 ![]() H1, h
H1, h ![]() H, because
H, because ![]() As h
As h ![]() H was arbitrary, this shows that (Kg)−1(H/K)Kg ⊆ H/K. Hence H/K
H was arbitrary, this shows that (Kg)−1(H/K)Kg ⊆ H/K. Hence H/K ![]() H1/K, as required.
H1/K, as required.
(5) and (6) These are left as Exercises 9 and 10.
If K ![]() G, the bijection H ↔ H/K in Theorem 5 pairs all subgroups H ⊇ K of G with all subgroups H/K of G/K. Not only is this correspondence a bijection, it also pairs normal subgroups with normal subgroups by (4) and preserves inclusion by (3). This last fact means that the lattice diagram of all subgroups of G/K has the same form as the lattice diagram of all subgroups of G that contain K. In particular, the bijection pairs G with G/K, and it pairs K with K/K = {K}—the trivial subgroup of G/K. This is illustrated in the following two examples.
G, the bijection H ↔ H/K in Theorem 5 pairs all subgroups H ⊇ K of G with all subgroups H/K of G/K. Not only is this correspondence a bijection, it also pairs normal subgroups with normal subgroups by (4) and preserves inclusion by (3). This last fact means that the lattice diagram of all subgroups of G/K has the same form as the lattice diagram of all subgroups of G that contain K. In particular, the bijection pairs G with G/K, and it pairs K with K/K = {K}—the trivial subgroup of G/K. This is illustrated in the following two examples.
Example 1. Let ![]() , where o(a) = 12, and let
, where o(a) = 12, and let ![]() and
and ![]() Draw the lattice diagram of all subgroups of G, and use the correspondence theorem to obtain the lattice of all subgroups of G/K and G/K1.
Draw the lattice diagram of all subgroups of G, and use the correspondence theorem to obtain the lattice of all subgroups of G/K and G/K1.
Solution. The subgroups of G are given by the divisors of 12, and the subgroup lattice for G appears on the left in the diagram (see Example 14 §2.4). The subgroups of G/K are thus determined (using the correspondence theorem) by the subgroups ![]() and K of G that contain K. Thus the lattice diagram for G/K shown in the center diagram can be “read off” from the diagram for G.
and K of G that contain K. Thus the lattice diagram for G/K shown in the center diagram can be “read off” from the diagram for G.

Similarly ![]() and K1 are the only subgroups containing K1, and they give the subgroup lattice for G/K1 on the right.
and K1 are the only subgroups containing K1, and they give the subgroup lattice for G/K1 on the right.
Example 2. Consider the octic group G = D4 = {1, a, a2, a3, b, ba, ba2, ba3}, where o(a) = 4, o(b) = 2 and aba = b. If K = {1, a2}, determine all the subgroups H of G such that K ⊆ H ⊆ G.
Solution. By Example 4 §2.9, K = Z(G), and G/K = {K, Ka, Kb, Kba} ≅ K4, the Klein group. Hence, the subgroups of G/K are {K}, G/K, and
![]()
The subgroup lattice diagram of G/K is shown at the left in the diagram.

The correspondence theorem ensures that, for each i, there is a unique subgroup Hi of G such that K ⊆ Hi and ![]() Explicitly, (2) of Theorem 5 gives
Explicitly, (2) of Theorem 5 gives
![]()
![]()
![]()
The correspondence theorem also shows that these are the only subgroups H such that K ⊆ H ⊆ G, and that the lattice of such subgroups (in the right diagram) has the same form as the subgroup lattice of G/K. Furthermore, the fact that ![]() , and
, and ![]() are normal in (the abelian group) G/K guarantees that H1, H2, and H3 are normal in G. (Of course this also follows because they are of index 2 in G.)
are normal in (the abelian group) G/K guarantees that H1, H2, and H3 are normal in G. (Of course this also follows because they are of index 2 in G.)
An important special case of the correspondence theorem describes when a factor group is simple. If K ![]() G, the group G/K is simple if and only if the only normal subgroups are the trivial subgroup K/K = {K} and the whole group G/K. Hence, the correspondence theorem shows that the only normal subgroups H such that K ⊆ H ⊆ G are H = K and H = G. A normal subgroup K ≠ G with this latter property is called a maximal normal subgroup of G. This discussion is summarized in
G, the group G/K is simple if and only if the only normal subgroups are the trivial subgroup K/K = {K} and the whole group G/K. Hence, the correspondence theorem shows that the only normal subgroups H such that K ⊆ H ⊆ G are H = K and H = G. A normal subgroup K ≠ G with this latter property is called a maximal normal subgroup of G. This discussion is summarized in
Theorem 6. A normal subgroup K ![]() G is a maximal normal subgroup if and only if G/K is simple.
G is a maximal normal subgroup if and only if G/K is simple.
Every finite group G ≠ {1} has maximal normal subgroups—choose any proper normal subgroup (possibly {1}) of maximal order. Hence, G has finite simple factor groups by Theorem 2, which shows that finite simple groups are quite common. In fact they serve as “ building blocks” by which we can study the structure of finite groups in general. We return to this topic in Chapter 9.
The correspondence theorem describes the subgroups of a factor group G/K, where K ![]() G. We now turn to the images of G/K. Of course they are all images of G, and so have the form G/H for some H
G. We now turn to the images of G/K. Of course they are all images of G, and so have the form G/H for some H ![]() G. They are described next by an important consequence of the isomorphism theorem that will be needed later.
G. They are described next by an important consequence of the isomorphism theorem that will be needed later.
Theorem 7. Third Isomorphism Theorem. Let K ⊆ H ⊆ G be groups, where K ![]() G and H
G and H ![]() G. Then H/K
G. Then H/K ![]() G/K and
G/K and
![]() .
.
Proof. Define α: G/K → G/H by α(Kg) = Hg for all g in G. This is well defined because Kg = Kg1 implies ![]() whence Hg = Hg1. With this it is easy to verify that α is an onto homomorphism, and ker (α) = {Kg
whence Hg = Hg1. With this it is easy to verify that α is an onto homomorphism, and ker (α) = {Kg ![]() Hg = H} = H/K. Hence, the isomorphism theorem (Theorem 4 §2.10) completes the proof.
Hg = H} = H/K. Hence, the isomorphism theorem (Theorem 4 §2.10) completes the proof.
Our final example provides a good illustration of how the second and third isomorphism theorems are used. A group G is called a metacyclic group if a normal subgroup K ![]() G exists such that both K and G/K are cyclic. Every cyclic group is metacyclic (take K = {1}) as is Dn (take K to be the cyclic subgroup of index 2). Thus, Dn is metacyclic but not cyclic.
G exists such that both K and G/K are cyclic. Every cyclic group is metacyclic (take K = {1}) as is Dn (take K to be the cyclic subgroup of index 2). Thus, Dn is metacyclic but not cyclic.
Example 3. Show that every subgroup and every image of a metacyclic group is again metacyclic.
Solution. Let G be metacyclic, say K and G/K are both cyclic where K ![]() G.
G.
If H is a subgroup of G then H ∩ K ![]() H, and H ∩ K is cyclic (being a subgroup of the cyclic group K). On the other hand, H/(H ∩ K) ≅ HK/K by the second isomorphism theorem, and HK/K is cyclic (it is a subgroup of G/K). It follows that H/(H ∩ K) is cyclic, whence H is metacyclic.
H, and H ∩ K is cyclic (being a subgroup of the cyclic group K). On the other hand, H/(H ∩ K) ≅ HK/K by the second isomorphism theorem, and HK/K is cyclic (it is a subgroup of G/K). It follows that H/(H ∩ K) is cyclic, whence H is metacyclic.
Now let G/N be any image of G, where N ![]() G. Then NK
G. Then NK ![]() G by Theorem 1, so NK/N
G by Theorem 1, so NK/N ![]() G/N. Moreover, NK/N is cyclic because NK/N ≅ K/(N ∩ K) is an image of the cyclic group K. On the other hand, (G/N)/(NK/N) ≅ G/NK is cyclic because G/NK ≅ (G/K)/(NK/K) is an image of the cyclic group G/K. This means that G/N is metacyclic.
G/N. Moreover, NK/N is cyclic because NK/N ≅ K/(N ∩ K) is an image of the cyclic group K. On the other hand, (G/N)/(NK/N) ≅ G/NK is cyclic because G/NK ≅ (G/K)/(NK/K) is an image of the cyclic group G/K. This means that G/N is metacyclic.
Exercises 8.1
1. Let S3 = {ε, σ, σ2, τ, τσ, τσ2} where σ3 = ε = τ2 and στσ = τ. Compute XY if:
a. X = {τ, τσ} and Y = {τ, τσ2}.
b. X = {σ, τσ} and Y = {σ, σ2}.
2. If α: G → C6 is an onto group homomorphism and show that and G has normal subgroups of orders 3, 6 and 9.
3. Use the correspondence theorem to show that each subgroup H of G with G′ ⊆ H is normal in G. (See Theorem 3 §2.9.)
4. In each case use Theorem 5 to find all subgroups of G that contain K.
a. G = D6 and K = Z(D6).
b. G = Q and K = Z(Q).
c. G = A4 and K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}.
5. In each case describe all maximal normal subgroups of G.
![]()
6. Let K ![]() G be such that both K and G/K are simple. Show that either K is the only proper normal subgroup of G, or G ≅ K × (G/K).
G be such that both K and G/K are simple. Show that either K is the only proper normal subgroup of G, or G ≅ K × (G/K).
7. Let K ![]() G and assume that G/K is cyclic,
G and assume that G/K is cyclic, ![]() and
and ![]() If m is an integer such that k|m and m|n, show that there is a unique subgroup H such that K ⊆ H ⊆ G and
If m is an integer such that k|m and m|n, show that there is a unique subgroup H such that K ⊆ H ⊆ G and ![]() [Hint: Theorem 9 §2.4.]
[Hint: Theorem 9 §2.4.]
8. If K ![]() G, show that the following conditions are equivalent. (1) The only subgroups H such that K ⊆ H ⊆ G are H = K and H = G. (2) G/K is cyclic and of prime order.
G, show that the following conditions are equivalent. (1) The only subgroups H such that K ⊆ H ⊆ G are H = K and H = G. (2) G/K is cyclic and of prime order.
9. Show that the correspondence theorem preserves intersections. More precisely, if K ⊆ H, H1 ⊆ G, H, H1, subgroups, K ![]() G, show that (H/K) ∩ (H1/K) = (H ∩ H1)/K.
G, show that (H/K) ∩ (H1/K) = (H ∩ H1)/K.
10. Show that the correspondence theorem preserves products. More precisely, if we have K ⊆ H ⊆ G and K ⊆ H1 ⊆ G where K ![]() G, H, H1 subgroups, show that (a) (H/K) · (H1/K) is a subgroup of G/K if and only if HH1 is a subgroup of G. (b) In this case (H/K) · (H1/K) = (HH1)/K.
G, H, H1 subgroups, show that (a) (H/K) · (H1/K) is a subgroup of G/K if and only if HH1 is a subgroup of G. (b) In this case (H/K) · (H1/K) = (HH1)/K.
11. If X and Y are nonempty subsets of some group, show that ![]() with equality if and only if
with equality if and only if ![]() [Hint: Lemma 2 §2.8.]
[Hint: Lemma 2 §2.8.]
12.
a. If H is a subgroup of a group G, show that H2 = H.
b. If X ≠ ∅ is a finite subset of G, show that X is a subgroup if and only if X2 ⊆ X.
13. Let G be a group with ![]() , where p, q and r are distinct primes. If H and K are subgroups,
, where p, q and r are distinct primes. If H and K are subgroups, ![]() and
and ![]() show that
show that ![]() [Hint: Lagrange's theorem.]
[Hint: Lagrange's theorem.]
14. Let ![]() be a cyclic group, and let
be a cyclic group, and let ![]() and
and ![]() Show that
Show that ![]() where d = gcd (a, b).
where d = gcd (a, b).
15. Let K, A and B be subgroups of G with K ![]() G and A
G and A ![]() B. Show that KA
B. Show that KA ![]() KB.
KB.
16. Let H, K and M be subgroups of a group G, and assume that H ⊆ M. If both H ∩ K = M ∩ K and HK = MK hold, show that H = M. [Hint: First show that M = (HK) ∩ M.]
17. Let ![]() where p is a prime and p does not divide m. If K
where p is a prime and p does not divide m. If K ![]() G satisfies
G satisfies ![]() show that K is the only subgroup of G of order pn. [Hint: Theorem 1.]
show that K is the only subgroup of G of order pn. [Hint: Theorem 1.]
18. If G is a group, M ![]() G is maximal normal, K
G is maximal normal, K ![]() G, and K6 ⊆ M, show that
G, and K6 ⊆ M, show that
a. G = KM.
b. K/(K ∩ M) is simple.
c. G/(K ∩ M) has a simple direct factor.
19. A group G is called a metabelian group if K ![]() G exists such that both K and G/K are abelian. (a) Show that every subgroup and factor group of a metabelian group is metabelian. (b) Show that G is metabelian if and only if the commutator subgroup G′ is abelian.
G exists such that both K and G/K are abelian. (a) Show that every subgroup and factor group of a metabelian group is metabelian. (b) Show that G is metabelian if and only if the commutator subgroup G′ is abelian.
20. Let ![]() be a nonempty family of groups closed under taking subgroups and images (for example the abelian or the cyclic groups). Call a group G meta-
be a nonempty family of groups closed under taking subgroups and images (for example the abelian or the cyclic groups). Call a group G meta-![]() if there exists K
if there exists K ![]() G such that both K and G/K are in
G such that both K and G/K are in ![]() Note that every group in
Note that every group in ![]() is meta-
is meta-![]() because the trivial group {1} is in
because the trivial group {1} is in ![]() If G is meta-
If G is meta-![]() show that every subgroup and factor group of G is meta-
show that every subgroup and factor group of G is meta-![]()
21. Let G be a group with subgroups H and K. Assume that ![]() and
and ![]() , where p ≠ q are primes. If
, where p ≠ q are primes. If ![]() show that
show that ![]()
22. Let G be a finite abelian group.
a. If G has two distinct elements of order 2, show that 4 divides ![]()
b. If G has three distinct elements of order 3, show that 9 divides ![]()
23. If G is a group, let M denote the monoid of nonempty subsets of G, and identify G ⊆ M by writing g = {g} for each g ![]() G. Show that G is the group of units of M.
G. Show that G is the group of units of M.
24. Let G be a group, let SG be the group of permutations of G, and write A = aut(G). If τa: G → G is defined by τa(g) = ag for all g ![]() G, let
G, let ![]() be the group of translations. Thus
be the group of translations. Thus ![]() by Cayley's theorem (Theorem 6 §2.5).
by Cayley's theorem (Theorem 6 §2.5).
a. Show that ![]() is a subgroup of SG called the holomorph of G.
is a subgroup of SG called the holomorph of G.
b. Show that ![]()
c. Show that ![]()
d. Show that ![]()
If p is a prime and G is a group of order pn, every element of G has order a power of p by Lagrange's theorem. The converse is also true. If every element of a finite group G has p-power order, then |G| = pn for some n ≥ 0. The proof of this result requires several theorems that are important in themselves and reveal many other properties of groups of p-power order.
Recall that two subgroups H and K of a group G are called conjugate in G if K = gHg−1 for some g ![]() G. This relation is an equivalence on the set of all subgroups of G, and the analogous equivalence on the elements of G is an important tool in this section. Thus, two elements a and b of a group G are said to be conjugate in G if b = gag−1 for some g
G. This relation is an equivalence on the set of all subgroups of G, and the analogous equivalence on the elements of G is an important tool in this section. Thus, two elements a and b of a group G are said to be conjugate in G if b = gag−1 for some g ![]() G. This is an equivalence on G and the equivalence class of a
G. This is an equivalence on G and the equivalence class of a ![]() G is denoted
G is denoted
classa = {x ![]() G
G ![]() x is conjugate to a} = {gag−1
x is conjugate to a} = {gag−1 ![]() g
g ![]() G},
G},
and is called the conjugacy class of a.
Hence the conjugacy classes partition a group G. Clearly, class1 = {1} in any group and, more generally, classa = {a} if and only if a ![]() Z(G). Also, if a and b are conjugate, then o(a) = o(b) because gag−1 is the image of a under an inner automorphism of G. Hence, all elements in a conjugacy class have the same order.
Z(G). Also, if a and b are conjugate, then o(a) = o(b) because gag−1 is the image of a under an inner automorphism of G. Hence, all elements in a conjugacy class have the same order.
Example 1. Partition D3 into conjugacy classes.
Solution. Let D3 = {1, a, a2, b, ba, ba2}, where o(a) = 3, o(b) = 2, and aba = b. We have class1 = {1}. As a and a2 are the only elements of order 3, we have classa ⊆ {a, a2}. But a2 = bab−1, so classa = {a, a2}. Similarly, classb = {b, ba, ba2} because aba−1 = ba and a2ba−2 = ba2.
It can be shown (Exercise 15) that two permutations in Sn are conjugate if and only if they have the same cycle structure; that is, when factored into disjoint cycles they have the same number of cycles of each length.
Example 2. The conjugacy classes of S4 are

If K is a normal subgroup of G, then gKg−1 = K for all g ![]() G, and so K contains the conjugacy class of each of its elements. Conversely, any subgroup that is a union of conjugacy classes must be normal (Exercise 5). This proves
G, and so K contains the conjugacy class of each of its elements. Conversely, any subgroup that is a union of conjugacy classes must be normal (Exercise 5). This proves
Theorem 1. If H is a subgroup of a group G, then H ![]() G if and only if H is a union of conjugacy classes.
G if and only if H is a union of conjugacy classes.
If D3 = {1, a, a2, b, ba, ba2}, as in Example 1, Theorem 1 shows that any normal subgroup K of D3 must be a union of the conjugacy classes {1}, {a, a2}, and {b, ba, ba2}. Because 1 ![]() K and |K| divides |D3| = 6, the only normal subgroups of D3 are {1}, {1, a, a2}, and D3. Similarly, Example 2 gives Example 3 (Exercise 17).
K and |K| divides |D3| = 6, the only normal subgroups of D3 are {1}, {1, a, a2}, and D3. Similarly, Example 2 gives Example 3 (Exercise 17).
Example 3. The normal subgroups of S4 are {ε}, A4, S4, and
K = {ε, (12)(34), (13)(24), (14)(23)}.
The relationship between conjugacy classes and normality is even closer than that shown in Theorem 1. If X ⊆ G is a nonempty subset, write
N(X) = NG(X) = {g ![]() G
G ![]() gXg−1 = X}.
gXg−1 = X}.
This is a subgroup of G for every X (Exercise 12), called the normalizer of X in G. We write N(X) = NG(X) if the group G must be emphasized, and we abbreviate N({a}) = N(a) for a ![]() G. Note that N(a) = {g
G. Note that N(a) = {g ![]() G
G ![]() ga = ag}. For this reason, N(a) is often called the centralizer of a in G. The normalizer of a subgroup has the following properties which explain the name.
ga = ag}. For this reason, N(a) is often called the centralizer of a in G. The normalizer of a subgroup has the following properties which explain the name.
Lemma 1. Let H be a subgroup of a group G.
1. H ![]() N(H)
N(H)
2. If H ![]() K, where K is a subgroup of G, then K ⊆ N(H).
K, where K is a subgroup of G, then K ⊆ N(H).
Proof. Let H ![]() K and k
K and k ![]() K. Then kHk−1 = H, so k
K. Then kHk−1 = H, so k ![]() N(H). Thus, K ⊆ N(H) proving (2). If we take K = H in (2), we get H ⊆ N(H), whence H
N(H). Thus, K ⊆ N(H) proving (2). If we take K = H in (2), we get H ⊆ N(H), whence H ![]() N(H).
N(H).
We can summarize Lemma 1 by saying that N(H) is the largest subgroup of G in which H is normal. In particular, H ![]() G if and only if N(H) = G. At the other extreme, it can happen that N(H) = H (consider H = {ε, (12)} in S3).
G if and only if N(H) = G. At the other extreme, it can happen that N(H) = H (consider H = {ε, (12)} in S3).
Much of the importance of normalizers stems from their connection with conjugation. Recall that |G: H| denotes the index in G of a subgroup H ⊆ G.
Theorem 2. Let G be a finite group.
1. |classa| = |G: N(a)|for each a ![]() G.
G.
2. The number of conjugates of a subgroup H of G is |G: N(H)|.
Proof. We prove (1); (2) is analogous (Exercise 13). Write N(a) = N. The index ![]() Since classa = {gag−1
Since classa = {gag−1 ![]() g
g ![]() G}, define a mapping
G}, define a mapping
ϕ: classa → {gN ![]() g
g ![]() G} by ϕ(gag−1) = gN.
G} by ϕ(gag−1) = gN.
It suffices to prove that ϕ is a bijection. Now N = {x ![]() G
G ![]() ax = xa}, so we have
ax = xa}, so we have
| gag−1 = hah−1 | (h−1g)a = a(h−1g) | |
| h−1g |
||
| gN = hN |
This shows that ϕ is well defined and one-to-one; as ϕ is onto, this proves (1).
Combining Theorem 2 with the fact that classa = {gag−1 ![]() g
g ![]() G} gives
G} gives
a ![]() Z(G)
Z(G) ![]() classa = {a}
classa = {a} ![]() N(a) = G.
N(a) = G.
In particular, the center Z(G) is the union of all the singleton conjugacy classes. This leads to the following useful theorem.
Theorem 3. The Class Equation. Let G be a finite group and let class a1, classa2, . . ., classan be the nonsingleton conjugacy classes. Then
![]()
Proof. The conjugacy classes partition G, so ![]() is the sum of the sizes of these classes. But the number of elements in classai is |G: N(ai)| by Theorem 2, and
is the sum of the sizes of these classes. But the number of elements in classai is |G: N(ai)| by Theorem 2, and ![]() is the number of singleton classes. The class equation follows.
is the number of singleton classes. The class equation follows.
Example 4. Consider the quaternion group Q = {1, − 1, i, − i, j, − j, k, − k} as in Example 9 §2.8. The conjugacy classes are {1}, { − 1}, {i, − i}, {j, − j}, and {k, − k}. We have N(i) = {1, − 1, i, − i} so that |Q: N(i)| = 2 = |classi|, as in Theorem 2. Because Z(Q) = {1, − 1}, the class equation is apparent.
The class equation is reminiscent of Lagrange's theorem in that it provides arithmetic information about the group. That Lagrange's theorem is useful is beyond doubt; the usefulness of the class equation lies in the fact that each term |G: N(a)| is a divisor of |G| which is not equal to 1 when a ∉ Z(G). This fact is particularly useful when |G| is a prime power as we shall see.
However, before doing so we use the class equation to prove an important theorem about general finite groups—due to A. L. Cauchy. If G is a finite group, the order of each element divides |G| by Lagrange's theorem. The converse is false. For example, |A4| = 12 but A4 has no element of order 6. However, a partial converse does hold.
Theorem 4. Cauchy's Theorem. If a prime p divides the order of a finite group G, then G has an element of order p.
Proof. If G is abelian, a (self-contained) proof has already been given (Lemma 1 §7.2). In general, we use induction on |G|. The theorem is easily verified if |G| ≤ 3. If |G| > 3, let classa1, . . ., classan denote the nonsingleton conjugacy classes so that |N(ai)| < |G|. If p divides |N(ai)| for any i, the proof is complete by induction. Otherwise, p divides |G: N(ai)| for each i, and hence p divides |Z(G)| by the class equation. As Z(G) is abelian, Lemma 1 §7.2 completes the proof.
As with many important theorems, the method of proof of Cauchy's theorem is at least as important as the result itself. In Section 8.3, we present a sweeping generalization of the class equation, which yields a wealth of information about finite groups.
p-Groups
We use Cauchy's theorem frequently below. One of the most important applications is to characterize groups of prime power order. If p is a prime, a group G is called a p-group if the order of every element of G is a power of p.
Lemma 2. If G is a finite group and p is a prime, then |G| is a power of p if and only if G is a p-group.
Proof. Assume that o(g) is a power of p for all g ![]() G. If |G| is not a power of p, let q divide |G|, where q ≠ p is a prime, Then Cauchy's theorem shows that G has an element of order q, contrary to hypothesis. Hence, |G| is a power of p. The converse follows by Lagrange's theorem.
G. If |G| is not a power of p, let q divide |G|, where q ≠ p is a prime, Then Cauchy's theorem shows that G has an element of order q, contrary to hypothesis. Hence, |G| is a power of p. The converse follows by Lagrange's theorem.
Thus, Lemma 2 characterizes the finite p-groups. The next result holds for all p-groups, finite or not, and we leave the routine proof as Exercise 21.
Theorem 5. Let K ⊆ G be groups with K ![]() G and let p be a prime. Then G is a p-group if and only if both K and G/K are p-groups.
G and let p be a prime. Then G is a p-group if and only if both K and G/K are p-groups.
Although infinite p-groups exist (Exercise 23), we focus on the finite case. Theorem 6 is fundamental, and the proof provides a good illustration of how to use the class equation.
Theorem 6. If p a prime and G ≠ {1} is a finite p-group, then Z(G) ≠ {1}.
Proof. Let classa1, . . ., classan denote the nonsingleton conjugacy classes in G. Because N(ai) ≠ G for each i by Theorem 2, and because |G: N(ai)| divides |G| for each i, it follows that p divides |G: N(ai)| for each i. But then p divides |Z(G)| by the class equation; in particular Z(G) ≠ {1}.
Theorem 6 is very useful in the study of p-groups where p is a prime. We give two applications; the first characterizes of all groups of order p2.
Theorem 7. If G is a group and |G| = p2 where p is a prime, then G is abelian and either ![]() or G ≅ Cp × Cp.
or G ≅ Cp × Cp.
Proof. To prove that G is abelian, we show that Z(G) = G. As Z(G) ≠ {1} by Theorem 6, it suffices to show that |Z(G)| = p is impossible. But, if it holds, then G/Z(G) is cyclic (it has order p), which implies that G is abelian by Theorem 2 §2.9, a contradiction. Hence |Z(G)| ≠ p, so Z(G) = G and G is abelian. Now assume that G is not cyclic so that every element g satisfies gp = 1. Choose a ≠ 1 in G and write ![]() Then choose b ∉ H and write
Then choose b ∉ H and write ![]() Because |K| = p = |H|, we have H ∩ K = {1}, so HK ≅ H × K by Theorem 3 §8.1. Hence |HK| = p2 = |G|, so G = HK ≅ H × K ≅ Cp × Cp.
Because |K| = p = |H|, we have H ∩ K = {1}, so HK ≅ H × K by Theorem 3 §8.1. Hence |HK| = p2 = |G|, so G = HK ≅ H × K ≅ Cp × Cp.
The extension of Theorem 7 to groups of order p3 is false: If p = 2, the nonabelian groups D4 and Q both have order 23. More generally, if p is an odd prime, Exercises 30 and 31 give nonabelian groups G1 and G2 of order p3 such that gp = 1 for all g ![]() G1, and G2 contains an element of order p2.
G1, and G2 contains an element of order p2.
The next result shows that, although a finite p-group need not be abelian, it has an abundance of normal subgroups; in fact, it has one of every possible order. The proof again depends on Theorem 6 and provides a tour de force through the methods we have developed for dealing with finite groups.
Theorem 8. Let G be a finite p -group of order pn. Then there exists a series
G = G0 ⊃ G1 ⊃ ![]() ⊃ Gn = {1}
⊃ Gn = {1}
of subgroups of G such that Gi ![]() G, |Gi| = pn−i, and |Gi/Gi+1| = p for all i.
G, |Gi| = pn−i, and |Gi/Gi+1| = p for all i.
Proof. The existence of such a series is obvious if n = 1, so we proceed by induction on n. If |G| = pn+1, we have Z(G) ≠ {1} by Theorem 6. By Cauchy's theorem, choose a ![]() Z(G) such that o(a) = p, and write
Z(G) such that o(a) = p, and write ![]() Then Gn
Then Gn ![]() G and G/Gn has order pn−1 so, by induction, let (G/Gn) ⊃ X1 ⊃
G and G/Gn has order pn−1 so, by induction, let (G/Gn) ⊃ X1 ⊃ ![]() ⊃ Xn = {Gn} be a series of subgroups of G/Gn such that Xi
⊃ Xn = {Gn} be a series of subgroups of G/Gn such that Xi ![]() G/Gn and |Xi/Xi+1| = p for each i. The correspondence theorem (Theorem 5 §8.1) ensures that each Xi has the form Xi = Gi/Gn, where Gi
G/Gn and |Xi/Xi+1| = p for each i. The correspondence theorem (Theorem 5 §8.1) ensures that each Xi has the form Xi = Gi/Gn, where Gi ![]() G and
G and ![]() Furthermore, Xi ⊃ Xi+1 implies that Gi ⊃ Gi+1, and Gi/Gi+1 ≅ Xi/Xi+1 by the third isomorphism theorem (Theorem 7 §8.1). Hence, G ⊃ G1 ⊃
Furthermore, Xi ⊃ Xi+1 implies that Gi ⊃ Gi+1, and Gi/Gi+1 ≅ Xi/Xi+1 by the third isomorphism theorem (Theorem 7 §8.1). Hence, G ⊃ G1 ⊃ ![]() ⊃ Gn ⊃ {1} is the required series for G.
⊃ Gn ⊃ {1} is the required series for G.
Note that Theorem 8 shows that if G is a p-group and ![]() n ≥ 1, then every subgroup H ⊆ G is contained in a subgroup M with
n ≥ 1, then every subgroup H ⊆ G is contained in a subgroup M with ![]() Such subgroups must be normal as we shall see in the Corollary to Theorem 1 §8.3, so G/M ≅ Cp and M is maximal.
Such subgroups must be normal as we shall see in the Corollary to Theorem 1 §8.3, so G/M ≅ Cp and M is maximal.
The existence of a series of subgroups such as that in Theorem 8 gives important information about the group. Such series are studied in Chapter 9.
Augustin Louis Cauchy (1789–1857) Cauchy was certainly one of the great mathematicians, and it is said that he and his contemporary Gauss were the last to know all the mathematics of their time. But, unlike Gauss, Cauchy published profusely (surpassed only by Euler and Cayley), and produced 789 papers on topics as diverse as optics, elasticity, differential equations, mechanics, determinants, permutation groups, and probability. He was the effective founder of the theory of functions of a complex variable. In addition he wrote three classic textbooks on analysis in which he firmly established standards of rigor that are now accepted by all analysts and carry down to today's calculus texts. We owe our modern notions of limit and continuity to him. In algebra, Cauchy is remembered as the first to formulate earlier work with permutations in an abstract way and so to create a formal theory of groups of permutations. This work led Cayley (in 1854) to the modern notion of an abstract group.
Cauchy was born in Paris and, after a stellar career in school, enrolled as an engineer in Napoleon's army. He continued his mathematical research and, at the age of 26, became a professor at the École Polytechnique. He soon established himself as the leading mathematician in France. He also enjoyed teaching, and this pedagogical bent probably accounts for the influence his books had.
Exercises 8.2
1. In each case partition G into conjugacy classes and find all the normal subgroups.
![]()
2. Partition Dn into conjugacy classes where n is odd. [Hint: All elements of order 2 are conjugate.]
3. Suppose that |a| = n in a finite group G. If am is conjugate to a in G, show that gcd (m, n) = 1. [Hint: If gag−1 = am, show first that ![]()
4. Show that ab and ba are conjugate in any group.
5. If a subgroup H of G is a union of conjugacy classes in G, show that H ![]() G.
G.
6. If H is a subgroup of prime index in a finite group G, show that either H ![]() G or N(H) = H.
G or N(H) = H.
7. If H and K are conjugate subgroups in G, show that N(H) and N(K) are conjugate.
8. If G is a group, let ![]() where a
where a ![]() G. Show that K
G. Show that K ![]() G.
G.
9. If a finite group G has an element with exactly two conjugates, show that G is not simple.
10. If G is a finite group and H ≠ G is a subgroup, show that G ≠ ![]() a
a![]() GaHa−1. [Hint: Theorem 2.]
GaHa−1. [Hint: Theorem 2.]
11. If H is a subgroup of G of finite index, show that H has only finitely many conjugates in G. [Hint: Exercise 31 §2.6.]
12. Show that N(X) is a subgroup of G for each nonempty subset X of G.
13. Prove (2) of Theorem 2.
14. Let D3 = {1, a, a2, b, ba, ba2}, where o(a) = 3, o(b)= 2, and aba = b. If H = {1, b}, show that N(H) = H.
15. Use Lemma 3 §2.8 to show that two permutations are conjugate in Sn if and only if they have the same cycle structure.
16. If γ = (1234) and δ = (123) in S4, compute N(γ) and N(δ). [Hint: Pre-ceding exercise.]
17. Write K = {ε, (12)(34), (13)(24), (14)(23)}.
a. Show that the only normal subgroups of S4 are {ε}, K, A4, and S4. [Hint: Exercise 15.]
b. Show that the only normal subgroups of A4 are {ε}, K, and A4. [Hint: Exercise 7 §2.8 and Lemma 2 §2.8.]
18. If n ≥ 5, show that {ε}, An, and Sn are the only normal subgroups of Sn. [Hint: Theorem 8 §2.8 and Exercise 7 §2.8.]
19. If G is a finite group with exactly two conjugacy classes, show that |G| = 2.
20. If G is a group and a ![]() G, define M(a) = {g
G, define M(a) = {g ![]() G
G ![]() [g, a]
[g, a] ![]() Z(G)}, where we write [g, a] = gag−1a−1 for the commutator. Show that M(a) is a subgroup of G and that there is a homomorphism M(a) → Z(G) with kernel N(a).
Z(G)}, where we write [g, a] = gag−1a−1 for the commutator. Show that M(a) is a subgroup of G and that there is a homomorphism M(a) → Z(G) with kernel N(a).
21. Prove Theorem 5.
22. Let G be a finite group. If p is a prime, show that G has a normal subgroup of index p if and only if p divides |G/G′|, where G′ is the commutator subgroup. [Hint: If p divides |G/G′| apply Theorem 8 to the p-primary component of G/G′.]
23. Let Gω be the group of sequences [gi) = (g0, g1, ![]() ) from a group G, with compo-nentwise multiplication [gi) · [hi) = [gihi). (See Exercise 37 §2.10). Show that, if G ≠ {1} is a finite p-group, then Gω is an infinite p-group.
) from a group G, with compo-nentwise multiplication [gi) · [hi) = [gihi). (See Exercise 37 §2.10). Show that, if G ≠ {1} is a finite p-group, then Gω is an infinite p-group.
24. If G is a finite p-group, show that G′ ≠ G. [Hint: Theorem 8.]
25. If H ![]() G, where G is a finite p-group and H ≠ {1}, show that H ∩ Z(G) ≠ {1}. [Hint: Theorem 1.]
G, where G is a finite p-group and H ≠ {1}, show that H ∩ Z(G) ≠ {1}. [Hint: Theorem 1.]
26. Let G be a nonabelian group of order p3, where p is a prime. Show that
a. Z(G) = G′ and this is the unique normal subgroup of G of order p.
b. G has exactly p2 + p − 1 distinct conjugacy classes.
27. Let G be a finite p-group and let H ![]() G. If |H| = pm and |G| = pn, strengthen Theorem 8 by showing that a series G = G0 ⊃ G1 ⊃
G. If |H| = pm and |G| = pn, strengthen Theorem 8 by showing that a series G = G0 ⊃ G1 ⊃ ![]() ⊃ Gn = {1} exists such that Gi
⊃ Gn = {1} exists such that Gi ![]() G and |Gi/Gi+1| = p for all i, and that Gn−m = H. [Hint: Exercise 25.]
G and |Gi/Gi+1| = p for all i, and that Gn−m = H. [Hint: Exercise 25.]
28. Let G be a group of order pn and let H1, ![]() , Hm be the distinct subgroups of G of index p. If N = H1 ∩
, Hm be the distinct subgroups of G of index p. If N = H1 ∩ ![]() ∩ Hm, show that N
∩ Hm, show that N ![]() G and that xp = 1 for every coset x in G/N. [Remark: In fact Hi
G and that xp = 1 for every coset x in G/N. [Remark: In fact Hi ![]() G for each i (see the Corollary of Theorem 1 §8.3).]
G for each i (see the Corollary of Theorem 1 §8.3).]
29. If H ≠ G is a subgroup of a finite p-group G, show that H ≠ N(H). [Hint: If C = coreH (Exercise 26 §2.8), let Z(G/C) = K/C, and show that K ![]() H and K ⊆ N(H).]
H and K ⊆ N(H).]
30. Let K ![]() G where G/K is a finite p-group, p a prime. Show that G has a normal subgroup of index p.
G where G/K is a finite p-group, p a prime. Show that G has a normal subgroup of index p.
31. If p is an odd prime, let ![]() and define an operation on G by (x, y, z) · (x1, y1, z1) = (x + x1, y + y1, z + z1 − yx1). Show that G is a nonabelian group of order p3 in which ap = 1 for all a
and define an operation on G by (x, y, z) · (x1, y1, z1) = (x + x1, y + y1, z + z1 − yx1). Show that G is a nonabelian group of order p3 in which ap = 1 for all a ![]() G.
G.
32. Let p be a prime and let X = {0, p, 2p, . . ., (p − 1)p} be the (additive) subgroup of ![]() generated by p. Define an operation on the cartesian product
generated by p. Define an operation on the cartesian product ![]() by (x, y) (x1, y1) = (x + x1, y + y1 − yx1). Show that G is a nonabelian group of order p3 that contains an element of order p2.
by (x, y) (x1, y1) = (x + x1, y + y1 − yx1). Show that G is a nonabelian group of order p3 that contains an element of order p2.
33. A G is called an FC-group if every conjugacy class is finite. Show that
a. If |G: Z(G)| is finite, then G is an FC-group.
b. If G is a finitely generated FC-group, show that |G: Z(G)| is finite. [Hint: Exercise 33 §2.6.]
c. If ![]() show that G is an FC -group if and only if |classx| is finite for all x
show that G is an FC -group if and only if |classx| is finite for all x ![]() X.
X.
d. Show that every subgroup and image of an FC-group is an FC -group.
e. If G is any group, show that G* = {a ![]() G
G ![]() classa is finite} is an FC-group which is a characteristic subgroup of G.
classa is finite} is an FC-group which is a characteristic subgroup of G.
A mathematician, like a painter or a poet, is a maker of patterns.
—Godfrey Harold Hardy
If G is a finite group of order n, Cayley's theorem asserts that there exists a one-to-one group homomorphism G → Sn. The proof proceed as follows. Given a ![]() G, we define the multiplication map σa: G → G by σa(g) = ag for all g
G, we define the multiplication map σa: G → G by σa(g) = ag for all g ![]() G. We can easily verify that σa is a bijection and so belongs to the group SG of all permutations of the set G. The proof is then completed by observing that the map G → SG given by a
G. We can easily verify that σa is a bijection and so belongs to the group SG of all permutations of the set G. The proof is then completed by observing that the map G → SG given by a ![]() σa is a one-to-one homomorphism and so embeds G in the permutation group SG. (Of course, SG ≅ Sn because |G| = n).
σa is a one-to-one homomorphism and so embeds G in the permutation group SG. (Of course, SG ≅ Sn because |G| = n).
The action of the permutation σa: G → G is left multiplication by a. The key observation in this section is that there are sets other than G on which an element of G can act by multiplication. For example, if H is a subgroup of G of index m, let X = {gH ![]() g
g ![]() G} denote the set of all left cosets. Then for a
G} denote the set of all left cosets. Then for a ![]() G we define
G we define
τa: X → X by τa(g) = a(gH) = agH, for all gH in X.
One verifies that τa is a (well defined) bijection for each a ![]() G and so τa
G and so τa ![]() SX. Moreover, τab = τaτb because τab(gH) = abgH = a(bgH) = τa[τb(gH)] for all g. Since this holds for all a and b, the map
SX. Moreover, τab = τaτb because τab(gH) = abgH = a(bgH) = τa[τb(gH)] for all g. Since this holds for all a and b, the map
ϕ: G → SX given by ϕ(a) = τa, for all a ![]() G
G
is a group homomorphism. However, unlike the map in Cayley's theorem, ϕ may have a nontrivial kernel:
| ker ϕ | = | {a |
| = | {a |
|
| = | {a |
|
| = |
This group is important enough to warrant a name.
If H is a subgroup of a group G, the core of H in G, denoted coreH, is defined to be the intersection of all the conjugates of H in G; that is,
coreH = {a ![]() G
G ![]() a
a ![]() gHg−1 for all g
gHg−1 for all g ![]() G} =
G} = ![]() g
g![]() GgHg−1.
GgHg−1.
Thus, coreH ![]() G by the preceding discussion, and coreH ⊆ H because H is a conjugate of itself. Furthermore, coreH is the largest normal subgroup of G that is contained in H. We record this fact for reference, and leave the proof as Exercise 9.
G by the preceding discussion, and coreH ⊆ H because H is a conjugate of itself. Furthermore, coreH is the largest normal subgroup of G that is contained in H. We record this fact for reference, and leave the proof as Exercise 9.
Lemma 1. Let H be a subgroup of a group G.
1. coreH ![]() G and coreH ⊆ H.
G and coreH ⊆ H.
2. If K ![]() G and K ⊆ H, then K ⊆ coreH.
G and K ⊆ H, then K ⊆ coreH.
Our present interest in coreH comes from Theorem 1.
Theorem 1. Extended Cayley Theorem. If H is a subgroup of finite index m in a group G, there is a group homomorphism θ: G → Sm with ker θ = coreH ⊆ H.
Proof. If X = {gH ![]() g
g ![]() G}, let ϕ: G → SX be defined as above. As |X| = m, there is an isomorphism δ: SX → Sm, so we obtain a homomorphism δϕ: G → Sm, and ker δϕ = ker ϕ = coreH by the preceding discussion. Then θ = δϕ does it.
G}, let ϕ: G → SX be defined as above. As |X| = m, there is an isomorphism δ: SX → Sm, so we obtain a homomorphism δϕ: G → Sm, and ker δϕ = ker ϕ = coreH by the preceding discussion. Then θ = δϕ does it.
This is Cayley's theorem when H = {1}. Example 1 illustrates how to use it.
Example 1. If |G| = 36 and G has a subgroup H of order 9, 189 then G is not simple. Indeed, |G: H| = 4 so, by Theorem 1, there is a homomorphism θ: G → S4, with ker θ ⊆ H. If ker θ = {1}, then G ≅ θ(G), a contradiction as |G| = 36 and |θ(G)| ≤ |S4| = 24. So ker θ ≠ {1} is normal in G.
In Section 2.8, we showed that any subgroup of index 2 is normal. The next result gives a generalization that is especially useful for finite p -groups.
Corollary. Let p be the smallest prime dividing the order of a finite group G. Then any subgroup of G of index p is normal in G.
Proof. Let |G| = pkqmrn ![]() , where p< q < r
, where p< q < r ![]() are primes. If |G: H| = p, then |H| = pk−1qmrn
are primes. If |G: H| = p, then |H| = pk−1qmrn ![]() . By Theorem 1 let θ: G → Sp be a homomorphism with ker θ ⊆ H and write K = ker θ. If
. By Theorem 1 let θ: G → Sp be a homomorphism with ker θ ⊆ H and write K = ker θ. If ![]() , then we have
, then we have ![]() divides |Sp| = p ! and so
divides |Sp| = p ! and so ![]() divides (p − 1) !. But this implies that k0 = m0 = n0 =
divides (p − 1) !. But this implies that k0 = m0 = n0 = ![]() = 0 because every divisor of (p − 1) ! is less than p. Hence, H = K
= 0 because every divisor of (p − 1) ! is less than p. Hence, H = K ![]() G.
G.
We give more applications of the extended Cayley theorem later; our present aim is to generalize it. The key to the theorem is the existence of the homomorphism ϕ: G → SX, where G is a group and X is some set. Because the image ϕ(G) of G is a subgroup of SX, the natural place to begin is to consider this situation.
Hence suppose that X is a nonempty set and that G is a subgroup of the group SX of all permutations of X. For x ![]() X and σ
X and σ ![]() G, the element σ(x) of X is specified, which amounts to a mapping G × X → X where (σ, x)
G, the element σ(x) of X is specified, which amounts to a mapping G × X → X where (σ, x) ![]() σ(x). We can now describe an apparently more general situation.
σ(x). We can now describe an apparently more general situation.
Group Actions
Let G be a group and let X be a nonempty set. A mapping G × X → X, denoted (a, x) ![]() a · x, is called an action of G if it satisfies the following conditions.
a · x, is called an action of G if it satisfies the following conditions.
A1 1 · x = x for all x ![]() X.
X.
A2 a · (b · x) = (ab) · x for all x ![]() X and for all a, b
X and for all a, b ![]() G.
G.
In this case, G is said to act on X and X is called a G-set.90
Hence an action of G on X is nothing more than a multiplication of any element x of X by any element a of G to yield a (uniquely determined) element a · x of X that satisfies axioms A1 and A2. There are many examples of such actions, and Example 2 recaptures the above discussion.
Example 2. If X is any nonempty set and G ⊆ SX is any group of permutations of X, define σ · x = σ(x) for all x ![]() X and σ
X and σ ![]() G. Then axioms A1 and A2 are clearly satisfied; in fact, A2 is the definition of composition of mappings.
G. Then axioms A1 and A2 are clearly satisfied; in fact, A2 is the definition of composition of mappings.
Example 3. Let H be a subgroup of a group G. Consider G as a set for the moment and let H act on G by h · x = hx for all x ![]() G, h
G, h ![]() H. This is clearly an action; and H is said to act on G by left multiplication.
H. This is clearly an action; and H is said to act on G by left multiplication.
Example 4. If G is a group, let G act on itself by a · x = axa−1 for all x ![]() G and a
G and a ![]() G. Then axiom A1 is clear and A2 holds because
G. Then axiom A1 is clear and A2 holds because
a · (b · x) = a(bxb−1)a−1 = (ab)x(ab)−1 = (ab) · x
for x ![]() G and a, b
G and a, b ![]() G. In this case, G is said to act on itself by conjugation.
G. In this case, G is said to act on itself by conjugation.
Example 5. Let H be a subgroup of a group G and let X = {gH ![]() g
g ![]() G} denote the set of left cosets of H in G. If a
G} denote the set of left cosets of H in G. If a ![]() G and gH
G and gH ![]() X then a · (gH) = agH is well defined (verify) and so is an action of G on X. As we have shown, this action plays an essential role in the derivation of the extended Cayley theorem.
X then a · (gH) = agH is well defined (verify) and so is an action of G on X. As we have shown, this action plays an essential role in the derivation of the extended Cayley theorem.
Example 6. If X is any set and G is any group, we define the trivial action by a · x = x for all x ![]() X and a
X and a ![]() G. Clearly, the axioms are satisfied.
G. Clearly, the axioms are satisfied.
Examples 2–6 show that group actions are commonly occurring phenomena, and other examples below underline this conclusion. Lemma 2 isolates two useful properties of group actions that we use repeatedly.
Lemma 2. Let X be a G -set, where G is a group, and let x, y ![]() X and a, b
X and a, b ![]() G.
G.
1. If a · x = a · y, then x = y.
2. a · x = b · y if and only if (b−1a) · x = y.
Proof. Clearly, (1) follows from (2) and axiom A1. If a · x = b · y, then
(b−1a) · x = b−1 · (a · x) = b−1 · (b · y) = (b−1b) · y = 1 · y = y,
which proves half of (2). The other implication is proved similarly.
We can now give a natural generalization of the extended Cayley theorem. If G is a group, X is a G-set and a ![]() G, define
G, define
σa: X → X by σa(x) = a · x for all x ![]() X.(*)
X.(*)
Then Lemma 2 shows that σa is a bijection and so is a member of the group SX of all permutations of X. Moreover, if a, b ![]() G, then axiom A2 gives
G, then axiom A2 gives
σab(x) = (ab) · x = a · (b · x) = σa[σb(x)] = (σaσb)(x)
for all x ![]() S. Hence, σab = σaσb so the map θ: G → SX, defined by θ(a) = σa for all a
S. Hence, σab = σaσb so the map θ: G → SX, defined by θ(a) = σa for all a ![]() G, is a group homomorphism. This gives parts (1) and (2) of
G, is a group homomorphism. This gives parts (1) and (2) of
Theorem 2. Let G be a group, let X be a G-set, and let σa be defined as in (*), where a ![]() G. Then
G. Then
1. σa ![]() SXfor all a
SXfor all a ![]() G.
G.
2. θ: G → SX given by θ(a) = σa is a group homomorphism.
3. ker θ = {a ![]() G
G ![]() a · x = x for all x
a · x = x for all x ![]() X}.
X}.
Proof. It remains to prove (3). But a ![]() ker θ means
ker θ means ![]() that is, σa(x) = x for all x
that is, σa(x) = x for all x ![]() X. This condition means that a · x = x for all x, as required.
X. This condition means that a · x = x for all x, as required.
If H is a subgroup of G, the extended Cayley theorem is clearly the special case of Theorem 2 where X = {gH|g ![]() G} and the action of G on X is given by a · (gH) = agH for all gH
G} and the action of G on X is given by a · (gH) = agH for all gH ![]() X and a
X and a ![]() G. In this case ker θ = coreH. In general, if X is a G-set then ker θ
G. In this case ker θ = coreH. In general, if X is a G-set then ker θ ![]() G is given by
G is given by
ker θ = {a ![]() G
G ![]() a · x = x for all x
a · x = x for all x ![]() X}.
X}.
The normal subgroup ker θ is called the fixer of the action. The reason for the name is that ker θ consists of the elements of G that fix every x ![]() X. Here an element x
X. Here an element x ![]() X is said to be fixed by a
X is said to be fixed by a ![]() G if a · x = x.
G if a · x = x.
Example 7. Let G be a group and let G act on itself by conjugation: a · x = axa−1 for all x ![]() G and a
G and a ![]() G. Here the bijection σa: G → G in Theorem 2 is the inner automorphism of G induced by a. Hence θ(G) = innG, where θ: G → SG is the homomorphism in Theorem 2, and the fixer is ker θ = {a
G. Here the bijection σa: G → G in Theorem 2 is the inner automorphism of G induced by a. Hence θ(G) = innG, where θ: G → SG is the homomorphism in Theorem 2, and the fixer is ker θ = {a ![]() G
G ![]() a · x = x for all x
a · x = x for all x ![]() G} = Z(G) in this case. Thus, Theorem 2 gives G/Z(G) ≅ innG, a result derived earlier (Theorem 5 §2.10).
G} = Z(G) in this case. Thus, Theorem 2 gives G/Z(G) ≅ innG, a result derived earlier (Theorem 5 §2.10).
Orbit Decomposition Theorem
So far, the theory of group actions has been motivated by the urge to generalize the extended Cayley theorem. However, the theory yields an additional bonus: It provides a fundamental, natural generalization of the class equation.
Recall that elements x and y in a group G are called conjugate in G if y = axa−1 for some a ![]() G. If we regard G as acting on itself by conjugation, this condition is y = a · x for some a
G. If we regard G as acting on itself by conjugation, this condition is y = a · x for some a ![]() G. This suggests a generalization: If X is a G-set, we define a relation ≡ on X as follows. If x, y
G. This suggests a generalization: If X is a G-set, we define a relation ≡ on X as follows. If x, y ![]() X, we write
X, we write
x ≡ y (modG), if y = a · x for some a ![]() G.
G.
One easily verifies that ≡ is an equivalence on X (Exercise 17). Moreover, we may describe the equivalence class [x] of an element x of X in terms of the action: [x] = {y ![]() X
X ![]() y ≡ x} = {a · x
y ≡ x} = {a · x ![]() a
a ![]() G}. This equivalence class is called the orbit of x under G and is denoted
G}. This equivalence class is called the orbit of x under G and is denoted
G · x = {a · x ![]() a
a ![]() G}.
G}.
Hence, if G acts on itself by conjugation, the orbits are just the conjugacy classes. Cosets also occur as orbits.
Example 8. Let H be a subgroup of a group G and let H act on G by left multiplication: h · x = hx for all x ![]() G, h
G, h ![]() H. Then the orbit of x
H. Then the orbit of x ![]() G is the right coset Hx = H · x.
G is the right coset Hx = H · x.
A key step in the derivation of the class equation is the observation that the number of elements in the conjugacy class of x ![]() G is just the index in G of the normalizer N(x) of x in G. Surprisingly, if X is any G-set, the size of each orbit is the index of a certain subgroup of G.
G is just the index in G of the normalizer N(x) of x in G. Surprisingly, if X is any G-set, the size of each orbit is the index of a certain subgroup of G.
Lemma 3. If X is a G -set and x ![]() X, write S(x) = {a
X, write S(x) = {a ![]() G
G ![]() a · x = x}. Then
a · x = x}. Then
1. S(x) is a subgroup of G for each x ![]() X.
X.
2. |G · x| = |G: S(x)| for each x ![]() X.
X.
Proof. The proof of (1) is left as Exercise 23. Given x ![]() X, write S(x) = S and define a function ϕ: G · x → {gS
X, write S(x) = S and define a function ϕ: G · x → {gS ![]() g
g ![]() G} by ϕ(g · x) = gS. Then
G} by ϕ(g · x) = gS. Then
g · x = h · x ![]() (h−1g) · x = x
(h−1g) · x = x ![]() h−1g
h−1g ![]() S
S ![]() gS = hS,
gS = hS,
so ϕ is well defined and one-to-one. Since ϕ is clearly onto, this proves (2) because ![]()
If X is a G-set and x ![]() X, the subgroup
X, the subgroup
S(x) = {a ![]() G
G ![]() a · x = x}
a · x = x}
is called the stabilizer 91 of x. If G acts on itself by conjugation the stabilizer of x in G is S(x) = {a ![]() G
G ![]() axa−1 = x} = N(x) is the normalizer of x, and the orbit of x is G · x = {gxg−1
axa−1 = x} = N(x) is the normalizer of x, and the orbit of x is G · x = {gxg−1 ![]() g
g ![]() G} = classx. Hence, Lemma 3 gives |classx| = |G: N(x)| in this case, a result proved earlier (Theorem 2 §8.2).
G} = classx. Hence, Lemma 3 gives |classx| = |G: N(x)| in this case, a result proved earlier (Theorem 2 §8.2).
If X is a G-set and x ![]() X, the orbit of x is G · x = {a · x
X, the orbit of x is G · x = {a · x ![]() a
a ![]() G}. Combining this with Lemma 3 gives equivalent conditions that the orbit is a singleton
G}. Combining this with Lemma 3 gives equivalent conditions that the orbit is a singleton
G · x = {x} ![]() a · x = x, for all a
a · x = x, for all a ![]() G
G ![]() S(x) = G.(**)
S(x) = G.(**)
The set of all such elements x is denoted
Xf = {x ![]() X
X ![]() a · x = x for all a
a · x = x for all a ![]() G}
G}
and is called the fixed subset of X under the action of G. With this we can give the promised generalization of the class equation.
Theorem 3. Orbit Decomposition Theorem. Let a group G act on a finite set X ≠ ∅ and let G · x1, G · x2, . . ., G · xn denote the nonsingleton orbits. Then
![]()
Proof. The fixed subset Xf is the union of the singleton orbits by (**). Because the orbits partition X, ![]() Now apply Lemma 3.
Now apply Lemma 3.
Theorem 3 becomes the class equation if X = G and G acts on itself by conjugation because the fixed subset is Gf = {x ![]() G
G ![]() axa−1 = x for all a
axa−1 = x for all a ![]() G} = Z(G).
G} = Z(G).
In the terminology of Theorem 3 the index |G: S(xi)| = |G · xi| is finite because X is a finite set and, if the group G is itself finite, it is a divisor of |G|. This property is particularly important when G is a finite p-group, where p is a prime, because then p divides |G: S(xi)| for each i. Hence, Theorem 3 shows that p divides |X| − |Xf| in this case, which is important enough to record as Theorem 4.
Theorem 4. Let p be a prime and let G be a finite p-group. If X is a finite G-set, then p divides |X| − |Xf|.
We use this result repeatedly in the next Section. For now we illustrate how to use it by proving an important property of finite p -groups that will recur in Chapter 9.
Theorem 5. Let G be a finite p -group, where p is a prime. If H ≠ G is a subgroup, then N(H) ≠ H.
Proof. Let X = {xH ![]() x
x ![]() G} denote the set of left cosets of H in G, and let H act on X by left multiplication: h · (xH) = hxH for all x
G} denote the set of left cosets of H in G, and let H act on X by left multiplication: h · (xH) = hxH for all x ![]() G and h
G and h ![]() H. Then p divides |X| = |G: H| and so |Xf| ≠ 1 by Theorem 4. Now
H. Then p divides |X| = |G: H| and so |Xf| ≠ 1 by Theorem 4. Now
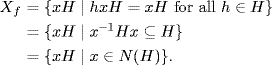
Hence, N(H) ≠ H since otherwise Xf = {H}, contrary to |Xf| ≠ 1.
We conclude this section by sketching J.H. McKay's beautiful proof 92 of Cauchy's theorem, which applies Theorem 4 and avoids proving the abelian case separately. If G is a group and p is a prime divisor of |G|, we must find an element of order p in G. McKay's idea is to consider the set of p-tuples with product 1:
X = {(a1, . . ., ap) ![]() ai
ai ![]() G, a1a2
G, a1a2 ![]() ap = 1}.
ap = 1}.
What is needed is a p-tuple (a, a, . . ., a) in X with a ≠ 1. To this end, let the (additive) group ![]() act on X by “ cycling” the p-tuples:
act on X by “ cycling” the p-tuples:
![]() , for all
, for all ![]()
We leave to the reader the task of verifying that this is an action (well defined) and that the fixed subset is Xf = {(a, a, . . ., a) ![]() ap = 1}. Hence, Cauchy's theorem follows if |Xf| ≠ 1, and this in turn holds (by Theorem 4) if p divides |X|. But this latter condition follows because p divides
ap = 1}. Hence, Cauchy's theorem follows if |Xf| ≠ 1, and this in turn holds (by Theorem 4) if p divides |X|. But this latter condition follows because p divides ![]() and |X| = |G|p−1 (indeed, in choosing (a1, . . ., ap) in X, the elements a1, . . ., ap−1 can be selected arbitrarily from G). This completes a most elegant proof.
and |X| = |G|p−1 (indeed, in choosing (a1, . . ., ap) in X, the elements a1, . . ., ap−1 can be selected arbitrarily from G). This completes a most elegant proof.
Exercises 8.3
1.
a. If |G| = 20, show that G has a normal subgroup of order 5.
b. If |G| = 28, show that G has a normal subgroup of order 7.
2. If |G| = 24 and G has a subgroup of order 8, show that G is not simple.
3. If p and q are primes, show that no group of order pq is simple.
4. Show that every group of order 15 is cyclic. [Hint: If o(a)= 5 and o(b)= 3, show that bab−1 = ak for some k. Deduce that ![]() for each n and hence k = 1.]
for each n and hence k = 1.]
5. If |G| = pm, where p is a prime and p > m, show that any subgroup of order p is normal in G. (Such subgroups exist by Cauchy's theorem.)
6. (a) If n ≥ 5 and p ≠ n is a prime, show that An has no subgroup of index p. (b) If p is a prime, show that Ap has a subgroup of index p.
7. If H and K are subgroups of G, show that core(H ∩ K) = coreH ∩ coreK.
8. If G is the group of all 2 × 2 invertible matrices over ![]() find coreH, where H is the group of diagonal matrices
find coreH, where H is the group of diagonal matrices ![]() in G.
in G.
9. Prove Lemma 1.
10. If H is a subgroup of G, define H0 = ![]() {σ(H)
{σ(H) ![]() σ
σ ![]() autG}. (a) Show that H0 is characteristic in G and H0 ⊆ H. (b) If K is characteristic in G and K ⊆ H, show that K ⊆ H0.
autG}. (a) Show that H0 is characteristic in G and H0 ⊆ H. (b) If K is characteristic in G and K ⊆ H, show that K ⊆ H0.
11. Show that the following are equivalent for a group G.
1. G has a nontrivial finite G-set.
2. G has a proper normal subgroup of finite index.
3. G has a proper subgroup of finite index.
12. Given m > 1, show that a finitely generated group G has at most a finite number of subgroups of index m. [Hint: If ![]() where |G: H| = m}, show that
where |G: H| = m}, show that ![]() is a finite set and that, given
is a finite set and that, given ![]() there are at most a finite number of subgroups H with K ⊆ H.]
there are at most a finite number of subgroups H with K ⊆ H.]
13. Let ![]() and define a · z = eiaz for all
and define a · z = eiaz for all ![]() and a
and a ![]() G. Show that
G. Show that ![]() is a G-set, describe the action geometrically, and find all orbits and stabilizers.
is a G-set, describe the action geometrically, and find all orbits and stabilizers.
14. Let ![]() the polynomial ring in the indeterminates x1, . . ., xn. Given σ
the polynomial ring in the indeterminates x1, . . ., xn. Given σ ![]() Sn and f = f(x1, . . ., xn)
Sn and f = f(x1, . . ., xn) ![]() X, define σ · f = f(xσ1, xσ2, . . ., xσn). Show that this is an action and describe the fixer. If n = 3, give three polynomials in the fixer and compute S3 · g and S(g), where g(x1, x2, x3) = x1 + x2.
X, define σ · f = f(xσ1, xσ2, . . ., xσn). Show that this is an action and describe the fixer. If n = 3, give three polynomials in the fixer and compute S3 · g and S(g), where g(x1, x2, x3) = x1 + x2.
15. Write Xn = {1, 2, . . ., n}. If σ ![]() Sn, write
Sn, write ![]() and let the elements of G act on Xn as mappings. Describe the relationship between the orbits of G in Xn and the factorization of σ into disjoint cycles.
and let the elements of G act on Xn as mappings. Describe the relationship between the orbits of G in Xn and the factorization of σ into disjoint cycles.
16. Let θ: G → SX be a group homomorphism, where X is a nonempty set. Show that θ arises, as in Theorem 2, from some action of G on X.
17. Let X be a G-set. Show that
a. Equivalence modulo G (defined prior to Example 8) is an equivalence on X.
b. Every equivalence on X arises, as in (a), from some group action on X.
18. Let X be a G-set. If F is the fixer, show that X is a G/F-set in a natural way and that the fixer is trivial (such actions are called faithful).
19. Show that a group G acts on its set of subgroups by conjugation and that Z(G) ⊆ F, where F is the fixer. Give an example where Z(G) ≠ F.
20. Is every normal subgroup of a group G the fixer of some action of G? Give reasons.
21. If H is a subgroup of G, find a G-set X and an element x ![]() X such that H = S(x).
X such that H = S(x).
22. If H ![]() G, define the centralizer of H in G as C(H) = {a
G, define the centralizer of H in G as C(H) = {a ![]() G
G ![]() ah = ha for all h
ah = ha for all h ![]() H}. Use Theorem 2 to show that C(H)
H}. Use Theorem 2 to show that C(H) ![]() G and that G/[C(H)] is isomorphic to a group of automorphisms of H.
G and that G/[C(H)] is isomorphic to a group of automorphisms of H.
23. Let X be a G-set and let x and y denote elements of X.
a. Show that S(x) is a subgroup of G.
b. If x ![]() X and b
X and b ![]() G, show that S(b · x) = bS(x)b−1.
G, show that S(b · x) = bS(x)b−1.
c. If S(x) and S(y) are conjugate subgroups, show that |G · x| = |G · y|.
24. Let X be a G-set with just one orbit (called a transitive action).
a. If K ![]() G, show that K ⊆ S(x) for some x
G, show that K ⊆ S(x) for some x ![]() X if and only if K is contained in the fixer. [Hint: Exercise 23.]
X if and only if K is contained in the fixer. [Hint: Exercise 23.]
b. If |X| ≥ 2, show that g ![]() G exists such that g · x ≠ x for all x
G exists such that g · x ≠ x for all x ![]() X. [Hint: Exercise 10 §8.2.]
X. [Hint: Exercise 10 §8.2.]
25. Let X be a G-set, let H be a subgroup of G, and let x ![]() X. Show that:
X. Show that:
a. H acts on the orbit G · x by h · (a · x) = (ha) · x for all h ![]() H and a · x
H and a · x ![]() G · x.
G · x.
b. If H ![]() G, the orbits of H in G · x all have the same cardinality.
G, the orbits of H in G · x all have the same cardinality.
26. Let G be a finite p-group. If {1}≠H ![]() G, show that H ∩ Z(G) ≠ {1}. [Hint: Let G act on H by conjugation.]
G, show that H ∩ Z(G) ≠ {1}. [Hint: Let G act on H by conjugation.]
27. If G is a finite p-group, show that the number of nonnormal subgroups of G is a multiple of p. [Hint: Let G act on its subgroups by conjugation.]
28. If G is a finite p-group, show that the number of subgroups of order pk is congruent (modulo p) to the number of normal subgroups of order pk.
29. Let H1, . . ., Hm be all the subgroups of index p in a finite p-group G. Show that ![]() is normal in G, that G/K is abelian, and that o(x)= p for all nonunity elements x
is normal in G, that G/K is abelian, and that o(x)= p for all nonunity elements x ![]() G/K. [Hint: Theorem 5 and Exercise 6 §8.2.]
G/K. [Hint: Theorem 5 and Exercise 6 §8.2.]
30. Let H and K be subgroups of a group G. Show that K has |H: H ∩ N(K)| distinct conjugates of the form hKh−1, where h ![]() H. Here N(K) = NG(K) is the normalizer.
H. Here N(K) = NG(K) is the normalizer.
31. If H and K are finite subgroups of some group, prove that |HK| · |H ∩ K| = |H| · |K| by letting H ∩ K act on H × K by a · (h, k) = (ha−1, ak). [Hint: Show that each orbit has the same number of elements.]
32. Let H and K be subgroups of a group G and let H × K act on G by (h, k) · x = hxk−1 for all x ![]() G and (h, k)
G and (h, k) ![]() H × K. Show
H × K. Show
a. This is an action and the orbit of x ![]() G is HxK (called a double coset).
G is HxK (called a double coset).
b. If x ![]() G, then |S(x)| = |H ∩ xKx−1| = |x−1Hx ∩ K|.
G, then |S(x)| = |H ∩ xKx−1| = |x−1Hx ∩ K|.
c. Frobenius' theorem: If Hx1K, Hx2K, . . ., HxnK are the distinct double cosets, then ![]()
33. If X and Y are G-sets, a map ϕ: X → Y is called a G-morphism if ϕ(a · x) = a · ϕ(x) holds for all x ![]() X and a
X and a ![]() G. If, in addition, ϕ is a bijection, it is called a G-isomorphism, and X and Y are called isomorphic G-sets. Call a G-set transitive if there is just one orbit. If H is a subgroup of G, let G/H denote the G-set of left H-cosets using left multiplication. (H need not be normal.)
G. If, in addition, ϕ is a bijection, it is called a G-isomorphism, and X and Y are called isomorphic G-sets. Call a G-set transitive if there is just one orbit. If H is a subgroup of G, let G/H denote the G-set of left H-cosets using left multiplication. (H need not be normal.)
a. Show that G/H is transitive for any subgroup H of G.
b. Show that every transitive G-set is G-isomorphic to G/H for some subgroup H.
34. Let ϕ: X → Y be an onto G-morphism, where X and Y are G-sets (Exercise 33). Define a relation ![]() on X by x
on X by x ![]() x1 if ϕ(x) = ϕ(x1). This relation is an equivalence (called thekernel equivalence of ϕ), and we denote the equivalence class of x
x1 if ϕ(x) = ϕ(x1). This relation is an equivalence (called thekernel equivalence of ϕ), and we denote the equivalence class of x ![]() X by [x] = {t
X by [x] = {t ![]() X
X ![]() ϕ(t) = ϕ(x)}. Finally, let X/ϕ = {[x]
ϕ(t) = ϕ(x)}. Finally, let X/ϕ = {[x] ![]() x
x ![]() X} denote the set of equivalence classes.
X} denote the set of equivalence classes.
a. Show that X/ϕ is a G-set via a · [x] = [a · x] for all [x] in X/ϕ and all a ![]() G.
G.
b. Find a G-isomorphism X/ϕ → Y (the G-set isomorphism theorem).
Lagrange's theorem asserts that the order of each subgroup of a finite group G is a divisor of |G|. The converse is false: A4 has no subgroup of order 6 even though |A4| = 12. However, if pk divides the order of G where p is a prime, then G does have a subgroup of order pk. This remarkable theorem was first proven in 1872 (for permutation groups) by the Norwegian mathematician Ludwig Sylow and has been ranked with Lagrange's theorem as being among the most important results about finite groups. The version presented here for abstract groups was proven in 1887 by Georg Frobenius, and this proof uses only Cauchy's theorem and the class equation. We give another more modern direct proof using the theory of group actions at the end of this section.
Theorem 1. Let G be a finite group. If p is a prime and pk divides |G| for some k ≥ 0, then G has a subgroup of order pk.
Proof. It is clear if k = 0, so assume k ≥ 1. Proceed by induction on |G|. The theorem is clear if |G| = 1, 2, or 3. In general, ![]() by the class equation, where classa1, . . ., classan are the nonsingleton conjugacy classes. If pk divides |N(ai)| for some i then N(ai) has a subgroup of order pk by induction because
by the class equation, where classa1, . . ., classan are the nonsingleton conjugacy classes. If pk divides |N(ai)| for some i then N(ai) has a subgroup of order pk by induction because ![]()
So assume that pk does not divide |N(ai)| for every i ≥ 1. Because pk divides ![]() for all i, it follows that p divides |G: N(ai)| for every i. Hence, p divides |Z(G)| by the class equation so, by Cauchy's theorem, choose a
for all i, it follows that p divides |G: N(ai)| for every i. Hence, p divides |Z(G)| by the class equation so, by Cauchy's theorem, choose a ![]() Z(G) with o(a) = p. If we write
Z(G) with o(a) = p. If we write ![]() then K
then K ![]() G and
G and ![]() Moreover, pk−1 divides
Moreover, pk−1 divides ![]() because pk divides
because pk divides ![]() Hence, again by induction, G/K has a subgroup H/K with
Hence, again by induction, G/K has a subgroup H/K with ![]() As
As ![]() we are done.
we are done.
Sylow originally proved Theorem 1 in the special case where pk is the highest power of the prime p that divides the order of the group.
Corollary. Sylow's First Theorem. If G is a group of order pnm, where p is a prime and p does not divide m, then G has a subgroup of order pn.
If G is a group of order pnm, where p is a prime and p does not divide m, any subgroup of order pn is called a Sylow p-subgroup of G.
Example 1. Write D3 = {1, a, a2, b, ba, ba2}, where o(a) = 3, o(b) = 2, and aba = b. Then H = {1, a, a2} is the unique Sylow 3-subgroup, but {1, b}, {1, ba}, and {1, ba2} are three Sylow 2-subgroups. Hence, the Sylow 2-subgroups may not be normal or unique. We show later that a Sylow p-subgroup is normal if and only if it is unique.
Example 2. If G is a finite abelian group and p is a prime divisor of |G|, let G(p) = {a ![]() G
G ![]() o(a) = pk for some k ≥ 0}. This set is a subgroup (because G is abelian) and so is a p -subgroup of G that contains every p-subgroup. It is thus the unique Sylow p-subgroup of G, called the p- primary component of G.
o(a) = pk for some k ≥ 0}. This set is a subgroup (because G is abelian) and so is a p -subgroup of G that contains every p-subgroup. It is thus the unique Sylow p-subgroup of G, called the p- primary component of G.
Corollary 2 of Theorem 3 §7.2 shows that every finite abelian group is isomorphic to the direct product of its primary components and thus of its distinct Sylow p-subgroups. We characterize when this happens in a nonabelian group in Section 9.3.
A Sylow p-subgroup P of a finite group G is a p-subgroup of G of maximum possible order (by Theorem 1). Note that each conjugate aPa−1 of P is also a Sylow p-subgroup because |aPa−1| = |P|. The converse is also true: Every Sylow p-subgroup is conjugate to P. In fact, every p-subgroup of G is contained in a conjugate of P (and so is contained in a Sylow p-subgroup of G)
Theorem 2. Let P be a Sylow p -subgroup of a finite group G. If H is any p-subgroup of G, then H ⊆ aPa−1 for some a ![]() G.
G.
Proof. Let X = {aP ![]() a
a ![]() G} be the set of left cosets of P in G and let H act on X by left multiplication: h · aP = haP for all h
G} be the set of left cosets of P in G and let H act on X by left multiplication: h · aP = haP for all h ![]() H. Write |G| = pnm, where p does not divide m. Then |X| = |G: P| = m, so p does not divide |X|. Hence (because H is a p -group) Theorem 4 §8.3 shows that p does not divide |Xf|, where Xf is the fixed subset. In particular, Xf is not empty, so let aP
H. Write |G| = pnm, where p does not divide m. Then |X| = |G: P| = m, so p does not divide |X|. Hence (because H is a p -group) Theorem 4 §8.3 shows that p does not divide |Xf|, where Xf is the fixed subset. In particular, Xf is not empty, so let aP ![]() Xf, a
Xf, a ![]() G. Then haP = h · aP = aP for all h
G. Then haP = h · aP = aP for all h ![]() H, whence a−1ha
H, whence a−1ha ![]() P for all h
P for all h ![]() H. Thus H ⊆ aPa−1, as required.
H. Thus H ⊆ aPa−1, as required.
Taking H to be any Sylow p-subgroup of G, we obtain
Corollary 1. Sylow's Second Theorem. If G is a finite group, any two Sylow p-subgroups of G are conjugate in G.
Because a subgroup of G is normal in G if and only if it equals all its conjugates in G, we get Corollary 2.
Corollary 2. A Sylow p -subgroup of a finite group G is normal in G if and only if it is unique.
Example 3. Given D3, as in Example 1, the Sylow 2-subgroups {1, b}, {1, ba}, and {1, ba2} must be conjugate. In fact, a{1, b}a−1 = {1, ba} and a2{1, b}a−2 = {1, ba2}.
The next result identifies a fundamental technique due to Giovanni Frattini. We return to this in Section 9.3.
Corollary 3. Frattini Argument. Let H ![]() G and let P be a Sylow p-subgroup of H. Then we have G = HNG(P), where NG(P) is the normalizer of P in G.
G and let P be a Sylow p-subgroup of H. Then we have G = HNG(P), where NG(P) is the normalizer of P in G.
Proof. Suppose g ![]() G. Then gPg−1 ⊆ H because H
G. Then gPg−1 ⊆ H because H ![]() G, so gPg−1 is also a Sylow p-subgroup of H. By Corollary 1, h(gPg−1)h−1 = P for some h
G, so gPg−1 is also a Sylow p-subgroup of H. By Corollary 1, h(gPg−1)h−1 = P for some h ![]() H, so hg
H, so hg ![]() NG(P). The result follows.
NG(P). The result follows.
If K ![]() G, Example 4, employs Theorem 2 to provide some useful information about the Sylow subgroups of K and G/K.
G, Example 4, employs Theorem 2 to provide some useful information about the Sylow subgroups of K and G/K.
Example 4. Let K ![]() G, where G is a finite group, and let p be a prime.
G, where G is a finite group, and let p be a prime.
1. A subgroup of K is a Sylow p-subgroup of K if and only if it has the form P ∩ K, where P is a Sylow p -subgroup of G.
2. A subgroup of G/K is a Sylow p-subgroup of G/K if and only if it has the form (PK)/K, where P is a Sylow p-subgroup of G.
Solution.
(1) We begin with one of the implications in (1).
Claim: If P is a Sylow p-subgroup of G then P ∩ K is a Sylow p-subgroup of K.
Proof. P ∩ K is a p-subgroup of K, so let P ∩ K ⊆ X where X is a Sylow p-subgroup of K. But X is a p -subgroup of G so X ⊆ aPa−1 for some a ![]() G by Theorem 2. It follows that
G by Theorem 2. It follows that
a−1(P ∩ K)a ⊆ a−1Xa ⊆ P ∩ (a−1Ka) = P ∩ K.
Hence, these sets are equal, and in particular P ∩ K = X. This proves the Claim.
Now if H is a Sylow p-subgroup of K, then H ⊆ P for some Sylow p-subgroup P of G. Hence, H ⊆ P ∩ K, so H = P ∩ K by the Claim. This proves (1).
(2) Let |G| = pnm where p does not divide m. By Lagrange's theorem, let ![]() where k ≤ n and r|m. Thus
where k ≤ n and r|m. Thus ![]() . Let
. Let ![]() be some Sylow p-subgroup of
be some Sylow p-subgroup of ![]() so
so ![]() . Then |H| = pnr. So if P is a Sylow p-subgroup of H, then P is a Sylow p-subgroup of G, and it remains to show PK = H. But
. Then |H| = pnr. So if P is a Sylow p-subgroup of H, then P is a Sylow p-subgroup of G, and it remains to show PK = H. But ![]() by the second isomorphism theorem (Theorem 1 §8.1), and |P ∩ K| = pk by (1). Hence,
by the second isomorphism theorem (Theorem 1 §8.1), and |P ∩ K| = pk by (1). Hence, ![]() so |PK| = pnr = |H|. Since PK ⊆ H, this gives PK = H, as required. The proof that each of the groups
so |PK| = pnr = |H|. Since PK ⊆ H, this gives PK = H, as required. The proof that each of the groups ![]() is a Sylow p -subgroup of
is a Sylow p -subgroup of ![]() is left to the reader.
is left to the reader.
The third Sylow theorem is concerned with the number of Sylow p -subgroups of a finite group G where p is a prime. We will denote this by np or np(G) if the group must be identified. Although determining np from the order of the group is not possible in general, we can deduce a good deal of numerical information.
Theorem 3. Sylow's Third Theorem. Let G be a group of order pnm, where p is a prime, n ≥ 1, and p does not divide m. If np denotes the number of distinct Sylow p-subgroups of G, then:
1. np ≡ 1 (modp).
2. np divides m.
3. np = |G: N(P)|, where P is any Sylow p-subgroup of G.
Proof. By Sylow's second theorem, (3) follows by Theorem 2 §8.2, so np divides |G| = pnm. Hence, (2) follows from (1) because (1) implies that gcd (p, np) = 1.
To prove (1), let X denote the set of all Sylow p-subgroups of G so that |X| = np. Fix P in X and let P act on X by conjugation. If Xf is the fixed subset, then np = |X| ≡ |Xf| modulo p by Theorem 4 §8.3, so it suffices to show that Xf = {P}. We have Xf = {Q ![]() X
X ![]() aQa−1 = Q for all a
aQa−1 = Q for all a ![]() P}, so P
P}, so P ![]() Xf is clear. If Q
Xf is clear. If Q ![]() Xf, then P ⊆ N(Q), so both P and Q are Sylow p -subgroups of N(Q) (they are p-subgroups of maximal order). But Q
Xf, then P ⊆ N(Q), so both P and Q are Sylow p -subgroups of N(Q) (they are p-subgroups of maximal order). But Q ![]() N(Q), so Q = P follows by Corollary 2 of Theorem 2. Hence Xf = {P}, as required.
N(Q), so Q = P follows by Corollary 2 of Theorem 2. Hence Xf = {P}, as required.
Examples 5–9 illustrate the power of the Sylow theorems and how to apply them to particular groups.
Example 5. If p and q are primes, show that no group G of order pq is simple.
Solution. If p = q, then G is abelian by Theorem 7 §8.2, so G is not simple because |G| = p2 is not a prime. So assume that p > q. Then np ≡ 1 (modp) and np|q by Theorem 3, so np = 1 because q < p. Thus, there is just one Sylow p-subgroup, and it is normal by Corollary 2 of Theorem 2.
Example 6. Show that every group of order 175 is abelian.
Solution. Observe |G| = 175 = 52 · 7. Then n5|7 and n5 ≡ 1 (mod5) by Theorem 3, from which n5 = 1. Hence, there is just one Sylow 5-subgroup P of G and so P ![]() G. Similarly n7|52 so n7 = 1, 5, or 25, and n7 ≡ 1 (mod7). Thus n7 = 1, so there is a unique Sylow 7-subgroup Q of G and Q
G. Similarly n7|52 so n7 = 1, 5, or 25, and n7 ≡ 1 (mod7). Thus n7 = 1, so there is a unique Sylow 7-subgroup Q of G and Q ![]() G. Now P ∩ Q = {1} because gcd (|P|, |Q|) = 1, so |PQ| = |P||Q| = |G|. Thus G = PQ, so G ≅ P × Q by Theorem 3 §8.1. But P and Q are abelian by Theorem 7 §8.2, so G is abelian.
G. Now P ∩ Q = {1} because gcd (|P|, |Q|) = 1, so |PQ| = |P||Q| = |G|. Thus G = PQ, so G ≅ P × Q by Theorem 3 §8.1. But P and Q are abelian by Theorem 7 §8.2, so G is abelian.
Example 7. Show that there is no simple group of order 56.
Solution. If |G| = 56 = 23 · 7, then n7 divides 8 and n7 ≡ 1 (mod7). This means that n7 = 1 or n7 = 8. If n7 = 1, then the Sylow 7-subgroup is normal. If n7 = 8, there are eight distinct cyclic subgroups in G of order 7. Because the intersection of any two of these subgroups equals {1}, there are 8 · 6 = 48 elements of order 7. This leaves eight elements, so the Sylow 2-subgroup is unique and hence normal.
Example 8. Show that there is no simple group of order 72.
Solution. If |G| = 72 = 23 · 32, then n2 = 1, 3, or 9 and n3 = 1 or 4 by Theorem 3, so the method in Example 7 fails. However, let P denote any Sylow 3-subgroup of G. If n3 = 1, then P ![]() G. If n3 = 4, then |G: N(P)| = 4 by Sylow's third theorem. Thus, Theorem 1 §8.3 provides a homomorphism θ: G → S4, with ker θ ⊆ N(P), and ker θ ≠ {1} because |G| = 72 does not divide |S4| = 24. As ker θ
G. If n3 = 4, then |G: N(P)| = 4 by Sylow's third theorem. Thus, Theorem 1 §8.3 provides a homomorphism θ: G → S4, with ker θ ⊆ N(P), and ker θ ≠ {1} because |G| = 72 does not divide |S4| = 24. As ker θ ![]() G and N(P) ≠ G, we are done.
G and N(P) ≠ G, we are done.
A famous theorem of William Burnside asserts that no group of order pnqm is simple where p and q are primes. The proof involves the theory of group representations and is beyond the scope of this book. However, we can do the following case.
Example 9. Show that no group of order p2q2 is simple when p and q are primes.
Solution. Let |G| = p2q2. If p = q, then Z(G) ≠ {1} by Theorem 6 §8.2 and we are finished. So assume that p > q. We have np = 1, q, or q2, and np ≡ 1 (modp). If np = 1, the Sylow p-subgroup is normal and we are done. The case np = q is impossible because q < p. So assume that np = q2, obtaining q2 ≡ 1 (modp). Then p divides q2 − 1 = (q − 1)(q + 1), so either p|(q − 1) or p|(q + 1). Because p > q, the first alternative is impossible; the second implies that q+ 1 ≥ p > q from which q + 1 = p. This means that p = 3 and q = 2, so |G| = 36. But then any Sylow 3-subgroup has index 4, so there is a homomorphism θ: G → S4 by Theorem 1 §8.3. This homomorphism cannot be one-to-one, so ker θ is normal in G.
We are now going to use the Sylow theorems to characterize the groups of order less than 16. It turns out that three of these groups belong to a family of groups that resemble the dihedral groups and are constructed in much the same way. We let n = 2m be an even positive integer, let ![]() and let
and let
![]() and
and ![]()
Then A and B are invertible complex matrices, and we can easily verify that |A| = n, ABA = B, and B2 = Am. One verifies that
G = {I, A, A2, . . ., An−1, B, BA, . . ., BAn−1}
is a subgroup of ![]() and |G| = 2n because
and |G| = 2n because ![]() has index 2 in G. As for Dn, we abstract this situation as follows.
has index 2 in G. As for Dn, we abstract this situation as follows.
If n = 2m, m ≥ 1, the dicyclic group Qn is the group of order 2n presented as
Qn = {1, a, ![]() , an−1, b, ba,
, an−1, b, ba, ![]() , ban−1}, where o(a) = n, aba = b, and b2 = am.
, ban−1}, where o(a) = n, aba = b, and b2 = am.
The condition that |Qn| = 2n amounts to the requirement that ![]() The group Qn is presented just like Dn, except that here n = 2m must be even and b2 = am (recall that b2 = 1 in the dihedral case). Again, akbak = b for all
The group Qn is presented just like Dn, except that here n = 2m must be even and b2 = am (recall that b2 = 1 in the dihedral case). Again, akbak = b for all ![]() so
so
akb = ba−k = ban−k, for all ![]()
This equation shows that (bak)2 = b2 = am for all k so, as |am| = 2, we get
|bak| = 4, for all ![]()
(in contrast to |bak| = 2 in Dn). Two of these dicyclic groups are already familiar, as we see in Example 10.
Example 10. Q2 ≅ C4 because |Q2| = 4. We claim that Q4 ≅ Q, the quaternion group (Section 2.8). Indeed Q = { ± 1, ± i, ± j, ± k} and, writing a = i and b = j, we have o(a) = 4, aba = b, and b2 = a2. Hence Q ≅ Q4.
Theorem 4. Every group G of order 8 is isomorphic to one of C8, C4 × C2, C2 × C2 × C2, D4, or Q4 = Q.
Proof. If G is abelian, then G is isomorphic to one of C8, C4 × C2, or C2 × C2 × C2 by Example 8 §2.8 (or by Corollary 2 of Theorem 6 §7.2). If G is not abelian, then x2 = 1 cannot hold for all x ![]() G, so there exists a
G, so there exists a ![]() G, o(a) = 4. Write
G, o(a) = 4. Write ![]() If b ∉ K, then G = K ∪ Kb, and we claim that aba = b. Indeed bab−1
If b ∉ K, then G = K ∪ Kb, and we claim that aba = b. Indeed bab−1 ![]() K because K
K because K ![]() G, and o(bab−1) = o(a) = 4. As bab−1 ≠ a because G is not abelian, we get bab−1 = a−1; that is, aba = b. Hence, if o(b) = 2 for some b ∉ K, then G ≅ D4. Otherwise, o(b) = 4 for all b ∉ K. But then a2 is the only element of G of order 2, so b2 = a2 for all b ∉ K. Thus G ≅ Q4.
G, and o(bab−1) = o(a) = 4. As bab−1 ≠ a because G is not abelian, we get bab−1 = a−1; that is, aba = b. Hence, if o(b) = 2 for some b ∉ K, then G ≅ D4. Otherwise, o(b) = 4 for all b ∉ K. But then a2 is the only element of G of order 2, so b2 = a2 for all b ∉ K. Thus G ≅ Q4.
In order to determine the groups of order 12, we need Lemma 1.
Lemma 1. The only subgroup of Sn of index 2 is An.
Proof. If |Sn: K| = 2, then K ![]() Sn and |Sn/K| = 2, so σ2
Sn and |Sn/K| = 2, so σ2 ![]() K for all σ
K for all σ ![]() Sn. If σ is a 3-cycle, then σ3 = ε so σ = σ4
Sn. If σ is a 3-cycle, then σ3 = ε so σ = σ4 ![]() K. But An is generated by the 3-cycles (Lemma 4 §2.8), so An ⊆ K. This implies that An = K because |Sn: An| = 2.
K. But An is generated by the 3-cycles (Lemma 4 §2.8), so An ⊆ K. This implies that An = K because |Sn: An| = 2.
Theorem 5. Every group of order 12 is isomorphic to one of C12, C6 × C2, A4, D6, or Q6.
Proof. Let P and Q be Sylow subgroups with |P| = 3 and |Q| = 4. If G is abelian, G ≅ P × Q, so either G ≅ C3 × C4 ≅ C12 or G ≅ C3 × C2 × C2 ≅ C6 × C2. If G is nonabelian, there is a homomorphism θ: G → S4 with ker θ ⊆ P. If ker θ = {1}, then G ≅ A4 by Lemma 2. So assume P ![]() G. Similarly, we have ϕ: G → S3 with ker ϕ ⊆ Q. Write ker ϕ = L. Then L ≠ {1}, and L = Q implies that Q
G. Similarly, we have ϕ: G → S3 with ker ϕ ⊆ Q. Write ker ϕ = L. Then L ≠ {1}, and L = Q implies that Q ![]() G, so G ≅ P × Q is abelian. Hence |L| = 2, so LP ≅ L × P ≅ C6.
G, so G ≅ P × Q is abelian. Hence |L| = 2, so LP ≅ L × P ≅ C6.
So let a ![]() G have order 6 and write
G have order 6 and write ![]() If b ∉ K, then G = K ∪ Kb and aba = b, as in Theorem 4. Finally, b2
If b ∉ K, then G = K ∪ Kb and aba = b, as in Theorem 4. Finally, b2 ![]() K because |G/K| = 2, and it remains to show that b2 = 1 (G ≅ D6) or b2 = a3 (G ≅ Q6). If b2 = a or a5, then o(b) = 12 and G is abelian. If b2 = a2, then b3 = ba2 = a−2b = a4b, so b2 = a4, a contradiction. Hence b2 ≠ a2 and, similarly, b2 ≠ a4.
K because |G/K| = 2, and it remains to show that b2 = 1 (G ≅ D6) or b2 = a3 (G ≅ Q6). If b2 = a or a5, then o(b) = 12 and G is abelian. If b2 = a2, then b3 = ba2 = a−2b = a4b, so b2 = a4, a contradiction. Hence b2 ≠ a2 and, similarly, b2 ≠ a4.
These results, together with earlier work, enable us to describe all the groups of order 15 or less. If p is a prime, the only group of order p is Cp. There are two groups of order 2p: C2p and Dp (Theorem 3 §2.6). And there are two groups of order p2: ![]() and Cp × Cp (Theorem 7 §8.2). We have already described the groups of order 8 or 12, and the only group of order 15 is C15 (Exercise 4). This list describes every group of order at most 15. The description of the groups of order 16 is more complicated (there are 14), and the general problem of describing all groups of a given order is extremely difficult.93
and Cp × Cp (Theorem 7 §8.2). We have already described the groups of order 8 or 12, and the only group of order 15 is C15 (Exercise 4). This list describes every group of order at most 15. The description of the groups of order 16 is more complicated (there are 14), and the general problem of describing all groups of a given order is extremely difficult.93
We conclude this section with an elegant direct proof of Theorem 1. The argument requires a number-theoretic fact. Recall that the binomial coefficient nr is defined by ![]() for 0 ≤ r ≤ n.
for 0 ≤ r ≤ n.
Lemma 2. Let p be a prime and let m, n, and k be positive integers. Then pn divides m if and only if pn divides pkmpk.
Proof. Since pkmpk = pkm(pkm − 1) ![]() (pkm − i)
(pkm − i) ![]() [pkm − (pk − 1)]pk(pk − 1)
[pkm − (pk − 1)]pk(pk − 1) ![]() (pk − i)
(pk − i) ![]() [pk − (pk − 1)], it suffices to show that
[pk − (pk − 1)], it suffices to show that
pn divides (pkm − i) ![]() pn divides (pk − i) for each i = 1, 2, . . ., pk − 1.
pn divides (pk − i) for each i = 1, 2, . . ., pk − 1.
Observe that if pn divides (pkm − i) then n < k (otherwise pk|i). Hence, the proof is completed by the observation that (pkm − i) = (pkm − pk) + (pk − i).
With this we can give Helmut Wielandt's elegant proof94 of Theorem 1, which does not use induction or Cauchy's theorem (and so provides another proof of Cauchy's theorem).
Proof of Theorem 1. If pk divides |G|, let X = {U ⊆ G ![]() U a subset, |U| = pk} and define an action of G on X by a · U = aU for all U in X and a in G. Given U in X, let S(U) = {a
U a subset, |U| = pk} and define an action of G on X by a · U = aU for all U in X and a in G. Given U in X, let S(U) = {a ![]() G
G ![]() aU = U} denote the stabilizer. Write |G| = pkm and write
aU = U} denote the stabilizer. Write |G| = pkm and write ![]() where p does not divide
where p does not divide ![]()
Claim. V in X exists such that pr+1 does not divide |G: S(V)|.
Proof. If not, pr+1 divides the order of every orbit in X (by Lemma 3 §8.3) and so divides |X|. But |X| = pkmpk, which means that pr+1 divides m by Lemma 3. Hence ![]() a contradiction. This proves the Claim.
a contradiction. This proves the Claim.
Now let V be as in the claim and write S = S(V). We show that |S| = pk, so S is the desired subgroup of G. Now pr+1 does not divide ![]() by the Claim, from which pk does divide |S|. In particular, pk ≤ |S|. But if
by the Claim, from which pk does divide |S|. In particular, pk ≤ |S|. But if ![]() then Sv ⊆ V by the definition of S, so |S| = |Sv| ≤ |V| = pk. Thus |S| = pk, as required.
then Sv ⊆ V by the definition of S, so |S| = |Sv| ≤ |V| = pk. Thus |S| = pk, as required.
Peter Ludvig Mejdell Sylow (1832–1918) Sylow was born in Norway and spent most of his professional life as a high school teacher in Halden. Despite onerous teaching duties, he found time to study the works of Abel and, in 1862–1863, he gave lectures on Galois theory and permutation groups at Christiania University in Oslo. The Sylow theorems were published in 1872 for permutation groups (Georg Frobenius extended them to abstract groups in 1887). These theorems are among the most important results on finite groups. Sylow applied them to show that any equation whose Galois group has prime-power order is solvable in radicals.
In addition to his study of groups, Sylow spent eight years editing the works of Abel. After his retirement from teaching high school, he was appointed to a chair at Christiania University, a position he held for the rest of his life.
Exercises 8.4
1. Find all Sylow 3-subgroups of S4 and show explicitly that all are conjugate.
2. Find all Sylow 2-subgroups of Dn, where n is odd, and show explicitly that all are conjugate.
3. If P is a Sylow p-subgroup of G, prove that it is the only Sylow p-subgroup of N(P).
4. Show that every group of order 15 is cyclic.
5. Show that there is only one group of order 1001.
6. Show that there are exactly two groups of order 99.
7. Show that a group G is not simple if
![]()
8. Show that no group of order 520 is simple.
9. Show that G has a cyclic normal subgroup of index 2 if
![]()
10. Show that G has a cyclic normal subgroup of index 5 if
![]()
11. (a) Show that G has a cyclic normal subgroup of index 3 if |G| = 105. (b) Show that G has an abelian normal subgroup of index 4 if |G| = 700.
12. If |G| = pq, where p < q are primes and p does not divide q − 1, show that G is cyclic.
13. If |G| = pnm, where n ≥ 1, p is a prime, and p > m, show that the Sylow p-subgroup of G is normal in G.
14. If |G| = p2q, where p and q are primes, show that G is not simple.
15. If P is a normal Sylow p-subgroup of a finite group G, show that P is fully invariant in G; that is, α(P) ⊆ P for every homomorphism α: G → G.
16. Let P ![]() H and H
H and H ![]() G. If P is a Sylow subgroup of G, show that P
G. If P is a Sylow subgroup of G, show that P ![]() G.
G.
17. If P is a Sylow p-subgroup of G, show that [N(P)]/P has no element of p-power order except the unity.
18. If P is a Sylow p-subgroup of G, let N(P) ⊆ H, H a subgroup of G.
a. Show that N(H) = H. [Hint: If a ![]() N(H), show that aPa−1 ⊆ H and use Sylow's second theorem.]
N(H), show that aPa−1 ⊆ H and use Sylow's second theorem.]
b. Show that p does not divide |G: H|.
19. If N(P) = P for some Sylow p-subgroup P of G, show that N(Q) = Q for every Sylow p-subgroup Q of G.
20. Suppose that N(P) = P for some Sylow p-subgroup of the finite group G. Show that G/G′ is an (abelian) p-group. [Hint: If q ≠ p is a prime divisor of |G/G′|, use Theorems 4 §7.2 and 8 §8.2 to find a subgroup H/G′ of index q in G/G′. If Q is a Sylow p -subgroup of H, show that N(Q) = Q by Exercise 18 and apply Exercise 19.]
21. Let K denote the intersection of all the Sylow p-subgroups of a finite group G. Show that K is a normal p-subgroup of G that contains every normal p-subgroup of G.
22. If n = 2m and m ≥ 2, show that Z(Qn) = {1, am}.
23. If k|n, k ≥ 4, and k is even, show that Qn has a subgroup isomorphic to Qk.
24. If k|n, k is even, and n/k is odd, show that K ![]() Qn exists such that Qn/K ≅ Qk.
Qn exists such that Qn/K ≅ Qk.
25. Show that, if G is a nonabelian group and 1 < |G| < 60, then G is not simple. (Of course, |A5| = 60 and A5 is simple).
There is no doubt that forming direct products is an important method of constructing groups using smaller groups: For example, all finite abelian groups can be constructed by forming direct products of cyclic groups. In this brief section, we describe a more general way to form a group from smaller groups.
Let K and H be subgroups of a group G and assume that G = KH, where K ∩ H = {1}. If both K ![]() G and H
G and H ![]() G then G ≅ K × H by Theorem 3 §8.1. In view of this, a natural question is what happens if only one of K and H is normal in G, say K
G then G ≅ K × H by Theorem 3 §8.1. In view of this, a natural question is what happens if only one of K and H is normal in G, say K ![]() G. Since G = KH and K ∩ H = {1}, each element g
G. Since G = KH and K ∩ H = {1}, each element g ![]() G has a unique representation as g = kh where k
G has a unique representation as g = kh where k ![]() K and h
K and h ![]() H. Given another element g1 = k1h1 of G, the key to understanding the group G is to describe the product gg1 in the same form. This can be accomplished as follows:
H. Given another element g1 = k1h1 of G, the key to understanding the group G is to describe the product gg1 in the same form. This can be accomplished as follows:
gg1 = khk1h1 = [k(hk1h−1)](hh1),(*)
where hk1h−1 ![]() K because K
K because K ![]() G.
G.
To describe this more formally, let a ![]() G and define a map σa: K → K by σa(k) = aka−1 for all k
G and define a map σa: K → K by σa(k) = aka−1 for all k ![]() K. This makes sense because K
K. This makes sense because K ![]() G, and σa is an automorphism of K for each a
G, and σa is an automorphism of K for each a ![]() G. Hence (*) becomes
G. Hence (*) becomes
(kh)(k1h1) = [k σh(k1)](hh1).(**)
Now observe that the map θ: H → aut(K) given by θ(h) = σh is a group homomorphism.95 This provides a way to turn this around: Starting with K, H, and θ, we can recreate G, using (**) to motivate the multiplication.
Theorem 1. Let K and H be groups and let θ: H → aut K be a homomorphism. Write θ(h) = σh for all h ![]() H. If G = K × H is the cartesian product, define an operation on G as follows:
H. If G = K × H is the cartesian product, define an operation on G as follows:
(k, h)(k1, h1) = (k σh(k1), hh1), for all (k, h) and (k1, h1) in G.
Write K1 = K × 1 and H1 = 1 × H. Then:
1. G is a group using this operation with unity (1K, 1H) and inverses given by ![]()
2. Then K1 and H1 are subgroups of G, with K1 ≅ K and H1 ≅ H.
3. G = K1H1, K1 ![]() G and K1 ∩ H1 = {1}.
G and K1 ∩ H1 = {1}.
Proof. (2) and (3) are routine verifications. As to (1), the operation is associative because the products [(k, h)(k1, h1)](k2, h2) and (k, h)[(k1, h1)(k2, h2)] each simplify to ![]() hh1h2). The verification of this, and of the rest of (1), is left to the reader.
hh1h2). The verification of this, and of the rest of (1), is left to the reader.
If K and H are groups and θ: H → aut K is a homomorphism, the group G constructed in Theorem 1 is called the semidirect product of K by H, and is denoted K × θH. Theorem 1, and the discussion preceding it, give an important characterization of semidirect products (often taken as the definition).
Theorem 2. Let G be a group.
1. G is a semidirect product if and only if it has subgroups K and H with G = KH, K ![]() G and K ∩ H = {1}.
G and K ∩ H = {1}.
2. In that case, G ≅ K × θH for some homomorphism θ: H → aut K. Indeed, θ(h) is (the restriction to K of) conjugation by h for each h ![]() H.
H.
Example 1. A direct product K × H is a semidirect product (let θ: H → aut K be the trivial homomorphism: θ(h) = 1K for each h ![]() H).
H).
Example 2. The dihedral group Dn = {1, a, . . ., an−1, b, ba, . . ., ban−1} is given by o(a) = n, o(b) = 2 and aba = b. If we write ![]() and
and ![]() then it is clear that Dn = KH, K
then it is clear that Dn = KH, K ![]() Dn (it has index 2) and K ∩ H = {1}, so
Dn (it has index 2) and K ∩ H = {1}, so
Dn ≅ Cn × θC2 for some θ: C2→ aut Cn.
In fact, the multiplication in Dn is given by akb = ba−k for all k, so bakb−1 = (ak)−1. Hence θ: C2→ aut Cn, where θ(b) is the automorphism x ![]() x−1.
x−1.
It is interesting to observe that D6 ≅ C3 × θC2 by Example 2, and C6 ≅ C3 × θC2 by Example 1. Hence, a semidirect product K × θH is not uniquely determined by K and H; the homomorphism θ must be specified.
The next result determines all groups of order pq where p and q are primes. The theorem illustrates the way that semidirect products can be used to give the detailed structure of all groups of a given order, and it extends the theorem (Theorem 3 §2.6) that every group of order 2p is either cyclic or dihedral.
Theorem 3. Let G be a group of order pq where p ≤ q are primes.
(1) If p = q then G is cyclic or G ≅ Cp × Cp.
(2) If p < q and q6 ≡ 1 (mod p) then G is cyclic.
(3) If p < q and q ≡ 1 (mod p) then either G is cyclic or ![]() whereo(a) = q, o(b) = p and ab = bam, and where 1 ≤ m ≤ q − 1 and mp ≡ 1 (mod q). [Here, all choices for m result in isomorphic groups.]
whereo(a) = q, o(b) = p and ab = bam, and where 1 ≤ m ≤ q − 1 and mp ≡ 1 (mod q). [Here, all choices for m result in isomorphic groups.]
Proof. By Cauchy's theorem, choose a, b ![]() G such that o(a) = q and o(b) = p, and write
G such that o(a) = q and o(b) = p, and write ![]() and
and ![]() Then K
Then K ![]() G by the Corollary to Theorem 1 §8.3. Clearly K ∩ H = {1}, so G = KH and it follows that G is a semidirect product by Theorem 2.
G by the Corollary to Theorem 1 §8.3. Clearly K ∩ H = {1}, so G = KH and it follows that G is a semidirect product by Theorem 2.
(1) This is Theorem 7 §8.2.
(2) As usual, let np denote the number of Sylow p-subgroups of G. Then Sylow's third theorem (Theorem 3 §8.4) gives np ≡ 1 (mod p) and np ![]() q. Hence if q6 ≡ 1 (mod p) then np = 1, so H
q. Hence if q6 ≡ 1 (mod p) then np = 1, so H ![]() G, and we have G ≅ K × H ≅ Cq × Cp ≅ Cpq.
G, and we have G ≅ K × H ≅ Cq × Cp ≅ Cpq.
(3) So assume q ≡ 1 (mod p). Since ![]() let
let
b−1ab = ax where ![]() (*)
(*)
Then ![]() Continuing in this way gives
Continuing in this way gives
![]() , for any k ≥ 1.
, for any k ≥ 1.
But bp = 1 so this gives ![]() and hence xp ≡ 1 (mod q). Since
and hence xp ≡ 1 (mod q). Since ![]() let
let ![]() have order p (by Cauchy's theorem). Then x = 1, m, m2, . . ., mp−1 are all solutions to xp ≡ 1 (mod q). Moreover, there are no other solutions because xp − 1 = 0 has at most p roots in
have order p (by Cauchy's theorem). Then x = 1, m, m2, . . ., mp−1 are all solutions to xp ≡ 1 (mod q). Moreover, there are no other solutions because xp − 1 = 0 has at most p roots in ![]() If x = 1 in (*) then ba = ab so G is abelian, and hence cyclic. If x = m in (*) then b−1ab = am so ab = bam and we have the situation in (3).
If x = 1 in (*) then ba = ab so G is abelian, and hence cyclic. If x = m in (*) then b−1ab = am so ab = bam and we have the situation in (3).
Finally, to realize the other solutions x = mr where 1 < r ≤ p − 1, we change the generators of G. If we put b1 = br then o(b1) = p and ![]() because o(b) = p is a prime. Hence
because o(b) = p is a prime. Hence ![]() Furthermore,
Furthermore, ![]() so this construction realizes the solution when x = mr in (*).
so this construction realizes the solution when x = mr in (*).
Other such theorems are possible, but we conclude by identifying one quite general situation in which a finite group G is necessarily a semidirect product, namely if G has a normal subgroup K and ![]() and
and ![]() are relatively prime. The next result of Issai Schur deals with the case when K is abelian.
are relatively prime. The next result of Issai Schur deals with the case when K is abelian.
Theorem 4. Schur's Theorem. Suppose G has an abelian normal subgroup K, where ![]() and
and ![]() are relatively prime. Then G has a subgroup of order
are relatively prime. Then G has a subgroup of order ![]()
Proof. Put ![]() and
and ![]() In each coset a of G/K select an element ga
In each coset a of G/K select an element ga ![]() G and assume that g1 = 1, where 1 denotes the unity of G/K. If a, b
G and assume that g1 = 1, where 1 denotes the unity of G/K. If a, b ![]() G/K then gagb = gabk(a, b) for a uniquely determined element k(a, b)
G/K then gagb = gabk(a, b) for a uniquely determined element k(a, b) ![]() K. If ga(gbgc) = (gagb)gc is written out it follows that
K. If ga(gbgc) = (gagb)gc is written out it follows that
k(a, bc) k(b, c) = k(ab, c) ![]() a, b)gc].(*)
a, b)gc].(*)
Now write k(b) = ∏ a![]() G/Kk(a, b). If the product of each side of equation (*) is taken as a ranges over G/K, we obtain (since K is abelian)
G/Kk(a, b). If the product of each side of equation (*) is taken as a ranges over G/K, we obtain (since K is abelian)
![]()
Now let nn′ ≡ 1 (mod m) and write k(a ![]() for all a
for all a ![]() G/K. Raising both sides of (**) to the power −n′ yields
G/K. Raising both sides of (**) to the power −n′ yields
(***) ![]()
Finally, write H ={gaka ![]() a
a ![]() G/K}, Then () gives
G/K}, Then () gives
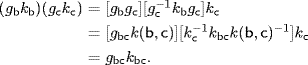
This means that H is a subgroup and that the map a ![]() gaka is an onto homomorphism G/K → H. It is one-to-one because gaka = gbkb implies that
gaka is an onto homomorphism G/K → H. It is one-to-one because gaka = gbkb implies that ![]() so ga = gb by the choice of these elements.
so ga = gb by the choice of these elements.
Along with I. Schur, H. Zassenhaus is also credited with the general version of the next theorem.96
Theorem 5. Schur-Zassenhaus Theorem. Let G be a group of order kn where k and n are relatively prime. Assume that G has a normal subgroup K of order k. Then G has a subgroup H of order n, and so is a semidirect product K × θH.
Proof. It suffices to show that H exists (then K ∩ H = {1} because the orders are relatively prime, and hence G = KH. We may assume that k > 1. The proof is by induction on ![]()
Case 1. K contains a proper subgroup M such that M ![]() G.
G.
Write ![]() Then
Then ![]() K/M
K/M ![]() G/M, and
G/M, and ![]() so G/M has a subgroup L/M of order n (by induction). But then
so G/M has a subgroup L/M of order n (by induction). But then ![]() M
M ![]() L and
L and ![]() so L contains a subgroup of order n (again by induction). Hence, the theorem is proved in this case.
so L contains a subgroup of order n (again by induction). Hence, the theorem is proved in this case.
Case 2. K contains no proper subgroup that is normal in G.
In this case let P be a Sylow p-subgroup of K, and let N = N(P) be the normalizer of P in G. Then P is a Sylow p-subgroup of G (because gcd(k, n) = 1), and so has ![]() conjugates in G. These are all in K so, as N ∩ K is the normalizer of P in K, we obtain
conjugates in G. These are all in K so, as N ∩ K is the normalizer of P in K, we obtain ![]() Hence
Hence ![]() so
so ![]() Consequently NK = G and so N/(N ∩ K) ≅ G/K has order n.
Consequently NK = G and so N/(N ∩ K) ≅ G/K has order n.
If it happens that N ≠ G this shows that N contains a subgroup of order n (by induction), and we are done. So assume that N = G. This means that P ![]() G, and hence that Z
G, and hence that Z ![]() G where Z is the center of P (being characteristic in P, see Corollary 3 of Theorem 3 §2.8). Since Z ≠ 1 by Theorem 6 §8.2, it follows that Z = K (we are in Case 2). Thus, K is abelian and we are done by Schur's theorem (Theorem 4).
G where Z is the center of P (being characteristic in P, see Corollary 3 of Theorem 3 §2.8). Since Z ≠ 1 by Theorem 6 §8.2, it follows that Z = K (we are in Case 2). Thus, K is abelian and we are done by Schur's theorem (Theorem 4).
Exercises 8.5
1.
a. Show that Sn ≅ An × θC2 for some θ.
b. Show that the following is false: If K is a maximal subgroup that is normal, in G, then G ≅ K × θH for some H and θ. [Hint: The quaternion group.]
2. Find all groups of order 55.
3. Find all groups of order 39.
4. Show that there are two nonisomorphic groups of order 105. [Hint: Exercise 11(a) §8.4.]
5. Show that there are four nonisomorphic groups of order 30: C30, D15, D5 × C3, and D3 × C5. [Hint: Find a normal subgroup of index 2.]
6. Let α: G → H be a group homomorphism, and write ker (α) = K. If there exists β: H → G such that αβ = 1H, show that G ≅ K × θH for some θ.
8.6 An Application to Combinatorics
A main theme in this chapter has been to apply counting arguments to gain information about a finite group G by defining G-sets and using the orbit decomposition theorem. In this section, we turn this successful technique around and use the group to gain information about the sets it acts on. Specifically, we get a formula for the number of distinct orbits, which is useful in solving certain combinatorial problems. We begin by deriving this formula that is of interest in its own right, and then describing how it applies to combinatorics.
If X is any G-set and x ![]() X, the stabilizer of x in X is the subgroup
X, the stabilizer of x in X is the subgroup
S(x) = {a ![]() G
G ![]() a · x = x}
a · x = x}
of all elements of G that fix x. Dually, if a ![]() G we write
G we write
F(a) = {x ![]() X
X ![]() a · x = x},
a · x = x},
the set of elements of X fixed by a. We refer to these sets frequently because of the following result of Cauchy and Frobenius.
Theorem 1. Cauchy-Frobenius Lemma. 97 Let X be a G -set and assume that G and X are finite. If n is the number of distinct orbits of G in X, then
n = 1|G| ∑ a![]() G|F(a)|.
G|F(a)|.
Proof. The proof proceeds by the time-honored method of counting the elements of a set Y in two ways and equating the results. In this case, consider the subset Y = {(a, x) ![]() x
x ![]() X, a
X, a ![]() G, a · x = x} of G × X. Then
G, a · x = x} of G × X. Then
|Y| = ∑ a![]() G|F(a)|(*)
G|F(a)|(*)
because, for each element a of G, there are exactly |F(a)| pairs in Y with first component a. In the same way, we obtain
|Y| = ∑ x![]() X|S(x)|.
X|S(x)|.
However, we can refine this second sum because X is partitioned into orbits by the action of G. If G · x1, . . ., G · xn are the n distinct orbits, then each x ![]() X belongs to exactly one orbit G · xi, so
X belongs to exactly one orbit G · xi, so
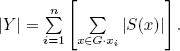 (**)
(**)
Now recall that |G · x| = |G: S(x)| holds for all x ![]() X (Lemma 3 §8.3). If x
X (Lemma 3 §8.3). If x ![]() G · xi, then G · x = G · xi and so |S(x)| = |S(xi)|. Hence (**) becomes
G · xi, then G · x = G · xi and so |S(x)| = |S(xi)|. Hence (**) becomes
![]()
Combining this with (*) gives n|G| = |Y| = ∑ a![]() G|F(a)|. The lemma follows.
G|F(a)|. The lemma follows.
As an illustration, let G act on itself by conjugation, so the orbits are the conjugacy classes. If a ![]() G, then F(a) = {x
G, then F(a) = {x ![]() G
G ![]() axa−1 = x} = N(a) is the normalizer of a in G. Thus, the Cauchy–Frobenius lemma gives the following Corollary.
axa−1 = x} = N(a) is the normalizer of a in G. Thus, the Cauchy–Frobenius lemma gives the following Corollary.
Corollary. A finite group G has (1/|G|) ∑ a![]() G|N(a)| distinct conjugacy classes.
G|N(a)| distinct conjugacy classes.
Before applying the Cauchy–Frobenius lemma, we must consider a technicality. If G is a group and X is a nonempty set, a function X × G → X, written (x, g) ![]() x · g, is called a right action of G on X if x · 1 = x and (x · a) · b = x · (ab) hold for all a, b
x · g, is called a right action of G on X if x · 1 = x and (x · a) · b = x · (ab) hold for all a, b ![]() G and all x
G and all x ![]() X. Clearly, all the results for G -sets can be proved for right actions. In fact, we can easily verify that a * x = x · a−1 defines a (left) action of F on X. The reason for mentioning this is that right actions occur naturally in the examples that follow.
X. Clearly, all the results for G -sets can be proved for right actions. In fact, we can easily verify that a * x = x · a−1 defines a (left) action of F on X. The reason for mentioning this is that right actions occur naturally in the examples that follow.
The combinatorial applications in which we are interested can all be described using the following format. Let D and C be nonempty finite sets and let CD denote98 the set of all mappings λ: D → C. Suppose that G is a subgroup of SD. Given σ ![]() G and λ
G and λ ![]() CD, we have D → σD → λC, so it is natural to define
CD, we have D → σD → λC, so it is natural to define
λ · σ = λσ = the composition of the maps.
This is a right action of G on the permutation group CD (the axioms are elementary properties of composition of mappings), and it plays a central role in our discussion. Example 1 is typical.
Example 1. If q colors are available, find the number of ways in which a pyramid can be painted if the edges of the base are all of length 1 and the sides are of length 2. Assume that each face is painted a single color.
Solution. Label the faces 1, 2, 3, and 4 as shown in the figure at the right. Then the labeled pyramid can be colored in q4 ways because there are q color choices for each face. The problem is that many of these colorings are indistinguishable when the labels are removed. The reason is that one labeled coloring may be carried to another by a motion of the pyramid, so both result in the same unlabeled coloring. To make this more precise, let

D = {1, 2, 3, 4} and C = the set of q colors.
Then each map λ: D → C determines a labeled coloring, the color of face i being λ(i). Conversely, each labeled coloring determines such a map, so we may identify CD with the set of labeled colorings. Now let G ⊆ SD = S4 be the group of motions of the pyramid, where a motion is identified with the permutation of the face labels that it induces. Then G acts on CD on the right as discussed previously, and we claim that the unlabeled colorings can be identified with the orbits of G in the set CD of labeled colorings. Indeed, if λ and μ are labeled colorings in CD, then
λ and μ lead to indistinguishable colorings when the labels are removed;
![]() λ is achieved by first moving the pyramid and then applying μ;
λ is achieved by first moving the pyramid and then applying μ;
![]() λ = μσ for some σ
λ = μσ for some σ![]() G;
G;
![]() λ and μ are in the same G -orbit.
λ and μ are in the same G -orbit.
Hence, the number of unlabeled colorings is equal to the number of orbits, so the Cauchy–Frobenius lemma applies. In this case G = {ε, σ, σ2}, where σ = (234). We have F(ε) = CD, so |F(ε)| = q4. Next,
F(σ) = {λ ![]() λσ = λ} = {λ
λσ = λ} = {λ ![]() λ(2) = λ(3) = λ(4)}.
λ(2) = λ(3) = λ(4)}.
Hence a coloring λ is in F(σ) just when sides 2, 3, and 4 are all the same color. We may choose this color in q ways and color the base in q ways, so |F(σ)| = q2. Similarly, |F(σ2)| = q2, so the number of orbits is ![]() by Theorem 1.
by Theorem 1.
The technique used in Example 1 can be used in the same way to count the number of ways to color the edges or vertices of a figure. In general, we label the objects to be colored as 1, 2, 3, . . ., n. The group G is the subgroup of Sn consisting of all permutations of these objects resulting from a rigid motion of the figure. We then identify the colorings with the set CD of all mappings from D = {1, 2, . . ., n} to the set C of colors. If λ is such a map and σ ![]() G, the map λσ colors object i the same as the map λ colors object σ(i). As σ is a motion of the figure, the results are indistinguishable when the labels are removed, so the number of distinguishable unlabeled colorings equals the number of orbits (as in Example 1). Hence, the Cauchy–Frobenius lemma applies.
G, the map λσ colors object i the same as the map λ colors object σ(i). As σ is a motion of the figure, the results are indistinguishable when the labels are removed, so the number of distinguishable unlabeled colorings equals the number of orbits (as in Example 1). Hence, the Cauchy–Frobenius lemma applies.
Before giving more examples, we describe a convenient way to compute |F(σ)| in the Cauchy–Frobenius lemma, where σ ![]() Sn, D = {1, 2, . . ., n}, and Sn acts on CD, as before. If σ is factored into disjoint cycles, we customarily ignore a cycle (k) of length 1 because σ fixes k. However, our present purpose requires that we include such cycles.
Sn, D = {1, 2, . . ., n}, and Sn acts on CD, as before. If σ is factored into disjoint cycles, we customarily ignore a cycle (k) of length 1 because σ fixes k. However, our present purpose requires that we include such cycles.
For example, if n = 7, we now think of σ = (14)(357) in S7 as a product of four disjoint cycles: σ = (14)(2)(357)(6). If q colors are available in C, we claim that |F(σ)| = q4. Indeed, given λ: D → C, we have
λ ![]() F(σ)
F(σ) ![]() λσ = λ
λσ = λ ![]() λ(1) = λ(4) and λ(3) = λ(5) = λ(7),
λ(1) = λ(4) and λ(3) = λ(5) = λ(7),
so there are q choices for each of the colors λ(1) = λ(4), λ(2), λ(3) = λ(5) = λ(7), and λ(6) and hence q4 possibilities for the map λ.
The obvious generalization is valid. If σ ![]() Sn, then |F(σ)| = qc, where c is the number of cycles in the factorization in Sn of σ into disjoint cycles (including cycles of length 1). The integer c is called the cycle index of σ and is denoted c = cycσ. We record this as Theorem 2.
Sn, then |F(σ)| = qc, where c is the number of cycles in the factorization in Sn of σ into disjoint cycles (including cycles of length 1). The integer c is called the cycle index of σ and is denoted c = cycσ. We record this as Theorem 2.
Theorem 2. Let C be a set of q colors and let Sn act on CD by composition of maps, where D = {1, 2, . . ., n}. Then
|F(σ)| = qcycσfor any σ ![]() Sn.
Sn.
If G is a subgroup of Sn, the number of orbits of G in CD is
(1/|G|) ∑ σ![]() Gqcycσ.
Gqcycσ.
Example 2. Suppose that a chemical molecule is modeled in the form of an equilateral triangle with the atoms at the vertices as shown in the figure below. If q colors are available and each atom is painted a single color, how many distinct ways can the molecule be colored? (The edges are not painted.)
Solution. Here the three vertices, labeled 1, 2, and 3, are permuted by motions in S3. Because of the high degree of symmetry of the equilateral triangle, every permutation in S3 can be achieved by a motion, so S3 is the group of motions. By Theorem 2 we get
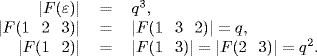
By Theorem 1 there are ![]() colorings (orbits).
colorings (orbits).
In Example 3, we vary the theme by insisting that no color is repeated. This amounts to labeling the various facets of the object with distinct colors.
Example 3. Suppose that children's blocks are to be constructed as cubes with each of the six faces painted a different color. If q ≥ 6 colors are available, how many distinct blocks can be made?
Solution. Let D = {1, 2, 3, 4, 5, 6} and let C be the set of q colors, as before. Because the faces are distinct colors, a coloring in this case is a one-to-one mapping λ: D → C. Let X ⊆ CD denote the set of all such mappings. If G is the group of motions of the cube, G acts on X by composition because λσ is one-to-one whenever σ ![]() G and λ
G and λ ![]() X. If σ ≠ ε in G, then F(σ) = {λ
X. If σ ≠ ε in G, then F(σ) = {λ ![]() λσ = λ} is empty. (If λ
λσ = λ} is empty. (If λ ![]() F(σ), then σ(i) = j implies that λ(j) = λ[σ(i)] = λ(i), from which i = j). Thus |F(σ)| = 0 if σ ≠ ε, whereas |F(ε)| = q !/[(q − 6) !] because F(ε) = X. Hence, the Cauchy–Frobenius lemma gives the number of colorings as q !/[|G|(q − 6) !], so it remains only to compute |G|. Label the faces of the cube 1, 2, 3, 4, 5, and 6. If we initially place the cube with side 1 on top, we determine a motion by choosing which side ends up on top (six choices) and then choosing one of four rotations fixing the top and bottom faces (four choices). Thus, there are 6 · 4 = 24 choices in all, so |G| = 24 and there are q / [24(q − 6) !] possible blocks. If q = 6 (the minimal number of colors), there are 6 !/‘ 24 = 30 possible blocks.
F(σ), then σ(i) = j implies that λ(j) = λ[σ(i)] = λ(i), from which i = j). Thus |F(σ)| = 0 if σ ≠ ε, whereas |F(ε)| = q !/[(q − 6) !] because F(ε) = X. Hence, the Cauchy–Frobenius lemma gives the number of colorings as q !/[|G|(q − 6) !], so it remains only to compute |G|. Label the faces of the cube 1, 2, 3, 4, 5, and 6. If we initially place the cube with side 1 on top, we determine a motion by choosing which side ends up on top (six choices) and then choosing one of four rotations fixing the top and bottom faces (four choices). Thus, there are 6 · 4 = 24 choices in all, so |G| = 24 and there are q / [24(q − 6) !] possible blocks. If q = 6 (the minimal number of colors), there are 6 !/‘ 24 = 30 possible blocks.
The argument in Example 3 gives the general result in Theorem 3.
Theorem 3. Let D = {1, 2, . . ., n}, let C be a set of q ≥ n colors, and let X ⊆ CD denote the set of one-to-one mappings D → C. If G is a subgroup of Sn, then G acts on X by composition of maps, and the number of orbits is q !/[|G|(q − n) !].
Needless to say, this theory has been developed further, and these examples provide only a glimpse of the possibilities. For example, we could ask how many ways a cube can be painted with q colors when exactly two faces are red or when at least two faces are red. In 1937, George Polya answered such questions, and many others, by giving an elegant and comprehensive generalization of the Cauchy–Frobenius lemma.99 This is beyond the scope of this book.
Exercises 8.6
1. If H is a subgroup of a finite group G, use the Cauchy–Frobenius lemma to compute the number of distinct right cosets of H in G.
2. Verify the Corollary to the Cauchy–Frobenius lemma when G = S3.
3.
a. If q colors are available, show that there are ![]() ways to paint the vertices of an isosceles triangle (not equilateral).
ways to paint the vertices of an isosceles triangle (not equilateral).
b. Derive the formula in (a) by using elementary counting methods.
4.
a. If q colors are available, show that there are ![]() ways to paint the faces of a tetrahedron (four faces, each an equilateral triangle). [Hint: Example 3 §2.7.]
ways to paint the faces of a tetrahedron (four faces, each an equilateral triangle). [Hint: Example 3 §2.7.]
b. Repeat (a) if q ≥ 4 and no two faces are the same color.
5.
a. If q colors are available, show that there are ![]() ways to paint the faces of a rectangular solid with square ends (not a cube).
ways to paint the faces of a rectangular solid with square ends (not a cube).
b. Repeat (a) if q ≥ 6 and no two faces are the same color.
6. If q colors are available, how many ways can
a. the vertices of a tetrahedron be painted?
b. the edges of a tetrahedron be painted?
7. How many ways can the faces of a cube be painted with q colors? [Hint: The group G of motions has |G| = 24. Here G consists of ε and various rotations: nine about a line through the centers of opposite faces, six about a line through the centers of opposite edges, and eight about a line through opposite vertices.]
8.
a. A circular disk is divided into six equal sections, as shown in the figure at the right. If q colors are available, how many ways can one side of the disk be painted if each section is painted a single color? How many if no two sections are the same color.
b. Repeat (a) if the sections are made of transparent glass and the circle can be turned over.

9. Show that there are 12[qn + q![]() (n+1)/2
(n+1)/2![]() ] ways to make a rectangular necktie with n stripes if there are q colors. (Here
] ways to make a rectangular necktie with n stripes if there are q colors. (Here ![]() k
k![]() denotes the greatest integer ≤k.)
denotes the greatest integer ≤k.)
10. Assume that q colors are available for painting the vertices and r colors are available for painting the edges of an equilateral triangle. Show that there are ![]() ways to paint both edges and vertices. [Hint: A motion σ of the triangle induces a permutation
ways to paint both edges and vertices. [Hint: A motion σ of the triangle induces a permutation ![]() of the vertices and a permutation σe of the edges. Let σ act in the obvious way on pairs (λ, μ), where λ and μ are vertex and edge colorings, respectively.]
of the vertices and a permutation σe of the edges. Let σ act in the obvious way on pairs (λ, μ), where λ and μ are vertex and edge colorings, respectively.]
11. Repeat Exercise 10 with a planar figure as shown at the right, where the four outer edges have the same length and the inner edge is shorter.
12. If G is a finite group, let p(G) denote the probability that ab = ba, where a and b are selected at random (with replacement) from G.
a. Show that p(G) = [k(G)]/|G|, where k(G) is the number of distinct conjugacy classes of G.
b. Show that ![]() if G is nonabelian, with equality for a suitable group G of order 8.
if G is nonabelian, with equality for a suitable group G of order 8.
Notes
89 Such a subgroup H must in fact exist (see Theorem 1 §8.4).
90 An action on the right may be defined by ![]() . This is nothing new because
. This is nothing new because ![]() is then an action in the present sense.
is then an action in the present sense.
91 Another name for S(x) is the isotropy group of x.
92 American Mathematical Monthly, Vol. 66, 1956, p. 119.
93. A lot is known about the number of groups of order pn for a prime p. For example there are 2328 groups of order 27, and 9310 groups of order 37. See O'Brien, I.A. and Vaughan-Lee, M.R. Journal of Algebra 292 (2005), 243–258, for more information.
94 Wielandt, H., Ein Bewise Fur die Existenz der Sylowgruppen, Archiv der Mathematik 10 (1959), 401–402.
95 This amounts to saying that ![]() is an action of the group G on K. Such actions were studied in Section 8.3, where K was only required to be a set.
is an action of the group G on K. Such actions were studied in Section 8.3, where K was only required to be a set.
96 The result was credited to Schur by Zassenhaus in his book The Theory of Groups, 2nd English Edition, Chelsea, 1958.
97 The lemma was known to Cauchy and Frobenius in the mid-1800s, and was rediscovered by William Burnside in 1900. Hence, it is also called Burnside's lemma.
98 This exponential notation is used because ![]() .
.
99 For an exposition of Polya's theory (by N. G. de Bruijn), see Beckenbach, E., ed., Applied Combinatorial Mathematics, New York: Wiley, 1964. Another good treatment appears in Roberts, F.S., Applied Combinatorics, Englewood Cliffs, NJ. Prentice-Hall, 1984, Chapter 7.
