Appendices

Appendix A Complex Numbers

The set of real numbers has deficiencies. For example, the equation x² + 1 = 0 has no real root; that is, no real number u exists such that u² + 1 = 0. This type of problem also exists for the set of natural numbers. It contains no solution of the equation x + 1 = 0, and the set of integers was invented to solve such equations. But is also inadequate (for example, 2x − 1 = 0 has no root in ), and hence the set of rational numbers was invented. Again, contains no solution to x² − 2 = 0, so the set of real numbers was created. Similarly, the set of complex numbers was invented that contains a root of x² + 1 = 0. More precisely, there is a complex number i such that

i² = − 1.

However, the process ends here. The complex numbers have the property that every nonconstant polynomial with complex coefficients has a (complex) root. In 1799, at the age of 22, Carl Friedrich Gauss first proved this result, which is known as the Fundamental Theorem of Algebra. We give a proof in Section 6.6.

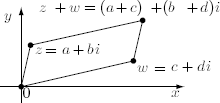
In this appendix, we describe the set of complex numbers. The set of real numbers is usually identified with the set of all points on a straight line. Similarly, the complex numbers are identified with the points in the euclidean plane by labeling the point with cartesian coordinates (a, b) as

(a, b) = a + bi.

Then the set of complex numbers is defined by

When this is done, the resulting Euclidean plane is called the complex plane.

Each real number a is identified with the point a = a + 0i = (a, 0) on the x-axis in the usual way, and for this reason the x-axis is called the real axis. The points

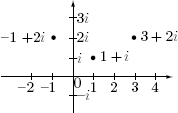
bi = 0 + bi = (0, b) on the y-axis are called imaginary numbers, and the y-axis is called the imaginary axis.¹³⁸ The diagram shows the complex plane and several complex numbers.

Identification of the complex number a + bi = (a, b) with the ordered pair (a, b) immediately gives the following condition for equality:

Equality Principle. a = bi = a′ + b′ i if and only if a = a′ and b = b′.

For a complex number z = a + bi, the real numbers a and b are called the real part of z and the imaginary part of z, respectively, and are denoted by a = rez and b = imz. Hence, the equality principle becomes as follows: Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal.

With the requirement that i² = − 1, we define addition and multiplication of complex numbers as follows:

These operations are analogous to those for linear polynomials a + bx, with one difference: i² = − 1. These definitions imply that complex numbers satisfy all the arithmetic axioms enjoyed by real numbers. Hence, they may be manipulated in the obvious fashion, except that we replace i² by −1 whenever it occurs.

Example 1. If z = 2 − 3i and

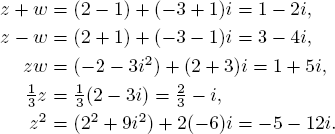
Example 2. Find all complex numbers z such that z² = − i.

Solution. Write z = a + bi, where a and b are to be determined. Then the condition z² = − i becomes

(a² − b²) + 2abi = 0 + (− 1)i.

Equating real and imaginary parts gives a² = b² and 2ab = − 1. The solution is

Theorem 1 collects the basic properties of addition and multiplication of complex numbers. The verifications are straightforward and left to the reader.

Theorem 1. If z, u, and are complex numbers, then

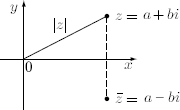
The following two notions are indispensable when working with complex numbers. If z = a + bi is a complex number, the conjugate and the absolute value (or modulus) |z| are defined by

Thus, is a complex number and is the reflec-tion of z in the real axis (see the diagram), whereas |z| is a nonnegative real number and equals the distance between z and the origin. Note that the absolute value of a real number a = a + 0i is using the definition of absolute value for complex num-bers, which agrees with the absolute value of a regarded as a real number.

Theorem 2. Let z and denote complex numbers. Then

Proof. (1) We prove (2), (5), and (7) and leave the rest to the reader. If z = a + bi and we compute

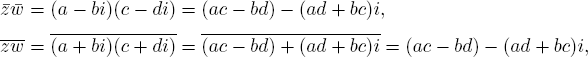
which proves (2). Next, (5) follows from

Finally (2) and (5) give

Then (7) follows when we take positive square roots.

Let z be a nonzero complex number. Then (6) of Theorem 2 shows that |z| ≠ 0, and so by (5). As a result, we call the complex number the inverse of z and denote it z⁻¹ = 1/z, which proves Theorem 3.

Theorem 3. If z = a + bi is a nonzero complex number, then z has an inverse given by

Hence, for real numbers, dividing by any nonzero complex number is possible. Example 3 shows how division is done in practice.

Example 3. Express in the form a + bi.

Solution. We multiply the numerator and denominator by the conjugate 2 − 5i of the denominator:

The addition of complex numbers has a geometric description. The diagram shows plots of the complex numbers z = a + bi and and their sum . These points, together with the origin, form the vertices of a parallelogram, so we can find the sum geometrically by completing the parallelogram. This method is the Parallelogram Law of Complex Addition and is a special case of vector addition, as students of linear algebra will recognize.

The geometric description of complex multiplication requires that complex num-bers be represented in polar coordinates. The circle with its center at the origin and radius 1 shown in the diagram below is called the unit circle. An angle θ measured counterclockwise from the real axis is said to be in standard po-sition. The angle θ determines a unique point P on this circle. The radian measure of θ is defined to be the length of the arc from 1 to P. Hence, the radian measure of a right angle is π/2 radians and that of a full circle is 2π radians. We define the cosine and sine of θ (written cos θ and sin θ) to be the x and y coordinates of P. Hence, P is the point (cos θ, sin θ) = cos θ + i sin θ in the complex plane. These complex numbers cos θ + i sin θ on the unit circle are denoted e^iθ = cos θ + i sin θ.

A complete discussion of why we use this notation lies outside the scope of this book.¹³⁹

The fact that e^iθ is actually an exponential function of θ is confirmed by verifying that the law of exponents holds, that is,

This law is analogous to the exponent rule e^ae^b = e^a+b for real exponents a and b, and it is an immediate consequence of the identities for sin (θ + ) and cos (θ + ):

We can now describe complex multiplication geometrically. We let z = a + bi be any complex number. The distance r from z to 0 is the modulus r = |z|. If z ≠ 0, it determines an angle θ, as shown in the diagram, called an argument of z. This angle is not unique (θ + 2πk would do as well for any k = 0, ± 1, ± 2, . . .,) but, as the diagram clearly shows,

always hold. Hence, in any case

This expression is the polar form of the complex number z. The geometric description of complex multiplication follows from the law of exponents.

Theorem 4. Multiplication Rule. If z = re^iθ and are two complex numbers in polar form, then

In other words, to multiply two complex numbers, simply multiply the absolute values and add the arguments. This method simplifies calculations and is valid for any arguments θ and .

Example 4. Multiply by first converting the factors to polar form.

Solution. The polar forms (see the diagram) are

Hence, the multiplication rule gives

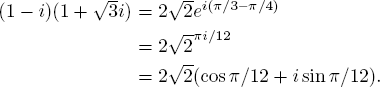
Of course, direct multiplication gives so equating real and imaginary parts gives the (somewhat unexpected) formulas

If z = re^iθ is given in polar form, z² = r²e^2iθ by the multiplication rule. Hence, z³ = (re^iθ)(r²e^2iθ) = r³e^3iθ. In general, we have Theorem 5 for any n ≥ 1 (we leave the proof for n ≤ 0 as Exercise 15(b)). The name honors Abraham DeMoivre (1667-1754).

Theorem 5. DeMoivre's Theorem. If θ is any angle and r > 0, then (re^iθ)ⁿ = rⁿe^inθ for all integers n.

Example 5. Verify that

The polar form is Hence DeMoivre's theorem gives

If n ≥ 1, a complex number u is called an nth root of unity if uⁿ = 1. DeMoivre's theorem gives a way to find all possibilities (there are n). If we write u = re^iθ in polar form and use DeMoivre's theorem, the condition uⁿ = 1 becomes

Comparing absolute values gives rⁿ = 1, so r = 1 (because r is real and positive). However, the arguments may differ by integral multiples of 2π, so all we can conclude is that nθ = 2kπ, where k is an integer; that is,

These arguments give distinct values of u on the unit circle for k = 0, 1, 2, . . ., n − 1, as shown in the di-agram. But every choice of k yields a value of θ differing from one of these by a multiple of 2π, so they give all the possible roots. This proves Theorem 6.

Theorem 6. The nth roots of unity are for k = 0, 1, 2, . . ., n − 1.

We find these roots geometrically as the distinct points on the unit circle, starting at 1, that cut the circle into n equal sectors. Note that if n = 2, the roots are 1 and −1, whereas the four 4^th roots of unity are 1, i, − 1, and −i. In general, if we write then the n^th then for each k ≥ 1, so the nth roots of unity are just the powers of

For this reason, is called a primitive nth root of unity. It follows easily (Exercise 16) that that is, the sum of the nth roots of unity is zero.

Exercises A

Appendix B Matrix Algebra

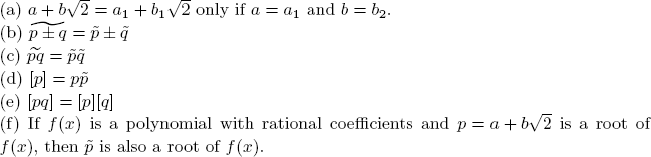
Matrix algebra will be familiar to most readers as it is standard fare in beginning linear algebra courses. The new ingredient here is that the matrices we consider will have entries drawn from an arbitrary commutative ring R, rather than from the real numbers A ring is an algebraic system in which there are two operations, addition and multiplication, for which the usual laws of arithmetic are valid (see Section 3.1). A ring R is called commutative if ab = ba for all a, b R. Examples include the familiar number systems and It is worth noting that the set of all 2 × 2 matrices over is a ring that is not commutative.

In this appendix, the standard results from linear algebra about matrices, adjugates, inverses, determinants, and so on, will be stated, with suitable minor modifications, over an arbitrary commutative ring R. We omit most proofs. When many proofs from linear algebra remain valid, but this is often not the case. It is important to note that it is essential that R is commutative in many arguments, especially when dealing with inverses and determinants. Hence,

R denotes a commutative ring throughout Appendix B.

Matrix Algebra

A rectangular array of elements of R is called a matrix and the elements themselves are called the entries of the matrix. Thus,

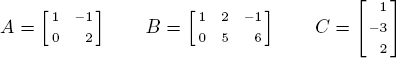
are matrices over The shape of a matrix depends on the number of rows and columns, and an m × n matrix is one with m rows and n columns. Two matrices are the same size if they have the same number of rows and the same number of columns. Thus, the preceding matrices A, B, and C are of size 2 × 2, 2 × 3, and 3 × 1, respectively. An n × n matrix is called a square matrix.

The rows and columns of a matrix are numbered from the top down and from left to right, respectively. Then the entry in row i and column j of a matrix A is called the (i, j)-entry of A. If the (i, j)-entry is denoted a_ij, then A has the form

which usually is abbreviated as A = [a_ij]. Two m × n matrices A = [a_ij] and B = [b_ij] are equal (written A = B) if they have the same size and corresponding entries are equal, that is

The set of all m × n matrices with entries from R is denoted M_mn(R). For A and B in M_mn(R), we obtain their sum A + B by adding corresponding entries. If A = [a_ij] and B = [b_ij], this is

This addition enjoys many of the properties of numerical addition. For example, if A, B, and C are in M_mn(R), then

A + B = B + A and A + (B + C) = (A + B) + C.

The matrix in M_mn(R) each of whose entries is zero is called the zero matrix of size m × n and is denoted 0 (or 0_mn if the size must be emphasized). Clearly,

A + 0 = A, for all A in M_mn(R).

So 0 plays the role in M_mn(R) that the number zero plays in We obtain the negative −A of a matrix A in M_mn(R) by negating every entry of A. Hence,

A + (− A) = 0, for all A in M_mn(R).

Finally we define subtraction by A − B = A + (− B). If A = [a_ij] and B = [b_ij],

−A = [− a_ij] and A − B = [a_ij − b_ij].

With these definitions, the additive arithmetic in M_mn(R) is entirely analogous to numerical arithmetic.

We also use the following notation: If A is a matrix and r R, the matrix rA is obtained by multiplying every entry of A by r. More formally

If A = [a_ij] then rA = [ra_ij].

This is called scalar multiplication and one verifies that it enjoys the following useful properties for all scalars r, s and matrices A, B:

Example 1. Given and in we have

Example 2. If and in M₂₃(R), find X in M₂₃(R) such that X + A = B.

Solution. We proceed as in numerical arithmetic and subtract A from both sides:

Multiplication of matrices is less natural than addition. To describe it, we define the dot product of a row matrix and a column matrix as follows:

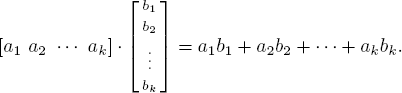
Now let A be an m × k matrix and B be a k × n matrix, chosen so that the rows of A and the columns of B have the same number k of entries. Then the product AB is defined to be the m × n matrix whose

(i, j)-entry is the dot product of row i of A and column j of B.

Thus to compute the (i, j)-entry, go across the ith row of A and down the jth column of B and form the dot product. Note: If A is m × k and B is k′ × n, then

AB is defined only if k = k′, and then the product AB is m × n.

Example 3. For and compute AB and BA.

Solution. We write out the dot products explicitly.

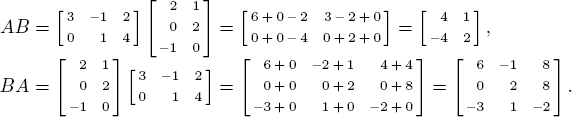
Example 4. If and compute A², AB, and BA.

Solution.

so A² = 0 can occur even when A ≠ 0. Next

Hence AB ≠ BA is possible even though they are both the same size.

Example 4 shows that two familiar properties of numerical algebra fail for matrices. Hence, it is surprising to learn that the following property does hold.

Theorem 1. Let A, B, and C be of sizes m × p, p × q, and q × n, respectively. Then (AB)C = A(BC).

Proof. Write A = [a_ij], B = [b_ij], and C = [c_ij]. Then AB = [x_ij] where we have and (AB)C = [y_ij] where Hence,

This last expression is the (i, j)-entry of A(BC), and the theorem follows. Note that we needed the associativity of R to get a_ik(b_ktc_tj) = a_ikb_ktc_tj = (a_ikb_kt)c_tj.

We express this result by saying that matrix multiplication is associative when the matrix sizes are such that the products involved are all defined.

The number 1 plays a neutral role in numerical multiplication in the sense that 1a = a and a 1 = a for every number a. The analogous role in matrix algebra is played by the identity matrices I_n. For each n ≥ 1, the matrix I_n is defined to be the n × n matrix with 1s along the main diagonal (upper left to lower right), and 0s elsewhere. Thus,

We use I without a subscript for the identity matrix when there is no need to emphasize the size. The reader can verify that the relations

hold whenever the matrix products are defined.

Note that rA = (rI)A for all r R and all matrices A. Moreover, since R is commutative we have (when the matrix multiplications are defined)

r(AB) = (rA)B = A(rB), for all r R.

Square Matrices and Inverses

We are interested primarily in square matrices. For convenience, we use the notation

M_n(R) = M_nn(R), for any n ≥ 2.

If A and B lie in M_n(R) then A + B and AB are both in M_n(R). Theorem 2 collects several properties of M_n(R) for reference later.

Theorem 2. Let A, B, and C be matrices in M_n(R). Then

Proof. The only property not discussed previously is (7), and we leave the verification as Exercise 12.

The reader may have noted that Theorem 2 shows that M_n(R) is a ring (noncommutative if n ≥ 2). It is also noteworthy that Theorem 2 holds even if the ring R is not commutative.

If A is a square matrix, a matrix B is called an inverse of A if

If it exists, this matrix B is uniquely determined by A. For if AC = I also holds, then AC = AB (both equal to I) so left multiplication by B gives C = B. A square matrix A is called invertible if it has an inverse, and in this case the (unique) inverse is denoted A⁻¹. Note that 0 has no inverse; in fact if AB = 0 for some B ≠ 0 then A has no inverse.

Write Rⁿ for the set of n × 1 column matrices with entries from R. If it is known that A is invertible if and only if the system AX = B of linear equations has a solution X for any This holds in general because AB = I in M_n(R) implies BA = I (Exercise 13). On the other hand, if it is known that A is invertible if and only if the homogeneous linear system AX = 0 has only the trivial solution X = 0. But this condition fails for (consider A = 2I). Hence if A is a square matrix, we need other ways to determine when A⁻¹ exists.

Again, it is well known that is invertible if and only if det A ≠ 0. If R is any commutative ring it turns out that the determinant of A M_n(R) can be defined in such a way that A is invertible if and only if det A is a unit in R (u R is a unit if uv = 1 = vu for some The idea is to define det A inductively. If n = 1 and A = [a], this holds if we define

det [a] = a.

If n ≥ 2, assume inductively that det A has been defined for all (n − 1) × (n − 1) matrices over R. If A is n × n write A_ij for the (n − 1) × (n − 1) matrix obtained from A by deleting row i and column j. Then, given 1 ≤ i, j ≤ n we define the (i, j) -cofactor of A by

c_ij(A) = (− 1)^i+j det A_ij.

With this, we define det A as follows:

(*) det A = a₁₁ c₁₁(A) + a₂₁ c₂₁(A) + + a_{n 1} c_{n 1}(A).

Then one shows that the following properties of determinants hold for rows:

With this one can prove a result first given (for in 1772 by Pierre Simon de Laplace.

Theorem 3. Cofactor Expansion Theorem. If A = [a_ij] is an n × n matrix over a commutative ring R, then

Furthermore, (a)–(e) above hold for rows and for columns.

We omit the details.¹⁴⁰ The expressions in (1) and (2) of Theorem 3 are called the cofactor expansions along column j and row i, respectively. In words, to find the cofactor expansion of det A along a row or column, multiply the entries of the row (column) by the corresponding cofactors, and add the results.

The cofactor expansion theorem has many important consequences, and the following result is necessary to describe them. Given an n × n matrix A = [a_ij], the transpose A^T of A is defined by

A^T = [b_ij], where b_ij = a_ji for all i and j.

This is an n × n matrix obtained from A by interchanging elements symmetric about the main diagonal. For example, if then The familiar elementary properties of the transpose hold

when the matrix operations are defined (even for nonsquare matrices). We omit the proof of the following theorem.

Theorem 4. Transpose Theorem. If A is a square matrix then det A^T = det A.

Surprisingly, the determinant function preserves matrix multiplication. Again we omit the proof.

Theorem 5. Multiplication Theorem. If A and B are n × n matrices then

det (AB) = det A det B.

Given an n × n matrix A = [a_ij] over a commutative ring R, we define the adjugate of A (also called the classical adjoint of A) as follows:

adj A = [c_ij(A)]^T.

This is also n × n and the cofactor expansion theorem (with some ingenuity) gives

Theorem 6. Adjugate Theorem. If A is n × n and d = det A, then

A (adj A) = dI_n = (adj A) A.

Again we omit the details.

If it happens that d = det A is a unit in R, then (as R is commutative) the adjugate theorem gives

A[d⁻¹ adj (A)] = I_n = [d⁻¹ adj (A)]A,

from which A is invertible and A⁻¹ = d⁻¹ adj (A). This proves part of

Theorem 7. Invertibility Theorem. If A is n × n then A is invertible if and only if det A is a unit in R. In this case det (A⁻¹) = (det A)⁻¹.

The rest of the proof follows from Theorem 5 (Exercise 14).

The case of 2 × 2 matrices is simple and so arises frequently in examples. The relevant facts are displayed next.

Example 5. If n = 2 and then we have adj and det A = ad − bc. Hence, if ad − bc is a unit in R then is a convenient formula for the inverse of A.

These results are enough to do most of the calculations in this book. A good reference source for this material (and much more) is the book by McDonald, B.R. Linear Algebra over Commutative Rings, Marcel Dekker Inc., New York, 1984.

Multilinear Approach

An n × n matrix A can be thought of as a row of columns in Rⁿ, and it is instructive to view matrices that way. Hence, we write A = [A₁, . . ., A_k, . . ., A_n], where A_k denotes column k of A. The determinant function det: M_n(R) → R has two basic properties from this point of view.

First, det is a multilinear function of the columns of a matrix, that is, it is a linear function of column k for each k (when we fix all other columns of A). More precisely, if we define

the requirement is that, for each k,

δ_k(rX + sY) = rδ_k(X) + sδ_k(Y) for all r, s R and X, Y Rⁿ.

Second, det is an alternating function of the columns of a matrix; that is if two distinct columns of A are interchanged to form B, then det B = − det A.

Before proceeding, write X_n = {1, 2, . . ., n} and recall the symmetric group S_n (see Section 1.4) of all permutations of X_n, that is all bijections σ: X_n → X_n. Each such σ is a product of transpositions, that is permutations that interchange two members of X_n. And σ is called even or odd according as it can be expressed as a product of an even, respectively odd, number of transpositions (the parity theorem ensures that this is well defined). The sign of σ is defined to be 1 or −1 according as σ is even or odd, and is written (− 1)^σ.

Hence, the fact that det is alternating means that if B is obtained from A by a series of column transpositions, then det B = (− 1)^σ det A where σ is the corresponding column permutation. With this it can be shown that d = det is the only multilinear, alternating function d: M_n(R) → R that satisfies d(I) = 1. Moreover, if we write σ(k) = σk when σ S_n and k X_n, the following characterization of det A can be proved.

Theorem 8. If A = [a_ij] is n × n then where the sum ranges over all n! elements σ of S_n.

Theorem 8 leads to other important properties of the determinant, and is often taken as the definition.

Exercises B

Throughout these exercises, R is assumed to be a commutative ring.

Appendix C Zorn's Lemma

The independent sets in a vector space are undeniably important, but the largest independent sets are the most important of all: they are the bases of the space. This theme that the “ largest” objects of a given type are the most interesting is universal in mathematics, certainly in algebra. Zorn's lemma is a set-theoretical principle that shows that maximal objects of various types exist and has become indispensable in many parts of mathematics. Clarifying what “ maximal” means is best formulated using the concept of a partial ordering.

A partial order on a nonempty set P is a relation¹⁴¹ ≤ on P that satisfies the following conditions (where x, y, and z denote elements of P):

A set P with a partial ordering is called a partially ordered set (poset for short). We say that (P, ≤) is a poset to assert that ≤ is a partial ordering on the set P. Posets occur everywhere in mathematics; here are a few examples.

The following are easily verified to be partial orders:

Inclusion ⊆ on any nonempty collection of sets.

Divisibility on any nonempty set of positive integers.

The usual ordering ≤ on the set of real numbers.

Nonempty subsets of a poset are again posets with the same partial order.

Other examples will occur later.

If ≤ is a partial order on a set P, we write x < y to mean x ≤ y and x ≠ y. An element m P is called maximal in P if there is no element x of P such that m < x, or equivalently,

For example, if U is any nonempty set, let denote the set of proper subsets X ⊂ U. Then the maximal members of (under inclusion) are the sets U {a} omitting one element a U. Here is a more algebraic example.

Example 1. If R is a ring, the maximal ideals of R (Section 3.3) are defined to be the maximal members of the poset is an ideal of R} partially ordered by inclusion. If R is commutative, corollary 1 of Theorem 6 §3.3 shows that an ideal A is maximal if and only if the factor ring R/A is a field.

Zorn's lemma gives a condition that guarantees that maximal elements exist in certain posets. To state it, we need some terminology. Let (P, ≤) be a poset. If X ⊆ P is a nonempty subset, an element u P is called an upper bound for X if x ≤ u for every x X. Note that u need not be an element of X. For example, in the poset the interval has no maximal member, but any number u ≥ 1 is an upper bound on X.

If we are looking for maximal elements in a poset P, choose x₁ P. If x₁ is maximal, we are done. Otherwise, x₁ < x₂ for some x₂ P. If x₂ is maximal, we are finished; otherwise x₁ < x₂ < x₃ for some x₃ P. Hence, either we find a maximal element at some stage, or we create elements x₁, x₂, x₃, . . . in P such that x₁< x₂ < x₃ < is a strictly increasing sequence. So it is plausible that guaranteeing the existence of maximal elements in P will require some restriction on such ascending sequences from P. In 1935, Max Zorn found a condition on P that does this and is reasonably easy to verify in specific situations.

Two elements x and y in a poset P are called comparable if either x ≤ y or y ≤ x, and the poset P is called a chain if any two elements are comparable. Thus, is a chain with respect to the usual partial ordering. A partially ordered set P is said to be inductive if every chain in P has an upper bound in P.

Theorem. Zorn's Lemma. Every inductive partially ordered set has a maximal element.

Note that to show that a poset is inductive, it is not enough to check that all countable¹⁴² chains x₁< x₂ < x₃ < have upper bounds in P. For example, consider the set of all countable subsets of partially ordered by inclusion. Then every countable chain in has an upper bound in , namely, its union (since unions of countable sets are again countable). But has no maximal member because such a maximal set would have to be itself, and is not a countable set.

Zorn's lemma has a wide variety of applications throughout mathematics; we give three examples from algebra. We begin with vector spaces. In Section 6.1, we proved that every finite dimensional vector space has a basis, but the proof that this holds in the infinite dimensional case requires Zorn's lemma. If V is a vector space over a field F, let X be a nonempty (possibly infinite) subset of V. Then X is called independent if every finite subset of X is independent (in the sense of Section 6.1), and X is said to span V if every element of V is a linear combination of (a finite number of) elements of X, Finally, X is called a basis of V if it is independent and spans V.

Example 2. If F is a field, show that every nonzero vector space V has a basis.

Solution. The idea is to show that any maximal independent set is a basis. Let denote the set of all independent sets in V and partially order by inclusion. We begin by using Zorn's lemma to show that has maximal members. First, is not empty since is in for all in V. Suppose that is a chain in if , we claim that X is independent. To see this, let {x₁, x₂, . . ., x_n} be a finite subset of X. Then each x_k is in some X_i, so, since X_i form a chain, {x₁, x₂, , x_n} ⊆ X_m for some m. Hence, {x₁, x₂, . . ., x_n} is independent (since X_m is in ), as required. This shows that X is in and so is an upper bound for in

Now Zorn's lemma shows that has a maximal member B, and we claim that B is a basis of V. Since it is independent (being in ), it remains to prove that span(B) = V, where span(B) consists of all linear combinations of vectors in B. Assume on the contrary that we show that is independent, contradicting the maximality of B.

So let X be a finite subset of we must show that X is independent. If X ⊆ B, this follows because If , then , so write , x_i B. Let a_i F. Then a₀ = 0 because otherwise , contrary to our choice (since exists in the field F). Hence, a₁x₁ + a₂x₂ + + a_nx_n = 0, so a_i = 0 for i ≥ 1, as required.

It is worth noting that Example 2 is true for any division ring in place of F. In fact, most of the theory of vector spaces goes through for division rings.

The next two examples of Zorn's lemma come from ring theory. An additive subgroup L of a ring R is called a left ideal if Ra ⊆ L for all a L, where Ra = {ra r R}. Right ideals are defined similarly, and the ideals of R (see Section 3.3) are just the left and right ideals. A maximal left ideal M is defined to be a maximal member of {L ≠ R L is a left ideal}, partially ordered by inclusion.

Example 3. If L ≠ R is any left ideal, then L is contained in a maximal left ideal.

Solution. Let is a left ideal and L ⊆ X ≠ R}, partially ordered by inclusion. Then is not empty ( so it suffices to show that contains a maximal element. By Zorn's lemma, it is enough to show that is inductive. Hence, let {X_i i I} be a chain from ; we show that is an upper bound for {X_i}. Clearly, X is a left ideal containing L, and we claim that X ≠ R. For if X = R, then 1 X, say 1 X_k for some k I. Since X_k is a left ideal, it follows that R = R 1 ⊆ X_k ⊆ R, so X_k = R, contrary to the fact that So X is an upper bound in on the chain {X_i}, as required.

As our last example of the use of Zorn's lemma, we prove a theorem that is of central importance in the theory of commutative rings. Let R be a commutative ring. An ideal P of R is called a prime ideal of R if R/P is an integral domain, or equivalently, if rs P, where r, s R, then either r P or s P (see Theorem 3 §3.3). Every commutative ring has at least one prime ideal by Example 3 (since maximal ideals are prime in any commutative ring).

An element a R is said to be nilpotent if aⁿ = 0 for some n ≥ 1, and the set nil(R) of all nilpotents in a commutative ring R is called the nil radical of R. It is easy to verify that nil(R) ⊆ P for every prime ideal P, and hence that nil(R) ⊆ ∩ {P P is a prime ideal of R}. The following example uses Zorn's lemma to show that this is in fact equality.

Example 4. If R is a commutative ring, nil(R) = ∩ {P P is a prime ideal of R}.

Solution. Let a P for every prime ideal P; by the above remarks, we must show that a is nilpotent. So we assume that a is not nilpotent and show (using Zorn's Lemma) that a ∉ P for some prime ideal P. To this end, let

is an ideal of R and aⁿ ∉ A for every n ≥ 1}.

Then is not empty as since a is not nilpotent. Suppose {A_i i I} is a chain from , and let A = _iIA_i. Then A is an ideal and if aⁿ A, then aⁿ A_k for some k, contradicting the fact that Hence, aⁿ ∉ A for each n, and so This shows that is inductive, so, by Zorn's lemma, let be a maximal member of Then certainly a = a¹ ∉ P, so it remains to show that P is a prime ideal. To that end, let rs P, where r, s R; we must show that r P or s P. Suppose, on the contrary, that r ∉ P and s ∉ P. Then

and P ⊂ Rr + P because r ∉ P. Since P is maximal in it follows that Rr + P is not in and hence that aⁿ Rr + P for some n ≥ 1, say aⁿ = t₁r + p₁, where t₁ R and p₁ P. Similarly, since s ∉ P, there exists m ≥ 1 such that a^m = t₂s + p₂, where t₂ R and p₂ P. But then

a^m+n = (t₁r + p₁)(t₂s + p₂) = (t₁t₂)rs + (t₁r)p₂ + (t₂s)p₁ + p₁p₁.

Hence, a^m+n P because rs, p₁, and p₂ are all in P. This contradiction completes the proof.

The proof of Zorn's lemma is difficult and will be omitted.¹⁴³ It requires (and is in fact equivalent to) the Axiom of Choice, which asserts that if is any family of nonempty sets, we can form a set containing one element of each of the sets in The axiom was first proposed in 1904 by Ernst Zermelo. At first glance, it seems self-evident, but there may be infinitely many choices of elements to make. For example, if consists of all the bounded intervals from , we can choose (say) the midpoint of each interval; but if consists of all nonempty subsets of , then it is not clear how to make all the choices. Bertrand Russell illustrates the point as follows: If a man has infinitely many pairs of shoes, and infinitely many pairs of socks, then he can easily choose one shoe from each pair (choose the left one, say), but choosing one sock from each pair requires the axiom of choice.

Mathematician's attitudes about the axiom of choice vary from never using it to making no distinction between mathematics assuming the axiom and mathematics not assuming it. Irving Kaplansky takes a middle position: “ I try to remember to make a note of it when I use it, but I do not hesitate to use it.” Whatever your attitude, Kurt Gödel showed in 1940 that the axiom of choice is consistent with the other axioms of set theory; that is, it cannot be disproved using these axioms. Then in 1963 Paul Cohen showed that the axiom of choice is independent of the other axioms; that is, it cannot be proved from these axioms.

Exercises C

Appendix D Proof of the Recursion Theorem

If A is a set, a mapping is called a sequence from A. Sequences are usually described as follows: If we write α(n) = a_n for each then the sequence is denoted a₀, a₁, a₂, a₃, . . ., a_n, . . . . The recursion theorem is concerned with recursively defined sequences wherein the first term a₀ is specified and the later terms are uniquely determined by the earlier ones. Such sequences are unique if they exist (see Theorem 3 §1.1); our task here is to prove existence.

Theorem. Recursion Theorem. Given a set A and a A, there is exactly one sequence a₀, a₁, a₂, a₃, . . ., a_n, . . . from A that satisfies the following requirements:

Proof. For each n ≥ 1, let β_n: Aⁿ → A be a mapping. We want to show that a sequence a₀, a₁, a₂, exists such that

a₀ = a and a_n = β_n(a₀, a₁, . . ., a_n−1), for each n ≥ 1.

The sequence is just a mapping such that α(n) = a_n, and we construct α as a set of ordered pairs in (see Section 0.3). Call a subset λ “ nice” if it satisfies the following two conditions:

is clearly “ nice”. Let α denote the intersection of all “ nice” subsets λ, that is

It is a routine verification that α is itself “nice”.

Claim 1. Given there exists x A such that (n, x) is in α.

Proof. If n = 0 then (0, a) is in α because α is nice. If n > 0 let (k, x_k) be in α for k = 0, 1, . . ., n − 1. Write x = β_n(x₀, . . ., x_n−1). Then (n, x) is in every “ nice” set λ by the definition of α, so (n, x) is in λ by (b). It follows that (n, x) is in α. This proves Claim 1.

Claim 2. If both (n, x) and (n, y) are in α then x = y.

Proof. If n = 0 suppose that (0, y) is in α where y ≠ a. Consider α′ = α {(0, y)}. It suffices to show that α′ is “ nice” since this contradicts the choice of α. Clearly (0, a) is in α′. If (k, x_k) is in α′ for k = 0, 1, . . ., n − 1 then all these pairs are in α, so (n, β_n(x₀, . . ., x_n−1)) is also in α. But n ≠ 0 so this is actually in α′. This shows that α′ is “ nice”. Now assume that Claim 2 is true for k = 0, 1, . . ., n − 1, and that (n, x) and (n, y) are both in α where x ≠ y. Then α^′′ = α {(n, y)} is “ nice” just as before, contrary to the choice of α. This proves Claim 2.

Finally let Then (n, a_n) is in α for some a_n A by Claim 1, and a_n is unique by Claim 2. Hence a₀, a₁, a₂, . . . is the desired sequence.

Notes

138 As the terms complex and imaginary suggest, these numbers met withsome resistance when they were first introduced. The names are misleading: Thesenumbers are no more complex than the real numbers, and i is nomore imaginary than −1. Descartes introduced the term imaginarynumbers.

139 An entire theory exists for the study of functions such as e^z, sin z, and cos z, where z is a complex variable. Many theorems can be proved in this theory, including the Fundamental Theorem of Algebra mentioned previously.

140 The argument when appears in Section 3.6 of Nicholson, W.K. Linear Algebra with Applications, 7th ed., McGraw-Hill Ryerson, 2012.

141 See Section 0.4.

142 A set X is called countable if it can be enumerated by the set of natural numbers, that is, if .

143 See Kaplansky, I. Set Theory and Metric Spaces, Boston: Allyn & Bacon, 1972, Section 3.3.