Selected Answers
Exercises 0.1 Proofs
1.
(a) If n = 2k, k an integer, then n2 = 4k2 is a multiple of 4. The converse is true: If n2 = 4k, then n must be even because n odd implies n2 odd.
(c) Verify that 23 − 6 · 22 + 11 · 2 − 6 = 0 and that 33 − 6 · 32 + 11 · 3 − 6 = 0.
The converse is false: 13 − 6 · 12 + 11 · 1 − 6 = 0 but 1 is not 2 or 3. Thus 1 is a counterexample.
2. (a) Either n is even or it is odd; that is, n = 2k or n = 2k + 1. Then n2 = 4k2 or n2 = 4(k2 + k) + 1.
3.
(a) If n is even, it cannot be prime unless n = 2 because, otherwise, 2 is a proper factor. The converse is false: 9 is an odd integer greater than 2, which is not prime.
(c) If ![]() then
then ![]() that is a > b, contrary to hypothesis. The converse is true: If
that is a > b, contrary to hypothesis. The converse is true: If ![]() then
then ![]() that is a ≤ b.
that is a ≤ b.
4. (a) If ![]() then
then ![]() Hence
Hence ![]() from which xy = 0; therefore x = 0 or 497 y = 0, contrary to hypothesis.
from which xy = 0; therefore x = 0 or 497 y = 0, contrary to hypothesis.
5. (a) n = 11 is a counterexample because then n2 + n + 11 has 11 as a factor.
Exercises 0.2 Sets
1. (a) {x ![]() x = 5k where
x = 5k where ![]()
2. (a) ![]()
3.
| (a) Not equal: −1 |
(c) Equal to {a, l, o, y} |
| (e) Not equal: 1 |
(g) Equal to { − 1, 0, 1} |
4.
| (a) ∅, {2} | (e) { 1}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} |
5. (a) True. As B ⊆ C, each element of B (in particular, A) is an element of C. (c) False. A = {1}, B = C = {{1}, 2}.
6. Every element of A ∩ B is in both A and B by definition, so A ∩ B ⊆ A and A ∩ B ⊆ B. If X ⊆ A and X ⊆ B, then x ![]() X implies that x
X implies that x ![]() A and x
A and x![]() B; that is, x
B; that is, x ![]() A ∩ B. Hence, X ⊆ A ∩ B.
A ∩ B. Hence, X ⊆ A ∩ B.
11. (a) (x, y) ![]() A × (B ∩ C) if and only if x
A × (B ∩ C) if and only if x ![]() A and y
A and y![]() B ∩ C; if and only if x
B ∩ C; if and only if x ![]() A and y
A and y ![]() B, and x
B, and x ![]() A and y
A and y![]() C; if and only if (x, y)
C; if and only if (x, y) ![]() A × B and (x, y)
A × B and (x, y)![]() A × C; if and only if (x, y)
A × C; if and only if (x, y) ![]() (A × B) ∩ (A × C). Hence A × (B ∩ C) and (A × B) ∩ (A × C) have the same elements.
(A × B) ∩ (A × C). Hence A × (B ∩ C) and (A × B) ∩ (A × C) have the same elements.
Exercises 0.3 Mappings
1.
(a) Not a mapping: α(1) = − 1 is not in ![]()
(c) Not a mapping: ![]() is not in
is not in ![]()
(e) Not a mapping: α(6) = α(2 · 3) = (2, 3) and α(6) = α(1 · 6) = (1, 6).
(g) Not a mapping: α(2) not defined.
2.
| (a) Bijective | (c) Onto, but not one-to-one |
| (e) One-to-one but not onto | (g) One-to-one but not onto if |B| ≥ 2 |
3.
(a) If c ![]() C, then c = βα(a) = β[α(a)] for some a
C, then c = βα(a) = β[α(a)] for some a ![]() A. As α(a)
A. As α(a) ![]() B, β is onto.
B, β is onto.
(c) If β(b) = β(b1), write b = α(a) and b1 = α(a1), where a, a1 ![]() A. Then β[α(a)] = β[α(a1)]; that is, βα(a) = βα(a1). Because βα is one-to-one, a = a1, which yields b = α(a) = α(a1) = b1.
A. Then β[α(a)] = β[α(a1)]; that is, βα(a) = βα(a1). Because βα is one-to-one, a = a1, which yields b = α(a) = α(a1) = b1.
7.
| (a) α−1(y) = 1a(y − b) | (c) α−1 = α |
9. If βα = 1A, then α is one-to-one so, as |A| = |B| is finite, α is also onto. Hence α−1 exists so α−1 = 1Aα−1 = βαα−1 = β1B = β. Then αβ = αα−1 = 1B and β−1 = (a−1)−1 = α.
11. ϕ−1(x, y) = α2 where α2(1) = x and α2(2) = y.
14. (b) ⇒ (c). If αγ = αδ, then γ = 1Aγ = (βα)γ = β(αγ) = β(αδ) = (βα)δ = 1Aδ = δ.
15. (c) ⇒ (a) If b0 ![]() B − α(A), choose a0
B − α(A), choose a0 ![]() A, and define β: B → B by:
A, and define β: B → B by:
![]() Deduce b0 = α(a0) using (c).
Deduce b0 = α(a0) using (c).
Exercises 0.4 Equivalences
1.
(a) Equivalence: [1] = [0] = [− 1] = {1, 0, − 1}, [2] = {2}, [− 2] = { − 2}.
(c) Not an equivalence: x ≡ x only if x = 1.
(e) Not an equivalence: 1 ≡ 2 but 26 ≡ 1.
(g) Not an equivalence: x ≡ x is never true.
(i) Equivalence: [(a, b)] = the line with slope 3 through (a, b).
2.
(a) A≡ = {[(1, 1)], [(1, 2)], [(1, 3)], [(2, 3)], [(3, 3)]}
(c) A≡ = {[(1, 1)], [(2, 1)], [(3, 1)]}
3.
(a) Kernel equivalence of ![]() where α(n) = n2; σ[n] = |n|.
where α(n) = n2; σ[n] = |n|.
(c) Kernel equivalence of ![]() where α(x, y) = y; σ[(x, y)] = y.
where α(x, y) = y; σ[(x, y)] = y.
7.
(a) Not well defined: ![]() and
and ![]()
(c) Not well defined: ![]() and
and ![]()
10. (c) |A≡| = |Q| = n by (c) of the preceding exercise.
Exercises 1.1 Induction
2. (e) ![]() .
.
3. (c) If 32k+1 + 2k+2 = 7m, then 32k+3 + 2k+3 = 7(9m − 2k+2).
7. Clear if n = 1. In general, such a (k + 1) digit number must end in 4, 5, or 6, and those are 3k of each by induction. We are done since 3 · 3k = 3k+1.
10. (a) If k ≥ 2 cents can be made up, there must be a 2-cent or a 3-cent stamp. In the first case, replace a 2-cent stamp by a 3-cent stamp; in the second case, replace a 3-cent stamp by two 2-cent stamps.
15. If p1 is true and pR ⇒ pR+1, show X = {n ![]() pnisfalse} is empty.
pnisfalse} is empty.
17. If pn is “ n has a prime factor”, then p2 is true. Assume p2, . . ., pk are all true. If k + 1 is a prime, we are done. If k + 1 = ab write 2 ≤ a ≤ k and 2 ≤ b ≤ k, then a (and b) has a prime factor by strong induction. Thus, k + 1 has a prime factor.
18.
| (a) an = 2(− 1)n | (c) |
24.
| (a) Verify p1 and p2. | (c) Verify p1, p2, . . ., p10. |
Exercises 1.2 Divisors And Prime Factorization
1. (a)
| (a) 391 = 23 · 17 + 0 | (c) −116 = (− 9)13 + 1 |
2. (a) n/d = 134.293 . . ., so q = 134. Then r = 113.
9.
| (a) 6 = 3 · 72 − 5 · 42 | (c) 3 = 1 · 327 − 6 · 54 |
| (e) 29 = 0 · 377 + 1 · 29 | (g) 1 = − 17 · 72 − 7 · (− 175) |
11. (a) If d = xm + yn, where ![]() then
then ![]()
15. If d = gcd (m, n) and d1 = gcd (m1, n1), then d ![]() m and d
m and d ![]() n, so d
n, so d ![]() m1 and d
m1 and d ![]() n1 by hypothesis. Thus d
n1 by hypothesis. Thus d ![]() d1.
d1.
19. If d = gcd (m, n) and d1 = gcd (km, kn), then d|m and d|n, so kd|km and kd|kn. Hence kd|d1. To show that d1|kd, write km = qd1 and kn = pd1. We have d = xm + yn where x and ![]() so kd = xkm + ykn = xqd1 + ypd1. Thus d1|kd.
so kd = xkm + ykn = xqd1 + ypd1. Thus d1|kd.
27. Let d = gcd(m, pk). Then d ![]() pk so d = pj, j ≤ k. Show that j > 0 contradicts gcd(m, pk) = 1.
pk so d = pj, j ≤ k. Show that j > 0 contradicts gcd(m, pk) = 1.
30.
| (a) 3473 | (c) 11 · 13 · 17 | (e) 241 |
31.
| (a) 5 and 16, 170 | (c) 139 and 278 |
33. (a) 25, 200 has 90 positive divisors.
41. (a) gcd(28, 665, 22, 869) = 63, and lcm(28, 665, 22, 869) = 10, 405, 395.
Exercises 1.3 Integers Modulo n
1.
![]()
2.
| (a) k ≡ 2 (mod7) | (c) k ≡ 0 (mod9) |
3.
| (a) 2, 5, 10 | (c) 3 |
8. (a) 7
9. (a) 7
15. One of a, a + 1 is even so 2 ![]() a(a + 1)(a + 2); similarly, one of a, a + 1, a + 2 is a multiple of 3. Since gcd(2, 3) = 1, it follows that 2 · 3 = 6 divides a(a + 1)(a + 2).
a(a + 1)(a + 2); similarly, one of a, a + 1, a + 2 is a multiple of 3. Since gcd(2, 3) = 1, it follows that 2 · 3 = 6 divides a(a + 1)(a + 2).
17. Compute ![]() for 0 ≤ a ≤ b.
for 0 ≤ a ≤ b.
22.
| (a) |
(c) |
25.
| (a) |
(c) No solution | (e) |
27.
| (a) |
(c) No solution |
31. (1)⇒(2). Let n = pka where p is a prime and p6 ![]() a. If a > 1 then gcd(n, a) = a > 1, so
a. If a > 1 then gcd(n, a) = a > 1, so ![]() has no inverse in
has no inverse in ![]() n. By (1), let
n. By (1), let ![]() in
in ![]() n. Then n
n. Then n ![]() ak, so p
ak, so p ![]() ak, so p
ak, so p ![]() a, a contradiction.
a, a contradiction.
35. (a) Working modulo p, ![]() means
means ![]() . Thus
. Thus ![]() so
so ![]() or
or ![]() by Theorem 7.
by Theorem 7.
Exercises 1.4 Permutations
1.
(a) ![]()
(c) ![]()
(e) ![]()
3.
(a) ![]()
(c) ![]()
(e) ![]()
7. (a) 24
11. (a) ![]()
13.
| (a) (148395276) | (c) (128)(367)(495) | (e) (138725) |
17. (a) (1432)(576)
18. Odd
19.
| (a) Even | (c) Even | (e) Odd |
25. It suffices to show that any pair of transpositions is a product of 3-cycles. If k, l, m, and n are distinct, this follows from (k l)2 = ε, (k l)(m n) = (k m l)(k m n), and (k l)(k m) = (k m l).
Exercises 2.1 Binary Operations
1.
(a) Not commutative or associative; no unity, so no units.
(c) Commutative, associative, unity is 0; if a ≠ 1, a−1 = aa − 1.
(e) Not commutative, associative; no unity, so no units.
(g) Commutative, associative; no unity, so no units.
(i) Not commutative, associative, unity is (1, 0, 1); if ![]()
2. (a)
| a | b | |
| a | a | b |
| b | b | a |
7. M × N is commutative if and only if both M and N are commutative. (m, n) is a unit if and only if both m and n are units, and then (m, n)−1 = (m−1, n−1).
9. (a) a24a = a25 = (a5)5 = (b5)5 = b25 = b24b = a24b. Cancel a 24 times
13. If ![]() , show that (vw)u = 1U.
, show that (vw)u = 1U.
18. (2)⇒(1). If (ab)−1 = x then (ab)x = 1, so a(bx) = 1. Then (bx)a = 1 by (2). So a is a unit. Similarly for b.
Exercises 2.2 Groups
1.
(a) Only 0 has an inverse.
(c) Group; unity is −1, a−1 is −a − 2.
(e) Not closed: (12)(13) = (132) is not in G.
(g) Group: unity is 16; each element is self-inverse.
(i) n ![]() 2n has no inverse in G.
2n has no inverse in G.
3.
(a) 

8. (a) Every element σ satisfies σ2 = ε.
13. α is onto because α(g−1) = g for all g![]() G; α is one-to-one because g−1 = h−1 implies that g = (g−1)−1 = (h−1)−1 = h.
G; α is one-to-one because g−1 = h−1 implies that g = (g−1)−1 = (h−1)−1 = h.
23. (a) If g = g−1, then g2 = gg−1 = 1; if g2 = 1, then g−1 = g−11 = g−1g2 = g.
29. (a) We first establish left cancellation: If gx = gy in G, then x = y. In fact, let hg = e. Then gx = gy implies x = ex = hgx = hgy = ey = y. With this, the fact that hg = e = e · e = hge gives g = ge by left cancellation. This shows that e is the unity. Finally, h(gh) = (hg)h = eh = h = he, so gh = e, again by left cancellation. Thus, h is the inverse of g.
Exercises 2.3 Subgroups
1.
| (a) No. 1 + 1 is not in H. | (c) No. 32 = 9 is not in H. | (e) No. (12)(34) · (13)(24) = (14)(23) is not in H. |
| (g) Yes. 6 = 0 is the unity. | (i) Yes. |
6. (a) 12 = 1. If x = g2, y = h2, then xy = (gh)2 and x−1 = (g−1)2.
7. (a) 1 = g0, gkgm = gk+m, and (gk)−1 = g−k; the subgroup test applies.
8. (a) 1 = xx−1![]()
![]() X
X ![]() . Clearly
. Clearly ![]() X
X![]() is closed. If
is closed. If ![]() , we obtain
, we obtain ![]() . Hence,
. Hence, ![]() X
X![]() is a subgroup; clearly x = x1
is a subgroup; clearly x = x1 ![]() X so X⊆
X so X⊆ ![]() X
X ![]() .
.
15.
(a) {1} and C5 are the only subgroups of C5.
![]()
(c) {ε}, K1 = {ε, (12)}, K2 = {ε, (13)}, K3 = {ε, (23)}, H = {ε, (123), (132)}, and S3.

17. ⇒. If H ![]() K, let h
K, let h ![]() H − K. If k
H − K. If k ![]() K, show kh ∉ K, hence kh
K, show kh ∉ K, hence kh ![]() H, whence k
H, whence k ![]() H.
H.
Exercises 2.4 Cyclic Groups And The Order Of An Element
1.
| (a) g, g2, g3, g4 | (c) g, g3, g5, g7, g9, g11, g13, g15 |
2.
| (a) 1, 2, 3, 4 | (c) 1, 3, 5, 7, 9, 11, 13, 15 |
4.
(a) ![]()
(c) ![]() is not cyclic; o(7) = o(9) = 2; o(3) = o(13) = o(5) = o(11) = 4
is not cyclic; o(7) = o(9) = 2; o(3) = o(13) = o(5) = o(11) = 4
7.
| (a) 10 | (c) 4 |
8. (a) (123)(45)
9.
(a) 
(b) 
(c)
11. (a) If G =![]() a
a ![]() where o(a) = n, let g = ak. Then gn = (ak)n = akn = (an)k = 1k = 1.
where o(a) = n, let g = ak. Then gn = (ak)n = akn = (an)k = 1k = 1.
16.
| (a) H = G | (c) |
(e) H = |
17. (a) X ⊆ Y ⊆ ![]() Y
Y ![]() ,
, ![]() Y
Y![]() a subgroup, so
a subgroup, so ![]() X
X![]() ⊆
⊆ ![]() Y
Y ![]() by Theorem 8.
by Theorem 8.
25. Let G =![]() g
g ![]() and H =
and H =![]() h
h ![]() where o(g) = m, o(h) = n. As |G × H| = |G| |H| = mn, it suffices to show that o((g, h)) = nm. We have (g, h)nm = (gnm, hnm) = (1, 1). If (g, h)k = (1, 1), then gk = 1 and hk = 1, so m
where o(g) = m, o(h) = n. As |G × H| = |G| |H| = mn, it suffices to show that o((g, h)) = nm. We have (g, h)nm = (gnm, hnm) = (1, 1). If (g, h)k = (1, 1), then gk = 1 and hk = 1, so m ![]() k and n
k and n ![]() k. But gcd(n, m) = 1, then implies nm
k. But gcd(n, m) = 1, then implies nm ![]() k (Theorem 5 §1.2)), so o(g, h) = mn, as required.
k (Theorem 5 §1.2)), so o(g, h) = mn, as required.
27. (a) If A ⊆ B, show that ga = gbq, ![]() Since |g| =∞, a = qb. Conversely, if a = qb, then ga
Since |g| =∞, a = qb. Conversely, if a = qb, then ga ![]() B, so A ⊆ B.
B, so A ⊆ B.
Exercises 2.5 Homomorphisms And Isomorphisms
8. (a) If ![]() let α(1) = m. Then α(k) = α(k · 1) = k[α(1)] = km. Thus, α is multiplication by m, and each such map is a homomorphism
let α(1) = m. Then α(k) = α(k · 1) = k[α(1)] = km. Thus, α is multiplication by m, and each such map is a homomorphism ![]() →
→![]()
12.
![]()
19. (a) If z ![]() Z(G), then σ(z)
Z(G), then σ(z) ![]() Z(G1) because, given g1 = σ(g) in G1, σ(z) · g1 = σ(zg) = σ(gz) = g1 · σ(z). Hence, σ: Z(G) → Z(G1) is a mapping. It is one-to-one because σ is, and
Z(G1) because, given g1 = σ(g) in G1, σ(z) · g1 = σ(zg) = σ(gz) = g1 · σ(z). Hence, σ: Z(G) → Z(G1) is a mapping. It is one-to-one because σ is, and ![]() clearly holds. If z1
clearly holds. If z1 ![]() Z(G1), let z1 = σ(z), z
Z(G1), let z1 = σ(z), z ![]() G. If g
G. If g ![]() G, then σ(gz) = σ(g) · z1 = z1 · σ(g) = σ(zg), so gz = zg because σ is one-to-one. Thus, z
G, then σ(gz) = σ(g) · z1 = z1 · σ(g) = σ(zg), so gz = zg because σ is one-to-one. Thus, z ![]() Z(G), and σ is onto.
Z(G), and σ is onto.
23. Write ![]() . Suppose
. Suppose ![]() is an isomorphism, write
is an isomorphism, write ![]() . Then
. Then ![]() so r = 1, so
so r = 1, so ![]() so
so ![]() , a con-tradiction.
, a con-tradiction.
25. ![]() is infinite cyclic, so
is infinite cyclic, so ![]() is infinite cyclic too, say
is infinite cyclic too, say ![]() In particular q2 = k0q, so
In particular q2 = k0q, so ![]() . Thus,
. Thus, ![]() a contradiction.
a contradiction.
31. If σ: G → G is an automorphism, then o(σ(a)) = 2, so σ(a) = a. Because σ(1) = 1, σ = 1G and autG = {1G}.
33. Let ![]() , o(a) =∞. If σ(a) = am,
, o(a) =∞. If σ(a) = am, ![]() , then a = σ(a)k = amk. As o(a) =∞ this gives 1 = mk, whence m = ± 1. If m = 1, then σ = 1G; if m = − 1 then σ(g) = g−1 for all g
, then a = σ(a)k = amk. As o(a) =∞ this gives 1 = mk, whence m = ± 1. If m = 1, then σ = 1G; if m = − 1 then σ(g) = g−1 for all g ![]() G.
G.
Exercises 2.6 Cosets And Lagrange's Theorem
1.
(a)
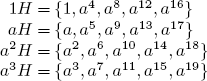
![]()
b

5. (a) a ≡ a because a−1a = 1 ![]() H. If a ≡ b then b−1a
H. If a ≡ b then b−1a ![]() H, and it follows that a−1b = (b−1a)−1
H, and it follows that a−1b = (b−1a)−1 ![]() H, so b ≡ a. Finally, if a ≡ b and b ≡ c then b−1a
H, so b ≡ a. Finally, if a ≡ b and b ≡ c then b−1a ![]() H and c−1b
H and c−1b ![]() H, so c−1a = (c−1b)(b−1a)
H, so c−1a = (c−1b)(b−1a) ![]() H and a ≡ c.
H and a ≡ c.
9.
(a) The sets of positive and negative numbers.
(c) If 0 ≤ t < 1, ![]() is the set of numbers at distance t to the right of an integer.
is the set of numbers at distance t to the right of an integer.
10. (a) 6
12. (a) If o(g) = m, we show m = 12. We have m ![]() 12 by Lagrange's theorem. If m ≠ 12, then m
12 by Lagrange's theorem. If m ≠ 12, then m ![]() 4 or m
4 or m ![]() 6, so g4 = 1 or g6 = 1, contrary to hypothesis.
6, so g4 = 1 or g6 = 1, contrary to hypothesis.
16. (a) If 1 = xm + yn, where ![]() then g = g1 = (gm)x(gn)y = 1x1y = 1.
then g = g1 = (gm)x(gn)y = 1x1y = 1.
25. (a) Because akbak = b implies that ak+1bak+1 = aba = b, it holds for k ≥ 0. But aba = b gives b = a−1ba−1, so a−kba−k = b follows for k ≥ 1 in the same way.
31. If ![]() , let Kh1, . . ., Khn be the distinct cosets of K in H. This means H = Kh1 ∪
, let Kh1, . . ., Khn be the distinct cosets of K in H. This means H = Kh1 ∪ ![]() ∪ Khn, a disjoint union. Then Hg ⊆ Kh1g ∪
∪ Khn, a disjoint union. Then Hg ⊆ Kh1g ∪ ![]() ∪ Khng is clear, and it is equality because K ⊆ H. Thus, each coset of H in G is the union of n K-cosets. If
∪ Khng is clear, and it is equality because K ⊆ H. Thus, each coset of H in G is the union of n K-cosets. If ![]() this gives
this gives ![]()
![]() . Conversely, if
. Conversely, if ![]() is finite, then
is finite, then ![]() is clearly finite and
is clearly finite and ![]() is finite by the hint since each H-coset is a union of K-cosets.
is finite by the hint since each H-coset is a union of K-cosets.
Exercises 2.7 Groups Of Motions And Symmetries
3. (a) If σ = (123), the group of motions is ![]()
4. (a) If σ = (1234), the group of motions is ![]()
6. (a) If σ = (123)(456) and τ = (14)(26)(35), the group G of motions is G = {ε, σ, σ2, τ, τσ, τσ2} ≅ D3.
Exercises 2.8 Normal Subgroups
1.
| (a) Not normal | (c) Normal |
2. If D4 = {1, a, a2, a3, b, ba, ba2, ba3}, where |a| = 4, |b| = 2, and aba = b, the normal subgroups are {1}, D4, Z = {1, a2} = Z(D4), ![]() K1 = {1, a2, b, a2b} and K1 = {1, a2, ba, ba3}.
K1 = {1, a2, b, a2b} and K1 = {1, a2, ba, ba3}.
5. First aKa−1 is a subgroup, by Theorem 5 §2.3, and aKa−1 ⊆ aHa−1 ⊆ H because H ![]() G. If h
G. If h ![]() H, we must show h(aKa−1)h−1 ⊆ aKa−1. We have h−1Kh = K as K
H, we must show h(aKa−1)h−1 ⊆ aKa−1. We have h−1Kh = K as K ![]() H, so h(aKa−1)h−1 = ha(h−1Kh)a−1h−1 = (hah−1)K(hah−1)−1 = K because K
H, so h(aKa−1)h−1 = ha(h−1Kh)a−1h−1 = (hah−1)K(hah−1)−1 = K because K ![]() G.
G.
11. Let H and K be subgroups of G with ![]() and
and ![]() . Then H ∩ K = {1} by Lagrange's theorem. Moreover, H
. Then H ∩ K = {1} by Lagrange's theorem. Moreover, H ![]() G because it is unique of its order, and similarly K
G because it is unique of its order, and similarly K ![]() G. Hence, G ≅ H × K by the Corollary to Theorem 6. Since p and q are primes, H and K are cyclic of relatively prime orders. Hence, H × K is cyclic by Exercise 25 §2.4.
G. Hence, G ≅ H × K by the Corollary to Theorem 6. Since p and q are primes, H and K are cyclic of relatively prime orders. Hence, H × K is cyclic by Exercise 25 §2.4.
15. (a) Conclude that Ka = G K = Kb−1, so ab ![]() K.
K.
17. (a) If H =![]() ad
ad ![]() , d
, d ![]() n, let n = md. Since bak is self-inverse for all k, we have (bak)−1adt(bak) = bakadtbak = b(ak+dt)bak = b · b · a−k−dt · ak = b2a−ka−dtak = a−dt
n, let n = md. Since bak is self-inverse for all k, we have (bak)−1adt(bak) = bakadtbak = b(ak+dt)bak = b · b · a−k−dt · ak = b2a−ka−dtak = a−dt ![]() H.
H.
24. (c) Let G = C2 × C2, where ![]() o(a) = 2, and let H = C × {1}. Then H
o(a) = 2, and let H = C × {1}. Then H ![]() G because G is abelian. But σ: G → G given by σ(x, y) = (y, x) is an automorphism and σ(H)
G because G is abelian. But σ: G → G given by σ(x, y) = (y, x) is an automorphism and σ(H) ![]() H. Thus, H is not characteristic in G.
H. Thus, H is not characteristic in G.
26. (a) Write K = core H = ∩ aaHa−1. Clearly 1 ![]() K. If g, g1
K. If g, g1 ![]() K, then gg1
K, then gg1 ![]() aHa−1 for all a, so gg1
aHa−1 for all a, so gg1 ![]() K. Also, g−1
K. Also, g−1 ![]() a−1H(a−1)−1 for all a, so g
a−1H(a−1)−1 for all a, so g ![]() K. Hence, K is a subgroup. If g
K. Hence, K is a subgroup. If g ![]() G, k
G, k ![]() K then gkg−1
K then gkg−1 ![]() g[(g−1a)H(g−1a)−1]g−1 = aHa−1 for all a, as required.
g[(g−1a)H(g−1a)−1]g−1 = aHa−1 for all a, as required.
Exercises 2.9 Factor Groups
1.
(a) If D6 = {1, a, . . ., a5, b, ba, . . ., ba5}, where o(a) = 6, o(b) = 2, and aba = b, then K = {1, a3} by Exercise 26 §2.6, and D6/K = {K, Ka, Ka2, Kb, Kba, Kba2}.

(c) K(a, b) = K(1, b) because (a, 1) ![]() K. Thus, G/K = {K(1, b)
K. Thus, G/K = {K(1, b) ![]() b
b ![]() B}. Moreover, K(1, b) · K(1, b1) = K(1, bb1), so the Cayley table is determined. Remark: The map K(1, b)
B}. Moreover, K(1, b) · K(1, b1) = K(1, bb1), so the Cayley table is determined. Remark: The map K(1, b) ![]() b is an isomorphism G/K → B.
b is an isomorphism G/K → B.
3. (a) 6, 4, 3, 12
4. (a) 12
5. (a) 1, 2, 2, 2
7. 
13.
(a) If z ![]() Z(G), then Kz
Z(G), then Kz ![]() Z(G/K), so z
Z(G/K), so z ![]() K by hypothesis. But then z
K by hypothesis. But then z ![]() Z(K), so z = 1.
Z(K), so z = 1.
(c) Given z ![]() G, let
G, let ![]() Then
Then ![]() so
so ![]() that is,
that is, ![]() Hence o(z) divides pn+m, so o(z) = pk for some k ≥ 0.
Hence o(z) divides pn+m, so o(z) = pk for some k ≥ 0.
19.
(a) G′ = {1}
(c) ![]() where D6 = {1, a, . . ., a5, b, ba, . . ., ba5}, o(a) = 6, o(b) = 2, aba = b.
where D6 = {1, a, . . ., a5, b, ba, . . ., ba5}, o(a) = 6, o(b) = 2, aba = b.
25. (a)
| [Ka, Kb] | = | Ka · Kb · Ka−1 · Kb−1 |
| = | K(aba−1b−1) | |
| = | K[a, b] |
Exercises 2.10 The Isomorphism Theorem
4. (a) 1 ![]() α−1(X) because α(1) = 1
α−1(X) because α(1) = 1![]() X; if g and h
X; if g and h ![]() α−1(X), then α(gh) = α(g)α(h)
α−1(X), then α(gh) = α(g)α(h) ![]() X and α(g)−1 = α(g−1)
X and α(g)−1 = α(g−1) ![]() X, shows that gh
X, shows that gh ![]() α−1(X) and g−1
α−1(X) and g−1 ![]() α−1(X). If X
α−1(X). If X ![]() α(G), let h
α(G), let h ![]() α−1(X), g
α−1(X), g ![]() G. Then α(ghg−1) = α(g)α(h)α(g)−1
G. Then α(ghg−1) = α(g)α(h)α(g)−1 ![]() α(g)Xα(g)−1 = X, so ghg−1
α(g)Xα(g)−1 = X, so ghg−1 ![]() α−1(X). Hence, α−1(X)
α−1(X). Hence, α−1(X) ![]() G.
G.
8. (a) If ![]() |g| = 6, then the choice of α(g)
|g| = 6, then the choice of α(g) ![]() K4 determines α: C6 → K4. If α(g) = 1, then α is trivial. If x ≠ 1 in K4, then o(x) = 2 and we define αx: C6 → K4 by αx(gk) = xk. This mapping is well defined because
K4 determines α: C6 → K4. If α(g) = 1, then α is trivial. If x ≠ 1 in K4, then o(x) = 2 and we define αx: C6 → K4 by αx(gk) = xk. This mapping is well defined because
gk = gm ⇒ 6|(k − m) ⇒ 2|(k − m) ⇒ xk = xm.
Hence, αx is a homomorphism and αx(g) = x. Thus, these are the only nontrivial homomorphisms.
(c) Let ![]() , where o(a) = 3, o(b) = 2, and aba = b, and let
, where o(a) = 3, o(b) = 2, and aba = b, and let ![]() , o(c) = 4. If α: D3 → C4 is a homomorphism, write K = ker α. Then K
, o(c) = 4. If α: D3 → C4 is a homomorphism, write K = ker α. Then K ![]() D3, so K = {1},
D3, so K = {1}, ![]() or K = D3. Now K = {1} is impossible as α is not one-to-one (|D3| = 6 does not divide |C4| = 4). If K = D3, then α is trivial. So assume that α is not trivial. Then α(G) ≅ G/K = {K, bK}, so α(G) is the unique subgroup of C4 of order 2: α(G) = {1, c2}. If ϕ: G → G/K is the coset map, there is an isomorphism σ: G/K → α(G) such that α = σϕ. Clearly, σ(K) = 1 and σ(bK) = c2. Hence
or K = D3. Now K = {1} is impossible as α is not one-to-one (|D3| = 6 does not divide |C4| = 4). If K = D3, then α is trivial. So assume that α is not trivial. Then α(G) ≅ G/K = {K, bK}, so α(G) is the unique subgroup of C4 of order 2: α(G) = {1, c2}. If ϕ: G → G/K is the coset map, there is an isomorphism σ: G/K → α(G) such that α = σϕ. Clearly, σ(K) = 1 and σ(bK) = c2. Hence
![]()
This is the only nontrivial homomorphism.
10. (a) No. If α: S3 → K4 were onto, then K4 ≅ S3/ker α, and |K4| = 4 would divide |S3| = 6.
(c) Yes. S3/A3 ≅ C2, say σ: S3/A3 → C2 is an isomorphism. If ϕ: S3 → S3/A3 is the (onto) coset map, then σϕ: S3 → C2 is an onto homomorphism.
13. Let G be simple. If α: G → G1 is nontrivial, ker α ≠ G, so ker α = {1} by sim-plicity. So α is one-to-one and G ≅ α(G) ⊆ G1. Conversely, if G1 has a subgroup G0 and σ: G → G0 is an isomorphism, then σ: G → G1 is a (one-to-one) homo-morphism, which is nontrivial because G0 ≠ {1} (it is simple).
17. (a) If g ![]() G′, write g = [a1, b1][a2, b2]
G′, write g = [a1, b1][a2, b2] ![]() [an, bn], where [a, b] = a−1b−1ab. Then
[an, bn], where [a, b] = a−1b−1ab. Then ![]() .
.
21. (a) Define ![]() because z ≠ 0). Then α is a homomorphism because
because z ≠ 0). Then α is a homomorphism because ![]() , and ker
, and ker ![]() . Thus, the isomorphism theorem gives
. Thus, the isomorphism theorem gives ![]()
33. (a) ![]() has subgroups H = {0}, {0, 2}, and
has subgroups H = {0}, {0, 2}, and ![]() . Hence
. Hence ![]() {1}, so these are the possible images.
{1}, so these are the possible images.
Exercises 2.11 An Application to Binary Linear Codes
1.
| (a) 5 | (c) 6 |
2.
| (a) 3 | (c) 7 |
7. (a) Detects 3, corrects 1.
11. (a) As k = 3 and t = 2, n must satisfy ![]() . If n = 3, 4, . . ., 8, this expression reads 7 ≤ 1, 11 ≤ 2, 16 ≤ 4, 22 ≤ 8, 29 ≤ 16, and 37 ≤ 32. Hence n ≥ 9. [Note: For n = 9, it reads 46 ≤ 64.]
. If n = 3, 4, . . ., 8, this expression reads 7 ≤ 1, 11 ≤ 2, 16 ≤ 4, 22 ≤ 8, 29 ≤ 16, and 37 ≤ 32. Hence n ≥ 9. [Note: For n = 9, it reads 46 ≤ 64.]
15. (a) If C is a (4, 2)-code that corrects one error, the weight of C must be at least 3 so that the nonzero words in C are contained in {1111, 1110, 1101, 0111}. But the sum of any two of these words is not in the set.
20.

21.
a. {0000, 1011, 0100, 1111}
c. {000000, 100101, 010110, 001001, 110011, 101100, 011111, 111010}
Exercises 3.1 Examples and Basic Properties
1. (a) Not an additive group.
(c) h(f + g) ≠ hf + hg can happen (try h(x) = x2).
3. (a) ![]() because the column sums are
because the column sums are
![]()
The rest of the subring test is routine.
7. ![]()
14. Compute (1 + sr) [1 − s(1 + rs)−1r].
15. (3) ⇒ (1). Let e be the unique right unity. Given b ![]() R, show that r(e + eb − b) = r for all r
R, show that r(e + eb − b) = r for all r ![]() R. Now use the uniqueness.
R. Now use the uniqueness.
16. (a) ![]() is a subring by Theorem 5. It is centered because s · (k1n) = ks = (k1n)s for all s
is a subring by Theorem 5. It is centered because s · (k1n) = ks = (k1n)s for all s ![]() R by Theorem 2.
R by Theorem 2.
18.
| (a) lcm(m, n) | (c) 0 |
21. (a) (1 − 2e)2 = 1 − 4e + 4e2 = 1
22. (a) If a = (1 − e)re then the fact that e2 = e gives ea = 0 and ae = a. It follows that a2 = (ae)a = a(ea) = a · 0 = 0.
23. (4) ⇒ (1). If r ![]() R, a = (1 − e)re is nilpotent so u = 1 + a is a unit and so commutes with e by (4). Conclude that re = ere.
R, a = (1 − e)re is nilpotent so u = 1 + a is a unit and so commutes with e by (4). Conclude that re = ere.
29.

36. (a) If ![]() is an isomorphism, then a = σ(i) satisfies a2 = − 1, a contradiction. (c) If
is an isomorphism, then a = σ(i) satisfies a2 = − 1, a contradiction. (c) If ![]() then
then ![]() is a division ring, a contradiction.
is a division ring, a contradiction.
Exercises 3.2 Integral Domains and Fields
1.
| (a) 1, −4 | (c) 0, 1 |
3. Idempotents ={0, 1}; nilpotents = {0}
7. If ab = 0 show that (ba)2 = 0.
9. Try ![]() for various primes p.
for various primes p.
15. If z ![]() Z(R) and za = 1, showing that a
Z(R) and za = 1, showing that a ![]() Z(R) is sufficient. Given r
Z(R) is sufficient. Given r ![]() R, (ra − ar)z = raz − arz = r · 1 − 1 · r = 0, so (as za = 1) ra − ar = 0.
R, (ra − ar)z = raz − arz = r · 1 − 1 · r = 0, so (as za = 1) ra − ar = 0.
16. (a) If o ≠ a ![]() K and ab = 1 with b
K and ab = 1 with b ![]() K, conclude that b = a−1 where a−1 is the inverse in F.
K, conclude that b = a−1 where a−1 is the inverse in F.
19. ![]() is a subfield of R by Example 4. If F is any subfield of R then
is a subfield of R by Example 4. If F is any subfield of R then ![]() (because 1
(because 1 ![]() R), and hence
R), and hence ![]() (because
(because ![]() for all n, m ≠ 0 in
for all n, m ≠ 0 in ![]() ). If also
). If also ![]()
![]()
![]() F, this means
F, this means ![]() for all
for all ![]() . Thus
. Thus ![]() .
.
23. If R = {r1, r2, . . ., rn} and 0 ≠ a ![]() R, then ar1, ar2, . . ., arn are distinct (ari = arj implies ri = rj as a ≠ 0). Hence {ar1, ar2, . . ., arn} has n elements, and so equals R. Hence, 1 = ari for some i.
R, then ar1, ar2, . . ., arn are distinct (ari = arj implies ri = rj as a ≠ 0). Hence {ar1, ar2, . . ., arn} has n elements, and so equals R. Hence, 1 = ari for some i.
26. (a) If ![]() and
and ![]() show
show ![]()
29. (a) If r = i and s = 1 in ![]() , consider a = r + sω in
, consider a = r + sω in ![]() . Then aa* = r2 + s2 = 0, but a ≠ 0 and a* ≠ 0 in
. Then aa* = r2 + s2 = 0, but a ≠ 0 and a* ≠ 0 in ![]() . Thus,
. Thus, ![]() is not a field. In
is not a field. In ![]() let a = 1 + 2ω. Then aa* = 12 + 22 = 0, and a ≠ 0 ≠ a*. So
let a = 1 + 2ω. Then aa* = 12 + 22 = 0, and a ≠ 0 ≠ a*. So ![]() is not a field. However,
is not a field. However, ![]() is a field. If a = r + si ≠ 0 in
is a field. If a = r + si ≠ 0 in ![]() then aa* = r2 + s2 and it suffices to show r2 + s2 ≠ 0 in
then aa* = r2 + s2 and it suffices to show r2 + s2 ≠ 0 in ![]() . Suppose r2 + s2 = 0. If r = 0 or s = 0 then a = 0, contrary to hypothesis. Thus r ≠ 0 ≠ s. Then 0 = s−1(r2 + s2) = (s−1r)2 + 1 so (s−1r)2 = − 1 in
. Suppose r2 + s2 = 0. If r = 0 or s = 0 then a = 0, contrary to hypothesis. Thus r ≠ 0 ≠ s. Then 0 = s−1(r2 + s2) = (s−1r)2 + 1 so (s−1r)2 = − 1 in ![]() . This is not the case because 02 = 0, 12 = 1 = 62, 22 = 4 = 52, 32 = 2 = 42 in
. This is not the case because 02 = 0, 12 = 1 = 62, 22 = 4 = 52, 32 = 2 = 42 in ![]() .
.
32. (a) If q is a unit in ![]() then 1 = N(1) = N(qq−1) = N(q)N(q−1), so N(q) is a unit in R. Conversely, qq* = N(q) shows q−1 = N(q)−1q* if N(q)
then 1 = N(1) = N(qq−1) = N(q)N(q−1), so N(q) is a unit in R. Conversely, qq* = N(q) shows q−1 = N(q)−1q* if N(q) ![]() R*.
R*.
Exercises 3.3 Ideals and Factor Rings
1.
| (a) No | (c) Yes | (e) No |
3. (c) If R is commutative then (r + A)(s + A) = rs + A = sr + A = (s + A)(r + A).
7. Let ![]() where a = (n, m), b = (k, l). Show that ml = 0.
where a = (n, m), b = (k, l). Show that ml = 0.
9. (a) A = R because i is a unit in R. So |R/A| = 1.
(c) R/A = {0 + A, 1 + A, 2 + A, 3 + A, 4 + A} and |R/A| = 5
10. If 0 ≠ z ![]() Z(R), then Rz is a nonzero ideal of R (it contains z ≠ 0) and so Rz = R. Hence 1
Z(R), then Rz is a nonzero ideal of R (it contains z ≠ 0) and so Rz = R. Hence 1 ![]() Rz, say 1 = az. It is enough to show that a
Rz, say 1 = az. It is enough to show that a ![]() Z(R). If r
Z(R). If r ![]() R, then
R, then
![]()
so ra = ar, as required.
11. (a) Show that A = {r ![]() R
R ![]() nr = 0} is an ideal of R.
nr = 0} is an ideal of R.
14. (a) X + Y is a subgroup because (1) 0 = 0+ 0 ![]() X + Y; (2) if r = x + y is in X + Y then −r = (− x) + (− y)
X + Y; (2) if r = x + y is in X + Y then −r = (− x) + (− y) ![]() X + Y; and (3) if also r′ = x′ + y′ is in X + Y then r + r′ = (x + x′) + (y + y′)
X + Y; and (3) if also r′ = x′ + y′ is in X + Y then r + r′ = (x + x′) + (y + y′) ![]() X + Y. We have X ⊆ X + Y because x = x + 0
X + Y. We have X ⊆ X + Y because x = x + 0 ![]() X + Y for all x
X + Y for all x ![]() X. Similarly Y ⊆ X + Y.
X. Similarly Y ⊆ X + Y.
15. A ∩ S is clearly an additive subgroup of S. If a ![]() A ∩ S and s
A ∩ S and s ![]() S, then sa
S, then sa ![]() A because A is an ideal and sa
A because A is an ideal and sa ![]() S because a
S because a ![]() S. Thus, sa
S. Thus, sa![]() A ∩ S; similarly, as
A ∩ S; similarly, as ![]() A ∩ S.
A ∩ S.
21. (a) (r + A)2 = r2 + A = r + A for all r ![]() R because r2 = r by hypothesis.
R because r2 = r by hypothesis.
22. (a) If e2 = e in R, show that (e + A)2 = e + A in R/A. By hypothesis, e ![]() A or 1 − e
A or 1 − e ![]() A. But 0 is the only nilpotent idempotent.
A. But 0 is the only nilpotent idempotent.
23.
| (a) 0 |
| (c) 2R = {0, 2, 4, 6, 8} |
25. (c) If u is a unit then u ![]() Ru implies Ru = R by Theorem 2. Conversely, if Ru = R then 1
Ru implies Ru = R by Theorem 2. Conversely, if Ru = R then 1 ![]() Ru, say 1 = vu,
Ru, say 1 = vu, ![]() . Hence, u is a unit (R is commutative).
. Hence, u is a unit (R is commutative).
33. (c) In ![]() is nilpotent. If
is nilpotent. If ![]() then
then ![]() is not nilpotent.
is not nilpotent.
34. (c) Write ![]()
![]() If
If ![]() is an ideal of
is an ideal of ![]()
![]() then
then ![]() so k
so k ![]() pn. Hence, k = pt for t ≤ n, so A ⊆ M where
pn. Hence, k = pt for t ≤ n, so A ⊆ M where ![]() It follows that M is the unique maximal ideal of
It follows that M is the unique maximal ideal of ![]()
![]() so
so ![]()
![]() is local and
is local and ![]()
Exercises 3.4 Homomorphisms
1.
| (a) No | (c) No | (e) Yes |
3. If ![]() is a general ring homomorphism, let θ(1) = e. Show that e2 = e so either e = 1or e = 0. In the last case θ(k) = θ(k · 1) = θ(k) · θ(1).
is a general ring homomorphism, let θ(1) = e. Show that e2 = e so either e = 1or e = 0. In the last case θ(k) = θ(k · 1) = θ(k) · θ(1).
9. 0 and R up to isomorphism
10. (4) Clearly, θ(r0) = θ(1) = 1 = θ(r)0. If θ(rn) = θ(r)n for some n ≥ 0, then θ(rn+1) = θ(rn · r) = θ(rn) · θ(r) = θ(r)n · θ(r) = θ(r)n+1. (5) Note first that θ(u) · θ(u−1) = θ(uu−1) = θ(1) = 1 and, similarly, that θ(u−1) · θ(u) = 1. So θ(u−1) = θ(u)−1. If k ≥ 0, then (4) gives (5): If k = − m, m > 0, then θ(uk) = θ[(u−1)m] = θ(u−1)m = [θ(u)−1]m = θ(u)k.
13. In ![]() 7 this is 4n2 = 2 and this has a solution (n = 2) in
7 this is 4n2 = 2 and this has a solution (n = 2) in ![]() 7. In
7. In ![]() 11 it is 7m2 = 9, or m2 = 8 · 9 = 72 = 6. But m2 = 0, 1, 3, 4, 5, 9 in
11 it is 7m2 = 9, or m2 = 8 · 9 = 72 = 6. But m2 = 0, 1, 3, 4, 5, 9 in ![]() 11, so there is no solution.
11, so there is no solution.
17. R ≅ R for any ring R because 1R: R → R is an isomorphism. If R ≅ S, say σ: R → S is an isomorphism, then σ−1: S → R is also an isomorphism, so S ≅ R. If also S ≅ T, where τ: S → T is an isomorphism, then τσ: R → T is an isomorphism and R ≅ T.
21. If ![]() is a ring homomorphism, then
is a ring homomorphism, then ![]() because 1 ∉ ker θ (θ(1) = 1 ≠ 0). Thus ker θ = 0 because
because 1 ∉ ker θ (θ(1) = 1 ≠ 0). Thus ker θ = 0 because ![]() is a field, from which
is a field, from which ![]() If θ(i) = a, then a2 = θ(i)2 = θ(i2) = θ(− 1) = − 1, a contradiction.
If θ(i) = a, then a2 = θ(i)2 = θ(i2) = θ(− 1) = − 1, a contradiction.
29. (a) The map ![]() given by
given by ![]() is an onto homomorphism with kernal
is an onto homomorphism with kernal ![]() .
.
37. Define ![]() by
by ![]() . Show that θ is a ring homomorphism and
. Show that θ is a ring homomorphism and ![]() .
.
41. If ![]() , show that e2 = e. If
, show that e2 = e. If ![]() is defined by σ(r) = re, show that σ is a ring isomorphism. Hence
is defined by σ(r) = re, show that σ is a ring isomorphism. Hence ![]()
Exercises 3.5 Ordered Integral Domains
3.
a. If a ≥ 0, then |a| = a ≥ 0. If a < 0, then −a = 0 − a ![]() R+, so |a| = − a > 0.
R+, so |a| = − a > 0.
c. If a = 0 or b = 0, then ab = 0 and |ab| = 0 = |a||b|. Assume that a ≠ 0 and b ≠ 0.
1. If a > 0 and b > 0, then ab > 0, so |ab| = ab = |a||b|.
2. If a > 0 and b < 0, then ab < 0, so |ab| = − ab = a(− b) = |a||b|.
3. If a < 0 and b > 0, the argument is like (2).
4. If a < 0 and b < 0, then ab > 0, so |ab| = ab = (− a)(− b) = |a||b|.
Hence, |ab| = |a||b| in every case.
Exercises 4.1 Polynomials
3. (a) 500
4. (a) In ![]() : 4, 5, 1, 2; in
: 4, 5, 1, 2; in ![]() : 4, 5
: 4, 5
5. (a) In ![]() : 0, 1; in
: 0, 1; in ![]() all four elements are roots; in
all four elements are roots; in ![]() : 0, 1, 3, 4
: 0, 1, 3, 4
7. (a) Let uxn and bxm be the leading terms of f and g, where u is a unit. The leading term of f g is ubxn+m because ub ≠ 0 (otherwise b = u−1(ub) = 0). Hence, f g ≠ 0 and deg (f g) = n + m = deg f + deg g.
14. (a) q = x3 + 3x2 − 3x + 5, r = − x − 3 = 5x + 3
| (c) q = 3x2 + 2x + 3, r(x) = 7 | (e) q = 3x + 2, r(x) = − 14x − 3 |
16. (a) 3, 5
17.
a. f = (x − 1)(x + 1)(x − 5)(x + 5)
c. f = (x − 1)(x + 2)(x + 3)
23.
| (a) 1 | (c) 3 |
25.
| (a) |
(c) 2, −1 | (e) None |
34. (c) If u![]()
![]() let
let ![]() denote the conjugate of u. Define
denote the conjugate of u. Define ![]()
![]() by
by ![]() This is a homomorphism (it is evaluation at 0 followed by conjugation) but it is not evaluation at a for any
This is a homomorphism (it is evaluation at 0 followed by conjugation) but it is not evaluation at a for any ![]()
![]() . Indeed, if θ = ϕa then
. Indeed, if θ = ϕa then ![]() while ϕa(i) = i.
while ϕa(i) = i.
38. (a) Show that R[x]/P[x] ≅ (R/A)[x] as rings (Exercise 37). Use Theorem 2.
Exercises 4.2 Factorization of Polynomials Over a Field
4.
| (a) Irreducible | (c) Not irreducible | (e) Irreducible |
5.
a. Yes, no, no, no, no, yes, yes
c. Yes, yes, no, yes, no, yes, yes
8. (a) As f is monic, we may assume that both factors are monic (Exercise 6). Hence ![]() Now equate coefficients.
Now equate coefficients.
15.
![]()
18.
a. 3x4 + 2 = 3(x − 1)(x + 1)(x − 3)(x + 3) in ![]()
c. x3 + 2x2 + 2x + 1 = (x + 1)(x + 3)(x + 5) in ![]()
e. x4 − x2 + x − 1 = (x − 1)(x − 2)(x2 + 3x + 6) in ![]()
22. (a) Eisenstein Criterion, with p = 3
23. (a) f(x + 1) = x4 + 4x3 + 6x2 + 6x + 2, so use the Eisenstein criterion with p = 2.
31. (a) If f is irreducible in K[x] it cannot factor properly in F[x].
35.
| (a) Already irreducible | (c) f = (x2 + 3x − 1)(x2 − x + 2) |
39.
a. 1 = (4x2 + 3x + 4)f − (4x + 2)g
c. ![]()
42. (a) Let 1 = mf + kg with m and k in F[x]. If h = pf and h = qg, then
h = hmf + hkg = (qg)mf + (pf)hg = (qm + pk)fg.
Exercises 4.3 Factor Rings of Polynomials Over a Field
2

3

5 ![]()
4. (a) Here t2 = t. Idempotents: 0, t, 1, 1− t; nilpotents: 0; units: a + bt, where a ≠ 0 ≠ a + b
7. (a) 5(− 1 + t + t2)
14.
(a) (x + t)(x + t2)(x + t + t2), where t3 = 1 + t
(c) (x − t)(x − 1 − t)(x + 1 − t), where t3 = t − 1
21. (a) If x2 + ax + b is not irreducible over F, it must have a root u ![]() F. Thus, u2 + au + b = 0. Take c = 2u + a. Then c2 = 4(u2 + ua) + a2 = − 4b + a2, con-trary to hypothesis.
F. Thus, u2 + au + b = 0. Take c = 2u + a. Then c2 = 4(u2 + ua) + a2 = − 4b + a2, con-trary to hypothesis.
25. (a) Write polynomials as f = f(x). Then d![]()
![]() f
f ![]() +
+ ![]() g
g ![]() because d = uf + vg for some
because d = uf + vg for some ![]() . On the other hand, f
. On the other hand, f![]()
![]() d
d ![]() and g
and g![]()
![]() d
d ![]() because d is a common divisor of f and g. Hence
because d is a common divisor of f and g. Hence ![]() f
f![]() ⊆
⊆ ![]() d
d ![]() and
and ![]() g
g![]() ⊆
⊆ ![]() d
d ![]() , so
, so ![]() f
f![]() +
+ ![]() g
g ![]() ⊆
⊆ ![]() d
d ![]() .
.
Exercises 4.4 Partial Fractions
2.
(a)![]()
(c)![]()
Exercises 4.5 Symmetric Polynomials
2. (a) (y2z2) + (x3 + xyz + x2z) + (x2 + xz − yz) + (3x − 3y)
7. (a) ![]()
3.
| (a) |
(c) |
11. ![]()
12. (a) ![]()
13. (a) x3 − 17x2 − 14x − 9
Exercises 5.1 Irreducibles and Unique Factorization
7. ±1
10.
| (a) Irreducible | (c) Not irreducible |
12.
| (a) Irreducible | (c) Not irreducible |
14.
| (a) Not irreducible | (c) Irreducible |
16. (a) If p ![]() q, suppose p is irreducible. If q = ab in R then p
q, suppose p is irreducible. If q = ab in R then p ![]() ab so p
ab so p ![]() a or p
a or p ![]() b. Thus q
b. Thus q ![]() a or q
a or q ![]() b, so q is irreducible. The converse is the same.
b, so q is irreducible. The converse is the same.
23. No. ![]()
![]()
27. Write d = gcd [a, gcd (b, c)] and d1 = gcd [gcd (a, b), c]. Then d divides a and gcd (b, c), so it divides all a, b, and c. Thus d divides gcd (a, b) and c, which gives d|d1. Similarly d1|d, so d ![]() d1. Moreover, this result shows that d divides a, b, and c and that every common divisor of a, b, and c divides d. Hence, gcd (a, b, c) exists and d
d1. Moreover, this result shows that d divides a, b, and c and that every common divisor of a, b, and c divides d. Hence, gcd (a, b, c) exists and d ![]() gcd (a, b, c).
gcd (a, b, c).
31. If m ![]() lcm(a1, . . ., an) exists in R then ai|m for each i shows
lcm(a1, . . ., an) exists in R then ai|m for each i shows ![]() m
m![]() ⊆
⊆ ![]() ai
ai ![]() for each i, and hence that
for each i, and hence that ![]() m
m ![]() ⊆ A where we write A =
⊆ A where we write A = ![]() ai
ai ![]() ∩
∩ ![]() ∩
∩ ![]() an
an ![]() . But r
. But r ![]() A means ai|r for each i, so m|r by definition. Thus, r
A means ai|r for each i, so m|r by definition. Thus, r![]()
![]() m
m ![]() and we have
and we have ![]() m
m ![]() = A. Conversely, if A =
= A. Conversely, if A =![]() m
m ![]() thenai|m for each i (because m
thenai|m for each i (because m ![]()
![]() ai
ai ![]() ); and, if ai|r for each i, then r
); and, if ai|r for each i, then r![]() A =
A = ![]() m
m ![]() so m|r. Thus, m is a least common multiple of the ai.
so m|r. Thus, m is a least common multiple of the ai.
35. Use Gauss' lemma.
37. If f = ug, u is a unit, write ![]() . Since f and g are primitive, show a
. Since f and g are primitive, show a ![]() b.
b.
39. (a) Show that R is a subring of ![]()
40. (a) Show ![]()
Exercises 5.2 Principal Ideal Domains
1. No, ![]() in
in ![]() .
.
5. Let A = ![]() a
a ![]() , a ≠ 0. If a is a unit then |R/A| = 1. Otherwise, by Theorem 4 §3.3, let B/A be any ideal of R/A, say B =
, a ≠ 0. If a is a unit then |R/A| = 1. Otherwise, by Theorem 4 §3.3, let B/A be any ideal of R/A, say B = ![]() b
b ![]() . Show that there are at most finitely many such divisors b of a up to associates.
. Show that there are at most finitely many such divisors b of a up to associates.
8. (a) Write ![]() R is a subring of R because
R is a subring of R because ![]() ,
, ![]() and
and ![]() and p does not divide nn′. Thus, R is an integral domain. Given
and p does not divide nn′. Thus, R is an integral domain. Given ![]() in R, if p does not divide m then
in R, if p does not divide m then ![]() is a unit in R (with inverse
is a unit in R (with inverse ![]() . Conversely, if
. Conversely, if ![]() is a unit, say
is a unit, say ![]() , then mm′ = nn′ so p does not divide m (it does not divide n or n′), so
, then mm′ = nn′ so p does not divide m (it does not divide n or n′), so ![]() does not divide m}.
does not divide m}.
13. (b) ![]() where
where ![]()
15. (b) a = 5b + (− 1), where δ(− 1) = 1 < 2 = δ(b)
24. (a) ![]()
26. (a) (1) ⇒ (2). Given a ≠ 0, b ≠ 0, let ![]() a, b
a, b ![]() =
= ![]() d
d ![]() . Then d = ra + sb for some r, s
. Then d = ra + sb for some r, s ![]() R, so if k|a and k|b in R then k|d. But d|a and d|b because a, b
R, so if k|a and k|b in R then k|d. But d|a and d|b because a, b ![]()
![]() d
d ![]() . (2) ⇒ (1). Given A =
. (2) ⇒ (1). Given A = ![]() a, b
a, b ![]() , clearly A is principal if a = 0 or b = 0. Otherwise let g = gcd(a, b)
, clearly A is principal if a = 0 or b = 0. Otherwise let g = gcd(a, b) ![]() d where d = ra + sb for r, s
d where d = ra + sb for r, s ![]() R. Then d
R. Then d ![]() A so
A so ![]() d
d ![]() ⊆ A. On the other hand, d|a and d|b so a
⊆ A. On the other hand, d|a and d|b so a![]()
![]() d
d ![]() and b
and b ![]()
![]() d
d ![]() . Hence
. Hence ![]() a, b
a, b ![]() ⊆
⊆ ![]() d
d ![]() .
.
35. No. If so, and ![]() , then
, then ![]() . But 2 = 1 + 1 > 0.
. But 2 = 1 + 1 > 0.
Exercises 6.1 Vector Spaces
1.
| (a) No | (c) No |
2.
| (a) Yes | (c) No |
7.
| (a) Dependent | (c) Independent |
11. {(1, − 1, 0), (1, 1, 1), (a, 0, 0)} for any a ≠ 0 in ![]()
15. I, A, A2, A3, A4 cannot be independent.
19. (a) {1, r, . . ., rn} is not independent because dim F(R) = n. So a0 + a1r + ![]() + anrn = 0 where the ai
+ anrn = 0 where the ai ![]() F are not all zero.
F are not all zero.
22. (b) If {u1, . . ., um} ⊆ {u1, . . ., um, . . ., un} then ![]() implies that
implies that ![]() where am+1 =
where am+1 = ![]() = an = 0. So ai = 0 for 1 ≤ i ≤ m.
= an = 0. So ai = 0 for 1 ≤ i ≤ m.
25. If ![]() is in
is in ![]() then
then ![]() so, writing ai = − 1,
so, writing ai = − 1, ![]() with ai ≠ 0. Hence
with ai ≠ 0. Hence ![]() is dependent. Conversely, if
is dependent. Conversely, if ![]() where some ai ≠ 0, then
where some ai ≠ 0, then ![]() is in
is in ![]()
31. (a) They are additive subgroups by group theory. If ![]() kerϕ then
kerϕ then ![]() for all a
for all a ![]() F. If
F. If ![]() im ϕ, say
im ϕ, say ![]() , then
, then ![]()
Exercises 6.2 Algebraic Extensions
1.
| (a) u4 − 16u2 + 4 = 0 | (c) u8 + 2u4 + 49 = 0 |
2.
| (a) x4 − 10x2 + 1 | (c) x4 − 2x2 − 2 |
3.
| (a) Algebraic | (c) Transcendental |
4. (a) x2 − 2x + 2
7. (a) ![]() so
so ![]() . We claim that the minimal poly-nomial is
. We claim that the minimal poly-nomial is ![]() . Its roots in
. Its roots in ![]() are
are ![]() and neither is in
and neither is in ![]() , so it is irreducible in
, so it is irreducible in ![]() , as required.
, as required.
12. (a) {1, u, u2}, where ![]() (c)
(c) ![]() where
where ![]() (e)
(e) ![]()
13.
| (a) 2 | (c) 2 |
17. If F(u) ⊇ L ⊇ F write p = [F(u): F] = [F(u): L][L: F]. Thus [L: F] = 1 or p; so L = F or [L: F] = [F(u): F], whence L = F(u) by Theorem 8 §6.1.
19. Let ![]() . Show that
. Show that ![]() with degree 2 exists such that f(u) = 0, say f = ax2 + bx + c. Conclude that
with degree 2 exists such that f(u) = 0, say f = ax2 + bx + c. Conclude that ![]() so
so ![]() . We may as-sume a, b, and c are integers, so
. We may as-sume a, b, and c are integers, so ![]() . If d = p2e,
. If d = p2e, ![]() , p a prime, then
, p a prime, then ![]() . Continue until
. Continue until ![]() where m is square free.
where m is square free.
21. (a) Write L = F(u), so ![]() Thus
Thus ![]() and [L: F] = m by hypothesis, and
and [L: F] = m by hypothesis, and ![]() Hence, we simply show that
Hence, we simply show that ![]() If p and m are the minimal polynomials of
If p and m are the minimal polynomials of ![]() over L and F, respectively, then p|m by Theorem 3, so
over L and F, respectively, then p|m by Theorem 3, so ![]()
23. If ![]() then
then ![]() , gcd(f, g) = 1. Then h(π) = 0, where h(x) = 2g2(x) − f2(x), and this is a contradiction if h ≠ 0 in
, gcd(f, g) = 1. Then h(π) = 0, where h(x) = 2g2(x) − f2(x), and this is a contradiction if h ≠ 0 in ![]() . But h = 0 means 2g2 = f2 so, since gcd(f, g) = 1, f|2. Thus f = ± 1, ±2, g2(x) = ± 1,
. But h = 0 means 2g2 = f2 so, since gcd(f, g) = 1, f|2. Thus f = ± 1, ±2, g2(x) = ± 1, ![]() . This forces deg g = 0;
. This forces deg g = 0; ![]() , g = ± 1,
, g = ± 1, ![]() . Thus g = ± 1,
. Thus g = ± 1, ![]() , a contradiction. Thus h ≠ 0 and
, a contradiction. Thus h ≠ 0 and ![]() has led to a contradiction. So
has led to a contradiction. So ![]()
26. (a) Let f(u2) = 0, 0 ≠ f ![]() F[x]. Use g where g(x) = f(x2) ≠ 0.
F[x]. Use g where g(x) = f(x2) ≠ 0.
31. (a) We show F(u) = Q, where Q = {f(u)g(u)−1| f, g ![]() F[x]; g(u) ≠ 0}. Since u is transcendental over F, f(u) ≠ 0 whenever f(x) ≠ 0. Thus Q is a subfield of E containing F and u, so F(u) ⊆ Q. But any subfield of E containing F and u must contain Q, so F(u) ⊇ Q. Thus F(u) = Q.
F[x]; g(u) ≠ 0}. Since u is transcendental over F, f(u) ≠ 0 whenever f(x) ≠ 0. Thus Q is a subfield of E containing F and u, so F(u) ⊆ Q. But any subfield of E containing F and u must contain Q, so F(u) ⊇ Q. Thus F(u) = Q.
33. Show that if u is algebraic over A then u ![]() A, contrary to hypothesis. If f(u) = 0 where f ≠ 0 in A[x], let
A, contrary to hypothesis. If f(u) = 0 where f ≠ 0 in A[x], let ![]() ,
, ![]() . Show that u
. Show that u ![]() L(u) where
L(u) where ![]() is a finite extension of F.
is a finite extension of F.
Exercises 6.3 Splitting Fields
1. (a) ![]() and [E: Q] = 2. (c)
and [E: Q] = 2. (c) ![]() and
and ![]()
2. (a) ![]()
4.
(a) ![]() u2+ u + 1 = 0; f(x) = (x + 1)(x + u)(x + 1 + u)
u2+ u + 1 = 0; f(x) = (x + 1)(x + u)(x + 1 + u)
(c) ![]() f(u) = 0; f(x) = (x + u)(x + u2)(x + 1 + u + u2)
f(u) = 0; f(x) = (x + u)(x + u2)(x + 1 + u + u2)
(e) ![]() u2 + 1 = 0, f(x) = (x − u)2(x + u)2
u2 + 1 = 0, f(x) = (x − u)2(x + u)2
6. (a) No. If ![]() were the splitting field of
were the splitting field of ![]() then
then ![]() . Thus
. Thus ![]() would be algebraic, contradicting the fact that π or e is transcendental.
would be algebraic, contradicting the fact that π or e is transcendental.
9. If gcd(f, g) = 1 let 1 = fh + gk; h, k in F[x]. Suppose E ⊇ F is an extension containing a common root u, that is f(u) = 0 = g(u). Then substitution gives 1 = f(u)h(u) + g(u)k(u) = 0, a contradiction. So no such extension E exists. Conversely, let d = gcd(f, g). If d ≠ 1 then degd ≥ 1 so let E ⊇ F be a field containing a root u of d. Then d|f and d|g means f(u) = 0 = g(u), contrary to hypothesis. So d = 1.
13. Show that the roots of xp − 1 are ![]() so
so ![]() is the splitting field. By Theorem 6, Appendix A, xp − 1 = (x − 1)Φp, where Φp = xp−1 + xp−2 +
is the splitting field. By Theorem 6, Appendix A, xp − 1 = (x − 1)Φp, where Φp = xp−1 + xp−2 + ![]() + x + 1 is irreducible over
+ x + 1 is irreducible over ![]() by Example 13 §4.2.
by Example 13 §4.2.
20. (a) We show ![]() Clearly
Clearly ![]() is algebraic. We must show that if u
is algebraic. We must show that if u ![]() E is algebraic over
E is algebraic over ![]() then u
then u ![]() A. Since u is algebraic over A, we show that u ∉ A implies u is transcendental over A. We have E = A(π) so this follows from Exercise 31 §6.2 if we can show that π is transcendental over A. But if π were algebraic over A it would be algebraic over
A. Since u is algebraic over A, we show that u ∉ A implies u is transcendental over A. We have E = A(π) so this follows from Exercise 31 §6.2 if we can show that π is transcendental over A. But if π were algebraic over A it would be algebraic over ![]() , contrary to the preceding exercise.
, contrary to the preceding exercise.
Exercises 6.4 Finite Fields
1.
| (a) 2 |
| (c) Any element of GF(8) except 0 and 1. |
4.
(a)
(c)

5. If GF(16) = {a + bt + ct2 + dt3 ![]() a, b, c, d in
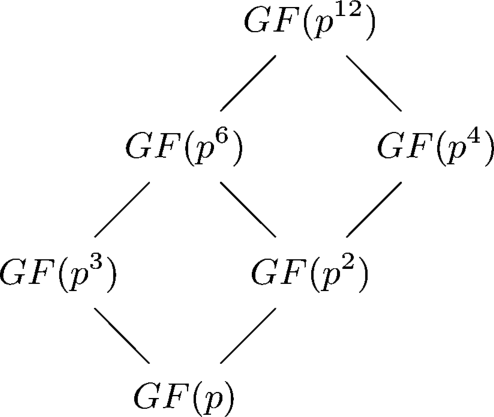
a, b, c, d in ![]() , then t is primitive. The subfields are
, then t is primitive. The subfields are ![]() , and
, and ![]()
8. ![]()
9. If G ⊆ C*, |G| = n, then ![]() where u = e2πi/n.
where u = e2πi/n.
17. Let d = gcd(f, f′) and write d = fg + f′h where g and h are in F[x]. If d = 1, suppose f has a repeated root a in E ⊇ F. Then x − a divides both f and f′ in E[x], and so divides d = 1, a contradiction. Conversely, if d ≠ 1, let E be a splitting field of f over F. Then d|f implies d has a root a in E, so x − a divides f and f′, a contradiction by Theorem 3.
22. (a) If ![]() is a field containing a root u of f, conclude that f is the minimal polynomial of u over
is a field containing a root u of f, conclude that f is the minimal polynomial of u over ![]() . If
. If ![]() then
then ![]() and so |E| = pn. Then u is a root of
and so |E| = pn. Then u is a root of ![]() so f|h in E[x], say h = qf. But h = q0f + r in
so f|h in E[x], say h = qf. But h = q0f + r in ![]() by the division algorithm, so this holds in E[x]. By the uniqueness in E[x], we get
by the division algorithm, so this holds in E[x]. By the uniqueness in E[x], we get ![]() and
and ![]()
Exercises 6.5 Geometric Constructions
3. Yes. Bisect 30![]() , after constructing that from a 30–60–90-triangle.
, after constructing that from a 30–60–90-triangle.
5. No. A sphere of radius 1 has volume ![]() and, if this is the volume of a cube with side a, then
and, if this is the volume of a cube with side a, then ![]() . But a is not constructible since it is not even algebraic over
. But a is not constructible since it is not even algebraic over ![]() . For if a is a root of
. For if a is a root of ![]() . Then π is a root of
. Then π is a root of ![]() . This is impossible as π is transcendental over
. This is impossible as π is transcendental over ![]()
Exercises 6.7 An Application to Cyclic and BCH Codes
5. (a) In B4: 1 + t, t + t2 = t(1 + t), t2 + t3 = t2(1 + t) and 1 + t3 = t3(1 + t). The other members 0, 1 + t2, t + t2 and 1 + t + t2 + t3 all lie in smaller ideals. (See Example 3.)
7. (a) 1 + x7 = (1 + x)(1 + x + x3)(1 + x2 + x3) so there are 2 · 2 · 2 = 8 divisors in all. Thus, there are 7 codes (excluding ![]() 1 + x7
1 + x7 ![]() = 0).
= 0).
11. Since g(x) = 1 + x + x4 has no root in ![]() , if it factorizes at all, it must do so as g(x) = (a + bx + cx2)(a′ + b′x + c′x2). Thus aa′ = 1 = cc′ so a = a′ = 1 = c = c′. Thus g(x) = (1 + bx + x2)(1 + b′x + x2) so (coefficient of x3) b + b′ = 0 and (co-efficient of x) b + b′ = 1. This is impossible.
, if it factorizes at all, it must do so as g(x) = (a + bx + cx2)(a′ + b′x + c′x2). Thus aa′ = 1 = cc′ so a = a′ = 1 = c = c′. Thus g(x) = (1 + bx + x2)(1 + b′x + x2) so (coefficient of x3) b + b′ = 0 and (co-efficient of x) b + b′ = 1. This is impossible.
17. (c) Write g(x) = 1 + x + x3. We have 1 + x7 = (1 + x)(1 + x2 + x3)g(x), a product of irreducibles. Hence, 1 + x7 = h(x)g(x), where h(x) = 1 + x + x2 + x4. We have 1 = xg(x) + 1 · h(x), so take e(x) = xg(x) = x + x2 + x4. Note that e(t)2 = e(t2) = t2 + t4 + t8 = t2 + t4 + t = e(t). So e(t) = t + t2 + t4 is the idempo-tent generator.
Exercises 7.1 Modules
1. (c) Using (a), x + (− x) = 0 = 0x = (1 + (− 1))x = 1x + (− 1)x = x + (− 1)x, so −x = (− 1)x.
2. (a) If α: M → N is onto and R-linear, and if M = Rx1 + ![]() + Rxn, then we have N = Rα(x1) +
+ Rxn, then we have N = Rα(x1) + ![]() + Rα(xn). Since some of the α(xi) may be zero, the result follows.
+ Rα(xn). Since some of the α(xi) may be zero, the result follows.
5. (a) If x = Σaiki then rx = Σ(rai)ki ![]() AK
AK
6. Let A = ΣiRai, ai ![]() A, and M = ΣjRx, xj
A, and M = ΣjRx, xj ![]() M. Use Exercise 5 to show that AM = Σi,jRaixj.
M. Use Exercise 5 to show that AM = Σi,jRaixj.
7. (a) Define α: N → K + NK by α(n) = n + K for all n ![]() N. Show that α is R -linear and kerα = N ∩ K. Every coset in K + NK has the form (k + n) + K, where k
N. Show that α is R -linear and kerα = N ∩ K. Every coset in K + NK has the form (k + n) + K, where k ![]() K and n
K and n ![]() N. But (k + n) + K = n + K = α(n), which proves that α is onto. Now the isomorphism theorem applies.
N. But (k + n) + K = n + K = α(n), which proves that α is onto. Now the isomorphism theorem applies.
11. (a) Yes. (m, n) = (n, n) + (m − n, 0) shows that M = K+ X; clearly K ∩ X = 0.
16. (a) We have M = π(M) + kerπ because m = π(m) + (m − π(m)) for each m ![]() M and π[m − π(m)] = π(m) − π2(m) = 0. If m
M and π[m − π(m)] = π(m) − π2(m) = 0. If m ![]() π(M) ∩ kerπ, let m = π(m1) with m1
π(M) ∩ kerπ, let m = π(m1) with m1 ![]() M. Then 0 = π(m) = π2(m1) = π(m1) = m, so π(M) ∩ kerπ = 0.
M. Then 0 = π(m) = π2(m1) = π(m1) = m, so π(M) ∩ kerπ = 0.
21. (a) If ![]() we must show that
we must show that ![]() Show that
Show that ![]() where ai
where ai ![]() A,
A, ![]() and apply the linearity of α.
and apply the linearity of α.
Exercises 7.2 Modules Over a PID
1. (c) ![]() ,
, ![]()
2. (a) The types are (4), (3, 1), (2, 2), (2, 1, 1) and (1, 1, 1, 1). Hence, representative groups are ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]()
3. (a) ![]() ,
, ![]()
4. (a) The types are: p-component (2), (1, 1); the q-component (3), (2, 1), (1, 1, 1); and the r-component (4), (3, 1), (2, 2), (2, 1, 1), (1, 1, 1, 1). Hence 2 · 3 · 5 = 30 in all.
7. (a) Thus G(2) has type (2, 2); G(3) has type (1, 1, 1) and G(5) has type (2, 1).
9. (a) The types are (2, 2, 2), (2, 2, 1, 1), (2, 1, 1, 1, 1), (1, 1, 1, 1, 1, 1).
12. (a) T(K) = {k ![]() K
K ![]() o(k) ≠ 0} = K ∩ {m
o(k) ≠ 0} = K ∩ {m ![]() M
M ![]() o(m) ≠ 0} = K ∩ T(M).
o(m) ≠ 0} = K ∩ T(M).
16. (a) Define σ: K → M/T(M) by σ(k) = k + T(M). This is a group homomor-phism and ker σ = {k ![]() K
K ![]() k
k ![]() T(M)} = K ∩ T(M) = T(K). Use the isomor-phism theorem.
T(M)} = K ∩ T(M) = T(K). Use the isomor-phism theorem.
20. (c) If m = Σxi then dm = 0 implies dxi = 0 for all i. Hence Ld(M) ⊆ ΣiLd(Mi).
22. (a) Here Lp(Rx) = {rx ![]() p(rx) = 0}. If prx = 0 then pr
p(rx) = 0}. If prx = 0 then pr ![]() ann
ann![]() say pr = spm. Since m ≥ 1 and R is a domain, this gives r = spm−1, and we have shown that (Rx)p ⊆ R(pm−1x). The other inclusion is because pmx = 0. Finally, p(Rx) = Rpx is a routine verification, and px = 0 if m = 1 because o(x) = pm.
say pr = spm. Since m ≥ 1 and R is a domain, this gives r = spm−1, and we have shown that (Rx)p ⊆ R(pm−1x). The other inclusion is because pmx = 0. Finally, p(Rx) = Rpx is a routine verification, and px = 0 if m = 1 because o(x) = pm.
27. (a) Lp(G) consists of 0 and the elements of order p. We have Lp(G) = Lp(G1) ⊕ ![]() ⊕ Lp(Gp) by Exercise 20, and |Lp(Gi)| = p for each i by Exercise 26.
⊕ Lp(Gp) by Exercise 20, and |Lp(Gi)| = p for each i by Exercise 26.
Exercises 8.1 Factors and Products
1. (a) XY = {ε, σ, σ2}. Note: XY is a subgroup here, but X and Y are not.
3. ![]() as
as ![]() is abelian. Hence H
is abelian. Hence H ![]() G by the correspondence theorem.
G by the correspondence theorem.
4.
(a) K, G, ![]() {1, a3, b, ba3}, {1, a3, ba, ba4}, {1, a3, ba2, ba5}.
{1, a3, b, ba3}, {1, a3, ba, ba4}, {1, a3, ba2, ba5}.
(c) K, A4
5.
(a) ![]() where p is any prime
where p is any prime
(c) If D10 = {1, a, . . ., a9, b, ba, . . ., ba9}, where |a| = 10, |b| = 2, and aba = b, the maximal subgroups are

9. (a) Clearly ![]() . If
. If ![]() let Kg = Kh, h
let Kg = Kh, h ![]() H. Then gh−1
H. Then gh−1 ![]() K ⊆ H, so g
K ⊆ H, so g ![]() H. Similarly g
H. Similarly g ![]() H1, so
H1, so ![]() .
.
12. (a) H2 ⊆ H because H is closed; H ⊆ H2 because 1 ![]() H.
H.
15. KA = AK and KB = BK are subgroups by Theorem 5 §2.8. Given kb in KB, Ab = bA and Kb = bK by hypothesis, so KA(kb) = AKkb = AKb = AbK = bAK = bKA = KbA = kKbA = (kb)KA. Thus KA ![]() KB.
KB.
22. (a) Let a ≠ b have order 2, show that H = {1, a, b, ab} is closed and apply La-grange's theorem.
Exercises 8.2 Cauchy'S Theorem
1. (a) {1}, {a, a3}, {a2}, {b, ba2}, {ba, ba3}. The normal subgroups are the unions {1}, {1, a2} and {1, a, a2, a3}, {1, b, a2, ba2} and {1, ba, a2, ba3}.
7. Let K = g−1Hg, so H = gKg−1. We claim N(K) = g−1N(H)g. Let a ![]() N(K) so a−1Ka = K. To show a
N(K) so a−1Ka = K. To show a ![]() g−1N(H)g it suffices to show gag−1
g−1N(H)g it suffices to show gag−1 ![]() N(H). But (gag−1)−1H(gag−1) = ga−1g−1Hgag−1 = ga−1Kag−1 = gKg−1 = H. HenceN(K) ⊆ g−1N(H)g. A similar argument shows that N(H) ⊆ gN(K)g−1 so g−1N(H)g ⊆ N(K).
N(H). But (gag−1)−1H(gag−1) = ga−1g−1Hgag−1 = ga−1Kag−1 = gKg−1 = H. HenceN(K) ⊆ g−1N(H)g. A similar argument shows that N(H) ⊆ gN(K)g−1 so g−1N(H)g ⊆ N(K).
11. Because H ⊆ N(H) ⊆ G, Exercise 31 §2.6 shows that |G: N(H)| is finite. Hence, Theorem 2 applies.
14. We have a−1Ha = {1, ba2} so ba2 ∉ N(H). Continue in this way.
16. ![]()
25. H is a union of conjugacy classes. Show that there exists a ≠ 1 such that {a} ⊆ H.
29. Since C ![]() G, let Z[G/C] = K/C. Since |G/C| > 1, Theorem 6 shows C ⊂ K. But K
G, let Z[G/C] = K/C. Since |G/C| > 1, Theorem 6 shows C ⊂ K. But K ![]() G so K
G so K ![]() H by Exercise 23 §2.8. If k
H by Exercise 23 §2.8. If k ![]() K then kC is in the center of G/C, so h−1k−1hk
K then kC is in the center of G/C, so h−1k−1hk ![]() C
C ![]() H. Hence k−1Hk ⊆ H, and similarly kHk−1 ⊆ H. Thus k
H. Hence k−1Hk ⊆ H, and similarly kHk−1 ⊆ H. Thus k ![]() N(H) and we have shown K ⊆ N(H).
N(H) and we have shown K ⊆ N(H).
Exercises 8.3 Group Actions
1. (a) By Cauchy's Theorem let a ![]() G, |a| = 5. If
G, |a| = 5. If ![]() then |G · H| = 4, so there is a homomorphism θ: G → S4 with ker θ ⊆ H. Then ker θ ≠ {1} because |G| = 20 does not divide |S4| = 24. Because H is simple, ker θ = H, so H
then |G · H| = 4, so there is a homomorphism θ: G → S4 with ker θ ⊆ H. Then ker θ ≠ {1} because |G| = 20 does not divide |S4| = 24. Because H is simple, ker θ = H, so H ![]() G.
G.
10. (a) H0 ⊆ H because H = 1G(H). If τ ![]() autG then τ−1σ
autG then τ−1σ ![]() autG for all σ
autG for all σ ![]() autG, so H0 ⊆ τ−1σ(H). Thus τ(H0) ⊆ σ(H) for all σ, so τ(H0) ⊆ H0. Simi-larly τ−1(H0) ⊆ H0, whence τ(H0) = H0. Thus H0 is characteristic in G.
autG, so H0 ⊆ τ−1σ(H). Thus τ(H0) ⊆ σ(H) for all σ, so τ(H0) ⊆ H0. Simi-larly τ−1(H0) ⊆ H0, whence τ(H0) = H0. Thus H0 is characteristic in G.
15. If σ = (k1k2 ![]() )(m1m2
)(m1m2 ![]() )(n1n2
)(n1n2 ![]() )
) ![]() , the orbits of the group G in Xn are G · k1 = {k1, k2, . . . }, G · m1 = {m1, m2, . . . }, G · n1 = {n1, n2, . . . },
, the orbits of the group G in Xn are G · k1 = {k1, k2, . . . }, G · m1 = {m1, m2, . . . }, G · n1 = {n1, n2, . . . }, ![]() . Clearly, G · k = {k} if and only if k is fixed by σ.
. Clearly, G · k = {k} if and only if k is fixed by σ.
17. (a) x ≡ x because x = x· 1; if x ≡ y, say y = x · a, a ![]() G, then x = y · a−1, so y≡ x; if x ≡ y and y ≡ z, say y = x · a, z = y · b, then z = (x · a) · b = x · (ab), so z ≡ x.
G, then x = y · a−1, so y≡ x; if x ≡ y and y ≡ z, say y = x · a, z = y · b, then z = (x · a) · b = x · (ab), so z ≡ x.
23. (a) If a, b ![]() S(x) then (ab) · x = a · (b · x) = a · x = x, so ab
S(x) then (ab) · x = a · (b · x) = a · x = x, so ab ![]() S(G). Similarly, a−1 · x = a−1 · (a · x) = (a−1 · a) · x = 1 · x = x, so a−1
S(G). Similarly, a−1 · x = a−1 · (a · x) = (a−1 · a) · x = 1 · x = x, so a−1 ![]() S(G). Finally 1 · x = x shows 1
S(G). Finally 1 · x = x shows 1 ![]() S(x), and we are done.
S(x), and we are done.
28. If X = {H ⊆ G|H is a subgroup and |H| = pk}, let G act on X by conjugation. Use Theorem 4.
32. (a) (1, 1) · x = 1x1−1 = x, and ![]() . The orbit is (H × K) · x = {(h, k) · x
. The orbit is (H × K) · x = {(h, k) · x ![]() h
h ![]() H, k
H, k ![]() K} = {hxk−1
K} = {hxk−1 ![]() h
h ![]() H, k
H, k ![]() K} = HxK.
K} = HxK.
Exercises 8.4 The Sylow Theorems
1. If P is a Sylow 3-subgroup, then ![]() where γ is a 3-cycle, say γ = (ijk). If
where γ is a 3-cycle, say γ = (ijk). If ![]() where {1, 2, 3, 4} = {i, j, k, x}, then σ(123)σ−1 = γ. Hence
where {1, 2, 3, 4} = {i, j, k, x}, then σ(123)σ−1 = γ. Hence ![]() so P is conjugate to
so P is conjugate to![]()
3. P is a Sylow p-subgroup of N(P), being a p-subgroup of maximal order. It is unique because it is normal in N(P).
7. (a) |G| = 40 = 23 · 5. Thus, n5 = 1, 2, 4, 8, and n5 ≡ 1 (mod5). Hence, n5 = 1, so the Sylow 5-subgroup is normal. (c) |G| = 48 = 24 · 3. If P is a Sylow 2-subgroup then |G: P| = 3, so a homomorphism θ: G → S3 exists. Clearly, ker θ ≠ {1}.
9. (a) |G| = 70 = 2 · 5 · 7. Then n5 = 1, 2, 7, 14, and n5 ≡ 1 (mod5), so n5 = 1. Similarly n7 = 1, so let P ![]() G and Q
G and Q ![]() G, where |P| = 5 and |Q| = 7. Because P ∩ Q = {1}, PQ ≅ P × Q ≅ C5 × C7 ≅ C35. Hence, |G: PQ| = 2, so PQ
G, where |P| = 5 and |Q| = 7. Because P ∩ Q = {1}, PQ ≅ P × Q ≅ C5 × C7 ≅ C35. Hence, |G: PQ| = 2, so PQ ![]() G.
G.
11. (a) |G| = 105 = 3 · 5 · 7. Then n7 = 1, 3, 5, 15, and n7 ≡ 1 (mod7), so n7 = 1, 15. Similarly, n5 = 1, 21. Let P and Q by Sylow 7-and 5-subgroups. If neither is normal in G, then G has 21 · 4 = 84 elements of order 5 and 15 · 6 = 90 elements of order 7, a contradiction. So P ![]() G or Q
G or Q![]() G; hence PQ is a subgroup, and |PQ| = |P||Q| = 35 because P ∩ Q = {1}. As |G: PQ| = 3, let θ: G → S3 be a homomorphism with ker θ ⊆ PQ. Then | ker θ| ≠ 1, 5, 7, so PQ = ker θ
G; hence PQ is a subgroup, and |PQ| = |P||Q| = 35 because P ∩ Q = {1}. As |G: PQ| = 3, let θ: G → S3 be a homomorphism with ker θ ⊆ PQ. Then | ker θ| ≠ 1, 5, 7, so PQ = ker θ ![]() G. Finally, P
G. Finally, P ![]() PQ and Q
PQ and Q ![]() PQ by the Sylow Theorems, so PQ ≅ P × Q ≅ C7 × C5 ≅ C35.
PQ by the Sylow Theorems, so PQ ≅ P × Q ≅ C7 × C5 ≅ C35.
13. Let P be a Sylow p -subgroup of G. Since p > m we have |P| = pn, so |G: P| = m. Apply Theorem 1 §8.3.
19. If Q is also a Sylow p -subgroup of G, then Q = a−1Pa by Sylow's second theorem. If g ![]() N(Q) then Q = g−1Qg; that is a−1Pa = g−1a−1Pag. This implies that aga−1
N(Q) then Q = g−1Qg; that is a−1Pa = g−1a−1Pag. This implies that aga−1 ![]() N(P) = P, whence g
N(P) = P, whence g ![]() a−1Pa = Q.
a−1Pa = Q.
Exercises 8.5 Semidirect Products
1. (a). Write σ = (1 2) ![]() Sn and
Sn and ![]() Then An ⊆ AnH ⊆ Sn As Sn/An ≅ C2, either AnH = Sn or AnH = An. Since σ ∉ An we have Sn = AnH. Similarly, An ∩ H ≠ {ε} means An ∩ H = H (because H is simple), contradicting h ∉ Anonce more. Hence An ∩ H = {ε} and the result follows from Theorem 2.
Then An ⊆ AnH ⊆ Sn As Sn/An ≅ C2, either AnH = Sn or AnH = An. Since σ ∉ An we have Sn = AnH. Similarly, An ∩ H ≠ {ε} means An ∩ H = H (because H is simple), contradicting h ∉ Anonce more. Hence An ∩ H = {ε} and the result follows from Theorem 2.
3. This is an instance of Theorem 3 (3), where p = 3 and q = 13. We have q ≡ 1 (mod p), so we look for m such that 1 ≤ m ≤ 12 and m5 ≡ 1 (mod 13). If m = 1 then G ≅ C13 × C3 ≅ C55. The first solution with m > 1 is m = 3, whence ![]() where o(a) = 11, o(b) = 3 and ab = ba3.
where o(a) = 11, o(b) = 3 and ab = ba3.
Exercises 8.6 An Application to Combinatorics
6. (a) ![]()
8. (a) ![]()
Exercises 9.1 The Jordan–HÖLder Theorem
1. (a) 3; C2, C2, C2 (c) 3; C2, C2, C2 (e) 3; C2, C2, C2
3. (a) If Hk is the unique subgroup of order k in C24, the series are
| C24 ⊃ H12 ⊃ H4 ⊃ H2 ⊃ {1} |
| C24 ⊃ H12 ⊃ H6 ⊃ H3 ⊃ {1} |
| C24 ⊃ H12 ⊃ H6 ⊃ H2 ⊃ {1} |
| C24 ⊃ H8 ⊃ H4 ⊃ H2 ⊃ {1} |
8. (a) Let n = p1p2 ![]() pm, where the pi are distinct primes. Then Cn has length 1 + 1 +
pm, where the pi are distinct primes. Then Cn has length 1 + 1 + ![]() + 1 = m by Example 8.
+ 1 = m by Example 8.
11. Induct on n. If n = 1 then G = G0 ⊃ G1 = {1} so G ≅ G0/G1 is finite. In gen-eral, G1 is finite by induction, and G/G1 = G0/G1 is finite by hypothesis. Thus G consists of |G/G1| cosets, each with |G1| elements. Hence G is finite. Now |G| = |G0/G1| · |G1|, and the formula follows by induction.
15. (a) If M ⊆ Cn is maximal normal, then Cn/M has order a prime q (being simple and abelian). Hence, q = pi for some i because q divides |Cn| = n. Thus, ![]() for some i = 1, 2, . . ., r. Since Cn is cyclic, it has exactly one subgroup of order
for some i = 1, 2, . . ., r. Since Cn is cyclic, it has exactly one subgroup of order ![]() by Theorem 9 §2.4.
by Theorem 9 §2.4.
Exercises 9.2 Solvable Groups
1. No, Z(S4) = {ε}.
3. No. S4 is solvable (Example 4) but ![]() is not abelian. Indeed
is not abelian. Indeed ![]() because S4/A4 is abelian. Thus
because S4/A4 is abelian. Thus ![]() , {ε} or K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}. But S4/{ε} and S4/K are not abelian (see Exercise 30 §2.9).
, {ε} or K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}. But S4/{ε} and S4/K are not abelian (see Exercise 30 §2.9).
8. (a) This is because α[a, b] = [α(a), α(b)] for every commutator [a, b] from G.
9. By Exercise 14 §8.4, let K ![]() G, K ≠ {1}, G. Then both |K| and |G/K| are in {p, q, p2, pq}. Hence, both are either abelian or of order pq and thus are solvable. Use Theorem 4.
G, K ≠ {1}, G. Then both |K| and |G/K| are in {p, q, p2, pq}. Hence, both are either abelian or of order pq and thus are solvable. Use Theorem 4.
15. If G is solvable and G = G0 ⊃ G1 ⊃ ![]() ⊃ Gp = {1} is a composition series, each simple factor is abelian and hence finite. Hence,
⊃ Gp = {1} is a composition series, each simple factor is abelian and hence finite. Hence, ![]() is finite (see Exercise 11 §9.1). The converse holds because every finite group has a composition series.
is finite (see Exercise 11 §9.1). The converse holds because every finite group has a composition series.
19. HK is a subgroup as K ![]() G, and
G, and ![]() is solvable by Theorem 3 (H is solvable). Done by Theorem 4.
is solvable by Theorem 3 (H is solvable). Done by Theorem 4.
21. (a) Because G ≠ {1}, G′ ≠ G by Theorem 5. Thus G/G′ is nontrivial and abelian.
23. (a) Write {K ![]() G
G ![]() G/K solvable} = {K1, K2, . . ., Km}. This set is nonempty as it contains G. Then
G/K solvable} = {K1, K2, . . ., Km}. This set is nonempty as it contains G. Then ![]() is normal and G/R is solvable by Exercise 18. If K
is normal and G/R is solvable by Exercise 18. If K ![]() G and G/K solvable, then R ⊆ K by definition.
G and G/K solvable, then R ⊆ K by definition.
27. (a) Write ![]() . Then V
. Then V ![]() G because the intersection of normal subgroups is normal. Note that the intersection is not empty because G
G because the intersection of normal subgroups is normal. Note that the intersection is not empty because G ![]() G and G/G is in
G and G/G is in ![]() . If V = K1 ∩ K2 ∩
. If V = K1 ∩ K2 ∩ ![]() ∩ Kn then G/V embeds in
∩ Kn then G/V embeds in ![]() (as in Exercise 18) and
(as in Exercise 18) and ![]() is in
is in ![]() by induction because
by induction because ![]() is closed under taking direct products. Hence G/V is in
is closed under taking direct products. Hence G/V is in ![]() , being isomorphic to a subgroup of a group in
, being isomorphic to a subgroup of a group in ![]()
Exercises 9.3 Nilpotent Groups
2. If H ![]() G and K
G and K ![]() G then a−1[h, k]a = [a−1ha, a−1ka]
G then a−1[h, k]a = [a−1ha, a−1ka] ![]() [H, K] for all h
[H, K] for all h ![]() H and k
H and k ![]() K.
K.
6. (a) By induction on n, it suffices to show that Γi(G × H) ⊆ Γi(G) × Γi(H). Do so by induction on i. If i = 0, then Γ0(G × H) = G × H = Γ0(G) × Γ0(H). If the relation holds for i ≥ 0, then Γi+1(G × H) = [Γi(G × H), G × H] ⊆ [Γi(G) × Γi(H), G × H], so it suffices to show that, if A ⊆ G, B ⊆ H, then [A × B, G × H] ⊆ [A, G] × [B, H]. This outcome follows because [(a, b), (g, h)] = ([a, g], [b, h]).
9. If n = 2k then |Dn| = 2k+1 so Dn is nilpotent by Example 3. Conversely, suppose n = 2km, m > 1 odd. Show that ![]() so Dm is nilpotent by Theorem 1. But in this case {1, b} is a Sylow 2-subgroup that is not normal, contradicting Theorem 4.
so Dm is nilpotent by Theorem 1. But in this case {1, b} is a Sylow 2-subgroup that is not normal, contradicting Theorem 4.
13. K ∩ Z(G) ≠ {1} by Exercise 11. Thus, K ∩ Z(G) = K by the condition on K. Now every subgroup of K is normal in G, so |K| is prime.
18. (a) H is itself nilpotent by Theorem 1 so, by Theorem 4, H is a product of p -groups. Now apply Theorem 6 §8.2.
21.
a. If H =![]() a2
a2 ![]() then H and
then H and ![]() are maximal.
are maximal.
b. If H =![]() ap
ap ![]() and H =
and H =![]() aq
aq ![]() then
then ![]() and
and ![]() are maximal, as is
are maximal, as is ![]() a2
a2![]() .
.
24. (1)⇒(2). We show that G′ ⊆ Φ, that is G′ ⊆ M for every maximal subgroup M of G. Show that this follows by (1) because M ![]() G.
G.
26. (a) Write Φ(G) = Φ and ![]() , where F
, where F ![]() G. If M is maximal in G then K ⊆ M (because K ⊆ Φ ⊆ M) and
G. If M is maximal in G then K ⊆ M (because K ⊆ Φ ⊆ M) and ![]() is maximal in
is maximal in ![]() . Hence
. Hence ![]() whence F ⊆ M. It follows that F ⊆ Φ. Conversely, let α: G → G/K be the coset map. Then α(Φ) ⊆ Φ(G/K) by the preceding exercise, so x
whence F ⊆ M. It follows that F ⊆ Φ. Conversely, let α: G → G/K be the coset map. Then α(Φ) ⊆ Φ(G/K) by the preceding exercise, so x ![]() Φ implies
Φ implies ![]() ; so x
; so x ![]() F. Thus Φ ⊆ F.
F. Thus Φ ⊆ F.
Exercises 10.1 Galois Groups and Separability
1. ε, σ−1 and στ all fix F when σ and τ do.
3. ![]() because σ(ai) = ai for ai
because σ(ai) = ai for ai ![]() F.
F.
5. If σ: E → E is an automorphism, show that σ(q) = q for all ![]()
7. C2
9. C2 × C2
11. Show that E = F(u) if u ![]() E F. If m is the minimal polynomial of u over F, show °m = 2.
E F. If m is the minimal polynomial of u over F, show °m = 2.
13. Construct σ and τ in gal![]() with σ(u) = iu, σ(i) = i, and τ(u) = u, τ(i) = − i.
with σ(u) = iu, σ(i) = i, and τ(u) = u, τ(i) = − i.
15. (a) ![]() and
and ![]() in Theorem 6.
in Theorem 6.
16. ![]() and
and ![]() in Theorem 6.
in Theorem 6.
17. See the Hint.
19. We proceed by induction on n. If n = 1 then E = F(u1) = {f(u1) ![]() f(x)
f(x) ![]() F[x]}. Hence σ(f(u1)) = g(σ(u1)) = g(τ(u1)) = τ(f(u1)) for all f, as required. In gen-eral, write K = F(u1, u2, . . ., un−1) so that E = K(un). By induction, σ = τ on K, so σ, τ
F[x]}. Hence σ(f(u1)) = g(σ(u1)) = g(τ(u1)) = τ(f(u1)) for all f, as required. In gen-eral, write K = F(u1, u2, . . ., un−1) so that E = K(un). By induction, σ = τ on K, so σ, τ![]() gal(K: F). Since σ(un) = τ(un) the result follows from the case n = 1.
gal(K: F). Since σ(un) = τ(un) the result follows from the case n = 1.
21. See the Hint.
22. (a) For (3)⇒(1), if f has a repeated root u in E ⊇ F, let 1 = fg + f′h in F[x] by (3).
23. If d = gcd (f, f′), show d = 1.
25. If E ⊇ F and q is an irreducible factor of f in E[x], write f = p1p2 ![]() pr in F[x], pi irreducible, and show that q|pi for some i.
pr in F[x], pi irreducible, and show that q|pi for some i.
27. If not, and u is a root of f in a splitting field E ⊇ F, show f = (x − u)p in E[x]. If q is an irreducible factor of f in F[x], show q = (x − u)t.
29. (a) If F is perfect, and a ![]() F, let E be the splitting field of f = xp − a. If u
F, let E be the splitting field of f = xp − a. If u ![]() E is a root of f show f = (x − u)p. If q is an irreducible factor of f in F[x] show that q = x − u. Use Theorem 4.
E is a root of f show f = (x − u)p. If q is an irreducible factor of f in F[x] show that q = x − u. Use Theorem 4.
30. (a) Let q be the minimal polynomial of u over F. If K = F(up) let m ![]() K[x] be the minimal polynomial of u over K. Then q
K[x] be the minimal polynomial of u over K. Then q ![]() K[x] and q(u) = 0, so m|q. But q has distinct roots by hypothesis, so m has distinct roots. On the other hand, xp − up
K[x] and q(u) = 0, so m|q. But q has distinct roots by hypothesis, so m has distinct roots. On the other hand, xp − up ![]() K[x] and xp − up = (x − u)p in E[x]. Hence m|(x − u)p so m = (x − u)r. Since m has distinct roots, r = 1 and so u
K[x] and xp − up = (x − u)p in E[x]. Hence m|(x − u)p so m = (x − u)r. Since m has distinct roots, r = 1 and so u ![]() K.
K.
32. (a) Let p and q be the minimal polynomials of u over F and K respectively. Then p ![]() K[x] and p(u) = 0, so q|p. Since p has distinct roots in some splitting field L ⊇ K, q is separable over K.
K[x] and p(u) = 0, so q|p. Since p has distinct roots in some splitting field L ⊇ K, q is separable over K.
Exercises 10.2 The Main Theorem of Galois Theory
1.
a. By Example 4 §10.1, ![]() , where σ(u) = u2. If
, where σ(u) = u2. If ![]() then H
then H![]() is the only intermediate field (except
is the only intermediate field (except ![]() ).
). ![]() .
.

c. By Exercise 9 §10.1, ![]() , where σ(i) = − i,
, where σ(i) = − i, ![]() ; and τ(i) = i,
; and τ(i) = i, ![]() . If
. If ![]() and
and ![]() , the lattice of fields is as shown.
, the lattice of fields is as shown. ![]() ;
; ![]() .
.

e. If ![]() then
then ![]() and, by Exercise 13 §10.1,
and, by Exercise 13 §10.1, ![]() where σ(u) = iu, σ(i) = i; and τ(u) = u, τ(i) = − i. The lattice diagram is shown. Primitive elements are
where σ(u) = iu, σ(i) = i; and τ(u) = u, τ(i) = − i. The lattice diagram is shown. Primitive elements are ![]()
![]() and
and ![]()

2. (a) Either ![]() :
:
or ![]() :
:

5. (a) Let ![]() show f(t)g(− t) = f(− t)g(t). If char F ≠ 2, write h(t) = f(t)g(− t). Show that h(t) = k(t2) for some polynomial k Similarly and g(t)g(− t) = l(t2) for some polynomial l. Continue.
show f(t)g(− t) = f(− t)g(t). If char F ≠ 2, write h(t) = f(t)g(− t). Show that h(t) = k(t2) for some polynomial k Similarly and g(t)g(− t) = l(t2) for some polynomial l. Continue.
7. Clear.
9. (a) An intermediate field K is closed if ![]()
11. Exercise 34 §2.6.
15. (a) Use the Galois connection.
17. If K = σ(K1) show ![]() If
If ![]() show K1 ⊆ σ−1(K), so σ(K1) ⊆ K, and similarly K ⊆ σ(K1).
show K1 ⊆ σ−1(K), so σ(K1) ⊆ K, and similarly K ⊆ σ(K1).
19. (a) Let E = F(u1, u2, . . ., um) where u1, . . ., um are the distinct roots of f, use Theorem 3 §10.1.
20. (a) Apply σ to the formulas for N(u) and T(u).
21. If ![]() show fτ = ∏ σ
show fτ = ∏ σ![]() G[x − τσ(u)] = f.
G[x − τσ(u)] = f.
Exercises 10.3 Insolvability of Polynomials
1. (a) ![]()
2. (a) f′ = 5x4 − 4 has roots ±a and ±ia, where ![]() Then f(a) < 0 and f(− a) > 0, so f has three real roots and two (conjugate) nonreal roots. As f is irreducible (Eisenstein), its Galois group is S5, as in Example 1.
Then f(a) < 0 and f(− a) > 0, so f has three real roots and two (conjugate) nonreal roots. As f is irreducible (Eisenstein), its Galois group is S5, as in Example 1.
3. Show that p = x7 − 14x + 2 has three distinct real roots and two (conjugate) complex roots. If ![]() is the splitting field, view
is the splitting field, view ![]() as a subgroup of SX where
as a subgroup of SX where ![]() are the roots. Then conjugation is a transposition and, if u is a real root, then
are the roots. Then conjugation is a transposition and, if u is a real root, then ![]() because p is the minimal polynomial of u over
because p is the minimal polynomial of u over ![]() Proceed as in Example 1.
Proceed as in Example 1.
5. Let X denote the set of roots of p in a splitting field E ⊇ F where p ![]() F[x]. View G = gal(E: F) ⊆ SX, so G embeds in S4.
F[x]. View G = gal(E: F) ⊆ SX, so G embeds in S4.
7. Since f′ = 3(x2 − 1), conclude that f has three real roots. In the cubic formula, p3 and q3 are roots of x2 + x + 1 which satisfy p3 + q3 = − 1 and pq = 1. The roots are ![]() and
and ![]() Show that p = e2πi/9 and
Show that p = e2πi/9 and ![]() . The roots are
. The roots are ![]() and
and ![]() Finally
Finally ![]()
8. (a) σ(Δ2) = Δ2 for all σ ![]() G because σ permutes the roots ui.
G because σ permutes the roots ui.
Exercises 10.4 Cyclotomic Polynomials and Wedderburn's Theorem
1.
![]()
3. Use the Hint and induction.
5. If ![]() , these fields are
, these fields are ![]() and
and ![]() respectively. Show that
respectively. Show that ![]() . (⊇ requires gcd (m, n) = 1).
. (⊇ requires gcd (m, n) = 1).
7. Write σ(n) = ∑ d|nμ(d). If ![]() and m = p1p2
and m = p1p2 ![]() pr, then σ(n) = σ(m). If d|m, show μ(d) = 1 if and only if d is the product of an even number (possibly 0) of the pi, and μ(d) = − 1 otherwise.
pr, then σ(n) = σ(m). If d|m, show μ(d) = 1 if and only if d is the product of an even number (possibly 0) of the pi, and μ(d) = − 1 otherwise.
8.

Exercises 11.1 Wedderburn'S Theorem
1. Show that M = Rx and use Theorem 1 §7.1.
3. Straight forward.
5. If L ⊆ eRe is a left ideal, consider RL.
7. Use the Corollary to Lemma 2 and Theorem 5 §7.1.
8.
a. Show there exists a minimal member of ![]() and X is finite}.
and X is finite}.
9. Let ![]() and p does not divide m}. If
and p does not divide m}. If ![]() where Y is a subgroup of X, show that there exists
where Y is a subgroup of X, show that there exists ![]() with n maximal. Then show that
with n maximal. Then show that ![]()
11.
a. If x ![]() M show that x− π(x)
M show that x− π(x) ![]() ker π. It follows that M = π(M)+ ker π. Continue.
ker π. It follows that M = π(M)+ ker π. Continue.
13.
a. If K = K1⊕ K2 ⊕ ![]() then K⊃ K2 ⊕ K3 ⊕
then K⊃ K2 ⊕ K3 ⊕ ![]() ⊃ K3 ⊕ K4 ⊃
⊃ K3 ⊕ K4 ⊃ ![]() and K1⊂ K1 ⊕ K2 ⊂ K1 ⊕ K2 ⊕ K3 ⊂
and K1⊂ K1 ⊕ K2 ⊂ K1 ⊕ K2 ⊕ K3 ⊂ ![]() .
.
15. Use the Hint.
17.
a. Show that ker(α)⊆ ker(α2) ⊆ ker(α3) ⊆ ![]() and apply the noetherian condition.
and apply the noetherian condition.
19.
a. To see that θ is multiplicative, let θ(r) = [rij] and θ(s) = [sij], so that ![]() and
and ![]() for each i. Compute uirs.
for each i. Compute uirs.
Exercises 11.2 The Wedderburn–Artin Theorem
2.
a. Show that R = L ⊕ M for some left ideal, and 1 = e + f where e ![]() L and f
L and f ![]() M.
M.
3.
a. The axioms are routinely verified.
5. Each ![]() is simple.
is simple.
7. Use the preceding exercise and Lemma 3 §11.1.
9. Show that R is simple as a left R-module.
11. The left ideals of the ring R/A are simultaneously left R-modules and left R/A-modules with the same action.
13. (2) ⇒ (1) If 0 ≠ x ![]() Re show that xax ≠ 0, a
Re show that xax ≠ 0, a ![]() R. Show that Rx = Re.
R. Show that Rx = Re.
15. Use Theorem 1(1) §11.1.
16. (a) (ML)2 = MLML. (b). (Ar)2 = ArAr.
17. Use Exercise 4.
19. Use Lemma 3 §3.3.
20. (a) Use the definition of domain.
21. Use Lemma 9 and Theorem 3.
22. (a) and (c) Use Schur's lemma.
Exercises A Complex Numbers
1.
| (a) x = 3 | (c) x = 0, x = 4i |
2.
![]()
3.
| (a) 1 − 3i | (c) |
(e) 2 + 3i |
5.
| (a) Unit circle | (c) Line y = x | (e) |
10.
| (a) |
(c) 2e5πi/6 | (e) 7e−πi/2 |
11.
| (a) −3 | (c) |
(e) |
12.
| (a) |
(c) 16 | (e) −64 |
14.
| (a) |
(c) 3i, |
19. If f(x) = z0 + z1x + z2x2 + ![]() + znxn, the coefficient of xk in
+ znxn, the coefficient of xk in ![]() is
is ![]() where the last term is real but missing if k is odd. Each of the other summands is also real, being a complex number plus its conjugate.
where the last term is real but missing if k is odd. Each of the other summands is also real, being a complex number plus its conjugate.
Exercises B Matrix Arithmetic
1. Use A−1.
2. (a) Use the definition of matrix multiplication.
3. Compute.
5. I and −I.
7. In general, show (A + B)(A − B) = A2 + AB − BA − B2.
9. A−1 = A2.
11. (a) In general, if AC = I = CA then A is invertible and A−1 = C. (c) If I + BA is invertible, compute (I + AB)(I − A(I + BA)−1B).
13. (a) Use Theorem 7.
15. (a) Use the definition of matrix multiplication. (c) aijEij has aij in the (i, j)-entry and zeros elsewhere.
Exercises C Zorn's Lemma
1.
a. Let ![]() is a submodule and K ∩ X = 0}. Then
is a submodule and K ∩ X = 0}. Then ![]() is nonempty because
is nonempty because ![]() so let {Xi
so let {Xi ![]() i
i ![]() I} be a chain from
I} be a chain from ![]() and put U = ∪ i
and put U = ∪ i![]() IXi. It is clear that U is a submodule, and K ∩ U = 0 because K ∩ U ⊆ K ∩ Xi = 0 for each i. Hence U is an upper bound for the chain {Xi
IXi. It is clear that U is a submodule, and K ∩ U = 0 because K ∩ U ⊆ K ∩ Xi = 0 for each i. Hence U is an upper bound for the chain {Xi ![]() i
i ![]() I}, so
I}, so ![]() contains maximal members by Zorn's lemma.
contains maximal members by Zorn's lemma.
