Chapter 2
Groups
Wherever groups disclose themselves, or could be introduced, simplicity crystallizes out of complete chaos.
—Eric Temple Bell
The origin of the modern theory of groups lies in the theory of equations. By the beginning of the nineteenth century, mathematicians had developed formulas for finding the roots of any cubic or quartic equation (analogous to the quadratic formula), and the best mathematicians of the day were trying to find such a formula for the quintic. It thus came as a great surprise when, in 1824, Niels Henrik Abel proved that no such formula exists. At about the same time, Evariste Galois showed that any equation of degree n has an associated group of permutations of the roots of the equation (that is, a set of permutations closed under compositions and inverses). He proved that the equation is solvable if and only if this group has a certain property (now called a solvable group). In particular, the fact that the group An of even permutations is not solvable for any n ≥ 5 implies that no formula exists for solving equations of degree n ≥ 5. This spectacular achievement led to modern Galois theory, but Galois' work went unrecognized until after his death at age 20.
Galois worked with groups of permutations. Then, in 1854, Arthur Cayley formulated the abstract group concept. While the study of permutation groups continues to occupy mathematicians, the abstract theory has the advantage that it isolates those properties of groups that do not depend on the underlying permutations and so can be applied more broadly. We pursue the abstract theory in this chapter (and in Chapters 7–9) with permutation groups as one of the most important examples. 71
Abstract algebra is primarily concerned with the study of operations analogous to the addition and multiplication of numbers. We define such operations in this section and examine some of their general properties. The addition process for numbers assigns to any ordered pair (a, b) of numbers a new number, their sum, denoted a + b. Similarly, multiplication assigns the product ab to the pair (a, b).
In general, a binary operation * on a set M is a mapping that assigns to each ordered pair (a, b) of elements of M an element a * b of M. In this case M is said to be closed under the binary operation. Binary operations are usually denoted by other symbols (for example, + for numbers) but, for the moment, we use the generic notation a * b.
A binary operation * is called commutative if a * b = b * a for all a, b in M, and * is called associative if a * (b * c) = (a * b) * c for all a, b, c in M. An element e in M is called a unity (or an identity)18 for * if a * e = a = e * a for all a in M. The unity for a binary operation is often denoted by different symbols (for example, 0 and 1 are the identities for addition and multiplication of numbers, respectively).
Theorem 1. If a binary operation has a unity, that unity is unique.
Proof. If e and f are both unities, then f = e * f and e * f = e. So e = f.
A set M is called a monoid if a binary operation is defined on M that is associative and has an unity19. We say that (M, *) is a monoid if the operation * is to be emphasized. If the operation is commutative, we say that M is a commutative monoid.
Example 1. The sets ![]() are all commutative monoids under both addition and multiplication. The additive unity is 0 in all cases (
are all commutative monoids under both addition and multiplication. The additive unity is 0 in all cases (![]() in
in ![]() ), and the multiplicative unity is 1 (
), and the multiplicative unity is 1 (![]() in
in ![]() ).
).
Example 2. The set ![]() of all n × n real matrices is a monoid under both matrix addition and matrix multiplication, the unities being 0 and I, respectively. The monoid
of all n × n real matrices is a monoid under both matrix addition and matrix multiplication, the unities being 0 and I, respectively. The monoid ![]() is commutative. However,
is commutative. However, ![]() is not commutative if n ≥ 2 (the proof of associativity is given in Appendix B).
is not commutative if n ≥ 2 (the proof of associativity is given in Appendix B).
Example 3. If U is a set, let M = {X ![]() X ⊆ U} denote the set of all subsets of U. Then (M, ∪) and (M, ∩) are both commutative monoids, the unities being ∅ and U, respectively.
X ⊆ U} denote the set of all subsets of U. Then (M, ∪) and (M, ∩) are both commutative monoids, the unities being ∅ and U, respectively.
Example 4. Sn is a monoid with unity ε, and it is noncommutative if n ≥ 3 (see Exercise 23 §1.4).
Example 5. If X is a nonempty set, let M = {α ![]() α: X → X is a mapping}. Then M is a monoid using composition of mappings as the operation and the identity mapping 1X as the unity (Theorem 3 §0.3). Moreover, M is noncommutative if X has at least two elements.
α: X → X is a mapping}. Then M is a monoid using composition of mappings as the operation and the identity mapping 1X as the unity (Theorem 3 §0.3). Moreover, M is noncommutative if X has at least two elements.
Example 6. Let * be the operation defined on ![]() by n * m = nm. This operation is neither commutative (2 * 3 = 8 but 3 * 2 = 9) nor associative ((2 * 3) * 2 = 64, but 2 * (3 * 2) = 512), and there is no unity (m = x * m for all m is impossible). Thus
by n * m = nm. This operation is neither commutative (2 * 3 = 8 but 3 * 2 = 9) nor associative ((2 * 3) * 2 = 64, but 2 * (3 * 2) = 512), and there is no unity (m = x * m for all m is impossible). Thus ![]() is not a monoid. Note, however, that m * 1 = m for all m.
is not a monoid. Note, however, that m * 1 = m for all m.
A comment on notation is in order here. Binary operations are denoted by many different symbols in mathematics. For example, + and · are universally used for addition and multiplication of numbers, but these symbols are also standard for the addition and multiplication of matrices. Similarly, ∩ and ∪ are well-established notations in set theory. When a binary operation has such a standard symbol, we use it along with any standard notation for the corresponding unity (as in the foregoing examples). However, when discussing monoids in general, we have been using * for the binary operation. But algebraists do not do this. They usually adopt one of the following two formats.
- Multiplicative Notation. Here a * b is written as ab (or sometimes a · b) and is called the product of a and b. The multiplicative unity is denoted 1 (or 1M if the monoid M must be emphasized).
- Additive Notation. Here a * b is written as a + b and is called the sum of a and b. The additive unity is denoted 0 (or 0M if the monoid M must be emphasized).
Multiplicative notation is the most popular format among algebraists. Hence we adopt the following convention.
Convention. In dealing with monoids in general, we use multiplicative notation, and denote the unity by 1.
Hence ab can mean many different things, depending on the monoid under discussion, but the meaning is nearly always clear from the context. The small amount of confusion is more than balanced by the simplicity and conciseness of the notation.
For a finite monoid M, defining the operation by means of a table is sometimes convenient (as in Example 7 below). Given x and y in M, the product xy is the entry of the table in the row corresponding to x and the column corresponding to y. Hence, for the table in Example 7, ab = b and ca = e. The elements of the monoid appear in the same order across the top of the table as down the left side. Such a table is called the Cayley table of the monoid, honoring Arthur Cayley who used it in 1854.
Example 7. If M = {e, a, b, c}, consider the binary operation shown in the table. The first row and column show that e is the unity. That the operation is commutative is also clear from the table because the entries are symmetric about the main diagonal (upper left to lower right). However, this operation is not associative. For example ![]()

If a, b, c, and d are elements in a monoid M, there are various ways to form the product abcd—for example [(ab)c]d and a[b(cd)]. Verifying that these forms are equal is not difficult using associativity. In fact, we have
Theorem 2. General Associativity. Let a1, a2, ![]() , an be elements of a monoid M. If the product a1a2
, an be elements of a monoid M. If the product a1a2 ![]() an is formed (in that order), the result is the same no matter which bracketing is used.
an is formed (in that order), the result is the same no matter which bracketing is used.
Proof20. Let the standard product ![]() be defined inductively by setting
be defined inductively by setting ![]() and
and ![]() for n ≥ 2. Thus,
for n ≥ 2. Thus, ![]() and so on. We use strong induction on n ≥ 1 to prove the following statement: If p is any product of a1, a2,
and so on. We use strong induction on n ≥ 1 to prove the following statement: If p is any product of a1, a2, ![]() , an in that order, then
, an in that order, then ![]() This is clear if n = 1 or n = 2; if n = 3, the only non-standard product is (a1a2)a3, which equals
This is clear if n = 1 or n = 2; if n = 3, the only non-standard product is (a1a2)a3, which equals ![]() by associativity. In general, because p is formed using multiplication, it must factor as p = qr, where q is a product of a1, a2,
by associativity. In general, because p is formed using multiplication, it must factor as p = qr, where q is a product of a1, a2, ![]() , ak and r is a product of ak+1,
, ak and r is a product of ak+1, ![]() , an for some k with 1 ≤ k ≤ n − 1. Hence
, an for some k with 1 ≤ k ≤ n − 1. Hence ![]() by induction. If k = 1, then
by induction. If k = 1, then
![]()
as required. If k > 1, then ![]() by induction, and
by induction, and
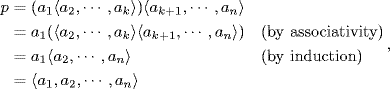
which completes the proof.
Theorem 2 enormously simplifies notation. It means that, in a monoid, we may (and do) write a1a2 ![]() an for the product of n elements with no ambiguity. If the operation were not associative, we would have to be careful about which bracketing we use. Of course, the order of the factors in a product does make a difference if the operation is not commutative.
an for the product of n elements with no ambiguity. If the operation were not associative, we would have to be careful about which bracketing we use. Of course, the order of the factors in a product does make a difference if the operation is not commutative.
Let a be an element of a monoid M. If n ≥ 0 is an integer, inductively define the nth power an of a as follows:
![]()
Thus, a1 = a, a2 = a · a, a3 = a · a · a, and so on. The following laws, familiar for numbers, hold for any monoid.
Theorem 3. Exponent Laws. Let a and b be elements of a monoid M.
1. anam = an+m for all n ≥ 0 and m ≥ 0.
2. (an)m = anm for all n ≥ 0 and m ≥ 0.
3. If ab = ba, then (ab)n = anbn for all n ≥ 0.
Proof. (1) Fix m ≥ 0 and prove (1) by induction on n ≥ 0. If n = 0 then a0am = 1am = am = a0+m. If n ≥ 1 then anam = (aan−1)am = a(an−1am). Since an−1am = an−1+m by induction, this gives anam = a(an−1+m) = an+m.
(2) Fix n ≥ 0 and induct on m using (1). If m = 0, then (an)0 = 1 = an·0. If m ≥ 1, then (an)m = an · (an)m−1 = anan(m−1) = an+n(m−1) = anm.
(3) This assertion follows by induction on n after first showing ban = anb for all n ≥ 0 (Exercise 10).
It is interesting to note that, in the monoids of Example 3 (with ∩ and ∪ as the operations), a2 = a for all a. Hence an = a for all n ≥ 1.
Inverses
If s is a nonzero real number, the inverse ![]() is the solution to the equation xs = 1. In this form the idea extends to any monoid. If a is an element in a monoid M, an element b of M is called an inverse of a if ab = 1 = ba. An element with an inverse is called a unit. Note that the definition is symmetric in a and b, so that a is an inverse of b if and only if b is an inverse of a.
is the solution to the equation xs = 1. In this form the idea extends to any monoid. If a is an element in a monoid M, an element b of M is called an inverse of a if ab = 1 = ba. An element with an inverse is called a unit. Note that the definition is symmetric in a and b, so that a is an inverse of b if and only if b is an inverse of a.
Theorem 4. If M is a monoid and a ![]() M has an inverse in M, then that inverse is unique .
M has an inverse in M, then that inverse is unique .
Proof. If both b and b′ are inverses of a, then ab = 1 = ba and ab′ = 1 = b′a. Hence b′ = b′1 = b′(ab) = (b′a)b = 1b = b.
Note the use of associativity in Theorem 4. In fact, its use is essential: In Example 7, both a and c are inverses of c.
If a is a unit in a multiplicative monoid, the inverse of a is denoted a−1. If the monoid is additive the inverse of a is denoted −a and is called the negative of a.
Example 8. Consider the additive monoids ![]() and
and ![]() Then every element is a unit and, in all cases, the usual negative −x of an element x is the (additive) inverse.
Then every element is a unit and, in all cases, the usual negative −x of an element x is the (additive) inverse.
Example 9. In the multiplicative monoids ![]() and
and ![]() every nonzero element is a unit. However, 0 has no inverse in either case.
every nonzero element is a unit. However, 0 has no inverse in either case.
Example 10. The units of ![]() are 1 and −1.
are 1 and −1.
Example 11. The units in ![]() are the residues
are the residues ![]() where a and n are relatively prime (Theorem 5 §1.3).
where a and n are relatively prime (Theorem 5 §1.3).
Example 12. If M = {α ![]() α: X → X is a mapping} under composition, the units in M are the bijections (onto and one-to-one mappings). (See Theorem 6 §0.3.)
α: X → X is a mapping} under composition, the units in M are the bijections (onto and one-to-one mappings). (See Theorem 6 §0.3.)
Example 12 is important, and we refer to it again. If X = {1, 2, ![]() , n}, the set of units is the symmetric group Sn of degree n (Section 1.4). If
, n}, the set of units is the symmetric group Sn of degree n (Section 1.4). If ![]() we get a monoid containing maps σ and τ such that στ = 1 but τσ ≠ 1. (Example 8 §0.3.)
we get a monoid containing maps σ and τ such that στ = 1 but τσ ≠ 1. (Example 8 §0.3.)
Example 13. The units in ![]() are the matrices A with det A ≠ 0, where det A denotes the determinant of A.21 This is discussed in Appendix B.
are the matrices A with det A ≠ 0, where det A denotes the determinant of A.21 This is discussed in Appendix B.
The next theorem collects several basic properties of units that will be used without comment throughout the book. This theorem will be familiar to students of linear algebra where it is proved for invertible matrices.
Theorem 5. Let a, b, a1, a2, ![]() , an−1, an denote elements in a monoid M.
, an−1, an denote elements in a monoid M.
1. 1 is a unit and 1−1 = 1.
2. If a is a unit so is a−1, and (a−1)−1 = a.
3. If a and b are units so is ab, and (ab)−1 = b−1a−1.
4. If a1, a2, ![]() , an−1, an are units, so is a1a2
, an−1, an are units, so is a1a2 ![]() an−1an, and
an−1an, and ![]()
5. If a is a unit so is an for any n ≥ 0, and (an)−1 = (a−1)n.
Proof. (1), (2), and (3) depend on the fact that, if ab = 1 = ba for some b then a is a unit and a−1 = b. Thus (1) follows from 1· 1 = 1; (2) follows from a−1a = 1 = aa−1, and (3) follows if we can show that
![]()
But (ab)(b−1a−1) = a(bb−1)a−1 = a1a−1 = aa−1 = 1. The other equation can be similarly verified.
Finally (4) follows from (3) by induction on n (Exercise 16), and (5) is the special case of (4) where a1 = a2 = ![]() = an = a.
= an = a.
Note that every monoid has at least one unit: the unity. Moreover, if M is the set of all subsets of a set U, then (M, ∩) and (M, ∪) are monoids in which the unity is the only unit. At the other extreme are the monoids (called groups) in which every element is a unit. These are the principal objects of study in this chapter. With this in mind, we extend the definition of nth powers to include negative powers of a unit. Since (a−1)n = (an)−1 by Theorem 5 for any unit a, we define the negative powers a−n, n ≥ 1, by
![]()
Then the laws of exponents extend as follows (the proof is left to the reader).
Theorem 6. Let a and b denote units in a monoid M.
(1) anam = an+m for all ![]()
(2) (an)m = anm for all ![]()
(3) If ab = ba, then (ab)n = anbn for all ![]()
2.1 Exercises
1. In each case a binary operation * is given on a set M. Decide whether it is com-mutative or associative, whether a unity exists, and find the units (if there is a unity).
(a) ![]() a * b = a − b
a * b = a − b
(b) ![]() ;
; ![]()
(c) ![]()
(d) M = any set with |M|≥ 2; a * b = b
(e) M = P × Q, where P and Q are sets with |P| ≥ 2 and |Q|≥ 2; (p, q) * (p′, q′) = (p, q′)
(f) ![]() m * n = max (m, n)—the larger of m and n
m * n = max (m, n)—the larger of m and n
(g) ![]()
(h) ![]()
(i) ![]()
(j) ![]()
2.
(a) If x, y, or z is 1, show that (xy)z = x(yz).
(b) Show that there are exactly two monoids with two elements.
(c) Let S be a set with an associative binary operation but with no unity. Choose an element 1 ∉ S, write M = {1} ∪ S, and define an operation on M by using the operation of S and 1s = s = s1 for all s ![]() S. Show that M is a monoid.
S. Show that M is a monoid.
3. Consider the partial Cayley tables: (1)
| a | b | |
| a | b | |
| b | a |
and (2)
| a | b | |
| a | a | |
| b | b |
(a) Show that there is only one way to complete table (1) so that the resulting op-eration is associative, and that the result makes {a, b} into a commutative monoid.
(b) Show that there are three associative completions of table (2), two making {a, b} into a commutative monoid and one having no unity.
4. If M is any monoid, let ![]() denote the set of all nonempty subsets of M and define an operation on
denote the set of all nonempty subsets of M and define an operation on ![]() by XY = {xy
by XY = {xy ![]() x
x ![]() X, y
X, y ![]() Y}. Show that
Y}. Show that ![]() is a monoid, commutative if M is, and find the units.
is a monoid, commutative if M is, and find the units.
5. Given an alphabet A, call an n-tuple (a1, a2, ![]() , an) with ai
, an) with ai ![]() A a word of length n from A and write it (as in English) as a1a2
A a word of length n from A and write it (as in English) as a1a2 ![]() an. Multiply two words by (a1a2
an. Multiply two words by (a1a2 ![]() an) · (b1b2
an) · (b1b2 ![]() bm) = a1a2
bm) = a1a2 ![]() anb1b2
anb1b2 ![]() bm, and call this product juxtaposition. Thus, the product of “ no” and “ on” is “ noon”. We decree the existence of an empty word λ with no letters. Show that the set W of all words from A is a monoid, noncommutative if |A| > 1, and find the units.
bm, and call this product juxtaposition. Thus, the product of “ no” and “ on” is “ noon”. We decree the existence of an empty word λ with no letters. Show that the set W of all words from A is a monoid, noncommutative if |A| > 1, and find the units.
6. Given a set X and a monoid M, let F = {σ ![]() σ: X → M is a mapping}. Given σ and τ in F, define σ · τ: X → M by (σ · τ)(x) = σ(x)τ(x). Show that this definition makes F into a monoid, commutative if M is, and find all the units.
σ: X → M is a mapping}. Given σ and τ in F, define σ · τ: X → M by (σ · τ)(x) = σ(x)τ(x). Show that this definition makes F into a monoid, commutative if M is, and find all the units.
7. If M and N are monoids, show that the cartesian product M × N is a monoid (called the direct product of M and N) using the operation (m, n)(m′, n′) = (mm′, nn′). When is M × N commutative? Describe the units.
8. An element e of a monoid M is called an idempotent if e2 = e.
(a) If a ![]() M satisfies am = am+n, where m ≥ 0 and n ≥ 1, show that some power of a is an idempotent. [Hint: am+r = am+kn+r for all k ≥ 1 and r ≥ 0.]
M satisfies am = am+n, where m ≥ 0 and n ≥ 1, show that some power of a is an idempotent. [Hint: am+r = am+kn+r for all k ≥ 1 and r ≥ 0.]
(b) If M is finite, show that some positive power of every element is an idempotent.
9. Assume that a is left cancelable in a monoid M (ab = ac implies that b = c).
(a) If a5 = b5 and a12 = b12 in M, show that a = b.
(b) If am = bm and an = bn where m and n are relatively prime, show that a = b.
10. If ab = ba in a monoid M, prove that (ab)n = anbn for all n ≥ 0 (Theorem 3(3)).
11. An element e is called a left (right) unity for an operation if ex = x (xe = x) for all x. If an operation has two left unities, show that it has no right unity.
12.
(a) If u is a unit in a monoid M, show that au = bu in M implies that a = b.
(b) If M is a finite monoid and au = bu in M implies that a = b, show that u is a unit. [Hint: If M = {a1, ![]() , an} show that a1u, . . ., anu are distinct.]
, an} show that a1u, . . ., anu are distinct.]
13. If uv is a unit in a monoid M, and if av = bv implies that a = b in M, show that u and ![]() are both units.
are both units.
14. If uv = 1, we say that u is a left inverse of ![]() and
and ![]() is a right inverse of u. If u has both a left and a right inverse in a monoid, show that u is a unit.
is a right inverse of u. If u has both a left and a right inverse in a monoid, show that u is a unit.
15. If M is a monoid and u ![]() M, let σ: M → M be defined by σ(a) = ua for all a
M, let σ: M → M be defined by σ(a) = ua for all a ![]() M.
M.
(a) Show that σ is a bijection if and only if u is a unit,
(b) If u is a unit, describe the inverse mapping σ−1: M → M.
16. If u1, u2, ![]() , un−1, un are units in a monoid, show that u1u2
, un−1, un are units in a monoid, show that u1u2 ![]() un−1un is also a unit and that
un−1un is also a unit and that ![]() (Theorem 5(4)).
(Theorem 5(4)).
17. Let u and ![]() be units in a monoid M.
be units in a monoid M.
(a) If ![]() show that
show that ![]()
(b) If a ![]() M and ua = au, show that u−1a = au−1.
M and ua = au, show that u−1a = au−1.
(c) If uv = vu, show that ![]()
18. Prove that the following are equivalent for a monoid M.
(1) If ab is a unit then both a and b are units.
(2) If ab = 1, then ba = 1.
19. If M is a finite monoid and uv = 1 in M, prove that vu = 1. [Hint: Exercise 12(b).]
20. Let M be a commutative monoid. Define a relation ![]() on M by a
on M by a ![]() b if a = bu for some unit u.
b if a = bu for some unit u.
(a) Show that ![]() is an equivalence on M.
is an equivalence on M.
(b) If ![]() denotes the equivalence class of a, let
denotes the equivalence class of a, let ![]() denote the set of all equivalence classes. Show that
denote the set of all equivalence classes. Show that ![]() is a well-defined operation on
is a well-defined operation on ![]()
(c) If ![]() is as in (b), show that
is as in (b), show that ![]() is a commutative monoid in which the unity
is a commutative monoid in which the unity ![]() is the only unit.
is the only unit.
21. If M is a monoid, define E(M) = {α: M → M ![]() α(xy) = α(x) · y for all x, y
α(xy) = α(x) · y for all x, y ![]() M}. If a
M}. If a ![]() M, define αa: M → M by αa(x) = ax for all x
M, define αa: M → M by αa(x) = ax for all x ![]() M.
M.
(a) Show that E(M) is a monoid under composition of mappings.
(b) Show that αa ![]() E(M) for all a
E(M) for all a ![]() M.
M.
(c) If θ: M → E(M) is defined by θ(a) = αa for all a ![]() M, show that θ is onto and one-to-one, θ(1) = 1M, and θ(ab) = θ(a) · θ(b) for all a, b
M, show that θ is onto and one-to-one, θ(1) = 1M, and θ(ab) = θ(a) · θ(b) for all a, b ![]() M.
M.
22. Show that there are exactly six monoids M with three elements. If M = {1, a, b}, consider first the case a2 = 1 (then only one multiplication table is possible). If a2 = b, then M = {1, a, a2} is commutative and there are three monoids. Then two more emerge if a2 = a. Note that, although associativity is used to force the multiplication table in every case, the associativity in the resulting table must be checked (Exercise 2(a) is useful).
A group is a monoid in which every element has an inverse. Because of its importance, we give the definition in full detail. A set G is called a group if it satisfies the following axioms.
G1 G is closed under a binary operation.
G2 The operation is associative.
G3 There is a unity element in G.
G4 Every element of G has an inverse in G.
The group G is called abelian22 if, in addition, it satisfies
G5 The operation is commutative.
If G is finite, the number |G| of elements in G is called the order of G.
The terminology used for groups (and other algebraic systems, such as monoids) is somewhat careless. Strictly speaking, a group (G, ·) consists of two things: a set G and a binary operation. However, common practice is simply to refer to a group G and not mention the operation. This practice usually causes no difficulty, because the operation in the group in question is understood. We adopt this loose notation because it is much simpler, and also to acquaint the reader with what is in fact used in more advanced books. When clarity is needed, we use terms such as the group (G, +) or the additive group G.
Examples 1–10 indicate the variety of ways that groups can occur, and we refer to many of them later. We leave verification of the axioms to the reader.
Example 1. {1}, {1, − 1}, and {1, − 1, i, − i} are all abelian groups of (complex) numbers under multiplication. Here −1 is self-inverse, and i and −i are inverses of each other.
Example 2. ![]() 23
23 ![]() and
and ![]() are all abelian groups under multiplication. In each case the inverse of an element a is a−1 = 1/a.
are all abelian groups under multiplication. In each case the inverse of an element a is a−1 = 1/a.
Example 3. The set of complex numbers
![]()
is a group under complex multiplication. Here eiθ = cos θ + i sin θ, as in Appendix A, and we have eiθei![]() = ei(θ+
= ei(θ+![]() ) and (eiθ)−1 = e−iθ. The group
) and (eiθ)−1 = e−iθ. The group ![]() is called the circle group because it consists of the points on the unit circle.
is called the circle group because it consists of the points on the unit circle.
Example 4. For n ≥ 1, the group ![]() is a group under complex multiplication, called the group of nth roots of unity. As in Appendix A, we have
is a group under complex multiplication, called the group of nth roots of unity. As in Appendix A, we have
![]()
Clearly, ![]() for all n ≥ 1, and U1, U2, and U4 are displayed in Example 1.
for all n ≥ 1, and U1, U2, and U4 are displayed in Example 1.
Example 5. The sets ![]() and
and ![]() are all abelian groups under addition. In each case the unity is 0 and the inverse of x is −x.
are all abelian groups under addition. In each case the unity is 0 and the inverse of x is −x.
Although we write most groups multiplicatively, many important groups are written additively (as in Example 5). Then the unity element is denoted 0 and is called zero, and the inverse of x is denoted −x and is called the negative of x.
Example 6. If ![]() is an additive abelian group with zero
is an additive abelian group with zero ![]() and the negative of
and the negative of ![]() being
being ![]() We write
We write ![]() in
in ![]() when no confusion can result.
when no confusion can result.
Henceforth, when we refer to one of the groups ![]() or
or ![]() we mean the additive group.
we mean the additive group.
Example 7. The set Sn of all permutations of {1, 2, . . ., n} is a group under composition (see Theorem 2 § 1.4), called the symmetric group of degree n.
The group Sn has historical significance because such groups of bijections were among the earliest examples of a group. They were used by Galois in his pioneering work on the theory of equations. In fact Galois was the first to use the term group.
Example 8. We single out S3 for special emphasis. Recall from Section 1.4 that
![]()
If we denote σ = (123) and τ = (12), then σ2 = (132), τσ = (23), and τσ2 = (13) as is easily verified. Hence we can list S3 as
![]()
The reason for doing this is that it provides an easy way to fill in the Cayley table. In fact, we can fill in the table by using three (easily verified) facts:
![]()
The resulting Cayley table is as follows

Note that
![]()
Then, for example, we compute the product (τσ)(τσ2) by
![]()
The other entries in the table are found in a similar manner (the reader should do this). The elements σ and τ are called generators for S3, and the equations σ3 = ε, τ2 = ε, and στσ = τ are called relations among the generators. We often describe S3 in this way.
Examples 9 and 10 display two other important groups of permutations.
Example 9. The set An of all even permutations in Sn is a group using the operation of Sn, called the alternating group of degree n (Theorem 8 §1.4).
Example 10. Given a (nonsquare) wire rectangle with vertices 1, 2, 3, and 4 as in the diagram, consider the permutations of the vertices induced by moving the rectangle in space (without bending). The 180![]() -rotations about vertical and horizontal axes (see the diagram) give permutations
-rotations about vertical and horizontal axes (see the diagram) give permutations
![]()

respectively. If we compute their product in S4 we obtain another motion στ = (13)(24) because the composite motion στ is the motion τ followed by the motion σ (the reader should verify this). Note that στ can also be viewed as the 180![]() -rotation in the plane of the rectangle about its center. Of course, we have another motion τσ, but this is not a new motion because
-rotation in the plane of the rectangle about its center. Of course, we have another motion τσ, but this is not a new motion because
![]()
is called the group of motions of the rectangle. Such groups of motions are important (for example they arise in the study of symmetries of molecules); we return to them in Section 2.7.
Recall that a set M with an associative operation that has a unity is called a monoid, and that an element u in M that has an inverse u−1 in M is called a unit. A monoid may not be a group, but its units form a group.
Theorem 1. If M is a monoid, the set M* of all units in M is a group using the operation of M, called the group of units of M.
Proof. From Theorem 5 §2.1, if u and ![]() are units, then uv is also a unit (the inverse is
are units, then uv is also a unit (the inverse is ![]() ), so M* is closed under the operation of M. The associativity of M* is inherited from M and 1
), so M* is closed under the operation of M. The associativity of M* is inherited from M and 1 ![]() M* (in fact 1−1 = 1), so M* itself is a monoid. Finally, if u
M* (in fact 1−1 = 1), so M* itself is a monoid. Finally, if u ![]() M*, then u−1
M*, then u−1 ![]() M* too (its inverse is u), so M* is a group.
M* too (its inverse is u), so M* is a group.
Theorem 1 provides many important examples of groups. For example, the multiplicative groups in Example 2 are ![]() and
and ![]()
Example 11. If X is a nonempty set, M = {α ![]() α: X → X is a mapping} is a monoid under composition and Theorem 6 §0.3 shows that the group M* of units consists of the bijections
α: X → X is a mapping} is a monoid under composition and Theorem 6 §0.3 shows that the group M* of units consists of the bijections
![]()
The bijections X → X are called permutations of X, and SX is the permutation group of X. Of course, if X = {1, 2, . . ., n} then SX = Sn.
Example 12. Consider ![]() where
where ![]() is regarded as a multiplicative monoid. Then Theorem 5 §1.3 gives
is regarded as a multiplicative monoid. Then Theorem 5 §1.3 gives
![]()
Hence ![]() if (and only if) p is a prime. Other examples include
if (and only if) p is a prime. Other examples include
![]()
We refer to these groups frequently.
Example 13. Let R denote ![]() . Then the set Mn(R) of all n × n matrices over R is a monoid using matrix multiplication. The group Mn(R)* of units consists of the invertible n × n matrices over R, that is the matrices such that det A is a unit in R—see Appendix B. It is called the general linear group of degree n over R, denoted GLn(R). Thus
. Then the set Mn(R) of all n × n matrices over R is a monoid using matrix multiplication. The group Mn(R)* of units consists of the invertible n × n matrices over R, that is the matrices such that det A is a unit in R—see Appendix B. It is called the general linear group of degree n over R, denoted GLn(R). Thus
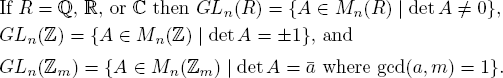
If G1, G2, ![]() , Gn are sets, recall that the cartesian product G1 × G2 ×
, Gn are sets, recall that the cartesian product G1 × G2 × ![]() × Gn is the set of all ordered n -tuples (g1, g2,
× Gn is the set of all ordered n -tuples (g1, g2, ![]() , gn), where gi
, gn), where gi ![]() Gi for each i. This set has a natural group structure when the Gi are themselves groups. If G1, G2,
Gi for each i. This set has a natural group structure when the Gi are themselves groups. If G1, G2, ![]() , Gn are groups, their direct product is the set G1 × G2 ×
, Gn are groups, their direct product is the set G1 × G2 × ![]() × Gn with the component-wise operation defined by
× Gn with the component-wise operation defined by
![]()
where ![]() is the product in Gi for each i. The routine proof of the next theorem is left to the reader.
is the product in Gi for each i. The routine proof of the next theorem is left to the reader.
Theorem 2. If G1, G2, ![]() , Gn are groups, so also is G1 × G2 ×
, Gn are groups, so also is G1 × G2 × ![]() × Gn, with unity (1, 1,
× Gn, with unity (1, 1, ![]() , 1) and inverses
, 1) and inverses ![]()
Because groups are monoids, all the properties of monoids presented in Section 2.1 are automatically properties of groups. In particular:
(1) The unity 1 is unique.
(2) The inverse g−1 of an element g is uniquely determined by g.
(3) General associativity holds (Theorem 2 §2.1).
The next theorem restates Theorem 5 §2.1 for units in monoids for reference.
Theorem 3. Let g, h, g1, g2, ![]() , gn−1, gn denote elements of a group G.
, gn−1, gn denote elements of a group G.
1. 1−1 = 1.
2. (g−1)−1 = g.
3. (gh)−1 = h−1g−1.
4. ![]() for all n ≥ 1.
for all n ≥ 1.
5. (gn)−1 = (g−1)n for all n ≥ 0.
Recall that negative powers of an element g in a group are defined by g−k = (g−1)k for k ≥ 1. The next theorem is a restatement of Theorem 6 §2.1.
Theorem 4. Exponent Laws. Let G be a group with elements g and h.
1. gngm = gn+m for all ![]()
2. (gn)m = gn·m for all ![]()
3. If gh = hg, then (gh)n = gnhn for all ![]()
These laws are important and play a prominent role in Section 2.4.
The assumption that every element of a group has an inverse is a very powerful axiom. In particular, it implies the cancellation laws, which we use countless times in this book.
Theorem 5. Cancellation Laws. Let g, h, and f be elements of a group.
1. If gh = gf, then h = f. (left cancellation)
2. If hg = fg, then h = f. (right cancellation)
Proof. If gh = gf, then left multiplication by g−1 gives (g−1g)h = (g−1g)f. Hence 1h = 1f; that is, h = f. This proves (1), and (2) follows similarly.
Note that “ mixed” cancellation is not valid in general: fg = gh does not imply that f = h. For example, in the group S3, we have (12)(13) = (13)(23) so (13) cannot be cancelled.
Example 14. If G is a finite group and g ![]() G, show that gn = 1 for some n ≥ 1.
G, show that gn = 1 for some n ≥ 1.
Solution. The elements g, g2, g3, ![]() in G cannot all be distinct because G is finite. So gm = gm+n for some m ≥ 1 and n ≥ 1. Thus gm · 1 = gm · gn, so 1 = gn by cancellation.
in G cannot all be distinct because G is finite. So gm = gm+n for some m ≥ 1 and n ≥ 1. Thus gm · 1 = gm · gn, so 1 = gn by cancellation.
Another consequence of the fact that all elements of a group have inverses is that equations gx = h and xg = h are always solvable.
Theorem 6. Let g and h be elements of a group G.
1. The equation gx = h has a unique solution x = g−1h in G.
2. The equation xg = h has a unique solution x = hg−1 in G.
Proof. If x = g−1h, then gx = gg−1h = 1h = h, so x is indeed a solution in (1). To prove that it is unique, let y also satisfy gy = h. Then gx = gy, so x = y by cancellation. This proves (1), and (2) follows in the same way.
Corollary. Every row (and column) of the Cayley table of a group G contains every element of G exactly once.
Proof. If g ![]() G, the row of the table corresponding to g consists of the elements gx as x ranges over G. This row contains every element h of G because gx = h is solvable for each h, and it contains h only once because the solution is unique. A similar argument applies to columns.
G, the row of the table corresponding to g consists of the elements gx as x ranges over G. This row contains every element h of G because gx = h is solvable for each h, and it contains h only once because the solution is unique. A similar argument applies to columns.
A group is determined completely by its Cayley table: associativity and existence of the unity and inverses, which are demanded by the group axioms, all depend entirely on the operation. Now consider the (multiplicative) group ![]() of units of
of units of ![]() and the (additive) group
and the (additive) group ![]() The Cayley tables are
The Cayley tables are
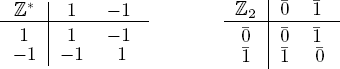
They are the same in the sense that the Cayley table of ![]() becomes that of
becomes that of ![]() if we replace the symbols 1 and −1 by
if we replace the symbols 1 and −1 by ![]() and
and ![]() respectively. Thus
respectively. Thus ![]() and
and ![]() are the same groups except for notation, and we say that they are isomorphic, or that they are the same up to isomorphism. We discuss this topic in more detail in Section 2.5; for now we prefer to treat the whole matter informally and call two groups isomorphic if they have the same Cayley table except for notation. As a result we can give an application of the Corollary to Theorem 6.
are the same groups except for notation, and we say that they are isomorphic, or that they are the same up to isomorphism. We discuss this topic in more detail in Section 2.5; for now we prefer to treat the whole matter informally and call two groups isomorphic if they have the same Cayley table except for notation. As a result we can give an application of the Corollary to Theorem 6.
Example 15. Show that, up to isomorphism, there is only one group G of order 1, 2, or 3, and that group can be described in the following manner.
- If |G| = 1, then G = {1}.
- If |G| = 2, then G = {1, g}, where g2 = 1.
- If |G| = 3, then G = {1, g, g2}, where g3 = 1.
In each case the Cayley table is determined by the laws of exponents.
Solution. In each case we show that there is only one way to fill in the Cayley table. Multiplication by 1 is prescribed. If |G| = 1, then G = {1} and the Cayley table is determined. If |G| = 2, let G = {1, g}, where g ≠ 1. The only entry in the Cayley table that is in doubt is whether g2 = g or g2 = 1. But g2 = g is impossible because it implies that g = 1 by cancellation. Hence g2 = 1 and the table is determined.
Turning to the case |G| = 3, write G = {1, g, h}. Then gh ≠ g and gh ≠ h by cancellation, so we must have gh = 1. Now repeated use of the Corollary to Theorem 6 (beginning with row 2 and column 3) gives the table on the left.
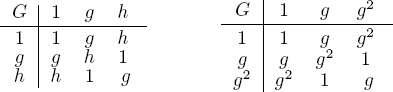
In particular, g2 = h, so G = {1, g, g2}, and g3 = gh = 1, as shown in the table on the right. This table is associative, a known realization being the group {ε, (123), (132)} of permutations.
The groups in Example 15 all have the rather special property that every element is a power of a particular element and are called cyclic groups. There exists a cyclic group of order n for every n ≥ 1. Indeed the group Un of nth roots of unity is cyclic of order n. In fact, if we write ![]() then
then ![]() has order n and
has order n and ![]()
We discuss cyclic groups in detail in Section 2.4 and treat them informally for now. They occur frequently, and the following generic notation is useful. Given n ≥ 1, the cyclic group of order n is the group Cn of order n:
![]()
We write ![]() in this case, and the element a is called a generator of Cn. Our insistence that |Cn| = n means that 1, a, a2, . . ., an−1 are distinct elements of Cn.
in this case, and the element a is called a generator of Cn. Our insistence that |Cn| = n means that 1, a, a2, . . ., an−1 are distinct elements of Cn.
The Cayley table of Cn is determined completely by the exponent laws and the condition an = 1. In fact, exponents in Cn can be reduced modulo n. That is, if k = qn + r, where 0 ≤ r ≤ n − 1, then ak = ar because ak = (an)qar = 1qar = ar. In particular,
![]()
This expression gives the Cayley table for Cn (below), and so is sufficient for all computations in Cn.

Example 16. Let C12 = {1, a, a2, . . ., a11}, a12 = 1, be a cyclic group of order 12. Compute a89 and a−40 in C12.
Solution. Because 89 = 7 · 12 + 5, we get a89 = (a12)7a5 = 17a5 = a5. Similarly, −40 = (− 4) · 12 + 8, so a−40 = (a12)−4a8 = 1−4a8 = a8.
Example 17. Show that bn = 1 for every element b of Cn.
Solution. Write ![]() where an = 1. Then b = ak for some k, so we have
where an = 1. Then b = ak for some k, so we have
![]()
Example 15 shows that every group of order 1, 2, or 3 is cyclic. However, this is not the case for groups of order 4.
Example 18. Show that there are only two groups of order 4, the cyclic group C4 and a noncyclic group K4 whose Cayley table is shown below.


table is the one on the left below. In that case a2 = c, a3 = ca = b, and a4 = c2 = 1, so ![]() is cyclic.
is cyclic.


Similarly if the product of any two of a, b, and c equals 1 then G is cyclic (possibly with a different generator). Thus, if G is not cyclic, the product of any two of a, b, and c must equal the third (for example, bc ≠ b, c, or 1, so bc = a). Hence we get the Cayley table on the right as required.
The group K4 = {1, a, b, c} in Example 18 is called the Klein group.24 The multiplication can be described as follows: a2 = b2 = c2 = 1, and the product of any two of a, b, and c is the third.
If you are nervous because we have not shown that K4 is associative, you can relax. The (associative) group ![]() has exactly the Cayley table of K4 if we write a = 3, b = 5, and c = 7. Another instance of K4 is the permutation group K = {ε, (12)(34), (13)(24), (14)(23)}. Example 18 shows that there are two groups of order 4: the cyclic group and the (noncyclic) Klein group. The reader should try to show that every group of order 5 is cyclic; in fact, if p is any prime, we show in Section 2.6 that every group of order p is cyclic.
has exactly the Cayley table of K4 if we write a = 3, b = 5, and c = 7. Another instance of K4 is the permutation group K = {ε, (12)(34), (13)(24), (14)(23)}. Example 18 shows that there are two groups of order 4: the cyclic group and the (noncyclic) Klein group. The reader should try to show that every group of order 5 is cyclic; in fact, if p is any prime, we show in Section 2.6 that every group of order p is cyclic.
Exercises 2.2
1. In each case either show that G is a group with the given operation or list the axioms that fail.
(a) ![]() addition
addition
(b) ![]() addition
addition
(c) ![]()
(d) ![]()
(e) G ={ε, (12), (13), (14)}; operation in S4
(f) G ={0, 2, 4, 6}; addition in ![]()
(g) G ={16, 12, 8, 4}; multiplication in ![]()
(h) ![]() multiplication
multiplication
(i) ![]() is one-to-one}; composition
is one-to-one}; composition
(j) G ={a, b, c, d}; multiplication given by

2. If G is a group, let Gop denote the set G with a new multiplication given by a ![]() b = ba. Show that Gop is a group.
b = ba. Show that Gop is a group.
3. In each case fill in the Cayley table, given that G = {1, a, b, c, d} is a group.


4. Is the empty set a group? Explain.
5. If M is a monoid, describe an easy way to determine whether M is a group by looking at the Cayley table.
6. If U is a set, let G = {X ![]() X ⊆ U}. Show that G is an abelian group under the operation ⊕ defined by X ⊕ Y = (X Y) ∪ (Y X).
X ⊆ U}. Show that G is an abelian group under the operation ⊕ defined by X ⊕ Y = (X Y) ∪ (Y X).
7. Show that the set 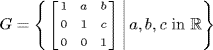 is a group under matrix multiplication.
is a group under matrix multiplication.
8. In each case show that G is a group using the operation of S4, and determine how many elements σ of G satisfy σ2 = ε.
(a) G = {ε, (12)(34), (13)(24), (14)(23)}
(b) G = {ε, (1234), (13)(24), (1432)}
9. Let σ = (123456) in S6. Show that G = {ε, σ, σ2, σ3, σ4, σ5} is a group using the operation of S6. Is G abelian? How many elements τ of G satisfy τ2 = ε? τ3 = ε?
10.
(a) If a4 = 1 and ab = ba2 in a group, show that a = 1.
(b) If a6 = 1 and ab = ba3 in a group, show that a2 = 1 and ab = ba.
(c) If a6 = 1 and ab = ba2 in a group, show that a3 = 1 and aba = b.
11.
(a) If (ab)n = 1 in a group where n ≥ 0, show that (ba)n = 1.
(b) Extend (a) to all ![]()
12. Let G be a group of order 4. Assume that 1, a, and b are distinct elements of G and that a2 = 1 and b2 = 1. Show that G = {1, a, b, ab} and fill in the Cayley table.
13. If G is any group, define α: G → G by α(g) = g−1. Show that α is onto and one-to-one.
14. Given a, b, and c in a group G, show that the equation a−1xb = c has a unique solution x ![]() G.
G.
15. Let a ![]() G where G is a group. If X ⊆ G is a finite subset, write Xa = {xa
G where G is a group. If X ⊆ G is a finite subset, write Xa = {xa ![]() x
x ![]() X}. Show that X and Xa have the same number of elements.
X}. Show that X and Xa have the same number of elements.
16. If fgh = 1 in a group G, show that ghf = 1. Must gfh = 1?
17. Recall that an element e in a monoid is called an idempotent if e2 = e. Describe all the idempotents in a group G.
18. If G is a group and g, h ![]() G, show that gh = hg if and only if g−1h−1 = h−1g−1.
G, show that gh = hg if and only if g−1h−1 = h−1g−1.
19. Show that a group G is abelian if and only if (gh)−1 = g−1h−1 for all g and h in G.
20. Show that a group G is abelian if g2 = 1 for all g ![]() G. Give an example showing that the converse is false.
G. Give an example showing that the converse is false.
21. Show that a group G is abelian if and only if (gh)2 = g2h2 for all g and h in G.
22. Show that a group G is abelian if (gh)3 = g3h3, (gh)4 = g4h4, and (gh)5 = g5h5 for all g and h in G.
23. Let g be an element of a group G. (a) Show that g2 = 1 if and only if g−1 = g. (b) If |G| is finite and even, show that g ≠ 1 in G exists such that g2 = 1.
24. Let a and b be elements of a group G. Prove that (aba−1)k = abka−1 holds for all ![]() (including negative k).
(including negative k).
25. If a5 = 1 and a−1ba = bm in a group, prove that ![]() [Hint: Exercise 24.]
[Hint: Exercise 24.]
26. Show that every cyclic group Cn of order n is abelian.
27. Show that the additive group ![]() is cyclic.
is cyclic.
28. Let a and b be elements of a group G. If an = bn and am = bm where gcd (m, n) = 1, show that a = b. [Hint: Theorem 4 §1.2.]
29. Let G be a set with an associative operation defined on it. In each case show that G is a group.
(a) There is a left unity e (eg = g for all g in G), and each element g has a left inverse (hg = e for some h in G).
(b) G is finite and both cancellation laws hold.
(c) Both gx = h and xg = h are solvable in G for all g and h in G.
(d) For all g and h in G, gx = h has a unique solution in G.
30. If G is an abelian group with n elements, show that gn = 1 for every g ![]() G. [Hint: See the proof of Theorem 8 §1.3.]
G. [Hint: See the proof of Theorem 8 §1.3.]
Many important groups arise as subsets of known groups. Therefore, we are interested in knowing which subsets H of a group G are themselves groups (with the same operation). Thus a subset H of a group G is called a subgroup of G if H itself is a group using the operation of G. For example, ![]() is a subgroup of
is a subgroup of ![]() However the multiplicative group
However the multiplicative group ![]() is not a subgroup of
is not a subgroup of ![]() even though
even though ![]() is a subset of
is a subset of ![]() because the operations are different.
because the operations are different.
Example 1. If G is any group, both {1} and G are subgroups of G. The subgroup {1} is the trivial subgroup of G. Any subgroup other than G is a proper subgroup.
Example 2. Each of the additive groups ![]() is a subgroup of the larger ones.
is a subgroup of the larger ones.
Example 3. An is a subgroup of Sn.
Example 4. ![]() denotes the circle group, then each of
denotes the circle group, then each of
![]()
is a subgroup of the larger ones.
In each of these examples, the subgroups of a group G not only have the same operation as G, but they also share the same unity element and the same inverses. This observation is true in general and, in fact, provides a very useful test for when a subset of a group is actually a subgroup.
Theorem 1. Subgroup Test. A subset H of a group G is a subgroup if and only if the following three conditions are satisfied .
(1) 1G ![]() H, where 1G is the unity of G.25
H, where 1G is the unity of G.25
(2) If h ![]() H and h1
H and h1 ![]() H, then hh1
H, then hh1 ![]() H.
H.
(3) If h ![]() H then h−1
H then h−1 ![]() H, where h−1 denotes the inverse of h in G.
H, where h−1 denotes the inverse of h in G.
In this case, H has the same unity as G and, if h ![]() H, its inverse in H is the same as its inverse in G.
H, its inverse in H is the same as its inverse in G.
Proof. If H satisfies (1), (2), and (3), then H is closed by (2), the unity of G is the unity for H by (1), and the inverse in G of an element h ![]() H serves as the inverse of h in H by (3). As H inherits the associative law from G, it is a subgroup.
H serves as the inverse of h in H by (3). As H inherits the associative law from G, it is a subgroup.
Conversely, if H is a subgroup, let e denote the unity of H. Then e2 = e = e · 1G, so e = 1G by cancellation in G. This proves (1), and (2) follows because H is closed under the operation of G. Finally, if h ![]() H, let h′ denote its inverse in H. If h−1 is the inverse in G, then hh′ = 1 = hh−1, so h′ = h−1 by cancellation in G. This proves (3) and the last sentence in the theorem.
H, let h′ denote its inverse in H. If h−1 is the inverse in G, then hh′ = 1 = hh−1, so h′ = h−1 by cancellation in G. This proves (3) and the last sentence in the theorem.
Theorem 1 is useful as the conditions are easily checked (see also Exercise 2).
Example 5. If R is one of ![]() or
or ![]() let
let ![]() Show that H is a group using matrix multiplication, called the special linear group.
Show that H is a group using matrix multiplication, called the special linear group.
Solution. We have ![]() —see Example 13 §2.2—so we show that it is a subgroup of
—see Example 13 §2.2—so we show that it is a subgroup of ![]() We have I
We have I ![]() H because det I = 1. If A and B
H because det I = 1. If A and B ![]() H, then det (AB) = det A det B = 1 · 1 = 1 and det A−1 = 1/det A = 1/1 = 1. These results show that AB
H, then det (AB) = det A det B = 1 · 1 = 1 and det A−1 = 1/det A = 1/1 = 1. These results show that AB ![]() H and A−1
H and A−1 ![]() H, so the subgroup test applies.
H, so the subgroup test applies.
Example 6. If n ≥ 0, write ![]() Show that
Show that ![]() is a subgroup of
is a subgroup of ![]()
Solution. The unity of ![]() is 0, and
is 0, and ![]() If a and b are in
If a and b are in ![]() write them as a = nk and b = nm, where
write them as a = nk and b = nm, where ![]() and
and ![]() Then a + b = n(k + m) and −a = n(− k) both lie in
Then a + b = n(k + m) and −a = n(− k) both lie in ![]() so
so ![]() is a subgroup of
is a subgroup of ![]() by the subgroup test.
by the subgroup test.
Theorem 2. Finite Subgroup Test. If H is a finite nonempty subset of a group G, then H is a subgroup of G if and only if H is closed (h, h1 ![]() H implies hh1
H implies hh1 ![]() H).
H).
Proof. If H is closed, let h ![]() H. Then each of h, h2, h3,
H. Then each of h, h2, h3, ![]() is in H so, because H is finite, they cannot all be distinct. Hence hn = hn+m for some n ≥ 1 and m ≥ 1. This means 1 = hm by cancellation, so 1
is in H so, because H is finite, they cannot all be distinct. Hence hn = hn+m for some n ≥ 1 and m ≥ 1. This means 1 = hm by cancellation, so 1 ![]() H by hypothesis. But then 1 = hm−1h implies that h−1 = hm−1, so h−1
H by hypothesis. But then 1 = hm−1h implies that h−1 = hm−1, so h−1 ![]() H, too. Because H is closed by hypothesis, it is a subgroup by Theorem 1. The converse is clear.
H, too. Because H is closed by hypothesis, it is a subgroup by Theorem 1. The converse is clear.
Example 7. Determine all subgroups of the Klein group K4 = {1, a, b, c}, where a2 = b2 = c2 = 1 and the product of two of a, b, and c is the third.
Solution. Each of Ha = {1, a}, Hb = {1, b}, and Hc = {1, c} is a subgroup by Theorem 2, because a2 = b2 = c2 = 1. Any subgroup H with |H| ≥ 3 must contain two of a, b, and c and so contains the other one (their product). Thus, H = G and the complete list of subgroups is {1}, Ha, Hb, Hc, and G.
Example 8. Determine all subgroups of C4 = {1, a, a2, a3}, a4 = 1.
Solution. Let H = {1, a2}. Then H is a subgroup by Theorem 2 because (a2)2 = a4 = 1. Suppose that K is a subgroup distinct from {1} and H. Then either a ![]() K or a3
K or a3 ![]() K. If a
K. If a ![]() K, then (because K is closed) each power a, a2, and a3 is in K, so K = C4. Similarly, H = C4 if a3
K, then (because K is closed) each power a, a2, and a3 is in K, so K = C4. Similarly, H = C4 if a3 ![]() H because, as the reader can verify, C4 = {1, a3, (a3)2, (a3)3}. Thus the subgroups are {1}, H = {1, a2}, and C4.
H because, as the reader can verify, C4 = {1, a3, (a3)2, (a3)3}. Thus the subgroups are {1}, H = {1, a2}, and C4.
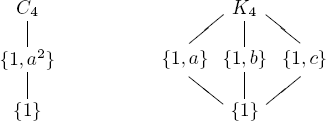
It is descriptive to draw the lattice diagram of all subgroups of a group G. Here the subgroups are shown in such a way that a line can be drawn up from K to H whenever K ⊆ H. The diagrams for K4 = {1, a, b, c} and for a cyclic group C4 = {1, a, a2, a3} of order 4 are given below.
If G is any group, the center of G is defined26 by
![]()
The elements in Z(G) are said to be central in G.
Theorem 3. If G is any group, then Z(G)is an abelian subgroup of G.
Proof. Use the subgroup test. Clearly 1 ![]() Z(G). If z
Z(G). If z ![]() Z(G), then zg = gz for all g
Z(G), then zg = gz for all g ![]() G, so multiplying this equation on the left by z−1 gives g = z−1gz. Then multiplication on the right by z−1 gives gz−1 = z−1g. Thus z−1
G, so multiplying this equation on the left by z−1 gives g = z−1gz. Then multiplication on the right by z−1 gives gz−1 = z−1g. Thus z−1 ![]() Z(G). Finally, if both y and z lie in Z(G), then, for all g
Z(G). Finally, if both y and z lie in Z(G), then, for all g ![]() G,
G,
![]()
Thus, yz ![]() Z(G), so Z(G) is a subgroup. It is clearly abelian.
Z(G), so Z(G) is a subgroup. It is clearly abelian.
Observe that Z(G) = G if and only if G is abelian. At the other extreme, it can happen that Z(G) = {1} so G is as far from abelian as it can be. In fact we have:
Example 9. If n ≥ 3, show that Z(Sn) = {ε}, where ε is the identity permutation.
Solution. If σ ![]() Sn, σ ≠ ε, we must find τ
Sn, σ ≠ ε, we must find τ ![]() Sn such that στ ≠ τσ. Because σ ≠ ε, choose k and m in Xn = {1, 2,
Sn such that στ ≠ τσ. Because σ ≠ ε, choose k and m in Xn = {1, 2, ![]() , n} such that σk = m ≠ k. Because n ≥ 3, let l, k, and m be distinct, with l
, n} such that σk = m ≠ k. Because n ≥ 3, let l, k, and m be distinct, with l ![]() Xn, and take τ to be the transposition τ = (kl). Then (τσ)k = τm = m and (στ)k = σl, so it suffices to show that σl ≠ m. But if σl = m then σl = σk, so l = k because σ is one-to-one, a contradiction.
Xn, and take τ to be the transposition τ = (kl). Then (τσ)k = τm = m and (στ)k = σl, so it suffices to show that σl ≠ m. But if σl = m then σl = σk, so l = k because σ is one-to-one, a contradiction.
We now turn to two important ways of manufacturing new subgroups from old ones. The straightforward proof of Theorem 4 is left as Exercise 16.
Theorem 4. Let H and K be subgroups of a group G. then their intersection
![]()
is also a subgroup of G.
Note that H ∩ K is a subgroup of both H and K, and is the largest such subgroup in the sense that if X is a subgroup of both H and K then X ⊆ H ∩ K. Incidentally, the union H ∪ K of two subgroups is almost never a subgroup (see Exercise 17).
The next theorem introduces another important type of subgroup.
Theorem 5. Let H be a subgroup of a group G. If g ![]() G, then
G, then
![]()
is a subgroup of G. These subgroups are called the conjugates of H in G.
Proof. Clearly, 1 = g1g−1 is an element of gHg−1. Given ghg−1, where h ![]() H,
H,
![]()
Finally (ghg−1)(gh1g−1) = g(hh1)g−1 for any h, h1 in H, which shows that gHg−1 is closed. Thus it is a subgroup by the subgroup test.
If H is a subgroup of G, then H = 1H1−1, so H is always a conjugate of itself. If H is the only conjugate of H in G (that is, gHg−1 = H for all g ![]() G), then H is said to be self-conjugate (or normal) in G. These subgroups play a fundamental role in group theory, and will be investigated in detail in Sections 2.8,2.9, and 2.10. Example 10 displays a subgroup that is not self-conjugate.
G), then H is said to be self-conjugate (or normal) in G. These subgroups play a fundamental role in group theory, and will be investigated in detail in Sections 2.8,2.9, and 2.10. Example 10 displays a subgroup that is not self-conjugate.
Example 10. Let S3 = {ε, σ, σ2, τ, τσ, τσ2}, where σ3 = ε = τ2 and στσ = τ. Find the conjugates of the subgroup H = {ε, τ}.
Solution. Clearly εHε−1 = H. Since σ−1 = σ2 and στσ = τ, we get
![]()
Similarly, σ2Hσ−2 = {ε, τσ2}. These are all the conjugates of H in G (verify).
Exercises 2.3
1. In each case determine whether H is a subgroup of G.
(a) ![]()
(b) ![]()
(c) ![]()
(d) H = {ε, (123)}, G = S3
(e) H = {ε, (12)(34), (13)(24)}, G = S3
(f) ![]()
(g) ![]()
(h) ![]()
(i) H = {(m, k) ![]() m + k is even},
m + k is even}, ![]()
2. If H is a subset of a group G, show that H is a subgroup if and only if H is nonempty and ab−1 ![]() H whenever a
H whenever a ![]() H and b
H and b ![]() H.
H.
3. If K is a subgroup of H, and H is a subgroup of G, must K be a subgroup of G? Justify your answer.
4. Let ![]() Show that G = {ε, λ1, λ2, μ1, μ2, μ3} is a subgroup of SX if ε(x) = x, λ1(x) = 1/(1 − x), λ2(x) = (x − 1)/x, μ1(x) = 1/x, μ2(x) = x/(x − 1), and μ3(x) = 1 − x, for all x
Show that G = {ε, λ1, λ2, μ1, μ2, μ3} is a subgroup of SX if ε(x) = x, λ1(x) = 1/(1 − x), λ2(x) = (x − 1)/x, μ1(x) = 1/x, μ2(x) = x/(x − 1), and μ3(x) = 1 − x, for all x ![]() X.
X.
5.
(a) If G is an abelian group, show that H = {a ![]() G
G ![]() a2 = 1} is a subgroup of G.
a2 = 1} is a subgroup of G.
(b) Give an example where H is not a subgroup.
6.
(a) If G is an abelian group, show that H = {g2 ![]() g
g ![]() G} is a subgroup of G.
G} is a subgroup of G.
(b) Give an example showing that the converse of (a) is false. (c) Show that H is not a subgroup if G = A4.
7.
(a) If G is a group and g ![]() G, show that
G, show that ![]() is a subgroup of G.
is a subgroup of G.
(b) If G is finite, show that ![]() is a subgroup of G for all g
is a subgroup of G for all g ![]() G.
G.
8. If X is a nonempty subset of a group G, let ![]() be the set of all products of powers of elements of X; more formally
be the set of all products of powers of elements of X; more formally
![]()
(a) Show that ![]() is a subgroup of G that contains X.
is a subgroup of G that contains X.
(b) Show that ![]() for every subgroup H such that X ⊆ H.
for every subgroup H such that X ⊆ H.
Thus, ![]() is the smallest subgroup of G that contains X, and is called the subgroup generated by X.
is the smallest subgroup of G that contains X, and is called the subgroup generated by X.
9. If G is a group and g ![]() G, define C(g) = {z
G, define C(g) = {z ![]() G
G ![]() zg = gz}. Show that C(g) is a subgroup of G (the centralizer of g in G).
zg = gz}. Show that C(g) is a subgroup of G (the centralizer of g in G).
10. Let X ⊆ {1, 2, ![]() , n} be a nonempty set. Show that {σ
, n} be a nonempty set. Show that {σ ![]() Sn
Sn ![]() σk = k for all k
σk = k for all k ![]() X} is a subgroup of Sn.
X} is a subgroup of Sn.
11. Let ![]() Show that G is a subgroup of
Show that G is a subgroup of ![]()
12. Show that ![]() is a subgroup of
is a subgroup of ![]()
13.
(a) If G is a group, show that {(g, g) ![]() g
g ![]() G} is a subgroup of G × G.
G} is a subgroup of G × G.
(b) Determine the groups G such that {(g, g−1) ![]() g
g ![]() G} is a subgroup of G × G.
G} is a subgroup of G × G.
14. If X is an infinite set, let G be the set of all permutations σ in SX such that σx = x for all but a finite number of elements x of X. Show that G is a subgroup of SX.
15. In each case determine all subgroups of G and draw the lattice diagram.
![]()
16. Let H and K be subgroups of a group G.
(a) Show that H ∩ K is a subgroup of G (Theorem 4).
(b) Show that H ∩ K is the largest subgroup contained in both H and K in the sense that it contains every subgroup contained in both H and K.
17. If H and K are subgroups of a group G, show that H ∪ K is a subgroup if and only if H ⊆ K or K ⊆ H.
18. If a and b are real numbers, define ![]() by τa,b(x) = ax + b for all
by τa,b(x) = ax + b for all ![]() Show that
Show that ![]() a ≠ 0} is a subgroup of
a ≠ 0} is a subgroup of ![]()
19. Let H and K be subgroups of a group G and let g ![]() G.
G.
(a) If G is abelian, describe the conjugates of H in G.
(b) Show that (gHg−1) ∩ (gKg−1) = g(H ∩ K)g−1.
20.
(a) If H is a subgroup of G and H ⊆ Z(G), show that H is self-conjugate in G.
(b) Let S3 = {ε, σ, σ2, τ, τσ, τσ2}, where σ3 = ε = τ2 and στσ = τ. Show that H = {ε, σ, σ2} is self-conjugate in G.
21. If ![]() find Z(G).
find Z(G).
22. Find ![]()
23. Can a group G have an abelian subgroup not contained in Z(G)? Defend your answer.
24. If ab = ba in a group G, let H = {g ![]() G
G ![]() agb = bga}. Show that H is a subgroup of G.
agb = bga}. Show that H is a subgroup of G.
25. If H and K are subgroups of G, define HK = {hk ![]() h
h ![]() H, k
H, k ![]() K}. Show that HK is a subgroup if and only if KH ⊆ HK.
K}. Show that HK is a subgroup if and only if KH ⊆ HK.
2.4 Cyclic Groups and the Order of an Element
We have already introduced the cyclic groups Cn, n ≥ 1, but discussed these groups only informally. Recall that Cn has the form Cn = {1, a, ![]() , an−1}, where an = 1, so Cn consists of powers of A. In this section, we classify groups consisting of all powers of a particular element and determine all subgroups of such groups. This endeavor is important because these groups are building blocks for all sufficiently “ small” abelian groups (including all finite ones).
, an−1}, where an = 1, so Cn consists of powers of A. In this section, we classify groups consisting of all powers of a particular element and determine all subgroups of such groups. This endeavor is important because these groups are building blocks for all sufficiently “ small” abelian groups (including all finite ones).
We begin by showing that the set of all powers of an element of a group G is an important subgroup of G.
Theorem 1. Let g be an element of a group G and write
![]()
Then ![]() is a subgroup of G, and
is a subgroup of G, and ![]() for every subgroup H of G with g
for every subgroup H of G with g ![]() H.
H.
Proof. Clearly, ![]() If
If ![]() write them as x = gk, y = gm. Then the exponent laws give
write them as x = gk, y = gm. Then the exponent laws give ![]() and
and ![]() and the subgroup test applies. Finally,
and the subgroup test applies. Finally, ![]() and if g
and if g ![]() H where H is a subgroup then
H where H is a subgroup then ![]() because gk
because gk ![]() H for all integers k.
H for all integers k.
Hence, if g ![]() G then
G then ![]() is the smallest subgroup of G containing the element g.
is the smallest subgroup of G containing the element g.
If g is an element of a group G, the subgroup ![]() is called the cyclic subgroup of G generated by g. If
is called the cyclic subgroup of G generated by g. If ![]() for some g
for some g ![]() G, we say that G is a cyclic group and that g is a generator of G. Thus, the generic cyclic group Cn = {1, a,
G, we say that G is a cyclic group and that g is a generator of G. Thus, the generic cyclic group Cn = {1, a, ![]() , an−1}, an = 1, is cyclic in the present sense, so the terminology is consistent.
, an−1}, an = 1, is cyclic in the present sense, so the terminology is consistent.
Example 1. If G is any group, ![]() is a cyclic subgroup of G.
is a cyclic subgroup of G.
Example 2. The group G = {1, − 1, i, − i} is cyclic. In fact, i2 = − 1 and i3 = − i show that ![]() Similarly,
Similarly, ![]() so both i and −i are generators. But −1 is not a generator, because all positive and negative powers of −1 are either 1 or −1. Hence
so both i and −i are generators. But −1 is not a generator, because all positive and negative powers of −1 are either 1 or −1. Hence ![]() is not all of G.
is not all of G.
If a group X is written additively, recall that the unity element is denoted 0 and the inverse of x ![]() X is denoted −x. The exponent xn (in multiplicative notation) becomes nx here, so the cyclic subgroup generated by x is
X is denoted −x. The exponent xn (in multiplicative notation) becomes nx here, so the cyclic subgroup generated by x is
![]()
consisting of the multiples of x. The laws of exponents translate as follows:
![]()
and if x and y commute
![]()
Here are two important examples of cyclic additive groups.
Example 3. Show that ![]() is cyclic and that 1 and −1 are the only generators.
is cyclic and that 1 and −1 are the only generators.
Solution. If ![]() then
then ![]() so
so ![]() Similarly,
Similarly, ![]() because k = (− k) · (− 1). Clearly
because k = (− k) · (− 1). Clearly ![]() , if n ≠ 1 and n ≠ − 1 (for example
, if n ≠ 1 and n ≠ − 1 (for example ![]()
Example 4. Show that ![]() is cyclic with generator
is cyclic with generator ![]()
Solution. We have ![]() where, for the moment, we revert to the formal
where, for the moment, we revert to the formal ![]() notation for residue classes. Given
notation for residue classes. Given ![]() in
in ![]() note that
note that ![]() is a multiple of
is a multiple of ![]() and so
and so ![]() It follows that
It follows that ![]() as required.
as required.
Example 5. In the multiplicative group ![]() of nonzero real numbers, the cyclic group
of nonzero real numbers, the cyclic group ![]() consists of all the powers (positive, zero, and negative) of 3. Note that these powers are all distinct in this case.
consists of all the powers (positive, zero, and negative) of 3. Note that these powers are all distinct in this case.
Example 6. Consider the group ![]() Here are the powers of 2:
Here are the powers of 2:
![]()
If the elements in the bottom row are read left to right they “ cycle” endlessly through the sequence 1, 2, 4 (this is the source of the term cyclic group). Clearly ![]() and the reason that
and the reason that ![]() has three elements is that 3 is the smallest positive integer n such that 2n = 1 in
has three elements is that 3 is the smallest positive integer n such that 2n = 1 in ![]()
Order of an Element
These examples point to one of the most useful concepts in group theory. Let g be an element of a group, and suppose that gk = 1 for some integer k ≠ 0. Since g−k = 1 also holds, we may assume that k ≥ 1, so the well-ordering principle guarantees that there is a smallest integer n ≥ 1 such that gn = 1. This integer n is called the order of g, and is denoted o(g) = n. If no such integer n exists we say that g has infinite order and write o(g) = ∞. To sum up:
1. If gk = 1 for some k ≠ 0 then o(g) = n is the smallest integer such that n ≥ 1 and gn = 1.
2. If gk = 1 only if k = 0 then o(g) = ∞.
In particular, in Example 5, o(3) =∞ in ![]() , while in Example 6, o(2) = 3 in
, while in Example 6, o(2) = 3 in ![]() Note that the unity element 1 is the only element of order 1 in any group.
Note that the unity element 1 is the only element of order 1 in any group.
Example 7. Find the order of each element in ![]() Is
Is ![]() cyclic?
cyclic?
Solution. We have o(1) = 1. Since 32 = 9 = 1 in ![]() it follows o(3) = 2. Similarly, o(5) = 2 and o(7) = 2. Hence no element of
it follows o(3) = 2. Similarly, o(5) = 2 and o(7) = 2. Hence no element of![]() has order 4, so
has order 4, so ![]() is not cyclic.
is not cyclic.
Example 8. Find ![]() in
in ![]()
Solution. Write ![]() Then
Then ![]() and
and ![]() so A6 = I. Since A4 ≠ I and A5 ≠ I, we conclude that
so A6 = I. Since A4 ≠ I and A5 ≠ I, we conclude that ![]()
Example 9. If γ = (k1k2 ![]() kr) is a cycle in Sn, then o(γ) = r is the length of γ.
kr) is a cycle in Sn, then o(γ) = r is the length of γ.
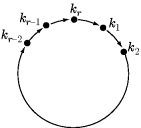
Solution. If the integers k1, k2, . . . kr are uniformly placed on a circle, the cycle γ moves each integer one position clockwise, as shown in the diagram. Hence γ2, γ3, . . . carry each in-teger 2, 3, . . . positions clockwise, respectively, so γn ≠ ε for 1 ≤ n ≤ r − 1, whereas γr = ε. This means that o(γ) = r.
Example 10. Show that o(g−1) = o(g) for any group element g.
Solution. If ![]() then (g−1)k = (gk)−1, and it follows that (g−1)k = 1 if and only if gk = 1. Hence the smallest positive integer n (if any) such that gn = 1 is the same as the smallest positive integer n such that (g−1)n = 1. That is, o(g−1) = o(g).
then (g−1)k = (gk)−1, and it follows that (g−1)k = 1 if and only if gk = 1. Hence the smallest positive integer n (if any) such that gn = 1 is the same as the smallest positive integer n such that (g−1)n = 1. That is, o(g−1) = o(g).
Example 11. If G is a finite group, show that every element g ![]() G has finite order.
G has finite order.
Solution. Since G is finite, the powers g, g2, g3, ![]() are not all distinct, so let gk = gm with k < m. Then gm−k = 1 where m − k > 0 so 0(g) is finite.
are not all distinct, so let gk = gm with k < m. Then gm−k = 1 where m − k > 0 so 0(g) is finite.
Computing the order of an element is simplified by the next theorem
Theorem 2. Let G be a group and let g ![]() G satisfy o(g) = n. Then
G satisfy o(g) = n. Then
1. gk = 1if and only if n|k.
2. gk = gmif and only if k ≡ m (modn).
3. ![]() where 1, g, g2,
where 1, g, g2, ![]() , gn−1 are all distinct.
, gn−1 are all distinct.
Proof. We use the laws of exponents.
(1) If n|k, say k = qn, then gk = (gn)q = 1q = 1. Conversely, if gk = 1, write k = qn + r with 0 ≤ r < n (division algorithm). But then we have gr = gk(gn)−q = 1(1)−q = 1. Since r < n, this contradicts the minimality of n unless r = 0. So r = 0 and n|k.
(2) We have gk = gm if and only if gk−m = 1. Now apply (1).
(3) Clearly, ![]() To prove the other inclusion, let
To prove the other inclusion, let ![]() say x = gk. As before, write k = qn + r, where 0 ≤ r ≤ n − 1. Then
say x = gk. As before, write k = qn + r, where 0 ≤ r ≤ n − 1. Then
![]()
which shows that ![]() Hence
Hence ![]() To complete the proof, suppose two of 1, g, g2,
To complete the proof, suppose two of 1, g, g2, ![]() , gn−1 are equal, say gk = gm, where 0 ≤ k ≤ m < n. Then gm−k = 1 and 0 ≤ m − k < n. This implies that m − k = 0 by the minimality of n, so gm = gk. Thus 1, g, g2,
, gn−1 are equal, say gk = gm, where 0 ≤ k ≤ m < n. Then gm−k = 1 and 0 ≤ m − k < n. This implies that m − k = 0 by the minimality of n, so gm = gk. Thus 1, g, g2, ![]() , gn−1 are distinct.
, gn−1 are distinct.
Theorem 2 asserts that if o(g) = n, then gk = 1 if and only if n|k. The following example illustrates how useful this is.
Example 12. Find the order of 2 in ![]()
Solution. We compute in ![]() : 23 = 8, so 26 = 64 = 7 and 29 = 56 = − 1. Hence 218 = 1, so o(2) divides 18 by Theorem 2. Thus, o(2) is 1, 2, 3, 6, 9, or 18. We have already eliminated 3, 6, and 9, so as 21 = 2 and 22 = 4, the only possibility remaining is o(2) = 18. Note that, since
: 23 = 8, so 26 = 64 = 7 and 29 = 56 = − 1. Hence 218 = 1, so o(2) divides 18 by Theorem 2. Thus, o(2) is 1, 2, 3, 6, 9, or 18. We have already eliminated 3, 6, and 9, so as 21 = 2 and 22 = 4, the only possibility remaining is o(2) = 18. Note that, since ![]() = 18, this shows that
= 18, this shows that ![]() is cyclic and that 2 is a generator.
is cyclic and that 2 is a generator.
The next result is the “ companion” of Theorem 2 for elements g with o(g) = ∞.
Theorem 3. Let G be a group and let g ![]() G satisfy o(g) = ∞. Then
G satisfy o(g) = ∞. Then
1. gk = 1if and only if k = 0.
2. gk = gm if and only if k = m.
3. ![]() , where the gi are distinct.
, where the gi are distinct.
Proof. (1) Clearly g0 = 1. If gk = 1, k ≠ 0, then g−k = (gk)−1 = 1−1 = 1, too. Hence gn = 1 for some n > 0, which implies that ![]() is finite, contrary to hypothesis. Thus gk = 1 implies that k = 0.
is finite, contrary to hypothesis. Thus gk = 1 implies that k = 0.
(2) We have gk = gm if and only if gk−m = 1. Apply (1).
(3) ![]() by definition, and these powers are distinct by (2).
by definition, and these powers are distinct by (2).
If o(g) = n, then ![]() too, by (3) of Theorem 2, so
too, by (3) of Theorem 2, so ![]() in this case. Since this also holds if o(g) = ∞, we have shown that our two uses of the word “ order” are compatible.
in this case. Since this also holds if o(g) = ∞, we have shown that our two uses of the word “ order” are compatible.
Corollary. We have o(g) = ![]() for every element g of any group.
for every element g of any group.
We now use Theorem 2 to derive an elegant formula for the order of any permutation σ in Sn. Recall that σ factors (uniquely) as a product of disjoint cycles γi (Theorem 5 §1.4). The order of σ turns out to be the least common multiple of the orders of the cycles γi (which are the lengths of the γi by Example 9).
Theorem 4. Let σ be a permutation in St with factorization σ = γ1γ2 ![]() γr into disjoint cycles. Then |σ| = lcm(o(γ1), o(γ2),
γr into disjoint cycles. Then |σ| = lcm(o(γ1), o(γ2), ![]() , o(γr)).
, o(γr)).
Proof. Write n = o(σ), ni = o(γi), and m = lcm(n1, n2, ![]() , nr). As ni|m for each i, we have
, nr). As ni|m for each i, we have ![]() and so
and so ![]() (because the γi commute). Hence n|m by Theorem 2. To show that m|n, it suffices to show that
(because the γi commute). Hence n|m by Theorem 2. To show that m|n, it suffices to show that ![]() for each i (then ni|n by Theorem 2 so m|n by the definition of the least common multiple). We show that
for each i (then ni|n by Theorem 2 so m|n by the definition of the least common multiple). We show that ![]() the others are similar. This requires proving that
the others are similar. This requires proving that ![]() for all 0 ≤ k ≤ n. This is clear if k is fixed by γ1, so let k be moved by γ1. Then k is fixed by each of γ2,
for all 0 ≤ k ≤ n. This is clear if k is fixed by γ1, so let k be moved by γ1. Then k is fixed by each of γ2, ![]() , γr, because the γi are disjoint. Thus, since
, γr, because the γi are disjoint. Thus, since ![]() we have
we have
![]()
It follows that ![]() as required.
as required.
Example 13. Find the order of
σ = ![]() .
.
Solution. Here σ = (151013414) (2712611) (39) is the cycle factorization, so Theorem 4 gives o(σ) = lcm(6, 5, 2) = 30.
The next result will be used several times below.
Theorem 5. Let o(g) = n for g in some group. If d|n, d ≥ 1, show that ![]()
Proof. Write ![]() for convenience. Then (gd)k = gn = 1, so we must show that k is the smallest such positive integer. Suppose (gd)r = 1, r ≥ 1. Then gdr = 1 so n|dr by Theorem 2, say dr = qn, q ≥ 1. But then dr = q(dk), so r = qk because these are integers and d ≠ 0. It follows that r ≥ k, as required.
for convenience. Then (gd)k = gn = 1, so we must show that k is the smallest such positive integer. Suppose (gd)r = 1, r ≥ 1. Then gdr = 1 so n|dr by Theorem 2, say dr = qn, q ≥ 1. But then dr = q(dk), so r = qk because these are integers and d ≠ 0. It follows that r ≥ k, as required.
Other Properties of Cyclic Groups
Theorem 6. Every cyclic group is abelian, but the converse does not hold.
Proof. Let ![]() be cyclic with generator g. If x, y
be cyclic with generator g. If x, y ![]() G, write x = gk, y = gm, where
G, write x = gk, y = gm, where ![]() Then the exponent laws give
Then the exponent laws give
![]()
so G is abelian. However ![]() is abelian but not cyclic by Example 7.
is abelian but not cyclic by Example 7.
As the proof of Theorem 6 illustrates, computations in a cyclic group depend entirely on the exponents of the generator. As these exponents are integers, the facts about ![]() derived in Chapter 1 turn out to be useful. In particular, the division algorithm plays a natural role in the proof of Theorem 7.
derived in Chapter 1 turn out to be useful. In particular, the division algorithm plays a natural role in the proof of Theorem 7.
Theorem 7. Every subgroup of a cyclic group is cyclic.
Proof. Suppose that ![]() is cyclic and let H be a subgroup of G. If H = {1}, then
is cyclic and let H be a subgroup of G. If H = {1}, then ![]() is cyclic. Otherwise, let gk
is cyclic. Otherwise, let gk ![]() H, k ≠ 0. Because H is a subgroup, g−k = (gk)−1
H, k ≠ 0. Because H is a subgroup, g−k = (gk)−1 ![]() H, and so we may assume that k > 0. Hence let m be the smallest positive integer such that gm
H, and so we may assume that k > 0. Hence let m be the smallest positive integer such that gm ![]() H. Then
H. Then ![]() and we claim this is equality. To see this, let gk
and we claim this is equality. To see this, let gk ![]() H and write k = qm + r, 0 ≤ r < m, by the division algorithm. It suffices to show that r = 0 (then
H and write k = qm + r, 0 ≤ r < m, by the division algorithm. It suffices to show that r = 0 (then ![]() ). But gr = (gm)−qgk
). But gr = (gm)−qgk ![]() H, which contradicts the minimality of m unless r = 0.
H, which contradicts the minimality of m unless r = 0.
A cyclic group ![]() can have other generators, for example,
can have other generators, for example, ![]() Theorem 8 explicitly describes all generators of a finite cyclic group.
Theorem 8 explicitly describes all generators of a finite cyclic group.
Theorem 8. Let ![]() be a cyclic group, where o(g) = n. Then
be a cyclic group, where o(g) = n. Then ![]() if and only if gcd (k, n) = 1.
if and only if gcd (k, n) = 1.
Proof. If ![]() then
then ![]() say g = (gk)m, where
say g = (gk)m, where ![]() Thus g1 = gkm, so n divides 1 − km by Theorem 2. Then 1 − km = qn for
Thus g1 = gkm, so n divides 1 − km by Theorem 2. Then 1 − km = qn for ![]() that is, 1 = km + qn, which implies that gcd (k, n) = 1. Conversely, if gcd (k, n) = 1 then 1 = xk + yn for some integers x and y by Theorem 4 §1.2. Hence
that is, 1 = km + qn, which implies that gcd (k, n) = 1. Conversely, if gcd (k, n) = 1 then 1 = xk + yn for some integers x and y by Theorem 4 §1.2. Hence
![]()
which implies that ![]()
Hence, for example, if o(g) = 12 the generators of ![]() are the powers gk where gcd (k, 12) = 1, that is g, g5, g7, and g11. In particular, the generators of the additive cyclic group
are the powers gk where gcd (k, 12) = 1, that is g, g5, g7, and g11. In particular, the generators of the additive cyclic group ![]() are the residues
are the residues ![]() and
and ![]()
Theorem 9 below gives a complete description of all subgroups of a finite cyclic group G. In particular, it shows that G has a unique subgroup of order k for every divisor k of n, and that these are the only subgroups of G.
Theorem 9. Fundamental Theorem of Finite Cyclic Groups. Let ![]() be a cyclic group of order n.
be a cyclic group of order n.
1. If H is a subgroup of G, then ![]() for some d|n. Hence |H| divides n.
for some d|n. Hence |H| divides n.
2. Conversely, if k|n, then ![]() is the unique subgroup of G of order k.
is the unique subgroup of G of order k.
Proof. (1) Theorem 7 implies that ![]() for some m. Let d = gcd (m, n); we show that
for some m. Let d = gcd (m, n); we show that ![]() We have d|m, say m = qd, so
We have d|m, say m = qd, so ![]() when
when ![]() On the other hand, d = xm + yn, for some
On the other hand, d = xm + yn, for some ![]() so
so
![]()
Hence ![]() so
so ![]() But then,
But then, ![]() by Theorem 5, so |H| divides n.
by Theorem 5, so |H| divides n.
(2) Suppose that K is any subgroup of G of order k where k|n. By (1) let ![]() where d|n. Then Theorems 2 and 5 give
where d|n. Then Theorems 2 and 5 give ![]() It follows that
It follows that ![]() so
so ![]() This proves (2).
This proves (2).
If G is finite and cyclic and H is a subgroup, part (1) of Theorem 9 shows that |H| divides |G|. In fact, this result is true for any finite group G, cyclic or not. The general result is called Lagrange's theorem, which we prove in Section 2.6.
Example 14. Find all subgroups of C12 and draw the lattice diagram.
Solution. Let ![]() , o(g) = 12. The divisors of 12 are 1, 2, 3, 4, 6, and 12. Using Theorem 5, the unique subgroup of each of these orders is, respectively,
, o(g) = 12. The divisors of 12 are 1, 2, 3, 4, 6, and 12. Using Theorem 5, the unique subgroup of each of these orders is, respectively,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
The lattice diagram is as shown at the right. Note that ![]() if and only if k|m.
if and only if k|m. ![]()

We speak of the cyclic subgroup ![]() as being generated by the single element g. We conclude this section with a brief discussion of subgroups generated by more than one element.
as being generated by the single element g. We conclude this section with a brief discussion of subgroups generated by more than one element.
Theorem 10. Let X be a nonempty subset of a group G and let
![]()
denote the set of all products of powers of (not necessarily distinct) elements of X. Then
1. ![]() is a subgroup of G containing X.
is a subgroup of G containing X.
2. If H is a subgroup of G with X ⊆ H, then ![]()
Proof. (1) Choose x ![]() X (because X ≠ ∅). Then
X (because X ≠ ∅). Then ![]() The set
The set ![]() is clearly closed and, if
is clearly closed and, if ![]() is in
is in ![]() then
then ![]() is also in
is also in ![]() Hence
Hence ![]() is a subgroup of G by the subgroup test.
is a subgroup of G by the subgroup test.
(2) If X ⊆ H and ![]() is in
is in ![]() then each
then each ![]() is in H because xi
is in H because xi ![]() X ⊆ H and H is a subgroup. Hence g
X ⊆ H and H is a subgroup. Hence g ![]() H, proving (2).
H, proving (2).
Thus, if X is a nonempty subset of a group G, the subgroup ![]() in Theorem 10 is the smallest subgroup of G that contains X (in the sense of (2) of Theorem 10). Hence
in Theorem 10 is the smallest subgroup of G that contains X (in the sense of (2) of Theorem 10). Hence ![]() is called the subgroup generated by X. If G has the form
is called the subgroup generated by X. If G has the form ![]() for some X ⊆ G, we call X a set of generators for G; if X is finite, we say that G is a finitely generated group.
for some X ⊆ G, we call X a set of generators for G; if X is finite, we say that G is a finitely generated group.
Obviously, ![]() so the cyclic groups are exactly the subgroups generated by singleton subsets. Similarly, it is customary to write
so the cyclic groups are exactly the subgroups generated by singleton subsets. Similarly, it is customary to write
![]()
for finitely generated groups.
Example 15. Consider the symmetric group S3 = {ε, σ, σ2, τ, τσ, τσ2}, where |σ| = 3, |τ| = 2, and στ = τσ2. Then ![]()
Example 16. The Klein group K4 = {1, a, b, ab} is generated by any two nonunity elements.
Exercises 2.4
1. Find all generators of the cyclic group ![]() if
if
![]()
2. Find all generators of
![]()
3. Find all generators of
![]()
4. In each case determine whether G is cyclic.
![]()
5.
(a) Is ![]() cyclic? Justify your answer.
cyclic? Justify your answer.
(b) Is ![]() cyclic? Justify your answer.
cyclic? Justify your answer.
6. If G is a group and g ![]() G, show that
G, show that ![]()
7. Let o(g)= 20 in a group G. Compute (a) o(g2) (b) o(g8) (c) o(g5) (d) o(g3)
8.
(a) Find an element of maximum order in S5.
(b) Find an element of maximum order in S7.
9. In each case find all subgroups of ![]() and draw the lattice diagram.
and draw the lattice diagram.
(a) o(g) = 8
(b) o(g) = 10
(c) o(g) = 18
(d) o(g)= p3, p is a prime.
(e) o(g) = pq, p and q are distinct primes.
(f) o(g)= p2q, p and q are distinct primes.
10.
(a) If gh = hg in a group and o(g) and o(h) are finite, show that o(gh) is finite.
(b) Show that (a) fails if gh ≠ hg by considering ![]() and
and ![]()
11. Let G be a cyclic group of order n.
(a) Show that gn = 1 for all g ![]() G.
G.
(b) If gm = 1 in G where gcd (m, n) = 1, show that g = 1.
12. Let ![]() in Un. Show that o(g) = n.
in Un. Show that o(g) = n.
13.
(a) If G = {g1, g2, ![]() , gr} is an abelian group, let a = g1g2
, gr} is an abelian group, let a = g1g2 ![]() gr. Show that a2 = 1.
gr. Show that a2 = 1.
(b) Prove Wilson's Theorem: (p − 1) ! ≡ − 1 (modp) if p is a prime. [Hint: ![]() ]
]
14. Suppose that G is a group in which {1} and G are the only subgroups. Show that G is finite and, in fact, is cyclic of order 1 or a prime.
15. Show that ![]() for all a and b in a group G.
for all a and b in a group G.
16. In each case, find the subgroup ![]() of G.
of G.
(a) ![]() is cyclic, x = a4, y = a3
is cyclic, x = a4, y = a3
(b) ![]() is cyclic, x = a6, y = a8
is cyclic, x = a6, y = a8
(c) ![]() is cyclic, x = am, y = ak, gcd (m, k) = d
is cyclic, x = am, y = ak, gcd (m, k) = d
(d) G = S3, x = (12), y = (23)
(e) ![]() o(a)= 4 = o(b), x = (a3, b), y = (a, b)
o(a)= 4 = o(b), x = (a3, b), y = (a, b)
(f) ![]() o(a)= 4, o(b)= 6, x = (a2, b), y = (a, b3)
o(a)= 4, o(b)= 6, x = (a2, b), y = (a, b3)
17.
(a) If X ⊆ Y in a group, show that ![]()
(b) Show that a nonempty subset X is a subgroup if and only if ![]()
18. If ![]() and
and ![]() show that
show that ![]()
19. If ![]() and xy = yx for all x, y
and xy = yx for all x, y ![]() X, show that G is abelian.
X, show that G is abelian.
20.
(a) Find three elements of C6 × C15 of maximum order.
(b) Find one element of maximum order in Cm × Cn.
21. Find the smallest positive integer n such that σn = ε for every σ ![]() S5.
S5.
22. If σ ![]() Sn and o(σ) = p is a prime, show that σ is a product of disjoint p-cycles.
Sn and o(σ) = p is a prime, show that σ is a product of disjoint p-cycles.
23.
(a) Show that o(h) = o(ghg−1) for all g, h ![]() G. [Hint: Example 10.]
G. [Hint: Example 10.]
(b) Show that o(gh) = o(hg) for all g, h ![]() G. [Hint: Example 10.]
G. [Hint: Example 10.]
24.
(a) If h is the only element of order 2 in a group G, show that h ![]() Z(G). [Hint: Exercise 23(a).]
Z(G). [Hint: Exercise 23(a).]
(b) If a is the unique element of order 3 in G, what can you say about a?
25. Let G and H be cyclic groups, with |G| = m and |H| = n. If gcd (m, n) = 1, show that G × H is cyclic. [Hint: If ![]() and
and ![]() use Theorem 5 §1.2 to show o((g, h))= mn.]
use Theorem 5 §1.2 to show o((g, h))= mn.]
26. Let o(g) = m and o(h) = n in a group G, where m and n are relatively prime.
(a) If gh = hg, show that o(gh) = mn. Is o(gh) = lcm(m, n) in general? [Hint: Theorem 5 §1.2.]
(b) If o(a) = mn, show that a = gh = hg for some g, h ![]() G with o(g) = m and o(h) = n. [Hint: Theorem 4 §1.2.]
G with o(g) = m and o(h) = n. [Hint: Theorem 4 §1.2.]
27. Let ![]() be a cyclic group and let
be a cyclic group and let ![]() and
and ![]() be cyclic subgroups.
be cyclic subgroups.
(a) If o(g) =∞, show that A ⊆ B if and only if a = qb for some ![]()
(b) If o(g) = n, show that A ⊆ B if and only if a ≡ qb (modn) for some ![]()
28. Let H be a subgroup of a group G and let a ![]() G, o(a) = n. If m is the smallest positive integer such that am
G, o(a) = n. If m is the smallest positive integer such that am ![]() H, show that m|n.
H, show that m|n.
29. If o(g) = n, show that o(gk) = n/d, where d = gcd (n, k). [Hint: Proof of Theorem 9.]
30. Let ![]() where o(g) = n. Given gk
where o(g) = n. Given gk ![]() G, show
G, show ![]() where d = gcd (k, n). [Hint: Theorem 3 §1.2.]
where d = gcd (k, n). [Hint: Theorem 3 §1.2.]
31. Let ![]() be a cyclic group and let
be a cyclic group and let ![]() and
and ![]()
(a) If o(g) =∞, show that ![]() where m = lcm(a, b).
where m = lcm(a, b).
(b) If o(g) = n, assume (Theorem 9) that a|n and b|n. Show that ![]() where m = lcm(a, b).
where m = lcm(a, b).
32. Show that the following conditions are equivalent for a finite group G.
(1) G is cyclic and |G| = pn, where p is a prime and n ≥ 0.
(2) If H and K are subgroups of G, either H ⊆ K or K ⊆ H. [Hint: For (1) ⇒ (2) use Theorem 8.]
33. If a group G has a finite number of subgroups, show that G must be finite.
34. Prove the Chinese Remainder Theorem. Let n1, n2, ![]() , nr be positive integers, relatively prime in pairs. Given integers m1, m2,
, nr be positive integers, relatively prime in pairs. Given integers m1, m2, ![]() , mr, show that there exists
, mr, show that there exists ![]() such that mi ≡ m (modni) for each i. [Hint: Extend Exercise 25 to r groups.]
such that mi ≡ m (modni) for each i. [Hint: Extend Exercise 25 to r groups.]
35.
(a) Let o(a) = m and o(b) = n in a group G. If ab = ba, show that an element c ![]() G exists, with o(c) = lcm(a, b). [Hint: Theorem 10 §1.2, Theorem 8, and Exercise 26(a).]
G exists, with o(c) = lcm(a, b). [Hint: Theorem 10 §1.2, Theorem 8, and Exercise 26(a).]
(b) Let G be an abelian group and assume that G has an element of maximal order n (always true if G is finite). Show that gn = 1 for all g ![]() G. [Hint: Part (a).]
G. [Hint: Part (a).]
36. Let m be the smallest positive integer such that σm = ε for all σ ![]() Sn. Show that m = lcm(2, 3, 4, 5,
Sn. Show that m = lcm(2, 3, 4, 5, ![]() , n).
, n).
37. For a deck of 2n distinct cards, a “ perfect shuffle” means cutting the deck into two equal halves and collating them as follows: If the cards were originally in the order 1, 2, 3, 4, ![]() , 2n, they end up in the order 1, n + 1, 2, n + 2,
, 2n, they end up in the order 1, n + 1, 2, n + 2, ![]() , n, 2n. In each case, determine the number of perfect shuffles required to bring the deck back into its original order.
, n, 2n. In each case, determine the number of perfect shuffles required to bring the deck back into its original order.
| (a) n = 4, 5, 6, and 7 | (b) n = 8, 9, and 10 |
| (c) n = 12 | (d) n = 26 (a regular deck) |
2.5 Homomorphisms and Isomorphisms
Mathematicians do not deal in objects, but in relations among objects; they are free to replace some objects by others so long as the relations remain unchanged. Content to them is irrelevant: they are interested in form only.
—Henri Poincaré
Up to this point we have ignored mappings from one group to another. The interesting ones are those that preserve the group multiplication in the following sense: If G and H are groups, a mapping α: G → H is called a homomorphism27 if
![]()
Of course the product ab here is in G while α(a) · α(b) is in H.
Homomorphisms arise in many forms as the following examples illustrate.
Example 1. The mapping ![]() given by α(a) = 3a is a homomorphism of additive groups because α(a + b) = 3(a + b) = 3a + 3b = α(a) + α(b) for all
given by α(a) = 3a is a homomorphism of additive groups because α(a + b) = 3(a + b) = 3a + 3b = α(a) + α(b) for all ![]()
Example 2. If a is an element of a group G, define the exponent map ![]() by α(k) = ak for all
by α(k) = ak for all ![]() Then α is a homomorphism because (as the operation in
Then α is a homomorphism because (as the operation in ![]() is addition)
is addition)
![]()
Example 3. Let ![]() denote the group of positive real numbers under multiplication. The absolute value map
denote the group of positive real numbers under multiplication. The absolute value map ![]() given by α(z) = |z| for all
given by α(z) = |z| for all ![]() is a homomorphism (in fact, onto) because
is a homomorphism (in fact, onto) because ![]() for all
for all ![]()
Example 4. Let ![]() denote the general linear group of n × n invertible matrices over
denote the general linear group of n × n invertible matrices over ![]() The determinant map
The determinant map ![]() given by A
given by A ![]() det A is a homomorphism because det (AB) = det A det B for all matrices A and B, and det A ≠ 0 if A is invertible.
det A is a homomorphism because det (AB) = det A det B for all matrices A and B, and det A ≠ 0 if A is invertible.
Example 5. The identity map 1G: G → G is a homomorphism for any group G because 1G(ab) = ab = 1G(a) · 1G(b) for all a, b in G.
Example 6. For groups G and H, there is at least one homomorphism from G to H, the trivial homomorphism α: G → H defined by α(g) = 1 for all g ![]() G.
G.
Example 7. If α: G → H and β: H → K are homomorphisms, show that the composite map βα: G → K is also a homomorphism.
Solution. This is because, for all a and b in G,
![]()
By definition, a homomorphism α: G → H is a mapping that preserves the operation in the sense that α(ab) = α(a)α(b) for all a and b in G. Theorem 1 shows that α is “ structure preserving” in the sense that it also preserves the unity, inverses, and powers.
Theorem 1. Let α: G → H be a group homomorphism. Then
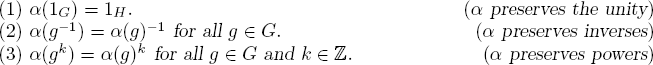
Proof.
(1) Here ![]() Now cancel in H.
Now cancel in H.
(2) From (1), α(g−1) · α(g) = α(g−1g) = α(1) = 1, which gives (2).
(3) For k = 0, α(g0) = α(1) = 1 = [a(g)]0. If (3) holds for some k ≥ 0, then
![]()
Hence (3) holds for all k ≥ 0 by induction. If k < 0, write k = − m, m > 0. Then (2) and the preceding calculation give
α(gk) = α[(gm)−1] = [α(gm)]−1 = [α(g)m]−1 = [α(g)]−m = [α(g)]k.
Thus [α(g)]k = α(gk) for all ![]()
Corollary 1. Let α: G → H be a homomorphism. If g ![]() G has finite order, then α(g) also has finite order, and o(α(g))divides o(g).
G has finite order, then α(g) also has finite order, and o(α(g))divides o(g).
Proof. If o(g) = n then gn = 1, so α(g)n = α(gn) = α(1) = 1. Hence o(α(g)) divides n by Theorem 2 §2.4.
Corollary 2. If α: G → H is a homomorphism, write α(G) = {α(g) ![]() g
g ![]() G}. Then α(G) is a subgroup of H.
G}. Then α(G) is a subgroup of H.
Proof. This follows from the subgroup test because of the following observations: 1H = α(1G) ![]() α(G); α(g)α(g1) = α(gg1)
α(G); α(g)α(g1) = α(gg1) ![]() α(G), and α(g)−1 = α(g−1)
α(G), and α(g)−1 = α(g−1) ![]() α(G).
α(G).
The group α(G) in Corollary 2 is called the image of α. Note that α: G → H is onto if and only if α(G) = H.
Example 8. Let α: G → H be an onto homomorphism.
1. If G is abelian show that H is abelian.
2. If ![]() is cyclic show that H is cyclic and
is cyclic show that H is cyclic and ![]()
Solution. Let h, h1 ![]() H. Since α is onto, write h = α(g) and h1 = α(g1), g, g1
H. Since α is onto, write h = α(g) and h1 = α(g1), g, g1 ![]() G.
G.
1. If G is abelian: hh1 = α(g)α(g1) = α(gg1) = α(g1g) = α(g1)α(g) = h1h.
2. Let ![]() If h
If h ![]() H, say h = α(g), let g = ak,
H, say h = α(g), let g = ak, ![]() It suffices to prove that
It suffices to prove that ![]() But
But ![]() as required.
as required.
Let G and H denote groups. In order to show that two mappings α: G → H and β: G → H are equal, we must verify that α(g) = β(g) holds for all g ![]() G. However, if α and β are homomorphisms, this need only be checked for all g in some generating set for G—see Theorem 10 §2.4.
G. However, if α and β are homomorphisms, this need only be checked for all g in some generating set for G—see Theorem 10 §2.4.
Theorem 2. Let α: G → H and β: G → H be homomorphisms and assume that ![]() is generated by a subset X. Then
is generated by a subset X. Then
![]()
Proof. If α = β, the condition is obvious. If the condition holds, let g ![]() G and write (Theorem 10 §2.4)
G and write (Theorem 10 §2.4) ![]() where xi
where xi ![]() X and
X and ![]() for each i. Then Theorem 1 gives
for each i. Then Theorem 1 gives
α(g) = α(x1)k1α(x2)k2 ![]() α(xn)kn = β(x1)1kβ(x2)2k
α(xn)kn = β(x1)1kβ(x2)2k ![]() β(xn)nk = β(g).
β(xn)nk = β(g).
As g ![]() G was arbitrary, this shows that α = β.
G was arbitrary, this shows that α = β.
Theorem 2 shows that a group homomorphism α: G → H is completely determined by its effect on a generating set for G. This is useful because many groups are generated by a relatively small number of elements.
Example 9. Show that there are at most six homomorphisms S3 → C6.
Solution. As in Example 8 §2.2 we write S3 = {1, σ, σ2, τ, τσ, τσ2} where o(σ) = 3, o(τ) = 2, and στσ = τ, and write ![]() o(c) = 6. Hence
o(c) = 6. Hence ![]() so Theorem 2 shows that a homomorphism α: S3 → C6 is determined by the choice of α(σ) and α(τ) in C6. Now α(σ)3 = α(σ3) = α(ε) = 1, so o(α(σ)) is 1 or 3. Hence there are three choices for α(σ): 1, c2, or c4. Similarly, α(τ)2 = 1, so α(τ) must be 1 or c3. Thus, there are at most 3 · 2 = 6 choices in all for α(σ).
so Theorem 2 shows that a homomorphism α: S3 → C6 is determined by the choice of α(σ) and α(τ) in C6. Now α(σ)3 = α(σ3) = α(ε) = 1, so o(α(σ)) is 1 or 3. Hence there are three choices for α(σ): 1, c2, or c4. Similarly, α(τ)2 = 1, so α(τ) must be 1 or c3. Thus, there are at most 3 · 2 = 6 choices in all for α(σ).
We hasten to note that not all the choices in Example 9 correspond to actual homomorphisms. In fact, there are only two homomorphisms from S3 to C6, and we return to this example later (see Example 9 §2.10).
Isomorphisms
We have shown that there are two distinct groups of order 4: the cyclic group and the noncyclic Klein group. Determining how to distinguish between distinct groups leads to the notion of isomorphic groups. Roughly speaking, the two groups are isomorphic if they are the same except for notation.
As an illustration, consider the groups G = {1, − 1} and ![]() The two Cayley tables are
The two Cayley tables are

Clearly, they are alike. In fact, because the way the unity multiplies is always specified, we can describe both by saying that the nonunity element squares to 1. Here is a more precise comparison: Consider the mapping ![]() given by
given by
![]()
Then α is a bijection, and we can obtain the entire Cayley table for ![]() from that of G by replacing a with σ(a) for every a in G. In other words, the two groups are the same except for notation; we obtain
from that of G by replacing a with σ(a) for every a in G. In other words, the two groups are the same except for notation; we obtain ![]() from G by changing symbols.
from G by changing symbols.
This works in general. If G and H are groups and σ: G → H is a bijection, we ask when the Cayley table for H results from applying σ to every element of the table for G. Looking at the diagram
the required condition is σ(ab) = σ(a)σ(b) for all a and b in G. In other words, σ must be is a homomorphism. This leads to the following definition.
If G and G1 are groups, a mapping
![]()
if σ is a bijection (one-to-one and onto) which is also a homomorphism. When an isomorphism exists from G to H we say that G is isomorphic to H and we write
![]()
Hence, if σ: G → H is an isomorphism, the group H is just G with the change of notation g ![]() σ(g). As in the preceding illustration, G and H are the same group except for the symbols used. It is useful to think of isomorphic groups as two different realizations of the same (abstract) group.28
σ(g). As in the preceding illustration, G and H are the same group except for the symbols used. It is useful to think of isomorphic groups as two different realizations of the same (abstract) group.28
Example 10. The set ![]() of even integers is an additive group, in fact a subgroup of
of even integers is an additive group, in fact a subgroup of ![]() Show that
Show that ![]()
Solution. The function ![]() given by σ(k) = 2k for all
given by σ(k) = 2k for all ![]() is clearly onto, and σ is one-to-one because σ(k) = σ(m) implies 2k = 2m, so k = m. Finally, σ is a homomorphism:
is clearly onto, and σ is one-to-one because σ(k) = σ(m) implies 2k = 2m, so k = m. Finally, σ is a homomorphism:
![]()
for all k and m in ![]() Thus σ is an isomorphism, so
Thus σ is an isomorphism, so ![]()
Note that the argument in Example 10 shows that ![]() for any integer n ≠ 0.
for any integer n ≠ 0.
Example 11. If ![]() show that G is a group using matrix multiplication, and that
show that G is a group using matrix multiplication, and that ![]()
Solution. Define ![]() by σ(n) =
by σ(n) = ![]() for all n in
for all n in ![]() Then σ is clearly one-to-one, and it is a homomorphism because
Then σ is clearly one-to-one, and it is a homomorphism because
![]()
Hence ![]() is a subgroup of
is a subgroup of ![]() by Corollary 2 of Theorem 1. Moreover, σ is a bijection
by Corollary 2 of Theorem 1. Moreover, σ is a bijection ![]() so
so ![]() is an isomorphism.
is an isomorphism.
Clearly, G ![]() G for any group G (the identity map G → G is an isomorphism). However, even though two groups are isomorphic, they sometimes appear to be quite different. As a remarkable example, the group
G for any group G (the identity map G → G is an isomorphism). However, even though two groups are isomorphic, they sometimes appear to be quite different. As a remarkable example, the group ![]() of all nonzero complex numbers is known to be isomorphic to the circle group
of all nonzero complex numbers is known to be isomorphic to the circle group ![]() of complex numbers on the unit circle.29 Here is a less spectacular example. Recall that
of complex numbers on the unit circle.29 Here is a less spectacular example. Recall that ![]()
Example 12. Show that ![]() where
where ![]() is additive and
is additive and ![]() is multiplicative.
is multiplicative.
Solution. Define ![]() by σ(r) = er, where ex is the exponential function. To show that σ is one-to-one, let σ(r) = σ(s), where
by σ(r) = er, where ex is the exponential function. To show that σ is one-to-one, let σ(r) = σ(s), where ![]() Then er = es so, if ln x denotes the natural logarithm of x, r = ln (er) = ln (es) = s. Thus σ is one-to-one. If
Then er = es so, if ln x denotes the natural logarithm of x, r = ln (er) = ln (es) = s. Thus σ is one-to-one. If ![]() then t > 0, so
then t > 0, so ![]() and σ(ln t) = elnt = t. Hence σ is onto. Finally,
and σ(ln t) = elnt = t. Hence σ is onto. Finally,
σ(r + s) = er+s = eres = σ(r) · σ(s), for all r and s in ![]()
which shows that σ is an isomorphism.
Example 13. If G ![]() G1 and H
G1 and H ![]() H1, show that G × G1
H1, show that G × G1 ![]() H × H1.
H × H1.
Solution. Let σ: G → G and τ: H → H1 be isomorphisms, and define a mapping μ: G × H → G1 × H1 by μ(g, h) = (σ(g), τ(h)). This is a homomorphism because
![]()
for all (g, h) and (g′, h′) in G × H. The proof that τ is onto and one-to-one is left to the reader.
Verifying that a particular mapping is an isomorphism requires checking three things: that it is onto; that it is one-to-one; and that it is operation-preserving. Even if a particular mapping α: G → H may fail one of these tests, the groups G and H may very well be isomorphic (for example r ![]() r + 1 is a bijection
r + 1 is a bijection ![]() but it is not an isomorphism). Conversely, showing that G and H are not isomorphic entails showing that no isomorphism exists from G to H. Examples 14 and 15 illustrate this situation.
but it is not an isomorphism). Conversely, showing that G and H are not isomorphic entails showing that no isomorphism exists from G to H. Examples 14 and 15 illustrate this situation.
Example 14. Show that ![]() is not isomorphic to
is not isomorphic to ![]()
Solution. Suppose that ![]() is an isomorphism. Then σ is onto, so let
is an isomorphism. Then σ is onto, so let ![]() satisfy σ(q) = 2, and write
satisfy σ(q) = 2, and write ![]() Since σ is a homomorphism, we have
Since σ is a homomorphism, we have
![]()
This is impossible because ![]() (Example 3 §0.1), so no such σ can exist.
(Example 3 §0.1), so no such σ can exist.
Example 15. Let G and H be cyclic groups with |G| = 9 and |H| = 3. Show that G and H × H are not isomorphic, even though both groups have order 9.
Solution. Suppose that σ: H × H → G is an isomorphism. If ![]() where o(a) = 9, let a = σ(x) with x
where o(a) = 9, let a = σ(x) with x ![]() H × H. Then x3 = 1 (this holds in H) so a3 = σ(x3) = 1, a contradiction. Hence
H × H. Then x3 = 1 (this holds in H) so a3 = σ(x3) = 1, a contradiction. Hence ![]()
The reason that ![]() in Example 15 is that, while x3 = 1 for every element x of H × H, this is not the case for G. The condition x3 = 1 for all x is a property of the Cayley table of H × H but not of the Cayley table of G. The fact that group isomorphisms preserve such properties is the reason that H × H is not isomorphic to G. More generally, we can often show two groups are not isomorphic by exhibiting such a property that holds in one but not the other.
in Example 15 is that, while x3 = 1 for every element x of H × H, this is not the case for G. The condition x3 = 1 for all x is a property of the Cayley table of H × H but not of the Cayley table of G. The fact that group isomorphisms preserve such properties is the reason that H × H is not isomorphic to G. More generally, we can often show two groups are not isomorphic by exhibiting such a property that holds in one but not the other.
Theorem 3. Let G, H, and K denote groups.
1. The identity map 1G: G → G is an isomorphism for every group G.
2. If σ: G → H is an isomorphism, the inverse mapping σ−1: H → G is also an isomorphism.
3. If σ: G → H and τ: H → K are isomorphisms, the composite map τσ: G → K is also an isomorphism.
Proof. (1) is clear.
(2) The inverse mapping σ−1: H → G exists because σ is a bijection, and σ−1 is also a bijection (Theorems 5 and 6 §0.3). So it remains to show that σ−1 is a homomorphism. If g1 and h1 are in G1, write g = σ−1(g1) and h = σ−1(h1). Then σ(g) = g1 and σ(h) = h1, so
σ−1(g1h1) = σ−1[σ(g) · σ(h)] = σ−1[σ(gh)] = gh = σ−1(g1) · σ−1(h1).
Therefore σ−1 is a homomorphism, and hence is an isomorphism.
(3) The map τσ is a bijection by Theorem 3 §0.3; now apply Example 7.
Corollary 1. The isomorphic relation ![]() is an equivalence for groups. That is
is an equivalence for groups. That is
1. G ![]() G for every group G.
G for every group G.
2. If G ![]() H then H
H then H ![]() G.
G.
3. If G ![]() H and H
H and H ![]() K then G
K then G ![]() K.
K.
Proof. (1), (2), and (3) follows from the corresponding items in Theorem 3.
As an illustration of Corollary 1, we show that if G and H are both cyclic of order n then G ![]() H. Indeed
H. Indeed ![]() and
and ![]() by Example 13, so G
by Example 13, so G ![]() H by Corollary 1.
H by Corollary 1.
Automorphisms
If G is a group, an isomorphism G → G is called an automorphism of G.
Corollary 2. If G is a group, the set of all automorphisms G → G forms a group under composition.
Proof. The automorphisms G → G are a subset of the group SG of all bijections G → G, and Theorem 3 shows that they are a subgroup of SG by the subgroup test.
The set of all automorphisms of G is called the automorphism group of G, and is denoted autG.
Example 16. If G is abelian, the mapping σ: G → G defined by σ(g) = g−1 for all g ![]() G is an automorphism of G. We leave the verification as Exercise 10.
G is an automorphism of G. We leave the verification as Exercise 10.
If G is a group and a ![]() G, define a mapping σa: G → G by
G, define a mapping σa: G → G by
![]()
This map σa is an automorphism of G (see Example 17 below), called the inner automorphism of G determined by a. Note that if H ⊆ G is a subgroup then σa(H) = aHa−1 is a conjugate of H.
Example 17. If G is any group and a ![]() G, show that
G, show that
1. For each a ![]() G, σa is an automorphism of G.
G, σa is an automorphism of G.
2. If θ: G → autG is defined by θ(a) = σa for each a ![]() G, then θ is a homomorphism, that is σab = σaσb for all a, b
G, then θ is a homomorphism, that is σab = σaσb for all a, b ![]() G.
G.
3. The image θ(G) = {σa ![]() a
a ![]() G} of θ is a subgroup of autG.
G} of θ is a subgroup of autG.
Solution. (1) We leave as Exercise 11 the verification that σa is a bijection for all a ![]() G. If g, h
G. If g, h ![]() G we have
G we have
σa(g) · σa(h) = aga−1 · aha−1 = ag1ha−1 = agha−1 = σa(gh).
Hence σa is an automorphism of G, proving (1).
(2) We must show that σaσb = σab for a, b ![]() G. But for any g
G. But for any g ![]() G:
G:
σaσb(g) = σa(bgb−1) = a(bgb−1)a−1 = (ab)g(ab)−1 = σab(g).
(3) This follows from (2) and Corollary 2 of Theorem 1.
In Example 17, the group θ(G) of all inner automorphisms G is denoted
![]()
The group innG is an important subgroup of autG, and it is easily described because each inner automorphism σa is given explicitly in terms of a. By contrast, the group autG can be difficult to determine. We do one simple case in Example 18 below.
Because it is a homomorphism, every isomorphism preserves the unity, inverses, and powers. But isomorphisms also preserve the order of an element (compare with Corollary 1 of Theorem 1).
Theorem 4. Let σ: G → G1 be an isomorphism. Then o(σ(g)) = o(g) for all g ![]() G.
G.
Proof. It suffices to show that gk = 1 if and only if [σ(g)]k = 1. If gk = 1, then [σ(g)]k = σ(gk) = σ(1) = 1 by Theorem 1. Conversely, if [σ(g)]k = 1, we have σ(gk) = [σ(g)]k = 1 = σ(1), so gk = 1 because σ is one-to-one.
Example 18. If G is cyclic of order 6, show that autG = {1G, λ}, where λ(g) = g−1 for all g ![]() G.
G.
Solution. Both 1G and (as G is abelian) λ are automorphisms of G. If σ: G → G is any automorphism, we show σ = 1G or σ = λ. Write ![]() where o(a) = 6. Theorem 2 shows that the choice of σ(a) completely determines σ. By Theorem 4, we have o(σ(a)) = o(a) = 6, so σ(a) = a, or σ(a) = a5 = a−1. If g
where o(a) = 6. Theorem 2 shows that the choice of σ(a) completely determines σ. By Theorem 4, we have o(σ(a)) = o(a) = 6, so σ(a) = a, or σ(a) = a5 = a−1. If g ![]() G, write g = ak for some
G, write g = ak for some ![]() , so that
, so that
![]()
If σ(a) = a, this gives σ(g) = ak = g for all g ![]() G, that is σ = 1G. If σ(a) = a−1, it shows that σ(g) = (a−1)k = (ak)−1 = g−1 for all g
G, that is σ = 1G. If σ(a) = a−1, it shows that σ(g) = (a−1)k = (ak)−1 = g−1 for all g ![]() G, that is σ = λ.
G, that is σ = λ.
Cayley's Theorem
We conclude this section with a proof of a theorem of Cayley (proved in 1878) that every finite group is isomorphic to a group of permutations. If X is a nonempty set, recall that SX denotes the group of all permutations of X (bijections X → X) under composition. We need one simple observation about these permutation groups: If a bijection σ: X → Y exists then SX ![]() SY. Indeed, if λ
SY. Indeed, if λ ![]() SX we have
SX we have
![]()
so σλσ−1 ![]() SY. But then
SY. But then ![]() : SX → SY given by
: SX → SY given by ![]() (λ) = σλσ−1 is an isomorphism, as can be readily verified. In particular, SX
(λ) = σλσ−1 is an isomorphism, as can be readily verified. In particular, SX ![]() Sn whenever |X| = n.
Sn whenever |X| = n.
Now let G be a group. We noted earlier that each row of the Cayley table of G is a permutation of G in the sense that each element appears exactly once. Since the row of a ![]() G is {ag
G is {ag ![]() g
g ![]() G}, this is just the assertion that g
G}, this is just the assertion that g ![]() ag is a bijection G → G. This is the connection that Cayley noticed between the groups G and SG.
ag is a bijection G → G. This is the connection that Cayley noticed between the groups G and SG.
Theorem 5. Cayley's Theorem. Every group G of order n is isomorphic to a subgroup of Sn.
Proof. By the preceding discussion, there is an isomorphism θ: SG → Sn. So if we can find a one-to-one homomorphism σ: G → SG, then G ![]() θσ(G) ⊆ Sn because θσ: G → θσ(G) is an isomorphism, and Cayley's theorem follows.
θσ(G) ⊆ Sn because θσ: G → θσ(G) is an isomorphism, and Cayley's theorem follows.
If a ![]() G, define μa: G → G by μa(g) = ag for all g
G, define μa: G → G by μa(g) = ag for all g ![]() G. Then it is easy to verify that μa is a bijection (so μa
G. Then it is easy to verify that μa is a bijection (so μa ![]() SG). Hence define θ: G → SG by σ(a) = μa for all a
SG). Hence define θ: G → SG by σ(a) = μa for all a ![]() G. Then θ is a homomorphism because μab = μaμb for all a, b
G. Then θ is a homomorphism because μab = μaμb for all a, b ![]() G (verify). Finally, θ is one-to-one because μa = μb implies that a = μa(1) = μb(1) = b. So σ is a one-to-homomorphism, as required.
G (verify). Finally, θ is one-to-one because μa = μb implies that a = μa(1) = μb(1) = b. So σ is a one-to-homomorphism, as required.
Cayley's theorem shows that every abstract group of order n is (up to isomor-phism) a subgroup of Sn. Hence, to study the groups of order n, we need only study the symmetric group Sn. At first this approach seems to be an advantage because Sn consists of concrete mappings that can be analyzed using tools (such as cycle factorization and parity) not available in an abstract group. However, these symmetric groups are extremely large, so a subgroup of order n is lost in Sn (for example, |S10| = 10 ! = 3, 628, 800). However, in Section 8.3 we give a generalization of Cayley's theorem that cuts down the size of the symmetric group and so provides more information about G.
Arthur Cayley (1821–1895) Cayley showed his mathematical talent at an early age, quickly excelling at school. After some initial reluctance, his merchant father sent him to Cambridge at the age of 17. During the following 8 years he read the works of the masters and published more than 20 papers on topics that would occupy him for the rest of his life. In addition, he developed broad interests in literature (he read Greek, German, and French, as well as English), architecture, and painting (he demonstrated talent in watercolors) and became an enthusiastic hiker and mountaineer.
At the age of 25, with no position as a mathematician in view, he began legal training and was admitted to the bar three years later. He earned a comfortable living as a lawyer but resisted the temptation to make a lot of money so as to free himself to do mathematics. And do it he did, publishing nearly 300 papers in 14 years. Finally, in 1863, he accepted the Sadlerian professorship at Cambridge and remained there for the rest of his life, valued for his administrative and teaching skills, as well as for his scholarship.
Although Cayley introduced the concept of an abstract group, his main accomplishments lay elsewhere. With his lifelong friend J. J. Sylvester, he founded the theory of invariants; he was one of the first to consider geometry of more than three dimensions; and he initiated matrix algebra. He also wrote on quaternions, the theory of equations, dynamics, and astronomy. He continued working until his death, leaving 966 papers filling 13 volumes of 600 pages each.
1. In each case show that α is a homomorphism and decide if it is onto or one-to-one.
(a) ![]() given by
given by ![]() for all r in
for all r in ![]()
(b) α: G → G × G given by α(g) = (g, g) for all g in the group G.
2. If G = G1 × G2 is a direct product of groups, define π1: G → G1 and σ1: G1 → G by π1(g1, g2) = g1 and σ1(g1) = (g1, 1). Show that π1 is an onto homomorphism (called the projection of G onto G1), and σ1 is a one-to-one homomorphism (called the injection of G1 into G).
3. If G is any group, define α: G → G by α(g) = g−1. Show that G is abelian if and only if α is a homomorphism.
4. If ![]() is fixed and G is an abelian group, define α: G → G by α(a) = am for all a
is fixed and G is an abelian group, define α: G → G by α(a) = am for all a ![]() G. Show that α is a homomorphism.
G. Show that α is a homomorphism.
5. Let σa be the inner automorphism of G determined by a. Show thatσa = 1G if and only if a ![]() Z(G).
Z(G).
6. Show that there are exactly two homomorphisms α: C6 → C4. [Hint: Example 9.]
7. If n ≥ 1, give an example of a group homomorphism σ: G → G1 and an element g ![]() G such that o(g)=∞ but o(α(g))= n.
G such that o(g)=∞ but o(α(g))= n.
8.
(a) Describe all group homomorphisms ![]()
(b) How many are onto?
9. If α: G → G1 is a homomorphism, show that K = {g ![]() G
G ![]() α(g) = 1} is a subgroup of G (called the kernel of α).
α(g) = 1} is a subgroup of G (called the kernel of α).
10. Define λ: G → G by λ(g) = g−1 for all g ![]() G. Show that λ is a bijection. If G is abelian, show that λ is an automorphism of G.
G. Show that λ is a bijection. If G is abelian, show that λ is an automorphism of G.
11. If G is a group and a ![]() G, show that the inner automorphism σa: G → G is a bijection.
G, show that the inner automorphism σa: G → G is a bijection.
12. In each case determine whether α: G → G1 is an isomorphism. Give reasons.
13. Show that ![]() is a subgroup of
is a subgroup of ![]() isomorphic to {1, − 1, i, − i}.
isomorphic to {1, − 1, i, − i}.
14. If G is an infinite cyclic group, show that ![]()
15. If ![]() is cyclic with o(a) = n, show that
is cyclic with o(a) = n, show that ![]() [Hint:
[Hint: ![]() if and only if ak = am by Theorem 2 §2.4.]
if and only if ak = am by Theorem 2 §2.4.]
16. Show that ![]() is an automorphism if
is an automorphism if ![]() for all
for all ![]() (here
(here ![]() denotes the complex conjugate of z).
denotes the complex conjugate of z).
17. If g and h are elements of a group G, show that ![]()
18. If G is a group of order 2, show that G × G ![]() K4.
K4.
19. If σ: G → G1 is an isomorphism, show that Z(G1) = σ[Z(G)], where we have σ[Z(G)] = {σ(z) ![]() z
z ![]() Z(G)}.
Z(G)}.
20. Write ![]() Show that
Show that ![]() whenever n ≠ 0 and m ≠ 0.
whenever n ≠ 0 and m ≠ 0.
21. Show that ![]() is not isomorphic to
is not isomorphic to ![]()
22. Show that ![]() is not isomorphic to
is not isomorphic to ![]()
23. Show that the circle group ![]() is not isomorphic to
is not isomorphic to ![]()
24. Find two nonisomorphic groups of order n2 for any integer n ≥ 2.
25. Are the additive groups ![]() and
and ![]() isomorphic? Support your answer.
isomorphic? Support your answer.
26. Show that ![]()
27. If ![]() and
and ![]() where o(a)= o(b) = 6, describe all isomorphisms G → G1.
where o(a)= o(b) = 6, describe all isomorphisms G → G1.
28. Show that ![]() where
where ![]() is the circle group.
is the circle group.
29. Define ![]() by τa,b(x) = ax + b for all
by τa,b(x) = ax + b for all ![]() and denote
and denote ![]() Let
Let ![]() Show that G and G1 are subgroups of
Show that G and G1 are subgroups of ![]() and
and ![]() respectively, and that G
respectively, and that G ![]() G1.
G1.
30. If ![]() show that G is a subgroup of
show that G is a subgroup of ![]() and that
and that ![]()
31. In each case, find autG, where ![]() is cyclic of order n: (a) n = 2 (b) n = 3
is cyclic of order n: (a) n = 2 (b) n = 3
32. If G is infinite cyclic, determine autG.
33. If Z(G) = {1}, show that G ![]() innG.
innG.
34. Given z ![]() Z(G), let Gz denote the set G with a new operation a * b = abz−1. Show that Gz is a group and Gz
Z(G), let Gz denote the set G with a new operation a * b = abz−1. Show that Gz is a group and Gz ![]() G.
G.
35. If G is a group and g ![]() G, let S(g) = {σ
G, let S(g) = {σ ![]() autG
autG ![]() σ(g) = g}.
σ(g) = g}.
(a) Show that S(g) is a subgroup of autG for all g ![]() G.
G.
(b) If g1 = τ(g), τ ![]() autG, show that S(g) and S(g1) are conjugate in autG.
autG, show that S(g) and S(g1) are conjugate in autG.
36. In a group G, write a ![]() b if b = gag−1 for some g
b if b = gag−1 for some g ![]() G (a is conjugate to b).
G (a is conjugate to b).
(a) Show that ![]() is an equivalence relation on G.
is an equivalence relation on G.
(b) Determine which elements of G have singleton equivalence classes.
37. If ![]() and σ: G → G1 is an onto homomorphism, show that
and σ: G → G1 is an onto homomorphism, show that ![]() where σ(X) = {σ(x)
where σ(X) = {σ(x) ![]() x
x ![]() X}.
X}.
38. Show that ![]()
2.6 Cosets and Lagrange's Theorem
He [Lagrange] would set to mathematics all the little themes on physical inquiries which his friends brought him, much as Schubert set to music any stray rhyme that took his fancy.
—Herbert Westron Turnbull
In this section we prove one of the most important theorems about finite groups, Lagrange's theorem, which asserts that the order of a subgroup of a finite group G is a divisor of |G|. This has far-reaching consequences as we shall see. The proof involves counting elements of G, and depends on the following basic notion.
Let H be a subgroup of a group G. If a ![]() G we identify two subsets of G:
G we identify two subsets of G:
![]()
We have H1 = H = 1H, so H is a right and left coset of itself. Also the fact that 1 ![]() H shows a
H shows a ![]() Ha and a
Ha and a ![]() aH for all a. Of course, if G is abelian then Ha = aH for all a
aH for all a. Of course, if G is abelian then Ha = aH for all a ![]() G and all subgroups H of G. However, this may not hold if G is not abelian (see Example 5 below).
G and all subgroups H of G. However, this may not hold if G is not abelian (see Example 5 below).
Example 1. Let K4 = {1, a, b, ab} be the Klein group where o(a) = o(b) = 2 and ab = ba. If H = {1, a}, find the cosets of H in K4.
Solution. H1 = H and Ha = {a, a2} = {a, 1} = H too. Similarly, Hb = {b, ab} and Hab = {ab, a2b} = {ab, b} = Hb. Thus, there are exactly two cosets of H in K4: H = {1, a} and Hb = {b, ab} = bH.
Note that the cosets H = {1, a} and {b, ab} form a partition30 of K4. This holds in general and, with the other properties in Theorem 1, makes finding cosets easier.
Theorem 1. Let H be a subgroup of a group G and let a, b ![]() G.
G.
(1) H = H1.
(2) Ha = H if and only if a ![]() H.
H.
(3) Ha = Hb if and only if ab−1 ![]() H.
H.
(4) If a ![]() Hb, then Ha = Hb.
Hb, then Ha = Hb.
(5) Either Ha = Hb or Ha ∩ Hb = ∅.
(6) The distinct right cosets of H are the cells of a partition of G.
Proof. First, (1) is clear because 1 ![]() H and (2) follows from (3) with b = 1.
H and (2) follows from (3) with b = 1.
(3). If Ha = Hb then a ![]() Ha = Hb, say a = hb, h
Ha = Hb, say a = hb, h ![]() H. Hence ab−1 = h
H. Hence ab−1 = h ![]() H.
H.
Conversely, suppose that ab−1 ![]() H. Then ha = h(ab−1)b
H. Then ha = h(ab−1)b ![]() Hb, so Ha ⊆ Hb. But ba−1 = (ab−1)−1
Hb, so Ha ⊆ Hb. But ba−1 = (ab−1)−1 ![]() H too, so Hb ⊆ Ha follows in the same way. Hence Ha = Hb.
H too, so Hb ⊆ Ha follows in the same way. Hence Ha = Hb.
(4) If a ![]() Hb then ab−1
Hb then ab−1 ![]() H so Ha = Hb by (3).
H so Ha = Hb by (3).
(5) If Ha ∩ Hb ≠ ∅, we show Ha = Hb. If x ![]() Ha ∩ Hb, then x
Ha ∩ Hb, then x ![]() Ha so Hx = Ha by (4). Similarly Hx = Hb, so Ha = Hx = Hb. This proves (5).
Ha so Hx = Ha by (4). Similarly Hx = Hb, so Ha = Hx = Hb. This proves (5).
(6) If Ha ≠ Hb then Ha and Hb are disjoint by (5). In other words, the set of right cosets is pairwise disjoint. Moreover, each a ![]() G belongs to some right coset of H (in fact a
G belongs to some right coset of H (in fact a ![]() Ha). This gives (6).
Ha). This gives (6).
Corollary. The analogue of Theorem 1 for left cosets also holds. In particular, (3) becomes aH = bH if and only if b−1a ![]() H. See Exercise 5.
H. See Exercise 5.
Mnemonic. The condition in (3) that Ha = Hb if and only if ab−1 ![]() H can be remembered by “ right multiplying” Ha = Hb by b−1. Similarly, aH = bH if and only if b−1a
H can be remembered by “ right multiplying” Ha = Hb by b−1. Similarly, aH = bH if and only if b−1a ![]() H can be recalled by “ left multiplying” by b−1.
H can be recalled by “ left multiplying” by b−1.
Example 2. Let ![]() where o(a) = 6. Find the right cosets of the subgroups
where o(a) = 6. Find the right cosets of the subgroups ![]() and
and ![]()
Solution. We have H = H1 = {1, a3}. Thus a3 ![]() H so H = Ha3 by (4) of Theorem 1. In the same way Ha = {a, a4} = Ha4, and Ha2 = {a2, a5} = Ha5. This exhausts G so the cosets are
H so H = Ha3 by (4) of Theorem 1. In the same way Ha = {a, a4} = Ha4, and Ha2 = {a2, a5} = Ha5. This exhausts G so the cosets are
H = {1, a3}, Ha = {a, a4}, and Ha2 = {a2, a5}.
Turning to K we find the partition in one step:
K = {1, a2, a4} and Ka = {a, a3, a5}.
In Example 2, the cosets of H (and those of K) do indeed partition G into pairwise disjoint cells, as Theorem 1(6) asserts. What is new here is that all the cosets of H have the same number of elements and, similarly, all the cosets of K have the same number of elements. This fact holds in general and lies at the heart of Lagrange's theorem, as we show shortly.
Example 3. Find all the right cosets of the subgroup ![]() in the additive group
in the additive group ![]()
Solution. The notation is additive, so the right coset of ![]() generated by a is
generated by a is ![]() For a = 0, we obtain the coset
For a = 0, we obtain the coset ![]() itself:
itself:
![]()
Now ![]() so it generates a new coset by Theorem 1:
so it generates a new coset by Theorem 1:
![]()
We continue in this way, with 2 and 3 generating new cosets:
![]()
This is a complete list of cosets, because every integer has the form 4k + r, where the remainder r is 0, 1, 2, or 3.
Example 4. In the group ![]() give a geometrical description of the cosets of the circle group
give a geometrical description of the cosets of the circle group ![]()
Solution. Recall that ![]() is the unit circle. If
is the unit circle. If ![]() then z = reiθ, where r = |z| > 0 and
then z = reiθ, where r = |z| > 0 and ![]() Hence
Hence ![]() . In other words,
. In other words, ![]() is the circle with its center at the origin and radius r = |z|.
is the circle with its center at the origin and radius r = |z|.
All these examples involve abelian groups so Ha = aH always holds. However, this does not hold in general as Example 5 shows.
Example 5. Let G = S3 = {ε, σ, σ2, τ, τσ, τσ2}, where σ3 = ε = τ2 and στσ = τ. Find the right and left cosets of H = {ε, τ}.
Solution. As στ = τσ−1 = τσ2, the cosets are
Observe that Hσ ≠ σH and Hσ2 ≠ σ2H in this case.
Note that, even though the right and left cosets of H may be different, they all have the same number of elements and there are the same number of them. This holds in general, even when the cosets are infinite sets.
Two sets X and Y are said to have the same cardinality if there is a bijection from one to the other, and in this case we write Of course if the sets are finite this means that they have the same number of elements, and this terminology is sometimes used for infinite sets too.
Lemma. Let H be a subgroup of a group G. Then
1. |H| = |Ha| = |aH| for all a ![]() G.
G.
2. The map Ha ![]() a−1H is a bijection {Ha
a−1H is a bijection {Ha ![]() a
a ![]() G} → {bH
G} → {bH ![]() b
b ![]() G}.
G}.
Proof. (1) |H| = |aH| since h ![]() ha is a bijection H → Ha. Similarly, |H| = |Ha|.
ha is a bijection H → Ha. Similarly, |H| = |Ha|.
(2) We have Ha = Hb ![]() ab−1
ab−1 ![]() H
H ![]() a−1H = b−1H by Theorem 1 and its Corollary. So the map in (2) is well defined and one-to-one. It is clearly onto.
a−1H = b−1H by Theorem 1 and its Corollary. So the map in (2) is well defined and one-to-one. It is clearly onto.
Part (2) of the Lemma shows that the sets of right and left cosets of a subgroup H of G have the same number of members (possibly infinite), and this common value has a name:
The index |G: H| of H in G is defined to be the number of distinct right (or left) cosets of H in G.
Note that a subgroup H can be of finite index in G even if both H and G are infinite (for example ![]() by Example 3).
by Example 3).
The Lemma enables us to prove the single most important theorem about finite groups: It introduces numerical relations into the theory.
Theorem 2. Lagrange's Theorem. Let H be any subgroup of a finite group G.
(1) Then |H| divides |G|.
(2) The quotient ![]() is the index of H in G.
is the index of H in G.
Proof. Write k = |G: H|, and let Ha1, Ha2, ![]() , Hak be the distinct right cosets of H in G. Then
, Hak be the distinct right cosets of H in G. Then
![]()
which is a disjoint union by Theorem 1. By the Lemma, |Hai| = |H| for each i, so
This proves (1), and it also proves (2) because |G||H| = k = |G: H|.
Note that Lagrange's theorem shows that both the order and the index of a subgroup of a finite group G are divisors of |G|.
Lagrange's theorem has many important consequences.
Corollary 1. If G is a finite group and g ![]() G, then o(g) divides |G|.
G, then o(g) divides |G|.
Proof. The cyclic subgroup ![]() generated by g has o(g) = |H| by the Corollary to Theorem 3 §2.4. So Lagrange's theorem applies.
generated by g has o(g) = |H| by the Corollary to Theorem 3 §2.4. So Lagrange's theorem applies.
Note that the converse of Lagrange's theorem (and of Corollary 1) is false. For example, |A4| = 12, but A4 has no subgroup of order 6 and hence no element of order 6 (Exercise 34).
Corollary 2. If G is a group and |G| = n, then gn = 1 for every g ![]() G.
G.
Proof. If o(g) = m then m|n by Corollary 1, say n = qm for some ![]() But then gn = (gm)q = 1q = 1.
But then gn = (gm)q = 1q = 1.
The next corollary will be referred to later, and illustrates how the numerical information in Lagrange's theorem can determine the structure of a finite group.
Corollary 3. If p is a prime, then every group G of order p is cyclic. In fact, ![]() for every element g ≠ 1 in G, so the only subgroups of G are {1} and G.
for every element g ≠ 1 in G, so the only subgroups of G are {1} and G.
Proof. Let g ≠ 1 in G and write ![]() Then |H| divides |G| = p, so |H| = 1 or |H| = p. But |H| ≠ 1 because H contains both 1 and g ≠ 1, so |H| = p = |G|. This implies that H = G because G is finite. Finally, if K ≠ {1} is a subgroup of G, and 1 ≠ k
Then |H| divides |G| = p, so |H| = 1 or |H| = p. But |H| ≠ 1 because H contains both 1 and g ≠ 1, so |H| = p = |G|. This implies that H = G because G is finite. Finally, if K ≠ {1} is a subgroup of G, and 1 ≠ k ![]() K, then
K, then ![]() and so K = G.
and so K = G.
Corollary 4. Let H and K be finite subgroups of a group G. If |H| and |K| are relatively prime, then H ∩ K = {1}.
Proof. As H ∩ K is a subgroup of both H and K, |H ∩ K| must divide both |H| and |K| by Lagrange's theorem. Since |H| and |K| are relatively prime, it follows that |H ∩ K| = 1. The Corollary follows.
Example 6. Let K ⊆ H ⊆ G be finite groups. If |G: K| is a prime, show that H = K or H = G.
Solution. By Lagrange's theorem, ![]() Since |G: K| is a prime, either |G: H| = 1 or |H: K| = 1; that is either H = G or H = K.
Since |G: K| is a prime, either |G: H| = 1 or |H: K| = 1; that is either H = G or H = K.
We showed earlier (Example 18 §2.2) that every group of order 4 = 22 is either cyclic or is isomorphic to the Klein group. In Example 7, Lagrange's theorem is used to give an analogous result for any prime p in place of 2.
Example 7. If G is a group and ![]() where p a prime, show that either G is cyclic or gp = 1 for every element g
where p a prime, show that either G is cyclic or gp = 1 for every element g ![]() G.
G.
Solution. Assume that G is not cyclic. Then o(g) ![]() p2, so o(g) = 1, p, or p2. But o(g) ≠ p2 because G is not cyclic, so o(g) is 1 or p. Either way gp = 1.
p2, so o(g) = 1, p, or p2. But o(g) ≠ p2 because G is not cyclic, so o(g) is 1 or p. Either way gp = 1.
Dihedral Groups
Recall (Example 8 §2.2) that the group S3 can be presented as follows:
S3 = {ε, σ, σ2, τ, τσ, τσ2}, o(σ) = 3, o(τ) = 2, and στσ = τ.
In fact, we can take σ = (123) and τ = (12), but the point here is that the three conditions o(σ) = 3, o(τ) = 2, and στσ = τ are themselves sufficient to fill in the Cayley table of the group.
We now construct a family of groups D2, D3, . . ., Dn, . . . each presented in much the same way as S3, and having D3 ![]() S3. We realize them as subgroups of the group
S3. We realize them as subgroups of the group ![]() of 2 × 2 invertible matrices with complex entries.
of 2 × 2 invertible matrices with complex entries.
Let n ≥ 2 be fixed and let ![]() (an nth root of unity). Then
(an nth root of unity). Then ![]() in
in ![]() Consider the matrices:
Consider the matrices:
![]()
in ![]() It is easy to verify that o(a) = n, o(b) = 2, and aba = b. This last equation shows that ab = ba−1 = ban−1, and hence that the finite set
It is easy to verify that o(a) = n, o(b) = 2, and aba = b. This last equation shows that ab = ba−1 = ban−1, and hence that the finite set
![]()
of matrices is closed under matrix multiplication (I is the 2 × 2 identity matrix). Hence G is a subgroup of ![]() by Theorem 2 §2.3. For convenience, write
by Theorem 2 §2.3. For convenience, write ![]() Then |A| = n and, as b ∉ A, the left cosets A and b A are disjoint. Hence |G| = 2n. We abstract this situation as follows.
Then |A| = n and, as b ∉ A, the left cosets A and b A are disjoint. Hence |G| = 2n. We abstract this situation as follows.
If n ≥ 2, the dihedral group Dn is the group of order 2n presented as follows:
Dn = {1, a, a2, . . ., an−1, b, ba, ba2, . . ., ban−1},
where o(a) = n, o(b) = 2, and aba = b.
Note that the requirement that |Dn| = 2n is equivalent to insisting that ![]() We can carry out all calculations in Dn by using the conditions o(a) = n, o(b) = 2, and aba = b. The equation aba = b implies that akbak = b for all
We can carry out all calculations in Dn by using the conditions o(a) = n, o(b) = 2, and aba = b. The equation aba = b implies that akbak = b for all ![]() by induction (Exercise 25), and so we obtain
by induction (Exercise 25), and so we obtain
akb = ba−k = ban−k and o(bak) = 2 for all ![]() .
.
In particular, ab = ban−1, and these formulas enable us to fill in the Cayley table for Dn. Hence the conditions o(a) = n, o(b) = 2, and aba = b completely determine the group Dn (up to isomorphism). The group D4 is called the octic group, and its Cayley table is as follows (the reader should verify this):

The group D3 is isomorphic to S3 because
D3 = {1, a, a2, b, ba, ba2}, o(a) = 3, o(b) = 2, and aba = b
which is the same as the presentation of S3 given previously. If n = 2,
D2 = {1, a, b, ba}, o(a) = 2, o(b) = 2, and aba = b.
We have a−1 = a here because o(a) = 2, so D2 is abelian (ba = a−1b = ab) and is isomorphic to the Klein group K4.
Thus, every group of order 4 is either cyclic or dihedral (Example 18 §2.2). The next theorem shows that this result holds for groups of order 2p where p is a prime.
Theorem 3. Let G be a group of order 2p where p is a prime. Then either G is cyclic or G ![]() Dp.
Dp.
Proof. First, the theorem is true if p = 2 because implies G is cyclic or G ![]() K4
K4 ![]() D2. Hence we assume that p is odd.
D2. Hence we assume that p is odd.
Assume that G is not cyclic. Hence o(g) = 1, 2, or p for every g ![]() G by Corollary 1 of Lagrange's theorem. We must show that G
G by Corollary 1 of Lagrange's theorem. We must show that G ![]() Dp.
Dp.
Claim 1. G has an element of order p.
Proof. If not, g2 = 1 for all g ![]() G, so G is abelian by Exercise 20 §2.2. Hence if 1, a, and b are distinct in G, then {1, a, b, ab} is a subgroup of order 4 by Theorem 2 §2.3, contrary to Lagrange's theorem. This proves Claim 1.
G, so G is abelian by Exercise 20 §2.2. Hence if 1, a, and b are distinct in G, then {1, a, b, ab} is a subgroup of order 4 by Theorem 2 §2.3, contrary to Lagrange's theorem. This proves Claim 1.
So let a ![]() G have order p and write
G have order p and write ![]()
Claim 2. If x ![]() G and x ∉ H, then o(x) = 2.
G and x ∉ H, then o(x) = 2.
Proof. We have G = H ∪ Hx so, because x2 ∉ Hx, we must have x2 ![]() H. If o(x) = p then, since p is odd,
H. If o(x) = p then, since p is odd, ![]() contrary to the choice of x. Thus o(x) ≠ p, so o(x) = 2 (x ≠ 1 because x ∉ H). This proves Claim 2.
contrary to the choice of x. Thus o(x) ≠ p, so o(x) = 2 (x ≠ 1 because x ∉ H). This proves Claim 2.
Now choose b ∉ H. Then G = H ∪ bH, a disjoint union, so we obtain
G = {1, a, a2, . . ., ap−1, b, ba, ba2, . . ., bap−1}.
As o(b) = 2 by Claim 2, it remains to show that aba = b. But ba ∉ H so (ba)2 = 1 again by Claim 2. But then aba = b−1(ba)2 = b−1 = b. Thus G ![]() Dp.
Dp.
Theorem 3 together with Corollary 3 determines all groups G with |G| ≤ 7:
![]()
Note that K4 ![]() C2 × C2, so every abelian group here is (isomorphic to) a direct product of cyclic groups. In fact this is true for every finite abelian group, an important result discussed in Chapter 7.
C2 × C2, so every abelian group here is (isomorphic to) a direct product of cyclic groups. In fact this is true for every finite abelian group, an important result discussed in Chapter 7.
Obviously, the list continues. We will show that there are five nonisomorphic groups of order 8: C8, C4 × C2, C2 × C2 × C2, D4, and another group Q called the quaternion group, to be introduced in Section 2.8. The groups of order 9 are C9 and C3 × C3—both abelian,) and there are two distinct groups of order 10; C10 and D5. The next interesting case is the groups of order 12 (there are five). However, it is not our intention to imply that all the distinct groups of order n have been determined for an arbitrary integer n. That is a very difficult task!
We conclude with an application of Lagrange's theorem to number theory. If n ≥ 2, the Euler function ![]() is defined by
is defined by
![]() (n) is the number of integers k
(n) is the number of integers k ![]() {1, 2,
{1, 2, ![]() , n − 1} with gcd (k, n) = 1.
, n − 1} with gcd (k, n) = 1.
We define ![]() (1) = 1. Hence
(1) = 1. Hence ![]() (2) = 1,
(2) = 1, ![]() (3) = 2,
(3) = 2, ![]() (4) = 2,
(4) = 2, ![]() (5) = 4, and
(5) = 4, and ![]() (6) = 2. Clearly,
(6) = 2. Clearly,
![]() (p) = p − 1 whenever p is a prime.
(p) = p − 1 whenever p is a prime.
Now recall (Theorem 5 §1.3) that, for n ≥ 2, the group of (multiplicative) units in ![]() is given by
is given by ![]() and gcd (k, n) = 1}. Hence
and gcd (k, n) = 1}. Hence
![]()
With this, Lagrange's theorem yields an elegant proof of the following famous result in number theory.
Theorem 4. Euler's Theorem. If a and n ≥ 2 are relatively prime integers, then a![]() (n) ≡ 1 (modn).
(n) ≡ 1 (modn).
Proof. We have ![]() Since
Since ![]() Lagrange's theorem (Corollary 2) gives
Lagrange's theorem (Corollary 2) gives ![]() in
in ![]() Euler's theorem follows.
Euler's theorem follows.
A special case gives another proof of Fermat's theorem (Theorem 8 §1.3).
Corollary. Fermat's Theorem. If p is a prime, then ap ≡ a(modp) for all integers a.
Proof. This is clear if a ≡ 0 (modp). Otherwise, a and p are relatively prime so, because ![]() (p) = p − 1, Euler's theorem gives ap−1 ≡ 1 (modp). Fermat's theorem follows.
(p) = p − 1, Euler's theorem gives ap−1 ≡ 1 (modp). Fermat's theorem follows.
Joseph Louis Lagrange (1736–1813) While his name sounds French, Lagrange was born in Italy and spent his early years in Turin. In 1766, he was appointed as Euler's successor at the Berlin Academy by Frederick the Great, who suggested that the “ greatest mathematician in Europe” should be at the court of the “ greatest king in Europe.” After the death of Frederick, Lagrange went to Paris at the invitation of Louis XVI. He remained there throughout the revolution and was made a count by Napoleon who called him the “ lofty pyramid of the mathematical sciences.”
Lagrange was one of the great mathematicians of all time. He made important contributions to many parts of mathematics, including number theory, the theory of equations, differential equations, celestial mechanics, and fluid dynamics. At age 19 he solved a famous problem, the so-called isoperimetrical problem, by inventing an entirely new method, known today as the calculus of variations. His work brought a new level of rigor to analysis. In addition to his mathematical achievements, he was a master of exposition, and his Mechanique Analytique is a masterpiece that William Rowan Hamilton described as a “ scientific poem,”.
In his work on the theory of polynomial equations, Lagrange studied the permutations of the roots of an equation in the hope of finding a general method of solution. He saw that, because the symmetric groups S2, S3, and S4 were sufficiently “ nice” a general solution can always be found if the degree is 2, 3, or 4. But he never discovered what it was about S5 that obstructed the solution of equations of degree 5. Abel, and later Galois, eventually clarified the matter. Nevertheless, Lagrange's work provided one of the sources from which the modern theory of groups evolved.
1. In each case find the right and left cosets in G of the subgroups H and K of G.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) G = D4 = {1, a, a2, a3, b, ba, ba2, ba3}, o(a) = 4, o(b) = 2, and aba = b; ![]()
(f) G = any group; H is any subgroup of index 2
2. If G is any group, describe the cosets in G of the subgroups {1} and G.
3. If H is a subgroup of G and Ha = Hb where a, b ![]() G, does it follow that aH = bH? Support your answer.
G, does it follow that aH = bH? Support your answer.
4. If K ⊆ H ⊆ G are finite groups, show that |G: K| = |G: H| · |H: K|.
5. If H is a subgroup of G and a, b ![]() G, define a ≡ b if b−1a
G, define a ≡ b if b−1a ![]() H.
H.
(a) Show that ≡ is an equivalence relation on G.
(b) Show that the equivalence class (Section 0.4.) of a ![]() G is the left coset aH.
G is the left coset aH.
6. Let ![]() with addition (x, y) + (x′, y′) = (x + x′, y + y′). Let H be the line y = mx through the origin:
with addition (x, y) + (x′, y′) = (x + x′, y + y′). Let H be the line y = mx through the origin: ![]() Show that H is a subgroup of G and describe the cosets H + (a, b) geometrically.
Show that H is a subgroup of G and describe the cosets H + (a, b) geometrically.
7. Let H be a subgroup of G and suppose that Ha = bH for a, b ![]() G. Show that aH = Hb.
G. Show that aH = Hb.
8. Let H and K be subgroups of G. If Ha ⊆ Kb for some a, b ![]() G, show that H ⊆ K.
G, show that H ⊆ K.
9. In each case give a geometric description of the cosets of H in G.
![]()
10.
(a) If ![]() and o(a) = 30, find the index of
and o(a) = 30, find the index of ![]() in G.
in G.
(b) Let ![]() o(a) = n. If d|n, find the index of
o(a) = n. If d|n, find the index of ![]() in G.
in G.
11. Let H and K be subgroups of some group G.
(a) Show that Ha ∩ Ka = (H ∩ K)a for all a ![]() G.
G.
(b) Given a, b ![]() G, show that either Ha ∩ Kb is empty or Ha ∩ Kb = (H ∩ K)c for some c
G, show that either Ha ∩ Kb is empty or Ha ∩ Kb = (H ∩ K)c for some c ![]() G.
G.
12. Let G denote a group and let g ![]() G. In each case show
G. In each case show ![]()
(a) |G| = 12, g4 ≠ 1, g6 ≠ 1.
(b) |G| = 40, g8 ≠ 1, g20 ≠ 1.
(c) |G| = 60, g30 ≠ 1, g20 ≠ 1, and g12 ≠ 1.
(d) Generalize. [Hint: Prime factorization.]
13. Let K = {ε, (12)(34), (13)(24), (14)(23)}, and let H be a subgroup of A4 containing K. If H contains any 3-cycle, show that H = A4.
14. Suppose that G has subgroups of orders 45 and 75. If |G| < 400, determine |G|.
15. If H and K are subgroups of a group and |H| is prime, show that either H ⊆ K or H ∩ K = {1}.
16. Let G be a group of order n and let m be an integer with gcd (m, n) = 1. (a) If gm = 1 in G, show that g = 1. [Hint: Theorem 4 §1.2.] (b) Show that each g ![]() G has an mth root, that is that g = am for some a
G has an mth root, that is that g = am for some a ![]() G.
G.
17. Let |G| = p2, where p is a prime. Show that every proper subgroup of G is cyclic.
18. Let |G| = p3, where p is a prime. If G is not cyclic, show that ![]() for all g
for all g ![]() G.
G.
19. Let ak = bk in a group. If o(a)= m and o(b)= n, where n and m are relatively prime, show that mn divides k. [Hint: Lagrange Corollary 4 and Theorem 5 §1.2.]
20. Show that ![]() is even if n ≥ 3. [Hint: Corollary 1 of Lagrange's theorem.]
is even if n ≥ 3. [Hint: Corollary 1 of Lagrange's theorem.]
21. Show that ![]() for every n ≥ 1.
for every n ≥ 1.
22. If G is a group of order n, define σ: G → G by σ(g) = gm for all g ![]() G. If gcd (m, n) = 1, show that σ is a bijection (an automorphism if G is abelian).
G. If gcd (m, n) = 1, show that σ is a bijection (an automorphism if G is abelian).
23. If G is a group of order pk, where p is a prime and k ≥ 1, show that G must have an element of order p. [Hint: Theorem 5 §2.4.]
24. If G is a group of order pq, where p and q are primes, show that every proper subgroup of G is cyclic.
25.
(a) In Dn, show that akbak = b for all ![]()
(b) In Dn, show that o(bak)= 2 for all ![]()
26. If n ≥ 3, show that Z(Dn) = {1} if n is odd, and that Z(D2m) = {1, am}.
27. Is D5 × C3 ![]() D3 × C5? Prove your answer.
D3 × C5? Prove your answer.
28. If k|n, k ≥ 2, show that Dn has a subgroup isomorphic to Dk.
29. Let G be a group and let p be a prime.
(a) If H and K are subgroups of order p, show that H = K or H ∩ K = {1}.
(b) If H1, H2, ![]() , Hk are distinct subgroups of order p, show that
, Hk are distinct subgroups of order p, show that
|H1 ∪ H2 ∪ ![]() ∪ H2| = 1 + k(p − 1).
∪ H2| = 1 + k(p − 1).
(c) If |G| = 15, show that G must have an element of order 3.
30. Let G be any group (possibly infinite) that has no subgroups except {1} and G. If |G| ≥ 2, show that G is finite and cyclic and that |G| is prime. (Converse of Corollary 3 of Lagrange's theorem.)
31. Let K ⊆ H ⊆ G be groups. Show that both |G: H| and |H: K| are finite if and only if |G: K| is finite, and then |G: K| = |G: H||H: K|.
[Hint: If |H: K| = n, let Kh1, Kh2, ![]() , Khn be the distinct cosets of K in H. Show that Hg = Kh1g ∪ Kh2g ∪
, Khn be the distinct cosets of K in H. Show that Hg = Kh1g ∪ Kh2g ∪ ![]() ∪ Khng is a disjoint union for all g
∪ Khng is a disjoint union for all g ![]() G.]
G.]
32. Let H and K be subgroups of a group G with |G: H| = m and |G: K| = n.
(a) Show that |G: H ∩ K| ≤ mn. [Hint:(H ∩ K)g = Hg ∩ Kg for all g ![]() G.]
G.]
(b) If gcd (m, n) = 1, show that |G: H ∩ K| = mn. [Hint: Exercise 31.]
33. Prove Poincaré 's Theorem: If H1, H2, ![]() , Hn are subgroups of a group G of finite index, then H1 ∩ H2 ∩
, Hn are subgroups of a group G of finite index, then H1 ∩ H2 ∩ ![]() ∩ Hn is also of finite index. [Hint: Exercise 32.]
∩ Hn is also of finite index. [Hint: Exercise 32.]
34. Show that A4 has no subgroup of order 6, and hence that the converse of Lagrange's theorem is false. [Hint: Theorem 3.]
35. If H and K are subgroups of a group G, define a relation ≡ on G by a ≡ b if a = hbk for some h ![]() H and k
H and k ![]() K.
K.
(a) Show that ≡ is an equivalence on G.
(b) Describe the equivalence classes (called double cosets).
36. If ![]() is the Euler function, show that n = ∑ d|n
is the Euler function, show that n = ∑ d|n![]() (d), where the sum is taken over all positive divisors of n. [Hint: Theorems 8 and 9, Section 2.4.]
(d), where the sum is taken over all positive divisors of n. [Hint: Theorems 8 and 9, Section 2.4.]
2.7 Groups of Motions and Symmetries
Group theory began with the study of subgroups of the symmetric group Sn. In this short section we discuss some of these groups, which arise from the symmetries of geometric figures. By a figure we mean a finite set of points called vertices, some pairs of which are joined by line segments. A motion of a geometric figure is a permutation of its vertices that can be realized by a rigid motion in space.
Given two motions σ and τ of a figure, the composite στ is also a motion obtained by first doing τ and then σ. Similarly, σ−1 is a motion achieved by reversing the motion that led to σ. Finally, the identity permutation ε is a motion (resulting from doing nothing at all). Hence the subgroup test gives Theorem 1.
Theorem 1. The set of motions of a figure with n vertices is a subgroup of Sn.
This theorem leads to many interesting groups.
Example 1. Find the group of motions of a (nonsquare) rectangle.

Solution. Label the vertices as shown. Then the motions (1 2)(3 4) and (1 4)(2 3) result from rotating the rectangle π radians (180![]() ) about the vertical and horizontal axes of symmetry, respectively. The composite of these is (1 3)(2 4), which is the motion obtained by a rotation of 180
) about the vertical and horizontal axes of symmetry, respectively. The composite of these is (1 3)(2 4), which is the motion obtained by a rotation of 180![]() in the plane of the rectangle. Hence
in the plane of the rectangle. Hence
G = {ε, (12)(34), (14)(23), (13)(24)}
is the group of motions. This group is isomorphic to the Klein group.
Example 2. Find the group of motions of an equilateral triangle.
Solution. Label the vertices as shown. The motions σ = (1 2 3) and σ2 = (1 3 2) are achieved by clockwise rotations of 2π/3 radians (120![]() ) and 4π/3 radians (240
) and 4π/3 radians (240![]() ), respectively. In addition, τ = (1 2) is realized by rotating the triangle π radians (180
), respectively. In addition, τ = (1 2) is realized by rotating the triangle π radians (180![]() ) about the line through vertex 3 and the midpoint of the opposite side. Similarly (1 3) and (2 3) are motions, so the group is
) about the line through vertex 3 and the midpoint of the opposite side. Similarly (1 3) and (2 3) are motions, so the group is
S3 = {ε, (1 2 3), (1 3 2), (1 2), (1 3), (2 3)}.
This shows that the equilateral triangle is highly symmetric because every possible permutation of the vertices can be obtained by a rigid motion in space.
It is vital that the rigid motions allowed in Example 2 are rigid motions in space. If the only motions allowed were those in the plane of the triangle, the group of motions would be {ε, (1 2 3), (1 3 2)}. The permutations (1 2), (1 3), and (2 3) cannot be achieved by rigid motions in the plane of the triangle.
A striking illustration of this phenomenon results when we consider the group G of motions of a tetrahedron. This figure is three-dimensional, with four vertices and six edges of equal length as in the diagram. Clearly (123) is a motion of the tetrahedron, obtained by a rotation of 2π/3 radians (120![]() ) about a line through vertex 4 and the center of the opposite face. Similarly, all 3 cycles are in G. The three permutations (1 2)(3 4), (1 3)(2 4), and (1 4)(2 3) are also motions, so A4 ⊆ G, where A4 is the alternating group of all even permutations:
) about a line through vertex 4 and the center of the opposite face. Similarly, all 3 cycles are in G. The three permutations (1 2)(3 4), (1 3)(2 4), and (1 4)(2 3) are also motions, so A4 ⊆ G, where A4 is the alternating group of all even permutations:

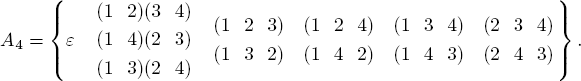
We claim that A4 = G. Suppose on the contrary that σ ![]() G is an odd motion. If γ = (1 2), write τ = γσ. Then τ is even so τ
G is an odd motion. If γ = (1 2), write τ = γσ. Then τ is even so τ ![]() G and hence γ = τσ−1 is in G because G is a group. But the transposition γ = (1 2) is not a motion of the tetrahedron, because interchanging vertices 1 and 2 by a rigid motion necessarily interchanges 3 and 4. It follows that
G and hence γ = τσ−1 is in G because G is a group. But the transposition γ = (1 2) is not a motion of the tetrahedron, because interchanging vertices 1 and 2 by a rigid motion necessarily interchanges 3 and 4. It follows that
Example 3. The group of motions of the tetrahedron is A4.
This situation is analogous to that for the equilateral triangle in Example 2, where the group of motions is A3 = {ε, (1 2 3), (1 3 2)} if the motions are restricted to the plane containing the triangle. Any odd permutation is achieved as a motion only if the triangle is pulled out of its plane, flipped over, and placed back in its plane. Similarly, no odd permutation of the vertices of a tetrahedron can be realized by a motion in 3-space. It can be achieved only if the figure is “ moved” into 4-space in the process.
Even so, these odd permutations of the vertices of a tetrahedron are symmetries of the figure in the intuitive sense of the word. To make this precise, we let d(x, y) denote the distance between two points x and y in space. As in Section 1.4, if σ ![]() Sn, we write σ(k) = σk for all integers k. Given a geometric figure with n vertices labeled 1, 2,
Sn, we write σ(k) = σk for all integers k. Given a geometric figure with n vertices labeled 1, 2, ![]() , n, a symmetry of the figure is a permutation σ of the vertices that preserves the distance between any two vertices; that is
, n, a symmetry of the figure is a permutation σ of the vertices that preserves the distance between any two vertices; that is
![]()
Clearly, any motion of a figure is a symmetry, but the converse is not true. For example, the transposition γ = (12) is a symmetry of the tetrahedron, but it is not a motion, as we have demonstrated.
Theorem 2. The symmetries of a figure with n vertices are a subgroup of Sn.
Proof. The identity permutation is clearly a symmetry. If σ and τ are symmetries, then for vertices k and m we have
d[(στ)k, (στ)m] = d[σ(τk), σ(τm)] = d(τk, τm) = d(k, m).
Hence στ is a symmetry. Finally, write σ−1k = k1 and σ−1m = m1. Then k = σk1 and m = σm1 so, since σ is a symmetry,
![]()
This shows that σ−1 is a symmetry and so completes the proof.
Now let G denote the group of symmetries of the tetrahedron. Then Example 3 gives A4 ⊆ G ⊆ S4, and A4 ≠ G because (12) ![]() G. This implies that G = S4 because |S4: A4| = 2 is a prime (see Example 6 §2.6). Hence
G. This implies that G = S4 because |S4: A4| = 2 is a prime (see Example 6 §2.6). Hence
Example 4. The group of symmetries of the tetrahedron is S4.
The group of motions (in 3-space) of a geometric figure is thus a subgroup of the group of symmetries, and the two may be distinct as the tetrahedron shows. However, if the figure can be drawn in a plane, the two groups coincide. The reason comes from a theorem of plane geometry. Call a mapping σ from the plane to itself an isometry if it preserves distance; that is if d[σ(x), σ(y)] = d(x, y) for all x and y. It can be shown that every isometry of the plane is a composite of translations, rotations about a point, and reflections in a line. Translations and rotations result from motions in the plane itself, whereas reflections can only be achieved by motions in 3 -space. Thus, every isometry of the plane (and hence every symmetry of a plane figure) is a motion in 3-space. Of course, this condition breaks down for a three-dimensional figure because reflections in a plane are isometries of 3-space that are not motions of 3-space.
We conclude this section by representing the dihedral group Dn as a group of motions. If n ≥ 3, a regular n -gon is a plane figure with n vertices evenly placed on a circle. Thus, a regular 3-gon is an equilateral triangle, a regular 4-gon is a square, and so on. Consider the group G of all motions of a regular n-gon. There are two obvious motions:
(1) σ = (123 ![]() n)—the clockwise rotation of 2π/n radians (360/n
n)—the clockwise rotation of 2π/n radians (360/n![]() ) about the center of the figure.
) about the center of the figure.
(2) τ = (1n− 1)(2n − 2)(3n − 3) ![]() —the rotation of π radians (180
—the rotation of π radians (180![]() ) about a line through the vertex n and the center of the figure.
) about a line through the vertex n and the center of the figure.
If n is odd, then τ fixes only the vertex n, whereas if n = 2m, then τ fixes n and m (see Figure 2.1). If λ is any motion of the n-gon, λ is determined by its effect λ1 and λ2 on vertices 1 and 2. If λ2 follows λ1 (clockwise round the n-gon) then λ = σk for some k. On the other hand, if λ2 precedes λ1, then λ = τσk for some k. For example, if n = 7 and the effect of λ is that shown in Figure 2.2, then λ can be achieved by τσ4 as shown in Figure 2.3.
Figure 2.1 The difference when n is odd or even.
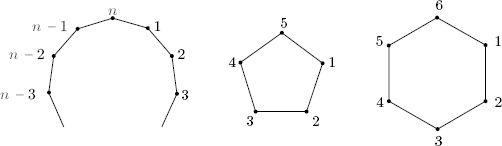
Figure 2.2 The effect of the motion λ.
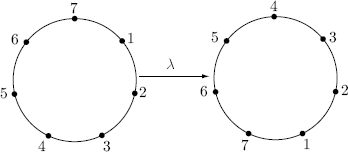
Figure 2.3 The effect of τσ4 is that of λ.
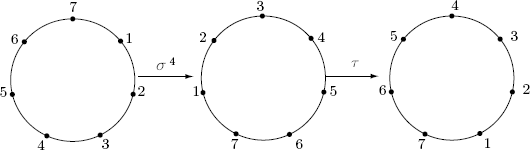
Because |σ| = n and |τ| = 2, it follows that
![]()
Thus ![]() so |G| = 2n. Moreover, the relation στσ = τ is valid as the following diagram shows.
so |G| = 2n. Moreover, the relation στσ = τ is valid as the following diagram shows.
Because |σ| = n, |τ| = 2, and στσ = τ, the definition of Dn (in § 2.6) proves
Theorem 3. The group of motions of a regular n-gon is isomorphic to Dn.
If n = 3, Theorem 3 shows that the group of motions of an equilateral triangle is isomorphic to D3, as is clear from Example 2. If n = 4, it shows that the group of motions of the square is isomorphic to the octic group D4.
1. Find the group of motions of the diamond shown—all edges, and the horizontal diagonal, of length 1.

2. Describe a symmetry of the cube that is not a (three-dimensional) motion.
3. Consider the figure where the base edges are of length 1 and the sloped edges are of length 2.
(a) Find the group of (three-dimensional) motions.
(b) Find the group of symmetries.
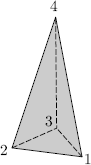
4. Consider the figure where all the edges have length 1 and the base is square.
(a) Find the group of (three-dimensional) motions.
(b) Find the group of symmetries.
5. If the double-marked edges of the square shown are painted blue, find the subgroup of the symmetries that carry blue edges to blue edges.
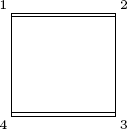
6.
(a) Find the group of (three-dimensional) motions of the figure where the triangle edges are of length 1 and the sides are 1 × 2 rectangles.
(b) Find the group of symmetries of the figure.

7. Find the groups of motions and symmetries of the figure where each face is a nonsquare rectangle.
If H is a subgroup of a group G, we have seen that aH = Ha may fail to hold for some a ![]() G (Example 2 below). A subgroup H of a group G is called a
G (Example 2 below). A subgroup H of a group G is called a
normal subgroup of G if gH = Hg holds for all g in G.
In this case H is said to be normal in G, written H ![]() G. These subgroups are of fundamental importance in group theory, and in this section we begin to see why.
G. These subgroups are of fundamental importance in group theory, and in this section we begin to see why.
Example 1. If G is any group, {1} ![]() G because g{1} = {g} = {1}g, and G
G because g{1} = {g} = {1}g, and G ![]() G because gG = G = Gg for all g
G because gG = G = Gg for all g ![]() G.
G.
Example 2. Let S3 = {ε, σ, σ2, τ, τσ, τσ2}, where o(σ) = 3, o(τ) = 2, and στσ = τ. If H = {ε, σ, σ2} and K = {ε, τ}, show that H ![]() S3 but that K/
S3 but that K/![]() S3.
S3.
Solution. Clearly, αH = H = Hα for all α ![]() H. Because στ = τσ2 and σ2τ = τσ, we get
H. Because στ = τσ2 and σ2τ = τσ, we get
Hτ = {τ, στ, σ2τ} = {τ, τσ2, τσ} = τH.
Similarly, Hτσ = τσH and Hτσ2 = τσ2H, so H ![]() S3.
S3.
However, σK = {σ, στ} and Kσ = {σ, σ2τ}, so σK ≠ Kσ. Hence K/![]() S3.
S3.
Let H be a subgroup of a group G. If g ![]() G satisfies gh = hg for all h
G satisfies gh = hg for all h ![]() H, then obviously gH = Hg. In particular, this condition holds if each element h of H is in the center Z(G) of G. This proves Theorems 1 and 2.
H, then obviously gH = Hg. In particular, this condition holds if each element h of H is in the center Z(G) of G. This proves Theorems 1 and 2.
Theorem 1. If G is a group, every subgroup of the center Z(G) is normal in G. In particular, Z(G) ![]() G.
G.
Theorem 2. If G is an abelian group, every subgroup of G is normal in G.
Note that, given g ![]() G, it is not necessary that gh = hg for all h
G, it is not necessary that gh = hg for all h ![]() H to ensure that gH = Hg. For example, to show that gH ⊆ Hg it is only necessary to show that, given h
H to ensure that gH = Hg. For example, to show that gH ⊆ Hg it is only necessary to show that, given h ![]() H, gh = h′g for some h′
H, gh = h′g for some h′ ![]() H.
H.
The converse of Theorem 1 is false: The subgroup H in Example 2 is normal in S3, but H is certainly not central in S3 (in fact, Z(S3) = {ε}). The converse of Theorem 2 is also false: Example 9 below exhibits a nonabelian group in which every subgroup is normal.
Example 3. If K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}, show that K ![]() A4.
A4.
Solution. If σ ![]() Sn and γ = (k1k2
Sn and γ = (k1k2 ![]() kr) is a cycle of length r, then σγσ−1 is also a cycle of length r, in fact σγσ−1 = (σk1σk2
kr) is a cycle of length r, then σγσ−1 is also a cycle of length r, in fact σγσ−1 = (σk1σk2 ![]() σkr)—see Lemma 3 below. With this, let (ab)(cd)
σkr)—see Lemma 3 below. With this, let (ab)(cd) ![]() K. If σ
K. If σ ![]() S4, then
S4, then
σ[(ab)(cd)]σ−1 = σ(ab)σ−1 σ(cd)σ−1 = (σaσb) (σcσd) ![]() K.
K.
It follows that K ![]() Sn, so certainly K
Sn, so certainly K![]() A4.
A4.
Theorem 3. Normality Test. The following conditions are equivalent for a subgroup H of a group G.
1. H is normal in G.
2. gHg−1 ⊆ H for all g ![]() G.
G.
3. gHg−1 = H for all g ![]() G.
G.
Proof. (1) ⇒ (2). Let x ![]() gHg−1, say x = ghg−1. Then gh
gHg−1, say x = ghg−1. Then gh ![]() gH = Hg by (1), say gh = h1g. Then x = ghg−1 = h1gg−1 = h1
gH = Hg by (1), say gh = h1g. Then x = ghg−1 = h1gg−1 = h1 ![]() H. This proves (2).
H. This proves (2).
(2) ⇒ (3). If g ![]() G then gHg−1 ⊆ H by (2). Taking g−1 in place of g in (2), we obtain g−1Hg ⊆ H. This implies H ⊆ gHg−1 (verify), so H = gHg−1, proving (3).
G then gHg−1 ⊆ H by (2). Taking g−1 in place of g in (2), we obtain g−1Hg ⊆ H. This implies H ⊆ gHg−1 (verify), so H = gHg−1, proving (3).
(3) ⇒ (1). Given g ![]() G, we have gHg−1 = H by (3). If x
G, we have gHg−1 = H by (3). If x ![]() gH, this shows that xg−1
gH, this shows that xg−1 ![]() H, so x
H, so x ![]() Hg. This proves gH ⊆ Hg. Since g−1Hg = H by (3) (with g−1 replacing g), a similar argument shows that Hg ⊆ gH. Now (1) follows.
Hg. This proves gH ⊆ Hg. Since g−1Hg = H by (3) (with g−1 replacing g), a similar argument shows that Hg ⊆ gH. Now (1) follows.
Conditions (2) and (3) in Theorem 3 become even more useful if G has a known set X of generators (see Theorem 10 §2.4). The proof is Exercise 13.
Corollary 1. If ![]() , a subgroup H is normal in G if and only if xHx−1 ⊆ H for all x
, a subgroup H is normal in G if and only if xHx−1 ⊆ H for all x ![]() X. In particular,
X. In particular, ![]() if and only if
if and only if ![]() for all g
for all g ![]() G.
G.
If H is a subgroup of G and g ![]() G, recall (Theorem 5 §2.3) that gHg−1 is also a subgroup of G which is isomorphic to H,31 and is called a conjugate of H in G. For this reason, normal subgroups of G are sometimes called self-conjugate subgroups. Incidentally, this discussion proves
G, recall (Theorem 5 §2.3) that gHg−1 is also a subgroup of G which is isomorphic to H,31 and is called a conjugate of H in G. For this reason, normal subgroups of G are sometimes called self-conjugate subgroups. Incidentally, this discussion proves
Corollary 2. If H is a subgroup of G, and if G has no other subgroups isomorphic to H, then H is normal in G.
In particular, if H is finite and H is the only subgroup of its order, then H ![]() G because |gHg−1| = |H| for all g
G because |gHg−1| = |H| for all g ![]() G.
G.
Theorem 3 suggests a stronger condition than normality. A subgroup H of a group G is called a characteristic subgroup of G if σ(H) = H for all automorphisms σ: G → G (equivalently if σ(H) ⊆ H for all automorphisms σ). The center Z(G) is characteristic in G, and other examples are given in Exercise 24. If σ = σa is the inner automorphism induced by a ![]() G then aHa−1 = σa(H), and it follows that characteristic subgroups are necessarily normal. However, the converse is false by Exercise 24 (c). The following result is often useful.
G then aHa−1 = σa(H), and it follows that characteristic subgroups are necessarily normal. However, the converse is false by Exercise 24 (c). The following result is often useful.
Corollary 3. If K ![]() G and H ⊆ K is characteristic in K, then necessarily H
G and H ⊆ K is characteristic in K, then necessarily H ![]() G.
G.
Proof. If a ![]() G, σa: K → K is an automorphism of K because K
G, σa: K → K is an automorphism of K because K ![]() G. It follows that σa(H) = H because H is characteristic in K. Hence K
G. It follows that σa(H) = H because H is characteristic in K. Hence K ![]() G.
G.
Corollary 3 fails if H is merely normal in K (Exercise 4). Many important subgroups are characteristic subgroups (for example, the center); some of their properties are given in Exercise 24.
Example 4. Let ![]() and let H be the subgroup of all matrices with determinant 1. Show that H
and let H be the subgroup of all matrices with determinant 1. Show that H ![]() G.
G.
Solution. If A ![]() G and B
G and B ![]() H, the properties of determinants give
H, the properties of determinants give
![]()
This shows that ABA−1 ![]() H, so H is normal in G by part (2) of Theorem 3.
H, so H is normal in G by part (2) of Theorem 3.
Theorem 4. If H is a subgroup of index 2 in G, then H is normal in G.
Proof. Let a ![]() G. If a
G. If a ![]() H, then Ha = H = aH. If a ∉ H then (because H has exactly 2 right cosets) G = H ∪ Ha, a disjoint union. Hence Ha = G H. Similarly aH = G H as H has two left cosets, so Ha = G H = aH. Thus, H
H, then Ha = H = aH. If a ∉ H then (because H has exactly 2 right cosets) G = H ∪ Ha, a disjoint union. Hence Ha = G H. Similarly aH = G H as H has two left cosets, so Ha = G H = aH. Thus, H ![]() G.
G.
Note that subgroups of index 3 need not be normal (Example 2).
Example 5. Show An ![]() Sn where An is the alternating group.
Sn where An is the alternating group.
Solution. The alternating group An is of index two in Sn (Theorem 8 §1.4).
Example 6. Let Dn = {1, a, a2, ![]() , an−1, b, ba, ba2,
, an−1, b, ba, ba2, ![]() , ban−1} denote the dihedral group, where o(a) = n, o(b) = 2, and aba = b. Then
, ban−1} denote the dihedral group, where o(a) = n, o(b) = 2, and aba = b. Then ![]() by Theorem 4 because
by Theorem 4 because ![]() has index 2 in Dn.
has index 2 in Dn.
We defined H ![]() G to mean gH = Hg for all g
G to mean gH = Hg for all g ![]() G, which is a kind of commutativity condition on H. The next result gives a situation where actual commuting of elements is implied. It will be referred to later.
G, which is a kind of commutativity condition on H. The next result gives a situation where actual commuting of elements is implied. It will be referred to later.
Lemma 1. Let H ![]() G and K
G and K ![]() G. If H ∩ K = {1}, then hk = kh for all elements h
G. If H ∩ K = {1}, then hk = kh for all elements h ![]() H and k
H and k ![]() K.
K.
Proof. Consider x = hkh−1k−1. Thinking of x = h(kh−1k−1) we see that x ![]() H because kh−1k−1
H because kh−1k−1 ![]() kHk−1 = H since H
kHk−1 = H since H ![]() G. Similarly, writing x = (hkh−1)k−1 shows that x
G. Similarly, writing x = (hkh−1)k−1 shows that x ![]() K because K
K because K ![]() G. Hence x
G. Hence x ![]() H ∩ K = {1} by hypothesis, so x = 1. But then hkh−1k−1 = 1, which gives hk = kh.
H ∩ K = {1} by hypothesis, so x = 1. But then hkh−1k−1 = 1, which gives hk = kh.
Let H and K be subgroups of a group G. The intersection H ∩ K is the largest subgroup of G contained in both H and K (it contains any such subgroup), and one wonders if there is a smallest subgroup of G containing both H and K. Note that, while H ∪ K is the smallest subset containing H and K, it is a subgroup only if H ⊆ K or K ⊆ H (see Exercise 17 §2.3). A much more useful construction turns out to be the product HK of the subgroups defined as follows:
HK = {hk ![]() h
h ![]() H, k
H, k ![]() K}.
K}.
Then HK contains both H and K, and is contained in any such subgroup, but HK need not be a subgroup (consider H = {ε, τ} and K = {ε, τσ} in S3 with the usual notation). However we do have the following result.
Lemma 2. The following are equivalent for subgroups H and K of a group G:
1. HK is a subgroup of G.
2. HK = KH.
3. KH is a subgroup of G.
Proof. We prove only (1) ![]() (2); then (1)
(2); then (1) ![]() (3) follows by interchanging H and K.
(3) follows by interchanging H and K.
(1) ⇒ (2). If kh ![]() KH, then kh = (h−1k−1)−1
KH, then kh = (h−1k−1)−1 ![]() HK by (1). This shows that KH ⊆ HK. On the other hand, if hk
HK by (1). This shows that KH ⊆ HK. On the other hand, if hk ![]() HK then k−1h−1 = (hk)−1
HK then k−1h−1 = (hk)−1 ![]() HK by (1), say k−1h−1 = h1k1. Hence
HK by (1), say k−1h−1 = h1k1. Hence ![]() so HK ⊆ KH.
so HK ⊆ KH.
(2) ⇒ (1). We use the subgroup test. Clearly 1 = 1 · 1 ![]() HK always holds. If hk
HK always holds. If hk ![]() HK then (hk)−1 = k−1h−1
HK then (hk)−1 = k−1h−1 ![]() KH = HK by (2). Finally, given hk and h1k1 in HK, we have kh1
KH = HK by (2). Finally, given hk and h1k1 in HK, we have kh1 ![]() KH = HK, say kh1 = h2k2. But then it follows that (hk)(h1k1) = h(h2k2)k1 = (hh2)(k2k1)
KH = HK, say kh1 = h2k2. But then it follows that (hk)(h1k1) = h(h2k2)k1 = (hh2)(k2k1) ![]() HK, which completes the proof of (1).
HK, which completes the proof of (1).
A note of caution is needed here: To say that HK = KH does not mean that hk = kh for all h ![]() H and k
H and k ![]() K. To show that HK ⊆ KH means that, if h
K. To show that HK ⊆ KH means that, if h ![]() H and k
H and k ![]() K are given, then hk = k1h1 for some h1
K are given, then hk = k1h1 for some h1 ![]() H and k1
H and k1 ![]() K.
K.
If G is abelian then HK is certainly a subgroup by Lemma 2. There is more:
Theorem 5. Let H and K be subgroups of a group G.
1. If H or K is normal in G, then HK = KH is a subgroup of G.
2. If both H and K are normal in G, then HK is also normal in G.
Proof. (1) Suppose that K is normal in G. If hk ![]() HK then hk = (hkh−1)h
HK then hk = (hkh−1)h ![]() KH because hkh−1
KH because hkh−1 ![]() hKh−1 = K. Hence HK ⊆ KH. The other inclusion is proved the same way, so Lemma 2 applies. A similar argument works if H
hKh−1 = K. Hence HK ⊆ KH. The other inclusion is proved the same way, so Lemma 2 applies. A similar argument works if H ![]() G.
G.
(2) If g ![]() G and hk
G and hk ![]() HK, then g−1(hk)g = (g−1hg)(g−1kg)
HK, then g−1(hk)g = (g−1hg)(g−1kg) ![]() HK because H
HK because H ![]() G and K
G and K ![]() G. This proves (2).
G. This proves (2).
Many groups arise as direct products of groups of smaller order, and the following useful theorem gives an important way to recognize when this is the case.
Theorem 6. If H ![]() G and K
G and K ![]() G satisfy H ∩ K = {1}, then HK
G satisfy H ∩ K = {1}, then HK ![]() H × K.
H × K.
Proof. First, HK is a subgroup of G by Theorem 5. Define
σ: H × K → HK by σ(h, k) = hk for all h ![]() H and k
H and k ![]() K.
K.
We show that σ is an isomorphism. Given (h, k) and (h1, k1) in H × K, we have h1k = kh1 by Lemma 1, so σ is a homomorphism because
σ[(h, k) · (h1, k1)] = σ(hh1, kk1) = hh1 kk1 = hk h1k1 = σ(h, k) · σ(h1, k1).
Since σ is clearly onto, it remains to show that σ is one-to-one. If σ(h, k) = σ(h1, k1), then hk = h1k1 so ![]() Thus
Thus ![]() so h = h1 and k = k1. But then (h, k) = (h1k1), proving that σ is one-to-one.
so h = h1 and k = k1. But then (h, k) = (h1k1), proving that σ is one-to-one.
The map σ in Theorem 6 is a bijection for any subgroups H and K. Hence
Corollary 1. If G is a finite group, and H and K are subgroups with H ∩ K = {1}, then
Corollary 2. Let G be a finite group and let H and K be normal subgroups such that H ∩ K = {1} and |H| |K| = |G|. Then G ![]() H × K.
H × K.
Proof. By Corollary 1, we have Hence G = HK because HK ⊆ G and G is finite, so Theorem 6 applies.
Examples 7 and 8 below illustrate how to use Theorem 6. It is easy to verify that the direct product of two cyclic groups of relatively prime orders is again cyclic (Exercise 25 §2.4). Example 7 is the converse. Recall that Cn denotes the generic cyclic group of order n.
Example 7. Let m and n be relatively prime positive integers. If G is a cyclic group of order mn, show that G ![]() Cm × Cn.
Cm × Cn.
Solution. Let ![]() where o(a) = mn, and write
where o(a) = mn, and write ![]() and
and ![]() Then |H| = o(an) = m and |K| = o(am) = n, so H
Then |H| = o(an) = m and |K| = o(am) = n, so H ![]() Cm and K
Cm and K ![]() Cn. Moreover, H ∩ K = {1} by Lagrange's theorem (Corollary 4). Also, H
Cn. Moreover, H ∩ K = {1} by Lagrange's theorem (Corollary 4). Also, H ![]() G and K
G and K ![]() G because G is abelian, and |H| · |K| = mn = |G|. Hence G
G because G is abelian, and |H| · |K| = mn = |G|. Hence G ![]() H × K by Corollary 2 of Theorem 6, that is G
H × K by Corollary 2 of Theorem 6, that is G ![]() Cm × Cn by Example 13 §2.5.
Cm × Cn by Example 13 §2.5.
The fundamental theorem of finite abelian groups asserts that every finite abelian group is isomorphic to a uniquely determined direct product of cyclic groups. We prove this assertion in Section 7.2. Example 8 gives a special case.
Example 8. Let G be an abelian group and assume that ![]() p a prime. Then either
p a prime. Then either ![]() is cyclic or G
is cyclic or G ![]() Cp × Cp.
Cp × Cp.
Solution. Assume that G is not cyclic. Then o(g) = p if 1 ≠ g ![]() G because o(g) divides p2. Choose a
G because o(g) divides p2. Choose a ![]() G with o(a) = p, and write
G with o(a) = p, and write ![]() Then H ≠ G, so choose b ∉ H, b
Then H ≠ G, so choose b ∉ H, b ![]() G, and write
G, and write ![]() Hence |K| = p too, so we have
Hence |K| = p too, so we have ![]() Moreover H
Moreover H ![]() G and K
G and K ![]() G because G is abelian. Finally, H ∩ K = {1} because, otherwise, H = H ∩ K = K by Corollary 3 of Lagrange's theorem. Thus G
G because G is abelian. Finally, H ∩ K = {1} because, otherwise, H = H ∩ K = K by Corollary 3 of Lagrange's theorem. Thus G ![]() H × K by Corollary 2 of Theorem 6, that is G
H × K by Corollary 2 of Theorem 6, that is G![]() Cp × Cp.
Cp × Cp.
We have already noted (Theorem 2) that every subgroup of an abelian group is normal. The converse is not true: A nonabelian group of order 8 exists in which every subgroup is normal. It is constructed as follows: Let
Q = { ± 1, ±i, ±j, ±k}
be a set of eight elements with multiplication determined by the following equations:

Here 1 and −1 multiply as usual, and the multiplication of i, j, and k is best remembered by the diagram above: The product of any two of i, j, and k taken clockwise around the circle is the next one, whereas the product counterclockwise is the negative of the next one. One realization of Q is in ![]() where, if
where, if ![]() satisfies
satisfies ![]() we take
we take
![]()
The group Q in the preceding discussion is called the quaternion group, and it rules out the converse to Theorem 2.
Example 9. Show that Q is a nonabelian group in which every subgroup is normal.
Solution. Q is nonabelian because ij = k while ji = − k. If a subgroup H contains one of ±i, ±j, or ±k, then |H| = 4 or 8 (because these elements have order 4), so H ![]() Q by Theorem 4. Otherwise, H ⊆ {1, − 1} ⊆ Z(Q) and again H
Q by Theorem 4. Otherwise, H ⊆ {1, − 1} ⊆ Z(Q) and again H ![]() Q.
Q.
Simple Groups
Lagrange's theorem shows that the cyclic groups G of prime order have no subgroups except {1} and G. More generally, if G is a group then we say that
G is simple if G ≠ {1} and the only normal subgroups of G are {1} and G.
Theorem 7. An abelian group G ≠ {1} is simple if and only if it is cyclic of prime order.
Proof. Suppose G is simple and abelian. Then the only subgroups of G are {1} and G (all subgroups are normal). If a ![]() G, a ≠ 1, this means that
G, a ≠ 1, this means that ![]() Then o(a)≠ ∞ because, otherwise,
Then o(a)≠ ∞ because, otherwise, ![]() does not equal {1} or G. So o(a) is finite, say o(a) = n ≥ 2. If p|n for some prime p, then
does not equal {1} or G. So o(a) is finite, say o(a) = n ≥ 2. If p|n for some prime p, then ![]() is a subgroup of order p by Theorem 5 §2.4. Hence
is a subgroup of order p by Theorem 5 §2.4. Hence ![]() is cyclic of prime order.
is cyclic of prime order.
The converse is by Lagrange's theorem.
Nonabelian finite simple groups are more difficult to find. We conclude with a proof that, although A4 is not simple by Example 3, the alternating groups An are all simple if n ≥ 5. This has applications in the theory of equations (Chapter 10). The proof requires three preliminary results, the first two of independent interest.
Lemma 3. If σ ![]() Sn and γ = (k1 k2
Sn and γ = (k1 k2 ![]() kr) is a cycle of length r, then σγσ−1 is also a cycle of length r. In fact, σγσ−1 = (σk1 σk2
kr) is a cycle of length r, then σγσ−1 is also a cycle of length r. In fact, σγσ−1 = (σk1 σk2 ![]() σkr).
σkr).
Proof. Write δ = (σk1σk2 ![]() σkr). Because σ is one-to-one, δ is a cycle of length r. We must show that σγσ−1 = δ, that is σγ = δσ, that is σ(γk) = δ(σk) for each k = 1, 2, . . ., n. The reader can verify that (writing kr+1 = k1)
σkr). Because σ is one-to-one, δ is a cycle of length r. We must show that σγσ−1 = δ, that is σγ = δσ, that is σ(γk) = δ(σk) for each k = 1, 2, . . ., n. The reader can verify that (writing kr+1 = k1)
σ(γki) = σki+1 = δ(σki) for each i = 1, 2, . . ., r.
But σ(γk) = σk = δ(σk) whenever k ∉ {k1, k2, ![]() , kr}because (as σ is one-to-one) this implies that σk ∉ {σk1, σk2,
, kr}because (as σ is one-to-one) this implies that σk ∉ {σk1, σk2, ![]() , σkr}. This is what we wanted.
, σkr}. This is what we wanted.
Lemma 4. If n ≥ 2, An is generated by the 3-cycles.
Proof. As each 3-cycle is in An, it suffices to show that each permutation σ ![]() An is either ε or a product of 3-cycles. But σ is even and so is a product of pairs of transpositions. Hence the following formulas complete the proof:
An is either ε or a product of 3-cycles. But σ is even and so is a product of pairs of transpositions. Hence the following formulas complete the proof:
(i j)(i j) = ε, (i j)(i k) = (i k j), and (i j)(k l) = (i l k)(i j k).
Lemma 5. Suppose that n ≥ 5. If H ![]() An and H contains a 3-cycle, then H = An.
An and H contains a 3-cycle, then H = An.
Proof. If (i j k) ![]() H we claim that (a j k), (i a k) and (i j a) are all in H for any a ∉ {i, j, k}. Indeed: Since n ≥ 5, choose b ∉ {a, i, j, k}. Then we have (a j k) = (i a b)(i j k)(i a b)−1
H we claim that (a j k), (i a k) and (i j a) are all in H for any a ∉ {i, j, k}. Indeed: Since n ≥ 5, choose b ∉ {a, i, j, k}. Then we have (a j k) = (i a b)(i j k)(i a b)−1 ![]() H by Lemma 3. Similarly, (i a k), (i j a)
H by Lemma 3. Similarly, (i a k), (i j a) ![]() H.
H.
Let σ = (1 2 3) ![]() H: by Lemma 4 we must show that every 3-cycle τ = (i j k) is in H. Write S = {1, 2, 3} and T = {i, j, k}. If then S = T so τ = σ
H: by Lemma 4 we must show that every 3-cycle τ = (i j k) is in H. Write S = {1, 2, 3} and T = {i, j, k}. If then S = T so τ = σ ![]() H or τ = σ−1
H or τ = σ−1 ![]() H. If say i = 1, j = 2 and k ≠ 3, then (1 2 3)
H. If say i = 1, j = 2 and k ≠ 3, then (1 2 3) ![]() H ⇒ τ = (1 2 k)
H ⇒ τ = (1 2 k) ![]() H by the first paragraph. If say i = 1 and {2, 3} ∩ {j, k} = ∅, then (1 2 3)
H by the first paragraph. If say i = 1 and {2, 3} ∩ {j, k} = ∅, then (1 2 3) ![]() H ⇒ (1 j 3)
H ⇒ (1 j 3) ![]() H ⇒ τ = (1 j k)
H ⇒ τ = (1 j k) ![]() H. Finally if then (1 2 3)
H. Finally if then (1 2 3) ![]() H ⇒ (i 2 3)
H ⇒ (i 2 3) ![]() H ⇒ (i j 3)
H ⇒ (i j 3) ![]() H ⇒ τ = (i j k)
H ⇒ τ = (i j k) ![]() H.
H.
Theorem 8. If n ≥ 5, the alternating group An is simple.
Proof. Let H ![]() An, H ≠ {ε}. Among all elements of H (excluding ε) let τ be one that moves the smallest number m of integers. Then m ≥ 3, because τ
An, H ≠ {ε}. Among all elements of H (excluding ε) let τ be one that moves the smallest number m of integers. Then m ≥ 3, because τ ![]() An is not a transposition. If m = 3 then τ is a 3-cycle, and we are done by Lemma 5. So assume m≥ 4; we show that this leads to a contradiction. Factor τ into disjoint cycles and consider two cases.
An is not a transposition. If m = 3 then τ is a 3-cycle, and we are done by Lemma 5. So assume m≥ 4; we show that this leads to a contradiction. Factor τ into disjoint cycles and consider two cases.
- Case 1: τ contains a cycle of length ≥ 3, say τ = (1 2 3
 )γ2
)γ2  γr. If τ moves exactly 4 integers, then τ = (1 2 3 k) is odd. So assume that τ moves (say) 4 and 5, as well as 1, 2, and 3. Let β = (3 4 5) and write τ1 = τ−1βτβ−1. Then τ1
γr. If τ moves exactly 4 integers, then τ = (1 2 3 k) is odd. So assume that τ moves (say) 4 and 5, as well as 1, 2, and 3. Let β = (3 4 5) and write τ1 = τ−1βτβ−1. Then τ1 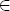 H because H
H because H 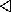 An, and τ1 ≠ ε because τ12 = τ−14 ≠ 2. Moreover, if k > 5 is fixed by τ, then k is also fixed by τ1 (because βk = k). Hence if τ1 moves k > 5, then τ also moves k. But τ1 fixes 1, whereas τ does not. Thus τ1 moves fewer elements than τ, a contradiction.
An, and τ1 ≠ ε because τ12 = τ−14 ≠ 2. Moreover, if k > 5 is fixed by τ, then k is also fixed by τ1 (because βk = k). Hence if τ1 moves k > 5, then τ also moves k. But τ1 fixes 1, whereas τ does not. Thus τ1 moves fewer elements than τ, a contradiction. - Case 2: τ is a product of disjoint transpositions, say, τ = (1 2)(3 4)
 . As before, let β = (3 4 5) and τ1 = τ−1βτβ−1. Now τ1 fixes 1 and 2 and any integer k > 5 that is fixed by τ. Because τ1 ≠ ε (for example, τ15 = 3), this is a contradiction, as in Case 1.
. As before, let β = (3 4 5) and τ1 = τ−1βτβ−1. Now τ1 fixes 1 and 2 and any integer k > 5 that is fixed by τ. Because τ1 ≠ ε (for example, τ15 = 3), this is a contradiction, as in Case 1.
Other infinite families of finite simple groups exist (in addition to the alternating groups An, n ≥ 5). The complete classification of these groups was first given in 1981. This was the culmination of more than 30 years of effort by hundreds of mathematicians, yielding thousands of pages of published work. It is certainly one of the greatest achievements of twentieth-century mathematics. One spectacular landmark came in 1963 when J. Thompson and W. Feit proved32 a long-standing conjecture of William Burnside that every finite nonabelian simple group has even order (the proof is more than 250 pages long!). Thompson went on to publish the “ N -group” paper in which he introduced many fundamental techniques, and which has been called the single most important paper in simple group theory.33 Then in the 1970s, M. Aschbacher carried the work forward in a series of papers, building on the methods of Thompson. The main difficulty was the existence of sporadic finite simple groups not belonging to any of the known families. R. L. Griess finally constructed the largest of these, called the monster (the order is approximately 8 × 1053). The complete classification encompasses several infinite families of finite simple groups and exactly 26 sporadic groups.34
Exercises 2.8
1. Consider D12 = {1, a, ![]() , a11, b, ba,
, a11, b, ba, ![]() , ba11}, where o(a) =12, o(b) =2, aba = b. In each case show that H is a subgroup of D12 and determine if H
, ba11}, where o(a) =12, o(b) =2, aba = b. In each case show that H is a subgroup of D12 and determine if H ![]() D12.
D12.
(a) H = {1, a6, b, ba6}
(b) H = {1, a4, a8, b, ba4, ba8}
(c) H = {1, a2, a4, a6, a8, a10, b, ba2, ba4, ba6, ba8, ba10}
2. Find all normal subgroups of D4. [Hint: Exercise 7 below.]
3. Let K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}. Show that K is the only normal subgroup of A4 apart from A4 and {ε}. [Hint: Exercise 34 §2.6.]
4. If D4 = {1, a, a2, a3, b, ba, ba2, ba3}, K = {1, b} and H = {1, a2, b, ba2} show that K ![]() H
H ![]() D4, but K/
D4, but K/![]() D4.
D4.
5. If K ![]() H and H
H and H ![]() G, show that aKa−1
G, show that aKa−1 ![]() H for all a
H for all a ![]() G. (See Theorem 5 §2.3.)
G. (See Theorem 5 §2.3.)
6. Let H be a subgroup of a group G. If for each a ![]() G there exists b
G there exists b ![]() G such that aH = Hb, show that H
G such that aH = Hb, show that H ![]() G.
G.
7. If H ![]() G and |H| = 2, show that H ⊆ Z(G). Is this true when |H| = 3?
G and |H| = 2, show that H ⊆ Z(G). Is this true when |H| = 3?
8. If H is a subgroup of G and K ![]() G, show that H ∩ K
G, show that H ∩ K ![]() H. Is H ∩ K
H. Is H ∩ K ![]() K?
K?
9. Given a group G, let D = {(g, g) ![]() g
g ![]() G}. Show that D is a normal subgroup of G × G if and only if G is abelian.
G}. Show that D is a normal subgroup of G × G if and only if G is abelian.
10. Let N ![]() G and K
G and K ![]() G. Show that N ∩ K
G. Show that N ∩ K ![]() G.
G.
11. Let p and q be distinct primes. If G is a group of order pq that has a unique subgroup of order p and a unique subgroup of order q, show that G is cyclic. [Hint: Corollary 2 of Theorem 6 and Exercise 25 §2.4.]
12. Let K ![]() G where K is cyclic. Show that every subgroup of K is normal in G.
G where K is cyclic. Show that every subgroup of K is normal in G.
13. Let X be a nonempty subset of a group G.
(a) If ![]() (see Theorem 10 § 2.4) and H is a subgroup of G, show that H
(see Theorem 10 § 2.4) and H is a subgroup of G, show that H ![]() G if and only if x−1Hx ⊆ H for all x
G if and only if x−1Hx ⊆ H for all x ![]() X.
X.
(b) Show that ![]() is normal in G if and only if
is normal in G if and only if ![]() for all g
for all g ![]() G.
G.
14. If G = H × K is finite, find H1 ![]() G and K1
G and K1 ![]() G such that H1 ≅ H, K1 ≅ K, H1 ∩ K1 = {1}, and |G| = |H1| · |K1|. (Converse of Theorem 6.)
G such that H1 ≅ H, K1 ≅ K, H1 ∩ K1 = {1}, and |G| = |H1| · |K1|. (Converse of Theorem 6.)
15. Let K be a subgroup of G of index 2.
(a) If a ![]() G K and b
G K and b ![]() G K, show that ab
G K, show that ab ![]() K.
K.
(b) If H is a subgroup of G and H ![]() K, show that |H: H ∩ K| = 2. [Hint: If h0
K, show that |H: H ∩ K| = 2. [Hint: If h0 ![]() H K, show that h
H K, show that h ![]() hh0 is a bijection H ∩ K → H (H ∩ K).]
hh0 is a bijection H ∩ K → H (H ∩ K).]
16. Show that innG ![]() autG for any group G.
autG for any group G.
17. Let Dn = {1, a, ![]() , an−1, b, ba,
, an−1, b, ba, ![]() , ban−1} with o(a)= n, o(b) = 2, and aba = b.
, ban−1} with o(a)= n, o(b) = 2, and aba = b.
(a) Show that every subgroup K of ![]() is normal in Dn.
is normal in Dn.
(b) If n is odd and K ![]() Dn, show that K = Dn or
Dn, show that K = Dn or ![]()
18.
(a) Let Q denote the quaternion group. If a = i and b = j show that Q has the form Q = {1, a, a2, a3, b, ba, ba2, ba3} where o(a)= 4, aba = b, and b2 = a2. Show further that these conditions determine the Cayley table of Q.
(b) If G is a nonabelian group of order 8, show that G ≅ D4 or G ≅ Q. [Hint: See Theorem 3 §2.6; use Theorem 4 and (a).]
19. If H and K are subgroups of G, show that HK is a subgroup if and only if HK ⊆ KH, if and only if KH ⊆ HK.
20. If G = HK where H and K are subgroups such that hk = kh for all h ![]() H and k
H and k ![]() K, show that H
K, show that H ![]() G and K
G and K ![]() G.
G.
21. If H ⊆ G and K ⊆ G are subgroups with HK = KH, show that ![]() (See Theorem 8 §2.4.)
(See Theorem 8 §2.4.)
22. Let G be a group with where m and n are relatively prime, and let H and K be subgroups where If hk = kh for all h ![]() H and k
H and k ![]() K, show that G ≅ H × K.
K, show that G ≅ H × K.
23.
(a) Let n = 2m, where m is odd. Show that Dn ≅ C2 × Dm, where C2 is cyclic of order 2. [Hint: Corollary 2 of Theorem 6.]
(b) Is D12 ≅ C3 × D4? Justify your answer.
24. A subgroup H of a group G is called a characteristic subgroup if σ(H) ⊆ H for all automorphisms σ of G.
(a) Show that every characteristic subgroup is normal.
(b) Show that if H is characteristic in G then σ(H) = H for all σ ![]() autG.
autG.
(c) If G = C2 × C2 show that H = C2 × {1} is normal in G but not characteristic. [Hint: Consider σ: G → G given by σ(x, y) = (y, x).]
(d) Show that the center Z(G) is characteristic in G.
(e) If H ⊆ K ![]() G and H is characteristic in K, show that H
G and H is characteristic in K, show that H ![]() G.
G.
(f) If K is characteristic in H and H is characteristic in G, show that K is characteristic in G. (Compare with Exercise 4.)
(g) Show that every subgroup of a cyclic group G is characteristic in G. Is this true if G is merely abelian?
(h) If H and K are characteristic in G, show that H ∩ K is characteristic in G.
(i) If H is a subgroup of G, let K = {g ![]() G
G ![]() g
g ![]() σ(H) for all σ
σ(H) for all σ ![]() autG}. Show that K is characteristic in G, that K ⊆ H, and that K contains every characteristic subgroup of G that is contained in H.
autG}. Show that K is characteristic in G, that K ⊆ H, and that K contains every characteristic subgroup of G that is contained in H.
25. If X is a nonempty subset of a group G, define the normalizer N(X) of X by N(X) = {a ![]() G
G ![]() aXa−1 = X}.
aXa−1 = X}.
(a) Show that N(X) is a subgroup of G.
(b) If H is a subgroup of G, show that H ![]() N(H).
N(H).
(c) If H is a subgroup of G, show that N(H) is the largest subgroup of G in which H is normal. That is, if H ![]() K, and K is a subgroup of G, then K ⊆ N(H).
K, and K is a subgroup of G, then K ⊆ N(H).
26. If H is a subgroup of G, define the core of H, denoted coreH, to be the intersection of all the conjugates of H in G; that is,
![]()
(a) Show that coreH ![]() G and coreH ⊆ H.
G and coreH ⊆ H.
(b) Show that coreH is the largest normal subgroup of G that is contained in H; that is, if K ![]() G and K ⊆ H, then K ⊆ coreH.
G and K ⊆ H, then K ⊆ coreH.
(c) Show that core(H ∩ K) = coreH ∩ coreK for all subgroups H and K.
27. If X is a nonempty subset of a group G, define the normal closure ![]() of X to be the intersection of all normal subgroups of G that contain X; that is,
of X to be the intersection of all normal subgroups of G that contain X; that is,
![]()
(a) Show that ![]() and
and ![]()
(b) Show that ![]() is the smallest normal subgroup of G that contains X; that is, X ⊆ N and N
is the smallest normal subgroup of G that contains X; that is, X ⊆ N and N ![]() G implies that
G implies that ![]()
(c) Show that ![]() for all subgroups H and K of G, and that this need not be equality.
for all subgroups H and K of G, and that this need not be equality.
28. If X is a nonempty subset of a group G, define the centralizer C(X) of X by C(X) = {c ![]() G
G ![]() cx = xc for all x
cx = xc for all x ![]() X}. Note that C(G) = Z(G).
X}. Note that C(G) = Z(G).
(a) Show that C(X) is a subgroup of G.
(b) If K ![]() G, show that C(K)
G, show that C(K) ![]() G.
G.
If n ≥ 2, recall the construction of ![]() in Section 1.3. Given the subgroup
in Section 1.3. Given the subgroup ![]() of
of ![]() the set
the set ![]() consists of all “ residue classes”
consists of all “ residue classes” ![]() (mod n)} where
(mod n)} where ![]() These classes are really cosets
These classes are really cosets ![]() Moreover, we defined addition in
Moreover, we defined addition in ![]() by
by ![]() that is,
that is,
![]()
This suggests a general definition: If K is a subgroup of a multiplicative group G, we could define an analogous multiplication on the set of right cosets by
![]()
However, this may not make sense for some subgroups K because cosets can have different generators: Ka = Ka1 can happen where a and a1 may not be equal.
More precisely, let x = Ka = Ka1 and y = Kb = Kb1 be cosets. If we multiply x = Ka and y = Kb using (*) we get xy = Kab, but if we view x and y as x = Ka1 and y = Kb1 we obtain xy = Ka1b1. Clearly, what is needed is:
![]()
In this case we say that the multiplication Ka Kb = Kab is well defined. This condition on K is equivalent to K being normal in G.
Lemma. The following conditions are equivalent for a subgroup K of G.
1. K is normal in G.
2. Ka Kb = Kab is a well defined multiplication of right cosets.
Proof. (1) ⇒ (2). If K ![]() G, let Ka = Ka1 and Kb = Kb1, that is
G, let Ka = Ka1 and Kb = Kb1, that is ![]() and
and ![]() We must show that Kab = Ka1b1, that is ab(a1b1)−1
We must show that Kab = Ka1b1, that is ab(a1b1)−1 ![]() K. Compute
K. Compute
![]()
because aKa−1 ⊆ K. This is what we wanted.
(2) ⇒ (1). If a ![]() G we must show that aka−1
G we must show that aka−1 ![]() K for all k
K for all k ![]() K. Clearly Ka = Ka and Kk = K1, so applying (2) gives Kak = Ka1, that is Kak = Ka. But then (ak)a−1
K. Clearly Ka = Ka and Kk = K1, so applying (2) gives Kak = Ka1, that is Kak = Ka. But then (ak)a−1 ![]() K, as required.
K, as required.
Theorem 1. Let K ![]() G and write G/K = {Ka
G and write G/K = {Ka ![]() a
a ![]() G} for the set of cosets.
G} for the set of cosets.
1. G/K is a group under the operation Ka Kb = Kab.
2. The mapping ![]() : G → G/K given by
: G → G/K given by ![]() (a) = Ka is an onto homomorphism.
(a) = Ka is an onto homomorphism.
3. If G is abelian, then G/K is abelian.
4. If ![]() is cyclic, then G/K is also cyclic; in fact,
is cyclic, then G/K is also cyclic; in fact, ![]()
5. If |G: K| is finite then |G/K| = |G: K|; if is finite then ![]()
Proof. (1) The operation on G/K is well defined by the Lemma. The unity of G/K is K = K1 because Ka K1 = Ka = K1 Ka for all Ka in G/K. We have Ka Ka−1 = K1 = Ka−1 Ka, so the inverse of the coset Ka is (Ka)−1 = Ka−1. Finally, associativity in G/K is inherited from G:
![]()
(2) We have ![]() (a)
(a) ![]() (b) = Ka Kb = Kab =
(b) = Ka Kb = Kab = ![]() (ab) for all a, b
(ab) for all a, b ![]() G, so
G, so ![]() is a homomorphism. It is clearly onto.
is a homomorphism. It is clearly onto.
(3) If G is abelian, Ka Kb = Kab = Kba = Kb Ka, proving (3).
(4) Let ![]() so every coset in G/K has the form Kak for some integer k. If
so every coset in G/K has the form Kak for some integer k. If ![]() is the map in (2), then Kak =
is the map in (2), then Kak = ![]() (ak) =
(ak) = ![]() (a)k = (Ka)k by Theorem 1 §2.5. It follows that
(a)k = (Ka)k by Theorem 1 §2.5. It follows that ![]() as required.
as required.
(5) As |G: K| is finite, |G/K| = |G: K| is the definition of the index |G: K|. If is finite, then |G/K| = |G|/|K| is (2) of Lagrange's theorem.
Thus, if n ≥ 2 in ![]() then
then ![]() as additive groups. If K is a normal subgroup of a group G, write G/K = {Ka
as additive groups. If K is a normal subgroup of a group G, write G/K = {Ka ![]() a
a ![]() G} as in Theorem 1. We make two definitions:
G} as in Theorem 1. We make two definitions:
The group G/K of all cosets of K in G is called the factor group of G by K.
The homomorphism ![]() : G → G/K where
: G → G/K where ![]() (a) = Ka is called the coset map.
(a) = Ka is called the coset map.
Hence the unity of G/K is K = K1, and inverses are given by (Ka)−1 = Ka−1. It is important for a student of group theory (and ring theory for that matter) to develop skill in working with factor groups. All the group theoretic techniques we have developed up to now apply to these groups; the only new aspect is that the elements are now cosets.
Example 1. If G is a group then we always have G ![]() G and {1}
G and {1} ![]() G.
G.
If K = G there is only one coset, so G/K = {G} is the group with one element.
If K = {1}, then Ka = {a} for each a ![]() G, so G/K is the set of all singleton
G, so G/K is the set of all singleton
subsets of G. The operation is {a}{b} = {ab}, so G/K ≅ G in this case.
Example 2. Let ![]() where o(a) = 12, and let
where o(a) = 12, and let ![]() Find all the cosets in G/K and write down the Cayley table.
Find all the cosets in G/K and write down the Cayley table.
Solution. Note first that K ![]() G because G is abelian. The cosets are
G because G is abelian. The cosets are
K = {1, a4, a8}, Ka = {a, a5, a9}, Ka2 = {a2, a6, a10}, Ka3 = {a3, a7, a11}.
Two computations are needed to fill in the Cayley table: Ka · Ka3 = K (because a4 ![]() K) and Ka2 · Ka3 = Ka5 = Ka (because a5
K) and Ka2 · Ka3 = Ka5 = Ka (because a5 ![]() Ka). Then
Ka). Then
We have ![]() as Ka2 = (Ka)2, Ka3 = (Ka)3, and K = Ka4 = (Ka)4. This confirms Theorem 1(4) in this case.
as Ka2 = (Ka)2, Ka3 = (Ka)3, and K = Ka4 = (Ka)4. This confirms Theorem 1(4) in this case.
Example 3. Let K = {ε, (12)(34), (13)(24), (14)(23)}. Show that K ![]() A4, find all the cosets in A4/K, and write down the Cayley table.
A4, find all the cosets in A4/K, and write down the Cayley table.
Solution. We showed that K ![]() A4 in Example 3 §2.8. The cosets are
A4 in Example 3 §2.8. The cosets are
The Cayley table is as shown.
Here the fact that K(132) = [K(123)]2 shows that ![]() is cyclic. Of course, this also follows from the fact that |G/K| = 3 is prime.
is cyclic. Of course, this also follows from the fact that |G/K| = 3 is prime.
Example 4. Consider the octic group D4 = {1, a, a2, a3, b, ba, ba2, ba3}, where o(a) = 4, o(b) = 2, and aba = b. Show that Z(D4) = {1, a2} and that D4/Z(D4) is isomorphic to the Klein group K4.
Solution. Write Z = Z(D4) for short. We have a(bak) = bak+3 ≠ bak+1 = (bak)a for each k, so bak ∉ Z. Similarly, ab = ba3 ≠ ba and a3b = ba ≠ ba3 show that a ∉ Z and a3 ∉ Z. Hence Z⊆ {1, a2}. However, a2b = ba2, so a2 commutes with both generators a and b of D4. This implies that a2 ![]() Z, so Z = {1, a2}.
Z, so Z = {1, a2}.
Of course, Z = Z(D4) is normal in D4, and the cosets are
![]()
Thus D4/Z = {Z, Za, Zb, Zba}, and the Cayley table is as shown.
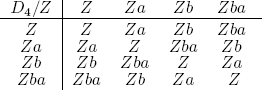
This is evidently the noncyclic group of order 4, that is D4/Z ≅ K4.
Example 5. Let ![]() where o(a) = 18, and let
where o(a) = 18, and let ![]() Find the order of the element Ka5 in G/K.
Find the order of the element Ka5 in G/K.
Solution 1. As K = {1, a6, a12}, we have |G/K| = |G|/|K| = 18/3 = 6. Then, from Lagrange's theorem, the order o(Ka5) of Ka5 is 1, 2, 3, or 6. Now
![]()
Hence o(Ka5) is not 1, 2, or 3, so it must be 6.
Solution 2. ![]() because gcd (5, 18) = 1, so
because gcd (5, 18) = 1, so ![]() . Hence
. Hence ![]() by Theorem 1. Because |G/K| = 6, this means that o(Ka5) = 6.
by Theorem 1. Because |G/K| = 6, this means that o(Ka5) = 6.
The next theorem provides a useful method of proving that a group is abelian. We include it for reference later.
Theorem 2. Suppose a group G has a subgroup K ⊆ Z(G) such that G/K is cyclic. Then G is abelian.
Proof. Let ![]() If a, b
If a, b ![]() G, this means that we can write Ka and Kb in the form Ka = Kgm and Kb = Kgn. Thus a = kgm and b = k1gn where k and k1 are in K (and hence are central in G by hypothesis). But then
G, this means that we can write Ka and Kb in the form Ka = Kgm and Kb = Kgn. Thus a = kgm and b = k1gn where k and k1 are in K (and hence are central in G by hypothesis). But then
![]()
This shows that G is abelian.
The Derived Subgroup
If H ![]() G there is a useful test for determining when a factor group G/H is abelian. To motivate it, consider the following way of deciding that two cosets Ha and Hb commute:
G there is a useful test for determining when a factor group G/H is abelian. To motivate it, consider the following way of deciding that two cosets Ha and Hb commute:
![]()
With this in mind, an element in a group G of the form aba−1b−1 is called a commutator and is denoted
![]()
Hence, if H ![]() G then G/H is abelian if and only if H contains every commutator.
G then G/H is abelian if and only if H contains every commutator.
The commutator subgroup or derived subgroup G′ of G is defined by
G′ = {all finite products of commutators from G}.
To see that G′ really is a subgroup of G, note that 1 = [a, a] is in G′ and that G′ is clearly closed under the operation of G. The fact that G′ is closed under inverses follows from the first of the following easily verified properties of commutators.
1. [a, b]−1 = [b, a].
2. g[a, b]g−1 = [gag−1, gbg−1] for all g ![]() G.
G.
These facts reveal the relationship between G′ and the abelian factor groups of G.
Theorem 3. Let G be a group and let H be a subgroup of G.
1. G′ is a normal subgroup of G and G/G′ is abelian.
2. G′ ⊆ H if and only if H is normal in G and G/H is abelian.
Proof. We have already established that G′ is a subgroup of G. Since (2) ⇒ (1) by taking H = G′, we prove only (2). If H ![]() G, the above argument shows that G/H is abelian if and only if every commutator belongs to H, that is, if and only if G′ ⊆ H. Hence it remains to show that G′ ⊆ H implies that H
G, the above argument shows that G/H is abelian if and only if every commutator belongs to H, that is, if and only if G′ ⊆ H. Hence it remains to show that G′ ⊆ H implies that H ![]() G. If G′ ⊆ H, let g
G. If G′ ⊆ H, let g ![]() G and h
G and h ![]() H. Then
H. Then
![]()
Thus gHg−1 ⊆ H, so H ![]() G as required.
G as required.
Hence G′ = {1} if and only if G is abelian. Since G is abelian if and only if Z(G) = G, this contrasts the way G′ and Z(G) measure the commutativity of the group G.
Theorem 3 asserts that G′ is the smallest normal subgroup H of G with the property that the factor group G/H is abelian. This fact can be very useful in computing G′, as Example 6 illustrates.
Example 6. Compute ![]() where D4 = {1, a, a2, a3, b, ba, ba2, ba3}, where o(a) = 4, o(b) = 2, and aba = b.
where D4 = {1, a, a2, a3, b, ba, ba2, ba3}, where o(a) = 4, o(b) = 2, and aba = b.
Solution. In Example 4 we showed that the center of D4 is Z = {1, a2} and that D4/Z is abelian. Hence ![]() by Theorem 3 and so, because |Z| = 2, either
by Theorem 3 and so, because |Z| = 2, either ![]() or
or ![]() But
But ![]() is impossible because D4/{1} ≅ D4 is not abelian. Hence
is impossible because D4/{1} ≅ D4 is not abelian. Hence ![]()
Exercises 2.9
1. In each case find the cosets in G/K, write down the Cayley table of G/K, and describe the group G/K.
(a) G = D6 and K = Z(D6)
(b) G = Q and K = Z(Q)
(c) G = A × B, A and B arbitrary groups, and K = {(a, 1) ![]() a
a ![]() A}
A}
(d) ![]() where o(a)= 8 and o(b) = 2, and
where o(a)= 8 and o(b) = 2, and ![]()
2. An integer n is called an exponent for a group G if gn = 1 for every g in G. If n is an exponent for G, show that it is an exponent for every factor group G/K.
3. If ![]() o(a)= 24, let
o(a)= 24, let ![]() and
and ![]()
(a) In G/K, find the order of the elements Ka2, Ka3, Ka4, and Ka5.
(b) In G/H, find the order of the elements Ha2, Ha3, Ha4, and Ha5.
4. Let ![]() where o(a)= 8 and o(b) = 12.
where o(a)= 8 and o(b) = 12.
(a) If ![]() find the order of K(a4, b) in G/K.
find the order of K(a4, b) in G/K.
(b) If ![]() find the order of K(a2, b) in G/K.
find the order of K(a2, b) in G/K.
5. Let ![]() where o(a) = 6, o(b) = 2, and aba = b.
where o(a) = 6, o(b) = 2, and aba = b.
(a) If ![]() find the order of Ka2, Ka3, Ka5, and Kba in G/K.
find the order of Ka2, Ka3, Ka5, and Kba in G/K.
(b) If ![]() find the order of Ka2, Ka5, and Kba2 in G/K.
find the order of Ka2, Ka5, and Kba2 in G/K.
6. If Q denotes the quaternion group, show that Q/Z(Q) has order 4. Is it cyclic or isomorphic to the Klein group? Support your answer.
7. Show that ![]() is an infinite abelian group in which every element has finite order.
is an infinite abelian group in which every element has finite order.
8. Let K ⊆ H ⊆ G be finite groups, with K ![]() G. Show that H/K = {Kh
G. Show that H/K = {Kh ![]() h
h ![]() H} is a subgroup of G/K, and
H} is a subgroup of G/K, and
9. If K ![]() G and o(g)= n, g
G and o(g)= n, g ![]() G, show that the order of Kg in G/K divides n.
G, show that the order of Kg in G/K divides n.
10. If K ![]() G has index m, show that gm
G has index m, show that gm ![]() K for all g
K for all g ![]() G.
G.
11. If K ![]() G has index m and if gcd (m, n) = 1, show that K contains every element of G of order n.
G has index m and if gcd (m, n) = 1, show that K contains every element of G of order n.
12. Let G be a finite group and let K ![]() G. If G/K has an element of order n, show that G has an element of order n.
G. If G/K has an element of order n, show that G has an element of order n.
13. Let K ![]() G. In each case, if both K and G/K have the given property, show that G also has the property.
G. In each case, if both K and G/K have the given property, show that G also has the property.
(a) Trivial center.
(b) Every element has finite order.
(c) Every element has order a power of a fixed prime p.
(d) Finitely generated.
14. If K ![]() G has prime index p, show that G = K ∪ Ka ∪
G has prime index p, show that G = K ∪ Ka ∪ ![]() ∪ Kap−1 is a disjoint union for some a
∪ Kap−1 is a disjoint union for some a ![]() G.
G.
15. If ![]() is generated by X, and if K
is generated by X, and if K ![]() G, show that G/K is generated by {Kx
G, show that G/K is generated by {Kx ![]() x
x ![]() X}.
X}.
16. Let H be a subset of G that is closed under the group operation. If g2 ![]() H for all g
H for all g ![]() G, show that H is a normal subgroup of G and G/H is abelian.
G, show that H is a normal subgroup of G and G/H is abelian.
17. If G is abelian, let T(G) denote the set of elements in G of finite order.
(a) Show that T(G) is a subgroup of G—the torsion subgroup.
(b) Call G a torsion-free group if T(G) = {1}. Show that G/T(G) is torsion free.
(c) Call G a torsion group if T(G) = G. If H is a subgroup of G, show that G is a torsion group if and only if both H and G/H are torsion groups.
18. Let K ⊆ H ⊆ G be groups, where K ![]() G and |G: K| is finite. Show that |G/K: H/K| is also finite and that |G/K: H/K| = |G: H|.
G and |G: K| is finite. Show that |G/K: H/K| is also finite and that |G/K: H/K| = |G: H|.
19. Find G′ in each case.
![]()
20. Show that G′ is a characteristic subgroup of G for every group G.
21. Show that (G × H)′ = G′ × H′.
22. If H is a subgroup of G, show that H′ ⊆ H ∩ G′. Show that this may not be equality.
23. Let K ![]() G.
G.
(a) If K ⊆ H where H is a subgroup of G, show that H/K is a subgroup of G/K.
(b) If ![]() is a subgroup of G/K, show that
is a subgroup of G/K, show that ![]() where H ={h
where H ={h ![]() G
G ![]() Kh
Kh ![]()
![]() is a subgroup of G containing K.
is a subgroup of G containing K.
24. If K ![]() G and K ∩ G′ = {1}, show that K ⊆ Z(G) and that
G and K ∩ G′ = {1}, show that K ⊆ Z(G) and that ![]() .
.
25. Let K ![]() G.
G.
(a) Show that [Ka, Kb] = K[a, b] for all a, b ![]() G.
G.
(b) If K ⊆ G′, show that (G/K)′ = G′/K.
26. Let K ⊆ Z(G) be a subgroup such that ![]() where xixj = xjxi in G for all i and j. Show that G is abelian. (This extends Theorem 2.)
where xixj = xjxi in G for all i and j. Show that G is abelian. (This extends Theorem 2.)
27. Let K ⊆ H ⊆ G be groups with K characteristic in G. If H/K is characteristic in G/K, show that H is characteristic in G. [See Exercise 24 §2.8.]
28.
(a) Show that |G: Z(G)| cannot be a prime for any group G.
(b) Show that G = D4 is a nonabelian group G such that G/Z(G) is abelian.
29. If k|n, k ≥ 2, show that Dn has a normal subgroup K such that Dn/K ≅ Dk. [Hint: If Dn is generated by a and b where o(a)= n, o(b)= 2, and aba = b, take ![]() ]
]
30. If K = {ε, (12)(34), (13)(24), (14)(23)}, show that S4/K ≅ D3. [Hint: Exercise 3 §2.8.]
31. Let G = C4 × C8.
(a) Find subgroups H and K of G such that H ≅ K but G/H6 ≅ G/K.
(b) Find subgroups P and Q of G such that G/P ≅ G/Q but P6 ≅ Q.
There is a connection between normal subgroups, homomorphisms and factor groups. The main relationship between these concepts is embodied in the isomorphism theorem, which is the principal result in this section and one of the most useful theorems in group theory. To describe it, we begin by identifying two subgroups associated with a group homomorphism α: G → H. The first is
![]()
This is a subgroup of H as was shown in Corollary 2 of Theorem 1 §2.5. We now turn to a subgroup of G determined by α: G → H:
The kernel of α, defined by ker α = {k ![]() G
G ![]() α(k) = 1}.
α(k) = 1}.
Theorem 1. Let α: G → H be a group homomorphism.
1. α(G) is a subgroup of H.
2. ker α is a normal subgroup of G.
Proof. (1) This is Corollary 2 of Theorem 1 §2.5.
(2) We have 1 ![]() ker α because α(1) = 1. If k, k′
ker α because α(1) = 1. If k, k′ ![]() ker α, then
ker α, then
![]()
Hence kk′ ![]() ker α and k−1
ker α and k−1 ![]() ker α, so ker α is a subgroup. If g
ker α, so ker α is a subgroup. If g ![]() G and k
G and k ![]() K then
K then
![]()
This shows that g(ker α)g−1 ⊆ ker α for all g ![]() G, and so proves that ker α
G, and so proves that ker α ![]() G.
G.
Note that the image of a homomorphism α: G → H need not be normal in H. For example, if K is any subgroup of H, define the inclusion mapping ı: K → H by ı(k) = k for all k ![]() K. This is a one-to-one homomorphism, but ı(K) = K need not be normal in H.
K. This is a one-to-one homomorphism, but ı(K) = K need not be normal in H.
Theorem 1 shows that kernels of homomorphisms from G are normal in G. Conversely, every normal subgroup of a group G arises as the kernel of some homo-morphism with G as domain:
Theorem 2. If K ![]() G, then K = ker
G, then K = ker ![]() where
where ![]() : G → G/K is the coset mapping.
: G → G/K is the coset mapping.
Proof. The coset map ![]() is defined by
is defined by ![]() (g) = Kg for all g
(g) = Kg for all g ![]() G and is a homo-morphism by Theorem 1 §2.9. Because K is the unity of the group G/K, we have g
G and is a homo-morphism by Theorem 1 §2.9. Because K is the unity of the group G/K, we have g ![]() ker
ker ![]() if and only if Kg = K, if and only if g
if and only if Kg = K, if and only if g ![]() K. Hence ker
K. Hence ker ![]() = K.
= K.
Many important subgroups are kernels of naturally occurring homomorphisms; indeed, the easiest way to verify that a subgroup of a group G is normal in G is often to exhibit it as the kernel of a homomorphism with G as domain.
Example 1. The absolute value homomorphism ![]() given by z
given by z ![]() |z| has kernel the circle group
|z| has kernel the circle group ![]()
Example 2. The kernel of the determinant homomorphism A ![]() det A from
det A from ![]() is the special linear group
is the special linear group ![]()
Example 3. If G is a group and g ![]() G has finite order n, let
G has finite order n, let ![]() be the exponent mapping given by α(k) = gk. Then
be the exponent mapping given by α(k) = gk. Then ![]() by Theorem 2 §2.4.
by Theorem 2 §2.4.
Example 4. Show that An ![]() Sn by exhibiting An as a kernel.
Sn by exhibiting An as a kernel.
Solution. Define the sign of a permutation σ ![]() Sn by
Sn by ![]()
Then the sign mapping α: Sn → {1, − 1} given by α(σ) = sgnσ is a homomorphism (see Exercise 29 §1.4). Clearly ker α = An.
Example 5. The trivial homomorphism G → H is the only one with G as kernel.
It is clear that a homomorphism α: G → H is onto if and only if α(G) = H, that is, if and only if the image α(G) is as large a subgroup of H as possible. The next theorem shows that α is one-to-one if and only if ker α is as small as possible.
Theorem 3. If α: G → H is a homomorphism, then α is one-to-one if and only if ker α = {1}.
Proof. If α is one-to-one, let g ![]() ker α. Thus α(g) = 1 = α(1), so g = 1 because α is one-to-one. Hence ker α = {1}. Conversely, let ker α = {1} and suppose that α(a) = α(b) where a and b are in G. Then α(ab−1) = α(a)α(b)−1 = 1, so ab−1
ker α. Thus α(g) = 1 = α(1), so g = 1 because α is one-to-one. Hence ker α = {1}. Conversely, let ker α = {1} and suppose that α(a) = α(b) where a and b are in G. Then α(ab−1) = α(a)α(b)−1 = 1, so ab−1 ![]() ker α = {1}. This shows that ab−1 = 1 and hence that a = b. Thus α is one-to-one.
ker α = {1}. This shows that ab−1 = 1 and hence that a = b. Thus α is one-to-one.
Theorem 3 is used frequently to test when a homomorphism is one-to-one.
We now come to one of the most useful theorems in group theory.
Theorem 4. Isomorphism Theorem35. Let α: G → H be a group homomorphism and write K = ker α. Then
![]()
Proof. Write K = ker α for simplicity, and define
![]()
First ![]() is well defined; that is, Kg = Kg1 implies that α(g) = α(g1). In fact,
is well defined; that is, Kg = Kg1 implies that α(g) = α(g1). In fact,
![]()
Hence ![]() is well defined (⇒) and one-to-one (⇐). As
is well defined (⇒) and one-to-one (⇐). As ![]() is clearly onto α(G), it remains to show that it is a homomorphism. But
is clearly onto α(G), it remains to show that it is a homomorphism. But
![]()
holds for all Kg and Kg1 in G/K.
If G is a group, a group of the form α(G) where α: G → H is some homomorphism is called a homomorphic image of G. Hence the isomorphism theorem shows that the factor groups of G and the homomorphic images of G are the same set of groups up to isomorphism.
Remark. The diagram to the right depicts the mappings α and ![]() in the isomorphism theorem. Here K = ker α as in the theorem, and the mapping
in the isomorphism theorem. Here K = ker α as in the theorem, and the mapping ![]() : G → G/K is the coset mapping. Note that
: G → G/K is the coset mapping. Note that ![]() is a factorization
is a factorization
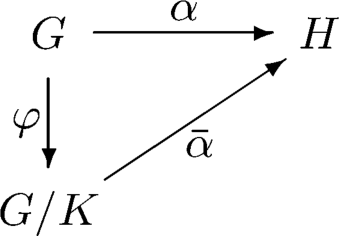
of the (arbitrary) homomorphism α as a composite where ![]() is onto and
is onto and ![]() is one-to-one. Indeed,
is one-to-one. Indeed, ![]() for all g
for all g ![]() G. Moreover,
G. Moreover, ![]() is the only homomorphism G/K → H with the property that
is the only homomorphism G/K → H with the property that ![]() Indeed, if this condition holds then the action of
Indeed, if this condition holds then the action of ![]() is determined:
is determined: ![]() for all Kg in G/K. Hence:
for all Kg in G/K. Hence:
Corollary. Let α: G → H be a group homomorphism. Then α factors uniquely as ![]() where
where ![]() : G → G/ker α is the coset map, and
: G → G/ker α is the coset map, and ![]() is defined in Theorem 4. Note that
is defined in Theorem 4. Note that ![]() is onto, and
is onto, and ![]() is one-to-one.
is one-to-one.
The isomorphism theorem is a marvelous result. It sheds light on nearly every situation to which it is applied. It is used as follows: If we want to show that G/K ≅ H, we find an onto homomorphism G → H with kernel K. As a bonus, the fact that K is a kernel automatically proves that it is normal in G. Examples 6–9 illustrate the use of the isomorphism theorem.
Example 6. If G is a cyclic group, show that ![]() or
or ![]()
Solution. Let ![]() and define
and define ![]() by α(k) = ak for all
by α(k) = ak for all ![]() This is an onto homomorphism and ker α = {k
This is an onto homomorphism and ker α = {k ![]() ak = 1}. If o(a) is infinite, ker α = {0} and the isomorphism theorem gives
ak = 1}. If o(a) is infinite, ker α = {0} and the isomorphism theorem gives ![]() If o(a) = n, then
If o(a) = n, then ![]() and
and ![]() =
=![]()
Example 7. Let K ![]() G and K1
G and K1 ![]() G1. Show that (K × K1)
G1. Show that (K × K1) ![]() (G × G1) and
(G × G1) and
![]()
Solution. We define α: (G × G1) → (G/K) × (G1/K1) by α(g, g1) = (Kg, K1g1). It is routine to verify that this is an onto homomorphism, and ker α = K × K1. The isomorphism theorem now gives all our assertions.
Example 8. Show that ![]() where
where ![]() is the circle group.
is the circle group.
Solution. We define ![]() by α(x) = e2πxi. We have
by α(x) = e2πxi. We have
![]()
so α is a homomorphism. It is clearly onto, and
![]()
Thus, ![]() and the isomorphism theorem does the rest.
and the isomorphism theorem does the rest.
If we are interested in determining all homomorphisms α: G → G1, the fact that α(G1) is isomorphic to G/(ker α) is useful because sometimes we can determine the normal subgroups of G. In Example 9 §2.5, we showed that there are at most six homomorphisms: S3 → C6, and hence at most 6 from D3 → C6. Using the isomorphism theorem, we can show that in fact there are only two.
Example 9. Write D3 = {1, a, a2, b, ba, ba2}, where o(a) = 3, o(b) = 2, and aba = b, and write ![]() where o(c) = 6. Show that there are only two homomorphisms, D3 → C6, the trivial one and
where o(c) = 6. Show that there are only two homomorphisms, D3 → C6, the trivial one and
![]()
Solution. We know that D3 has only three normal subgroups: {1}, D3, and ![]() . Thus if α: D3 → C6 is a homomorphism, ker α must be one of them. It is impossible that ker α = {1} because then α(D3) ≅ D3 would be a nonabelian subgroup of C6. If ker α = D3 then α is the trivial homomorphism. So assume that
. Thus if α: D3 → C6 is a homomorphism, ker α must be one of them. It is impossible that ker α = {1} because then α(D3) ≅ D3 would be a nonabelian subgroup of C6. If ker α = D3 then α is the trivial homomorphism. So assume that ![]() . In this case, let
. In this case, let ![]() : D3 → D3/K be the coset map. If α exists, the corollary to the isomorphism theorem guarantees that α = σ
: D3 → D3/K be the coset map. If α exists, the corollary to the isomorphism theorem guarantees that α = σ![]() , whereσ: D3/K → α(D3) is an
, whereσ: D3/K → α(D3) is an

isomorphism. In this case D3/K = {K, bK} is cyclic of order 2, so α(D3) is the (unique) subgroup of order 2 in C6; that is α(D3) = {1, c3}. Clearly, σ(K) = 1 and σ(bK) = c3, so α = σ![]() is given by
is given by
α(bkam) = σ![]() (bkam) = σ(bkamK) = σ(bK)k · σ(aK)m = (c3)k · 1m = c3k.
(bkam) = σ(bkamK) = σ(bK)k · σ(aK)m = (c3)k · 1m = c3k.
We conclude this section with one more result using the isomorphism theorem. Recall (Example 18 §2.5) that the set innG of all inner automorphisms of a group G is a subgroup of the group autG of all automorphisms of G.
Theorem 5. If G is any group, then G/Z(G) ≅ innG.
Proof. If a ![]() G, recall that the inner automorphism σa: G → G is defined by σa(g) = aga−1 for all g
G, recall that the inner automorphism σa: G → G is defined by σa(g) = aga−1 for all g ![]() G. Then σaσb = σab for all a, b
G. Then σaσb = σab for all a, b ![]() G (Example 17 §2.5), and so θ(a) = σa defines a group homomorphism θ: G → autG. Clearly, θ(G) = innG, and
G (Example 17 §2.5), and so θ(a) = σa defines a group homomorphism θ: G → autG. Clearly, θ(G) = innG, and
![]()
The result now follows from the isomorphism theorem.
Example 10. Show that innS3 ≅ S3. Show further that innS3 = autS3.
Solution. Z(S3) = {ε} is easily verified, so S3 ≅ innS3 by Theorem 5. Hence so, since innS3 ⊆ autS3, it suffices to show that But S3 = {1, σ, σ2, τ, τσ, τσ2} where o(σ) = 3 and o(τ) = 2. So if θ: S3 → S3 is an automorphism then o(θ(σ)) = o(σ) = 3, so θ(σ) = σ or σ2. Similarly θ(τ) = τ, τσ or τσ2, so there are at most 2 · 3 = 6 choices for θ because ![]() .
.
Exercises 2.10
1. Let ![]() and
and ![]() , subgroups of GL
, subgroups of GL![]() Show that K
Show that K ![]() G by exhibiting K as the kernel of a group homomorphism G→
G by exhibiting K as the kernel of a group homomorphism G→![]()
2. Show that the following are equivalent for a group homomorphism α: G → G1.
| (a) α is trivial | (b) ker α = G | (c) α(G) = {1} |
3. Let H be a subgroup of G with |G: H| = 2, and define α: G → {1, − 1} by ![]() . Show that α is a homomorphism and that ker α = H.
. Show that α is a homomorphism and that ker α = H.
4. If α: G → G1 is a group homomorphism and if X is a subgroup of α(G), the preimage of X under α is defined by α−1(X) = {g ![]() G
G ![]() α(g)
α(g) ![]() X}. For example α−1({1}) = ker α. [Note: The notation α−1 here is not intended to imply that α is an isomorphism.]
X}. For example α−1({1}) = ker α. [Note: The notation α−1 here is not intended to imply that α is an isomorphism.]
(a) Show that α−1(X) is a subgroup of G, normal if X ![]() α(G).
α(G).
(b) Show that X ⊆ Y if and only if α−1(X) ⊆ α−1(Y).
(c) Show that α−1(X ∩ Y) = α−1(X) ∩ α−1(Y).
5. Let ρm: G → G be the m-power map: ρm(g) = gm. Assume G is abelian and |G| = n.
(a) Show that ker ρm = {g ![]() gd = 1} where d = gcd (m, n).
gd = 1} where d = gcd (m, n).
(b) If m and n are relatively prime, show that ρm is an automorphism.
(c) If ![]() is cyclic, show that every automorphism of G arises as in (b).
is cyclic, show that every automorphism of G arises as in (b).
6. Let α: G → G1 be a group homomorphism with ker α = K. For a ![]() G, show that Ka = {g
G, show that Ka = {g ![]() G
G ![]() α(g) = α(a)}.
α(g) = α(a)}.
7. If α: G → G1 is a group homomorphism and both α(G) and ker α are finitely generated, show that G is finitely generated.
8. Find all group homomorphisms
![]()
9. If K = {ε, (12)(34), (13)(24), (14)(23)}, is there a group homomorphism α: S4 → A4, with ker α = K? Support your answer.
10. Determine if there exists an onto group homomorphism in each case:
(a) α: S3 → K4
(b) α: S3 → C3
(c) α: S3 → C2
(d) ![]()
11. If G is a group, let θ: G → G × G be defined by θ(g) = (g, g).
(a) Show that θ is a one-to-one group homomorphism.
(b) Show that the following conditions are equivalent: (1) G is abelian; (2) θ(G) is normal in G× G; and (3) θ(G) = ker ![]() for some homomorphism
for some homomorphism ![]() : G × G → G.
: G × G → G.
12. Show that a group G is simple if and only if every nontrivial group homomorphism G → G1 is one-to-one.
13. If G is a simple group, show that there is a nontrivial group homomorphism G → G1 if and only if G1 has a subgroup isomorphic to G.
14. If n is odd, show that there are at most 36 group homomorphisms Dn → A4.
15. If |G| ≥ 2 and autG is cyclic, show that G is abelian and that autG is finite and of even order. [Hint: Theorem 2 §2.9 and Theorem 5.]
16. If aut G is simple, show that G is abelian or G/Z(G) is simple. [Hint: Exercise 16 §2.8.]
17. Let α: G → G1 be a group homomorphism, as shown in the figure at the right.
(a) Show that ![]() . [Hint: Show α([a, b]) = [α(a), α(b)] for all a, b
. [Hint: Show α([a, b]) = [α(a), α(b)] for all a, b ![]() G.]
G.]
(b) If ![]() : G → G/G′ and
: G → G/G′ and ![]() are the coset maps, show that a unique homomorphism
are the coset maps, show that a unique homomorphism ![]() exists such that
exists such that ![]() (see the diagram).
(see the diagram).
18. If G = H × K and K1 = {(1, k) ![]() k
k ![]() K}, show that K1
K}, show that K1 ![]() G, K1 ≅ K and G/K1 ≅ H.
G, K1 ≅ K and G/K1 ≅ H.
19. Let ![]() let K = {A
let K = {A ![]() det A = 1} and let K1 = {A
det A = 1} and let K1 = {A ![]() det A = ± 1}.
det A = ± 1}.
(a) Show K ![]() G and
G and ![]()
(b) Show K1 ![]() G and
G and ![]()
20. Let ![]() If
If ![]() show that K
show that K ![]() G and
G and ![]()
21. Show that ![]() where
where ![]() is the circle group.
is the circle group.
22. Show that ![]()
23. If ![]() define
define ![]() by τa,b(x) = ax + b for all
by τa,b(x) = ax + b for all ![]() It follows that
It follows that ![]() is a subgroup of
is a subgroup of ![]() Show that
Show that ![]() is a normal subgroup of G and
is a normal subgroup of G and ![]()
24. Consider ![]() as a group under addition. For n ≥ 2, show that
as a group under addition. For n ≥ 2, show that ![]() and
and ![]() —all additive groups.
—all additive groups.
25. If G is abelian, let K = {(g, g, g) ![]() g
g ![]() G}. Show that K
G}. Show that K ![]() G × G × G and G × G × G/K ≅ G × G.
G × G × G and G × G × G/K ≅ G × G.
26. If G/K ≅ H, show that there is an onto homomorphism α: G → H with ker α = K.
27. If α: G → G1 is a group homomorphism and K ![]() G with ker α ⊆ K, show that α(K)
G with ker α ⊆ K, show that α(K) ![]() α(G) and α(G)/α(K) ≅ G/K.
α(G) and α(G)/α(K) ≅ G/K.
28. Let G be a finite abelian group. Show that the following conditions are equivalent for an integer m: (1) gm = 1 in G implies that g = 1; and (2) every element g ![]() G has an mth root, that is, g = am for some a
G has an mth root, that is, g = am for some a ![]() G. Compare your results with those of Exercise 16 §2.6.
G. Compare your results with those of Exercise 16 §2.6.
29. Let 
(a) Show that G is a subgroup of ![]() and that
and that ![]()
(b) Show that ![]()
30. Use the isomorphism theorem to show that, if m|n, then ![]()
31. Let s = lcm(m, n). Show that ![]() is isomorphic to a subgroup of
is isomorphic to a subgroup of ![]() [Hint: Think of
[Hint: Think of ![]() as
as ![]() ]
]
32. Show that every infinite homomorphic image of ![]() is isomorphic to
is isomorphic to ![]()
33. Describe the homomorphic images of each group.
| (a) |
(b) A simple group G | (c) A4 [Hint: Exercise 3 §2.8.] |
34. If |G| ≥ 3, show that G has at least two automorphisms. [Hint: Theorem 5.]
35. Let α: G → G1 be an onto group homomorphism. If X is a subgroup of G1, define α−1(X) = {g ![]() G
G ![]() α(g)
α(g) ![]() X} as in Exercise 4. If X
X} as in Exercise 4. If X ![]() G1 show that α−1(X)
G1 show that α−1(X) ![]() G and G/α−1(X) ≅ G1/X.
G and G/α−1(X) ≅ G1/X.
36. If X and Y are additive abelian groups, let hom (X, Y) denote the set of all group homomorphisms α: X → Y. If α, β ![]() hom (X, Y), define α + β: X → Y by (α + β)(x) = α(x) + β(x) for all x
hom (X, Y), define α + β: X → Y by (α + β)(x) = α(x) + β(x) for all x ![]() X.
X.
(a) Show that hom (X, Y) is an abelian group under this addition.
(b) Show that ![]() for every additive abelian group Y.
for every additive abelian group Y.
(c) Show that ![]() where d = gcd (m, n). [Hint: If e = n/d, define
where d = gcd (m, n). [Hint: If e = n/d, define ![]() by
by ![]() where
where ![]() and
and ![]() ]
]
37. If G is a group and gi ![]() G for all i ≥ 0, let [gi) = (g0, g1, g2,
G for all i ≥ 0, let [gi) = (g0, g1, g2, ![]() ) denote an infinite sequence from G. Define [gi) = [hi) if and only if gi = hi for all i ≥ 0 and define [gi) · [hi) = [gihi). Write Gω = {[gi)
) denote an infinite sequence from G. Define [gi) = [hi) if and only if gi = hi for all i ≥ 0 and define [gi) · [hi) = [gihi). Write Gω = {[gi) ![]() gi
gi ![]() G}.
G}.
(a) Show that Gω is a group with the preceding multiplication.
(b) Show that G0 = {[gi) ![]() g0
g0 ![]() G, gi = 1 for all i ≥ 1} is a normal subgroup of Gω, and Gω/G0 ≅ Gω.
G, gi = 1 for all i ≥ 1} is a normal subgroup of Gω, and Gω/G0 ≅ Gω.
(c) Let F denote the set of mappings ![]() and, if f, g
and, if f, g ![]() F, define fg
F, define fg ![]() F by fg(i) = f(i) · g(i) for all
F by fg(i) = f(i) · g(i) for all ![]() Show that F is a group. What is the relationship between F and Gω? Support your answer.
Show that F is a group. What is the relationship between F and Gω? Support your answer.
38. If K ![]() G show that C(K)
G show that C(K) ![]() G and G/[C(K)] is isomorphic to a subgroup of autK, where C(K) = {a
G and G/[C(K)] is isomorphic to a subgroup of autK, where C(K) = {a ![]() G
G ![]() ak = ka for all k
ak = ka for all k ![]() K}. [Hint: Theorem 5.]
K}. [Hint: Theorem 5.]
2.11 An Application to Binary Linear Codes
The value of mathematics in any science lies more in disciplined analysis and abstract thinking than in particular theories or techniques.
—Alan Tucker
Coding theory is concerned with the transmission of information over a channel that is affected by noise. The noise causes errors, and the general aim is to detect such errors when they occur and to correct them if possible. Such codes are used every day in communication systems such as radio, television, and telephone; in data storage systems such as those used by banks; in the internal circuits of computers; and in many other systems where information is being processed. With the advent of computers, information is often expressed in digital form, that is as strings of 0s and 1s which computers can easily handle. Consequently we deal with binary codes that are based on ![]()
General coding theory originated in the 1940s, primarily with the work of Claude Shannon. He created a mathematical theory of information and proved that certain codes exist which can transmit information at near optimal rates with arbitrarily small chance of error. In 1950, Richard W. Hamming discovered the error-detecting and error-correcting codes that now bear his name. Many of these codes are widely used today.
Example 1 concretely illustrates many of the features of general coding.
Example 1. Suppose that a spacecraft is orbiting the moon, and assume that the message 1 or 0 is to be sent instructing the mission commander to land or not. Because of static interference (noise) the probability36 is 0.1 that an error will occur during transmission (and hence a probability of 0.9 that no error will occur). To ensure accuracy, the earth station transmits five signals: 11111 instead of 1 and 00000 for 0. The spacecraft computer receives a five-digit message and decodes it by a simple majority: It concludes that 11111 was sent if more 1s than 0s are received and that 00000 was sent otherwise. For example, if it receives 11001 it concludes that 11111 was sent. Thus, the spacecraft computer will get the wrong message if and only if three or more errors occur in transmission and (assuming successive errors occur independently) the probability of this happening37 is 0.00856. This probability is less than 1 %, even though there is a 10% chance of error on any one transmission. This decision method is called maximum likelihood decoding.
Example 1 is a good illustration of the way coding works. A sender has a message to send (say, 1 in Example 1). It is encoded (as 11111) and transmitted over a noisy channel where it is received (as, say, 11001) and decoded (as 1) before being sent to the receiver. In Example 1, the coding process can detect errors and correct them with a probability of less than 0.01 of being wrong.
In general, it is desirable to have more messages than 1 or 0 available for encoding and transmission. For convenience (and due to the ubiquity of computers) we assume that our messages, and the encoded messages to be transmitted, are strings of 0s and 1s. We use the following notation. If n ≥ 1, let
![]()
denote the direct product of n copies of the (additive abelian) group ![]() The elements of Bn are called words of length n and, for convenience, we write them as strings of 0s and 1s rather than as n-tuples. Thus, 110101 in B6 stands for (1, 1, 0, 1, 0, 1). We call the individual 0s and 1s the bits of the word (an abbreviation for binary digits). A subset C of Bn, with |C| ≥ 2, is called an n -binary code (or simply an n-code). The words in C are called code words.
The elements of Bn are called words of length n and, for convenience, we write them as strings of 0s and 1s rather than as n-tuples. Thus, 110101 in B6 stands for (1, 1, 0, 1, 0, 1). We call the individual 0s and 1s the bits of the word (an abbreviation for binary digits). A subset C of Bn, with |C| ≥ 2, is called an n -binary code (or simply an n-code). The words in C are called code words.
We describe the general coding process in the diagram.

A set of words, called message words, is given in Bk. They are paired with a set C of longer words in Bn, n ≥ k, which will actually be transmitted. Thus C is an n-code, and the process of passing from a message to the corresponding code word is called encoding. Only code words are transmitted but, as some bits may be altered during transmission, words other than code words may be received. The sole purpose of the encoding process is to enable the receiver to detect errors and, if there are not too many, to correct them. The encoding and transmission processes are usually quite simple. The message words in Bk are paired with code words in Bn in such a way that passing back and forth is easy. A common method is to add extra bits (called check bits) to the end of the message so that the message itself forms the first k bits of the code word (making retrieval easy). The transmission process is more complex, and the design of codes that are easy and inexpensive to transmit (using, say, shift registers) is an important problem that we do not consider here. The most mathematically interesting part of the process is decoding. A method must be devised to detect bit errors in the received word and, hopefully, to correct them and so reconstruct the transmitted code word. The transmission and decoding part of the process begins and ends with code words, so we concentrate on constructing codes and pay less attention to encoding and retrieving.
In Example 1, the 5-code {00000, 11111} has so few code words that a system (majority rule) of decoding can correct errors with a small probability of error. However, sometimes (for example, when retransmission is easy and inexpensive) all that is needed is to detect errors. Example 2 gives one such system that is commonly used.
Example 2. Parity-check Codes are n-codes that are constructed as follows. The message words are the elements of Bn−1, and we form the code words by adding one extra bit at the end, selecting it so that the total number of 1 s is even (equivalently, the sum of the bits (in ![]() ) is 0). Such words are said to have even parity. Thus, the 4-parity-check code C is
) is 0). Such words are said to have even parity. Thus, the 4-parity-check code C is
![]()
If a member of C is transmitted and one error occurs, the received word will have an odd number of 1s (odd parity) and so the error is detected. This code can thus detect any odd number of errors, but it cannot detect an even number of errors and it cannot correct any errors. Nonetheless, it is used in banking (the last digit of an account number is often a control digit) and in the internal arithmetic of digital computers.
Nearest Neighbor Decoding
Many important error-correcting codes operate in the following way. A method is found to define the distance between two words in Bn. Then a code C ⊆ Bn is found whose members are so far apart that, if any one bit (say) in a code word c is changed, the new word ![]() is still closer to c than to any other word in the code. Thus, if c is transmitted and one error occurs, the received word
is still closer to c than to any other word in the code. Thus, if c is transmitted and one error occurs, the received word ![]() can be corrected by replacing it with the code word closest to it. We state this more compactly as follows.
can be corrected by replacing it with the code word closest to it. We state this more compactly as follows.
Nearest Neighbor Decoding Let C be an n -code. If a word ![]() is received, it is decoded as the code word in C closest to it.(If more than one candidate appears, choose arbitrarily38.)
is received, it is decoded as the code word in C closest to it.(If more than one candidate appears, choose arbitrarily38.)
Codes can be constructed that will correct any finite number of errors using nearest neighbor decoding.
Of course the whole thing depends on the existence of an appropriate distance function on Bn. If a word c is transmitted and t errors occur, the received word ![]() will differ from c in exactly t bits. This is the distance between c and
will differ from c in exactly t bits. This is the distance between c and ![]()
More precisely, let ![]() and
and ![]() be words in Bn. The Hamming distance 39
be words in Bn. The Hamming distance 39 ![]() between
between ![]() and
and ![]() is the number of coordinates at which their corresponding bits differ. Thus, if
is the number of coordinates at which their corresponding bits differ. Thus, if ![]() and
and ![]() where the
where the ![]() and
and ![]() are the bits, then
are the bits, then ![]() is the number of indices i such that
is the number of indices i such that ![]() Define the Hamming weight of
Define the Hamming weight of ![]() by
by ![]() Thus,
Thus, ![]() is the number of 1s occurring as bits of the word
is the number of 1s occurring as bits of the word ![]()
The following theorem gives some fundamental properties of the Hamming weight and distance functions. The proof uses the fact that Bn is an additive group under componentwise operations. Thus two words are added by adding corresponding bits modulo 2. For example,
![]()
Note that the unity is the word 000 ![]() 0, each of whose bits is 0, which we denote 0. Also,
0, each of whose bits is 0, which we denote 0. Also, ![]() for each word
for each word ![]() in Bn, but we write
in Bn, but we write ![]() for clarity.
for clarity.
Theorem 1. Let ![]() and
and ![]() be words in Bn.
be words in Bn.
1. ![]()
2. ![]()
3. ![]() if and only if
if and only if![]()
4. ![]()
Proof. (1) A bit of ![]() is a 1 if and only if
is a 1 if and only if ![]() and
and ![]() differ at that coordinate. Hence the number of bits of
differ at that coordinate. Hence the number of bits of ![]() that are 1 s equals the number of coordinates where
that are 1 s equals the number of coordinates where ![]() and
and ![]() differ. This is (1).
differ. This is (1).
(2), (3). We leave the proofs to the reader.
(4) Write ![]() and
and ![]() so that
so that ![]() Then, using (1), condition (4) becomes wt(x + y) ≤ wtx + wty. Now let xi and yi denote the ith bits of x and y, respectively. Then the wt(x + y) is the number of values of i for which xi + yi = 1. Hence (4) certainly holds if xi + yi = 1 implies that xi = 1 or yi = 1. But this implication is clear because xi = 0 = yi implies that xi + yi = 0.
Then, using (1), condition (4) becomes wt(x + y) ≤ wtx + wty. Now let xi and yi denote the ith bits of x and y, respectively. Then the wt(x + y) is the number of values of i for which xi + yi = 1. Hence (4) certainly holds if xi + yi = 1 implies that xi = 1 or yi = 1. But this implication is clear because xi = 0 = yi implies that xi + yi = 0.
Properties (2), (3), and (4) of Theorem 1 justify calling d a distance function on Bn. The first two are clearly true of ordinary distance. With respect to
property (4), we may regard ![]() , and
, and ![]() as the vertices of a triangle (see the figure). Then (4) asserts that the length of one side of a triangle is not greater than the sum of the lengths of the other two sides. For this reason we call (4) the triangle inequality.
as the vertices of a triangle (see the figure). Then (4) asserts that the length of one side of a triangle is not greater than the sum of the lengths of the other two sides. For this reason we call (4) the triangle inequality.

This geometric terminology for Hamming distance is useful for discussing nearest neighbor decoding. If ![]() is a word in Bn and r ≥ 0 is a real number, the set
is a word in Bn and r ≥ 0 is a real number, the set
![]()
is called the ball of radius r about w or simply the r-ball about ![]() ). We use this to describe how to construct a code C that can detect (or correct) t errors.
). We use this to describe how to construct a code C that can detect (or correct) t errors.
Suppose that a code word c is transmitted and a word ![]() is received with s errors, where 1 ≤ s ≤ t. Then s is the number of coordinates at which the digits of c and
is received with s errors, where 1 ≤ s ≤ t. Then s is the number of coordinates at which the digits of c and ![]() differ; that is,
differ; that is, ![]() Hence St(c) consists of all possible received words where at most t errors have occurred. We first assume that C has the property that no code word lies in the t-ball of another code word. Because
Hence St(c) consists of all possible received words where at most t errors have occurred. We first assume that C has the property that no code word lies in the t-ball of another code word. Because ![]() and
and ![]() this means that
this means that ![]() is not a code word and that the error has been detected. If we strengthen the assumption on C to require that the t-balls about code words are pairwise disjoint, then
is not a code word and that the error has been detected. If we strengthen the assumption on C to require that the t-balls about code words are pairwise disjoint, then ![]() belongs to a unique ball (that about c), so
belongs to a unique ball (that about c), so ![]() will be correctly decoded as c.
will be correctly decoded as c.
To describe when this happens, let C be an n-code. The minimum distance d of C is defined to be the smallest distance between two distinct code words in C. That is,
![]()
Theorem 2. Let C be an n -code with minimum distance d. Assume that nearest neighbor decoding is used.
1. If t + 1 ≤ d, then C can detect 40 t errors.
2. If 2t + 1 ≤ d, then C can correct t errors.
Proof. (1) If c ![]() C, the t-ball St(c) contains no other code word because t < d. Hence C can detect t errors by the preceding discussion.
C, the t-ball St(c) contains no other code word because t < d. Hence C can detect t errors by the preceding discussion.
(2) If 2t + 1 ≤ d, it suffices (by the preceding discussion) to show that the t-balls about distinct code words are pairwise disjoint. But if c ≠ c′ in C and ![]() then the triangle inequality gives
then the triangle inequality gives
![]()
by the hypothesis, a contradiction.
Example 3. The following 7-code has minimum distance 3, so it can detect 2 errors and correct 1 error.
{0000000, 0101010, 1010101, 1110000, 1011010, 0100101, 0001111, 1111111}.
If c is any word in Bn, a word ![]() satisfies
satisfies ![]() if and only if
if and only if ![]() and c differ in exactly r bits. Hence there are exactly nr such words
and c differ in exactly r bits. Hence there are exactly nr such words ![]() (where nr is the binomial coefficient), because there are nr ways to choose r bits of c to change. Therefore
(where nr is the binomial coefficient), because there are nr ways to choose r bits of c to change. Therefore
![]()
This leads to a useful bound on the size of error-correcting codes.
Theorem 3. Hamming Bound. If an n-code C can correct t errors, then
![]()
Proof. Write N = n0 + n1 + ![]() + nt. The t-balls centered at distinct code words each contain N words, and there are |C| of them. Hence they contain N|C| distinct words (being pairwise disjoint). Hence N|C| ≤ 2n because |Bn| = 2n. This proves the theorem.
+ nt. The t-balls centered at distinct code words each contain N words, and there are |C| of them. Hence they contain N|C| distinct words (being pairwise disjoint). Hence N|C| ≤ 2n because |Bn| = 2n. This proves the theorem.
An n-code C is called perfect if there is equality in Theorem 3 or, equivalently, if every word in Bn lies in exactly one t-ball about a code word. Such codes exist. For example, if n = 3 and t = 1, then 30 + 31 = 4 and the Hamming bound is 23/4 = 2. The 3 -code C = {000, 111} has minimum distance 3, so by Theorem 2 it can correct 1 error. Hence C is perfect. We present another example of a perfect code later.
Binary Linear Codes and Coset Decoding
Up to this point we have regarded any nonempty subset of Bn as an n-code. However, many important codes are subgroups. The group Bn has order 2n so, by Lagrange's theorem, each subgroup has order 2k for some k = 0, 1, ![]() , n. Given integers k and n, with 1 ≤ k ≤ n, an additive subgroup C of Bn of order 2k is called an (n,k)-binary linear code (or simply an (n,k)-code). Note that we do not regard the trivial subgroup (k = 0) as a code.
, n. Given integers k and n, with 1 ≤ k ≤ n, an additive subgroup C of Bn of order 2k is called an (n,k)-binary linear code (or simply an (n,k)-code). Note that we do not regard the trivial subgroup (k = 0) as a code.
Example 4. The code {00000, 11111} in Example 1 is a (5, 1)-code.
Example 5. The n-parity-check codes in Example 2 are (n, n − 1)-codes, because the sum of two words of even parity also has even parity.
Example 6. {0000, 0101, 1010, 1111} is a (4, 2) -code. The following is a (4, 3)-code: {0000, 0010, 0101, 0111, 1000, 1010, 1101, 1111}.
Many of the properties of the general n-codes take a simpler form for linear codes. The first part of the next theorem gives a much easier way to find the minimum distance of a linear code, the second and third parts strengthen Theorem 2, and the fourth part reformulates the Hamming bound.
Theorem 4. Let C be an (n, k) -code with minimum distance d.
1. ![]() 41
41
2. C can detect t errors if and only if t + 1 ≤ d.
3. C can correct t errors if and only if 2t + 1 ≤ d.
4. If C can correct t errors, then n0 + n1 + ![]() + nt ≤ 2n−k.
+ nt ≤ 2n−k.
Proof. (1) Write ![]() If
If ![]() then
then ![]() by the definition of d. Hence d′ ≥ d. However, Theorem 1 gives
by the definition of d. Hence d′ ≥ d. However, Theorem 1 gives ![]() for all
for all ![]() in C, so
in C, so ![]() because
because ![]() (C is a group). Hence d ≥ d′.
(C is a group). Hence d ≥ d′.
(2) Assume that C can detect t errors. If ![]() the t -ball about
the t -ball about ![]() contains no other code word (see the discussion preceding Theorem 2). In particular, it does not contain the code word 0, so
contains no other code word (see the discussion preceding Theorem 2). In particular, it does not contain the code word 0, so ![]() Hence t + 1 ≤ d by (1). The converse is part of Theorem 2.
Hence t + 1 ≤ d by (1). The converse is part of Theorem 2.
(3) If C corrects t errors, the t-balls about code words are pairwise disjoint (see the discussion preceding Theorem 2). It suffices to show that wtc ≥ 2t + 1 for all c ![]() C, c ≠ 0, since then d ≥ 2t + 1.
C, c ≠ 0, since then d ≥ 2t + 1.
So assume, on the contrary, that wtc ≤ 2t. We show that then St(0) ∩ St(c) ≠ ∅, a contradiction. Since c ∉ St(0), we have wt(c) > t, so c has more than t ones as bits. Form ![]() by changing exactly t of these ones to zeros, and leaving the other bits of c as they were. Then
by changing exactly t of these ones to zeros, and leaving the other bits of c as they were. Then ![]() , so
, so ![]() . But c has at most 2t ones as digits (wt(c) ≤ 2t), so
. But c has at most 2t ones as digits (wt(c) ≤ 2t), so ![]() will have at most t ones. Hence
will have at most t ones. Hence ![]() ; that is
; that is ![]() that is
that is ![]() . So St(0) ∩St(c) ≠ Φ, as required.
. So St(0) ∩St(c) ≠ Φ, as required.
(4) Because |C| = 2k, this assertion restates Theorem 3.
In practice, an (n, k)-code C contains a large number of words, so implementing nearest neighbor decoding by computing the distance between a received word and all 2k code words is impractical at best. Fortunately, methods exist for reducing the amount of work required. One of these methods, called coset decoding, is based on the fact that the group Bn is partitioned into cosets by the subgroup C. In fact, there are 2n/2k = 2n−k cosets ![]() where
where ![]() The method depends on the following notion.
The method depends on the following notion.
In each coset of C in Bn, choose a word e of minimum weight, called the coset leader for that coset. Note that there may be more than one candidate for coset leader. For example, if C is the code in Example 3 and ![]() the coset
the coset
![]()
has two members of minimum weight 2.
After choosing the coset leaders, we can easily state the decoding procedure.
Coset Decoding Let C be an (n, k) -code. If a word ![]() is received, and if e is any coset leader for
is received, and if e is any coset leader for ![]() decode
decode ![]() as
as ![]()
Theorem 5. Coset decoding is nearest neighbor decoding.
Proof. Let C be an (n, k)-code. If a word ![]() is received and e is any coset leader in
is received and e is any coset leader in ![]() then
then ![]() is a code word in C (because e is in
is a code word in C (because e is in ![]() ). We must show that
). We must show that ![]() is as close to c as any other element d of C. We have
is as close to c as any other element d of C. We have ![]() so
so ![]() by the choice of e in C. Hence
by the choice of e in C. Hence
![]()
which is what we wanted.
Example 7. Consider the (6, 3)-code:
![]()
If ![]() and
and ![]() are received, decode them using coset decoding.
are received, decode them using coset decoding.
Solution. The cosets generated by ![]() and
and ![]() are
are
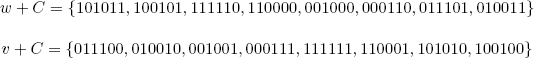
One of the coset leaders in ![]() is e = 001000, so
is e = 001000, so ![]() decodes as
decodes as ![]() However,
However, ![]() has three potential coset leaders: f = 010010, g = 001001, and h = 100100. These leaders decode
has three potential coset leaders: f = 010010, g = 001001, and h = 100100. These leaders decode ![]() as 001110, 010101, and 111000, respectively. Note that C has minimum distance 3, so it will correct one error by Theorem 4. Since
as 001110, 010101, and 111000, respectively. Note that C has minimum distance 3, so it will correct one error by Theorem 4. Since ![]() is one error away from 100011 (in C), the code corrects
is one error away from 100011 (in C), the code corrects ![]() But
But ![]() for every word c in C, so the code does not correct
for every word c in C, so the code does not correct ![]() Note that 001110, 010101, and 111000 are all the elements of C at distance 2 from
Note that 001110, 010101, and 111000 are all the elements of C at distance 2 from ![]()
Given an (n, k)-code C for which |C| = 2k is not too large, we can carry out coset decoding by constructing a table (called a standard array for C), the rows of which are the various cosets ![]() of C in Bn. The coset C = 0 + C is listed in the top row with 0 in column 1. (Note that 0 is the coset a for C.) In general, if e is any coset leader for
of C in Bn. The coset C = 0 + C is listed in the top row with 0 in column 1. (Note that 0 is the coset a for C.) In general, if e is any coset leader for ![]() then
then ![]() and we place the elements of this coset in a row of the table with e in column 1 and e + c in the column headed by c for each c
and we place the elements of this coset in a row of the table with e in column 1 and e + c in the column headed by c for each c ![]() C. We then decode as follows: If we receive a word
C. We then decode as follows: If we receive a word ![]() we locate it in the table (so
we locate it in the table (so ![]() where e is a coset leader) and decode it as the code word c at the head of its column. Here is an example.
where e is a coset leader) and decode it as the code word c at the head of its column. Here is an example.
Example 8. Construct the standard array for the (4, 2)-code C = {0000, 0110, 1011, 1101}.
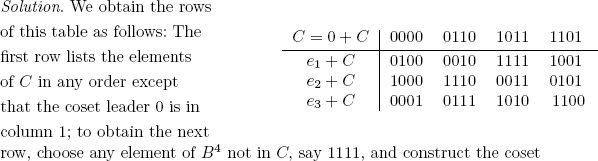
row, choose any element of B4 not in C, say 1111, and construct the coset
![]()
Next, we choose a coset leader, say, e1 = 0100, (0010 would do as well), and obtain row 2 of the table by adding e1 to the elements of row 1 in order. Thus, for example, the word 1111 in column 3 is the sum of e1 and the word 1011 (in C) at the head of column 3.
We complete the rest of the table in the same way. To form any row, we choose an element of B4 not yet listed, find a coset leader in its coset, and list the coset as a row. The remaining coset leaders are e2 = 1000 and e3 = 0001 (each the unique word of minimum weight in its coset).
With the table complete, decoding is easy. For example, if we receive ![]() we decode
we decode ![]() as c = 1011 because
as c = 1011 because ![]() is in column 3 of the table.
is in column 3 of the table.
This method is impractical for large linear codes. For example, a (40, 10) -code has 230 > 109 cosets, so finding the coset leaders is practically impossible. Hence large codes are constructed using more systematic methods.
Matrix Methods
One convenient way to obtain codes is by using matrix multiplication. Here we take the original messages to be the elements of Bk. We regard them as 1 × k row matrices with entries from ![]() and encode by multiplying by a fixed binary matrix (entries from
and encode by multiplying by a fixed binary matrix (entries from ![]() ). We use the usual rules for matrix multiplication, except that we do arithmetic modulo 2.
). We use the usual rules for matrix multiplication, except that we do arithmetic modulo 2.
Example 9. The Hamming (7, 4)-code.42 We use the binary matrix
The message words are the elements of B4; for example, u = 1011 is encoded as uG = 1011001 because of the matrix product
![]()
In the chart below, the code words corresponding to all entries of B4 appear on the right. Here each nonzero code word has weight at least 3, so the code can detect two errors and correct one error by Theorem 4.

Observe that the first four columns of the matrix G in Example 9 form the 4 × 4 identity matrix I4. This ensures that the first four digits of each code word uG form the original message word. The general situation is described using the following terminology.
An (n, k)-code C is called a systematic code if each message word in Bk forms the first k digits of exactly one code word. A k × n matrix of the form43
![]()
is a standard generator matrix if Ik is the k × k identity matrix and A is a k × (n − k) binary matrix. Thus, the matrix G in Example 9 is a 4 × 7 standard generator matrix G = [I4A] where

The code itself is given as C = {uG ![]() u
u ![]() Bk}.
Bk}.
Theorem 6. Let G be a k × n standard generator matrix. Then
![]()
is a systematic (n, k)-code. Conversely, every systematic (n, k)-code is given in this way by a standard generator matrix G.
Proof. Define σ: Bk → Bn by σ(u) = uG for all u ![]() Bk. Then σ is a group homomorphism because matrix multiplication satisfies
Bk. Then σ is a group homomorphism because matrix multiplication satisfies ![]() As σ is clearly onto C, this shows that C is a subgroup of Bn. In fact, σ is one-to-one. To see this, write G = [IkA], where A is k × (n − k). Then
As σ is clearly onto C, this shows that C is a subgroup of Bn. In fact, σ is one-to-one. To see this, write G = [IkA], where A is k × (n − k). Then
![]()
Hence σ is one-to-one because ![]() implies that [uuA] = [vvA], when
implies that [uuA] = [vvA], when ![]() Thus Bk and C are isomorphic groups and, in particular, |C| = |Bk| = 2k. Thus C is an (n, k)-code; it is systematic because σ(u) = [uuA] for all u
Thus Bk and C are isomorphic groups and, in particular, |C| = |Bk| = 2k. Thus C is an (n, k)-code; it is systematic because σ(u) = [uuA] for all u ![]() Bk. This proves the first part of Theorem 6; we leave the converse as Exercise 26.
Bk. This proves the first part of Theorem 6; we leave the converse as Exercise 26.
Example 10. The (6, 3)-code
![]()
in Example 7 is systematic, and the reader can verify that it is generated by the standard generator matrix

That is, C = {uG ![]() u
u ![]() B3}.
B3}.
If C is a systematic (n, k)-code, we can easily write down a standard generator matrix for C. Because C is systematic, it contains a word ci whose first k digits form row i of Ik. Let G be the k × n matrix whose rows are c1, c2, ![]() , ck in order:
, ck in order:

Then G is a standard generator matrix and C = {uG ![]() u
u ![]() Bk} (See Exercise 26). Incidentally, we say that C is generated by G when C = {uG
Bk} (See Exercise 26). Incidentally, we say that C is generated by G when C = {uG ![]() u
u ![]() Bk}. In this case C consists of 0 and all sums of (1 or more) of the generating words c1, c2,
Bk}. In this case C consists of 0 and all sums of (1 or more) of the generating words c1, c2, ![]() , ck. This is illustrated in Example 11.
, ck. This is illustrated in Example 11.
Example 11. Both the codes {0000, 0101, 1010, 1111} and
![]()
in Example 6 are systematic with matrices ![]() and
and  .
.
On the other hand, the (7, 3)-code in Example 3 is not systematic. Nonetheless, every (n, k)-code is close to being systematic in the sense that it contains k words with the following property: If F is the k × n matrix with these words as rows, F contains every column of the k × k identity matrix Ik (Exercise 27).
The use of a standard generator matrix is a convenient method of generating (n, k)-codes not only because retrieval is easy but also because a k × n matrix has only kn entries to store, whereas the code contains 2k words of n entries each. Moreover, the process of encoding with a systematic code is simple: Multiply the message word by the generator matrix. Hence it is not surprising that matrix methods give a simple way to detect and correct errors.
To understand why, let C be a systematic binary (n, k)-code with standard generator matrix G = [IkA], where A is a k × (n − k) binary matrix. The parity-check matrix44 for C is the n × (n − k) matrix given in block form by
![]()
If ![]() is a word in Bn, the word wH in Bn−k is called the syndrome of
is a word in Bn, the word wH in Bn−k is called the syndrome of ![]() Note that each of G and H completely determines the other, so either matrix determines the code C.
Note that each of G and H completely determines the other, so either matrix determines the code C.
Example 12. The Hamming (7, 4)-code in Example 9 has the generator matrix

Hence the parity-check matrix is H =  .
.
In Example 12, the reader can verify that GH = 0 is the zero matrix. This relation holds in general.
Lemma. If G and H are the standard generator matrix and the parity-check matrix of a systematic(n, k)-code, then GH = 0.
Proof. Write G = [IkA] so that ![]() Then block multiplication gives
Then block multiplication gives
![]()
where A + A = 0 because A is binary and x + x = 0 for all ![]()
Theorem 7. Orthogonality Theorem. Let C be a systematic (n, k)-code with parity-check matrix H.
1. ![]()
2. Words ![]() and
and ![]() in Bn lie in the same C-coset if and only if wH = vH.
in Bn lie in the same C-coset if and only if wH = vH.
Proof. (1) Let G = [IkA] be the generator matrix for C, so ![]() Define α: Bn → Bn−k by
Define α: Bn → Bn−k by ![]() for all
for all ![]() Then α is a group homomorphism because
Then α is a group homomorphism because ![]() and (1) amounts to showing that C = ker α. We first verify that α is onto. If
and (1) amounts to showing that C = ker α. We first verify that α is onto. If ![]() let
let ![]() be the word whose first k bits are zero and which ends with
be the word whose first k bits are zero and which ends with ![]() Then
Then
![]()
Hence α is onto, so imα = Bn−k. Now the isomorphism theorem (Theorem 4 §2.10) gives Bn/(ker α) ≅ Bn−k, so |Bn|/|ker α| = |Bn−k|. Therefore | ker α| = 2k and so | ker α| = |C|. Then to prove that C = ker α, it suffices to show that C ⊆ ker α. But if c ![]() C, then c = uG for some u
C, then c = uG for some u ![]() Bk (Theorem 6), so α(c) = cH = uGH = u0 = 0 by the lemma. Hence C ⊆ ker α.
Bk (Theorem 6), so α(c) = cH = uGH = u0 = 0 by the lemma. Hence C ⊆ ker α.
(2) For ![]() and
and ![]() in Bn, we have a chain of equivalences
in Bn, we have a chain of equivalences
![]()
where the first equivalence comes from Theorem 1 §2.6, the second is by (1), and the third is because ![]()
The orthogonality theorem enables us to reformulate the coset decoding algorithm entirely in terms of the parity-check matrix.
Syndrome Decoding Let C be a systematic (n, k)-code with parity-check matrix H. If ![]() is received, compute its syndrome wH and find a word e
is received, compute its syndrome wH and find a word e ![]() Bn of minimal weight with the same syndrome (that is, wH = eH). Decode
Bn of minimal weight with the same syndrome (that is, wH = eH). Decode ![]() as
as ![]()
The advantage of this method is that it requires knowing only the syndromes of the coset leaders (rather than the entire standard array), and sometimes the coset leaders can be discovered without finding the whole array.
Nearest neighbor decoding, as we have described it, is complete decoding in the sense that every received word is decoded. However, in many cases (especially where retransmission is easy) a better approach is to use a partial decoding procedure that corrects t errors and calls for retransmission when more than t errors are detected. We conclude by describing one such algorithm.
In this section, we have merely touched the surface of algebraic coding theory. For example, these results generalize with very little change if an (n, k)-code is defined to be a k-dimensional subspace of an n-dimensional vector space V over a finite field F (in our discussion, V = Bn and ![]() ). Even more sophisticated coding algorithms exist that use ring theory and field theory as well as group theory and linear algebra (see Section 6.7 for one such application).45
). Even more sophisticated coding algorithms exist that use ring theory and field theory as well as group theory and linear algebra (see Section 6.7 for one such application).45
Exercises 2.11
1. Find the Hamming weight of each word.
| (a) 10110110 | (b) 11010110 |
| (c) 00101011011 | (d) 010110101011 |
2. Find the Hamming distance between each pair of words.
| (a) 101101 and 010101 | (b) 10110101 and 01110111 |
| (c) 1110111 and 0001000 | (d) 10110111 and 01001011 |
3. Show that ![]() for all
for all ![]() and
and ![]() in Bn.
in Bn.
4. What is the maximum value of ![]() when
when ![]() Describe the pairs of words
Describe the pairs of words ![]() and
and ![]() in Bn with
in Bn with ![]() as large as possible.
as large as possible.
5. Let ![]() be the word obtained from
be the word obtained from ![]() by changing every bit.
by changing every bit.
(a) Show that ![]() for all
for all ![]()
(b) Show that ![]() for all
for all ![]()
6. Let C be the (7, 3)-code in Example 3. Find the nearest neighbors to each of the following words in B7 and so correct them (if possible).
![]()
7. How many errors can be detected or corrected by each of the following codes?
(a) 
(b) 
8. Let c be a word in Bn and let 0 ≤ t ≤ n. Show that ![]()
9.
(a) Show that the Hamming bound is equality if t = 1 in the (7, 4)-Hamming code.
(b) What is the maximum number of errors that an (8, 3)-code can correct? (c) Is there a (7, 2)-code of minimum distance 5?
10.
(a) If a systematic (n, 2)-code corrects one error, use the Hamming bound to show that n ≥ 5 and find a (5, 2)-code that corrects one error.
(b) If a systematic (n, 2)-code corrects two errors, use the Hamming bound to show that n ≥ 7. Show that no (7, 2)-code can correct two errors. Is there an (8, 2)-code that corrects two errors? Justify your answer.
11.
(a) If an (n, 3)-code corrects two errors, show that n ≥ 9.
(b) Find a (10, 3)-code that corrects two errors. It can be shown that there is no (9, 3)-code that corrects two errors.
12. Given r ≥ 2, write n = 2r − 1 and k = 2r − r − 1 so that n − k = r. Define H to be the n × r parity-check matrix consisting of all n = 2r − 1 nonzero elements of Br with Ir forming the last r rows. The corresponding (n, k)-code is called a Hamming code. (The (7, 4)-Hamming code is the case r = 3). Show that every Hamming code corrects one error.
13. If a code word c is transmitted and ![]() is received, show that coset decoding will correctly decode
is received, show that coset decoding will correctly decode ![]() if and only if
if and only if ![]() is a coset leader in
is a coset leader in ![]()
14. Suppose that an (n, k)-code C has the property that each word e ![]() Bn, with wte ≤ t, is a coset leader in e + C. Show that C corrects t errors by using coset decoding.
Bn, with wte ≤ t, is a coset leader in e + C. Show that C corrects t errors by using coset decoding.
15.
(a) Show that no (4, 2)-code can correct single errors.
(b) Construct a (5, 2)-code that can correct a single error.
16.
(a) Show that no (6, 3)-code can correct two errors.
(b) Construct a (6, 3)-code that can correct a single error. (c) Show that no (7, 3)-code can correct two errors.
17. Given words ![]() , define their product vw to be the word whose ith digit is the product
, define their product vw to be the word whose ith digit is the product ![]() where
where ![]() and
and ![]() are the ith digits of
are the ith digits of ![]() and
and ![]()
(a) Show that ![]()
(b) Deduce the triangle inequality: ![]() (See Theorem 1.)
(See Theorem 1.)
(c) Show that equality holds in (b) if and only if the ith bit of ![]() is 0 whenever the ith bit of
is 0 whenever the ith bit of ![]() is 1.
is 1.
18. If ![]() show that
show that ![]() with equality if and only if the ith bit of
with equality if and only if the ith bit of ![]() is 1 whenever the ith bit of
is 1 whenever the ith bit of ![]() is 1. [Hint: Preceding exercise.]
is 1. [Hint: Preceding exercise.]
19. If C is an (n, k)-code, ![]() and
and ![]() show that
show that ![]() is an (n, k + 1)-code.
is an (n, k + 1)-code.
20. Write down the standard generator matrix G and the parity-check matrix H for each of the following systematic codes.
(a) C = {00000, 11111}.
(b) C = any systematic (n, 1)-code.
(c) The code in Exercise 7(a). (d) The code in Exercise 7(b).
21. List the codes generated by each standard generator matrix.
| (a) |
(b) |
(c)  |
(d)  |
22. If C is the (n, n − 1)-parity-check code (Example 2), show that C is systematic and describe the standard generating matrix G and the parity-check matrix H.
23. (Requires matrix algebra) Prove Theorem 7(a) without using the isomorphism theorem by writing each ![]() such that wH = 0 as
such that wH = 0 as ![]() where u consists of the first k bits of
where u consists of the first k bits of ![]() and
and ![]() is the last n − k bits of
is the last n − k bits of ![]()
24. (Requires matrix algebra) Let C and C′ be (n, k) -codes, with standard generator matrices G and G′, and parity-check matrices H and H′, respectively.
(a) Show that C = C′ if and only if G = G′.
(b) Show that C = C′ if and only if H = H′.
25. Let C be an (n, k)-code.
(a) Show that either each word in C has even weight or exactly half have even weight.
(b) Show that either each word in C has nth bit 0 or exactly half have nth bit 0.
(c) Generalize.
26. Show that every systematic (n, k)-code C is generated by a k × n standard generator matrix G; that is, C = {uG ![]() u
u ![]() Bk}. [Hint: Let c1, c2,
Bk}. [Hint: Let c1, c2, ![]() , ck be the rows of Ik; that is, ci has the ith bit 1 and all other bits 0. If
, ck be the rows of Ik; that is, ci has the ith bit 1 and all other bits 0. If ![]() is the unique element of C with ci as its first k bits, take G = [IkA], where the rows of A are
is the unique element of C with ci as its first k bits, take G = [IkA], where the rows of A are ![]() ]
]
27. (Requires linear algebra) Show that every (n, k)-code C contains k words c1, c2, ![]() , ck such that the k × n matrix K =
, ck such that the k × n matrix K = ![]() contains every column of the k × k identity matrix Ik. [Hint: Regard C as a vector space over
contains every column of the k × k identity matrix Ik. [Hint: Regard C as a vector space over ![]() and let {b1,
and let {b1, ![]() , bk} be a basis. If B =
, bk} be a basis. If B = ![]() , carry B to reduced row-echelon form B → R and let ci be row i of R.]
, carry B to reduced row-echelon form B → R and let ci be row i of R.]
Notes
18. The term “identity” is often used here but it has other meanings in algebra. So we use the term unity.
19. A set with an associative binary operation, but possibly no unity, is called a semigroup.
20. This proof will not be used below and so may be omitted at a first reading. By contrast, the theorem will be used hundreds of times.
21. See Nicholson, W.K., Linear Algebra with Applications, 7th ed., McGraw-Hill Ryerson, 2012 (Theorem 2 §3.2).
22. The name honors the Norwegian mathematician Niels Henrik Abel.
23. If X and Y are sets the set difference is defined by ![]() .
.
24. The name honors Felix Klein. This group is also called the four group.
25. To avoid confusion, we sometimes denote the unity of a group G by 1G when other groups are present.
26. The notation Z(G) comes from zentrum, the German word for center.
27. Homomorphisms were first used explicitly (for permutation groups) by Jordan in 1870.
28. The term isomorphism comes from isos, meaning equal, and morphe, meaning shape.
29. See, for instance, Clay, J.R., The punctured plane is isomorphic to the unit circle, Journal of Number Theory, 1, (1964), 500–501.
30. Recall (Section 0.4) that a partition of a nonempty set X is a collection of nonempty subsets of X (called the cells of the partition) which are pairwise disjoint (distinct cells are disjoint) and every element of X is in some cell (hence in exactly one cell).
31. In fact ![]() where
where ![]() is the inner automorphism determined by g.
is the inner automorphism determined by g.
32. Thompson, J. G., and Feit, W., Solvability of Groups of Odd Order, Pacific Journal of Mathematics, 13 (1963), 775–1029.
33. John Thompson was awarded the Fields Medal in 1970, the highest honor a mathematician can receive.
34. More information can be found in Chapter 17 of “Finite Groups” by D. Gorenstein, Chelsea, 1980.
35. This result goes back to Camille Jordan (1838–1922) in his book Traité des Substitutions (1870), where the concept of a homomorphism was introduced.
36. We treat probability informally here. The probability that an event occurs is the long-term proportion of the time that the event does indeed occur. Thus probabilities are numbers between 0 and 1. A probability of 0 means that the event in question is impossible; a probability of 1 means that the event is certain to occur; and a probability of 0.5 means that the event is as likely as not to occur.
37. The probability is computed as ![]() . It is based on the assumption that at most one error occurs in each digit transmitted and that these errors occur independently.
. It is based on the assumption that at most one error occurs in each digit transmitted and that these errors occur independently.
38. If it is feasible, retransmission may be called for in this case.
39. The name honors Richard W. Hamming. Distance functions are also called metrics.
40. If C can detect (correct) t or fewer errors, we say simply that C detects (corrects) t errors.
41. Because of this the minimum distance of a linear code is sometimes called the minimum weight of the code.
42. This code was the first nontrivial example of an error correcting code given in the groundbreaking paper in which information theory was originated (Shannon, C.E., A mathematical theory of communication, Bell Systems Technical Journal 27 (1948), 623–656).
43. If A and B are k × m and k × n matrices, the notation [A B] indicates the k × (m + n) matrix with A occupying the first m columns and B occupying the last n columns. The matrix [A B] is said to be given in block form.
44. Systematic binary codes are often defined using the parity-check matrix. Then the transpose of H is referred to as the parity-check matrix.
45. An introduction to the subject is given in Pless, V., Introduction to the Theory of Error Correcting Codes, New York: Wiley, 1982. A more thorough treatment (with an extensive bibliography) is that by MacWilliams, F.I., and Sloan, N.J.A., The Theory of Error Correcting Codes, Vols. I and II, New York: North Holland, 1977. Finally, a useful survey is contained in Chapter 4 of Lidl, R., and Pilz, G., Applied Abstract Algebra, New York: Springer-Verlag, 1984.
