Chapter 9
Series of Subgroups
In the future, as in the past, the great ideas must be simplifying ideas.
—André Weil
If G is a finite abelian group, it can be shown that G is isomorphic to a direct product of cyclic groups (see Chapter 7). This result is an example of a structure theorem, that is, a theorem showing that every group in a suitable defined class may be constructed in a systematic way from well understood groups in the class. Such theorems are hard to come by, and the result for finite abelian groups is a stunning example. The structure of nonabelian finite groups is much more complicated.
Suppose that groups K and H are given. It is a very difficult problem to describe all groups G that have a normal subgroup K1 isomorphic to K such that G/K1 is isomorphic to H. If we could solve this extension problem, the solution would give an inductive method for constructing all finite groups. Direct and semidirect products solve this problem in very special cases. Although the general problem is far from being solved, the classes of groups that can be built up this way are of interest.
To illustrate, suppose that we use only abelian groups as building blocks. Starting with an abelian group G0, we construct G1 ⊇ G0 such that G0 ![]() G1 and G1/G0 is abelian. Next, we extend G1 to obtain G2 ⊇ G1 such that G1
G1 and G1/G0 is abelian. Next, we extend G1 to obtain G2 ⊇ G1 such that G1 ![]() G2 and G2/G1 is abelian. After n steps, we have a chain
G2 and G2/G1 is abelian. After n steps, we have a chain
G = 389Gn ⊇ Gn−1 ⊇ ![]() ⊇ G1 ⊇ G0,
⊇ G1 ⊇ G0,
where Gi ![]() Gi+1 and Gi+1/Gi is abelian for each i. Such a group G is called solvable, and the theory of these groups is successful in the following sense: The class of solvable groups is large (it contains all finite groups of odd order), but at the same time, many theorems are true for all solvable groups but do not hold in general. We investigate solvable groups in Section 9.2.
Gi+1 and Gi+1/Gi is abelian for each i. Such a group G is called solvable, and the theory of these groups is successful in the following sense: The class of solvable groups is large (it contains all finite groups of odd order), but at the same time, many theorems are true for all solvable groups but do not hold in general. We investigate solvable groups in Section 9.2.
If we use simple groups as building blocks in this way, the resulting groups are those studied in Section 9.1. In this case, the above chain of subgroups is called a composition series for G, and the famous Jordan–Hö lder theorem asserts that G uniquely determines the series of groups Gn/Gn−1, Gn−1/Gn−2, . . ., G1/G0, G0. This leads to the useful notion of the composition length of a group.
Section 9.3 deals with somewhat more specialized central series and begins the study of finite nilpotent groups. These groups are characterized as the groups that are the direct product of their Sylow subgroups, equivalently if every Sylow subgroup is normal. In addition, the Frattini subgroup is defined for every finite group and shown to be nilpotent.
Much of what we do in this chapter is concerned with groups G that admit a chain of subgroups with certain nice properties. A subnormal series for G is a chain
G = G0 ⊇ G1 ⊇ G2 ⊇ ![]() ⊇ Gn = {1}
⊇ Gn = {1}
of subgroups of G such that Gi+1 ![]() Gi for each i. The factor groups Gi/Gi+1 are called the factors of the subnormal series. Note that we do not insist that the subgroups Gi are normal in G. Moreover, by possibly deleting some of the groups Gi, we clearly may assume that Gi ≠ Gi+1 for each i.
Gi for each i. The factor groups Gi/Gi+1 are called the factors of the subnormal series. Note that we do not insist that the subgroups Gi are normal in G. Moreover, by possibly deleting some of the groups Gi, we clearly may assume that Gi ≠ Gi+1 for each i.
Example 1. G ⊇ {1} is a subnormal series for any group G. The only factor is G.
Example 2. A4 ⊃ K ⊃ H ⊃ ε is a subnormal series for A4, we have K = {ε, (12)(34), (13)(24), (14)(23)} and H = {ε, (12)(34)}. The factors are C3, C2, and C2 in order. Note that H is not normal in A4.
The most interesting cases are the groups that admit a subnormal series in which every factor is abelian or every factor is simple. We investigate the first case in Section 9.2; the second calls for another definition.
If G is a group, a subnormal series G = G0 ⊃ G1 ⊃ ![]() ⊃ Gn = {1} is called a composition series for G if each factor Gi/Gi+1 is simple. In this case, the factors Gi/Gi+1 are called composition factors of G, and the integer n is called the length of the composition series. If G = {1}, we say that G has a composition series of length 0.
⊃ Gn = {1} is called a composition series for G if each factor Gi/Gi+1 is simple. In this case, the factors Gi/Gi+1 are called composition factors of G, and the integer n is called the length of the composition series. If G = {1}, we say that G has a composition series of length 0.
Example 3. The simple groups are those with a composition series of length 1.
Example 4. Every finite group G has a composition series. This holds by definition if G = {1}. If G ≠ {1}, write G = G0 and choose a maximal normal subgroup G1 of G0 (it exists because G is finite). Then G0/G1 is simple by Theorem 6 §8.1. If G1 ≠ {1}, choose a maximal normal subgroup G2 of G1 and continue in this way. The series G = G0⊃ G1 ⊃ G2 ⊃ ![]() must reach {1} eventually because G is finite, so it is a composition series.
must reach {1} eventually because G is finite, so it is a composition series.
The converse of Example 4 is false: Any infinite simple group has a composition series of length 1. However, the converse does hold for abelian groups.
Example 5. An abelian group G has a composition series if and only if G is finite. Indeed, if G = G0 ⊃ G1 ⊃ ![]() ⊃ Gn = {1} is a composition series, each composition factor Gi/Gi+1 is a simple abelian group and so is finite. Hence (Exercise 11), |G| = |G/G1||G1/G2|
⊃ Gn = {1} is a composition series, each composition factor Gi/Gi+1 is a simple abelian group and so is finite. Hence (Exercise 11), |G| = |G/G1||G1/G2| ![]() |Gn−1/Gn| is also finite.
|Gn−1/Gn| is also finite.
The finite abelian groups are not the only ones having all composition factors abelian. Theorem 8 §8.2 shows that every finite p-group has this property:
Example 6. If p is a prime, each finite p -group has a composition series in which every composition factor is isomorphic to Cp.
A group may have several different composition series. For example, let G be a cyclic group of order 12 and, for each divisor d of 12, let Hd be the unique subgroup of G of order d. Then G has three composition series. These series, along with their composition factors, are
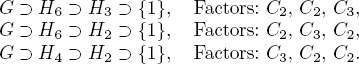
Note that the length is 3 in each case and the factors are also the same except for the order in which they appear. Hence, these series are all equivalent in the following sense: Two composition series for a group are said to be equivalent if they have the same length and the composition factors can be paired in such a way that corresponding factors are isomorphic. This is clearly an equivalence relation on the set of all composition series of a group G (assuming that there is one). The remarkable thing is that any two composition series for G are equivalent. This is the most important theorem in this section.
Theorem 1. Jordan–Hölder Theorem. If a group has a composition series, any two composition series are equivalent.
We will give the proof at the end of this section.
If a group G has a composition series, it uniquely determines the length of the series and the composition factors (including multiplicities). Hence, we can speak of the composition length of the group G, denoted lengthG, and of the composition factors of G.
Composition series were first discussed by Camille Jordan. In 1869, he showed (for groups of permutations) that the orders of the composition factors are the same for every composition series of the group. However, it was not until 20 years later, after the abstract definition of a group had been given, that Otto H ölder observed that the group uniquely determines the composition factors themselves and that they are the same in any composition series.
Example 7. If n ≥ 5, then Sn ⊃ A5 ⊃ {ε} is a composition series because An is simple (Theorem 8 §2.8). Hence, Sn has length 2 and the composition factors are C2 ≅ Sn/An and An. If n = 4, we get a composition series
S4 ⊃ A4 ⊃ K ⊃ H ⊃ {ε},
where K = {ε, (12)(34), (13)(24), (14)(23)} and H = {ε, (12)(34)}. Hence, S4 has length 4 and the composition factors are C2, C3, C2, and C2.
The Jordan–Hölder theorem is a type of unique factorization theorem. In the following corollary, we use it to give another proof that the factorization of an integer n into primes is unique. Here, the composition factors play the role of primes.
Corollary. The factorization of an integer n ≥ 2 into primes is unique.
Proof. Let n = p1p2 ![]() pr, where pi are (not necessarily distinct) primes. If
pr, where pi are (not necessarily distinct) primes. If ![]() is a cyclic group of order n, then
is a cyclic group of order n, then
![]()
is a composition series for G because the factors are ![]() (Indeed,
(Indeed, ![]() for each k by Theorem 5 §2.4.) Since any other factorization of n into primes must yield the same composition factors, it follows that n uniquely determines the number r = lengthG and the primes pi.
for each k by Theorem 5 §2.4.) Since any other factorization of n into primes must yield the same composition factors, it follows that n uniquely determines the number r = lengthG and the primes pi.
If K ![]() G and G/K ≅ H, the group G is called an extension of K by H. So if
G and G/K ≅ H, the group G is called an extension of K by H. So if
G = G0 ⊃ G1 ⊃ ![]() ⊃ Gr = {1}
⊃ Gr = {1}
is a composition series for G, then each Gi is an extension of Gi+1 by a simple group. Thus, each finite group G is the result of a finite number of extensions by finite simple groups, and the Jordan–Hö lder theorem shows that G uniquely determines the simple groups used (up to order). Moreover, we know all the finite simple groups (see the discussion at the end of Section 2.8), so the complete description of all finite groups comes down to the extension problem: For a simple group H, describe all extensions of a given group G by H. This is a very difficult task.
We are going to prove that subgroups and homomorphic images of groups with a composition series again have composition series. The proof requires the follow-ing technical lemma that gives important information about subnormal series in general and will be referred to again later. For composition series, we use it to deduce some important properties of the length of a group and prove the Jordan–Hölder theorem itself.
Lemma 1. Let G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn = {1} be a subnormal series for the group G and let K
⊇ Gn = {1} be a subnormal series for the group G and let K ![]() G.
G.
1. K = K ∩ G0 ⊇ K ∩ G1 ⊇ ![]() ⊇ K ∩ Gn = {1} is a subnormal series for K, and the factor (K ∩ Gi)/(K ∩ Gi+1) is isomorphic to a normal subgroup of Gi/Gi+1 for each i.
⊇ K ∩ Gn = {1} is a subnormal series for K, and the factor (K ∩ Gi)/(K ∩ Gi+1) is isomorphic to a normal subgroup of Gi/Gi+1 for each i.
2. G/K = (KG0)/K ⊇ (KG1)/K ⊇ ![]() ⊇ (KGn)/K = {K} is a subnormal series for G/K, and the factor [(KGi)/K]/[(KGi+1)/K] is a homomorphic image of Gi/Gi+1 for each i.
⊇ (KGn)/K = {K} is a subnormal series for G/K, and the factor [(KGi)/K]/[(KGi+1)/K] is a homomorphic image of Gi/Gi+1 for each i.
Proof. We leave to the reader the verification that the series are subnormal.
(1) Define α: K ∩ Gi → Gi/Gi+1 by α(x) = xGi+1. This is clearly a group homomorphism and ker α = {x ![]() K ∩ Gi
K ∩ Gi ![]() x
x ![]() Gi+1} = K ∩ Gi+1. Hence, it remains to prove that α(K ∩ Gi)
Gi+1} = K ∩ Gi+1. Hence, it remains to prove that α(K ∩ Gi) ![]() (Gi/Gi+1). But if x
(Gi/Gi+1). But if x ![]() K ∩ Gi and y
K ∩ Gi and y ![]() Gi, then
Gi, then
(yGi+1)α(x)(yGi+1)−1 = (yxy−1)Gi+1 = α(yxy−1) ![]() α(K ∩ Gi)
α(K ∩ Gi)
because yxy−1 ![]() (yKy−1) ∩ Gi = K ∩ Gi.
(yKy−1) ∩ Gi = K ∩ Gi.
(2) Since KGi+1 ![]() KGi (Exercise 15 §8.1), the third isomorphism theorem (Theorem 7 §8.1) shows that
KGi (Exercise 15 §8.1), the third isomorphism theorem (Theorem 7 §8.1) shows that
![]()
To show that (KGi)/(KGi+1) is an image of Gi/Gi+1, define
![]() by α(xGi+1) = xKGi+1 for all x
by α(xGi+1) = xKGi+1 for all x ![]() Gi.
Gi.
This is well defined because xGi+1 = yGi+1 implies that y−1x ![]() Gi+1 ⊆ KGi+1. It is clearly a group homomorphism, and (as K
Gi+1 ⊆ KGi+1. It is clearly a group homomorphism, and (as K ![]() G) it is onto because
G) it is onto because
kxKGi+1 = x(x−1kx)KGi+1 = xKGi+1 = α(xGi+1)
holds for all k ![]() K and x
K and x ![]() Gi.
Gi.
Now suppose that G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn = {1} is a composition series for G. If K
⊇ Gn = {1} is a composition series for G. If K ![]() G, the subnormal series for K and G/K in Lemma 1 are also composition series. Indeed, in both cases, the factors are isomorphic to either normal subgroups or images of the simple groups Gi/Gi+1 and so are all either simple or {1}. Hence, after we eliminate equalities, these series become composition series for K and G/K, respectively, each with factors from G. This proves part of Theorem 2.
G, the subnormal series for K and G/K in Lemma 1 are also composition series. Indeed, in both cases, the factors are isomorphic to either normal subgroups or images of the simple groups Gi/Gi+1 and so are all either simple or {1}. Hence, after we eliminate equalities, these series become composition series for K and G/K, respectively, each with factors from G. This proves part of Theorem 2.
Theorem 2. Let G be a group and let K ![]() G. Then G has a composition series if and only if both K and G/K have composition series. Moreover, in this case,
G. Then G has a composition series if and only if both K and G/K have composition series. Moreover, in this case,
1. length G = length K + length G/K.
2. The composition factors of G are exactly those of K and G/K.
3. G has a composition series containing K.
Proof. If G has a composition series, we have already seen that this is true of K and G/K. Conversely, suppose
K = K0 ⊃ K1 ⊃ ![]() ⊃ Km = {1} and
⊃ Km = {1} and ![]()
are composition series for K and G/K. Because GiGi+1 ≅ Gi/KGi+1/K, the series
G = G0 ⊃ G1 ⊃ ![]() ⊃ Gr = K = K0 ⊃ K1 ⊃
⊃ Gr = K = K0 ⊃ K1 ⊃ ![]() ⊃ Km = {1}
⊃ Km = {1}
is a composition series for G. Now (1)–(3) are apparent.
Corollary 1. If θ: G → H is a homomorphism, then G has a composition series if and only if both ker θ and θ(G) have composition series. In this case,
lengthG = length ker θ + lengthθ(G).
Proof. Since G/ker θ ≅ θ(G), Theorem 2 applies with K = ker θ.
Corollary 2. If G1, G2, ![]() , Gn are groups, then G1 × G2 ×
, Gn are groups, then G1 × G2 × ![]() × Gn has a composition series if and only if the same is true of each Gi. In this case,
× Gn has a composition series if and only if the same is true of each Gi. In this case,
length(G1 × G2 × ![]() × Gn) = lengthG1 + lengthG2 +
× Gn) = lengthG1 + lengthG2 + ![]() + lengthGn.
+ lengthGn.
Solution. We prove it for n = 2, and then the general case follows by induction. Define θ: G1 × G2 → G2 by θ(g1, g2) = g2 for all g1 ![]() G1 and g2
G1 and g2 ![]() G2. Then θ is a homomorphism, ker θ = G1 × {1} ≅ G1, and θ(G1 × G2) = G2. Use Corollary 1.
G2. Then θ is a homomorphism, ker θ = G1 × {1} ≅ G1, and θ(G1 × G2) = G2. Use Corollary 1.
Example 8. Let G be an abelian group of order ![]() where pi are distinct primes. Show that lengthG = n1 + n2 +
where pi are distinct primes. Show that lengthG = n1 + n2 + ![]() + nr.
+ nr.
Solution. Proceed by induction on |G|. If |G| = 1, it is clear. In general, let K be a maximal (normal) subgroup of G. Then |G/K| is a prime divisor of |G|, say |G/K| = p1. Hence, ![]() so induction and Theorem 2 give
so induction and Theorem 2 give
![]()
We conclude this section with a proof of the Jordan–Hölder theorem. The proof requires the following lemma.
Lemma 2. Let G be a group and let H and K be distinct maximal normal subgroups of G. Then H ∩ K is maximal normal in both H and K. Moreover,
![]() and
and ![]()
Proof. We first claim that KH = G. Indeed, H ⊆ KH ![]() G and K ⊆ KH
G and K ⊆ KH ![]() G, so if KH ≠ G, the fact that H and K are maximal normal in G implies that H = KH = K, contrary to assumption. Hence, KH = G, so the second isomorphism theorem (Theorem 1 §8.1) gives GK = KHK ≅ HH ∩ K. Because G/K is simple, this shows that K ∩ H is maximal normal in H. The rest is proved in the same way.
G, so if KH ≠ G, the fact that H and K are maximal normal in G implies that H = KH = K, contrary to assumption. Hence, KH = G, so the second isomorphism theorem (Theorem 1 §8.1) gives GK = KHK ≅ HH ∩ K. Because G/K is simple, this shows that K ∩ H is maximal normal in H. The rest is proved in the same way.
Proof of the Jordan–Hölder Theorem. Suppose the group G has a composition series
(1) ![]()
of length n. We show by induction on n that every composition series
(2) ![]()
for G is equivalent to series (1). If n = 1, then G is simple, so G1 = {1} = H1 and the theorem holds. So assume that n ≥ 2 and that the theorem holds for all groups with a composition series of length less than n. In particular, it holds for G1 because G1 ⊃ G2 ⊃ ![]() ⊃ Gn = {1} has length n − 1. If it happens that H1 = G1, then G1 ⊃ H2 ⊃
⊃ Gn = {1} has length n − 1. If it happens that H1 = G1, then G1 ⊃ H2 ⊃ ![]() ⊃ Hm = {1} is another composition series for G1 and so is equivalent to G1 ⊃ G2 ⊃
⊃ Hm = {1} is another composition series for G1 and so is equivalent to G1 ⊃ G2 ⊃ ![]() ⊃ Gn = {1} by induction and the theorem follows.
⊃ Gn = {1} by induction and the theorem follows.
So assume that H1 ≠ G1 and let H1 ∩ G1 = L0 ⊃ L1 ⊃ ![]() ⊃ Ls = {1} be a composition series for H1 ∩ G1 by Theorem 2 as H1 ∩ G1
⊃ Ls = {1} be a composition series for H1 ∩ G1 by Theorem 2 as H1 ∩ G1 ![]() G. Now consider the following series for G:
G. Now consider the following series for G:
(3) ![]()
(4) ![]()
As H1 ≠ G1, Lemma 2 asserts that H1 ∩ G1 is maximal normal in each of H1 and G1, so both (3) and (4) are composition series for G. Moreover, G/G1 ≅ H1/(H1 ∩ G1) and G/H1 ≅ G1/(H1 ∩ G1) by Lemma 2, so (3) and (4) are equivalent; denote this as (3) ![]() (4). Note that this equivalence holds even if s = 0, that is, if H1 ∩ G1 = {1}.
(4). Note that this equivalence holds even if s = 0, that is, if H1 ∩ G1 = {1}.
Now G1 ⊃ G2 ⊃ ![]() ⊃ Gn = {1} and G1 ⊃ (H1 ∩ G1) ⊃ L1 ⊃
⊃ Gn = {1} and G1 ⊃ (H1 ∩ G1) ⊃ L1 ⊃ ![]() ⊃ Ls = {1} are composition series for G1 and so are equivalent by induction. This implies that (1)
⊃ Ls = {1} are composition series for G1 and so are equivalent by induction. This implies that (1) ![]() (3) and also that n − 1 = s + 1. But then the composition series H1 ⊃ (H1 ∩ G1) ⊃ L1 ⊃
(3) and also that n − 1 = s + 1. But then the composition series H1 ⊃ (H1 ∩ G1) ⊃ L1 ⊃ ![]() ⊃ Ls = {1} has length n − 1 and so (again by induction) is equivalent to H1 ⊃ H2 ⊃
⊃ Ls = {1} has length n − 1 and so (again by induction) is equivalent to H1 ⊃ H2 ⊃ ![]() ⊃ Hm = {1}. This in turn implies that (2)
⊃ Hm = {1}. This in turn implies that (2) ![]() (4). Piecing these equivalent series together gives (1)
(4). Piecing these equivalent series together gives (1) ![]() (3)
(3) ![]() (4)
(4) ![]() (2), which proves the Jordan–Hölder theorem.
(2), which proves the Jordan–Hölder theorem.
Exercises 9.1
1. In each case, find the length of the group and exhibit the composition factors.
(a) C8 (b) C12 (c) D4 (d) A4 (e) Q (see Section 2.8)
2. If n ≥ 1 and p is prime, show that ![]() has exactly one composition series.
has exactly one composition series.
3. Find all composition series for
a. C24
b. C30
4. Find two nonisomorphic finite groups with identical composition factors.
5. Find all composition series for C4 × C2.
6. If ![]() find the length of Dn. [Hint: Example 8.]
find the length of Dn. [Hint: Example 8.]
7. Find a composition series for D16 that contains the center Z(D16) and find one that does not contain Z(D16).
8.
a. For each m ≥ 2, find a group of length m.
b. For each m ≥ 2, find a group of length 1 with a subgroup of length m.
9. Let G = K0 × K1 × ![]() × Kr, where each Ki is simple. Show that the groups Ki are the composition factors of G.
× Kr, where each Ki is simple. Show that the groups Ki are the composition factors of G.
10. Describe the groups of length 2 by using Exercise 6 §8.1.
11. Let G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn= {1} be any subnormal series. If each factor Gi/Gi+1 is finite, show that G is finite and that |G| = |G0/G1| · |G1/G2|
⊇ Gn= {1} be any subnormal series. If each factor Gi/Gi+1 is finite, show that G is finite and that |G| = |G0/G1| · |G1/G2| ![]() |Gn−1/Gn|.
|Gn−1/Gn|.
12. If p is a prime, show that a finite group is a p-group if and only if all its composition factors are isomorphic to Cp.
13. Suppose that G is a group with a composition series. Show that any subnormal series G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn ={1} can be refined (by inserting groups if necessary) to a composition series for G.
⊇ Gn ={1} can be refined (by inserting groups if necessary) to a composition series for G.
14. Suppose that G has a composition series with no two factors isomorphic.
a. Show that no two proper normal subgroups of G are isomorphic. [Hint: If H ![]() G and K
G and K ![]() G, find a composition series through HK, H, and H ∩ K and one through HK, K, and H ∩ K. Use Exercise 13.]
G, find a composition series through HK, H, and H ∩ K and one through HK, K, and H ∩ K. Use Exercise 13.]
b. Show that every normal subgroup of G is characteristic in G.
15. Let ![]() where the pi are distinct primes and each ni ≥ 1.
where the pi are distinct primes and each ni ≥ 1.
a. Show that Cn has exactly r maximal normal subgroups.
b. If m = n1 + n2 + ![]() + nr, show that Cn has m ! n1 ! n2 !
+ nr, show that Cn has m ! n1 ! n2 ! ![]() nr ! composition series. [Hint: induct on m.]
nr ! composition series. [Hint: induct on m.]
16. Prove the Zassenhaus lemma:100 Let H1 ![]() H and K1
H and K1 ![]() Kbe subgroups of a group G. Then H1(H ∩ K1)
Kbe subgroups of a group G. Then H1(H ∩ K1) ![]() H1(H ∩ K), K1(H1 ∩ K)
H1(H ∩ K), K1(H1 ∩ K) ![]() K1(H ∩ K), and we have H1(H ∩ K)H1(H ∩ K1) ≅ K1(H ∩ K)K1(H1 ∩ K). [Hint: Each group is isomorphic to H ∩ K(H1 ∩ K)(H ∩ K1) by Theorem 4 §2.10.]
K1(H ∩ K), and we have H1(H ∩ K)H1(H ∩ K1) ≅ K1(H ∩ K)K1(H1 ∩ K). [Hint: Each group is isomorphic to H ∩ K(H1 ∩ K)(H ∩ K1) by Theorem 4 §2.10.]
17. Prove the Schreier refinement theorem:101 Two subnormal series G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn ={1} and H = H0 ⊇ H1 ⊇
⊇ Gn ={1} and H = H0 ⊇ H1 ⊇ ![]() ⊇ Hm = 1 can be refined (by inserting groups) in such a way that the resulting series are equivalent. [Hint:
⊇ Hm = 1 can be refined (by inserting groups) in such a way that the resulting series are equivalent. [Hint:
Gi = Gi+1(Gi ∩ H0) ⊇ Gi+1(Gi ∩ H1) ⊇ ![]() ⊇ Gi+1(Gi ∩ Hm) = Gi+1.
⊇ Gi+1(Gi ∩ Hm) = Gi+1.
Do a similar construction with the Hj and use the Zassenhaus lemma.]
18. Use the Schreier refinement theorem to prove the Jordan–Hö lder theorem.
In Section 9.1, we were concerned with groups that admit a composition series, that is, a subnormal series in which all the factors are simple. Although those groups are of interest, we obtain an even more important class of groups when the factors are required to be abelian rather than simple.
A group G is called a solvable group102 if there exists a subnormal series
G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn = {1}
⊇ Gn = {1}
such that each factor Gi/Gi+1 is abelian. Such a series is called a solvable series for G. Note that {1} is solvable.
Example 1. Every abelian group G is solvable because G ⊇ {1} is a solvable series.
Example 2. If p is a prime, every finite p -group is solvable. In fact, it has a composition series in which each factor is isomorphic to Cp (Theorem 8 §8.2).
Example 3. Dn is solvable for each n. Indeed, Dn has a cyclic subgroup H of index 2, so H ![]() Dn and Dn ⊇ H ⊇ {1} is a solvable series.
Dn and Dn ⊇ H ⊇ {1} is a solvable series.
Example 4. S4 is solvable because S4 ⊇ A4 ⊇ K ⊇ {ε} is a solvable series, where K = {ε, (12)(34), (13)(24), (14)(23)}.
Example 5. If p and q are primes, show that any group of order pq is solvable.
Solution. Because G is not simple by the Sylow theorems (Example 5 §8.4), let K ≠ {1} be a proper normal subgroup. Then |K| = p or |K| = q; either way G ⊃ K ⊃ {1} is a solvable series with factors Cp and Cq.
Suppose that G1 is an abelian group. It is difficult to describe how to construct all groups G2 such that G1 ![]() G2 and G2/G1 is abelian. Nonetheless, suppose we carry out this construction and then repeat it to construct a group G3 such that G2
G2 and G2/G1 is abelian. Nonetheless, suppose we carry out this construction and then repeat it to construct a group G3 such that G2 ![]() G3 and G3/G2 is abelian. If we continue this procedure, each group constructed is clearly solvable, and we can obtain every solvable group in this way—constructed from the bottom up, as it were. Viewing solvable groups in this way is useful, but an analogous top–down construction is actually more important. It is based on the derived subgroup introduced in Section 2.9.
G3 and G3/G2 is abelian. If we continue this procedure, each group constructed is clearly solvable, and we can obtain every solvable group in this way—constructed from the bottom up, as it were. Viewing solvable groups in this way is useful, but an analogous top–down construction is actually more important. It is based on the derived subgroup introduced in Section 2.9.
Recall that an element of the form aba−1b−1 in a group G is called a commutator, denoted [a, b]. The set G′ of all products of commutators is a subgroup, called the derived subgroup of G, and has the following properties (Theorem 3 §2.9):
1. G′ ![]() G and G/G′ is abelian.
G and G/G′ is abelian.
2. If K ![]() G and G/K is abelian, then G′ ⊆ K.
G and G/K is abelian, then G′ ⊆ K.
For a group G, repeatedly taking the derived subgroup leads to a subnormal series of subgroups G⊇ G′ ⊇ G′′ ⊇ G′′′ ⊇ ![]() in which each factor is abelian. There is a standard notation for these subgroups. Given a group G, construct subgroups G(0), G(1), G(2),
in which each factor is abelian. There is a standard notation for these subgroups. Given a group G, construct subgroups G(0), G(1), G(2), ![]() of G as follows:
of G as follows:
1. Define G(0) = G.
2. If G(i) has been constructed for i ≥ 0, define G(i+1) = [G(i)]′.
Thus, G(1) = G′, G(2) = G′′, G(3) = G′′′, and so on. Furthermore, G(i+1) ![]() G(i) for each i and the subnormal series
G(i) for each i and the subnormal series
G = G(0)⊇ G(1) ⊇ G(2) ⊇ ![]()
is called the derived series for G. Note that G(i)/G(i+1) is abelian for each i by Theorem 3 §2.9. The groups G(i) are called the higher derived subgroups of G, and they are actually normal in G as the next theorem shows. The proof requires the following lemma; we leave the proof as Exercise 8.
Lemma 1. Let G denote a group and let H be a subgroup.
1. If α: G → G is a homomorphism, then α(G′) ⊆ G′.
2. G′ ⊆ H if and only if H ![]() G and G/H is abelian.
G and G/H is abelian.
3. If H ⊆ G is a subgroup, then H′ ⊆ G′.
Theorem 1. If G is a group, we have G(i) ![]() G for all i ≥ 0.
G for all i ≥ 0.
Proof. We use induction on i ≥ 0. It is clear if i = 0, so assume inductively that G(i) ![]() G for some i. If a
G for some i. If a ![]() G then σa(G(i)) = G(i), where σa is the inner automorphism of G determined by a. But then Lemma 1 gives
G then σa(G(i)) = G(i), where σa is the inner automorphism of G determined by a. But then Lemma 1 gives
σa[G(i+1)] = σa[(G(i))′] ⊆ (G(i))′ = G(i+1).
This shows that G(i+1) ![]() G and so completes the induction.
G and so completes the induction.
The solvable groups G are just those for which the derived series reaches {1}.
Theorem 2. A group G is solvable if and only if G(n) = {1} for some n ≥ 1.
Proof. If G(n) = {1}, then
G = G(0) ⊇ G(1) ⊇ G(2) ⊇ ![]() ⊇ G(n) = {1}
⊇ G(n) = {1}
is a solvable series for G because G(i)/G(i+1) = G(i)/[G(i)]′ is abelian for each i. Conversely, let G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn = {1} be a solvable series for G. It suffices to show that G(i) ⊆ Gi holds for each i. This is clear if i = 0, so assume that G(i) ⊆ Gi for some i ≥ 0. As Gi/Gi+1 is abelian, we have
⊇ Gn = {1} be a solvable series for G. It suffices to show that G(i) ⊆ Gi holds for each i. This is clear if i = 0, so assume that G(i) ⊆ Gi for some i ≥ 0. As Gi/Gi+1 is abelian, we have ![]() Hence,
Hence,
![]()
by Lemma 1, which completes the induction.
If G is solvable, then G(i) ⊃ G(i+1) is strictly for all i by Corollary 1 of Theorem 3.
Theorem 2 provides a quick method of establishing several basic properties of solvable groups. We begin with the following result.
Theorem 3. Every subgroup and image of a solvable group is again solvable.
Proof. Suppose that G is solvable and let G(n) = {1}. If H is a subgroup of G, it suffices to show that H(i) ⊆ G(i) for each i. This follows by induction: It is clear when i = 0, and if H(i) ⊆ G(i), then Lemma 1 gives
H(i+1) = [H(i)]′ ⊆ [G(i)]′ = G(i+1).
Now let α: G → K be an onto group homomorphism. It suffices to show that K(i) ⊆ α[G(i)] for each i. This is clear if i = 0 because α is onto, so assume that K(i) ⊆ α(G(i)). Then, given x and y in K(i), write x = α(a) and y = α(b), where a, b ![]() G(i). Hence,
G(i). Hence,
[x, y] = [α(a), α(b)] = α([a, b]) ![]() α(G(i+1)),
α(G(i+1)),
so K(i+1) ⊆ α(G(i+1)) because K(i+1) = (K(i))′.
Corollary 1. If H ≠ {1} is a subgroup of a solvable group G, then H′ ≠ H.
Proof. If H′ = H, then H(2) = [H′]′ = H′ = H and an induction shows that H(i) = H ≠ {1} holds for each i. As H is solvable by Theorem 3, this result contradicts Theorem 2.
Corollary 2. A simple group is solvable if and only if it is abelian (of prime order).
Proof. Let G be solvable. If G is simple, then either G′ = {1} (so G is abelian) or G′ = G, (contradicting Corollary 1). The converse is clear.
Example 6. If n ≥ 5, the symmetric group Sn is not solvable. For if Sn were solvable, An would be solvable by Theorem 3 so, as An is simple, Corollary 2 would imply that An is abelian, which is not the case. Hence, Sn is not solvable.
Example 6 explains the origin of the term solvable. A classical problem in the theory of equations was to find a formula for the roots of a real polynomial xn + an−1xn−1 + ![]() + a1x + a0 in terms of the coefficients ai. If n = 2, the solution is the famous quadratic formula:
+ a1x + a0 in terms of the coefficients ai. If n = 2, the solution is the famous quadratic formula: ![]() In general, such a formula should give the roots in terms of the coefficients ai using only arithmetic operations and the extraction of roots. Such formulas were found for n = 3 and n = 4, but the case n = 5 proved to be difficult. Call a polynomial f solvable if such a formula exists. It will be shown in Chapter 10 that f is solvable if and only if a certain group (called the Galois group of f) is a solvable group. For example, the polynomial x5 − 6x + 2 has Galois group S5 (Example 1 §10.3) and so cannot be solvable. Incidentally, the first proof that a nonsolvable polynomial exists was given in 1824 by the young Norwegian mathematician Niels Henrik Abel, building on the work of Paolo Ruffini.
In general, such a formula should give the roots in terms of the coefficients ai using only arithmetic operations and the extraction of roots. Such formulas were found for n = 3 and n = 4, but the case n = 5 proved to be difficult. Call a polynomial f solvable if such a formula exists. It will be shown in Chapter 10 that f is solvable if and only if a certain group (called the Galois group of f) is a solvable group. For example, the polynomial x5 − 6x + 2 has Galois group S5 (Example 1 §10.3) and so cannot be solvable. Incidentally, the first proof that a nonsolvable polynomial exists was given in 1824 by the young Norwegian mathematician Niels Henrik Abel, building on the work of Paolo Ruffini.
Theorem 4 gives a useful way to show that a group is solvable.
Theorem 4. If K ![]() G, then G is solvable if and only if both K and G/K are solvable.
G, then G is solvable if and only if both K and G/K are solvable.
Proof. Assume that K and G/K are solvable and let
![]() and
and ![]()
be solvable series. Then
G = G0 ⊇ G1 ⊇ ![]() ⊇ Gr = K = K0 ⊇ K1 ⊇
⊇ Gr = K = K0 ⊇ K1 ⊇ ![]() ⊇ Km = {1}
⊇ Km = {1}
is a subnormal series for G and the factors are abelian because GiGi+1 ≅ Gi/KGi+1/K for each i. Hence, G is solvable. The converse follows by Theorem 3.
Example 7. If G1, G2, ![]() , Gn are groups, then G1 × G2 ×
, Gn are groups, then G1 × G2 × ![]() × Gn is solvable if and only if the same is true of each Gi.
× Gn is solvable if and only if the same is true of each Gi.
Solution. By induction, it suffices to prove it for n = 2. Let θ: G1 × G2 → G2 be the projection given by θ(g1, g2) = g2. Then (G1 × G2)/ker θ ≅ θ(G1 × G2) = G2 and ker θ = G1 × {1} ≅ G1 are both solvable, so Theorem 4 applies.
The above theorems are valid for arbitrary groups. We now give some conditions equivalent to solvability in a finite group.
Theorem 5. The following conditions are equivalent for a finite group G.
1. G is solvable.
2. The composition factors of G are all abelian.
3. H′ ≠ H for every subgroup H ≠ {1} of G.
Proof. Note first that G has a composition series because it is finite.
(1) ⇒ (2). Each composition factor is simple and solvable (Theorem 3), and so is abelian by Corollary 2 of Theorem 3.
(2) ⇒ (3). Any composition series for G is a solvable series by (2).
(3) ⇒ (1). The derived series G = G(0)⊇ G(1) ⊇ G(2) ⊇ ![]() reaches {1} because G is finite and G(i) ⊃ (G(i))′ = G(i+1) for each i by (3).
reaches {1} because G is finite and G(i) ⊃ (G(i))′ = G(i+1) for each i by (3).
Example 8. Let R be any ring. If n ≥ 3, show that the group G of all invertible n × n matrices over R is not solvable.
Solution. Let Eij denote the n × n matrix with (i, j)-entry 1 and zeros elsewhere. Then EijEjk = Eik, whereas EijElk = 0 if j ≠ l. If I is the n × n identity matrix, this shows that I + Eij is in G whenever i ≠ j and that (I + Eij)−1 = I − Eij. Now let H be the subgroup of G generated by the matrices I + Eij, i ≠ j. If i, j, and k are distinct indices (they exist because n ≥ 3), compute
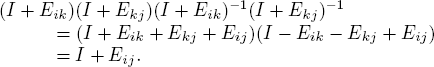
This shows that every generator of H is a commutator from H and hence H′ = H. Thus, G is not solvable by Corollary 1 of Theorem 3.
If F is a field, Example 8 shows that the general linear group GLn(F) of all n × n invertible matrices over F is not solvable if n ≥ 3. If F is finite, Theorem 5 shows that a nonabelian simple group is lurking among the composition factors of GLn(F). In fact, such a group exists even if F is infinite. The mapping A ![]() det A is an onto homomorphism GLn(F) → F* and the kernel is the special linear group SLn(F) of all matrices with determinant 1. It is not difficult to verify that the center of SLn(F) consists of all scalar matrices aI, where a
det A is an onto homomorphism GLn(F) → F* and the kernel is the special linear group SLn(F) of all matrices with determinant 1. It is not difficult to verify that the center of SLn(F) consists of all scalar matrices aI, where a ![]() F satisfies an = 1. The factor group
F satisfies an = 1. The factor group
![]()
is called the projective special linear group (of degree n) over F. These groups comprise another infinite family of finite, simple, nonabelian groups (in addition to the alternating groups An, n ≥ 5). The theorem was proved in 1870 by Camille Jordan for ![]() a prime and, in early 1900, Leonard Eugene Dickson proved it for all finite fields.
a prime and, in early 1900, Leonard Eugene Dickson proved it for all finite fields.
Theorem 6. Jordan–Dickson Theorem. If F is a finite field, then PSLn(F) is a finite nonabelian simple group for all n ≥ 2, except for ![]() and
and ![]()
The proof is beyond the scope of this book.103
The class of solvable groups is large. Of course, it contains all abelian groups, and a celebrated theorem of William Burnside asserts that every group of order pnqm is solvable, where p and q are primes. In a different direction, Georg Frobenius showed that every group of square-free order is solvable. In 1911, Burnside conjectured that every nonabelian finite simple group has even order, equivalently (Exercise 13) that every group of odd order is solvable. This conjecture remained an open question until 1963 when two American algebraists Walter Feit and John Thompson proved that it is true. The proof is 254 pages long and fills an entire issue of the Pacific Journal of Mathematics,104 and it is widely regarded as the best single paper in finite group theory. Thompson went on to classify all minimal finite simple groups, that is, those in which every proper subgroup is solvable, and played an important role in the classification of all finite simple groups. He was awarded the Fields Medal in 1970, the highest honor a mathematician can attain.
Even though the class of solvable groups is very large, many theorems are true for solvable groups that are not true of groups in general. One such theorem, a fundamental strengthening of the Sylow theorems in any solvable group, was first proved in 1928 by the British mathematician Philip Hall.
Theorem 7. Hall's Theorem. Let G be a group of order nm, where n and m are relatively prime. If G is solvable, then
1. G has a subgroup of order n and any two are conjugate.
2. If k|n, each subgroup of order k is contained in a subgroup of order n.
We omit the proof.105 Hall went on to develop the theory of finite solvable groups and influenced an entire generation of group theorists.
Exercises 9.2
1. Is Z(G)≠{1} for every solvable group G ≠ {1}? Support your answer.
2. If G is solvable, is N(H) ≠ H for each subgroup H ≠ G? Support your answer.
3. Is G′ abelian for every solvable group G? Support your answer.
4. Does every solvable group of order n have a subgroup of order m for each divisor m of n? Support your answer.
5. Give an example of a nonsolvable group in which every Sylow subgroup is abelian.
6. Show that a nonsolvable group of minimal order must be simple.
7. Suppose G has a solvable, maximal normal subgroup. Either prove G is solvable or give a counterexample.
8. Prove Lemma 1.
9. If |G| = p2q, p, q primes, show that G is solvable. [Hint: Exercise 14 §8.4.]
10. If |G| = p2q2, p, q primes, show that G is solvable. [Hint: Example 9 §8.4 and the preceding exercise.]
11.
a. Show that
![]()
is a solvable group for any field F.
b. Show that
![]()
is a solvable group for any field F.
12. If p and q are primes, show that every group of order pmqn is solvable if and only if the only simple groups of this type are the cyclic groups of order p or q. (Burnside proved that these statements are true.)
13. Show that every group of odd order is solvable if and only if every finite nonabelian simple group has even order. (These statements are true by Feit and Thompson.)
14. Find the composition length of a solvable group of order ![]() where pi are distinct primes. [Hint: Example 8 §9.1.]
where pi are distinct primes. [Hint: Example 8 §9.1.]
15. Show that a solvable group is finite if and only if it has a composition series.
16. Show that the following are equivalent for a group G.
(a) G is solvable. (b) G′ is solvable. (c) G/Z(G) is solvable.
17. If H ![]() G and K
G and K ![]() G show that G/(H ∩ K) is solvable if and only if the product (G/H) × (G/K) is solvable.
G show that G/(H ∩ K) is solvable if and only if the product (G/H) × (G/K) is solvable.
18. If Ki ![]() G for i = 1, 2,
G for i = 1, 2, ![]() , n, put K = K1 ∩ K2 ∩
, n, put K = K1 ∩ K2 ∩ ![]() ∩ Kn. If G/Ki is solvable for each i, show that G/K is solvable.
∩ Kn. If G/Ki is solvable for each i, show that G/K is solvable.
19. If H and K are solvable subgroups of G and K ![]() G, show that HK is solvable.
G, show that HK is solvable.
20.
a. If G is a finite group and Z(G/K) is nontrivial for all K ![]() G, K ≠ G, show that G is solvable.
G, K ≠ G, show that G is solvable.
b. Show that the converse of (a) is false for a finite group G.
21. If G ≠ 1 is solvable, show that
a. G has a nontrivial abelian factor group.
b. G has a nontrivial abelian normal subgroup.
22. Show that the following are equivalent for a nontrivial finite group G.
1. G is solvable.
2. Every nontrivial normal subgroup of G has a nontrivial abelian factor group.
3. Every nontrivial factor group of G has a nontrivial abelian normal subgroup.
23. If G is a finite group, define R = R(G) = ![]() {K
{K ![]() G
G ![]() G/K is solvable}.
G/K is solvable}.
a. Show that R = R(G) is the smallest normal subgroup of G such that G/R is solvable. [Hint: Exercise 18.]
b. Show that G is solvable if and only if R(G) = {1}.
c. If α: G→H is a group homomorphism, show that α[R(G)] ⊆ R(H). Hint: Consider {k ![]() α(k)
α(k) ![]() R(H)}.
R(H)}.
d. If H ⊆ G is a subgroup, show that R(H) ⊆ H ∩ R(G), with equality if H ![]() G.
G.
24. If G is a finite group, define S(G) = ∏ {K ![]() G
G ![]() K is solvable}.
K is solvable}.
a. Prove S(G) is the largest solvable, normal subgroup of G. [Hint: Exercise 19.]
b. Prove G is solvable if and only if S(G) = G.
c. If α: G→H is an onto group homomorphism, show that α[S(G)] ⊆ S(H).
d. If H ⊆ G is a subgroup, show that H ∩ S(G) ⊆ S(H), with equality if H ![]() G.
G.
e. Show that S(G/S) = {1}.
25. A group G is called polycyclic if it has a solvable series with every factor cyclic.
a. Show that every finite solvable group is polycyclic.
b. Show that every polycyclic group is finitely generated.
c. Show that every subgroup and homomorphic image of a polycyclic group is polycyclic. [Hint: Lemma 1 §9.1.]
d. If K ![]() G, show that G is polycyclic if and only if K and G/K are polycyclic.
G, show that G is polycyclic if and only if K and G/K are polycyclic.
e. Show that the following are equivalent for a group G. [Hint: Theorem 3 §7.2.]
i. G is polycyclic
ii. Every subgroup of G is solvable and finitely generated.
iii. Every normal subgroup of G is solvable and finitely generated.
26. A class ![]() of groups is called a subvariety if
of groups is called a subvariety if ![]() and each subgroup and ho-momorphic image of a group in
and each subgroup and ho-momorphic image of a group in ![]() is again in
is again in ![]() . Examples: abelian groups, p-groups for a fixed prime p and torsion groups (each element has finite order). If
. Examples: abelian groups, p-groups for a fixed prime p and torsion groups (each element has finite order). If ![]() is a subvariety, a group G is called
is a subvariety, a group G is called ![]() -solvable if there is a subnormal series G = G0 ⊃ G1 ⊃
-solvable if there is a subnormal series G = G0 ⊃ G1 ⊃ ![]() ⊃ Gn= {1} with Gi/Gi+1 in
⊃ Gn= {1} with Gi/Gi+1 in ![]() for each i. If G is a group and K
for each i. If G is a group and K ![]() G, show that G is
G, show that G is ![]() -solvable if and only if both K and G/K are
-solvable if and only if both K and G/K are ![]() -solvable. [Hint: Lemma 1 §9.1.]
-solvable. [Hint: Lemma 1 §9.1.]
27. A subvariety ![]() of groups (Exercise 26) is called a variety if, in addition, G × H is in
of groups (Exercise 26) is called a variety if, in addition, G × H is in ![]() whenever G and H are in
whenever G and H are in ![]() . Examples: abelian groups, p -groups for a fixed prime p, torsion groups, and
. Examples: abelian groups, p -groups for a fixed prime p, torsion groups, and ![]() -solvable groups, where
-solvable groups, where ![]() is any subvariety (by Exercise 26). If
is any subvariety (by Exercise 26). If ![]() is a variety and G is a finite group, the
is a variety and G is a finite group, the ![]() -derived subgroup of G is defined to be
-derived subgroup of G is defined to be ![]() is in
is in ![]() Let G denote a finite group. (a) Show that
Let G denote a finite group. (a) Show that ![]() and
and ![]() is in
is in ![]() (b) If K
(b) If K ![]() G, show that G/K is in
G, show that G/K is in ![]() if and only if
if and only if ![]() (c) If H is a subgroup of G, show that
(c) If H is a subgroup of G, show that ![]() [Hint: Lemma 2 §9.1.] (d) If α: G → H is a homomorphism of groups, show that
[Hint: Lemma 2 §9.1.] (d) If α: G → H is a homomorphism of groups, show that ![]()
28. If ![]() is a variety of finite groups, define
is a variety of finite groups, define ![]() and
and ![]() for each k ≥ 0. Let G denote a finite group. Show that (a) If α: G → H is a group homomorphism, then
for each k ≥ 0. Let G denote a finite group. Show that (a) If α: G → H is a group homomorphism, then ![]() for all k. (b)
for all k. (b) ![]() for each k. (c) G is
for each k. (c) G is ![]() -solvable if and only if
-solvable if and only if ![]() {1} for some k. (d) Every subgroup of a
{1} for some k. (d) Every subgroup of a ![]() -solvable group is
-solvable group is ![]() -solvable. (e) G is
-solvable. (e) G is ![]() -solvable if and only if
-solvable if and only if ![]() for all subgroups H≠{1} of G.
for all subgroups H≠{1} of G.
If G is a group, the definition of the derived subgroup G′ guarantees that G is abelian if and only if G′ = {1}. If the process of taking the derived subgroup is iterated, the derived series G = G(0)⊇ G(1) ⊇ G(2) ⊇ ![]() is obtained, and G is solvable if and only if this series (of normal subgroups of G) reaches {1} in a finite number of steps (Theorem 2 §9.2). Note that G(1) = G′. Now the center Z(G) plays an analogous role to G′ in the sense that G is abelian if and only if Z(G) = G. In view of this, an irresistible question arises: Is there a way to iterate the formation of the center so as to create a series {1} = Z0⊆ Z1 ⊆ Z2 ⊆
is obtained, and G is solvable if and only if this series (of normal subgroups of G) reaches {1} in a finite number of steps (Theorem 2 §9.2). Note that G(1) = G′. Now the center Z(G) plays an analogous role to G′ in the sense that G is abelian if and only if Z(G) = G. In view of this, an irresistible question arises: Is there a way to iterate the formation of the center so as to create a series {1} = Z0⊆ Z1 ⊆ Z2 ⊆ ![]() of normal subgroups of G (with Z(G) = Z1) such that G is solvable if and only if this series reaches G in a finite number of steps? The answer is yes and no. Yes, there is a natural way to define such a series. No, it does not characterize the solvable groups in this way. Rather, it characterizes a smaller class of groups called the nilpotent groups. In this section, we define these groups and show that the finite ones are precisely the finite groups that are isomorphic to the direct product of their Sylow subgroups.
of normal subgroups of G (with Z(G) = Z1) such that G is solvable if and only if this series reaches G in a finite number of steps? The answer is yes and no. Yes, there is a natural way to define such a series. No, it does not characterize the solvable groups in this way. Rather, it characterizes a smaller class of groups called the nilpotent groups. In this section, we define these groups and show that the finite ones are precisely the finite groups that are isomorphic to the direct product of their Sylow subgroups.
Central Series
If G is a group, define a series Z0(G), Z1(G), Z2(G), . . . of normal subgroups of G inductively as follows:
1. Take Z0(G) = {1}.
2. If Zi(G) ![]() G has been constructed, define Zi+1(G) the unique normal subgroup of G that contains Zi(G) and satisfies
G has been constructed, define Zi+1(G) the unique normal subgroup of G that contains Zi(G) and satisfies ![]()
Then Zi+1(G) ⊇ Zi(G) and Zi(G) ![]() Zi+1(G) for each i ≥ 0, and the series
Zi+1(G) for each i ≥ 0, and the series
{1} = Z0(G)⊆ Z1(G) ⊆ Z2(G) ⊆ ![]()
is called the ascending central series of G. Note that
![]()
The ascending central series may never reach G, even if G is solvable:
Example 1. Suppose Z(G) = {1} where G ≠ {1}—for example the solvable group S3. Then Z1(G) = Z(G) = {1}, so we have ![]() Hence, Z2(G) = {1}, and this process continues inductively to show that Zk(G) = {1} for all k.
Hence, Z2(G) = {1}, and this process continues inductively to show that Zk(G) = {1} for all k.
To characterize the groups G for which the ascending central series reaches G, it is useful to define a related descending central series. This requires a new notion. Recall that the derived subgroup G′ is generated by the commutators [a, b] = aba−1b−1 in G. We extend this idea as follows. If H and K are subgroups of a group G, define
![]()
to be the subgroup generated by the commutators [h, k], with h ![]() H and k
H and k ![]() K. Note that [h, k]−1 = [k, h] for all h
K. Note that [h, k]−1 = [k, h] for all h ![]() H and k
H and k ![]() K. Hence, [H, K] = [K, H], and this group consists of all products of commutators of the form [h, k] or [k, h], where h
K. Hence, [H, K] = [K, H], and this group consists of all products of commutators of the form [h, k] or [k, h], where h ![]() H and k
H and k ![]() K. In particular, [G, G] = G′. Lemma 1 collects several other useful facts about these subgroups.
K. In particular, [G, G] = G′. Lemma 1 collects several other useful facts about these subgroups.
Lemma 1. Let H, K, H1, and K1 be subgroups of a group G.
1. [H, K] = [K, H].
2. If H ⊆ H1 and K ⊆ K1, then [H, K] ⊆ [H1, K1].
3. If H ![]() G and K
G and K ![]() G, then [H, K]
G, then [H, K] ![]() G.
G.
4. H ![]() G if and only if [H, G] ⊆ H.
G if and only if [H, G] ⊆ H.
5. Suppose that K ⊆ H ⊆ G and K ![]() G. Then H/K ⊆ Z(G/K) if and only if [H, G] ⊆ K.
G. Then H/K ⊆ Z(G/K) if and only if [H, G] ⊆ K.
Proof. We prove (5) and leave the rest as Exercise 2. If ![]() , then we have hKgK = gKhK for all g
, then we have hKgK = gKhK for all g ![]() G and h
G and h ![]() H; that is, [h, g]
H; that is, [h, g] ![]() K. Hence, [H, G] ⊆ K. Since this argument works in reverse, we have proved (5).
K. Hence, [H, G] ⊆ K. Since this argument works in reverse, we have proved (5).
Now, given a group G, define a series Γ0(G), Γ1(G), Γ2(G), . . . of subgroups of G inductively as follows:
1. Take Γ0(G) = G.
2. If Γi(G) has been constructed, define Γi+1(G) = [Γi(G), G].
Then Γi(G) ![]() G for all i ≥ 0 by induction on i (using (3) of Lemma 1), whence Γi+1(G) = [Γi(G), G] ⊆ Γi(G) for each i by (4) of Lemma 1. Thus, we obtain a series of normal subgroups
G for all i ≥ 0 by induction on i (using (3) of Lemma 1), whence Γi+1(G) = [Γi(G), G] ⊆ Γi(G) for each i by (4) of Lemma 1. Thus, we obtain a series of normal subgroups
G = Γ0(G) ⊇ Γ1(G) ⊇ Γ2(G) ⊇ ![]() .
.
This is called the descending central series of G. The name comes from the fact that, using (5) of Lemma 1,
![]()
holds for each i ≥ 0. Note that
Γ1(G) = [G, G] = G′ is the derived subgroup of G.
If G is an abelian group, then Z1(G) = G and Γ1(G) = {1}. On the other hand, there are groups (even solvable ones by Example 1) for which the ascending central series does not reach G and the descending central series does not reach 1. However, if either possibility occurs, so does the other.
Lemma 2. The following are equivalent for a group G and an integer n ≥ 0:
1. Γn(G) = {1}.
2. Zn(G) = G.
3. A series G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn = {1} exists with Gi
⊇ Gn = {1} exists with Gi ![]() G for each i and Gi/Gi+1 ⊆ Z(G/Gi+1).
G for each i and Gi/Gi+1 ⊆ Z(G/Gi+1).
Proof. Write Γi(G) = Γi and Zi(G) = Zi for each i.
(1) ⇒ (2). If Γn = {1}, we show that Γn−i ⊆ Zi for each i = 0, 1, 2, . . . (so Zn = G). This is clear if i = 0 by (1), so assume Γn−i ⊆ Zi, where i > 0. If a ![]() Γn−i−1, then, for all g
Γn−i−1, then, for all g ![]() G, [a, g]
G, [a, g] ![]() [Γn−i−1, G] = Γn−i ⊆ Zi. Thus, aZi is in the center of G/Zi and so a
[Γn−i−1, G] = Γn−i ⊆ Zi. Thus, aZi is in the center of G/Zi and so a ![]() Zi+1. Hence, Γn−i−1 ⊆ Zi+1 as required.
Zi+1. Hence, Γn−i−1 ⊆ Zi+1 as required.
(2) ⇒ (3). Given (2), use G = Zn ⊇ Zn−1 ⊇ ![]() ⊇ Z0 = {1} in (3).
⊇ Z0 = {1} in (3).
(3) ⇒ (1). Given (3), we show that Γi ⊆ Gi for each i = 0, 1, 2, . . . (so Γn = {1}). This is clear if i = 0, so assume that Γi ⊆ Gi for some i > 0. We must show that [Γi, G] = Γi+1 ⊆ Gi+1, so we show that [a, g] ![]() Gi+1 for all a
Gi+1 for all a ![]() Γi, g
Γi, g ![]() G. But
G. But ![]() by (3), so a
by (3), so a ![]() Γi ⊆ Gi implies that aGi+1 commutes with gGi+1 for all g
Γi ⊆ Gi implies that aGi+1 commutes with gGi+1 for all g ![]() G. This in turn implies that [a, g]
G. This in turn implies that [a, g] ![]() Gi+1, as required.
Gi+1, as required.
A group G is called a nilpotent group if the conditions in Lemma 2 are satisfied for some n ≥ 0. The smallest integer n for which Γn(G) = {1}, equivalently Zn(G) = G, is called the nilpotency class of G. Thus, if G is nilpotent, then G has class 1 if and only if it is abelian, and (Exercise 11) G has class 2 if and only if it is nonabelian and G′ ⊆ Z(G).
A series as in (3) of Lemma 2 is called a central series for G. Suppose that G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn = {1} is any central series for a nilpotent group G. Then the proof that (3) ⇒ (1) in Lemma 2 derives the first of the following inclusions:
⊇ Gn = {1} is any central series for a nilpotent group G. Then the proof that (3) ⇒ (1) in Lemma 2 derives the first of the following inclusions:
![]()
We leave the second inclusion for the reader (Exercise 7). Hence, we often call the series G =Γ0(G) ⊇ Γ1(G) ⊇ Γ2(G) ⊇ ![]() and 1 = Z0(G)⊆ Z1(G) ⊆ Z2(G) ⊆
and 1 = Z0(G)⊆ Z1(G) ⊆ Z2(G) ⊆ ![]() the lower and upper central series, respectively.
the lower and upper central series, respectively.
Example 2. Every abelian group is nilpotent.
Example 3. If p is a prime, every finite p -group is nilpotent. In fact, if we write Zi(G) = Zi for each i, Theorem 6 §8.2 shows that Zi+1/Zi = Z(G/Zi) is not trivial if Zi ≠ G because G/Zi is a p-group. Hence, 1 ⊂ Z1 ⊂ Z2 ⊂ ![]() , which eventually reaches G because G is finite.
, which eventually reaches G because G is finite.
Example 4. Show that every nilpotent group G is solvable, but not conversely.
Solution. If G is nilpotent, the series {1} = Z0(G) ⊆ ![]() ⊆ Zn(G) = G is a solvable series. However, S3 is solvable but not nilpotent by Example 1.
⊆ Zn(G) = G is a solvable series. However, S3 is solvable but not nilpotent by Example 1.
Theorem 1. Every subgroup and image of a nilpotent group is again nilpotent.
Proof. Let G be nilpotent. To show that a subgroup K ⊆ G is nilpotent, it suffices to show that Γi(K) ⊆ Γi(G) for each i. This is clear if i = 0. If Γi(K) ⊆ Γi(G) for some i, then the induction goes through because
Γi+1(K) = [Γi(K), K] ⊆ [Γi(G), G] = Γi+1(G).
Now let α: G → H be an onto homomorphism; we show that Γi(H) ⊆ α[Γi(G)] for each i. If i = 0, it is because α is onto. In general, let Γi(H) ⊆ α(Γi(G)), and let y ![]() Γi(H) and h
Γi(H) and h ![]() H. Write y = α(x), where x
H. Write y = α(x), where x ![]() Γi(G), and (as α is onto) write h = α(g), g
Γi(G), and (as α is onto) write h = α(g), g ![]() G. Then
G. Then
[y, h] = [α(x), α(g)] = α[x, g] ![]() α[Γi(G), G] = α(Γi+1(G)).
α[Γi(G), G] = α(Γi+1(G)).
Hence, Γi+1(H) = [Γi(H), H] ⊆ α(Γi+1(G)), as required.
Corollary. A group G is nilpotent if and only if G′ is nilpotent.
Proof. Write D = G′. If D(n) = {1}, then G(n+1) = D(n) = {1}.
By Theorem 1, if K ![]() G and G is nilpotent, then both K and G/K are nilpotent. The converse is false (S3 is again a counterexample) in contrast to the situation for solvable groups. However, the converse does hold when K ⊆ Z(G).
G and G is nilpotent, then both K and G/K are nilpotent. The converse is false (S3 is again a counterexample) in contrast to the situation for solvable groups. However, the converse does hold when K ⊆ Z(G).
Theorem 2. If G is a group, K ⊆ Z(G), and G/K is nilpotent, then G is nilpotent.
Proof. Assume that G/K is nilpotent, and let θ: G → G/K be the coset map. By hypothesis, let θ(G) = X0 ⊇ X1 ⊇ ![]() ⊇ Xn = {K} be a central series for θ(G), where
⊇ Xn = {K} be a central series for θ(G), where ![]() for 0 ≤ i ≤ n − 1. Write Xi = Gi/K = θ(Gi) for 0 ≤ i ≤ n. Then we obtain the series
for 0 ≤ i ≤ n − 1. Write Xi = Gi/K = θ(Gi) for 0 ≤ i ≤ n. Then we obtain the series
G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn = K ⊇ Gn+1 = {1}.
⊇ Gn = K ⊇ Gn+1 = {1}.
We show this is a central series for G. First, ![]() because K ⊆ Z(G). To see that
because K ⊆ Z(G). To see that ![]() for 0 ≤ i < n, let a
for 0 ≤ i < n, let a ![]() Gi. Then θ(a)
Gi. Then θ(a) ![]() θ(Gi) = Xi, so θ(a) Xi+1 commutes with θ(g) Xi+1 for all g
θ(Gi) = Xi, so θ(a) Xi+1 commutes with θ(g) Xi+1 for all g ![]() G. Thus, θ[a, g] = [θ(a), θ(g)]
G. Thus, θ[a, g] = [θ(a), θ(g)] ![]() Xi+1 = θ(Gi+1), say θ[a, g] = θ(b), b
Xi+1 = θ(Gi+1), say θ[a, g] = θ(b), b ![]() Gi+1. Thus, [a, g]b−1
Gi+1. Thus, [a, g]b−1 ![]() ker θ = K ⊆ Gi+1, so [a, g]
ker θ = K ⊆ Gi+1, so [a, g] ![]() Gi+1b = Gi+1. This means aGi+1 commutes with gGi+1, that is,
Gi+1b = Gi+1. This means aGi+1 commutes with gGi+1, that is, ![]() , as required.
, as required.
The next result will be needed in Theorem 4.
Theorem 3. If G1, G2, ![]() , Gn are nilpotent, so also is G1 × G2 ×
, Gn are nilpotent, so also is G1 × G2 × ![]() × Gn.
× Gn.
Proof. This follows because Γi(G1 × G2 × ![]() × Gn) ⊆ Γi(G1) ×
× Gn) ⊆ Γi(G1) × ![]() × Γi(Gn) for each i, a fact that we leave as Exercise 6.
× Γi(Gn) for each i, a fact that we leave as Exercise 6.
Theorem 3 and Example 3 combine to show that any finite direct product of finite p-groups (for various primes p) is nilpotent. In fact, every finite nilpotent group is isomorphic to such a direct product. We need the following notion.
A subgroup M of a group G is said to be maximal in G if M ≠ G and the only subgroups H such that M ⊆ H ⊆ G are H = M and H = G. Clearly, every proper subgroup K of a finite group is contained in a maximal subgroup—one of maximal order containing K. If G is finite, every subgroup of prime index is maximal by Example 6 §2.6.106 The converse is not necessarily true (any subgroup of index 4 in A4 is maximal), but it does hold in a finite p-group. Moreover, in this case, the maximal subgroups (of index p) are necessarily normal (see the corollary to Theorem 1 §8.3). This property characterizes the finite nilpotent groups.
Theorem 4. Burnside–Wielandt Theorem. 107 The following conditions are equivalent for a finite group G ≠ {1}:
1. G is nilpotent.
2. N(H) ≠ H for all subgroups H ≠ G of G.
3. Every maximal subgroup of G is normal in G.
4. Every Sylow subgroup of G is normal in G.
5. G is isomorphic to the direct product of its Sylow subgroups.
Proof. (1) ⇒ (2). Write Zi = Zi(G) for each i and assume that Zn = G. If H ≠ G is a subgroup of G, then Z0 ⊆ H but Zn ![]() H, so an integer k ≥ 0 exists such that Zk ⊆ H but Zk+1
H, so an integer k ≥ 0 exists such that Zk ⊆ H but Zk+1 ![]() H. Choose a
H. Choose a ![]() Zk+1, a ∉ H. Then aZk is in the center of G/Zk, so if h
Zk+1, a ∉ H. Then aZk is in the center of G/Zk, so if h ![]() H, aZk and hZk commute. Hence, hah−1a−1
H, aZk and hZk commute. Hence, hah−1a−1 ![]() Zk ⊆ H, from which aHa−1 ⊆ H. Thus, a
Zk ⊆ H, from which aHa−1 ⊆ H. Thus, a ![]() N(H), and so N(H) ≠ H.
N(H), and so N(H) ≠ H.
(2) ⇒ (3). Let M be a maximal subgroup of G. Since M ⊆ N(M) ⊆ G, (2) implies that N(M) = G. Hence, M ![]() G.
G.
(3) ⇒ (4). Suppose P is a nonnormal Sylow p-subgroup of G. Then N(P) ≠ G, so let N(P) ⊆ M, where M is a maximal subgroup of G. Because P ⊆ M, (3) gives aPa−1 ⊆ aMa−1 = M for all a ![]() G. Hence, both P and aPa−1 are Sylow p-subgroups of M and so are conjugate in M, say P = m(aPa−1)m−1 for some m
G. Hence, both P and aPa−1 are Sylow p-subgroups of M and so are conjugate in M, say P = m(aPa−1)m−1 for some m ![]() M. But then ma
M. But then ma ![]() N(P), so a
N(P), so a ![]() M. Because a
M. Because a ![]() G was arbitrary, this means G ⊆ M, a contradiction. This proves (4).
G was arbitrary, this means G ⊆ M, a contradiction. This proves (4).
(4) ⇒ (5). Let P1, P2, ![]() , Pr denote the distinct Sylow subgroups of G.
, Pr denote the distinct Sylow subgroups of G.
Claim 1. P1P2 ![]() Pk ≅ P1 × P2 ×
Pk ≅ P1 × P2 × ![]() × Pk for each k = 2, 3,
× Pk for each k = 2, 3, ![]() , r.
, r.
Proof. It is clear if k = 1. Assume inductively that P1P2 ![]() Pk ≅ P1 × P2 ×
Pk ≅ P1 × P2 × ![]() × Pk for some k > 1. Then (P1P2
× Pk for some k > 1. Then (P1P2 ![]() Pk) ∩ Pk+1 = {1} because elements in the two subgroups have relatively prime orders. By Theorem 6 §2.8,
Pk) ∩ Pk+1 = {1} because elements in the two subgroups have relatively prime orders. By Theorem 6 §2.8,
(P1P2 ![]() Pk)Pk+1 ≅ (P1 × P2 ×
Pk)Pk+1 ≅ (P1 × P2 × ![]() × Pk) × Pk+1 ≅ P1 × P2 ×
× Pk) × Pk+1 ≅ P1 × P2 × ![]() × Pk+1
× Pk+1
because P1P2 ![]() Pk
Pk ![]() G and Pk+1
G and Pk+1 ![]() G. This proves the claim.
G. This proves the claim.
The claim gives |P1P2 ![]() Pr| ≅ |P1||P2|
Pr| ≅ |P1||P2| ![]() |Pr| = |G|. Hence G = P1P2
|Pr| = |G|. Hence G = P1P2 ![]() Pr and (5) follows, again by the Claim.
Pr and (5) follows, again by the Claim.
(5) ⇒ (1). This follows from Theorem 3 and Example 3.
It is interesting to compare (2) in Theorem 4 with the result (Theorem 5 §9.2) that a finite group G is solvable if and only if H′ ≠ H for every subgroup H ≠ {1}.
Since every finite abelian group is nilpotent, the implication (1) ⇒ (5) in Theorem 4 gives another proof of the primary decomposition theorem for finite abelian groups (Corollary 2 of Theorem 3 §7.2). We reformulate (1)![]() (5) as
(5) as
Corollary 1. A finite group G is nilpotent if and only if G is isomorphic to a finite direct product of p-groups for various primes p.
Frattini and Fitting Subgroups
One of the most important aspects of the study of nilpotent groups is that every finite group G contains a nilpotent subgroup Φ, which is characteristic in G (that is, σ(Φ) = Φ for every automorphism σ of G—these subgroups are discussed in Corollary 3 of Theorem 3 §2.8). We now turn to a discussion of this.
If G ≠ {1} is a finite group, define the Frattini subgroup
Φ(G) = ![]() {M ⊆ G
{M ⊆ G ![]() M is a maximal subgroup of G}.
M is a maximal subgroup of G}.
Define Φ{1} = {1}. This was introduced in 1885 by Giovanni Frattini.
Example 5. Φ(A4) = {ε}. Indeed, K = {ε, (12)(34), (13)(24), (14)(23)} is maximal, being of index 3, and M = {ε, (123), (132)} is maximal (it has index 4, but A4 has no subgroup of index 2). Hence, we have Φ(A4) ⊆ K ∩ M = {ε}.
Example 6. If Q = { ± 1, ± i, ± j, ± k} is the quaternion group, then Φ(Q) = {1, − 1} because ![]() and
and ![]() are the only maximal subgroups.
are the only maximal subgroups.
Example 7. If ![]() and o(a) = pn, where p is a prime,
and o(a) = pn, where p is a prime, ![]() because
because ![]() is the unique maximal subgroup (of index p).
is the unique maximal subgroup (of index p).
Theorem 5. Let G be a group and write Φ = Φ(G). Then the following hold:
1. If α: G → H is an onto group homomorphism, then α(Φ) ⊆ Φ(H).
2. In particular, Φ is a characteristic subgroup of G.
3. G is nilpotent if and only if G′ ⊆ Φ.
Proof. (1) If U ⊆ H is a maximal subgroup, we must show that α(Φ) ⊆ U. If we define M = {m ![]() G
G ![]() α(m)
α(m) ![]() U}, then it suffices to show that M is a maximal subgroup of G (since then Φ ⊆ M). But if M ⊆ K ⊆ G are subgroups of G then α(M) ⊆ α(K) ⊆ α(G). Since α is onto, this is U ⊆ α(K) ⊆ H, so α(K) = U or σ(K) = H. These imply that K = M or K = G.
U}, then it suffices to show that M is a maximal subgroup of G (since then Φ ⊆ M). But if M ⊆ K ⊆ G are subgroups of G then α(M) ⊆ α(K) ⊆ α(G). Since α is onto, this is U ⊆ α(K) ⊆ H, so α(K) = U or σ(K) = H. These imply that K = M or K = G.
(2) This follows from (1) if H = G and α is an automorphism of G.
(3) G′ ⊆ Φ if and only if G′ ⊆ M for each maximal subgroup M of G, if and only if M ![]() G for each M, and if and only if G is nilpotent by Theorem 4.
G for each M, and if and only if G is nilpotent by Theorem 4.
Corollary 1. The following are equivalent for a finite group G:
1. G is nilpotent.
2. G/Φ(G) is abelian.
3. G/Φ(G) is nilpotent.
Proof. (1)![]() (2) restates (3) of Theorem 5 and (2)⇒(3) is obvious.
(2) restates (3) of Theorem 5 and (2)⇒(3) is obvious.
(3)⇒(1). Given (3), we show that every maximal subgroup M of G is normal. Write Φ = Φ(G). Since Φ ⊆ M, the subgroup M/Φ is maximal in G/Φ by the correspondence theorem, so M/Φ ![]() G/Φ by (3) and Theorem 4. But then M
G/Φ by (3) and Theorem 4. But then M ![]() G, again by the correspondence theorem.
G, again by the correspondence theorem.
To see that Φ(G) is a nilpotent group, we first characterize it in terms of the following concept. An element t ![]() G is called a nongenerator in G if it can be omitted from any generating set X of G; that is, if
G is called a nongenerator in G if it can be omitted from any generating set X of G; that is, if ![]() , then
, then ![]()
Theorem 6. Let G denote any finite group. Then the following hold:
1. Φ(G) = {t ![]() t is a nongenerator of G}.
t is a nongenerator of G}.
2. Φ(G)is a nilpotent group.
Proof. For convenience, write Φ = Φ(G).
(1) Write N = {t ![]() t is a nongenerator of G} and let a
t is a nongenerator of G} and let a ![]() Φ. If a ∉ N, then X ⊆ G exists such that
Φ. If a ∉ N, then X ⊆ G exists such that ![]() but
but ![]() So let
So let ![]() where M is a maximal subgroup of G. Then a
where M is a maximal subgroup of G. Then a ![]() M because Φ ⊆ M, whence
M because Φ ⊆ M, whence ![]() a contradiction. Hence, Φ ⊆ N. Conversely, if t
a contradiction. Hence, Φ ⊆ N. Conversely, if t ![]() N and M is a maximal subgroup of G, then g
N and M is a maximal subgroup of G, then g ![]() M (otherwise
M (otherwise ![]() ). Hence, N ⊆ Φ.
). Hence, N ⊆ Φ.
(2) By Theorem 4 we show that every Sylow p-subgroup P of Φ is normal in G. If g ![]() G, then gPg−1 ⊆ gΦg−1 = Φ by (2) of Theorem 5. Hence, both gPg−1 and P are Sylow p-subgroups of Φ and so are conjugate in Φ, say t(gPg−1)t−1 = P, where t
G, then gPg−1 ⊆ gΦg−1 = Φ by (2) of Theorem 5. Hence, both gPg−1 and P are Sylow p-subgroups of Φ and so are conjugate in Φ, say t(gPg−1)t−1 = P, where t ![]() Φ. Thus, tg
Φ. Thus, tg ![]() N(P), which yields G = ΦN(P). But then
N(P), which yields G = ΦN(P). But then ![]() so, as Φ is finite,
so, as Φ is finite, ![]() by (1). Hence, P
by (1). Hence, P ![]() G as required.
G as required.
Note the proof of (2) shows that Sylow p-subgroups of Φ(G) are normal in G.
Corollary 1. Assume that Φ(G) is finitely generated (for example, if G is finite). If HΦ(G) = G, where H is a subgroup, then H = G.
Proof. Write Φ(G) = Φ. If ![]() then
then ![]() and the nongenerators ti can be removed one by one.
and the nongenerators ti can be removed one by one.
The next result extends a useful theorem about finite p-groups.
Theorem 7. If G is a nilpotent group and {1} ≠ H ![]() G, then H ∩ Z(G) ≠ {1}.
G, then H ∩ Z(G) ≠ {1}.
Proof. Write Γi = Γi(G) for each i. We have G = Γ0 ⊇ Γ1 ⊇ ![]() ⊇ Γn = {1} for some n, so H ∩ Γn = {1} while H ∩ Γ0 ≠ {1}. So there exists k such that H ∩ Γk ≠ {1} while H ∩ Γk+1 = {1}. Choose 1 ≠ h
⊇ Γn = {1} for some n, so H ∩ Γn = {1} while H ∩ Γ0 ≠ {1}. So there exists k such that H ∩ Γk ≠ {1} while H ∩ Γk+1 = {1}. Choose 1 ≠ h ![]() H ∩ Γk. If g
H ∩ Γk. If g ![]() G, then [h, g]
G, then [h, g] ![]() [Γk, G] = Γk+1. Also, [h, g] = h−1g−1hg
[Γk, G] = Γk+1. Also, [h, g] = h−1g−1hg ![]() H(g−1Hg) = H because H
H(g−1Hg) = H because H ![]() G. So [h, g]
G. So [h, g] ![]() H ∩ Γk+1 = {1}, whence hg = gh. Thus, h
H ∩ Γk+1 = {1}, whence hg = gh. Thus, h ![]() Z(G) ∩ H.
Z(G) ∩ H.
In 1938, Hans Fitting identified a largest nilpotent normal subgroup in every finite group. His key result was
Theorem 8. Fitting's Theorem. If H and K are nilpotent, normal subgroups of a finite group G, so also is HK.
Proof. We proceed by induction on We have HK ![]() G, so we may assume (by induction) that G = HK and that H ≠ {1} ≠ K. Write W = Z(K). Then W ≠ {1} by Theorem 7. Also, W
G, so we may assume (by induction) that G = HK and that H ≠ {1} ≠ K. Write W = Z(K). Then W ≠ {1} by Theorem 7. Also, W ![]() G being characteristic in K
G being characteristic in K ![]() G. If we write N = [W, H], the proof falls into two cases.
G. If we write N = [W, H], the proof falls into two cases.
Case 1. N = {1}. Then W centralizes H (and K), so W ⊆ Z(HK) = Z(G). But ![]()
![]() Moreover,
Moreover, ![]() and
and ![]() are both nilpotent by Theorem 1, so
are both nilpotent by Theorem 1, so ![]() is nilpotent by induction. Hence, G is nilpotent by Theorem 2.
is nilpotent by induction. Hence, G is nilpotent by Theorem 2.
Case 2. N ≠ {1}. We have N ⊆ W ∩ H because W ![]() G and H
G and H ![]() G. In particular, V = N ∩ Z(H) ≠ {1} again by Theorem 7. As before,
G. In particular, V = N ∩ Z(H) ≠ {1} again by Theorem 7. As before, ![]()
![]() and both
and both ![]() and
and ![]() are nilpotent, so
are nilpotent, so ![]() is nilpotent by induction. But V centralizes H, and it also centralizes K because V ⊆ N ⊆ W = Z(K). Hence, V ⊆ Z(HK) = Z(G), so G is nilpotent by Theorem 2 and we are done in this case too.
is nilpotent by induction. But V centralizes H, and it also centralizes K because V ⊆ N ⊆ W = Z(K). Hence, V ⊆ Z(HK) = Z(G), so G is nilpotent by Theorem 2 and we are done in this case too.
Now let G be any finite group. If N1 = {1}, N2, . . ., Nk denote all the nilpotent, normal subgroups of G, define the Fitting subgroup F(G) of G by
![]()
Then F(G) ![]() G, and it is nilpotent by Theorem 8 and induction on k. This proves
G, and it is nilpotent by Theorem 8 and induction on k. This proves
Theorem 9. If G is a finite group, then F(G) is the largest nilpotent, normal subgroup of G in the sense that it contains every such subgroup.
Corollary 1. If α: G → H is an onto homomorphism, then α[F(G)] ⊆ F(H).
Proof. α[F(G)] ![]() H because α is onto, and it is nilpotent by Theorem 1.
H because α is onto, and it is nilpotent by Theorem 1.
Hence, a finite group G is nilpotent if and only if F(G) = G. Clearly, Z(G) ⊆ F(G), and Φ(G) ⊆ F(G) because it is nilpotent (Theorem 6) and normal in G (Theorem 5). Moreover, F(G) is a characteristic subgroup of G by the above corollary.
Lemma 3. If G is finite and N ![]() G, then N is nilpotent if and only if N′ ⊆ Φ(G).
G, then N is nilpotent if and only if N′ ⊆ Φ(G).
Proof. Write Φ(G) = Φ. If N′ ⊆ Φ, then N′ is nilpotent by Theorem 6, and so N is nilpotent by the corollary to Theorem 1. Conversely, if N is nilpotent, then N′ ⊆ Φ(N) by Theorem 5, and it remains to show that Φ(N) ⊆ Φ. Write Φ(N) = H and suppose H6 ⊆ Φ. Then H6 ⊆ M for some maximal subgroup M of G, so HM = G. Since H ⊆ N, the modular law (Lemma 1 §8.1) gives
N = G ∩ N = HM ∩ N = H(M ∩ N).
Thus, ![]() and H = Φ(N) consist of (a finite number of) non-generators of N. Hence, N = M ∩ N, whence N ⊆ M, a contradiction.
and H = Φ(N) consist of (a finite number of) non-generators of N. Hence, N = M ∩ N, whence N ⊆ M, a contradiction.
We can now describe the relationship between the Frattini and Fitting subgroups in a finite group.
Theorem 10. Let G be a finite group and write Φ = Φ(G) and F = F(G).
1. F′ ⊆ Φ ⊆ F.
2. F(G/Φ) = F/Φ.
Proof. (1) We have F′ ![]() G because it is characteristic in F
G because it is characteristic in F ![]() G, so F′ ⊆ Φ by Lemma 3 because F is nilpotent. On the other hand, Φ ⊆ F by Theorem 9 because Φ is nilpotent. This proves (1).
G, so F′ ⊆ Φ by Lemma 3 because F is nilpotent. On the other hand, Φ ⊆ F by Theorem 9 because Φ is nilpotent. This proves (1).
(2) This follows from a more general result (Theorem 11).108
Theorem 11. If G is a finite group and Φ(G) ⊆ N ![]() G, then N is nilpotent if and only if N/Φ(G) is nilpotent.
G, then N is nilpotent if and only if N/Φ(G) is nilpotent.
Proof. Write Φ(G) = Φ. If N is nilpotent, so is its image ![]() For the converse, assume that
For the converse, assume that ![]() is nilpotent. To show that N is nilpotent, we show that every Sylow p -subgroup P of N is normal in N (and invoke Theorem 4). First,
is nilpotent. To show that N is nilpotent, we show that every Sylow p -subgroup P of N is normal in N (and invoke Theorem 4). First, ![]() is a Sylow p-subgroup of
is a Sylow p-subgroup of ![]() (by Example 4 §8.4), whence
(by Example 4 §8.4), whence ![]() by hypothesis. But then
by hypothesis. But then ![]() is characteristic in
is characteristic in ![]() and it follows that
and it follows that ![]() Thus, ΦP
Thus, ΦP ![]() G. But P is a Sylow p-subgroup of ΦP (because ΦP ⊆ N), so G = (ΦP)NG(P) by Lemma 1 §8.4. Since G is finite and Φ consists of nongenerators, it follows that G = P NG(P) = NG(P). Hence, P
G. But P is a Sylow p-subgroup of ΦP (because ΦP ⊆ N), so G = (ΦP)NG(P) by Lemma 1 §8.4. Since G is finite and Φ consists of nongenerators, it follows that G = P NG(P) = NG(P). Hence, P ![]() G, so certainly P
G, so certainly P ![]() N as required.
N as required.
There is much more information available on nilpotent groups in books on group theory.109
Exercises 9.3
1.
a. Show that An is not nilpotent if n ≥ 3.
b. Show that every nilpotent group is solvable, but not conversely.
2. Prove (1)–(4) in Lemma 1.
3. If H and K are subgroups of G and α: G → G1 is a homomorphism, show that α[H, K] = [α(H), α(K)]. Conclude that [H, K] is normal in G (characteristic in G) if the same is true of H and K.
4. If α: G → H is any homomorphism, show that α[Γi(G)] = Γi[α(G)].
5. If G(k) is the kth derived subgroup of G (see Theorem 1, Section 9.2), show that G(k+1) = [G(k), G(k)] for each k ≥ 0.
6.
a. Show that Γi(G1 × ![]() × Gn) ⊆ Γi(G1) ×
× Gn) ⊆ Γi(G1) × ![]() × Γi(Gn) for all i ≥ 0.
× Γi(Gn) for all i ≥ 0.
b. Show that equality holds in (a).
7. If G = G0 ⊇ G1 ⊇ ![]() ⊇ Gn= {1} is any central series for a group G, show that Gn−i ⊆ Zi(G) for each i.
⊇ Gn= {1} is any central series for a group G, show that Gn−i ⊆ Zi(G) for each i.
8. Let
![]()
where F is a field. Is G nilpotent?
9. Show that Dn is nilpotent if and only if n is a power of 2.
10. Show that a finite group is nilpotent if and only if any two elements of relatively prime orders commute.
11. Show that a group G is nilpotent of class 2 if and only if G is nonabelian and G′ ⊆ Z(G).
12. Show that a finite group G is nilpotent if and only if Z(G/K) is nontrivial for all K ![]() G, K ≠ G. [Hint: Theorem 7.]
G, K ≠ G. [Hint: Theorem 7.]
13. If G is a finite nilpotent group, let K be of minimal order in {K ![]() {1} ≠ K
{1} ≠ K ![]() G}. Show that K ⊆ Z(G) and that |K| is a prime. [Hint: Theorem 7.]
G}. Show that K ⊆ Z(G) and that |K| is a prime. [Hint: Theorem 7.]
14. If H ![]() G and K
G and K ![]() G, show that G/(H ∩ K) is nilpotent if and only if the product group (G/H) × (G/K) is nilpotent.
G, show that G/(H ∩ K) is nilpotent if and only if the product group (G/H) × (G/K) is nilpotent.
15. Show that a finite group G is nilpotent if and only if G has a normal subgroup of order m for every divisor m of |G|.
16. A subgroup H of a group G is called subnormal in G if a chain of subgroups H = H0 ⊆ H1 ⊆ ![]() ⊆ Hn = G exists such that Hi
⊆ Hn = G exists such that Hi ![]() Hi+1 for each i. Show that a finite group G is nilpotent if and only if every subgroup is subnormal.
Hi+1 for each i. Show that a finite group G is nilpotent if and only if every subgroup is subnormal.
17. If K ⊆ Z(G) and G/K is nilpotent, show that G is nilpotent using only (3) of Theorem 4.
18.
a. If G is nilpotent, show that Z(H)≠{1} for all subgroups H ≠ {1}.
b. Show that the converse is false by considering Q6.
19. If G is nilpotent and G/G′ is cyclic, show that G is abelian. [Hint: Apply Theorem 2 §2.9 to G/[Γ2(G)] and conclude that Γ2(G) = Γ1(G).]
20. If G is a finite group show that (2) ![]() (3)
(3) ![]() (4) and (2) ⇒ (1), but (1) ⇒/(2).
(4) and (2) ⇒ (1), but (1) ⇒/(2).
(1) G′ is abelian. (2) G/Z(G) is abelian. (3) Γ2(G) = {1}. (4) Z2(G) = G.
21. Let ![]() where o(a) = n, o(b) = 2, and aba = b. Show that (a) Φ(D4) = {1, a2}, (b) Φ(D12) ⊆ {1, a6}, and (c) Φ(Dpq) ={1}, where p ≠ q are primes. [Hint: If
where o(a) = n, o(b) = 2, and aba = b. Show that (a) Φ(D4) = {1, a2}, (b) Φ(D12) ⊆ {1, a6}, and (c) Φ(Dpq) ={1}, where p ≠ q are primes. [Hint: If ![]() has index m, show that
has index m, show that ![]() is a subgroup of index m.]
is a subgroup of index m.]
22. If o(a)![]() where pi are distinct primes, show that
where pi are distinct primes, show that ![]() , where m = p1p2
, where m = p1p2 ![]() pr.
pr.
23. Let |G| = p3, where p is a prime. If G is nonabelian, show that Φ(G) = G′ = Z(G) and that this subgroup has order p. [Hint: Exercise 26 §8.2.]
24. If G is a finite group, write Φ = Φ(G). Show that the following are equivalent:
(1) G is nilpotent (2) G/Φ is abelian (3) G/Φ is nilpotent
25. If K ![]() G, where G is finite, and Φ(G/K) = {K}, show that Φ(G) ⊆ K.
G, where G is finite, and Φ(G/K) = {K}, show that Φ(G) ⊆ K.
26.
a. If G is finite, K ![]() G, and K ⊆ Φ(G), show that Φ(G/K) = Φ(G)/K.
G, and K ⊆ Φ(G), show that Φ(G/K) = Φ(G)/K.
b. Show that Φ(G/Φ(G)) = {1}.
27. Show that Φ(G × H) = Φ(G) × Φ(H) for finite groups G and H.
28. If G is a finite group and H ![]() G, show that Φ(H) ⊆ H ∩ Φ(G). [Hint: If Φ(H)
G, show that Φ(H) ⊆ H ∩ Φ(G). [Hint: If Φ(H) ![]() M, where M is maximal in G, show that G = Φ(H)M and apply Lemma 1 §8.1.]
M, where M is maximal in G, show that G = Φ(H)M and apply Lemma 1 §8.1.]
29.
a. If G is a finite group and M ⊆ G is a maximal subgroup, show that either Z(G) ⊆ M or G′ ⊆ M. [Hint: MZ(G) = G implies that M ![]() G.]
G.]
b. Show that Z(G) ∩ G′ ⊆ Φ(G) for all finite groups G.
30. Show that a finite group G can be generated by n elements if and only if the same is true of G/Φ(G).
31. If G is a finite p-group, p a prime, show that ![]()
Notes
100. Due to Hans Zassenhaus.
101. Due to Otto Schreier.
102. These groups are also called soluble groups.
103. See Kargapolov, M.I. and Merzljakov, J.I., Fundamentals of the Theory of Groups, Springer-Verlag, 1979; Rotman, J.J., The Theory of Groups: An Introduction, 2nd ed., Boston: Allyn & Bacon, 1973; Artin, E., Geometric Algebra, New York: Interscience, 1957. For an elementary proof when n = 2, see Lang, S., Undergraduate Algebra, Berlin: Springer-Verlag, 1987.
104. Feit, W. and Thomson, J.G., Solvability of groups of odd order, Pacific Journal of Mathematics, 13 (1963), 775–1029.
105. See Kargapolov, M.I. and Merzljakov, J.I., Fundamentals of the Theory of Groups, Springer-Verlag, 1979; MacDonald, I.D., The Theory of Groups, London: Oxford University Press, 1968; Rotman, J.J., The Theory of Groups: An Introduction, 2nd ed., Boston: Allyn & Bacon, 1973.
106. This is also true if G is infinite by Exercise 31, §2.6.
107. The name honors William Burnside and Helmut Wielandt.
108. Because of (2) and the corollary to Theorem 9, the Fitting subgroup of G is also called the nilpotent radical of G.
109. The following books contain excellent introductions to the theory of nilpotent groups: Mac-Donald, I.D., The Theory of Groups, London: Oxford University Press, 1968; Rose, J.S., A Course on Group Theory, Cambridge, England: Cambridge University Press, 1978; Kargapolov, M.I. and Merzljakov, J.I., Fundamentals of the Theory of Groups, New York: Springer-Verlag, 1979; Gorenstsein, D., Finite Groups, 2nd ed., New York: Chelsea, 1980.
