Preface

This book is a self-contained introduction to the basic structures of abstract algebra: groups, rings, and fields. It is designed to be used in a two-semester course for undergraduates or a one-semester course for seniors or graduates. The table of contents is flexible (see the chapter summaries that follow), so the book is suitable for a traditional course at various levels or for a more application-oriented treatment. The book is written to be read by students with little outside help and so can be used for self-study. In addition, it contains several optional sections on special topics and applications.

Because many students will not have had much experience with abstract thinking, a number of important concrete examples (number theory, integers modulo n, permu-tations) are introduced at the beginning and referred to throughout the book. These examples are chosen for their importance and intrinsic interest and also be-cause the student can do actual computations almost immediately even though the examples are, in the student's view, quite abstract. Thus, they provide a bridge to the abstract theory and serve as prototype examples of the abstract structures themselves. As an illustration, the student will encounter composition and inverses of permutations before having to fit these notions into the general framework of group theory.

The axiomatic development of these structures is also emphasized. Algebra provides one of the best illustrations of the power of abstraction to strip concrete examples of nonessential aspects and so to reveal similarities between ostensibly different objects and to suggest that a theorem about one structure may have an analogue for a different structure. Achieving this sort of facility with abstraction is one of the goals of the book. This goes hand in hand with another goal: to teach the student how to do proofs. The proofs of most theorems are at least as important for the techniques as for the theorems themselves. Hence, whenever possible, techniques are introduced in examples before giving them in the general case as a proof. This partly explains the large number of examples (over 450) in the book.

Of course, a generous supply of exercises is essential if this subject is to have a lasting impact on students, and the book contains more than 1450 exercises (many with separate parts). For the most part, computational exercises appear first, and the exercises are given in ascending order of difficulty. Hints are given for the less straightforward problems, and answers are provided to odd numbered (parts of) computational exercises and to selected theoretical exercises. (A student solution manual is available.) While exercises are vital to understanding this subject, they are not used to develop results needed later in the text.

An increasing number of students of abstract algebra come from outside mathematics and, for many of them, the lure of pure abstraction is not as strong as for mathematicians. Therefore, applications of the theory are included that make the subject more meaningful and lively for these students (and for the mathematicians!). These include cryptography, linear codes, cyclic and BCH codes, and combinatorics, as well as “theoretical” applications within mathematics, such as the impossibility of the classical geometric constructions. Moreover, the inclusion of short historical notes and biographies should help the reader put the subject into perspective. In the same spirit, some classical “gems” appear in optional sections (one example is the elegant proof of the fundamental theorem of algebra in Section 6.6, using the structure theorem for symmetric polynomials). In addition, the modern flavor of the subject is conveyed by mentioning some unsolved problems and recent achievements, and by occasionally stating more advanced theorems that extend beyond the results in the book.

Apart from that the material is quite standard. The aim is to reveal the basic facts about groups, rings, and fields and give the student the working tools for applications and further study. The level of exposition rises slowly throughout the book and no prior knowledge of abstract algebra is required. Even linear algebra is not needed. Except for a few well-marked instances, the aspects of linear algebra that are needed are developed in the text. Calculus is completely unnecessary. Some preliminary topics that are needed are covered in Chapter 0, with appendices on complex numbers and matrix algebra (over a commutative ring).

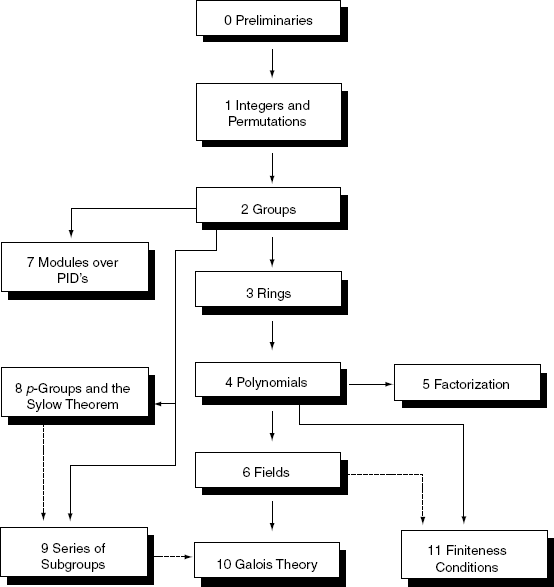
Although the chapters are necessarily arranged in a linear order, this is by no means true of the contents, and the student (as well as the instructor) should keep the chapter dependency diagram in mind. A glance at that diagram shows that while Chapters 1–4 are the core of the book, there is enough flexibility in the remaining chapters to accommodate instructors who want to create a wide variety of courses. The jump from Chapter 6 to Chapter 10 deserves mention. The student has a choice at the end of Chapter 6: either change the subject and return to group theory or continue with fields in Chapter 10 (solvable groups are adequately reviewed in Section 10.3, so Chapter 9 is not necessary). The chapter summaries that follow, and the chapter dependency diagram, can assist in the preparation of a course syllabus.

Our introductory course at Calgary of 36 lectures touches Sections 0.3 and 0.4 lightly and then covers Chapters 1–4 except for Sections 1.5,2.11, 3.5, and 4.4–4.6. The sequel course (also 36 lectures) covers Chapters 5, 6, 10, 7, 8, and 9, omitting Sections 6.6, 6.7, 8.5, 8.6, and 10.4 and Chapter 11.

Features

This book offers the following significant features:

• Self-contained treatment, so the book is suitable for self-study.
• Preliminary material for self-study or review available in Chapter 0 and in Appendices A and B.
• Elementary number theory, integers modulo n, and permutations done first as a bridge to abstraction.
• Over 450 worked examples to guide the student.
• Over 1450 exercises (many with parts), graded in difficulty, with selected answers.
• Gradual increase in level throughout the text.
• Applications to number theory, combinatorics, geometry, cryptography, coding, and equations.
• Flexibility in syllabus construction and choice of optional topics (see chapter dependency diagram).
• Historical notes and biographies.
• Several special topics (for example, symmetric polynomials, nilpotent groups, and modules).
• Solution manual containing answers or solutions to all exercises.
• Student solution manual available with solutions to all odd numbered (parts of) exercises.

Changes in the Third Edition (2007)

The important concept of a module was introduced and used in Chapters 7 and 11.

• Chapter 7 on finitely generated abelian groups was completely rewritten, modules were introduced, direct sums were studied, and the rank of a free module was defined (for commutative rings). Then the structure of finitely generated modules over a PID was determined.
• Chapter 11 was upgraded from finite dimensional algebras to rings with the descending chain condition. Wedderburn's characterization of simple artinian rings and the Wedderburn–Artin theorem on semisimple rings were proved.
• A new section on semidirect products of groups was added.
• Appendices on Zorn's lemma and the recursion theorem were added.
• More solutions to theoretical exercises were included in the Selected Answers section.

Changes in the Fourth Edition

The changes in the Third Edition primarily involved new concepts (modules, semi-direct products, etc). However, the changes in the Fourth Edition are more “microscopic” in nature, having more to do with clarity of exposition and making the “flow” of arguments more natural and inevitable. Of course, minor editorial changes are made through the book to correct typographical errors, improve the exposition, and in some cases remove unnecessary material. Here are some more specific changes.

• Because of the increasing importance of modules in the undergraduate curriculum, the new material on modules over a PID (Chapter 7) and the Wedderburn theorems (Chapter 11) introduced in the Third Edition was thoroughly reviewed for clarity of exposition.
• More generally, in an effort to make the book more accessible to students, the writing was carefully edited to ensure readability and clarity, the goal being to make arguments flow naturally and, as much as possible, effortlessly. Of course, this is in accord with the goal of making the book more suitable for self-study.
• Appendix B is expanded to an exposition of matrix algebra over a commuta-tive ring.
• Two notational changes are introduced. First, the symbol o(g) replaces for the order of an element g in a group, reducing confusion with the cardinality of a set. Second, polynomials f(x) are written simply as f.
• In Chapter 2, proofs of two early examples of “structure theorems” are given to motivate the subject: A group of order 2p (p a prime) is cyclic or dihedral, and an abelian group of order p² is or C_p × C_p.
• More emphasis is placed on characteristic subgroups and on the product HK of subgroups H and K.
• Wilson's theorem is included in §1.3 with later applications to number theory and fields.
• In Chapter 5, it is shown that an integral domain is a UFD if and only if it has the ACC on principal ideals and either (a) every irreducible is prime, or (b) any two nonzero elements have a greatest common divisor. This shortens the original proof (with (a) only) at the expense of a lemma of independent interest.
• In Chapter 6, a simpler proof is given that any finite multiplicative subgroup of a field is cyclic.
• The first section of Chapter 8 has been completely rewritten with several results added.
• In Chapter 9, several new results on nilpotent groups have been included. In particular, the Fitting subgroup of any finite group G is introduced, several properties are deduced, and its relationship to the Frattini subgroup is explained.
• In Chapter 10, many arguments are rewritten and clarified, in particular the lemma explaining the basic Galois connection between the subgroups of the Galois group of a field extension and the intermediate fields of the extension.
• In Chapter 11, a new elementary proof is given that R = Lⁿ, where L is a simple left ideal of the simple ring R. This directly leads to Wedderburn's theorem, and the proof does not involve the theory of semisimple modules.
• A student solution manual is now available giving detailed solutions to all odd numbered (parts of) exercises.

Chapter Summaries

Chapter 0. Preliminaries. This chapter should be viewed as a primer on mathematics because it consists of materials essential to any mathematics major. The treatment is self-contained. I personally ask students to read Sections 0.1 and 0.2, and I touch briefly on the highlights of Sections 0.3 and 0.4. (Our students have had complex numbers and one semester of linear algebra, so a review of Appendices A and B is left to them.)

Chapter 1. Integers and Permutations. This chapter covers the fundamental properties of the integers and the two prototype examples of rings and groups: the integers modulo n and the permutation group S_n. These are presented naively and allow the students to begin doing ring and group calculations in a concrete setting.

Chapter 2. Groups. Here, the basic facts of group theory are developed, including cyclic groups, Lagrange's theorem, normal subgroups, factor groups, homomorphisms, and the isomorphism theorem. The simplicity of the alternating groups A_n is established for n ≥ 5. An optional application to binary linear codes in included.

Chapter 3. Rings. The basic properties of rings are developed: integral domains, characteristic, rings of quotients, ideals, factor rings, homomorphisms and the isomorphism theorem. Simple rings are studied, and it is shown that the ring of n × n matrices over a division ring is simple.

Chapter 4. Polynomials. After the usual elementary facts are developed, irreducible polynomials are discussed and the unique factorization of polynomials over a field is proved. The factor rings of polynomials over a field are described in detail, and some finite fields are constructed. In an optional section, symmetric polynomials are discussed and the fundamental structure theorem is proved.

Chapter 5. Factorization in Integral Domains. Unique factorization domains (UFDs) are characterized in terms of irreducibles, primes, and greatest common divisors. The fact that being a UFD is inherited by polynomial rings is derived. Principal ideal domains and euclidean domains are discussed. This chapter is self-contained, and the material presented is not required elsewhere.

Chapter 6. Fields. After a minimal amount of vector space theory is developed, splitting fields are constructed and used to completely describe finite fields. This topic is a direct continuation of Section 4.3. In optional sections, the classical results on geometric constructions are derived, the fundamental theorem of algebra is proved, and the theory of cyclic and BCH codes is developed.

Chapter 7. Modules over Principal Ideal Domains. Motivated by vector spaces (Section 6.1) and abelian groups, the idea of a module over a ring is introduced. Free modules are discussed and the uniqueness of the rank is proved for IBN rings. With abelian groups as the motivating example, the structure of finitely generated modules over a principal ideal domain is determined, yielding the fundamental theorem for finitely generated abelian groups.

Chapter 8. p -Groups and the Sylow Theorems. This chapter is a direct con-tinuation of Section 2.10. After some preliminaries (including the correspondence theorem), the class equation is developed and used to prove Cauchy's theorem and to derive the basic properties of p-groups. Then group actions are introduced, motivated by the class equation and an extended Cayley theorem, and used to prove the Sylow theorems. Semidirect products are presented. An optional application to combinatorics is also included.

Chapter 9. Series of Subgroups. The chapter begins with composition series and the Jordan–Hölder theorem. Then solvable series are introduced, including the derived series, and the basic properties of solvable groups are developed. Sections 9.1 and 9.2 depend only on the second and third isomorphism theorems and the correspondence theorem in Section 8.1. Finally, in Section 9.3, central series are discussed and nilpotent groups are characterized as direct products of p-groups, and the Frattini and Fitting subgroups are introduced.

Chapter 10. Galois Theory. Galois groups of field extensions are defined, separable elements are introduced, and the main theorem of Galois theory is proved. Then it is shown that polynomials of degree 5 or more are not solvable in radicals. This requires only Chapter 6 (the reference to solvable groups in Section 10.3 is adequately reviewed there). Finally, cyclotomic polynomials are discussed and used (with the class equation) to prove Wedderburn's theorem that every finite division ring is a field.

Chapter 11. Finiteness Conditions for Rings and Modules. The ascending and descending chain conditions on a module are introduced and the Jordan–Hölder theorem is proved. Then endomorphism rings are used to prove Wedderburn's theorem that a simple, left artinian ring is a matrix ring over a division ring. Next, semisimple modules are studied and the results are employed to prove the Wedderburn–Artin theorem that a semisimple ring is a finite product of matrix rings over division rings. In addition, it is shown that these semisimple rings are characterized as the rings with every module projective and as the semiprime, left artinian rings.

Chapter Dependency Diagram

A Dashed arrow indicates minor dependency.