What are the key components of the rational portfolio?
Once you have conceded that you don’t have an edge on the market, unfortunately you are not done. In fact you have only arrived at the starting point of your rational journey!
Doing nothing with our assets is not a sensible solution: we need to put our money to use to get the best return for the risk we take, just like we would if we claimed we had an edge. Figure 3.1 shows a list of issues that a rational investor needs to think about. The remainder of this book covers these issues.
Asset split in a rational investment portfolio
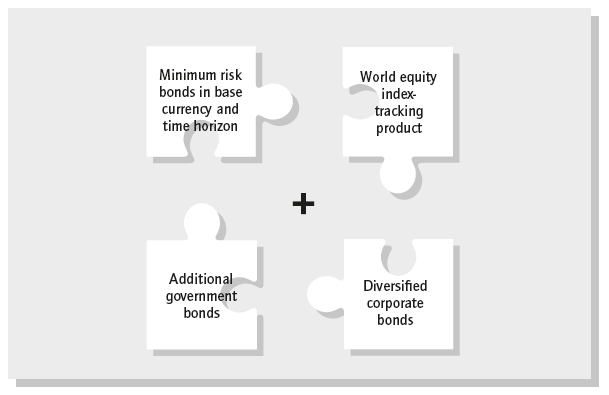
In creating the rational portfolio we split our assets into the lowest-risk assets that preserve capital and risky assets that have to generate returns, and combine the two according to our risk preference. In the low-risk bucket we should have the highest-rated and liquid government bonds, ideally available in the base currency of our investments.
If we want to achieve anything other than the very unexciting return profile of low-risk government bonds we have to turn to riskier assets. We acquire these riskier assets not for the sake of adding risk, but because we hope to get great investment returns from them. The majority of rational investors are best off with a cheaply bought index tracker of world equities as their risky assets. It is a major evolution in the investing world that products tracking these indices are now readily available: just 15 years ago they were not.
Some books on investing involve intricate arguments about why certain geographical areas or sectors of the equity markets will outperform and provide a safe haven for the investor. On the contrary, the most diversified portfolio you can find offers the greatest protection against regional declines. Also, since we are simply saying ‘buy the world’, the product is very simple and should be super cheap. Over the long run that will matter greatly.
Someone willing to add a bit of complexity to the very simple portfolio of world equities and minimal-risk government bonds could add other government and corporate bonds (see Figure 3.2). While these additions make a lot of sense and I have them in my personal portfolio, unfortunately the product offerings in the space still leave something to be desired. Creating broad and cheap index-type exposure for bond portfolios is not as simple as for equities and there is a tendency for the products to be dominated by US and European securities in particular.
Elements of the rational portfolio are summarised as follows:
| Asset class | Description |
| Minimal risk asset | UK, US, German, etc. or equivalent. Credit quality of maturity matching investor’s time horizon. |
| Equities | World equity index or as broad as possible. |
| Other government bonds | Diversified return generating government bonds of varying maturities, countries and currencies; we have used those rated sub-AA as a good indicator. |
| Corporate bonds | Broad range of corporate bonds of varying maturity, credit risk, currency, issuer and geography. |
You may have noticed that there are some investments that are not part of this portfolio: property, private equity/venture capital, commodities, hedge funds, private investments (including angel capital, etc.) and so on. Buying these asset classes requires an edge. Whether you invest in regional property, a private equity fund or buy coal, you are claiming that you know something about future performance that the rest of the world does not. Also some of those investments are similar to the exposure you already have through your broad market exposures (at a small fraction of the cost) and are often very illiquid. The liquidity of the rational portfolio is one of its most underappreciated features; having the ability to readily realise cash can be critical in some circumstances and something the rational portfolio provides.
Even during the darkest days of 2008–09, unless you had assets similar in size to a really rich oil sheik, you could unwind your portfolio at short notice if need be. If you badly need liquidity then having that option is priceless.
Understand the level of risk you are comfortable with
The products that rational investors use may be similar, but the proportions are not. If you have £105 and need £100 for heart surgery in a year, your risk profile is very different from someone with £100 at the age of 30 who needs £150 40 years hence. Our needs change over time as we age or our circumstances change. The risk you are willing to take at age 60 is typically very different from what you were willing to take at 40. Everyone is different and individual circumstances will determine what your mix of low-risk and riskier assets (like the equity markets) will be. The elements of the portfolio don’t change, but the proportions of the risky assets do.
We need to gauge current market risk, but also think about less fun stuff like the risk of money in the bank, or the risk of markets heading down as badly as they have occasionally done in the past. With a large number of caveats, I want to use our understanding of the risks of the market to be better informed about risks in our investing.
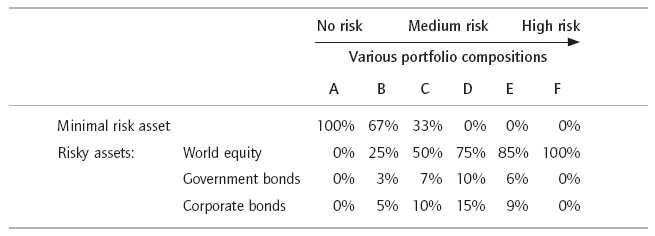
In Table 3.1 I show how you should split your portfolio into its component parts, depending on your risk levels.
So someone with £100 to invest and a medium ‘C’ risk profile could do as follows:
| Allocation | Investment |
| £33 | UK government bond tracker with maturity matching investor’s time horizon |
| £50 | World equity index tracker product |
| £7 | Diversified return generating government bonds of varying maturities, countries and currencies, rated sub-AA |
| £10 | Broad range of corporate bonds of varying maturity, credit risk, currency, issuer and geography. |
I will discuss how I came up with the allocations above. Whilst the allocations are not an exact science and therefore do not have to be implemented in exactly the proportions illustrated, you would do very well if you implement your portfolio in a similar manner.
Of course our risk tolerances differ. Let’s say that we have $100 now and need $110 in 10 years’ time, and that we invest in the world equity markets where we expect real returns of about 5% a year. If we assume that performance every year will in fact be 5% we know that in 10 years our $100 will have become $162 and be far in excess of what we need. But that is not the whole story.
Since the equity markets are inherently risky, what can we say about the probability that we don’t reach $110? Is it 1%, 2% or 20%? The answer depends on the risk of the equity markets. If we believe our expected return is $162 are we willing to move our allocations away from risky equities and into lower-risk bonds if it meant increasing our chances of reaching the $110, but with lower expected assets (because the bonds have lower expected returns)? Some people may, for example, be so risk averse that they would rather have expected assets of $120 with a 2% risk of not reaching $110, instead of expected assets of $162, but a 15% risk of not having $110 in assets. Which of the two types you are depends on your individual circumstance and attitude towards risk.
The numbers above may look complicated, but we can use them to think about the risk of our allocations in the context of our financial planning. Investment performance at times will differ significantly from average; how different will depend on the risk we take, and thinking ahead to how we react to bad outcomes will help us prepare for any eventuality.
Don’t put all your non-investment eggs in one basket
As individual or institutional investors, the investment portfolio is only one out of several parts of our investing life. This is true when we consider risk, liquidity and taxes, but also when we consider the best investment portfolio.
Perhaps without thinking about it in those terms, many investors run the risk of putting all their eggs in the same basket. Someone may have a €1 million house with a €750,000 mortgage and a €100,000 investment portfolio. The investor has more than 90% of her gross assets tied up in the property market; if she were to invest in local property on top of this she would be buying more of an exposure that she already has plenty of. Similarly, if this was an Italian-based investor she already has plenty of exposure to the Italian economy. Putting her investments into Italian stocks would not diversify her exposure away from local exposure, as an investment into a broader index would.
There is a tendency for investors to be over-invested in their home markets; the British invest in the UK, Americans in the US, etc. Historically it was impractical and expensive to buy foreign securities, and perhaps the home bias has become an ingrained habit. Aim to diversify beyond the national borders. While many domestic firms may have international exposures as part of the business mix, as an investor you probably already have plenty of exposure to your home economy.
Incorporating non-investment assets in portfolio thinking is not a scientific optimisation, but rather a gut feeling. So when you consider your overall portfolio of assets and liabilities it is mainly the risk of interconnection between your assets you should worry about. Is there some event or risk that would affect all your assets in the same way? Could this event even lead to a crisis in your local bank and thus risk your deposits? Is there a way for you to diversify away from that risk in some of your non-investment assets, or are you at least making sure that your investment assets are diversified? Depending on your circumstances, factors such as your job prospects, the value of your education, a potential future inheritance, etc. may move more in tandem than you expect. A broadly diversified investment portfolio could one day be your safe haven in a nasty local storm.
Reducing tax has a large impact on long-term returns
The average individual or institutional investor should make good use of tax planning advice. The optimal portfolio and risk profile we have discussed above can be put together without too much outside help, but in the case of tax expert advice can make a huge difference.
Tax is a constant challenge. I will describe the tax benefits of the rational portfolio, but also discuss ways to save tax generally. Considering that taxes could take a huge chunk out of your returns, it’s important to get it right.
Paying too much in fees destroys asset growth
One of the key drivers of long-term returns for the rational investor is low fees and expenses. The products involved in the creation of the optimal rational portfolio are fairly generic investment products and are cheap as a result. We are not paying anyone with the expectation that they do anything particularly clever – we are asking them to replicate an index (see Figure 3.3). Perhaps a monkey couldn’t do it, but a computer certainly could.
The world of finance seems impossibly complex when it should be simple and transparent. Lower fees are a major benefit of simplifying a complex world, but importantly this has to be done while creating a stronger portfolio. We are not doing cheap for cheapness sake, but because it is a happy by-product of the simple portfolio construction that gives us the best risk/return profile. Throughout this book I will hammer home the point of low fees. If the only thing you take away from this book is getting charged a little bit less for a financial product the next time you invest, the book and time you spent reading it will have repaid itself many times over.
The benefit of paying lower fees may not look obvious at first. It typically does not reveal itself for a long time, until the compounding of better returns are really obvious, and even then there will always be some active manager or stock picker who claimed that you missed something obvious by not investing with him. Think of it as making a little bit of money while you’re sleeping; the lower fees and sensible investment strategy should make you sleep soundly at night. However, it’s not one that leaves you sleepless with giddy excitement because of great outperformance compared to the general markets.
Implementation
The indices I suggest for your portfolio are extremely broad, transparent and liquid. As a result they should also be extremely cheap. The exact method of buying this index exposure depends on the specific tax situation, but since the underlying assets are so broadly traded, good products are generally available.
The past decade has seen a massive increase in the number of exchange traded funds (ETFs) and the amount of money invested in them. Similarly, index funds have had large asset inflows. Both developments are very positive for investors as it has increased choice when implementing the rational portfolio. With the greater number of product offerings, the fees charged have also declined. US-based Vanguard – one of the world’s largest asset management firms – has been a major player in the drive for lower fees and even today has among the best product offerings at the lowest prices.
Because the development of index-tracking products continues to be so strong, future product development may well provide even better opportunities. At a fee of around 0.25% a year for world equity products there may not be much scope to significantly improve on the annual charges. But other features like tax structures or better indices to follow may improve the execution of the rational portfolio.
Generally, as a catch-all, I call any product that cheaply recreates an index-type exposure an index tracker. This could be an ETF or index fund, but also note that just because something is called an index does not make it a good choice for the rational investor. An index of companies with CEOs named Bob is an index, but that does not make it a relevant option in achieving our portfolio.
Speculate less, sleep better!
Becoming a rational investor can be a very significant moment in the investing life of some people, and those who have spent a large part of their investing lives frustrated with their inability to outperform the markets may find it a huge relief.
So what actually happens as a rational investor? The short answer is not a lot, and that is the point. But there are some on-going tasks that you could do or have someone help you with:
- You should see if there are better or cheaper products coming on the market to replicate the rational portfolio.
- You should consider if your risk characteristics have changed significantly, or if the world around you has changed so much that the portfolio mix no longer matches your risk profile.
- You should think about your tax situation and if there are better ways of optimising it.
- If your non-investment situation changes significantly you should consider how that affects your investment portfolio.
The points above may seem like a lot to do, but really are not. These are things you should consider irrespective of whether or not you are pursuing a rational portfolio, so there is no extra work involved.
The main non-financial benefit comes from the peace of mind a rational portfolio gives the investor. Someone who has accepted the fact that they do not have an edge should naturally be investing cost efficiently for the long term. They will not be spending a lot of time and financial resources contemplating the next hot stock tip from their golfing buddy or local tip sheet (even though the tipsters are very quick and vocal to boast about their winners). They will be doing other things with their lives and slowly get richer as a result.
For the brave: portfolio theory and the rational investor
Writing about portfolio theory is probably even less fun than reading about it, but this part is important so stay with me if you are interested in the theory behind this book. You should know that the investing style and portfolio construction in this book is not something I have come up with. It is a practical implementation of the generally acknowledged most advanced theory on the subject. Implementing advanced portfolio theory in the real world gives us the best possible portfolio and is actually very easy and logical for someone that does not have an edge on the markets.
The foundation of portfolio theory is that you have a riskless investment that you can optimally combine with a series of other investments. These combinations of investments create different portfolios with a range of individual risk profiles. Because of the optimal investment combination you get the best expected return for any level of risk.
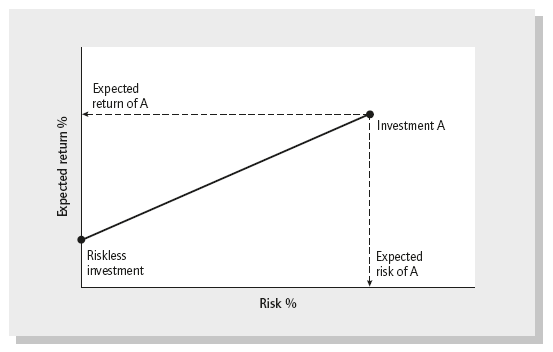
Imagine the simple scenario where you can choose between investing only in two different things: the riskless investment and investment A. Since we know what return we will get from the riskless investment (otherwise it would not be riskless) we can plot the two options on a simple chart (see Figure 3.4).
The line between the riskless investment and A represent different proportions of the riskless investment and investment A; from 0–100% (all A) to 100–0% (all riskless).
In academic theory, the riskless investment was generally acknowledged to be short-term US government bonds. For practical purposes there was no risk that the US government would default overnight: thus ‘riskless’. Those short-term US bonds still provided a return and that return was appropriately called the riskless return. The presence of this riskless return suggested that if you were not willing to take any risk with your investments whatsoever there would be the choice of investing in short-term US government bonds. Because this was the lowest risk security it was also accepted that it should be expected to carry the lowest expected return: there is no such thing as a free lunch.
Of course in today’s world the term ‘riskless investment’ sounds almost like a contradiction in terms. At the time of writing the credit rating of the US, UK and French governments have been downgraded from the highest rating, the financial press is flooded with stories of government debt and deficits, and the number of issuers with the highest credit rating have dwindled since 2007. Granted that in the run up to 2007 investors acted as if everything was riskless, but that is another story.1
Investment A can be almost anything, but think of it as a share in Microsoft. Investment A carries a higher expected return than the riskless asset, but there is also some risk associated with that return. More risk for a higher expected return; again, no free lunch.
If you want no risk, you go all riskless, and if you want more risk, you buy investment A. If you want risk between the two, you combine them.
Adding assets
Now we introduce the possibility of another investment, B. Like A, B has its own expected risk/return profile. Importantly though, the movement in the price of A and B are not entirely independent of each other, measured by the correlation (relationship) between those stocks. Remember that word – correlation. It is one of the most important, yet overused, words in the world of finance.
Correlation gives an idea of how A and B move relative to each other. With a correlation of zero there is no relationship between the two, and a correlation of 1 suggests that they move in perfect tandem. If A goes up, so will B. At the danger of oversimplifying complex statistics, most stocks within a general stock market have correlations of roughly 0.5–0.9 with each other, although correlations can change a lot over time. This means that most stocks tend to move in the same direction. You would expect Microsoft and Apple to have a high correlation, while Microsoft and the price of wheat would be less correlated. The lower that two investments’ correlation is, the more there are diversifying benefits of lower risk from investing in both of them instead of just one.
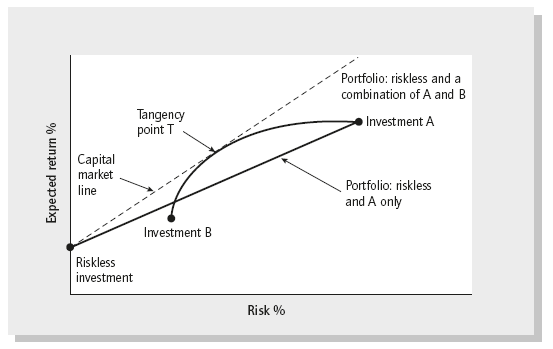
Adding the possibility of investing in investment B to Figure 3.4 gives the choices shown in Figure 3.5.
The line between A and B is not straight – this is because we assume A and B are not perfectly correlated and we benefit from the diversification of having two investments. Instead of a straight line, the curved line between A and B represents different proportions of A and B.
We can combine an investment in the riskless investment with any combination of A and B (any point on the curved line between A and B). As you see on Figure 3.5, if we draw a tangent line from the riskless investment point to the curved line then point T is where they meet. T is called the tangency point, and the line between the riskless investment and T is called the capital market line. Looking at the chart in this example, point T consists of roughly 40% of investment A and 60% of investment B (you can see point T is closer to B). You can also see from the chart that if you want the risk of point T or less, you get the highest expected return from combining point T and the riskless investment.
If we want more risk in our portfolio than point T (so on the dotted line to the right of point T) the best solution is to add leverage and invest the additional capital in the combination of 40% of A and 60% of B in this example. By adding leverage and buying more of the 40/60% T combination2 we achieve a higher return than if we had allocated more to investment A to get more risk in the portfolio. You can see that the tangent line that continues on from point T is above the curved line where the combination consists increasingly of only investment A.
The optimised market – minimise risk and maximise returns
All of this material may seem abstract and theoretical, but I hope to show how the implications for the rational investor are simple and straightforward as the combined forces of the market have already done the work for you.
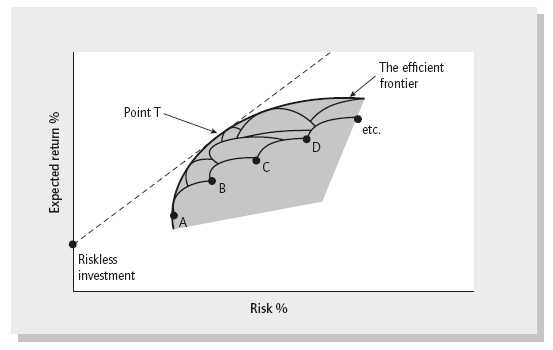
Extending the theory discussed above to the whole market, there are endless combinations. Instead of just A and B we can combine thousands of investments as illustrated in Figure 3.6.
As shown in the chart, the new tangency portfolio T is no longer a combination of just two securities but a combination of the various combinations. By combining securities in different proportions we are able to create any risk/return portfolio in the shaded area. Since we want higher returns for a given level of risk we chose combinations of securities that get us to the bold curve. In portfolio theory this curve is called the efficient frontier. What the curve is telling us is that for each level of risk there is a combination of securities in the market that gives us the highest expected return. And by combining one of those points on the efficient frontier (point T) with the riskless asset we can create portfolios with the highest level of expected return for any level of risk.
I imagine some of my old economics professors would be aghast at the simplicity of the paragraphs above and the absence of long mathematical formulas. If you are interested in the maths and theory behind this summary of portfolio theory then Modern Portfolio Theory and Investment Analysis by Edwin Elton et al. (John Wiley & Sons, 2003) is a good textbook on the subject.
Bullshit in, bullshit out
One of the things I disliked about investment banking was building massive 50-page Excel models, outlining projections of companies and industries. We would often have little to go on in terms of projections other than short analyst reports which we would use to extrapolate all sorts of data to get 5–10 year projections with all the bells and whistles. We would call this ‘bullshit in, bullshit out’, suggesting that the financial models were only as good as the assumptions we put into them.
As with the large investment banking financial models, optimal portfolio theory is subject to getting our assumptions right. You probably noticed how casually the theory suggested that you input the expected risk and return for individual securities, and the correlation between them, and voilà, the efficient frontier and the tangency point are revealed. Or rather for about £50 you can buy software that will do that for you. But the world is obviously not that simple. Ask 10 market participants about the expected risk and return over the next year on Apple shares and its correlation with Microsoft, and you will get 10 different answers. Now ask the same people to do the same thing for all listed stocks and they will tell you that you are crazy – it’s not realistic to have this kind of expectation for more than a small portfolio of shares, and besides, risk and return expectations, and correlations, change all the time. It simply can’t be done.
The beautiful shortcut – follow the crowd
But here is the beautiful thing. If you generally believe in efficient markets, you don’t need to worry about the portfolio theory above or collecting millions of correlations and thousands of risk-return profiles. The market’s ‘invisible hand’ has already done all that for you. We don’t think we are able to reallocate between securities in such a way that we have a higher risk/return profile than what the aggregate knowledge of the market provides. Buying the entire market is essentially like buying the tangency point T.
To some people it will seem like too bold an assumption that capital has seamlessly flowed between countries and industries in such a way that world markets are efficiently allocated. But if we asked: which country/industry/company is it that you want to reallocate money to/from contrary to the combined information and analytical power of millions of investors allocating trillions of dollars, and why? Accepting that investing internationally gives us greater choice and diversification than only investing in one country, we need to figure out some way to allocate between those choices. If we picked the countries/industries/companies on anything other than their relative market sizes we would essentially be claiming we knew something more than the markets.3
You can of course disagree with all of this and make claims like ‘Microsoft will go up 20% next year regardless of the market and there is almost no risk that I am wrong’. Of course you might be right, but you are also clearly claiming an edge in knowing or seeing something that the rest of the market does not. Do that consistently and you’ll be rich.
Going back to the example of having only the choice of the riskless investment and investment A, that is essentially where we end up. If we replace investment A with the world equity portfolio, and replace the riskless investment with the minimal risk asset, we have moved on from the world of portfolio theory to the real world with investments we can actually implement. We will see later that the minimal risk asset depends on the base currency of your investments.
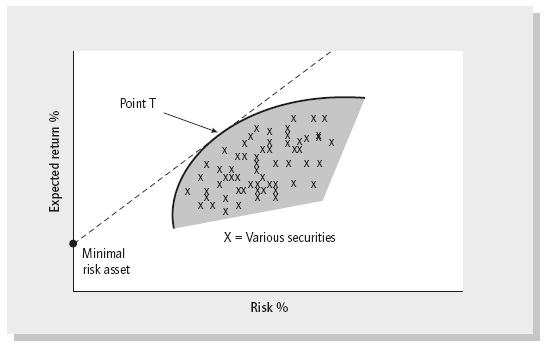
Investment A in the chart, therefore, consists of many thousands of underlying equities from all over the world in the portfolio (see later). By combining the minimal risk asset and A (world equities) in various proportions we choose various risk/return levels in the most efficient way, from minimal risk to the risk of the world equity markets, or greater than that if we borrow money. Point T is already the tangency point, or optimal portfolio, and we don’t think we can reallocate money between the many securities in such a way that we end up with better risk/return characteristics (see Figure 3.7).
Later, when we add other government and corporate bonds, we will see that this is akin to when we added the possibility of investment B earlier. While adding a bit of complexity to the portfolio, the other government and corporate bonds enhance the risk/return profile of the whole portfolio.
The best theoretical and actual portfolio
The rational portfolio is a compromise: a compromise between what we would like to create in a theoretical world and what is available practically. In an ideal (theoretical) world we should own a small slice of all of the world’s assets to maximise diversification and returns. This clearly is not possible in reality, but the rational portfolio is a very good simplification that we can actually implement. Because the asset classes of the rational portfolio have active and liquid markets for the pricing of thousands of individual securities, we don’t need any specific insight to select securities in those markets. And because government bonds, equities and corporate bonds give a very good representation of the world’s assets, a portfolio representing those asset classes is a very good simplification of what we should ideally be striving for in a portfolio. We can accept the premise that market forces have set a price on individual securities and the aggregate market at a level that is consistent with the risk/return characteristics of that asset class. Because equities are riskier, we get higher expected returns, etc. For other investments left out of the rational portfolio there is typically not a liquid and efficient market to set prices for the individual investments, so someone without an edge is unable to simply buy into the whole asset class and expect to get its overall risk/return.
So there is no theoretical inconsistency in being a rational investor – on the contrary. We don’t think we know any better than the market about the risk/return profiles of individual securities or how they move relative to one another. By pricing securities, the market effectively incorporates the views of thousands of investors and presents us with the results of the market as it currently stands.
So what is ‘the market’?
In equities, the market has often meant your local stock market. And if you invest in your local index in a cheap way you are doing better than by picking individual stocks or active mutual funds, but not as well as you could be. You could be picking a much broader geographical range of the world stock markets in proportion to their values.
So only publicly listed equities?
In order to keep things simple, we typically refer to the markets as the listed equity markets. If you invest in a combination of the minimal-risk asset and broad-listed equity markets in a cheap and tax efficient way, you are doing better than most. If you are willing to add a bit of complexity there’s a lot of merit in adding other government and corporate bonds to your portfolio (see later).
Summary
- The ‘invisible hand’ of the markets has optimised the values of the investments available. We should celebrate this simplicity and buy the whole market. We don’t think we can reallocate between securities to get a better risk/return profile.
- Combine the world equity markets with investing in the minimal risk asset to get to the kind of risk profile you want.
- The markets could mean for you only a broad range of equities, but adding other government and corporate bonds has a lot of merit.
1 An important point on portfolio theory and the minimal risk asset that will be discussed later. In accepting that the minimal risk asset is not entirely without risk the line between it and investment A is theoretically not straight, but a curve. Depending on how the minimal risk asset and investment A move relative to each other you might actually end up in a situation where the lowest risk combination of the two is not the 100% minimal risk asset, but instead has some investment A in it. For the purpose of simplicity, I have ignored this possibility.
2 This leveraged portfolio assumes that we can borrow money at the riskless rate to invest in more of the T combination, which we can’t. In reality, the cost of borrowing would be higher and the line would be flatter to the right of T than it would be to the left of T, to reflect this. If you were unwilling or unable to borrow money, the optimal portfolio at higher risk levels than T would consist increasingly of A and would be represented graphically on the curved line from T to A.
3 We are here assuming that capital can flow easily between countries and industries, which is increasingly a fair assumption.