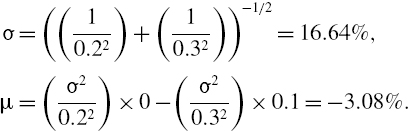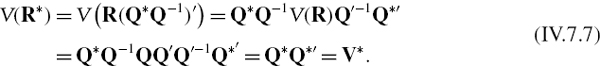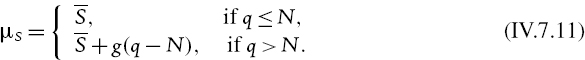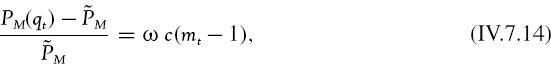IV.7
Scenario Analysis and Stress Testing
IV.7.1 INTRODUCTION
Previous chapters have focused on VaR estimates that are based on historical asset or risk factor returns. Believing these data capture the market circumstances that are assumed to prevail over the risk horizon, we then obtain a distribution of the returns (or P&L) on a portfolio and estimate the VaR and ETL at the required confidence level over the risk horizon. Whilst such a belief may seem fairly tenuous over risk horizons that are longer than a few months, experience proves that in the absence of a shock, such as the terrorist attacks on the US in 2001, market behaviour and characteristics are unlikely to alter completely over a risk horizon of a few days or weeks. It is therefore reasonable to base short-term VaR and ETL estimation on historical data, provided it is adjusted to reflect current market conditions, but as the risk horizon increases the case for using other beliefs than ‘history will repeat itself’ becomes stronger.
A main focus of this chapter is to describe the application of a particular type of belief, which is called a stress scenario, to risk models. Stress testing is a risk management tool for quantifying the size of potential losses under stress events, and for quantifying the scenarios under which such losses might occur. A traditional definition of a stress event is an exceptional but credible event in the market to which the portfolio is exposed. Then, in a stress test one subjects the risk factor returns to shocks, i.e. extreme but plausible movements in risk factors.
But how can we define the terms ‘credible’ or ‘plausible’, or similar terms such as ‘reasonable’, ‘rational’, ‘realistic’ etc., except in terms of probabilities? People tend to use such verbal descriptors because it is more difficult to phrase beliefs in terms of probability distributions. One of the main aims of this chapter is to help risk analysts to develop the mathematical framework for scenario analysis, and in particular the means to represent beliefs as probability distributions rather than using vague linguistic terminology. We shall, of course, be covering the traditional approach to stress testing in which stress scenarios are usually based on a worst case loss. However, the concept of a worst case loss is not only imprecise, it is mathematically meaningless. Indeed, there is no such thing as a ‘worst case’ loss other than losing the entire value of the investment.1 In summary, to attempt to derive a ‘worst case’ loss resulting from a ‘realistic’ scenario is to apply a mathematically meaningless quantity to an imprecise construction. So, rather than waste much time on this, after describing the traditional approaches we introduce mathematically meaningful frameworks for stress testing, with illustrative examples that are supported by simple Excel spreadsheets.
Scenario analysis and stress testing actually pre-date VaR modelling. The first commercial application of stress testing was by the Chicago Mercantile Exchange (CME) during the 1980s. The CME requires margins of 3–4 times what could be lost in a single day, as do most futures exchanges. In the early 1980s these margins were contract-specific and so some contracts such as calendar spreads (which trade a long and a short futures, with different maturities, on the same underlying) had zero margins. In 1988 the CME adopted the Standard Portfolio Analysis of Risk® (SPAN)2 system in which daily margin requirements are based on a set of standard stress scenarios including not only parallel shift but also tilts in the yield curve.3 This system has since been adopted by many exchanges.
The purpose of this chapter is to explain how risk models may be applied to scenario data and how the analyst can formalize his beliefs about the behaviour of the market over a risk horizon in a mathematically coherent framework. A complete formalization of beliefs provides a multivariate distribution of risk factor returns, to which one can apply the mapping of any portfolio and hence derive a scenario-based returns (or P&L) distribution for the portfolio over the risk horizon. The main applications of this scenario-based distribution are the same as the usual applications of return or P&L distributions that are based on historical data, i.e. to risk assessment and optimal portfolio selection.
We shall distinguish between single case scenarios that provide just one value for the vector of risk factor returns, as in the SPAN system, and distribution scenarios that prescribe an entire multivariate distribution of risk factor returns. We shall also distinguish between historical scenarios and hypothetical scenarios. A single hypothetical parallel shift of 100 basis points on a yield curve is an example of a single case hypothetical scenario. It aims to provide an ‘extreme but plausible’ value for the vector of risk factor returns, and the analyst can use the portfolio mapping to derive a ‘worst case’ loss resulting from this scenario. But he cannot assign a probability to this loss. A simple example of a hypothetical distribution scenario is that changes in yields are perfectly correlated and normally distributed, and they all have mean 100 basis points and standard deviation 50 basis points.4 Distribution scenarios provide a mathematically coherent framework for scenario analysis and stress testing. That is, because they specify an entire multivariate distribution rather than just a single vector of risk factor changes, probabilities may be assigned to different levels of loss.
Given the tremendous number of historical and hypothetical scenarios that are possible, the analyst needs to have some tool that restricts the number of scenarios that are explored. Often he will perform a preliminary sensitivity analysis that examines the loss profile of a portfolio as a function of possible values for all of its risk factors. This helps him to distinguish between the main risk drivers and the minor risk factors for his portfolio, so he can focus his scenarios on movements in the factors that are most likely to affect his portfolio adversely. It may be the case, especially in option portfolios that have highly non-linear loss profiles, that it is a small movement rather than a large movement in a major risk factor that incurs the largest losses.
The outline of this chapter is as follows. Section IV.7.2 provides a classification of the scenarios that we usually consider in market risk analysis. We also comment on the process of constructing hypothetical scenarios that are consistent with the views of the analyst and of senior management. Section IV.7.3 explains how to apply distribution scenarios in a risk model framework, to derive a scenario VaR and ETL. We consider a number of increasingly complex scenarios that are based on both parametric and non-parametric return distributions and take care to distinguish between the different use of information in scenario VaR and Bayesian VaR.
Section IV.7.4 introduces the traditional approach to stress testing portfolios, in which a ‘worst case’ loss is derived by applying the portfolio mapping to a set of possible stress scenarios, taking the maximum loss over all scenarios considered. We review the Basel Committee's recommendations for stress testing and provide an overview of the traditional approach based on worst case scenarios.
Section IV.7.5 presents a coherent framework for stress testing, illustrated with many empirical examples. We begin by focusing on stressed covariance matrices and how they are used in the three broad types of VaR models, including historical simulation, to derive stressed VaR and ETL estimates. Then we explain how to derive hypothetical stressed covariance matrices, ensuring that they are positive semi-definite. Section IV.7.5.3, on the use of principal component analysis in stress tests, highlights their facility to reduce the complexity of the stress test at the same time as focusing attention on the types of market movements that are most likely to occur. Section IV.7.5.4 describes how to estimate liquidity-adjusted VaR, differentiating between exogenous and endogenous liquidity effects. We end this chapter by explaining how to incorporate volatility clustering effects, which can have a significant impact on stress VaR and ETL when the position is held for several days.
IV.7.2 SCENARIOS ON FINANCIAL RISK FACTORS
Historical data on financial assets and market risk factors are relatively easy to obtain, compared with credit risk factors (e.g. default intensities) and especially compared with operational risk factors (e.g. the loss associated with low probability events such as major internal fraud). Market risk analysts can usually obtain many years of daily historical data for their analysis, but this is not always the case. For instance, when estimating the equity risk of a portfolio containing unlisted stocks or the credit spread risk of a portfolio of junk bonds, a market risk analyst typically has little or no historical data at his disposal. Nevertheless, so much of the documented analysis of market risk is based on historical data, that analysts may not know how to proceed when they have little or no ‘hard’ data available. By contrast, operational risk analysts are used to having virtually no history of experienced large losses in their firm. As a result operational risk analysts have developed methods based on their own personal views – in other words, based on hypothetical scenarios on risk factors.
Market risk analysis has developed in an environment where, typically, a wealth of historical data on market risk factor returns is available. For this reason risk analysts tend to rely on historical data for quantifying market risks far more than they do for operational risks, or even for credit risks. But there is a real danger in such reliance because excessive losses due to market risk factors are often incurred as a result of a scenario that is not captured by the historical data set. For instance, the Russian bond default in 1998, the bursting of the technology bubble in 2000, the credit crunch in 2007 and the banking crisis in 2008 all induced behaviour in risk factor returns that had no historical precedent at the time they occurred.
In my opinion the quantity of historical data that is commonly available for market risk analysis has hampered the progress of this subject. Market risk managers may be lulled into a false sense of security, believing that the availability of historical data increases the accuracy of their risk estimates. But risk is a forward looking measure of uncertainty, and it may be based on any distribution for risk factor returns, not only a historical one. In this text we have, until now, been estimating the parameters of these distributions using purely historical data. But this is in itself a subjective view – i.e. that history will repeat itself! So now we extend our analysis to encompass other subjective views, which could be entirely personal to the risk analyst and need not have any foundation in historical events at all.
At the time of writing the majority of financial institutions apply very simple stress tests and scenarios, using only the portfolio mapping part of the risk model to derive ‘worst case’ losses without associating any probability with these losses. The aim of this section is to help market risk analysts to think ‘out of the box’; to use their entire risk model – not just the portfolio mapping – to report on the extent of losses that could be incurred when the unexpected happens; and to do all of this within a mathematically coherent framework.
IV.7.2.1 Broad Categorization of Scenarios
We shall categorize scenarios on the risk factors of a given portfolio using two dimensions: first, the type of changes that we consider in risk factors; and second, the data that are used to derive these changes. Within the first dimension we consider two separate cases:
- Single case scenarios. These scenarios are for a single vector of the risk factor returns, such as a shift of a given magnitude in a yield curve, or a single value for the return on each major stock index. With a single case scenario we can apply the risk factor mapping model to the scenario and hence obtain a single profit or loss for our portfolio resulting from the scenario. Single case scenarios include the worst case scenarios that are applied in the traditional approach to stress testing, the base case scenarios that are used in decision analysis to capture the event that current market conditions continue to prevail over the risk horizon, and any scenario between these two extremes.
- Distribution scenarios. In a distribution scenario our beliefs are encapsulated by a continuous, multivariate distribution of risk factor returns. Applying the risk factor mapping model to such a scenario yields an entire distribution of portfolio returns or P&L. Thus, a distribution scenario allows the estimation of a scenario VaR and ETL of our portfolio.5 We shall also be extending simple distribution scenarios to compound distribution scenarios, where our beliefs are encapsulated by a discrete distribution over scenario distributions.
Regarding the data that are used, we also consider two separate cases:
- Historical scenarios. These concern a repeat of a historical event such as the global equity crash of 1987 or the banking crisis of 2008. By saving the market data from this period we can apply them to the current portfolio mapping or, better, to the entire risk model since this allows us to derive a coherent scenario analysis for our portfolio.
- Hypothetical scenarios. These can involve any changes in any risk factors and they need not have any historical precedent. For instance, a single case scenario when the vector of risk factor returns is a term structure of AA credit spreads could be that the curve shifts upwards by 50 basis points at all maturities.
Hence, there are four broad scenario categories that institutions could consider and these are summarized, along with simple illustrative examples for the iTraxx credit spread index, in Table IV.7.1.
Table IV.7.1 Scenario categorization, with illustration using the iTraxx index
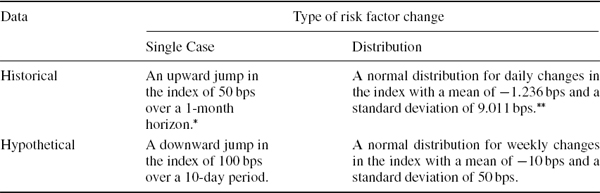
* The index was at 91 bps on 15 February, and by 13 March it had risen to a historical high of 141 bps.
** This is the high volatility component of a mixture of two normal distributions that was fitted to the iTraxx daily changes using data from June 2004 to March 2008. See the case study in Section IV.2.12.
IV.7.2.2 Historical Scenarios
Both single case and distribution scenarios can be based on historical events. By storing the market data that were recorded at the time of a specific event, we could apply either a worst case scenario (e.g. based on the total drawdown that was experienced on major risk factors over a specified time horizon) or a distribution scenario (based on an experienced distribution of risk factor returns over a specified time horizon).
Common examples of historical scenarios include: the 1987 global equity crash; the 1992 European Exchange Rate Mechanism crisis; the 1994 and 2003 bond market sell-offs; the 1997 Asian property crisis; the 1998 Russian debt default and the ensuing falls in equities induced by the threat of insolvency of the Long Term Capital Management hedge fund; the burst of the technology stock bubble that started in 2000 and lasted several years; the terrorist attacks on the US in 2001; the credit crunch of 2007 and the banking crisis of 2008. The following example illustrates how historical data from one of these crisis periods can be used to formulate both a worst case scenario and a distribution scenario.
EXAMPLE IV.7.1: HISTORICAL WORST CASE AND DISTRIBUTION SCENARIOS
Use historical data on daily closing prices of the FTSE 100 index during the period of the 1987 global equity crash to estimate the worst case daily return and worst case monthly return corresponding to this scenario. Also estimate the first four sample moments of daily returns over this period and hence estimate the 100α% daily VaR for a linear exposure to the FTSE index, comparing the results obtained for α = 0.1, 0.01 and 0.001 using a Cornish–Fisher expansion with those based on a normal distribution assumption.
SOLUTION Daily closing prices on the FTSE index were downloaded from Yahoo! Finance for the period from 13 October to 20 November 1987.6 The maximum loss over 1 day, which occurred between 19 and 20 October, was 12.22% of the portfolio value, and over the entire data period the loss on a linear exposure to the index was 30.5%. Both these figures could be used as worst case scenarios but over different time horizons, i.e. 1 day and 30 days. For instance, if we have an exposure of £10 million to the FTSE index, then the worst case daily loss according to this scenario is approximately £1.222 million and the worst case monthly loss is approximately £3.05 million.
For the distribution scenario we need to estimate the sample moments of daily returns. The results are: mean = −1.21%, standard deviation = 3.94%, skewness = −0.3202 and excess kurtosis = 1.6139. The distribution scenario allows us to compute the VaR of a linear exposure to the FTSE index, with different degrees of confidence, conditional on the occurrence of this historical scenario. Using the same calculations as were used in Example IV.3.4 to estimate the daily VaR based on a Cornish–Fisher expansion, we obtain the results shown in the column headed ‘CF VaR’ in Table IV.7.2. The last column shows the normal VaR estimates that assume the skewness and excess kurtosis are both zero. Due to the strong negative skewness and positive excess kurtosis in the sample, the CF VaR is greater than the normal VaR and the difference between the CF VaR and the normal VaR increases as we move to higher confidence levels.
Table IV.7.2 VaR estimates based on historical scenarios

We might conclude from this example that if there was a repeat of the global stock market crash of 1987 starting tomorrow and if we did nothing to hedge our position for 24 hours, we could be 90% confident that we would not lose more than 6.0% of the portfolio's value and 99% confident that we would not lose more than 12.6% of the portfolio's value over a 24-hour period.7 It is a very simple example, but it already demonstrates how distribution scenarios can provide more information than worst case loss scenarios, because we can associate a probability with each given level of loss.
IV.7.2.3 Hypothetical Scenarios
The advantage of using historical scenarios is that they are certainly credible, having actually been experienced in the past. The limitation is that they are restricted to losses that have actually occurred. Hence, most institutions also apply hypothetical scenarios in their risk analysis. To give the reader a sense of the hypothetical single case scenarios that financial institutions may be using, the following worst case scenarios were recommended by the Derivatives Policy Group in 1995:8
- a parallel shift in a yield curve of ±100 basis points;
- a linear tilt in a yield curve of ±25 basis points;9
- a parallel change in credit spreads of ±20 basis points;
- a stock index return of ±10%;
- a return of ±6% on a major currency pair, or of ±20% for a minor currency against another currency;
- a relative change in volatility of ±20%.
If the portfolio has a non-linear pay-off it is quite possible that the maximum loss will not occur at one of the extremes, such as a stock index return of +10% (for a short position) or −10% (for a long position). Hence, more recently regulators of financial institutions require them to run scenarios that are specific to their portfolios individual characteristics. Further details on the new regulations for stress testing in banking institutions are given in Section IV.7.4.1.
Hypothetical scenarios such as those defined above may be applied individually or simultaneously. If simultaneously, they may or may not respect the codependence between risk factors. For instance, no such dependency is respected in the factor push stress testing methodology that is described in Section IV.7.4.3. On the other hand, the analyst may feel that the simultaneous scenario of a 10% fall in a stock index and a 20% relative fall in its volatility is so improbable that it will not be considered.
More complex single case hypothetical scenarios can be designed that respect a sequence of events on the different risk factors of a portfolio that, in the analyst's view, is plausible. For example, suppose that a US bank announces that it must write off $20 billion of tier one capital due to defaults on loans and credit derivatives. Here is an example of a single case scenario encompassing the behaviour of US credit spreads, US money market rates, dollar exchange rates, global equity prices and stock volatility over the week following this announcement:
- US credit spreads in the US banking sector increase by 80 basis points.
- Other credit spreads on investment grade US companies increase by between 50 and 200 basis points, depending on their credit rating.10
- To compensate for higher spreads, the Federal Reserve cuts base rates by 25 basis points. As a result money market rates decrease by between 25 and 50 basis points, depending on maturity.11
- Funds flow out of the dollar into other major currencies, against which the dollar depreciates by 5%.
- The Dow Jones and S&P 500 stock indices fall 10% on fears about the US economy, and some other major stock markets that are highly correlated with the US markets follow suit.
- The volatility of US stocks (and of other highly correlated stock markets) increases by 20%, relative to its value before the announcement.
This way the analyst can think through the repercussions of his hypothetical event on the behaviour of all the relevant risk factors. It is also possible to associate a time scale with the risk factor changes, as we have done above. However, what we cannot do with single case scenarios is associate a probability with the sequence of events. For this we need to construct a distribution scenario.
We now explain how to design a mathematically coherent hypothetical distribution scenario for a vector of risk factors of the portfolio. First we state the steps to be followed and then we provide an illustrative example.
- State the hypothetical scenario event in as much detail as possible. For instance, the scenario event could be that Georgia joins NATO, Russia invades Georgia and NATO troops defend Georgia.
- Identify the risk drivers. Often there will be a single risk factor that drives the scenario, for instance a fall in the S&P 500 index or rises in the values of the US dollar and gold.
- Specify conditional scenarios on the main risk driver. That is, specify a distribution that represents your beliefs about the possible values of the main risk driver resulting from the scenario event. Note that the conditional scenarios can be a set of distributions, each referring to a different time horizon. For instance, when specifying conditional scenarios on the government yield curve in Singapore, conditional on an unpegging of their currency from the US dollar, the analyst may specify the distribution of interest rate changes over the next week, the next month, the next three months and so on.
- Conditional on each possible value for the main risk driver, specify scenarios on other risk factors of the portfolio. For instance, suppose the scenario event is that, as a result of the credit crisis, a major US bank becomes insolvent. Given the nervousness in the market at the time of writing, credit spreads on AA bonds could rise to 150 basis points within a month.12 Conditional on this, what could happen to the secondary drivers, i.e. interest rates and equities prices? Perhaps it is more likely that the government will bring down interest rates than raise them, and it is also more likely that equity prices would fall. So, conditional on a 150 basis points rise in AA spreads over the next month we have a distribution of interest rate changes and another distribution of equity returns over the next month. These distributions refer to the same time horizon as the change in the main risk driver that they are conditional upon.
EXAMPLE IV.7.2: HYPOTHETICAL DISTRIBUTION SCENARIO: BANK INSOLVENCY
One of the major US banks announces that it must write off $10 billion of tier one capital due to defaults on loans and credit derivatives. Formulate your hypothetical distribution for credit spreads and US interest rates.
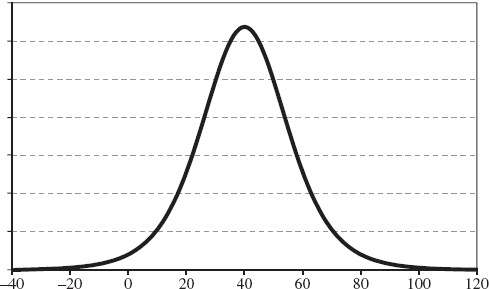
SOLUTION The main risk driver of this scenario is a credit spread index for the banking sector in the US. Figure IV.7.1 depicts my personal view about the possible changes in this index over the next week.13
Now, conditional on each of the possible changes in the credit spread index I must formulate a view on the possible weekly change in interest rates. Figures IV.7.2 and IV.7.3 depict two distributions for interest rate changes, each conditional on a different level for the credit spread.
Figure IV.7.1 A personal view on credit spread change during the week after a major banking crisis
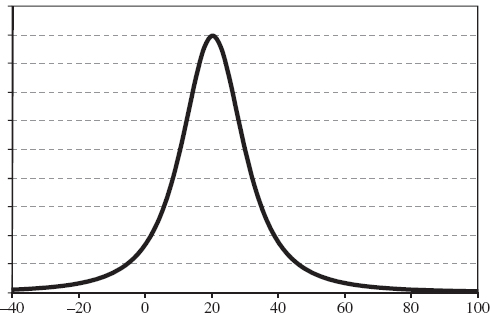
Figure IV.7.2 Distribution of interest rate changes conditional on a 20 basis point fall in the credit spread
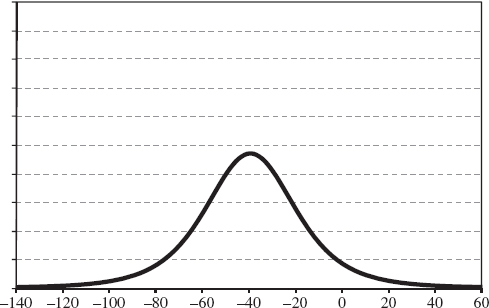
Figure IV.7.3 Distribution of interest rate changes conditional on a 40 basis point rise in the credit spread
My view assumes that there is a negative correlation between interest rates and credit spread changes, and that my uncertainty surrounding interest rate changes is directly proportional to the absolute change in spread. For instance, conditional on the credit spread increasing by 40 basis points, my beliefs about the interest rate are captured by the distribution shown in Figure IV.7.3, which has a lower mean and a higher standard deviation (i.e. more uncertainty) than my subjective distribution conditional on the spread decreasing by 20 basis points, which is shown in Figure IV.7.2.
IV.7.2.4 Distribution Scenario Design
The encoding of subjective beliefs into probability distributions has been studied by many cognitive psychologists and by the Stanford Research Institute (SRI) in particular.14 A number of cognitive biases are known to be present, one of which is that most people have a tendency to be overconfident about uncertain outcomes.
For instance, consider the following experiment that was conducted by SRI researchers during the 1970s. A subject is asked to estimate a quantity which is known but about which they personally are uncertain.15 Ask the subject first to state a value they believe is the most likely value for this quantity: this is the median. Then ask them to state an interval within which they are sufficiently sure the quantity lies – sufficiently sure to place a double-or-nothing bet on being correct. This is the interquartile range. Then, by associating ranges with other bets, elicit responses for 90%, 95% and 99% confidence intervals for the value of the quantity in question. Finally, reveal the true value, and mark the quantile where it lies in the subject's distribution. Repeat this for a large number of different uncertain quantities and for a large number of different subjects. If the subjects were encoding their beliefs accurately we should find that 10% of the marks fall outside the subject's 90% confidence intervals, 5% fall outside the 95% intervals and 1% fall outside the 99% confidence intervals. However, the empirical results from SRI established that these intervals were far too narrow. For instance, approximately 15% of marks fell outside the 99% confidence intervals.
This type of bias is particularly relevant for analysts who wish to encode a senior manager's beliefs into a quantifiable scenario distribution that is to be used for stress testing, since the effect of the bias is to reduce the probability in the tails. In other words, people have the tendency to assign a lower probability to a stress scenario than they should. Spetzler and Staël von Holstein (1977) describe a general methodology for encoding a subject's probability distribution about an uncertain quantity using a series of simple questions. The methodology is designed to deal with a variety of cognitive biases, such as the tendency towards overconfidence that most subjects exhibit in their responses. Armed with such a methodology, how could it then be applied to formulate distribution scenarios for stress testing?
The first distribution to encode should relate to the main risk driver of the scenario, such as changes in the credit spread or the oil price. Then encode the distributions for related risk factors conditional on different values for the main risk driver. For instance, conditional on the BBB-rated credit spread increasing by 100 basis points or more, encode the subjective distribution of the change in the base interest rate. Let X denote the change in the credit spread and Y denote the change in the interest rate, both in basis points. From the first encoding we obtain P(X ≥ 100) and from the second we obtain P(Y ≤ y | X ≥ 100) for different values of y, e.g. for y = −50. Then the joint probability of credit spreads increasing by 100 basis points or more and the interest rate decreasing by 50 basis points or more is P(Y ≤ −50 and X ≥ 100) = P(Y ≤ −50 | X ≥ 100) P(X ≥ 100).
The sequential encoding of conditional distributions aims to assign a probability to any vector of risk factor returns, and to a vector corresponding to extreme returns in particular. Then, substituting this vector into the portfolio mapping, we obtain a worst case loss with a specified subjective probability. However, the method described above is very subjective, and depends heavily on the analyst's ability to encode complex beliefs into quantifiable distributions. There are more tangible ways in which one can associate a probability with a loss that is incurred under a stress scenario, some of which are described in the next section.
IV.7.3 SCENARIO VALUE AT RISK AND EXPECTED TAIL LOSS
In this section we describe how to apply VaR models to either historical or hypothetical distribution scenarios, focusing on the latter case. We begin by considering the simplest, normally distributed scenarios for risk factors and then explain how these scenarios have a natural extension to a compound distribution scenario using the normal mixture framework. Then we explain how to derive scenario VaR and ETL using a more general non-parametric framework for compound distribution scenarios. Finally, we describe how ‘hard’ data based on the historical evolution of risk factors may be combined with ‘soft’ data based on the analyst's personal views in a Bayesian VaR analysis.
IV.7.3.1 Normal Distribution Scenarios
The normal linear VaR formula (IV.2.5) depends on two parameters of the portfolio's h-day discounted return distribution, its expected value μh and its standard deviation σh, which until now have been estimated from historical data on the portfolio returns.16 It is important to note that the standard deviation represents the uncertainty about the expected value, i.e. the dispersion of the discounted return distribution about its centre. It does not represent uncertainty about any other value. Thus, to apply the formula (IV.2.5) to a scenario VaR estimate, the analyst should express his views about the discounted expected return on the portfolio using his point forecast of the discounted expectation and his uncertainty about this forecast, in the form of a standard deviation.
We now present some numerical examples that show how to estimate a normal distribution scenario VaR and ETL based on increasingly complex, but plausible scenarios.
EXAMPLE IV.7.3: SCENARIO BASED VAR FOR UNLISTED SECURITIES
You hold a large stake in an unlisted company. Based on analysts’ forecasts you believe that over the next month the asset value will grow by 2% in excess of the risk free rate. But you are fairly uncertain about this forecast: in fact, you think there is a 25% chance that it will in fact grow by 3% less than the risk free rate. Using a normal distribution scenario, estimate the 10% 1-month scenario VaR and ETL, expressing both as a percentage of your investment in the company.
SOLUTION Suppose X denotes the return on the company's asset value over the next month. Your discounted expected return over 1 month is 2% and we can express your uncertainty forecast as
![]()
Applying the standard normal transformation gives
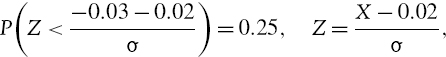
where Z is a standard normal variable. Thus
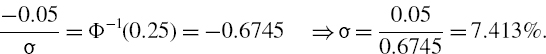
We now apply the normal linear VaR formula to obtain the VaR estimate
![]()
The 10% 1-month normal scenario VaR estimate is 7.5%, so we are 90% sure that you will lose no more than 7.5% of your investment over the next month.
Next, applying the formula (IV.2.84) for the normal ETL, we obtain
![]()
Thus, if you do lose more than 7.5% of your investment you should expect to lose about 11% of your money over the next month.
EXAMPLE IV.7.4: SCENARIO INTEREST RATE AND CREDIT SPREAD VAR
A bank has an exposure of $0.25 billion to 5-year BBB-rated interest rates in the US. The interest rate is currently 6.5%. Over the next 3 months you expect that BBB-rated 5-year credit spreads will increase by 50 basis points and that 5-year LIBOR rates will fall by 75 basis points. You express your uncertainty about these expected values using a bivariate normal distribution scenario with the following parameters:
- 5-year LIBOR volatility = 100 bps
- 5-year spread volatility = 125 bps
- LIBOR–spread correlation = −0.25.
Estimate the 0.1% scenario VaR over the next 3 months that is due to changes in interest rates and credit spreads.
SOLUTION We shall use the normal linear VaR formula (IV.2.14), i.e.
where θ denotes the 2 × 1 vector of the exposure's PV01 to LIBOR rates and credit spreads and Ωh and μh are defined below, for a risk horizon of 3 months. Using the approximation (IV.2.27), we obtain the PV01 of a $5 billion exposure at 5 years over a 3-month risk horizon when the interest rate is 6.5% as
![]()
Thus the sensitivity vector to LIBOR and credit spread changes is θ′ = (85,667 85,667)′. The expected changes in LIBOR and spread over the next 3 months are summarized in the vector
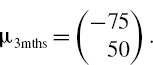
The covariance matrix that expresses your uncertainty about this expectation is17
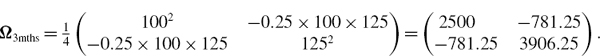
Now substituting these values into the VaR formula with α = 0.001 gives the 0.1% 3-month VaR as $20,566,112. This is 8.23% of the exposure. Thus, according to our scenario we are 99.9% confident that the bank will not lose more than 8.23% of the exposure due to changes in credit spreads and interest rates over the next 3 months.
EXAMPLE IV.7.5: SCENARIO BASED VAR FOR COMMODITY FUTURES
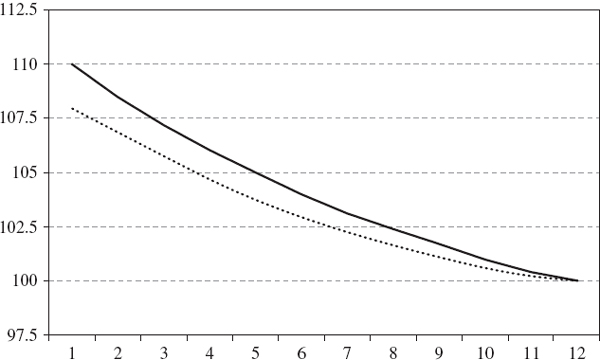
An oil company produces 10 million barrels of crude oil per month. Figure IV.7.4 depicts, by the black line, the current term structure of crude oil prices for the 1- to 12-month futures contracts. The dotted line in the figure shows the company's expectation for the term structure of futures prices one week from now. The current prices and the expected changes in the prices are given in Table IV.7.3.
Suppose the company's uncertainty about the percentage returns at each maturity is represented by a standard deviation equal to the absolute value of the expected percentage return. For instance, the standard deviation of the 1-month futures is
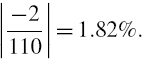
We also assume the correlation between the returns on i-month futures and j-month futures is 0.96|i−j|.
Figure IV.7.4 Term structure of crude oil futures now and in one week
Table IV.7.3 Prices for crude oil futures ($/barrel)

Table IV.7.4 Expected weekly returns, standard deviations and correlations
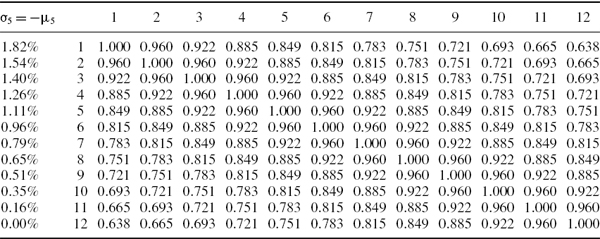
The first column of Table IV.7.4 shows the assumed vector of standard deviations of the returns over the next week (which is set equal to the absolute value of the expected return) at different maturities. The rest of the table displays their assumed correlation matrix. Based on these hypothetical data, use a multivariate normal distribution scenario to estimate the 1% 10-day scenario VaR of this exposure (ignoring discounting, for simplicity). What is the difference between this result and the result based on a scenario where the expected futures price change is zero for all maturities, but where the uncertainty is still specified by Table IV.7.4?
SOLUTION The expected weekly return μ5 is given by −1 times the first column of Table IV.7.4 and the weekly covariance matrix Ω5 is obtained using the usual matrix product DCD where D is the diagonal matrix of weekly standard deviations given in the first column of Table IV.7.4. Here C is the correlation matrix shown in the remaining part of the table. The weekly covariance matrix is computed in the spreadsheet for this example. Since Table IV.7.4 refers to weekly returns, for a 10-day VaR we multiply both the expected weekly return and the weekly covariance matrix by 2.
Now we apply formula (IV.7.1) where θ denotes the vector of the nominal exposures to each futures contract, which is calculated by multiplying the current price of each futures contract by 10 million, this being the number of barrels produced each month. In the spreadsheet we calculate the VaR with and without the expected return term, obtaining a 1% 10-day VaR of $347 million when we ignore the expected loss in revenues, and $607 million including the expected loss in revenues.
A couple of comments are required about the practical aspects of the above example. First, we have ignored the oil company's production costs. If they are significantly less than the current price of oil then they will be making a large profit, and do not need to hold any capital against expected losses, or against their uncertainty about expected losses. Second, even when production costs are large and profits are jeopardized by an expected price fall, most large corporations employ historical accounting, not mark-to-market accounting, for their production. So their corporate treasury will not necessarily use VaR as a risk metric.18
IV.7.3.2 Compound Distribution Scenario VaR
Compound distribution scenarios lend themselves to situations where the analyst believes there is more than one possible distribution scenario for the evolution of his portfolio value, and when he has a subjective estimate of the probability of each distribution scenario. In this subsection we illustrate a simple compound distribution scenario based on a normal mixture distribution. A mixture of two normal distributions can be used to represent beliefs about a market crash, when the probability of a crash during the risk horizon is specified. Two numerical examples illustrate the application to credible scenarios on equities and credit spreads. Then we define a general theoretical framework in which the component distributions in the scenario are not constrained to be normal.
The application of normal mixture scenarios to long-term VaR has more mathematical (as well as economic and financial) meaning than the blind extrapolation of short term market risks to very long horizons, based on totally unjustified statistical assumptions. We should question the standard practice of estimating VaR over a short risk horizon and then scaling the estimate to a longer horizon under the assumption that the portfolio returns are i.i.d. The i.i.d. assumption is seldom justified, and it introduces a considerable model risk in long-term VaR estimates. In this section we demonstrate how the analyst could use his knowledge of financial markets and economic policy to formulate a subjective view on the long-term return distribution, and hence obtain an appropriate VaR estimate, in the normal mixture framework.
EXAMPLE IV.7.6: SCENARIO VAR WITH A SMALL PROBABILITY OF A MARKET CRASH
A portfolio has shown a steady positive return in excess of the risk free rate of 3% per annum with a volatility of 25%. The portfolio manager believes there is a small chance, say 1 in 100, that the market will crash during the next 10 days, in which case he believes that the expected portfolio excess return over a 10-day period will be −10% with an annual volatility around this of 100%. What is the 100α% 10-day normal mixture VaR and how does it compare with the VaR under the assumption of that no crash can possibly occur? Compute the answer as a percentage of the portfolio value, and for α = 0.05, 0.01, 0.005 and 0.001.
SOLUTION To answer this we use the implicit formula for the mixture VaR that is derived in Section IV.2.9.2 with two 2-component normal densities and where:
- π is the probability of regime 1 (i.e. 0.01),
- μ1,10 is the 10-day excess return in regime 1 (i.e. −0.1),
- σ1,10 is the 10-day excess return standard deviation in regime 1 (i.e. 0.2),
- μ2,10 is the 10-day excess return in regime 2 (i.e. 0.03/25 = 0.0012), and
- σ2,10 is the 10-day standard deviation in regime 2 (i.e. 0.25/
 = 0.05)
= 0.05)
Using the Excel spreadsheet for this example with Solver (or Goal Seek) applied each time we change the significance level, we obtain the normal mixture VaR figures in the first row of Table IV.7.5.
Table IV.7.5 Normal mixture VaR versus normal VaR

The two set of figures corresponding to normal VaR, shown in the last two rows of Table IV.7.5, are calculated using a single value for the discounted returns standard deviation and expected value over the holding period. The ‘normal VaR 2’ figures are computed using the second (i.e. ‘ordinary market circumstances’) distribution of excess returns. That is, we ignore the possibility of a market crash in the ‘ordinary’ normal VaR and use the expected value of 0.0012 and standard deviation of 0.05. For the ‘normal VaR 1’ figures shown in the table we apply the normal linear VaR using a density that has the same mean and standard deviation as the normal mixture density. By (IV.2.73) the standard deviation is the square root of
![]()
and the mean is πμ1,10 + (1 − π)μ2,10. These adjust the ‘ordinary’ market mean and standard deviation to take account of the possibility of a crash, but after this the VaR is computed using a normal assumption for portfolio returns.
From the results in Table IV.7.5 it is clear that ignoring the possibility of a crash can seriously underestimate the VaR at high confidence levels. The normal mixture VaR estimates are based on a distribution with extremely high excess kurtosis, because the probability of a market crash is very small. Hence it is only at the very high confidence of 99.5% and 99.8% that the normal mixture scenario VaR exceeds the normal VaR estimates. Even if one were always to assume a normal distribution, comparing the normal VaR 2 results (which exclude the manager's beliefs about the crash entirely) with the normal VaR 1 results, the latter is larger especially at the high confidence levels.
Readers may use the spreadsheet for the above example to compute the scenario VaR during periods of intense volatility, such as October 2008, when the analyst's view on the crash probability may be considerably greater than 1% and, if the market recovers, the expected daily excess return could be considerably greater than 0.12%.
To demonstrate how flexible normal mixture scenario VaR is, the next example considers the case where a risk analyst estimates the annual VaR of a 5-year BBB-rated bond at the 99.9% confidence level. The VaR estimate is based on his personal beliefs about the possible values of the bond's credit spread one year from now, which are summarized in a distribution that is derived from a mixture of three normal distributions with different means and variances. The density function for this distribution is shown in Figure IV.7.5.19
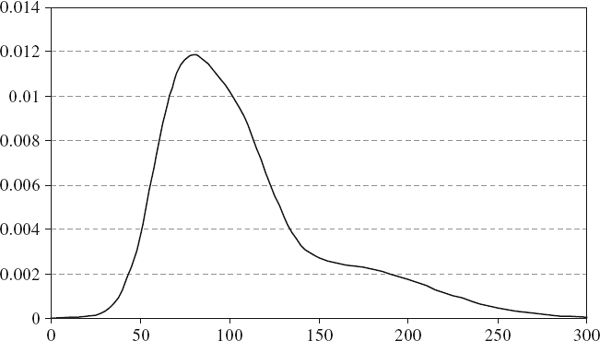
Figure IV.7.5 Personal view on credit spread of bond, one year from now
EXAMPLE IV.7.7: CREDIT SPREAD NORMAL MIXTURE SCENARIO VAR
You have invested several million dollars in a 5-year BBB-rated zero coupon bond. The PV01 of your exposure at 5 years is $1000 and the current credit spread on this bond is 100 basis points. You believe that, 1 year from now, there are only three possibilities. The bond will either be upgraded to an A rating, downgraded to a BB rating, or remain in the same credit rating, and your subjective probabilities for the occurrence of these three scenarios are 0.3, 0.3 and 0.4, respectively. Your beliefs about the change in the credit spread, in basis points and over an annual horizon, are summarized in Table IV.7.6. Assuming that your uncertainty about each of the three component scenarios is captured by a normal distribution, the resulting mixture distribution is depicted in Figure IV.7.5. Use this personal view to estimate the 0.1% annual VaR and ETL for your exposure to this bond.
Table IV.7.6 Analyst's beliefs about credit spreads

SOLUTION In the spreadsheet for this example we use the Solver to back out the VaR from the normal mixture VaR formula derived in Section IV.2.9.2 with three component normal densities. The result is an estimate of 0.1% annual VaR equal to $78,942. The reader may change the personal view and/or the VaR parameters and recalculate the VaR, but note that a suitable starting value in cell B10 is sometimes needed for Solver to converge.
Compound distribution scenarios that involve Student t distributions can be dealt with in the simple framework illustrated by the two previous examples, simply by replacing one or more of the normal components in the mixture VaR formula (IV.2.72) by Student t distributions with specified degrees of freedom.20
We now explain a general simulation method for simulating scenario VaR and ETL using component distribution scenarios that need not be Student t or normally distributed. Suppose beliefs are captured by a compound distribution scenario, similar to the normal mixture scenarios described in the examples above, but now we allow the distribution function for each scenario to be any distribution we like. For instance, one or more components could be non-parametric distributions based on empirical observations on risk-factor returns drawn from different historical periods. Or we could use one or more empirical distribution components plus one or more parametric distribution components with parameters that are assigned subjectively according to our views about the return distribution in the case that this scenario pertains. We also require a subjective estimate for the mixing law of the compound distribution, i.e. a probability vector whose components correspond to our subjective probability assigned to each scenario.21
For simplicity we shall henceforth assume that there are only two components in the compound distribution scenario, since the extension to more than two (but still a finite number of) components is straightforward to extrapolate from this description. Thus we represent the mixing law by a vector (π, 1 − π) with 0< π < 1, and we denote the two component distribution functions G(x) and H(x) where x is the return on our portfolio.22 The compound scenario is represented by the distribution
The VaR and ETL corresponding to this scenario are then estimated using the following twostep simulation algorithm:
- Draw a random number u from a standard uniform distribution: if u < π then select the distribution G(x), otherwise select H(x).
- Simulate a return from the selected distribution using the standard (historical or Monte Carlo) approach.
- Return to step 1 and repeat thousands of times to obtain an empirical, simulated return distribution.
This way we simulate from the compound return distribution (IV.7.2) that represents our beliefs, and thereafter we can estimate the VaR and ETL from the simulated return distribution in the usual manner.
IV.7.3.3 Bayesian VaR
The classical or ‘frequentist’ approach to statistics focuses on the question: what is the probability of the data, given the model parameters? This probability is measured by the likelihood function of the data, which is introduced in Section I.3.6.1. The functional form and the parameters of the distribution are assumed to be fixed, although unknown, but the point to emphasize is that classical statisticians assume that at any point in time there is one true value for each model parameter. Hence, they only make probabilistic statements about the likelihood of the sample data, given that the assumed distribution is the true distribution.
Bayesian statistics, on the other hand, focuses on our uncertainty about model parameters.23 There may be a true value for each parameter at any point in time, but we shall never know for sure what it is. Bayesians represent the possibilities for true values of a parameter by a probability distribution. In this way probabilistic statements can be made about model parameters, thus turning the classical question around, to ask: what is the probability of the parameters, given the data?
The Bayesian process of statistical estimation is one of continuously revising and refining our subjective beliefs about the state of the world as more data become available. It can be considered as an extension of, rather than an alternative to, classical inference: indeed, some of the best classical estimators may be regarded as restricted forms of Bayesian estimator.24 Bayesian estimators are based on a combination of prior beliefs and sample information. The idea is to express uncertainty about the true value of a model parameter with a prior distribution on the parameter that describes one's beliefs about this true value. Beliefs, i.e. personal views, can be entirely subjective, but more ‘objective’ information may be added to these prior beliefs when it becomes available, in the form of the likelihood of an observed sample of data. The likelihood function is used to update the prior distribution to a posterior distribution using Bayes’ rule.
Bayes’ rule, the cornerstone of Bayesian analysis, is based on the theorem of conditional probability which is described in Section I.3.2.2. There we stated Bayes’ rule for two probabilistic events A and B as
When Bayes’ rule is applied to distributions about model parameters we let A be the parameters and B be the data, and Bayes’ rule is usually written as25
![]()
We identify P(parameters) with the prior density, often based entirely on a subjective view about the possible values for each parameter, and P(data parameters) with the sample likelihood which, for Bayesian VaR analysis, will usually be based on historical data. Then P(parameters data) is the posterior density on possible parameter values, which takes account of the extra information we have obtained by observing the sample data.
Hence Bayes’ rule may be written26
Note that the posterior will be normal if both the likelihood and the prior are normal, because the product of two normal density functions is another normal density function. In fact, if the sample distribution is ![]() and the prior distribution is
and the prior distribution is ![]() then the posterior distribution is N(μ,σ2) with
then the posterior distribution is N(μ,σ2) with
To prove this, write the product of the two normal density functions as
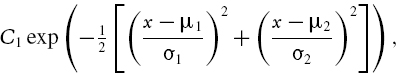
where C1 is a constant (i.e. it does not depend on x). Now, after some algebra it may be shown that the term in square brackets above may be written in the form
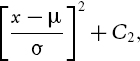
with μ and σ given by (IV.7.5) and where C2 is another constant. We can ignore the constants, because we will normalize the posterior density after multiplying the two density functions representing the likelihood and the prior, as explained above.
When formulating prior distribution scenarios one should always use a prior that reflects all the information, views and opinions that one has a priori – no more, no less. This is crucial for rational descriptions and decision making. Note that if there is no prior information, then the prior beliefs are that all possible values of parameters are equally likely. In this case the prior distribution is just the uniform distribution. Then the posterior density is just the same as the sample likelihood, so the Bayesian VaR and ETL estimates will be identical to the standard VaR and ETL estimates.
EXAMPLE IV.7.8: COMPARISON OF BAYESIAN VAR AND SCENARIO VAR
Consider two ways of forming a personal view about the portfolio's annual return distribution:
- (a) Analyst A believes that there is a 1 in 10 chance that some major political event will occur during the next year, in which case the portfolio's expected return over the next year will be −10%, with a volatility of 30%.
- (b) Analyst B has the prior belief, in the absence of any historical information on the portfolio's performance, that the portfolio will return −10% over the next year, with a volatility of 30%.
Now both analysts observe some ‘objective’ sample data on the portfolio's returns. These have mean zero and volatility 20%. Assuming both the objective data and the personal views have distributions that are normal, combine the beliefs with the objective data to estimate the 5% and the 1% annual VaR expressing the result as a percentage of the portfolio value.
SOLUTION The difference between case (a) and case (b) is subtle. In case (a), which corresponds to a normal mixture scenario, we have more information about the probability with which each scenario will occur than we do in case (b), which represents the Bayesian view. The view of analyst A is that there is a 90% chance that the objective sample represents the return distribution and a 10% chance that some adverse political event will occur. But this information is not used for the Bayesian view. That is, case (a) uses a weighted sum of normal densities, which is not another normal density, but case (b) takes the product of the densities, which is another normal density. We now describe the distribution of returns in each case and estimate the VaR.
Analyst A
The analyst's view is represented by a normal mixture distribution with parameters
![]()
This is depicted by the grey curve in Figure IV.7.6. Using Solver to back out the VaR in the usual way, we obtain: 5% VaR = 36.37%, 1% VaR = 54.27%.
Analyst B
We find the posterior density by multiplying together two normal density functions: the likelihood has mean zero and standard deviation 0.2 and the prior has mean −0.1 and standard deviation 0.3. Hence, by (IV.7.5) the posterior distribution is a normal distribution with
Using these in the normal linear VaR gives the result: 5% VaR = 30.45%, 1% VaR = 41.79%.
The Bayesian posterior density corresponding to analyst B is depicted by the normal black curve in Figure IV.7.6.27 Notice that the normal mixture scenario corresponding to analyst A has a heavier lower tail than the Bayesian posterior distribution, so the normal mixture scenario VaR at high confidence levels could be much greater than the Bayesian VaR.
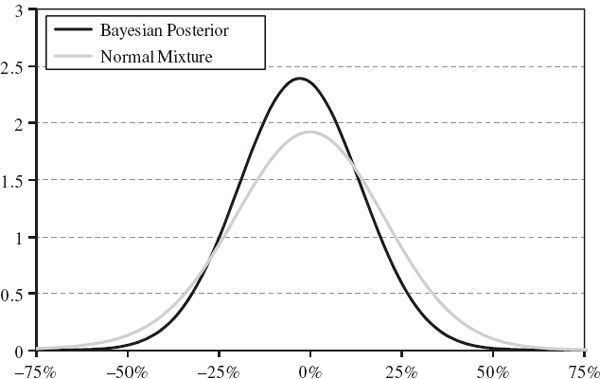
Figure IV.7.6 Comparison of normal posterior with normal mixture
IV.7.4 INTRODUCTION TO STRESS TESTING
Since the 1990s regulators of financial institutions have been encouraging risk managers to look beyond the standard risk metrics such as volatility and VaR, and to think for themselves about circumstances that could generate extreme losses. Mechanically reapplying the same risk metric to the same risk model each day, where the only difference is that the portfolio sensitivities and the corresponding data for the risk factors have been updated, is like playing the same score on a pianola, day after day.28
If estimating VaR is like playing a pianola then stress testing is like performing on a concert grand. Over the course of the last decade the design, structure and implementation of risk models have all evolved considerably, and what was state-of-the-art 10 years ago now seems simplistic in the extreme. Today, in most major financial institutions, advances in theoretical financial risk analysis, computational power and database design have combined to produce sophisticated models for measuring market risk. Regulators lay down few prescriptive rules for stress testing, leaving analysts a fairly free choice of what to ‘play’ on their risk model. But all too often they only play some variation on Chopsticks.29
If the risk analysts are musicians then the senior managers and board members that are responsible for the overall solvency of the firm are the conductors. It is the task of the most senior members of the firm to define the stress scenarios that are used, and to formulate dynamic contingency plans under each scenario, just as it is the conductor's task to direct the musicians in the orchestra. At the time of writing the majority of conductors are directing some version of Chopsticks where the score (not that Chopsticks really requires a score) is a ‘worst case’ scenario (not that this actually means anything).
The challenge facing the profession today is that many senior managers and board members are unaware how to direct analysts to produce meaningful results. With the new professional standards that we have been setting since the 1990s, risk analysts should now be sufficiently well trained; it is the senior managers who all too often fail to understand the risk model properly. Yet, to assess risks in a coherent mathematical framework, they must learn to conduct a score that is a little more complex than Chopsticks.
Well, one can take analogies only so far, so – although I could easily continue because I feel in need of some light relief, having worked so long on these books – let me now summarize my views and close by focusing on an important learning point. After nearly two decades of rapid development, market risk management systems and the analysts that work with them have evolved to an extent that meaningful stress tests can be performed. But in order to do this, analysts must first ask senior managers the right questions, and senior managers must learn to understand these questions. ‘What is the worst case scenario’ is not the right sort of question, because an analyst cannot apply his risk model to such a scenario; he can only apply the portfolio mapping. And, in this case, the result is meaningless because there is no probability associated with a ‘worst case’ loss. Instead the analyst needs to design a simple set of questions that aim to encode the senior manager's beliefs about changes in major risk factors into a distribution scenario. Given this distribution the analyst can use his entire risk model – not only the portfolio mapping – to apply meaningful and coherent stress tests corresponding to each such scenario.
IV.7.4.1 Regulatory Guidelines
The internal calculations for market risk capital are based on 1% 10-day VaR estimates that are derived using historical data, but these calculations cannot reveal the extreme losses that could be incurred in unexpected exceptional circumstances. Since the end of 1997, financial institutions using internal VaR models to assess capital adequacy have been required to implement stress testing. The 1996 Market Risk Amendment to the 1988 Basel Accord specified that a bank wishing to use an internal model for market risk capital must have in place a rigorous and comprehensive stress testing program designed to identify events or influences that could have a significant impact on the bank's capitalization. Stress scenarios need to cover a range of factors that can create extraordinary losses in trading positions. The results of stress tests should be routinely communicated to senior management, and periodically to directors.
Consequently, for the past 10 years banks have been considering low probability events on all major risk factors – without assigning any numerical value for this probability – and from these events they have been deriving extreme scenarios for the risk factors that, when input to a portfolio mapping, produce a so-called ‘worst case’ loss. Regulators require that banks do this for both linear and non-linear exposures and that they provide a qualitative as well as a quantitative analysis in their stress testing reports to supervisors. The quantitative report describes ‘plausible’ stress scenarios that could have a significant impact on their particular exposures in numerical terms, and evaluates the total loss incurred by the bank under such scenarios. The qualitative report evaluates the bank's capacity to absorb losses of this magnitude and identifies the bank's strategy for reducing risk and conserving capital under a stress scenario.
More recently regulators have emphasized the importance of stress test results for determining capital adequacy in banks, by requiring that a bank's minimum regulatory capital for market risk covers the losses that are quantified in stress tests. Specifically, the Basel II Accord, which was adopted in the EU countries in January 2007 and in the US in January 2008,30 states that ‘A bank must ensure that it has sufficient capital to meet the minimum capital requirements set out in the Market Risk Amendment and to cover the results of its stress testing required by that amendment.’ Moreover, in addition to the stress tests recommended in the Basel I Amendment, banks must consider stress tests relating to a number of specific scenarios, including illiquidity,31 concentrated positions, gapping of prices,32 one-way markets and default events.
The results of stress tests help regulators to assess the capital adequacy of a particular institution, and in particular they are supposed to give regulators an idea – however crude – of the likelihood of insolvency over some future time horizon.33 Banking supervisors will want to see:
- a document describing the stress testing methodologies used;
- the results of a portfolio sensitivity analysis that aims to identify the key risk factors for each of the major lines of business;34 and
- full details of the largest losses that were recorded during the reporting period – how they were incurred and whether the loss exceeded the VaR estimate at the time of the loss.
The main effect of the Basel II Accord on market risk capital is that supervisors can impose an additional capital charge under Pillar 2 if they deem it appropriate.35 Hence, if they are concerned that the bank has insufficient capital to cover its stress testing results, the regulatory risk capital requirement could be increased.
IV.7.4.2 Systemic Risk
Systemic risk is the risk that the insolvency of a few large firms spreads throughout the sector, and possibly into other sectors of the economy. Local regulators can gain some idea of the extent to which mass insolvency could affect their sector of the global banking system by aggregating the stress test results, usually based on standard stress scenarios, over all banks under their supervision.
The three main factors that contribute to systemic risk are the similarities of risk assessment and risk management procedures, collateral shortages and illiquid markets. We discuss each of these in turn.
The regulations governing financial institutions actually encourage institutions to assess and manage risk in a similar fashion. Under Pillar 3 of the new Accord banks must declare the methods used to assess risks and their Pillar 1 regulatory capital requirements. The public disclosure of risk capital based on a standard methodology (i.e. usually a VaR model) coupled with the rapid dissemination of information that is facilitated by technological advances (e.g. via electronic trading platforms) can precipitate a sequence of rapid responses to an adverse event that culminates in institutions displaying herd behaviour, where traders have virtually simultaneous, similar responses. Market participants attempt to ‘beat the herd’ by trading first, shocks are augmented because short term volatility increases, and a one-way market may ensue.
Many financial institutions hold sufficient collateral to cover only ‘normal’ contingencies and long term average liquidity demands. But a stress event can create a collateral shortage that is contagious. Suppose counterparty A defaults on counterparty B because it lacks collateral. Counterparty B must absorb a large fraction of the loss and, as a result, may now have difficulty meeting its own obligations, so it may default on counterparty C, and so the contagion spreads.
A market's liquidity is reflected by the size of the bid–ask spread (exogenous liquidity) and the market depth (i.e. the ability to do large trades with little price effect, which is an endogenous form of liquidity). In the event of a crisis, exogenous illiquidity can spill over from one market to another, because an increase in one market's bid–ask spread can increase demand in another market. For instance, traders may be using a market for hedging because it is the cheapest of several alternative markets to trade in, but if spreads widen in that market then traders will seek to use another market for hedging. A sudden increase in demand in this second market could then decrease its liquidity; in other words, a reduction in liquidity in one market may affect liquidity in other markets.
IV.7.4.3 Stress Tests Based on Worst Case Loss
A ‘worst case’ loss purports to quantify the tails of the distribution of losses beyond the threshold (typically 99%) used in VaR analysis. It is derived from a set of simplistic extreme scenarios on the risk factor returns. Each extreme scenario is a vector of risk factor returns and the worst case loss is the maximum loss that is recorded over all the identified scenarios. But since a worst case loss is not based on a distribution of risk factor returns the result is a loss to which we cannot assign a probability, so the output is impossible to interpret in any meaningful way. Nevertheless, this approach to stress testing remains popular at the time of writing, mainly because it is easy to understand and cheap to implement. To derive a ‘worst case’ loss one only has to substitute some extreme value for each risk factor return in the portfolio mapping, and the portfolio mapping is the only part of the risk model that is used.
The application of worst case scenarios to stress tests may be based on hypothetical or historical events. A common hypothetical event is a six sigma event, meaning a loss that is at least six standard deviations from the expectation of a distribution.36 Simply put, if the historical (or hypothetical) P&L standard deviation is ![]() dollars, then the worst case loss is 6
dollars, then the worst case loss is 6![]() dollars. More generally, suppose we are stress-testing a portfolio that has k risk factors whose returns are denoted X1,…, Xk and whose P&L is denoted f(X1,…, Xk). Given an estimated or hypothesized value for the means
dollars. More generally, suppose we are stress-testing a portfolio that has k risk factors whose returns are denoted X1,…, Xk and whose P&L is denoted f(X1,…, Xk). Given an estimated or hypothesized value for the means ![]() i and the standard deviations
i and the standard deviations ![]() i, i = 1,…, k, the six sigma loss is defined as f(
i, i = 1,…, k, the six sigma loss is defined as f(![]() 1 ± 6
1 ± 6![]() 1,…,
1,…, ![]() k ± 6
k ± 6![]() k), where the + or − is chosen independently for each risk factor in order to maximize the loss.
k), where the + or − is chosen independently for each risk factor in order to maximize the loss.
This is an example of the factor push methodology for stress testing, in which each risk factor is ‘pushed’ by a certain amount, in a direction that will incur the greatest loss, without respecting any assumption about the risk factor correlations. More generally, a factor push method generates a P&L of the form
![]()
where the integers a1,…, ak can be positive or negative. This method is commonly used by traders for assessing the risks of their own positions, but since it takes no account of risk factor correlations the factor push methodology has limited application to firm-wide solvency assessment.
EXAMPLE IV.7.9: A FACTOR PUSH STRESS TEST
A UK bank has invested £5 million in a US equity index. Assuming the $/£ exchange rate is currently 2, with a volatility of 10%, and the equity risk factor volatility is 25%, find the six sigma daily return in each risk factor and hence estimate the worst case loss to the UK investor over a daily horizon.
SOLUTION The daily standard deviation of the forex rate is ![]() and that of the equity index is
and that of the equity index is ![]() . The six sigma daily return is six times these, i.e. 3.79% for the forex rate, 9.49% for the equity index.37 The original value of the position, based on a forex rate of 2, is $10 million. With a positively stressed equity return of 9.49% the new position value is 10 × exp(0.0949) = $10,995,141, and with a positively stressed forex return the new exchange rate is 2 × exp(0.0379) = 2.077. Hence the stressed value of the new position is $10,995,141/2.077 = £5,292,861. So, under this scenario, the position would make profit of £292,861.
. The six sigma daily return is six times these, i.e. 3.79% for the forex rate, 9.49% for the equity index.37 The original value of the position, based on a forex rate of 2, is $10 million. With a positively stressed equity return of 9.49% the new position value is 10 × exp(0.0949) = $10,995,141, and with a positively stressed forex return the new exchange rate is 2 × exp(0.0379) = 2.077. Hence the stressed value of the new position is $10,995,141/2.077 = £5,292,861. So, under this scenario, the position would make profit of £292,861.

The P&L corresponding to the four possible directions of the changes in the two risk factor returns is displayed in the last row of Table IV.7.7. From this it is clear that the worst case loss of £621,868 occurs when the exchange rate appreciates and the equity index falls.
The factor push approach does not respect correlations between risk factors and, although these may indeed change during stressful periods, there are some correlations that must always be respected if the market is to be arbitrage free. For instance, it is impossible for interest rates along a yield curve to move independently by any amount and in any direction without creating arbitrage opportunities using calendar spreads.
A more sophisticated method for estimating worst case loss, developed by Studer and Lüthi (1997), uses a trust region in risk factor returns space to derive a worst case loss that respects correlations between risk factors. Denote the risk factor covariance matrix by Ω and the risk factor returns vector by x = (X1,…, Xk)′. If the risk factor returns have a multivariate normal distribution then the regions defined by x′Ω−1 x = c for some constant c are concentric ellipsoids. For instance, if k = 2 then the ellipsoid curves are ordinary two-dimensional ellipses. They correspond to the level sets of the bivariate normal density function. By requiring x′Ω−1x ≤ c for some constant c, we are therefore requiring that the risk factor returns lie in a confidence region that is determined by c. This region is called a ‘trust’ region because the smaller the value of c the smaller the possible range for risk factors returns about their expected value, and therefore the more likely they are to occur.
The matrix Ω may be specified according to historical returns behaviour, or by a stressed covariance matrix such as those described in Section IV.7.5. Either way we can derive a constrained maximum loss as the solution to the following optimization problem:
where f(x) is the P&L for the portfolio, according to the portfolio mapping f.
EXAMPLE IV.7.10: WORST CASE LOSS IN SPECIFIED TRUST REGION
A UK bank holds £5 million in S&P 500 futures and £5 million in FTSE 100 futures and the $/£ exchange rate is 2. The two equity indices each have a volatility of 25% and the forex rate has a volatility of 10%. The correlation between the forex rate and S&P 500 dollar returns is 0.25, the correlation between the forex rate and the FTSE 100 index is −0.15, and the correlation between the local currency returns on the equity indices is 0.5. Use these data to set up the optimization problem (IV.7.6) for trust levels c = 0.05, 0.1 and 0.25, each time recording the vector of optimally stressed risk factor returns and the corresponding worst case loss on the portfolio.
SOLUTION The optimization problem is set up in the spreadsheet for this example, using the Solver settings shown there. Readers are free to change the covariance matrix and/or the trust level, but must remember to reapply Solver each time. The results are summarized in Table IV.7.8. The first three rows show the optimized returns on each of the risk factors and the last row shows the worst case loss under these risk factor returns. As c increases the optimized vector of risk factor returns may be less likely to occur. In other words, as the worst case loss shown in the table increases from £502,768 to £1,159,302 it may also become less likely under a multivariate normal distribution for the returns.38
Table IV.7.8 Results of worst case loss optimization

IV.7.5 A COHERENT FRAMEWORK FOR STRESS TESTING
The most straightforward method of encoding stress scenarios for distributions of risk factor returns is to assume that the functional form of the risk factor return distributions remains the same in stressful markets.39 For instance, if the risk factor returns have a multivariate Student t distribution with 8 degrees of freedom in ‘normal’ market circumstances, then we assume that they still have a multivariate Student t distribution with 8 degrees of freedom during stressful periods; the only change is to the mean and covariance parameters of this distribution.
This section will illustrate the use of a stressed covariance matrix to calculate VaR and ETL corresponding to stressful scenarios.40 This way, a stress test is derived from the entire risk model, not only the portfolio mapping, and so we can quote the result of a stress test as a probabilistic statement. Note that we should stress not only the covariance matrix but also the expected risk factor returns in the stress test. The vector of expected returns can contain many extreme values that impact the portfolio with substantial losses, so accounting for the expected return could have a significant effect on the stressed VaR and ETL even over a very short time horizon.
One of the methods that regulators recommend for constructing stressed covariance matrices is to ‘make up’ a hypothetical covariance matrix. But in so doing there is no guarantee that the matrix will in fact represent a covariance matrix, because when correlations are altered in an arbitrary fashion the matrix need not be positive semi-definite. We discuss this problem in Section IV.7.5.2, and explain how to find the ‘nearest’ covariance matrix to the one that is specified in our hypothetical example. Section IV.7.5.3 addresses the problem of dimension in the context of stress testing. Stress tests commonly involve changing a very large number of risk factors, many of which are often highly correlated. We already know how to use principal component analysis to reduce the dimension of the risk factor space, and this subsection illustrates the application of stress tests to principal components of a large number of correlated risk factors. Section IV.7.5.4 explains how to model liquidity effects in stress tests, distinguishing between exogenous effects where illiquidity is reflected in an increase in the bid–ask spread, and endogenous effects which include the impact of the quantity traded on the mid price in the market. We explain how to model the gradual liquidation of a position – or the gradual hedging – over a period of several days, and how to incorporate this into a liquidity - adjusted estimate in the stressed VaR calculation. Finally, we discuss volatility clustering, which has a significant influence on VaR and ETL even in ‘normal’ market circumstances. In stressful markets this effect becomes even more pronounced, as we demonstrate in Section IV.7.5.5.
IV.7.5.1 VaR Based on Stressed Covariance Matrices
The 1996 Amendment to the Basel Accord recommended that banking regulators require stress tests to be performed using stressed risk factor covariance matrices. Such matrices could be obtained using historical data on daily risk factor returns from a crisis period in the past. The crisis period should cover the period where there is a concentration of extreme returns. For instance, the next example computes a simple covariance matrix for the FTSE 100 and S&P 500 indices using data from around the period of the global stock market crash.
EXAMPLE IV.7.11: COVARIANCE MATRIX FROM GLOBAL EQUITY CRASH OF 1987
Use daily prices on the FTSE 100 and S&P 500 indices from just before and after the global stock market crash in October 1987 to derive a historical covariance matrix for these two risk factors. Use this matrix, and the other sample moments from the same period, to estimate the 0.1% daily equity VaR of a portfolio with equal amounts invested in the two indices, and discuss your results.
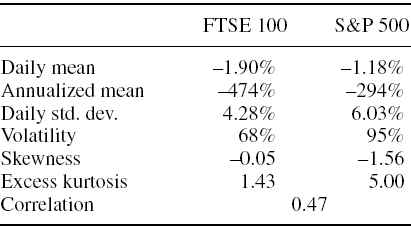
SOLUTION Data from 13 October to 20 November 1987 were downloaded from Yahoo! Finance.41 Figure IV.7.7 shows that the FTSE index fell on most of the days from 13 October until 10 November.42 Based on the 20 observations from 13 October to 10 November, the sample moments are displayed in Table IV.7.9.
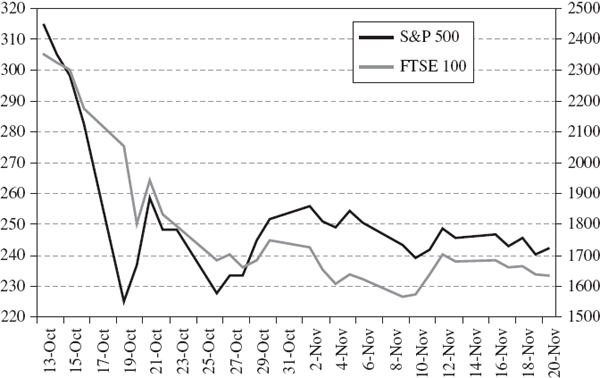
Figure IV.7.7 S&P 500 and FTSE 100 indices during global crash of 1987
Table IV.7.9 Sample moments of S&P 500 and FTSE 100 index returns during global crash period
The covariance matrix based on these data, expressed in annual terms, is
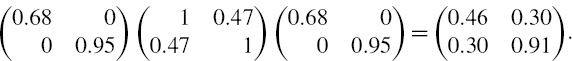
It is clear from the high negative sample skewness and positive sample excess kurtosis that a normal distribution assumption is not appropriate. We shall consider instead the Student t VaR formula (IV.2.63), using the negative mean returns to pick up the negative skewness. First, just for comparison, we shall use the above matrix in the normal linear formula.
The portfolio weights vector is (0.50.5)′ and the mean return vector is (−0.0190 − 0.0118)′.43 Thus the 0.1% daily normal equity VaR, expressed as a percentage of the portfolio value, is
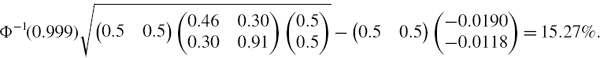
Note that ignoring the mean adjustment gives a result that is only 13.73% of the portfolio value, so the adjustment is important even over a 1-day horizon.
Now we use a simple method of moments to estimate the degrees of freedom for a Student t distribution of each return. Using (IV.2.60), we can set ν = 6![]() −1 + 4 where
−1 + 4 where ![]() 0.5 0.5 − 0.50.5 −0.0190 −0.0118 is the sample excess kurtosis. Solving this gives a degrees of freedom parameter of 8.2 for the FTSE 100 index and 5.2 for the S&P 500 index. We could then use a normal copula for the multivariate return distribution, but this would require simulation, and to keep this illustration simple we prefer a closed-form VaR formula. We therefore use (IV.2.63) where ν is the average of the two degrees of freedom, i.e. 6.7.44
0.5 0.5 − 0.50.5 −0.0190 −0.0118 is the sample excess kurtosis. Solving this gives a degrees of freedom parameter of 8.2 for the FTSE 100 index and 5.2 for the S&P 500 index. We could then use a normal copula for the multivariate return distribution, but this would require simulation, and to keep this illustration simple we prefer a closed-form VaR formula. We therefore use (IV.2.63) where ν is the average of the two degrees of freedom, i.e. 6.7.44
Based on this approximation, the 0.1% daily Student t equity VaR, expressed as a percentage of the portfolio value, is estimated as
This time ignoring the mean adjustment gives a result of 19.38%. Either way, our VaR estimate at the 99.9% confidence level would be very seriously underestimated if we ignored the leptokurtosis in returns during market crises and tried to estimate a stressed VaR based on a normal distribution. Still, we have not accounted properly for the strong negative skewness in equity returns at the time of a crash – this could be captured using a Cornish–Fisher approximation or a normal mixture VaR formula – but these extensions are left to the interested reader.
Normal or Student t Monte Carlo VaR models are also based on a covariance matrix, so using a stressed covariance matrix with these models produces a stressed VaR estimate – and these are applicable to non -linear portfolios. We may also use a stressed covariance matrix to estimate historical VaR. Using an idea that was introduced by Duffie and Pan (1997), we can change the covariance structure of the historical data on risk factor returns to reflect the covariances during the crisis period. The idea is simply an extension of the volatility adjustment of historical returns, already described in the case study of Section IV.3.5.2.
Suppose there are k risk factors and T observations on each factor in the historical sample. Denote the T × k matrix of historical risk factor returns by R, denote their covariance matrix by V and denote the Cholesky matrix of V by Q. So
![]()
Now take a stressed covariance matrix for these risk factor returns, denote this by V* and denote the Cholesky matrix of V* by Q*. So
![]()
Now set R* = R (Q* Q−1)′. Then
Thus R* is a stress-adjusted set of historical returns, i.e. returns that are adjusted to have the stressed covariance matrix V*.
After adjusting the historical returns as above, i.e. so that their covariance structure is that of the stressed market throughout, we apply the portfolio mapping to the standard historical simulation model to derive a stressed portfolio return distribution. Then we estimate the stressed historical VaR as an extreme quantile of this distribution.
EXAMPLE IV.7.12: STRESSED HISTORICAL VAR
Use daily historical returns on the FTSE 100 and S&P 500 indices from 3 January 1996 to 21 April 2008 to estimate the 0.1% daily historical equity VaR for a portfolio with equal amounts invested in the two indices, where the returns are adjusted to have the stressed covariance matrix that was derived in the previous example.
SOLUTION The spreadsheet first derives the covariance matrix based on daily returns over the whole historical period. This is
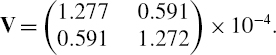
For the stressed covariance matrix use the daily covariance matrix from the 1987 stock market crash, derived in the previous example, i.e.
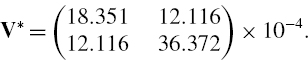
Clearly both volatilities and the correlation are far higher during the period of the global stock market crash in 1987. Now we adjust the historical returns using a transformation that is based on historical and stressed Cholesky matrices, which are
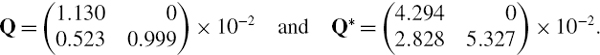
The transformation matrix is given by
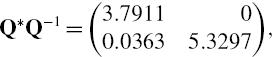
and post-multiplying the transpose of this matrix by the returns gives the stress-adjusted returns. The historical stressed equity VaR is minus the 0.1% quantile of this return distribution, which is calculated in the spreadsheet as 19.63% of the portfolio value. This should be compared with the ordinary historical 0.1% daily equity VaR on 21 April 2008, which is just 4.32%.
IV.7.5.2 Generating Hypothetical Covariance Matrices
Stressed covariance matrices may also be based on hypothetical scenarios for the risk factor volatilities and correlations. In fact, the Basel Committee recommended this in their stress testing guidelines of the 1996 Market Risk Amendment. For instance, we could assume that the volatility of a risk factor is five times the current level of volatility. Provided volatilities are positive, the stressed covariance matrix will be positive semi-definite if and only if its associated correlation matrix is positive semi-definite.45 Risk factor correlations tend to be augmented during crisis periods, so we could likewise assume that a risk factor correlation increases by 50% of its current level. However, although we are free to change volatilities to any positive quantity that we like, we are not free to change correlations. In doing so we could be specifying a matrix which is not positive semi-definite and which therefore cannot, in fact, be a correlation matrix.
Nevertheless risk analysts and portfolio analysts find it very useful to ‘make up’ correlation matrices to represent their own personal views on the market behaviour over the risk or investment horizon. So we need to check hypothetical ‘correlation’ matrices to test whether they are positive semi-definite.46 If not, we need to transform a matrix into another matrix that is positive semi-definite and that is, in some sense, as ‘close’ as possible to the hypothesized matrix.
There are several measures of ‘closeness’ that can be applied to two matrices. Any such measure is defined using a matrix norm, which is a generalization of the concept of ‘length’ for a vector.47 Perhaps the most popular matrix norm is the Frobenius norm which, for a real matrix A, is defined as
where ‘tr’ denotes the trace operator (i.e. the sum of the diagonal elements of a square matrix). For our purposes we have two square symmetric matrices, C and ![]() where C is the hypothesized matrix (and which we suppose is not a correlation matrix because it is not positive semi-definite) and
where C is the hypothesized matrix (and which we suppose is not a correlation matrix because it is not positive semi-definite) and ![]() is the closest correlation matrix to C. In other words,
is the closest correlation matrix to C. In other words, ![]() is a symmetric, positive semi-definite matrix such that the matrix
is a symmetric, positive semi-definite matrix such that the matrix
![]()
has the smallest possible matrix norm. Moreover, both C and ![]() must have 1s along the diagonal, and off-diagonal elements that are less than or equal to 1 in absolute value.
must have 1s along the diagonal, and off-diagonal elements that are less than or equal to 1 in absolute value.
To find ![]() we have to perform an optimization. This takes the form of minimizing (IV.7.8) or some other matrix norm, with A = C −
we have to perform an optimization. This takes the form of minimizing (IV.7.8) or some other matrix norm, with A = C − ![]() , and subject to the constraints that A has zero diagonal elements and
, and subject to the constraints that A has zero diagonal elements and ![]() has off-diagonal elements that are less than or equal to 1 in absolute value.
has off-diagonal elements that are less than or equal to 1 in absolute value.
EXAMPLE IV.7.13: FINDING THE ‘NEAREST’ CORRELATION MATRIX
Suppose an analyst hypothesizes that the returns on four risk factors have the ‘correlation’ matrix
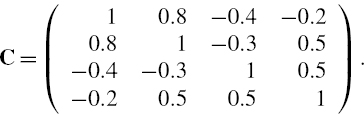
Show that this is not in fact a correlation matrix, because it is not positive semi-definite. Then use the Frobenius norm to find the nearest correlation matrix to the hypothesized matrix.
SOLUTION First we use the determinant test for positive definiteness described in Section I.2.2.8. That is, we find the matrices of the successive principal minors, i.e. of the 2 × 2 and 3 × 3 matrices with diagonal elements along the main diagonal, and the determinant of the matrix itself. These are 0.36, 0.302 and −0.1284. Not all of these are non-negative, so the matrix is not positive semi-definite.
Next we apply Solver to find the nearest positive semi-definite matrix, subject to the constraints on the elements described above. We shall impose a non-trivial lower bound for the determinant test on the result; otherwise the optimization is likely to return a matrix that has a zero determinant, so it will only be positive semi-definite. In this example we have required that all principal minors be greater than or equal to 0.01.48 The result of the optimization is the positive definite matrix

IV.7.5.3 Stress Tests Based on Principal Component Analysis
Regulators recommend that portfolios be stress-tested for parallel and tilt movements in term structures. For instance, the Derivatives Policy Group recommended that yield curves be subject to a parallel shift of 100 basis points in either direction, and also to a linear tilt of 25 basis points. In the light of the recent credit crisis, their recommendation that credit spreads be subject to a parallel shift of 20 basis points along the maturity curve may seem rather too mild to be classed as a stress scenario. This is so often the case – after the event!
The problem with simple scenarios such as parallel shifts is not so much the magnitude of the shock – after all, it is simple to make this as large we like – but whether in fact parallel shifts and linear tilts in a term structure of interest rates are truly capturing the weak spots of the portfolio. Indeed, portfolios may be hedged against parallel movements,49 and in this case stress tests against parallel moves in interest rates of all maturities will not produce extreme losses for a ‘worst case’ scenario.
Here again we have an example where the term ‘worst case’ loss is totally inappropriate. Not only because ‘worst case’ is a logical misnomer whenever it is used, but because by far the most common type of movement in a highly correlated yield curve is the movement captured by the first principal component. Typically this is not a parallel shift, and because it is the most commonly occurring type of movement (given the historical data used in the analysis) it is this movement that a trader should really be hedging against.50 If the portfolio has only been hedged against a parallel shift, stress testing with a parallel shift will not produce an extreme loss; but stressing the first principal component could produce a significant loss. In short, principal component analysis is not only a very useful tool for hedging, it is an ideal method for generating more realistic ‘shocked’ term structures than parallel shifts and linear tilts.
Principal component analysis also reduces the complexity of a stress test. Typically a three-component representation is all that we need to capture about 99% of the historical variation of yield curves, or credit spread curves, or term structures of futures or forwards, or even volatilities of different maturities. Hence, there is a large dimension reduction and this greatly simplifies the stress test. Principal component analysis produces a small number of new, uncorrelated risk factors. Because they are uncorrelated there is no need to consider their dependency in the stress test. Thus, instead of stress-testing the simultaneous, correlated movements of, say, 60 correlated risk factors we can stress test separately the movements of 3 uncorrelated ones! That is, each stress test can be performed by shocking just one of these components to an extreme value, such as a six standard deviation move, in either direction. Or, we could change all the components simultaneously, by different positive or negative amounts.
In Section II.2.4.6 we presented an empirical example of a stress test of a UK bond portfolio that was based on principal component analysis. The first component corresponded to a roughly parallel shift in interest rates longer than 18 months’ maturity, but with considerably less movement in the money market rates. The intuition that this type of movement is the most commonly occurring type of variation in UK interest rates rests on the observation that short rates are tied to monetary policy targets, and were less variable than long rates over the historical period considered.
In this example the portfolio incurred the worst loss, amongst all the scenarios considered, when the first principal component experienced a six sigma downward movement, but not all linear portfolios will experience worst case losses as a result of a large movement in the first principal component (i.e. a roughly parallel shift). It depends on the hedging strategy for the portfolio, as demonstrated by the following example.
EXAMPLE IV.7.14: PRINCIPAL COMPONENT STRESS TESTS
Consider the bond portfolio in Example IV.2.9. In that example we derived a three principal component factor model representation for the P&L of this portfolio, i.e.
![]()
We know from Table IV.2.9 that this representation captures over 99% of the historical variation in the portfolio. The standard deviations of the first three principal components were calculated in that example as:
![]()
Find the maximum loss incurred from uncorrelated six sigma adverse changes in each of the principal components separately.51
SOLUTION Denote by βi the portfolio's sensitivity to the ith component so, for example, β1 = £428. Set Pi = −6βiσi for i = 1, 2 and 3 separately, and hence obtain the worst case loss corresponding to a six sigma change in each component. The results are a loss of £75,169 for the six sigma move in the first component, £112,871 for the second component and £18,894 for the third component. Thus the portfolio is more exposed to an unusual tilt in the curve than it is to a shift or a change in convexity.
However, our results in Example IV.2.9 showed that movements in the first component accounted for over 93% of the historical variation in the yield curve, whereas the second component only accounted for about 5% of the movements. In this example the loss incurred through an extreme change in the first principal component is less than the loss resulting from an extreme change in the second component, but the first type of loss is far more likely to occur, if we assume the historical data to be representative of the future.
To summarize, the use of principal component analysis for worst case loss calculations provides:
- a reduction in the complexity of stress tests through the use of a few, uncorrelated risk factors that can be stressed separately;
- stress tests against the scenarios that are most likely to occur, according to historical experience; and
- an indication of the relative likelihood, according to historical experience, of the losses that we compute.
IV.7.5.4 Modelling Liquidity Risk
There are two types of liquidity risk:
- Market liquidity risk is the risk associated with an inability to perform market transactions at the current mark-to-market value. Market liquidity is commonly measured by an exogenous factor, i.e. the relative size of the bid–ask spread, and by an endogenous factor, i.e. market impact. Market impact relates to market depth, i.e. the ability to trade a substantial amount without seriously impacting the mid price.
- Funding liquidity risk refers to the inability to raise funds or collateral to meet obligations.
Funding illiquidity is a prime risk driver of default risk, but not of market risk. Hence this section focuses only on market liquidity risk, and in particular on methods that incorporate exogenous and endogenous illiquidity effects into stressed VaR calculations.
Standard VaR analysis assumes that all trades are at the mid market price. It ignores the increase in the bid–ask spread and the reduction in market depth that so often occurs at the time of a stress event. However, traders attempting to close out or hedge large positions in stressful market conditions may find that they cannot transact efficiently, resulting in exposure to adverse market conditions for longer periods and additional losses resulting from wider spreads.
Liquidity varies between markets and over time, as illustrated by Borio (2000), and in many markets it decreases as market volatility increases, as observed by Bangia et al. (2002). These authors also propose a methodology for estimating a liquidity-adjusted VaR that captures exogenous liquidity effects via an ‘add-on’ to the changes in mid price that we usually model in a stress test, where the size of the add-on depends on the size of the bid–ask spread. They assume that extreme market events are perfectly correlated with extreme liquidity events because this simplifies the analysis considerably, and it is also fairly realistic.
Define the relative bid–ask spread by
where PA, PB and PM are the ask, bid and mid prices respectively, and ![]() . We assume that S is a random variable and thence define the cost of exogenous liquidity, Cα, t at the α quantile at time t by
. We assume that S is a random variable and thence define the cost of exogenous liquidity, Cα, t at the α quantile at time t by
where PM,t denotes the current mid price and x1−α, t denotes the 1 − α quantile of the spread distribution. The motivation for this definition is that standard VaR calculations assume transactions are at the mid price, but on average we expect the ask price to be ![]() above this price, and the bid price to be
above this price, and the bid price to be ![]() below it, where μS denotes the expected value of the spread. The definition (IV.7.10) thus adjusts the transaction price to be at the 1 − α quantile of the spread distribution, where α corresponds to the quantile of the VaR estimate. Then the liquidity-adjusted 100α% VaR (or ETL) is the standard VaR (or ETL) plus the cost of exogenous liquidity. The next example illustrates the calculation under the assumption that the spread is lognormally distributed.
below it, where μS denotes the expected value of the spread. The definition (IV.7.10) thus adjusts the transaction price to be at the 1 − α quantile of the spread distribution, where α corresponds to the quantile of the VaR estimate. Then the liquidity-adjusted 100α% VaR (or ETL) is the standard VaR (or ETL) plus the cost of exogenous liquidity. The next example illustrates the calculation under the assumption that the spread is lognormally distributed.
EXAMPLE IV.7.15: STRESSED VAR WITH EXOGENOUS ILLIQUIDITY
Suppose an investor has equal amounts invested in FTSE 100 and S&P 500 index futures. Assume that spreads are perfectly correlated in these markets and that in each market the relative bid–ask spread is lognormally distributed. Suppose that historical observations on the relative spread during stressful markets indicate that the mean and standard deviation of the spread in each market are given by52
![]()
Estimate the cost of liquidity for this position at the 99.9% confidence level, and compare your result with the historical stressed VaR that was estimated in Example IV.7.12.
SOLUTION In the spreadsheet for this example we apply the Excel LOGINV function to estimate the 99.9% quantile of the lognormal spread distribution for each pair of mean and standard deviation parameters. The result is 0.1645% for the S&P 500 and 0.2713% for the FTSE 100 index. Since our position has equal amounts invested in each futures market, the cost of liquidity expressed as a percentage of the portfolio mid price is
![]()
This is negligible compared with the 0.1% stressed VaR of the portfolio, which was estimated to be 19.64% of the portfolio value in Example IV.7.12.
The above example demonstrates that this type of exogenous liquidity adjustment to stressed VaR is of negligible importance in the world's main futures markets. Bangia et al. (2002) also report that no significant liquidity adjustment is necessary for major currency markets. Readers are free to change the parameters used in the previous example to reflect the behaviour of bid–ask spreads in less liquid markets.
There are two drawbacks to the methodology just described. First, it takes no account of endogenous liquidity, i.e. the relationship between the price that is realized and the size or quantity of the transaction relative to the normal lot size in the market. Secondly, it is not easy to assess the appropriate value of the quantile of a spread distribution in stressful market conditions because, typically, only a few empirical observations are available.
Angelidis et al. (2004) suggest a method that accounts for the market impact of trades that are larger than normal. For instance, for quantities in excess of the normal market lot size N we could assume a linear or quadratic increasing function for the expected size of the spread as a function of the quantity transacted. Specifically, we could assume that the expected value of the relative spread μS is related to the quantity q that is traded as
Here g denotes some increasing linear or quadratic function such that g(0) = 0. For instance, if g is linear then
Estimation of the value of k could be based on dealers’ quotations during a crisis in the past, or on the subjective judgement of experienced traders.
EXAMPLE IV.7.16: STRESSED VAR WITH ENDOGENOUS LIQUIDITY
An illiquid stock has a bid–ask spread that is assumed to follow a lognormal distribution. The mean relative spread is 0.4% and its standard deviation is 0.2%. Find the cost of liquidity adjustment that should be made to the VaR at the 99.9% confidence level. Now assume the normal lot size is 1000 and that we need to make a transaction of 50,000 shares. Assume the quantity impact on the mean relative spread is given by (IV.7.11) where g is given by (IV.7.12) with k = 10−7. Find a revised estimate of the cost-of-liquidity adjustment to be made to the VaR.
SOLUTION In the spreadsheet we use Solver to back out the appropriate mean and standard deviation of the log spread, since these are the parameters used in the Excel LOGINV function. Thereafter the first case is a straightforward repeat of the calculations used in the previous example, and we obtain a cost-of-liquidity adjustment of 0.2684% to the 99.9% VaR, expressed as a percentage of the investment value.
The second part of the calculation assumes the mean relative spread is only 0.4% when 1000 shares are transacted. Since we are trading 50 times this amount, we use the function (IV.7.12) with k = 10−7 and q − N = 49,000 to obtain an adjustment to the mean spread of 0.49%. Hence, with this quantity adjustment the new mean relative spread is 0.89%. Leaving the standard deviation unchanged and repeating the calculation gives a cost-of-liquidity adjustment of 0.7276% of the portfolio value.
It is clear from the above examples that spread adjustment has a relatively small impact on the stressed VaR, except in highly illiquid markets. However, spread size is not the most important variable that is adversely affected by the quantity traded; the main liquidity effect arises from movements in the mid price itself as it comes under pressure in a one-way market. For instance, in liquid stock markets the daily average trading volume (DATV) is approximately 0.5% of the market capitalization of the stock. So to effect a sale of, say, 1% of the market cap the dealer will divide the order into normal size lots and execute each order over a period of time.53 But if he does this too quickly, for example over the course of only one day, there comes a point when a downward price pressure is exerted on the mid price. Thus both bid and ask prices could trend upward during a buyers market, or downward during a seller's market.
It may be necessary to introduce gradual liquidation of a period over several days. For example, one might assume that a large position is divided into three parts, each a multiple of the standard lot size Q, and then traded on successive days. Then, denoting the quantity traded on day t by qt, the mid-price at time t may be adjusted by assuming a linear price impact relationship of the form
where ![]() M is the mid price just before the trade occurs, ω = +1 for a purchase order and ω = −1 for a sell order, and the constant k is set relative to the standard lot size, for instance using the judgement of experienced traders. Setting k = c / Q for some constant c, and setting qt = mtQ, rearrangement of (IV.7.13) gives an alternative expression for the price impact relationship as
M is the mid price just before the trade occurs, ω = +1 for a purchase order and ω = −1 for a sell order, and the constant k is set relative to the standard lot size, for instance using the judgement of experienced traders. Setting k = c / Q for some constant c, and setting qt = mtQ, rearrangement of (IV.7.13) gives an alternative expression for the price impact relationship as
where the left-hand side is the percentage return due to the price impact of the trade. To account for the price impact effect, the absolute value of this return should be added to the VaR that is estimated without accounting for the quantity impact, assuming the VaR is expressed as a percentage of the portfolio value.
EXAMPLE IV.7.17: ADJUSTING VAR FOR PRICE-QUANTITY IMPACT
Suppose daily log returns, based on the mid price of an illiquid asset, are i.i.d. and normally distributed with volatility 30%. We have to sell 50% of the DATV, which itself is equal to 1000 standard lots. Assume the quantity impact on the mid price is given by (IV.7.14) with c = 5 × 10−5. Calculate the price impact of the quantity traded when it is traded on one day, and when it is traded in parcels of 100 times the standard lot size on each of five successive days. In each case show how we should adjust the 1% VaR to account for the expected price depreciation resulting from the unusual size of our position. Is it better to liquidate the position immediately, or to spread the liquidation uniformly over 5 days? How does your conclusion change if the quantity impact coefficient increases to c = 2 × 10−4?
SOLUTION We must sell 500 standard lots, and with c = 5 × 10−5 and ω = −1 the price impact on the return (IV.7.14) is
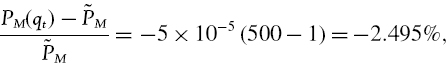
assuming the sale is made on one day. The 1% daily VaR is given by the usual normal linear VaR formula, so if we ignore the price-quantity impact we have
![]()
Adding the absolute value of the return created by the price-quantity impact, the total 1% VaR, including the price-quantity impact, is 6.909%.
Now consider the case where we divide the sale into five lots of 100, traded over five successive days. Although the price impact is less on each day, the position remains open for 5 days instead of 1, and so we must compute a 5-day VaR instead of a 1-day VaR. On each day the price-quantity impact induces a negative return of only
![]()
instead of 2.495%, but we must account for the gradual stepping down of the exposure over the five successive days.
On the first day we have 1% daily VaR of 4.414% and an add-on for the price impact of 100 lot sizes traded of 0.495%, so the total daily VaR is 4.909%. On the second day the 1% daily VaR is (4/5) × 4.414% = 3.531% and the add-on for the price impact is (4/5) × 0.495% = 0.396% so the total daily VaR on the second day is 3.927%. On the third, fourth and fifth day we continue to step down the exposure uniformly, until on the last day the 1% daily VaR is (1/5) × 4.414% = 0.883% and the add-on for the price impact is (1/5) × 0.495% = 0.099%, so the total daily VaR on the last day is only 0.982% of the original value of our position.
To find the total VaR we need to aggregate the daily VaRs obtained above in accordance with our risk model. Since this assumes the returns are normal and i.i.d., returns are additive. So the total price-quantity impact is just the sum of the add-ons due to the negative returns given by the price-impact function. The VaR in this model is a constant multiple of volatility, but it is variance not volatility that is additive in our risk model. So to find the total VaR, unadjusted for the price impact, we take the square root of the sum of the squared daily VaRs. The results are set out in Table IV.7.10, where the aggregates in the last row are obtained as the square root of the sum of the squares for the unadjusted VaR, and as a simple sum for the add-ons that account for the price quantity impact. Thus the total 1% VaR, including the price-quantity impact, which is now measured over a 5-day horizon, is 6.547% + 1.485% = 8.032%. Since this is greater than 6.909%, we conclude that the quantity impact is low enough for it to be preferable to liquidate the position immediately.
Table IV.7.10 Adjusting VaR for uniform liquidation
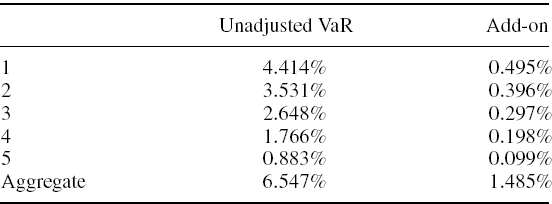
Readers may change the constant c in the spreadsheet to alter the cost of liquidation, and will see that when the price impact of large trades is great, it pays to liquidate more slowly. For instance, if we change cell B5 to c = 2 × 10−4 the price-quantity impact is very significant. If the entire job is executed in one day the effect on the return is –9.98% and so the daily VaR corresponding to immediate liquidation jumps up to 14.394%. However, gradual liquidation over a 5-day period yields a total 5-day VaR of 12.487%, so in this case it pays to liquidate the position more slowly.
IV.7.5.5 Incorporating Volatility Clustering
In the previous subsection the model of gradual liquidation assumed the returns were normal and i.i.d. This assumption led to a simple analysis but it is not very realistic. In this subsection we explain how to incorporate volatility clustering into stressed VaR calculations when the exposure is hedged or liquidated gradually, over a horizon of several days. The importance of volatility clustering effects for stressed VaR calculations cannot be understated. For example, in an extensive empirical analysis of VaR-based stress tests in which many different frameworks for estimating VaR are compared, Alexander and Sheedy (2008) show that it is only the risk models that incorporate volatility clustering that are able to provide accurate predictions of VaR at extreme quantiles in stressful currency markets.
Here we shall illustrate the methodology in the framework of two VaR models: the filtered historical simulation (FHS) model that was introduced in Section IV.3.3.4 and the Monte Carlo VaR model with volatility clustering, introduced in Section IV.4.3.2. Both frameworks utilize a simple volatility clustering model for the conditional return distribution, and this effect is incorporated into our VaR calculations. An illustration of the FHS approach was given in Example IV.3.2, and applications of volatility clustering models to multi-step Monte Carlo were provided in Examples IV.4.6 and IV.4.7.
In Example IV.3.2 we estimated 10-day VaR at various quantiles and performed a simple scenario analysis based on shocking the current volatility. But for a stress test based on FHS we should shock both the current volatility and the current return. For example, we might assume that both are shocked to six times their normal value, and that the return is negative for a long exposure or positive for a short exposure. The following example extends Example IV.3.2 in this manner.
EXAMPLE IV.7.18: USING FHS FOR STRESS TESTING
The asymmetric GARCH model with parameters given in Table IV.3.5 is the model for S&P 500 returns that was estimated in Example IV.3.1. Use this model to estimate the 0.1% 10-day VaR following a shock to the daily return of −10% and a simultaneous shock to volatility, so that it is 60% in annual terms. Apply the FHS approach, bootstrapping the sample of returns that was used to estimate the GARCH model, and assume the exposure is liquidated uniformly over a 10-day period.
SOLUTION The spreadsheet for this example is an adaptation of the FHS spreadsheet for Example IV.3.2. We use the same asymmetric GARCH model as in that spreadsheet and the only differences are that (a) we now use shocked values for the returns and volatility, and (b) we step down the exposure so that the total return is a weighted sum of the returns over the next 10 days.54
The shock to the daily return is −10% and the shock to the daily standard deviation is ![]() . Based on 10,000 simulations we obtain a 0.1% 10-day stressed VaR of approximately 35% of the portfolio value.55 This more than double the 0.1% VaR estimate in Example IV.3.2, which was computed under ‘normal’ market circumstances. Finally we illustrate the use of multi-step Monte Carlo to incorporate volatility clustering into stress tests. In fact, Example IV.4.7 already performed a simple stress test by shocking the daily return to be ±10%. We used the example to show that, because the GARCH model is asymmetric, the losses following a negative shock to the return are greater than those following a positive shock.56 In the next example we shock the current volatility as well as the current return.
. Based on 10,000 simulations we obtain a 0.1% 10-day stressed VaR of approximately 35% of the portfolio value.55 This more than double the 0.1% VaR estimate in Example IV.3.2, which was computed under ‘normal’ market circumstances. Finally we illustrate the use of multi-step Monte Carlo to incorporate volatility clustering into stress tests. In fact, Example IV.4.7 already performed a simple stress test by shocking the daily return to be ±10%. We used the example to show that, because the GARCH model is asymmetric, the losses following a negative shock to the return are greater than those following a positive shock.56 In the next example we shock the current volatility as well as the current return.
EXAMPLE IV.7.19: USING GARCH WITH MONTE CARLO FOR STRESS TESTING
Use the asymmetric GARCH model of the previous example to estimate the 100α% 10-day VaR following a shock to the daily return of −10% and a simultaneous shock to volatility, so that it is currently 60% per annum. Again assume the exposure is liquidated uniformly over a 10-day period, but this time apply conditional normal Monte Carlo simulation for the returns.
SOLUTION We use α = 0.001, 0.01, 0.05 and 0.1 in the spreadsheet and the results are calculated based on 10,000 simulations. One set of simulations gives the results shown in Table IV.7.11. Notice that the 0.1% 10-day stressed VaR is 32.49%, which is less than that of the previous example, even though both examples use the same GARCH model. This is because here we have used standard normal simulations for the returns rather than bootstrapping them from an empirical and leptokurtic return distribution.
Table IV.7.11 Stressed VaR at different confidence levels based on Monte Carlo GARCH

IV.7.6 SUMMARY AND CONCLUSIONS
Historical data on major market risk factors are usually easily available. As a result, market risk analysts have developed a tendency to rely on these data when forecasting the market risk of a portfolio, even over a long risk horizon. In doing so the analyst is implicitly adopting a subjective view that history will repeat itself. However, when the risk horizon is more than a few days, there is much to be said for using an alternative subjective view that is not necessarily tied rigidly to historical experience. In my view there is far too much reliance on historical data when computing VaR, and analysts should develop the confidence to use their own personal views as well. In any case, this becomes essential when there are little or no historical data available. Any critics of the subjective nature of the methodology we have proposed in this chapter should bear in mind that, so far, each new financial crisis entails events, and precipitates market behaviour, for which we have no historical precedent.
Scenarios can be categorized by the type of data that are used to construct them, and by the mathematical quantity that the scenario concerns. The data can be based on either historical experience or hypothetical views. The mathematical quantity in the scenario can be a single vector of risk factor returns (as it is in ‘worst case’ scenarios) or one or more parameters of the risk factor return distribution (as it is in the covariance matrices that regulators recommended for use in stress testing). One may also apply empirical risk factor return distribution scenarios, without specifying a parametric form, such as those that were experienced during stress events in the past. When a scenario is on a single vector of risk factor returns, we apply the portfolio mapping to derive the portfolio's P&L associated with the scenario, and we ignore the rest of the risk model. It is only when scenarios concern the distribution of risk factor returns that we can use the risk model in the stress test, and it is only when we use the risk model that can we associate a probability with the resulting P&L.
Financial institutions and regulators regard stress testing as an essential complement to the VaR and ETL calculations that are based on ‘normal’ market circumstances. There is no single standard approach to stress testing, and the methodology that is chosen often depends on the context in which the results will be used. But stress testing, as it is practised by many institutions today, is an art without a proper mathematical foundation. Stress scenarios are chosen to result in a so-called ‘worst case’ loss, but there is nothing to guarantee that the loss that is calculated will not be exceeded, and no statement of the probability that this loss will occur.
The main focus of this chapter has been to develop a coherent framework for stress testing, in the context of the risk model that is used for standard VaR and ETL calculations. Personal views of the analysts may be used to forecast the market VaR of a portfolio in both ‘ordinary’ and stressful market conditions. We have focused on some empirical examples that incorporate the use of scenarios for portfolio returns over a long horizon, and have contrasted the differing ways that subjective information is used in scenario VaR and in Bayesian VaR. We have described the impact of scenarios for returns on stressed VaR. We have also shown how to obtain the correlation matrix that is ‘closest’ to a hypothesized matrix that cannot be a correlation matrix because it is not positive semi-definite. We have advocated the use of principal component analysis for stress testing on a highly correlated set of risk factors such as a yield curve, or credit spreads of different maturities. We have also explained how to adjust VaR and ETL by adding on a cost of liquidity adjustment that accounts for exogenous liquidity effects on the bid–ask spread in illiquid markets, and endogenous liquidity effects on the price impact of trading quantities that are large, relative to the DATV. The cost of endogenous liquidity effects is usually much greater than the cost of exogenous effects, except in highly illiquid markets, and we have demonstrated how a trader's liquidation or hedging strategy can be tailored to the size of the liquidation costs. The chapter ends with a description of the use of both FHS and standard Monte Carlo simulation to incorporate volatility clustering effects into a stress test, when positions are liquidated or hedged only gradually over a period of several days, so as to minimize the liquidity costs.
1 Or, for a short position, losing so much that the firm becomes insolvent.
2 See http://www.cme.com/span/fordetails.
3 A parallel shift in a yield curve will leave the value of a one-for-one calendar spread unchanged, but a tilt in the yield curve affect its value. For example, if the short rate increases but the long rate decreases, then a spread position that is long the short-maturity futures and short the long-maturity futures will increase in value.
4 Or, the correlations could be less than one and the standard deviation could be different for yields of different maturities, as indeed could the mean. Neither is it necessary to assume changes in yields have a multivariate normal distribution: for instance, a multivariate Student t distribution, a normal mixture distribution or a general distribution based on a copula may be preferred.
5 Given a distribution of portfolio returns or P&L we can of course obtain any quantile of this distribution and hence estimate the VaR and/or corresponding ETL.
6 The symbol is ∘FTSE.
7 Notice that a normal assumption would lead to a much more conservative conclusion.
8 The Derivatives Policy Group was comprised of principals representing CS First Boston, Goldman Sachs, Morgan Stanley, Merrill Lynch, Salomon Brothers, and Lehman Brothers. It was organized to respond to public policy issues raised by the over-the-counter derivatives activities of unregulated broker-dealers and futures commission merchants, including the need to gain information on the risk profile of professional intermediaries and the quality of their internal controls.
9 That is, the shortest rate moves up (or down) by 25 bps and the longest rate moves down (or up) by 25 bps, and the movements in other rates are determined by linear interpolation.
10 For instance, AA spreads increase by 50 basis points and B-rated spreads increase by 200 basis points.
11 For example, 50 basis points for overnight rates and 25 basis points for the annual rate.
12 They almost reached this level at the beginning of the credit crisis and so it is plausible that they could do so again.
13 This is a Student t distribution with 6 degrees of freedom, a mean of 40 bps and a standard deviation of 15 bps.
14 Interested readers are recommended the excellent paper by Spetzler and Staël von Holstein (1977).
15 Such as the height of Nelson's Column in Trafalgar Square, London.
16 When the risk horizon h is small we usually assume the expected value is zero, i.e. that the portfolio is expected to return the discount rate. It is only when the risk horizon exceeds several months that the discounted expectation has a significant effect on the VaR estimate.
17 Note that the factor of ![]() here expresses the fact that we have a 3-month covariance matrix, not an annual one.
here expresses the fact that we have a 3-month covariance matrix, not an annual one.
18 The historical and mark-to-market accounting frameworks are explained, briefly, in Section IV.8.2.2.
19 Readers may change the parameters of the normal mixture distribution in the spreadsheet until they are satisfied that the distribution represents their own beliefs about the credit spread on a BBB-rated bond in 1 year's time. Since mixtures with three normal components are very flexible, a great variety of shapes may be obtained.
20 See the numerical examples provided in Section IV.2.9.4 for further illustration.
21 For example, in Example IV.7.7 the probability vector representing the mixing law was (0.3, 0.3, 0.4).
22 More generally, we could replace x by a vector of risk factor returns x, and use multivariate distribution functions for G(x) and H(x). Then at the second simulation stage we must apply a multivariate method – see Section IV.4.4.1 for further details.
23 The Bayesian approach is named after Rev. Thomas Bayes, whose ‘Essay Towards Solving a Problem in the Doctrine of Chances’ was published posthumously in the Philosophical Transactions of the Royal Society of London in 1764.
24 Bayesian estimates of parameters are usually based on an assumed loss function (e.g. a quadratic loss function) and it is only for certain types of loss function that we recover the classical estimates as a special case of Bayesian estimates. For instance, the maximum likelihood estimator of a parameter is a Bayesian estimator with a non -informative prior (i.e. the prior distribution is uniform) and a zero–one loss function (i.e. the loss is zero if the estimator has no error, and one for any other value). Thus the maximum likelihood estimator – the jewel in the crown or classical statistics – is the most basic of all Bayesian estimators, because it is based on no prior information and a very crude loss function.
25 The unconditional probability of the data P(B) is regarded as a scaling constant, k, whose value is set to ensure that the distribution on the left-hand side is normalized (so that its sum or integral is one).
26 The symbol? denotes ‘is proportional to’.
27 Notice that the posterior distribution has a volatility that is less than both the historical and the prior's volatility. This will always be the case when the likelihood and the prior are both normal. The rationale that justifies this result is that additional information should reduce one's uncertainty. However, when the likelihood and prior are not both normal, the uncertainty in the posterior distribution need not be less than in both the likelihood and the prior.
28 A pianola is a mechanical piano (see www.pianola.org).
29 Chopsticks is the name given to extremely simple piano pieces that can be played with two fingers, acting like chopsticks (see http://en.wikipedia.org/wiki/Chopsticks_(music)).
30 Simple methods only: However, advanced credit and operational risk models were adopted in the UK in January 2008.
31 They specifically mention deep out-of-the-money options positions. Also the exogenous and endogenous aspects of liquidity should be considered. See Section IV.7.5.4 for further details.
32 That is, a very large difference between yesterday's closing price and today's opening price.
33 In fact most credit rating agencies such as Standard and Poor's, Moody's and Fitch also require firms to provide stress testing results that support their claims about capital adequacy.
34 This analysis should be designed around the bank's current trading positions and also take account of current market circumstances. For instance, at the time of writing, volatile oil prices and credit spreads are the two main risk drivers that could be affecting the solvency of a bank.
35 The three ‘pillars’ of the new Basel Accord are: Pillar 1, capital requirements; Pillar 2, enhanced supervision; and Pillar 3, public disclosure and market discipline (see Section IV.8.2.3 for further details).
36 The six sigma methodology was originally developed as a set of practices designed to improve manufacturing processes and eliminate defects. See http://en.wikipedia.org/wiki/Six_Sigma for more information.
37 Note that the latter is the dollar return, not the return in pounds sterling, and we assume that all returns are log returns.
38 It is also possible – though complex – to associate a probability with a worst case loss that is derived using this method by computing the value of the multivariate normal distribution function at x, when x′Ω−1x = c. See Studer and Lüthi (1997).
39 However, Berkowitz (1999) has argued that the distribution of an asset or risk factor during periods of market stress is very different from its usual distribution.
40 The Basel Committee recommends the use of both hypothetical stressed covariance matrices, and those derived from historical crisis periods.
41 Codes^FTSE and^GSPC. Note that the closing prices are not contemporaneous, as the UK market closes 4.5 hours before the US market, and hence the correlation is likely to be underestimated.
42 The S&P index is on the left-hand scale and the FTSE 100 index is on the right-hand scale.
43 We can ignore discounting with no real loss of accuracy since the risk horizon is only 1 day.
44 This is, of course, a crude approximation. But then the functional form we have chosen is fairly arbitrary anyway, since the Student t distribution is symmetric. On the plus side, (IV.2.63) is just as easy to compute as the normal linear VaR, and at least it is a more accurate reflection of the data than a normal distribution.
45 For the proof of this see Section I.2.4.3.
46 We can check a matrix for positive semi-definiteness either by finding its eigenvalues and checking that none of these are negative, or by checking that all its principal minors have positive or zero determinant. See Sections I.2.2.8 and I.2.3.7.
47 See http://en.wikipedia.org/wiki/Matrix_norm.
48 Without this, the resulting matrix has determinant 2.75 × 10−8.
49 For instance, bond portfolios are commonly ‘immunized’ against parallel movements – see Section III.1.5.6 for further details.
50 For details on how to do this, see Section II.2.4.4.
51 Note that the first component is not a parallel shift, as we can see from Figure IV.2.3.
52 These values are very small, reflecting the fact that FTSE 100 and S&P 500 futures are major markets that tend to remain highly liquid even in stressful circumstances. Note that the parameters of a lognormal distribution are the mean and standard deviation of the corresponding normal distribution, i.e. the mean and standard deviation of the log spread in this case. The figures here for the spread mean and standard deviation are actually derived from choosing suitable values for the mean and standard deviation of the log spread. See (I.3.40) and (I.3.41) for the formulae used in the spreadsheet to relate the mean and standard deviation of the log spread to the corresponding parameters for the spread.
53 The normal lot size is 100 for US stocks and 1000 for UK stocks, since the price per share of US stocks tends to be higher than it is in the UK. Normal lot sizes for currencies are usually in units of $1000. Transactions at multiples of $1000 usually have smaller spreads than transactions at intermediate amounts.
54 The formula used in cell AH2 accounts for uniform liquidation over a 10-day period.
55 As usual, readers should extend the number of simulations by filling down, after copying the spreadsheet from the CD-ROM to their hard disk. But due to the limitations of Excel we are not able to simulate very many 10-day returns for the empirical distribution that forms the basis of our stressed VaR estimation; that is why our results are based on only 5000 simulations.
56 This depends on the sign of the asymmetric coefficient λ, which was positive in this case. But if λ were negative then the losses following a positive shock to the return would be greater than those following a negative shock.