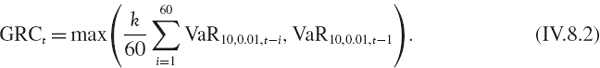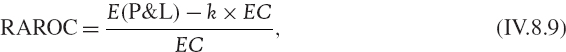IV.8
Capital Allocation
IV.8.1 INTRODUCTION
The senior management and board of directors of a financial institution have an important role, which is to ensure that capitalization is sufficient to cover the risks that are being taken. Their duty is to the shareholders and, in banking, also to the regulators. Thus, a major task facing the risk manager in a bank or financial firm is to assess the level of risk relative to the capitalization, at various activity levels and within each line of business. Also, the value of the firm is reflected by its credit rating, which is linked to the probability of default over a long time horizon. Thus, good risk management should encompass a rigorous stress testing programme that is designed to increase the probability that the firm remains solvent over this time horizon.
The solvency of banks is particularly important for the stability of the financial system. Governments, central banks and the Basel Committee have a strong interest in systemic risk, where insolvency in one sector of an economy can lead to a national – if not global – economic crisis. Thus the global recession following the stock market crash of 1987 prompted a revision of banking regulations and, in the mid 1990s, new minimum requirements for the regulatory risk capital owned by banks were imposed on all banks in the G10 countries, and these were later adopted by most of the developed countries in the world.
The computation of regulatory capital for various activities in each line of business is an important task for the risk managers in a bank. But, unlike economic capital, when estimating the legal minimum level of capitalization required for the bank as security against its market risk exposures, the manager is not free to use the risk models, risk metrics and data that he deems most appropriate. He may even use no risk model at all, and merely apply the standardized rules that are set by the regulators. Alternatively, he could use an internal risk model to estimate risk capital, provided it is validated by the regulator and provided that the risk management structure in the bank satisfies certain qualitative criteria. However, the internal model must conform to some fairly strict quantitative criteria. In most countries it can be one of two broad types, either a scenario model or a VaR model;1 and regulatory capital is based on an aggregate maximum loss if the scenario model is used or the 1% 10-day VaR if the value-at-risk approach is used.
By contrast, the computation of economic capital can be based on any internal risk model, any risk metric and any data. The only proviso is that the methodology is acceptable to the board of directors. An economic capital model could be based on any assumptions about risk factor evolution over the risk horizon and the data that are used could be purely historical, purely hypothetical (e.g. as in hypothetical stressed VaR) or a combination of the two. The risk manager is also free to recommend whatever risk metric or metrics he believes to be appropriate, and apply these to the economic capital model. In fact, for economic capital estimation many large banks use ETL rather than VaR, and they may also use at least some data from historical or hypothetical market crises.
At the elemental level, economic capital does not need to correspond to real capital. It is a risk measure, such as VaR or ETL, at a fairly high confidence level and assessed over a fairly long horizon. The confidence level 1 − α and risk horizon h are linked to the solvency condition, whereby the total economic capital for the firm as a whole can be interpreted as the minimum level of capitalization required so that the probability of insolvency over a risk horizon h is no greater than α. But capital reserves do not have to match economic capital in the same way that they must match minimum regulatory capital. In fact, many institutions carry a much higher level of capital than they need to justify their credit rating, as a signal of confidence to their investors and their counterparties.
In a large organization it is usual to assess risks first at a fairly elemental level, then progressively aggregate positions into larger and larger portfolios. This is because different individuals assess market risks for different reasons. Starting at the most granular level, each trader is concerned with the accurate assessment of the risk of every instrument in his book, the risk of portfolios of similar instruments and, finally, the risk of the book as a whole. Both he and the head of the desk should be monitoring these risks, and limits will be placed on the total risks that each trader can take. The head of desk will be monitoring portfolios consisting of each single book, up to a portfolio that contains all the instruments in all his trading books. Then the risk manager at the head of the business unit has the job of ensuring that the market risks taken by the head of each desk in the business unit remains within reasonable limits, as he monitors the total market risk taken by the unit as a whole. Finally, the global head of market risk examines the market risks of each business unit and the total market risk at the company or group level, and reports these to the board of directors. Thus a ‘portfolio’ can be anything from a single instrument to all the positions in the entire firm.
In other words, we first assess the risk of individual instruments, then of portfolios of similar instruments, and then we aggregate the risks in a (hopefully) intelligent manner to obtain the risk for progressively larger and larger portfolios containing different aggregate positions. At some stage, often at the business unit level, the total market risk is aggregated with the total credit risk and the total operational risk, to produce a combined estimate for the total risk of the business unit. Finally, the business unit risks are aggregated to obtain a firm-wide estimate of risk against which the total capitalization of the firm may be assessed. This so-called ‘bottomup’ approach is the most common risk assessment paradigm.
By contrast, the process of economic capital allocation takes a ‘top-down’ approach. Having assessed the total, firm-wide risk and made a judgement on the required level of total economic capital for the firm, this capital is then assigned to different business units, and to different activities within each unit. Finally, economic capital is assigned to the desk level and possibly even to the level of the trader. The greater the economic capital assigned, the greater the risks that can be taken, and the freer the desk or trader becomes. Hence, the increase or withdrawal of an economic capital allowance becomes a useful tool whereby senior managers can control different activities in the organization. Nowadays most large organizations have a management structure that is driven by economic capital, because it is a tool that allows the risks of all the different activities in the firm to be compared on a standard scale, and because it can be aggregated for the purpose of ‘bottom-up’ firm-wide risk capital estimation and disaggregated for ‘top-down’ capital allocation, in a mathematically coherent framework.
One of the major disadvantages of the ‘bottom-up’ approach to risk assessment is that most risk analysts use a simple dependency metric, i.e. correlation, for the aggregation of risks, as if all dependencies were linear and normal. Aggregation risk is the model risk that arises through inappropriate assumptions on risk factor dependencies when assessing portfolio risk, and this is the major source of model risk in firm-wide risk capital assessment. The ‘bottom-up’ paradigm also assumes that we know the current value of all our positions precisely. Yet only a limited number of positions can be marked to market. These include the liquid exchange traded contracts and some over-the-counter (OTC) contracts, if quoted by the brokers. Many other positions will need to be valued by marking to model, and this introduces a pricing model risk, as opposed to risk model risk, that can be very significant indeed.
The remainder of this chapter is structured as follows. Section IV.8.2 deals with the estimation of the minimum market risk capital requirements for banks. Here we describe the Basel regulations, which were broadly defined in the 1996 Market Risk Amendment and later refined with the new Basel II Accord; we summarize the differences between the accounting frameworks that are used in the banking and trading books (typically, market risks are only assessed on the trading book); we describe the regulatory framework for estimating minimum capital requirements for market risks, using both internal models and the standardized rules that the Basel Committee recommends for adoption into national regulations; and then we describe the ‘add-ons’ to the general market risk capital charge that account for specific risks, and the incremental risk charge that the Basel Committee has recently recommended for banks that use internal models with specific risk recognition.
Section IV.8.3 introduces economic capital: the methods used to assess it and the optimal allocation of economic capital as a risk management tool. We show that the aggregate economic capital for a firm, defined as the minimum level of capitalization that the firm should aim for in order to achieve a high probability of remaining solvent over some future time horizon, is a risk metric which corresponds to a quantile, like VaR. But, unlike regulatory capital for banks, firms are free to choose whatever metric they like for economic capital, provided it is acceptable to shareholders. The risk-adjusted performance of each activity in the firm may be assessed by combining forecasts of expected profits and losses with a measure of economic capital for this activity. Finally, we show how to achieve an efficient allocation of economic capital to different activities, by optimizing the firm-wide risk-adjusted performance, focusing on the maximization of risk adjusted return on capital (RAROC) which is one of the performance measures that is most commonly applied in the industry today.
IV.8.2 MINIMUM MARKET RISK CAPITAL REQUIREMENTS FOR BANKS
This section focuses on the 1996 Market Risk Amendment to the 1988 Basel Accord, and the modifications to market risk capital requirements under the new Basel II Accord. Section IV.8.2.1 describes the history of the Basel Committee and its regulatory initiatives; Section IV.8.2.2 defines the banking and trading books and provides an overview of the accountancy frameworks used in each; Section IV.8.2.3 describes the regulatory framework for controlling market risk in the banking system, which is based on three ‘pillars’ of regulation. Thereafter we focus on the Pillar 1 capital charge, explaining how the general, specific and incremental market risk charges are calculated using an internal model, or using a set of standardized rules defined by the Basel Committee.
IV.8.2.1 Basel Accords
In 1974 the central bank governors of the G10 countries created a forum to debate and coordinate best practices for risk management and banking supervision. The Bank for International Settlements (BIS), located in Basel, offered its premises and facilities for meetings and a permanent secretariat, hence the name Basel Committee on Banking Supervision (BCBS or ‘the Committee’).2 The Committee now has about 30 workgroups and task forces addressing various issues affecting banks and their supervisors, focusing on broad standards and statements of best practice. The recommendations put forward in the two Basel Accords are now almost universally adopted into national legislation. However, whilst the Committee has great influence, it has no legal power.
The defining initiative of the Committee was the 1988 Basel Accord which was implemented in the G10 countries in 1992. Prior to this, banking supervisors were content with requiring disclosure of exposures (mostly foreign exchange and interest rate) and setting some limits on concentrations of risks (large exposure limits, and country risks). Adequacy of capital was a topic of discussion between supervisors and banks, but there were no strict requirements. The main contribution of the 1988 Basel Accord was to set core principles for adequate supervision and minimum capital standards. At the same time, regulatory convergence and coordination were sought across countries as well as between banking and securities’ businesses.
For the first time, the 1998 Basel Accord set quantitative minimum capital requirements for banks based on the level of credit risk in their assets. The Accord, and its subsequent 1996 Amendment for Market Risk in the Trading Book,3 has been progressively adopted into legal regulations by over 100 countries, so that the Accord has now become the global standard for evaluating banking risk. An important initiative in the 1996 Amendment was a long technical appendix that responded to the industry calls for the use of internal models, rather than standardized rules, to assess market risk capital.
Extensive revisions to the assessment of credit risks and the introduction of a capital charge to cover operational risks were the main features of the new Basel II Accord in 2005.4 Developments in credit derivatives and the rapid growth in the markets for credit default swaps and collateralized debt obligations in particular, meant that sophisticated credit mitigation techniques were no longer recognized efficiently under the old Accord. And because of the increasing complexity of financial markets there was greater need for transparency of accounts and risk disclosures. But, in contrast to the 1996 Amendment, the initiative for a new Accord was driven by regulators, not by the industry. Industry consultation on Basel II took almost 6 years and many contentions remain even now, after its implementation in major countries.
The primary objectives of the old accord were safety and market stability. In addition to maintaining these prime objectives, the Basel II Accord aims to harmonize banking regulations among countries and to foster better risk management in an evolutionary approach, starting with simple rules for all banks but providing incentives in the form of reduced capital requirements for banks with more sophisticated risk management. The new regulations should not affect global capital requirements, but they do introduce greater risk discrimination, and this will lead to a redistribution of capital among financial firms.
The market risk capital requirements under Basel II are largely unchanged from the 1996 Amendment, except for the definition of the trading book as positions in financial instruments and commodities held either with trading intent or to hedge other elements of the trading book.5 And now, under the new Accord, exceptional market risks should be monitored in the banking book. For example, the Basel Committee have recommended that interest rate exposure be stress-tested by assuming a 200 basis point parallel shift in the zero coupon curve. However, any additional capital charges for market risks in the banking book are left to the discretion of national supervisors.
IV.8.2.2 Banking and Trading Book Accounting
In the current spectrum of accounting standards, banks currently apply these forms of accounting:
- In historical (also called accrual or cost) accounting, cash flows are recorded as they occur, and assets are held at cost. This form of accounting does not reflect the current value of a business. Therefore, for prudence, it is accompanied by a ‘reserves and provisioning’ policy that is designed to cover future potential losses, in which provisions (but not reserves) are limited, to avoid manipulation of profit and tax avoidance.
- Fair value accounting is reserved for positions that have a visible value in a liquid market (positions that can be marked to market) or that have a value which can be objectively and accurately estimated (positions that can be marked to model).
Cost accounting is easier to understand than fair value accounting, being based on observed cash flows rather than complex marking-to-model calculations. And there is less subjectivity in cost accounting than there is in fair value accounting. The only subjective elements of the cost accounting framework are in the reserves and provisions that are made. Since these reserves and provisions are to cover expected losses, not worst case losses, the accent of cost accounting will be on a conservative valuation of assets and liabilities, based on their historical cost. But cost accounting is backward looking, so it is not an appropriate starting point for the evaluation of risk. It does not assess variations in economic value about its fair (i.e. expected) value. In fact, it does not even assess the fair economic value of a business.
In fair value accounting the accent is on ‘true and fair’ assessment of asset values, although the interpretation of these concepts is somewhat subjective.6 As a result, fair value accounting is more subjective than cost accounting. At the same time, being based on market (or model) prices of financial instruments, it is also less consistent across different countries and businesses (e.g. banks, securities firms and insurance companies) than cost accounting. However, it is forward looking, since market prices provide a signal about traders’ expectations. The disadvantages of fair value accounting are that it can be complex, costly and unreliable. For instance, it would be very difficult to reach a consensus on the expected losses due to counterparty default in illiquid markets. Nevertheless, it is in fair value rather than cost accounting that we find the appropriate foundation for risk evaluation.
The trading book contains on and off balance sheet positions that are held with the intent of deriving short term profits. This implies that they are liquid enough to be closed down rapidly and can be easily valued by marking to market. Derivative instruments such as futures, swaps and options are off balance sheet instruments that are marked in the trading book. The banking book contains all transactions that cannot be valued easily or are held for the long term with no trading intent. They are usually accounted for on an accrual basis with adequate reserves and provisions for potential losses, but marking to market is permitted where safe. Thus the distinction between the two books is based on an accounting issue, i.e. that of valuing liquid versus illiquid assets. Banks normally use fair value accounting in the trading book and cost accounting for most of the positions in the banking book.
Reporting standards for basic accounts (or supplementary risk disclosures) play a critical role in risk evaluation and capital allocation. These are essential for the evaluation of performance, the disclosure of risks and the enforcement of market as well as supervisory discipline. Accounting standards need to be global, to facilitate comparisons across nations and businesses. International accounting standards also save costs and facilitate access to international capital markets. However, despite the extensive work that has been carried out by the International Accounting Standards Committee (IASC) since its creation in 1974, progress is slow because of differences in national traditions and legal systems.
Like the BCBS, the standards developed by the IASC have no legal power until accepted and enacted by national authorities. In 2000 the Securities and Exchange Commission (SEC) in the US adopted the FAS 133 standards in which derivatives are recorded in the trading book at fair value.7 Since January 2005 the EU has required quoted companies to produce accounts according to the much more comprehensive IAS 39 standards.8
IV.8.2.3 Regulatory Framework for Market Risk
The Basel II Accord reaffirmed the three pillars of regulation that were defined in the first Accord:
- Pillar 1 – minimum capital standards. This sets the minimum level of eligible capital that banks must hold as insurance against risk.
- Pillar 2 – supervisory review. This sets out the recommendations for inspection and the reporting requirements for banks.
- Pillar 3 – public disclosure and market discipline. This aims to support the supervisor by enhancing market scrutiny by competitors, clients and shareholders.
The three pillars are seen as equally important. They are also complementary. For example, the flexibility to use internal models for calculating risk capital in Pillar 1 means greater responsibility for the supervisor to inspect and approve these models under Pillar 2.
The central concept in the Pillar 1 capital requirement is a solvency ratio, called the Cooke ratio, which is defined as the ratio of eligible capital to the total capital charge, both of which are defined below. The minimum solvency ratio is the minimum value for the Cooke ratio that is set by the national regulator, and for well-managed banks with at least an A credit rating it is at least 8%. National supervisors are entitled to set higher ratios for poor-quality or less well-managed banks, and to set different minimum solvency ratios for the trading and banking books within a bank.
The numerator in the solvency ratio, eligible capital, consists of three tiers, defined in decreasing order of reliability for capital reserves:
- Tier 1 (core capital) consists of paid up share capital plus audited retained P&L on investing this capital;
- Tier 2 (supplementary capital) consists of undisclosed reserves, revaluation reserves, general provisions, hybrid instruments and subordinated debt with maturity at issue of at least 5 years;
- Tier 3 (sub-supplementary capital) consists of subordinated debt with maturity at issue of 2–5 years.9
For eligibility under Tier 2 or Tier 3 capital, instruments must be free from any restrictive covenants on their tradability, or they must be able to be hedged completely. Tier 2 capital must also be less than Tier 1 capital.
The denominator in the solvency ratio, the risk weighted assets, is the sum of risk measures for market, credit and operational risks. The market risk capital charge (MRC) applies to all on and off balance sheet positions in a trading book.10 The MRC is defined as the sum of a general risk charge (GRC), plus a specific risk charge (SRC) or an incremental risk charge (IRC):
The specific or incremental risk components of the MRC may be applied to both equity and interest rate exposures under the Basel recommendations, but they do not apply to commodities or currencies.
Subject to certain qualitative requirements on its risk management procedures and quantitative requirements on the structure of the risk model, set out below, banks may use an internal risk model to estimate the MRC.11 The qualitative criteria that must be satisfied for use of an internal model to assess MRC include:
- independence between risk control and business trading, with risk managers reporting directly to the senior management of the bank;
- a regular backtesting programme, as well as initial and ongoing validation of the internal model;
- involvement of the board of directors and senior management in the risk control process, to which they must be committed;
- use tests whereby the internal model is closely integrated into daily risk management, including its use in conjunction with trading and exposure limits;
- a routine and rigorous programme for stress testing, with results being regularly reviewed by senior management, and dynamic contingency plans must be in place;
- documentation for the technical framework of the risk model, and for internal policies, controls and procedures for operating the model;
- the regular internal auditing of the risk model, to assess the above.
Regulators pay particular attention to the possibility of large losses, that is, to the negative tail of a return distribution. Consequently, they focus on VaR to determine the minimum level of regulatory capital. The quantitative criteria recommended by the Basel Committee for the use of internal models are as follows:
- The 1% 10-day VaR must be estimated on a daily basis. For linear portfolios this may be computed as
 times the 1% 1-day VaR.
times the 1% 1-day VaR. - The historical sample must be at least 1 year (or, for banks that use a weighting scheme or other methods, the weighted average time lag of the individual observations must be at least 6 months). Also data must be updated at least every 3 months or when there has been a sharp change in prices.12
- No particular type of model is prescribed. So banks are free to use models based, for example, on covariance matrices, historical simulations, or Monte Carlo simulations. Discretion may be exercised to recognize empirical correlations within and across broad risk categories, including implied volatilities in each risk factor category, provided that the supervisory authority is satisfied that a bank's system for measuring correlations is ‘sound and implemented with integrity’.
- Models must capture the risks associated with option portfolios accurately using a 10-day price shock, corresponding to static rather than dynamic options VaR;13 they must also capture option portfolios’ non-linear price characteristics (i.e. gamma risk) and the volatility of underlying rates or prices (i.e. vega risk).14
IV.8.2.4 Internal Models
For banks that use an internal VaR model to estimate the MRC the general risk charge is calculated as k times the average of the 1% 10-day VaR over last 60 days, or yesterday's VaR on the current portfolio, if this is greater:
The multiplier k takes a value between 3 and 4 depending on the model's backtesting results. If backtests reveal statistical inaccuracies in the VaR estimates, k takes a higher value or the VaR model may be disallowed.15
It is easy to show that a multiplier of between 3 and 4 produces a much higher (i.e. far more conservative) risk measure than a 99.9% annual VaR. For example, even when k takes its lowest value 3 and the returns are normal and i.i.d., we have
![]()
Hence, the GRC is approximately 7σ away from the expected portfolio return. The probability of a return that is less than this, in a 10-day period during which the portfolio is static, can be found using standard normal tables: it is approximately 1.5 × 10−12. Hence, it is extremely unlikely that the GRC would be exceeded over a 10-day horizon.
But what about exceeding the GRC over an annual horizon – how likely is this? We should not just extrapolate the GRC to an annual horizon using the square-root-of-time rule, i.e. by multiplying it by ![]() , because the portfolio is likely to be rebalanced, except in cases of extreme illiquidity. If the portfolio is rebalanced every 10 days then it is reasonable to assume the 10-day returns are i.i.d., and in this case the probability of not exceeding 3 × 1% 10-day VaR over an annual horizon is (1−1.5 × 10−12)25. So the probability of exceeding a level of loss that is set at 3 × 1% 10-day VaR, over 250 days, is
, because the portfolio is likely to be rebalanced, except in cases of extreme illiquidity. If the portfolio is rebalanced every 10 days then it is reasonable to assume the 10-day returns are i.i.d., and in this case the probability of not exceeding 3 × 1% 10-day VaR over an annual horizon is (1−1.5 × 10−12)25. So the probability of exceeding a level of loss that is set at 3 × 1% 10-day VaR, over 250 days, is
![]()
Clearly, this is much more stringent than using a 99.9% confidence level over a 250-day horizon.
In a steady market the GRC will be dominated by k times the average VaR and, as we have just demonstrated, it is unlikely that losses would exceed the capital requirement in this case. The averaging process also smoothes out sharp variations in MRC and reduces the procyclical tendency for capital requirements. However, if there is a sharp increase in the bank's aggregated market risk, the average VaR term in (IV.8.2) is replaced by yesterday's VaR, that is, the VaR estimate does not increase enough when the portfolio make a large loss. This increases the risk sensitivity of the MRC. Problems will arise, however, if the risk model that is used to estimate VaR is insufficiently risk-sensitive, that is, the VaR estimate does not increase enough when the portfolio make a large loss. This is one reason why regulators require the VaR model to pass certain quantitative backtesting requirements.
EXAMPLE IV.8.1: CALCULATING GRC FOR A LONG-ONLY POSITION USING VAR
In Example II.1.2 we considered a portfolio of two US stocks, American Express (AXP) and Cisco (CSCO) in the S&P 100 index. Using daily data from 3 January 2000 to 31 December 2007, we estimated the stock's betas and the specific volatility of the portfolio. Estimate the GRC for the same portfolio, which is continually rebalanced to have 60% invested in American Express and the rest in Cisco. Assume the GRC multiplier k = 3 and use the normal linear model based on 250 daily returns to estimate the portfolio beta and the 1% 10-day VaR.
SOLUTION We estimate the 1% 10-day VaR using the normal linear VaR formula
![]()
where βt and σt are the portfolio beta and the standard deviation of the S&P 100 index returns respectively, both based on equal weighting over the last 250 observations. Then we apply the GRC formula (IV.8.2). This result of rolling this calculation over the sample period is the series shown by the black line in Figure IV.8.1, measured on the left-hand scale. The S&P 100 index volatility is also shown on the left-hand scale and the procyclical tendency of the GRC, to move with the market volatility, is clear.
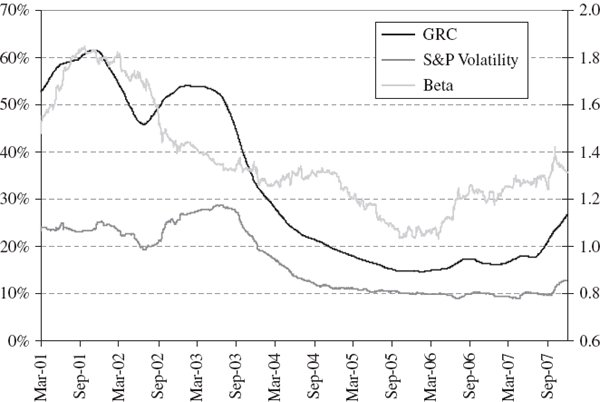
Figure IV.8.1 GRC for the US stock portfolio and S&P 100 volatility
The portfolio beta, shown on the right-hand scale, is always greater than 1. Hence, this is a ‘high risk’ portfolio, and this explains why the GRC is so large. Around 50% of the portfolio value would need to be held as the general risk capital charge in the early part of the period, but during 2004–2006 it reduced to less than 20% of the portfolio value. It rose again at the end of the data period due to the credit crunch, which had a serious impact on US stock market volatility.
In some jurisdictions banks may be allowed to use another approach to compute the GRC using an internal model.16 This is the scenario analysis approach to estimating GRC, in which exposures in each division of the trading book are subjected to hypothetical changes to major risk factors, as if the position has a risk factor sensitivity of 1.17 The extent of the hypothetical change depends on the type of risk factors. For instance, equity indices are subjected to a maximum of ±8% changes in price and ±25% relative changes in volatility.18 Within these limits a two-dimensional ‘grid’ of possible price and volatility changes is drawn, and the P&L of the book as a whole is calculated at several points within this grid. The aim is to quantify the maximum loss that could be made and, for non-linear exposures, the maximum loss may occur at an interior point, not necessarily at one of the extremes. For each type of risk and within each geographical zone, the maximum loss is recorded for each book, and these losses are then summed over all books covering different risk types and geographical zones, to produce the market GRC for the bank. Small ‘boutique’ banks that have just a few large exposures may find that this approach produces lower GRC estimates than would be obtained under the standardized rules, and which may be easier to estimate than VaR-based GRC.
IV.8.2.5 Standardized Rules
An alternative to using internal models to estimate capital requirements is to apply a ‘building block’ approach, in which separate charges for equity, currency, commodity and interest rate exposures are estimated and then summed across the four categories of risk.19 In the standardized approach the MRC is based on instrument-specific rules. For equity exposures the GRC is 8% of the exposure (long or short, with netting allowed within a book) summed over all books. Then there is an additional specific risk charge (SRC) for equity risk because, in the risk factor mapping of a stock portfolio's returns, idiosyncratic risk could be significant. This risk cannot be overlooked, except when all equity books contain large, well-diversified portfolios. The SRC for equities is calculated, without netting long and short exposures in the same book, as a percentage of nominal exposure. The SRC is 8%, unless the portfolio is both liquid and well diversified, in which case the charge is 4%. Then the SRC is summed over all books to obtain the total SRC for equity risk.
The SRC add-on may apply to internal models as well as the standardized rules. Banks using internal VaR models to calculate the GRC for equities may already be capturing specific risk when the only significant risks are those due to the risk factors that they are using in the risk model. If a bank's internal model has gained specific risk model recognition (i.e. if the bank can convince the supervisor that the model is capturing specific risk adequately), then it is exempt from the SRC. Otherwise it must add on the SRC that is calculated according to these standardized rules.
For example, the GRC for the portfolio in Example IV.8.1, when based on the standardized rules, is 8% of the portfolio value. To this we must add a specific risk charge of 8%, because the portfolio is not well diversified. So, the MRC under the standardized rules will be 16% of the portfolio value. But the internal model produced a GRC of more than 16% throughout the data period considered. Moreover, it is unlikely that this model would gain specific risk recognition, so the bank would still need to add on an SRC of 8%.20 Hence, the use of an internal model in this simple example would lead to a much higher VaR estimate than the application of the standardized rules.
The standardized rules for currencies and gold require the nominal amount (or net present value) of the net position in each foreign currency and in gold to be converted at spot rates into the reporting currency. The overall net open position is measured by aggregating the sum of the net short positions or the sum of the net long positions in currencies, whichever is the greater; plus the net position (long or short) in gold, regardless of sign. Then the GRC is 8% of the overall net open position. There is no specific risk charge for currencies and gold, so MRC ≡ GRC.
The standardized rules for interest rates are more complex.21 For general interest rate risk due to discount curve movements, exposures within each currency are banded into duration or maturity bands. The bands are then grouped into three zones, according to the duration or maturity of the band. In each band the exposures (long and short) are weighted by a series of factors that depend on the zone.22 Then ‘vertical and horizontal disallowances’ are calculated. First, we net long and short exposures within each band and find the matched amount and an excess amount. The excesses are then matched within the zone, giving a second matched amount, the vertical disallowance, and an excess. These excesses are matched across different zones, giving the horizontal disallowance, and a final net unmatched amount. Thus the GRC is the sum of these components:23
- (i) a small percentage of the matched positions in each zone;
- (ii) a larger percentage of matched positions across different zones;
- (iii) the net (long or short) position in the whole trading book.
Separate maturity ladders are used for each currency and capital charges are calculated for each currency separately, and then summed with no offsetting between positions of opposite sign, to obtain the total GRC for interest rate risk.
The reason for an additional specific charge for interest rate risk is that a single discount curve for the risk factors of an interest rate sensitive portfolio ignores the risk due to changes in credit spreads. The SRC for interest rate exposures depends on the credit rating of the issuer. For example, the SRC for a government security varies from 0% (for a government with at least an AA– rating) to 12% (for a government with a rating below B–). Banks using internal VaR models to calculate the GRC may already be using credit spread curves as risk factors, in which case the model may have gained specific risk recognition, and then it is exempt from the SRC. Otherwise it must add on the SRC that is calculated according to the standardized rules. Full details are given in BCBS (2005).
The standardized approach for commodity risk entails a maturity ladder with position matching that is similar to that used for interest rate exposures. The percentages used to calculate the GRC depend on maturity, except when a simplified method is used. In the simplified method the GRC for directional risk is 15% of the net position, long or short, in each commodity. Added to this is an additional capital charge equivalent to 3% of the bank's gross position (i.e. long plus short) in that particular commodity, to cover basis risk. There is no specific risk charge for commodities, so MRC ≡ GRC.
IV.8.2.6 Incremental Risk Charge
After the credit crunch that began in 2007 a new requirement for banks using internal models, for holding capital against default risk, was proposed by the Committee, and this is incremental to any default risk already captured. Regulators are concerned that the VaR framework ignores important differences in the underlying liquidity of trading book positions, and that it may not fully reflect large but infrequent daily losses, or losses that occur as a result of large cumulative price movements over periods of several weeks or months. Also, following the Committee's recommendations, many banks are using VaR models with equal weighting of about 250 days of historical data. Now the Committee is concerned that this approach yields insufficient capital to be held against trading positions following periods of relative calm in financial markets.
In July 2008 the Basel Committee introduced an incremental risk charge, which applies to default risk in the trading book, in response to the increasing credit risk exposure in banks’ trading books where the illiquidity of certain products is not reflected in standard VaR estimates.24 The IRC represents an estimate of the trading book's overall exposure to systematic and specific default, credit migration, credit spread and equity price risks over a 1-year horizon at a 99.9% confidence level, taking into account the liquidity horizons of positions.25
Current proposals are that the IRC must capture all material risks affecting prices of IRC covered positions that are attributable to IRC market risk factors, irrespective of whether they are already incorporated into a bank's 1% 10-day VaR estimate. For example, the IRC would capture price risks associated with movements in broad indices of stock prices and market credit spreads even though typically such price risks are already captured in a bank's VaR calculations.26
The Committee expects banks to develop their own models for calculating the IRC, and broad guidelines for these models are provided in BCBS (2008). Note that banks are now required to meet these guidelines in order to receive specific risk model recognition. For portfolios or products for which banks have already received specific risk model recognition under the 1996 Market Risk Amendment, banks are required to implement the IRC in January 2010. For banks without specific risk model recognition, and in particular for banks that apply the standardized rules, the current rules for calculating capital charges remain unchanged.
The guidelines set out in BCBS (2008) require that banks pay particular attention to the appropriate liquidity horizon in their IRC models. This represents the time required to sell the position or to hedge all risks related to the IRC market factors in a stressful market. The minimum liquidity horizon has a floor equal to:
- 1 month for equities traded on a recognized exchange, and for exposures to broad equity market indices, and benchmark interest rate spreads traded in liquid markets;
- 1 year for re-securitizations; and
- 3 months for all other IRC covered positions.
Alternatively, if this is greater, the liquidity horizon is set to be consistent with the bank's actual experience. Thus, the size of the IRC will depend very much on the liquidity of the exposure.
We now discuss how large the IRC might be for a specific, highly liquid portfolio. Most banks actively hedge their portfolios and so Example IV.8.1, which was used to demonstrate the methods that may be used to calculate MRC, is not very realistic in practice. The next example is also very simple, but it is more relevant than the previous one because we examine a liquid, hedged portfolio. If the portfolio is exactly hedged all the time, and the bank has specific risk model recognition, then the internal models-based GRC should be zero, and the MRC will simply be equal to the IRC. However, we shall assume that the hedge is rebalanced only once per day, so the portfolio's daily P&L is non-zero. Also, we shall assume there is a position risk in the hedged portfolio which depends on the size of the exposure.27
Normally, banks are not allowed to buy each other's shares, because this would allow them to increase their capitalization without using any capital. Two banks could merely swap shares, without any money changing hands. However, small amounts of another bank's shares may be held for market making purposes, when a bank's brokerage business needs to fulfil the orders from its clients, and so forth.
EXAMPLE IV.8.2: COMPARISON OF INTERNAL AND STANDARDIZED MRC FOR A HEDGED POSITION
A bank holds 10,000 shares in Barclays and each day it rebalances the short position in Lloyds TSB shares needed to match, as closely as possible, the value of the Barclays shares. It can only trade Lloyds TSB shares in units of 100. What is the MRC associated with this hedged portfolio, according to the standardized rules and based on an internal model?
SOLUTION We shall use daily data from 3 January 2005 until 14 November 2008 to answer this question.28 Over this period, the prices (in pence) of the two shares are shown in Figure IV.8.2. The effect of the banking crisis in 2008 is clear, as both share prices tumbled from about £5 per share to less than £2 per share, even though these banks were cash-rich retail banks that fared much better than many other banks during the crisis.
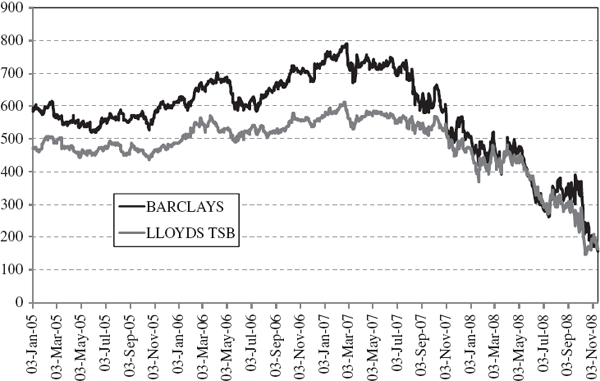
Figure IV.8.2 Price of Barclays and Lloyds TSB shares (in pence)
The hedge is rebalanced once each day, and we shall ignore transactions costs. So the market risk on the hedged portfolio arises from the daily P&L, as the previous day's portfolio is marked to market before rebalancing. There is also a small position risk, since we can only trade shares in units of 100. The standard deviation of the hedged portfolio's P&L determines the VaR.
Each day we use the past 250 observations on daily P&L to calculate its standard deviation. Then the normal linear VaR is calculated by applying the usual formula and we use (IV.8.2) to estimate the GRC. The standardized rules require holding 8% of the hedged portfolio value for the GRC plus 8% of the gross exposure (long and short, no netting) for the SRC. Hence the SRC is the main component of the standardized rules-based MRC (as can be seen by comparing the size of the figures in columns N and P in the spreadsheet). Rolling the calculation of capital charges daily over the entire sample gives the black line labelled GRC (Internal) and the grey line labelled MRC (Standardized) in Figure IV.8.3.
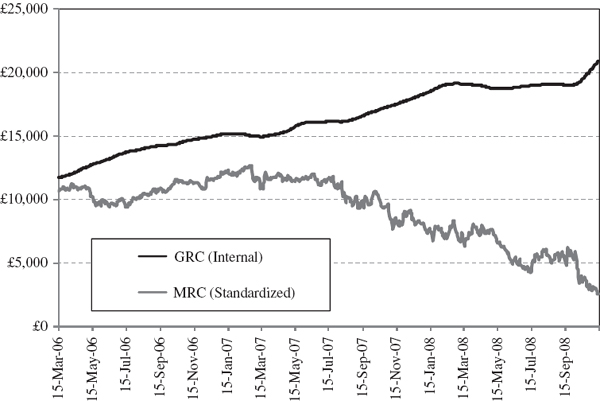
Figure IV.8.3 Internal GRC and standardized MRC for hedged portfolio
If the internal model does not have specific risk recognition, then the specific risk charge would be added to the internal model-based GRC to obtain the MRC. And if it does have specific risk recognition, then the Basel Committee are now recommending that a new, incremental risk charge should be added to the internal model-based GRC to obtain the MRC. Either way, the use of an internal VaR model will lead to a charge that is far greater than it would be under the standardized rules. As can be seen in Figure IV.8.3, the GRC (internal) is already greater than the standardized rules-based MRC. In fact, although the two were fairly close at the beginning of the sample, by November 2008 the GRC (internal) was about 8 times large than the MRC (standardized).
The Basel Committee have proposed the IRC because they believe that internal models with specific risk recognition could induce a bank to hold relatively little risk capital against hedged portfolios. However, the above example demonstrates that the capital charges based on internal models may be substantially greater than those based on the standardized rules, for hedged portfolios as well as for unhedged portfolios. Therefore, if the proposed IRC is adopted into national regulations, then some banks may have the incentive to revert to the standardized rules for calculating MRC, if they are allowed to do so.
IV.8.3 ECONOMIC CAPITAL ALLOCATION
Innovation and progress in financial risk management have been driven by the regulators but led by the industry, and risk professionals in the industry have always questioned the methods that regulators propose for estimating regulatory risk capital. The standardized rules approach is extremely crude and imprecise, and even the internal models that most large banks use for calculating regulatory risk capital are based on questionable assumptions. For example, using a square-root scaling rule for assessing VaR of linear exposures assumes that daily returns on portfolios are normal and i.i.d., but we know this is very unlikely from observing historical samples. Another very imprecise practice is to adopt a value for the GRC multiplier that depends on only a single year of backtesting results. Moreover, it is extremely unlikely that the GRC will be exceeded over a 1-year horizon.29 And there are many other ways in which the regulatory rules are being questioned by industry practitioners.
Financial firms are bound by fewer modelling constraints when they assess their internal risk capital, i.e. their economic capital (EC). There may be an external demand, from rating agencies, who use EC as one indicator of the firm's solvency, and it is not uncommon for a rating agency to place some requirements on a firm's economic capital measurement methodology. An internal constraint is that senior managers should adopt an EC measurement approach that is in line with shareholders’ personal views.30 Other than this, financial firms are free to use any methodology they wish to arrive at a figure that they choose to label the ‘economic capital’ associated with an activity; the only provisions being that it is acceptable to the shareholders and the rating agencies used by the firm.
IV.8.3.1 Measurement of Economic Capital
Economic capital is the name that is usually given to a particular risk metric, estimated according to internal methods. The aggregate EC for the entire firm, which is derived by accounting for the firm's diversification of activities, reflects the desirable level of capital the firm would like to hold for insurance against its risks. However, the components of EC that are allocated to individual activities need not refer to real capital at all. Real capital should add up, but EC is a risk metric and its aggregation should account for the correlation between different components.
Definitions of economic capital vary across firms; EC estimates are generally based on a quantification of extreme losses, and although the assessment methods are free from regulatory constraints, they tend to ape the Basel methodology. Thus, whereas some firms base EC on stress testing alone, others use risk metrics such as VaR or ETL at extreme quantiles, or a mixture of VaR and ‘worst case’ losses.
We now use a simple, stylized framework to show that aggregate EC corresponds to a minimum level of capitalization for a firm, defining the firm's capitalization as its net asset value, i.e. the asset value minus the value of all the liabilities of the firm. The firm's aggregate EC can be thought of the current net asset value such that there is a high probability that the asset value remains positive for one year. In other words, the EC is the current net asset value which guarantees (at some confidence level) that the firm remains technically solvent over a one year horizon.
Having defined the basic framework, we now introduce some notation. The current value of the firm's assets is known and denoted by A0, and the annual return on assets RA is uncertain. Hence, 1 year from now, the asset value is AT = A0(1 + RA) and the α quantile of the asset value distribution is AT, α = A0(1 + RA, α), where RA, α denotes the α quantile of the asset return distribution. The current liabilities, or debt is denoted D0 and we assume there is a constant annual rate of debt financing, RD. Hence, the value of the debt, including the financing cost, 1 year from now is DT = D0(1 + RD).
To find the minimum level of capitalization we ask what is the minimum level of debt, ![]() , such that the probability that the firm is insolvent 1 year from now is very small. More precisely:
, such that the probability that the firm is insolvent 1 year from now is very small. More precisely:
![]()
The important observation here is that, by definition,
Then, since AT, α = A0(1 + RA, α),
![]()
In other words, if the current level of debt is no greater than
![]()
then the capitalization is at least
and consequently there is a high probability, of 1 − α, that the firm remains solvent by the end of the year.
Expression (IV.8.4) defines the EC as the minimum level of capital that must be assigned to the firm to meet the solvency condition, i.e.
![]()
Hence, with definition (IV.8.5), EC is the present value of E(AT) − AT, α, where the expected asset value, E(AT) is discounted at rate E(RA) and the value of the debt AT, α is discounted at rate RD. This shows that EC, defined as the minimum requirement of real capital, or net asset value, for the firm to remain solvent over a period of time, is a risk metric. EC is the present value of the difference between the expected asset value 1 year from now and the α quantile of the future asset value distribution, AT, α. The expectation refers to the assets of the firm, and the α quantile AT, α represents the liabilities side of the firm's balance sheet: it corresponds to the maximum level of liabilities so that the probability of insolvency in one year is no greater than 1 − α. Note that, when discounting the EC risk metric to present value terms, the assets and liabilities in the definition of EC are discounted at different rates.
Figure IV.8.4 depicts the relationship between EC, the expected asset value and the maximum value of the liabilities such that the firm remains solvent with probability 1 − α after one year. The grey curve represents the asset value distribution 1 year from now, and the EC is the distance between the current asset value, A0 and the maximum present value of the liabilities, ![]() .
.
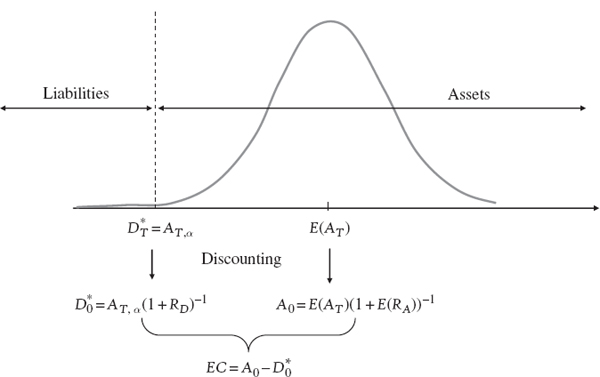
Figure IV.8.4 Relationship between economic capital and capitalization
EXAMPLE IV.8.3: MRC AND ECONOMIC CAPITAL
A firm has a current asset value of £50 million and the annual return on assets is normally distributed with mean 5%, and volatility 10%. The total liabilities of the firm are £40 million and debt is financed at a rate of 3% per annum. Find the probability that the firm becomes insolvent 1 year from now. How low should the firm's current liabilities be to ensure there is no more than 1 chance in 1000 that the firm becomes insolvent at the end of the year? Derive the EC corresponding to this level of liabilities.
SOLUTION Since the expected asset return is 5% the expected asset value in 1 year is
![]()
And, since the standard deviation of the asset return is 10%, the standard deviation of AT is
![]()
The value of the liabilities in 1 year is
![]()
Since AT is normally distributed, we can use Excel to look up the probability that AT < DTu using the NORMSDIST function.32 That is, we find
![]()
In other words, applying the standard normal transformation, we seek
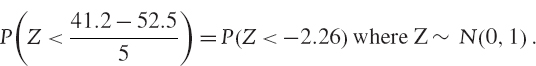
The result is NORMSDIST (−2.26) = 1.19%. This is the probability that the firm goes bankrupt by the end of the year.
Now we compute the EC in two equivalent ways. First, we use the Excel Solver to find the value of the current debt that would lead to a probability of bankruptcy of only 0.1%. The Solver settings are shown in the spreadsheet, and the result is £35,969,746. With this level of debt the firm's net asset value would be £14,030,254 and this is the minimum level of capitalization required to ensure the solvency condition, i.e. the EC.
Secondly, we calculate the EC (in non-discounted terms first of all) as the difference between the expected asset value and the 0.1% quantile of the asset value distribution. That is,
![]()
Then we discount each term using the appropriate rate, i.e. using the return on assets for the expected return and using the debt financing rate for the quantile, since the quantile is the value of the debt 1 year from now, by definition. Hence,
![]()
as before.
Many firms base EC measures on risk metrics such as VaR or ETL at extreme quantiles, although they are free to choose whatever metric they like (unlike regulatory capital for banks). The most important criteria for an EC measurement approach are that it:
- (i) refers to an appropriate risk horizon,
- (ii) is based on coherent mathematical assumptions, and
- (iii) utilizes intelligent risk aggregation methods.
A minimal requirement for aggregating risks is that they are based on a common horizon. EC is often defined with reference to risks over a 1-year risk horizon and with reference to a quantile that is consistent with the target credit rating of the firm. For instance, the quantile could be 0.03% for an AA-rated firm, or 0.10% for an A-rated firm. Whilst credit and operational risks are often assessed over a 1-year horizon, market risks are typically assessed over a much shorter term. Thus, to aggregate market risks with credit and operational risks, market risk measures will need extending to a longer risk horizon.
In contrast to credit and operational risks, market risks are typically highly liquid, so it makes no sense to extend a daily VaR to a 1-year horizon using a scaling rule such as the square root of time over the full 250-day period. In adverse market circumstances most exposures can be hedged or closed out easily, typically within a period of no more than a few weeks, and the scaling horizon should refer only to the time period during which there is an exposure. For instance, a gradual stepping down of the exposure could be made, at a rate that depends on the liquidity in the market.33
Another important criterion is that the EC model be based on coherent mathematical assumptions. Unfortunately, many models fall far short on this criterion. EC models tend to focus on measuring the risks that are relatively easy to quantify, ignoring the risks that are difficult to measure. Furthermore, totally different mathematical assumptions and accounting frameworks are applied to measure market, credit and operational risks. Because of this it is impossible to aggregate the three main risk types in a proper mathematical framework. Even within a given risk type – and we are concerned here with market risk – the bottom-up approach to EC measurement tends to apply a single figure such as VaR at an early stage in the aggregation, forgetting about the underlying distribution of which the VaR is the quantile. Distribution aggregation is relatively straightforward, given some assumptions on the dependency between risks; but if we forget about the distributions and simply summarize the risk with a single figure such as VaR, then it is not at all straightforward to aggregate risk estimates in a mathematically coherent way.
The ‘intelligent aggregation’ criterion is extremely important because EC measurement is usually approached within the ‘bottom-up’ paradigm. That is, a detailed model of individual positions or activities is applied at the portfolio level, and then for a particular activity, and then for an entire line of business, and so on. At each stage the EC measure is progressively aggregated into EC measures for larger and larger portfolios, until we arrive at an EC measure for the entire firm. Simply summing the component risk capital estimates ignores the diversification of the firm's activities and will lead to a gross overestimate of the total EC. The aggregation of market, credit and operational EC (which can be done at any level, from a single portfolio to the entire firm) also needs to be performed in an intelligent manner, taking account of diversification effects and avoiding double-counting of risks.
IV.8.3.2 Banking Applications of Economic Capital
However it is measured, EC is primarily a tool for risk budgeting. That is, its main purpose is to set a limit on the risks that can be taken by each of the risky activities in a firm, by placing an upper limit on the EC itself or by increasing the cost of risk capital and allowing the line managers to determine their own maximum EC. Decisions about risk budgeting are typically based on the maximization of a risk adjusted performance measure (RAPM). EC is commonly used as the denominator in a RAPM, and in this case the optimal allocation of risk capital to cover various risky activities can be determined by maximizing the value of this RAPM. That is what we mean by economic capital allocation, and we shall describe this process in more detail below.
A bank (normally) has easy access to funding; essentially, it only requires capital as a buffer against risk. The risk management structure in most major banks is economic capital driven because they use risk capital, as measured by EC, rather than real capital as the prime risk management tool. This is because many of the higher-risk activities within a bank – and derivatives trading in particular – do not require a significant amount of real capital for funding their activities, because they are highly leveraged. But, precisely because they are highly leveraged, there is considerable uncertainty about the returns on these activities, so they do need a significant amount of risk capital. Hence, in the process of risk budgeting, funding costs may be negligible, but we can still associate a cost of risk capital with every activity.
Rating agencies assess the credit quality of debt issues, usually with maturities of several years, and by extrapolation they assess the long term credit-worthiness of firms. The capitalization of a bank is one of the many important factors that will affect their credit rating. Banks wish to hold sufficient EC because they care about their credit rating: it gives an important signal to their customers, and their debt holders. The main customers in a retail or commercial bank are the depositors and mortgage holders, and for an investment bank the customers include the counterparties to OTC transactions. All these customers must have confidence in the solvency of the bank. Indeed, without this confidence the bank could fail.
Here is a recent example where lack of counterparty and investor confidence precipitated the bankruptcy of a UK retail bank, Northern Rock, whose prime business was mortgage lending. To finance its loans the bank borrowed short term funds in the inter-bank market and then periodically securitized its mortgages to repay its borrowings. With the onset of the banking crisis in 2008, credit spreads soared and the higher costs in the inter-bank loan market led to considerable uncertainty about the credit quality of all counterparties. Northern Rock in particular found it difficult to secure short-term funds in the inter-bank market because, like several other retail banks in the UK, it depended very heavily on securitization – issuing mortgage backed securities (MBS) and collateralized debt obligations (CDO) – rather than funding through depositors. When the MBS and CDO markets dried up Northern Rock found it could not raise funds, either on the inter-bank market (where LIBOR rates had jumped to more than 200 basis points above base rates) or by securitizing its mortgages. Since no private banks would deal with Northern Rock, they sought help from the Bank of England. This request became public knowledge, and signalled a crisis to the bank's depositors who then withdrew their funds. Due to European regulations on subsidization the Bank of England could not provide special loan facilities. Currently an administrator has been appointed by the government and Northern Rock has effectively been nationalized.
IV.8.3.3 Aggregation Risk
Since the components of risk capital that are assigned to different activities need not refer to real capital, risk capital need not be aggregated by simply summing its components. Indeed, this ignores the effects of diversifying into activities whose returns are not perfectly correlated. Aggregation risk is a form of risk model risk that stems from the aggregation of component risk capital into a total risk capital measure. It refers, in particular, to an inappropriate assumption about the dependencies between two or more risks when aggregating risk capital.
A very basic example of aggregation risk arises in an assessment of portfolio volatility, when we assume an incorrect value for the correlation between the returns on the constituent assets. More generally, whenever we make an inappropriate assumption about dependencies between the different components of total risk, we have aggregation risk. Aggregation risk can be huge; indeed, it is likely to be by far the most important source of model risk in any firm-wide risk assessment system. We now provide some simple but illustrative examples that support this assertion.
EXAMPLE IV.8.4: AGGREGATION OF ECONOMIC CAPITAL
A firm measures EC for market risk using a 4-week VaR at the 99.9% confidence level.34 The firm undertakes two different activities, labelled A and B, with $25 million dollars invested in each activity. Suppose that the joint distribution of the returns to the two activities, in excess of financing costs at the risk free rate, is a bivariate normal distribution, with volatilities 25% and 40% and with correlation 0.2. Suppose also that the annual expected excess return is 5% for activity A and 10% for activity B. Estimate the EC for each activity. Now aggregate these EC estimates according to the risk model. How different would your result be if you simply added the two EC estimates?
SOLUTION The mathematical problem is conceptually identical to the risk aggregation problems in a multivariate normal setting that we considered in Chapter IV.2. There are small differences due to the time horizon and the use of non-zero excess returns in the EC estimates, which are also based on VaR estimates at a very low quantile. But the general framework for the solution is identical to that used in previous examples.35
The EC estimates are obtained using the normal linear VaR formula with a mean adjustment, due to the non-zero expected excess returns on these activities. That is, if X denotes the returns over the risk horizon of the EC estimate,
In our example, we have set α = 0.1% and a risk horizon of 4 weeks. Hence, for activity A,
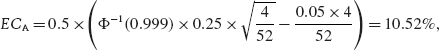
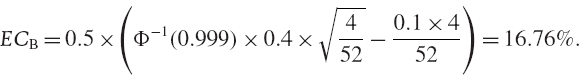
Note that the initial multiplication by 0.5 arises because we have expressed the resulting EC as a percentage of the total sum invested in the two activities, i.e. as a percentage of the firm value.
To estimate the aggregate EC for the firm as a whole we find the weighted sum of the returns to the two activities and use the correlation between the returns to derive the overall volatility of the firm's returns. Thus in (IV.8.6) we use the values
![]()
and
![]()
Hence,
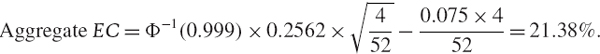
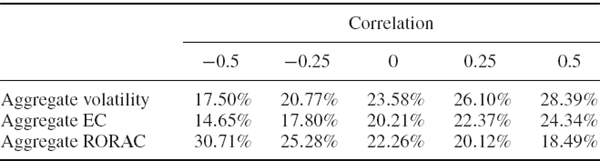
The results for each activity and for the firm as a whole are summarized in Table IV.8.1. Here we express the EC first as a percentage of the firm value of $50 million, and then in nominal terms.
Table IV.8.1 Aggregation of economic capital

The risk capital that is allocated to cover the risks of both activities is 21.38% of the total sum invested, i.e. $10,689,561. Of the £50 million invested 10.52%, i.e. $5,260,573, is required to cover the risks of activity A and 16.76%, i.e. $8,378,455, is required to cover the risks of activity B. Since the correlation is less than 1 the aggregate EC is less than the sum of the two EC estimates. Because of the diversification effect from spreading the investment equally over two different activities, we can hold considerably less risk capital than 27.28%, i.e. $13,639,027, and still cover both the risks.
Correlation is a very important determinant of the aggregate EC: the lower the correlation, the lower the aggregate EC. During stressful markets equity volatilities and correlations tend to increase. The assumed correlation has no effect on the individual EC estimates, but it has a significant effect on the aggregate EC, and it is this effect that we associate with aggregation risk. We now continue the previous example by supposing the correlation between returns of the two activities is different from 0.2, and then we compare the aggregate EC obtained using different correlations. This illustrates the extent to which our assumption about correlation affects the EC allocated to the two activities.
EXAMPLE IV.8.5: SIMPLE ILLUSTRATION OF AGGREGATION RISK
Suppose that the correlation between returns of the two activities in Example IV.8.4 is 0.6 rather than 0.2. By how much does the aggregate EC in that example underestimate the total EC that should be allocated to the two activities?
SOLUTION By changing the value for the correlation in cell B8 of the spreadsheet to 0.6 we estimate an aggregate EC of 24.5% of the total sum invested, i.e. $12,251,314. This is 14.6% greater than the aggregate EC estimate derived under the assumption that the returns on the activities have a correlation of 0.2.
Figure IV.8.5 illustrates how the aggregate EC estimate depends on the assumed value for the correlation, keeping the volatilities and expected excess returns of the two activities fixed. The assumed value for the correlation is shown on the horizontal axis, and the resulting aggregate EC estimate is depicted by the grey curve, expressed on the vertical axis as a proportion of the total capital invested in the two activities. The straight lines show the individual EC estimates and their sum, which do not depend on correlation.
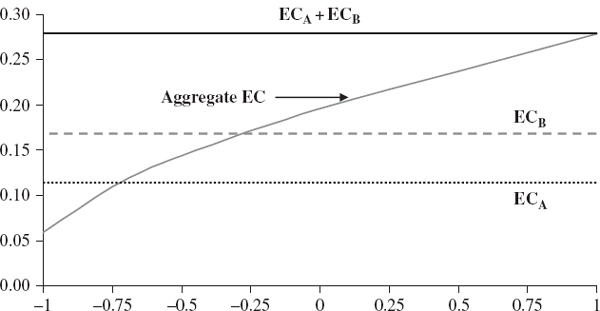
Figure IV.8.5 Effect of correlation on aggregate EC
The figure shows how important correlation is for determining the aggregate EC. The diversification that arises from investing in two activities increases as their correlation decreases, and so the aggregate EC decreases. At the two extremes we would have to allocate 27.28% of our capital to cover both risks if the returns on the two activities were perfectly correlated, compared with only 5.85% of our capital if the returns were perfectly negatively correlated.
IV.8.3.4 Risk Adjusted Performance Measures
A business may be considered as a collection of investments in risky activities, with a common set of constraints and funded from a common pool of resources. Not all risks are undesirable. Some risks are expected to be well rewarded because they have substantial diversification properties that can reduce the overall risk of the business. Efficient EC management does not necessarily reduce all risks; its aim is to achieve the best mix of business activities. But what do we mean by ‘best’? And how certain are we that this ‘best mix’ of activities will be achieved? These are the questions that we try to answer with the theory of optimal capital allocation.
A standard objective for optimal capital allocation is to achieve the best risk adjusted performance or the best reward to risk ratio. To define ‘performance’ or ‘rewards’ we require a comprehensive description of the good and the bad consequences of an allocation; typically there are many attributes to consider, such as profit, reputation, agreements with competitors and so forth, and the consequences are realized over a period of time. In this general framework the risk associated with an allocation refers to our uncertainty about the results, and which is the ‘best’ allocation depends on a criterion that associates some performance measure with each probability distribution of results. To simplify this problem, we assume that all the results of an investment are represented by the distribution of its return, and that an investor always prefers a larger return to a smaller one. That is, the return scale satisfies what economists call the principle of non-satiation, i.e. ‘the more the better’. This still leaves a wide choice, and there is no ‘best’ choice of performance measure, only choices more or less well suited to a decision situation.36
In general a risk adjusted performance measure (RAPM) is a ratio of expected reward to a risk measure. It is designed to choose the best mix of risky activities under restrictive circumstances, such as when a risk free asset is available, or to judge the relative attractiveness of various risky activities.37 But a RAPM cannot indicate how much should be invested in the best portfolio of risky activities; in general it can only be used to rank various activities. RAPMs have been designed to suit different risk types (e.g. those with symmetric, skewed, or heavy tailed return distributions) and to suit different contexts (e.g. total, systematic, or specific risks). Given the limitations of the ordinary Sharpe ratio and in view of the non-normal characteristics of many financial return distributions, many RAPMs have been designed in an ad hoc manner to focus only on downside risks.38
The RAPMs that are commonly applied in the context of optimal EC allocation, are commonly based on the risk measures VaR or ETL. The inputs to the firm's RAPM (i.e. expected returns, risks and correlations) are forecasts, and so they cannot be predicted with certainty. Past performance may give a useful indication of future performance in a stable environment, but may be unreliable if the allocation of resources is changed dramatically or if circumstances (e.g. competition, technology, regulation) evolve.
A simple example is the return on risk adjusted capital (RORAC), usually defined as the ratio of the expected net profit of an activity to the EC associated with that activity. When EC is defined as a percentage of the investment,
where E(R) is the expected return on an activity in excess of funding and operating costs and after tax. Alternatively, as in the example below, when EC is defined in nominal terms,
where E(P&L) is the expected profit (or loss) after accounting for funding and operating costs and after tax.
EXAMPLE IV.8.6: CALCULATING RORAC
A firm has an asset value of £130 million with expected return of 5%, and a debt value of £98 million with cost of debt of 3%. It pays a tax on net profits of 40% and its total EC over a 1-year horizon is £15 million. Calculate the firm's RORAC.
SOLUTION The expected profit on the firm's assets less the funding cost is 130 × 0.05 − 98 × 0.03 = £3.56 million. After paying 40% tax on this, the expected after-tax profit is £2.136 million. The RORAC is the expected after-tax profit per unit of risk:
![]()
EXAMPLE IV.8.7: AGGREGATING RORAC
Calculate the RORAC for each of the activities defined in Example IV.8.4, and the total RORAC on the two activities. Assume that funding is available at the risk free rate and there is a 40% tax on profits. As in Example IV.8.4, assume the EC is based on a 4-week VaR at a 99.9% confidence level, and derive the aggregate RORAC as a function of the correlation between the returns on the two activities.
SOLUTION Half of the firm's capital is invested in each activity, and the EC estimates that were derived in Example IV.8.4 were expressed as a percentage of the firm's total capitalization. So that the expected excess return that appears in the numerator of the RORAC is the excess return on the total capital, we multiply the expected excess return on each activity by 0.5. Hence, the RORAC for activity A, whose expected excess return is 5%, is
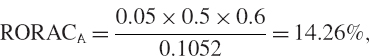
and similarly, since activity B has expected excess return 10%,
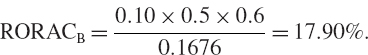
The total expected excess return after tax is
![]()
which is independent of the correlation between the two activities. But the aggregate volatility, and hence also the aggregate EC and the aggregate RORAC, depends on the correlation, i.e. it depends on the diversification that the firm achieves with its mix of activities.
Table IV.8.2 displays the aggregate volatility, EC and RORAC for correlation values between −0.5 and +0.5. The EC increases with the volatility of the net returns which itself increases as diversification effects decrease. Hence, as correlation increases, diversification effects decrease and the aggregate EC increases. Since the numerator of the RORAC is unaffected by correlation, the RORAC increases as the aggregate EC decreases, i.e. as the correlation decreases.
Table IV.8.2 Aggregate RORAC as a function of correlation
Risk adjusted performance measurement began in the late 1970s when Bankers Trust, prompted by the growing role of trading and the development of new financial instruments, introduced the risk adjusted return on capital (RAROC) as its preferred performance metric. This metric has now been adopted by many major banks (e.g. Deutsche Bank, ING and CIBC) and insurance companies (e.g. Swiss Re) to price and rank the profitability of deals, for EC allocation and even for compensation schemes.
A general definition of RAROC is the ratio of risk adjusted expected net income after tax to EC. But, just as there are numerous ways to define EC, so there are numerous ways to define risk adjusted expected net income. Many banking activities – trading in derivatives in particular – require very little real capital for their operation. However, they do require risk capital to insure against potential losses. Hence, a simple risk adjustment to expected net income after tax is to subtract the cost of risk capital that is allocated to that activity. For instance, we could define39
where k is some multiplier, called the cost of capital coefficient.
Equation (IV.8.9) may be applied to obtain an aggregate RAROC for the entire firm, and it may be applied to individual activities or mixes of activities in the firm. At the level of the firm, the EC term in (IV.8.9) is the aggregate EC of the firm and, as shown in Section IV.8.3.1, this should be greater than or equal to the minimum level of capitalization for the firm required to meet the solvency condition. When aggregate EC is equal to the minimum level of capitalization for the firm, the cost of capital coefficient k is equal to the real funding cost for the firm. For instance, we might assume that k is the risk free rate plus some margin.
In general, it is not optimal for a firm to favour or reward activities with the largest RAROC. It is the incremental contribution of an activity to total EC that is important. Assigning different values for k, the cost of capital coefficient, to different activities is just an artifice, to achieve the maximum global RAROC without forcing each business line to consider its incremental contribution to global risk.
When we apply the RAROC formula to an individual activity, such as a trading desk in a bank, then the EC term in (IV.8.9) need not refer to real capital at all. In this case, the cost of capital coefficient k is set by senior management. In general, the value of k for each activity should increase with the total demand for capital within the firm, relative to the total capitalization of the firm. If the total demand for real or risk capital is high relative to the capitalization of the firm, the cost of capital coefficient k would increase for all activities. But if senior managers wish to reward an activity – perhaps because it is particularly well managed or because it provides a good source of diversification – they may encourage it to grow by reducing its cost of capital. The ability to assign different values for the cost of capital coefficient to different activities is a management tool that can be used to alter the mix of activities in the firm over a period of time.
We also need to distinguish between funded and unfunded activities. In funded activities, such as trading securities, real capital is allocated to the activity in addition to economic (risk) capital. Then the financing cost of the real capital should be included in the expected P&L before accounting for tax. Alternatively, if funded activities are not operating as separate budgetary units, in which case no financing costs are accounted for in the expected P&L, the adjustment term in the numerator of (IV.8.9) could be set at some multiple k of the total capital, i.e. the funding capital plus the risk capital, that is allocated to the activity.
We illustrate the application of (IV.8.9) by continuing the previous example, to estimate the firm's aggregate RAROC as a function of both the correlation between the activities and the cost of capital coefficient k, which is assumed to take values between 0 and 25%. The results are shown in Table IV.8.3. Like the firm's RORAC, the total RAROC decreases as the opportunity for diversification in the firm's mix of activities decreases (i.e. as the returns correlation of the activities increases). But now, the cost of risk capital also affects the performance measure. As the cost of capital increases, the RAROC declines. When the cost of capital is high and there is low diversification in the firm's activities, the RAROC even becomes negative.
Table IV.8.3 Effect of cost of capital and correlation on aggregate RAROC
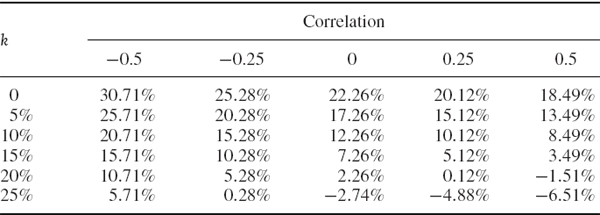
The next example distinguishes between two types of activities in an investment bank: a highly leveraged activity that requires no real capital for financing (other than operating costs), even though the notional size of the business is huge; and a funded activity that requires funding of the full notional size. In each case the expected P&L term in the numerator of RAROC is the expected revenue from the activity, less expected losses, less any funding and operating costs, and this total is adjusted to be after tax.
EXAMPLE IV.8.8: COMPARING RAROC FOR SWAPS AND BONDS
A UK bank has an interest rate swaps desk with a notional size of £100 billion. The profit margin built into each deal is 3 basis points, the annual operating costs are 1 basis point and the EC is 5 basis points. The same bank has a corporate bond desk that buys bonds and finances these transactions through loans from depositors, loans on the inter-bank market and securitization of low grade bonds. The notional size of the bond portfolio is £10 billion, the expected revenue from the portfolio over the next year is 10%, the expected losses due to defaults are 3%, the financing cost is 6%, the operating cost is 10 basis points and the EC allocated to this portfolio is 3% of the notional. Assuming that the bank pays a profits tax of 30% and charges each desk a 15% cost of risk capital, calculate the RAROC for each desk, before and after tax.
SOLUTION For the swaps desk we have:
| Profit margin | £30 million |
| Operating costs | £10 million |
| Net expected profit | £20 million |
| Economic capital | £50 million |
So before tax,
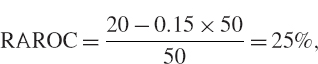
and after tax,
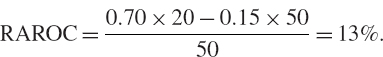
For the bond desk we have:
| Expected revenue | £1 billion |
| Expected losses due to default: | £300 million |
| Financing costs | £600 million |
| Operating costs | £10 million |
| Net expected profit | £90 million |
| Economic capital | £300 million |
So before tax,
![]()
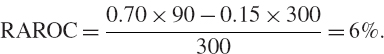
In this example the results are actually independent of the notional size of each business, because the expected profits, losses, costs and tax are all defined as proportional to size. The reason why we have set up this example to include a figure for the notional size of each business is that we shall be using this example in the next subsection to illustrate how the bank may prefer to alter the relative size of each business, to optimize the aggregate RAROC.
IV.8.3.5 Optimal Allocation of Economic Capital
Since the portfolio theory of Markowitz (1959) modern finance theory has attempted to explain the balance between risks and returns in securities markets. In Chapter I.6 we explained how this balance affects the optimal allocation of scarce resources to risky investments, taking account of portfolio diversification effects through the correlation of the returns on different investments. There we adopted the perspective of a global asset manager who evaluates the performance of different portfolios of a set of risky assets, and hence decides how to allocate his capital in an optimal manner, according to his utility function. But, as noted in Section I.6.1, another main application of optimal capital allocation theory is to the allocation of EC in a financial institution. This is the perspective that we adopt in the present section.
In fund management investors are free to select assets according to their expected returns, volatilities and correlations. A risk free asset is usually available, at least for investment. An optimal investment strategy can therefore be designed in three steps:40
- Construct the opportunity set of all investment opportunities and determine its efficient frontier in risk–return space.
- Determine the tangency portfolio which yields the maximum Sharpe ratio, or by maximizing another RAPM that is consistent with the CAPM.
- Construct the optimal portfolio as the combination of the tangency portfolio and the risk free asset that maximizes expected utility, or the certain equivalent of the portfolio.
An optimal EC allocation strategy follows a similar design, since it is based on a very similar mathematical framework. In business, shareholders switch their investments to maximize some RAPM, such as RAROC. Hence, senior managers should adopt a similar objective. A critical element in the consistent application of a RAPM is that one should compare bundles of business units, or activity mixtures, to investigate the ideal mix for the firm. Thus, the optimum notional capital allocation to a business unit depends on its correlation with other business units as well as on its own profile of risk and return. This is a problem equivalent to the selection of an optimal portfolio of securities, but with additional constraints. The three steps to follow in an optimal capital allocation strategy are as follows:
- Assess the EC of all activities, for instance within each line of business.
- Aggregate the EC across activities, taking into account their dependencies.
- Change the capital allocated to different activities, or the cost of risk capital charged to the activity, to maximize the RAPM, taking account of any risk capital constraints.
In the last step, after solving the allocation problem for the complete business, subject to a constraint on the total EC, one can either budget EC or set a cost for EC for each business unit. In the latter case the internal costs for risk capital will depend on correlations between businesses.
EXAMPLE IV.8.9: MAXIMIZING RAROC FOR OPTIMAL CAPITAL ALLOCATION
Suppose a firm measures EC for market risk using a 4-week VaR at the 99.9% confidence level, and that the firm has $1 billion to invest in two diversified activities, A and B. Assume the joint distribution of the two returns in excess of the risk free rate is a bivariate normal distribution, having volatilities 30% and 50% and correlation −0.25. The expected excess annual return is 5% for activity A and 12% for activity B and there is no tax. The firm charges a cost of capital of 10% to each activity, and the overall cost of economic capital is 6%. First, assuming that equal amounts are invested in each activity, calculate the RAROC for each activity and the aggregate RAROC. Now find the optimal allocations to the two activities that will maximize the aggregate RAROC.
SOLUTION When exactly half the capital is invested in each activity we have, using (IV.8.6) with α = 0.1% and a risk horizon of 4 weeks,
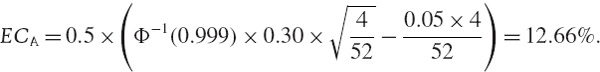
Hence, for activity A,

And, for activity B,
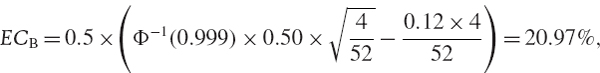
and
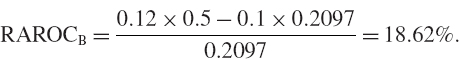
The multiplication by 0.5 arises because we have expressed the result as a percentage of the total sum invested in the two activities.
To estimate the aggregate EC we use (IV.8.6) with the values
![]()
and
![]()

and
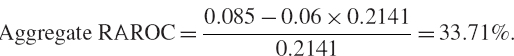
In nominal terms, we have an aggregate risk capital of 21.41% of $1 billion, i.e. $214,065,036. The component risks are 12.66% of $1 billion, i.e. $126,638,358, for activity A and 20.97% of $1 billion, i.e. $209,653,674, for activity B.
We now ask whether we could change the proportions invested in each activity to increase the aggregate RAROC. The optimization problem is set up in the spreadsheet, using the Solver, and we find that we could increase the aggregate RAROC to 34.33% if we invested $572,872,462 in activity A and $427,127,538 in activity B, instead of investing of $0.5 billion in each activity. With this optimal mix of activities we would increase the allocation of EC for activity A to $145,095,256 and decrease the EC allocation to activity B to $179,097,715. We would also have a lower aggregated EC: it is reduced from $214,065,036 to $198,108,377.
The final example illustrates how to implement a constraint on the optimal allocation of EC where the aggregate EC must be equal to a bank's minimum regulatory capital.
EXAMPLE IV.8.10: CONSTRAINED ECONOMIC CAPITAL ALLOCATION
Consider again the interest rate swaps and corporate bond desks of a UK bank in Example IV.8.8. Calculate the:
- (i) aggregate EC when the two desks have a returns correlation of 0.5, assuming that equal amounts are invested in each activity;
- (ii) aggregate RAROC when the bank pays a 6% cost for financing, and the cost of overall EC is also 6%;
- (iii) optimal EC allocation to the two desks when the aggregate EC is equal to minimum regulatory capital covering these activities, and this is £80 billion.
SOLUTION Using our results from Example IV.8.8, on the swaps desk we have an expected net return after tax of £14 million, with an EC of £50 million, and on the corporate bond desk an expected net return after tax of £63 million, with an EC of £300 million.
(i) The aggregate EC is calculated using the formula
where EC1 and EC2 are the EC of each desk and ![]() is the returns correlation. Using the results from Example IV.8.8, we have
is the returns correlation. Using the results from Example IV.8.8, we have
![]()
(ii) The aggregate RAROC is thus
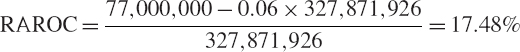
(iii) The above results may be seen in the spreadsheet by changing cell C3 to 100 and cell G3 to 10. The constrained optimum aggregate RAROC is found by changing the notional size of each desk to maximize the RAROC, subject to the constraint that the aggregate EC is £80 million. The EC of the bond desk alone is £300 million, which far exceeds the minimum risk capital required. Hence a constrained optimization of RAROC will reduce the size of the corporate bond trading desk quite substantially. Using the Solver, just as we did in the previous example, but now adding the EC constraint, we find that we should increase the notional on the swaps desk to £128,102,523,043 and decrease the notional on the corporate bond desk from £10 billion to only £854,016,820. The new EC allocations are now £64,051,262 for the swaps desk and just £25,620,505 for the bond desk and, taking account of the correlation between the two activities, the aggregate EC is exactly £80 million. With these new allocations, the overall RAROC of the two desks would be increased to 23.14% and the bank would be holding no more than the minimum risk capital required by the regulators.
In the above examples the firm implements the optimum RAROC by changing the allocation of EC to each activity. Alternatively, a firm could adjust the cost of capital rather than change the EC allocation and let the line managers determine their own EC subject to a lower limit on the RAROC of their business. This allows more freedom for the internal risk management in each activity.
Optimal capital allocation may recommend a very significant change in EC allocations, especially when subject to minimum regulatory capital constraints. But it is difficult to alter the business mix rapidly. Instead, hedging could be considered as an intermediate step. We also need to understand how the performance of an activity and its correlation with others will change with a significant redistribution of the sizes of various activities. In reality we may only know the marginal change in profitability for a relatively small change in size, and have very little idea about the effect of scale on correlations. For all these reasons the determination of an optimal EC allocation in practice is an iterative process giving, at each step, only a direction for improvement rather than leading in one step to a realistic optimum.
IV.8.4 SUMMARY AND CONCLUSIONS
This chapter has described how regulators, senior managers and the board of directors may use VaR, ETL and/or stress scenarios to estimate the minimum level of a firm's capitalization that ensures a high probability of solvency over a fixed time horizon. Regulators have required a minimum level of capitalization for banks to cover market risks since the 1990s. Consequently, developments in the assessment of risk capital have been driven by banking regulators, who themselves have been led by the Basel Committee. However, more than a decade before minimum regulatory risk capital requirements were enforced, the banking system had already adopted a framework for risk management that is based on the optimization of an enterprise-wide risk adjusted performance metric. Nowadays virtually all the major banks have risk management systems that are driven by an allocation of internal risk capital – called economic capital – which is based on an optimization of risk adjusted performance. In this way, over a period of time, senior managers and the board of directors may alter the preferred mix of business units within the bank.
The minimum requirements for market risk capital that are prescribed by regulators are based on a minimum solvency ratio, i.e. a minimum value for the Cooke ratio of eligible capital to a minimum risk capital requirement. There are strict rules for the methods used to assess the minimum risk capital requirement. For capital covering market risks a bank can either adopt the standardized rules approach, which prescribes rather onerous capital requirements, at least for hedged positions, or an internal models approach where minimum market risk capital is usually assessed using a 1% 10-day VaR measure, aggregated over all the lines of business in the bank. But risk capital does not add up like real capital. Indeed, the whole point is to account for the less-than-perfect correlation between activities so that the aggregate risk capital is less than the sum of the components.
In addition to a general risk capital charge, the Basel Committee has recently recommended that banks which use internal models that have specific risk recognition, so that they are exempt from the specific risk charges in the standardized rules, should increase their risk capital charge by adding an incremental risk charge to cover equity and credit spread risk. At the time of writing the incremental risk charge has not yet been adopted in national regulations: it is a recent innovation of the Basel Committee, suggested in response to the credit crisis that began in 2007, more than a year after the new Basel Accord. However, a capital charge that is calculated using internal models is likely to favour banks that are better able to net their exposures. Hence the current rules for internal models and the proposed incremental risk charge may favour the large banks that are dominating the industry. In view of the greater systemic risk posed by failures of very large banks, a better alternative may be to require capital charges to be directly proportional to the bank's size.
A financial institution is free to use any method it wishes for the assessment of EC, provided it is acceptable to the shareholders and, if the firm's issues have credit ratings, the rating agencies. The aggregate EC for the entire firm reflects the desirable level of capital the firm would like to hold for insurance against its risks. It is important for the firm to hold a level of EC that is sufficient to justify its credit rating. And achieving a satisfactory level of total capitalization is particularly important for banks, since inadequate capitalization can adversely affect the confidence of both investors and counterparties, as was the case during the banking crisis in October 2008.
When EC is allocated to different activities within the firm, it need not refer to real capital at all; it merely corresponds to a risk metric. Many activities such as derivatives trading do not require much real capital for funding their activities, because they are very highly leveraged, but they do require a capital buffer to cover their risks. Hence risk budgeting is a process of economic capital allocation rather than the allocation of real capital to fund different activities.
Shareholders switch their investments to maximize a risk adjusted performance measure, so senior managers should do likewise. The most prevalent risk adjusted performance measure that is used in financial risk management today is the risk adjusted return on capital (RAROC). This is the ratio of risk adjusted expected net income after tax to EC. Since EC appears in the denominator of RAROC, the maximization of aggregate RAROC (or a similar risk adjusted performance metric) for the entire firm or for various mixes of business activities allows managers to set limits on the EC, and therefore also limit the risks that can be taken at every level of the firm. In this way, senior managers and the board of directors use EC allocation to influence the mix of business activities undertaken by the firm.
But it is difficult to forecast EC, since it typically depends on the volatilities and correlations of business activities over a long time horizon. It is also difficult to forecast future net income, which appears in the numerator of the risk adjusted performance metric. Moreover, when the aggregate risk adjusted performance metric for a bank is maximized subject to the constraint that it is greater than or equal to the bank's minimum regulatory capital, the preferred mix of business activities may require a very significant change in the size of some operations. Thus, economic capital allocation in practice is a process that takes time, in which only gradual steps towards improving risk adjusted performance should be taken at any point.
1 Most major banks would adopt a VaR model, but some regulators allow scenario models to be used by smaller banks.
2 See the Bank's website, www.bis.org for further details about the BIS and the BCBS. In particular, for more detailed information on the structure and activities of the BCBS, see http://www.bis.org/bcbs/
3 See BCBS (1996). This was implemented in the G10 countries in January 1998.
4 See BCBS (2005). A compilation of this paper and some key previous publications by the Basel Committee may also be found in BCBS (2006).
5 Trading intent may be evidenced by a clearly documented trading strategy that is approved by senior management, and/or by clearly defined policies and procedures for the active management of the position.
6 The Financial Accounting Standards Board in the US defines fair value as ‘the amount at which an asset could be bought or sold in a current transaction between willing parties, that is, other than being forced into liquidation’. Therefore, the assessment of fair value is straightforward if quoted market prices exist. If they do not, the instrument can be marked to model, but not without introducing pricing model risk.
7 Financial Accounting Standards (FAS) Board Statement No. 133, Accounting for Derivative Instruments and Hedging Activities. Available from www.fasb.org/derivatives.
8 International Accounting Standards 39: Financial Instruments: Recognition and Measurement.
9 Tier 3 capital is not counted in the assessment of the credit risk capital requirement.
10 The risk measure for market risk is 12.5 times the market risk capital charge evaluated directly. Market risks for non-traded positions in a banking book are largely ignored, except possibly as a small additional charge under Pillar 2.
11 These criteria are stated in more detail in BCBS (2005).
12 Supervisors may also require a bank to use a shorter historical period if this is justified by a significant upsurge in price volatility.
13 For evaluating market risks of option portfolios banks are ultimately expected to move towards the application of a full 10-day price change. But in the interim, they may adjust their capital measure through other methods, e.g. via periodic simulations or by stress testing.
14 Banks with relatively large and/or complex option portfolios should measure the volatilities of options positions broken down by different maturities. This requires a form of vega bucketing or, preferably, volatility beta mapping, as described in Section III.5.6.
15 See Section IV.6.4.2 for further details on the way that supervisors set the value for k. If the model is disallowed the MRC must be calculated using the standardized rules.
16 For example, the Financial Services Authority in the UK may allow scenario-based internal models to be used by some banks.
17 In this approach, and in the standardized rules approach, a capital charge is assessed, initially, for each part of the trading book (e.g. UK equities, US bonds, currencies and gold, etc.).
18 The scenario method is basically an extension of the standardized rules that are described in the next subsection, since the maximum changes for the risk factors as well as the duration or maturity banding of interest rate exposures are defined in a similar way.
19 Gold is included in currency risk, not commodity risk.
20 It is difficult to obtain specific risk recognition with such a simple model and such a small portfolio. Indeed, in the spreadsheet for Example IV.8.1 we also calculate the GRC based on the portfolio returns – i.e. without using a portfolio mapping – and find that it is considerably greater than the GRC based on the portfolio beta mapping, especially during the early part of the sample.
21 Readers are referred to BCBS (1996) or its amended version, BCBS (2005), for complete details and numerical examples.
22 And on coupon, if the maturity band approach is used.
23 An additional charge is required for positions in options, where appropriate.
24 This encompasses all positions subject to the 1996 Market Risk Amendment, regardless of their perceived liquidity, except those positions whose valuations depend solely on commodity prices, foreign exchange rates, or the term structure of default-free interest rates. So it includes debt securities, equities, securitizations of commercial and consumer products, structured credit products as well as derivatives on such instruments. Full details are given in BCBS (2008).
25 This is similar to the credit and operational risk capital charges.
26 A bank's IRC model should normally incorporate credit default and migration risks for positions subject to credit risk and, by January 2010, must incorporate all remaining price risks for credit positions (that are unrelated to defaults or credit migrations) as well as all price risks for equity positions. At the time of writing the Committee has not determined whether to allow a bank's IRC to be adjusted for double-counting of risks that are already included in the 10-day VaR capital calculation.
27 Position risk arises when it is not possible to take a position with size equal to the size of an optimal contract. For instance, it is not possible to buy or sell a non-integer number of shares.
28 Data downloaded from Yahoo! Finance, codes BARC.L and LLOY.L.
29 Even when k = 3 the probability of exceeding the GRC over 1 year is less than 10−10. See our comments in Section IV.8.2.4.
30 For instance, if stress scenarios are used to determine economic capital then these scenarios should confirm to shareholder's beliefs.
31 Since α is the probability of default over 1 year, firms set α according to their target credit rating. For instance, for a AAA rated firm a typical value for α would be 0.03%.
32 In fact, in the spreadsheet we use the NORMDIST function, so we do not need to apply the standard normal transformation.
33 Then a scaled market VaR could be set, for example, following the liquidity adjusted VaR framework that was introduced in Section IV.7.5.4.
34 This is consistent with the 99.9% confidence level that the Basel Committee have adopted as standard, and is also consistent with a 1-year horizon if we assume that 1 month is enough time to liquidate or hedge any positions in any adverse circumstances.
35 For instance, see Example IV.2.14 which refers to the aggregation of equity risk with forex risk in the normal linear VaR model.
36 Nevertheless, some of the performance measures described in Chapter I.6 are difficult to justify theoretically because they cannot be linked directly to a utility function, or because the implied utility function has strange characteristics.
37 For instance, in Section I.6.5 we introduced the concept of the Sharpe ratio, which is a RAPM that is linked to the capital asset pricing model (CAPM) and which is relevant when there is the possibility of unlimited risk free lending and borrowing. It is defined as the ratio of the expected return in excess of the risk free rate to the standard deviation of the return distribution. Thus, when an investor uses the Sharpe ratio, his preferences are entirely determined by the knowledge of the expected return and the standard deviation of the return. However, even the standard Sharpe ratio, along with other RAPMs that are derived in the CAPM framework, does not satisfy the basic axiom of weak stochastic dominance. Yet no rational investor would prefer a investment that is weakly stochastically dominated by another.
38 These include the Sortino ratio and the kappa and omega indices that were introduced in Section I.6.5.6.
39 The precise definition of RAROC is determined by senior managers in consultation with the shareholders and the board. Although RAROC is the most common RAPM used in banking, numerous other performance metrics are used in the financial industry. Some of these are defined relative to assets rather than capital, for instance Matten (2000) lists return on assets (ROA), risk adjusted return on assets (RAROA) and return on risk adjusted assets (RORAA). The ROA and a related performance metric, the return on accounting capital (ROC), are not often used because they ignore the relative risk of different activities; RORAA, like RORAC, applies a risk adjustment to the denominator only; only RAROC and its related measure, RORAA, apply an risk adjustment to both the numerator and the denominator of the RAPM.
40 See Section I.6.3 for further details.