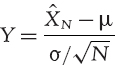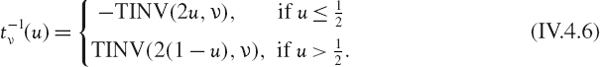IV.4
Monte Carlo VaR
IV.4.1 INTRODUCTION
Monte Carlo simulation is an extremely flexible tool that has numerous applications to finance. It is often used as a method of ‘last resort’ when analytic solutions do not exist, or when other numerical methods fail. Its drawback has been the amount of time it takes to resolve a problem accurately using simulation, but as computers become more powerful this disadvantage becomes less relevant.
The purpose of this chapter is to provide a pedagogical introduction to Monte Carlo simulation with a specific focus on its applications to VaR estimation. There are two equally important design aspects of Monte Carlo VaR: the sampling algorithm and the model to which the algorithm is applied. Section IV.4.2 focuses on the first of these. It begins by explaining how pseudo-random numbers are generated. Then we introduce the sampling techniques that are based on low discrepancy sequences, which are commonly termed quasi Monte Carlo methods. The section then explains how to transform random numbers into simulations from a parametric distribution for risk factor returns, a process called structured Monte Carlo. Then we describe the technique of multi-step Monte Carlo, which is important for accounting for the dynamic properties of risk factor returns, such as volatility clustering.
The main aim of this chapter is to describe the different types of statistical models for risk factor returns that are used to underpin the simulation algorithm. A huge variety of static and dynamic models are available: static models are based on the assumption that each risk factor return is an independent and identically distributed process, in which case we only need to specify the multivariate unconditional distribution for the risk factor returns. But we can use a dynamic model to introduce time series effects such as volatility clustering and mean reversion. In this case we must specify how the multivariate conditional distributions for the risk factor returns evolve over time.
Section IV.4.3 focuses on describing various parametric static and dynamic models that are appropriate for different types of risk factor returns. As we know from previous chapters, volatility clustering can be a very important feature to capture in the VaR estimate. So here we apply exponentially weighted moving average and generalized autoregressive conditional heteroscedasticity processes to model volatility clustering in a single risk factor returns series. Later on, in Section IV.4.5.4, we give a practical example that illustrates the extension of this framework to a multivariate setting.
Section IV.4.4 focuses on modelling the interdependence between different types of risk factor returns. First we describe the standard multivariate normal and multivariate Student t distributions for i.i.d. returns. But Monte Carlo simulation is so flexible that we can very easily use copulas instead of correlation as the dependence metric. We end the section with a case study on the use of non-linear regression in the context of bivariate Monte Carlo simulation.
Section IV.4.5 builds on the three previous sections to demonstrate how Monte Carlo methods are used to estimate the VaR and expected tail loss of a portfolio, assuming it has a linear mapping to its risk factors (Monte Carlo VaR for option portfolios is dealt with in the next chapter). The section begins by outlining both static and dynamic (multi-step) algorithms for estimating Monte Carlo VaR and ETL for a linear portfolio, based on a generic model for the multivariate distribution of the risk factor returns.
Then we provide specific examples that are designed to emphasize different aspects of the Monte Carlo algorithm and different features of the returns model. We begin by considering cash-flow portfolios, firstly using different copulas to model credit spread changes and hence to estimate the credit spread VaR, and secondly using Monte Carlo simulation on principal component risk factors to estimate the interest rate VaR of a large portfolio of interest rate sensitive securities. In the interest rate VaR example we focus on the efficiency gains from dimension reduction and advanced sampling techniques, rather than on the specification of the multivariate return distribution.
The next example illustrates the use of Monte Carlo with a multivariate normal mixture distribution, using a stock portfolio to emphasize the advantages of this approach for scenario analysis. Finally, we extend the volatility clustering simulation model that was introduced earlier for a single risk factor, to a currency portfolio where forex log returns have a conditional multivariate Student t distribution and their dynamics are governed by a multivariate GARCH model. We use another empirical example to demonstrate that the VaR estimate is significantly affected by non-normality in conditional return distributions and by volatility and correlation clustering in risk factor returns, even over a relatively short risk horizon such as 10 days. Section IV.4.6 summarizes and concludes.
Besides the technical tools for modelling VaR with Monte Carlo simulation, the main message of this chapter is that we need to control two sources of model risk in Monte Carlo VaR models: that stemming from simulation errors and that resulting from inappropriate behavioural models for risk factor returns. There are many books about Monte Carlo techniques that focus on methods for reducing simulation error, most notably the comprehensive and classic text by Glasserman (2004). For this reason, I have provided only a short introduction to sampling methods and instead have devoted most of this chapter to the construction of a statistical model for risk factor returns that provides an appropriate basis for Monte Carlo VaR estimation.
There are many empirical examples for this chapter in Excel workbooks on the CD-ROM. To reduce file size each workbook is saved using only 100 or 1000 simulations. Before use, all the spreadsheets containing simulations and calculations on those simulations need to be extended by the reader after copying the workbooks onto their hard drive. Just take the last row of all the simulated vectors in each spreadsheet and fill down. I have turned the automatic calculation of results to manual so that new simulations are not repeated each time the spreadsheet is altered.1 Due to the size constraints in Excel (especially before Excel 2007) many of our empirical results in the text are based on only 10,000 simulations. This is sufficient to illustrate the important points of each example, but without additional variance reduction there will be substantial sampling error in the results.
IV.4.2 BASIC CONCEPTS
We begin this section by outlining some efficient algorithms for generating pseudo-random numbers. Section I.5.7 provided only a very brief and basic introduction to this vast subject, so this section develops the material in a little more depth. Then we move on to advanced sampling techniques for improving the efficiency of Monte Carlo simulation. We describe the use of low discrepancy sequences to cover the hypercube with the minimum number of simulations, and two simple variance reduction methods, i.e. antithetic sampling and stratified sampling.
By necessity, our treatment in these three subsections is extremely selective, and readers interested in commercial implementation of Monte Carlo VaR models are advised to consult texts that are specifically devoted to Monte Carlo algorithms and the control of simulation error. As mentioned in the previous section, I can particularly recommend the classic textbook written by Glasserman (2004).
It may be relatively straightforward, if time-consuming, to reduce sampling error, but it is not at all straightforward to select the appropriate behavioural model for risk factor returns in a Monte Carlo VaR framework.2 So the next three sections will focus on the statistical aspects of a Monte Carlo VaR model. This section of the chapter gives an introduction to univariate and multivariate simulation and the subsequent estimation of Monte Carlo VaR, assuming that we already know the appropriate risk factor returns model.
IV.4.2.1 Pseudo-Random Number Generation
Random number generation is the first step in a Monte Carlo simulation algorithm. Its aim is to produce a sequence of numbers between 0 and 1 that are uniformly distributed, independent and non-periodic. That is, each number in the unit interval (0, 1) is equally likely to occur in the sequence, the ith number is independent of the j th number for all i ≠ j, and the sequence does not repeat itself however long it becomes.
The only way to generate random numbers is to measure, without error, a physical phenomenon that is truly random. In practice computers generate pseudo-random numbers, which should be impossible to distinguish from a set of realizations of truly independent standard uniform random variables. These pseudo-random numbers are generated by an initial seed, such as the time of the computer's clock, and thereafter follow a deterministic sequence. In Excel, the function RAND () produces a pseudo-random number.3
A simple but common type of generator is a linear congruential generator. This takes the form of an iteration that is based on the idea of congruence. For some fixed integer m, we say that two integers x and y are congruent modulo m, written
![]()
if m divides x − y.4 To generate a linear congruential sequence we fix two positive integer values m and c greater than 1, start the sequence with a positive integer seed x0 between 1 and m − 1 and perform the iteration
each time choosing the unique integer value for xi+ +1 in [1, m − 1]. Then, for each i set ui = m−1xi, and the resulting sequence {u0, u1, u2,…, uN} is our pseudo-random number sequence where N is the number of simulations. The following example shows that m should be a prime number.
EXAMPLE IV.4.1: LINEAR CONGRUENTIAL RANDOM NUMBER GENERATION
Generate a sequence of pseudo-random numbers using (IV.4.1) with m = 13, c = 2 and x0 = 1. What happens if you use the same values of c and x0 but set m = 12?
SOLUTION With m = 13 the sequence for x is
![]()
where ‘…’ here means that the sequence continues to cycle through the same sub-sequence {1, 2, 4, 8, 3, 6, 12, 11, 9, 5, 10, 7}. Dividing the numbers in this subsequence by 13 gives a sequence of 12 distinct pseudo-random numbers:
![]()
Now change the value of m from 13 to 12 in the spreadsheet for this example. The sequence of integers is {1, 2, 4, 8, 4, 8, 4, 8,…}. Whereas the first sequence had full periodicity, i.e. the full set of integers between 1 and m − 1 are visited in the repeating subsequence, the second sequence has a periodicity of only 2. Hence setting m = 12, c = 2 is not a good choice for generating a sequence of pseudo-random numbers.
All random number generators have a periodicity, i.e. at some point in the sequence the numbers start repeating themselves. But one of the reasons why linear congruential generators are so popular is that they will have full periodicity if c is a primitive root of m.5 In practice, m is chosen to be a very large prime number so that the sequence does not repeat itself too soon and very many distinct random numbers can be simulated in the cycle. That is, long sequences of pseudo-random numbers are easier to generate if we choose m to be a very large prime number.
A Mersenne prime is a prime number of the form 2n − 1, and many Mersenne primes are known for very large values of n.6 For instance, one of the best generators, called the Mersenne twister, sets m = 219,937 − 1. Since this m is prime, there will be 219,937 − 1 distinct pseudo-random numbers in the associated linear congruential generator.
IV.4.2.2 Low Discrepancy Sequences
Most portfolios have several risk factors, and simulations of a portfolio's P&L distribution are based on simulations of the returns on these risk factors. For this, we require a sequence of random numbers for each factor, and if there are k risk factors we need to generate k such sequences. We label these ![]() where, typically, the number of simulations N in each sequence will be a very large number.7
where, typically, the number of simulations N in each sequence will be a very large number.7
For the ith simulation on the risk factor returns we start with a vector (u1i,…, uki) of numbers with each uji∈(0, 1). For instance, if k = 2, the ith simulation could be based on a vector such as (0.643278, 0.497123). This can be thought of as a point in the unit square, i.e. the square with sides along the two axes from 0 to 1. The two elements represent the coordinates of the point. If k = 3the ith simulation is a point in the unit cube, and more generally the vector (u1i,…, uki) is a point in the k-dimensional unit hypercube.
We now motivate the concept of the discrepancy of a sequence with a simple numerical example.
EXAMPLE IV.4.2: DISCREPANCY OF LINEAR CONGRUENTIAL GENERATORS
Generate a sequence of pseudo-random numbers using the linear congruential generator (IV.4.1) with m = 127 and c = 3. Then plot the numbers (ui, ui+1), i = 1, 2,… on the two-dimensional unit cube.
SOLUTION The spreadsheet for this example is similar to that for the previous example. The resulting plot of consecutive pseudo-random numbers, displayed in Figure IV.4.1, shows that the points are not uniformly covering the cube. Instead they lie along three distinct lines.
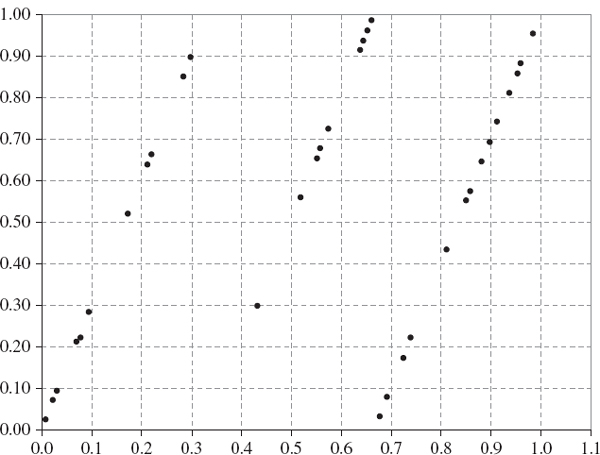
Figure IV.4.1 Consecutive pseudo-random numbers plotted as points in the unit cube
The feature illustrated in Figure IV.4.1 is not particular to our choice of m = 127 and c = 3, and nor is it particular to a plot of two consecutive points. The same features are apparent in all linear congruential generators, and are evident in n-dimensional plots of n consecutive numbers for n > 2. That is, the points generated by such generators will lie in proper subspaces of the hypercube. This means that there can be large areas of the hypercube that contain no points. But if the hypercube is not covered uniformly the final result of the Monte Carlo simulation, which in our case is a VaR or ETL estimate, will not be robust. This is because we would cover different areas of the hypercube each time we perform another set of N simulations, starting with a different seed.
A low discrepancy sequence is a method for generating sequences of numbers that are not uniformly distributed random numbers at all; instead they are designed to cover the n-dimensional hypercube uniformly. The name low discrepancy means that the deviations from a uniform covering of the hypercube are minimal.8 In other words, the purpose of a low discrepancy sequence is to cover the hypercube without gaps, using fewer simulations than are required from a pseudo-random generator, for the same uniformity of coverage.
After an initial seed, the remaining numbers in the sequence follow a deterministic path. Common examples of low discrepancy sequences are the Faure and Sobol sequences, both of which are based on van der Corput sequences. The technical details on generating these sequences are very well described in Glasserman (2004, Chapter 5).
IV.4.2.3 Variance Reduction
The computation time required for generating large numbers of pseudo- or quasi-random numbers is minimal. However, this is only the first step in Monte Carlo simulation. The computation time required by the application of the VaR model can be huge, for example if it requires complex models for repricing non-linear instruments on each set of simulations. For this reason we try to restrict the number of simulations to be as small as possible without sacrificing the accuracy of the resulting VaR or ETL estimate.
To assess the trade-off between speed and accuracy we need a measure of the extent to which the VaR or ETL estimates change each time the simulations are repeated. A common measure of this sampling uncertainty is the variance of the simulation error.
- When simulating a quantity such as an expected value or VaR, here simply denoted
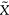 , the simulation error is defined as
, the simulation error is defined as 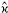 N −
N − 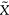 , where
, where 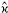 N denotes the estimator of
N denotes the estimator of 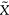 based on N simulations.
based on N simulations. - If the estimator is unbiased, E(
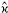 N −
N − 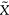 ) = 0, in other words, E(
) = 0, in other words, E(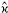 N) =
N) = 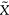 .
. - Since
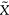 is a constant, although it is unknown, the variance of the simulation error is equal to V(
is a constant, although it is unknown, the variance of the simulation error is equal to V(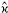 N).
N).
If ![]() denotes an expected value, then
denotes an expected value, then ![]() N =
N = ![]() is the sample mean based on N observations. Let μ and σ denote the mean and standard deviation of the distribution of the underlying random variable, X. By the central limit theorem, which is described in Section I.3.5.2, we know that the random variable
is the sample mean based on N observations. Let μ and σ denote the mean and standard deviation of the distribution of the underlying random variable, X. By the central limit theorem, which is described in Section I.3.5.2, we know that the random variable
has a distribution that converges to a standard normal distribution as N increases. In other words, as N increases the distribution of ![]() N converges to a normal distribution with expectation μ and variance N−1σ2. Thus, the variance of the simulation error is approximately equal to N−1σ2 for large N.
N converges to a normal distribution with expectation μ and variance N−1σ2. Thus, the variance of the simulation error is approximately equal to N−1σ2 for large N.
Now suppose ![]() is an α quantile of an h-day portfolio return distribution. The asymptotic distribution for the number of returns X (N, α) that are less than the α quantile is described in Section II.8.4.1. From this we know that as N increases, the distribution of the proportion of returns that are less than the α quantile, i.e.
is an α quantile of an h-day portfolio return distribution. The asymptotic distribution for the number of returns X (N, α) that are less than the α quantile is described in Section II.8.4.1. From this we know that as N increases, the distribution of the proportion of returns that are less than the α quantile, i.e. ![]() N = N−1X (N, α), converges to a binomial distribution with expectation α and variance N−1α (1 − α). Hence the variable
N = N−1X (N, α), converges to a binomial distribution with expectation α and variance N−1α (1 − α). Hence the variable
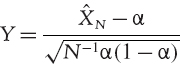
has a distribution that converges to a standard normal distribution as N increases. In other words, the variance of the simulation error is approximately equal to N−1α (1 − α) for large N.
In both the cases above, the variance of the estimator decreases with N, that is, the accuracy in our simulations increases as N increases. In other words, we should use as many simulations as possible. But, as mentioned above, computation time can be a substantial constraint on the size of N.
We now describe two sampling techniques that have the effect of decreasing the variance of an estimator based on a given number of simulations. The simplest of these techniques, based on antithetic variables, is illustrated in the next example.
EXAMPLE IV.4.3: ANTITHETIC VARIANCE REDUCTION
Suppose we wish to estimate the expected value of a standard uniform variable using just 20 simulations.
(a) Use the Excel random number generator to simulate 20 realizations {u1,…, u20} on independent standard uniform variables and repeat the simulations 10 times, each time estimating the sample mean. Compute the sample standard deviation of the sample means obtained from the 10 different simulations.
(b) Now repeat this process, but this time use the Excel random number generator to simulate only the first 12 random numbers {u1,…, u12}. For the next 8 numbers simply take 1 minus the first 8 of these 12 numbers. More generally, base your sample mean estimates on the sample {![]() 1,…,
1,…, ![]() 20} where, for some n such that 10 ≤ n < 20, we set
20} where, for some n such that 10 ≤ n < 20, we set ![]() i = ui for i = 1,…, n, and
i = ui for i = 1,…, n, and ![]() i = 1 − ui − n for i = n + 1,…, 20.
i = 1 − ui − n for i = n + 1,…, 20.
For different values of n, compare the sample standard deviations obtained in case (a) and case (b), and comment on your results.
SOLUTION In the spreadsheet for this example we use the Excel RAND () function to generate 20 pseudo-random numbers for part (a). Then, in each set of simulations, the first 12 realizations {u1,…, u12} for (b) are identical to those in (a), but for the last 8 realizations they are {1 − u1,…, 1 − u8}. Note that the last 8 realizations are still drawn from a standard uniform distribution, but they are no longer independent of the first 8 realizations.
With a sample size of only 20 the sampling variation over the 10 sets of simulations is very large in both cases. Nevertheless, the standard deviation of the means in (b) is virtually always considerably less than the standard deviation of the means (a). Readers can verify this by pressing F9 to repeat the simulations many times.
More generally, the value for n can be anywhere between 10 and 20. If n = 10 we obtain the maximum possible variance reduction, in fact in this case the sample mean estimates are all identical, so their variance is zero. Thus the variance reduction decreases as n increases until, when n = 20, there is no variance reduction at all.
We now provide a slightly more formal introduction to the concept of antithetic sampling of standard uniform random variables, and explain why this technique can reduce the variance of estimators when estimates are based on simulated samples. We shall again use an estimator of a sample mean for illustration.
Denote by {X1,…, XN} a sample of N i.i.d. random variables having distribution function F. Now let ![]() denote another sample of N i.i.d. random variables, with the same distribution function F, and having a constant correlation with the first sample:
denote another sample of N i.i.d. random variables, with the same distribution function F, and having a constant correlation with the first sample:
![]()
Finally, denote by {X1,…, X2N} a set of 2N i.i.d. random variables with distribution function F.
Consider the estimators of the sample mean based on a sample of size 2N using realizations from (a) {X1,…, X2N}, and (b) ![]() . These are:
. These are:
(a) ![]() , and
, and
(b) ![]() where
where ![]()
What is the variance of the estimator in each case? Suppose the distribution F has variance σ2.
Then in case (a),
since the variables are independent. However, although the variables Yi, i = 1,…, N are independent their variance is not σ2, but
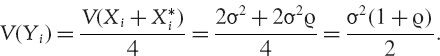
Hence, in case (b),
So the variance of the estimator in case (b) will be less than the variance of the estimator in case (a) if and only if
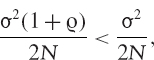
that is, if and only if ![]() < 0.
< 0.
This shows that a necessary and sufficient condition for antithetic sampling to reduce the variance of the estimator of a sample mean is that the antithetic variables have negative correlation with the original variables. The antithetic pairs in Example IV.4.3 were chosen to have correlation −1.9 Then, by (IV.4.3), the variance of the sample mean estimator is zero when we use the same number of realizations on the antithetic variables as on the original variables.10 This is true for any linear estimator, not just for the sample mean.11
In Monte Carlo simulation we often require a non-linear estimator; for instance, we shall be focusing on an estimator of a quantile. Nevertheless, there is considerable potential for the use of antithetic pairs to reduce the variance of a Monte Carlo VaR estimate as well.
We now introduce an alternative method for variance reduction, which may be applied in conjunction with antithetic sampling. The next example provides a simple illustration of the principle of stratified sampling on the unit interval, after which we generalize this concept to stratified sampling on the hypercube.
EXAMPLE IV.4.4: STRATIFIED SAMPLING FROM STANDARD UNIFORM DISTRIBUTIONS
Repeat the exercise from Example IV.4.3, but this time in case (b) set:
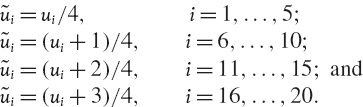
SOLUTION The solution is implemented in the spreadsheet. Note that our construction for case (b) now generates random numbers in the intervals (0,0.25], (0.25,0.5], (0.5,0.75] and (0.75,1) respectively. The reader can verify that the standard deviation of the sample means is exactly ![]() of the standard deviation of the mean in case (a).
of the standard deviation of the mean in case (a).
The above example illustrates that by stratifying the sample space (0, 1) into n non-overlapping subspaces of equal size, the standard deviation of a linear estimator becomes n−1 times the standard deviation of the estimator based on a non-stratified sample. Another advantage is that when n is large, stratified sampling can provide a more uniform coverage of the unit interval than a standard unstratified sampling method.
A simple way to generalize this concept to multiple dimensions is to use Latin hypercube sampling. For instance, to generate a stratified sample on the two-dimensional unit cube (i.e. the unit square) we can create nm simulations on pairs (u1, u2) in the unit square by:
(i) taking two independent stratified samples on (0, 1), in each case dividing the interval into n non-overlapping equal length sub-intervals and taking a random sample size m from each sub-interval; and
(ii) randomly permuting the first column and, independently, randomly permuting the second column – i.e. we ‘shuffle up’ each sample of m random numbers separately.
EXAMPLE IV.4.5: LATIN HYPERCUBE SAMPLING
Generate two independent stratified samples of the unit interval with n = 6, and take a random sample size m = 5 from each sub-interval. Plot the 30 points that are generated in this way in the unit square. Now ‘shuffle’ each sample of 30 observations independently, and again plot the 30 points.
SOLUTION In Figure IV.4.2 the ‘unshuffled’ stratified sample is plotted on the left and the ‘shuffled’ sample is plotted on the right. Clearly, step (ii) above is necessary otherwise all the points would lie along the diagonal blocks within the unit square, as seen in the left-hand figure. However, after shuffling the sample is uniformly distributed over the unit square.
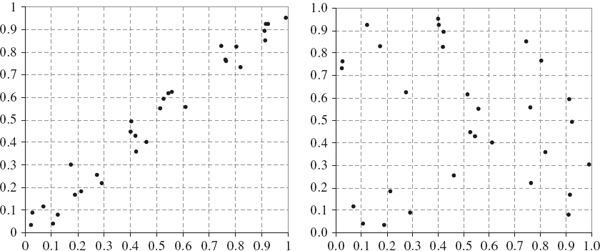
Figure IV.4.2 Effect of independently permuting stratified samples
Stratified sampling is a useful technique for generating initial values of a simulated process. For instance, it can be used in one-step Monte Carlo for an h-day VaR, when we are simulating the h-day risk factor returns directly. But it cannot be used to generate consecutive values along a simulated path of an i.i.d. process, because the stratification introduces dependence into the process.12 Hence, it should not be applied to each step in a multi-step Monte Carlo VaR model.
IV.4.2.4 Sampling from Univariate Distributions
Until this point we have focused on efficient methods for constructing random samples on standard uniform distributions. Now we show how to transform a random sample from a single standard uniform variable U into a random sample from a distribution of a random variable X with a given continuous distribution function, F. Since the values of F lie between 0 and 1, given a random number u in (0, 1) we obtain the corresponding value of x by setting
In other words, given a random number u, the corresponding simulation for X is the u quantile of its distribution.
For example, Figure IV.4.3 illustrates this transformation in the case of a standard normal distribution when the random number generated is 0.3.13 Note that given the sigmoid shape of the distribution function a uniform series of random numbers will be converted into simulations where more observations occur around the expected value than in the tails of the distribution.
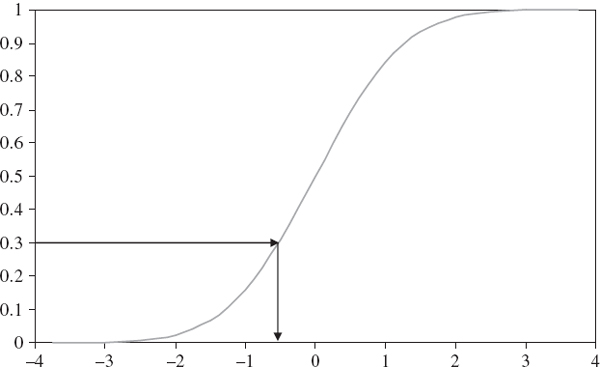
Figure IV.4.3 Simulating from a standard normal distribution
A sample from a standard normal distribution can be translated into a sample from any other normal distribution using the inverse of the standard normal transformation.14 That is, we obtain a simulation on a normal variable with mean μ and standard deviation σ using
More generally, we can use the inverse distribution of any univariate distribution in the transformation. For instance, in Excel we transform a standard uniform simulation u into a simulation on a standard Student t variable with ν degrees of freedom using the command
Note that the standard Student t distribution has mean zero and variance ν (ν − 2)−1, so to transform the simulations ![]() to simulations from a general Student t distribution with mean μ and standard deviation σ, we use the transformation
to simulations from a general Student t distribution with mean μ and standard deviation σ, we use the transformation
Excel also provides inverse distribution functions for several other distributions. Table IV.4.1 shows the command for generating simulations from each, where u = RAND ().
Table IV.4.1 Excel commands for simulations

The variance reduction techniques that were described in the previous section can be translated into variance reduction for simulations based on other univariate distributions. For instance, if X has a normal, Student t, or any other symmetric distribution F then
Hence antithetic sampling from a uniform distribution is equivalent to antithetic sampling from any symmetric distribution.
Stratified samples on a standard uniform distribution also correspond to stratified samples on any other distribution, because a distribution function is monotonic increasing. If the sub-intervals used for the stratification have equal probabilities under the standard uniform distribution, they will also have equal probabilities under a non-uniform distribution. For example, if the equiprobable sub-intervals for uniform stratification are
![]()
then the equiprobable sub-intervals for standard normal stratification are
![]()
However, the sub-intervals no longer have equal length.
Figure IV.4.4 compares the histogram of a stratified sample from a lognormal distribution with that based on an unstratified sample. The two empirical densities are based on the same sample of 500 random numbers, but the density shown in black is based on a stratified sample with 50 observations taken from 10 equiprobable sub-intervals of (0, 1). The mean and the standard deviation of the lognormal variable were both set equal to 1. The density based on the stratified sample should be closer to the theoretical distribution.
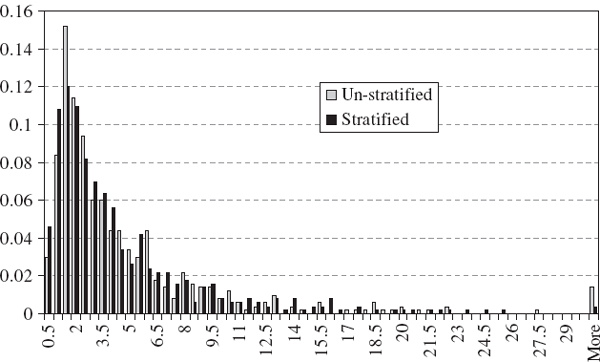
Figure IV.4.4 Densities based on stratified and unstratified samples
IV.4.2.5 Sampling from Multivariate Distributions
Several chapters in Volumes I and II of the Market Risk Analysis series have explained how to transform a random sample on several independent standard uniform variables U1,…, Uk into a random sample from a multivariate distribution of several, non-independent and nonuniform random variables X1,…, Xk.15 First we generate independent simulations on each marginal distribution, then we impose the dependence structure using either the Cholesky matrix of the correlation matrix,16 or for more general distributions, the copula. We shall not repeat the theory here. The main focus of this chapter is to provide empirical examples and case studies of Monte Carlo VaR where simulations are based on realistic risk factor returns models.
IV.4.2.6 Introduction to Monte Carlo VaR
We know how to obtain variance reduced simulations on the returns to the risk factors of a portfolio, or indeed on the returns to any dependent set of asset prices. But how do we compute the portfolio's VaR and ETL?17 The process is completely analogous to the estimation of VaR and ETL using historical simulation, only now we use Monte Carlo simulations instead of historical simulations. That is, we simulate a distribution for the portfolio's h-day returns, or for its h-day P&L, and the 100α% h-day VaR estimate is estimated empirically as −1 times the α quantile of this distribution.18 The ETL is estimated empirically, by taking −1 times the average of the returns that are less than the VaR (or the losses that exceed the VaR).
When we base the portfolio's returns or P&L distribution on a portfolio mapping, each vector of simulations on the risk factor returns is input to this mapping to obtain one simulated portfolio return. Using a very large number N of simulated vectors on the risk factor returns gives N simulated portfolio returns, from which we derive their distribution. On the other hand, if we price the portfolio exactly, each vector of simulations on the risk factor or asset returns is used to derive values for the risk factors themselves, and these are used in the appropriate pricing model. Then the simulation of the portfolio's P&L is the difference between the simulated portfolio price and the current price of the portfolio.19 Again, N simulations on vectors of risk factor returns give N points upon which to base the portfolio P&L distribution.
In the next chapter we shall make a strong case that Monte Carlo simulation is the most reliable method for estimating the VaR for option portfolios. Historical simulation is good when the risk horizon is 1 day and the confidence level is not too high, but it is very difficult to extend the model to longer risk horizons or higher confidence levels without introducing model risk in some form or another. And analytic approximations to the VaR for an option portfolio are usually too inaccurate to be of much use.
Monte Carlo simulation may also be applied to the VaR estimation of linear portfolios. Here the main advantage of Monte Carlo over historical simulation is the absence of restrictions on historical sample size. The calibration of the parametric distributions for risk factor or asset returns can be based on very little historical data, indeed we could just use scenario values for the parameters of the distributions. And if the parameters are calibrated on only very recent history, the Monte Carlo VaR estimates will naturally reflect these market circumstances.
The advantage of Monte Carlo VaR compared with parametric VaR estimates for linear portfolios is the large number of alternative risk factor return distributions that can be assumed. However, readers are warned that, if insufficient thought and effort have been invested in choosing and developing the statistical model of risk factor returns, this can be the major drawback of using Monte Carlo simulation to estimate VaR. It is important to apply simulations to a dynamic model of risk factor returns that captures path-dependent behaviour, such as volatility clustering, as well as the essential non-normal features of their multivariate conditional distributions. Without such a model, volatility adjusted historical simulation may be the better alternative, except for static option portfolios.
The next two sections of this chapter develop the risk factor returns models that underpin the Monte Carlo VaR estimate. Then, in Section IV.4.5 we illustrate these models with empirical examples for different types of linear portfolios. Linear portfolios of interest rate sensitive instruments, cash or futures positions on equities, currency forwards, and commodities are all treated in slightly different ways. First, if risk factor sensitivities are in value rather than percentage terms (e.g. for interest rate sensitive portfolios) we require absolute changes rather than returns in the risk factor mapping. Second, the essential features of the risk factor returns model differ according to the portfolio. For example, volatility clustering is more important in credit spreads than in interest rates, and asymmetry is more important in equities than in currencies.
IV.4.3 MODELLING DYNAMIC PROPERTIES IN RISK FACTOR RETURNS
This section describes the empirical characteristics of a single time series for a financial asset or risk factor and summarizes the econometric models that are commonly used to capture these characteristics. Since this is a vast subject we assume the reader is already armed with the relevant background knowledge. This can be found in Market Risk Analysis Volume II, the most important parts being:
- EWMA and GARCH models and their application to Monte Carlo simulation (see Chapters II.3 and II.4, and Section II.4.7 in particular);
- univariate time series models of stationary processes (see Chapter II.5, and Section II.5.2 in particular); and
- advanced econometric models (see Chapter II.7, and Section II.7.5 in particular).
When risk factor returns are assumed to be i.i.d., we simulate h-day returns on each risk factor, and hence estimate VaR and ETL in one step. However, when the risk factors have dynamic properties such as autocorrelation and volatility clustering, these properties will influence the Monte Carlo VaR estimate. Hence we must consider simulations of time series on risk factor returns, over the risk horizon. We begin with a general description of the multi-step framework for simulating time series that capture the dynamic behaviour of financial returns. We then introduce the concept of importance sampling as a useful means of decreasing computation time without sacrificing too much accuracy. If there is one overriding feature of financial returns that a dynamic model should necessarily capture, it is volatility clustering. To do this properly requires a technical background in statistical models for time varying volatility, but the exposition below is presented at a relatively low technical level. For equity, forex and currency exposures the major market risk factors are prices, and mean reversion in prices is weak, if it exists at all, at the daily level. But volatility is usually a rapidly mean-reverting time series so we should try to include this feature in a multi-step Monte Carlo framework for option portfolios. The last part of this section provides a gentle introduction to the inclusion of volatility regime-switching behaviour in Monte Carlo models for long term VaR estimation.
IV.4.3.1 Multi-Step Monte Carlo
The previous section focused on efficient algorithms for generating a very large number N of simulations on k variables. In the context of Monte Carlo VaR, these variables could represent the h-day returns on the k risk factors for a portfolio. Each row vector of simulations on the risk factors gives one simulated value for the portfolio, via the portfolio mapping.20 Hence, we obtain N simulated portfolio values.
Commonly we would use one-step Monte Carlo to simulate h-day risk factor returns directly. But in many cases – such as estimating the VaR for a path-dependent option, or for estimating the VaR of a linear portfolio without ignoring the dynamic features of daily returns – it can be very important to capture the characteristics of daily returns in the simulation model. For this we need to use a multi-step Monte Carlo framework. For a linear portfolio, with simulations at the daily frequency, this consists of simulating an h-day log return by summing h consecutive daily log returns, and then just evaluating the portfolio once, h days ahead. But for an option portfolio, and particularly one with path-dependent products, we would evaluate the portfolio value on every consecutive day over the risk horizon.21
Multi-step Monte Carlo for a single risk factor is illustrated in Figure IV.4.5. Here we assume that the number of risk factors k = 1 and the risk horizon is h = 10 days, and we perform N = 5 simulations based on the assumption of i.i.d. lognormally distributed returns. We use log returns to simulate the price of our portfolio on each day over the risk horizon, starting from the current price, which we assume is 100, and ending in 10 days' time with five simulated prices. Hence, we simulate five paths for the daily log returns over the next 10 days. This means that, when we are estimating the risk of an option portfolio, the simulated daily log returns can be used to calculate the price tomorrow, the price in 2 days' time, and so on up to the risk horizon (of 10 days, in this case). It is these price paths that we depict in the figure.
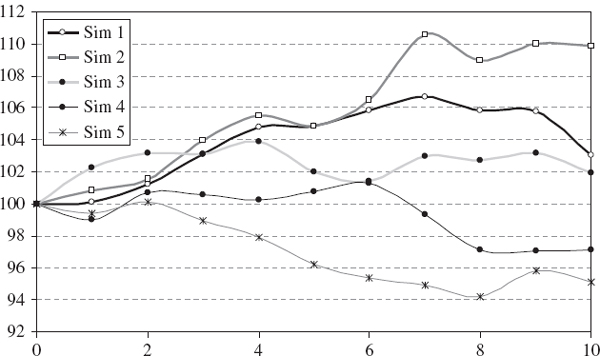
Figure IV.4.5 Multi-step Monte Carlo price paths
If the current price is 100, the simulated price in 10 days' time based on one-step Monte Carlo is 100 exp(r10), where r10 is a simulated 10-day log return. To take path dependence such as volatility clustering into account, we should use multi-step Monte Carlo to simulate each r10 as the sum of 10 consecutive daily log returns. If the log returns are i.i.d. this would be a waste of time, unless we are pricing a path-dependent product. When returns are i.i.d. the sum of 10 consecutive daily log returns should be the 10-day log return, so the result is theoretically the same whether we use 50 simulations for five 10-step paths, or use just five simulations on 10-day returns.22 And the latter is 10 times quicker. However, if returns are not i.i.d. then multi-step Monte Carlo over h consecutive days will not give the same theoretical results as one-step h-day Monte Carlo, even for linear portfolios.
Multi-step Monte Carlo requires considerable effort compared with the one-step case. For instance, in Figure IV.4.5 we generated only five prices at the 10-day horizon but we needed 50 random numbers. In general, multi-step methods at the daily frequency over an h-day risk horizon require h times more simulations than one-step methods. And it is not just the extra simulations that take time: path-dependent products often require complex pricing models, and these have to be implemented at each step along the path.
Importance sampling is a technique for focusing simulations on the most important path. For instance, suppose we are using multi-step Monte Carlo to estimate the 10-day VaR of an up-and-out call option where the underlying asset price has a strong positive trend and the current price is not very far below its barrier. Then there is a reasonably high chance that within 10 days the underlying price will hit the barrier and knock out the option. If we simulated 50,000 10-day paths for this option – requiring 500,000 random numbers to be generated and 500,000 associated pricings for the barrier option – then perhaps about 20,000 of these paths could result in a zero price for the option. In other words, we would have wasted about 40% of the simulation time in generating paths for the underlying price that all lead to the same price for the option, i.e. zero.
Suppose the underlying asset price has a strong negative trend, instead of a strong upward trend, although the volatility remains unchanged.23 Then relatively few of the price paths would result in a zero price for the up-and-out barrier option. As a result, our option price, which is computed as the average over all simulated discounted pay-offs, would be more accurate based on the same number of simulations. However, without modifying this price in some way, it would also be wrong, because it is based on the wrong drift for the process.
Importance sampling makes an artificial change to the drift in the price process, in order to shift the price density to one where more of the paths lead to informative simulated prices for the option. The only problem is that the average of such prices is not the option price we want. It is a price that has been simulated in the wrong measure.24 However, we can derive the option price in the original measure from the price that we have simulated under the new measure. We just multiply each simulated option price by the ratio of the original underlying price density to the ‘shifted’ underlying price density, both evaluated at the simulated underlying price, before taking the average.25
In so far as it helps to price complex products, importance sampling based on a change of measure is a very useful technique for simulating VaR for large portfolios with exotic, path-dependent options. However, VaR is related to a quantile, not an expected value, so different techniques are required for the application of importance sampling to VaR estimation. For instance, Glasserman et al. (2000) apply importance sampling via an exponential twisting technique to the delta – gamma representation of the P&L of an option portfolio.
IV.4.3.2 Volatility Clustering and Mean Reversion
One of the most important features of high frequency returns on equity, currency and commodity portfolios is that volatility tends to come in clusters. Certainly at the daily frequency, but also when returns are sampled weekly if not monthly, large returns tend to follow large returns of either sign. Whilst returns themselves may show little or no autocorrelation, there is a strong positive autocorrelation in squared returns. We refer to this feature as generalized autoregressive conditional heteroscedasticity because the conditional volatility varies over time, as markets pass through periods with low and high volatility.
Chapter II.4 provided a comprehensive introduction to GARCH modelling, and to understand the current subsection readers are also referred to Sections II.3.8, which introduced exponentially weighted moving averages, a simple method for generating time varying estimates of volatility. It is not easy to estimate GARCH models in Excel without special add-ins. Nevertheless a number of spreadsheets that illustrated the use of Excel Solver to estimate GARCH parameters were provided with Chapter II.4. So as not to obscure the important learning points here, the examples in this subsection will be illustrated with user-defined GARCH parameters, or using a simple EWMA model. First, we illustrate the effect of volatility clustering on Monte Carlo VaR estimates using the simplest possible example, with EWMA volatility at the portfolio level.
When based on multi-step Monte Carlo simulations, the EWMA variance estimate ![]() at time t is computed using the recurrence
at time t is computed using the recurrence
where λ is a constant called the smoothing constant, and rt −1 is the simulated log return in the previous simulation. In the normal EWMA model for simulating log returns we set ![]() where zt is a simulation from a standard normal variable and
where zt is a simulation from a standard normal variable and ![]() t is computed using (IV.4.9).
t is computed using (IV.4.9).
The next example shows that when EWMA is used to capture volatility clustering, the h-day Monte Carlo VaR estimates can be considerably greater than the equivalent constant volatility VaR estimates (even over short risk horizons) if the current return is relatively large.
EXAMPLE IV.4.6: MULTI-STEP MONTE CARLO WITH EWMA VOLATILITY
Compare the 10-day log returns that are obtained using multi-step Monte Carlo based on
(a) independent zero-mean normal log returns with a constant conditional volatility of 20%, and
(b) independent zero-mean normal log returns with a time-varying volatility estimate given by a EWMA model. Assume that the current conditional volatility is 25%, the current daily return is 1% and thereafter conditional volatilities are generated using EWMA with daily smoothing constant 0.9.
How do the 10-day VaR estimates that are based on the two return distributions compare? What happens if the current daily log return is 10%?
SOLUTION We compute the 10-day log returns under each model using the same random numbers. The 10 standard normal realizations used for daily log returns are shown in columns B to K of the spreadsheet for this example. The log returns under the constant volatility model (a) are simulated by multiplying each standard normal realization zi(i = 1,…, 10) by the daily standard deviation, then these are summed to obtain the simulated 10-day log return shown in column V.
The log returns under the EWMA model (b) are based on the model (IV.4.9) with λ = 0.9. These are constructed in two interconnected parts. First we simulate the EWMA variance ![]() , using the model (IV.4.9) with r0 = 0.01 and
, using the model (IV.4.9) with r0 = 0.01 and ![]() . Then we multiply the same standard normal realization z1 that was used to simulate the 1-day-ahead daily log return in model (a) by
. Then we multiply the same standard normal realization z1 that was used to simulate the 1-day-ahead daily log return in model (a) by ![]() 1, to obtain r1, the 1-day-ahead daily log return in model (b). Then we use
1, to obtain r1, the 1-day-ahead daily log return in model (b). Then we use ![]() and
and ![]() in (IV.4.9) to obtain
in (IV.4.9) to obtain ![]() , and multiply the same standard normal realization z2 that was used to simulate the 2-day-ahead daily log return in model (a) by
, and multiply the same standard normal realization z2 that was used to simulate the 2-day-ahead daily log return in model (a) by ![]() 2, to obtain r2, the 2-day-ahead daily log return in model (b). This process is repeated up to the 10-day-ahead daily log return and then the 10 log returns are summed to obtain the simulated 10-day log return shown in column AQ.
2, to obtain r2, the 2-day-ahead daily log return in model (b). This process is repeated up to the 10-day-ahead daily log return and then the 10 log returns are summed to obtain the simulated 10-day log return shown in column AQ.
Table IV.4.2 compares 10 simulated 10-day log returns that are generated using each model. The first two columns are returns that are simulated using the current daily log return r0 = 1%, and these show that the return with EWMA volatility may be greater than or less than the constant volatility return, depending on the simulation. The second two columns of simulations set r0 = 10%, and with such a large daily shock, almost all the returns have greater magnitude, whether positive or negative, when based on the volatility clustering model.
Table IV.4.2 Simulated returns based on constant and EWMA volatilities
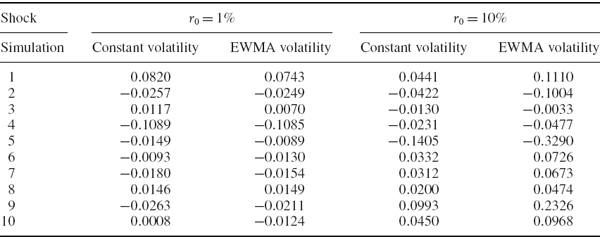
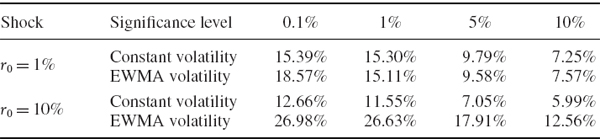
After extending the simulations to a sufficiently large number, readers can use the spreadsheet for this example to compare the 10-day VaR estimates that are based on the 10-day return distributions generated by the two different volatility models. The first two rows of Table IV.4.3 report the results for 0.1%, 1%, 5% and 10% VaR estimates, expressed as a percentage of the portfolio value, based on the same set of 10,000 random numbers. Repeating the simulations shows that the P&L distribution becomes more leptokurtic when the simulations include volatility clustering. The second two rows of the table report the results from the same set of 10,000 random numbers – note these are different simulations from those used in the top part of the table – when the current daily log return is 10%. Notice that the constant volatility model is not influenced by the size of the shock.26 But when volatility clustering is included in the returns model, all the VaR estimates are considerably greater following a shock of 10% than of 1%.
Table IV.4.3 Multi-step Monte Carlo VaR based on constant and EWMA volatilities
The above example demonstrates that introducing volatility clustering in the dynamic model of portfolio returns produces heavier tails in the 10-day return distribution, and to capture this effect we need to use multi-step Monte Carlo simulation.
However, the EWMA model takes no account of the asymmetric relationship between returns and volatility. That is, the results in Example IV.4.5 would be similar to those presented here if the current daily returns were −1% and −10% respectively. EWMA ignores the fact that the volatility of equity portfolio returns increases considerably following a large negative return, but increases little, if at all, following a positive return of the same magnitude. That is, there is no asymmetric volatility clustering in EWMA. It also assumes there is no mean reversion in volatility.
To capture asymmetric volatility clustering and mean reversion in volatility following a shock, we can use an asymmetric GARCH model. The following example uses a similar methodology to that explained in the previous example, but now the EWMA model (IV.4.9) for the conditional variance of the returns is replaced by an A-GARCH model. This model takes the form27
where the parameter λ will be positive if the volatility increases more following a negative return than it does following a positive return of the same magnitude.28 Here ∈t denotes the unexpected return, which is commonly set equal to its deviation from a constant mean. The EWMA model assumes this mean is zero, and we shall also assume this in the following example, hence we assume ∈t = rt for all t.
EXAMPLE IV.4.7: MULTI-STEP MONTE CARLO WITH ASYMMETRIC GARCH VOLATILITY
Compare the multi-step VaR estimates that are obtained using
(a) a constant volatility model with volatility 25%, and
(b) an A-GARCH model (IV.4.10) with the parameters shown in Table IV.4.4 (note that the unconditional volatility of this model is 25%).29
Table IV.4.4 A-GARCH model parameters
| Parameter | Value |
| ω | 4 × 10−6 |
| α | 0.06 |
| λ | 0.01 |
| β | 0.9 |
Estimate the 10-day VaR at the 0.1%, 1%, 5% and 10% significance levels, following a positive return of 10% and following a negative return of 10%. Use the same set of standard normal realizations to drive each model.
SOLUTION The spreadsheet for this example is very similar to the spreadsheet for the previous example, the only difference being that we use an A-GARCH model instead of EWMA. The 10-day VaR estimates based on one set of 10,000 simulations are displayed in Table IV.4.5. The simulations for the constant volatility model are based on the same random numbers as those used in Example IV.4.6.
Table IV.4.5 Multi-step Monte Carlo A-GARCH VaR with positive and negative shocks

The VaR estimates based on constant volatility are identical those shown in Table IV.4.3, since the same 10,000 standard normal simulations were used. But the A-GARCH VaR estimates are considerably lower than the EWMA estimates in Table IV.4.3. This is because the volatility should revert quite rapidly following such a large shock, and this does not happen in the EWMA model. Instead, the EWMA model is highly reactive to the market because it has a reaction coefficient of 0.1. By comparison the GARCH model has a reaction coefficient of 0.06.
The asymmetric volatility response to positive and negative shocks is evident on comparing the last two rows in Table IV.4.5. At high levels of confidence the A-GARCH VaR based on a negative shock is greater than the VaR based on the same model, but following a positive shock of the same size. This asymmetric clustering effect is controlled by the λ parameter. When it is zero there is no differential effect, and when it is negative the A-GARCH VaR following a positive shock would be the greater. However, the asymmetric clustering effect is minor compared with the volatility mean reversion effect that all GARCH models capture.
To see this mean reversion in action, Figure IV.4.6 shows two simulations of daily returns over 10 days based on the same random numbers but using the EWMA (in grey) and the A-GARCH model (in black).30 The asymmetric effect in the GARCH model is very small, in fact in these simulations, noting the scale of the returns, the volatility is greater following a very small positive first return (above) than following a large negative return (below). Both graphs illustrate the pronounced mean reversion in the A-GARCH volatility model. The EWMA model has volatility that remains higher for longer, because of the EWMA model's higher reaction coefficient.
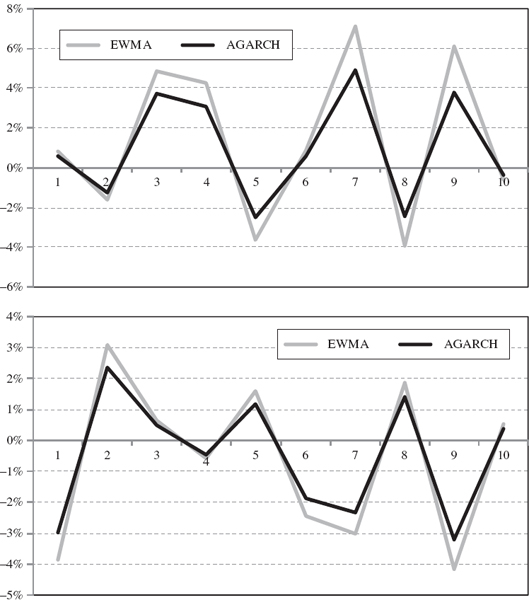
Figure IV.4.6 Simulated returns based on EWMA and GARCH following shock
I am often asked why we cannot use analytic volatility term structure forecasts, such as those derived for various asymmetric GARCH models in Section II.4.3, to estimate VaR with volatility clustering. That is, why can we not take the h-day GARCH volatility for the portfolio, for which there is an analytic formula, and multiply this by the standard normal critical value, just as we would to estimate VaR under the assumption of i.i.d. returns? There are two reasons. First, the h-day returns are not normal or i.i.d., because their volatility is time varying. Secondly, whilst these analytic formulae give us forecasts of h-day GARCH volatility, a forecast is only an expected value. Analytic GARCH volatility forecasts are based on the assumption that the squared return on every day between now and the risk horizon is equal to its expected value. The use of analytic forecasts therefore ignores a very considerable source of uncertainty in the 10-day log return distribution.31 But the risk of the portfolio as measured by the 10-day VaR – or indeed as measured by the standard deviation or any other dispersion metric for 10-day returns – is a measure of the uncertainty of these returns. Therefore, the use of analytic formulae for GARCH volatility term structures, which ignores the most important part of this uncertainty, will tend to underestimate the VaR substantially.
To summarize, the advantage of using GARCH models in VaR estimates based on multi-step Monte Carlo is that these models include a mean reversion effect in volatility. That is, if the returns over the risk horizon were all equal to their expected value (which was assumed to be zero above) then the volatility would converge to its long term average value. Whenever a return is different from its expected value, GARCH volatility will react, but will also display mean reversion. Mean reversion in equity prices or in forex rates is negligible, in commodity prices it is questionable, and even in interest rates mean reversion tends to occur over a very long cycle.32 But volatility is known to mean-revert relatively rapidly. Hence, volatility is a risk factor for which a mean reversion effect is important when designing dynamic models of market returns.
There are several papers on the ability of GARCH models to capture volatility clustering in the VaR estimation literature. Mittnik and Paolella (2000) and Giot and Laurent (2003) employ an asymmetric generalized t conditional distribution in the GARCH model; Venter and de Jongh (2002) use the normal inverse Gaussian distribution and Angelidis et al. (2004) apply the Student t EGARCH model. Both So and Yu (2006) and Alexander and Sheedy (2008) find that the Student t GARCH model performs well in VaR estimation for major currency returns. GARCH Monte Carlo VaR models also have important applications to stress testing portfolios, as we shall see in Chapter IV.7.
IV.4.3.3 Regime Switching Models
Our discussion of Monte Carlo simulation with GARCH models in Section II.4.7 made the case that Markov switching GARCH is the only model that properly captures the type of volatility clustering behaviour that we observe in most financial markets. In this section we explain how this model provides a useful framework for deriving VaR estimates over a long risk horizon, during which it is possible that volatility passes through different regimes. We use a risk horizon of 250 days, although such long risk horizons are rare when we assess market risks.
Figure IV.4.7 is based on the same Markov switching GARCH model as was used in Section II.4.7.2. Each graph is generated from a different series of 250 simulated realizations of a returns process with a regime switching volatility. Notice how different the two simulations are, even though they are based on the same GARCH model. The sum of the 250 consecutive log returns is 29.23% for the upper graph but −26.29% for the lower graph in Figure IV.4.7. Also note that the initial return in the upper graph is quite large, and hence a high volatility cluster appears immediately, whereas the initial return in the lower graph is small and so the initial regime is one of low volatility. However, in this particular case it is the path in the lower graph that experiences the most volatility, especially between days 50 and 150. The path in the upper graph has smaller bursts of volatility that are less extreme than in the lower graph.
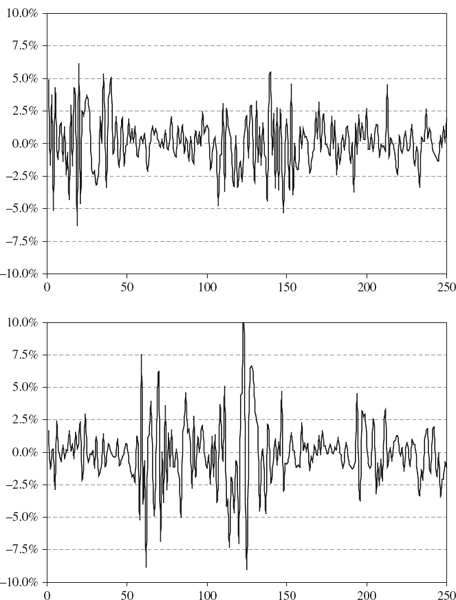
Figure IV.4.7 Log returns simulated under Markov switching GARCH
Each time we repeat the simulations the sum of the log returns can change considerably, even though we do not change the model parameters. For example, I have repeated the simulations ten times and obtained the following simulated values for the sum of the log returns:
![]()
We conclude that volatility clustering regimes introduce an additional source of uncertainty into long term return distributions. This could significantly increase the long term VaR estimate, depending on the volatility at the time is VaR is measured, compared with a constant volatility VaR estimate. For instance, the VaR could be measured at a time when the market was relatively tranquil, but there may still be a prolonged period of high volatility over the risk horizon, as in the lower graph in Figure IV.4.7.
Unfortunately, without VBA code it is beyond the scope of Excel to simulate many thousands of such annual returns, in order to estimate the Markov switching GARCH annual VaR. And so we end the illustration here, leaving the development of the spreadsheet for Figure IV.4.7 into a Markov switching GARCH model for long term VaR as an exercise for the reader.
IV.4.4 MODELLING RISK FACTOR DEPENDENCE
The primary purpose of a risk model is to disaggregate portfolio risk into components corresponding to different types of risk factors. That is why we use a portfolio mapping to derive the portfolio returns or P&L, rather than modelling the returns or P&L distribution directly at the portfolio level. All risk metrics, including VaR, should take account of portfolio diversification effects when aggregating risks across different types of risk factors.
In the traditional view of portfolio theory, diversification effects arise when there is less than perfect correlation between the assets or risk factors for a portfolio. More recently, we have widened this to include any type of less-than-perfect dependence between risk factors, where dependence in general is captured using a copula. In the elliptical copulas (i.e. normal and Student t copulas) dependence is captured by a correlation matrix. But in other copulas, different parameters govern dependence.
In this section we summarize the relevant material from Volumes I and II on statistical models for dependence between risk factors and explain how they are implemented in a Monte Carlo framework to simulate dependent vectors of risk factor returns. Several numerical examples are provided, for which you will need to install the Matrix.xla Excel add-in.33
IV.4.4.1 Multivariate Distributions for i.i.d. Returns
Useful background reading for this section is the brief introduction to Monte Carlo simulation of correlated variables in Section I.5.7, the material on multivariate elliptical distributions in Section I.3.4, and Section II.6.7 on simulation with copulas.
We shall describe the process for estimating Monte Carlo VaR based on risk factor mapping, but a similar algorithm applies to estimate Monte Carlo VaR using asset returns rather than risk factor returns in the simulations. The only difference is that instead of applying the risk factor sensitivities in the portfolio mapping to compute the portfolio return, we use the portfolio weights.
We shall also assume that the portfolio mapping is based on returns rather than on changes in the equity, currency and commodity risk factors, so that the mapping yields a portfolio return. Hence, the VaR will be measured as a percentage of the portfolio value. But for interest rate sensitive portfolios the risk factor mapping is normally based on changes in interest rates, with the PV01 vector of sensitivities to these changes. Then the portfolio mapping gives the portfolio P&L, not the portfolio return, corresponding to each vector of interest rates changes.34
Multivariate Normal
The most basic algorithm for generating correlated simulations on k risk factor returns is based on a k-dimensional, i.i.d. normal process. So the marginal distribution of the ith risk factor's return is ![]() , for i = 1,…, k, and the risk factor correlations are represented in a k × k matrix C. The algorithm begins with k independent simulations on standard uniform variables, transforms these into independent standard normal simulations, and then uses the Cholesky matrix of the risk factor returns covariance matrix to transform these into correlated zero-mean simulations with the appropriate variance. Then the mean excess return is added to each variable.
, for i = 1,…, k, and the risk factor correlations are represented in a k × k matrix C. The algorithm begins with k independent simulations on standard uniform variables, transforms these into independent standard normal simulations, and then uses the Cholesky matrix of the risk factor returns covariance matrix to transform these into correlated zero-mean simulations with the appropriate variance. Then the mean excess return is added to each variable.
With the above notation the risk factor excess returns covariance matrix Ω may be written
where D = diag (σ1,…, σk). Its Cholesky matrix is a lower triangular k × k matrix Q such that Ω = QQ′. We also write the expected returns in a vector, as μ =(μ1,…, μk)′. Then the k × 1 multivariate normal vectors x are generated by simulating a k × 1 independent standard normal vector z, and setting x = Qz + μ.
We simulate a very large number N of such vectors x and apply the portfolio mapping to each simulation, thus producing N simulations on the portfolio returns. When the returns are i.i.d. we use one-step rather than multi-step Monte Carlo, so the expectations vector μ and standard deviation matrix D of the risk factor returns are h-day expected excess returns and standard deviations. Then we simulate N h-day portfolio excess returns, find their empirical distribution, find the α quantile of this distribution, multiply this by −1 and that is the h-day VaR estimate. And the corresponding ETL is −1 times the average of the returns below the α quantile.
EXAMPLE IV.4.8: MULTIVARIATE NORMAL MONTE CARLO VAR
A linear portfolio has five correlated risk factors, labelled A–E, which we assume have i.i.d. normal returns. The annual expected excess returns on each risk factor, the risk factor volatilities and the current risk factor sensitivities are displayed in Table IV.4.6. Below these the table displays the risk factor returns correlation matrix. Use Monte Carlo simulation to estimate the 1% 10-day VaR of the portfolio.
Table IV.4.6 Risk factor returns, volatilities, sensitivities and correlations
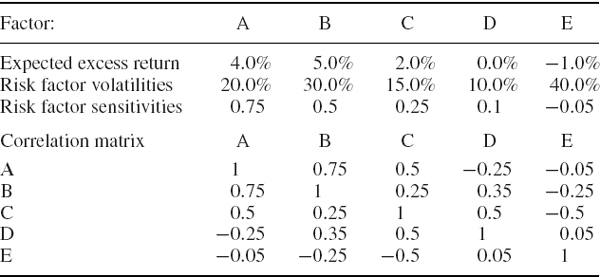
SOLUTION Note that it is easier to represent the simulated vectors in the spreadsheet as row vectors, although we used columns vectors (as usual) in the mathematical description of the algorithm above. First the 10-day Cholesky matrix Q10 is calculated, and this is shown in cells B17:F21 of the spreadsheet. Then we simulate five independent standard normal realizations as a row vector z′, post-multiply this by the transpose of the 10-day Cholesky matrix and add on the 10-day mean vector μ′10. This gives x′10 = z′Q′10 + μ′10, i.e. one simulation of a row vector of correlated risk factor returns. Having simulated N such row vectors, we apply the linear risk factor mapping to each one of these, using the sensitivities shown in Table IV.4.6, to obtain N simulated portfolio 10-day returns. Finally, the 1% VaR is −1 times the 1% quantile of the distribution of these returns, and with N = 10, 000 simulations we obtain a Monte Carlo VaR estimate of approximately 14% of the portfolio value.
Multivariate Student t
The above example illustrated the most basic risk factor mapping, i.e. a simple linear function, and the most basic risk factor returns model, i.e. where the multivariate distribution is normal and the risk factor returns are i.i.d. However, risk factor returns at the daily or weekly frequency rarely have normal distributions. In particular, for estimating Monte Carlo VaR over short risk horizons of up to a few weeks it is important to include leptokurtosis in the risk factor return distributions. The easiest way to do this is to use a multivariate Student t distribution, which has the distribution function specified in Section I.3.4.8. Note that there is only one degrees of freedom parameter ν in this distribution, so the marginal distributions of all risk factor returns are assumed to have the same excess kurtosis. But in the next subsection, when we introduce copulas, we show how this assumption may be relaxed.
The Monte Carlo VaR algorithm for i.i.d. multivariate Student t distributed risk factor returns is very similar to the multivariate i.i.d. normal algorithm. The only difference is that the vector z is replaced by a vector t containing simulations from a standardized multivariate Student t distribution, i.e. the distribution with zero mean, unit variance marginals. Since a Student t distributed variable with ν degrees of freedom parameter has mean zero but variance ν (ν − 2)−1, we obtain t by multiplying independent standard Student t simulations by ![]() .
.
EXAMPLE IV.4.9: MULTIVARIATE STUDENT T MONTE CARLO VAR
Suppose the risk factors in the previous example have a multivariate Student t distribution with 6 degrees of freedom, but otherwise the portfolio and the risk factors have the same characteristics as those displayed in Table IV.4.6. Re-estimate the 1% 10-day VaR based on this assumption.
SOLUTION The spreadsheet for this example is similar to that for Example IV.4.8, except that now we use an extra set of five columns to produce the standardized uncorrelated simulations, one set to simulate standard Student t distributed returns with 6 degrees of freedom,35 and a second set which transforms these to have unit variance. Otherwise the spreadsheet is unchanged from the previous example. With 10,000 simulations we obtain a 1% 10-day Monte Carlo VaR that is approximately 15% of the portfolio value.
Due to the leptokurtosis in the Student t distribution this is greater than the VaR estimate based on normally distributed risk factor returns.36 The difference between the two VaR estimates becomes more pronounced at more extreme quantiles, but at the 5% quantile there may be little difference between the estimates, and at 10% the Student t VaR estimate may be less than the normal VaR estimate.
Multivariate Normal Mixture
It is possible to apply Monte Carlo to many distributions – indeed, this is one of the main advantages of Monte Carlo methods VaR. We now explain how to use Monte Carlo methods when risk factor returns have a multivariate normal mixture distribution, i.e. each multivariate normal in the mixture distribution has its own mean vector and covariance matrix. This is a simple way to capture non-zero skewness as well as leptokurtosis in the risk factor returns.
By way of illustration, let us suppose we have only two multivariate normal distributions in the mixture. In fact, this is often sufficient to capture the leptokurtosis and/or skewness that we often observe in risk factor returns. Suppose one multivariate normal occurs with a low probability π, has mean vector μ1 and covariance matrix Ω1 and reflects ‘market crash’ conditions, and the other, which occurs with probability 1 − π, has mean vector μ2 and covariance matrix Ω2 and reflects ordinary market circumstances. The normal mixture distribution function on n random variables x = (x1,…, xn)′ may then be written
where Φ is the multivariate normal distribution function.
Monte Carlo simulation on (IV.4.12) is performed in two stages. First we take a random draw on a Bernoulli variable with success probability π. Then we sample from the first multivariate normal if the result is a ‘success’ and otherwise we sample from the second multivariate normal. Equivalently, when we perform a very large number N of simulations, we apply μ1and Ω1 to π N of the independent standard normal simulations and μ2 and Ω2 to (1 − π ) N of them. An empirical illustration of normal mixture Monte Carlo is given in Example IV.4.13 below.
Copulas
In the examples considered so far all the risk factor returns were assumed to have identical marginal distributions. To allow for heterogeneous risk factor return distributions we must model dependence using a copula distribution. Copulas are multivariate distributions with uniform marginals that may be used to construct a huge variety of risk factor return distributions. The copula only models dependence; the marginal distribution of each of the risk factor returns may be anything we like. For instance, one risk factor could have a Student t return distribution with 6 degrees of freedom, another could have a normal return distribution, another could have a gamma distribution, and so on.
Normal (also called Gaussian) and Student t copulas capture dependency through a correlation matrix, which is a limited measure of only linear association. But there are many other copulas that capture more general dependency. One very attractive class of copulas, which have very parsimonious parameterizations, are the Archimedean copulas. See Sections II.6.4.4, II.6.5.4 and II.6.7.4 for further details.
Suppose the risk factor returns have some assumed marginal distributions, which need not be identical, and that their dependency is modelled with a copula. The simulation algorithm begins with simulations on independent uniform random variables. Then the inverse conditional copula functions are applied to obtain realizations of dependent uniform variables. Finally, the dependent uniform realizations are translated into simulations on the risk factor returns by applying the relevant inverse marginal distribution function to each realization.
The elliptical copulas (i.e. normal and Student t copulas) have dependency structure that is captured by a correlation matrix, and this makes simulation based on these copulas very easy, with risk factors that may have a variety of marginal distributions. In the next example we show how to estimate VaR based on simulated returns to five risk factors, each having different Student t marginal distributions, but with a normal copula. Because the marginals already have a variance different from one, for a normal or Student t copula we use the Cholesky matrix of the correlation matrix, not of the covariance matrix, to impose the dependency structure.
EXAMPLE IV.4.10: MONTE CARLO VAR BASED ON COPULAS
Suppose the risk factors have the same expected excess returns and volatilities as in the two previous examples and that their dependency is described by a normal copula with the same correlation matrix. The portfolio's risk factor sensitivities are also assumed to be the same as in the previous examples. However, now suppose that each risk factor return has a different univariate Student t marginal distribution. The degrees of freedom, in order of the five risk factors are: 5, 4, 6, 10, and 5. Re-estimate the 1% 10-day VaR based on this assumption.
SOLUTION The result is only marginally less than that in the previous example: based on 10,000 simulations, the 1% 10-day VaR is approximately 14.75% of the portfolio value. The use of a normal copula rather than a Student t copula tends to decrease the VaR, but some of the marginals have more leptokurtosis than in the previous example, which tends to increase the VaR.
The purpose of the above example is not to discuss how the VaR behaves under different behavioural assumptions for the risk factors; it is merely to illustrate the algorithm for estimating VaR based on simulation from a normal copula with different marginals. The steps are as follows:
- Simulate independent standard uniform observations, one column for each risk factor.
- Transform these into independent standard normal observations, using the inverse standard normal distribution function.
- Transform the independent standard normal observations into correlated multivariate standard normal observations, using the Cholesky matrix of the correlation matrix.
- Transform the correlated multivariate standard normal observations into simulations from a normal copula, by applying the standard normal distribution function.
- Transform the simulations from a normal copula into standard Student t observations with normal copula, using the inverse distribution function for the Student t with the required degrees of freedom. Note that the degrees of freedom can be different for each marginal. Indeed, the marginals do not have to have Student t distributions, we have just used these for illustration.
- Use the required h-day mean and h-day standard deviation to transform the standard Student t observations with normal copula into simulations on h-day risk factor returns, with general Student t marginals, but still with dependency captured by a normal copula.
- Apply the risk factor mapping and hence obtain simulated portfolio returns.
- Estimate the α quantile of the simulated portfolio return distribution, and multiply this by −1 to obtain the 100α% VaR. If required, estimate the 100α% ETL as −1 times the average of the returns less than the α quantile.
Algorithms for simulation from bivariate distributions using various copulas are illustrated in the workbook ‘Copula_Simulations_II.6.7.xls’ that accompanies Volume II. Also in that workbook is an example on VaR estimation under various copulas, described in Section II.6.8.1. Readers may wish to study that workbook and then change the spreadsheet for the above example so that it uses a different copula and/or different marginals. For example, with a Student t copula with ν degrees of freedom, the transformation at step 2 is performed using the inverse Student t distribution with ν degrees of freedom, and then its distribution function is applied at step 4. But for other copulas we would not use a correlation matrix at all. For instance, for simulations under a Clayton copula the risk factor dependency is described by a single parameter.
IV.4.4.2 Principal Component Analysis
Principal component analysis is a standard statistical tool for orthogonalizing risk factors and for reducing dimensions of the risk factors. In other words, PCA is a technique for extracting a few key, uncorrelated risk factors – which are called the principal components – from a larger set of correlated risk factors. It works best when the original risk factors are highly correlated, since then we need only a few principal components to represent the system. The first component will be the most important, and in a highly correlated system it usually represents a common trend.
PCA works especially well when the risk factors are a highly correlated, ordered system since then all the principal components and not just the first one will have an intuitive financial meaning. This is why much of Chapter II.2 dealt with the principal component factor models for term structures of interest rates, credit spreads, futures, forwards or volatilities. The input to a PCA is either a covariance matrix or a correlation matrix. Then the principal components are derived from the eigenvectors of this matrix, which are ordered so that the first eigenvector belongs to the largest eigenvalue, and therefore the first component explains the most variation in the system. In very highly correlated systems this component captures an almost parallel shift in all variables, and more generally it is labelled the common trend component, because it captures the most often experienced type of common movement in all risk factors. The second eigenvector belongs to the second largest eigenvalue, and therefore the second component explains the second most variation in the system. In ordered and highly correlated systems such as a term structure this eigenvector captures an almost linear tilt in the variables, so it is commonly labelled the tilt component. The third most important component usually comes from an eigenvector that is an approximate quadratic function of the ordered variables, so it has the interpretation of convexity or curvature. Similarly, higher order principal components in ordered, highly correlated systems capture changes in risk factors that are cubic, quartic, quintic and so forth.
The ability of PCA to reduce dimensions, combined with the use of orthogonal variables for risk factors, makes this technique an extremely attractive option for Monte Carlo simulation. In highly correlated term structures of interest rates, credit spreads and volatilities the replacement of the original risk factors by just a few orthogonal risk factors introduces very little error into the simulations, and increases the efficiency of the simulations enormously, because it reduces the number of risk factors.
However, the application of PCA to Monte Carlo simulations of equity and currency risk factors, or to portfolios with different types of commodity futures, is limited. Typically, these systems are neither very highly correlated nor ordered. So a large number of principal components would usually be required in the representation, to avoid introducing a substantial risk model error. This means that there is less scope for computational efficiency gains.
Each volume of Market Risk Analysis has contained numerous empirical examples and case studies on the application of PCA to different types of risk factors. Here are some references to just a selection of these:
- equity indices – Section I.2.6.3;
- individual stocks – Section II.2.5.3;
- interest rate term structures – Section II.2.3;
- forward currency exposures – Section II.2.4.2;
- energy futures – III.2.6.3;
- implied volatility smiles – Section III.4.4.2;
- volatility term structures – Section III.5.7.
In this chapter we provide yet another illustration of the power of this technique. Example IV.4.12 in Section IV.4.5.2 presents an empirical example on Monte Carlo interest rate VaR based on principal component risk factors.
IV.4.4.3 Behavioural Models
One of the reasons why copulas are used in multivariate simulations is that the dependency between risk factor returns is not necessarily linear. When there are only a few risk factors, an alternative to copulas is to model the risk factor returns relationship using non-linear regression. For example, suppose there are two risk factors whose returns X and Y have a quadratic rather than a linear relationship, i.e.
Since X and Y are stochastic the relationship will not be exact, so we add an error term on the right-hand side of (IV.4.13). The error has zero mean and often we assume it is homoscedastic (i.e. has constant standard deviation, which we denote σ) and normally distributed. These are the standard assumptions for ordinary least squares regression (OLS).37 Then we use T historical observations on the returns X and Y to estimate the model parameters α, β1, β2 and σ using OLS on the regression:
Other non-linear models are usually easy to estimate provided the right-hand side is only a non-linear function of the variables and not of the parameters. For instance, we may hypothesize a relationship of the form
Again the parameters may be estimated using OLS multiple regression, provided we make the standard assumption about homoscedasticity of the error term. Or, if the risk factor return Y is thought to be non-linearly related to two other risk factor returns, X1 and X2, their relationship could be of the form
for example. Since this is linear in the parameters, we may estimate them using OLS.38
IV.4.4.4 Case Study: Modelling the Price – Volatility Relationship
Consider Figure IV.4.8, which depicts a scatter plot of the daily log returns on the S&P 500 index (horizontal scale) and Vix index (vertical scale). The negative dependence and leptokurtosis are apparent and the grey curve is drawn through the scatter plot to highlight their non-linear relationship. We shall capture the relationship between implied volatility and the underlying price using a simple quadratic regression of daily log returns to the Vix index on the S&P 500 log returns over the same sample period.
Figure IV.4.8 Scatter plot of S&P 500 and Vix daily log returns
In the case study workbook we estimate a quadratic regression via the data analysis tools in Excel. Using daily data from 2 January 2000 until 25 April 2008, the result is the estimated model
where Y denotes the log return on the Vix, X denotes the log return on the S&P 500 index and the error term has standard deviation equal to the standard error of the regression, which is estimated to be 3.77%. The figures in parentheses denote the t statistics of the coefficients above them, so both the S&P 500 returns and the squared returns are very highly significant. This is to be expected, given the evident non-linearity in the scatter plot above.
However, no significant non-linearity is apparent in the weekly returns relationship. Using weekly data from 2 January 2000 until 28 April 2008, the result is the estimated model
where the estimated standard error of the regression is 7.54%. The quadratic term is no longer significant, and so we conclude that non-linearities in the S&P500 – Vix relationship are only important when simulations are at the daily frequency.
We can use the estimated model (IV.4.17) to simulate a daily log return Y on the Vix for any simulated daily log return X on the S&P 500. Because of their non-linear relationship, this is better than using a covariance matrix to capture their dependence. We shall return to this model in Section IV.5.5.3, where we use it to estimate the VaR for an option portfolio.
IV.4.5 MONTE CARLO VALUE AT RISK FOR LINEAR PORTFOLIOS
In Chapter IV.2 we showed how to extend the normal linear VaR formula to Student t and normal mixture VaR, and how to use a scaling constant that reflects autocorrelation in returns. If we use one these models for the returns on the risk factors of a linear portfolio then there is no point in applying Monte Carlo to estimate the VaR.39 The only difference between the Monte Carlo and the parametric linear VaR estimates would be due to simulation error, and it is the analytic formula that gives the correct result. The more simulations used, the more accurate the Monte Carlo VaR estimate, and as the number of simulations used increases the Monte Carlo VaR estimate converges to the parametric linear VaR estimate that is based on the same distributional model for returns.
So what is the advantage of using Monte Carlo to estimate VaR for a linear portfolio, compared with parametric linear VaR? The advantage is that the risk factor returns model is not limited to the simple models that we considered in Chapter IV.2, i.e. multivariate normal, Student t or mixture returns that are either i.i.d. or have a simple first order autoregressive structure. As we have seen in the previous two sections, a great variety of conditional multivariate distributions may be used as a basis for simulation. We may also want to use multi-step Monte Carlo simulations to introduce path dependence, either in an option's pay-off or in the volatility clustering behaviour of risk factor returns.
Compared with historical simulation, the advantage of using Monte Carlo to estimate VaR for a linear portfolio is that we can generate as many h-day returns as we like.40 Whilst historical VaR is a natural way to capture the complex behaviour in and between risk factor returns it is, at least initially, limited to the 1-day horizon. This is because we simply do not have enough relevant historical data to use non-overlapping h-day returns.41 But we can extend the standard historical simulation model to filtered historical simulation (FHS) which applies a statistical bootstrap on a parametric, dynamic model for return distributions, such as a GARCH model. This filtering allows h-day return distributions to be generated from overlapping samples and we can also increase the number of observations used for building the h-day portfolio return distribution through the use of the bootstrap. But FHS is in fact a hybrid method combining some attractive features of both historical and Monte Carlo VaR models.42
What is the effect on VaR of using parametric but non-normal distributions for the risk factors returns? We can use Monte Carlo VaR to answer this question, by comparing the Monte Carlo VaR estimates based on simple risk factor returns models with those based on more complex distributions. The result will depend on both the risk horizon and the type of portfolio. For instance, one might expect the i.i.d. multivariate normal or Student t distribution to be less appropriate for daily changes in credit spreads than it is for daily changes interest rates. But over a monthly risk horizon many risk factors might well be assumed to have i.i.d. multivariate normal or Student t distributions.
The purpose of this section is to illustrate the application of the risk factor returns models that we introduced in Sections IV.4.3 and IV.4.4 to the estimation of Monte Carlo VaR and ETL. We shall apply a different returns model to four different types of portfolios:
- elliptical copulas for credit spreads;
- principal component analysis for interest rates;
- multivariate normal mixture distributions for equities;
- volatility clustering for currencies.
Although we apply these different assumptions for Monte Carlo VaR in the framework of a particular type of portfolio, this is primarily for the purpose of illustrating each technique rather than a practical recommendation. For example, equity portfolios could benefit from modelling volatility clustering, as well as capturing the asymmetry and leptokurtosis in the conditional return distributions using multivariate normal mixture distributions.43
IV.4.5.1 Algorithms for VaR and ETL
The following summarizes the general one-step algorithm for estimating VaR and ETL when the risk factor mapping expresses the portfolio return as a linear combination of risk factor returns:
- Simulate N independent 1 × k vectors of standard uniform observations, where k is the number of risk factors and N is the number of simulations.
- Use the i.i.d. risk factor returns model to transform these standard uniform observations into simulations on h-day risk factor returns, as described in Section IV.4.4.
- Apply the risk factor mapping to the simulations on h-day risk factor returns to produce N simulated h-day returns on the portfolio, and discount these to today.
- As a percentage of the portfolio value, the 100α% h-day VaR is −1 times the α quantile of the h-day return distribution and the 100α% h-day ETL is −1 times the average of all the h-day returns that are less than the α quantile. Multiplying these by the portfolio value today gives the VaR and ETL in value terms.
Depending on the type of portfolio, we may simulate h-day changes in risk factor values at step 2 instead of h-day returns. That is, we may take the simulated value of a risk factor in h days' time minus value of this risk factor today (i.e. the time when the VaR is measured).44 In addition, or alternatively, the risk factor mapping may produce N simulated h-day P&Ls on the portfolio, discounted to today.45 In that case the VaR and ETL estimated at step 4 will already be expressed in value terms.
To account for path dependence such as volatility clustering in risk factor returns, the general algorithm above is modified for multi-step Monte Carlo as follows:
- Simulate N independent 1 × k vectors of standard uniform observations, where k is the number of risk factors and N is the number of simulations.
- Use the conditional 1-day risk factor log returns model to transform these standard uniform observations into simulations on 1-day risk factor log returns.
- Return to step 1 and repeat h times, using the dynamic returns model to simulate each subsequent risk factor log return, as described in Section IV.4.3.
- For each risk factor and for each of the N simulated paths, sum the log returns to obtain N simulated h-day log returns on each risk factor.
- Apply the risk factor mapping to produce N simulated h-day returns on the portfolio, and discount these to today.
- As a percentage of the portfolio value, the 100α% h-day VaR is −1 times the α quantile of the h-day return distribution and the 100α% h-day ETL is −1 times the average of all the h-day returns that are less than the α quantile. Multiplying these by the portfolio value today gives the VaR and ETL in value terms.
We now present some empirical implementations of these algorithms in the context of cash flow, equity and currency portfolios.
IV.4.5.2 Cash-Flow Portfolios: Copula VaR and PC VaR
A cash flow is mapped to a vector of default-free interest rates r at fixed maturities, and to a vector of credit spreads s, also at fixed maturities. As explained in Section IV.2.3, the risk factor sensitivities are the PV01 of the mapped cash flows at each vertex, and the risk factors are the absolute changes in these interest rates and credit spreads, expressed in basis point terms. When an interest rate sensitive portfolio is represented as a cash flow the risk factor mapping therefore takes the form
where θr and θs are the PV01 vectors with respect to the interest rate and credit spread risk factors, and Δr and Δs are the basis point changes in these risk factors.46 Since the PV01 is already in present value terms the algorithms described in the previous subsection provide N simulated values for the discounted P&L, from which we estimate the VaR and ETL.
The next example illustrates the estimation of Monte Carlo credit spread VaR based on elliptical copulas with different elliptical marginals. The parameters in the spreadsheet can be changed to reflect suitable distributions for any type of risk factors, such as interest rates, currencies, commodities or equities if so desired.
EXAMPLE IV.4.11: MONTE CARLO CREDIT SPREAD VAR
A portfolio of BBB-rated corporate bonds and swaps is mapped to vertices at 1 year, 2 years, 3 years, 4 years and 5 years. Table IV.4.7 shows the PV01 vector, along with the annual volatilities and correlations of the credit spread risk factors.47 Compare the 10-day Monte Carlo VaR of this portfolio at different significance levels based on the assumption that changes in credit spreads have:
(a) a multivariate normal distribution;
(b) a normal copula and marginal Student t distributions having 5 degrees of freedom, and
(c) a multivariate Student t distribution with 5 degrees of freedom.
In case (b), readers may change the degrees of freedom to be different for each credit spread in the spreadsheet.
Table IV.4.7 Volatilities and correlations of LIBOR and credit spreads
SOLUTION We adapt the spreadsheets for Examples IV.4.8, IV.4.9 and IV.4.10 for parts (a), (b) and (c), respectively. We use the same 10,000 standard uniform simulations for each distribution, and the results for one set of 10,000 simulations are shown in Table IV.4.8.
Table IV.4.8 Comparison of Monte Carlo VaR estimates for credit spreads

The results for (a) and (b) are similar at the 10% significance level, but as the confidence level of the VaR increases the difference between the normal copula VaR with Student t marginals and the normal VaR increases. This is due to the leptokurtosis in the Student t marginal distributions. The multivariate Student t VaR estimates (c) are greater than those in (b), readers may change the degrees of freedom to be different for each credit spread in the spreadsheet, because they are based on the same Student t marginals but have a Student t copula dependence, and the Student t copula has a greater tail dependency than the normal copula.
In practice cash flows are mapped to a very large number of fixed maturity interest rates and credit spreads. But interest rate risk factors are very highly correlated and so PCA can be applied to reduce the dimension of the risk factor space. Moreover, the construction of the principal components guarantees that they are uncorrelated, because they are generated by orthogonal eigenvectors. Thus, their correlation matrix is diagonal, and its Cholesky decomposition is also diagonal. The combination of dimension reduction and zero correlation reduces the complexity of the simulation algorithm considerably. Thus, using principal component risk factors will speed up the calculation of Monte Carlo VaR, with little loss of accuracy.
For instance, in Examples IV.2.8 and IV.2.10 we estimated the normal linear VaR of a cash flow characterized by the PV01 vector shown in Figure IV.2.2. We found that the 1% 10-day principal component VaR was £175,457, compared with £176,549 when calculated on the interest rates directly. Hence, interest rate VaR based on PCA tends to be very accurate, provided the interest rates of different maturities are highly correlated.48
When using principal components as risk factors, the mechanics of Monte Carlo VaR computation are basically identical to those outlined in the previous section. The dimension of the risk factor space is considerably reduced, which speeds up the computation. Also, with multivariate normal or Student t VaR, the steps are computationally simpler and therefore faster to execute, because the covariance matrix of the risk factors is diagonal.49 In fact, the Cholesky matrix is already known from the PCA. Because the variance of the ith component is the ith eigenvalue, the Cholesky matrix is just a diagonal matrix with ith diagonal element equal to the square root of the ith largest eigenvalue.
The next example demonstrates how to perform simulations on the first few principal components alone, and then uses the results of each simulation in the PCA risk factor mapping (IV.2.39) to compute the associated discounted P&L of the portfolio.
EXAMPLE IV.4.12: MONTE CARLO INTEREST RATE VAR WITH PCA
Recall the case study on estimating VaR for a UK bond portfolio, presented in Section IV.2.4. In Example IV.2.10 the 1% 10-day normal linear VaR based on a three principal component representation was estimated as £175,457. Now estimate the VaR based on this same PCA representation, but use Monte Carlo simulation on the principal components. What is the effect on the PC VaR of assuming that the principal components have a multivariate Student t distribution with 6 degrees of freedom?
SOLUTION The first three eigenvalues of the daily covariance matrix were found in the case study of Section IV.2.4 to be 856.82, 45.30 and 9.15. Hence the 10-day Cholesky matrix has diagonal elements
![]()
as shown in Table IV.4.9. In the first row of this table we show the net PC sensitivities of the bond portfolio. These were already calculated in the case study of Section IV.2.4, and they are obtained by multiplying each PV01 by the corresponding element of the eigenvector that defines the principal component.
The normal VaR spreadsheet in the workbook for this example estimates the multivariate normal linear VaR using Monte Carlo simulation. Without simulation error, this should be £175,457, i.e. the PC VaR based on the exact analytic solution.50 The t VaR spreadsheet estimates the multivariate Student t linear VaR using Monte Carlo simulation. Based on 10,000 simulations this is approximately £185,000. Predictably, it is greater than the normal VaR, since the Student t distribution with 6 degrees of freedom has an excess kurtosis of 3.
Table IV.4.9 PC sensitivities and the PC Cholesky matrix
This illustrates the basic framework for Monte Carlo VaR calculations when the dimension of the risk factor space is reduced by using principal components. For clarity, the above example used only a simple i.i.d. model for the principal component factors, but it could easily be extended, to include volatility clustering for the principal components. The point to note is that it would take much longer to perform the simulations if we applied 100,000 or more simulations to 60 highly correlated interest rates, instead of to three uncorrelated principal components. And the error introduced by using principal component risk factors instead of the interest rates themselves will still be very small compared with the simulation error.
IV.4.5.3 Equity Portfolios: ‘Crash’ Scenario VaR
In the following we use x = (X1,…, Xk) to denote a set of asset or risk factor returns for an equity portfolio. When a long-only stock portfolio is not mapped to broad market indices or other risk factors, the portfolio return Y may be written
where w is the vector of portfolio weights and here x denotes a vector of stock returns. If the portfolio is mapped to a set of risk factors then the portfolio return may be written
where β is the vector of net risk factor betas, expressed as a percentage of the portfolio value and here x denotes the risk factor returns.51
Now Monte Carlo VaR is based on the usual algorithm, using simulations of x. We shall assume the portfolio is characterized by its current weights or betas, and that these are constant over the risk horizon. This assumption implies that the portfolio is rebalanced each time a stock price or risk factor changes. However, a long-short portfolio may have price zero, so returns are difficult to define. In this case it is standard to represent the P&L, not the return, as a linear sum. Here the coefficients will be the portfolio holdings and the risk factors are the P&L on each stock, and we assume the holdings are kept constant over the risk horizon, i.e. that the portfolio is not rebalanced.
This section demonstrates the flexibility of Monte Carlo simulation by applying it to the measurement of scenario VaR for a simple equity portfolio. Of course, volatility clustering is also an important feature of equity portfolios, and could easily be added by using EWMA or GARCH covariance matrices in a multi-step simulation framework, as will be demonstrated for currency portfolios in Example IV.4.14. However, here we want to focus on applying the unconditional normal mixture returns model that was described in Section IV.4.4. This framework is very useful for equity portfolios, because a mixture of two multivariate normal distributions can capture the leptokurtosis and asymmetry that characterize equity markets. We could use a mixture of three or more multivariate normal distributions, but two is often sufficient.
The analyst is required to assign, subjectively, a probability π to a market crash during the risk horizon. During such a crash he has a scenario for a negative excess return on each stock in the portfolio, and we denote these returns by the vector μ1. The stock returns also become much more volatile and highly correlated, and the analyst summarizes this by assuming some covariance matrix Ω1 that he believes best reflects ‘market crash’ conditions. But with probability 1 − π ‘ordinary’ market conditions will prevail throughout the risk horizon, and these conditions are captured by the expected excess return vector μ2 and covariance matrix Ω2. Any of these parameters may, if the analyst wishes, be estimated using historical data.
We know from Section IV.4.4.1 that the risk factor return distribution will take the form
![]()
Now given N independent standard normal simulations, we apply μ1 and Ω1 to π N of the simulations and μ2 and Ω2 to the remaining (1 − π)N simulations. Hence, we obtain simulations for the stock returns, or the risk factor returns, that are used in the estimation of Monte Carlo VaR. This approach is illustrated in the next example.
EXAMPLE IV.4.13: MONTE CARLO VAR WITH NORMAL MIXTURE DISTRIBUTIONS
Suppose an equally weighted portfolio contains three stocks having the regime dependent returns parameters shown in Table IV.4.10. Based on a normal mixture distribution for the stocks' returns with these parameters, compute the 100α% 10-day Monte Carlo VaR for α =5%, 1% and 0.1%. Compare these results with the multivariate normal Monte Carlo VaR when the stocks have expected returns, volatilities and correlations equal to their expected values under the two-regime distribution.
Table IV.4.10 Parameters of normal mixture distribution for three stocks
SOLUTION We perform the Monte Carlo simulation in two stages. First we take a random draw on a Bernoulli variable with success probability 1%. Then we sample from the first multivariate normal, representing the crash regime, if the result is a ‘success’ and otherwise we sample from the ‘ordinary’ multivariate normal. For the comparison with a straightforward multivariate normal VaR, we use the parameters shown in Table IV.4.11, i.e. the expected values of the parameters under the regime distribution.
Table IV.4.11 Parameters of normal distribution for three stocks
Monte Carlo VaR estimates, expressed as a percentage of the portfolio value and based on one set of 10,000 simulations, are displayed in Table IV.4.12. As expected, the higher the confidence levels, the greater the difference between the normal mixture VaR and the VaR based on a normal distribution, because the normal mixture VaR is based on a negatively skewed and leptokurtic distribution. Because the probability of a crash is very small the normal mixture distribution has extremely long thin tails. The effect is to reduce the VaR, compared with the normal VaR, at the 5% and 1% quantiles but to increase it tremendously at the 0.1% quantile.
Table IV.4.12 Comparison of normal and normal mixture Monte Carlo scenario VaR

Since the VaR at extreme quantiles is significantly influenced by a very small probability of a crash, the above example suggests that normal mixtures could be applied to stress testing portfolios in a VaR framework. In fact, this is only one of many ways that VaR models can be used for scenario analysis, as we shall see in Section IV.7.3.2.
IV.4.5.4 Currency Portfolios: VaR with Volatility Clustering
Currency portfolios have the simplest possible risk factor mapping. Given nominal exposures n = (N1,…, Nk)′ to k foreign exchange rates with returns x = (X1,…, Xk)′, the portfolio P&L is just n′x.52
Before implementing this risk factor mapping in the next example, we ask: what are the important features to capture in multivariate forex return distributions? The unconditional marginal distributions may be more symmetric than the return distributions for most other financial assets, but they still have a high leptokurtosis. What features should we include in the conditional marginals, and how should we model conditional and unconditional dependence between forex returns?
In every financial market skewness and leptokurtosis in unconditional return distributions have two main sources: they stem from occasional large jumps in prices, and from volatility clustering. Large price jumps introduce skewness and leptokurtosis into the conditional distributions. But even when the conditional distributions are fairly close to normality, if they have pronounced asymmetric volatility clustering, the unconditional distributions will still be skewed and leptokurtic. The dependency between two financial asset returns also has conditional and unconditional features. Asymmetric dependence may be captured using a copula. But even when the dependency is symmetric and is captured by a correlation matrix, we should still ensure that this is time-varying, so that correlation clustering can be modelled.
In the next example we show how to estimate Monte Carlo VaR for a portfolio of two US dollar exchange rates. We shall capture both sources of leptokurtosis, by using multivariate Student t conditional distributions and a symmetric multivariate GARCH model to capture volatility and correlation clustering. This model entails a multi-step framework for the simulations, as described in Section IV.4.3. To estimate VaR with volatility clustering we must set a value for the current return on each forex rate, at the time that the VaR is measured. We shall call this return the ‘shock’ for short.
Asymmetric GARCH models and skewed multivariate conditional distributions may be appropriate, especially in equity markets, but our example examines forex portfolios, which have less asymmetry than equity portfolios. Besides, we prefer to use a relatively simple specification for the risk factor returns model because our main purpose is to illustrate the framework as clearly as possible, without too many technicalities.
EXAMPLE IV.4.14: VAR WITH VOLATILITY AND CORRELATION CLUSTERING
A bank has $15 million exposure to forex 1 and $10 million exposure to forex 2. A simple symmetric bivariate GARCH model of the daily log returns on the two forex rates is estimated and the parameters are shown in Table IV.4.13. Use a multi-step Monte Carlo framework, with volatility and correlation clustering based on this bivariate GARCH model, to estimate the 1% 10-day VaR of the portfolio following shocks of 1%, 3% and 5%, assuming there is the same shock to each forex rate. In each case compare the results obtained when we assume the conditional distributions are bivariate normal, with those obtained under the assumption that the conditional distributions are bivariate Student t with 6 degrees of freedom. Also, use the model with constant volatility and correlation as a benchmark for your results.
Table IV.4.13 Bivariate GARCH model parameters
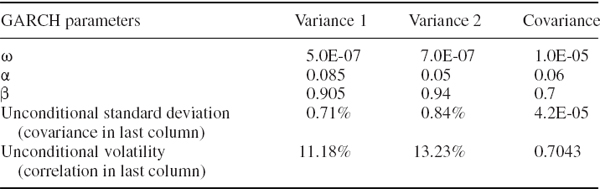
SOLUTION To fully understand the rather complex spreadsheet for this problem, readers are advised to familiarize themselves with some other spreadsheets first: the multi-step simulation model of Example IV.4.6, the correlated normal and Student t simulations of Examples IV.4.8 and IV.4.9, and the ‘Diag Vech’ spreadsheet in the GARCH_Simulations_II.4.xls workbook.
For each shock we shall compare results based on the same set of 10,000 standard uniform simulations over 10 consecutive days. These simulations, one for each forex return, are shown in the spreadsheet labelled ‘VaR’ in the workbook for this example. Then two further spreadsheets have an identical structure, except for two sets of ten columns which contain standard normal simulations in one spreadsheet and standardized Student t simulations in the other. The algorithm in each spreadsheet is as follows:
- Generate independent standard normal (or standardized Student t) returns for each day and for each forex rate. (The simulations on the second forex rate will subsequently be adjusted, as explained in step 4, to capture the conditional dependency.)
- Use the GARCH parameters to simulate a path for each GARCH variance over the 10-day period, following the shock that we have assumed.
- Also simulate the GARCH covariance over the 10-day period, and on each day divide this by square root of the product of the GARCH variances to obtain the GARCH correlation simulated on each day.
- Use the GARCH correlation to adjust the return on forex 2 that was simulated at step 1, changing it so that instead of being independent of the simulation for forex 1, they are correlated with the GARCH correlation. That is, if from step 1 we have independent returns f1t and f2t simulated at time t, and if
 t is the GARCH correlation simulated at time t, then set
t is the GARCH correlation simulated at time t, then set
Now f1t and
 2t will have correlation
2t will have correlation  t.
t. - Next, multiply f1t by the square root of the GARCH variance for forex 1 at time t, and multiply
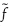 2t by the square root of the GARCH variance for forex 2 at time t. This gives two paths for log returns over 10 days, one for each forex rate, which display both volatility and correlation clustering.
2t by the square root of the GARCH variance for forex 2 at time t. This gives two paths for log returns over 10 days, one for each forex rate, which display both volatility and correlation clustering. - Sum the log returns over each path to obtain a 10-day log return on each forex rate, and then use the risk factor mapping described at the beginning of this section to obtain one simulated 10-day P&L for the portfolio.
- Repeat N times, and then the 100α% 10-day VaR estimate is −1 times the 100α% quantile of the distribution based on the N simulated 10-day P&Ls.
We also simulate paths under the assumption that parameters are constant, at the unconditional values shown in Table IV.4.13. As we have shown in Section IV.4.3, multi-step methods are unnecessary in this case. However, we do this to provide a benchmark against which to interpret our results, which for comparison are based on the same standard uniform simulations as those used in the conditional model.
In the first row of Table IV.4.14 we show the results based on constant volatility and correlation, and in the second row the results are based on the volatility and correlation clustering that is defined by the bivariate GARCH model. For each shock (1%, 3% and 5%) we display the result based on both normal and Student t marginal distributions for the forex returns, the Student t distributions each having 6 degrees of freedom.
Table IV.4.14 Comparison of normal GARCH and Student t GARCH VaR
The GARCH VaR estimates are always greater than the estimates based on our benchmark model with no volatility and correlation clustering. The bigger the shock, the greater the difference between the GARCH and the constant parameter VaR estimates. The difference is also more pronounced when we assume the return distributions are Student t with 6 degrees of freedom. We see that the VaR estimate could easily be doubled or halved, simply by changing our assumptions about the risk factor returns model.
These conclusions are fairly obvious. We do not need to build a complex Excel workbook to demonstrate them. But the aim of this above example, as with every example in this chapter, is to provide readers with an Excel template for building advanced Monte Carlo VaR models. Simple Monte Carlo models, such as those based on i.i.d. normal risk factor returns, are not usually justified, at least for short term risk horizons. Mixture, Student t or copula models with volatility clustering effects are generally thought to be more appropriate for short term VaR estimation.
IV.4.6 SUMMARY AND CONCLUSIONS
The parametric linear VaR model is used when returns are assumed to have a multivariate normal, Student t or normal mixture distribution. So why should we use Monte Carlo VaR for a linear portfolio? The reason is that Monte Carlo VaR is much more flexible than linear VaR. It can be applied with any assumed distribution for risk factor returns. We can also use multi-step Monte Carlo to simulate time-varying risk factor volatilities and correlations, or to account for path-dependent behaviour in options or in contingent cash flows.
Historical VaR has the distinct advantage that it does not need to impose a parametric model on risk factor return distributions. Instead the empirical risk factor return distribution is naturally embedded in the VaR estimate. In the next chapter we shall demonstrate that standard historical simulations have limited application to estimating VaR for option portfolios, but why should we use Monte Carlo VaR in preference to historical VaR for linear portfolios? The reason is that, whatever the portfolio, the limited size of a historical sample places a severe constraint on the accuracy of historical VaR estimates. Standard historical simulation cannot be based on overlapping h-day returns, because this truncates the tail of the P&L distribution. For this reason many practitioners scale up the 1-day historical VaR to an h-day VaR estimate, but this introduces a major model risk in VaR calculations, even for linear portfolios. We can only increase the number of simulations by using a parametric statistical bootstrap, as in filtered historical simulation. However, this is really a hybrid approach, a mixture between historical and Monte Carlo simulation, because it is based on simulations from a parametric, dynamic model for the returns process such as GARCH.
The great advantage of Monte Carlo VaR is that historical data place no restrictions on simulations. We can simulate as much data on risk factor returns as we like (and the more simulations used the more accurate the VaR estimate) since there are relatively few computational time constraints with the powerful computers used today. With Monte Carlo methods, the simulations do not necessarily have any basis in historical data. For instance, in scenario VaR calculations the analyst could use his own personal views about the values of the parameters of the risk factor returns model.
The first part of this chapter gave a brief survey of the sampling methods that form the basis of a Monte Carlo VaR estimate. We provided examples of pseudo-random number generation using linear congruential generators and introduced some basic advanced sampling methods and variance reduction techniques, again with numerical examples in Excel. Because sampling error can be controlled, the main source of model risk in Monte Carlo VaR models lies with the specification of the statistical model for the risk factor returns. These models are used to translate standard uniform simulations into risk factor returns simulations, and then the risk factor mapping is used to translate these into simulations on the portfolio returns or P&L. Finally, we derive the Monte Carlo VaR from a quantile of the simulated portfolio returns or P&L distribution.
Much of this chapter is devoted to developing adequate statistical models for static and dynamic risk factor returns, because this is a major source of model risk in Monte Carlo VaR estimates. Yet it requires considerable skill to develop a suitable risk factor returns model, even for a linear portfolio where we might feasibly assume that risk factor returns have i.i.d. multivariate normal or i.i.d. multivariate Student t distributions. In that case we can use an h-day covariance matrix to transform independent draws from a standard normal or standardized Student t distribution into correlated h-day returns on the risk factors. We have also shown how more complex returns models can be used to estimate Monte Carlo VaR. For instance, the risk factors may have different marginal distributions and their dependency may be captured by a copula.53 We also explained how to design multi-step Monte Carlo for linear portfolios with risk factors that exhibit volatility and correlation clustering. All these features have been illustrated, for teaching purposes, using Excel workbooks.
1 This is an Excel option, found in the Tools menu of Excel 2003 or in Excel 2007 under Options | Formulas from the Excel Office button. Press F9 to repeat the calculations manually. Note that calculations are repeated on all open workbooks each time F9 is pressed.
2 Risk factor model selection requires very thorough backtesting, as described in Chapter IV.6, and this can entail months of research.
3 See http://support.microsoft.com/kb/828795 for more details about their random number generator.
4 For instance, 2 ≡ 5mod(3).
5 We call c a ‘primitive root’ of m if m − 1 is the smallest positive integer value of n such that cn ≡ 1mod (m). In our example therefore, 212 ≡ 1mod (13) and n = 12 is the lowest power n of 2 such that 13 divides 2n − 1.
6 Marin Mersenne (1588–1648) was a French philosopher, mathematician and music theorist. For more details, see http://en.wikipedia.org/wiki/Mersenne.
7 For instance, N = 100, 000 or 1,000,000. Smaller values for N are usually acceptable only if some variance reduction technique is applied, as we shall see presently.
8 Low discrepancy sequences are sometimes called quasi-random numbers. See Glasserman (2004, Section 5.1.1) for several formal definitions of discrepancy.
9 In Section IV.4.2.5 we see that the antithetic sampling realization (u, 1 − u) on a standard uniform variable translates into a realization (F−1(u), F−1(1 − u)) where F is the distribution function for our risk factor. But if F is symmetric then F−1(1 − u) =− F−1(u), so we have a set of antithetic pairs ![]() that still have correlation −1.
that still have correlation −1.
10 This is why when we take n = 10 in Example IV.4.3, each set of simulations has a sample mean of exactly 0.5 and the standard deviation of the sample means is zero.
11 A linear estimator is an estimator that is a linear function of the random variables.
12 For instance, in the above example the first five simulations were all taken from the interval (0, 1/6].
13 In Excel, RAND () generates a standard uniform simulation and, for instance, NORMSINV (RAND ()) generates a simulation Φ−1(u) from a standard normal variable.
14 See Section I.3.3.4 for the specification of the standard normal distribution.
15 For instance, refer to Section I.5.7.5 for details on generating simulations from correlated normal or Student t distributed variables and to Section II.6.7 for simulations on a multivariate distribution, with marginal distributions that may have different parametric forms and where the dependence structure is represented by a copula.
16 In the case of the multivariate normal or Student t distributions, we could simulate realizations of standardized normal or t variables, and then impose the variance as well as the correlation using the Cholesky matrix of the covariance matrix.
17 When these estimates are based on Monte Carlo simulations we call them ‘Monte Carlo VaR’ and ‘Monte Carlo ETL’ for short.
18 As usual, if the α quantile is of the return distribution, the VaR is expressed as a percentage of the portfolio's value, and if the α quantile is of the P&L distribution, the VaR is expressed in value terms.
19 This is for a long exposure to the portfolio – and for a short portfolio the simulated P&L is the current price minus the simulated price.
20 Or, if the simulations are on the asset returns, we obtain the portfolio return using constant portfolio weights.
21 Indeed, for path-dependent products we may also wish to simulate portfolio values at a higher frequency than daily.
22 However, due to sampling variation, the two results are not the same, as demonstrated in the spreadsheet for Figure IV.4.5.
23 Thus the underlying price density is the same shape as before, but it has been shifted to the left because the drift has been reduced.
24 This is because a change of drift in the price process is a change in the measure. An option price is a discounted expectation (which is why we can obtain the simulated price as an average) and we use the subscript on the expectation operator to denote the measure under which the expectation is taken. In this case we have two measures, the original price distribution P and the price distribution Q which is used to estimate the price after changing the drift so that more of the paths avoid the barrier. See Section III.3.2.3 for further details.
25 This ratio is called the likelihood ratio, or the Radon – Nykodym derivative of the two measures. Further details are given in Section III.3.2.3.
26 In fact, because we used different simulations, and not nearly enough of them for good levels of accuracy, the constant volatility model actually has a lower VaR estimate in the second part of the table.
27 Note that we do not use the caret ‘^’ for the variance here, because the model conditional variances are time-varying in the GARCH framework. In the EWMA framework the true conditional variance is constant, with only its estimates varying over time.
28 Not to be confused with the EWMA λ, which measures the persistence of volatility following a market shock (the GARCH parameter β plays this role); in the EWMA model 1 − λ captures the reaction of volatility to a market shock (the GARCH parameter α plays this role). The GARCH parameter ω affects the unconditional (i.e. long term average) volatility of the GARCH model. Readers should consult Section II.4.2.6 if they require further information on the association between GARCH and EWMA volatility models.
29 The unconditional volatility is derived using the formula for the long term variance given in Section II.4.3.1.
30 For this model set the A-GARCH parameter λ to zero.
31 However, see Alexander et al. (2009) for a quasi-analytic form for the distribution of returns under GARCH processes. Having derived analytic formulae for the first eight moments of the aggregated returns from a very general asymmetric GARCH process, we fit a distribution to h-day returns. The resulting VaR estimates, which are very quick to compute, are very close to those based on simulation.
32 See Section III.1.4.4 for further details and an empirical study.
33 We use version 2.3 of this add-in, which is kindly provided free from http://digilander.libero.it/foxes by Leonardo Volpi of Foxes team, Italy. To install this add-in to Excel 2003, in the Tools menu of Excel click ‘Add-ins’ then ‘Browse’. Find the location of Matrix.xla on your machine, highlight the icon and click OK. Once added in, it remains on your menu of possible add-ins, and unless you deselect it, it will be automatically loaded when you start Excel just like any other add-in. In Excel 2007 use the Excel Office button to find the Excel options, and then browse the add-ins. Note that the software is not supported and, for Vista users, the Help file requires the Windows Help program (WinHlp32.exe) for Windows Vista (as do all help files from earlier Microsoft operating systems!).
34 The differences between portfolio mappings for different types of risk factors were discussed in detail in Chapter III.5 and, if not already clear, this will be clarified in Section IV.4.5 when we provide specific examples for each different type of portfolio.
35 Note that the cumbersome form of the TINV function in Excel requires a conditional statement in these simulations. See Section I.3.5.3 for further details.
36 The excess kurtosis of each marginal is 6/(ν − 4) = 3 when ν = 6.
37 Since the model is linear in the parameters it may be regarded as a special case of multivariate regression. See Section I.4.4 for an introduction. Note that the normality assumption is not required to use OLS, but it is necessary to make inference on the model, for instance about the importance of each explanatory variable as given by the t-ratio. See Section I.4.2 for further details.
38 See Section II.7.4.1 for a numerical method for deriving least squares estimates when the model is a non-linear function of the parameters, such as
![]()
39 By contrast, Monte Carlo simulation is the only reliable method for estimating the VaR for an option portfolio over a risk horizon of more than 1 day, as we demonstrate in the next chapter.
40 Computation time is not an issue with linear VaR in practice, since the linear mapping can be performed in a few microseconds.
41 We can try to scale a 1-day VaR using an approximate scale exponent, but this scaling can be a great source of model risk in historical VaR estimates, especially in option portfolios. If we use overlapping h-day returns on the risk factors, this will distort the tail behaviour of the return distributions, leading to significant error in the VaR estimates at extreme quantiles.
42 See Sections IV.3.2.3, IV.3.2.4 and IV.5.4 for further details about these three approaches to estimating h-day historical VaR.
43 We do not provide an example on commodity portfolios in this section, but these would benefit from all the techniques that we illustrate here. The construction of a non-normal conditional model with GARCH volatility clustering and principal component risk factors, if the portfolio contains commodity forwards or futures of different maturities, is left as an exercise for experienced readers.
44 Or, if we are short the portfolio, the current value minus simulated value represents the P&L.
45 This is the case when the risk factor sensitivities are expressed in value rather than percentage terms.
46 Recall that for cash-flow portfolios the non-linearity of the portfolio P&L is captured by the PV01 sensitivities, so the risk factor mapping is a linear map with respect to interest rates and credit spreads.
47 The PV01 vector is based on an exposure of $1 million at each maturity.
48 The number of principal components used will depend on the required degree of accuracy. For well-behaved yield curves three components are often sufficient to capture 95% of the historical variations in interest rates, but the less well-behaved the yield curve, the more components will be required.
49 Because the risk factors are the principal components and these are uncorrelated.
50 But since we have used only 10,000 unstructured simulations in this example, the result can vary considerably each time the simulations are repeated.
51 However, if β is expressed in value terms then β′x is the portfolio P&L.
52 For instance, if k = 2, n = ($1m, $2m)′ and we simulate x = (5%, 1%)′ then the simulated P&L is $50,000 + $20,000 = $70,000.
53 Experienced readers requiring further details are recommended to consult the path-breaking work of Patton (2008) in this area. Note that Matlab code is available from Andrew Patton's website. (http://www.economics.ox.ac.uk/members/andrew.patton/), and see the copula toolbox in particular.