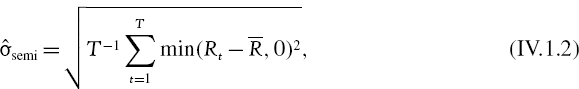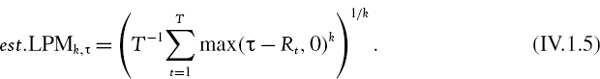IV.1

Value at Risk and Other Risk Metrics

IV.1.1 INTRODUCTION

A market risk metric is a measure of the uncertainty in the future value of a portfolio, i.e. a measure of uncertainty in the portfolio's return or profit and loss (P&L). Its fundamental purpose is to summarize the potential for deviations from a target or expected value. To determine the dispersion of a portfolio's return or P&L we need to know about the potential for individual asset prices to vary and about the dependency between movements of different asset prices. Volatility and correlation are portfolio risk metrics but they are only sufficient (in the sense that these metrics alone define the shape of a portfolio's return or P&L distribution) when asset or risk factor returns have a multivariate normal distribution. When these returns are not multivariate normal (or multivariate Student t) it is inappropriate and misleading to use volatility and correlation to summarize uncertainty in the future value of a portfolio.¹

Statistical models of volatility and correlation, and more general models of statistical dependency called copulas, are thoroughly discussed in Volume II of Market Risk Analysis. The purpose of the present introductory chapter is to introduce other types of risk metric that are commonly used by banks, corporate treasuries, portfolio management firms and other financial practitioners.

Following the lead from both regulators and large international banks during the mid-1990s, almost all financial institutions now use some form of value at risk (VaR) as a risk metric. This almost universal adoption of VaR has sparked a rigorous debate. Many quants and academics argue against the metric because it is not necessarily sub-additive,² which contradicts the principal of diversification and hence also the foundations of modern portfolio theory. Moreover, there is a closely associated risk metric, the conditional VaR, or what I prefer to call the expected tail loss (ETL) because the terminology is more descriptive, that is sub-additive. And it is very simple to estimate ETL once the firm has developed a VaR model, so why not use ETL instead of VaR? Readers are recommended the book by Szegö (2004) to learn more about this debate.

The attractive features of VaR as a risk metric are as follows:

• It corresponds to an amount that could be lost with some chosen probability.
• It measures the risk of the risk factors as well as the risk factor sensitivities.
• It can be compared across different markets and different exposures.
• It is a universal metric that applies to all activities and to all types of risk.
• It can be measured at any level, from an individual trade or portfolio, up to a single enterprise-wide VaR measure covering all the risks in the firm as a whole.
• When aggregated (to find the total VaR of larger and larger portfolios) or disaggregated (to isolate component risks corresponding to different types of risk factor) it takes account of dependencies between the constituent assets or portfolios.

The purpose of this chapter is to introduce VaR in the context of other ‘traditional’ risk metrics that have been commonly used in the finance industry. The assessment of VaR is usually more complex than the assessment of these traditional risk metrics, because it depends on the multivariate risk factor return distribution and on the dynamics of this distribution, as well as on the risk factor mapping of the portfolio. We term the mathematical models that are used to derive the risk metric, the risk model and the mathematical technique that is applied to estimate the risk metrics from this model (e.g. using some type of simulation procedure) the resolution method.

Although VaR and its related measures such as ETL and benchmark VaR have recently been embraced almost universally, the evolution of risk assessment in the finance industry has drawn on various traditional risk metrics that continue to be used alongside VaR. Broadly speaking, some traditional risk metrics only measure sensitivity to a risk factor, ignoring the risk of the factor itself. For instance, the beta of a stock portfolio or the delta and gamma of an option portfolio are examples of price sensitivities. Other traditional risk metrics measure the risk relative to a benchmark, and we shall be introducing some of these metrics here, including the omega and kappa indices that are currently favoured by many fund managers.³

The outline of the chapter is as follows. Section IV.1.2 explains how and why risk assessment in banking has evolved separately from risk assessment in portfolio management. Section IV.1.3 introduces a number of downside risk metrics that are commonly used in portfolio management. These are so called because they focus only on the risk of underperforming a benchmark, ignoring the ‘risk’ of outperforming the benchmark.

The reminder of the chapter focuses on VaR and its associated risk metrics. We use the whole of Section IV.1.4 to provide a thorough definition of market VaR. For instance, when VaR is used to assess risks over a long horizon, as it often is in portfolio management, we should adjust the risk metric for any difference between the expected return and the risk free or benchmark return.⁴ However, a non-zero expected excess return has negligible effect when the risk horizon for the VaR estimate is only a few days, as it usually is for banks, and so some texts simply ignore this effect.

Section IV.1.5 lays some essential foundations for the rest of this book by stating some of the basic principles of VaR measurement. These principles are illustrated with simple numerical examples where the only aim is to measure the VaR

• at the portfolio level,⁵ and where
• the portfolio returns are independent and identically distributed (i.i.d.).

Section IV.1.6 begins by stressing the importance of measuring VaR at the risk factor level: without this we could not quantify the main sources of risk. This section also includes two simple examples of measuring the systematic VaR, i.e. the VaR that is captured by the entire risk factor mapping.⁶ We consider two examples: an equity portfolio that has been mapped to a broad market index and a cash-flow portfolio that has been mapped to zero-coupon interest rates at standard maturities.

Section IV.1.7 discusses the aggregation and disaggregation of VaR. One of the many advantages of VaR is that is can be aggregated to measure the total VaR of larger and larger portfolios, taking into account diversification effects arising from the imperfect dependency between movements in different risk factors. Or, starting with total risk factor VaR, i.e. systematic VaR, we can disaggregate this into stand-alone VaR components, each representing the risk arising from some specific risk factors.⁷ Since we take account of risk factor dependence when we aggregate VaR, the total VaR is often less than the sum of the stand-alone VaRs. That is, VaR is often sub-additive. But it does not have to be so, and this is one of the main objections to using VaR as a risk metric. We conclude the section by introducing marginal VaR (a component VaR that is adjusted for diversification, so that the sum of the marginal VaRs is approximately equal to the total risk factor VaR) and incremental VaR (which is the VaR associated with a single new trade).

Section IV.1.8 introduces risk metrics that are associated with VaR, including the conditional VaR risk metric or expected tail loss. This is the average of the losses that exceed the VaR. Whilst VaR represents the loss that we are fairly confident will not be exceeded, ETL tells us how much we would expect to lose given that the VaR has been exceeded. We also introduce benchmark VaR and its associated conditional metric, expected shortfall (ES). The section concludes with a discussion on the properties of a coherent risk metric. ETL and ES are coherent risk metrics, but when VaR and benchmark VaR are estimated using simulation they are not coherent because they are not sub-additive.

Section IV.1.9 introduces the three fundamental types of resolution method that may be used to estimate VaR, applying each method in only its most basic form, and to only a very simple portfolio. After a brief overview of these approaches, which we call the normal linear VaR, historical VaR and normal Monte Carlo VaR models, we present a case study on measuring VaR for a simple position of $1000 per point on an equity index. Our purpose here is to illustrate the fundamental differences between the models and the reasons why our estimates of VaR can differ so much depending on the model used. Section IV.1.10 summarizes and concludes.

Volume IV of the Market Risk Analysis series builds on the three previous volumes, and even for this first chapter readers first require an understanding of:⁸

• quantiles and other basic concepts in statistics (Section I.3.2);
• the normal distribution family and the standard normal transformation (Section I.3.3.4);
• stochastic processes in discrete time (Section I.3.7.1);
• portfolio returns and log returns (Section I.1.4);
• aggregation of log returns and scaling of volatility under the i.i.d. assumption (Section II.3.2.1);
• the matrix representation of the expectation and variance of returns on a linear portfolio (Section I.2.4);
• univariate normal Monte Carlo simulation and how it is performed in Excel (Section I.5.7).
• risk factor mappings for portfolios of equities, bonds and options, i.e. the expression of the portfolio P&L or return as a function of market factors that are common to many portfolios (e.g. stock index returns, or changes in LIBOR rates) and which are called the risk factors of the portfolio (Section III.5).

There is a fundamental distinction between linear and non-linear portfolios. A linear portfolio is one whose return or P&L may be expressed as a linear function of the returns or P&L on its constituent assets or risk factors. All portfolios except those with options or option-like structures fall into the category of linear portfolios.

It is worth repeating here my usual message about the spreadsheets on the CD-ROM. Each chapter has a folder which contains the data, figures, case studies and examples given in the text. All the included data are freely downloadable from websites, to which references for updating are given in the text. The vast majority of examples are set up in an interactive fashion, so that the reader or tutor can change any parameter of the problem, shown in red, and then view the output in blue. If the Excel data analysis tools or Solver are required, then instructions are given in the text or the spreadsheet.

IV.1.2 AN OVERVIEW OF MARKET RISK ASSESSMENT

In general, the choice of risk metric, the relevant time horizon and the level of accuracy required by the analyst depend very much on the application:

• A typical trader requires a detailed modelling of short-term risks with a high level of accuracy.
• A risk manager working in a large organization will apply a risk factor mapping that allows total portfolio risk to be decomposed into components that are meaningful to senior management. Risk managers often require less detail in their risk models than traders do. On the other hand, risk managers often want a very high level of confidence in their results. This is particularly true when they want to demonstrate to a rating agency that the company deserves a good credit rating.
• Senior managers that report to the board are primarily concerned with the efficient allocation of capital on a global scale, so they will be looking at long-horizon risks, taking a broad-brush approach to encompass only the most important risks.

The metrics used to assess market risks have evolved quite separately in banking, portfolio management and large corporations. Since these professions have adopted different approaches to market risk assessment we shall divide our discussion into these three broad categories.

IV.1.2.1 Risk Measurement in Banks

The main business of banks is to accept risks (because they know, or should know, how to manage them) in return for a premium paid by the client. For retail and commercial banks and for many functions in an investment bank, this is, traditionally, their main source of profit. For instance, banks write options to make money on the premium and, when market making, to make profits from the bid–ask spread. It is not their business, at least not their core business, to seek profits through enhanced returns on investments: this is the role of portfolio management. The asset management business within a large investment bank seeks superior returns on investments, but the primary concern of banks is to manage their risks.

A very important decision about risk management for banks is whether to keep the risk or to hedge at least part of it. To inform this decision the risk manager must first be able to measure the risk. Often market risks are measured over the very short term, over which banks could hedge their risks if they chose to, and over a short horizon it is standard to assume the expected return on a financial asset is the risk free rate of return.⁹ So modelling the expected return does not come into the picture at all. Rather, the risk is associated with the unexpected return – a phrase which here means the deviation of the return about its expected value – and the expected rate of return is usually assumed to be the risk free rate.

Rather than fully hedging all their risks, traders are usually required to manage their positions so that their total risk stays within a limit. This limit can vary over time. Setting appropriate risk limits for traders is an important aspect of risk control. When a market has been highly volatile the risk limits in that market should be raised. For instance, in equity markets rapid price falls would lead to high volatility and equity betas could become closer to 1 if the stock's market correlation increased. If a proprietary trader believes the market will now start to rise he may want to buy into that market so his risk limits, based on either volatility or portfolio beta, should be raised.¹⁰

Traditionally risk factor exposures were controlled by limiting risk factor sensitivities. For instance, equity traders were limited by portfolio beta, options traders operated under limits determined by the net value Greeks of their portfolio, and bond traders assessed and managed risk using duration or convexity.¹¹ However, two significant problems with this traditional approach have been recognized for some time.

The first problem is the inability to compare different types of risks. One of the reasons why sensitivities are usually represented in value terms is that value sensitivities can be summed across similar types of positions. For instance, a value delta for one option portfolio can be added to a value delta for another option portfolio;¹² likewise the value duration for one bond portfolio can be added to the value duration for another bond portfolio. But we cannot mix two different types of sensitivities. The sum of a value beta, a value gamma and a value convexity is some amount of money, but it does not correspond to anything meaningful. The risk factors for equities, options and bonds are different, so we cannot add their sensitivities. Thus, whilst value sensitivities allow risks to be aggregated within a given type of trading activity, they do not aggregate across different trading units. The traditional sensitivity-based approach to risk management is designed to work only within a single asset class.

The second problem with using risk factor sensitivities to set traders' limits is that they measure only part of the risk exposure. They ignore the risks due to the risk factors themselves. Traders cannot influence the risk of a risk factor, but they can monitor the risk factor volatility and manage their systematic risk by adjusting their exposure to the risk factor.¹³

In view of these two substantial problems most large banks have replaced or augmented the traditional approach. Many major banks now manage traders’ limits using VaR and its associated risk metrics.

New banking regulations for market risk introduced in 1996 heralded a more ‘holistic’ approach to risk management. Risk is assessed at every level of the organization using a universal risk metric, such as VaR, i.e. a metric that applies to all types of exposures in any activity; and it relates not only to market risks, but also to credit and operational risks. Market VaR includes the risk arising from the risk factors as well as the factor sensitivities; it can be aggregated across any exposures, taking account of the risk factor correlations (i.e. the diversification effects) to provide an enterprise-wide risk assessment; and it allows risks to be compared across different trading units.¹⁴ As a result most major banks have adopted VaR, or a related measure such as conditional VaR, to assess the risks of their operations at every level, from the level of the trader to the entire bank.

Banking risks are commonly measured in a so-called ‘bottom-up’ framework. That is, risks are first identified at the individual position level; then, as positions are aggregated into portfolios, we obtain a measure of portfolio risk from the individual risks of the various positions. As portfolios are aggregated into larger and larger portfolios – first aggregating all the traders' portfolios in a particular trading unit, then aggregating across all trading units in a particular business line, then aggregating over all business lines in the bank – the risk manager in a bank will aggregate the portfolio's risks in a similar hierarchy. A further line of aggregation occurs for banks with offices in different geographical locations.

IV.1.2.2 Risk Measurement in Portfolio Management

One of the reasons why risk assessment in banking has developed so rapidly is the impetus provided by the new banking regulations during the 1990s. Banks are required by regulators to measure their risks as accurately as possible, every day, and to hold capital in proportion to these risks. But no such regulations have provided a catalyst for the development of good risk management practices in the fund management industry. The fund manager does have a responsibility to report risks accurately, but only to his clients. As a result, in the first few years of this century major misconceptions about the nature of risk relative to a benchmark still persisted amongst some major fund managers.

Until the 1990s most funds were ‘passive’, i.e. their remit was merely to track a benchmark. During this time an almost universal approach to measuring risk relative to a benchmark was adopted, and this was commonly called the tracking error. Most managers were not allowed to sell short,¹⁵ for fear of incurring huge losses if one of the shares that was sold short dramatically rose in price; clients used to limit mutual fund managers to long-only positions on a relatively small investment universe.¹⁶

Then, during the 1990s actively managed funds with mandates to outperform a benchmark became popular. So, unlike banking, in portfolio management risks are usually measured relative to a benchmark set by the client. However, as portfolio managers moved away from passive management towards the so-called alpha strategies that are commonly used today, problems arose because the traditional control ranges which limited the extent to which the portfolio could deviate from the benchmark were dropped and many large fund managers used the tracking error as a risk metric instead. But tracking error is not an appropriate risk metric for actively managed funds.¹⁷

Also, with the very rapid growth in hedge funds that employ diverse long-short strategies on all types of investment universe, the risks that investors face have become very complex because hedge fund portfolio returns are highly non-normal. Hence, more sophisticated risk measurement tools have recently been developed. Today there is no universal risk metric for the portfolio management industry but it is becoming more and more common to use benchmark VaR and its associated risk metrics such as expected shortfall.

In portfolio management the risk model is often based on the expected returns model, which itself can be highly developed. As a result the risk metrics and the performance metrics are inextricably linked. By contrast, in banks the expected return, after accounting for the normal cost of doing business, is most often set equal to the risk free rate.

Another major difference between risk assessment in banking and in portfolio management is the risk horizon, i.e. the time period over which the risk is being forecast. Market risk in banking is assessed, at least initially, over a very short horizon. Very often banking risks are forecast at a daily frequency. Indeed, this is the reason why statistical estimates and forecasts of volatilities, correlations and covariance matrices are usually constructed from daily data. Forecasts of risks over a longer horizon are also required (e.g. 1-year forecasts are needed for the computation of economic capital) but in banking these are often extrapolated from the short-term forecasts. But market risk in portfolio management is normally forecast over a much longer horizon, often 1 month or more. This is linked to the frequency of risk reports that clients require, to data availability and to the fact that the risk model is commonly tied to the returns model, which often forecasts asset returns over a 1-month horizon.

IV.1.2.3 Risk Measurement in Large Corporations

The motivation for good financial risk management practices in large corporations is the potential for an increase in the value of the firm and hence the enhancement of value for shareholders and bondholders. Also, large corporations have a credit rating that affects the public value of their shares and bonds, and the rating agency requires the risk management and capitalization of the firm to justify its credit rating. For these two reasons the boards and senior managements of large corporations have been relatively quick to adopt the high risk management standards that have been set by banks.

Unlike portfolio management, market risks for corporations are not usually measured relative to a benchmark. Instead, risks are decomposed into:

• idiosyncratic or reducible risk which could be diversified away by holding a sufficiently large and diversified portfolio; and
• undiversifiable, systematic or irreducible risk, which is the risk that the firm is always exposed to by choosing to invest in a particular asset class or to operate in a particular market.

Like banks, the expected returns to various business lines in a major corporation are usually modelled separately from the risks. The expected return forecasts are typically based on economic models for P&L predictions based on macroeconomic variables such as inflation, interest rates and exchange rates. Like banks, corporations will account for the normal ‘cost’ of doing business, with any expected losses being provisioned for in the balance sheet. Hence, from the point of view of the risk manager in a corporate treasury, the expected returns are taken as exogenous to the risk model.

The financial risks taken by a large corporation are typically managed using economic capital. This is a risk adjusted performance measure which does not necessarily have anything to do with ordinary capital.¹⁸ The risk part of the risk adjusted performance measure is very commonly measured using a quantile risk metric such as VaR, or conditional VaR, to assess the market, credit and ‘other’ risks of:

• individual positions;
• positions in a trading book;
• trading books in the ‘desk’;
• desks in a particular activity or ‘business unit’;
• business units in the firm.

That is, the risk assessment proceeds from the bottom up, just as it does in a bank. Risks (and returns) are first assessed at the most elemental level, often instrument by instrument, and according to risk type, i.e. separately for market, credit and other risks such as operational risks. Then, individual positions are progressively aggregated into portfolios of similar instruments or activities, these are aggregated up to the business units, and then these are aggregated across all business units in the firm. Then, usually only at the very end, VaR is aggregated across the major types of risks to obtain a global representation of risks at the company or group level.

Expected returns are also assessed at the business unit level, and often also at the level of different types of activities within the business unit. The economic capital can thus be calculated at a fairly disaggregated level, and used for risk budgeting of the corporation's activities. To provide maximum shareholder value, the firm will seek to leverage those activities with the best risk adjusted performance and decrease the real capital allocation to activities with the worst risk adjusted performance, all else being equal.

The rating agency will assess the capitalization of the entire corporation. To justify its credit rating the corporation must demonstrate that it has a suitably low probability of default during the next year. As shown in Section IV.8.3.1, this probability is related to the total VaR of the firm, i.e. the sum of the market, credit and operational VaR over all the firm's activities. For instance, the AA credit rating corresponds to a 0.03% default probability over a year. This means that to obtain this credit rating the corporation may need to hold sufficient capital to cover the 99.97% total VaR at a 1-year horizon.

IV.1.3 DOWNSIDE AND QUANTILE RISK METRICS

In this section we introduce the downside risk metrics that are popular for portfolio management. A downside risk metric is one that only focuses on those returns that fall short of a target or threshold return. The target or threshold return can be the benchmark return (appropriate for a passive fund) or some percentage above the benchmark return (appropriate for an active fund). Downside risk metrics are now common in active risk management, and there are a large number of possible risk metrics to choose from which are described below.

IV.1.3.1 Semi-Standard Deviation and Second Order Lower Partial Moment

The semi-standard deviation is the square root of the semi-variance, a concept introduced by Markovitz (1959). Semi-variance is a measure of the dispersion of only those realizations on a continuous random variable X that are less than the expectation of X.¹⁹ It is defined as

But since E(min(X − E(X), 0)) ≠ 0,

Hence, the terms semi-variance and semi-standard deviation are misnomers, even though they are in common use.

The ex post semi-standard deviation that is estimated from a sample {R₁,…, R_T} of T returns is

where is the sample mean return. Like most risk metrics, including the other lower partial moment metrics that we define in the next section, this is normally quoted in annualized terms. A numerical example is provided below.

We can extend the operator (IV.1.1) to the case where a target or threshold return τ is used in place of the expected return. We call this the lower partial moment (LPM) of order 2, or second order lower partial moment, and denote it LPM_2,τ. The following example illustrates how an ex post estimate may be calculated.

EXAMPLE IV.1.1: SEMI-STANDARD DEVIATION AND SECOND ORDER LPM

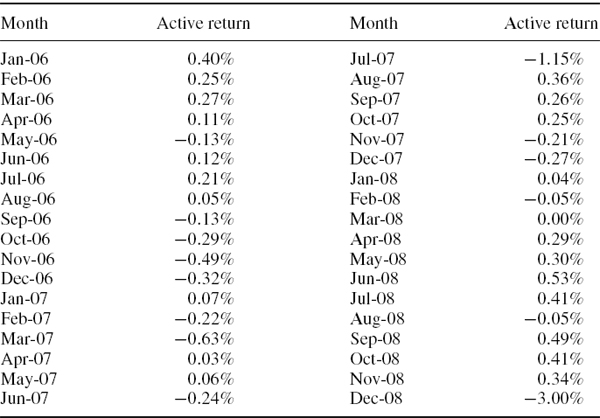
A historical sample of 36 active returns on a portfolio is shown in Table IV.1.1. Calculate (a) the semi-standard deviation and (b) the second order LPM relative to a threshold active return of 2% per annum.

Table IV.1.1 Active returns

SOLUTION The spreadsheet for this example includes a column headed min (AR_t − x, 0) where AR_t is the active return at time t and where

(a) x is the sample mean active return (−0.03%) for the semi-standard deviation, and

(b) x = 0.165% for the LPM. Remember the active returns are monthly, so the target active return of 2% per annum translates into a target of 0.165% per month.

Dividing the sum of the squared excess returns by 36, multiplying by 12 and taking the square root gives the value in annualized terms: 1.81% for the semi-standard deviation and 2.05% for the second order LPM.

IV.1.3.2 Other Lower Partial Moments

More generally LPMs of order k can be defined for any positive k. The LPM operator is:

where τ is some target or threshold return and k is positive, but need not be a whole number.²⁰ For instance the LPM of order 1, which is also called the regret, is

It follows immediately from (IV.1.4) that the regret operator is the expected pay-off to a put option with strike equal to the target return τ. So, like any put option, it has the intuitive interpretation of an insurance cost.²¹ It is the cost of insuring the downside risk of a portfolio. Like semi-standard deviation, regret is able to distinguish ‘good risk’ from ‘bad risk’.

As k increases, the kth order LPM places more weight on extremely poor returns. An ex post estimate of an LPM based on a sample {R₁,…, R_T} of T returns is

Note that LPM_3,0 is sometimes called the semi-skewness and LPM_4,0 is sometimes called the semi-kurtosis.

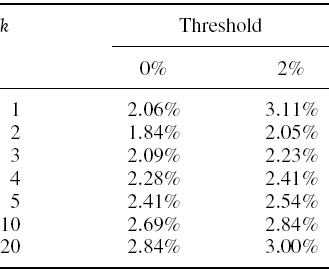
EXAMPLE IV.1.2: LPM RISK METRICS

Calculate the kth order LPMs for k = 1, 2, 3, 4, 5, 10 and 20 based on the sample of active returns in Example IV.1.1 and using (a) a threshold active return of 0%; and (b) a threshold active return of 2% per annum.

SOLUTION The calculations are very similar to (b) in the previous example, except that this time we use a power k of the series on max (τ − R_t, 0) and take the kth root of the result. By changing the threshold for different values of k in the spreadsheet the reader will see that increasing the threshold increases the LPM, and for thresholds of 0% and 2% we obtain the results shown in Table IV.1.2. For k ≥ 2, LPM measures also increase with k. However, this is not a general rule, it is because of our particular sample: as the order increases the measures put progressively higher weights on the very extreme active return of −3% in December 2008, which increases the risk considerably. In general, the behaviour of the LPM metrics of various orders as the threshold changes depends on the specific characteristics of the sample.

Table IV.1.2 LPM of various orders relative to two different thresholds

IV.1.3.3 Quantile Risk Metrics

For any α between 0 and 1 the α quantile of the distribution of a continuous random variable X is a real number x_α such that²²

If we know the distribution function F(x) of X then the quantile corresponding to any given value of α may be calculated as

When a target return is an α quantile of the return distribution the probability of underperforming the target is α. For instance, if the 5% quantile of a return distribution is −3% then we are 95% confident that the return will not be lower than −3%. So a quantile becomes a downside risk metric when α is small, and very often we use standard values such as 0.1%, 1%, 5% or 10% for α.

In market risk, X is usually a return or P&L on an investment, and α is often assumed to be small so that the α quantile corresponds to a loss that we are reasonably certain will not be exceeded. The time horizon over which the potential for underperformance is measured is implicit in the frequency of returns or P&L. For instance, it would be measured over a month if X were a monthly return.

The next example considers a return that is assumed to be i.i.d. and normally distributed, with mean μ and standard deviation σ. Then, for any α ∈(0, 1) applying the standard normal transformation gives

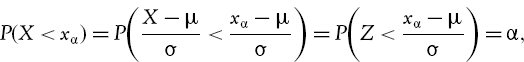
where Z is a standard normal variable. For instance, if a return is normally distributed with mean 10% and standard deviation 25% then the probability of returning less than 5% is 42%, because

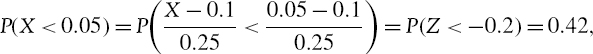
using the fact that −0.2 is the 42% quantile of the standard normal distribution.²³

EXAMPLE IV.1.3: PROBABILITY OF UNDERPERFORMING A BENCHMARK

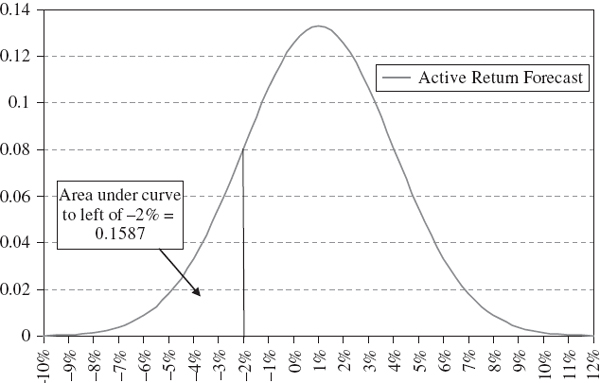
Consider a fund whose future active returns are normally distributed, with an expected active return over the next year of 1% and a standard deviation about this expected active return (i.e. tracking error) of 3%. What is the probability of underperforming the benchmark by 2% or more over the next year?

SOLUTION The density function for the active return is X~N(0.01, 0.0009), as illustrated in Figure IV.1.1. We need to find P(X < −0.02). This is²⁴

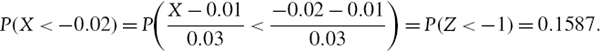
Hence, the probability that this fund underperforms the benchmark by 2% or more is 15.87%. This can be also seen in Figure IV.1.1, as the area under the active return density function to the left of the point −0.02.

Figure IV.1.1 Probability of underperforming a benchmark by 2% or more

In the above example, we found the probability of underperforming the benchmark by knowing that −1 is the 15.87% quantile of the standard normal distribution. In the next section we shall show that the quantile of a distribution of a random variable X is a risk metric that is closely related to VaR. But, unlike LPMs, quantiles are not invariant to changes in the returns that are greater than the target or threshold return. That is, the quantile is affected by ‘good returns’ as well as ‘bad returns’. This is not necessarily a desirable property for a risk metric.

On the other hand, quantiles are easy to work with mathematically. In particular, if Y = h(X), where h is a continuous function that always increases then, for every α, the α quantile y_α of Y is just

where x_α is the α quantile of X. For instance, if Y = ln (X) and the 5% quantile of X is 1 then the 5% quantile of Y is 0, because ln (1) = 0.

IV.1.4 DEFINING VALUE AT RISK

Value at risk is a loss that we are fairly sure will not be exceeded if the current portfolio is held over some period of time. In this section we shall assume that VaR is measured at the portfolio level, without considering the mapping of portfolios to their risk factors. More detailed calculations of VaR based on risk factor mappings are discussed later in this chapter and throughout the subsequent chapters.

IV.1.4.1 Confidence Level and Risk Horizon

VaR has two basic parameters:

• the significance level α (or confidence level 1 − α);
• the risk horizon, denoted h, which is the period of time, traditionally measured in trading days rather than calendar days, over which the VaR is measured.

Often the significance level is set by an external body, such as a banking regulator. Under the Basel II Accord, banks using internal VaR models to assess their market risk capital requirement should measure VaR at the 1% significance level, i.e. the 99% confidence level. A credit rating agency may set a more stringent significance level, i.e. a higher confidence level (e.g. the 0.03% significance or 99.97% confidence level). In the absence of regulations or external agencies, the significance/confidence level for the VaR will depend on the attitude to risk of the user. The more conservative the user, the lower the value of α, i.e. the higher the confidence level applied.

The risk horizon is the period over which we measure the potential loss. Different risks are naturally assessed over different time periods, according to their liquidity.²⁵ For instance, under the Basel banking regulations the risk horizon for the VaR is 10 days. In the absence of internal or external constraints (e.g. regulations) the risk horizon of VaR should refer to the time period over which we expect to be exposed to the position. An exposure to a liquid asset can usually be closed or fully hedged much faster than an exposure to an illiquid asset. And the time it takes to offload the risk depends on the size of the exposure as well as the market liquidity. Some of the most liquid positions are on major currencies and they can be closed or hedged extremely rapidly – usually within hours, even in a crisis. On the other hand private placements are highly illiquid:²⁶ there is no quotation in a market and the only way to sell the issue is to enter into private negotiations with another bank.

When the traders of liquid positions are operating under VaR limits they require real-time, intra-day VaR estimates to assess the effect of any proposed trade on their current level of VaR. The more liquid the risk, the shorter the time period over which the risk needs to be assessed, i.e. the shorter the risk horizon for the VaR model. Liquid risks tend to evolve rapidly and it would be difficult to represent the dynamics of these risks over the long term. Markets also tend to lose liquidity during stressful and volatile periods, when there can be sustained shortages of supply or demand for the financial instrument. Hence, the risk horizon should be increased when measuring VaR in stressful market circumstances.

At the desk level a risk manager often assesses only the liquid market risks, initially at least over a daily risk horizon. This will then be extended to a 10-day risk horizon when using an internal VaR model to assess minimum risk capital for regulatory purposes, and to a longer horizon (e.g. 1 year) for internal capital allocation purposes and for credit rating agencies.

The confidence level also depends on the application. For instance:

• VaR can be used to assess the probability of company insolvency, or the probability of default on its obligations. This depends on the capitalization of the company and the risks of all its positions over a horizon such as 6 months or 1 year. Credit rating agencies would only award a top rating to those companies that can demonstrate a very small probability of default, such as 0.03% over the next year for an AA rated company. So companies aiming for AA rating would apply a confidence level of 99.97% for enterprise-wide VaR over the next year.
• Regulators that review the regulatory capital of banks usually allow this capital to be assessed using an internal VaR model, provided they have approved the model and that certain qualitative requirements have also been met. In this case a 99% confidence level must be applied in the VaR model to assess potential losses over a 2-week risk horizon, i.e. a 1% 10-day VaR. This figure is then multiplied by a factor of between 3 and 4 to obtain the market risk capital requirement.²⁷
• When setting trading limits based on VaR, risk managers may take a lower confidence level and a shorter risk horizon. For instance, the manager may allow traders to operate under a 5% 1-day VaR limit. In this case he is 95% confident that traders will not exceed the VaR overnight while their open positions are left unmanaged. By monitoring the traders’ losses that exceed his VaR limit, further scrutiny could be given to traders who exceed their limit too often. A higher confidence level than 95% or a longer risk horizon than 1 day may give traders too much freedom.

IV.1.4.2 Discounted P&L

VaR assumes that current positions will remain static over the chosen risk horizon, and that we only assess the uncertainty about the value of these positions at the end of the risk horizon.²⁸

Assuming a portfolio remains static means that we are going to assess the uncertainty of the unrealized or theoretical P&L, i.e. the P&L based on a static portfolio. However, the realized or actual P&L accounts for the adjustment in positions as well as the costs of all the trades that are made in practice.

To have meaning today, any portfolio value that might be realized h trading days into the future requires discounting. That is, the P&L should be expressed in present value terms, discounting it using a risk free rate, such as the London Inter Bank Offered Rate (LIBOR).²⁹

Hence, in the following when we refer to ‘P&L’ we mean the discounted theoretical h-day P&L, i.e. the P&L arising from the current portfolio, assumed to be static over the next h trading days, when expressed in present value terms.

Let P_t denote the value of the portfolio and let B_ht denote the price of a discount bond that matures in h trading days, both prices being at the time t when the VaR is measured. The value of the portfolio at some future time t +h, discounted to time t, is B_htP_t+h and the discounted theoretical P&L over a risk horizon of h trading days is therefore

Although we can observe the portfolio value and the value of the discount bond at time t, the portfolio value at time t +h is uncertain, hence the discounted P&L (IV.1.7) is a random variable. Measuring the distribution of this random variable is the first step towards calculating the VaR of the portfolio.

IV.1.4.3 Mathematical Definition of VaR

We have given a verbal definition of VaR as the loss, in present value terms, due to market movements, that we are reasonably confident will not be exceeded if the portfolio is held static over a certain period of time. We cannot say anything for certain about a portfolio's P&L because it is a random variable, but we can associate a confidence level with any loss. For instance, a 5% daily VaR, which corresponds to a 95% level of confidence, is a loss level that we anticipate experiencing with a frequency of 5%, when the current portfolio is held for 24 hours. Put another way, we are 95% confident that the VaR will not be exceeded when the portfolio is held static over 1 day. Put yet another way, we anticipate that this portfolio will lose the 5% VaR or more one day in every 20. Sometimes we quote results in terms of the confidence level 1 − α instead of the significance level α. For instance, if

then we are 99% confident that we would lose no more than $2 million from holding the portfolio for 1 day.

A loss is a negative return, in present value terms. In other words, a loss is a negative excess return. If the portfolio is expected to return the risk free discount rate, i.e. if the expected excess return is zero, then the α% VaR is the α quantile of the discounted P&L distribution. For instance, the 1% VaR of a 1-day discounted P&L distribution is the loss, in present value terms that would only be equalled or exceeded one day in 100. Similarly, a 5% VaR of a weekly P&L distribution is the loss that would only be equalled or exceeded one week in 20.

Assuming the portfolio returns the risk free rate the discounted P&L has expectation zero. The two VaR estimates depicted in Figure IV.1.2 assume this, and also that discounted P&L is normally distributed. In the figure we assume daily P&L has a standard deviation of $4 million and weekly P&L has a standard deviation of $9 million.

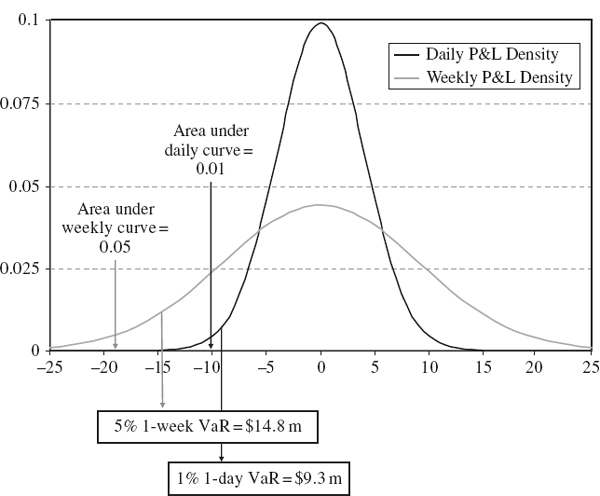
Figure IV.1.2 Illustration of the VaR metric

In mathematical terms the 100α% h-day VaR is the loss amount (in present value terms) that would be exceeded with only a small probability α when holding the portfolio static over the next h days. Hence, to estimate the VaR at time t we need to find the α quantile x_{ht, α} of the discounted h-day P&L distribution. That is, we must find x_{ht, α} such that

and then set VaR_{ht, α} = −x_{ht, α}. We write VaR_{ht, α} when we want to emphasize the time t at which the VaR is estimated. However, in the following chapters we usually make explicit only the dependence of the risk metric on the two basic parameters, i.e. h (the risk horizon) and α (the significance level), and we drop the dependence on t.

When VaR is estimated from a P&L distribution it is expressed in value (e.g. dollar) terms. However, we often prefer to analyse the return distribution rather than the P&L distribution. P&L is measured in absolute terms, so if markets have been trending the P&Ls at different moments in time are not comparable. For instance, a loss of €10,000 when the portfolio has a value of €1 million has quite a different impact than a loss of €10,000 when the portfolio has a value of €10 million. We like to build mathematical models of returns because they are measured in relative terms and are therefore comparable over long periods of time, even when price levels have trended and/or varied considerably. But when the portfolio contains long and short positions, or when the risk factors themselves can take negative values, the concept of a return does not make sense, since the portfolio could have zero value. In that case VaR is measured directly from the distribution of P&L.

When VaR is estimated from a return distribution it is expressed as a percentage of the portfolio's current value. Since the current value of the portfolio is observable it is not a random variable. So we can perform calculations on the return distribution and express VaR as a percentage of the portfolio value and, if required, we can then convert the result to value terms by multiplying the percentage VaR by the current portfolio value.³⁰

In summary, if we define the discounted h-day return on a portfolio as the random variable

then we can find x_{ht, α}, the α quantile of its distribution, that is,

and our current estimate of the 100α% h-day VaR at time t is:

IV.1.5 FOUNDATIONS OF VALUE-AT-RISK MEASUREMENT

In this section we derive a formula for VaR under the assumption that the returns on a linear portfolio are i.i.d. and normally distributed. After illustrating this formula with a numerical example we examine the assumption that the portfolio remains static over the risk horizon and show that this assumption determines the way we should scale the VaR over different risk horizons. Then we explain how the VaR formula should be adjusted when the expected excess return on the portfolio is non-zero. As the expected return deviates more from the risk free rate this adjustment has a greater effect, and the size of the adjustment also increases with the risk horizon. The adjustment can be important for risk horizons longer than a month or so. But when the risk horizon is relatively short, any assumption that returns are not expected to equal the risk free rate has only a very small impact on the VaR measure, and for this reason it is often ignored.

IV.1.5.1 Normal Linear VaR Formula: Portfolio Level

Suppose we only seek to measure the VaR of a portfolio without attributing the VaR to different risk factors. We also make the simplifying assumption that the portfolio's discounted h-day returns are i.i.d. and normally distributed. For simplicity of notation we shall, in this section, write the return as X, dropping the dependence on both time and risk horizon. Thus we assume

We will derive a formula for x_α, the α quantile return, i.e. the return such that P(X < x_α) = α. Then the 100α% VaR, expressed as a percentage of the portfolio value, is minus this α quantile. Using the standard normal transformation, we have

where Z~N (0, 1). So if P(X < x_α) = α, then

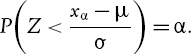
But by definition, P(Z < Φ⁻¹(α )) = α, so

where Φ is the standard normal distribution function. For instance, Φ⁻¹(0.01) = 2.3264.

But x_α = −VaR_α by definition, and Φ⁻¹(α) = −Φ⁻¹(1 − α) by the symmetry of the standard normal distribution. Substituting these into (IV.1.14) yields an analytic formula for the VaR for a portfolio with an i.i.d. normal return, i.e.

If we want to be more precise about the risk horizon of our VaR estimate, we may write

This is a simple formula for the 100α% h-day VaR, as a percentage of the portfolio value, when the portfolio's discounted returns are i.i.d. normally distributed with expectation μ_h and standard deviation σ_h.

To obtain the VaR in value terms, we simply multiply the percentage VaR by the current value of the portfolio:

where P_t is the value of the portfolio at the time t when the VaR is measured. Note that when we express VaR in value terms, VaR will depend on time, even under the normal i.i.d. assumption using a constant mean and standard deviation for the portfolio return.

EXAMPLE IV.1.4: VAR WITH NORMALLY DISTRIBUTED RETURNS

What is the 10% VaR over a 1-year horizon of $2 million invested in a fund whose annual returns in excess of the risk free rate are assumed to be normally distributed with mean 5% and volatility 12%?

SOLUTION Let the random variable X denote the annual returns in excess of the risk free rate, so we have

We must find the 10% quantile of the discounted return distribution, i.e. that x such that P(X < x) = 0.1. So we apply the standard normal transformation to X, and then find x such that

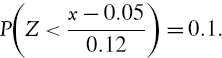
From standard normal statistical tables or using NORMSINV (0.1) in Excel. We know that

Hence,

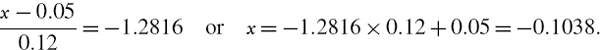
Thus the 10% 1-year VaR is 10.38% of the portfolio value. With $2 million invested in the portfolio the VaR is $2m × 0.1038 = $207,572. In other words, we are 90% confident that we will lose no more than $207,572 from investing in this fund over the next year.

Since we have assumed returns are i.i.d., the formula (IV.1.15) for the normal VaR, expressed as a percentage of the portfolio value, depends on the risk horizon h but it does not depend on time. That is, under the i.i.d. normal assumption VaR is a constant percentage of the portfolio value. However, to estimate VaR we need to use forecasts of σ_h and μ_h – forecasts that are based on an i.i.d. model for returns – and in practice these forecasts will change over time simply because the sample data change over time, or because our scenarios change over time. Hence, even though the model predicts that VaR is a constant percentage of the portfolio value, the estimated percentage will change over time, merely due to sample variations.

It is important to realize that all the problems with moving average models of volatility that we have discussed in Chapter II.3 will carry over to the normal linear VaR model. Since the returns are assumed to have a constant volatility, this should be estimated using an equally weighted moving average, which gives an unbiased estimator of the returns variance. But equally weighted average volatility estimates suffer from ‘ghost features’. As a result, VaR will remain high for exactly T periods following one large extreme return, where T is the number of observations in the sample. Then it jumps down T periods later, even though nothing happened recently. See Section II.3.7 for further details.

In Section IV.3.3.1 we show that the choice of T has a very significant impact on an equally weighted VaR estimate – in fact, this choice has much more impact than the choice between using a normal linear (analytic) VaR estimate as above, and an estimate based on historical simulation. The larger T is, the less risk sensitive is the resulting VaR estimate, i.e. the less responsive is the VaR estimate to changing market conditions. For this reason many institutions use an exponentially weighted moving average (EWMA) methodology for VaR estimation, e.g. using EWMA to estimate volatility in the normal linear VaR formula. These estimates, if not the estimator, take account of volatility clustering so that EWMA VaR estimates are more risk sensitive than equally weighted VaR estimates. For example, the RiskMetrics^TM methodology and supporting database allows analysts to choose between these two approaches. See Section II.3.8 for further details.

IV.1.5.2 Static Portfolios

Market VaR measures the risk of the current portfolio over the risk horizon, and in order to measure this we must hold the portfolio over the risk horizon. A portfolio may be specified at the asset level by stating the value of the holdings in each risky asset. If we know the value of the holdings then we can find the portfolio value and the weights on each asset. Alternatively, we can specify the portfolio weights on each asset and the total value of the portfolio. If we know these we can determine the holding in each asset.

Formally, consider a portfolio with (long or short) holdings {n₁, n₂,…, n_k} in k risky assets, so n_i is the number of units long (n_i > 0) or short (n_i < 0) in the ith asset, and denote the ith asset price at time t by p_it. Then the value of the holding in asset i at time t is is n_ip_it, and the portfolio value at time t is

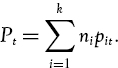
We can define the portfolio weight on the ith asset at time t as

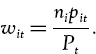
In a long-only portfolio each n_i > 0 and so P_t > 0. In this case, the weights in a fully funded portfolio sum to one.

Note that even when the holdings are kept constant, i.e. the portfolio is not rebalanced, the value of the holding in asset i changes whenever the price of that asset changes, and the portfolio weight on every asset changes, whenever the price of one of the assets changes. So when we assume the portfolio is static, does this mean that the portfolio holdings are kept constant over the risk horizon, or that the portfolio weights are kept constant over the risk horizon? We cannot assume both. Instead we assume either

• no rebalancing – the portfolio holdings in each asset are kept constant, so each time the price of an asset changes, the value of our holding in that asset will change and hence all the portfolio weights will change; or
• rebalancing to constant weights – to keep the portfolio weights constant we must rebalance all the holdings whenever the price of just one asset changes.

Similar comments apply when a portfolio return (or P&L) is represented by a risk factor mapping. Most risk factor sensitivities depend on the price of the risk factor. For instance, the delta and the gamma of an option depend on the underlying price, and the PV01 of a cash flow depends on the level of the interest rate at that maturity. So when we say that a mapped portfolio is held constant, if this means that the risk factor sensitivities are held constant then we must rebalance the portfolio each time the price of a risk factor changes.

The risk analyst must specify his assumption about rebalancing the portfolio over the risk horizon. We shall distinguish between the two cases described above as follows:

• Static VaR assumes that no trading takes place during the risk horizon, so the holdings are kept constant, i.e. there is no rebalancing. Then the portfolio weights (or the risk factor sensitivities) will not be constant: they will change each time the price of an asset (or risk factor) changes. This assumption is used when we estimate VaR directly over the risk horizon, without scaling up an estimate corresponding to a short risk horizon to an estimate corresponding to a longer risk horizon. It does not lead to a tractable formula for the scaling of VaR to different risk horizons, as the next subsection demonstrates.
• Dynamic VaR assumes the portfolio is continually rebalanced so that the portfolio weights (or risk factor sensitivities, if VaR is estimated using a risk factor mapping) are held constant over the risk horizon. This assumption implies that the same risks are faced every trading day during the risk horizon, if we also assume that the asset (or risk factor) returns are i.i.d., and it leads to a simple scaling rule for VaR.

IV.1.5.3 Scaling VaR

Frequently market VaR is measured over a short-term risk horizon such as 1 day and then scaled up to represent VaR over a longer risk horizon. How should we scale a VaR that is estimated over one risk horizon to a VaR that is measured over a different risk horizon? And what assumptions need to be made for such a scaling?

The most tractable framework for scaling VaR is based on the assumption that the returns are i.i.d. normally distributed and that the portfolio is rebalanced daily to keep the portfolio weights constant. Similarly, if the VaR is based on a risk factor mapping, it is mathematically tractable to assume the risk factor sensitivities are constant over the risk horizon, and that the risk factor returns are i.i.d. and have a multivariate normal distribution. As a result the returns on a linear portfolio will be i.i.d. normally distributed.³¹ So in the following we derive a formula for scaling VaR from a 1-day horizon to an h-day horizon under this assumption.

For simplicity of notation, from here onward we shall drop the t from the VaR notation, unless it is important to make explicit the time at which the VaR estimate is made. Also, in this section we do not include the discounting of the returns (or, equivalently, the expression of returns as excesses over the risk free rate) since this does not affect the scaling result, and it only makes the notation more cumbersome. Hence, to derive formulae (IV.1.18) and (IV.1.21) below we may, without loss of generality, assume the risk free rate is zero.

Suppose we measure VaR over a 1-day horizon, and assume that the daily return is i.i.d. normal. Then we have proved above that the 1-day VaR is given by

where μ₁ and σ₁ are the expectation and standard deviation of the normally distributed daily returns. We now use a log approximation to the daily discounted return. To be more specific, we let³²

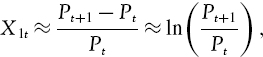
where P_t denotes the portfolio price at time t. We use this approximation because it is convenient, i.e. log returns are additive. That is, the h-day discounted log return is the sum of h consecutive daily discounted log returns. Since the sum of normal variables is another normal variable, the h-day discounted log returns are normally distributed with expectation μ_h =h μ₁and standard deviation , as proved in Section II.3.2.1.

We now approximate the h-day log return with the ordinary h-day return, and deduce that this is (approximately) normally distributed. Then the h-day VaR is given by the approximation

This approximation is reasonably good when h is small, but as h increases the approximation of the h-day log return with the ordinary h-day return becomes increasingly inaccurate.

What happens if we drop the assumption of independence but retain the assumption that the returns have identical normal distributions? In Section IV.2.2.2 we prove that if the daily log return follows a first order autoregressive process with autocorrelation then the expectation of the h-day log return is μ_h =h μ₁ (so autocorrelation does not affect the scaling of the mean) but the standard deviation of the h-day log return is

with

Hence, in this case,

with defined by (IV.1.20).

EXAMPLE IV.1.5: SCALING NORMAL VAR WITH INDEPENDENT AND WITH AUTOCORRELATED RETURNS

A portfolio has daily returns, discounted to today, that are normally and identically distributed with expectation 0% and standard deviation 1.5%. Find the 1% 1-day VaR. Then find the 1% 10-day VaR under the assumption that the daily excess returns (a) are independent, and (b) follow a first order autoregressive process with autocorrelation 0.25. Does positive autocorrelation increase or decrease the VaR?

SOLUTION Using formula (IV.1.17), the 1% 1-day VaR is

i.e. 3.4895% of the portfolio value. Now we scale the VaR under the assumption of i.i.d. normal returns. By (IV.1.18) the 1% 10-day VaR is approximately times the 1% 1-day VaR, because the discounted expected return is zero. So the 1% 10-day VaR is approximately

Finally, with h = 10 and = 0.25 the scaling factor (IV.1.20) is not 10, but 15.778. So under the assumption that returns have an autocorrelation of 0.25, the 1% 10-day VaR is approximately

A positive autocorrelation in daily returns increases the standard deviation of h-day returns, compared with that of independent returns. Hence, positive autocorrelation increases VaR, and the longer the risk horizon the more the VaR will increase. On the other hand, a negative autocorrelation in daily returns will decrease the VaR, especially over long time horizons. Readers may verify this by changing the parameters in the spreadsheet for this example.

Scaling VaR when returns are not normally distributed is a complex question to answer, so we shall address it later in this book. In particular, see Sections IV.2.8 and IV.3.2.3.

IV.1.5.4 Discounting and the Expected Return

We now examine the effect of discounting returns on VaR and ask two related questions:

• Over what time horizon does it become important to include any non-zero expected excess return in the VaR calculation?
• If we fail to discount P&L in the VaR formula, i.e. if we do not express returns as excess over the risk free rate, does this have a significant effect on the results?

Banking regulators often argue that the expected return on all portfolios should be equal to the risk free rate of return. In this case the discounted expected P&L will be zero or, put another way, the expected excess return will be zero. If we do assume that the expected excess return is zero the normal linear VaR formula becomes even simpler, because the second term is zero and the h-day VaR, expressed as a percentage of the current portfolio value, is just the standard deviation of the h-day return, multiplied by the standard normal critical value at the confidence level 1 − α.

The situation is different in portfolio management. When quoting risk adjusted performance measures to their clients, fund managers often believe that they can provide returns greater than the risk free rate by judicious asset allocation and stock selection. However, expectations are highly subjective and could even be a source of argument between a fund manager and his client, or between a bank and its regulator. Corporate treasurers, on the other hand, are free to assume any expected return they wish. They are not constrained by regulators or clients.

We now prove that when portfolios are expected to return a rate different from the risk free rate this should be included as an adjustment to the VaR. This is obvious in the normal i.i.d. framework described above, since the discounted mean return appears in the VaR formula. But it is also true in general. To see why, consider the distribution of P&L at time t + h, as seen from the current time t. This is the distribution of P_t+h − E_t(P_t+h) where E_t(P_t+h) is the conditional expectation seen from time t of the portfolio value at time t + h. That is, it is conditional on the information available up to time t.

Denote by y_{ht, α} the α quantile of this distribution, discounted to time t. That is,

where B_ht is the value at time t of a discount bond maturing in h trading days. Now (IV.1.22) may be rewritten as

or as

where ∈_ht = P_t − B_htE_t(P_t+h) is the difference between the current portfolio price and its expected future price, discounted at the risk free rate.³³

Note that ∈_ht is only zero if the portfolio is expected to return the risk free rate, i.e. if E_t(P_th = (B_ht)⁻¹P_t. Otherwise, comparing (IV.1.23) with (IV.1.8), we have

Hence, the VaR is minus the α quantile of the discounted P&L distribution plus ∈_ht, if this is not zero. When the expected return on the portfolio is greater than the risk free rate of return, ∈_ht will be negative, resulting in a reduction in the portfolio VaR. The opposite is the case if the portfolio is expected to return less than the risk free rate, and in this case the VaR will increase.

The following example shows that this adjustment term ∈_ht, which we call the drift adjustment to the VaR, can be substantial but only when VaR is measured over a risk horizon of several months or more.

EXAMPLE IV.1.6: ADJUSTING VAR FOR NON-ZERO EXPECTED EXCESS RETURNS

Suppose that a portfolio's return is normally distributed with mean 10% and standard deviation 20%, both expressed in annual terms. The risk free interest rate is 5% per annum. Calculate the 1% VaR as a percentage of the portfolio value when the risk horizon is 1 week, 2 weeks, 1 month, 6 months and 12 months.

SOLUTION The calculations are set out in the spreadsheet and results are reported in Table IV.1.3 below. As anticipated, the reduction in VaR arising from the positive expected excess return increases with the risk horizon. Up to 1 month ahead, the effect of the expected excess return is very small: it is less than 0.5% of the portfolio value. However, with a risk horizon of one year (as may be used by hedge funds, for instance) the VaR can be reduced by almost 5% of the portfolio value if we take account of an expected excess return of 5%.

Table IV.1.3 Normal VaR with drift adjustment

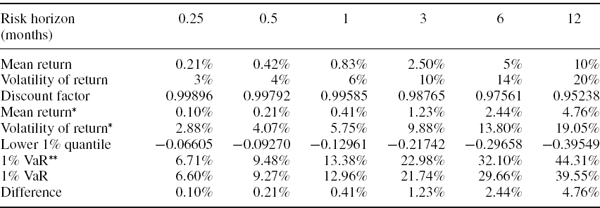
Note:^* denotes that the quantities are discounted, and^** denotes that the VaR is based on a zero mean excess return.

Readers may use the spreadsheet to verify the following:

• Keep the mean return at 10% but change the volatility of the portfolio return. This has a great effect on the values of the VaR estimates but it has no influence on the difference shown in the last row; the only thing that affects the difference between the non-drift adjusted VaR and the drift adjusted VaR is the expected excess return (and the portfolio value, if the VaR is expressed in value terms).
• Keep the portfolio volatility at 20%, but change the expected return. This shows that when the portfolio is expected to return x% above the risk free rate, the reduction in VaR at the 1-year horizon is a little less than x% of the portfolio value.³⁴

IV.1.6 RISK FACTOR VALUE AT RISK

In the previous section we described one simple model for measuring the VaR of a linear portfolio at the portfolio level. We also obtained just one figure, for the total VaR of the portfolio, but this is not where VaR measurement stops – if it were, this book would be considerably shorter than it is. In practice, VaR measures are based on a risk factor mapping of the portfolio, in which case the model provides an estimate of the systematic VaR, also called the total risk factor VaR. The systematic VaR may itself be decomposed into the VaR due to different types of risk factors. The specific VaR, also called residual VaR, measures the risk that is not captured by the mapping.

A risk factor mapping entails the construction of a model that relates the portfolio return, or P&L, to variations in its risk factors. For example, with an international equity portfolio having positions on cash equity and index futures we would typically consider variations in the following risk factors:

• major market spot equity indices (such as S&P 500, FTSE 100, CAC 40);
• spot foreign exchange (forex) rates (such as $/£, $/€);
• dividend yields in each major market;
• spot LIBOR rates of maturity equal to the maturity of the futures in the domestic and foreign currencies (such as USD, GBP and EUR).

In the factor model, the coefficient parameters on the risk factor variations are called the portfolio's sensitivities to variations in the risk factors. For instance, the international equity portfolio above has:

• a sensitivity that is called a beta with respect to each of the major stock indices;
• a sensitivity that is one with respect to each exchange rate;
• a sensitivity that is called a PV01 with respect to each interest rate, or each dividend yield.³⁵

The whole of Chapter III.5 was devoted to describing risk factor mappings and risk factor sensitivities for different types of portfolios, and it is recommended that readers are familiar with this, or similar material.

IV.1.6.1 Motivation

The process of risk attribution is the mapping of total risk factor VaR to component VaRs corresponding to different types of risk factors. The reason why risk managers map portfolios to their risk factors is that the analysis of the components of risk corresponding to different risk factors provides an efficient framework for hedging these risks, and for capital allocation. Risk factors are often common to several portfolios, for instance:

• Foreign exchange rates are common to all international portfolios, whether they contain equities, commodities or bonds and other interest rate sensitive instruments. The enterprise-wide exposures to forex rates are often managed centrally, so that these risks can be netted across different portfolios. But a manager of an international equity or bond portfolio will still want to know his forex risk, as measured by his forex VaR. So will the risk manager and senior managers, since they need to know which activities are the main contributors to each type of risk.
• Zero-coupon yield curves are common to any portfolio containing futures or forwards, as well as to interest rate sensitive portfolios. And if the portfolio is international then yield curves in different currencies are risk factors. Interest rate risk is the uncertainty about the present value of future cash flows, and this changes as discount rates change from day to day. Except for portfolios consisting entirely of interest rate sensitive instruments, interest rate risk is often one of the smallest risks. The firm can use the VaR model to net these risks when aggregating interest rate VaR across different activities.

Another reason why we base VaR on a risk factor mapping is that typical portfolios are too large to measure VaR by mapping to all of its instruments. It is technically infeasible to analyse the risk of most portfolios without the aid of risk factor mapping. For example, measuring VaR at the level of each asset in a stock portfolio containing 1000 stocks requires modelling the multivariate distribution of 1000 stock returns. Usually we try to summarize this distribution using only the returns covariance matrix, but in this example we would still have to deal with an enormous matrix.

Only a few portfolios are so small that they do not require risk factor mapping. For instance, we do not really need to map a private investor's portfolio that has cash positions in only a few stocks, or any other small portfolio containing similar and straightforward positions. But small, cash portfolios are not the business of financial institutions. Typically, the institution will handle tens of thousands of complex positions with exposures to hundreds of different risk factors. Hence, even measuring VaR at the risk factor level is a formidable challenge.

Another advantage of risk factor mapping is that it provides a convenient framework for the daily work of a market risk manager. He requires many stress tests of current positions and an overall assessment of whether capital is available to cover these risks. Stress tests are usually conducted by changing risk factor values – firstly because this gives the risk manager further insight into his risk attribution, and secondly because it would be impossible to investigate different scenarios for each individual asset.

When we measure VaR on portfolios that are mapped to risk factors there are three important sources of model risk in the VaR estimate:

• The choice of risk factor mapping is subjective. A different risk manager might choose a different set of risk factors.
• The risk factor sensitivities may have estimation errors. For stock portfolios the risk factor sensitivities, which are called risk factor betas, depend on a model, and their estimation is subject to sampling error, as we have seen in Section II.1.2.
• The specific risk of the portfolio is ignored. By measuring VaR based on a risk factor mapping, all we capture is the systematic VaR.

There are many other sources of model risk in a VaR model and a full discussion of this is given in Chapter IV.6.

IV.1.6.2 Normal Linear Equity VaR

We now provide some very simple examples of the measurement of VaR based on a risk factor mapping. In this subsection we consider the case of a cash equity portfolio with excess return Y and we assume it has a single risk factor, such as a broad market index, with excess return X. Then the factor model may be written

where and β are constant parameters and ∈_t is the specific return.³⁶ We suppose the risk factor excess returns X are normally distributed, and that the expected excess return over the next h days is μ_h with a standard deviation of σ_h. Then the portfolio's excess returns due to the movements in the index will also be normally distributed, with expectation + βμ_h and standard deviation βσ_h.

Since the portfolio's alpha is idiosyncratic to the portfolio, it does not enter the systematic part of the risk; instead it enters the specific risk component of the VaR. Thus to measure the systematic VaR of the portfolio, which is here called the equity VaR since the only risk factor is an equity index, we assume the portfolio's excess return are normally distributed with expectation βμ_h and standard deviation βσ_h.

Now, using the same argument as in Section IV.1.5.1 when we derived the normal linear VaR formula at the portfolio level, the normal linear systematic VaR of the portfolio is

The following example illustrates a simple application of this formula for a two-stock portfolio with one risk factor.

EXAMPLE IV.1.7: EQUITY VAR

A portfolio contains cash positions on two stocks: $1 million is invested in a stock with a beta of 1.2 and $2 million is invested in a stock with a beta of 0.8 with respect to a broad market index. If the excess returns on the index are i.i.d. and normally distributed with expectation 5% and volatility 20% per annum, what is the 1% 10-day VaR of the portfolio?

SOLUTION The net portfolio beta is measured in dollar terms as

Note that using the dollar beta in (IV.1.26) gives the equity VaR in dollar terms, not as a percentage of the portfolio value. The 10-day expected excess return on the risk factor is

and the 10-day standard deviation of the excess returns on the market index is

Hence, the 1% 10-day equity VaR is

IV.1.6.3 Normal Linear Interest Rate VaR

This subsection introduces the interest rate VaR of bonds, swaps and loans portfolios that can be represented as a series of cash flows. In Section III.5.2.1 we explained how to represent an interest rate sensitive portfolio using an approximate linear risk factor model, called a cash-flow map, the salient details of which are summarized below for convenience.³⁷

The discounted P&L on the portfolio is the net change in present value of the entire cash flow series, and the linear approximation derived in Section III.5.2.1 is

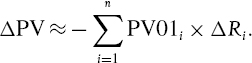
Alternatively, using the matrix algebra that was introduced in Chapter I.2, this may be written in matrix form as

where

• θ = (PV01₁,…, PV01_n)′ is the vector of risk factor sensitivities, that is, θ is a vector whose ith element is the PV01 of the cash flow that is mapped to the ith vertex;³⁸ and
• Δr = (ΔR₁,…, ΔR_n)′ is the vector of changes (measured in basis points) in interest rates at the standard maturities (which are also called the vertices of the risk factor mapping).

Since the PV01 is the present value of a basis point change, the change in the portfolio value given by the risk factor representation (IV.1.27) is already measured in present value terms.

Suppose that Δr has a multivariate normal distribution with mean μ and covariance matrix Ω. Then, based on the linear mapping (IV.1.27), the discounted P&L also has a normal distribution with expectation −θ′μ and variance θ′Ωθ. It is particularly important to understand the quadratic form θ′Ωθ for the variance, since this will be used many times in Chapter IV.2.³⁹The minus sign appears in the expectation because the PV01 measures the sensitivity to a one basis point fall in interest rates. Thus, applying the normal linear VaR formula (IV.1.15), the VaR of the cash flow is

We often assume that the same interest rate risk factors are used for discounting, in which case θ′μ, the expected change in portfolio value, is zero. We also measure the covariance matrix over a specific h-day period. Thus, denoting the h-day interest rate covariance matrix by Ω_h, the formula for the normal linear 100α% h-day VaR for a cash flow becomes

EXAMPLE IV.1.8: NORMAL VAR OF A SIMPLE CASH FLOW

Find the 1% 10-day VaR of a cash flow that is mapped to a 1-year and a 2-year vertex with PV01 of $50 and $75, respectively. Assume the absolute changes in 1-year and 2-year interest rates over the next 10 days have a multivariate normal distribution with expectation 0, correlation 0.9 and with annual volatilities of 100 basis points for the change in the 1-year rate and 80 basis points for the change in the 2-year rate.

SOLUTION We use the formula (IV.1.28) with h = 10, α = 0.01, θ = (50, 75)′ and where Ω₁₀ is the 10-day covariance matrix of the risk factor changes, expressed in basis points. We have the annual covariance matrix

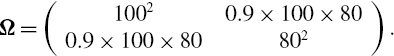
So the 10-day matrix is

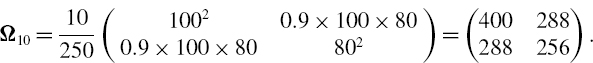
Hence,

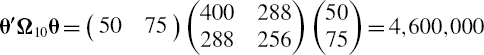
and

The 1% 10-day VaR is therefore 2.32635 × $2144.76 = $4989.

IV.1.7 DECOMPOSITION OF VALUE AT RISK

This section explains how to aggregate VaR over different activities and disaggregate it into components corresponding to different types of risk factors. The level of discussion is very general and we do not provide any examples. However, numerous numerical and empirical examples are given in later chapters as we investigate each of the three VaR models in greater depth.

The ability to aggregate and disaggregate VaR is an essential management tool. The aggregation of VaR allows total risk to be assigned to different activities. Indeed, this is the fundamental tool for the risk budgeting process, which is the allocation of economic capital to activities, the allocation of (VaR-based) limits for traders, and the estimation of the size of the regulatory capital requirement for market risk. Or they may call for further supervision of high risk activities. The disaggregation of VaR helps a risk analyst to understand the main sources of risk in a portfolio. Good risk managers use VaR decomposition to be better informed about the risks that need to be hedged, about the limits that traders should be set, and about the risks of potential trades or investments.

IV.1.7.1 Systematic and Specific VaR

The total risk of a portfolio may be decomposed into systematic risk, i.e. the risk that is captured by mapping the portfolio to risk factors, and specific risk, i.e. the risk that is not captured by the portfolio mapping. Some numerical and empirical illustrations of this type of VaR disaggregation are provided in Sections IV.2.5.2–IV.2.5.4.

For an example of specific risk, consider portfolios of commodity futures which use spot prices as risk factors. Here a specific risk arises due to fluctuations in carry costs, if these are not captured by the portfolio mapping. Another example is when a factor model is used to map an equity portfolio to its risk factors. Few factor models can provide perfect descriptions of portfolio returns. There will be a model residual that may have high volatility, especially when portfolios are not well diversified. In large diversified portfolios the specific returns on each stock that are left to the model's residuals tend to cancel each other out if the factor model is well specified. But if inappropriate (or too few) risk factors are used in the factor model, the specific risk of the portfolio can be large. In that case we can measure the specific risk by saving the factor model residuals and applying the VaR model directly to these.

The total VaR includes both the systematic and the specific VaR components. To calculate this directly we forget about the risk factor mapping and measure the VaR at the portfolio level, i.e. using a univariate series of portfolio returns or P&L. In the simple normal linear model this could be based on an assumed (or estimated) value for portfolio volatility; in the historical VaR model we build an empirical distribution using a time series for the portfolio returns or P&L; and in the Monte Carlo VaR model we simulate this distribution using a parametric model for the portfolio's P&L.

An alternative to the direct calculation of the total VaR is to assume the specific and systematic risks are approximately uncorrelated. Of course, this would only be the case when the factor model is capturing most of the variation in the portfolio. Then, in the normal linear model, the total VaR will be the square root of the sum of the systematic VaR squared and the specific VaR squared.⁴⁰ Just adding up the systematic and specific risks is not a good way to estimate the total risk, because this assumes the systematic and specific risks are perfectly correlated! Thus, the systematic risk should dominate the total risk, but this happens only if it is much larger than the specific risk of the portfolio. The regulatory requirements for specific risk are that a specific risk ‘add-on’ must be applied to the systematic risk to obtain the total risk, unless the risk model allows one to incorporate the specific risk into the total VaR estimate.⁴¹

IV.1.7.2 Stand-alone VaR

We may also decompose the systematic risk of a portfolio into ‘stand-alone’ components that correspond to fundamental risk factors. The aim is to disaggregate VaR into the risk associated with particular asset classes: equity VaR, interest rate VaR, forex VaR and commodity VaR.⁴² This allows the forex and interest rate risks of all types of securities in international portfolios to be individually assessed, and then combined and managed by separate desks. The disaggregation of VaR into stand-alone components is important even for domestic portfolios. For instance, the systematic risk of commodity futures portfolios would be based on movements in spot commodity prices, if we used these as the risk factors, but under such a mapping portfolios also have interest rate and net carry cost VaR components.

The decomposition of systematic VaR into stand-alone components can be applied whatever the assumptions made about the evolution of risk factors, and for any type of portfolio. Stand-alone VaR is calculated by setting all the sensitivities to other risk factors to zero. The precise computation depends on the VaR model used and further details are given throughout the remaining chapters.⁴³

Stand-alone VaR measures the risk of an asset class in isolation. It is stand-alone capital that should be used to compare the performance of different trading activities. Assuming the trading desks are managed separately, any diversification benefits should be excluded when assessing their risks. No single desk should be rewarded or penalized for diversification in the overall businesses. The correlation between different risk factors, e.g. the correlation between equity returns and changes in interest rates, is taken into account only when we aggregate stand-alone VaR estimates.

Stand-alone components of VaR do not ‘add up’, unless we assume that portfolios are linear and everything is perfectly correlated. In the normal linear VaR model the total risk factor VaR will be equal to the sum of the stand-alone component VaRs if and only if all the risk factors are perfectly correlated. Otherwise, the total VaR will be less than the sum of the stand-alone component VaRs, a property that is known as sub-additivity.⁴⁴ This is because the VaR is determined by the volatility of portfolio returns in the linear model, and variance (i.e. the square of the volatility) obeys nice mathematical rules.

More generally, we use some type of simulation to resolve the risk model. Then VaR is measured as a quantile and quantiles need not be sub-additive, as we shall demonstrate below. But if the sum of the stand-alone component VaRs does exceed the total VaR, then stand-alone capital is not appropriate for risk budgeting. Individual portfolios could be within their risk limits yet the business overall could be in breach of limits. The reason why many large economic capital driven organizations (mainly large banks and corporations) prefer to use conditional VaR (expected tail loss) instead of VaR for risk budgeting purposes is that conditional VaR is sub-additive, whatever the resolution method in the risk model.

IV.1.7.3 Marginal and Incremental VaR

An alternative way to disaggregate VaR is to decompose it into marginal VaR components. Marginal VaR assigns a proportion of the total risk to each component, and hence provides the risk manager with a description of the relative risk contributions from different factors to the systematic risk of a diversified portfolio. Unlike stand-alone VaR, marginal VaR is additive, by virtue of its definition as a proportion. In other words, the sum of the marginal VaR components is the systematic VaR. For this reason, marginal VaR can be used to allocate real capital which, being money, must add up.

As its name suggests, marginal VaR is the sensitivity of VaR to the risk factor model parameters, i.e. the sensitivity of VaR to the risk factor sensitivities θ = (θ₁, …,θ_n)′.⁴⁵ Note that θ can usually be measured in either percentage or value terms, and this determines whether VaR itself is measured in percentage or value terms.

We now derive an expression for the marginal VaR, by writing VaR as a function of these parameters, and using some elementary calculus.⁴⁶ That is, we assume that

for some unspecified but differentiable function f. The gradient vector of first partial derivatives is

where

Hence, a first order Taylor approximation to VaR is

Each term θ_if_i(θ) in the sum is called the ith marginal component VaR, or just the ith marginal VaR for short.

When the portfolio is linear and the VaR is estimated from the normal linear VaR model then the approximation in (IV.1.30) is exact. In this case the sum of the marginal VaRs is always equal to the total risk factor VaR. But for other portfolios, and also when VaR is estimated using simulation, the sum of the marginal VaRs is only approximately equal to the total risk factor VaR.

The gradient vector (IV.1.29) can also be used to approximate the VaR impact of a small trade. For instance, it can be used to assess the impact of a partial hedge on a trader's VaR limit. We use a first order Taylor approximation to the change in VaR for a small change in θ. Suppose θ changes from θ₀ to θ₁. Then the associated change in VaR is

This change in VaR is called the incremental VaR.

IV.1.8 RISK METRICS ASSOCIATED WITH VALUE AT RISK

Active portfolio managers are usually required to benchmark their risk as well as their returns. During the last decade this task caused considerable confusion. Even the phrase ‘the risk of returns relative to the benchmark’ is ambiguous, as discussed in Section II.1.6. This section begins by introducing benchmark VaR, a metric that is suitable for measuring risk relative to a benchmark.

Unless VaR is measured using a simple model, such as the normal linear model, it is not sub-additive. That is, the sum of the stand-alone component VaRs may be greater than the total VaR. In this case the whole concept of risk budgeting flies out of the window. Traders could keep within risk limits for each portfolio but the total limit for the desk could be exceeded. Desk managers could adhere to strict limits, but the total risk budget for the organization as a whole could still be exceeded. Hence, for risk budgeting purposes most large economic capital driven organizations use a risk metric that is associated with VaR, and which is sub-additive. This is a conditional VaR metric that we call expected tail loss or, if measured relative to a benchmark, expected shortfall. Conditional VaR satisfies all the properties for being a coherent risk metric, in a sense that will presently be made precise.

IV.1.8.1 Benchmark VaR

When returns are measured relative to a benchmark we consider the active return, which we assume is the difference between the portfolio return and the benchmark return.⁴⁷ Then, expressing VaR in percentage terms, the benchmark VaR is the α quantile of the h-day active return distribution, discounted to today.

EXAMPLE IV.1.9: BENCHMARK VAR WITH NORMALLY DISTRIBUTED RETURNS

What is the 1% benchmark VaR over a 1-year horizon for $10 million invested in a fund with an expected active return equal to the risk free interest rate and a tracking error of 3%?⁴⁸

SOLUTION Since the expected active return is equal to the risk free rate, the discounted active return has expectation zero. The tracking error is the standard deviation of the active return. Hence, we apply the normal linear VaR formula (IV.1.15) with

The standard normal critical value is Φ⁻¹(0.99) = 2.3264, hence the 1% 1-year benchmark VaR is

Multiplying this by the portfolio value of $10 million gives the 1% benchmark VaR of $697,904. Thus we are 99% confident that losses relative to the benchmark will not exceed $697,904 when holding this portfolio over the next year.

Compared with tracking error, benchmark VaR has two main advantages. Firstly, it measures the risk of underperforming the benchmark and not the ‘risk’ of outperforming it. Secondly, the expected active return does affect the benchmark VaR, whereas tracking error says nothing about the expected active return on the fund.⁴⁹

The expected active return has a linear effect on the benchmark VaR, and we demonstrate this by reconsidering the previous example, this time allowing the expected active return to be different from zero. Figure IV.1.3 shows that, keeping the tracking error constant at 3%, the annual benchmark VaR decreases linearly as we increase the expected active return on the fund, shown on the horizontal axis. As we increase this from −5% up to 5%, the corresponding 1% 1-year benchmark VaR decreases from almost $1.2 million to only $200,000.⁵⁰

Figure IV.1.3 Effect of expected active return on benchmark VaR

In short, when a portfolio is expected to outperform a benchmark then the risk of the portfolio reduces if it is measured by benchmark VaR, but not if it is measured by the tracking error. Similarly, when a portfolio is expected to underperform a benchmark then the risk of the portfolio as measured by benchmark VaR increases. This is not a feature of the tracking error, because that metric only measures the risk relative to the expected active return and is not affected by the level of the expected active return.

IV.1.8.2 Conditional VaR: Expected Tail Loss and Expected Shortfall

VaR defines a level of loss that one is reasonably sure will not be exceeded. But VaR tells us nothing about the extent of the losses that could be incurred in the event that the VaR is exceeded. However, we obtain information about the average level of loss, given that the VaR is exceeded, from the conditional VaR.

There are two conditional VaR measures, depending on whether we are measuring the VaR relative to a benchmark or not. The 100α% h-day expected tail loss is the conditional VaR defined as

where X_h denotes the discounted h-day return on the portfolio, VaR_{h, α} is the 100α% h-day VaR expressed as a percentage of the portfolio's value and P is the current value of the portfolio.

The 100α% h-day expected shortfall is the conditional benchmark VaR defined as

where _h denotes the discounted h-day active return on the portfolio and BVaR_h,α is the 100α% h-day benchmark VaR expressed as a percentage of the portfolio's value.

The distinction between VaR, benchmark VaR, ETL and ES can be illustrated by considering 1000 P&Ls for a portfolio and for its benchmark and looking at (a) the absolute losses on the portfolio, and (b) the relative losses, measured relative to a benchmark. Both losses are in present value terms. Then:

• the 1% VaR is the 10th largest absolute loss;
• the 1% ETL is the average of the 10 largest absolute losses;
• the 1% benchmark VaR is the 10th largest relative loss;
• the 1% ES is the average of the 10 largest relative losses.

Their difference is further illustrated by the following example, which is based on an empirical approach to VaR estimation which we shall later describe as historical simulation.

EXAMPLE IV.1.10: COMPARISON OF DIFFERENT VAR METRICS

The spreadsheet for this example contains a time series of daily values for the Dow Jones Industrial Average (DJIA) index and for a (hypothetical) portfolio of stocks that closely tracks the DJIA. The data in the spreadsheet are from 5 January 1998 to 31 December 2001 and at the end of this period the portfolio value was $1,007,580, which is similar to a $100 per point position on the DJIA index.

(a) Find the 1% 1-day VaR and the 1% 1-day ETL on the portfolio on 31 December 2001.

(b) Using the DJIA as benchmark, calculate the 1% 1-day benchmark VaR and expected shortfall for the portfolio on 31 December 2001.

SOLUTION (a) There are exactly 1000 returns in the spreadsheet, so the 1% quantile is the tenth largest negative return. This is the return of −3.549% on 15 October 1999, as shown on the left-hand side of Table IV.1.4.⁵¹ The 1% daily VaR is minus this return, multiplied by the current value of the portfolio and discounted by 1 day. But the risk free interest rate on 31 December 2001 was only approximately 4%, so the 1-day discount factor is almost one and we have set it to one.⁵² Hence, we compute the portfolio VaR on 31 December 2001 as⁵³

This tells us that we are 99% confident of not losing more than $35,764 between 31 December 2001 and 1 January 2002.

The ETL is the average of the ten largest negative returns that are shown in the first columns of Table IV.1.4, again multiplied by −1 and by the current portfolio value (ignoring the discounting as before). That is,

This tells us that if we do exceed the VaR, which we expect to happen with a probability of 1%, on average we would lose $46,505 from our position. The conditional VaR is much greater than the ordinary VaR, as is often the case.⁵⁴

Table IV.1.4 The tail of the return distribution and of the active return distribution

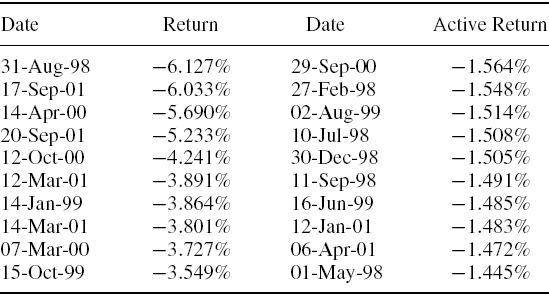
(b) The benchmark VaR and ES are calculated using a similar process to that in (a), but this time using the active returns relative to the DJIA benchmark rather than the returns on the portfolio itself. The tenth largest negative active return was −1.445% on 1 May 1998, and this and the other 9 largest negative active returns are shown on the right-hand side of Table IV.1.4. Recalling that the value of the portfolio on 31 December 2001 was $1,007,580, we calculate the benchmark VaR and the expected shortfall as:

and

Hence, we are 99% confident of not losing more than $14,557 more than we would with a $100 per point position on the DJIA, over a 1-day period. And if we do exceed this figure then the expected loss, relative to the DJIA position, would be $15,129.

IV.1.8.3 Coherent Risk Metrics

A risk metric is a single number that is used to summarize the uncertainty in a distribution. For instance, volatility is a risk metric that summarizes the dispersion over the whole range of a distribution. Other risk metrics, such as the downside risk metrics introduced in Section IV.1.3, only summarize the uncertainty over a restricted range for the random variable.

How do we choose an appropriate risk metric? In portfolio management we choose risk metrics that have an associated risk adjusted performance measure that ranks investments in accordance with a utility function – and hopefully, a utility function with desirable properties. But in banking we tend to choose risk metrics that have certain ‘intuitive’ properties. For instance, we prefer risk metrics that can aggregate risks in a way that accounts for the effects of diversification.

What other intuitive properties should a ‘good’ risk metric possess? In Section I.6.5.2 we introduce a property called weak stochastic dominance. Suppose one investment A dominates another investment B in the sense that the probability of the return exceeding any fixed value is never greater with investment B than it is with investment A. Any rational investor should rank A above B. Yet some basic risk adjusted performance measures such as the Sharpe ratio (see Sharpe, 1994) do not preserve this property, as have seen in Section I.6.5.2. We can construct two investments A and B where the Sharpe ratio of A is less than that of B even though A weakly stochastically dominates B.

Clearly, requiring a risk metric to preserve stochastic dominance is not a trivial property. We shall now phrase this property as the first of several ‘axioms’ that should be satisfied by a ‘good’ risk metric. In the following we use the notation to denote an arbitrary risk metric.⁵⁵

Monotonicity

If A weakly stochastically dominates B then A should be judged as no more risky than B according to our risk metric. We write this property mathematically as

Sub-additivity

Furthermore, as mentioned above, we would like the risk metric to aggregate risks in an intuitive way, accounting for the effects of diversification. We should ensure that the risk of a diversified portfolio is no greater than the corresponding weighted average of the risks of the constituents. For this we need

Without sub-additivity there would be no incentive to hold portfolios. For instance, we could find that the risk of holding two stocks with agent 1, who can then net the risk by taking into account the correlation between the stock returns, is greater than the risk of holding stock A with agent 1 and stock B with agent 2, with no netting of the two agents' positions. As remarked in the introduction to this section, without sub-additivity the risk metric cannot be used for risk budgeting.

Homogeneity

Note that a risk metric is simply a measure of uncertainty in a distribution; it says nothing at all about the risk attitude of an investor. It is not a risk premium. For this reason some authors believe that another intuitive axiom is that if we double our bet, then we double our risk. More generally, for any positive constant k the homogeneity axiom requires

This axiom states that risk preference has nothing to do with the risk metric, or at least if users are endowed with a utility function then they must be risk neutral. Risk aversion or risk loving behaviour is, rather, in homogeneity, in that the marginal utility of wealth typically depends on the level of wealth. Of all the four axioms for a coherent risk metric, it is this axiom that states that a risk metric is a measure of uncertainty, rather than of an agent's perception of risk. For this reason, several authors find the homogeneity axiom rather contentious and prefer to use an axiom that can link the risk metric with risk attitude.

Risk free condition

Finally, we note that some risk metrics, such as VaR, may be measured in value terms (e.g. in dollars or euros). Others, such as volatility of returns, are measured on a relative scale. It is more convenient to represent risks on a value scale because then the capital that is at risk can be offset by capital held in cash or a risk free asset.

For example, suppose that risk is measured in US dollars and that we have capital of $1 million of which 90% is invested in a risky portfolio A and 10% is held in a risk free asset. Suppose further that the risk of our $0.9 million capital invested in A is $250,000 according to our risk metric . In other words, (A) = $250,000. So we have capital at risk of $250,000 but risk free capital of $100,000. Then, according to the risk free axiom, the net capital at risk should be $150,000. The intuition behind this is that we could use the $100,000 of risk free capital to cover the risk on the risky asset.

More generally, suppose we divide our capital into an investment A and amount γ earning the risk free return. Then the net capital at risk is

Artzner et al. (1999) introduced the label coherent for any risk metric that satisfies the four axioms above. They showed that lower partial moment risk metrics are coherent, and that conditional VaR, i.e. expected shortfall and expected tail loss, are also coherent risk metrics. But many common risk metrics are not coherent. For instance, any risk metric expressed in relative terms, like volatility or tracking error, will not satisfy the risk free condition.

VaR is measured in value terms, but it is only coherent under special assumptions about the distribution of returns. When returns are normally distributed VaR is a coherent risk metric, because it behaves like the volatility of returns (converted into value terms). But more generally, VaR is not coherent because quantiles, unlike the variance operator, do not obey simple rules such as sub-additivity unless the returns have an elliptical distribution. The next example constructs a portfolio containing only two instruments for which VaR is not sub-additive.

EXAMPLE IV.1.11: NON-SUB-ADDITIVITY OF VAR

Suppose we write the following two binary options: option A pays $10,000 if the monthly return on the S&P 500 index is at least 20% and option B pays $10,000 if the monthly return on gold is at least 20%. Both options are sold for $1000. We assume that the returns on the S&P 500 and gold are independent and that each has a probability of 0.02532 of returning at least 20%.⁵⁶ Show that the sum of the 5% VaRs on each separate position is less than the 5% VaR when the two options are taken together in a portfolio.

SOLUTION First consider each position separately: in each individual position there is only a 2.532% chance that we pay out $10,000. Put another way, the P&L distribution is exactly

This is depicted in Figure IV.1.4.

We cannot lose more than $9000, so this is the 1% VaR, i.e. P(P&L ≤ −$9000) = 1%. And indeed, $9000 is also the 2.5% VaR. But what is the 5% VaR, i.e. the amount X such that P(P&L ≤ −X) = 5%? It is important to note that the P&L is truly discrete for this binary option, it is not just a discrete approximation to a continuous random variable. Either we make a profit of $1000 or we lose $9000. These are the only alternatives. It makes no sense to interpolate between these outcomes, as if we could obtain a P&L between them. We know the distribution function is exactly as shown Figure IV.1.4, so we can read off the 5% quantile: it is +$1000. The sum of the two 5% VaRs is thus −$2000.

Now consider a portfolio containing both the options. The most we can lose is $18,000, if both options are called. By the independence assumption, this will happen with probability 0.02532² = 0.000642. We could also lose exactly $9000 if one option is called and the other is not. The probability of this happening is 2 × 0.02532 × (1 − 0.02532) = 0.049358.

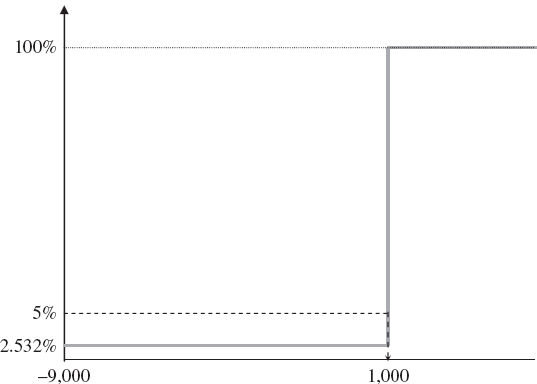
Figure IV.1.4 P&L distribution for one binary option

Figure IV.1.5 P&L distribution for a portfolio of two binary options

Hence, the probability that we lose $9000 or more is 4.9358% + 0.0642% = 5%. Hence, as depicted in Figure IV.1.5, the 5% VaR of the portfolio is $9000. This is greater than −$2000, i.e. the sum of the VaR on the two individual positions taken separately. Hence, the VaR is not sub-additive.

IV.1.9 INTRODUCTION TO VALUE-AT-RISK MODELS

The material presented in this section, which provides essential background reading for the remainder of the book, introduces the three basic types of VaR models:

• the normal linear VaR model, in which it is assumed that the distribution of risk factor returns is multivariate normal and the portfolio is required to be linear;
• the historical simulation model, which uses a large quantity of historical data to estimate VaR but makes minimal assumptions about the risk factor return distribution; and
• the Monte Carlo VaR model, which in its most basic form makes similar assumptions to the normal linear VaR model.

It is easy to estimate VaR once we have the discounted return distribution, but constructing this distribution can take considerable effort. The only differences between the three VaR models are due to the manner in which this distribution is constructed. All three approaches may be developed and generalized, as will be explained in the next three chapters. The Monte Carlo framework is the most flexible of all, and may be used with a great diversity of risk factor return distributions. And, like historical simulation, it also applies to option portfolios.

IV.1.9.1 Normal Linear VaR

A note on terminology is appropriate first. The risk factor (or asset) returns covariance matrix is central to this approach and for this reason some people call this approach the covariance VaR model. However, I find this terminology slightly ambiguous for two reasons. Firstly, in its most basic form the Monte Carlo VaR model also uses the risk factor returns covariance matrix. Secondly, a parametric linear VaR model need not summarize the risk factor dependency with a single covariance matrix. For instance, we could use several covariance matrices in the normal or Student t mixture linear VaR model, as we shall see in the next chapter.

In fact, the parametric linear VaR models have been given many different names by many different authors. Some refer to them as the analytic VaR models, but analytic expressions for VaR may also be derived for non-linear portfolios. Other authors call normal linear VaR the delta–normal VaR, but we do not actually need to assume that risk factors are normally distributed for this approach and the use of the term ‘delta’ gives the impression that it always refers to a linearization of the VaR for option portfolios.

The parametric linear VaR model is only applicable to a portfolio whose return or P&L is a linear function of its risk factor returns or its asset returns. The most basic assumption in the model is that risk factor returns are normally distributed, and that their joint distribution is multivariate normal, so the covariance matrix of risk factor returns is all that is required to capture the dependency between the risk factor returns. Under these assumptions it is possible to derive an explicit formula for the VaR, and we have already demonstrated this in Sections IV.1.5.1, IV.1.6.2 and IV.1.6.3.

VaR is usually measured over a short risk horizon, and we have shown in Section IV.1.5.2 that it is a reasonable approximation to assume that the excess return on the portfolio is zero over such an horizon. Then the normal linear VaR formula takes a very simple form. As a percentage of the portfolio value, the 100α% normal linear VaR is simply minus the standard normal α quantile, multiplied by the standard deviation of the portfolio returns over the risk horizon. In a linear portfolio, this standard deviation may be represented as the square root of a quadratic form that is based on the risk factor sensitivity vector and the risk factor covariance matrix over the risk horizon.⁵⁷

The next chapter is a very long chapter, completely devoted to discussing the parametric linear VaR model. We shall see that it is not necessary to assume that risk factors returns have a multivariate normal distribution in order to derive a formula for the VaR. It is also possible to derive a formula when risk factor returns have a multivariate Student t distribution, or when they have a mixture of normal or Student t distributions. However, in the mixture case the formula gives VaR as an implicit rather than an explicit function, so a numerical method needs to be applied to solve for the VaR.

Furthermore, it is not necessary to assume that each risk factor return follows an i.i.d. process, although this is a standard assumption for scaling VaR over different risk horizons. It is possible to find a simple scaling rule for linear VaR when the risk factor returns are autocorrelated, provided there is no time-varying volatility.⁵⁸

IV.1.9.2 Historical Simulation

The historical VaR model assumes that all possible future variations have been experienced in the past, and that the historically simulated distribution is identical to the returns distribution over the forward looking risk horizon. Again, a note on terminology is in order. Some authors call this model the non-parametric VaR model, but I do not like this nomenclature because parametric distributions can be a useful addition to this framework when estimating VaR at very high quantiles. Having said this, the term ‘historical VaR’ is a little unfortunate, since both of the other models can use historical data, if required. For instance, we may use a risk factor return covariance matrix forecast that is based on historical data for the risk factors.

Historical scenarios on contemporaneous movements in risk factors are used to simulate many possible portfolio values in h days' time. For this, we need to apply the risk factor mapping (e.g. the factor model for equities, the cash-flow map for interest rate sensitive portfolios, or the Taylor expansion for options) to each one of these contemporaneous simulated risk factor returns. We assume the risk factor sensitivities are held constant at their current levels, as discussed in Section IV.1.5.2. Then the risk factor mapping changes each set of correlated risk factor returns into one possible return for the portfolio over the risk horizon of the VaR model. This h-day return is discounted to today, if necessary, using the h-day discount rate.⁵⁹

Taking all the simulated discounted portfolio returns together, we can build an empirical distribution of the h-day portfolio return or P&L. Then the 100α% h-day VaR is minus the α quantile of the historically simulated distribution. If the distribution is of portfolio returns then VaR is expressed as a percentage of the current portfolio value, and if the distribution is of portfolio P&L VaR is expressed in value terms.

One such simulated P&L density is depicted in Figure IV.1.6. The lower 1% quantile of the distribution is −0.04794 million dollars. This is calculated in the spreadsheet using linear interpolation. Hence the 1% VaR based on this set of simulations is $47,940.

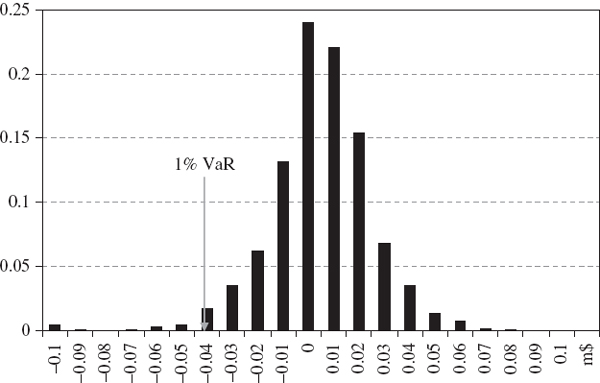
Figure IV.1.6 Simulated P&L density showing 1% VaR

The main limitations of historical VaR stem from the constraints imposed by the sample size. The number of data points used to construct the historical distribution is equal to the number of observations on each risk factor return in the simulation. This number should be as large as possible, otherwise there would be very few points in the lower tail of the distribution and the VaR, especially at high confidence levels, would be imprecise. The historical data should be sampled at the daily frequency and should span many years into the past. This is because we need very many data points to estimate the quantiles of an empirical distribution, especially those quantiles in the extreme lower tail (which are required for VaR estimates at high confidence levels). Gathering such data can be a difficult and time-consuming task. We should try not to use overlapping h-day returns in the model, for reasons that will be clarified in Section IV.3.2.7. So even if we have many, many years of daily data on each risk factor we can initially measure VaR at the daily risk horizon only. If we require VaR over a longer horizon we need to scale up the daily VaR estimate somehow. The problem is that scaling historical VaR estimates is very tricky. This is fully discussed in Section IV.3.2.

On the other hand, one great advantage of historical VaR is that it makes few distributional assumptions. No assumption is made about the parametric form of the risk factor return distribution, least of all multivariate normality. For instance, we do not need to assume that the risk factor returns covariance matrix can capture all the complex dependencies between risk factors. The only distributional assumption is that the multivariate distribution of the risk factor returns over the risk horizon will be identical to the distribution in the past. Also, if we scale the historical VaR to a longer risk horizon, we need to assume the risk factor returns are i.i.d. They need not be normally distributed; as long as they have a ‘stable distribution’⁶⁰ we can derive a scaling rule for historical VaR.

In summary, a major advantage of historical VaR is that it bases risk factor dependencies on experienced risk factor returns and comovements between these, rather than on a parametric model for their distribution. However, the model also suffers from a major drawback. Due to sample size constraints historical VaR needs to be assessed initially at the daily horizon, and then scaled up to longer horizons. The scaling of historical VaR from a daily to a longer risk horizon requires a detailed investigation of the nature of the empirical return distribution. Usually it is not appropriate to apply the square-root-of-time scaling rule, as we do for normal i.i.d. returns. Moreover, historical VaR has only limited applications to option portfolios because any type of scaling will distort their gamma effects, as we shall demonstrate in Section IV.5.4.

IV.1.9.3 Monte Carlo Simulation

In its most basic form the Monte Carlo VaR model uses the same assumptions as the normal linear VaR model, i.e. that the risk factor returns are i.i.d. with a multivariate normal distribution. In particular, it assumes that the covariance matrix is able to capture all possible dependency between the risk factor returns. However, the Monte Carlo VaR model is extremely flexible and many different assumptions about the multivariate distribution of risk factor returns can be accommodated. For instance, we could use a copula to model the dependence and specify any type of marginal risk factor return distributions that we like.⁶¹

In the i.i.d. multivariate normal Monte Carlo VaR model we simulate independent standard normal vectors and these are transformed to correlated multivariate normal vectors using the Cholesky decomposition of the risk factor returns covariance matrix.⁶² Then the portfolio mapping is applied to each vector of simulated risk factor changes to obtain a simulated portfolio value at the end of the risk horizon, one for each simulated vector of correlated risk factor returns. To reduce the sampling error we generate a very large number of simulations and apply techniques to reduce the error variance.⁶³

For example, if we use 100,000 simulations then we have 100,000 simulated portfolio values at the risk horizon in h days' time, and hence also 100,000 simulated returns on the portfolio. These are expressed in present value terms and then the 100α% h-day VaR is obtained as minus the lower α quantile of the discounted h-day portfolio return distribution.

Both the multivariate normality and the i.i.d. assumptions can be generalized, and we shall discuss how this is done in Sections IV.4.3 and IV.4.4. Another essential difference between the Monte Carlo VaR and parametric linear VaR models is that the Monte Carlo approach can be applied to non-linear portfolios, and to option portfolios in particular.

Clearly the normal linear VaR and the normal Monte Carlo VaR models are very similar because they make identical assumptions about risk factor distributions. The only difference between the two models is that the evolution of the risk factors is simulated in the Monte Carlo VaR model whereas it is obtained analytically in the normal linear VaR model. Thus the normal linear VaR is precise, albeit based on an assumption that is unlikely to hold, whilst the normal Monte Carlo VaR estimate is subject to simulation error. Thus, the normal Monte Carlo VaR estimate should be similar to the normal linear VaR estimate. If it is different, that can only be because an insufficient number of simulations were used. In fact, it is a waste of time to apply normal Monte Carlo VaR to a linear portfolio, because this merely introduces sampling errors that are not present in the normal linear VaR model. Nevertheless, there is still a good reason for applying Monte Carlo VaR to a linear portfolio, and this is that the Monte Carlo VaR can be based on virtually any multivariate distribution for risk factor returns, whereas closed-form solutions for parametric linear VaR only exist for a few select distributions.

IV.1.9.4 Case Study: VaR of the S&P 500 Index

The aim of this subsection is to illustrate the three standard VaR models, in their most basic form, by applying them to measure the VaR of a very simple portfolio with a position of $1000 per point on the S&P 500 index. We use the case study to illustrate the different ways in which the three models build the portfolio return distribution, and to give the reader some insight into the reasons why different VaR models give different results. A more thorough discussion of this topic is left until Chapter IV.6, after we have reviewed all three models in detail.

Daily historical data on the S&P 500 index from 3 January 2000 until 8 January 2008 are downloaded from Yahoo! Finance.⁶⁴ Using the same data set for each, we apply the three models to estimate the VaR of a position of $1000 per point on the index on 8 January 2008. Since the index closed at 1390.19 on that day, the nominal value of our position is P = $1,390,190.

Normal Linear VaR

Here we assume a normal distribution for the portfolio's daily returns, and we use the log approximation since this is usually very accurate over a 1-day horizon. From the historical price series in the spreadsheet we compute the daily log returns over the whole sample, and hence estimate the standard deviation σ of these returns as .⁶⁵ Under the assumption that the log returns are i.i.d. we can use the square-root-of-time rule, setting the h-day standard deviation . For example, .

For simplicity, and because it will not detract from the illustration, we assume that the expected return on our position and the risk free rate are both zero, so that no discounting or drift adjustment needs to be made to the returns before calculating the VaR. Hence, we set

For example,

Historical VaR

The historical VaR estimate uses exactly the same historical daily log returns as above, but now no parametric form is assumed for the log returns distribution. The α quantile is calculated on the actual daily (log) returns that were realized over the sample.⁶⁶ This is then multiplied by −1 and by the nominal value of the portfolio, to convert the quantile into a 1-day VaR in nominal terms. For comparison with the other models we also apply a square-root scaling law to the historical 1-day VaR to obtain the h-day historical VaR, even though there may be no theoretical justification for the use of this rule. Thus we multiply the 1-day historical VaR by to obtain the h-day historical VaR.

For example, the 1% quantile of the empirical return distribution in our case study is −2.959%, so the 1% 10-day historical VaR estimate is

Monte Carlo VaR

For the Monte Carlo VaR we take the same standard deviation estimate _h as that used in the normal linear VaR model. Using the Excel command = NORMSINV (RAND ())^* _h, as explained in Section I.5.7, we simulate a very large number of hypothetical h-day returns. Only 5000 are set into the spreadsheet, but readers may increase the number of simulations by filling down column D. Then we apply the Excel PERCENTILE function to find the α quantile of their distribution. This is multiplied by the nominal value of the portfolio to convert the quantile into a 100α% h-day VaR in nominal terms.

The Monte Carlo simulations are automatically repeated each time you change any data in the spreadsheet, unless you turn the automatic calculation option to manual. To repeat the simulations at any time just press F9. We use no variance reduction technique here, so unless a very large number of simulations are used the result can change considerably each time. Table IV.1.5 summarizes results for α = 1% and 5% and for h = 1 and 10. Of course, in the spreadsheet readers will see a different value for Monte Carlo VaR than that shown in the right-hand column of Table IV.1.5. Remember, the linear VaR gives the exact figure and the Monte Carlo VaR is subject to simulation errors, but the variance of this error decreases as we increase the number of simulations.⁶⁷

Table IV.1.5 Comparison of estimates from different VaR models

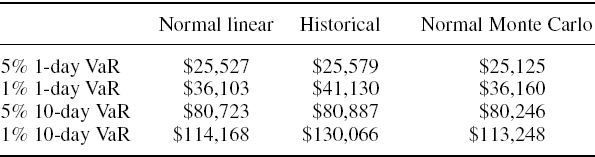
The difference between the normal linear and the historical VaR estimates is more apparent at the 1% significance level. At the 5% level the two estimates are similar, but the historical return distribution is leptokurtic. That is, it has heavier tails than the normal distribution, so the VaR at extreme quantiles is greater when estimated using the historical simulation approach. The square-root scaling rule may not appropriate for historical VaR, but even without this potential error the 1% 1-day VaR estimates are already very different. The estimated VaR is about 14% greater when based on historical simulation. Relative to the portfolio value of $1,390,190, we have a 1% 1-day VaR of:

• 36,103/1,390,190 = 2.6% according to the normal linear VaR model, but
• 41,130/1,390,190 = 2.96% according to the historical VaR model.

The reason is that the normal linear VaR model assumes the returns have a normal distribution, whereas the sample excess kurtosis of the daily log returns is 2.538. Such a high positive excess kurtosis indicates that the empirical S&P 500 return distribution has heavy tails, so the assumption of normality that is made in the linear and Monte Carlo VaR models is not validated by the data.

IV.1.10 SUMMARY AND CONCLUSIONS

We opened this chapter by discussing the risk metrics that are commonly used by fund managers, banks and corporations. In the fund management industry risk is commonly measured in the context of a returns model, whereas in banking and corporate treasury the risk model is usually separate from the returns model. Hence, quite different risk metrics were traditionally used in these industries.

A market risk metric is a single number which measures the uncertainty in a portfolio's P&L, or in its return. Its fundamental purpose is to summarize the portfolio's potential for deviations from a target or expected return. A typical risk metric for passive fund management is tracking error, which is the volatility of the active return. Unfortunately tracking error has also been adopted by many active portfolio managers, even though it is not an appropriate risk metric for actively managed funds. One of the reasons for this is that tracking error is not a downside risk metric. Many downside risk metrics have been developed for active fund managers and several of these have better properties than tracking error. Increasingly, portfolio managers are adopting VaR-based downside risk metrics, such as benchmark VaR and expected shortfall, because these metrics tell clients about the probability of losing money. Tracking error is more difficult for clients to understand, particularly when it is linked to the (possibly erroneous) assumption that the portfolio returns are normally distributed. VaR does not have to assume that returns are normally distributed.

VaR is a quantile risk metric. But when returns are normal every quantile is just a multiple of the standard deviation, so in this special case VaR obeys the same rules as a standard deviation. Otherwise, VaR does not obey nice rules and it may not even be sub-additive.

VaR and its associated risk metrics have become the universal risk metrics in banking and corporate treasury. The reason why large companies measure risks using a VaR model is that these firms often have a management structure that is based on economic capital allocation. Most major banks use VaR to measure both economic and regulatory capital. Economic capital affects the bank's credit rating, and is a primary tool for management. Regulatory capital is determined by either standardized rules or an internal VaR model. We shall return to this topic in the final chapter of this book.

There are many reasons why banks like to use VaR, which are listed in the introduction and explained in this chapter. But VaR has some undesirable properties. It is not a coherent risk metric, unless we make some simplifying assumptions about the behaviour of the risk factors and the portfolio is a linear portfolio. However, the conditional VaR metric is always coherent, so many banks use a conditional VaR such as expected tail loss in their internal economic capital calculations.

In the bottom-up risk assessment paradigm that is prevalent today, risks are assessed first at the individual position level, and then positions are progressively aggregated into larger and larger portfolios. A portfolio can contain anything from a single instrument to all the positions in the entire firm. At each stage of aggregation VaR is estimated and decomposed into the VaR due to different classes of risk factors. This decomposition allows the VaR due to risk factors in different asset classes to be identified, monitored and hedged efficiently. It also allows capital to be allocated in accordance with a universal risk metric, used for all the activities in the firm.

The disaggregation of VaR allows risk to be allocated to different activities and risk capital to be allocated accordingly. VaR can be decomposed into systematic and specific components, and systematic VaR can be further decomposed into stand-alone or marginal VaR components belonging to different types of risk factors. Thus, taking all the positions in the entire bank, we estimate stand-alone and/or marginal VaR for equity, interest rates, credit spreads, commodity groups, and forex. Stand-alone VaR is used in performance measures that determine the internal allocation of economic capital. It measures the risk of an activity (e.g. proprietary trading, or swaps) in isolation. It does not reduce the risk of any component by accounting for any diversification benefits (e.g. between equities and interest rates). Marginal VaR can be used to allocate real capital. It tells us the proportion of total risk stemming from different activities and it accounts for diversification benefits between the components. Marginal VaR can be extended to the concept of incremental VaR, i.e. the impact on the portfolio's VaR of adding a small new position to the portfolio.

Aggregation of VaR provides information about the total risk faced by a firm and the adequacy of its total capital to cover risky positions given an adverse market move. Marginal VaR is constructed in such as way that the sum of marginal VaRs is the total risk factor VaR. But stand-alone VaR estimates do not sum to the total risk factor VaR. Since stand-alone VaR measures risk in isolation, the aggregation of stand-alone component VaRs takes no account of diversification.

We have defined several distinct steps to take when building a VaR model, and provided a preliminary discussion on the choice available at each step. The model building process may be summarized as follows:

1. Define the portfolio and identify its risk factors. Portfolios may be characterized by their asset holdings, and long-only portfolios may be characterized by the portfolio weights.
2. Set the basic parameters for the model. The basic parameters of a VaR model are the confidence level and the risk horizon, and a VaR estimate increases with both these parameters. The choice of these parameters depends on the end use of the model. For instance, trading limits may be set at 95% confidence and a horizon of 1 day, whereas economic capital estimates may be based on 99.9% confidence with a risk horizon of 1 year.
3. Map the portfolio to its risk factors. This entails building a model for the portfolio return, or P&L, as a function of the absolute or percentage returns to its risk factors. The risk factor mapping process greatly facilitates (a) the subsequent VaR computations, which indeed in many cases would be impossible without a risk factor mapping; and (b) the efficient firm-wide hedging of risks, as the fundamental risk factors can be isolated and the exposures netted centrally.
4. Model the evolution of the risk factors over the risk horizon. It is here that the three different VaR models adopt different approaches. Both the parametric linear VaR and Monte Carlo VaR models assume we know a functional form for the multivariate stochastic process generating the time series of risk factor returns. For instance, they could assume that an independent, normally distributed process generates each risk factor returns series. In that case the returns on each risk factor have no autocorrelation or time-varying volatility, but the risk factor returns at any particular point in time are assumed to be correlated with each other. The historical VaR model uses an empirical risk factor return distribution, without assuming it takes any specific parametric form. It is only based on the risk factor variations and dependencies that have been experienced in a historical sample. Importantly, it does not rely on a covariance matrix to capture all the risk factor variations and dependencies.
5. Revalue the portfolio for each realization of the risk factors. Here we typically assume the risk factor sensitivities are held constant over a risk horizon of h days. But these sensitivities depend on the risk factor values and the risk factor values change over the risk horizon. Hence, there is an implicit assumption that the portfolio is rebalanced to maintain constant risk factor sensitivities.
6. Build a distribution for the portfolio return or P&L. Which of these distributions is used will depend on the risk factor mapping. In some cases (e.g. interest rates or long-short portfolios) it is more natural to generate the P&L distribution, in others it is more natural to use the return distribution. The h-day portfolio return or P&L must also be expressed in present value terms. If the expected return on the portfolio is very different from the discount rate, then the return distribution should be modified to account for this. When VaR is measured over a long horizon such as a year, this adjustment may result in a significant reduction in VaR. This is particularly important when VaR is used to assess the absolute risk of funds, which typically expect to return more than the risk free rate and have risks that are measured over long horizons. However, when the risk of funds is benchmarked, in which case the VaR is based on the active returns rather than the ordinary returns on the fund, there may be little justification to suppose that the expected active return will be any different from zero whatever the fund manager tells you.
7. Calculate the VaR and ETL. The 100α% h-day VaR is (minus) the α quantile of the discounted h-day distribution. If we build a P&L distribution, the VaR and ETL will be measured in value terms and if we build a return distribution they will be expressed as a percentage of the portfolio value. It is possible to obtain the quantiles using analytical methods in parametric linear VaR models. Otherwise, the returns or P&L distribution must be simulated, and the quantile is calculated using interpolation on the simulated distribution. Often we assume that an i.i.d. process generates each risk factor return; then we can measure the VaR initially over a 1-day horizon, and scale this up to a VaR estimate for a longer risk horizon. Under some conditions we can use a square - root scaling rule for VaR, for instance when the discounted portfolio returns are i.i.d. and normally distributed with mean zero.

For a linear portfolio with i.i.d. normally distributed returns, the normal linear VaR should be identical to the normal Monte Carlo VaR. But in the ensuing chapters we shall see that both the parametric linear VaR model and the Monte Carlo VaR model may be generalized to make other distributional assumptions. The Monte Carlo VaR model is particularly flexible in that the returns may be assumed to have any parametric distribution that we care to specify.

An obvious problem with the historical VaR model is the severe constraints that are imposed by sample size limitations. In their basic form the other two models only require a covariance matrix, and this can be based on only very recent historical data – or indeed, it can be set according to the personal views of the analyst, using no historical data at all. But in historical VaR one has to re-create an artificial history for the portfolio, holding its current weights, holdings or risk factor sensitivities constant over a very long historical period. Even when this is possible, it is not necessarily desirable because the market conditions in the recent past and the immediate future may have been very different from those experienced many years ago. As its name suggests, the historical model assumes that the distribution of the portfolio returns or P&L over the risk horizon is the same as the historical distribution. This makes it more difficult to perform scenario analysis in the historical model, although we shall demonstrate how to do this in Section IV.7.5.1.

A further distinguishing feature between the models is that a normal linear VaR estimate can only be applied when the portfolio return is a linear function of its risk factor returns. This restriction does not apply to the Monte Carlo VaR and historical VaR models, although the application of historical VaR to option portfolios is fairly limited, as explained in Section IV.5.4.

To summarize the main advantage of each approach:

• The normal linear VaR model is analytically tractable.
• Historical VaR makes no (possibly unrealistic) assumption about the parametric form of the distribution of the risk factors.
• The Monte Carlo VaR model is very flexible, and it can be applied to any type of position, including non-linear, path-dependent portfolios.

To summarize the main limitations of each approach:

• The normal linear VaR model is restricted to linear portfolios and it can only be generalized to a few simple parametric forms, such as a Student t or a mixture of normal or Student t distributions.
• Historical VaR assumes that all possible future variation has been experienced in the past. This imposes very stringent, often unrealistic, requirements on data.
• Monte Carlo VaR is computationally intensive and without sophisticated sampling methods, simulation errors can be considerable.

The chapter concluded with a case study that highlights the similarities and the differences between the three VaR models, using a simple position on the S&P 500 index as an illustration. We used an i.i.d. normal assumption in the linear and Monte Carlo VaR models, so the two VaR estimates should be identical for every significance level and risk horizon. However, even with many thousand simulations and a very simple portfolio, the simulation errors in Monte Carlo VaR were considerable. Also, there was a highly significant excess kurtosis in the S&P return distribution, and for this reason the normal linear and Monte Carlo VaR estimates were significantly lower than the historical VaR estimates at the 1% significance level. However, at the 5% significance level, all three models gave similar results.