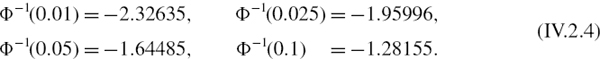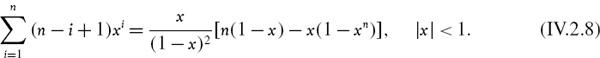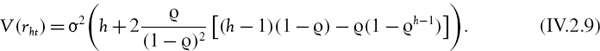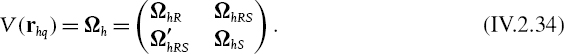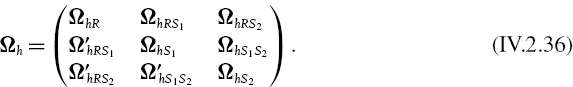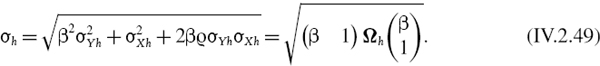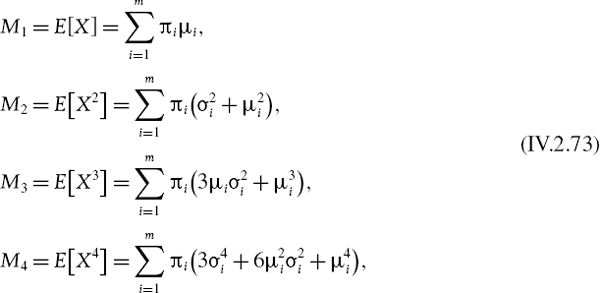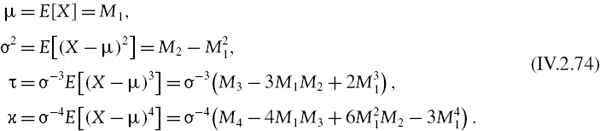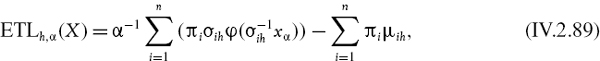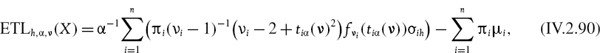IV.2

Parametric Linear VaR Models

IV.2.1 INTRODUCTION

The parametric linear model calculates VaR and ETL using analytic formulae that are based on an assumed parametric distribution for the risk factor returns, when the portfolio value is a linear function of its underlying risk factors. Specifically, it applies to portfolios of cash, futures and/or forward positions on commodities, bonds, loans, swaps, equities and foreign exchange. The most basic assumption, discussed in the previous chapter, is that the returns on the portfolio are independent and identically distributed with a normal distribution. Now we extend this assumption so that we can decompose the portfolio VaR into VaR arising from different groups of risk factors, assuming that the risk factor returns have a multivariate normal distribution with a constant covariance matrix. We derive analytic formulae for the VaR and ETL of a linear portfolio under this assumption and also when risk factor returns are assumed to have a Student t distribution, or a mixture of normal or Student t distributions.

In bond portfolios, and indeed in any interest rate sensitive portfolio that is mapped to a cash flow, the risk factors are the interest rates of different maturities that are used to both determine and discount the cash flow. When discounting cash flows between banks we use a term structure of LIBOR rates as risk factors. Additional risk factors may be introduced when a counterparty has a credit rating below AA. For instance, the yield on a BBB-rated 10-year bond depends on the appropriate spread over LIBOR, so we need to add the 10-year BBB-rated credit spread to our risk factors. More generally, term structures of credit spreads of different ratings may also appear in the market risk factors: when portfolios contain transactions with several counterparties having different credit ratings, one credit spread term structure is required for each different rating.

There is a non-linear relationship between the value of a bond or swaps portfolio and interest rates. However, this non-linearity is already captured by the sensitivities to the risk factors, which are in present value of basis point (PV01) terms. Hence, we can apply the parametric linear VaR model by representing the portfolio as a cash flow, because the discount factor that appears in the PV01 is a non-linear function of the interest rate.

We may also base parametric linear VaR and ETL estimates on an equity factor model, provided it is linear, which is very often the case. Foreign exchange exposures are based on a simple linear proportionality, and commodity portfolios can be mapped as cash flows on term structures of constant maturity forwards or interest rates. Thus, the only portfolios to which the parametric linear VaR method does not apply are portfolios containing options, or portfolios containing instruments with option-like pay-offs. That is, whenever the portfolio's P&L function is a non-linear function of the risk factors, the model will not apply.

In the parametric linear VaR model, all co-dependencies between the risk factors are assumed to be represented by correlations. We represent these correlations, together with the variance of each risk factor over some future risk horizon h, in an h-day covariance matrix. It is this covariance matrix – and in mixture linear VaR models there may be more than one covariance matrix – that really drives the model. To estimate the covariance matrix we employ a moving average model.¹ These models assume the risk factors are i.i.d. From this it follows that the h-day covariance matrix is just h times the 1-day covariance matrix, a result that is commonly referred to as the square-root-of-time rule.²

In the standard parametric linear VaR model we cannot forecast the covariance matrix using a GARCH model.³ When a return is modelled with a GARCH process it is not i.i.d.; instead it exhibits volatility clustering. As a result the square-root-of-time rule does not apply. However, this is not the reason why we cannot use a GARCH process in the parametric linear VaR model. The problem is that when a return follows a GARCH process we do not know the exact price distribution h days from now. We know this distribution when the returns are i.i.d., because it is the same as the distribution we have estimated over a historical sample. But the h-day log return in a GARCH model is the sum of h consecutive daily log returns and, due to the volatility clustering it is the sum of non-i.i.d. variables. Thus far, we only know the moments of the h-day log return distribution, albeit for a general GARCH process.⁴

The outline of this chapter is as follows. In Section IV.2.2 we introduce the basic concepts for parametric linear VaR. Starting with VaR estimation at the portfolio level (i.e. we consider the returns or P&L on a portfolio, without any risk factor mapping), we examine the properties of the i.i.d. normal linear VaR model and then extend this assumption to the case where returns are still normally distributed, but possibly autocorrelated. This assumption only affects the way that we scale VaR estimates over different risk horizons; the formula for 1-day VaR remains the same. An extension of the normal linear VaR formula for h-day VaR is derived for the case where daily returns are autocorrelated, and this is illustrated with a numerical example.

Then we consider the more general case, in which we assume the portfolio has been mapped to its risk factors using an appropriate mapping methodology.⁵ We provide the mathematical definitions, in the general context of the normal linear VaR model, of the different components of the total VaR of a portfolio. The total VaR may be decomposed into systematic (or total risk factor) VaR and specific (or residual) VaR, where the systematic VaR is the VaR that is captured by the risk factor mapping. The systematic VaR may be further decomposed into stand - alone VaR or marginal VaR components, depending on our purpose:

• Stand-alone VaR estimates are useful for estimating the risk of a particular activity in isolation, without considering any netting or diversification effects that this activity may have with other activities in the firm. Diversification effects are accounted for when aggregating stand-alone VaRs to a total risk factor VaR. The ordinary sum of the stand-alone VaRs is usually greater than the total risk factor VaR, and in the normal linear VaR model it can never be less that the total risk factor VaR.
• Marginal VaR estimates are useful for the allocation of real capital (as opposed to economic capital) because the sum of all the marginal VaR estimates is equal to the total risk factor VaR (and real capital must always add up).

The next five sections provide a large number of numerical and empirical examples, and two detailed case studies, on the application of the normal linear model to the estimation of total portfolio VaR. We focus on the decomposition of the systematic VaR into components corresponding to different types of risk factor. Each section provides a detailed analysis of a different type of asset class.

• Section IV.2.3 examines the VaR of interest rate sensitive portfolios. These portfolios are represented as a sequence of cash flows that are mapped to standard maturities along a term structure of interest rates. Their risk factors are the LIBOR curve and usually one or more term structures of credit spreads. The risk factor sensitivities are the PV01s of the mapped cash flows. Here we use numerical examples to show how to disaggregate the total VaR into LIBOR VaR and credit spread VaR components.
• Section IV.2.4 presents the first case study of this chapter, on the estimation of VaR for a portfolio of UK bonds. We demonstrate how to use principal component analysis to reduce the dimension of the risk factors from 60 to only 3, and describe some risk management applications of this technique.
• Section IV.2.5 examines the normal linear VaR for stock portfolios, from a small portfolio with just a few positions on selected stocks, to a large international portfolio that has been mapped to broad market risk factors. We focus on the decomposition of VaR into systematic and specific factors, and the moving average methods that are used to estimate the covariance matrix.
• Section IV.2.6 shows how to estimate the total VaR for an international stock portfolio, how to decompose this into specific and systematic VaR, and how to disaggregate total VaR into equity VaR, foreign exchange (forex) VaR and interest rate VaR components. We use numerical and empirical examples to calculate stand-alone and marginal VaR components for different types of risk factor, and to illustrate the sub-additivity property of normal linear VaR when component VaRs are aggregated.
• Section IV.2.7 presents a case study on the normal linear VaR of a commodity futures trading desk, using constant maturity futures as risk factors.

There are three other parametric linear VaR models that have analytic solutions for VaR. These are the Student t, the normal mixture and the Student t mixture models. They are introduced and illustrated in Sections IV.2.8 and IV.2.9. Of course, other parametric forms are possible for return distributions but these do not lead to a simple analytic solution and instead we must use Monte Carlo resolution methods. The formulae that we derive in Section IV.2.8 are based on the assumption that returns are i.i.d. We describe a simple technique to extend these formulae so that they assume autocorrelated returns. However, to include volatility clustering we would normally use Monte Carlo simulation for the resolution.⁶

Section IV.2.10 explains how exponentially weighted moving averages (EWMAs) are applied in the parametric linear VaR model, with a particular emphasis on the advantages and limitations of the RiskMetrics^™ VaR methodology that was introduced by JP Morgan in the 1990s. Section IV.2.11 derives analytic formulae for the expected tail loss associated with different parametric linear VaR models. The formal derivation of each formula is then illustrated with numerical examples. Section IV.2.12 presents a case study on estimating the VaR and ETL for an exposure to the iTraxx Europe 5-year credit spread index. The distribution of daily changes in the iTraxx index has a significant negative skew and a very large excess kurtosis and, of the alternatives considered here, we demonstrate that its highly non-normal characteristics are best captured by a mixture linear VaR model. Section IV.2.13 concludes by summarizing the main results in this long chapter. As usual there are numerous interactive Excel spreadsheets on the CD-ROM to illustrate virtually all of the examples and all three case studies.

IV.2.2 FOUNDATIONS OF NORMAL LINEAR VALUE AT RISK

This section introduces the normal linear VaR formula, first when VaR is measured at the portfolio level and then when the systematic VaR is measured by mapping the portfolio to its risk factors. We also discuss the rules for scaling normal linear VaR under both i.i.d. and autocorrelated returns. Then we derive the risk factor VaR, and its disaggregation into stand-alone VaR components and into marginal VaR components. We focus on consequences of the normal linear model's assumptions for aggregating VaR. Finally, we derive the incremental VaR, i.e. the impact on VaR of a small trade, in a linear portfolio with i.i.d. normally distributed returns.

IV.2.2.1 Understanding the Normal Linear VaR Formula

The formal definition of VaR was given in Section IV.1.4, and we summarize it here for convenience. Let

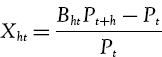
be the discounted h-day return on a portfolio. Here B_ht denotes the price of a discount bond maturing in h trading days and P_t denotes the value of the portfolio at time t. Then the 100α% h-day VaR estimated at time t is

where x_{ht, α} is the lower α quantile of the distribution of X_ht, i.e. P(X_ht < x_{ht, α}) = α.

Derivation of the Formula

The normal linear VaR formula was derived in Section IV.1.5.1. It is convenient to summarize that derivation here, but readers should return to Section IV.1.5 if the following is too concise. In the normal linear VaR model we assume the discounted h-day returns on the portfolio follow independent normal distributions, i.e. X_ht is i.i.d. and

The parameters μ_ht and σ_ht are the forecasts made at time t of the portfolio's expected return over the next h days, discounted to today, and its standard deviation. Amongst other things, these will depend on both the risk horizon and the point in time at which they are forecast.

Applying the standard normal transformation to (IV.2.2) gives⁷

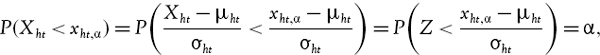
where Z is a standard normal variable. Thus

where Φ⁻¹(α) is the standard normal α quantile value, such as

By the symmetry of the normal distribution function,

Hence, substituting the above and (IV.2.1) into (IV.2.3) gives the 100α% h-day parametric linear VaR at time t, expressed as a percentage of the portfolio value, as

To estimate normal linear VaR we require forecasts of the h-day discounted mean and standard deviation of the portfolio return, and to obtain these forecasts we can make up scenarios for their values, scenarios that would normally be based on the portfolio's risk factor mapping, so that we can find separate scenario estimates for the different risk factor component VaRs. Alternatively, we can base the forecasts for the mean and standard deviation of the portfolio return on historical data for the assets or risk factors. This is useful, to compare with the results based on the historical simulation model using identical data.

When using historical data, for a long-only portfolio we would create a constant weighted historical return series based on the current allocations.⁸ Then we base our (ex-ante) forecasts of the mean and standard deviation on the (ex-post) sample estimates of mean and variance.

For a long-short portfolio we use changes (P&L) on the risk factors and keep the holdings constant rather than the portfolio weights constant. For a cash-flow map, we keep the PV01 vector constant, and use absolute changes in interest rates and credit spreads. In both cases we produce a P&L series for the portfolio. Then the mean and standard deviation of the P&L distribution, and hence also the VaR, are estimated directly in value terms.

Drift Adjustment

From the discussion in Section IV.1.5.2 we know that a non-zero discounted expected return μ_ht can be important. Fund managers, for instance, may sell their services on the basis of expecting returns in excess of the discount rate. Figure IV.2.1 illustrates how a positive mean discounted return will have the effect of reducing the VaR. We have drawn here a normally distributed h-day discounted returns density at time t, with positive mean μ_ht and where the area under the curve to the left of the point μ_ht − Φ⁻¹(1 − α)σ_ht is equal to α, by the definition of VaR.

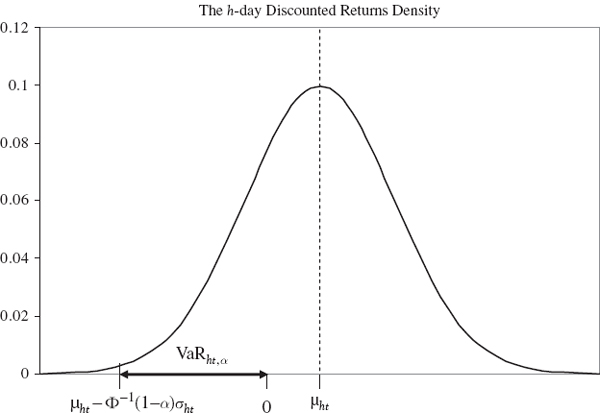
Figure IV.2.1 Illustration of normal linear VaR

In Section IV.1.5.2 we showed that it is only for long risk horizons and when a portfolio is expected to return substantially more than the discount rate that the drift adjustment to VaR, i.e. the second term in (IV.2.5), will have a significant effect on VaR. Hence, we often assume the portfolio is expected to return the risk free rate so that μ_ht, the present value of the expected return, is zero. We shall assume this in the following, unless explicitly stated otherwise.

Without the drift adjustment, the normal linear VaR formula is simply

Henceforth in this chapter we shall also drop the implicit dependence of the VaR estimate on the time at which the estimate is made, and write simply

for the 100α% h-day VaR estimate made at the current point in time, when the portfolio's expected return is the discount rate.

Scaling VaR to Different Risk Horizons

When normal linear VaR estimates are based on daily returns to the portfolio, we obtain a 1-day VaR estimate using the daily mean μ₁ and standard deviation σ₁ in the VaR formula. How can we scale this 1-day VaR estimate up to a 10-day VaR estimate, or more generally to an h-day VaR estimate?

The normal linear VaR estimate assumes that the daily returns are i.i.d. We have to approximate the returns by the log returns, as explained in Section IV.1.5.4, then

• the h-day mean is h × daily mean, μ_h = hμ₁;
• the h-day variance is h × daily variance, .

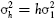In this case, it now follows directly from (IV.2.5) that

So, under the assumption of i.i.d. returns, it is only when the portfolio is expected to return the discount rate, i.e. μ₁ = 0, that

Note that the scaling argument above applies to any base frequency for the VaR. For instance, we could replace ‘day’ with ‘month’ above. Then the square-root-of-time scaling rule will apply to scaling the 1-month VaR to longer horizons, but only if we assume the monthly return on the portfolio is the risk free (discount) rate. For example, if this assumption holds and the 1-month VaR is 10% of the portfolio value, then the 6-month VaR will be of the portfolio value. When returns are normal and i.i.d. and the expected return on the portfolio is the risk free rate, we could also apply the square-root law for scaling from longer to shorter horizons. For example, annual VaR = 25%⇒ monthly VaR = 25% × 12^−½ = 7.22%.

However, the square-root scaling rule should be applied with caution. Following our discussion in Section IV.1.5.4, we know that even when the returns are i.i.d. the square-root scaling rule is not very accurate, except for scaling over a few days, because we have to make a log approximation to returns and this approximation is only accurate when the return is very small.⁹ Moreover, it does not usually make sense to scale 1-day VaR to risk horizons longer than a few days, because the risk horizon refers to the period over which we expect to be able to liquidate (or completely hedge) the exposure. Typically portfolios are rebalanced very frequently and the assumption that the portfolio weights or risk factor sensitivities remain unchanged over more than a few days is questionable. Hence, to extrapolate a 1-day VaR to, for instance, an annual VaR using a square-root scaling rule is meaningless.

How Large is VaR?

The assumption that portfolio returns are i.i.d. and normal is usually not justified in practice, so the normal linear VaR model gives only a very crude estimate for VaR. However, this is still very useful as a benchmark. It provides a sort of ‘plain vanilla’ VaR estimate for a linear portfolio, against which to measure more sophisticated models.

Table IV.2.1 illustrates the normal linear VaR given by (IV.2.6) for different levels of volatility and some standard choices of significance level and risk horizon. All VaR estimates are expressed as a percentage of the portfolio value. Each row corresponds to a different volatility, and these volatilities range from 5% to 100%. We only include risk horizons of 1 day and 10 days in the table, since the VaR for other risk horizons can easily be derived from these. In fact, we only really need to display the 1-day VaR figures, because the corresponding 10-day VaR is just times the 1-day VaR under the i.i.d. normal assumption.

Table IV.2.1 Normal linear VaR for different volatilities, significance levels and risk horizons

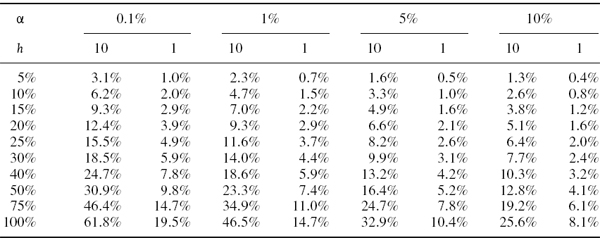
In our empirical examples we shall very often calculate the 1% 10-day VaR, as this is the risk estimate that is used for market risk regulatory capital calculations. Hence, from the results in Table IV.2.1:

• in major currency portfolios that have recently had volatility in the region of 10%, we would expect the 1% 10-day VaR estimate to be about 5% of the portfolio value;
• equity portfolios, with volatilities running at 40–60% at the time of writing, could have 1% 10-day VaR of about 25% of the portfolio value;
• credit spreads have been extremely volatile recently and so interest rate VaR is unusually high at the moment, unless all counterparties have AA credit rating;
• energy portfolios, and many other commodity portfolios, tend to have the highest VaR. With oil prices being highly volatile at the time of writing, the 1% 10-day VaR for energy portfolios could be up to 40% of the portfolio value!

IV.2.2.2 Analytic Formula for Normal VaR when Returns are Autocorrelated

It is important to simplify models when they are applied to thousands of portfolios every day. A very common simplification is that returns are not only normally distributed but also generated by an i.i.d. process. But in most financial returns series this assumption is simply not justified. Many funds, and hedge funds in particular, smooth their reported results, and this introduces a positive autocorrelation in the reported returns. Even when returns are not autocorrelated, squared returns usually are, when they are measured at the daily or weekly frequency. This is because of the volatility clustering effects that we see in most markets.

There are no simple formulae for scaling VaR when returns have volatility clustering. Instead, we could apply a GARCH model to simulate daily returns over the risk horizon, as explained in Sections IV.3.3.4 and IV.4.3. In this section we derive a formula for scaling VaR under the assumption that the daily log returns r_t are not i.i.d. but instead they follow a first order autoregressive process where is the autocorrelation, i.e. the correlation between adjacent log returns.¹⁰

Write the h-period log return as the sum of h consecutive one-period log returns:

Assuming the log returns are identically distributed, although no longer independent, we can set μ = E(r_t+i) and σ² = V(r_t+i) for all i. Autocorrelation does not affect the scaling of the expected h-period log return, since . So the h-day expected log return is the same as it is when the returns are i.i.d.

But autocorrelation does affect the scaling standard deviation. Under the first order autoregressive model the variance of the h-period log return is

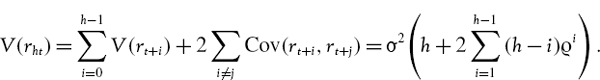
Now we use the identity

Setting x = and n = h − 1 in (IV.2.8) gives

This proves that when returns are autocorrelated with first order autocorrelation coefficient then the scaling factor for standard deviation is not but , where

Hence, we should scale normal linear VaR as

Even a small autocorrelation has a considerable effect on the scaling of volatility and VaR. The following example shows that this effect is much more significant than the effect of a mean adjustment term when the portfolio is not expected to return the risk free rate. Thus for the application of parametric linear VaR to hedge funds, or any other fund that smoothes its returns, the autocorrelation adjustment is typically more important than an adjustment to the VaR that accounts for a positive expected excess return.

EXAMPLE IV.2.1: ADJUSTING NORMAL LINEAR VAR FOR AUTOCORRELATION

Suppose a portfolio's daily log returns are normally distributed with a standard deviation of 1% and a mean of 0.01% above the discount rate. Calculate (a) the portfolio volatility and (b) the 1% 10-day normal linear VaR of the portfolio under the assumption of i.i.d. daily log returns and under the assumption that daily log returns are autocorrelated with first order autocorrelation = 0.2.

SOLUTION Under the i.i.d. assumption and assuming 250 trading days per year, the annual excess return is 0.01% × 250 = 2.5% and the volatility is

The 1% 10-day VaR is

That is, the 1% 10-day VaR is 7.26% of the portfolio's value.

But under the assumption that daily log returns have an autocorrelation of 0.2, the volatility and the VaR will be greater. The adjustment factor, i.e. the second term on the right-hand side of (IV.2.10) is calculated in the spreadsheet. It is 124.375 for h = 250, and 4.375 for h = 10. Hence, the volatility is

and the 1% 10-day VaR is

That is, the 1% 10-day VaR is now 8.72% of the portfolio's value.

Following this example, some general remarks are appropriate.

• Even this relatively small autocorrelation of 0.2 increases the 1% 10-day VaR by about one-fifth, whereas the daily mean excess return of 0.01% (equivalent to an annual expected return of 2.5% above the discount rate) only decreases the 1% 10-day VaR by 0.1%.
• The higher the autocorrelation and the longer the risk horizon, the greater the effect that a positive autocorrelation has on increasing the VaR. For higher autocorrelation and longer risk horizons, the VaR could easily double when autocorrelation is taken into account. And of course, negative autocorrelation decreases the VaR in a similar fashion.

IV.2.2.3 Systematic Normal Linear VaR

For reasons that have been discussed in the previous chapter, it is almost always the case that the risk manager will map each portfolio to a few well-chosen risk factors.¹¹ The systematic return or P&L on a portfolio is the part of the return that is explained by variations in the risk factors. In a linear portfolio it may be represented as a weighted sum,

where X_i denotes the return or P&L on the ith risk factor and the coefficients θ_i denote the portfolio's sensitivity to the ith risk factor.¹² If we use the risk factor returns on the right-hand side of (IV.2.12) rather than their P&L, and the sensitivities are measured in percentage terms, then Y is the systematic return; otherwise Y is the systematic P&L on the portfolio.¹³

To calculate the systematic normal linear VaR we need to know the expectation E(Y_h) and variance V(Y_h) of the portfolio's h-day systematic return or P&L. We can use the factor model (IV.2.12) to express these in terms of the expectations, variances and covariances of the risk factors. To see this, write the vector of expected excess returns on the risk factors as

write the vector of current sensitivities to the m risk factors as θ =(θ₁,…, θ_m)′ and denote the m × m covariance matrix of the h-day risk factor returns by Ω_h. Then the mean and variance of the portfolio's h-day systematic returns or P&L may be written in matrix form as¹⁴

The normal linear VaR model assumes that risk factors have a multivariate normal distribution; hence, the above mean and variance are all that is required to specify the entire distribution. Substituting (IV.2.13) into (IV.2.5) gives the following formula for the 100α% h-day systematic VaR:

In many cases we assume that the expected systematic return is equal to the discount rate, in which case the discounted mean P&L will be zero and (IV.2.14) takes a particularly simple form:

The above shows how the systematic normal linear VaR can be obtained straight from the risk factor mapping. We only need to know the current:

• estimate of the risk factor sensitivities θ;
• forecast of the h-day risk factor returns covariance matrix Ω_h.

Note that both these inputs can introduce significant errors into the VaR estimate, as will be discussed in detail in Chapter IV.6.

A common assumption is that each of the risk factors follows an i.i.d. normal process. In the absence of autocorrelation or conditional heteroscedasticity in the processes, the square-root-of-time rule applies. In this case,

In other words, each element in the 1-day covariance matrix is multiplied by h. Thus, just as for the total VaR in (IV.2.7), the h-day systematic VaR (IV.2.15) can be scaled up from the 1-day systematic VaR using a square-root scaling rule:

Two simple numerical examples of normal linear systematic VaR have already been given in Section IV.1.6. A large number of much more detailed examples and case studies on normal linear systematic VaR for cash flows, stock portfolios, currency portfolios and portfolios of commodities will be given in this chapter and later in the book.

IV.2.2.4 Stand-Alone Normal Linear VaR

In Section IV.1.7 we explained, in general non-technical terms, how systematic VaR may be disaggregated into components consisting of either stand-alone VaR or marginal VaR, due to different types of risk factor. The stand-alone VaR is the systematic VaR due to a specific type of risk factor. So, depending on the type of risk factor, stand-alone VaR may be called equity VaR, forex VaR, interest rate VaR, credit spread VaR or commodity VaR.

Due to the diversification effect between risk factor types, and using the summation rule for the variance operator, in the normal linear model the sum of the stand-alone VaRs is greater than or equal to the total systematic VaR, with equality only in the trivial case where all the risk factors are perfectly correlated. However, in the next subsection we show how to transform each stand-alone VaR into a corresponding marginal VaR, where the sum of the marginal VaRs is equal to the total risk factor VaR.

In this subsection we specify the general methodology for calculating stand-alone VaRs in the normal linear VaR model. Although the derivation of theoretical results is set in the context of the normal linear VaR model, it is important to note that similar aggregation and decomposition rules apply to the other parametric linear VaR models that we shall introduce later in this chapter.

For the disaggregation of systematic VaR into different components we need to partition the risk factor covariance matrix Ω_h into sub-matrices corresponding to equity index, interest rate, credit spread, forex and commodity risk factors. In the following we illustrate the decomposition when there are just three risk factor types, and we shall assume these are the equity, interest rate and forex factors. Although we do not cover this explicitly here, other classes of risk factor may of course be included.

Let the risk factor sensitivity vector θ, estimated at the time that the VaR is measured, be partitioned as

where θ_E, θ_R and θ_X are column vectors of equity, interest rate and forex risk factor sensitivities. For simplicity we assume the interest rate exposure is to only one risk free yield curve, but numerical examples of interest rate VaR when there are several yield curve risk factors and the exposures are to lower credit grade entities are given in Section IV.2.3.

For ease of aggregation it is best if all three vectors θ_E, θ_R and θ_X are expressed in percentage terms, or all three are expressed in nominal terms. Table IV.2.2 explains how these vectors are measured, and here we assume the numbers of equity, interest rate and forex risk factors are n_E, n_R and n_X respectively. We also use the notation:

• P to denote the value of the portfolio in domestic currency at the time the VaR is measured;
• β_i to denote the portfolio's percentage beta with respect to the ith equity risk factor;
• PV01_i to denote the portfolio's PV01 with respect to the ith interest rate risk factor;
• X_i to denote the portfolio's nominal exposure to the ith foreign currency in domestic terms.

Table IV.2.2 Risk factor sensitivities

Now we partition the h-day covariance matrix Ω_h into sub-matrices of equity risk factor return covariances Ω_Eh, interest rate risk factor return covariances Ω_Rh and forex risk factor return covariances Ω_Xh and their cross-covariance matrices Ω_ERh, Ω_EXh and Ω_RXh. Thus we write the risk factor covariance matrix in the form

This partitioned matrix has off-diagonal blocks equal to the cross-covariances between different types of risk factors. For instance, if there are five equity risk factors and four foreign exchange risk factors, the 5 × 4 matrix Ω_EXh contains the 20 pairwise h-day covariances between equity and foreign exchange factors, with i,jth element equal to the covariance between the ith equity risk factor and the jth forex risk factor.

Ignoring any mean adjustment, the systematic normal linear VaR is given by (IV.2.15) with θ partitioned as in (IV.2.17) and with Ω_h given by (IV.2.18). With this notation it is easy to isolate the different risk factor VaRs.

• Equity VaR, i.e. the risk due to equity risk factors alone: Set θ_R = θ_X = 0 and (IV.2.15) yields

  

• Interest rate VaR, i.e. the risk due to interest rate risk factors alone: Set θ_E = θ_X = 0 and (IV.2.15) yields

  

• Forex VaR, i.e. the risk due to forex risk factors alone: Set θ_E = θ_R = 0 and (IV.2.15) yields

  

Even if the cross-covariance matrices are all zero the total VaR would not be equal to the sum of these three ‘stand-alone’ VaRs. The only aggregation rules we have are that the sum of the stand-alone components equals the total systematic VaR if and only if the risk factors are all perfectly correlated, and that the sum of the squared stand-alone VaRs is equal to the square of the total VaR if the cross correlations between risk factors are all zero.¹⁵

IV.2.2.5 Marginal and Incremental Normal Linear VaR

In Section IV.1.7.3 we showed that the total systematic VaR is equal to the sum of the marginal component VaRs, to a first order approximation. In the normal linear model the gradient vector (IV.1.29) is obtained by differentiating (IV.2.15) with respect to each component in θ.

Using our partition of the covariance matrix as in (IV.2.18) above, and the risk factor sensitivities vector θ partitioned as in (IV.2.17), the equity marginal VaR is given by the approximation (IV.1.30) with θ_R = θ_X = 0, and so forth for the other component VaRs. That is, we set the other risk factor sensitivities in θ to zero, compute the gradient vector and then approximate the marginal VaR as

In Section IV.1.7.3 we also showed how to use the gradient vector to assess the VaR impact of a trade, i.e. to compute the incremental VaR. In the specific case of the normal linear VaR model the incremental VaR is, to a first order approximation, given by

where θ is the original risk factor sensitivity vector and Δθ is the change in the risk factor sensitivity vector as a result of the trade. Note that this approximation can lead to significant errors if used on large trades. The approximation rests on a Taylor linearization of the parametric linear VaR, but the parametric linear VaR is actually a quadratic function of the sensitivity vector.

To apply the general formulae (IV.2.22) and (IV.2.23) we must derive the gradient vector g(θ) under the normal linear VaR model assumptions. The 100α% h-day normal linear systematic VaR is given by (IV.2.25). Differentiating this, using the chain rule, gives the gradient vector of first partial derivatives, which in this case is

The gradient vector, which Garman (1996) calls the DelVaR vector, has elements equal to the derivative of VaR with respect to each of the components in θ. Now using (IV.2.22) gives the marginal VaR. A numerical illustration of the formula is given in Example IV.2.5 below.

Specific examples of the decomposition of normal linear VaR into stand-alone and marginal VaR components, and of the calculation of incremental VaR, will be given below. For instance, see Examples IV.2.4–IV.2.6 for cash flows and Examples IV.2.14–IV.2.16 for international equity portfolios.

IV.2.3 NORMAL LINEAR VALUE AT RISK FOR CASH-FLOW MAPS

This section analyses the normal linear VaR of a portfolio of bonds, loans or swaps, each of which can be represented as a cash flow. The risk factors are one or more yield curves, i.e. sets of fixed maturity interest rates of a given credit rating. Later in this section we shall decompose each interest rate into a LIBOR rate plus a credit spread. In that case the risk factors are the LIBOR curves and possibly also one or more term structures of credit spreads with different credit ratings.

The excess return on the portfolio over the discount rate will be significantly different from zero only when the portfolio has many exposures to low credit quality counterparties and when the risk horizon is very long. Since the PV01 vector is expressed in present value terms, and since there is no constant term in the risk factor mapping of a cash flow, the discounted expected return on the portfolio is zero, so it is only the volatility of the portfolio P&L that determines the VaR.

In this section all cash flows are assumed to have been mapped to standard maturity interest rates in a present value and volatility invariant fashion. Since we have covered cash-flow mapping in considerable detail in Section III.5.3, and furnished several numerical examples there, we shall assume the reader is familiar with cash-flow mapping in the following. We characterize a portfolio by its mapped cash flow at standard vertices, or by its PV01 sensitivity vector directly.

IV.2.3.1 Normal Linear Interest Rate VaR

We begin by considering only the interest rate risk factors, without decomposing these into LIBOR and credit spread components. In Section IV.1.6.3 we derived a formula for normal linear interest rate VaR, repeated here for convenience:

where θ = (PV01₁,…, PV01_n)′ is the vector of PV01 sensitivities to the various interest rates that are chosen for the risk factors.

A simple example of normal linear VaR for a cash-flow portfolio was given in Section IV.1.6.3, and the first remark that we make here is that in that example the covariance matrix was expressed in basis points. The reason for this is that the PV01 vector contains the risk factor sensitivities to absolute, basis point changes in interest rates, and not to relative changes.

In highly developed markets, returns on fixed income portfolios are usually measured in terms of changes, rather than relative terms. This is natural because the change in the interest rate is the percentage return on the corresponding discount bond. Volatilities of changes in interest rates are often of the order of 100 basis points. But in some countries, such as Brazil or Turkey (at the time of writing), interest rates are extremely high and variable and their volatilities are so high that they are commonly quoted in percentage terms. In this case care should be taken to ensure that the PV01 sensitivities are also adjusted to relate to percentage changes in interest rates or, when PV01 sensitivities relate to changes, the covariance matrix of interest rates must be converted to basis point terms. The following example illustrates how to do this, assuming the returns are normal and i.i.d.

EXAMPLE IV.2.2: CONVERTING A COVARIANCE MATRIX TO BASIS POINTS

Suppose two interest rates have a correlation of 0.9, that one interest rate is at 10% with a volatility of 30% and the other is at 8% with a volatility of 25%. What is the daily covariance matrix in basis point terms?

SOLUTION For the 10% rate with 30% volatility, the volatility is 0.1 × 0.3 = 300 basis points; for the 8% rate with 25% volatility, the volatility is 0.08 × 0.25 = 200 basis points. For the correlation of 0.9, the covariance is 0.9 × 300 × 200 = 54,000 in basis points squared. Hence the annual covariance matrix is

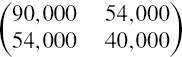
and, assuming 250 trading days per year, the daily covariance matrix is, in basis point terms

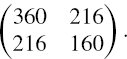
IV.2.3.2 Calculating PV01

Consider a cash flow C_T at some fixed maturity T, measured in years, which we assume for simplicity is an integer.¹⁶ The present value of the cash flow based on a discretely compounded discount rate R_T, expressed in annual terms, is

Then, by definition,

A useful and very accurate approximation to (IV.2.27) is derived in Section III.1.8.2. It is repeated here for convenience:

Again, this is valid when T is an integer number of years. Otherwise a small adjustment should be made to the discount factor, as explained in Section III.1.8.2.

Because of the unwanted technical details when working with discretely compounded rates, practitioners usually convert discretely compounded rates into their continuously compounded equivalents for calculations. Using the continuously compounded rate r_T that gives the same present value as the discretely compounded rate, we have, for any maturity T, not necessarily an integral number of years,

Thus the PV01 approximation for any T may be written

See Section III.1.8.2 for further details and numerical examples.

The examples in the remainder of this section assume that a cash flow has been previously mapped to the interest rate risk factors, and that the values of the mapped cash flows are not discounted to present value terms. This is because the PV01 vector θ of risk factor sensitivities themselves will convert the change in portfolio value at some time in the future into present value terms.

We now consolidate the application of the normal linear VaR model to cash-flow portfolios by considering a simple numerical example. We make the assumption that the interest rate risk factors are the same as those used for discounting, so there is no drift adjustment term in the VaR formula. We also assume that interest rate changes are generated by i.i.d. multivariate normal processes, so that we can scale the normal linear VaR using the square-root-of-time rule. In particular, the h-day covariance matrix is just h times the 1-day covariance matrix.

EXAMPLE IV.2.3: NORMAL LINEAR VAR FROM A MAPPED CASH FLOW

Consider a cash flow of $1 million in 1 year and of $1.5 million in 2 years' time. Calculate the volatility of the discounted P&L of the cash flows, given that:

• the 1-year interest rate is 4% and the 2-year interest rate is 5%;
• the volatility of the 1-year rate is 100 basis points, and the volatility of the 2-year rate is 75 basis points; and
• their correlation is 0.9.

Hence calculate the 5% 1-day and the 1% 10-day normal linear VaR.

SOLUTION In the spreadsheet we use (IV.2.27) to calculate the PV01 vector as

Then we calculate the covariance matrix in basis point terms from the volatilities and correlation, as described above, yielding

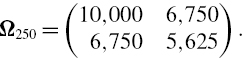
Now the volatility of discounted P&L is

To convert this into a 100α% h-day VaR figure we use the relevant standard normal critical value from (IV.2.4) and the square-root-of-time rule. Assuming 250 risk days per year, the 5% 1-day VaR corresponding to the volatility of $28,052 is

Similarly, assuming the number of 10-trading-day periods per year is 25, the 1% 10-day VaR is

IV.2.3.3 Approximating Marginal and Incremental VaR

The gradient vector (IV.2.24) allows us to express, to a first order approximation, the incremental effect on VaR resulting from each of the cash flows in a trade. Denote the change in the PV01 cash-flow sensitivity vector as a result of a small trade by Δθ. Each incremental VaR corresponding to a cash flow at one specific maturity is an element of another vector Δθ ⊗ g(θ), where ⊗ denotes the column vector obtained as the element by element product of two column vectors. The net incremental VaR of the new trade is given by the sum of the separate components of this vector, i.e. by (IV.2.23). Using this in (IV.2.23) will give a first order approximation to the change in VaR when any of the PV01 cash-flow sensitivities change.

The following example illustrates how we can approximate the effect of a new trade on the VaR by considering only the cash flow resulting from the proposed trade, thus avoiding the need to revalue the VaR for the entire portfolio each time a new trade is considered.

EXAMPLE IV.2.4: INCREMENTAL VAR FOR A CASH FLOW

Consider a cash-flow map with the following sensitivity vector:

Suppose the interest rates at maturities 1, 2 and 3 years have volatilities of 75 basis points, 60 basis points and 50 basis points and correlations of 0.95 (1yr, 2yr), 0.9 (1yr, 3yr), and 0.975 (2yr, 3yr). Find the 1% 10-day normal linear VaR. Now assume that interest rates are 4%, 4.5% and 5% at the 1-year, 2-year and 3-year vertices and suppose that a trader considers entering into a swap with the following cash flow:

What is the incremental VaR of the trade?

SOLUTION The 1-day risk factor covariance matrix, in basis point terms, is

For instance, the top left element 22.5 for the 1-day variance of the 1-year rate is obtained as 75²/250 = 22.5. We are given

and so

The square root of this, i.e. $16,443, is the 1-day standard deviation of the discounted P&L. The 10-day standard deviation is obtained, using the square-root-of-time rule, as

Hence the 1% 10-day normal linear VaR is

For a 10-day risk horizon,

From above we have . Hence the DelVaR vector is

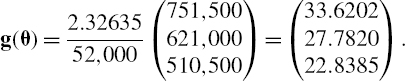
Calculating the PV01 sensitivity vector of the swap's cash flows, using (IV.2.27) gives

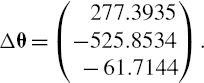
Hence, the components of the incremental VaR are

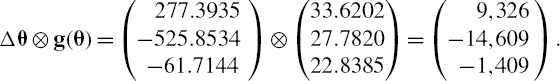
This shows that the positive cash flow at 1 year increases the VaR by approximately $9326 but both of the negative cash flows on the swap will decrease the VaR, by approximately $14,609 and $1409 respectively. The total incremental VaR for the swap is the sum of these, i.e. approximately −$6693. Hence, adding the swap would reduce the VaR of the portfolio.

Incremental VaR is based on a linear approximation to the VaR, which is a non-linear function of the risk factor sensitivities, so it should only be applied to assess the effect of trades that are small relative to the overall size of the portfolio. Also, in order to properly compare the incremental VaR of several different trades, the cash flows from these trades need to be normalized. Obviously, if trade A has double the magnitude of the cash flows of trade B, the incremental VaR of trade A will be twice that of trade B. That is, we should normalize the trades, so that the incremental VaRs per unit of cash flow are compared. There are several ways of doing this. For instance, we could divide each PV01 by the sum of the absolute values of all PV01s in the sensitivity vector of the trade, or we could divide each PV01 by the square root of the sum of the squared PV01s. More details are given in Garman (1996).

IV.2.3.4 Disaggregating Normal Linear Interest Rate VaR

In this subsection we continue with simple numerical examples of normal linear interest rate VaR to examine the case of an exposure to two yield curves. Such an exposure arises in many circumstances: it can result from an international portfolio containing interest rate sensitive securities; or from any type of foreign investment in forwards and futures;¹⁷ even in international commodity portfolios, where we may prefer to use constant maturity futures as risk factors, the forex risk is usually managed by hedging with forex forwards and these are mapped to the spot forex rate. A forex forward mapping thus gives rise to an exposure to the foreign LIBOR curve.

In equity and commodity portfolios the interest rate risk factors are usually much less important than the equity or commodity risk factors and, for international portfolios, the forex risk factors. Usually the equity, commodity, interest rate and forex risk exposures are managed by separate desks. Hence, in the examples in this section we keep things simple by considering only the interest rate part of the risk.

EXAMPLE IV.2.5: NORMAL LINEAR VAR FOR AN EXPOSURE TO TWO YIELD CURVES

In Table IV.2.3 we display the PV01 vectors, both in US dollars, for a portfolio with exposures to the UK and US government yield curves. For simplicity we assume the portfolio has been mapped to only the 1-year, 2-year and 3-year interest rates in each county, and the basis point volatilities for these interest rates are given below each PV01. The correlation matrix of daily interest rates is given in Table IV.2.4. Calculate the 1% 10-day normal linear interest rate VaR, the stand-alone VaR due to the US and UK yield curve risk factors, and the marginal VaRs of these risk factors.

Table IV.2.3 PV01 of cash flows and volatilities of UK and US interest rates

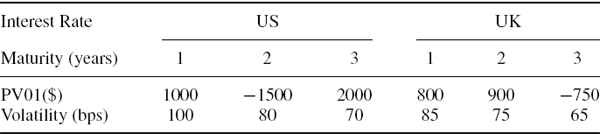
Table IV.2.4 Correlations between UK and US interest rates

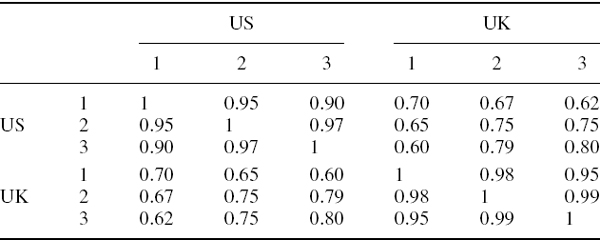
SOLUTION Using the information given in Tables IV.2.3 and IV.2.4, the annual covariance matrix is written in partitioned form as

where

We also write the PV01 vector as

where

Under the usual normal i.i.d. assumption, the 1% 10-day total risk factor VaR is then

For the stand-alone US interest rate VaR we simply use Ω_US and θ_US in place of Ω and θ (and similarly, we use Ω_UK and θ_UK for the UK interest rate VaR). The results, which are calculated in the spreadsheet for this example, are:

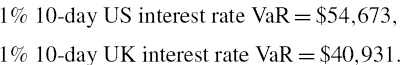
So the sum of the stand-alone VaRs is $95,604, which is considerably more than the total interest rate VaR.

However, the marginal VaRs do add up to the total interest rate VaR. To calculate these we first compute the DelVaR vector g (θ) using (IV.2.24). Working at the annual level,¹⁸ we have

Now we can recover the 1% annual total interest rate VaR as θ′g (θ) and the two 1% annual marginal VaRs as

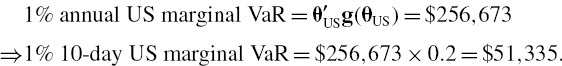
Similarly,

The sum of the marginal VaRs is $87,688, which is identical to the total interest rate VaR.

IV.2.3.5 Normal Linear Credit Spread VaR

An exposure to curves with different credit ratings arises from a portfolio with investments in company bonds, corporate loans or swaps, asset backed securities, collateralized debt obligations and non-bank loans such as mortgages. All exposures can be mapped as cash flows at standard vertices, and for each vertex we represent the risk factors as the LIBOR rate of that maturity and the various spreads over LIBOR for each credit rating.

We now explain how to decompose the linear VaR of an interest rate sensitive portfolio into LIBOR and spread components, using continuous compounding (because the mathematics is so much easier). In this case we may write an interest rate of a given credit rating as the sum of the continuously compounded LIBOR rate and the continuously compounded credit spread for that rating. That is, for maturity T and at time t,

where r(t, T) denotes the spot LIBOR rate with maturity T at time t, and r_q(t, T) and s_q(t, T) respectively denote the interest rate and credit spread, both with credit rating q.

The VaR is calculated in exactly the same way as above, and the only difference is that the variance of the interest rate r_q(t, T) can, if we wish, be decomposed into three terms: the variances of the LIBOR rate and the credit spread, and their covariance. This variance decomposition is obtained by applying the variance operator to (IV.2.31):

We now explain how to decompose the total interest rate VaR into LIBOR VaR and credit spread VaR, for a portfolio of a given credit rating, in the context of the normal linear model. Dropping the time and maturity dependence for simplicity, we denote the set of interest rates of credit rating q with different maturities by the vector r_q, the LIBOR rates of these maturities by r and the corresponding credit spreads by s_q.

We account for the correlations between interest rates using the yield curve covariance matrix, and now we partition this matrix into LIBOR and spread covariance matrices, and their cross-covariance matrix, as

If we want to make the risk horizon of the matrix explicit, then the covariance matrix corresponding to h-day changes in interest rates is written as

Suppose there are n LIBOR rate and n credit spread risk factors at the same maturities. The four matrices in the partition on the right-hand side of (IV.2.34) are then n × n matrices and Ω has dimension 2n × 2n. Now, what is the 2n × 1 risk factor sensitivity vector? The PV01 sensitivity to the change in interest rate of a given maturity is the change in the present value of the cash flow for a one basis point fall in that interest rate. But since the interest rate is the sum of the LIBOR rate and the credit spread, this one basis point fall could be in either the LIBOR rate or the credit spread of that maturity. Thus, assuming the vertices of the risk factor mapping are the same for LIBOR and credit spreads, the PV01 is same for both LIBOR and the credit spread. In other words, with the decomposition (IV.2.34) of the covariance matrix, the corresponding PV01 is the vector with the PV01s at the n vertices in the LIBOR rate risk factor set, and then these are repeated for the vertices in the credit spread risk factor set. Thus where in this case

But due to the limitations of historical data, it usually the case that the maturities at which credit spreads are recorded are a proper subset of the maturities in the LIBOR rate risk factor set.¹⁹ So in general, θ_R ≠ θ_S because they do not even have the same dimension.

Now the total VaR due to LIBOR and spread is given by the usual formula,

Setting θ_R = 0 gives the stand-alone credit spread VaR, and setting θ_S = 0 gives the stand-alone LIBOR VaR. The marginal contributions to VaR and the incremental VaR of a new trade are all calculated using the gradient vector in the usual way.

The extension of this decomposition to a portfolio containing exposures with several credit ratings is straightforward. For example, with two credit ratings in the portfolio we decompose the covariance matrix thus:

and the PV01 vector is written as the column vector

where θ_R is the PV01 of the combined exposure to the two different credit ratings, θ_S1 is the PV01 of the exposure to the first credit rating, and θ_S2 is the PV01 of the exposure to the second credit rating.

The following example illustrates the decomposition of interest rate VaR for a portfolio with exposures to a single credit rating.

EXAMPLE IV.2.6: SPREAD AND LIBOR COMPONENTS OF NORMAL LINEAR VAR

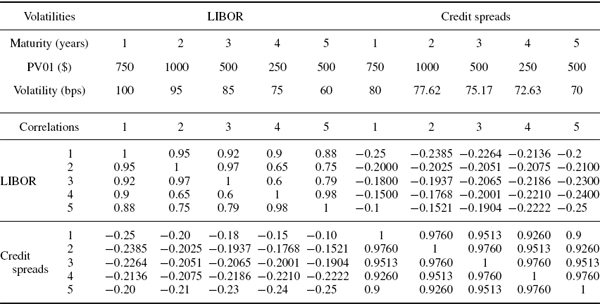
A portfolio of A-rated corporate bonds and swaps has its cash flows mapped to vertices at 1 year, 2 years, 3 years, 4 years and 5 years. The volatilities of the LIBOR rates (in basis points per annum) and PV01 vector of the portfolio are shown in Table IV.2.5. The correlations of the LIBOR rates are shown in Table IV.2.6.

The 1-year and 5-year A-rated credit spreads are, like the LIBOR parameters, assumed to have been estimated from a historical sample. Suppose the 1-year spread has volatility 80 basis points per annum and the 5-year spread has volatility 70 basis points per annum, and their correlation is 0.9. Suppose the cross correlations between these credit spreads and the LIBOR rates of different maturities are as shown in Table IV.2.7. Estimate the 1% 10-day total interest rate VaR and decompose the total VaR into the VaR due to LIBOR rate uncertainty, and the VaR due to credit spread uncertainty. Then estimate the marginal VaR of the LIBOR and credit spread components.

Table IV.2.5 PV01 of cash flows and volatilities of LIBOR rates

Table IV.2.6 Correlations between LIBOR rates

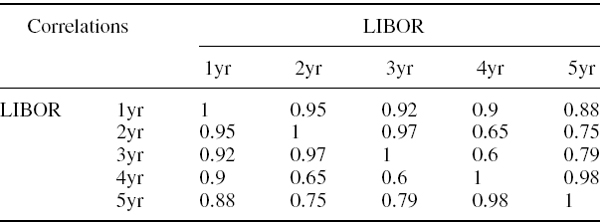
Table IV.2.7 Cross correlations between credit spreads and LIBOR rates

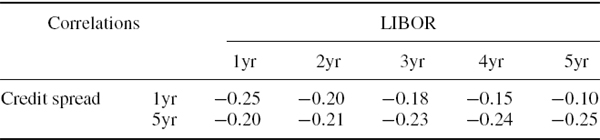
SOLUTION We shall employ a simple linear interpolation between variances and between squared correlations to fill in the elements of the matrices Ω_S and Ω_RS.²⁰ The full matrix Ω is a10 × 10 matrix, and the volatilities and correlations in this matrix are shown in Table IV.2.8.

The PV01 vector is

with

This yields the 1% annual total risk factor VaR:

Table IV.2.8 Volatilities and correlations of LIBOR and credit spreads

Multiplying this by gives the 1% 10-day total risk factor VaR as $137,889.

For the stand-alone LIBOR VaR we simply use Ω_R and θ_R in place of Ω and θ (and similarly, we use Ω_S and θ_S for the credit spread VaR). The results, which are calculated in the spreadsheet for this example, are:

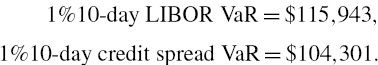
So the sum of the stand-alone VaRs is $220,224, which is much larger than the total VaR, due to the negative correlation between interest rates and credit spreads.

As usual, the marginal VaRs sum to the total VaR. To calculate these we first compute the annual gradient vector using the usual formula. This gives

The 1% annual total VaR is and this has already been calculated as $689,443. The two 1% annual marginal VaRs are

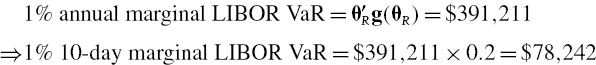
and

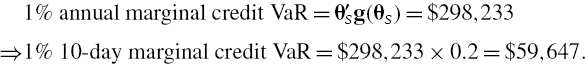
The sum of the marginal VaRs is identical to the total VaR.

IV.2.4 CASE STUDY: PC VALUE AT RISK OF A UK FIXED INCOME PORTFOLIO

The above example employed a cash-flow mapping to just five vertices, and included just one credit rating. But in practice there could be 50 or 60 vertices, and several credit ratings. With n vertices and k credit ratings there will be kn risk factors, so the risk factor correlation matrix could have a very large dimension indeed. However, the risk factors are very highly correlated and for this reason lend themselves to dimension reduction through the use of principal component analysis (PCA).²¹ This section demonstrates how to apply PCA to reduce the dimension of the risk factor space when estimating the VaR of interest rate sensitive portfolios so that the new risk factors (i.e. the principal components) are uncorrelated variables that capture the most commonly experienced moves in interest rates.

We consider a portfolio of UK bonds (and/or swaps) on 31 December 2007. We ignore the credit spread risk and suppose that its cash flows have been mapped to the spot market rates at intervals of one month using the volatility, present value and duration invariant cash-flow map described in Section III.5.3. Then the PV01 of the mapped cash flow is computed as explained in Section III.1.8 and the resulting PV01 vector is depicted in Figure IV.2.2.

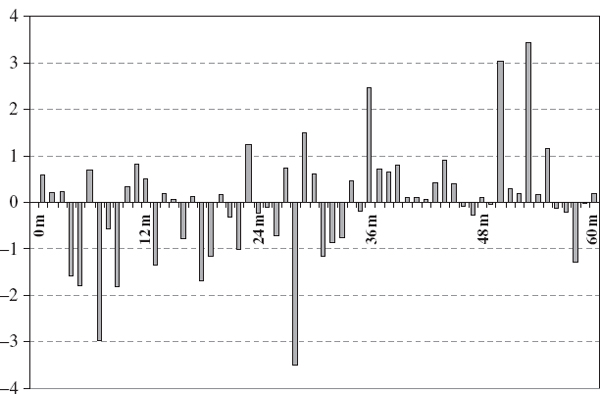
Figure IV.2.2 PV01 vector of a UK fixed income portfolio (£000)

Given the size of the PV01 sensitivities shown in Figure IV.2.2, with several exceeding ±£1000, there must be cash flows of ±£5 million or more at several maturities.²² Hence, the portfolio could contain long positions on bonds with face value of around £1 billion, and short positions on bonds with face value of around £1 billion or more. The present value of the portfolio may be much less than £1 billion of course, because it has a rough balance of positive and negative cash flows.

IV.2.4.1 Calculating the Volatility and VaR of the Portfolio

This section contains two examples, the first showing how to use the cash-flow map and the second showing how to compute the volatility and VaR of the portfolio.

EXAMPLE IV.2.7: APPLYING A CASH-FLOW MAP TO INTEREST RATE SCENARIOS

Consider the portfolio of UK bonds and swaps with PV01 vector θ shown in Figure IV.2.2. Find an approximation to the change in the portfolio's value given that UK interest rates change as follows:

(a) The UK yield curve moves upward with a parallel shift of 10 basis points at all maturities.

(b) There is a tilt in the UK yield curve where the 1-month rate increases by 35 basis points, the 2-month rate by 34 basis points, the 3-month rate by 33 basis points and so on up to the 59-month rate decreasing by 23 basis points and the 60-month rate decreasing by 24 basis points.

SOLUTION In the spreadsheet for this example we apply the relationship (IV.1.25), i.e.

with the basis point changes in interest rates specified in (a) and (b) above. Hence:

(a) Δr =(10, 10,…, 10)′ gives PV = £9518; and

(b) Δr =(35, 34,…, −23, −24)′ gives ΔPV = £396,478.

Since the portfolio has a balance of long and short exposures, its present value does not change much when the yield curve shifts parallel, as is evident in case (a) above. But the portfolio is much more exposed to a change in slope of the yield curve; Figure IV.2.2 shows that the portfolio is predominately short in bonds with maturities up to 3 years but its positions on bonds with maturities between 3 and 5 years are predominately long. Hence, the portfolio will increase in value if the yield curve shifts up at the short end and down at the long end. Indeed, under the scenario for interest rates in (b) above, the portfolio would make a profit of £396,478.

In the next three examples, all of which are contained in the case study workbook, we use an equally weighted covariance matrix Ω₁ of the absolute daily changes in UK interest rates based on data from 2 January 2007 until 31 December 2007.²³ The covariance matrix has dimension 60 × 60, so we do not show it here, although it can be seen in the Excel spreadsheet accompanying the following example.

EXAMPLE IV.2.8: VAR OF UK FIXED INCOME PORTFOLIO

Use the 1-day covariance matrix Ω₁ given in the spreadsheet to find the volatility of the discounted P&L of the portfolio with PV01 vector θ shown in Figure IV.2.2. Assuming that each interest rate change is i.i.d. normally distributed, calculate the 1% 10-day VaR on 31 December 2007.

SOLUTION We first obtain the 1-day variance of the portfolio P&L as

But θ was given in units of £1000. Hence to convert this figure to the P&L volatility we must take the square root, multiply this by the square root of 250 (assuming there are 250 risk days per year) and then also multiply by £1000. The result is

Hence,

IV.2.4.2 Combining Cash-Flow Mapping with PCA

Principal component analysis is a powerful tool for representing any highly correlated system. In Chapter II.2 we explained how to apply PCA to a set of interest rates, and in Section II.2.3 we used the UK bonds that we are considering in this case study as an example. In this section we shall combine a principal component representation with the PV01 vector shown in Figure IV.2.2. In this way we obtain a set of sensitivities to a new set of interest rate risk factors: the first three principal components of the UK yield curve.

The general expression for a principal component representation of the changes in interest rates Δr_t at time t is

where the factor weights matrix W^* is the n × k matrix whose columns are the first k eigenvectors of the covariance matrix of absolute changes in returns; n is the number of risk factors, i.e. the dimension of the covariance matrix; and is the k × 1 column vector of the first k principal components at time t.

We use (IV.2.38) to derive the representation of our UK bond portfolio P&L in terms of sensitivities β to just k orthogonal risk factors (i.e. the principal components) instead of sensitivities to n highly correlated risk factors. Combining (IV.2.37) with (IV.2.38) gives

Hence, the new factor sensitivity vector is the k × 1 vector of constants obtained by taking (minus) the product of the transpose of the component factor weights matrix, W*′, which has dimension k × n, and the n × 1 PV01 vector θ. This way the number of risk factors has been reduced from n to k.

Now the interest rate VaR based on the principal component risk factors is

or, equivalently,

where D = diag (λ₁,…, λ_k) is the diagonal matrix of the first k eigenvalues of the h-day risk factor covariance matrix Ω_h. Note that if n = k (i.e. we only make the risk factors uncorrelated and do not reduce the number of risk factors) then W* = W, i.e. the matrix of all n eigenvectors, and WDW′ = Ω_h. So unless we use PCA to reduce dimensions, the PC VaR estimate is identical to the ordinary interest rate VaR estimate.

The approximation (IV.2.39) of portfolio P&L is now based on new risk factors, i.e. the first k principal components. These are uncorrelated, whereas interest rate risk factors themselves are highly correlated. Moreover, the new sensitivity vector β is just a k × 1 vector, whereas the old PV01 sensitivity vector was an n × 1 vector, where n is much larger than k. In practice it is typical for n to be around 50 or 60 and for k to be only 3 or 4. So there is a huge reduction in dimension from basing VaR measurement on (IV.2.39) rather than using the ordinary risk factor VaR. Yet, the loss of accuracy from using PC VaR as an approximation to the interest rate VaR is negligible, particularly when it is set in the context of all the other sources of model risk in the normal linear VaR model.

The next example shows how to derive the quantities in (IV.2.40) and applies this formula to measure the PC VaR of our UK bond portfolio.

EXAMPLE IV.2.9: USING PRINCIPAL COMPONENTS AS RISK FACTORS

Suppose that the cash-flow representation of the bond portfolio whose PV01 vector is shown in Figure IV.2.2 was taken on 31 December 2007. Also suppose that we base our daily interest rate covariance matrix Ω₁ on daily changes in the UK spot curve for maturities measured at monthly intervals up to 5 years, using the data period from 2 January to 31 December 2007.²⁴ Find a principal component representation based on Ω₁ with three principal components, and specify the diagonal matrix D that has their standard deviations along its diagonal. Then use this principal component representation to calculate the UK bond portfolio's sensitivities to the three principal component risk factors.

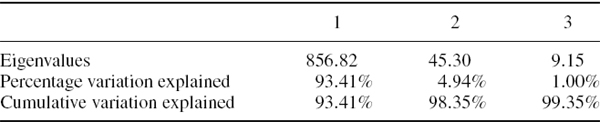
SOLUTION A PCA on the 60 × 60 covariance matrix is given in the Excel workbook for this case study. The first three eigenvalues are shown in Table IV.2.9, and we see that together the first three components explain over 99% of the total variation in UK interest rates over the past year. The first component alone accounts for 93.41% of the variation, so the rates were extremely highly correlated along the yield curve during 2007.

Table IV.2.9 Eigenvalues of covariance matrix of UK spot rates – short end

The first three eigenvectors belonging to these eigenvalues are plotted, as a function of the maturity of the interest rate, in Figure IV.2.3. These have the usual ‘trend–tilt–curvature’ interpretation that we are accustomed to when PCA is applied to a highly correlated yield curve, such as the Bank of England liability curves. However, as is usual for money market rates which are frequently affected by manipulation from the central bank, the very short term rates are less volatile than others, giving the eigenvectors a characteristic ‘dip’ at the short end. For instance, if the first principal component increases but the other components are unchanged, then the 1-month rate will hardly change, but the interest rates at maturities greater than 2 years will all change by a similar amount, i.e. by approximately 15% of the change in the first principal component.

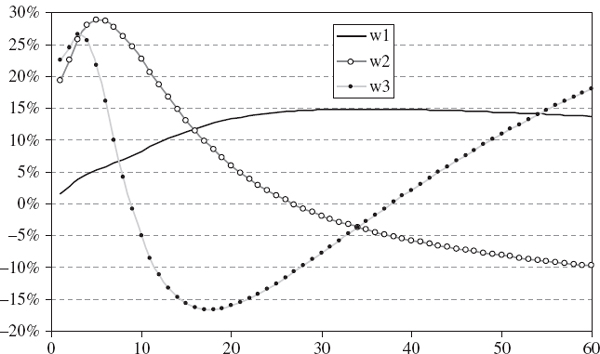
Figure IV.2.3 Eigenvectors of covariance matrix of UK spot rates – short end

The diagonal matrix of standard deviations of the principal components has elements equal to the square root of the eigenvalues in Table IV.2.9, i.e.

Since by definition the first principal component has much the largest standard deviation, this would be the main determinant of the VaR if the sensitivity to each PC were the same. We estimate the PC sensitivity vector β using (IV.2.39), i.e. multiplying the matrix W* whose columns contain the first three eigenvectors by the 60 × 1 vector of PV01 sensitivities shown in Figure IV.2.2. In this way we obtain the new 3 × 1 sensitivity vector β for the principal component factors shown in Table IV.2.10. In fact, the sensitivity to the first PC is the smallest of the three.

Table IV.2.10 Net sensitivities on PC risk factors

Figure IV.2.4 shows the first principal component, which is obtained from the first eigenvector. Since it is based on a covariance matrix that is expressed in basis point terms, the principal component is also measured in basis points. The coefficient of £428 on P1 means that a 100 basis point increase in the first principal component leads, approximately, to a £42,800 increase in the present value of the portfolio. From the first eigenvector in Figure IV.2.3 we see that a 100 basis point increase in the first component would be approximately equivalent to a yield curve movement that is up 15 basis points at maturities over 2 years, but up much less at shorter maturities. Our portfolio has some very large positive cash flows at maturities over 2 years so an upward shift of 15 basis points at the longer maturities, with less movement at the short end, will induce a much larger gain in the portfolio than a parallel shift of 15 basis points. The eigenvalues given in Table IV.2.1 tell us that the first principal component captured a very common type of movement in the yield curve. In fact, it accounts for 93.41% of the variation experienced in the UK government yield curve during 2007. By contrast, the exact parallel shift scenario that we used in Example IV.2.7 is not nearly as common.

Figure IV.2.4 First principal component of the UK spot rates – short end

EXAMPLE IV.2.10: COMPUTING THE PC VAR

Estimate the VaR of the portfolio based on the mapping to the first three principal components, i.e. based on (IV.2.40), and compare this with the full evaluation interest rate VaR from Example IV.2.8.

SOLUTION The spreadsheet for this example first gives the result of estimating the P&L volatility using the β vector shown in Table IV.2.3 and the diagonal covariance matrix of the principal components given by (IV.2.42). This gives

Then we compute the 1% 10-day VaR from this volatility, by multiplying it by the critical value Φ⁻¹(0.99) = 2.32635 and by the scaling factor , giving the 1% 10-day PC VaR as £175,457, compared with £176,549 under full evaluation. The PC approximation leads to only a very small error in VaR (of about 0.6%). The error is a result of taking only three principal components, but this ignores only a small fraction of the variation in the risk factors.

IV.2.4.3 Advantages of Using PC Factors for Interest Rate VaR

In addition to the advantage of dimension reduction, the principal component risk factors make it much easier to apply meaningful scenarios to interest rates. By changing just the first principal component, for instance, we obtain the change in our portfolio's value corresponding to the most likely shift in the yield curve, given the historical data used in the PCA. This is not usually a parallel shift in all yields, but it is approximately parallel at longer maturities, so for a portfolio with a high duration this scenario gives a portfolio sensitivity that is similar to that obtained via the standard duration approximation. But, since interest rates do not normally shift exactly parallel all the time, using a change in the first principal component is more representative of historical movements in yields than a parallel shift.

Moreover, the representation (IV.2.39) provides a more detailed analysis of our portfolio's responses than duration–convexity analysis. In addition to a roughly parallel shift, by changing the second principal component we can find the change in portfolio value corresponding to a specific tilt in the yield curve, i.e. the tilt that is most likely to occur, based on the historical yield curve movements. On changing the third principal component we obtain our portfolio's response to a specific (most likely) change in the yield curve convexity, and so on if more than three principal components are used in (IV.2.39).

Covariance matrix scenarios, which form the basis of many stress tests, are also very easy to implement using PCA. For instance, suppose the original cash-flow mapping of the portfolio is to 50 different maturities of interest rates. Then their covariance matrix is very large, i.e. 50 × 50. Performing stress tests on this matrix will not be a simple task. However, when using the principal component representation (IV.2.39) of the portfolio's P&L, stress tests need only be performed on a k × k covariance matrix, where typically k = 3. PC-based stress tests also take on a meaningful interpretation, i.e. stressing the most common changes in trend, tilt and curvature of interest rates.

Finally, by choosing only the first few components in the representation we have cut down the ‘noise’ in the data that we would prefer not to contaminate our risk measures. In highly correlated yield movements there is very little ‘noise’ and for this reason a three-component representation captures over 99% of the variations in our example. But in less highly correlated yields, much of the idiosyncratic variation in yields may not be useful for risk analysis, especially over the longer term. We saw a small reduction in the PC VaR estimate, compared with the usual VaR estimate, and this is to be expected if some of the variation is ignored. But with the yield curves in major currencies this reduction will be very small indeed. However, other systems such as implied volatilities or equities have much more noise and in this case the use of principal components could reduce VaR more significantly.

IV.2.5 NORMAL LINEAR VALUE AT RISK FOR STOCK PORTFOLIOS

Starting with the simplest case of just a few cash stock positions, we shall consider many linear equity portfolios in this section, including cash and futures positions with and without foreign exchange risk. The systematic parametric linear VaR estimates of an equity portfolio are based on forecasts of expected returns and standard deviations of returns, taken in the context of an equity factor model. Hence, this section draws on the material presented in Chapter II.1, where we covered the different types of factor models that are used for mapping equity portfolios.

IV.2.5.1 Cash Positions on a Few Stocks

In Section I.2.4 we showed how to compute the volatility of portfolio P&L, when the portfolio is characterized by its holdings in each of n stocks and we are given the covariance matrix of the stocks returns. Denote the n × 1 vector of portfolio weights on each stock by w, where each element of w is the holding in that stock divided by the total amount invested, i.e. the current price of the portfolio P. Denote the n × n stock returns annual covariance matrix by V.²⁵ Then the portfolio return volatility is and the P&L volatility is Pσ.

In Section IV.2.2 we showed how to convert a portfolio volatility into a 100α% h-day normal linear VaR estimate, for an arbitrary portfolio, under the assumption that the risk factor returns are multivariate normal and i.i.d. with zero expected excess returns. We ignore the effect on VaR of an expected return that is different from the discount rate, since this is very small unless h is very large. Then, with h measured in days and assuming there are 250 trading days per year, we have

More generally, and particularly when estimating the VaR for long term investments in equity funds, we may wish to include the possibility that the portfolio grows at a rate different from the discount rate over a long risk horizon. In this case we would include the drift adjustment to the VaR, as explained in Sections IV.1.5.1 and IV.2.2.

In the general case, to apply the normal linear VaR formula (IV.2.43) we need to forecast, over a risk horizon of h days, the standard deviation and mean of the portfolio returns. Let

• w denote the current vector of portfolio weights,
• E (x_h) be the n × 1 vector of the stocks' expected excess h-day returns, and
• V_h be the h-day covariance matrix of stock returns.

Then the 100α% h-day normal linear VaR of the portfolio, under the assumption that the risk factor returns are multivariate normal and i.i.d. and expressed as a percentage of the portfolio value P is

The application of this formula is illustrated in the following example.

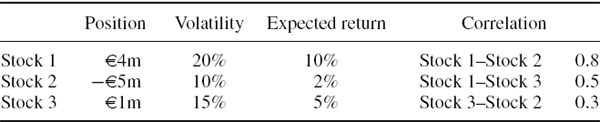
EXAMPLE IV.2.11: VAR FOR CASH EQUITY POSITIONS

Calculate the 1% 10-day parametric linear VaR for a portfolio that has the characteristics defined in Table IV.2.11, discounting using a risk free rate of 5%. How much is the VaR reduced by the mean adjustment? Repeat your calculations for a risk horizon of 1 year.

Table IV.2.11 Stock portfolio characteristics

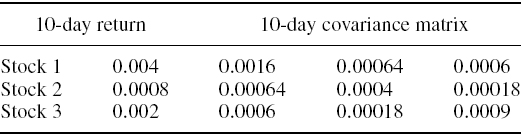
SOLUTION The calculations are performed in the accompanying spreadsheet, using the 10-day expected returns and the covariance matrix of 10-day returns displayed in Table IV.2.12. This gives an expected P&L of €14,000, a P&L standard deviation of €117,898 and a 1% 10-day VaR of €259,765. But without the mean adjustment, i.e. without the second term on the right-hand side of (IV.2.44), the 1% 10-day VaR is €273,738. Hence, the mean adjustment reduces the VaR by about 5%. Over a 1-year risk horizon the 1% VaR is €1,384,864 without the mean adjustment and €1,051,530 with the mean adjustment. Hence, over 1 year the drift adjustment is very important, as it leads to a 24% reduction in VaR.

Table IV.2.12 Characteristics of 10-day returns

Another way of looking at the results in the above example is to use Table IV.2.1, which tells us that the 1% 10-day VaR is very approximately about 10% of the portfolio value, depending of course on the portfolio volatility. So very approximately the VaR is about €100,000 per €1 million invested. In the above example the discount factor over 10 days corresponding to a 5% discount rate is 0.99805, and its effect is therefore about €(1 − 0.99805) million, i.e. approximately €195 per €1 million invested. This is negligible compared with the VaR. However, over a 1-year horizon the VaR is about 50% of the portfolio value, again depending on the portfolio volatility. And the discount factor over 1 year corresponding to a 5% discount rate is 0.95238. So its effect is about (1 − 0.95238) million euros, i.e. approximately €47,620 per €1 million invested, which is not insignificant compared with the VaR.

For simplicity, we shall often ignore discounting when VaR is measured over a short horizon such as 10 days, just as we shall often ignore the mean return. It is only when VaR is measured over a risk horizon of several weeks or months that the errors induced by ignoring the effects of discounting and of a non-zero discounted mean return really affect the accuracy of the VaR estimate. However, and we have stressed this before, such long term VaR estimates are only meaningful to investors who hold positions constant over a long term risk horizon without liquidating or hedging when market conditions are adverse.

IV.2.5.2 Systematic and Specific VaR for Domestic Stock Portfolios

In Section IV.1.7.1 we introduced, in general terms, the disaggregation of total VaR into systematic and specific components. Now we use the normal linear VaR model to provide some numerical examples that illustrate this decomposition for stock portfolios.

Portfolios that contain a large number of equities in the same currency are mapped to their risk factors via a factor model. The set of risk factors may include broad stock market indices, style indices such as value and growth indices of different capitalizations, or statistical factors such as those obtained using PCA. When portfolio returns are represented by a factor model, the systematic parametric linear VaR can be calculated using (IV.2.14) where:

• θ is the vector of stock betas with respect to each risk factor;²⁶
• E(x_h) is the vector of the risk factors’ expected h-day returns; and
• Ω_h is the h-day covariance matrix of the risk factor returns.

For risk assessment (rather than returns forecasting, which is another use of the factor model) the portfolio betas should be as risk sensitive as possible. Hence an exponentially weighted moving average (EWMA) on recent daily data maybe preferred to ordinary least squares (OLS) on weekly or monthly data over a long period. Note that if the betas are estimated using EWMAs, a time series of beta estimates is obtained over the sample period but it is only the last (today's) forecast that we use in the calculation.

EXAMPLE IV.2.12: SYSTEMATIC VAR BASED ON AN EQUITY FACTOR MODEL

A linear model with two risk factors indicates that a stock portfolio has net betas of 0.8 and 1.2 with respect to these factors. The factors have volatility 15% and 20% respectively, and a correlation of −0.5. If the portfolio is expected to return the risk free rate over the next month, calculate the 5% 1-month systematic VaR on an investment of $20 million in the portfolio.

SOLUTION The risk factors' monthly covariance matrix is

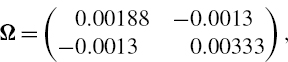
so the portfolio variance due to the risk factors is

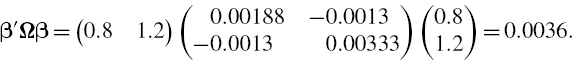
Hence the monthly standard deviation is and the systematic VaR is therefore

In Section II.1.2.5 we decomposed the total volatility of a stock portfolio into two portions, that due to the risk factors (the systematic risk) and that due to the idiosyncratic volatility (the specific or residual risk). Since the parametric linear VaR is a linear transformation of the portfolio volatility, this decomposition carries over into a decomposition of total VaR into systematic and specific VaR components.

The relationship between the total VaR, systematic VaR and specific VaR is easily explained using a simple factor model with only one risk factor, i.e. the market factor, as in Section II.1.2.5. Write the model as

where Y_t is the return on the portfolio, X_t is the return on the market and ∈_t is the specific return, all at time t. Taking variances gives

or, in parameter notation,

where is the correlation between the market and the specific returns. This may be written in the alternative form

The market volatility, i.e. the volatility due to the market risk factor, is βσ_X, so (IV.2.46) may be expressed in words as

But in the parametric linear VaR model, the VaR behaves just like volatility, assuming we ignore any adjustment for a non-zero discounted mean return. Hence, an expression similar to (IV.2.46) also holds with VaR in place of volatility:

Hence, the total VaR is equal to the sum of the systematic VaR and the specific VaR if and only if , the correlation between the return explained by the risk factors and the specific return, is equal to 1. But, on the contrary, it is usually assumed that the factor model explains the portfolio return so well that = 0. Also, if the factor model is estimated by OLS, then = 0 by construction. Under this assumption the total VaR is the square root of the sum of the squared systematic VaR and the squared specific VaR.

In the more general case, when is not 0 but less than 1, the total VaR will be less than the sum of the systematic VaR and the specific VaR. This property, which is an example of the sub-additivity property of parametric linear VaR models, is a necessary property for the risk metric to be coherent. It implies that the risk of investing in a portfolio is no greater than the risk resulting from an equivalent sized investment in any single asset of that portfolio. It is related to the portfolio diversification effect that was introduced and discussed in Section I.6.3.1. There we showed that the volatility of a portfolio is never greater than the volatility of any of its constituent assets, and that the volatility of a fully funded long-only portfolio decreases with the asset returns correlations. Hence, to reduce risk (as measured by volatility), investors have the incentive to hold a diversified portfolio, i.e. a portfolio with investments distributed over many assets that have as low a correlation as possible.²⁷ The sub-additivity property of parametric linear VaR amounts to exactly the same thing as portfolio diversification, but now the portfolio risk is measured by its systematic and specific VaR and not its volatility.²⁸

IV.2.5.3 Empirical Estimation of Specific VaR

The normal linear specific risk of an equity portfolio can be calculated in three different ways:

1. Save a time series of residuals from the factor model, and calculate the normal linear specific VaR directly from the residual variance.
2. First calculate the normal linear total VaR using the variance of the portfolio return.²⁹ Then calculate the systematic VaR using 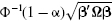and the specific VaR using (IV.2.47), under the assumption that 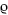= 0.
3. Use a standardized rule, such as setting specific risk = 8% of portfolio value (see Section IV.8.2.5).

An advanced risk assessment system should have a database of historical prices on all stocks and risk factors that enables the more precise estimation of specific VaR using method 1. Based on these data, the factor betas and the risk factor covariance matrix, and hence also the systematic VaR and (from the factor model residuals) the specific VaR, may all be estimated in-house. Holding the current portfolio weights constant, historical data on stock returns may be used to construct a current weighted returns series for the portfolio.³⁰ Then the total VaR may be estimated directly from the current weighted returns.³¹ An empirical illustration, for a portfolio of stocks in the S&P 100 index, is provided in the next subsection.

However, method 2 is often used, even though it is based on the assumption that the specific returns and the systematic returns are uncorrelated, which may not be warranted. This would only be the case if the factor model were doing an excellent job of explaining the stock's returns, and the portfolio is well diversified, but often this is not the case.

EXAMPLE IV.2.13: DISAGGREGATION OF VAR INTO SYSTEMATIC VAR AND SPECIFIC VAR

Suppose the volatility of the portfolio returns in Example IV.2.12 is 25%. Find the 5% 10-day total VaR and the 5% 10-day specific VaR using the normal linear model, based on method 2 above.

SOLUTION Since the portfolio volatility is 25%,

The systematic VaR was found, in Example IV.2.12, to be $1,973,824. Hence, assuming a zero correlation between the residual and the market returns, the specific VaR may be calculated as the square root of the difference between the square of the total VaR and the square of the systematic VaR, i.e.:

Which of the three methods is used to estimate specific risk depends very much on the data available. If the risk factor betas are obtained directly from a data provider then method 1 cannot be used. If the risk factor returns covariance matrix Ω is also obtained from a data provider, or provided in-house, then we can calculate the systematic VaR but not the total VaR, and in that case a standardized rule (see Section IV.8.2.5. must be applied to estimate the specific risk.

IV.2.5.4 EWMA Estimates of Specific VaR

When ordinary least squares is used to estimate both the factor model betas and the covariance matrix, on an identical sample, methods 1 and 2 above for estimating specific VaR will produce identical results.³² However, OLS is not necessarily the best method to use. Indeed, OLS estimates merely represent an average value over the time period covered by the sample and will not reflect current market conditions. Risk managers often prefer to use more risk sensitive estimates of factor model betas and the covariance matrix, such as those obtained using the exponentially weighted moving average methodology. This approach for estimating risk sensitive betas was introduced and illustrated in Section II.1.2.3, and full details of the EWMA methodology were given in Section II.3.8.

We now show that when EWMA is applied to estimate portfolio betas we should use method 1 rather than method 2 (described in the previous subsection) to obtain the specific VaR. Using EWMA estimates instead of OLS, these two methods no longer yield identical results; in fact, method 2 could produce negative values for the specific VaR because the assumption that = 0 is not valid.

For simplicity we suppose the portfolio with returns Y has only one risk factor, with returns X. Then the EWMA beta is estimated by dividing the EWMA covariance by the EWMA variance with the same smoothing constant, i.e.

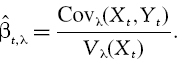
Having estimated beta, we obtain the residual returns series

Then, using method 1, the normal linear specific VaR is estimated from the EWMA standard deviation of these residuals, using the usual formula, i.e.³³

This method will always gives a positive specific VaR that is less than the total VaR. To see this, substitute EWMA variances in (IV.2.45) and rearrange, yielding

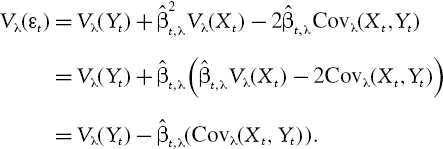
But so the specific VaR is always less than the total VaR, and because it is a variance it is always positive.

Figure IV.2.5 illustrates the application of the EWMA methodology for estimating total, systematic and specific VaR to a portfolio of stocks in the S&P 100 index. The 1% 10-day VaR is here expressed as a percentage of the portfolio value and the smoothing constant used for the figure is λ = 0.95 (but this, as well as the portfolio weights and the VaR model parameters, may be changed by the reader in the spreadsheet). Although the portfolio is fairly highly correlated with the index most of the time, there are short intervals when the specific VaR is greater than the systematic VaR, but never greater than total VaR.

Figure IV.2.5 Systematic and specific VaR based on EWMA

In summary, both OLS and EWMA estimates for the factor model betas and the covariance matrix allow VaR decomposition into systematic and specific VaR, but the EWMA approach yields more risk sensitive estimates. It is inadvisable to mix methodologies, for instance, by using OLS for the covariance matrix and EWMA for the factor model betas, and when EWMA is used take care to follow the procedure outlined above. For consistency, all variances, covariances and betas should be estimated using the same smoothing constant in the EWMA.

IV.2.6 SYSTEMATIC VALUE-AT-RISK DECOMPOSITION FOR STOCK PORTFOLIOS

In Section IV.2.2 we explained how systematic VaR, i.e. total risk factor VaR, can be attributed to different risk factors under the normal linear VaR model. This section illustrates this VaR decomposition by considering several equity portfolios with different types of risk factor exposures, showing how to decompose the systematic VaR into stand-alone and marginal VaR components. Although we remain with the normal linear VaR model for our empirical examples, the decomposition method applies equally well to other types of parametric linear VaR model.

IV.2.6.1 Portfolios Exposed to One Foreign Currency

To purchase securities on foreign exchanges one has first to purchase the local currency. Hence, portfolios with international equities have forex rates as risk factors where the nominal factor sensitivity is equal to the amount invested in the currency. In this section we consider a stock portfolio with exposure to just one foreign currency, to illustrate the VaR decomposition into equity and forex components, assuming for simplicity that both domestic and foreign interest rates are zero. As usual, the discounted expected return on the portfolio is also assumed to be negligible over the risk horizon, so all we need to consider for the systematic VaR calculations is the covariance matrix of the risk factors.

We first prove that in the parametric linear VaR model the systematic VaR is sub-additive. That is, the total systematic VaR is never greater than the sum of the stand-alone component VaRs. To prove this we begin by noting that log returns are additive, so the log return in domestic currency on an exposure to a foreign equity market may be written as

where R_h is the h-day log return on the portfolio in foreign currency and X_h is the h-day log return on the domestic/foreign exchange rate.

Now consider the factor model representation of the equity log return in foreign currency, i.e. set

where Y_h is the h-day log return on the foreign risk factor (e.g. the foreign market index). Then the standard deviation σ_h of the h-day log return in domestic currency is the standard deviation of βY_h + X_h. That is,

In the above, denotes the quanto correlation between the foreign market index returns in foreign currency terms and the exchange rate returns, and

is the h-day covariance matrix of these returns.

Decomposition into stand-alone components

Knowing σ_h, we can compute

expressed as a percentage of portfolio value. The equity and forex components of the systematic VaR are

and

Rewriting (IV.2.49) as

and using the expressions for equity and forex VaR above gives an exact decomposition of systematic VaR as

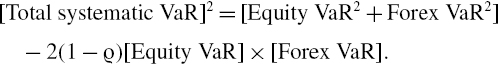
Hence,

with equality if and only if = 1.

However, it is extremely unlikely that = 1. Indeed, since quanto correlations can be small and are often very difficult to forecast, the quanto correlation might be assumed to be zero. In that case the decomposition into stand-alone VaR components becomes

If the quanto correlation is large and negative it is possible that the systematic VaR is less than both the stand-alone equity VaR and the forex VaR, as illustrated in Example IV.2.14.

Decomposition into marginal components

For the decomposition of total systematic VaR into marginal components we use the approximation described in Section IV.2.2.4. In the case of the parametric linear VaR model the gradient vector is given by

where θ is the vector of risk factor sensitivities.

Following our discussion in Section IV.2.2.3, the ith marginal component VaR is obtained by multiplying the ith component of the gradient vector by the ith nominal sensitivity. Note that

and so the total systematic VaR is the sum of the marginal VaR components. The next numerical example illustrates this construction.

EXAMPLE IV.2.14: EQUITY AND FOREX VAR

A US investor buys $2 million of shares in a portfolio of UK (FTSE 100) stocks and the portfolio beta is 1.5. Suppose the FTSE 100 and $/£ volatilities are 15% and 20% respectively, and their correlation is 0.3. What is the 1% 10-day systematic VaR in US dollars? Decompose the systematic VaR into (a) stand-alone and (b) marginal equity and forex components.

SOLUTION Given the data, the 10-day risk factor covariance matrix has the following elements:

• FTSE 100 variance 0.0225/25 = 0.0009;
• $/£ variance 0.04/25 = 0.0016;
• with a correlation of 0.3, the 10-day covariance is

The 10-day returns variance is thus

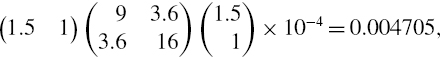
so the 10-day 1% systematic VaR is of the portfolio value. Since the portfolio has $2 million invested in it, its 1% 10-day systematic VaR is 15.9571% of $2,000,000, i.e. $319,142.

(a) Consider the stand-alone component VaRs:

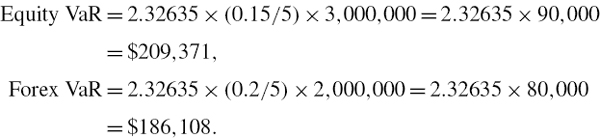
Hence

which is greater than the total systematic VaR.

(b) For the marginal VaRs we first compute the gradient vector. Since

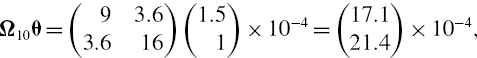
the gradient vector is

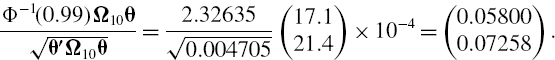
Hence the marginal VaRs are:

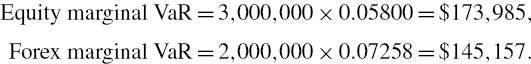
and the sum of these is $319,142, which is equal to the total VaR.

When marginal VaRs are expressed as a percentage of the total VaR they tell the investor how much risk stems from each risk factor in a diversified portfolio. Hence

• 173,985/319,142 = 54.5% of the risk is associated with the equity exposure, and
• 145,157/319,142 = 45.5% of the risk is from the foreign exchange exposure.

When the quanto correlation is large and negative it may be that the total risk factor VaR is less than either the equity VaR or the forex VaR, and in fact it can be less than both of them. To illustrate this point we change the quanto correlation in the above example between −1 and +1, and this gives different figures for the total risk factor VaR shown by the grey line in Figure IV.2.6. We see that when the quanto correlation is less than about −0.6, the total systematic VaR due to both equity and forex factors becomes less than both the equity VaR and the forex VaR.

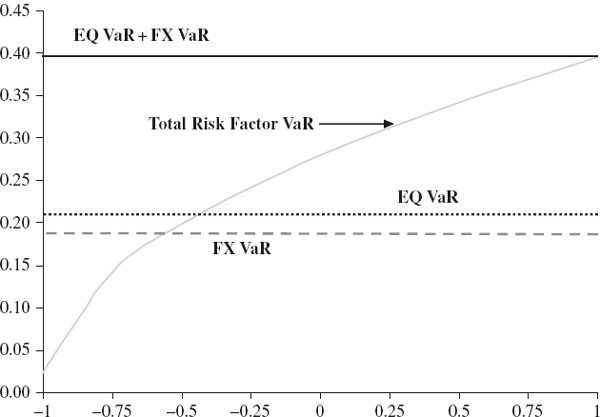
Figure IV.2.6 Total risk factor VaR versus quanto correlation

The general point to take away from this section is that the total systematic VaR is always equal to the sum of the marginal VaRs, but it is almost always less than the sum of the stand-alone VaRs, because stand-alone VaR measures the risk due to a factor in isolation and does not account for any diversification effects. Indeed, the total systematic VaR could be less than either, or both, of the stand-alone VaRs. It would only be equal to the sum of the stand-alone VaRs if the risk factor correlations were all equal to 1, which is extremely unlikely.

IV.2.6.2 Portfolios Exposed to Several Foreign Currencies

We now consider stock portfolios with investments in several different countries, using a broad market index as the single equity risk factor in each country. Following our general discussion in Sections IV.2.2.3 and IV.2.2.4, it is convenient to partition the risk factors into equity and foreign exchange factors. For the moment we retain the assumptions that both domestic and foreign interest rates are zero (and that the discounted expected return on the portfolio is also zero) so there are no interest rate risk factors.

Denote by θ_E and θ_X the vectors of equity and forex rate risk factor sensitivities. The stand-alone VaR decomposition is based on the variance decomposition:

where and

is the h-day risk factor covariance matrix, partitioned into equity and forex risk factors. Note that the quanto correlation between equity returns and forex returns is often negative. If it is both large and negative, the total systematic VaR can be less than either the equity VaR or the forex VaR, or both, as we have seen (for the single risk factor case) in Example IV.2.14 above.

EXAMPLE IV.2.15: VAR FOR INTERNATIONAL EQUITY EXPOSURES

Consider a US dollar investment in a large international stock portfolio with the characteristics shown in Table IV.2.13. Suppose that the correlation between all equity risk factors is 0.75, the correlation between the two forex risk factors is 0.5, and the quanto correlations are each 0.2. Find the 1% 10-day systematic VaR of this portfolio and decompose this into (a) stand-alone and (b) marginal equity and forex components.

Table IV.2.13 Characteristics of an international equity portfolio

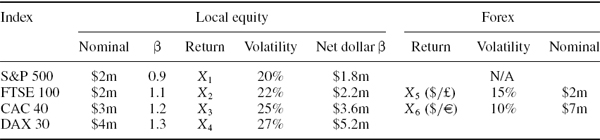
SOLUTION In Table IV.2.13 the net dollar beta is the product of the percentage beta and the nominal dollar exposure to the index. With these dollar betas, and the notation defined in the table, we can write the systematic P&L, Y in US dollars as

Given the data on risk factor volatilities and correlations, we construct the annual risk factor covariance matrix Ω shown in Table IV.2.14, with the partition drawn as in (IV.2.57).

Table IV.2.14 Annual covariance matrix Ω of equity and forex risk factor returns

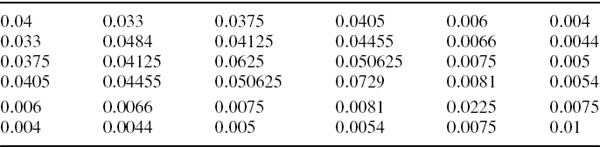
The total P&L annual variance due to all risk factors is given by θ′Ω θ, where Ω is as above and θ = (1.8, 2.2, 3.6, 5.2, 2, 7)′. The value of θ′Ωθ is calculated in the Excel spreadsheet and the result is 10.2679. To find the systematic normal linear VaR of this portfolio, we simply take the square root of the P&L variance and use the square-root-of-time rule. Hence the 1% 10-day systematic VaR due to all risk factors is:

(a) We use (IV.2.56) to decompose the total P&L variance due to all risk factors into

• the variance due to the equity factors,

  

• the variance due to the forex factors,

  

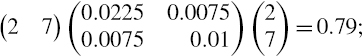
• and the covariance due to the ‘quanto’ factors,

  

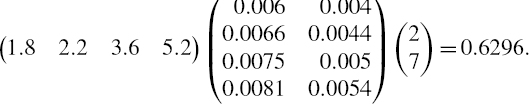
Taking the square root of the equity and forex variances, multiplying by the relevant critical value of the standard normal distribution and diving by 5 (to convert the annual VaRs into 10-day VaRs), the decomposition of the 1% 10-day total systematic VaR is summarized in Table IV.2.15.

Table IV.2.15 VaR decomposition for diversified international stock portfolio

Equity VaR	$1,333,847
FX VaR	$413,541
Sum of stand-alone VaRs	$1,747,388
Total systematic	VaR $1,490,889

(b) To estimate the marginal VaRs we first compute the gradient vector, in annual terms. Since

the annual gradient vector is

The marginal VaRs are, therefore,³⁴

and

As usual, the sum of these is equal to the total VaR. Hence, approximately

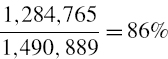
of the risk, on a diversified basis, stems from the equity exposure and only

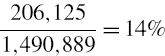
of the risk arises from the forex exposure. Notice that the marginal forex VaR is less than half of the stand-alone forex VaR; the forex exposure has this effect because the diversification benefit is significant, due to the low quanto correlation.

IV.2.6.3 Interest Rate VaR of Equity Portfolios

Exposures to interest rates arise in equity portfolios that are hedged with futures or when the foreign currency exposures that arise in international equity portfolios are transacted on the forward currency market.³⁵ Assuming that an investment of $N in a foreign equity index is financed by taking a foreign currency forward position, there are equal and opposite exposures of +$N and −$N to the foreign and domestic zero-coupon interest rates of maturity equal to the maturity of the currency forward.

EXAMPLE IV.2.16: INTEREST RATE VAR FROM FOREX EXPOSURE

A US investor buys $2 million of sterling 10 days forward, when the 10-day Treasury bill rate is 5% and the 10-day spot rate is 4.5% in the UK. If these interest rates have volatilities of 100 basis points for the Treasury bill and 80 basis points for the UK rate, and a correlation of 0.9, calculate the 1% 10-day interest rate VaR.

SOLUTION The interest rate risk arises from the cash flows of $2 million on the UK interest rate and −$2 million on the US interest rate. The PV01 vector is calculated in the spreadsheet using the method described in Section III.1.8. First we compute the change in each discount factor for a one basis point decrease in the corresponding interest rate and then we multiply these changes by the exposures of $2 million and −$2 million, respectively. This gives the PV01 vector θ =(5.47, −5.46)′ in US dollars. The annual covariance matrix of the interest rates, in basis points, is

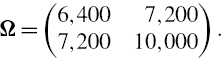
Now using the usual formula (θ′Ω θ) for the variance and calculating the 1% 10-day VaR in the usual way gives a grand total of $114 for the interest rate VaR.

This example shows that interest rate VaR on equity portfolios arising from foreign exchange forward positions is very small indeed. Unless there are large interest rate differentials between the domestic and foreign currencies and the forward date for the forex transaction is very distant, the interest rate risks arising from this type of transaction are negligible compared with the equity and forex risks.

IV.2.6.4 Hedging the Risks of International Equity Portfolios

Foreign investors wishing to accept risks only on equity markets can hedge the forex risk by taking an equal and opposite position in the currency, so that the forex VaR is zero. For instance, in Example IV.2.15 where the US investor has a long sterling exposure of $2 million and a long exposure to the euro of $7 million, if the investor wants to hedge the forex risk he should take a short position of $2 million on sterling and a short position of $7 million on the euro. Then the net currency exposure is zero, so the forex VaR is zero. Thus the total systematic VaR is equal to the equity VaR.

The forex hedges introduce a new systematic VaR due to the interest rate risk factors, but we have seen from the previous example that the interest rate VaR is very small compared with the equity VaR, and compared with the specific VaR of a stock portfolio. Nevertheless, for the sake of completeness, the following example shows how to measure all the sources of risk for a typical, hedged stock portfolio.

EXAMPLE IV.2.17: VAR FOR A HEDGED INTERNATIONAL STOCK PORTFOLIO

A European investor has $5 million invested a portfolio of volatile S&P 500 stocks, with an S&P 500 market beta of 1.5. The volatilities of the S&P 500 and €/$ rate are 20% and 15% respectively, and their correlation is −0.5.

(a) Find the 1% 1-day total systematic VaR and the VaR due to each risk factor.

(b) He now hedges the portfolio's equity exposure by selling a 3-month future on the S&P 500 index and further hedges the currency exposure with a short position on US dollars, 3 months forward. The 3-month US dollar and euro interest rates are 4% and 3.5% respectively, and the dividend yield on the S&P 500 is 3%. The volatilities and correlations of these risk factors are summarized in Table IV.2.16. Find the 1% 1-day VaR due to each of the risk factors.

(c) If the portfolio volatility is 35%, calculate the hedged portfolio's 1% 1-day specific VaR.

Table IV.2.16 Volatilities and correlations of risk factors

SOLUTION

(a) The initial VaR calculations, before hedging, are based on the same method as Example IV.2.14 and the results are shown in Table IV.2.17.

Table IV.2.17 VaR decomposition into equity and forex factors

Total systematic VaR	$191,129
Equity VaR	$220,697
Forex VaR	$110,348

(b) The equity and forex hedges introduce three new risk factors: the 3-month euro interest rate, with an exposure of $5 million because he has sold $5 million 3 months forward against the euro; the S&P 500 dividend yield, with an exposure of $7.5 million because, with a beta of 1.5, this is the amount he sells of the 3-month S&P 500 future for the equity hedge; and the 3-month US interest rate with an exposure of −$5 million from the forex hedge and an additional −$7.5 million from the equity hedge, making a total exposure of −$12.5 million to the US interest rate.

We now calculate the sensitivities of these exposures. With a 4% (annual) 3-month interest rate, the discount factor is (1.01)⁻¹ = 0.9901 and, as shown in the spreadsheet, the change in the discount factor for a one basis point decrease in the interest rate, i.e. the δ01, is

Similarly the euro interest rates and the US dividend yield have δ01s that are calculated in the spreadsheet to be 0.246 × 10⁻⁴.

The exposure to the US interest rate, the euro interest rate and the dividend yield respectively is {−12.5, 5, 7.5} in millions of dollars. Hence, the PV01 vector in dollars is³⁶

Given the risk factor volatilities and correlations in Table IV.2.16, the 1-day covariance matrix of the risk factor returns is

For instance, 25.6 = 80²/250, and so forth. Hence, the 1-day variance of the P&L is

So, after the hedges the 1% 1-day total systematic VaR is:

The 1% 1-day VaR due to each risk factor is

where σ_{1, i} is the 1-day standard deviation of the ith risk factor. Hence,

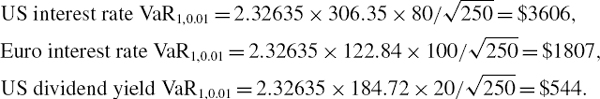
Note that the US interest rate VaR is larger than the total VaR, which is not unusual when we have opposite positions in positively correlated risk factors.

(c) By far the largest residual VaR after the equity and forex hedge is going to arise from the specific VaR, i.e. from the tracking error of this portfolio. This is because we are hedging a portfolio that has a market beta of 1.5 with an index futures contract. Assuming the residuals are uncorrelated with the futures, the specific variance, in annual terms, is

Hence, the 1% 1-day specific VaR is

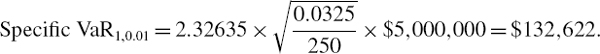
IV.2.7 CASE STUDY: NORMAL LINEAR VALUE AT RISK FOR COMMODITY FUTURES

In this section we calculate the normal linear VaR for two commodity futures trading desks, one trading natural gas futures and the other trading silver futures. We shall calculate the VaR for each desk, and then aggregate these into a total VaR covering both the desks. The data used in this study are NYMEX futures on natural gas and silver with maturities up to 6 months. Each natural gas futures contract is for 10,000 million British thermal units and each silver futures contract is for 5000 troy ounces.

The desks can take long or short positions on the futures according to their expectations and we assume the traders have mapped their positions to constant maturity futures at 1, 2, 3, 4 and 5 months using the commodity futures mapping described in Section III.5.4.2.

Applying linear interpolation to daily data on the NYMEX traded futures prices, we first construct a historical series of daily data on constant maturity futures from 3 January 2006 to 31 January 2007. We shall use these data to measure the VaR on 31 January 2007. The constant maturity futures on the two commodities over the sample period are shown in Figures IV.2.7 and IV.2.8.

Figure IV.2.7 Constant maturity futures prices, silver

Figure IV.2.8 Constant maturity futures prices, natural gas

The natural gas futures prices have a very strong contango (upward sloping term structure) during the summer of 2006. Like the spot price, near term futures prices were rather low in the summer of 2006 because storage was almost full to capacity. The silver futures prices are much closer to each other than the natural gas futures prices. The silver term structure is very flat most of the time and there is no seasonality in the prices. Price jumps are quite common, due to speculation, because silver is an investment asset as well as being used in industrial processes.

Table IV.2.18 shows the volatilities and correlations of each set of constant maturity futures returns. These are calculated from the daily returns over the entire sample. Both are highly correlated along their own term structures and natural gas futures returns are more volatile than silver futures returns.

Table IV.2.18 Volatilities and correlations of natural gas and silver futures

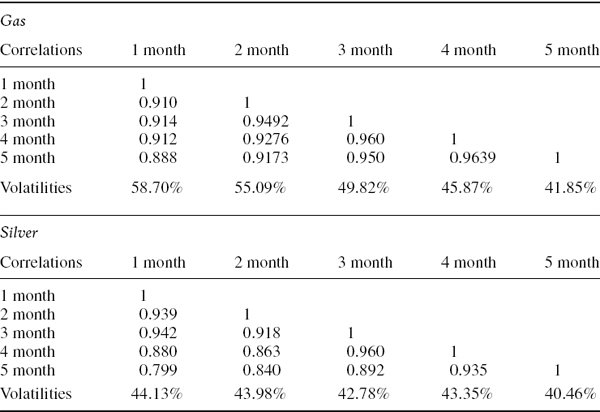
We now consider the positions taken on each trading desk on 31 January 2007. These are shown in Table IV.2.19. First we show the price and number of units of each futures contract, then the position values are calculated as the product of the number of contracts and the price of the contract, multiplied by either 10,000 (the trading unit for natural gas futures) or 5000 (the trading unit for silver futures).

Table IV.2.19 Commodities trading desk positions on natural gas and silver

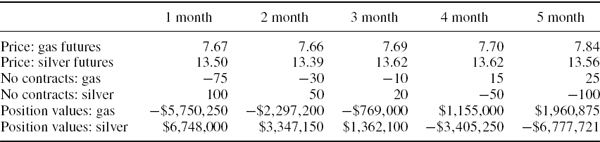
The commodities trading desks are betting on an imminent fall in price for natural gas, since it has short positions on the short maturities and long positions on longer maturities, and an imminent rise in price for silver, taking long positions in shorter maturities and short positions in longer maturities.

The 1% 10-day stand-alone VaR for each desk is calculated in the spreadsheet using the formula

where θ is the position value vector given in the last rows of Table IV.2.19 and Ω₁ is the 5 × 5 1-day covariance matrix of the constant maturity gas or silver futures daily returns. A similar formula is applied to obtain the total VaR aggregated over both desks, now using the position value vector in the last two rows of Table IV.2.19 combined, and the 10 × 10 1-day covariance matrix of natural gas and silver futures daily returns. The marginal VaRs were calculated using the methodology described in Section IV.2.2.4.³⁷

The results are shown in Table IV.2.20. The marginal VaRs tell us that trading on gas futures contributes 69% of the total risk and trading on silver futures contributes 31% of the total risk, after adjusting for the diversification effects from the two activities.³⁸

The stand-alone VaRs measure risk without accounting for diversification. Hence, the sum of the two stand-alone VaRs is greater than the total VaR – this is because the natural gas and silver futures have less than perfect correlation. If the correlation between natural gas and silver futures changed, all else remaining the same, this would not affect the stand-alone VaRs. But it would affect the total VaR and hence also the marginal VaRs.

Table IV.2.20 1% 10-day VaR of commodity futures desks

IV.2.8 STUDENT t DISTRIBUTED LINEAR VALUE AT RISK

In this section we shall extend the analytic formula for normal linear VaR to the case where the portfolio returns and the risk factor returns are assumed to have a Student t distribution. First, to motivate this formula, Section IV.2.8.1 describes the effect that leptokurtosis has on a VaR estimate. Then Section IV.2.8.2 derives a parametric linear VaR formula for the case where the portfolio's returns are generated by a Student t distribution, and extends this to systematic VaR when the risk factor returns have a multivariate Student t distribution. Empirical examples are provided in Section IV.2.8.3.

IV.2.8.1 Effect of Leptokurtosis and Skewness on VaR

A leptokurtic distribution is one whose density function has a higher peak and greater mass in the tails than the normal density function of the same variance. In a symmetric unimodal distribution, i.e. one whose density function has only one peak, leptokurtosis is indicated by a positive excess kurtosis.³⁹

Leptokurtosis is one of the basic ‘stylized facts’ emerging from examination of the empirical distributions of financial asset returns. Also apparent is the skewness of return densities, particularly for equity returns which often have a strong negative skew (heavier lower tail). With leptokurtosis and negative skewness in risk factor return distributions the normal linear VaR formula is likely to underestimate the VaR at high confidence levels. In commodity returns a positive skew (heavier upper tails) is often seen, but for companies that are short commodity futures, losses are made following price rises, and here the positive skewness effect compounds the leptokurtosis effect on VaR. Again, the normal linear VaR formula is likely to underestimate the VaR at high confidence levels.

Figure IV.2.9 illustrates the impact of leptokurtosis on the VaR estimate. Both of the density functions shown in the figure are symmetric, but the density depicted by the black line is leptokurtic, i.e. it has a higher peak and heavier tails than the ‘equivalent’ normal density (i.e. the normal density with the same variance) which is shown in grey. For each density the corresponding 1% and 5% VaR estimates are shown. We observe the following:

Figure IV.2.9 Comparison of normal VaR and leptokurtic VaR

• For low significance levels (e.g. 5%), the normal assumption can overestimate VaR if the return distribution is leptokurtic.
• For higher significance levels (e.g. 0.5%), the normal assumption can seriously underestimate VaR if the return distribution is leptokurtic.
• The significance level at which the VaR becomes greater under the leptokurtic distribution depends on the extent of the excess kurtosis. If the excess kurtosis is large, the leptokurtic VaR will exceed the normal VaR even at 10% significance levels. For an empirical illustration of this, see Example IV.2.20.

As the confidence level of the VaR estimate increases (i.e. α becomes smaller) there always comes a point at which the leptokurtic VaR exceeds the normal VaR. Referring to Figure IV.2.9, and noting the ‘intermediate’ region where the leptokurtic density curve lies below the equivalent normal density, the reason for this becomes clear. In the tails (and the centre) the leptokurtic density function lies above the equivalent normal density function; hence the leptokurtic VaR will be the greater figure for all significance levels above some threshold. But in the intermediate region, the ordering may be reversed.

We know from Section I.3.3.7 that Student t distributions are leptokurtic. When significant positive excess kurtosis is found in empirical financial return distributions, the Student t distribution is likely to produce VaR estimates that are more representative of historical behaviour than normal linear VaR. However, by the central limit theorem, the excess kurtosis in financial returns decreases as the sampling interval increases. Thus, whilst daily returns may have a large positive excess kurtosis, weekly returns have lower kurtosis and monthly returns may even have excess kurtosis that is close to zero.

IV.2.8.2 Student t Linear VaR Formula

In this subsection we derive an analytic formula for the Student t VaR.⁴⁰ It is useful when VaR is estimated over a short risk horizon, as positive excess kurtosis can be pronounced over a period of a few days or even weeks. But for risk horizons of a month or more, returns are likely to be approximately normally distributed, by the central limit theorem.

The standard Student t distribution with ν degrees of freedom was introduced in Section I.3.3.7. If a random variable T has a Student t distribution with ν degrees of freedom we write T~t_ν, and its density function is

where the gamma function Γ is an extension of the factorial function to non-integer values.⁴¹

The distribution has zero expectation and zero skewness. For ν > 2 the variance of a Student t distributed variable is not 1, but

Its excess kurtosis is finite for ν > 4, and is given by

The Student t density has a lower peak than the standard normal density, and it converges to the standard normal density as ν →∞. But the density is leptokurtic, since when we compare it with the equivalent normal density, i.e. the one having the same variance as (IV.2.59), the peak in the centre of the distribution is higher than the peak of the equivalent normal density, and the tails are heavier.

The α quantile of the standard Student t distribution is denoted by . Since quantiles translate under monotonic transformations,⁴² the α quantile of the standardized Student t distribution with ν degrees of freedom, i.e. the Student t distribution with mean 0 and variance 1, is . Let X denote the daily return on a portfolio and suppose it has standard deviation σ and discounted mean μ. To apply a Student t linear VaR formula to the portfolio we need to use the quantiles from a generalized Student t distribution, i.e. the distribution of the random variable X = μ + σ T, where T is a standardized Student t random variable.

Note that the ordinary Student t quantiles satisfy

because the distribution is symmetric about a mean of zero. So, using the same argument that we used in Section IV.2.2 to derive the normal linear VaR formula, it follows that

The Student t distribution is not a stable distribution,⁴³ so the sum of i.i.d. Student t variables is not another Student t variable. Indeed, by the central limit theorem the sum converges to a normal variable as the number of terms in the sum increases. When h is small, a very approximate formula for the 100α%h-day VaR, as a percentage of the portfolio value, is

But when h is more than about 10 days (or even less, if ν is relatively large) the normal linear VaR formula should be sufficiently accurate.

The extension of (IV.2.63) to the systematic VaR for a linear portfolio that has been mapped to m risk factors with sensitivities θ =(θ₁,…, θ_m)′ is, assuming the risk factors have a multivariate Student t distribution with ν degrees of freedom,

where Ω_h denotes the m × m covariance matrix of the risk factor returns and μ_h denotes the m × 1 vector of expected excess returns over the h-day risk horizon.

IV.2.8.3 Empirical Examples of Student t Linear VaR

The critical value can be found in statistical tables or using the Excel function TINV.⁴⁴ The degrees of freedom parameter ν is estimated by fitting the distribution using maximum likelihood estimation (MLE). Example I.3.17 and its accompanying spreadsheet explain how to do this in practice. Alternatively, a quick approximation to ν may be obtained using a simple ‘moment matching’ method called the method of moments, which entails equating the sample moments to population moments.⁴⁵ We shall compare both methods in the following example.

EXAMPLE IV.2.18: ESTIMATING STUDENT T LINEAR VAR AT THE PORTFOLIO LEVEL

Using the daily FTSE 100 data from 4 January 2005 to 7 April 2008 shown in Figure IV.2.10, estimate the degrees of freedom parameter for a generalized Student t distribution representation of the daily returns, using (a) the method of moments and (b) MLE.⁴⁶ Then compute the 1% 1-day Student t VaR, as a percentage of portfolio value, using both estimates for the degrees of freedom parameter.

SOLUTION The method of moments gives an estimate = 6.07 for the degrees of freedom parameter, but MLE gives = 4.14.⁴⁷ The resulting estimates of 1% 1-day VaR are 2.81% for the method of moments estimate and 2.94% for the maximum likelihood estimate. Both estimates are ignoring the possibility of non-zero skewness, because the Student t distribution is symmetric. But in fact the sample skewness is −0.258. This is because of the large falls in the FTSE 100 index that are evident from Figure IV.2.10.

Figure IV.2.10 FTSE 100 index price

EXAMPLE IV.2.19: COMPARISON OF NORMAL AND STUDENT T LINEAR VAR

Using the maximum likelihood estimate of the degrees of freedom for the Student t representation of the FTSE 100 index returns from the previous example, compare the Student t linear VaR with the normal linear VaR over a 1-day horizon, at the 0.1%, 1% and 10% significance levels. Express your results as a percentage of the portfolio value.

SOLUTION The spreadsheet for the previous example is extended to include the normal linear VaR, and using the three different significance levels. The results are displayed in Table IV.2.21.

Table IV.2.21 Normal and Student t linear VaR

The 1-day Student t VaR is considerably greater than the normal VaR at the 0.1% significance level, it is a little greater than the normal VaR at the 1% level, and at the 10% significance level the normal VaR is greater than the Student t VaR. This is because the tails of the Student t density have greater mass and the peak at the centre is higher than the normal density with the same variance. Hence, for quantiles lying further toward the centre there may be less mass in the tail of the Student t density than in the tail of the normal density.

The above examples show that the model risk arising from the assumption that returns are normally distributed is very significant, especially when VaR is measured at high confidence levels such as 99.9%. The Student t VaR model provides a more accurate representation of most financial asset returns, but a potentially significant source of model risk arises from assuming the return distribution is symmetric. Although there are skewed versions of the Student t distribution (see McNeil et al. (2005) and references therein), the non-linear transformations that underpin these distributions remove the possibility of simple parametric linear VaR formulae. By far the easiest way to extend the parametric linear VaR model to accommodate the skewness that is so often evident in financial asset returns is to use the mixture linear VaR model, which is explained in the next section.

IV.2.9 LINEAR VALUE AT RISK WITH MIXTURE DISTRIBUTIONS

In this section we show how mixtures of normal or Student t distributions can be used to estimate VaR, capturing both leptokurtosis and skewness in return distributions. Section IV.2.9.1 provides a gentle introduction to the subject by summarizing the important features of simple mixtures of two distributions. Section IV.2.9.2 explains how to calculate VaR when the portfolio return distribution is assumed to be a normal mixture or a Student t mixture distribution. In this case the parametric linear VaR is given by an analytic formula that does not have an explicit solution, so we use numerical methods to find the mixture linear VaR. Section IV.2.9.3 explains how mixture distribution parameters are estimated from historical data and Section IV.2.9.4 provides empirical examples. Section IV.2.9.5 illustrates the potential for mixture VaR to be applied in a scenario VaR setting, when using little or no historical data on a portfolio's returns. Finally, Section IV.2.9.6 considers the case where the portfolio is mapped to risk factors whose returns are generated by correlated i.i.d. normal mixture processes with two multivariate normal components.

IV.2.9.1 Mixture Distributions

The mixture setting is designed to capture different market regimes. For instance, in a mixture of two normal distributions, there are two regimes for returns: one where the return has mean μ₁ and variance and another where the return has mean μ₂ and variance . The other parameter of the mixture is the probability π with which the first regime occurs, so the second regime occurs with probability 1 − π.

The distribution function of a mixture distribution is a probability-weighted sum of the component distribution functions. For instance, a mixture of just two normal distributions has distribution function defined by

where denotes the normal distribution function with mean μ_i and variance , for i = 1, 2, and where π is the probability associated with the normal component with mean μ₁ and variance . Differentiating (IV.2.65) gives the corresponding normal mixture density function

where denotes the normal density function with mean μ_i and variance , for i = 1, 2. Full details about normal mixture distributions are given in Section I.3.3.6.

We illustrate the basic properties of mixture distributions by considering a simple mixture of two zero-mean normal components, i.e. where μ₁ = μ₂ = 0. In this case the variance of the normal mixture distribution is

The skewness is zero and the kurtosis is

For instance, Figure IV.2.11 shows four densities:

• three zero-mean normal densities with volatility 5%, 10% (shown in grey) and 7.906% (shown as dotted line);
• a normal mixture density, shown in black, which is a mixture of the first two normal densities with probability weight of 0.5 on each of the grey normal densities, and which has volatility 7.906%.

Figure IV.2.11 Comparison of a normal mixture with a normal density of the same variance

The variance of the mixture distribution is 0.5 × 5² + 0.5 × 10² = 62.5. Since , the mixture has the same variance as the dashed normal curve. However, it has a kurtosis of 4.87. In other words it has an excess kurtosis of 1.87, which is significantly greater than zero (zero being the excess kurtosis of the equivalent (dashed) normal density in the figure).

Normal mixture distributions provide a simple means of capturing the empirically observed skewness and excess kurtosis of financial asset returns. It is always the case that zero-mean normal mixture densities have zero skewness but positive excess kurtosis: they have higher peaks and heavier tails than normal densities with the same variance. Taking different means in the component normal densities gives a positive or negative skew. See Figure I.3.14 for an example.

IV.2.9.2 Mixture Linear VaR Formula

When the excess return X on a linear portfolio has a normal distribution, the analytic formula (IV.2.5) for normal linear VaR follows directly from the definition of VaR. But there is no explicit formula for estimating VaR under the assumption that portfolio returns follow a mixture density. However, using exactly the same type of argument as in Section IV.2.2.1, we can derive an implicit formula that we can solve using a numerical algorithm.

For instance, suppose there are only two components in a mixture density for the portfolio's returns, and write

where denotes the distribution function with mean μ_i and variance , for i = 1, 2, and where π is the probability associated with the component with mean μ₁ and variance . Note that F₁ and F₂ need not be both normal; one or both of them could be a Student t distribution, in which case the degrees of freedom ν_i should be included in their list of parameters.

We have

and when P(X < x_α) = α, then x_α is the α quantile of the mixture distribution. Let X_i be the random variable with distribution function . Then

But

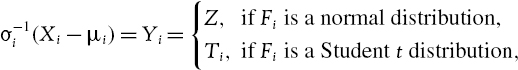
where Z is a standard normal variable and T_i is a standardized Student t variable with ν_i degrees of freedom. Hence,

But since Y_i is a standardized Student t or normal variable, we know its quantiles. That is, we know everything in the above identity except the mixture quantile, x_α. Hence, the mixture quantile can be ‘backed out’ from (IV.2.71) using an iterative approximation method such as the Excel Goal Seek or Solver algorithms (see Section I.5.2.2). Finally, we find the mixture VaR by setting VaR_α = − x_α.

For greater flexibility to fit the empirical return distribution we may also include more than two component distributions in the mixture. The general formula for the mixture VaR, now making the risk horizon h over which the returns are measured explicit, is therefore

As before, backing out x_{h, α} from the above gives VaR_{h, α} = −x_{h, α}.

IV.2.9.3 Mixture Parameter Estimation

The 100α% h-day mixture VaR that is implicit in (IV.2.72) will be expressed as a percentage of the portfolio value if μ_ih and σ_ih are the expectation and standard deviation of the component returns, and it will be expressed in nominal terms if μ_ih and σ_ih are the expectation and standard deviation of the component P&L. But how do we estimate these component means and variances?

The estimation of the mixture parameters from historical data is best performed using the EM algorithm, especially when the mixture is over more than two distributions. A description of this algorithm and a case study illustrating its application to financial data are given in Section I.5.4. Empirically, we often find that we can identify two significantly different regimes: a regime that occurs most of the time and governs ordinary market circumstances, and a second ‘high volatility’ regime that occurs with a low probability. In an equity portfolio the low probability, high volatility regime is usually captured by a component with a large and negative mean; in other words, this component usually corresponds to a crash market regime.

As the number of distributions in the mixture increases the probability weight on some of these components can become extremely small. However, in finance it is seldom necessary to use more than two or three components in the mixture, since financial asset return distributions are seldom so irregular as to have multiple modes. When there are only a few components the method of moments may be used estimate the parameters of a normal mixture distribution in Excel. In this approach we equate the first few sample moments (one moment for each parameter to be estimated) to the corresponding theoretical moments of the normal mixture distribution.

The theoretical moments for normal mixture distributions are now stated for the general case where there are m normal components with means and standard deviations μ_i and σ_i, for i = 1, 2,…, m. The vector of probability weights, i.e. the mixing law for the normal mixture, is denoted by π =(π₁,…, π_m) where . The non-central moments are

and the mean, variance, skewness and kurtosis are

Hence, when the method of moments is applied to estimate the parameters of a normal mixture distribution, we equate (μ, σ, τ, x) to the first four sample moments by changing the parameters of the normal mixture distribution. An empirical example is given in the next subsection.

IV.2.9.4 Examples of Mixture Linear VaR

In a case study in Section I.5.4.4 we applied the EM algorithm to fit a mixture of two normal distributions to the daily returns on the FTSE 100 index, and likewise for the S&P 500 index and the $/£ exchange rate. For convenience, Table IV.2.22 states the sample moments and Table IV.2.23 states the normal mixture parameter estimates for each of these variables, based on the EM algorithm. In both tables the means and standard deviations are quoted in annualized terms, assuming the returns are i.i.d.

Table IV.2.22 Moments of the FTSE 100 and S&P 500 indices and of the $/£ forex rate

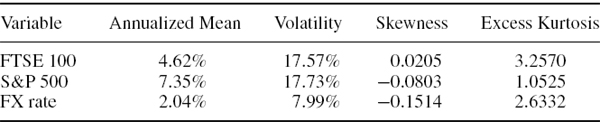
Table IV.2.23 Estimated parameters of normal mixture distributions (annualized)

In the next example we use these parameters to estimate the normal mixture VaR for a US investor in the FTSE 100 and S&P 500 indices.

EXAMPLE IV.2.20: ESTIMATING NORMAL MIXTURE VAR FOR EQUITY AND FOREX

Use the parameters in Table IV.2.23 to estimate the 100α% 10-day normal mixture VaR for a US investment in the FTSE 100 and S&P 500 indices. Report your results as a percentage of the local currency exposure to each risk factor and compare them with the normal estimate of VaR. Use significance levels of α = 10%, 5%, 1% and 0.1%.

SOLUTION For each of the three risk factors we use Solver or Goal Seek to back out the normal mixture VaR from the formula (IV.2.71).⁴⁸ The results are reported in Table IV.2.24, where they are compared with the equivalent normal VaR. Compared with the normal VaR, the normal mixture VaR is greater than the normal VaR at higher significance levels. As expected, the extent to which it exceeds the normal VaR increases as we move to a greater confidence level in the VaR estimate, and the difference is most pronounced in the S&P 500 since this has the largest negative skewness of all three risk factors. In both VaR models the forex risk is much the smallest, since the forex volatility is considerably lower than the volatility of the equity risk factors.

Table IV.2.24 Comparison of normal mixture and normal VaR

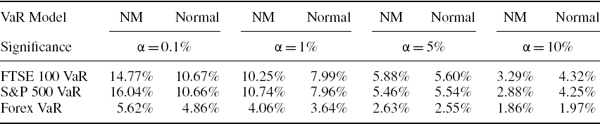
The next example further investigates the effect that a large negative skewness has on the normal mixture VaR estimate. It also illustrates the application of the method of moments to the estimation of the normal mixture parameters.

EXAMPLE IV.2.21: COMPARISON OF NORMAL MIXTURE AND STUDENT T LINEAR VAR

Using the daily FTSE 100 index data from 4 January 2005 to 7 April 2008 shown in Figure IV.2.10, apply the method of moments to estimate the parameters for a mixture of two normal distributions representation of the daily returns. Then, using both the maximum likelihood and the method of moments estimate of the degrees of freedom for the Student t density representation of the FTSE 100 index returns from Example IV.2.18, compare the Student t linear VaR with the normal mixture linear VaR over a 10-day horizon, at the 0.1%, 1% and 5% significance levels. Express your results as a percentage of the portfolio value.

SOLUTION The sample moments that we want to match are shown in Table IV.2.25. The sample is of daily log returns between January 2006 and April 2008.

Table IV.2.25 Sample moments of daily returns on the FTSE 100 index

Moment	Estimate
Mean	0.012%
Standard deviation	1.097%
Skewness	−0.2577
Excess kurtosis	2.9049

The application of Solver to the problem of estimating the parameters of a mixture of two normal distributions is highly problematic. Firstly, with five parameters there would be no unique solution even if the system were linear – and the optimization problem here is highly non-linear. Secondly, we require a better optimization algorithm (such as the EM algorithm) than the simple Newton or conjugate gradient methods employed by Solver. So the user needs to ‘nurse’ the optimization through stages, trying to equate each moment in turn. Without going into details, I was able to match the sample and population moments to five decimal places and the resulting parameter estimates are shown in Table IV.2.26.⁴⁹

Table IV.2.26 Normal mixture parameters for FTSE 100 returns FTSE 100 π μ₁ μ₂ σ₁ σ₂

We now compare the results obtained using the normal mixture distribution with the Student t VaR results from Examples IV.2.18 and IV.2.19. The 100α% 10-day VaR estimates are displayed in Table IV.2.27, for different values of α. The Student t VaR estimates ignore the large negative skewness of the FTSE 100 returns, and as a result they tend to underestimate the VaR. The only Student t VaR estimate that exceeds the normal mixture VaR is the one based on the maximum likelihood estimate of the degrees of freedom, at the 0.1% significance level.

Table IV.2.27 Comparison of normal and Student t linear VaR

The final example in this section illustrates the application of a mixture of Student t distributions to the estimation of VaR, comparing the result with the normal mixture VaR. Note that we require the standardized t distribution in (IV.2.71), and Excel only has the ordinary Student t distribution function. Even this has some strange properties, so that in the example we must set⁵⁰

EXAMPLE IV.2.22: COMPARISON OF NORMAL MIXTURE AND STUDENT T MIXTURE VAR

For α = 0.1%, 1%, 5% and 10%, compute the 100α% 10-day VaR of a mixture of two distributions, the first with mean 0 and volatility 20% and the second with (annualized) mean −10% and volatility 40%. The probability weight associated with the first distribution is 75% and the daily returns are assumed to be i.i.d. Compare two cases: in the first case the two component distributions are assumed to be normal, and in the second case the first component distribution is a Student t distribution with 10 degrees of freedom and the second is a Student t distribution with 5 degrees of freedom.

SOLUTION In each case the implicit formula (IV.2.71) is implemented in the spreadsheet, based on the data in the question, and set up to back out the mixture VaR using Solver. Solver is reapplied to obtain both VaR estimates each time we change the significance level (or if we were to change any other parameter). The results, expressed as a percentage of the portfolio value, are summarized in Table IV.2.28. Predictably, the Student t mixture VaR is the greater at all significance levels, and the difference increases as we move to higher significance levels.

Table IV.2.28 Comparison of mixture VaR estimates

EXAMPLE IV.2.23: MIXTURE VAR IN THE PRESENCE OF AUTOCORRELATED RETURNS

Recalculate the normal mixture and Student t mixture 1% 10-day VaR estimates from the previous example when daily returns are assumed to have autocorrelation +0.25, and when the are assumed to have autocorrelation −0.25.

SOLUTION The calculation proceeds as before, but instead of scaling daily returns by = 3.1623 for the 10-day standard deviation, we use the scale factor based on (IV.2.10). This is

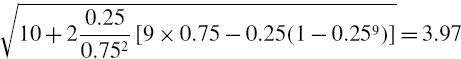
when the autocorrelation is 0.25, and

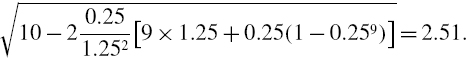
when the autocorrelation is −0.25. Using this scaling factor for the standard deviations in (IV.2.71), and then applying Solver to back out the VaR, we obtain the results for 1% 10-day VaR shown in Table IV.2.29.

Table IV.2.29 Effect of autocorrelation on mixture VaR

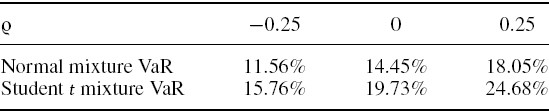
As when the distribution is normal, the effect of positive autocorrelation on non-normal parametric linear VaR will be to increase the VaR estimate, relative to the case where autocorrelation is assumed to be zero; and the opposite is the case when there is negative autocorrelation.

IV.2.9.5 Normal Mixture Risk Factor VaR

In applications of the parametric linear VaR model we use a cash-flow mapping to represent interest rate sensitive portfolios, equity portfolios are represented by a linear factor model and the log returns on commodity futures are a linear function of the log spot returns and the carry cost. Then the variance of the systematic return (i.e. the return that is explained by the risk factor mapping) is given by a quadratic form θ′Ωθ, where θ denotes the vector of sensitivities to the risk factors and Ω denotes the risk factor returns covariance matrix. There is only one covariance matrix and in the normal linear VaR model we assume that all risk factor returns are normally distributed.

We now extend the normal linear risk factor VaR model to the mixture framework, in the case where there are two risk factors and each marginal risk factor return distribution is a mixture of two normal components. In this case the risk factor covariance structure may be captured by four covariance matrices and the portfolio return distribution will be a mixture of four normal components.

To see why this is the case, suppose we have two risk factors X₁ and X₂ with return densities that have correlated normal mixture distributions. The marginal densities of the risk factors are

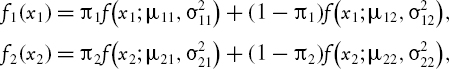
where denotes the normal density function for a random variable X with mean μ and variance σ². Thus, we may assume that so that each risk factor representation has

• a ‘core’ normal density with weight 1 − π_i in the mixture and with the lower volatility,
• a ‘tail’ normal density with weight π_i in the mixture and a higher volatility.

Since each risk factor return density has two normal components, their joint density is a bivariate normal mixture density of the form

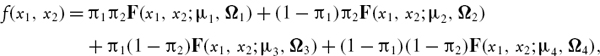
where F (x₁, x₂; μ, Ω) is the bivariate normal density function with mean vector μ and covariance matrix Ω and

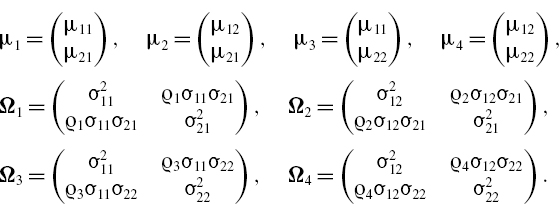
The covariance matrix Ω₁ represents the volatilities and correlation in the ‘tails’ of the two distributions and Ω₄ represents the volatilities and correlation in the ‘core’ of the two distributions. The other two matrices Ω₂ and Ω₃ represent the volatilities and correlation when one risk factor is in the ‘core’ of its distribution and the other is in the ‘tail’.

Then the portfolio return will have a normal mixture distribution with four normal components and parameters given by the mixing law

the component means

and the component variances

where θ is the vector of sensitivities of the portfolio to the two risk factors. Hence, to estimate the normal mixture VaR of the portfolio we apply Solver, or a similar numerical algorithm, to (IV.2.72) when the number of normal components is four and the mixing law, means and variances are given by (IV.2.75)– (IV.2.77).

As the number of risk factors increases, the number of components in the normal mixture distribution for the portfolio return increases. However, since the component means are different, the portfolio return may remain quite skewed and/or leptokurtic.

EXAMPLE IV.2.24: NORMAL MIXTURE VAR – RISK FACTOR LEVEL

A portfolio has two risk factors with percentage sensitivities to these risk factors of 0.8 and 1, respectively. The risk factor returns have a bivariate normal mixture distribution with the mean excess returns and volatilities shown in Table IV.2.30. Calculate the 1% 10-day VaR of the portfolio.

Table IV.2.30 Normal mixture parameters for risk factors

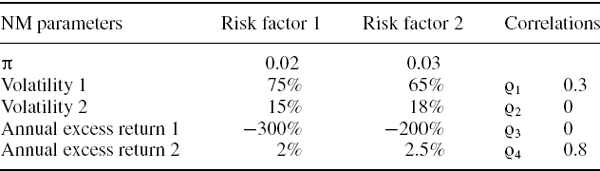
SOLUTION Using the data in Table IV.2.27 with the sensitivity vector θ = (0.8, 1)^′ we calculate the means and variances of the four components in the normal mixture distribution of the portfolio return, using (IV.2.76) and (IV.2.77) above. Then the 1% 10-day VaR of the portfolio is calculated in the spreadsheet, using Excel Goal Seek (or Solver) to ‘back out’ the VaR from the formula (IV.2.72), just as in the previous examples. The result is a 1% 10-day normal mixture VaR that is 16.88% of the portfolio's value.

IV.2.10 EXPONENTIAL WEIGHTING WITH PARAMETRIC LINEAR VALUE AT RISK

Until now, when historical volatility estimates have been used they have been based on the the equally weighted unconditional variance estimate, which was introduced and illustrated in Section II.3.4. For instance, denoting the portfolio return at time t by r_t and assuming these returns are i.i.d. with zero mean, the equally weighted sample variance based on the most recent T returns is

If these returns are daily then our estimate at time t of the h-day standard deviation is _t.⁵¹ A formula similar to (IV.2.78) but based on cross products rather than squared returns, yields an equally weighted average covariance estimate. Dividing the covariance by the square root of the product of the two variances gives the equally weighted correlation. Since the variance and covariance of i.i.d. returns both scale with h, the correlation does not scale with the risk horizon of the returns.

Whilst equally weighted averages are useful for estimating VaR over a long term risk horizon, they have limited use for estimating VaR over a short term horizon. This is because they provide an estimate of the un conditional parameter, and the estimate represents only the average value of the corresponding conditional parameter over the historical sample of returns. For instance, if we use three years of data to estimate volatility, the equally weighted average represents the average sample volatility over the last three years. This may be fine for long-term VaR estimation, but short-term VaR estimates are supposed to reflect the current market conditions, and not the average conditions of the past three years. For this we need a forecast of the conditional volatility, which is time-varying, or at least we need a time-varying estimate of volatility.⁵²

This section explains how the exponentially weighted moving average methodology may be used to provide more accurate short term VaR estimates than the standard equally weighted method for parameter estimation. Throughout this section all risk factors are assumed to have i.i.d. daily returns. Hence, in our empirical examples we use the square-root-of-time rule to scale VaR over different risk horizons.

IV.2.10.1 Exponentially Weighted Moving Averages

This section summarizes the EWMA statistical methodology as it is applied to estimating time series of volatilities and correlations. The EWMA methodology is described in full in Section II.3.8.1, to which readers are referred for further information.

The EWMA formula for the variance estimate at time t of a time series of returns {r_t} is most easily expressed in a recursive form, as

where λ denotes the smoothing constant, and 0< λ < 1.⁵³ The EWMA volatility is obtained by annualizing (IV.2.79) and taking the square root. For instance, if {r_t} denotes a series of daily returns and there are 250 daily returns per year, then the EWMA volatility at time t is , where is given by (IV.2.79).

Figure IV.2.12 depicts the EWMA volatility of the FTSE 100 index for two different values of the smoothing constant. This shows that the smoothing constant captures the persistence of variance from one time period to the next. The larger the value of λ, the smoother the resulting time series of variance estimates. The effect that a non-zero market return at time t − 1 has on the variance estimate at time t depends on 1 − λ, and the lower the value of λ the more reactive the variance is to market events.

Figure IV.2.12 EWMA volatility of the FTSE 100 for different smoothing constants

Another way of viewing an EWMA estimate of volatility is as an equally weighted volatility estimate on exponentially weighted returns. That is, we multiply the return from n periods in the past by λ^(n−1)/2, for n = 1,…., T where T is the sample size. Then the EWMA variance estimate at time t is the equally weighted variance estimate based on the series λ^(n−1)/2r_t−n, n = 1,…, T, but instead of dividing by T, we multiply by 1 − λ.⁵⁴ Thus an alternative expression to (IV.2.79), valid only as T →∞, is

But since 0< λ < 1, λ^k → 0as k →∞, and so as returns move further into the past they will have less influence on the EWMA estimate (IV.2.80).

The EWMA covariance of two contemporaneous time series of returns {r_1t} and {r_2t} may also be expressed in a recursive form, as

The EWMA correlation is obtained by computing three series based on the same value of the smoothing constant, two EWMA variances that are estimated using (IV.2.79) for each of the returns, and the EWMA covariance (IV.2.81). Then the covariance estimate at time t is divided by the square root of the product of the variance estimates at time t, and the result is the EWMA correlation estimate at time t.

As an example, we estimate the EWMA correlation between the NASDAQ 100 technology and S&P 500 indices, using daily log returns based on closing index prices.⁵⁵ The evolution of the two indices is depicted in Figure IV.2.13, where the effects on the NASDAQ 100 of the technology bubble at the turn of the century are clearly visible. Then, using daily log returns on the closing prices, the spreadsheet for Figure IV.2.14 computes the EWMA index volatilities for any value for the smoothing constant. For the graph shown here we have used the RiskMetrics^™ daily smoothing constant of 0.94.

Figure IV.2.13 NASDAQ 100 and S&P 500 indices

Next we compute the daily EWMA covariance, using (IV.2.81) with the same value of λ, i.e. 0.94, for the two volatilities shown in Figures IV.2.14. Dividing this covariance by the square root of the product of the two daily variances gives the EWMA correlation. The resulting correlations are compared in Figure IV.2.15. In the spreadsheet for this figure readers may like to change the value of the smoothing constant and see the smoothing effect on the EWMA correlation as λ increases. Notice that, for any choice of λ, the average of the EWMA correlations over the sample is approximately 82%, i.e. the same as the equally weighted average correlation estimate over the entire sample.

Figure IV.2.14 EWMA volatilities of NASDAQ and S&P 500 indices

Figure IV.2.15 EWMA correlations of NASDAQ and S&P 500 indices

IV.2.10.2 EWMA VaR at the Portfolio Level

The previous subsection demonstrated that EWMA volatilities and correlations are more risk sensitive than equally weighted average estimates of the same parameters. That is, they respond more rapidly to changing market circumstances, particularly for low values of the smoothing constant λ. It is not easy to make equally weighted average parameter estimates risk sensitive, because as the sample size over which the average is taken decreases, the estimates become more seriously biased by ghost features of extreme market movements in the sample.⁵⁶

In this section we present some empirical examples to illustrate the effect of using EWMA on VaR estimation at the portfolio level, compared with VaR based on equally weighted estimates of the portfolio volatility. The i.i.d. normal assumption is retained, and the portfolio value is assumed to be a linear function of the prices of its assets or risk factors. Hence, the EWMA daily VaR estimate may be scaled to longer horizons using the square-root-of-time rule.⁵⁷

Given an EWMA estimate _t of the daily standard deviation of the portfolio return or P&L at time t, when the VaR is measured, the normal linear EWMA estimate of the 100α% h-day VaR is⁵⁸

We illustrate the application of this formula in the next example.

EXAMPLE IV.2.25: EWMA NORMAL LINEAR VAR FOR FTSE 100

Use an EWMA volatility series to estimate the 100α% 10-day normal linear VaR for a position on the FTSE 100 index on 18 April 2008. How does the choice of smoothing constant affect the result?

SOLUTION We do not need a long period of historical data to compute the EWMA VaR. The spreadsheet for this example uses data from January 2006 until 18 April 2008, i.e. 580 daily returns.⁵⁹ The formula (IV.2.82) is implemented in the spreadsheet and the results are displayed in Table IV.2.31. In the last column we show the equally weighted VaR estimate over the whole sample of 580 observations, which is identical to the EWMA estimate with a smoothing constant of 1.

Table IV.2.31 EWMA VaR for the FTSE 100 on 18 April 2008

As usual, all VaR estimates increase with the significance level. Also, at each significance level, each of the EWMA volatility estimates are greater than the equally weighted VaR estimate shown in the last column. This is because April 2008 was a fairly volatile period for the FTSE 100, as the effects of the credit crunch were still taking their toll on the financial sector of the UK economy. But the most interesting point to note about these results is that lower values of lambda do not necessarily give higher or lower VaR estimates, just because they use only very recent data. In fact, in our case the estimates based on λ = 0.95 are the greatest, at each significance level. This is because the FTSE 100 index was also very volatile during the latter half of 2007, and not just in the first quarter of 2008. Of the three values used for λ, it seems that setting λ = 0.95 maximizes the total weight put on these more volatile data. Results for other values of λ and for different significance levels and risk horizons may be obtained by changing the parameters in the spreadsheet.

IV.2.10.3 RiskMetrics^™ VaR Methodology

When the systematic VaR of a large portfolio is disaggregated into stand-alone or marginal component VaRs, we could base the systematic VaR on the normal linear VaR formula (IV.2.15). For a short-term VaR estimate to be more risk sensitive, the covariance matrix in this formula may be based on an EWMA covariance matrix, instead of using equally weighted averages of squared returns and their cross products. However, unless we apply the orthogonal EWMA methodology, which is described in Section II.3.8.7, the smoothing constant must be the same for the variance and covariance estimates in the matrix. Otherwise the matrix need not be positive semi-definite.⁶⁰

The RiskMetrics group provides daily estimates of volatilities and correlations, summarized in three very large covariance matrices, with risk factors that include most commodities, government bonds, money markets, swaps, foreign exchange and equity indices for over 40 currencies. The three covariance matrices provided by the RiskMetrics group are as follows:⁶¹

1. Regulatory matrix. An equally weighted average matrix based on the last 250 days.
2. Daily matrix. An EWMA covariance matrix with λ = 0.94 for all elements.
3. Monthly matrix. An EWMA covariance matrix with λ = 0.97 for all elements and then multiplied by 25.⁶²

In addition, the group provides VaR software based on these data and a number of documents, including a technical document, which describes its portfolio mapping procedures and the VaR methodology.

In the next example we use a portfolio of US stocks in the S&P 500 and NASDAQ 100 indices to illustrate the application of the RiskMetrics methodology and the decomposition of systematic VaR into stand-alone components.

EXAMPLE IV.2.26: COMPARISON OF RISKMETRICS^™ REGULATORY AND EWMA VAR

Consider a large portfolio of US stocks having a percentage beta with respect to the S&P 500 index of 1.1 and a percentage beta with respect to the NASAQ 100 index of 0.85. Assume that $3 million is invested in the S&P 500 stocks and $1 million is invested in the NASDAQ 100 stocks. Compare the 1% 10-day normal VaR of this portfolio on 18 April 2008, based on the RiskMetrics regulatory matrix and based on the daily matrix, and in each case disaggregate the VaR into S&P 500 and NASDAQ 100 stand-alone VaR.

SOLUTION We use the data shown in Figure IV.2.16, starting on 3 January 2006 and ending on 18 April 2008.⁶³ The NASDAQ 100 index is on the left-hand scale and the S&P index is on the right-hand scale.

Figure IV.2.16 NASDAQ 100 and S&P 500 indices, 2006–2008

The EWMA variances and covariances are estimated as explained above, but we are not interested in a time series of variances and covariances, only in the covariance matrix on 18 April 2006, because we are only estimating VaR on this day. The volatilities and correlation estimated on 18 April 2006, based on an EWMA with λ = 0.94 and based on an equally weighted average of the last 250 returns, are shown in Table IV.2.32, and the resulting annual covariance matrices are shown in Table IV.2.33. Note that the US was still very much feeling the effects of the credit crisis in April 2008 and so, being based on more recent data, the EWMA volatilities and correlations are higher than the RiskMetrics regulatory estimates.

Table IV.2.32 Volatilities of and correlation between S&P 500 and NASAQ 100 indices

Table IV.2.33 Annual covariance matrix based on Table IV.2.32

The spreadsheet for this example implements the normal linear VaR formula (IV.2.15) where Ω_h is the h-day matrix that is derived from the relevant annual matrix in Table IV.2.33, using the square-root-of-time rule, and θ is the vector of nominal portfolio betas, that is, ($3.3m, $0.85m)′. We assume the excess return on each index is zero. Since θ is expressed in value terms, the VaR will also be expressed in value terms.

The stand-alone VaRs are estimated using the individual volatilities shown in Table IV.2.32, each scaled to a 10-day standard deviation using the square-root-of-time rule. Since both volatility estimates are lower when based on an equally weighted average over the last 250 days, we expect the stand-alone VaRs to be lower when they are based on the regulatory matrix. However, since the regulatory correlation estimate is also lower, the total systematic VaR could be greater than or less than the corresponding EWMA estimate, depending on the portfolio composition. The results for the portfolio given in the question are shown in Table IV.2.34.⁶⁴

Table IV.2.34 RiskMetrics VaR for US stock portfolio

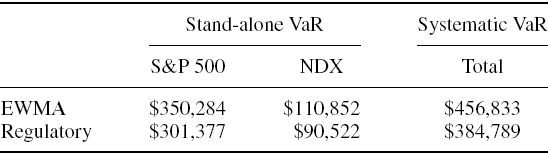
In both cases the sum of the stand-alone VaRs exceeds the total systematic VaR, due to the usual diversification effect in the total VaR. However, since the two risk factors have a high correlation, this diversification effect is small. Both stand-alone VaRs, and the total VaR estimate, are greater when based on the EWMA covariance matrix, because this captures the current, more volatile market circumstances, whereas the regulatory covariance matrix is based on an average over 1 year.

The Basel regulations that were introduced in 1996, specified that internal models which are used to calculate the market risk capital requirements must use at least 250 days of historical data. Hence the EWMA methodology, which effectively uses less than 250 days, due to the exponential weighting of returns, has been disallowed. However, following the credit crisis, in July 2008 the Basel Committee proposed extra capital charges for equity and credit spread risks, precisely because the use of 250 days or more of historical data is now thought to produce VaR estimates that are insufficiently risk sensitive. It is unfortunate that the Committee took so long to realise this fact. It is also unfortunate that the Committee believe that imposing additional capital charges is the appropriate response to the credit and banking crises.

IV.2.11 EXPECTED TAIL LOSS (CONDITIONAL VAR)

Section IV.1.8.2 introduced expected tail loss, also called conditional VaR. The ETL is defined by (IV.1.32) and its interpretation is the expected loss (in present value terms) given that the loss exceeds the VaR. The ETL risk metric is more informative than VaR, because VaR does not measure the extent of exceptional losses. VaR merely states a level of loss that we are reasonably sure will not be exceeded: it tells us nothing about how much could be lost if VaR is exceeded. However, ETL tells us how much we expect to lose, given than the VaR is exceeded. Clearly ETL gives a fuller description of the risks of a portfolio than just reporting the VaR alone. Since ETL is also a coherent risk metric (see Section IV.1.8.3. ETL is sub-additive even when VaR is not.⁶⁵ This means that ETL is a better risk metric to use for regulatory and economic capital allocation, a subject that we shall return to in Chapter 8.

We now present a mathematical description of ETL. Let X denote the discounted h-day return, and set

where x_α denotes the α quantile of the distribution of X, i.e. P(X < x_α) = α. The definition of ETL, when it is expressed as a percentage of the portfolio value, is

Since the ETL is a conditional expectation, it is obtained by dividing the probability weighted average of the values of X that are less than x_α by P(X < x_α). But P(X < x_α) = α so if X has density function f(x) then

In this section we derive formulae for ETL when VaR is estimated using the parametric linear model, beginning with the normal linear model and then extending this to Student t linear ETL, to normal mixture linear ETL and to Student t mixture ETL. We shall express the ETL as a percentage of portfolio value throughout.

IV.2.11.1 ETL in the Normal Linear VaR Model

Let the random variable X denote a portfolio's discounted h-day return. If then

where and Φ denote the standard normal density and distribution functions. Hence, Φ⁻¹(α) is the α quantile of the standard normal distribution and (Φ⁻¹(α)) is the height of the standard normal density at this point.

To prove (IV.2.84) we first calculate the ETL of a standard normal variable Z. Since the standard normal density function is

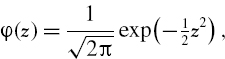
we have

Now we use the standard normal transformation to write X in the form

By the definition (IV.2.83) of ETL,⁶⁶

and this proves (IV.2.84).

EXAMPLE IV.2.27: NORMAL ETL

Suppose a portfolio is expected to return the risk free rate with a volatility of 30%. Assuming the returns are i.i.d., find the 1% 10-day parametric linear VaR and ETL as a percentage of the portfolio's value.

SOLUTION The 10-day standard deviation is . So the 1% 10-day normal ETL is

That is, the 1% 10-day normal ETL is about 16% of the portfolio's value. This should be compared with the 1% 10-day normal linear VaR, which is only 13.96% of the portfolio's value. By definition, the ETL is always at least as great as the corresponding VaR, and often it is much greater than the VaR.

IV.2.11.2 ETL in the Student t Linear VaR Model

Again let the random variable X denote a portfolio's discounted h-day return. In this section we show that if X has a Student t distribution with mean μ_h, standard deviation σ_h and ν degrees of freedom then

where x_α(ν) denotes the α quantile of the standardized Student t distribution (i.e. the one with zero mean and unit variance) having ν degrees of freedom, and f_ν(x_α(ν)) is the value of its density function at that point. The standardized Student t density function is derived in Section I.3.3.7 as

The result (IV.2.86) follows if we can prove that the ETL in a standardized Student t distribution with ν degrees of freedom is given by

where T denotes a standardized Student t variable with ν degrees of freedom. By the definition (IV.2.83) of ETL, we need to evaluate

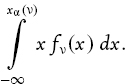
To shorten our notation, note that we may write (IV.2.87) more briefly as

where

Then,

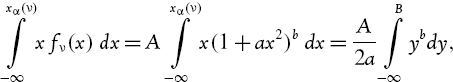
where we have set y = 1 +ax² and B = 1 +(ν − 2)⁻¹x_α(ν)². Then

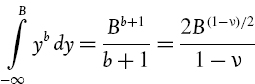
and

So

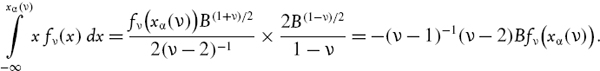
Now substituting in the above for B and using (IV.2.83) yields (IV.2.88).

EXAMPLE IV.2.28: STUDENT T DISTRIBUTED ETL

As in the previous example, suppose that a portfolio is expected to return the risk free rate with a volatility of 30%, but now suppose that its returns are i.i.d. with a Student t distribution with ν degrees of freedom. Find the 1% 10-day Student t VaR and ETL, as a percentage of the portfolio's value, for ν = 5, 10, 15, 20 and 25.

SOLUTION We base the calculations in the spreadsheet on (IV.2.63) for the VaR, and (IV.2.88) for the ETL. Thus we calculate the standardized t ETL, and transform the standardized t ETL to obtain the ETL for our return distribution using (IV.2.86). The results are summarized in Table IV.2.35 and, for comparison, the last column of this table reports the normal VaR and ETL for the same portfolio, with the results obtained from the previous example. For highly leptokurtic distributions (i.e. for low values for the degrees of freedom) the ETL is far greater than the VaR. For instance, the ETL is almost twice as large as the VaR under the t₅ distribution. But as the degrees of freedom increase, the Student t distribution converges to the normal distribution, so VaR and ETL converge toward to the normal VaR and ETL.

Table IV.2.35 VaR and ETL for Student t distributions

IV.2.11.3 ETL in the Normal Mixture Linear VaR Model

First suppose that a portfolio's discounted h-day return X has a normal mixture distribution G₀ with zero means in the components where

is the mixing law and the component variances are . We set

so that − x_α is the 100α% h-day VaR under the zero-mean normal mixture. Write the density function as , where each f_i(x) is a zero-mean normal density with standard deviation σ_ih. Then, by extending the argument used in the normal case, we have

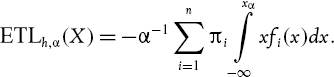
Using an argument similar to that in (IV.2.85), it can be shown that

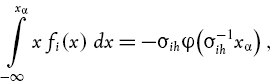
where is the standard normal density function. Hence, we have

Now suppose a portfolio's discounted h-day is expected to return are represented by a mixture of n normal distributions with distribution function G. That is, , where π and are defined above and the component means are μ_h =(μ_1h,…, μ_nh). Then the expected value of the normal mixture is and, again by extending the argument used in the normal case, we have

where − x_α is the 100α% h-day VaR under the corresponding zero-mean normal mixture.

EXAMPLE IV.2.29: NORMAL MIXTURE ETL

As in Examples IV.2.27 and IV.2.28, suppose that a portfolio is expected to return the risk free rate with a volatility of 30%, but now suppose that its returns are i.i.d. with a normal mixture distribution with discounted mean returns of zero, but with two normal components having different volatilities: with probability 0.2 the volatility is 60% and with probability 0.8 the volatility is 15%. Find the 1% 10-day normal mixture VaR and ETL as a percentage of the portfolio's value.

SOLUTION We remark that the volatility of the normal mixture is the same as that in the previous two examples, since

Hence, we can compare the results with those in the previous examples for the normal and Student t ETL. First the spreadsheet uses Excel Solver or Goal Seek optimizer to back out the 1% 10-day normal mixture VaR using formula (IV.2.72). The normal mixture VaR is 19.74% of the portfolio's value. This is significantly greater than the normal VaR found in Example IV.2.27.

The normal mixture ETL is also much greater than the normal ETL derived in Example IV.2.27. A volatility of 60% corresponds to a 10-day standard deviation of 0.12 and a volatility of 15% corresponds to a 10-day standard deviation of 0.03. Thus, applying (IV.2.89), we have

So under the normal mixture distribution with an overall volatility of 30%, the 1% 10-day ETL is nearly 25% of the portfolio value, compared with approximately 16% if the distribution were normal with volatility 30%.

IV.2.11.4 ETL under a Mixture of Student t Distributions

It can be shown that when the return distribution is assumed to be a mixture of Student t distributions with different means, variances and degrees of freedom as in Section IV.5.2.7, then⁶⁷

where

and x_α(ν) is minus the Student t mixture VaR. Here ν denotes the vector of degrees of freedom for each component in the mixture. The next example illustrates the implementation of this formula, and compares the results with those in the previous examples.

EXAMPLE IV.2.30: STUDENT T MIXTURE ETL

As in Examples IV.2.27–IV.2.29, suppose that a portfolio is expected to return the risk free rate with a volatility of 30%, but now suppose that its is expected to return are i.i.d. with a Student t mixture distribution. Both Student t distributed components have a discounted mean return of zero, but the two components have different volatilities and degrees of freedom: with probability 0.2 the distribution has 5 degrees of freedom and a volatility of 45% and with probability 0.8 the distribution has 10 degrees of freedom and volatility of 25%.⁶⁸ Find the 100α% h-day VaR and ETL as a percentage of the portfolio's value for α = 0.1% and 1% and h = 1 and 10. Compare your results with those obtained above, using a normal, normal mixture and individual Student t distributions.

SOLUTION Table IV.2.36 compares the 100α% h-day VaR and ETL from all the distributions considered in these examples, for the different values of α and h.⁶⁹ The normal VaR and ETL are the smallest, which is as expected, due to the high significance level of the VaR and the leptokurtic nature of the other distributions. Comparing the normal mixture with the individual Student t estimates, the normal mixture VaR exceeds both the Student t VaR estimates, but the normal mixture ETL estimates lie between the two Student t ETL estimates. Although greater than the ETL estimates based on 10 degrees of freedom, the normal mixture ETL is substantially less than the Student t ETL with 5 degrees of freedom.⁷⁰ The Student t mixture VaR is less than the normal mixture VaR at the 1% level, but greater than the normal mixture VaR at the 0.1% level, and the Student t mixture ETL is greater than the normal mixture ETL at both the 1% and 0.1% levels.

Table IV.2.36 VaR and ETL for normal, Student t and mixture distributions

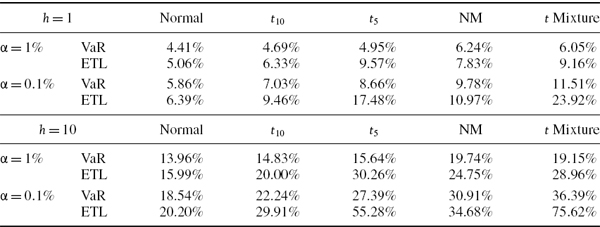
The above example shows that it is not only the excess kurtosis that determines the ETL: it is also very much influenced by the tail behaviour. The tails of a normal mixture distribution decline exponentially, but the tails of a Student t distribution decline more slowly than this. Hence, when the two distributions have similar excess kurtosis, the normal mixture ETL will be lower than the Student t ETL.

IV.2.12 CASE STUDY: CREDIT SPREAD PARAMETRIC LINEAR VALUE AT RISK AND ETL

We end the chapter with a short case study on estimating VaR and ETL for a highly non-normal and autocorrelated risk factor. The purpose of the study is to highlight the huge model risk that arises from the choice of VaR model. That is, we show that very different VaR estimates can be obtained even when we fix the same:

• broad methodology – i.e. the VaR estimates are based on different parametric linear VaR models;
• sample data – we shall use the same sample for all estimates;
• risk factor model – we consider the VaR and ETL from an exposure to a single credit spread risk factor.

IV.2.12.1 The iTraxx Europe Index

The risk factor we have chosen for this study is the iTraxx Europe 5-year index. In June 2004 the iBoxx and Trac-x credit default swap (CDS) indices merged to form the Dow Jones iTraxx index family, which consists of the most liquid single-name credit default swaps in the European and Asian markets. As well as representing an important risk factor for interest rate sensitive portfolios, the iTraxx indices for maturities of 3, 5, 7 and 10 years are traded over the counter (OTC), the 5- and 10-year maturities being the most liquid. Also, many major banks have been entering OTC trades on iTraxx options during the last few years. Their clients include hedge funds, proprietary trading desks, insurance companies, investment managers and index CDS traders who use options for the risk management of their positions. In March 2007 Eurex, the world's largest derivative exchange, launched exchange traded futures and will soon introduce other credit derivative products on iTraxx indices.

The main Europe index series, which is shown in Figure IV.2.17, is an equally weighted CDS spread, measured in basis points, and based on 125 single firm investment grade CDSs. Every six months a new series for each of the iTraxx indices is introduced in which defaulted, merged, sector changed or downgraded entities are replaced by the next most liquid ones. We splice the older series together with the most recent series to produce the data shown in the figure.

Figure IV.2.17 shows the iTraxx index's evolution, and its daily changes between 21 June 2004 and 10 April 2008.⁷¹ The effects of the credit crunch that was precipitated by the sub-prime mortgage crisis in the US in the latter half of 2007 are clearly visible. In June 2007 credit spreads were at a historical low, having been trending down for several years. However, by mid-March 2008, with the onset of the crisis, the iTraxx Europe spread for investment grade CDSs rose from less than 3 basis points to an unprecedented high of over 140 basis points. Then, by the beginning of April 2008, the index fell to less than 60 basis points.

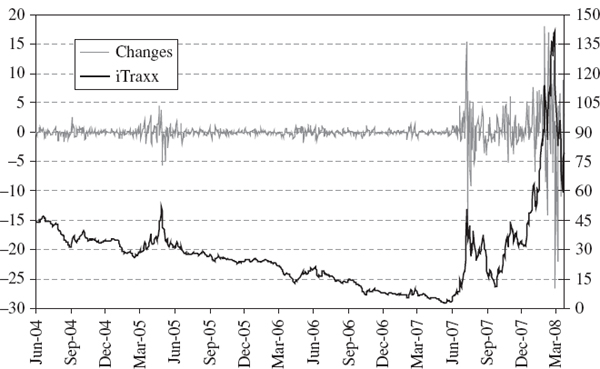
Figure IV.2.17 iTraxx Europe 5-year index

Table IV.2.37 shows the sample statistics, with approximate standard errors, and the ratio of the statistic to its standard error, based on all 970 data points. All statistics except the mean appear to be highly significant, and in particular we have significant negative skewness, positive excess kurtosis and positive autocorrelation.

Table IV.2.37 Sample statistics for iTraxx Europe 5-year index

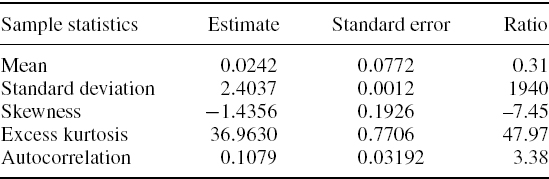
The annualized volatility of the index depends on the assumption made about the dynamics. Based on the i.i.d. assumption, it is

But the autocorrelation of 0.1079 is positive and significant, and using the autocorrelation adjusted scaling factor (IV.2.10) we obtain a higher volatility, of

Thus we expect that when the sample autocorrelation is taken into account the VaR and ETL estimates will be higher than when we assume the daily changes are i.i.d.

IV.2.12.2 VaR Estimates

We shall estimate the VaR and ETL for a simple linear exposure, with a PV01 of €1000, to the daily changes in the iTraxx Europe 5-year index. Using the PV01 approximation described in Section IV.2.3.2, we see that this represents a cash flow at 5 years of approximately €2.5 million.

Different VaR and ETL estimates will be based on the normal, Student t and normal mixture models that we have introduced in this chapter. Our focus is on the model risk arising from the choice of risk factor distribution, so we shall base all the estimates on the same, objective sample data. That is, we use all the data on iTraxx index changes shown in Figure IV.2.17. There are 970 daily changes, covering almost 4 years.

When estimating the 1% 10-day VaR and ETL, we consider two assumptions about the index dynamics: that daily changes are (a) i.i.d. and (b) autocorrelated. Thus, using exactly the same data in each case, we obtain six different estimates of the parametric linear VaR and six corresponding estimates of the ETL, over a risk horizon of 10 days and at the 99% confidence level.

The estimation of the model parameters is based on the method of moments. For the Student t degrees of freedom we follow Example IV.2.18, and for normal mixture parameters we use the same methodology as that described in Section IV.2.8.3 and applied in Example IV.2.21.⁷²

The method of moments estimate of the Student t degrees of freedom is 4.1623, which matches the sample excess kurtosis of 36.963. But note that the skewness is assumed to be zero under the Student t distribution.

The mixture distribution assumes only two components, one to represent the stable downward trending regime which prevailed most of the time prior to the credit crisis, and another to represent the volatile regime where credit spreads have the tendency to jump up rapidly and jump down even more rapidly. The estimated parameters, quoted in basis points per annum, are displayed in Table IV.2.38.⁷³

Table IV.2.38 Normal mixture parameter estimates: iTraxx Europe 5-year index

The VaR and ETL estimates are obtained in the spreadsheet labelled ‘VaR and ETL’ in the case study workbook, using the methodology described in Sections IV.2.2 and IV.2.8, and the results are summarized in Table IV.2.39. The VaR estimates range from €17,683 for the normal i.i.d. VaR model, to €43,784 for the normal mixture model with the autocorrelation adjustment. Similarly, the ETL estimates range from €20,259 for the normal i.i.d. VaR model, to €48,556 for the Student t model with the autocorrelation adjustment.

All the estimates are based on exactly the same data, but the assumptions made by the normal i.i.d. model are clearly not justified for the daily changes in the iTraxx index. The normal i.i.d. VaR model ignores not only the autocorrelation, but also the large negative skewness and the extremely high excess kurtosis (of almost 37 – see Table IV.2.37); instead both are assumed to be zero.

Table IV.2.39 VaR and ETL estimates for iTraxx Europe 5-year index

The Student t model has a high ETL, like the normal mixture model, but the VaR estimates based on the Student t distribution are much lower than those from the normal mixture. This is because the large negative skewness, which is ignored by the Student t model and is only captured by the normal mixture model, increases the VaR significantly.

The model that makes the most appropriate assumptions is the autocorrelated normal mixture model. This is able to capture all the features of the data, and in particular, it captures the two different regimes in credit spreads during the data period. Therefore the VaR and ETL estimates based on this model are, amongst all the estimates reported in Table IV.2.39, the most representative of the historical sample.

IV.2.13 SUMMARY AND CONCLUSIONS

The parametric linear VaR model is applicable to all portfolios except those containing options, or any other instruments with non-linear price functions. If we assume the portfolio returns have either a normal distribution or a Student t distribution it is possible to derive VaR as an explicit solution to an analytic formula. It is also possible to back out the VaR from a formula, using a simple numerical algorithm (such as Excel's Goal Seek or Solver) under the assumption that the portfolio return has a mixture of normal or Student t distributions. All these formulae, and the corresponding ETL formulae, have been derived in this chapter, and we have provided a very large number of numerical examples and empirical illustrations based on different types of linear portfolios.

The analytic VaR formulae hold for any confidence level and over any risk horizon. The general formulae contain an adjustment for the case where the portfolio is expected to grow at a rate different from the discount rate, but this adjustment is very small except for long risk horizons and when a portfolio has an expected return very different from the discount rate.

We do not need to assume the returns are i.i.d. It is also possible to adjust the general parametric linear VaR formula to account for autocorrelation in log returns. When the daily log returns are autocorrelated an adjustment needs to be made to the h-day standard deviation. No adjustment is required for the discounted expected return, if this is included in the VaR estimate. With positive or negative autocorrelation the h-day standard deviation is no longer σ, where σ is the standard deviation of daily log returns, but σ where > h for positively autocorrelated daily log returns and < h for negatively autocorrelated daily log returns. Hence positive or negative autocorrelation can result in a significant increase or decrease in h-day VaR, even for short risk horizons.

When the portfolio has a discounted expected return of zero, parametric linear VaR behaves like volatility and so its aggregation rule can be derived from the rule for the variance of a sum. We first examined the disaggregation of the total VaR of a portfolio into a systematic VaR component that is explained by the mapping to risk factors, and a specific VaR or residual component. Our empirical examples here focused on the decomposition of the VaR for a stock portfolio into the systematic VaR due to the market risk factors, and a residual VaR.

Further, systematic VaR can be decomposed in two different ways. The first is the decomposition of systematic VaR into stand-alone VaR components that are due to each type of risk factor. Thus we have equity VaR, interest rate VaR, credit spread VaR, forex VaR, commodity VaR, and so forth. The stand-alone VaRs represent the risk taken by each individual trading activity without allowing for any diversification effects from other trading activities in the same firm. But when we measure VaR at an aggregate level, we take account of diversification. Hence, the sum of the stand-alone VaRs is not equal to the total systematic VaR. In fact, when VaR is measured by the parametric linear model, the sum of the stand-alone VaRs is always greater than or equal to the total systematic VaR. That is, parametric linear VaR is sub-additive. We have also shown how the total systematic VaR can be decomposed into marginal VaR components which are additive. Thus marginal VaRs are useful for the allocation of real capital which (unlike regulatory or economic capital) must be additive.

In the context of the normal linear VaR model we have derived simple formulae that may be applied to estimate the stand-alone and marginal VaR, and the corresponding ETL, for any given risk factor class. Another formula which, like marginal VaR, is based on the gradient vector, is derived for the incremental VaR that measures the impact of a small trade on the VaR of a given, large portfolio.

The normal linear VaR model can be extended to the case where the portfolio's returns, or the risk factor returns, have leptokurtic and skewed distributions. We have derived formulae for Student t distributed VaR, for normal mixture VaR and for Student t mixture distributed VaR. The mixture linear VaR models result in an implicit rather than an explicit formula for VaR. They provide an ideal framework for scenario VaR in the presence of two or more possible regimes, or states of the world. In Section IV.7.2 we shall illustrate this by considering the credit spread 1-year VaR of a BBB bond under three scenarios, i.e. that it is downgraded, upgraded, and that its rating remains the same by the end of the year.

The expected tail loss is the expected loss, in present value terms, given that VaR is exceeded. It is also called the conditional VaR. ETL is more informative than VaR because it provides information of the average or expected loss when the VaR is exceeded. We have derived general formulae for the ETL under the assumption that a portfolio's returns have normal, Student t and mixtures of these distributions. Empirical examples show that the normal mixture ETL and the Student t distributed ETL may be considerably greater than the normal ETL, when returns have leptokurtic and skewed distributions.

The examples in this chapter have focused on portfolios represented by cash flows, international equity portfolios and commodity futures portfolios. In each case we assumed the portfolio has been mapped to a set of standard risk factors following the techniques described in Chapter III.5. We have used these portfolios to:

• show that adjusting VaR and ETL for a non-zero discounted expected return only has a significant effect when the risk horizon is very long and the discounted expected return is very large;
• illustrate how to adjust VaR and ETL for autocorrelation in portfolio returns;
• estimate the systematic VaR and specific VaR for an equity portfolio using (a) equally and (b) exponentially weighted estimates for the portfolio volatility and its market beta;
• decompose total systematic VaR into different stand-alone and marginal VaR components, due to different classes of risk factors;
• aggregate stand-alone VaRs into the total risk factor VaR, in a sub-additive manner;
• measure the incremental VaR of adding a single swap to a large swaps portfolio;
• demonstrate how the different theoretical assumptions made by normal, Student t and mixture VaR models affect the VaR and ETL estimates; and
• explain how EWMA covariance matrices may be applied in the context of the parametric linear VaR model.

Our first case study was on a UK bond portfolio where the risk factors are fixed maturities along a zero coupon yield curve. We explained how to use principal component analysis to reduce the dimensions of the risk factor space: instead of 60 risk factors (constant maturity interest rates) we used only three risk factors (the first three principal components), and the approximation error was very small indeed. That is, the VaR was almost exactly the same whether we used 60 or three risk factors. It can also be argued that the VaR based on only three risk factors is the more accurate of the two, because the dimension reduction allows us to ignore extraneous ‘noise’ in the data that should not affect the VaR estimate.

The second case study examined the risks facing a commodity futures trading business with desks trading silver and natural gas. The study highlighted the very different characteristics of these two commodities and disaggregated the total VaR of the trading activities into the stand-alone and marginal VaRs due to trading in both natural gas and silver futures.

The last case study illustrated the application of different parametric linear models to estimate both the VaR and the ETL for an exposure to the iTraxx Europe 5-year credit spread index. The historical distribution of this risk factor is highly non-normal, with a large negative skewness and an extremely high excess kurtosis, and its daily changes have a significant positive autocorrelation. Hence, the normal i.i.d. model is totally inappropriate. The most representative parametric linear VaR model is the normal mixture VaR model with autocorrelated returns. This model provided 1% 10-day VaR and ETL estimates that are approximately 2.5 times the size of the normal i.i.d. VaR and ETL estimates! Clearly the use of a normal i.i.d. model would seriously underestimate the risk of such an exposure.