The Normal Density

There is a plethora of books on probability and statistics that cover the important normal distribution, and I recommend one among many excellent texts, the volume by Ross [99], especially Chapters 5, 6, and 7, where most of the elementary facts can be found.

Recall that a continuous random variable X is normally distributed with parameters μ and σ if its density function is defined, for all i, by

(A.1)

It is known that E(X) = μ and Var(X) = σ². Suppose we have n independent samples X₁, X₂, . . . , X_n from a normal distribution having an unknown mean that is now designated as θ in order to be consistent with the notation used in Chapter 5. The samples are most likely clustered about the value of the mean where the normal density peaks. An interesting ploy to find a good estimate of θ is to treat it as a variable and keep the samples fixed and then forming a product function

in which f(X_j, θ) is the normal density evaluated at X_j, with mean θ. The idea is to choose θ so as to maximize L(θ), effectively sliding the normal density back and forth, until the sample values give a best fit to the mean, in the sense that the probability L has its largest value. This can be done most easily by taking logarithms, since the optimum θ is also optimum:

(allowing σ to equal 1 without any real loss). This is known as the maximum-likelihood method. Using straightforward calculus, one solves for the root of ∂L(θ)/∂θ = 0 to obtain

from which we find the optimal estimate of θ as the sample mean X^∗ = 1/n ∑X_j. Note that X^∗ is unbiased, in the sense that E(X^∗) = θ.

It can be shown, in the case of the normal distribution, that the best estimate of the mean—in the sense of minimizing the variance of an unbiased function g(X₁, . . . , X_n) of the sample values, namely, the minimum of E(g(X₁, . . . , X_n) – θ)², where g can be nonlinear—is again the sample mean X^∗. I do not show this here, even though the proof is not that hard. What is important here is that the minimum-variance unbiased estimate of the mean is also the maximum-likelihood estimate in the case of normal densities.

In terms of the Central Limit Theorem, whose proof is beyond the scope of these notes, one gets an estimate for the value of the sample mean X^∗ in terms of the integral Φ(a) of the normal density function from –∞ to some value a, its cumulative distribution function, prob (|X^∗ – θ|/σ/√n < a), tends to the value Φ(a) – Φ(–a) as n → ∞, or, since the normal density is symmetrical about its mean, to the value 2Φ(a) – 1. Multiplying by n, one gets the equivalent statement that prob (|∑X_j – nθ| < aσ√n) tends to 2Φ(a) – 1 as n increases. These estimates were utilized in Section 5.8.

Now suppose that Z₁ and Z₂ are independent and normally distributed variables with mean zero and unit variance, and form the linear combinations

Let X = (X₁, X₂), Z = (Z₁, Z₂), and θ = (θ_1, θ₂). Since X – θ is a combination of independent normal variables, its components are normally distributed with zero means, variances σ₁² = a₁₁² + a₁₂², σ₂² = a₂₁² + a₂₂², and covariance a₁₁a₂₁ + a₁₂ a₂₂. Since covariance equals σ₁σ₂ρ, where ρ is the usual correlation coefficient, the covariance matrix takes on the form

Assuming that the matrix A of coefficients a_ij is nonsingular, the equation X – θ = AZ can be solved to give Z in terms of the X variables as Z = A^–1(X – θ).

Because Z₁ and Z₂ are independent, we can integrate their joint density function f(z₁, z₂) to obtain

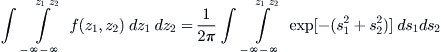
Using the change-of-variables formula for multiple integrals, with Jacobean determinant 1/[σ₁σ₂(1 – ρ)^1/2], the details of which I forego here, the foregoing expression transforms into the double integral of the density function f(x₁, x₂) for the variables X₁ and X₂, and this is given by

(A.2)

where (x – θ)^TΛ^–1(x – θ) = u/(1 – ρ²) and

(A.3)

The variables X₁ and X₂ are said to have a bivariate normal distribution. When there is only a single variable, the foregoing expression reduces to the usual univariate normal density (A.1).

Now suppose that X and Y have a joint bivariate normal distribution. The conditional density of X₁ given that Y equals some specific value y can be computed from Bayes’ formula f(x|y) = f(x, y)/f(y), in which the denominator is the marginal density of the variable Y and f(x, y) is the bivariate density derived earlier. It is a remarkable fact, as is shown in Ross in a straightforward but lengthy proof [99, Section 6.5], that X is again normally distributed with a mean value of

(A.4)

and variance

(A.5)

Note the mean is a linear function of y. It is also true that the marginal density of X is normal, with mean θ_x and variance σ_x². A totally symmetrical result holds for the conditional density of Y given that X = x.

As an aside, recall that if any two variables X, Y are independent, then their covariance, and hence ρ, will be zero. But the converse is also true when the variables are normally distributed, since the density function (A.2) splits into the product of the two marginal densities when ρ = 0, and this shows that X, Y must be independent.

At this point we are in a position to explain the result stated in Section 5.7 regarding Bayes’ estimators. To start with, let X and θ be random variables such that the conditional distribution of X, given that θ takes on a particular value θ, is normal with mean θ and unit variance. Next, suppose that θ itself is normally distributed with mean μ and variance σ². This is the prior distribution of θ, and we want to find the posterior distribution given that X = x.

By Bayes’ formula, the joint density of X and θ, namely, f(x, θ), can be written as f(x, θ) = f(x|θ)f(θ), where the last factor is the marginal density of θ. The conditional density is normal with mean θ and variance equal to 1. Now let Z be normally distributed and independent of θ, with zero mean and unit variance. Then the conditional density of Z₀ = Z + θ, given that θ = θ, is also normal, with mean θ and variance 1. Therefore the joint density of Z₀ and θ is the same as the joint density of X and θ. But the former density is bivariate normal because each variable is separately a linear combination of independent normal variables Z and θ (it suffices to replace θ by θ – θ for it to have a zero mean). It follows that X and θ also have a bivariate normal density and that E(X) = E(Z₀) = E(Z + θ) = μ and Var(X) = Var(Z + θ) = 1 + σ².

By definition of covariance we find that Cov(X, θ) = Cov(Z + θ, θ) = E(Zθ + θ²) – E(Z + θ)E(θ) = μ, and hence the correlation coefficient ρ satisfies the relation ρ[Var(Z + θ)Var(θ)]^1/2 = Cov(Z + θ, θ) = μ.

Because the variables X, θ have a bivariate normal distribution, we obtain, from (A.4) and (A.5),

(A.6)

and

(A.7)