Chapter 4. Nuclear Processes

Nuclear Reactions—those in which atomic nuclei participate—may take place spontaneously, as in radioactivity or may be induced by bombardment with a particle or ray. Nuclear reactions are much more energetic than chemical reactions, but they obey the same physical laws—conservation of momentum, energy, number of particles, and charge.

The number of possible nuclear reactions is extremely large, because there are approximately 2000 known isotopes and many particles that can either be projectiles or products—photons, electrons, protons, neutrons, alpha particles, deuterons, and heavy charged particles. In this chapter we will emphasize induced reactions, especially those involving neutrons.

4.1. Transmutation of Elements

The conversion of one element into another, a process called transmutation, was first achieved in 1919 by Rutherford in England. He bombarded nitrogen atoms with α particles from a radioactive source to produce an oxygen isotope and a proton, according to the equation

We note that on both sides of the equation the A values add to 18 and the Z values add to 9. Figure 4.1 shows Rutherford's experiment. It is difficult for the positively charged α particle to enter the nitrogen nucleus because of the force of electrical repulsion between charged particles. The α particle thus must have several MeV of energy.

Figure 4.1. Transmutation by nuclear reaction.

Nuclear transmutations can also be achieved by charged particles that are electrically accelerated to high speeds. The first such example discovered was the reaction

Another reaction,yields a gamma ray and an isotope of nitrogen. The latter decays with a half-life of 10.3 min, releasing a positron, the positive counterpart of the electron.

Because the neutron is a neutral particle, it does not experience electrostatic repulsion and can readily penetrate a target nucleus. Neutrons are thus especially useful as projectiles to induce reactions. Several examples are chosen on the basis of interest or usefulness. The conversion of mercury into gold, the alchemist's dream, is described by

The production of cobalt-60 is governed bywhere a capture gamma ray is produced. Neutron capture in cadmium, often used in nuclear reactor control rods, is given by

A reaction that produces tritium, which may be a fuel for controlled fusion reactors of the future, is

A shorthand notation is used to represent nuclear reactions. Let an incoming particle a strike a target nucleus X to produce a residual nucleus Y and an outgoing particle b, with equation a + X = Y + b. The reaction may be abbreviated X(a, b)Y, where a and b stand for the neutron (n), alpha particle (α), gamma ray (γ), proton (p), deuteron (d), and so on. For example, Rutherford's experiment can be written ¹⁴N(α, p)¹⁷O and the reaction in control rods ¹¹³Cd(n, γ)¹¹⁴Cd. The Z value can be omitted, because it is unique to the chemical element.

The interpretation of nuclear reactions often involves the concept of compound nucleus. This intermediate stage is formed by the combination of a projectile and target nucleus. It has extra energy of excitation and breaks up into the outgoing particle or ray and the residual nucleus.

Later, in Section 6.1, we will discuss the absorption of neutrons in uranium isotopes to cause fission.

The reaction equations can be used to calculate balances in properties such as mass-energy, visualizing conditions before and after. In place of the symbols, the atomic masses are inserted. Strictly the masses of the nuclei should be used, but in most reactions, the same number of electrons appears on both sides of the equation and cancels out. In the case of reactions that produce a positron, however, either nuclear masses or atomic masses with the subtraction of the mass-energy required to create an electron-positron pair should be used, 0.0011 amu or 1.02 MeV.

4.2. Energy and Momentum Conservation

The conservation of mass-energy is a firm requirement for any nuclear reaction. Recall from Chapter 1 that the total mass is the sum of the rest mass m⁰ and the kinetic energy E^k (in mass units). Let us calculate the energy released when a slow neutron is captured in hydrogen, according to

This process occurs in reactors that use ordinary water. Conservation of mass-energy says

We use accurately known masses, as given in the Appendix, along with a conversion factor 1 amu = 931.49 MeV,from which E^k = 0.002388 amu with an energy release per capture of 2.22 MeV. This energy is shared by the deuterium atom and the gamma ray, which has no rest mass.

A similar calculation can be made for the proton-lithium reaction of the previous section. Suppose that the target nucleus is at rest and that the incoming proton has a kinetic energy of 2 MeV, which corresponds to 2/931.49 = 0.002147 amu. The energy balance statement is

Then E^k = 0.02077 amu = 19.3 MeV. This energy is shared by the two α particles.

The calculations just completed tell us the total kinetic energy of the product particles but do not reveal how much each has or what the speeds are. To find this information we must apply the principle of conservation of momentum. Recall that the linear momentum p of a material particle of mass m and speed υ is p = mυ. This relation is correct in both the classical and relativistic senses. The total momentum of the interacting particles before and after the collision is the same.

For our problem of a very slow neutron striking a hydrogen atom at rest, we can assume the initial momentum is zero. If it is to be zero finally, the and γ-ray must fly apart with equal magnitudes of momentum p^d = p^γ. The momentum of a γ-ray having the speed of light c may be written p^γ = mc if we regard the mass as an effective value, related to the γ energy E^γ by Einstein's formula E = mc². Thus

Most of the 2.22-MeV energy release of the neutron capture reaction goes to the γ-ray, as shown in Exercise 4.5. Assuming that to be correct, we can estimate the effective mass of this γ-ray. It is close to 0.00238 amu, which is very small compared with 2.014 amu for the deuterium. Then from the momentum balance, we see that the speed of recoil of the deuterium is much smaller than the speed of light.

The calculation of the energies of the two α particles is a little complicated even for the case in which they separate along the same line that the proton entered. The particle speeds of interest are low enough that relativistic mass variation with speed is small, and thus the classical formula for kinetic energy can be used, E^k = (1/2)m⁰ υ ². If we let m be the α particle mass and υ¹ and υ² be their speeds, with p^H the proton momentum, we must solve the two equations

4.3. Reaction Rates

When any two particles approach each other, their mutual influence depends on the nature of the force between them. Two electrically charged particles obey Coulomb's relation F ~ q¹q²/r², where the q's are the amounts of charge and r is the distance of separation of centers. There will be some influence no matter how far they are apart. However, two atoms, each of which is neutral electrically, will not interact until they get close to one another (≅10⁻¹⁰ m). The special force between nuclei is limited still further (≅10⁻¹⁵ m).

Although we cannot see nuclei, we imagine them to be spheres with a certain radius. To estimate that radius, we need to probe with another particle—a photon, an electron, or a γ-ray. But the answer will depend on the projectile used and its speed, and thus it is necessary to specify the apparent radius and cross sectional area for the particular reaction. This leads to the concept of cross section as a measure of the chance of collision.

We can perform a set of imaginary experiments that will clarify the idea of cross section. Picture, as in Figure 4.2(A), a tube of end area 1 cm² containing only one target particle. A single projectile is injected parallel to the tube axis, but its exact location is not specified. It is clear that the chance of collision, labeled σ (sigma) and called the microscopic cross section, is the ratio of the target area to the area of the tube, which is 1 cm². In Computer Exercise 4.A, the programs MOVENEUT and CURRENT show graphically the flow of neutrons in a column.

Figure 4.2. Particle collisions.

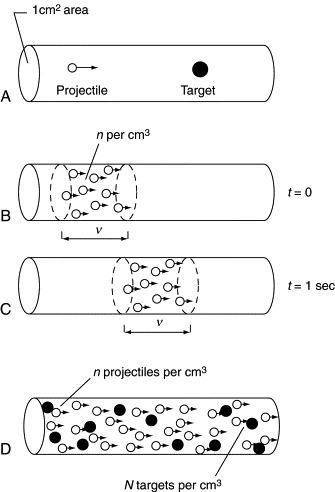
Now let us inject a continuous stream of particles of speed υ into the empty tube (see Figure 4.2[B]). In a time of 1 second, each of the particles has moved along a distance υ cm (see Figure 4.2(C)). All of them in a column of volume (1 cm²) (υ cm) = υ cm³ will sweep past a point at which we watch each second. If there are n particles per cubic centimeter, then the number per unit time that crosses any unit area perpendicular to the stream direction is nυ, called the current density.

Finally, in Figure 4.2(D) we fill each unit volume of the tube with N targets, each of area σ as seen by incoming projectiles (we presume that the targets do not “shadow” each other). If we focus attention on a unit volume, there is a total target area of Nσ. Again, we inject the stream of projectiles. In a time of 1 second, the number of them that pass through the target volume is nυ; and because the chance of collision of each with one target atom is σ, the number of collisions is nυ Nσ. We can thus define the reaction rate per unit volume,

We let the current density nυ be abbreviated by j and let the product Nσ be labeled Σ (capital sigma), the macroscopic cross section, referring to the large-scale properties of the medium. Then the reaction rate per cubic centimeter is simply R = jΣ. We can easily check that the units of j are cm⁻² s⁻¹ and those of Σ are cm⁻¹, so that the unit of R is cm⁻³ s⁻¹.

In a different experiment, we release particles in a medium and allow them to make many collisions with those in the material. In a short time, the directions of motion are random, as sketched in Figure 4.3. We will look only at particles of the same speed υ, of which there are n per unit volume. The product nυ in this situation is no longer called current density but is given a different name, the flux, symbolized by φ (phi). If we place a unit area anywhere in the region, there will be flows of particles across it each second from both directions, but it is clear that the current densities will now be less than nυ. It turns out that they are each nυ/4, and the total current density is nυ/2. The rate of reaction of particles with those in the medium can be found by adding up the effects of individual projectiles. Each behaves the same way in interacting with the targets, regardless of direction of motion. The reaction rate is again nυ Nσ or, for this random motion, R = φ Σ.

Figure 4.3. Particles in random motion.

The random motion of particles can be simulated mathematically by the use of random numbers, which form a collection of decimal fractions that are independent and are uniformly distributed over the range 0 to 1. They are useful for the study of neutron and gamma ray processes, both of which are governed by statistics. Computer Exercise 4.B describes their generation by three small programs RANDY, RANDY1, and RANDY2.

When a particle such as a neutron collides with a target nucleus, there is a certain chance of each of several reactions. The simplest is elastic scattering, in which the neutron is visualized as bouncing off the nucleus and moving in a new direction with a change in energy. Such a collision, governed by classical physics, is predominant in light elements. In the inelastic scattering collision, an important process for fast neutrons in heavy elements, the neutron becomes a part of the nucleus; its energy provides excitation; and a neutron is released. The cross section σ^s is the chance of a collision that results in neutron scattering. The neutron may instead be absorbed by the nucleus, with cross section σ^a. Because σ^a and σ^s are chances of reaction, their sum is the chance for collision or total cross section σ = σ^a + σ^s. Computer Exercise 4.A also introduces a program called CAPTURE related to neutron capture and another called HEADON describing a scattering collision of a neutron with a nucleus in which the neutron direction is exactly reversed.

Let us illustrate these ideas by some calculations. In a typical nuclear reactor used for training and research in universities, a large number of neutrons will be present with energies near 0.0253 eV. This energy corresponds to a most probable speed of 2200 m/s for the neutrons viewed as a gas at room temperature, 293 K. Suppose that the flux of such neutrons is 2 × 10¹² cm⁻²−s⁻¹. The number density is then

Although this is a very large number by ordinary standards, it is exceedingly small compared with the number of water molecules per cubic centimeter (3.3 × 10²²) or even the number of air molecules per cubic centimeter (2.7 × 10¹⁹). The “neutron gas” in a reactor is almost a perfect vacuum.

Now let the neutrons interact with uranium-235 fuel in the reactor. The cross section for absorption σ^a is 681 × 10⁻²⁴ cm². If the number density of fuel atoms is N = 0.048 × 10²⁴ cm⁻³, as in uranium metal, then the macroscopic cross section isThe unit of area 10⁻²⁴ cm² is conventionally called the barn.* If we express the number of targets per cubic centimeter in units of 10²⁴ and the microscopic cross section in barns, then Σ^a = (0.048) (681) = 32.7 cm⁻¹ as previously shown. With a neutron flux φ = 3 × 10¹³ cm⁻²-s⁻¹, the reaction rate for absorption is

^* As the story goes, an early experimenter observed that the cross section for U-235 was “as big as a barn.”

This is also the rate at which uranium-235 nuclei are consumed.

The average energy of neutrons in a nuclear reactor used for electrical power generation is approximately 0.1 eV, almost four times the value used in our example. The effects of the high temperature of the medium (approximately 600°F) and of neutron absorption give rise to this higher value.

4.4. Particle Attenuation

Visualize an experiment in which a stream of particles of common speed and direction is allowed to strike the plane surface of a substance as in Figure 4.4. Collisions with the target atoms in the material will continually remove projectiles from the stream, which will thus diminish in strength with distance, a process we label attenuation. If the current density incident on the substance at position z = 0 is labeled j⁰, the current of those not having made any collision on penetrating to a depth z is given by^[†]where Σ is the macroscopic cross section. The similarity in form to the exponential for radioactive decay is noted, and one can deduce by analogy that the half-thickness, the distance required to reduce j to half its initial value, is z^H = 0.693/Σ. Another more frequently used quantity is the mean free path λ, the average distance a particle goes before making a collision. By analogy with the mean life for radioactivity, we can write^[‡]

^† The derivation proceeds as follows. In a slab of material of unit area and infinitesimal thickness dz, the target area will be Nσdz. If the current at z is j, the number of collisions per second in the slab is jNσdz, and thus the change in j on crossing the layer is dj = −jΣdz, where the reduction is indicated by the negative sign. By analogy with the solution of the radioactive decay law, we can write the formula cited.

^‡ This relation can be derived directly by use of the definition of an average as the sum of the distances the particles travel divided by the total number of particles. When integrals are used, this is .

Figure 4.4. Neutron penetration and attenuation.

This relation is applicable as well to particles moving randomly in a medium. Consider a particle that has just made a collision and moves off in some direction. On the average, it will go a distance λ through the array of targets before colliding again. For example, we can find the mean free path of 1 eV neutrons in water, assuming that scattering by hydrogen with cross section 20 barns is the dominant process. Now the number of hydrogen atoms is N^H = 0.0668 × 10²⁴ cm⁻³, σ^s is 20 × 10⁻²⁴ cm², and Σ^s = 1.34 cm⁻¹. Thus the mean free path for scattering λ^s is approximately 0.75 cm.

The cross sections for atoms interacting with their own kind at the energies corresponding to room temperature conditions are of the order of 10⁻¹⁵ cm². If we equate this area to π r², the calculated radii are of the order of 10⁻⁸ cm. This is in rough agreement with the theoretical radius of electron motion in the hydrogen atom 0.53 × 10⁻⁸ cm. On the other hand, the cross sections for neutrons interacting with nuclei by scattering collisions, those in which the neutron is deflected in direction and loses energy, are usually very much smaller than those for atoms. For the case of 1 eV neutrons in hydrogen with a scattering cross section of 20 barns (i.e., 20 × 10⁻²⁴ cm²), one deduces a radius of approximately 2.5 × 10⁻¹² cm. These results correspond to our earlier observation that the nucleus is thousands of times smaller than the atom.

4.5. Neutron Cross Sections

The cross section for neutron absorption in materials depends greatly on the isotope bombarded and on the neutron energy. For consistent comparison and use, the cross section is often cited at 0.0253 eV, corresponding to neutron speed 2200 m/s. Values for absorption cross sections for a number of isotopes at that energy are listed in order of increasing size in Table 4.1. The dependence of absorption cross section on energy is of two types, one called 1/υ, in which σ^a varies inversely with neutron speed, the other called resonance, in which there is a very strong absorption at certain neutron energies. Many materials exhibit both variations. Figures 4.5 and 4.6 show the cross sections for boron and natural uranium. The use of the logarithmic plot enables one to display the large range of cross section over the large range of energy of interest. Neutron scattering cross sections are more nearly the same for all elements and have less variation with neutron energy. Figure 4.7 shows the trend of σ^s for hydrogen as in water. Over a large range of neutron energy the scattering cross section is nearly constant, dropping off in the million-electron-volt region. This high-energy range is of special interest, because neutrons produced by the fission process have such energy values.

Table 4.1. Selected Thermal Neutron Absorption Cross Sections (in order of increasing size)^[†]

Isotope or Element	σa (Barns)
	≅ 0
	0.00019
	0.00051
	0.0035
Zr	0.19
	0.332
	2.7
Mn	13.3
In	197
	681
	1022
	3840
	2,650,000

^† CRC Handbook of Chemistry and Physics.

Figure 4.5. Absorption cross section for elemental boron.

Figure 4.6. Cross section for natural uranium.

Figure 4.7. Scattering cross section for hydrogen.

The competition between scattering and capture for neutrons in a medium is statistical in nature. The number of scattering collisions that occur before an absorption removes the neutron may be none, one, a few, or many. Computer Exercise 4.C discusses the program ABSCAT, which simulates the statistical competition.

4.6. Neutron Migration

When fast neutrons, those of energy of the order of 2 MeV, are introduced into a medium, they make inelastic or elastic collisions with nuclei. On each elastic collision neutrons are deflected in direction, they lose energy, and they tend to migrate away from their origin. Each neutron has a unique history, and it is impractical to keep track of all of them. Instead, we seek to deduce average behavior. First, we note that the elastic scattering of a neutron with an initially stationary nucleus of mass number A causes a reduction in neutron energy from E⁰ to E and a change of direction through an angle θ (theta), as sketched in Figure 4.8. The length of arrows indicates the speeds of the particles. The example shown is but one of a great variety of possible results of scattering collisions. For each final energy, there is a unique angle of scattering, and vice versa, but the occurrence of a particular E and θ pair depends on chance. The neutron may bounce directly backward, θ = 180 °, dropping down to a minimum energy α E⁰, where α = (A − 1)²/(A + 1)², or it may be undeflected, θ = 0 ° and retain its initial energy E⁰, or it may be scattered through any other angle, with corresponding energy loss. For the special case of a hydrogen nucleus as scattering target, A = 1 and α = 0, so that the neutron loses all of its energy in a head-on collision. As we will see later, this makes water a useful material in a nuclear reactor.

Figure 4.8. Neutron scattering and energy loss.

The process of neutron scattering with energy loss is graphically displayed by application of the program SCATTER, see Computer Exercise 4.D.

The average elastic scattering collision is described by two quantities that depend only on the nucleus, not on the neutron energy. The first is , the average of the cosines of the angles of scattering, given by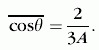

For hydrogen it is 2/3, meaning that the neutron tends to be scattered in the forward direction; for a very heavy nucleus such as uranium it is near zero, meaning that the scattering is almost equally likely in each direction. Forward scattering results in an enhanced migration of neutrons from their point of appearance in a medium. Their free paths are effectively longer, and it is conventional to use the transport mean free path instead of λ^s to account for the effect. We note that λ^t is always the larger. Consider slow neutrons in carbon, for which σ^s = 4.8 barns and N = 0.083 (in units of 10²⁴ as in Section 4.3), so that Σ^s = 0.4 cm⁻¹ and λ^s = 2.5 cm. Now , and λ^t = 2.5/0.994 = 2.7 cm.

The second quantity that describes the average collision is ξ (xi), the average change in the natural logarithm of the energy, given by

For hydrogen, it is exactly 1, the largest possible value, meaning that hydrogen is a good “moderator” for neutrons, its nuclei permitting the greatest neutron energy loss; for a heavy element it is ξ ≅ 2/(A + 2/3), which is much smaller than 1 (e.g., for carbon, A = 12, it is 0.16).

To find how many collisions C are required on the average to slow neutrons from one energy to another, we merely divide the total change in ln E by ξ, the average per collision. In going from the fission energy 2 × 10⁶ eV to the thermal energy 0.025 eV, the total change is ln (2 × 10⁶) − ln(0.025) = ln(8 × 10⁷) = 18.2. Then C = 18.2/ξ. For example in hydrogen, ξ = 1, C is 18, whereas in carbon ξ = 0.16, C is 114. Again, we see the virtue of hydrogen as a moderator. The fact that hydrogen has a scattering cross section of 20 barns over a wide range, whereas carbon has a σ^s of only 4.8 barns, implies that collisions are more frequent and the slowing takes place in a smaller region. The only disadvantage is that hydrogen has a larger thermal neutron absorption cross section, 0.332 barns vs. 0.0035 barns for carbon.

The statistical nature of the neutron slowing process is demonstrated in Computer Exercise 4.E, which uses the program ENERGY to calculate the number of collisions to go from fission energy to thermal energy in carbon.

The movement of individual neutrons through a moderator during slowing consists of free flights, interrupted frequently by collisions that cause energy loss. Picture, as in Figure 4.9, a fast neutron starting at a point and migrating outward. At some distance r away, it arrives at the thermal energy. Other neutrons become thermal at different distances, depending on their particular histories. If we were to measure all of their r values and form the average of r², the result would be , where τ (tau) is called the “age” of the neutron. Approximate values of the age for various moderators, as obtained from experiment, are listed below:

 

Moderator	τ, Age to Thermal (cm2)
H2O	26
D2O	125
C	364

Figure 4.9. Neutron migration during slowing.

We thus note that water is a much better agent for neutron slowing than is graphite because of the larger scattering and energy loss.

As neutrons slow into the energy region that is comparable to thermal agitation of the moderator atoms, they may either lose or gain energy on collision. Members of a group of neutrons have various speeds at any instant and thus the group behaves as a gas in Maxwellian distribution, as was shown in Figure 2.1 and discussed in Exercise 2.15. The neutron group has a temperature T that is close to that of the medium in which they are found. Thus if the moderator is at room temperature 20° C, or 293°K, the most likely neutron speed is approximately 2200 m/s, corresponding to a kinetic energy of 0.0253 eV. The neutrons are said to be thermal, in contrast to fast or intermediate.

Another parameter that characterizes neutron migration while at thermal energy is the diffusion length, symbolized by L. By analogy to the slowing process, the average square distance between origin and absorption is given by . Approximate values of L for three moderators are listed below.

 

Moderator	L, Diffusion Length (cm)
H2O	2.85
D2O	116
C	54

According to theory, , where D = λ^t /3. This shows that the addition of an absorber to pure moderator reduces the distance neutrons travel, as expected.

The process of diffusion of gas molecules is familiar to us. If a bottle of perfume is opened, the scent is quickly observed, because the molecules of the substance migrate away from the source. Because neutrons in large numbers behave as a gas, the descriptions of gas diffusion may be applied. The flow of neutrons through a medium at a location is proportional to the way the concentration of neutrons varies, in particular to the negative of the slope of the neutron number density. We can guess that the larger the neutron speed υ and the larger the transport mean free path λ^t, the more neutron flow will take place. Theory and measurement show that if n varies in the z-direction, the net flow of neutrons across a unit area each second, the net current density, is

This is called Fick's law of diffusion, derived long ago for the description of gases. It applies if absorption is small compared with scattering. In terms of the flux φ = nυ and the diffusion coefficient D = λ^t /3, this may be written compactly j = − D φ′ where φ′ is the slope of the neutron flux.

4.7. Summary

Chemical and nuclear equations have similarities in the form of equations and in the requirements on conservation of particles and charge. The bombardment of nuclei by charged particles or neutrons produces new nuclei and particles. Final energies are found from mass differences and final speeds from conservation of momentum. The cross section for interaction of neutrons with nuclei is a measure of the chance of collision. Reaction rates depend mutually on neutron flows and macroscopic cross section. A stream of uncollided particles is reduced exponentially as it passes through a medium. Neutron absorption cross sections vary greatly with target isotope and with neutron energy, whereas scattering cross sections are relatively constant. Neutrons are slowed readily by collisions with light nuclei and migrate from their point of origin. On reaching thermal energy, they continue to disperse, with the net flow dependent on the spatial variation of flux.

4.8. Exercises

1. The energy of formation of water from its constituent gases is quoted to be 54 500 cal/mole. Verify that this corresponds to 2.4 eV per molecule of H²O.
2. Complete the following nuclear reaction equations:
3. Using the accurate atomic masses listed below, find the minimum amount of energy an α particle must have to cause the transmutation of nitrogen to oxygen.
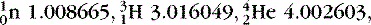4. Find the energy release in the reaction , noting the masses , and .
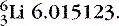5. A slow neutron of mass 1.008665 amu is caught by the nucleus of a hydrogen atom of mass 1.007825 and the final products are a deuterium atom of mass 2.014102 and a γ-ray. The energy released is 2.22 MeV. If the γ-ray is assumed to have almost all of this energy, what is its effective mass in kg? What is the speed of the particle in m/s, using equality of momenta on separation? What is the recoil energy of in MeV? How does this compare with the total energy released? Was the assumption about the γ-ray reasonable?
6. Calculate the speeds and energies of the individual α particles in the reaction , assuming that they separate along the line of proton motion. Note that the mass of the lithium-7 atom is 7.016005.
7. Calculate the energy release in the reactionThe atomic masses are and the masses of the positron and electron are 0.000549. Calculate (a) using nuclear masses, subtracting the proper number of electron masses from the atomic masses, and (b) using atomic masses with account for the energy of pair production.
8. Calculate the macroscopic cross section for scattering of 1 eV neutrons in water, using N for water as 0.0334 × 10²⁴ cm⁻³ and cross sections 20 barns for hydrogen and 3.8 barns for oxygen. Find the mean free path λ^s.
9. Find the speed υ and the number density of neutrons of energy 1.5 MeV in a flux 7 × 10¹³ cm⁻² − s⁻¹.
10. Compute the flux, macroscopic cross section and reaction rate for the following data: n = 2 × l0⁵ cm⁻³, υ = 3 × l0⁸ cm/sec, N = 0.04 × 10²⁴ cm⁻³, σ = 0.5 × 10⁻²⁴ cm².
11. What are the values of the average logarithmic energy change ξ and the average cosine of the scattering angle for neutrons in beryllium, A = 9? How many collisions are needed to slow neutrons from 2 MeV to 0.025 eV in Be-9? What is the value of the diffusion coefficient D for 0.025 eV neutrons if Σ^s is 0.90 cm⁻¹?
12. (a) Verify that neutrons of speed 2200 m/s have an energy of 0.0253 eV. (b) If the neutron absorption cross section of boron at 0.0253 eV is 760 barns, what would it be at 0.1 eV? Does this result agree with that shown in Figure 4.5?
13. Calculate the rate of consumption of U-235 and U-238 in a flux of 2.5 × 10¹³ cm⁻² − s⁻¹ if the uranium atom number density is 0.0223 × 10²⁴ cm⁻³, the atom number fractions of the two isotopes are 0.0072 and 0.9928, and cross sections are 681 barns and 2.7 barns, respectively. Comment on the results.
14. How many atoms of boron-10 per atom of carbon-12 would result in an increase of 50% in the macroscopic absorption cross section of graphite? How many ¹⁰B atoms would there then be per million ¹²C atoms?
15. Calculate the absorption cross section of the element zirconium using the isotopic data in the following table:

     

    Mass number	Abundance (Atom %)	Cross Section (Barns)
    90	51.45	0.014
    91	11.22	1.2
    92	17.15	0.2
    94	17.38	0.049
    96	2.80	0.020

    Compare the result with the figure given in Table 4.1.
16. The total cross section for uranium dioxide of density 10 g/cm³ is to be measured by a transmission method. To avoid multiple neutron scattering, which would introduce error into the results, the sample thickness is chosen to be much smaller than the mean free path of neutrons in the material. Using approximate cross sections for UO² of σ^s = 15 barns and σ^a of 7.6 barns, find the macroscopic cross section Σ = Σ^a+ Σ^s. Then find the thickness of target t such that t/λ = 0.05. How much attenuation in neutron beam would that thickness give?
17. The manganese content of a certain stainless steel is to be verified by an activation measurement. The activity induced in a sample of volume V by neutron capture during a time t is given byA foil of area 1 cm² and thickness 2 mm is irradiated in a thermal neutron flux of 3 × 10¹²/cm² − s for 2 h. Counts taken immediately yield an activity of 150 mCi for the induced Mn-56, half-life 2.58 h. Assuming that the atom number density of the alloy is 0.087 in units of 10²⁴ and that the cross section for capture in Mn-55 is 13.3 barns, find the percent of Mn in the sample.
18. For fast neutrons in uranium-235 metal, find the density ρ, the number of atoms per cubic centimeter N, the macroscopic cross section Σ^a and Σ^t, the transport mean free path λ^t, the diffusion coefficient D, and the diffusion length L. Note: the density of natural U (99.3% U-238) is approximately 19.05 g/cm³; for U-235, σ^c = 0.25 barns, σ^f = 1.4 barns, and σ^t = 6.8 barns (Report ANL-5800, p. 581).
19. When a projectile of mass m¹ and vector velocity u¹ collides elastically with a target of mass m² and vector velocity u², the final velocities are:Find the velocities if u² = 0 and m² >> m¹. Discuss the results.
20. A neutron of energy E⁰ collides head-on with a heavy nucleus of mass number A. Using the velocity equations of Exercise 4.19, verify that the minimum neutron energy after collision is E¹ = α E⁰, where α = [(A − 1)/(A + 1)]². Evaluate α and ξ for U-238.
21. Show for the case of u² = 0 (Exercise 4.19) that kinetic energy is conserved.

Computer Exercises

1. Several computer programs provide visual images of neutron processes. MOVENEUT merely shows a moving particle; CURRENT gives a flow of many particles; CAPTURE allows a moving neutron to be captured by a stationary target nucleus. Run the programs to help visualize the processes. The program HEADON demonstrates an elastic collision in which neutron direction is reversed. Run the program with various choices of mass number A: 12 (carbon), 2 (deuterium), 238 (uranium), and 1 (hydrogen). Note and report on differences.
2. Random variables are numbers between 0 and 1 that are statistically independent. They are at the heart of the method known as Monte Carlo (after the gambling casino in Monaco). Such numbers are produced by the command RND(X).
   • Program RANDY generates and prints out a sequence of random numbers. Run the program two or three times to see results. Then delete the command RANDOMIZE TIMER and repeat. Comment on the effect.
   • Program RANDY1 is the same as RANDY except that the average value is calculated. Run the program with increasing values of input NT, the total number of random numbers, to see what happens. What would you expect?
   • Program RANDY2 is the same as RANDY1 except that additional statistical features are calculated. Run the program; note and comment on the results.
3. On average, scattering and absorption of neutrons is determined by the macroscopic cross sections Σ^s, and Σ^a. For a given neutron, however, by chance the number of scatterings before being absorbed varies widely. The program ABSCAT uses random numbers to describe the process. Run the program several times to note the variation. Explain how the expected number of scatterings per absorption is calculated.
4. The computer program SCATTER shows the general elastic collision of a neutron with a stationary nucleus, in which the neutron loses energy and moves off at an angle from the original direction, while the struck nucleus recoils in another direction. (a) Run the program several times to see the variety of final motions. (b) Change the mass ratio A (line 330) to 1, or 12, or 238, and observe differences.
5. The energy loss of a neutron in an elastic collision with a nucleus can range from zero to E⁰ (l − α). Thus there is considerable statistical variation in the number of collisions C required to go between two energies. By use of random numbers, the computer program ENERGY shows a set of values of C for neutron slowing in carbon between fission and thermal energies. (a) Run the program to note the variation about the average of 114 collisions. (b) Change the A value to 238 as for U-238 and run again. (c) Repeat for A = 1 as for hydrogen. (d) Make a large change in the number of histories (e.g., decrease or increase by a factor of 10) and note the effect.
6. Apply computer program ALBERT (See Chapter 1) to find a more accurate pair of numbers (e.g., 7 significant figures) than 2200 m/s and 0.0253 eV to describe room temperature 20° C neutrons at absolute temperature T = 293.15 K. Note: 1 eV = 1.60217646 × 10⁻¹⁹ J and Boltzmann's constant in E = kT is 1.3806503 × 10⁻²³ J/K. What limits the accuracy of the result?

4.9 References

Bethe et al., 1986 Hans A. Bethe, Robert F. Bacher, M. Stanley Livingston, Basic Bethe: Seminal Articles on Nuclear Physics, 1936–1937 1986 American Institute of Physics Reprints of classic literature on nuclear processes

Neutron Cross Sections Neutron Cross Sections, Vol. 1, Neutron Resonance Parameters and Thermal Cross Sections, S. F. Mughabghab, Part B, Z = 61 - 100, 1981; S. F. Mughabghab, M. Divadeenam, and N. E. Holden, Part A, Z = 1 - 60, 1984; Vol. 2, Neutron Cross Section Curves, Victoria McLane, Charles L. Dunford, and Philip F. Rose, 1988; Academic Press, New York.

Tables of Thermal Cross Sections Tables of Thermal Cross Sections

http://ie.lbl.gov/ngdata/sig.txt http://ie.lbl.gov/ngdata/sig.txt.

Some of the same information as in the preceding book Some of the same information as in the preceding book, at a Web site maintained by Lawrence Berkeley Laboratory.

Mughabghab, 2006 Said F. Mughabghab, Atlas of Neutron Resonances, 5th Ed.: Resonance Parameters and Thermal Cross Sections, Z = 1 − 100 2006 Elsevier Science Amsterdam

Explanations, theory, and cross section data Explanations, theory, and cross section data. An updated version of Neutron Cross Sections.

National Nuclear Data Center (NNDC) National Nuclear Data Center (NNDC)

http://www.nndc.bnl.gov/masses http://www.nndc.bnl.gov/masses

2003 atomic mass evaluation 2003 atomic mass evaluation. Latest and perhaps last.

Atomic Mass Data Center Atomic Mass Data Center

http://amdc.in2p3.fr http://amdc.in2p3.fr

Select AME Select AME. Mirror site to BNL's.

The Isotope Project The Isotope Project (Lawrence Berkeley National Laboratory)

http://isotopes.lbl.gov http://isotopes.lbl.gov

Data centers and links to Web sites Data centers and links to Web sites.

Bertulani and Danielewicz, 2004 C.A. Bertulani, P. Danielewicz, Introduction to Nuclear Reactions 2004 Taylor and Francis

Lamarsh and Baratta, 2001 John R. Lamarsh, Anthony J. Baratta, Introduction to Nuclear Engineering 3rd Ed. 2001 Prentice-Hall Upper Saddle River, NJ Update of classic textbook

Murray, 1957 Raymond L. Murray, Nuclear Reactor Physics 1957 Prentice-Hall Englewood Cliffs, NJ Elementary theory, analysis, and calculations

Lamarsh, 1972 John R Lamarsh, Introduction to Nuclear Reactor Theory 1972 Addison-Wesley Reading, MA Widely used textbook. Paperback reprint by American Nuclear Society, La Grange Park, IL, 2002

Henry, 1975 Allen F. Henry, Nuclear Reactor Analysis 1975 MIT Press Cambridge Advanced textbook

Duderstadt and Hamilton, 1976 James J. Duderstadt, Louis J. Hamilton, Nuclear Reactor Analysis 1976 John Wiley & Sons New York Thorough treatment

Stacey, 2001 Weston M. Stacey, Nuclear Reactor Physics 2001 John Wiley & Sons New York Advanced textbook

Faw and Shultis, 2002 Richard E. Faw, J. Kenneth Shultis, Fundamentals of Nuclear Science and Engineering 2002 Marcel Dekker New York

Bodansky, 2003 David Bodansky, Nuclear Energy: Principles, Practices, and Prospects 2nd Ed. 2003 Springer/AIP Press New York