Chapter 5 Rotational Motion

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

In this chapter, we will discuss rotational motion. We will apply our equations to wheels, motors, and anything else that rotates (Figure 5.1).

FIGURE 5.1 A top.

Any point on a circle can be described by its radius r from the center and an angle θ. The angle can be measured in degrees, revolutions, or radians (Figure 5.2).

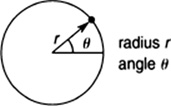
FIGURE 5.2 A point on a circle can be described by its radius r from the center and an angle θ measured in degrees, revolutions, or radians.

Comparing the three units:

1 rev = 360 ° = 2 π rad

See Figure 5.3 for a comparison of angular units.

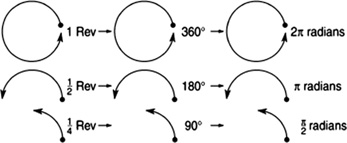
FIGURE 5.3 A comparison of angular units.

The unit radians may be unfamiliar. It has its origin in nature. Take any circle and place a string around it to measure its circumference. Then measure its diameter. Divide the circumference by the diameter, and the number 3.14159…, which is written as π, will result.

Converting between angular units,

1 rev = 360 ° = 2 π rad

Example 5.1

How many revolutions are there in 180°?

\begin{matrix} θ = & 180 ° \\ 1 rev = & 360 ° \\ 180^{ϕ} (\frac{1 rev}{360^{ϕ}}) = & 0.50 rev \end{matrix}

Example 5.2

How many radians are there in 320°?

\begin{matrix} θ = 320 ° \\ 2 π rad = 360 ° \\ 320^{ϕ} (\frac{2 π rad}{360^{ϕ}}) = 5.6 rad \end{matrix}

Example 5.3

How many radians are there in 200 rev?

\begin{matrix} θ = 20 \bar{0} rev \\ 1 rev = 2 π rad \\ 20 \bar{0} rev (\frac{2 π rad}{1 rev}) = 1, 256 rad \end{matrix}

5.1 MEASURING ANGLES

Aside from using a protractor, there are a number of electronic ways of measuring an angle (Figure 5.4).

FIGURE 5.4 A protractor.

5.1.1 Potentiometer

A potentiometer connected to the center of rotation can be used to determine the angular position of something undergoing a rotation (Figure 5.5).

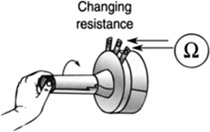
FIGURE 5.5 A potentiometer used to measure angular orientation.

5.1.2 Mechanical Rotary Encoder

A mechanical rotary encoder consists of a shaft that opens and closes a switch during the rotation of the shaft. Counting the number of switch activations determines the angle that the shaft rotates through (Figure 5.6).

FIGURE 5.6 A rotary encoder, courtesy of adafruit.com.

5.1.3 Optical Rotary Encoder

An old type of computer mouse contains two small wheels with spokes that are driven by the ball at the bottom of the mouse. A light source and detector are placed on either side of the wheel. The light detector measures how many times the light beam is broken as the wheel turns. Simply counting the number of interruptions of the light beam determines the angle through which the ball rotates or the distance the mouse has moved (Figure 5.7).

FIGURE 5.7 A computer mouse converts the revolutions of the ball using an optical encoder in the mouse to a position on the computer screen.

5.1.4 Gyroscope

A mechanical gyroscope consists of a spinning wheel mounted sideways on a frame. Because the wheel is spinning, its momentum resists having its orientation changed. As the instrument is rotated, the spinning wheel keeps pointing in the same direction. The angle measured is the angle between the instrument and the spinning wheel with the fixed orientation (Figure 5.8).

FIGURE 5.8 A gyroscope demonstrated using a spinning bicycle wheel hanging by a cable.

5.2 DISTANCE MEASUREMENTS ALONG A CIRCLE

Any motion that takes place in the circle can be described with two parameters:

The distance (r) by which the object is away from the center of rotation.
The angle (θ) through which it moves.

Suppose a point travels along the arc of a circle. How far has this point traveled?

\begin{array}{l} d = r \cdot θ \leftarrow θ must be in radians \\ Distance along an arc = radius \times angle(in radians) \end{array}

If a wheel of radius r rolls along a surface through an angle θ, the wheel has traveled a distance d (Figure 5.9).

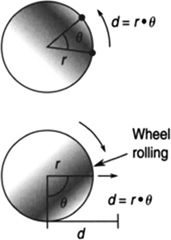
FIGURE 5.9 If a wheel of radius r rolls along a surface through an angle θ, the wheel has traveled a distance d, d = r·θ, θ must be in radians.

\begin{array}{l} d = r \cdot θ \leftarrow θ must be in radians \\ Distance a wheel rolls = radius \times angle(in radians) \end{array}

Example 5.4

A point on the rim of a wheel with a radius of 2.0 ft travels through an angle of 1.5 rad (Figure 5.10). (a) How far did the point travel on the wheel? (b) If the wheel was rolling on the ground, how far did it roll?

(a)

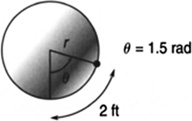
FIGURE 5.10 A point on the rim of a wheel with a radius of 2.0 ft travels through an angle of 1.5 rad.

\begin{matrix} r = 2.0 ft \\ θ = 1.5 rad \\ d = ? \\ d = r \times θ \\ d = (2.0 ft) (1.5 rad) \\ d = 3.0 ft \leftarrow We don’t retain the unit rad. \end{matrix}

(b)

The distance the wheel rolls for is the same as the distance the point travels through on the rim, d = 3.0 ft.

Note that the unit radian drops out in the calculation of d = r⋅θ because the unit radian is dimensionless.

When using the formula d = r⋅θ, if θ was in any unit other than radians, the answer would be wrong. Why are there so many different units for angles, and when do you use which one? The answer depends on the context of the problem.

As a general rule, however, always use radians when a calculation involves an angle times another quantity.

Example 5.5

A wheel with a radius of 12 in. rotates through an angle of 320°. How far has this wheel traveled?

In order to use this formula, θ must be in radians (Figure 5.11).

FIGURE 5.11 How far has this wheel rolled?

\begin{array}{l} r = 12 in. \\ θ = 320 ° \\ d = ? \\ d = r \cdot θ \Leftarrow In order to use this fomula θ must be in radians. \\ (320 °) (\frac{2 π}{360 °}) = 5.6 rad \\ d = (12 in.) (5.6 rad) \\ d = 67 in. \end{array}

Example 5.6

Suppose a wheel with a radius of 1.3 m rolls along the ground through an angle of 1.5 revolutions (Figure 5.12). How far has the wheel traveled?

FIGURE 5.12 How far has the wheel traveled?

\begin{array}{l} r = 1.3 m \\ θ = 1.5 Rev \\ d = ? \\ d = r \cdot θ \Leftarrow In order to use this fomula θ must be in radians. \\ (1.5 rev) (\frac{2 π}{1 rev}) = 9.4 rad \\ d = (1.3 m) (9.4 rad) \\ d = 12.25 m \end{array}

5.3 ANGULAR VELOCITY

Angular velocity is the measure of how fast something is spinning (Figure 5.13). Everyone is familiar with the unit revolutions/min (rpm), which is a measure of how fast something is spinning. It describes how many revolutions a shaft or a wheel turns in 1 min.

FIGURE 5.13 Angular velocity is a measure of how fast something is spinning.

Example 5.7

A shaft on a motor turns 6,000 rev in 1 min. What is its angular velocity?

\begin{array}{l} 6, 000 rev/ 1 \min = 6, 000 rpm \\ (1 rpm = 1 rev/ \min) \end{array}

5.3.1 Measuring Angular Velocity

If a shaft or wheel is moving slowly enough, simply counting the number of revolutions in a given amount of time is enough to determine the angular velocity. However, it’s more probable that the wheel is turning too fast to perform such a measurement, and therefore another means is necessary.

5.3.2 Tachometer

A tachometer is used to determine angular velocity. There are a number of types of tachometers. Typically, they are simply proximity sensors such as the one described below.

5.3.3 Magnetic Pickup Coil Tachometer

In Figure 5.14, a coil is placed near the rotating gear. The inductance of the coil will change as a tooth on the gear positions itself directly below the coil. This change in inductance will be monitored and converted into a pulse and counted for some interval of time. If one knows the number of teeth on the gear and the number of pulses occurring in some interval of time, the angular velocity can be found.

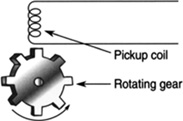
FIGURE 5.14 A coil used as a proximity sensor functioning as a tachometer.

MEMS Gyroscope: A MEMS (microelectromechanical systems) gyroscope is micro machined, about the size of a human hair, silicon wafer mass suspended by polysilicon springs. The wafer has a plate attached to it that acts as a plate of a capacitor, while the other plate is fixed, Figure 5.15. There are three of these wafers, one along each axis, Figure 5.16. During a rotation along a particular axis, the mass is displaced and the capacitance between the plates changes. This change in capacitance produces a change in voltage that is proportional to the angular velocity (Figure 5.17).

FIGURE 5.15 A MEMS gyroscope is micro machined silicon wafer mass suspended by polysilicon springs. During a rotation the mass is displaced, the distance between the plates changes, producing a small electrical signal.

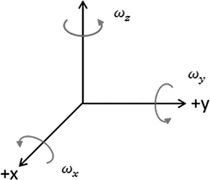
FIGURE 5.16 Rotations along x, y, and z axes.

FIGURE 5.17 A three-axis gyroscope capable of measuring rotation in the x, y, and z axes from adafruit.com.

5.4 ANGULAR VELOCITY CALCULATIONS

The average angular velocity is a rate at which an angle changes and is given by:

\begin{matrix} ω = \frac{Δ θ}{Δ t} \\ {Angular velocity}_{average} = \frac{Change in angle}{Change in time} \end{matrix}

ω has units of (degrees or revolutions or radians)/(time unit).

Example 5.8

A wheel turns 720° in 3 s (Figure 5.18). What is its angular velocity?

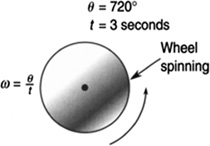
FIGURE 5.18 A wheel turns 720° in 3 s.

\begin{array}{l} ω = \frac{Δ θ}{Δ t} \\ ω = \frac{720 °}{3 s} \\ ω = 240 ° /s \end{array}

Example 5.9

A top revolves 4.2 rad in 2 s (Figure 5.19). What is its angular velocity?

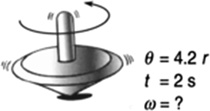
FIGURE 5.19 A top revolves 4.2 radians in 2 s.

\begin{array}{l} ω = \frac{Δ θ}{Δ t} \\ ω = \frac{4.2 rad}{2 s} \\ ω = 2.1 \frac{rad}{s} \end{array}

Example 5.10

Suppose a gear is rotating and being monitored by the tachometer described above. If the gear has ten teeth and produces a count of 500 counts in 1 min, what is the angular velocity of the gear?

Since the gear has ten teeth, in one complete revolution there will be ten pulses out of the tachometer. Therefore, we want to convert 500 counts into revolutions (Figure 5.20).

FIGURE 5.20 What is the angular velocity of the gear?

\begin{array}{l} 500 counts (\frac{1 rev}{10 counts}) = 50 rev \\ ω = \frac{θ}{t} \\ ω = \frac{50 rev}{1 \min} = 50 rpm \end{array}

5.5 CIRCULAR VELOCITY

We can now calculate the velocity of an object moving in a circular path. Recall that velocity $v = \frac{d}{t}$ .

For a circle:

\begin{array}{l} d = r \cdot θ \\ ω = \frac{Δ θ}{Δ t} \end{array}

We can write $ω = \frac{θ}{t}$ instead of $ω = \frac{Δ θ}{Δ t}$ , when ω and t start at 0.

Therefore,

\begin{array}{l} v = \frac{d}{t} \\ v = \frac{r \cdot θ}{t} \\ v = r \cdot \frac{θ}{t} \\ v = r \cdot ω \end{array}

velocity (m/s) = radius (m) \times angular velocity (rad/s)

In the English system,

Velocity (ft/s) = radius (ft) \times angular velocity (rad/s)

v = r \cdot ω

This equation is the velocity of an object moving in a circle or it can describe the velocity of a wheel rotating at ω rolling along a surface (Figure 5.21).

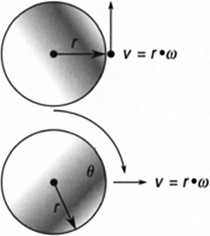
FIGURE 5.21 Velocity of an object moving in a circle (ω in radians/time) or the velocity of a wheel rolling along a surface can be determined by the equation v = r· ω.

Example 5.11

A wheel with a radius of 1.25 ft is rotating at 4.2 rad/s. How fast is the car moving? (See Figure 5.22.)

FIGURE 5.22 The speed of the car depends on how fast the wheels are spinning and their radius.

\begin{matrix} r = 1.25 ft \\ θ = 4.2 \frac{rad}{s} \\ v = ? \\ v = r \cdot ω \\ r = 1.25 ft \\ θ = 4.2 \frac{rad}{s} \\ v = ? \\ v = r \cdot ω \\ v = (1.25 ft) (4.2 \frac{rad}{s}) \\ v = 5.3 \frac{ft}{s} \Leftarrow Note that radians does not appear in \\ the answer because it is dimensionless. \end{matrix}

5.6 CENTRIPETAL ACCELERATION

An object moving in a circle has a velocity vector that is constantly changing, because its direction is constantly changing. The object may be moving at a constant speed as it moves around the circle, but because it is changing direction it is accelerating. Recall, a change in velocity is an acceleration. This change in velocity is directed toward the center and is called centripetal acceleration. Centripetal acceleration is given by (Figure 5.23):

FIGURE 5.23 A mass accelerating in a circle.

\begin{matrix} a_{c} = r \cdot ω^{2} \\ {acceleration}_{centripetal} (\frac{m}{s^{2}}) = radius (m) \times angular velocity {(\frac{rad}{s})}^{2} \end{matrix}

The centripetal acceleration can be rewritten in another form if we use the formula for circular velocity.

\begin{array}{l} v = r \cdot ω \\ ω = v / r \\ a_{c} = r \cdot ω^{2} \leftarrow substitute in for ω, \frac{v}{r} \\ a_{c} = r \cdot {(\frac{v}{r})}^{2} \end{array}

a_{c} = \frac{v^{2}}{r}

Example 5.12

A wheel of radius 0.4 m in a car is spinning at an angular velocity of 100 rad/s. What is the centripetal acceleration of the wheel?

a_{c} = r \cdot ω^{2} = (0.4 m) {(100 r a d / s)}^{2}

a_{c} = 4, 000 \frac{m}{s^{2}}

Example 5.13

A shoe in a dryer is spinning at 1.5 m/s in a drum of radius 0.5 m. What is the centripetal acceleration of the shoe?

\begin{array}{l} a_{c} = \frac{v^{2}}{r} \\ a_{c} = \frac{{(1.5 \frac{m}{s})}^{2}}{0.5 m} \\ a_{c} = 4.5 {m/s}^{2} \end{array}

5.7 CENTRIPETAL FORCE

Changing the motion of something means acceleration, and the force on a body that is accelerating is given by F = m × a. If a body is being accelerated in a circular path, it is accelerating toward the center of the circle and its acceleration is a_c = r·ω². Therefore, the centripetal force is directed toward the center of rotation and is given by:

\begin{matrix} F_{c} = m \cdot a_{c} \\ {Force}_{centripetal} = mass (kg) \cdot centripetal acceleration ({m/s}^{2}) \end{matrix}

Example 5.14

What is the centripetal force on a shoe in a washing machine if the shoe has a mass of 0.35 kg and the inside of the machine is rotating at 120 rpm and has a radius of 0.30 m (Figure 5.24)?

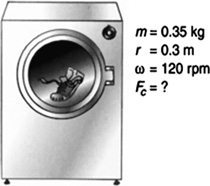
FIGURE 5.24 What is the centripetal force on the shoe in a washing machine?

\begin{array}{l} Converting ω to \frac{radians}{s} \\ ω = (120 \frac{rev}{\min}) (\frac{2 π rad}{1 rev}) (\frac{1 \min}{60 s}) = 13 rad/s \\ F_{c} = m \cdot a_{c} \\ F_{c} = m \cdot r \cdot ω^{2} \\ F_{c} = 0.35 kg \cdot 0.30 m \cdot {(13 \frac{rad}{s})}^{2} \\ F_{c} = 18 N \end{array}

5.8 CENTRIFUGAL FORCE

When driving in a car turning a corner, you feel yourself being pushed in the opposite direction to that you are turning. The faster or the tighter you make the turn, the greater the force. This force is called centrifugal force. The origin of this force can be explained as follows. When driving a car straight, your body has momentum straight ahead. When making a turn, in order for your body to move with the car, you must hold on to the wheel tightly to “force” your body into this new direction, otherwise you would move in a straight path. This force is called a fictitious force because there is no real force pushing you. It is a result of your body’s inertia resisting the change in direction. Although fictitious, we can still use this centrifugal force to calculate correctly the behavior of rotating objects. The centrifugal force has the same equation as the centripetal force; only it is directed in the opposite direction (Figures 5.25 and 5.26).

FIGURE 5.25 The driver experiences a centrifugal force.

FIGURE 5.26 The mass experiences a centrifugal force.

\begin{matrix} F_{c} = m \cdot a_{c} \\ {Force}_{centrifugal = mass (kg) \cdot centripetal accleration (m/ s^{2})} \end{matrix}

Example 5.15

A rock is tied to the end of a 1.0 m long string. How fast must it be rotated so that it does not fall? The rock must be rotated fast enough so that the force downward due to gravity equals the centrifugal force upward. Setting the two forces equal to each other (Figure 5.27):

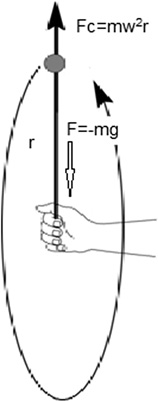
FIGURE 5.27 How fast must the rock be rotated so that it does not fall?

\begin{array}{l} F_{centrifugal} = F_{gravity} \\ m \cdot r \cdot ω^{2} = m \cdot g \\ ω^{2} = g / r \\ ω = \sqrt{g / r} \\ ω = \sqrt{\frac{9.8 \frac{m}{s^{2}}}{1.0 m}} \\ ω = 3.13 rad/s \end{array}

5.8.1 Geosynchronous Orbits

A satellite can be placed in an orbit around the earth so that it remains fixed at one point over the earth. This orbit is called a geosynchronous orbit. A geosynchronous satellite has the same angular velocity as the earth and remains at a fixed distance from the earth (Figure 5.28).

FIGURE 5.28 A satellite in a geosynchronous orbit.

To find the geosynchronous orbit distance, consider the forces on the satellite.

F = m a = F_{centrifugal} - F_{gravity} = m \cdot ω^{2} \cdot r - G \frac{m \cdot M_{Earth}}{r^{2}}

a = \frac{F}{m} = ω^{2} \cdot r - G \frac{M_{Earth}}{r^{2}}

For a geosynchronous orbit, the distance to the satellite is fixed and therefore the acceleration in the radial direction r equals zero.

a = 0 \to ω^{2} \cdot r = G \frac{M_{Earth}}{r^{2}}

Solving for r \to r = {(G \frac{M_{Earth}}{ω^{2}})}^{\frac{1}{3}}

r = {(G \frac{M_{Earth}}{ω^{2}})}^{\frac{1}{3}} = {(6.67 \times 10^{- 11} \frac{m^{3}}{kg s^{2}} \times \frac{5.97 \times 10^{24} kg}{{(7.3 \times 10^{- 5} \frac{rad}{s})}^{2}})}^{\frac{1}{3}}

r = 42.1 \times 10^{6} m with respect to the center of the earth

The earth has a mean radius of 6.4 × 10⁶m, therefore the distance to the satellite from the earth’s surface is:

\begin{matrix} r = 42.1 \times 10^{6} m - 6.4 \times 10^{6} m \\ r = 35.7 \times 10^{6} m or approximately 22, 000 miles above the surface of the earth \end{matrix}

5.9 TRANSMISSIONS

Gears and wheels can be coupled in such a way as to change their speed, direction of rotation, and torque capability (Figure 5.29).

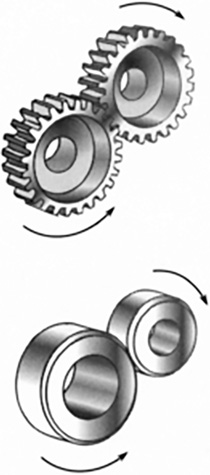
FIGURE 5.29 Couple gears and wheels together to change speed, direction of rotation, and torque capability.

To determine the speed of rotation of a wheel or gear being driven by a driving wheel or gear, we use the following formulas:

\begin{array}{l} N \cdot S = n \cdot s \\ N = angle or angular speed of the driver \\ S = size of driving diameter or number of teeth \\ n = angle or angular speed of the driven \\ s = size of driven diameter or number of teeth \end{array}

Example 5.16

A wheel of diameter 3 in. spinning at 32 rpm is driving a wheel of diameter 6 in. (Figure 5.30). How fast is the driven wheel spinning?

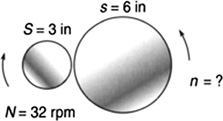
FIGURE 5.30 How fast is the driven wheel spinning?

\begin{matrix} S = 3 in. \\ s = 6 in. \\ N = 32 rpm \\ n = ? \\ N S = n s \end{matrix}

\begin{matrix} n = \frac{N S}{s} \\ n = \frac{(32 rpm) (3 in.)}{6 in.} \\ n = 16 rpm \end{matrix}

Example 5.17

If a wheel that must spin at 3,600 rpm is being driven by a wheel of diameter 2 cm spinning at 180 rpm, what diameter should the driven wheel have? (Figure 5.31)

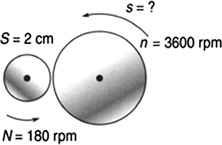
FIGURE 5.31 What diameter does the driven wheel have?

\begin{matrix} S = 2 cm \\ N = 180 rpm \\ n = 3, 600 rpm \\ s = ? \\ N S = n s \\ \frac{N S}{n} = \frac{n s}{n} \\ s = \frac{N S}{n} \\ s = \frac{(180 rpm) (2 cm)}{3, 600 rpm} \\ s = 0.1 cm \end{matrix}

A distance can separate the driving and driven wheels or gears by using a belt or chain, and the two wheels or gears now rotate in the same direction (Figure 5.32).

FIGURE 5.32 A distance can separate the driving and driven wheels or gears by using a belt or chain, and the two wheels or gears now rotate in the same direction.

Two wheels can be made to rotate in the opposite directions if the belt is twisted (Figure 5.33).

FIGURE 5.33 Two wheels can be made to rotate in opposite directions if the belt is twisted.

Example 5.18

A gear with 80 teeth spinning at 100 rpm is driving a gear with 20 teeth (Figure 5.34). How fast is the driven gear spinning?

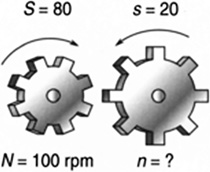
FIGURE 5.34 How fast is the driven gear spinning?

\begin{matrix} S = 80 teeth \\ s = 20 teeth \\ N = 100 rpm \\ n = ? \\ N S = n s \\ \frac{N S}{s} = \frac{n s}{s} \leftarrow solving for n \\ n = \frac{N S}{s} \\ n = \frac{(100 rpm) (80 teeth)}{20 teeth} \\ n = 400 rpm \end{matrix}

Multiple wheels and gears can be connected to create multiple speeds and rotations (Figure 5.35). To solve problems such as these, apply these equations to two wheels or gears at a time.

FIGURE 5.35 Multiple wheels and gears can be connected to create multiple speeds and rotations.

5.10 TORQUE

Everyone who has ever used a wrench knows that it is easier to turn a wrench with a long handle than a short one. The longer wrench has more torque (Figure 5.36).

FIGURE 5.36 A longer wrench has more torque than a shorter one.

Torque is defined mathematically as:

\begin{matrix} T = F \cdot r \\ Torque (N/m) = Force (N/m) = Force (N) \times radius arm (m) \end{matrix}

In the English system,

Torque (ft lb) = Force (lb) \times radius arm (ft)

Torque has units of foot pounds or newton meters. The force is applied perpendicular to the radius arm as shown in Figure 5.37.

FIGURE 5.37 Force is applied perpendicular to the radius arm to generate the torque.

Example 5.19

A torque wrench measures the torque applied to a bolt (see Figure 5.38). Suppose a torque wrench handle is 1 ft long and that 100 lb is applied to the handle. What does the torque wrench read?

FIGURE 5.38 A mechanic’s torque wrench.

F = 100 lb

r = 1 ft

T = ?

T = F \times r

T = (100 lb) (l ft)

T = 100 ft lb

5.11 TORQUE AND POWER

Every motor has horsepower and torque as two of its specifications. Torque is a measure of a motor’s strength to rotate something connected to its shaft some distance from the center of rotation. Torque and power are related by:

\begin{matrix} P = T \cdot ω \\ Power (W) = Torque (Nm) \times angular velocity (rad/s) \end{matrix}

In the English system,

Power (ft lb / s) = Torque (ft lb) \times angular velocity (rad/s)

Example 5.20

A motor connected to a wheel drives a cart. The cart requires 15 lb of force to move it. The wheel has a radius of 0.5 ft and is rotating at 3.0 rad/s (Figure 5.39). (a) What torque is the motor putting out? (b) What power is the motor generating? (c) What is this power in horsepower and watts?

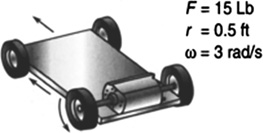
FIGURE 5.39 A motor connected to a wheel drives a cart.

(a)

\begin{matrix} F = 15 lb \\ r = 0.5 ft \\ ω = 3.0 \frac{rad}{s} \\ 1 hp = 550 \frac{ft lb}{s} \\ 1 hp = 746 W \\ T = ? \\ T = F \cdot r \\ T = (15 lb) (0.5 ft) = 7.5 ft lb \end{matrix}

(b)

\begin{matrix} P = ? \\ P = T \cdot ω \\ P = (7.5 ft lb) (3 \frac{rad}{s}) = 23 \frac{ft lb}{s} \end{matrix}

23 \frac{ft lb}{s} (\frac{1 hp}{550 \frac{ft lb}{s}}) = 0.042 hp

Converting horsepower into watts,

0.042 hp (\frac{746 W}{1 hp}) = 31 W

5.12 CHANGING TORQUE

Sometimes it is necessary to increase the torque delivered to a wheel, for example, when driving up a hill. The torque can be changed in multiple wheel or gear systems by changing the relative size of the driving and driven gears or wheels (Figure 5.40) according to:

FIGURE 5.40 The torque can be changed in multiple wheel or gear systems by changing the relative size of the driving and driven gears or wheels.

\begin{array}{l} \frac{T_{d}}{T_{D}} = \frac{s}{S} \\ T_{D} = driving torque \\ T_{d} = driving torque \\ S = size of driving diameter or number of teeth \\ s = size of driven diameter or number of teeth \end{array}

Example 5.21

What is the increase in torque when the driving torque is 12 ft lb, the driving wheel diameter is 0.16 ft, and the driven wheel is 2 ft in diameter? (Figure 5.41)

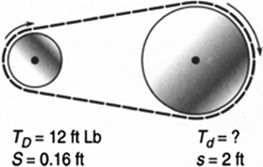
FIGURE 5.41 Centripetal force generated by changing the motion of a body into a circular path.

\begin{array}{l} T_{D} = 12 ft lb \\ S = 0.16 ft \\ s = 2.0 ft \\ T_{d} = ? \\ \frac{T_{d}}{T_{D}} = \frac{s}{S} \\ T_{d} = T_{D} \frac{s}{S} \\ T_{d} = 12 ft lb (\frac{2.0 ft}{0.16 ft}) \\ T_{d} = 150 ft lb \end{array}

5.13 CHAPTER SUMMARY

Symbols used in this chapter:

1 rev = 360 ° = 2 pi rad

d = r \cdot θ \Leftarrow θ must be in radians.

distance = radius \times angle (in radians)

If a wheel of radius r rolls along a surface through an angle θ, the wheel has traveled a distance d, where $d = r \cdot θ \Leftarrow θ must be in radians$ .

$\begin{matrix} ω = \frac{Δ θ}{Δ t} \\ Angular {velocity}_{average} = \frac{Change in angle}{Change in time} \end{matrix}$

$\begin{matrix} v = r \cdot ω \\ velocity = radius \times angular velocity \end{matrix}$

$\begin{matrix} a_{c} = r \times ω^{2} \\ {acceleration}_{centripetal} (\frac{m}{s^{2}}) = radius (m) \times angular velocity {(\frac{rad}{s})}^{2} \end{matrix}$

Alternatively:

$a_{c} = \frac{v^{2}}{r}$

$\begin{matrix} F_{c} = m \times a_{c} \\ {Force}_{centripetal} (N) = mass (kg) \cdot a_{c} (\frac{m}{s^{2}}) \leftarrow Force directed inward \\ {Force}_{centrifugal} (N) = mass (kg) \cdot a_{c} (\frac{m}{s^{2}}) \leftarrow Force directed outward \end{matrix}$

$\begin{matrix} N \cdot S = n \cdot s \\ N = Angle or angular speed of the driver. \\ S = Size of driving diameter or number of teeth. \\ n = Angle or angular speed of the driven. \\ s = Size of driven diameter or number of teeth. \end{matrix}$

$\begin{matrix} T = F \cdot r \\ Torque = Force \times radius arm \\ Torque has units of ft lb or N m \end{matrix}$

$\begin{matrix} P = T \cdot ω \\ Power = torque \times angular velocity (in radians/time) \end{matrix}$

\frac{T_{d}}{T_{D}} = \frac{s}{S}

\begin{array}{l} T_{D} = Driving torque. \\ T_{d} = Driven torque. \\ S = Size of driving diameter or number of teeth \\ s = Size of driven diameter or number of teeth \end{array}

PROBLEM SOLVING TIPS

∎ Always use angular units in radians for ω andθ when calculating.

$Distance: d = r \cdot θ \Leftarrow θ must be in radians.$

$Velocity: v = r \cdot ω \leftarrow ω in radians/time$

$Power: P = T \cdot ω \leftarrow ω in radians/time$

$Force: F_{c} = m r ω^{2} \leftarrow ω in radians/time$
∎ When solving transmission problems, capital letters refer to the drivers, lowercase to the driven.

PROBLEMS

A point on a CD rotates through an angle of 1 rev. The radius of the CD is 2.25 in. How far has this point traveled? Remember that θ must be in radians.
Suppose you are fixing a broken CD player because it is not spinning fast enough. You measure that the CD completes 5 rev in 1 s. What is the angular velocity in rpm?
You are asked to design a robot that moves at a speed of 120 in./min. The drive wheel is connected to a motor spinning at 25 rpm. What should the radius of the wheel be?
A wheel of diameter 3 in. is being driven by another wheel of diameter 6 in. How many times faster is the driven wheel spinning compared with the driving wheel?
A gear with 100 teeth is being driven by another gear. The driven gear is spinning at 10 rpm, and the driving gear is spinning at 5 rpm. How many teeth does the driving gear have?
A wrench with an 8 in. handle is used to tighten a bolt. Twenty-two pounds of force is applied to the handle. What is the torque in ft lb applied to the bolt?
A motor drives a conveyer belt. If the motor’s angular speed is 1,870 rpm and its torque is 35 ft lb, what is its horsepower? Remember that 1 hp = 550 ft lb/s.
Using two gears, how can you double the torque of a motor?
A motor of torque 12 ft lb is driving a wheel of 2 in. in diameter. This wheel is connected by a belt to another driven wheel of 1 in. diameter. What is the torque of the 1 in. wheel?
What is the angular velocity of the earth on its own axis?
A floppy disk in a computer rotates at 31.4 rad/s. How many revolutions does it make in a 30 s reading of the disk? (Be careful of the units!)
Suppose you wanted to build an elevator to outer space by attaching a 5.98 × 10²⁴kg mass in space to a cable 22,000 miles long and drop the other end of the cable to the earth and anchor it to the ground. The centripetal force would keep the cable taut, and you could ride up the cable to space. What would the centripetal force be on the cable? Why doesn’t NASA do this?
What is the centripetal acceleration of the tip of a fan blade moving at 1.1 m/s at a distance of 0.5 m from the axis of rotation?
To prevent a car from skidding on a turn, the frictional force of the tire on the road must be greater than or equal to the centripetal force. How fast can the car make a turn if the coefficient of the tire with the road is μ = 0.9, the car weighs 9,345 N, and the radius of the turn is 25 m. Hint: Maximum speed occurs when F_c = F_f.
If you build an electric cart and the drive motor that rotates at 1,750 rpm is connected to a drive wheel of radius 6.0 in., how fast will this cart move?
A motor rotates at 3,600 rpm. Convert this number into rad/s.
A go-kart is made by mounting a washing machine motor onto a cart. The motor drives a wheel of radius 6 in. If the motor is spinning at 2.0 rad/s, how fast is the cart moving in in./s?
A wheel of diameter 10 cm is spinning at 200 rpm and is driving another wheel of diameter 5 cm. How fast is the driven wheel spinning (in rpm)?
The head bolts on a certain car require that they be tightened with a torque of 110 ft lb. You are able to push on the wrench with 50 lb of force. How long should the wrench be?
The specification plate on a motor states that the motor puts out 452.4 W of power and runs at 3,600 rpm. What is the torque of this motor? (Remember to convert rpm into rad/s!)
The transmission on a car is designed to change the rpm and torque of an engine to the proper levels at the wheels to drive the car effectively. If the engine has 130 ft lb of torque and the torque at the wheels is 260 ft lb, how many times bigger is the driven wheel compared to the driving wheel?
What is the centripetal force on a 75 kg man turning a corner of radius 100 m in a car at an angular velocity of 1.1 rad/s?
A 2,000 lb car exits off the expressway onto an exit ramp at 45 mph or 66 ft/s. The ramp had a turning radius of 300 ft. What is the centripetal force on the car? (Remember to convert weight to mass!)
A robot moves across the floor on wheels of radius 2 in. rotating at 25 rpm. How fast is the robot moving in in./s?
A conveyer belt requires 22 lb of force to move. Mounted on the shaft of the motor that drives the belt is a wheel of radius 6 in. What torque must the motor have in ft lb?
A motor is spinning at 1,750 rpm. What is this in rad/s?
What is the angular velocity of the earth on its own axis in rpm?
The carriage on a copy machine is translated back and forth on wheels of radius 1.0 cm. If the wheels are spinning at 5 rpm, how fast is the carriage moving in cm/min?
A motor rotating at 50 rpm is connected to a wheel of radius 12 cm. This wheel is driving another wheel of radius 4 cm. How fast is the 4 cm wheel spinning?
A cart on wheels requires 8 N of force to keep it moving steadily. If the cart is driven by a motor connected to a wheel of radius 0.03 m, what torque is the motor generating?
If the motor in the previous problem is spinning at 25 rpm, how much power is the motor generating?
A motor has a torque of 1.1 Nm with a gear on its shaft with 20 teeth. Another gear is being driven by this gear with 60 teeth. What is the torque of the driven gear?
A mass of 0.4 kg is placed on a turntable at a distance of 0.10 m from the center of rotation. If the turntable is spinning at 45 rpm, what is the centripetal force on the mass?
The wheels on a cart of radius 2.0 in. turn through 50 rev. How far has the cart moved?
A wheel of diameter 10 cm spinning at 200 rpm drives another wheel of diameter 5 cm. How fast is the driven wheel spinning?
A wheel starts from rest and reaches an angular velocity of 20 rad/s in 4 s. What was its angular acceleration?
What is the centrifugal force on the driver of a car if she has a mass of 72 kg and is turning a corner of radius 10 m at a velocity of 10 m/s?

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 5 Rotational Motion

Create new playlist

Sign In

Sign Up

Table of Contents for
Chapter 5 Rotational Motion