The previous chapters have shown that concurrent programs can have subtle errors, that the errors cannot be discovered by debugging and that corrections cannot be checked by testing. For this reason, formal specification and verification of correctness properties are far more important for concurrent programs than they are for sequential programs. In this chapter we will explore several such methods.
We begin with a short section on the specification of correctness properties and then present the most important technique for proving properties, inductive proofs of invariants. This technique is used to prove that mutual exclusion holds for the third attempt. Inductive proofs are easy to carry out once you know what the invariants are, but they can be quite difficult to discover.
We have already discussed the construction of state diagrams and their use for proving correctness properties. Unfortunately, the full state diagram of even the simplest concurrent program is quite large, so it is not practical to manually construct such diagrams. In fact, for algorithms after the first attempt, we did not bother to construct full diagrams, and limited ourselves to displaying interesting fragments. Even if we could display a large diagram, there remains the task of reasoning with the diagram, that is, of finding forbidden states, cycles that lead to starvation of a process, and so on.
However, we can use a computer program not only to construct the diagram, but also to simultaneously check a correctness property. Such a program is called a model checker, because it checks if the state diagram of the concurrent program is a model (satisfying interpretation) of a formula specifying a correctness property of the program. Model checkers have become practical tools for verifying concurrent programs, capable of checking properties of programs that have billions of states. They use advanced algorithms and data structures to deal efficiently with large numbers of states.
Before discussing model checking in general and the Spin tool in particular, we present a system of temporal logic. Temporal logics have proved to be the most effective formalism for specifying and verifying concurrent programs. They can be used deductively to verify programs as will be shown in Section 4.5; temporal logics are also used to specify correctness properties for model checkers, and as such must be mastered by every student of concurrency. We have (more or less arbitrarily) divided the presentation of temporal logic into two sections: Section 4.3 should suffice for readers interested in using temporal logic to specify elementary correctness properties in Spin, while Section 4.4 covers more advanced aspects of the logic.
For further study of temporal logics, consult [9, 50, 51]. You may want to examine the STeP system, [12] which provides computer support for the construction of deductive proofs, and the Temporal Logic of Actions (TLA) [41], developed by Leslie Lamport for specifying concurrent programs.
We assume that you understand the basic concepts of the propositional calculus, as summarized in Appendix B.
The atomic propositions will be propositions about the values of the variables and the control pointers during an execution of a concurrent program. Given a variable of boolean type such as wantp, the atomic proposition wantp is true in a state if and only if the value of the variable wantp is true in that state. These two fonts will be used to denote the program variables and the associated symbols in logic. Similarly, boolean-valued relations on arithmetic variables are atomic propositions: turn ≠ 2 is true in a state if and only if the value of the variable turn in that state is not 2.
Each label of a statement of a process will be used as an atomic proposition whose intended interpretation is “the control pointer of that process is currently at that label.” We again use fonts to distinguish between the label p1 and the proposition p1 that may be true or false, depending on the state of the computation. Of course, since the control pointer of a single process can only point to one statement at a time, if pi is true, then pj is false for all j ≠ i; we will use this fact implicitly in our proofs.
To give a concrete example, let use write some formulas related to Algorithm 3.8, the third attempt. The formula
p1 ∧ q1 ∧ ¬ wantp ∧ ¬ wantq
is true in exactly one state, (p1,q1,false,false), where the control pointers of both processes are at the initial statements and the values of both variables are false. The formula is certainly true in the initial state of any computation (by construction of the program), and just as certainly is false in the second state of any computation (because either p1 or q1 will become false), unless, of course, both processes halt in their non-critical sections, in which case the computation remains in this state indefinitely.
A more interesting formula is
p4 ∧ q4,
which is true if the control pointers of both processes point to critical section; in other words, if this formula is true, the mutual exclusion property is not satisfied. Therefore, the program satisfies the mutual exclusion property in states in which
¬(p4 ∧ q4),
the negation of p4 ∧ q4, is true.
p1 ∧ q1 ∧ ¬ wantp ∧ ¬ wantp is an example of a formula that is true in some states (the initial state of the computation), but false in (most) other states, in particular, in any state in which the control pointers of the processes are at statements other than p1 and q1. For the program to satisfy the mutual exclusion property, the formula ¬(p4 ∧ q4) must be true in all possible states of all possible computations. The next section shows how to prove such claims.
The formula ¬(p4 ∧ q4) is called an invariant because it must invariably be true at any point of any computation. Invariants are proved using induction, not over the natural numbers, but over the states of all computations. (You may want to review Appendix B.2 on arithmetical induction before reading on.)
Prove that A holds in the initial state. This is called the base case.
Assume that A is true in all states up to the current one, and prove that A is true in the next state. This is called the inductive step, and the assumption that A is true in the current and previous states is called the inductive hypothesis. In a concurrent program, there may be more than one possible successor to the current state, so the inductive step must be proved for each one of them.
If (a) and (b) can be proved, we can conclude that A is true for all states of all computations.
Given an invariant, a proof by induction over all states is easier than it sounds. First, it is only necessary to take into account the effect of statements that can potentially change the truth of the atomic propositions in the formula. For example, it is trivial to prove the invariance of (turn = 1) ∨ (turn = 2) in the first attempt or in Dekker’s algorithm. The initial value of the variable turn is 1. The only two statements that can affect the truth of the formula are the two assignments to that variable; but one assigns the value 1 and the other assigns the value 2, so the inductive step is trivial to prove.
Second, many correctness claims are implications of the form p4 → wantp, that is, if a control pointer is at a certain statement, then a formula on the values of the variables is true. By the properties of material implication, if the formula is assumed true by the inductive hypothesis, it can be falsified in only two very limited ways; see Appendix B.3 for a review of this property of material implication. We now show how to prove that the third attempt satisfies the mutual exclusion property.
Algorithm 3.8, the third attempt at solving the critical section problem, is repeated here for convenience:
Example 4.1. Lemma
The formula A = p3..5 → wantp is invariant.
Proof: The base case is trivial because p1 is true initially so p3..5 is false.
Let us prove the inductive step, assuming the truth of A. Trivially, the execution of any statement by process q cannot change the truth of A, because A is expressed in terms of locations in process p that process q cannot change, and a variable wantp whose value is changed only by statements of p. Trivially, executing p1: noncritical section cannot change the truth of A. Only slightly less trivially, executing p3 or p4 does not change the truth of A: these statements do not assign to wantp and executing p3 (respectively, p4) moves the control pointer to p4 (respectively p5), maintaining the truth of p3..5.
So, the only two statements that can possibly falsify A are p2 and p5. Normally, of course, we wouldn’t go through such a long list of trivialities; we would just begin the proof by saying: the only statements that need to be checked are p2 and p5.
Executing p2 makes p3..5 true, but it also makes wantp true, so A remains true. Executing p5 makes p3..5 false, so by the properties of material implication A remains true, regardless of what happens to wantp. Therefore, we have proved by induction that A = p3..5 → wantp is true in all states of all computations.
The converse of formula A is also easily proved:
Example 4.2. Lemma
The formula B = wantp → p3..5 is invariant.
Proof: The base case is trivial because wantp is false initially. Again, the only statements that can falsify B are p2 and p5. p2 makes wantp “suddenly” become true, but it also makes p3..5 true, preserving the truth of B. p5 makes p3..5 false, but it also falsifies wantp.
Combining the two lemmas and symmetrical proofs for process q, we have:
Example 4.4. Theorem
The formula ¬(p4 ∧ q4) is invariant.
Proof: The proof will be easier to understand if, rather than show that ¬(p4 ∧ q4) is an invariant, we show that p4 ∧ q4 is false in every state. Clearly, p4 ∧ q4 is false in the initial state. So assume that p4 ∧ q4 is false; what statements might make it “suddenly” become true? There are only two: (successfully) executing p3: await wantq=false when q4 is true, and (successfully) executing q3: await wantp=false when p4 is true. Since the program is symmetrical, it is sufficient to consider one of them.
p3: await wantq=false can be successfully executed only if wantq is false; but by Lemma 4.3, if process q is at q4 then wantq is true. We conclude that the await statement in p3 cannot be successfully executed when q4 is true, so p4 ∧ q4 cannot become true.
In the usual study of mathematical logic, an assignment of truth values to atomic propositions is used to give an interpretation to a formula; in the interpretation, the formula will be either true or false. But within the context of the execution of a program, the assignment may change from state to state. For example, if A is the proposition turn = 1, then the proposition is true in the initial state of Dekker’s algorithm, but it will become false in any state that immediately follows the execution of the statement turn ← 2. In other words, turn = 1 is sometimes true and sometimes false, and a new system of logic is needed to deal with such situations.
Temporal logic is a system of formal logic obtained by adding temporal operators to propositional or predicate logic. In this section, we will informally present a logic called (propositional) linear temporal logic (LTL).
Atomic propositions like turn = 1 can be either true or false in a state s of a computation. The temporal operators will also be defined as being true or false in a state s of a computation, but their truth will depend on other states of the computation, not just on s.
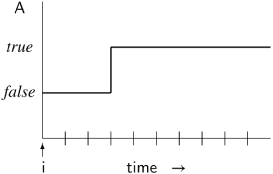
The meaning of □A is shown in the following diagram, where time flows in discrete units from left to right on the x-axis, while the y-axis has two levels for the two possible values of the formula A, true and false:
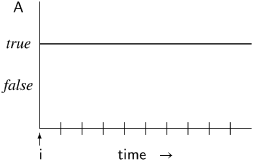
The origin of the x-axis is the index i of the state si at which the truth of the formula is being evaluated; this is not necessarily the beginning of the computation.
In Section 2.6, correctness properties were divided into safety and liveness properties. □A is a safety property because it specifies what must always be true. For example, the specification of the mutual exclusion property discussed previously can be expressed as □ ¬(p4 ∧ q4). Read this as always ¬(p4 ∧ q4), or in every state ¬(p4 ∧ q4) is true.
The meaning of 
A is shown in the following diagram:
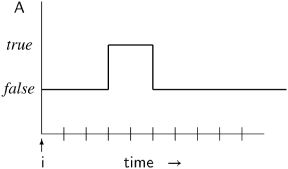
Note that if A is true in si because A is true in sj (j ≥ i), then A may subsequently become false in a later state sk, k > j. In the example, A is true in state si because A is true in state si+3 (and in state si+4), although it subsequently becomes false in state si+5 and remains false in subsequent states.
The eventually operator is used to specify liveness properties, for example, the freedom from starvation for the third attempt. Since the algorithm is symmetric, it is sufficient to specify for one process, say p, that it must enter its critical section. The formula p2 → p4 means that if the computation is at a state in which the control pointer of process p is at statement p2 (indicating that it wishes to enter the critical section), then eventually the control pointer will be at p4. More precisely, freedom from starvation should be specified as □(p2 → p4), so that we require that any state in which p2 is true is followed by a state in which p4 is true.
The meaning of the operator is consistent with our model of concurrency, in that it only specifies that eventually some proposition must be true, without specifying if that will happen immediately, soon, or after many millions of execution steps.
There is a duality to temporal operators, similar to the duality of deMorgan’s laws:
¬(A ∧ B) ↔ (¬A ∨ ¬B),
¬(A ∨ B) ↔ (¬A ∧ ¬B).
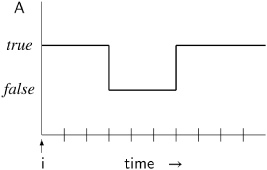
¬ □A (it is false that A is always true) is equivalent to ¬ A (eventually A is false):
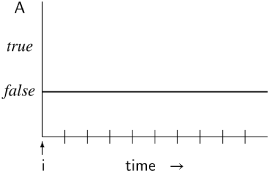
¬ A (it is false that A is eventually true) is equivalent to □ ¬ A (A is always false):
The meaning of the formula □A with a compound temporal operator is shown in the following diagram:
Eventually A will be come true and remain true; in the diagram, A is false for the first three units of time, but then it becomes and remains true.
The meaning of □A is different:
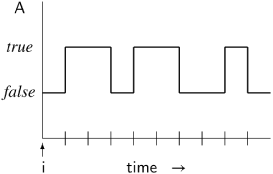
At every point in time, there is a time in the future when A becomes true; later, it may return to have the value false, but if so, it must become true again.
The always and eventually operators have limited expressive power, because they are applied to only one formula. Many specifications of correctness properties involve two or more propositions. For example, we may want to specify that process p1 enters its critical section at most once before process p2 enters its critical section.
The until operator 
is a binary temporal operator. A B means that eventually B becomes true and that A is true until that happens:
This is shown in the diagram below, where the truth value of A is represented by the thin line and the truth value of B by the thick line:
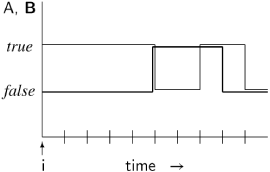
At the fifth state from the origin, B becomes true, and until then, A is true. What happens afterwards is not relevant to the truth of A B. Note that A is not required to remain true when B becomes true. By reflexivity, A B is true if B is true at the initial state; in this case the requirement on A is vacuous.
There is also an operator called weak until, denoted 
. For the weak operator, the formula B is not required to become true eventually, though if it does not, A must remain true indefinitely.
The semantics of linear temporal logic are defined over the sequence of states of a computation over time. Thus, in any state, it makes sense to talk of the next state. The corresponding unary temporal operator is denoted 
or ◯.
The next operator is rarely used in specifications because the interleaving semantics of concurrent computation are not sensitive to the precise sequence of states, only to their relative order. For example, given the following statements in a process:
integer x ← 0 x ← 1 x ← 2
it makes sense to claim that (x = 1) → (x = 2) (assuming that the computation is fair), but not to claim (x = 1) → ◯(x = 2). We don’t know how many states may occur between the execution of the first assignment statement and the second, nor do we usually care.
If the precise behavior of the system in the interval between the execution of the statements is important, we would use an until formula because we want to specify something about all intervening states and not just the next one. For example, (x = 1)(x = 2) claims that x = 1 remains true in all states between the execution of these two statements.
Temporal logic is a formal system of deductive logic with its own axioms and rules of inference [9]. Similarly, the semantics of concurrent programs can be formalized within temporal logic, and then the logic can be used to rigorously prove correctness properties of programs. Here we will show how semi-formal reasoning can be used to prove formulas of temporal logic. This type of reasoning will be used in the next section to prove freedom from starvation in Dekker’s algorithm.
Here is a formula that is a theorem of temporal logic:
(□A1 ∧ □A2) → □(A1 ∧ A2).
To prove an implication, we have to prove that if the antecedent is true, then so is the consequent. The antecedent is a conjunction, so we assume that both its subformulas are true. Let us now use the definitions of the temporal operators. □A1 is true if there is some state sk1 such that □A1 is true in sk1; this holds if A1 is true for all states sj such that j ≥ k1. For □A2 to be true, there must be some sk2 with a similar property. The following diagram shows what it means for the antecedent to be true.
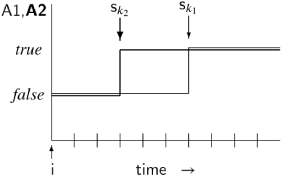
Let k be the larger of k1 and k2. Clearly, A1 ∧ A2 is true in all states sj such that j ≥ k. By definition of □, □(A1 ∧ A2) is true in sk, and then by definition of , □(A1 ∧ A2) is true in the initial state si.
Let us now consider the similar formula
(□A1 ∧ □A2) → □(A1 ∧ A2).
Suppose that A1 is true at s3, s6, s9, . .. and that A2 is true at s1, s2, s4, s5, s7, s8, . .., as shown in the following diagram:
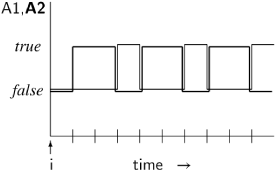
Clearly, the antecedent is true and the consequent is false, so we have falsified the formula, showing that it is not a theorem of temporal logic.
In the exercises, you are asked to prove or disprove other important formulas of temporal logic.
Consider the following scenario:
Process p tries to enter its critical section, but does so only after process q tries and successfully enters its critical section one thousand times. The scenario is not an example of starvation, because it remains true that eventually p enters its critical section. This scenario shows that freedom from starvation is a very weak property.
To ensure that a process enters its critical section within a reasonable amount of time, we can specify that an algorithm satisfy the property of k-bounded overtaking, meaning that from the time a process p attempts to enter its critical section, another process can enter at most k times before p does:
The bakery algorithm for the critical section problem to be discussed in Chapter 5 satisfies the property of 1-bounded overtaking: if process p tries to enter its critical section, any other process can enter its critical section at most once before p does. This property can be expressed using the weak until operator :
Let us interpret this formula on the following diagram, where the execution of p is represented by thin lines and that of q by thick lines:
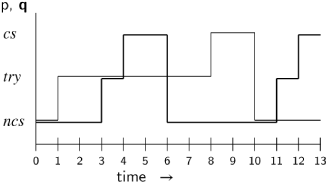
We want the formula to be true at time 1 when tryp is true. Between 1 and 4, ¬ csq is true, so we have to check the truth of (csq) (¬ csq) (csp) at time 4. Now csq is true from time 4 to time 6, so it remains to check if (¬ csq) (csp) is true at time 6. And, in fact, ¬ csq remains true until csp becomes true at time 8.
Note that the formula does not specify freedom from starvation, because the operator does not require that its right operand ever becomes true. Therefore, the formula is true in an execution in which both csp and csq are always false. In the exercises, we ask you to modify the formula so that it also specifies freedom from starvation.
In this section we give a full deductive proof of the correctness of Algorithm 3.10, Dekker’s algorithm, repeated as Algorithm 4.2 for convenience. The following lemma is a direct result of the structure of the program and its proof is very similar to that of Lemma 4.3.
Table 4.2. Dekker’s algorithm
boolean wantp ← false, wantq ← false integer turn ← 1 | ||
|
| |
loop forever p1: non-critical section p2: wantp ← true p3: while wantq p4: if turn = 2 p5: wantp ← false p6: await turn = 1 p7: wantp ← true p8: critical section p9: turn ← 2 p10: wantp ← false |
loop forever q1: non-critical section q2: wantq ← true q3: while wantp q4: if turn = 1 q5: wantq ← false q6: await turn = 2 q7: wantq ← true q8: critical section q9: turn ← 1 q10: wantq ← false | |
The statement and proof that mutual exclusion holds for Dekker’s algorithm is similar to that of Theorem 4.4 and is left as an exercise.
Invariants can be used to specify and verify safety properties like mutual exclusion, but they cannot be used for proving liveness properties like freedom from starvation. To prove a liveness property, we must reason about progress, that is, if the computation is in a state satisfying A, it must progress to another state in which B is true. We will now explain how to reason about progress and then use the techniques to prove the freedom from starvation of Dekker’s algorithm.
We will assume that all computations are weakly fair (Section 2.7). In terms of progress, this means that if a statement of a process can be executed, then eventually it will be executed. Weak fairness is needed to rule out trivial counterexamples; if a process is never allowed to execute, then of course it may be starved. We are only interested in scenarios for counterexamples that are the result of a lack of synchronization among processes.
Assignment statements: Clearly, if the control pointer of a process p points to an assignment statement var←expression and if (by weak fairness) p is eventually allowed to execute, then the execution eventually completes. Therefore, progress holds for assignment statements, meaning that in any such computation, there are states si and si+1, such that si+1 is obtained from si by changing the control pointer of p—it is incremented to the next statement—and changing the value of var to be the value of expression as evaluated in si.
Critical and non-critical sections: By assumption (Section 3.2), critical sections progress while non-critical sections need not. In Dekker’s algorithm, progress for the critical section means that p8 → p9 must always be true, or equivalently, □(p8 → p9) must be true. For the non-critical section, we cannot claim p1 → p2, because it is possible that □p1, if, from some point in time, process p remains at p1 indefinitely.
Control statements: The situation is more complicated in the case of control statements with conditions like if, while and await statements. Consider for example, statement p4: if turn = 2. Neither of the following formulas is true:
p4 ∧ (turn = 2) → p5,
p4 ∧ ¬(turn = 2) → p3.
Suppose that the control pointer of process p is actually at p4 and that the value of the variable turn is actually 2. It does not follow that the process p eventually reaches p5. This does happen in interleavings in which the next step is taken from process p, but there are interleavings in which process q executes an arbitrary number of statements, among which might be q9: turn←1. When p is next allowed to execute, it will continue to statement p3, not to p5.
To prove that a specific branch of a conditional statement is taken, we must first prove that the condition is held at a certain value indefinitely:
p4 ∧ □(turn = 2) → p5.
This may seem to be too strong a requirement, because turn = 2 may not be true forever, but it is important that it be true indefinitely, until process p is allowed to execute the if statement and continue to statement p5.
A proof rule for progress: Frequently, we will have a pair of lemmas of the form: (a) □A → B, meaning that if (from now) A remains true then B is eventually true, and (b) □A, meaning that eventually A remains true indefinitely. We would like to conclude B. If (b) had been □A, this would follow immediately from (a) by modus ponens. Nevertheless, the inference is sound, as we ask you to show in an exercise.
We now turn to the proof of freedom from starvation of Dekker’s algorithm. Semi-formal reasoning will be used about progress. When we say that a formula B becomes true “by progress,” we mean that the statements of the program and formulas of the form □A that have already been proved constrain the program to execute statements making B eventually true.
We will prove freedom from starvation under the assumption that q always progresses out of its critical section: □ ¬ q1; this will be called the progress assumption on q. The full proof follows from additional invariants that you are asked to prove in the exercises.
The intended interpretation of the following lemma is that if p insists on entering its critical section then eventually q will defer to it. Read it as: if wantp and turn = 1 are always true, then eventually wantq will be indefinitely false.
Example 4.11. Lemma
□wantp ∧ □turn = 1 → □ ¬ wantq.
Proof: If the antecedent □wantp ∧ □turn = 1 is true, by the progress assumption on q and the progress of the other statements of q, process q will eventually reach q6: await turn=2, and it will remain there because □turn = 1. Invariant (4.4) implies that wantq eventually becomes false and remains false, making the consequent true.
Example 4.12. Theorem
p2 → p8.
Proof: To prove the theorem, we assume its negation p2 ∧ ¬ p8 and derive a contradiction.
If □turn = 2, then p2 ∧ ¬ p8 implies by progress that □p6 (eventually process p remains p6: await turn=1). By invariant (4.3), this implies □ ¬ wantp. By the progress assumption for q and progress of the other statements in process q, □turn = 2 and □ ¬ wantp imply that eventually q9: turn ← 1 is executed, so turn = 1. This contradicts the assumption □turn = 2, establishing the truth of ¬ □turn = 2, which is equivalent to turn = 1 by invariant (4.2).
By assumption, p2∧ ¬ p8, so process p will never execute p9: turn ← 2; therefore, turn = 1 implies □turn = 1. By progress, it follows that process p is eventually looping at the two statements p3: while wantq and p4: if turn=2. Invariant (4.3) then implies □wantp, and from Lemma 4.11 it follows that □ ¬ wantq, contradicting the claim that p repeatedly executes p3 without entering the critical section.
If the number of reachable states in a program is not too large, it is possible to construct a diagram of the states and transitions, and to check correctness properties by examining the diagram. Clearly, if we use variables of types like integer or floating point, the number of possible states is astronomical. Nevertheless, constructing state diagrams is a practical tool for verification for several reasons.
First, algorithms for concurrency typically use variables which take on only a few values or which can be modeled by just a few values. If we want to verify a communications protocol, for example, we need not include the rich structure of the messages themselves, as it is sufficient to represent any message by a small number representing its type.
Second, the construction of the state diagram can be incremental, starting with the initial state. The structure of the program often limits the number of states that can actually be accessible in an execution. Furthermore, we can perform model checking: checking the truth of a correctness specification as the incremental diagram is constructed, so that if a falsifying state is found, the construction need not be carried further.
Third, we do not actually have to display the state diagram. The diagram is just a data structure which can be constructed and stored by a computer program. It is a directed graph whose nodes contain tuples of values, and the size of a tuple (the number of bits needed to store it) is fixed for any particular program.
In this book we will explain how to perform model checking using Spin (Appendix D.2). Spin is a model checker that has become very popular in both academic research and in industrial software development, because it is extremely efficient and yet easy to use. There are many other model checkers intended for use with different languages, models and logics. We draw your attention in particular to Java PathFinder (JPF) [69] and to the tools developed by the SAnToS research group. They are intended to be used for the verification of programs written in Java, in contrast with Spin which is intended for use in the modeling and design of concurrent and distributed systems.
In this section we present the Promela language that is used in Spin to write concurrent programs. Promela is a programming language with syntax and semantics like any other language, but it is called a modeling language, because it contains a
Example 4.1. Dekker’s algorithm in Promela
1 bool wantp = false, wantq = false; 2 byte turn = 1; 3 4 active proctype p() { 5 do :: wantp = true; 6 do :: ! wantq –> break; 7 :: else –> 8 if :: (turn == 1) 9 :: (turn == 2) –> 10 wantp = false; 11 (turn == 1); 12 wantp = true 13 fi 14 od; 15 printf ("MSC: p in CS "); 16 turn = 2; 17 wantp = false 18 od 19 } 20 21 active proctype q() { /* similar */ }
limited number of constructs that are intended to be used to build models of concurrent systems. Designing such a language is a delicate balancing act: a larger language is more expressive and easier to use for writing algorithms and programs, but a smaller language facilitates efficient model checking. We will not give the details of the syntax and semantics of Promela, as these are readily available in the Spin online documentation and in the reference manual [33]. Instead, we will describe how it can be used to model and verify the algorithms that are used in this textbook.
The description of the language will refer to Listing 4.1 which shows Dekker’s algorithm in Promela. The syntax and semantics of declarations and expressions are similar to those of C. The control structures might be unfamiliar, as they use the syntax and semantics of guarded commands, frequently used in theoretical computer science. To execute an if statement, the guards are evaluated; these are the first expressions following the :: in each alternative. If some of them evaluate to true, one of them is (nondeterministically) selected for execution; if none evaluate to true, the statement blocks. In the algorithm, the guards of the if statement:
if :: (turn == 1) :: (turn == 2) –> . . . fi
are exhaustive and mutually exclusive (because the value of turn is either 1 or 2), so there is no blocking and no nondeterminism. A do statement is executed like an if statement, except that after executing the statements of one alternative, the execution loops back to its beginning. A break statement is needed to exit a loop.
An else guard is used to obtain the semantics of a non-blocking if or do statement as shown in line 7. The meaning of this guard is that if all other guards evaluate to false, then this alternative is selected.
Of course, the concept of blocking the execution of statement makes sense only within the context of a concurrent program. So writing:
if :: (turn == 1) –> /* Do nothing */ fi
makes sense. There is only one guard turn==1 and if it is false, the statement will block until some other process assigns 1 to turn, making the statement executable. In fact, in Promela, any boolean expression will simply block until it evaluates to true, so the above if statement can be expressed simply as:
(turn == 1)
as shown in line 9.
A process is declared as a proctype, that is, a process declaration is a type and you can instantiate several processes from the process type. We have used active as a shortcut to both declare the types, and instantiate and activate a procedure of each type.
An array-like syntax can be used to activate several procedures of the same type:
#define NPROCS 3 active [NPROCS] proctype p() { . . . }
Note the use of the C-language preprocessor to parameterize the program. Alternatively, processes can be declared without active and then explicitly activated within a special initialization process:
proctype p(byte N) { . . . } init { int n = . . .; atomic { run p(2*n); run p(3*n); } }
This is useful if you want to compute initial parameters and pass their values to the processes. (See, for example, the algorithm in Section 8.3.) atomic was discussed in Section 2.13.
Within each process, the predefined identifier _pid gives a unique identifier for each process, and can be used, for example, in output statements or to index arrays:
bool want[NPROCS] = false; . . . want[_pid] = true; printf ("MSC: process %d in critical section ", _pid);
In Section 4.3, logical formulas expressing correctness specifications used atomic propositions like p1 that are true if and only if the control pointer of a process is at that label. In Spin correctness specifications are expressed using auxiliary variables. For example, to prove that Dekker’s algorithm satisfies mutual exclusion, we add an auxiliary variable critical that is incremented and then decremented when the processes are in their critical sections:
byte critical = 0; active proctype p() { /* preprotocol */ critical ++; printf ("MSC: p in CS "); critical −−; /* postprotocol */ }
The values of these variables are not otherwise used in the computation (and you will receive a warning message to that effect when you compile the program), so they cannot affect the correctness of the algorithm. However, it is clear that the boolean-valued expression critical ≤ 1 is true if and only if at most one process is in its critical section. A state in which critical > 1 is a state in which mutual exclusion is violated.
The printf statements are not used in the proof of correctness; they serve only to display information during simulation.
We are now ready to ask Spin to verify that Dekker’s algorithm satisfies mutual exclusion. The simplest way to do this is to attach an assertion to each critical section claiming that at most one process is there in any state:
critical ++;
assert(critical <= 1);
critical −−;Clearly, if mutual exclusion is violated then it is violated when the two processes are in their critical sections, so it is sufficient to check within the critical sections that the property is always true. Running a Spin verification in Safety mode will return the answer that there are no errors. (Verification of Promela models in Spin is described in greater detail in Appendix D.2.)
An alternative way of proving that the algorithm satisfies mutual exclusion is to use a formula in temporal logic. Atomic propositions in Spin must be identifiers, so we start by defining an identifier that is true when mutual exclusion holds:
#define mutex (critical < = 1)We can now execute a verification run of Spin in Acceptance mode with the temporal logic formula []mutex. The two-character symbol [] is used for the temporal operator always □, and the two-character symbol <> is used for the temporal operator eventually . Spin will report that there are no errors.
Let us introduce an error into the program; for example, suppose that we forget to write the not symbol ! in the guard in line 6. Running a verification will cause Spin to report an error: claim violated. To assist the user in diagnosing the error, Spin writes a trail, which is a representation of a scenario that leads to the claim being violated. You can now run Spin in simulation mode on the trail to examine this scenario, and you will in fact discover that the execution reaches a state in which critical = 2, falsifying the proposition mutex.
We can use Spin to verify that Dekker’s algorithm is free from starvation. Since the algorithm is symmetric, it is sufficient to prove this for one of the processes, say process p. First we define a proposition that is true if p is in its critical section:
bool PinCS = false; #define nostarve PinCS active proctype p() { /* preprotocol */ critical ++; PinCS = true; PinCS = false; critical −−; /* postprotocol */ }
The property we want to verify is given by the following temporal logic formula:
[]<> nostarve
and a verification run shows that this holds. By default, Spin will check all scenarios, even those that are not weakly fair (Section 2.7). To prove freedom from starvation of Dekker’s algorithm, you must specify that only weakly fair scenarios are to be checked.
Verification of concurrent and distributed programs is a dynamic field. A central goal of this introductory book is to prepare you for further study of verification by introducing a variety of techniques and tools, instead of choosing and presenting a unified approach. A few words are in order to compare the various approaches, and you may wish to return to this discussion again as you progress in your studies.
The basic concept in defining the semantics of any program is that of the state, consisting of the control pointers and the contents of the memory. Executing a statement of a program simply transforms one state into another. The correctness specification of a sequential program is straightforward: it relates the final state at termination to the initial state. (See Appendix B.4 for an example.) Concurrent programs are much more difficult to verify, both because of the nondeterministic nature of the computation, and also because of the complexity of the correctness specifications. There are basically two classes of specifications: safety properties and liveness properties.
A safety property must be true at all states, so—needless to say—you have to check that it is true at all states. There are two ways of doing this: generate all possible states and check that each one satisfies the property, or show that any state that may be generated satisfies the property. The former technique is used by model checkers and the latter by deductive systems. Model checking is basically a “mindless” mechanical enumeration of all the possible states of the computation. Practical model checkers like Spin are thus characterized by the clever and sophisticated techniques they employ for incrementally and efficiently constructing and checking the set of states, not by any insight they provide into the structure of a concurrent algorithm. They are primarily used for debugging high-level system specifications, because if a verification run fails, the model check will provide the detailed scenario of a counterexample to the property. Receiving the message errors: 0 is a cause for rejoicing, but it doesn’t help you understand why an algorithm is correct.
Deductive systems are similar to those used in mathematics. A safety property in the form of an invariant is proved by induction over the structure of the algorithm: if it is true initially and if its truth is preserved by all statements in the program, then it will be true in any possible state. This we know without actually creating any states. The first advantage a deductive proof has over model checking is that it can handle state spaces of indefinite size that might overwhelm a model checker; since no states are actually created, there is no problem of computational resources. The second advantage is the insight that you get from working through the steps of the induction. The are two disadvantages of deductive proofs relative to model checking. First, it can require some ingenuity to develop the proof, so your failure to prove an algorithm may just be the result of failing to find the right invariant. Second, although mechanical systems are available to help develop deductive proofs [12], most proofs are done by hand and thus are prone to human error, unlike a well-debugged model checker which does not make mistakes.
Deductive proofs and model checking complement each other, which is why they are both included in this book. For example, while it is easy and important to verify Barz’s algorithm by model checking in Spin, the complex deductive proof in Section 6.10 gives insight into how the algorithm works.
A liveness property claims that a state satisfying a property will inevitably occur. It is not sufficient to check states one by one; rather, all possible scenarios must be checked. This requires more complex theory and software techniques. More resources are required for checking liveness properties and this limits the complexity of models that can be checked. In deductive proofs, it is not sufficient to check the inductive steps of individual statements; the proof rules needed are much more sophisticated, as shown by the proof of the freedom from starvation of Dekker’s algorithm.
The proof of safety properties of concurrent programs like mutual exclusion is usually straightforward. The difficulty is to discover the right invariants, but once the invariants are specified, checking them is relatively easy. Deductive proofs of liveness properties require complex reasoning in temporal logic. A practical alternative is to use computer programs called model checkers to conduct a systematic search for counterexamples to the correctness assertions. The Spin model checker and its language Promela were described.
By now you must be totally bored solving the critical section problem within the model of atomic load and store to global memory. If so, skip to Chapter 6 to continue your study with new models and new problems. Eventually, you will want to return to Chapter 5 to study more advanced algorithms for the critical section problem.
1. | Give invariants for the first attempt (Algorithm 3.2) and show that mutual exclusion holds. | |||||||||
2. | Prove Lemma 4.10 and use it to prove that Dekker’s algorithm satisfies the mutual exclusion property. | |||||||||
3. | What is the difficulty in proving freedeom from starvation in Dekker’s algorithm for the case where process | |||||||||
4. | Prove the proof rule for progress: □A → | |||||||||
5. | Express □ and | |||||||||
6. | Prove that □ distributes over conjunction (□A ∧ □B) ↔ □(A ∧ B) and that | |||||||||
7. | It follows that strings of unary temporal operators “collapse” to a single operator or to a pair of distinct operators. | |||||||||
8. | Using the operator | |||||||||
9. | The temporal operator leads to, denoted | |||||||||
10. | Prove the correctness of Peterson’s algorithm, repeated here for convenience: Table 4.3. Peterson’s algorithm
First show that are invariant, and then use them to prove that mutual exclusion holds. To prove liveness for process and deduce a contradiction. | |||||||||
11. | Show that Peterson’s algorithm does not satisfy the LCR restriction (page 27). Write a Promela program for the algorithm that does satisfy the restriction. | |||||||||
12. | Write a Promela program for the frog puzzle of Section 2.14 with six frogs and use Spin to find a solution. Hint: use | |||||||||
13. | In the Promela program for Dekker’s algorithm, is it sufficient to add the assertion to just one of the processes | |||||||||
14. | Modify the Promela program for Dekker’s algorithm to prove that □ | |||||||||
15. | (Ruys [56]) To check a safety property P of a Promela program, we use the LTL formula active proctype monitor() { assert(P) } Discuss the advantages and disadvantages of the two approaches. Similarly, discuss the following alternatives for the active proctype monitor() { !P –> assert(P) } active proctype monitor() { do :: assert(P) od } | |||||||||
