In this chapter we present two advanced algorithms for the critical section problem. These algorithms are important for two reasons: first, they work for an arbitrary number of processes, and second, they raise additional issues concerning the concurrency abstraction and the specification of the critical section problem. Both algorithms were developed by Leslie Lamport.
In the bakery algorithm, a process wishing to enter its critical section is required to take a numbered ticket, whose value is greater than the values of all outstanding tickets. The process waits until its ticket has the lowest value of all outstanding tickets and then enters its critical section. The name of the algorithm is taken from ticket dispensers used at the entrance of bakeries and similar institutions that wish to serve customers on a first-come, first-served basis. Before looking at the full bakery algorithm, let us examine a simplified version for two processes:
np and nq hold the ticket numbers of the two processes. A value of 0 indicates that the process does not want to enter its critical section, while a positive value represents an implicit queue of the processes that do want to enter, with lower ticket numbers denoting closeness to the head of the queue. If the ticket numbers are equal, we arbitrarily assign precedence to process p.
Example 5.1. Lemma
The following formulas are invariant:
np = 0 ↔ p1 ∨ p2, |
nq = 0 ↔ q1 ∨ q2, |
p4 → (nq = 0) ∨ (np ≤ nq), |
q4 → (np = 0) ∨ (nq < np). |
Proof: The first two invariants follow trivially from the structure of the program, since np is only assigned to in process p and nq is only assigned to in process q.
Let us prove the third invariant as the proof of the fourth is symmetric. Clearly, p4 → (nq = 0) ∨ (np ≤ nq) is true initially. Suppose that it is true because both the antecedent and consequent are false; can it be falsified by the antecedent “suddenly” becoming true? This will occur if process p executes p3, successfully passing the await statement. But, by the condition, nq = 0 ∨ (np ≤ nq) must be true, so the consequent cannot have been false.
Suppose now that the formula is true because both the antecedent and consequent are true; can it be falsified by the consequent “suddenly” becoming false? For the antecedent to remain true, process p must remain at p4, so the values of the variables can be changed only by process q. The only possibility is to change the value of nq, either in statement q2 or in statement q5. But q2 makes np ≤ nq true and q5 makes nq = 0 true, so the consequent remains true.
Example 5.2. Theorem
The bakery algorithm for two processes satisfies the mutual exclusion property.
Proof: Combining the third and fourth invariants from Lemma 5.1, we get:
(p4 ∧ q4) → ((nq = 0) ∨ (np ≤ nq)) ∧ ((np = 0) ∨ (nq < np)). |
By the first two invariants of the lemma, if p4 ∧ q4 is true, then neither np = 0 nor nq = 0 is true, so the formula simplifies to:
(p4 ∧ q4) → (np ≤ nq) ∧ (nq < np). |
The consequent is clearly false by the properties of arithmetic, so we can deduce that p4 ∧ q4 is always false, and therefore ¬(p4 ∧ q4) is invariant, proving that the mutual exclusion property holds.
Example 5.3. Theorem
The two-process bakery algorithm is free from starvation.
Proof: Let us prove that process p is not starved: p2 → ![]() p4. Suppose to the contrary that p2 and ¬
p4. Suppose to the contrary that p2 and ¬ ![]() p4 are true. By progress of the assignment statement
p4 are true. By progress of the assignment statement p2, p3 becomes true; together with ¬ ![]() p4, this implies
p4, this implies ![]() □p3. By the first invariant of Lemma 5.1, □
□p3. By the first invariant of Lemma 5.1, □![]() p3 implies 32 (np = k) for some k >0. Furthermore, □
p3 implies 32 (np = k) for some k >0. Furthermore, □![]() p3 is true only if eventually the
p3 is true only if eventually the await statement at p3 is never executed successfully. By weak fairness, p must attempt to execute p3 infinitely often only to find the condition false. Therefore,
□![]() ¬(nq = 0 ∨ np ≤ nq)
¬(nq = 0 ∨ np ≤ nq)
must be true. From deMorgan’s laws and the distributive laws of temporal logic, specifically:
□ (A ∧ B) → (□A ∧ □B) and ![]() (A ∧ B) → (
(A ∧ B) → (![]() A ∧
A ∧ ![]() B),
B),
this formula implies
□![]() (nq ≠ 0) ∧ □
(nq ≠ 0) ∧ □![]() (nq < np).
(nq < np).
□![]() (nq ≠ 0) means that process
(nq ≠ 0) means that process q leaves the critical section infinitely often, so by progress, q executes q2: nq ← np+1 infinitely often. By ![]() □ (np = k), □
□ (np = k), □![]() (nq = k + 1), for k >0, contradicting □
(nq = k + 1), for k >0, contradicting □![]() (nq < np).
(nq < np).
We have assumed that the assignments at statements p2 and q2 are atomic. This can be unrealistic, because each involves computing an expression with the value of one variable and assigning the result to another. In the exercises you are asked to find a scenario that violates mutual exclusion when the normal load and store model is used, and to prove the correctness of another version of the algorithm.
Here is the bakery algorithm for N processes:
Each of the N processes executes the same algorithm, except that i is set to a different constant in the range 1 to N, called the ID number of the process.
The statement for all other processes j is an abbreviation for
for j from 1 to N if j ≠ i
The notation (number[i] ≪ number[j]) is an abbreviation for:
(number[i] < number[j]) or
((number[i] = number[j]) and (i < j))that is, either the first ticket number is lower than the second, or they are equal and the first process ID number is lower than the second.
Each process chooses a number that is greater than the maximum of all outstanding ticket numbers. A process is allowed to enter its critical section when it has a lower ticket number than all other processes who want to enter their critical sections. In case of a tie in comparing ticket numbers, the lower numbered process is arbitrarily given precedence. Again we are making an unrealistic assumption, namely, that computing the maximum of the values of an array is atomic. As shown in the next section, these assumptions can be removed at the cost of complicating the algorithm.
The bakery algorithm is elegant because it has the property that no variable is both read and written by more than one process (unlike the variable turn in Dekker’s algorithm). Despite this elegance, the bakery algorithm is impractical for two reasons. First, the ticket numbers will be unbounded if some process is always in the critical section. Second, each process must query every other process for the value of its ticket number, and the entire loop must be executed even if no other process wants to enter its critical section.
See [48, Section 10.7] for a proof of the correctness of the bakery algorithm. The ideas used in the algorithm are also used in the Ricart–Agrawala algorithm for distributed mutual exclusion (Section 10.3).
The model of concurrency that we use throughout this book is that of interleaved execution of atomic statements, where each access to a variable in memory (load or store) is atomic. In a sense, we are “passing the buck,” because we are depending on a hardware-level synchronization mechanism to ensure mutual exclusion of memory accesses. Here is the original bakery algorithm for N processes, which is correct under weaker assumptions than the atomicity of load and store to global variables:
Table 5.3. Bakery algorithm without atomic assignment
boolean array[1..n] choosing ← [false,. . . ,false] integer array[1..n] number ← [0,. . . ,0] | |
loop forever
p1: non-critical section
p2: choosing[i] ← true
p3: number[i] ← 1 + max(number)
p4: choosing[i] ← false
p5: for all other processes j
p6: await choosing[j] = false
p7: await (number[j] = 0) or (number[i] ≪ number[j])
p8: critical section
p9: number[i] ← 0 | |
Algorithm 5.3 differs from Algorithm 5.2 by the addition of a boolean array choosing. If choosing[i] is true, a process is in the act of choosing a ticket number, and other processes must wait for the choice to be made before comparing numbers.
Each global variable is written to by exactly one process, so there are no cases in which multiple write operations to the same variable can overlap. It is also reasonable to assume that if a set of read operations to a variable does not overlap a write operation to that variable, then they all return the correct value. However, if read operations overlap a write operation, it is possible that inconsistent values may be obtained. Lamport has shown that the bakery algorithm is correct even if such read operations return arbitrary values [36].
In the bakery algorithm, a process wishing to enter its critical section must read the values of all the elements of the array number to compute the maximum ticket number, and it must execute a loop that contains await statements that read the values of all the elements of the two arrays. If there are dozens of processes in the system, this is going to be extremely inefficient. The overhead may be unavoidable: if, in general, processes attempt to enter their critical sections at short intervals, there will be a lot of contention, and a process really will have to query the state of all the other processes. If, however, contention is low, it makes sense to search for an algorithm for the critical section problem that is very efficient, in the sense that only if there is contention does the process incur the significant overhead of querying the other processes.
An algorithm for the critical section problem is fast, if in the absence of contention a process can access its critical section by executing pre- and postprotocols consisting of a fixed (and small) number of statements, none of which are await statements. The first fast algorithm for mutual exclusion was given by Lamport in [40], and this paper initiated extensive research into algorithms that are efficient under various assumptions about the characteristics of a system, such as the amount of contention and the behavior of the system under errors. Here we will describe and prove Lamport’s algorithm restricted to two processes and then note the changes needed for an arbitrary number of processes.
Here is the outline of the algorithm, where we assume that the process identifiers p and q are encoded as nonzero integer constants so that their values can be assigned to variables and compared with the values of these variables:
Table 5.4. Fast algorithm for two processes (outline)
| ||
|
| |
loop forever
non-critical section
p1: gate1 ← p
p2: if gate2 ≠ 0 goto p1
p3: gate2 ← p
p4: if gate1 ≠ p
p5: if gate2 ≠ p goto p1
critical section
p6: gate2 ← 0 |
loop forever
non-critical section
q1: gate1 ← q
q2: if gate2 ≠ 0 goto q1
q3: gate2 ← q
q4: if gate1 ≠ q
q5: if gate2 ≠ q goto q1
critical section
q6: gate2 ← 0 | |
(To simplify the proof of correctness, we have given an abbreviated algorithm as was done in the previous chapters.)
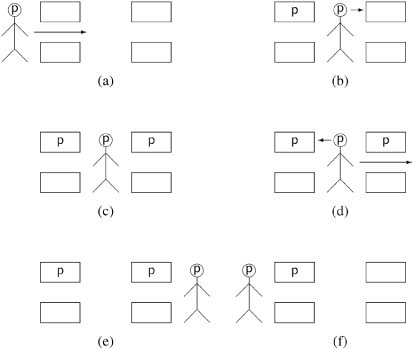
The concept of the algorithm is displayed graphically in Figures 5.1–5.3. A process is represented by a stick figure. The non-critical section is at the left of each diagram; a process must pass through two gates to reach the critical section on the right side of the diagram. Figure 5.1 shows what happens in the absence of contention. The process enters the first gate, writing its ID number on the gate [p1, (a)]. (The notation correlates the line number p1 in the algorithm with diagram (a) in the figure.) It then looks at the second gate [p2, (b)]; in the absence of contention, this gate will not have an ID written upon it, so the process writes its ID on that gate also [p3, (c)]. It then looks back over its shoulder at the first gate to check if its ID is still written there [p4, (d)]. If so, it enters the critical section [p6, (e)]. Upon leaving the critical section and returning to the non-critical section, it erases its ID from the second gate [p6, (f)].
In the absence of contention, the algorithm is very efficient, because a process can access its critical section at the cost of three statements that assign a constant to a global variable (p1, p3, p6), and two if statements that check that the value of a global variable is not equal to a constant (p2, p4).
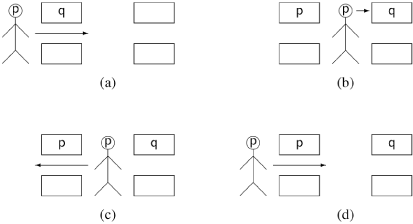
The case of contention at the second gate is shown in Figure 5.2. The process enters the first gate [p1, (a)], but when it checks the second gate [p2, (b)], it sees that the other process q has already written its ID, preparing to enter the critical section. Since q has gotten through both gates sooner, process p returns to before the first gate [p2, (c)] to try again [p1, (d)].
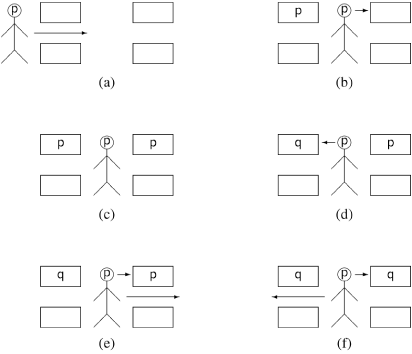
In the case of contention at the first gate, the algorithm is a bit more complex (Figure 5.3). Initially, the algorithm proceeds as before [p1, (a)], [p2, (b)], [p3, (c)], until looking back over its shoulder, process p perceives that process q has entered the first gate and written its ID [p4, (d)]. There are now two possibilities:
the ID of process p is still written on the second gate; if so, it continues into the critical section [p5, (e)]. Or, process q has passed process p and written its ID on the second gate; if so, the new process defers and returns to the first gate [p5, (f)].
The outline of the algorithm is not correct; in the exercises you are asked to find a scenario in which mutual exclusion is not satisfied. We will now partially prove the outline of the algorithm and then modify the algorithm to ensure correctness.
To save turning pages, here is the algorithm again:
Table 5.5. Fast algorithm for two processes (outline)
| ||
|
| |
loop forever
non-critical section
p1: gate1 ← p
p2: if gate2 ≠ 0 goto p1
p3: gate2 ← p
p4: if gate1 ≠ p
p5: if gate2 ≠ p goto p1
critical section
p6: gate2 ← 0 |
loop forever
non-critical section
q1: gate1 ← q
q2: if gate2 ≠ 0 goto q1
q3: gate2 ← q
q4: if gate1 ≠ q
q5: if gate2 ≠ q goto q1
critical section
q6: gate2 ← 0 | |
We assume the truth of this lemma and use it to prove the following lemma:
Example 5.5. Lemma
The following formulas are invariant:
Mutual exclusion follows immediately from invariants (5.4) and (5.6).
Proof: By symmetry of the algorithm, it is sufficient to prove that (5.3) and (5.4) are invariant. Trivially, both formulas are true initially.
Proof of 5.3: Executing p3 makes p4, the first conjunct of the antecedent, true, but it also makes gate2 = p, so the consequent is true. Executing statement p1 makes the second conjunct of the antecedent gate1 = p true, but p4, the first conjunct, remains false. Executing q6 while process p is at p4 can make the consequent false, but by the inductive hypothesis, (5.6) is true, so p3 ∨ p4 → gate1 ≠ p, and therefore the antecedent remains false.
Proof of 5.4: There are two transitions that can make the antecedent p6 true—executing p4 or p5 when the conditions are false:
p4 to p6: By the if statement, gate1 ≠ p is false, so gate1 = p is true; therefore, by the inductive hypothesis for (5.3), gate2 ≠ 0, proving the truth of the first conjunct of the consequent. Since gate1 = p is true, gate1 ≠ q, so the third conjunct is true. It remains to show ¬ q6. Suppose to the contrary that q6 is true. By the inductive hypothesis for (5.6), if both q6 and p4 are true, then so is gate1 ≠ p, contradicting gate1 = p.
p5 to p6: By the if statement, gate2 = p, so gate2 ≠ 0, proving the truth of the first conjunct. By the assumed invariance of (5.1), ¬(q3 ∨ q4 ∨ q6), so ¬ q6, which is the second conjunct, is true, as is the third conjunct since its antecedent is false.
Assume now that the antecedent is true; there are five transitions of process q that can possibly make the consequent false:
q6: This statement cannot be executed since ¬ q6 by the inductive hypothesis.
q4 to q6 : This statement cannot be executed because q3 ∨ q4 → gate1 ≠ q by the inductive hypothesis.
q5 to q6: This statement cannot be executed. It can only be executed if gate2 ≠ q is false, that is, if gate2 = q. By the assumed invariance of (5.2) this can be true only if ¬(p3 ∨ p4 ∨ p6), but ¬ p6 contradicts the truth of the antecedent p6.
q1: This can falsify gate1 ≠ q, but trivially, q3 ∨ q4 will also be false.
q2 to q3: This can falsify the third conjunct if gate1 ≠ q is false. But the statement will be executed only if gate2 = 0, contradicting the inductive hypothesis of the first conjunct.
Lemma 5.4 is not true for Algorithm 5.5. The algorithm must be modified so that (5.1) and (5.2) are invariant without invalidating the invariants we have already proved. This is done by adding local variables wantp and wantq with the usual meaning of wanting to enter the critical section (Algorithm 5.6). Clearly, these additions do not invalidate the proof of Lemma 5.5 because the additional variables are not referenced in the proof, and because await statements can affect the liveness of the algorithm, but not the truth of the invariants.
Table 5.6. Fast algorithm for two processes
integer gate1 ← 0, gate2 ← 0 boolean wantp ← false, wantq ← false | ||
|
| |
loop forever
non-critical section
p1: gate1 ← p
wantp ← true
p2: if gate2 ≠ 0
wantp ← false
goto p1
p3: gate2 ← p
p4: if gate1 ≠ p
wantp ← false
await wantq = false
p5: if gate2 ≠ p goto p1
else wantp ← true
critical section
p6: gate2 ← 0
wantp ← false |
loop forever
non-critical section
q1: gate1 ← q
wantq ← true
q2: if gate2 ≠ 0
wantq ← false
goto q1
q3: gate2 ← q
q4: if gate1 ≠ q
wantq ← false
await wantp = false
q5: if gate2 ≠ q goto q1
else wantq ← true
critical section
q6: gate2 ← 0
wantq ← false | |
Let use now prove that 5.1 is invariant in Algorithm 5.6.
Example 5.6. Lemma
p5 ∧ gate2 = p → ¬(q3 ∨ q4 ∨ q6) is invariant.
Proof: Suppose that the antecedent is true; then gate2 = p prevents the execution of both q2 to q3 and q5 to q6, so the consequent cannot be falsified.
Suppose now that the consequent is false; can the antecedent become true? The conjunct gate2 = p in the antecedent cannot become true, because gate2 is not assigned the value p when executing p4 (making p5 true) nor by any statement in process q.
Consider now executing p4 to p5 to make p5 true. By assumption, the consequent ¬(q3 ∨ q4 ∨ q6) is false, so the control pointer of process q is at q3 or q4 or q6. It follows trivially from the structure of the program that wantq ↔ (q2 ∨ q3 ∨ q4 ∨ q6) is invariant. Therefore, await wantq = false will not allow the control pointer of process p to reach p5.
To generalize Algorithm 5.6 to an arbitrary number of processes, use an array of boolean variables want so that each process writes to its own variable. Replace the statement await wantq = false by a loop that waits in turn for each want variable to become false, meaning that that process has left its critical section:
for all other processes j
await want[j] = falseThe N-process algorithm is still a fast algorithm, because in the absence of contention it executes a fixed number of statements, none of which is an await-statement. Only if there is contention will the loop of await statements be executed. This algorithm does not prevent starvation of an individual process (though there are other algorithms that do satisfy this requirement). However, since starvation scenarios typically involve a high rate of contention, if (as assumed) little contention occurs, a process will not be indefinitely starved.
A complete verification of the bakery algorithm cannot be done in Spin because the ticket numbers are unbounded, so either variables will overflow or the number of states will overflow the memory allocated to Spin. The depth of search can be increased to some large value (say, pan-m1000); then, you can claim that if mutual exclusion is satisfied to that depth, there is unlikely to be a counterexample.
This chapter has presented advanced algorithms for the critical section problem that improve on earlier algorithms in two areas. First, algorithms have been developed for models that are weaker than atomic load and store to global memory. While this model is adequate to describe multitasking on a single CPU, the required level of atomicity cannot be guaranteed for multiprocessor architectures. Second, early algorithms for solving the critical section problem required that a process wishing to enter its critical section interrogate every other process. This can be highly inefficient if the number of processes is large, and newer algorithms can reduce this inefficiency under certain assumptions.
In most systems, higher-level synchronization constructs are used to simplify the development of concurrent programs. The next chapter introduces the semaphore, the first such construct.
1. | The correctness proof of the two-process bakery algorithm (Algorithm 5.1) assumed that the assignment statements | |||||
2. | Show that Algorithm 5.1 as modified in the previous exercise is correct if the statement | |||||
3. | Construct a scenario for the bakery algorithm showing that the ticket numbers can be unbounded. | |||||
4. | (Fisher, cited in [40]) Show that the following algorithm solves the critical section problem for n processes provided that | |||||
5. | Show that mutual exclusion does not hold for Algorithm 5.4. | |||||
6. | Show that Algorithm 5.6 is free from deadlock. | |||||
7. | Construct a scenario that leads to starvation in Algorithm 5.6. | |||||
8. | (Lamport [39]) Show that mutual exclusion and freedom from deadlock hold for the following algorithm: Table 5.8. Lamport’s one-bit algorithm
Show that starvation is possible. Prove that mutual exclusion is satisfied even if a process | |||||
9. | (Manna and Pnueli [51, p. 232]) Show that mutual exclusion and freedom from deadlock (but not starvation) hold for the following algorithm with a server process and n client processes: Table 5.9. Manna–Pnueli central server algorithm
|