14. Mathematics
This chapter describes modules for performing various kinds of mathematical operations. In addition, the decimal module, which provides generalized support for decimal floating-point numbers, is described.
decimal
The Python float data type is represented using a double-precision binary floating-point encoding (usually as defined by the IEEE 754 standard). A subtle consequence of this encoding is that decimal values such as 0.1 can’t be represented exactly. Instead, the closest value is 0.10000000000000001. This inexactness carries over to calculations involving floating-point numbers and can sometimes lead to unexpected results (for example, 3*0.1 == 0.3 evaluates as False).
The decimal module provides an implementation of the IBM General Decimal Arithmetic Standard, which allows for the exact representation of decimals. It also gives precise control over mathematical precision, significant digits, and rounding behavior. These features can be useful if interacting with external systems that precisely define properties of decimal numbers. For example, if writing Python programs that must interact with business applications.
The decimal module defines two basic data types: a Decimal type that represents a decimal number and a Context type that represents various parameters concerning computation such as precision and round-off error-handling. Here are a few simple examples that illustrate the basics of how the module works:

Decimal Objects
Decimal numbers are represented by the following class:
Decimal([value [, context]])
value is the value of the number specified as either an integer, a string containing a decimal value such as '4.5', or a tuple (sign, digits, exponent). If a tuple is supplied, sign is 0 for positive, 1 for negative; digits is a tuple of digits specified as integers; and exponent is an integer exponent. The special strings 'Infinity', '-Infinity', 'NaN', and 'sNaN' may be used to specify positive and negative infinity as well as Not a Number (NaN). 'sNaN' is a variant of NaN that results in an exception if it is ever subsequently used in a calculation. An ordinary float object may not be used as the initial value because that value may not be exact (which defeats the purpose of using decimal in the first place). The context parameter is a Context object, which is described later. If supplied, context determines what happens if the initial value is not a valid number—raising an exception or returning a decimal with the value NaN.
The following examples show how to create various decimal numbers:

Decimal objects are immutable and have all the usual numeric properties of the built-in int and float types. They can also be used as dictionary keys, placed in sets, sorted, and so forth. For the most part, you manipulate Decimal objects using the standard Python math operators. However, the methods in the following list can be used to carry out several common mathematical operations. All operations take an optional context parameter that controls the behavior of precision, rounding, and other aspects of the calculation. If omitted, the current context is used.

Context Objects
Various properties of decimal numbers, such as rounding and precision, are controlled through the use of a Context object:
This creates a new decimal context. The parameters should be specified using keyword arguments with the names shown. prec is an integer that sets the number of digits of precision for arithmetic operations, rounding determines the rounding behavior, and traps is a list of signals that produce a Python exception when certain events occur during computation (such as division by zero). flags is a list of signals that indicate the initial state of the context (such as overflow). Normally, flags is not specified. Emin and Emax are integers representing the minimum and maximum range for exponents, respectively. capitals is a boolean flag that indicates whether to use 'E' or 'e' for exponents. The default is 1 ('E').
Normally, new Context objects aren’t created directly. Instead, the function getcontext() or localcontext() is used to return the currently active Context object. That object is then modified as needed. Examples of this appear later in this section. However, in order to better understand those examples, it is necessary to explain these context parameters in further detail.
Rounding behavior is determined by setting the rounding parameter to one of the following values:

The traps and flags parameters of Context() are lists of signals. A signal represents a type of arithmetic exception that may occur during computation. Unless listed in traps, signals are ignored. Otherwise, an exception is raised. The following signals are defined:
These signal names correspond to Python exceptions that can be used for error checking. Here’s an example:

Like exceptions, the signals are organized into a hierarchy:

The Overflow and Underflow signals appear more than once in the table because those signals also result in the parent signal (for example, an Underflow also signals Subnormal). The decimal.DivisionByZero signal also derives from the built-in DivisionByZero exception.
In many cases, arithmetic signals are silently ignored. For instance, a computation may produce a round-off error but generate no exception. In this case, the signal names can be used to check a set of sticky flags that indicate computation state. Here’s an example:

When flags get set, they stay set until they are cleared using the clear_flags() method. Thus, one could perform an entire sequence of calculations and only check for errors at the end.
The settings on an existing Context object c can be changed through the following attributes and methods:
c.capitals
Flag set to 1 or 0 that determines whether to use E or e as the exponent character.
c.Emax
Integer specifying maximum exponent.
c.Emin
Integer specifying minimum exponent.
c.prec
Integer specifying digits of precision.
c.flags
Dictionary containing current flag values corresponding to signals. For example, c.flags[Rounded] returns the current flag value for the Rounded signal.
c.rounding
Rounding rule in effect. An example is ROUND_HALF_EVEN.
c.traps
Dictionary containing True/False settings for the signals that result in Python exceptions. For example, c.traps[DivisionByZero] is usually True, whereas c.traps[Rounded] is False.
c.clear_flags()
Resets all sticky flags (clears c.flags).
c.copy()
Returns a copy of context c.
c.create_decimal(value)
Creates a new Decimal object using c as the context. This may be useful in generating numbers whose precision and rounding behavior override that of the default context.
Functions and Constants
The following functions and constants are defined by the decimal module.
getcontext()
Returns the current decimal context. Each thread has its own decimal context so this returns the context of the calling thread.
Creates a context manager that sets the current decimal context to a copy of c for statements defined inside the body of a with statement. If c is omitted, a copy of the current context is created. Here is an example of using this function that temporarily sets the precision to five decimal places for a series of statements:
![]()
setcontext(c)
Sets the decimal context of the calling thread to c.
BasicContext
A premade context with nine digits of precision. Rounding is ROUND_HALF_UP; Emin is -999999999; Emax is 999999999; and all traps are enabled except for Inexact, Rounded, and Subnormal.
DefaultContext
The default context used when creating new contexts (the values stored here are used as default values for the new context). Defines 28 digits of precision; ROUND_HALF_EVEN rounding; and traps for Overflow, InvalidOperation, and DivisionByZero.
ExtendedContext
A premade context with nine digits of precision. Rounding is ROUND_HALF_EVEN, Emin is -999999999, Emax is 999999999, and all traps are disabled. Never raises exceptions. Instead, results may be set to NaN or Infinity.
Inf
The same as Decimal("Infinity").
negInf
The same as Decimal("-Infinity").
NaN
The same as Decimal("NaN").
Examples
Here are some more examples showing basic usage of decimal numbers:
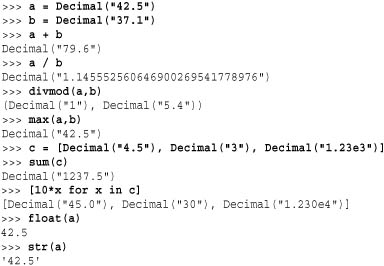
Here’s an example of changing parameters in the context:

Notes
• The Decimal and Context objects have a large number of methods related to low-level details concerning the representation and behavior of decimal operations. These have not been documented here because they are not essential for the basic use of this module. However, you should consult the online documentation at http://docs.python.org/library/decimal.html for more information.
• The decimal context is unique to each thread. Changes to the context only affect that thread and not others.
• A special number, Decimal("sNaN"), may be used as a signaled-NaN. This number is never generated by any of the built-in functions. However, if it appears in a computation, an error is always signaled. You can use this to indicate invalid computations that must result in an error and must not be silently ignored. For example, a function could return sNaN as a result.
• The value of 0 may be positive or negative (that is, Decimal(0) and Decimal ("-0")). The distinct zeros still compare as equals.
• This module is probably unsuitable for high-performance scientific computing due to the significant amount of overhead involved in calculations. Also, there is often little practical benefit in using decimal floating point over binary floating point in such applications.
• A full mathematical discussion of floating-point representation and error analysis is beyond the scope of this book. Readers should consult a book on numerical analysis for further details. The article “What Every Computer Scientist Should Know About Floating-Point Arithmetic” by David Goldberg, in Computing Surveys, Association for Computing Machinery, March 1991 is also a worthy read (this article is easy to find on the Internet if you simply search for the title).
• The IBM General Decimal Arithmetic Specification contains more information and can be easily located online through search engines.
fractions
The fractions module defines a class Fraction that represents a rational number. Instances can be created in three different ways using the class constructor:
Fraction([numerator [,denominator]])
Creates a new rational number. numerator and denominator have integral values and default to 0 and 1, respectively.
Fraction(fraction)
If fraction is an instance of numbers.Rational, creates a new rational number with the same value as fraction.
Fraction(s)
If s is a string containing a fraction such as "3/7" or "-4/7", a fraction with the same value is created. If s is a decimal number such as "1.25", a fraction with that value is created (e.g., Fraction(5,4)).
The following class methods can create Fraction instances from other types of objects:
Fraction.from_float(f)
Creates a fraction representing the exact value of the floating-point number f.
Fraction.from_decimal(d)
Creates a fraction representing the exact value of the Decimal number d.
Here are some examples of using these functions:

An instance f of Fraction supports all of the usual mathematical operations. The numerator and denominator are stored in the f.numerator and f.denominator attributes, respectively. In addition, the following method is defined:
f.limit_denominator([max_denominator])
Returns the fraction that has the closest value to f.max_denominator specifies the largest denominator to use and defaults to 1000000.
Here are some examples of using Fraction instances (using the values created in the earlier example):

The fractions module also defines a single function:
gcd(a, b)
Computes the greatest common divisor of integers a and b. The result has the same sign as b if b is nonzero; otherwise, it’s the same sign as a.
math
The math module defines the following standard mathematical functions. These functions operate on integers and floats but don’t work with complex numbers (a separate module cmath can be used to perform similar operations on complex numbers). The return value of all functions is a float. All trigonometric functions assume the use of radians.

The following constants are defined:

Notes
• The floating-point values +inf, -inf, and nan can be created by passing strings into the float() function—for example, float("inf"), float("-inf"), or float("nan").
• The math.fsum() function is more accurate than the built-in sum() function because it uses a different algorithm that tries to avoid floating-point errors introduced by cancellation effects. For example, consider the sequence s = [1, 1e100, -1e100]. If you use sum(s), you will get a result of 0.0 (because the value of 1 is lost when added to the large value 1e100). However, using math.sum(s) produces the correct result of 1.0. The algorithm used by math.sum() is described in “Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates” by Jonathan Richard Shewchuk, Carnegie Mellon University School of Computer Science Technical Report CMU-CS-96-140, 1996.
numbers
The numbers module defines a series of abstract base classes that serve to organize various kinds of numbers. The numeric classes are organized into a hierarchy in which each level progressively adds more capabilities.
A class that serves as the top of the numeric hierarchy.
Complex
A class that represents the complex numbers. Numbers of this type have real and imag attributes. This class inherits from Number.
Real
A class that represents the real numbers. Inherits from Complex.
Rational
A class that represents fractions. Numbers of this type have numerator and denominator attributes. Inherits from Real.
Integral
A class that represents the integers. Inherits from Rational.
The classes in this module are not meant to be instantiated. Instead, they can be used to perform various kinds of type checks on values. For example:

If one of these type checks returns True, it means that x is compatible with all of the usual mathematical operations associated with that type and that a conversion to one of the built-in types such as complex(), float(), or int() will work.
The abstract base classes can also be used as a base class for user-defined classes that are meant to emulate numbers. Doing this is not only just a good idea for type checking, but it adds extra safety checks that make sure you implement all of the required methods. For example:

Notes
• Refer to Chapter 7 (“Classes and Object-Oriented Programming”) for more information on abstract base classes.
• PEP 3141 (http://www.python.org/dev/peps/pep-3141) has more information about the type hierarchy and intended use of this module.
random
The random module provides a variety of functions for generating pseudo-random numbers as well as functions for randomly generating values according to various distributions on the real numbers. Most of the functions in this module depend on the function random(), which generates uniformly distributed numbers in the range [0.0, 1.0) using the Mersenne Twister generator.
Seeding and Initialization
The following functions are used to control the state of the underlying random number generator:
seed([x])
Initializes the random number generator. If x is omitted or None, the system time is used to seed the generator. Otherwise, if x is an integer or long integer, its value is used. If x is not an integer, it must be a hashable object and the value of hash(x) is used as a seed.
getstate()
Returns an object representing the current state of the generator. This object can later be passed to setstate() to restore the state.
setstate(state)
Restores the state of the random number generator from an object returned by getstate().
jumpahead(n)
Quickly changes the state of the generator to what it would be if random() were called n times in a row. n must be a nonnegative integer.
Random Integers
The following functions are used to manipulate random integers.
getrandbits(k)
Creates a long integer containing k random bits.
randint(a,b)
Returns a random integer, x, in the range a <= x <= b.
randrange(start,stop [,step])
Returns a random integer in range(start,stop,step). Does not include the endpoint.
Random Sequences
The following functions are used to randomize sequence data.
choice(seq)
Returns a random element from the nonempty sequence seq.
Returns a sequence length, len, containing elements chosen randomly from the sequence s. The elements in the resulting sequence are placed in the order in which they were selected.
shuffle(x [,random])
Randomly shuffles the items in the list x in place. random is an optional argument that specifies a random generation function. If supplied, it must be a function that takes no arguments and returns a floating-point number in the range [0.0, 1.0).
Real-Valued Random Distributions
The following functions generate random numbers on real numbers. Distribution and parameter names correspond to the standard names used in probability and statistics. You will need to consult an appropriate text to find out more details.
random()
Returns a random number in the range [0.0, 1.0).
uniform(a,b)
Returns a uniformly distributed random number in the range [a, b).
betavariate(alpha, beta)
Returns a value between 0 and 1 from the Beta distribution. alpha > -1 and beta > -1.
cunifvariate(mean, arc)
Circular uniform distribution. mean is the mean angle, and arc is the range of the distribution, centered around the mean angle. Both of these values must be specified in radians in the range between 0 and pi. Returned values are in the range (mean - arc/2, mean + arc/2).
expovariate(lambd)
Exponential distribution. lambd is 1.0 divided by the desired mean. Returns values in the range [0, +Infinity).
gammavariate(alpha, beta)
Gamma distribution. alpha > -1, beta > 0.
gauss(mu, sigma)
Gaussian distribution with mean mu and standard deviation sigma. Slightly faster than normalvariate().
lognormvariate(mu, sigma)
Log normal distribution. Taking the natural logarithm of this distribution results in a normal distribution with mean mu and standard deviation sigma.
normalvariate(mu, sigma)
Normal distribution with mean mu and standard deviation sigma.
Pareto distribution with shape parameter alpha.
triangular([low [, high [, mode]]])
Triangular distribution. A random number n in the range low <= n < high with mode mode. By default, low is 0, high is 1.0, and mode is set to the midpoint of low and high.
vonmisesvariate(mu, kappa)
von Mises distribution, where mu is the mean angle in radians between 0 and 2 * pi and kappa is a nonnegative concentration factor. If kappa is zero, the distribution reduces to a uniform random angle over the range 0 to 2 * pi.
weibullvariate(alpha, beta)
Weibull distribution with scale parameter alpha and shape parameter beta.
Notes
• The functions in this module are not thread-safe. If you are generating random numbers in different threads, you should use locking to prevent concurrent access.
• The period of the random number generator (before numbers start repeating) is 2**19937–1.
• The random numbers generated by this module are deterministic and should not be used for cryptography.
• New types of random number generators can be created by subclassing random.Random and implementing the random(), seed(), getstate(), getstate(), and jumpahead() methods. All the other functions in this module are actually internally implemented as methods of Random. Thus, they could be accessed as methods of an instance of the new random number generator.
• The module provides two alternative random number generators classes—WichmannHill and SystemRandom—that are used by instantiating the appropriate class and calling the preceding functions as methods. The WichmannHill class implements the Wichmann-Hill generator that was used in earlier Python releases. The SystemRandom class generates random numbers using the system random number generator os.urandom().

