4.1. Introduction

Beginning with the 1950s, a new branch of queueing theory – RQ system – was introduced to the theory and engineering practice. The main peculiarity of such systems consists of the existence of a number of so-called orbits to which a rejected customer is directed so that it can make periodical attempts (retrials) until a time of vacation of the service facility. Well known monographs and surveys on retrial queues include Artalejo and Gomez-Corral (2008); Bocharov et al. (2004); Falin and Templeton (1997); Artalejo (2010) and others. As a disciple and co-author with a distinguished scientist Boris V. Gnedenko, I would like to refer to some relevant works from B.V. Gnedenko’s scientific school: Falin (2008, 2010); Afanasyeva (1984); Afanasyeva and Gnedenko (1985); Anisimov (1999); Anisimov and Artalejo (2001); Anisimov and Kurtulush (2001). Most of these works are connected to applied problems. For instance, L.G. Afanasyeva studied RQ models of aviation flows.

4.2. A contribution by Laszlo Lakatos and his disciples

In 1994, the Hungarian mathematician Laszlo Lakatos, on an order from aviation traffic researcher Vaclav Ceric, introduced a new type of retrial queue (Lakatos 1994), with Markovian input and service time, constant orbit time and moreover FCFS queueing discipline. Applying a suitable embedded Markov chain, Lakatos derived an elegant ergodicity condition of this chain as follows:

where λ is the arrival rate, μ is the service rate and T is a constant orbit time of a customer.

Moreover, Lakatos derived the ergodic distribution of the embedded Markov chain (k_n) denoting a queue size just before the arrival of the nth customer.

For further works by the school of Lakatos, see Lakatos (2002, 2006); Langaris (1999); Kárász and Farcas (2005); Lakatos (2018); Lakatos et al. (2013); Rogiest et al. (2006, 2007).

4.3. A contribution by E.V. Koba

My disciple Elena V. Koba has investigated a number of generalizations of Lakatos-type queueing systems. She studied GI/G/1 retrial FCFS systems with generally distributed orbit times for customers. The stability conditions of such systems were derived. The main point of Koba’s argument consists of the following. Let W_n denote the waiting time of the nth customer. Then, under usual convergence conditions,

where t_n are arrival epochs and Y_n are service times of customers. U_n is an excess of a renewal process controlling orbit intervals. Thus, one can prove that this limit is negative.

In particular, if an orbit time is a non-latticed random variable V_n, then the sequence is stable as soon as

A more general case of Markovian dependence of variables is considered as well (see Koba (2002, 2004)).

4.4. An Erlangian and hyper-Erlangian approximation for a Laszlo Lakatos-type queueing system

In the preceding section, Koba’s results on stability/ergodicity conditions for GI/G/1 RQ systems were outlined. It is interesting to note that in some cases, it is possible to derive elementary analytical equations for such conditions. Indeed, one such example is studied in a paper by Kovalenko (2018).

Consider a GI/G/1 FCFS RQ system with a constant orbit time T. We denote by X an interarrival time and by Y a service time. Assume that they possess complementary distribution functions (d.f.)

and

with probability density functions (p.d.f.)

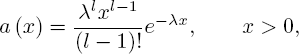
and

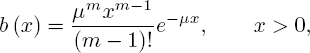
respectively.

Consider non-negative random variables

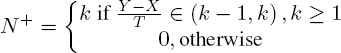
and

Further, consider the difference

Then obviously

It is easily to show that the system is stable iff

E N < 0

We have the equations

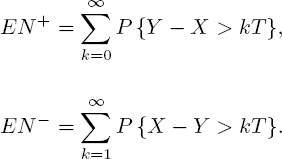
For any x > 0, we get equations

and

Taking into account the equations for cumulative d.f. and p.d.f. of Erlangian laws, one obtains the equations

and

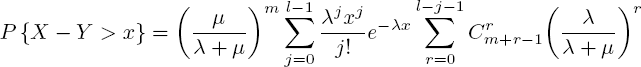
for any x ≥ 0.

To obtain the expressions for E N⁺ and E N⁻, it suffices to sum up these equations in x for x = kT, k ≥ 0 and x = kT, k ≥ 1, respectively.

It should be noted that infinite series like

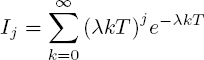
can be computed through a term-wise differentiation of infinite series. Indeed, obviously

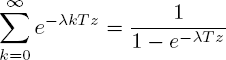
for any non-negative z. The j-fold term-wise differentiation in z leads to the equation

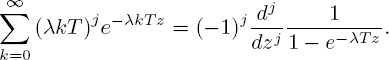
Setting z = 1, one obtains the sum I_j.

Further, we assume that the distributions A (x) and B (x) are hyper-Erlangian. This case can be easily reduced to the above-considered case. Indeed, the p.d.f. a (x) and b (x) are mixtures of some Erlangian p.d.f. e(x∣λ_g,l_g) and e(x∣μ_h,m_h).It is easy to see that this property implies the corresponding property of the functional N.

4.5. Two models with a combined queueing discipline

A Lakatos-type RQ system reflects the peculiarities of some engineering systems (Koba and Pustova 2012). Meanwhile, a negative aspect of such systems is that long intervals between service times are practically lost for the serving process; thus mean waiting time is rather long. So an idea arises naturally as follows: to combine the FCFS principle with the possibility of a partial servicing of some customers within free intervals. One of the possible disciplines leads to the following model.

Each incoming customer gets its service period on its arrival so that it cannot be changed afterwards. We denote by t_n the nth arrival time provided t_n < t_n+1 by Y_n > 0 the associated service time.

For the definiteness, assume that t_n form a recurrent process; t_n – t_n−1 are i.i.d.r.v. with a d.f. A(x) = P{t_n – t_n−1 ≤ x }. Y_n are i.i.d.r.v. with a d.f. B (x) = P {Y_n ≤ x}. Also assume that both t_n – t_n−1 and Y_n are positive almost surely.

In our model, each customer is serviced either immediately on its arrival, if a required time allows this, or, if not, then the customer is directed to the orbit taking the last place in the queue of “orbited” customers. The rule of reserving time for such customers is controlled by a renewal process. This will be explained later. In such cases, the service time of the customer equals Y′_n, where Y′_n = Y_n (model 1) or Y′_nis a newly generated r.v. with the d.f. B (x) (model 2).

Thus, let denote a number of customers who entered before t_n and were not fully serviced before the instant t_n; , where . These quantities will be interpreted in such a way that time intervals being seen from time t_n are complete or residual service times of customers who are not fully served up to time t_n. At last, set . In the same way, , where . Also set . Hereinafter, the lower index n relates to an arrival time, whereas the upper signs “-” and “+” relate to prearrival and postarrival moments, respectively.

The variables are adjusted to the temporary coordinate system with the origin t_n. These symbols mean the variables as relating to time just after the arrival time of the nth customer instead of The dynamics of the servicing process can be described by recurrence equations enabling one to make a transfer from to and from to

Consider the “- to +” case. In any case, .If , then ; , . These equations mean that the nth customer is taken for servicing at time t_n (see Figure 4.1 for example).

If or , then _i, , To finish the definition, we must use a concept from renewal theory. The variables and are assumed to be defined through independent renewal processes (U_nj ,j ≥ 0) for which U_n0 = 0; U_nj − U_n,_j−1 are positive i.i.d.r.v. with a d.f. C (x)=P {U_nj − U_n,j−1 ≤ x}, n ≥ 1. Assume that is defined. Then .

One can observe that in the case that a customer cannot be served from the very beginning, then this customer is directed to the end of the queue. Obviously, in the model introduced by Laszlo Lakatos, all the customers follow the FCFS queueing discipline.

At last, consider the to transfer. if If , then .If , for some , then ^.

If for some , then .

See also a paper by Koba (2017) for a special queueing retrial discipline on the Markov level. The paper considers the RQ system M/M/1/0 with combined discipline of service, namely, a customer from the orbit is served in its turn, but in case of a free channel an arrival from the original flow is serviced immediately. The author obtained the expressions for state probabilities as well as the ergodicity conditions. The system is compared with the Lakatos type system (see also Kovalenko (2015)).