When you get a high correlation between two continuous variables, you might want to express the relation between them in a functional way; that is, one variable as a function of the other one. The linear function between two variables is a line determined by its slope and its intercept. Here is the formula for the linear function:

 

You can imagine that the two variables you are analyzing form a two-dimensional plane. Their values define coordinates of the points in the plane. You are searching for a line that fits all the points best. Actually, it means that you want the points to fall as close to the line as possible. You need the deviations from the line—that is, the difference between the actual value for the Y_i and the line value Y'. If you use simple deviations, some are going to be positive and others negative, so the sum of all deviations is going to be zero for the best-fit line. A simple sum of deviations, therefore, is not a good measure. You can square the deviations, like they are squared to calculate the mean squared deviation. To find the best-fit line, you have to find the minimal possible sum of squared deviations. Here are the formulas for the slope and the intercept:

  

 

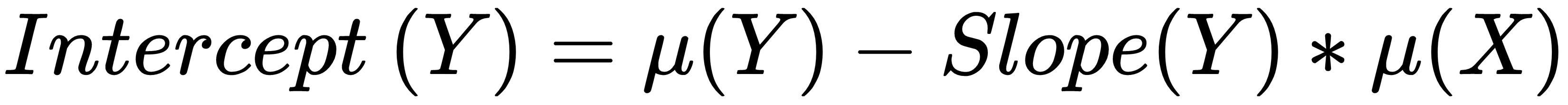
Linear regression can be more complex. In a multiple linear regression, you use multiple independent variables in a formula. You can also try to express the association with a polynomial regression model, where the independent variable is introduced in the equation as an n^th order polynomial.

The following code creates another data frame as a subset of the original data frame, this time keeping only the first 100 rows. The sole purpose of this action is the visualization at the end of this section, where you will see every single point in the graph. The code also removes the TM data frame from the search path and adds the new TMLM data frame to it:

TMLM <- TM[1:100, c("YearlyIncome", "Age")]; 
detach(TM); 
attach(TMLM); 

The following code uses the lm() function to create a simple linear regression model, where YearlyIncome is modeled as a linear function of Age:

LinReg1 <- lm(YearlyIncome ~ Age); 
summary(LinReg1); 

If you check the summary results for the model, you can see that there is some association between the two variables; however, the association is not that strong. You can try to express the association with polynomial regression, including squared Age in the formula:

LinReg2 <- lm(YearlyIncome ~ Age + I(Age ^ 2)); 
summary(LinReg2); 

If you plot the values for the two variables in a graph, you can see that there is a non-linear dependency between them. The following code plots the cases as points in the plane, and then adds a linear and a lowess line to the graph. A lowess line calculation is more complex; it is used here to represent the polynomial relationship between two variables:

plot(Age, YearlyIncome,  
     cex = 2, col = "orange", lwd = 2); 
abline(LinReg1, 
       col = "red", lwd = 2); 
lines(lowess(Age, YearlyIncome), 
      col = "blue", lwd = 2); 

The following screenshot shows the results:

You can see that the polynomial line (the curve) fits the data slightly better. The polynomial model is also more logical: you earn less when you are young, then you earn more and more, until at some age your income goes down again, probably after you retire. Finally, you can remove the TMLM data frame from the search path:

detach(TMLM);