In this chapter, we discuss the design of the test oracle, that is, the agent whose task is to observe executions of the candidate program on sample test data and to rule on whether the program does or does not behave according to its specification. We review, in turn, the tradeoffs that arise in oracle design, how to design an oracle from a relational specification, and how to design an oracle for a state-based software product.

11.1 DILEMMAS OF ORACLE DESIGN

All the test data in the world do not help us unless we have an oracle, a correct oracle, to reliably check whether the candidate program behaves according to its specification. The choice of an oracle is both critical and difficult.

• It is critical to have a reliable oracle because otherwise we run the risk of overlooking faults (if failures are not detected) and the risk of acting on faulty diagnoses (if correct behavior is reported to be incorrect).
• It is difficult and error prone to monitor the behavior of a program by having a human operator watch its inputs and outputs; but developing automated oracles poses challenges of its own, which we discuss in this section.

The general framework in which an oracle is invoked can be written as follows (where g is the program under test and S is the space of the program):

main ()
      {s = testdata;  s_init=s;
      g;   //  modifies s, keeps s_init intact
      assert(oracle(s_init,s));}

The design of the oracle is subject to the following criteria:

• Simplicity. The oracle must be simple enough that we can ensure its reliability with a great degree of confidence. In particular, it must be significantly simpler to write and analyze than candidate programs. If the oracle is as complex as the program being tested, then it is as likely to have faults as the candidate program; this, in turn, defeats the purpose of using the oracle to test the program.
• Strength. Ideally, we want the oracle to capture all the clauses of the requirements specification, so as to test all the relevant functional properties of the program. But this may prove too complex (hence violating the first criterion), too inefficient (in terms of resource usage), or too impractical (requiring a great deal of context, for example). Hence we may often have to settle for capturing a subset of the target requirements.

The criteria of strength and simplicity must be balanced against each other to reach a tradeoff where we derive an oracle that is sufficiently strong to be useful, yet sufficiently simple to be reliable. This tradeoff is very easy when it is easier to check that a final state is correct than to compute a correct final state. Consider for example a program that computes the roots of a quadratic equation: The space of this program is defined by real variables a, b, c that represent the coefficients of the quadratic equation, and real variables x1and x2 that hold the roots. A specification of the quadratic equation may be written as follows:

This specification provides that the quadratic equation is assumed to have two distinct roots, and that candidate programs are expected to produce the smaller root in x1 ′ and the larger root in x2 ′. To account for possible loss of precision in computer arithmetic, predicates positive and root are defined with respect to selected precision thresholds; for example,

for some small positive constant, ε. Whereas the program computes the roots of the quadratic equation constructively, the oracle merely checks that the computed values are indeed roots of the equation, and that they are distinct (hence the program is returning all the roots, rather than twice the same root). We can think of many other examples where computing a result is significantly more complex than checking that a computed result is correct:

• Consider the problem of computing the roots of a polynomial of higher degree, or the roots of a functional that has no polynomial form altogether, where no constructive solutions are known: candidate programs may compute the roots by some iterative method of successive approximations; yet all the oracle has to do is simply to check that the delivered values are indeed roots to the equation.
• Solving a large system of linear equations may be a complex affair (e.g., Gaussian elimination), where we have to worry not only about the correctness of the algorithm, but also about controlling round-off errors; yet checking that the solution is correct amounts to little more than multiplying a matrix by a vector.
• Computing the inverse of a matrix involves complex calculations (e.g., N systems of linear equations), which are made all the more complex by the need to control round off errors; yet checking that the solution is correct amounts to little more than computing the product of two matrices.
• Computing the eigenvalues and eigenvectors of a matrix involves solving polynomials of degree N, followed by solving systems of N linear equations, where again the control of runaway round-off errors is a major concern; yet checking that the solution is correct amounts to little more than multiplying a matrix by a vector.

In all these cases, it is possible to test a complex program using a simple, reliable oracle. There are ample cases, however, where checking that a final program state is correct is not much easier than generating a correct final state; in such cases, we may have to settle for generating an oracle that tests only some aspects of the target requirements specification, deferring the other aspects to other verification/quality assurance methods. As a simple illustrative example, consider the specification of a gcd program on natural variables x and y. The specification can be written as:

If we are given the initial values of variable x and y, and the final value x ′ of variable x, we have no easy way to tell whether x ′ is the gcd of x and y, except possibly to compute the gcd of x and y independently and compare it with x ′. But doing so defeats the purpose of the oracle because it violates the requirement of simplicity: if the oracle is as complex as the program we are testing, we have no reason to trust the correctness of the oracle more than the correctness of the candidate program. As a substitute, we may want to settle for checking that x ′ is a common divisor of x and y, and renounce checking that it is the greatest common divisor. The specification that corresponds to such a scaled-down oracle can then be written as:

11.2 FROM SPECIFICATIONS TO ORACLES

Let g be a program on space S and let R be the specification against which we are testing g; as we discussed in the previous section, the general format for testing program g looks as follows:

main ()
      {s = testdata;  s_init=s;
      g;   //  modifies s, keeps s_init intact
      assert(oracle(s_init,s));}

The question we wish to address in this section is: How do we derive the oracle from specification R? A naïve solution would be to simply let oracle(s_init,s) be defined as: . As we will see in the following example, this is not a valid choice. We consider the following specification on space S defined by natural variables x and y (where we want to compute the greatest common divisor of integers greater than 10):

and we consider the following program:

    //  gcd program
    void   gcd() {while (x!=y) {if (x>y) {x=x-y;} else {y=y-x;}};}

Because of the difficulties we have alluded to above, we resolve to test this program against a simpler specification than R, which checks that the final value of x is a common divisor of the original values of x and y, but not the greatest common divisor; this yields the following relation,

Let us consider the following program, whose goal is to check the correctness of program gcd against specification R ′ for the input data .

#include <iostream>
using namespace std;
int x, y, x_init; y_init;  void gcd();
int main () {x=0; y=0;  x_init=x; y_init=y;
      gcd();   //  modifies  x  and  y, keeps  x_init and  y_init  intact
      if (!(x_init>0 && y_init>0 &&  x_init%x==0 && x_init%y==0))
            {cout << “test failure”;}
      else {cout << “test success”;}}

When we run this program on test data , it prints “test failure,” which appears to suggest that the program is incorrect, when in fact this program is correct. The reason for this inconsistency is that the specification includes clauses on the initial state and clauses on the final state, which have different interpretations:

• Clauses on the initial state represent the conditions that candidate programs may assume to hold prior to their call, whereas
• Clauses on the final state represent the conditions that candidate programs are expected to ensure upon their execution.

An oracle ought to treat these two conditions separately:

1. If the condition on the initial state does not hold, then the program is off the hook: since its assumption does not hold, whatever it does must be considered correct.
2. The output condition of the specification is checked only if the input condition holds.

Hence the following proposition:

In Programming terms, we can write the generic form of the oracle as follows:

   bool oracle (s_init, s)
     {return (!(domR(s_init)) || R(s_init,s));}

As an example, we consider again the gcd program, and we rewrite it as follows:

#include <iostream>//   1
using namespace std;//   2
int x, y, x_init, y_init;  void gcd ();//   3
bool oracle (int x_init, int y_init, int x, int y);//   4
bool domR(int x_init, int y_init);//   5
bool R(int x_init, int y_init, int x, int y);//   6
int main () {x=355; y=215; x_init=x; y_init=y;//   7
   gcd();  // changes x, y, keeps x_init and y_init//   8
   if (oracle(x_init,y_init,x,y)) //   9
      {cout << “test success” << endl;}//  10
   else {cout << “test failure” << endl;}   }//  11
void gcd()
     {while (x!=y) {if (x>y) {x=x-y;} else {y=y-x;}};}//  12
bool oracle(int x_init, int y_init, int x, int y)//  13
   {return (!(domR(x_init,y_init)) || R(x_init,y_init,x,y));}//  14
bool domR(int x_init, int y_init)
   {return (x_init>10 && y_init>10);}//  15
bool R(int x_init, int y_init, int x, int y)//  16
   {return (x_init>10 && y_init>10 && x_init%x==0);}//  17

The code of method ‘bool oracle’ can be used as a general template for oracles (modulo differences in the state space): for any specification R, we must define Boolean functions domR() and R() with the appropriate parameters and let function oracle use them according to the formula of the proposition above.

As a second example, we consider the specification of the quadratic equation, which we define on space S represented by variables a, b, c (coefficients of the equation) and variables x1 and x2 (roots of the equation):

From this definition, we infer the domain of this relation as:

Hence the oracle can be written as:

bool oracle
  (float a_init, float b_init, float c_init, float x1_init, float x2_init, float a, float b, float c, float x1, float x2)
   {return (!(domR(a_init,b_init, c_init, x1_init,   x2_init)) ||
   R(a_init, b_init, c_init, x1_init, x2_init, a, b, c,  x1, x2));}

Where predicates domR and R are defined as follows:

bool domR
(float a_init, float b_init, float c_init, float x1_init,   float x2_init)
   {return (positive(b_init*b_init-4*a_init*c_init));}
bool R(float a_init,float b_init, float c_init,
    float x1_init, float x2_init,
    float a, float b, float c, float x1, float x2)
  {return      (positive(b_init*b_init-4*a_init*c_init)&&root(x1)&&root(x2) && positive(x2-x1));}
bool positive(float x) {return (x>epsilon);}
bool root(float x)
   {return (abs(a_init*x*x+b_init*x+c) <epsilon);}

The following segment shows how this code is called to run the quadratic equation program and test its operation:

int main ()
   {a=1; b=8; c=9; x1=0; x2=0; 
     a_init=a; b_init=b; c_init=c; x1_init=x1; x2_init=x2; //saving init state
   quadratic();  // changes current state, keeps initial state
   if (oracle(a_init, b_init, c_init, x1_init, x2_init, a, b, c, x1, x2))
     {cout << “test success” << endl;}
   else {cout << “test failure” << endl;}}

where function quadratic is defined as follows:

void quadratic() 
   {float delta; delta = b*b-4*a*c; delta=sqrt(delta); 
   x1=(-b-delta)/2.*a; x2=(-b+delta)/2.*a;}

We have seen in Chapter 7 that the specification against which we test a software product depends to a great extent on the goal of the test; in particular, if our goal is to find (and remove) the maximum number of faults, then it is important to use the most refined (strongest) specification possible, namely one that capture every functional detail of the program as written. Hence, for the quadratic equation program, for example, the specification that captures all the functional detail would look like:

Also, for the gcd program, the specification that captures all the functional detail would look like:

As a tradeoff between simplicity and strength, we can use the following specification as a substitute for R:

This relation provides that x ′ is a common divisor of x and y, and that y ′ is equal to x ′; but it does not provide that x ′ is the greatest common divisor of x and y; to ensure this latter property, we can write the following Boolean function:

bool greatest(int x_init, int y_init, int x)
   {// no number greater than x is a divisor of x_init and y_init;
     int min;
       if (x_init<y_init) {min=x_init;} else {min=y_init;};
    bool isgreatest;  isgreatest=true;
    for (int i=x+1; i<=min; i++) 
         {isgreatest = isgreatest && !(x_init%i==0 && y_init%i==0);};
    return isgreatest;}

11.3 ORACLES FOR STATE-BASED PRODUCTS

In the previous section, we have discussed how to choose a specification against which we test a program and then how to derive a test oracle from a specification. In particular, we have focused our attention on two possible specifications:

• A specification that is appropriate for acceptance testing, which is the weakest specification that a user is willing to accept as a criterion for considering that the contract (between the software provider and the software user) is fulfilled.
• A specification that is appropriate for fault removal, which is the strongest possible specification that the candidate program must fulfill, reflecting the intent of the programmer and the minute details of the program.

In this section, we consider software products that are based on an internal state. As we have seen in Chapter 4, such products can be specified by means of relations from input histories to outputs. The main advantage of this specification model is that it absolves us from talking about system states, leaving this matter as a design decision rather than a specification decision.

We consider a specification of the form (X, Y, R), where R is a relation from to Y and we let g be a candidate implementation of the specification, in the form of a class (in the object oriented programming (OOP) sense). If we are interested in testing class g for the purpose of fault removal, then we can specify each of its methods in terms of how it affects the system state and how it generates outputs accordingly. Each individual method can be viewed as a simple software component mapping an initial state into a final state; testing such components falls under the model we discussed in the previous section. Hence we focus our attention in this section on testing a state-based system against a specification of the form (X, Y, R), where R is a relation from to Y. We assume that such specifications are represented by means of axioms and rules, as we discuss in Chapter 4. The question then becomes: how do we test a candidate implementation against such a specification? More specifically, how do we map such an axiomatic specification into an oracle? In the following section we discuss, in turn, how we generate oracles from axioms and how we generate oracles from rules. In the discussions that follow, we assume that implementation g is a class that has a method for each symbol in X; for the sake of simplicity, we assume that each method has the same name as the corresponding symbol; we postfix method names with parentheses, even when they have no parameters.

vtype y;  y=y0;  //  y0:  output specified by the axiom
g.m1();  g.m2();  g.m3(); … g.mk(); // sequence h’
if (g.vop==y) {successfultest;} else {unsuccessfultest;}

bool y;  y=false; //  data type returned by empty
g.init(); g.push(a); // sequence h’, arbitrary a
if (g.empty==y) {successfultest;} else {unsuccessfultest;}

11.3.2 From Rules to Oracles

The vast majority of rules in axiomatic specifications has the form of an equality between the images of two histories and expresses the property that two histories are equivalent for all subsequent input sequences. Typically the two histories are ordered (one is more complex than the other) and such rules can be used to infer the output of the complex history from the output of the simpler history. We focus on such rules first and then we consider other forms of rules.

Such rules can be written in generic form as:

and can be interpreted as follows: for any input sequence h, the input sequence h ′. h yields the same outcome as the input sequence h ′′. h; in other words, the histories h ′ and h ′′ are equivalent now (if h is empty) and at any time in the future (if h is not empty). Examples of such rules, in the stack specification given in Chapter 4, include the following:

• stack(h′.init.h) = stack(init.h).
• stack(init.pop.h) = stack(init.h).
• stack(init.h.push(a).pop.h+) = stack(init.h.h+).
• stack(init.h.top.h+) = stack(init.h.h+).
• stack(init.h.size.h+) = stack(init.h.h+).
• stack(init.h.empty.h+) = stack(init.h.h+).

Some rules have h+ (nonempty sequences) instead of h (possibly empty), but they could be converted into rules with h by replacing h+ by xxx.h for each symbol xxx in X. Hence we make no distinction between rules that end with an arbitrary history h and rules that end with a nonempty history . The same input sequence may lend itself to more than one rule, yielding a different oracle for each rule, as we discuss below. As an example, we consider the following input sequence:

• init.pop.push(a).size.push(b).pop.top.push(c).

We leave it to the reader to check that this input sequence lends itself to the following rules:

• The Init-Pop Rule that reduces the sequence to
  • init.push(a).size.push(b).pop.top.push(c).
• The VX Rule (for size and top) that reduces the sequence to
  • init.pop.push(a).push(b).pop.push(c).
• The Push-Pop Rule that reduces the sequence to
  • init.pop.push(a).size.top.push(c).

Each one of these rules provides that the original sequence places the stack in the same state as the simpler input sequence; since we want to write the oracle by inspecting the specification rather than candidate implementations (and we want the same oracle to work for all possible implementations), we abstain from referring to states. The question that arises then is: how can we say that two states are identical if we cannot refer to the states? The answer is that, as an approximation, we consider that two states are identical if all the VX operations return the same values at these two states. Hence if we have a rule of the form:

• R(init.h′.h) = R(init.h″.h),

where h″ is simpler than h′, then the general template for an oracle that is derived from the above rule is the following segment:

g.init(); g.m1(); g.m2(); … g.mk();  //  sequence init.h’
if oracle()  {successfultest();}
  else {unsuccessfultest();}

where oracle() is defined as follows:

 bool oracle()
 {vx1type vx1;  vx2type vx2; vx3type vx3;  //  VX types
 vx1 = g.vop1(); vx2 = g.vop2(); vx3 = g.vop3();
 //  storing the current state, following init.h’
 g.init(); g.m1’(); g.m2’(); … g.mh′(); //  sequence  init.h”
 return ((vx1==g.vop1()) && (vx2==g.vop2()) && (vx3==g.vop3()));}

As an illustration, we consider the following input sequence:

• init.pop.push(a).size.push(b).pop.top.push(c).

and we generate oracles to test it, according to various applicable rules.

• The Init-Pop Rule. In order to test this sequence against the Init-Pop rule, we apply the code pattern shown above, which we specialize to this rule.

itemtype a, b, c, v;  int n;               // working variables
g.init(); g.pop(); g.push(a); n=g.size(); g.push(b); g.pop(); v=g.top(); g.push(c);
if oracleinitpop(){successfultest();}
   else {unsuccessfultest();}

where we define oracle() as follows:

bool oracleinitpop()
{bool sempty;  int ssize; itemtype stop; // VX values
sempty=g.empty(); ssize=g.size(); stop=g.top();
g.init(); g.push(a); n=g.size(); g.push(b); g.pop(); 
v=g.top(); g.push(c);
return ((sempty == g.empty()) && (ssize==g.size) && (stop==g.top()));}

• The VX Rule (for size). In order to test this sequence against the VX rule for size, we apply the code pattern shown above, which we specialize to this rule.

itemtype a, b, c, v;  int n;                // working variables
g.init(); g.pop(); g.push(a); n=g.size(); g.push(b);
g.pop(); v=g.top(); g.push(c);
if oracleVXsize(){successfultest();}
   else {unsuccessfultest();}

where we define oracle() as follows:

bool oracleVXsize()
{bool sempty;  int ssize; itemtype stop;  // VX values
sempty=g.empty(); ssize=g.size(); stop=g.top();
g.init(); g.pop(); g.push(a); g.push(b); g.pop();
v=g.top(); g.push(c);
return ((sempty == g.empty()) && (ssize==g.size) && (stop==g.top()));}

• The VX Rule (for top). In order to test this sequence against the VX rule for top, we apply the code pattern shown above, which we specialize to this rule.

itemtype a, b, c, v;  int n;                // working variables
g.init(); g.pop(); g.push(a); n=g.size(); g.push(b);
g.pop(); v=g.top(); g.push(c);
if oracleVXtop(){successfultest();}
else {unsuccessfultest();}

where we define oracle() as follows:

bool oracleVXtop()
{bool sempty;  int ssize; itemtype stop;  // VX values
sempty=g.empty(); ssize=g.size(); stop=g.top();
g.init(); g.pop(); g.push(a); n=g.size(); g.push(b);
g.pop(); g.push(c);
return ((sempty == g.empty()) && (ssize==g.size) && (stop==g.top()));}

• The Push-Pop Rule. In order to test this sequence against the Push-Pop rule, we apply the code pattern shown above, which we specialize to this rule.

itemtype a, b, c, v;  int n;                // working variables
g.init(); g.pop(); g.push(a); n=g.size(); g.push(b);
g.pop(); v=g.top(); g.push(c);
if oraclepushpop(){successfultest();}
   else {unsuccessfultest();}

where we define oracle() as follows:

bool oraclepushpop()
{bool sempty;  int ssize; itemtype stop; // VX values
sempty=g.empty(); ssize=g.size(); stop=g.top();
g.init(); g.pop(); g.push(a); n=g.size(); v=g.top(); 
g.push(c);
return ((sempty == g.empty()) && (ssize==g.size) && (stop==g.top()));}

Whereas some rules provide that distinct input histories are equivalent, other rules describe how the value of a VX method depends on the structure of the input history. We write their general form as follows:

• C(R(init.h.vop), R(init.h′.vop)),

where C is a binary predicate between values returned by vop. As such, these rules are potentially applicable to any input sequence that ends with a vop symbol. The general format of their oracle can be written as follows, where we assume that sequence h is more complex than sequence h ’:

g.init(); g.m1(); g.m2(); … g.mk();    //  sequence init.h
if oraclevoprule()  {successfultest();}
else {unsuccessfultest();}

where oraclevoprule() is defined as follows:

bool oraclevoprule()
{vxtype vx; vx = g.vop();                     //  store R(init.h.vop)  
g.init(); g.m1’(); g.m2’(); … g.mh′();        //  sequence init.h’
return (C(vx, g.vop);}

As an illustration, we consider the following input sequence

• init.pop.push(a).push(b).size.push(a).top.push(c).size

and we generate an oracle for it on the basis of the size rule. As we recall, the Size Rule of the stack specification provides:

• stack(init.h.push(a).size) = 1 + stack(init.h.size).

We find:

itemtype a, b, c, v;  int n;             // working variables
g.init(); g.pop(); g.push(a); g.push(b); n=g.size();
g.push(a); v=g.top(); g.push(c);         //  sequence init.h
if oraclesize()  {successfultest();}
   else {unsuccessfultest();}

where oraclesize() is defined as follows:

bool oraclesize()
{int ssize; ssize = g.size();       //  store R(init.h.vop)  
g.init(); g.pop(); g.push(a); g.push(b); n=g.size();
g.push(a); v=g.top();              //  sequence init.h’
return (ssize==g.size()+1);}

To illustrate the generation of oracles from the empty rules, we consider the following input sequence:

• init.pop.empty.push(a).push(b).size.pop.push(a).size.push(c).empty.

Using the two empty rules (copied from Chapter 4):

• stack(init.h.push(a).h′.empty) ⇒ stack(init.h.h′.empty)
• stack(init.h.h′.empty) ⇒ stack(init.h.pop.h′.empty)

From these rules, we generate the following oracles:

itemtype a, b, c, v;  int n;  bool e;    // working  variables
g.init(); g.pop(); e=g.empty(); g.push(a); g.push(b);
n=g.size();
g.pop; g.push(a); n=g.size(); g.push(c); //  sequence init.h
if oracleempty1()  {successfultest();}
   else {unsuccessfultest();}

where oracleempty1() is defined as follows:

bool oracleempty1()
{bool sempty; sempty = g.empty();         //  store R(init.h.vop)  
g.init(); g.pop(); e=g.empty(); g.push(a); g.push(b);
n=g.size();
g.pop; n=g.size(); g.push(c); //  sequence init.h’
return (!(sempty) || (g.empty()));}  
// stack(init.h.push(a).h′.empty) →
// stack(init.h.h′.empty)

Whereas the first empty rule provides that removing a push operation makes the stack more empty (so to speak), the second empty rule provides that adding a pop operation also makes the stack more empty. Its oracle can be defined as follows, for the selected input sequence:

itemtype a, b, c, v;  int n;  bool e;    // working variables
g.init(); g.pop(); e=g.empty(); g.push(a); g.push(b); n=g.size();
g.push(a); n=g.size(); g.push(c); //  sequence init.h
if oracleempty2()  {successfultest();}
   else {unsuccessfultest();}

where oracleempty2() is defined as follows:

bool oracleempty2()
{bool sempty; sempty = g.empty();       //  store R(init.h.vop)  
g.init(); g.pop(); e=g.empty(); g.push(a); g.push(b); n=g.size();
g.pop(); g.push(a); n=g.size(); g.push(c); //  sequence init.h’
return (!(sempty) || (g.empty()));}  
        // stack(init.h.h′.empty) →
        // stack (init.h.pop.h′.empty)

So far we have used axioms and rules to generate test data and design oracles; but in fact, test data generation ought to be driven by coverage criteria. In Chapter 9, we had explored ways to generate test data for state-based software products, using the criteria that all states and all state transitions be visited at least once. In Chapter 12, we will see how the data generated in Chapter 9 can be combined with the oracles introduced herein to build test drivers.

11.4 CHAPTER SUMMARY

The subject of this chapter is the derivation of test oracles from relational specifications. This chapter covers two main themes, pertaining to the two main formats that specifications may take:

• For simple programs that operate by mapping an initial state to a final state, we find that if the specification of the program is a relation R, then the oracle has the form Oracle(s,s′) ≡ (s∈dom(R)→ (s,s′)∈R).
• For state-based programs that maintain an internal state, we find that if the specification of such programs is represented by axioms and rules, then any sequence of method calls can be tested using an oracle derived from the axioms or from the rules (depending on the structure of the method call sequence).

We make it a point to separate the generation of test data from the generation of test oracles; in Chapter 12, we see how these two artifacts are put together to produce operational test drivers.

11.5 EXERCISES

1. 11.1 We are interested in testing a program that searches an item x in an array a[1..N] of the same type as x. If x is in a, the array returns its index; if not, it returns 0.
   1. Write a specification that is appropriate for acceptance testing. Use it to derive a test oracle.
   2. Write a specification that is appropriate for fault removal, if you know that the candidate program operates by linear search starting from 1. Use it to derive a test oracle.
   3. Write a specification that is appropriate for fault removal, if you know that the candidate program operates by linear search starting from N. Use it to derive a test oracle.
   4. Write a specification that is appropriate for fault removal, if you know that the candidate program operates by binary search. Use it to derive a test oracle.
2. 11.2 We are interested in testing a program that solves a system of linear equations of the form .
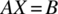   1. Write a specification for this problem, to be used in acceptance testing, modulo some precision ε.
   2. Use it to write a test oracle, assuming that you have a built-in function that computes the determinant of a square matrix.
3. 11.3 We are interested in testing a program that solves a cubic equation of the form .
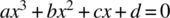   1. Write a specification for this problem, which provides that the equation has three distinct roots, and that candidate programs must return these roots in variables x1, x2, and x3. Note: In order for a cubic equation to have three roots, its discriminant must be positive, where the discriminant is defined as .
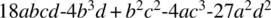   2. Use this specification to write a test oracle for acceptance testing.
   3. Write a program to solve this equation constructively (using analytical formulas for the roots) and derive a corresponding oracle for fault removal.
   4. Write a program to solve this equation iteratively (find the roots of the derivative and use these roots to apply the bisection method) and derive a corresponding oracle for fault removal.
4. 11.4 Consider the specification of the queue in Chapter 4. Generate oracles for all the axioms of this specification and apply them to appropriate input sequences.
5. 11.5 Consider the specification of the queue in Chapter 4. Generate an oracle for the Init Dequeue Rule of this specification and apply it to an appropriate input sequence.
6. 11.6 Consider the specification of the queue in Chapter 4. Generate an oracle for the Enqueue Dequeue Rule of this specification and apply it to an appropriate input sequences.
7. 11.7 Consider the specification of the queue in Chapter 4. Generate oracles for the Size Rule and the Empty Rules of this specification and apply them to appropriate input sequences.
8. 11.8 Consider the specification of the queue in Chapter 4. Generate oracles for all the VX Rules of this specification and apply them to appropriate input sequences.
9. 11.9 Consider the specification of the set in Chapter 4. Generate oracles for all the axioms of this specification and apply them to appropriate input sequences.
10. 11.10 Consider the specification of the set in Chapter 4. Generate an oracle for the Null Delete Rule of this specification and apply it to an appropriate input sequence.
11. 11.11 Consider the specification of the set in Chapter 4. Generate an oracle for the Insert Delete Rule of this specification and apply it to an appropriate input sequences.
12. 11.12 Consider the specification of the set in Chapter 4. Generate an oracle for the Commutativity Rule of this specification and apply it to an appropriate input sequences.
13. 11.13 Consider the specification of the set in Chapter 4. Generate oracles for the Size Rules of this specification and apply them to appropriate input sequences.
14. 11.14 Consider the specification of the set in Chapter 4. Generate oracles for the Inductive Rules of this specification and apply them to appropriate input sequences.
15. 11.15 Consider the specification of the set in Chapter 4. Generate oracles for all the VX Rules of this specification and apply them to appropriate input sequences.
16. 11.16 Following the example of Section 11.3.2, generate applicable oracles for the following input sequence in the stack specification: init.push(_).push(_).push(a).push(b).
17. 11.17 Following the example of Section 11.3.2, generate applicable oracles for the following input sequence in the stack specification: init.push(_).push(_).push(a).push(b).size().
18. 11.18 Following the example of Section 11.3.2, generate applicable oracles for the following input sequence in the stack specification: init.push(_).push(_).push(a).push(b).empty().