12
Counting, Sorting, and Distributed Coordination
12.1 Introduction
This chapter shows how some important problems that seem inherently sequential can be made highly parallel by “spreading out” coordination tasks among multiple parties. What does this spreading out buy us?
To answer this question, we need to understand how to measure the performance of a concurrent data structure. There are two measures that come to mind: latency, the time it takes an individual method call to complete, and throughput, the overall rate at which method calls complete. For example, real-time applications might care more about latency, and databases might care more about throughput.
In Chapter 11 we saw how to apply distributed coordination to the EliminationBackoffStack class. Here, we cover several useful patterns for distributed coordination: combining, counting, diffraction, and sampling. Some are deterministic, while others use randomization. We also cover two basic structures underlying these patterns: trees and combinatorial networks. Interestingly, for some data structures based on distributed coordination, high throughput does not necessarily mean low latency.
12.2 Shared Counting
We recall from Chapter 10 that a pool is a collection of items that provides put() and get() methods to insert and remove items (Fig. 10.1). Familiar classes such as stacks and queues can be viewed as pools that provide additional fairness guarantees.
One way to implement a pool is to use coarse-grained locking, perhaps making both put() and get() synchronized methods. The problem, of course, is that coarse-grained locking is too heavy-handed, because the lock itself creates both a sequential bottleneck, forcing all method calls to synchronize, as well as a hot spot, a source of memory contention. We would prefer to have Pool method calls work in parallel, with less synchronization and lower contention.
Let us consider the following alternative. The pool’s items reside in a cyclic array, where each array entry contains either an item or null. We route threads through two counters. Threads calling put() increment one counter to choose an array index into which the new item should be placed. (If that entry is full, the thread waits until it becomes empty.) Similarly, threads calling get() increment another counter to choose an array index from which the new item should be removed. (If that entry is empty, the thread waits until it becomes full.)
This approach replaces one bottleneck: the lock, with two: the counters. Naturally, two bottlenecks are better than one (think about that claim for a second). We now explore the idea that shared counters need not be bottlenecks, and can be effectively parallelized. We face two challenges.
1. We must avoid memory contention, where too many threads try to access the same memory location, stressing the underlying communication network and cache coherence protocols.
2. We must achieve real parallelism. Is incrementing a counter an inherently sequential operation, or is it possible for n threads to increment a counter faster than it takes one thread to increment a counter n times?
We now look at several ways to build highly parallel counters through data structures that coordinate the distribution of counter indexes.
12.3 Software Combining
Here is a linearizable shared counter class using a pattern called software combining. A CombiningTree is a binary tree of nodes, where each node contains bookkeeping information. The counter’s value is stored at the root. Each thread is assigned a leaf, and at most two threads share a leaf, so if there are p physical processors, then there are p/2 leaves. To increment the counter, a thread starts at its leaf, and works its way up the tree to the root. If two threads reach a node at approximately the same time, then they combine their increments by adding them together. One thread, the active thread, propagates their combined increments up the tree, while the other, the passive thread, waits for the active thread to complete their combined work. A thread may be active at one level and become passive at a higher level.
For example, suppose threads A and B share a leaf node. They start at the same time, and their increments are combined at their shared leaf. The first one, say, B, actively continues up to the next level, with the mission of adding 2 to the counter value, while the second, A, passively waits for B to return from the root with an acknowledgment that A’s increment has occurred. At the next level in the tree, B may combine with another thread C, and advance with the renewed intention of adding 3 to the counter value.
When a thread reaches the root, it adds the sum of its combined increments to the counter’s current value. The thread then moves back down the tree, notifying each waiting thread that the increments are now complete.
Combining trees have an inherent disadvantage with respect to locks: each increment has a higher latency, that is, the time it takes an individual method call to complete. With a lock, a getAndIncrement() call takes O(1) time, while with a CombiningTree, it takes O(log p) time. Nevertheless, a CombiningTree is attractive because it promises far better throughput, that is, the overall rate at which method calls complete. For example, using a queue lock, p getAndIncrement() calls complete in O(p) time, at best, while using a CombiningTree, under ideal conditions where all threads move up the tree together, p getAndIncrement() calls complete in O(log p) time, an exponential improvement. Of course, the actual performance is often less than ideal, a subject examined in detail later on. Still, the CombiningTree class, like other techniques we consider later, is intended to benefit throughput, not latency.
Combining trees are also attractive because they can be adapted to apply any commutative function, not just increment, to the value maintained by the tree.
12.3.1 Overview
Although the idea behind a CombiningTree is quite simple, the implementation is not. To keep the overall (simple) structure from being submerged in (not-so-simple) detail, we split the data structure into two classes: the CombiningTree class manages navigation within the tree, moving up and down the tree as needed, while the Node class manages each visit to a node. As you go through the algorithm’s description, it might be a good idea to consult Fig. 12.3 that describes an example CombiningTree execution.
This algorithm uses two kinds of synchronization. Short-term synchronization is provided by synchronized methods of the Node class. Each method locks the node for the duration of the call to ensure that it can read–write node fields without interference from other threads. The algorithm also requires excluding threads from a node for durations longer than a single method call. Such long-term synchronization is provided by a Boolean locked field. When this field is true, no other thread is allowed to access the node.
Every tree node has a combining status, which defines whether the node is in the early, middle, or late stages of combining concurrent requests.
enum CStatus{FIRST, SECOND, RESULT, IDLE, ROOT};
These values have the following meanings:
![]() IDLE: This node is not in use.
IDLE: This node is not in use.
![]() FIRST: One active thread has visited this node, and will return to check whether another passive thread has left a value with which to combine.
FIRST: One active thread has visited this node, and will return to check whether another passive thread has left a value with which to combine.
![]() SECOND: A second thread has visited this node and stored a value in the node’s value field to be combined with the active thread’s value, but the combined operation is not yet complete.
SECOND: A second thread has visited this node and stored a value in the node’s value field to be combined with the active thread’s value, but the combined operation is not yet complete.
![]() RESULT: Both threads’ operations have been combined and completed, and the second thread’s result has been stored in the node’s result field.
RESULT: Both threads’ operations have been combined and completed, and the second thread’s result has been stored in the node’s result field.
![]() ROOT: This value is a special case to indicate that the node is the root, and must be treated specially.
ROOT: This value is a special case to indicate that the node is the root, and must be treated specially.
Fig. 12.1 shows the Node class’s other fields.
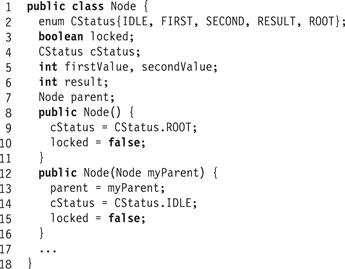
Figure 12.1 The Node class: the constructors and fields.
To initialize the CombiningTree for p threads, we create a width ![]() array of Node objects. The root is node[0], and for 0 < i < w, the parent of node[i] is node[(i-1)/2]. The leaf nodes are the last (w + 1)/2 nodes in the array, where thread i is assigned to leaf i/2. The root’s initial combining state is ROOT and the other nodes combining state is IDLE. Fig. 12.2 shows the CombiningTree class constructor.
array of Node objects. The root is node[0], and for 0 < i < w, the parent of node[i] is node[(i-1)/2]. The leaf nodes are the last (w + 1)/2 nodes in the array, where thread i is assigned to leaf i/2. The root’s initial combining state is ROOT and the other nodes combining state is IDLE. Fig. 12.2 shows the CombiningTree class constructor.

Figure 12.2 The CombiningTree class: constructor.
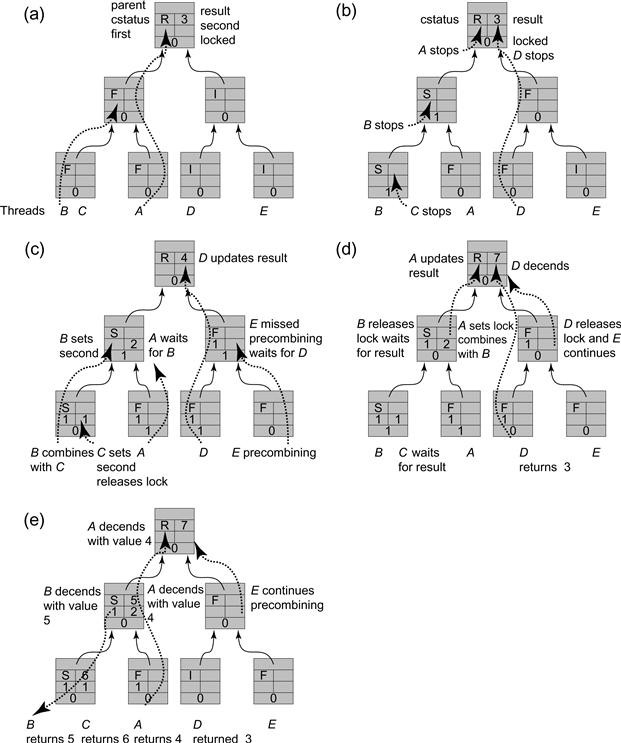
Figure 12.3 The concurrent traversal of a width 8 combining tree by 5 threads. The structure is initialized with all nodes unlocked, the root node having the CStatus ROOT and all other nodes having the CStatus IDLE.
The CombiningTree’s getAndIncrement() method, shown in Fig. 12.4, has four phases. In the precombining phase (Lines 16 through 19), the CombiningTree class’s getAndIncrement() method moves up the tree applying precombine() to each node. The precombine() method returns a Boolean indicating whether the thread was the first to arrive at the node. If so, the getAndIncrement() method continues moving up the tree. The stop variable is set to the last node visited, which is either the last node at which the thread arrived second, or the root. For example, Part (a) of Fig. 12.3 shows a precombining phase example. Thread A, which is fastest, stops at the root, while B stops in the middle-level node where it arrived after A, and C stops at the leaf where it arrived after B.

Figure 12.4 The CombiningTree class: the getAndIncrement() method.
Fig. 12.5 shows the Node’s precombine() method. In Line 20, the thread waits until the locked field is false. In Line 21, it tests the combining status.

Figure 12.5 The Node class: the precombining phase.
IDLE
The thread sets the node’s status to FIRST to indicate that it will return to look for a value for combining. If it finds such a value, it proceeds as the active thread, and the thread that provided that value is passive. The call then returns true, instructing the thread to move up the tree.
FIRST
An earlier thread has recently visited this node, and will return to look for a value to combine. The thread instructs the thread to stop moving up the tree (by returning false), and to start the next phase, computing the value to combine. Before it returns, the thread places a long-term lock on the node (by setting locked to true) to prevent the earlier visiting thread from proceeding without combining with the thread’s value.
ROOT
If the thread has reached the root node, it instructs the thread to start the next phase.
Line 31 is a default case that is executed only if an unexpected status is encountered.
Pragma 12.3.1
It is good programming practice always to provide an arm for every possible enumeration value, even if we know it cannot happen. If we are wrong, the program is easier to debug, and if we are right, the program may later be changed even by someone who does not know as much as we do. Always program defensively.
In the combining phase, (Fig. 12.4, Lines 21–28), the thread revisits the nodes it visited in the precombining phase, combining its value with values left by other threads. It stops when it arrives at the node stop where the precombining phase ended. Later on, we traverse these nodes in reverse order, so as we go we push the nodes we visit onto a stack.
The Node class’s combine() method, shown in Fig. 12.6, adds any values left by a recently arrived passive process to the values combined so far. As before, the thread first waits until the locked field is false. It then sets a long-term lock on the node, to ensure that late-arriving threads do not expect to combine with it. If the status is SECOND, it adds the other thread’s value to the accumulated value, otherwise it returns the value unchanged. In Part (c) of Fig. 12.3, thread A starts ascending the tree in the combining phase. It reaches the second level node locked by thread B and waits. In Part (d), B releases the lock on the second level node, and A, seeing that the node is in a SECOND combining state, locks the node and moves to the root with the combined value 3, the sum of the FirstValue and SecondValue fields written respectively by A and B.

Figure 12.6 The Node class: the combining phase. This method applies addition to FirstValue and SecondValue, but any other commutative operation would work just as well.
At the start of the operation phase (Lines 29 and 30), the thread has now combined all method calls from lower-level nodes, and now examines the node where it stopped at the end of the precombining phase (Fig. 12.7). If the node is the root, as in Part (d) of Fig. 12.3, then the thread, in this case A, carries out the combined getAndIncrement() operations: it adds its accumulated value (3 in the example) to the result and returns the prior value. Otherwise, the thread unlocks the node, notifies any blocked thread, deposits its value as the SecondValue, and waits for the other thread to return a result after propagating the combined operations toward the root. For example, this is the sequence of actions taken by thread B in Parts (c) and (d) of Fig. 12.3.

Figure 12.7 The Node class: applying the operation.
When the result arrives, A enters the distribution phase, propagating the result down the tree. In this phase (Lines 31–36), the thread moves down the tree, releasing locks, and informing passive partners of the values they should report to their own passive partners, or to the caller (at the lowest level). The distribute method is shown in Fig. 12.8. If the state of the node is FIRST, no thread combines with the distributing thread, and it can reset the node to its initial state by releasing the lock and setting the state to IDLE. If, on the other hand, the state is SECOND, the distributing thread updates the result to be the sum of the prior value brought from higher up the tree, and the FIRST value. This reflects a situation in which the active thread at the node managed to perform its increment before the passive one. The passive thread waiting to get a value reads the result once the distributing thread sets the status to RESULT. For example, in Part (e) of Fig. 12.3, the active thread A executes its distribution phase in the middle level node, setting the result to 5, changing the state to RESULT, and descending down to the leaf, returning the value 4 as its output. The passive thread B awakes and sees that the middle-level node’s state has changed, and reads result 5.

Figure 12.8 The Node class: the distribution phase.
12.3.2 An Extended Example
Fig. 12.3 describes the various phases of a CombiningTree execution. There are five threads labeled A through E. Each node has six fields, as shown in Fig. 12.1. Initially, all nodes are unlocked and all but the root are in an IDLE combining state. The counter value in the initial state in Part (a) is 3, the result of an earlier computation. In Part (a), to perform a getAndIncrement(), threads A and B start the precombining phase. A ascends the tree, changing the nodes it visits from IDLE to FIRST, indicating that it will be the active thread in combining the values up the tree. Thread B is the active thread at its leaf node, but has not yet arrived at the second-level node shared with A. In Part (b), B arrives at the second-level node and stops, changing it from FIRST to SECOND, indicating that it will collect its combined values and wait here for A to proceed with them to the root. B locks the node (changing the locked field from false to true), preventing A from proceeding with the combining phase without B’s combined value. But B has not combined the values. Before it does so, C starts precombining, arrives at the leaf node, stops, and changes its state to SECOND. It also locks the node to prevent B from ascending without its input to the combining phase. Similarly, D starts precombining and successfully reaches the root node. Neither A nor D changes the root node state, and in fact it never changes. They simply mark it as the node where they stopped precombining. In Part (c) A starts up the tree in the combining phase. It locks the leaf so that any later thread will not be able to proceed in its precombining phase, and will wait until A completes its combining and distribution phases. It reaches the second-level node, locked by B, and waits. In the meantime, C starts combining, but since it stopped at the leaf node, it executes the op() method on this node, setting SecondValue to 1 and then releasing the lock. When B starts its combining phase, the leaf node is unlocked and marked SECOND, so B writes 1 to FirstValue and ascends to the second-level node with a combined value of 2, the result of adding the FirstValue and SecondValue fields.
When it reaches the second level node, the one at which it stopped in the precombining phase, it calls the op() method on this node, setting SecondValue to 2. A must wait until it releases the lock. Meanwhile, in the right-hand side of the tree, D executes its combining phase, locking nodes as it ascends. Because it meets no other threads with which to combine, it reads 3 in the result field in the root and updates it to 4. Thread E then starts precombining, but is late in meeting D. It cannot continue precombining as long as D locks the second-level node. In Part (d), B releases the lock on the second-level node, and A, seeing that the node is in state SECOND, locks the node and moves to the root with the combined value 3, the sum of the FirstValue and SecondValue fields written, respectively, by A and B. A is delayed while D completes updating the root. Once D is done, A reads 4 in the root’s result field and updates it to 7. D descends the tree (by popping its local Stack), releasing the locks and returning the value 3 that it originally read in the root’s result field. E now continues its ascent in the precombining phase. Finally, in Part (e), A executes its distribution phase. It returns to the middle-level node, setting result to 5, changing the state to RESULT, and descending to the leaf, returning the value 4 as its output. B awakens and sees the state of the middle-level node has changed, reads 5 as the result, and descends to its leaf where it sets the result field to 6 and the state to RESULT. B then returns 5 as its output. Finally, C awakens and observes that the leaf node state has changed, reads 6 as the result, which it returns as its output value. Threads A through D return values 3 to 6 which fit the root’s result field value of 7. The linearization order of the getAndIncrement() method calls by the different threads is determined by their order in the tree during the precombining phase.
12.3.3 Performance and Robustness
Like all the algorithms described in this chapter, CombiningTree throughput depends in complex ways on the characteristics both of the application and of the underlying architecture. Nevertheless, it is worthwhile to review, in qualitative terms, some experimental results from the literature. Readers interested in detailed experimental results (mostly for obsolete architectures) may consult the chapter notes.
As a thought experiment, a CombiningTree should provide high throughput under ideal circumstances when each thread can combine its increment with another’s. But it may provide poor throughput under worst-case circumstances, where many threads arrive late at a locked node, missing the chance to combine, and are forced to wait for the earlier request to ascend and descend the tree.
In practice, experimental evidence supports this informal analysis. The higher the contention, the greater the observed rate of combining, and the greater the observed speed-up. Worse is better. Combining trees are less attractive when concurrency is low. The combining rate decreases rapidly as the arrival rate of increment requests is reduced. Throughput is sensitive to the arrival rate of requests.
Because combining increases throughput, and failure to combine does not, it makes sense for a request arriving at a node to wait for a reasonable duration for another thread to arrive with a increment with which to combine. Not surprisingly, it makes sense to wait for a short time when the contention is low, and longer when contention is high. When contention is sufficiently high, unbounded waiting works very well.
An algorithm is robust if it performs well in the presence of large fluctuations in request arrival times. The literature suggests that the CombiningTree algorithm with a fixed waiting time is not robust, because high variance in request arrival rates seems to reduce the combining rate.
12.4 Quiescently Consistent Pools and Counters
First shalt thou take out the Holy Pin. Then shalt thou count to three, no more, no less. Three shall be the number thou shalt count, and the number of the counting shall be three…. Once the number three, being the third number, be reached, then lobbest thou thy Holy Hand Grenade of Antioch towards thy foe, who, being naughty in my sight, shall snuff it.
From Monty Python and the Holy Grail.
Not all applications require linearizable counting. Indeed, counter-based Pool implementations require only quiescently consistent1 counting: all that matters is that the counters produce no duplicates and no omissions. It is enough that for every item placed by a put() in an array entry, another thread eventually executes a get() that accesses that entry, eventually matching put() and get() calls. (Wrap-around may still cause multiple put() calls or get() calls to compete for the same array entry.)
12.5 Counting Networks
Students of Tango know that the partners must be tightly coordinated: if they do not move together, the dance does not work, no matter how skilled the dancers may be as individuals. In the same way, combining trees must be tightly coordinated: if requests do not arrive together, the algorithm does not work efficiently, no matter how fast the individual processes.
In this chapter, we consider counting networks, which look less like Tango and more like a Rave: each participant moves at its own pace, but collectively the counter delivers a quiescently consistent set of indexes with high throughput.
Let us imagine that we replace the combining tree’s single counter with multiple counters, each of which distributes a subset of indexes (see Fig. 12.9). We allocate w counters (in the figure w = 4), each of which distributes a set of unique indexes modulo w (in the figure, for example, the second counter distributes 2, 6, 10, … i ⋅ w + 2 for increasing i). The challenge is how to distribute the threads among the counters so that there are no duplications or omissions, and how to do so in a distributed and loosely coordinated style.
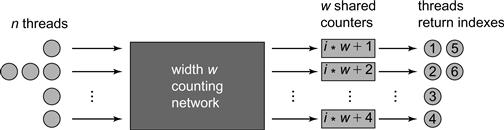
Figure 12.9 A quiescently consistent shared counter based on w = 4 counters preceded by a counting network. Threads traverse the counting network to choose which counters to access.
12.5.1 Networks That Count
A balancer is a simple switch with two input wires and two output wires, called the top and bottom wires (or sometimes the north and south wires). Tokens arrive on the balancer’s input wires at arbitrary times, and emerge on their output wires, at some later time. A balancer can be viewed as a toggle: given a stream of input tokens, it sends one token to the top output wire, and the next to the bottom, and so on, effectively balancing the number of tokens between the two wires (see Fig. 12.10). More precisely, a balancer has two states: up and down. If the state is up, the next token exits on the top wire, otherwise it exits on the bottom wire.
![]()
Figure 12.10 A balancer. Tokens arrive at arbitrary times on arbitrary input lines and are redirected to ensure that when all tokens have exited the balancer, there is at most one more token on the top wire than on the bottom one.
We use x0 and x1 to denote the number of tokens that respectively arrive on a balancer’s top and bottom input wires, and y0 and y1 to denote the number that exit on the top and bottom output wires. A balancer never creates tokens: at all times.
![]()
A balancer is said to be quiescent if every token that arrived on an input wire has emerged on an output wire:
![]()
A balancing network is constructed by connecting some balancers’ output wires to other balancers’ input wires. A balancing network of width w has input wires x0, x1, …, xw − 1 (not connected to output wires of balancers), and w output wires y0, y1, …, yw − 1 (similarly unconnected). The balancing network’s depth is the maximum number of balancers one can traverse starting from any input wire. We consider only balancing networks of finite depth (meaning the wires do not form a loop). Like balancers, balancing networks do not create tokens:
![]()
(We usually drop indexes from summations when we sum over every element in a sequence.) A balancing network is quiescent if every token that arrived on an input wire has emerged on an output wire:
![]()
So far, we have described balancing networks as if they were switches in a network. On a shared-memory multiprocessor, however, a balancing network can be implemented as an object in memory. Each balancer is an object, whose wires are references from one balancer to another. Each thread repeatedly traverses the object, starting on some input wire, and emerging at some output wire, effectively shepherding a token through the network.
Some balancing networks have interesting properties. The network shown in Fig. 12.11 has four input wires and four output wires. Initially, all balancers are up. We can check for ourselves that if any number of tokens enter the network, in any order, on any set of input wires, then they emerge in a regular pattern on the output wires. Informally, no matter how token arrivals are distributed among the input wires, the output distribution is balanced across the output wires, where the top output wires are filled first. If the number of tokens n is a multiple of four (the network width), then the same number of tokens emerges from each wire. If there is one excess token, it emerges on output wire 0, if there are two, they emerge on output wires 0 and 1, and so on. In general, if
![]()
then
![]()
We call this property the step property.
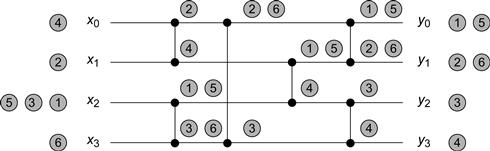
Figure 12.11 A sequential execution of a BITONIC [4] counting network. Each vertical line represents a balancer, and each balancer’s two input and output wires are the horizontal lines it connects to at the dots. In this sequential execution, tokens pass through the network, one completely after the other in the order specified by the numbers on the tokens. We track every token as it passes through the balancers on the way to an output wire. For example, token number 3 enters on wire 2, goes down to wire 3, and ends up on wire 2. Notice how the step property is maintained in every balancer, and also in the network as a whole.
Any balancing network that satisfies the step property is called a counting network, because it can easily be adapted to count the number of tokens that have traversed the network. Counting is done, as we described earlier in Fig. 12.9, by adding a local counter to each output wire i, so that tokens emerging on that wire are assigned consecutive numbers i, i + w, …, i + (yi − 1)w.
The step property can be defined in a number of ways which we use interchangeably.
12.5.2 The Bitonic Counting Network
In this section we describe how to generalize the counting network of Fig. 12.11 to a counting network whose width is any power of 2. We give an inductive construction.
When describing counting networks, we do not care about when tokens arrive, we care only that when the network is quiescent, the number of tokens exiting on the output wires satisfies the step property. Define a width w sequence of inputs or outputs x = x0, …, xw − 1 to be a collection of tokens, partitioned into w subsets xi. The xi are the input tokens that arrive or leave on wire i.
We define the width-2k balancing network MERGER [2k] as follows. It has two input sequences of width k, x and x′, and a single output sequence y of width 2k. In any quiescent state, if x and x′ both have the step property, then so does y. The MERGER [2k] network is defined inductively (see Fig. 12.12). When k is equal to 1, the MERGER [2k] network is a single balancer. For k > 1, we construct the MERGER [2k] network with input sequences x and x′ from two MERGER [k] networks and k balancers. Using a MERGER [k] network, we merge the even subsequence x0, x2, …, xk − 2 of x with the odd subsequence ![]() of x′ (that is, the sequence
of x′ (that is, the sequence ![]() is the input to the MERGER [k] network), while with a second MERGER [k] network we merge the odd subsequence of x with the even subsequence of x′. We call the outputs of these two MERGER [k] networks z and z′. The final stage of the network combines z and z′ by sending each pair of wires zi and
is the input to the MERGER [k] network), while with a second MERGER [k] network we merge the odd subsequence of x with the even subsequence of x′. We call the outputs of these two MERGER [k] networks z and z′. The final stage of the network combines z and z′ by sending each pair of wires zi and ![]() into a balancer whose outputs yield y2i and y2i+1.
into a balancer whose outputs yield y2i and y2i+1.
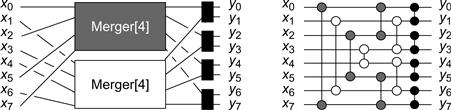
Figure 12.12 On the left-hand side we see the logical structure of a MERGER [8] network, into which feed two BITONIC [4] networks, as depicted in Fig. 12.11. The gray MERGER [4] network has as inputs the even wires coming out of the top BITONIC [4] network, and the odd ones from the lower BITONIC [4] network. In the lower MERGER [4] the situation is reversed. Once the wires exit the two MERGER [4] networks, each pair of identically numbered wires is combined by a balancer. On the right-hand side we see the physical layout of a MERGER [8] network. The different balancers are color coded to match the logical structure in the left-hand figure.
The MERGER [2k] network consists of log 2k layers of k balancers each. It provides the step property for its outputs only when its two input sequences also have the step property, which we ensure by filtering the inputs through smaller balancing networks.
The BITONIC [2k] network is constructed by passing the outputs from two BITONIC [k] networks into a MERGER [2k] network, where the induction is grounded in the BITONIC [2] network consisting of a single balancer, as depicted in Fig. 12.13. This construction gives us a network consisting of ![]() layers each consisting of k balancers.
layers each consisting of k balancers.
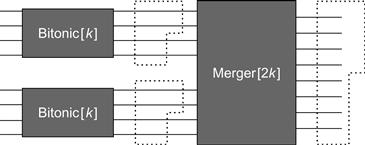
Figure 12.13 The recursive structure of a BITONIC [2k] Counting Network. Two BITONIC [k] counting networks feed into a MERGER [2k] balancing network.
A Software Bitonic Counting Network
So far, we have described counting networks as if they were switches in a network. On a shared-memory multiprocessor however, a balancing network can be implemented as an object in memory. Each balancer is an object, whose wires are references from one balancer to another. Each thread repeatedly traverses the object, starting on some input wire and emerging at some output wire, effectively shepherding a token through the network. Here, we show how to implement a BITONIC [2] network as a shared-memory data structure.
The Balancer class (Fig. 12.14) has a single Boolean field: toggle. The synchronized traverse() method complements the toggle field and returns as output wire, either 0 or 1. The Balancer class’s traverse() method does not need an argument because the wire on which a token exits a balancer does not depend on the wire on which it enters.

Figure 12.14 The Balancer class: a synchronized implementation.
The Merger class (Fig. 12.15) has three fields: the width field must be a power of 2, half[] is a two-element array of half-width Merger objects (empty if the network has width 2), and layer[] is an array of width/2 balancers implementing the final network layer.

Figure 12.15 The Merger class.
The class provides a traverse(i) method, where i is the wire on which the token enters. (For merger networks, unlike balancers, a token’s path depends on its input wire.) If the token entered on the lower width/2 wires, then it passes through half[0], otherwise half[1]. No matter which half-width merger network it traverses, a balancer that emerges on wire i is fed to the ith balancer at layer[i].
The Bitonic class (Fig. 12.16) also has three fields: width is the width (a power of 2), half[] is a two-element array of half-width Bitonic[] objects, and merger is a full width Merger network width. If the network has width 2, the half[] array is uninitialized. Otherwise, each element of half[] is initialized to a half-width Bitonic network.

Figure 12.16 The Bitonic[] class.
The class provides a traverse(i) method. If the token entered on the lower width/2 wires, then it passes through half[0], otherwise half[1]. A token that emerges from the half-merger subnetwork on wire i then traverses the final merger network from input wire i.
Notice that this class uses a simple synchronized Balancer implementation, but that if the Balancer implementation were lock-free (or wait-free) the network implementation as a whole would be lock-free (or wait-free).
Proof of Correctness
We now show that BITONIC [w] is a counting network. The proof proceeds as a progression of arguments about the token sequences passing through the network. Before examining the network itself, here are some simple lemmas about sequences with the step property.
Lemma 12.5.2
If a sequence has the step property, then so do all its subsequences.
Lemma 12.5.3
If x0, …, xk − 1 has the step property, then its even and odd subsequences satisfy:
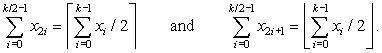
Proof
Either x2i = x2i+1 for ![]() , or by Lemma 12.5.1, there exists a unique j such that x2j = x2j+1 + 1 and x2i = x2i+1 for all i ≠ j,
, or by Lemma 12.5.1, there exists a unique j such that x2j = x2j+1 + 1 and x2i = x2i+1 for all i ≠ j, ![]() . In the first case,
. In the first case, ![]() , and in the second case
, and in the second case ![]() and
and ![]() .
.
Lemma 12.5.4
Let x0, …, xk−1 and y0, …, yk−1 be arbitrary sequences having the step property. If ![]() , then xi = yi for all
, then xi = yi for all ![]() .
.
Proof
Let ![]() . By Lemma 12.5.1,
. By Lemma 12.5.1, ![]() .
.
Lemma 12.5.5
Let x0, …, xk−1 and y0, …, yk−1 be arbitrary sequences having the step property. If ![]() , then there exists a unique j,
, then there exists a unique j, ![]() , such that xj = yj + 1, and xi = yi for i ≠ j,
, such that xj = yj + 1, and xi = yi for i ≠ j, ![]() .
.
Proof
Let ![]() . By Lemma 12.5.1,
. By Lemma 12.5.1, ![]() and
and ![]() . These two terms agree for all i,
. These two terms agree for all i, ![]() , except for the unique i such that i = m − 1 (mod k).
, except for the unique i such that i = m − 1 (mod k).
We now show that the MERGER [w] network preserves the step property.
Lemma 12.5.6
If MERGER [2k] is quiescent, and its inputs x0, …, xk−1 and ![]() both have the step property, then its outputs y0, …, y2k−1 also have the step property.
both have the step property, then its outputs y0, …, y2k−1 also have the step property.
Proof
We argue by induction on log k. It may be worthwhile to consult Fig. 12.17 which shows an example of the proof structure for a MERGER [8] network.
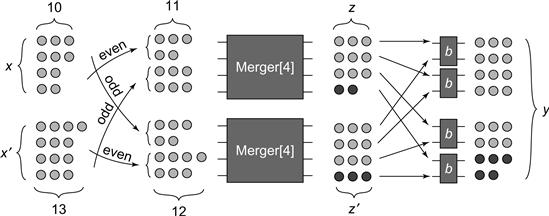
Figure 12.17 The inductive proof that a MERGER [8] network correctly merges two width 4 sequences x and x’ that have the step property into a single width 8 sequence y that has the step property. The odd and even width 2 subsequences of x and x’ all have the step property. Moreover, the difference in the number of tokens between the even sequence from one and the odd sequence from the other is at most 1 (in this example, 11 and 12 tokens, respectively). It follows from the induction hypothesis that the outputs z and z’ of the two MERGER [4] networks have the step property, with at most 1 extra token in one of them. This extra token must fall on a specific numbered wire (wire 3 in this case) leading into the same balancer. In this figure, these tokens are darkened. They are passed to the southern-most balancer, and the extra token is pushed north, ensuring the final output has the step property.
If 2k = 2, MERGER [2k] is just a balancer, and its outputs are guaranteed to have the step property by the definition of a balancer.
If 2k > 2, let z0, …, zk−1 be the outputs of the first MERGER [k] subnetwork which merges the even subsequence of x with the odd subsequence of x′. Let ![]() be the outputs of the second MERGER [k] subnetwork. Since x and x′ have the step property by assumption, so do their even and odd subsequences (Lemma 12.5.2), and hence so do z and z′ (induction hypothesis). Furthermore,
be the outputs of the second MERGER [k] subnetwork. Since x and x′ have the step property by assumption, so do their even and odd subsequences (Lemma 12.5.2), and hence so do z and z′ (induction hypothesis). Furthermore, ![]() and
and ![]() (Lemma 12.5.3). A straightforward case analysis shows that
(Lemma 12.5.3). A straightforward case analysis shows that ![]() and
and ![]() can differ by at most 1.
can differ by at most 1.
We claim that ![]() for any i < j. If
for any i < j. If ![]() , then Lemma 12.5.4 implies that
, then Lemma 12.5.4 implies that ![]() for
for ![]() . After the final layer of balancers,
. After the final layer of balancers,
![]()
and the result follows because z has the step property.
Similarly, if ![]() and
and ![]() differ by one, Lemma 12.5.5 implies that
differ by one, Lemma 12.5.5 implies that ![]() for
for ![]() , except for a unique
, except for a unique ![]() such that
such that ![]() and
and ![]() differ by one. Let
differ by one. Let ![]() and
and ![]() for some nonnegative integer x. From the step property for z and z′ we have, for all
for some nonnegative integer x. From the step property for z and z′ we have, for all ![]() ,
, ![]() and for all
and for all ![]()
![]() . Since
. Since ![]() and
and ![]() are joined by a balancer with outputs
are joined by a balancer with outputs ![]() and
and ![]() , it follows that
, it follows that ![]() and
and ![]() . Similarly, zi and
. Similarly, zi and ![]() for
for ![]() are joined by the same balancer. Thus, for any
are joined by the same balancer. Thus, for any ![]() , y2i = y2i+1 = x + 1 and for any
, y2i = y2i+1 = x + 1 and for any ![]() , y2i = y2i+1 = x. The step property follows by choosing
, y2i = y2i+1 = x. The step property follows by choosing ![]() and applying Lemma 12.5.1.
and applying Lemma 12.5.1.
The proof of the following theorem is now immediate.
Theorem 12.5.1
In any quiescent state, the outputs of BITONIC [w] have the step property.
A Periodic Counting Network
In this section, we show that the Bitonic network is not the only counting network with depth O(log2w). We introduce a new counting network with the remarkable property that it is periodic, consisting of a sequence of identical subnetworks, as depicted in Fig. 12.18. We define the network BLOCK [k] as follows. When k is equal to 2, the BLOCK [k] network consists of a single balancer. The BLOCK [2k] network for larger k is constructed recursively. We start with two BLOCK [k] networks A and B. Given an input sequence x, the input to A is xA, and the input to B is xB. Let y be the output sequence for the two subnetworks, where yA is the output sequence for A and yB the output sequence for B. The final stage of the network combines each ![]() and
and ![]() in a single balancer, yielding final outputs
in a single balancer, yielding final outputs ![]() and
and ![]() .
.

Figure 12.18 A PERIODIC [8] counting network constructed from 3 identical BLOCK [8] networks.
Fig. 12.19 describes the recursive construction of a BLOCK [8] network. The PERIODIC [2k] network consists of log k BLOCK [2k] networks joined so that the ith output wire of one is the ith wire of the next. Fig. 12.18 is a PERIODIC [8] counting network.2
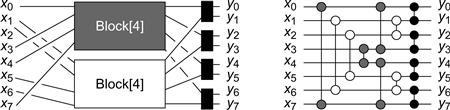
Figure 12.19 The left-hand side illustrates a BLOCK [8] network, into which feed two PERIODIC [4] networks. The right-hand illustrates the physical layout of a MERGER [8] network. The balancers are color-coded to match the logical structure in the left-hand figure.
A Software Periodic Counting Network
Here is how to implement the Periodic network in software. We reuse the Balancer class in Fig. 12.14. A single layer of a BLOCK [w] network is implemented by the LAYER [w] network (Fig. 12.20). A LAYER [w] network joins input wires i and w − i − 1 to the same balancer.

Figure 12.20 The Layer network.
In the BLOCK [w] class (Fig. 12.21), after the token emerges from the initial LAYER [w] network, it passes through one of two half-width BLOCK [w/2] networks (called north and south).

Figure 12.21 The BLOCK [w] network.
The PERIODIC [w] network (Fig. 12.22) is implemented as an array of log w BLOCK [w] networks. Each token traverses each block in sequence, where the output wire taken on each block is the input wire for its successor. (The chapter notes cite the proof that the PERIODIC [w] is a counting network.)

Figure 12.22 The Periodic network.
12.5.3 Performance and Pipelining
How does counting network throughput vary as a function of the number of threads and the network width? For a fixed network width, throughput rises with the number of threads up to a point, and then the network saturates, and throughput remains constant or declines. To understand these results, let us think of a counting network as a pipeline.
![]() If the number of tokens concurrently traversing the network is less than the number of balancers, then the pipeline is partly empty, and throughput suffers.
If the number of tokens concurrently traversing the network is less than the number of balancers, then the pipeline is partly empty, and throughput suffers.
![]() If the number of concurrent tokens is greater than the number of balancers, then the pipeline becomes clogged because too many tokens arrive at each balancer at the same time, resulting in per-balancer contention.
If the number of concurrent tokens is greater than the number of balancers, then the pipeline becomes clogged because too many tokens arrive at each balancer at the same time, resulting in per-balancer contention.
![]() Throughput is maximized when the number of tokens is roughly equal to the number of balancers.
Throughput is maximized when the number of tokens is roughly equal to the number of balancers.
If an application needs a counting network, then the best size network to choose is one that ensures that the number of tokens traversing the balancer at any time is roughly equal to the number of balancers.
12.6 Diffracting Trees
Counting networks provide a high degree of pipelining, so throughput is largely independent of network depth. Latency, however, does depend on network depth. Of the counting networks we have seen, the most shallow has depth ![]() . Can we design a logarithmic-depth counting network? The good news is yes, such networks exist, but the bad news is that for all known constructions, the constant factors involved render these constructions impractical.
. Can we design a logarithmic-depth counting network? The good news is yes, such networks exist, but the bad news is that for all known constructions, the constant factors involved render these constructions impractical.
Here is an alternative approach. Consider a set of balancers with a single input wire and two output wires, with the top and bottom labeled 0 and 1, respectively. The TREE [w] network (depicted in Fig. 12.23) is a binary tree structured as follows. Let w be a power of two, and define TREE [2k] inductively. When k is equal to 1, TREE [2k] consists of a single balancer with output wires y0 and y1. For k > 1, construct TREE [2k] from two TREE [k] trees and one additional balancer. Make the input wire x of the single balancer the root of the tree and connect each of its output wires to the input wire of a tree of width k. Redesignate output wires y0, y1, …, yk−1 of the TREE [k] subtree extending from the “0” output wire as the even output wires y0, y2, …, y2k−2 of the final TREE [2k] network and the wires y0, y1, …, yk−1 of the TREE [k] subtree extending from the balancer’s “1” output wire as the odd output wires y1, y3, …, y2k−1 of final TREE [2k] network.
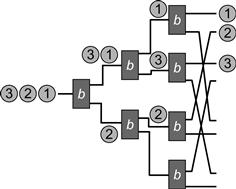
Figure 12.23 The TREE [8] class: a tree that counts. Notice how the network maintains the step property.
To understand why the TREE [2k] network has the step property in a quiescent state, let us assume inductively that a quiescent TREE [k] has the step property. The root balancer passes at most one token more to the TREE [k] subtree on its “0” (top) wire than on its“1” (bottom) wire. The tokens exiting the top TREE [k] subtree have a step property differing from that of the bottom subtree at exactly one wire j among their k output wires. The TREE [2k] outputs are a perfect shuffle of the wires leaving the two subtrees, and it follows that the two step-shaped token sequences of width k form a new step of width 2k where the possible single excess token appears at the higher of the two wires j, that is, the one from the top TREE [k] tree.
The TREE [w] network may be a counting network, but is it a good counting network? The good news is that it has shallow depth: while a BITONIC [w] network has depth log2w, the TREE [w] network depth is just log w. The bad news is contention: every token that enters the network passes through the same root balancer, causing that balancer to become a bottleneck. In general, the higher the balancer in the tree, the higher the contention.
We can reduce contention by exploiting a simple observation similar to one we made about the EliminationBackoffStack of Chapter 11:
If an even number of tokens pass through a balancer, the outputs are evenly balanced on the top and bottom wires, but the balancer’s state remains unchanged.
The basic idea behind diffracting trees is to place a Prism at each balancer, an out-of-band mechanism similar to the EliminationArray which allowed tokens (threads) accessing a stack to exchange items. The Prism allows tokens to pair off at random array locations and agree to diffract in different directions, that is, to exit on different wires without traversing the balancer’s toggle bit or changing its state. A token traverses the balancer’s toggle bit only if it is unable to pair off with another token within a reasonable period of time. If it did not manage to diffract, the token toggles the bit to determine which way to go. It follows that we can avoid excessive contention at balancers if the prism can pair off enough tokens without introducing too much contention.
A Prism is an array of Exchanger<Integer> objects, like the EliminationArray. An Exchanger<T> object permits two threads to exchange T values. If thread A calls the object’s exchange() method with argument a, and B calls the same object’s exchange() method with argument b, then A’s call returns value b and vice versa. The first thread to arrive is blocked until the second arrives. The call includes a timeout argument allowing a thread to proceed if it is unable to exchange a value within a reasonable duration.
The Prism implementation appears in Fig. 12.24. Before thread A visits the balancer’s toggle bit, it visits associated Prism. In the Prism, it picks an array entry at random, and calls that slot’s exchange() method, providing its own thread ID as an exchange value. If it succeeds in exchanging ids with another thread, then the lower thread ID exits on wire 0, and the higher on wire 1.

Figure 12.24 The Prism class.
Fig. 12.24 shows a Prism implementation. The constructor takes as an argument the capacity of the prism (the maximal number of distinct exchangers). The Prism class provides a single method, visit(), that chooses the random exchanger entry. The visit() call returns true if the caller should exit on the top wire, false if the bottom wire, and it throws a TimeoutException if the timeout expires without exchanging a value. The caller acquires its thread ID (Line 13), chooses a random entry in the array (Line 14), and tries to exchange its own ID with its partner’s (Line 15). If it succeeds, it returns a Boolean value, and if it times out, it rethrows TimeoutException.
A DiffractingBalancer (Fig. 12.25), like a regular Balancer, provides a traverse() method whose return value alternates between 0 and 1. This class has two fields: prism is a Prism, and toggle is a Balancer. When a thread calls traverse(), it tries to find a partner through the prism. If it succeeds, then the partners return with distinct values, without creating contention at the toggle(Line 11). Otherwise, if the thread is unable to find a partner, it traverses (Line 16) the toggle (implemented as a balancer).

Figure 12.25 The DiffractingBalancer class: if the caller pairs up with a concurrent caller through the prism, it does not need to traverse the balancer.
The DiffractingTree class (Fig. 12.26) has two fields. The child array is a two-element array of child trees. The root field is a DiffractingBalancer that alternates between forwarding calls to the left or right subtree. Each DiffractingBalancer has a capacity, which is actually the capacity of its internal prism. Initially this capacity is the size of the tree, and the capacity shrinks by half at each level.

Figure 12.26 The DiffractingTree class: fields, constructor, and traverse() method.
As with the EliminationBackoffStack, DiffractingTree performance depends on two parameters: prism capacities and timeouts. If the prisms are too big, threads miss one another, causing excessive contention at the balancer. If the arrays are too small, then too many threads concurrently access each exchanger in a prism, resulting in excessive contention at the exchangers. If prism timeouts are too short, threads miss one another, and if they are too long, threads may be delayed unnecessarily. There are no hard-and-fast rules for choosing these values, since the optimal values depend on the load and the characteristics of the underlying multiprocessor architecture.
Nevertheless, experimental evidence suggests that it is sometimes possible to choose these values to outperform both the CombiningTree and CountingNetwork classes. Here are some heuristics that work well in practice. Because balancers higher in the tree have more contention, we use larger prisms near the top of the tree, and add the ability to dynamically shrink and grow the random range chosen. The best timeout interval choice depends on the load: if only a few threads are accessing the tree, then time spent waiting is mostly wasted, while if there are many threads, then time spent waiting pays off. Adaptive schemes are promising: lengthen the timeout while threads succeed in pairing off, and shorten it otherwise.
12.7 Parallel Sorting
Sorting is one of the most important computational tasks, dating back to Hollerith’s Nineteenth-Century sorting machine, through the first electronic computer systems in the 1940s, and culminating today, when a high fraction of programs use sorting in some form or another. As most Computer Science undergraduates learn early on, the choice of sorting algorithm depends crucially on the number of items being sorted, the numerical properties of their keys, and whether the items reside in memory or in an external storage device. Parallel sorting algorithms can be classified in the same way.
We present two classes of sorting algorithms: sorting networks, which typically work well for small in-memory data sets, and sample sorting algorithms, which work well for large data sets in external memory. In our presentation, we sacrifice performance for simplicity. More complex techniques are cited in the chapter notes.
12.8 Sorting Networks
In much the same way that a counting network is a network of balancers, a sorting network is a network of comparators.3 A comparator is a computing element with two input wires and two output wires, called the top and bottom wires. It receives two numbers on its input wires, and forwards the larger to its top wire and the smaller to its bottom wire. A comparator, unlike a balancer, is synchronous: it outputs values only when both inputs have arrived (see Fig. 12.27).
![]()
Figure 12.27 A comparator.
A comparison network, like a balancing network, is an acyclic network of comparators. An input value is placed on each of its w input lines. These values pass through each layer of comparators synchronously, finally leaving together on the network output wires.
A comparison network with input values xi and output values yi, i ∈ {0 … 1}, each on wire i, is a valid sorting network if its output values are the input values sorted in descending order, that is, ![]() .
.
The following classic theorem simplifies the process of proving that a given network sorts.
Theorem 12.8.1
(0-1-principle)
If a sorting network sorts every input sequence of 0s and 1s, then it sorts any sequence of input values.
12.8.1 Designing a Sorting Network
There is no need to design sorting networks, because we can recycle counting network layouts. A balancing network and a comparison network are isomorphic if one can be constructed from the other by replacing balancers with comparators, or vice versa.
Theorem 12.8.2
If a balancing network counts, then its isomorphic comparison network sorts.
Proof
We construct a mapping from comparison network transitions to isomorphic balancing network transitions.
By Theorem 12.8.1, a comparison network which sorts all sequences of 0s and 1s is a sorting network. Take any arbitrary sequence of 0s and 1s as inputs to the comparison network, and for the balancing network place a token on each 1 input wire and no token on each 0 input wire. If we run both networks in lock-step, the balancing network simulates the comparison network.
The proof is by induction on the depth of the network. For level 0 the claim holds by construction. Assuming it holds for wires of a given level k, let us prove it holds for level k + 1. On every comparator where two 1s meet in the comparison network, two tokens meet in the balancing network, so one 1 leaves on each wire in the comparison network on level k + 1, and one token leaves on each wire in the balancing network on level k + 1. On every comparator where two 0s meet in the comparison network, no tokens meet in the balancing network, so a 0 leaves on each level k + 1 wire in the comparison network, and no tokens leave in the balancing network. On every comparator where a 0 and 1 meet in the comparison network, the 1 leaves on the north (upper) wire and the 1 on the south (lower) wire on level k + 1, while in the balancing network the token leaves on the north wire, and no token leaves on the south wire.
If the balancing network is a counting network, that is, it has the step property on its output level wires, then the comparison network must have sorted the input sequence of 0s and 1s.
The converse is false: not all sorting networks are counting networks. We leave it as an exercise to verify that the OddEven network in Fig. 12.28 is a sorting network but not a counting network.

Figure 12.28 The OddEven sorting network.
Corollary 12.8.1
Comparison networks isomorphic to BITONIC [] and PERIODIC [] networks are sorting networks.
Sorting a set of size w by comparisons requires ![]() comparisons. A sorting network with w input wires has at most O(w) comparators in each level, so its depth can be no smaller than
comparisons. A sorting network with w input wires has at most O(w) comparators in each level, so its depth can be no smaller than ![]() .
.
Corollary 12.8.2
The depth of any counting network is at least ![]() .
.
A Bitonic Sorting Algorithm
We can represent any width-w sorting network, such as BITONIC [w], as a collection of d layers of w/2 balancers each. We can represent a sorting network layout as a table, where each entry is a pair that describes which two wires meet at that balancer at that layer. (E.g., in the BITONIC [4] network of Fig. 12.11, wires 0 and 1 meet at the first balancer in the first layer, and wires 0 and 3 meet at the first balancer of the second layer.) Let us assume, for simplicity, that we are given an unbounded table bitonicTable[i][d][j], where each array entry contains the index of the associated north (0) or south (1) input wire to balancer i at depth d.
An in-place array-based sorting algorithm takes as input an array of items to be sorted (here we assume these items have unique integer keys) and returns the same array with the items sorted by key. Here is how we implement BitonicSort, an in-place array-based sorting algorithm based on a Bitonic sorting network. Let us assume that we wish to sort an array of 2 ⋅ p ⋅ s elements, where p is the number of threads (and typically also the maximal number of available processors on which the threads run) and p ⋅ s is a power of 2. The network has p ⋅ s comparators at every layer.
Each of the p threads emulates the work of s comparators. Unlike counting networks, which act like uncoordinated raves, sorting networks are synchronous: all inputs to a comparator must arrive before it can compute the outputs. The algorithm proceeds in rounds. In each round, a thread performs s comparisons in a layer of the network, switching the array entries of items if necessary, so that they are properly ordered. In each network layer, the comparators join different wires, so no two threads attempt to exchange the items of the same entry, avoiding the need to synchronize operations at any given layer.
To ensure that the comparisons of a given round (layer) are complete before proceeding to the next one, we use a synchronization construct called a Barrier (studied in more detail in Chapter 17). A barrier for p threads provides an await() method, whose call does not return until all p threads have called await(). The BitonicSort implementation appears in Fig. 12.29. Each thread proceeds through the layers of the network round by round. In each round, it awaits the arrival of the other threads (Line 12), ensuring that the items array contains the prior round’s results. It then emulates the behavior of s balancers at that layer by comparing the items at the array positions corresponding to the comparator’s wires, and exchanging them if their keys are out of order (Lines 14 through 19).

Figure 12.29 The BitonicSort class.
The BitonicSort takes ![]() time for p threads running on p processors, which, if s is constant, is
time for p threads running on p processors, which, if s is constant, is ![]() time.
time.
12.9 Sample Sorting
The BitonicSort is appropriate for small data sets that reside in memory. For larger data sets (where n, the number of items, is much larger than p, the number of threads), especially ones that reside on out-of-memory storage devices, we need a different approach. Because accessing a data item is expensive, we must maintain as much locality-of-reference as possible, so having a single thread sort items sequentially is cost-effective. A parallel sort like BitonicSort, where an item is accessed by multiple threads, is simply too expensive.
We attempt to minimize the number of threads that access a given item through randomization. This use of randomness differs from that in the DiffractingTree, where it was used to distribute memory accesses. Here we use randomness to guess the distribution of items in the data set to be sorted.
Since the data set to be sorted is large, we split it into buckets, throwing into each bucket the items that have keys within a given range. Each thread then sorts the items in one of the buckets using a sequential sorting algorithm, and the result is a sorted set (when viewed in the appropriate bucket order). This algorithm is a generalization of the well-known quicksort algorithm, but instead of having a single splitter key to divide the items into two subsets, we have p − 1 splitter keys that split the input set into p subsets.
The algorithm for n items and p threads involves three phases:
1. Threads choose p − 1 splitter keys to partition the data set into p buckets. The splitters are published so all threads can read them.
2. Each thread sequentially processes n/p items, moving each item to its bucket, where the appropriate bucket is determined by performing a binary search with the item’s key among the splitter keys.
Barriers between the phases ensure that all threads have completed one phase before the next starts.
Before we consider Phase one, we look at the second and third phases.
The second phase’s time complexity is (n/p) log p, consisting of reading each item from memory, disk, or tape, followed by a binary search among p splitters cached locally, and finally adding the item into the appropriate bucket. The buckets into which the items are moved could be in memory, on disk, or on tape, so the dominating cost is that of the n/p accesses to the stored data items.
Let b be the number of items in a bucket. The time complexity of the third phase for a given thread is ![]() , to sort the items using a sequential version of, say, quicksort.4 This part has the highest cost because it consists of read–write phases that access relatively slow memory, such as disk or tape.
, to sort the items using a sequential version of, say, quicksort.4 This part has the highest cost because it consists of read–write phases that access relatively slow memory, such as disk or tape.
The time complexity of the algorithm is dominated by the thread with the most items in its bucket in the third phase. It is therefore important to choose the splitters to be as evenly distributed as possible, so each bucket receives approximately n − p items in the second phase.
The key to choosing good splitters is to have each thread pick a set of sample splitters that represent its own n − p size data set, and choose the final p − 1 splitters from among all the sample splitter sets of all threads. Each thread selects uniformly at random s keys from its data set of size n − p. (In practice, it suffices to choose s to be 32 or 64 keys.) Each thread then participates in running the parallel BitonicSort (Fig. 12.29) on the s ⋅ p sample keys selected by the p threads. Finally, each thread reads the p − 1 splitter keys in positions s, 2s, …, (p − 1)s in the sorted set of splitters, and uses these as the splitters in the second phase. This choice of s samples, and the later choice of the final splitters from the sorted set of all samples, reduces the effects of an uneven key distribution among the n − p size data sets accessed by the threads.
For example, a sample sort algorithm could choose to have each thread pick p − 1 splitters for its second phase from within its own n/p size data set, without ever communicating with other threads. The problem with this approach is that if the distribution of the data is uneven, the size of the buckets may differ greatly, and performance would suffer. For example, if the number of items in the largest bucket is doubled, so is the worst-case time complexity of sorting algorithm.
The first phase’s complexity is s (a constant) to perform the random sampling, and ![]() for the parallel Bitonic sort. The overall time complexity of sample sort with a good splitter set (where every bucket gets O(n/p) of the items) is
for the parallel Bitonic sort. The overall time complexity of sample sort with a good splitter set (where every bucket gets O(n/p) of the items) is
![]()
which overall is O((n/p) log(n/p)).
12.10 Distributed Coordination
This chapter covered several distributed coordination patterns. Some, such as combining trees, sorting networks, and sample sorting, have high parallelism and low overheads. All these algorithms contain synchronization bottlenecks, that is, points in the computation where threads must wait to rendezvous with others. In the combining trees, threads must synchronize to combine, and in sorting, when threads wait at barriers.
In other schemes, such as counting networks and diffracting trees, threads never wait for one another. (Although we implement balancers using synchronized methods, they could be implemented in a lock-free manner using compareAndSet().) Here, the distributed structures pass information from one thread to another, and while a rendezvous could prove advantageous (as in the Prism array), it is not necessary.
Randomization, which is useful in many places, helps to distribute work evenly. For diffracting trees, randomization distributes work over multiple memory locations, reducing the chance that too many threads simultaneously access the same location. For sample sort, randomization helps distribute work evenly among buckets, which threads later sort in parallel.
Finally, we saw that pipelining can ensure that some data structures can have high throughput, even though they have high latency.
Although we focus on shared-memory multiprocessors, it is worth mentioning that the distributed algorithms and structures considered in this chapter also work in message-passing architectures. The message-passing model might be implemented directly in hardware, as in a network of processors, or it could be provided on top of a shared-memory architecture through a software layer such as MPI.
In shared-memory architectures, switches (such as combining tree nodes or balancers) are naturally implemented as shared-memory counters. In message-passing architectures, switches are naturally implemented as processor-local data structures, where wires that link one processor to another also link one switch to another. When a processor receives a message, it atomically updates its local data structure and forwards messages to the processors managing other switches.
12.11 Chapter Notes
The idea behind combining trees is due to Allan Gottlieb, Ralph Grishman, Clyde Kruskal, Kevin McAuliffe, Larry Rudolph, and Marc Snir [47]. The software CombiningTree presented here is a adapted from an algorithm by PenChung Yew, Nian-Feng Tzeng, and Duncan Lawrie [151] with modifications by Maurice Herlihy, Beng-Hong Lim, and Nir Shavit [65], all based on an original proposal by James Goodman, Mary Vernon, and Philip Woest [45].
Counting networks were invented by Jim Aspnes, Maurice Herlihy, and Nir Shavit [16]. Counting networks are related to sorting networks, including the ground breaking Bitonic network of Kenneth Batcher [18], and the periodic network of Martin Dowd, Yehoshua Perl, Larry Rudolph, and Mike Saks [35]. Miklós Ajtai, János Komlós, and Endre Szemerédi discovered the AKS sorting network, an O(log w) depth sorting network [8]. (This asymptotic expression hides large constants which make networks based on AKS impractical.)
Mike Klugerman and Greg Plaxton [84, 85] were the first to provide an AKS-based counting network construction with O(log w) depth. The 0-1 principle for sorting networks is by Donald Knuth [86]. A similar set of rules for balancing networks is provided by Costas Busch and Marios Mavronicolas [25]. Diffracting trees were invented by Nir Shavit and Asaph Zemach [143].
Sample sorting was suggested by John Reif and Leslie Valiant [132] and by Huang and Chow [73]. The sequential Quicksort algorithm to which all sample sorting algorithms relate is due to Tony Hoare [70]. There are numerous parallel radix sort algorithms in the literature such as the one by Daniel Jiménez-González, Joseph Larriba-Pey, and Juan Navarro [82] or the one by Shin-Jae Lee and Minsoo Jeon and Dongseung Kim and Andrew Sohn [101].
Monty Python and the Holy Grail was written by Graham Chapman, John Cleese, Terry Gilliam, Eric Idle, Terry Jones, and Michael Palin and co-directed by Terry Gilliam and Terry Jones [27].
Exercise 134. Prove Lemma 12.5.1.
Exercise 135. Implement a trinary CombiningTree, that is, one that allows up to three threads coming from three subtrees to combine at a given node. Can you estimate the advantages and disadvantages of such a tree when compared to a binary combining tree?
Exercise 136. Implement a CombiningTree using Exchanger objects to perform the coordination among threads ascending and descending the tree. What are the possible disadvantages of your construction when compared to the CombiningTree class presented in Section 12.3?
Exercise 137. Implement the cyclic array based shared pool described in Section 12.2 using two simple counters and a ReentrantLock per array entry.
Exercise 138. Provide an efficient lock-free implementation of a Balancer.
Exercise 139. (Hard) Provide an efficient wait-free implementation of a Balancer (i.e. not by using the universal construction).
Exercise 140. Prove that the TREE [2k] balancing network constructed in Section 12.6 is a counting network, that is, that in any quiescent state, the sequences of tokens on its output wires have the step property.
Exercise 141. Let ![]() be a width-w balancing network of depth d in a quiescent state s. Let n = 2d. Prove that if n tokens enter the network on the same wire, pass through the network, and exit, then
be a width-w balancing network of depth d in a quiescent state s. Let n = 2d. Prove that if n tokens enter the network on the same wire, pass through the network, and exit, then ![]() will have the same state after the tokens exit as it did before they entered.
will have the same state after the tokens exit as it did before they entered.
In the following exercises, a k-smooth sequence is a sequence y0, …, yw−1 that satisfies
![]()
Exercise 142. Let X and Y be k-smooth sequences of length w. A matching layer of balancers for X and Y is one where each element of X is joined by a balancer to an element of Y in a one-to-one correspondence.
Prove that if X and Y are each k-smooth, and Z is the result of matching X and Y, then Z is (k + 1)-smooth.
Exercise 143. Consider a BLOCK [k] network in which each balancer has been initialized to an arbitrary state (either up or down). Show that no matter what the input distribution is, the output distribution is (log k)-smooth.
Hint: you may use the claim in Exercise 142.
Exercise 144. A smoothing network is a balancing network that ensures that in any quiescent state, the output sequence is 1-smooth.
Counting networks are smoothing networks, but not vice versa.
A Boolean sorting network is one in which all inputs are guaranteed to be Boolean. Define a pseudo-sorting balancing network to be a balancing network with a layout isomorphic to a Boolean sorting network.
Let ![]() be the balancing network constructed by taking a smoothing network
be the balancing network constructed by taking a smoothing network ![]() of width w, a pseudo-sorting balancing network
of width w, a pseudo-sorting balancing network ![]() also of width w, and joining the ith output wire of
also of width w, and joining the ith output wire of ![]() to the ith input wire of
to the ith input wire of ![]() .
.
Show that ![]() is a counting network.
is a counting network.
Exercise 145. A 3-balancer is a balancer with three input lines and three output lines. Like its 2-line relative, its output sequences have the step property in any quiescent state. Construct a depth-3 counting network with 6 input and output lines from 2-balancers and 3-balancers. Explain why it works.
Exercise 146. Suggest ways to modify the BitonicSort class so that it will sort an input array of width w where w is not a power of 2.
Exercise 147. Consider the following w-thread counting algorithm. Each thread first uses a bitonic counting network of width w to take a counter value v. It then goes through a waiting filter, in which each thread waits for threads with lesser values to catch up.
The waiting filter is an array filter[] of w Boolean values. Define the phase function
![]()
A thread that exits with value v spins on filter[(v−1) mod n] until that value is set to ϕ(v − 1). The thread responds by setting filter[v mod w] to ϕ(v), and then returns v.
1. Explain why this counter implementation is linearizable.
2. An exercise here shows that any linearizable counting network has depth at least w. Explain why the filter[] construction does not contradict this claim.
3. On a bus-based multiprocessor, would this filter[] construction have better throughput than a single variable protected by a spin lock? Explain.
Exercise 148. If a sequence X = x0, … xw−1 is k-smooth, then the result of passing X through a balancing network is k-smooth.
Exercise 149. Prove that the Bitonic[w] network has depth ![]() and uses
and uses ![]() balancers.
balancers.
Exercise 150. (Hard) Provide an implementation of a DiffractingBalancer that is lock-free.
Exercise 151. Add an adaptive timeout mechanism to the Prism of the DiffractingBalancer.
Exercise 152. Show that the OddEven network in Fig. 12.28 is a sorting network but not a counting network.
Exercise 153. Can counting networks do anything besides increments? Consider a new kind of token, called an antitoken, which we use for decrements. Recall that when a token visits a balancer, it executes a getAndComplement(): it atomically reads the toggle value and complements it, and then departs on the output wire indicated by the old toggle value. Instead, an antitoken complements the toggle value, and then departs on the output wire indicated by the new toggle value. Informally, an antitoken “cancels” the effect of the most recent token on the balancer’s toggle state, and vice versa.
Instead of simply balancing the number of tokens that emerge on each wire, we assign a weight of +1 to each token and −1 to each antitoken. We generalize the step property to require that the sums of the weights of the tokens and antitokens that emerge on each wire have the step property. We call this property the weighted step property.
Fig. 12.30 shows how to implement an antiTraverse() method that moves an antitoken though a balancer. Adding an antiTraverse() method to the other networks is left as an exercise.
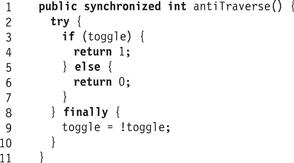
Figure 12.30 The antiTraverse() method.
Let ![]() be a width-w balancing network of depth d in a quiescent state s. Let n = 2d. Show that if n tokens enter the network on the same wire, pass through the network, and exit, then
be a width-w balancing network of depth d in a quiescent state s. Let n = 2d. Show that if n tokens enter the network on the same wire, pass through the network, and exit, then ![]() will have the same state after the tokens exit as it did before they entered.
will have the same state after the tokens exit as it did before they entered.
Exercise 154. Let ![]() be a balancing network in a quiescent state s, and suppose a token enters on wire i and passes through the network, leaving the network in state s′. Show that if an antitoken now enters on wire i and passes through the network, then the network goes back to state s.
be a balancing network in a quiescent state s, and suppose a token enters on wire i and passes through the network, leaving the network in state s′. Show that if an antitoken now enters on wire i and passes through the network, then the network goes back to state s.
Exercise 155. Show that if balancing network ![]() is a counting network for tokens alone, then it is also a balancing network for tokens and antitokens.
is a counting network for tokens alone, then it is also a balancing network for tokens and antitokens.
Exercise 156. A switching network is a directed graph, where edges are called wires and node are called switches. Each thread shepherds a token through the network. Switches and tokens are allowed to have internal states. A token arrives at a switch via an input wire. In one atomic step, the switch absorbs the token, changes its state and possibly the token’s state, and emits the token on an output wire. Here, for simplicity, switches have two input and output wires. Note that switching networks are more powerful than balancing networks, since switches can have arbitrary state (instead of a single bit) and tokens also have state.
An adding network is a switching network that allows threads to add (or subtract) arbitrary values.
We say that a token is in front of a switch if it is on one of the switch’s input wires. Start with the network in a quiescent state q0, where the next token to run will take value 0. Imagine we have one token t of weight a and n −1 tokens t1, …, tn−1 all of weight b, where b > a, each on a distinct input wire. Denote by ![]() the set of switches that t traverses if it traverses the network by starting in q0.
the set of switches that t traverses if it traverses the network by starting in q0.
Prove that if we run the t1, …, tn−1 one at a time though the network, we can halt each ti in front of a switch of ![]() .
.
At the end of this construction, n − 1 tokens are in front of switches of ![]() . Since switches have two input wires, it follows that t’s path through the network encompasses at least n − 1 switches, so any adding network must have depth at least n − 1, where n is the maximum number of concurrent tokens. This bound is discouraging because it implies that the size of the network depends on the number of threads (also true for CombiningTrees, but not counting networks), and that the network has inherently high latency.
. Since switches have two input wires, it follows that t’s path through the network encompasses at least n − 1 switches, so any adding network must have depth at least n − 1, where n is the maximum number of concurrent tokens. This bound is discouraging because it implies that the size of the network depends on the number of threads (also true for CombiningTrees, but not counting networks), and that the network has inherently high latency.
Exercise 157. Extend the proof of Exercise 156 to show that a linearizable counting network has depth at least n.
1 See Chapter 3 for a detailed definition of quiescent consistency.
2 While the BLOCK [2k] and MERGER [2k] networks may look the same, they are not: there is no permutation of wires that yields one from the other.
3 Historically sorting networks predate counting networks by several decades.
4 If the item’s key size is known and fixed, one could use algorithms like Radixsort.
