If is a term or a formula, i₁,...,i_n are pairwise distinct variables and t₁,...,t_n are arbitrary terms, then

is the term or formula obtained from by the simultaneous substitution of t₁,...,t_n for i₁,..., i_n, which it is unnecessary to define. When there is no possible confusion regarding which variables are substituted, we will write simply

Lemma A.1 Let be a term or a formula and i k.

(1) If i does not occur free in t2 and k does not occur free in t1, then

(2) If a is an individual constant, and the variables i, k are not quantified in , then

Remark

On occasion we will need to replace a fleeing term with a constant or a variable. This operation will always be performed on formulas without quantifiers, and the variables that replace the fleeing terms will be different from the ones that the formula possesses. This type of substitution consists in inserting in the place of the fleeing term the variable or constant that replaces it. I have not included this case in the previous definition so as not to complicate its formulation.

A.3 SEMANTICS

A.3.1 Assignments

From now on we will always suppose that the language L does not have individual constants. If D is a nonempty set, L_D will be the language that in addition to the symbols of L has the elements of D as individual constants. We assume that no element of D is a combination of symbols of L. We will refer to D as the domain, and L_D as the language associated with the domain D. Clearly, if R is an n-place predicate symbol of L and a₁,...,a_n are elements of the domain, then Ra₁...a_n is a formula of L_D.

If k_r1..._rn is a fleeing term of L_D and I is the set of variables on which it depends, the terms of L_D generated by k_r1..._rn in D are those of the form

where m 0, i₁,...,i_m are distinct variables of I, and a₁,...,a_m are elements of D. For example, if D = {0, 1, 2}, then k_i11, k₁₀₂, and k_1jh are terms of L_D generated by k_ijh. Evidently, if c is an element of the domain, the set of terms generated in D by k_r1..._rn(ⁱc) is a subset of the set generated by k_r1..._rn.

An assignment for L in a domain D is a function v from the set of terms of L_D into D such that for every c D, v(c) = c. As can be seen, we do not impose any special restriction for the case of the fleeing terms. The element assigned to a fleeing term is independent of the elements assigned to its subindices. For example, it may be that v(i) = v(j), but v(k_i) v(k_j). In consequence, the fleeing terms are not functional terms. For them to behave functionally, it would suffice to require that v meets

The next proposition shows that every assignment gives rise naturally to another one that treats fleeing terms functionally.

Proposition A.2 For every assignment v for L in D, there exists a unique assignment for L in D such that

(1) for every simple term t of L_D, v(t) = (t);

(2) if a₁,...,a_n D, then v(k_a1..._an) = (k_a1..._an);

(3) if r₁,...,r_n are simple terms of L_D, then v(k_r1..._rn) = v(k_v(r1)..._v(rn)).

Proof. If v is an assignment for L in D, the function from the set of terms of LD into D defined by

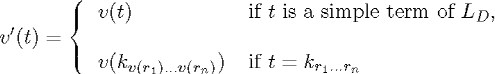
is an assignment for L in D that meets (1), (2), and (3).

A.3.2 Satisfaction

A solution for L in a domain D is a function S from the set of atomic sentences of LD into {0, 1} such that

Let D be a nonempty set, S a solution for L in D. and v an assignment for L in D. We define by recursion a function (S, v) from the set of sentences of L_D into {0, 1} in the following way:

2. (S.v) (Rt1 ... tn) = 1 iff S(Rv(t1) ... v(tn)) = 1;²

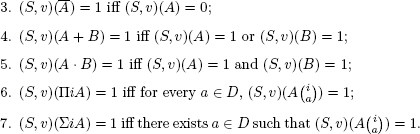
If S is a solution for L in a domain D and v an assignment for L in D, the function (S, v) will be an interpretation for L in D. If (S, v)(A) = 1, we will say that the interpretation (S, v) satisfies A in D or that A is satisfied by (S, v) in D or that A is true under (S, v) in D.

A formula A of L is satisfiable in D iff there exist a solution S and an assignment v in D such that (S, v)(A) = 1. More succinctly, A is satisfiable in D iff there exists an interpretation for L in D that satisfies it. A formula A of L is logically valid in D iff (S, v) satisfies A for every solution S for L in D and every assignment v for L in D. In abbreviated form, A is valid in D if every interpretation for L in D satisfies it.

A set of formulas Σ of L is satisfiable iff there exist a solution S and an assignment v in a domain D such that for every A Σ, (S, v)(A) = 1. If A is a formula of L, we will say that A is satisfiable iff it is satisfiable in some domain. A is logically valid iff it is logically valid in every domain.

If A and B are formulas of L, we say that A implies B iff for every domain D, every solution S for L in D and every assignment v for L in D, if (S, v)(A) = 1, then (S, v)(B) = 1.

If A and B are any two formulas of L, we say that A is logically equivalent to B iff for every domain D and every interpretation (S, v) for L in D, (S, v)(A) = (S, v)(B).

Remark

Regarding fleeing indices, we can differentiate among three cases: all subindices are variables; some subindices are variables and some are individual constants; and all subindices are constants. Löwenheim does not take into account fleeing indices of the second type; his examples only contain fleeing indices of the first type, and the variables on which they depend are all simultaneously replaced by constants. In practice, these indices can be assimilated to those of the first type. Löwenheim refers to indices of the first and third types as “fleeing indices,” but the term only genuinely applies to indices of the first type, since the indices whose subindices are all constants are treated as normal individual variables.

Although the semantics of quantified (genuine) fleeing indices is one of the aspects analyzed in this book, in the languages I have presented fleeing indices are never quantified. The reason is that this type of quantification does not actually intervene in Löwenheim's proof. Nonetheless, this does not prevent us from seeing how the definition of satisfaction would be extended if the language allowed it.

Let k_i1..._in be a fleeing term of L, v an assignment for L in D, T the set of terms generated by k_i1..._in in D and f a function from T into D. We define an assignment v_f for L in D, as follows:

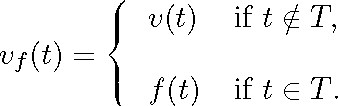
If S is a solution for L in D, we can now complete the definition of satisfaction with the following clause:

(A.1) (S, v)(k_i1..._inA) = 1 iff there exists a function f from T into D such that (S, v_f )(A) = 1.

The clause corresponding to the universal quantifier is the dual of theclause above.³

Note that this is the way in which we defined the concept of satisfaction for quantified fleeing indices in chapter 3. More specifically, (A.1) expresses the same idea as (3.11).⁴ The differences between the two formulations derive from the greater formal rigor and generality that I have just given. This becomes clear when we think of the assumptions under which we proceeded in chapter 3.

If we assume, as Schröder and Löwenheim do, that existentially quantified fleeing indices are followed by all of their universally quantified subindices, then there is no need for f to assign elements of the domain to all the terms generated by k_i1..._in; it suffices that f be a function from {k_a1..._an | a₁,...,a_n D} into D.⁵ If, to move even closer to (3.11), we suppose that the fleeing term has only one subindex, it will suffice that f be a function from {k_a | a D} into D. Clearly, in this case, the function f coincides essentially with the indexed family of elements of the domain mentioned in (3.11).

A tacit assumption that Schröder and Löwenheim both make—expressed in present day terminology—is that the formulas do not have free variables. The whole of chapter 3 is written under this assumption. However, in order to know whether a formula without free variables is satisfied or not by a solution in a given domain, the only terms whose assignment we need to know are those generated by its fleeing indices; this is precisely the information that the function f provides.

If we make all the assumptions I have just mentioned, we can simplify (A.1) as follows:

S(k_iIIiA) = 1 iff there exists a function f from {k_a | a D} into D such that (S,f)(IIiA) = 1.Obviously, in the context of the definition of satisfaction this statement expresses the same as (3.11).

It can be seen that, as stated in chapter 3 (subsection 3.4.4), this way of interpreting quantified fleeing indices is compatible with the nonfunctional character of these indices. If we want them to be functional, what we need to do is not to modify (A.1), but to restrict the concept of assignment in the way I have already described. The statement (3.11), then, tells us nothing at all about whether the fleeing terms have a functional character or not. In the same way, we observe that is a quantification over functions even if the fleeing terms do not behave functionally, since, put slightly informally, it means that there exists a function of a certain type.

Finally, as I state in subsection 6.2.2 of chapter 6, it is evident that A is satisfiable in a domain D if and only if A is satisfiable in the same domain. Indeed, if A is satisfiable in D, there are a solution S and an assignment v in D such that (S, v)(A) = 1. If we take f in such a way that v_f = v, it is obvious that (S, vf )(A) = 1. This shows that A is satisfiable in D. The other conditional is immediate.

A.3.3 Coincidence and substitution lemmas

Lemma A.3 (of coincidence) Let A be any formula of LD. If v and are assignments in D that agree on the free variables of A, on the fleeing terms of A, and on the terms generated in D by the fleeing terms of A, then for every solution S in D, (S, v)(A) = (S, )(A).

Observe that if the assignments v and only agree on the free variables in A, it may be that (S, v)(A) 6= (S, )(A).

Corollary A.3.1 Let v and be assignments in D and A any formula of LD whose fleeing terms depend only on elements of the domain. If for every term t that occurs in A, v(t) = (t), then for every solution S in D, (S, v)(A) = (S, )(A).

Corollary A.3.2 If A is a sentence of LD without fleeing indices and S is a solution for L in D, then for every assignment v and in D, (S, v)(A) = (S, )(A).

By virtue of this lemma, if A is a sentence of L_D without fleeing indices, we can omit the reference to the assignment and simply write S(A). If S(A) = 1; we will say that the solution S satisfies A in D or that A is satisfied by S in D.

Lemma A.4 Let (S, v) be an interpretation for L in D and (, ) an interpretation for L in such that D, the restriction of S to , and an assignment for L in . If A is a formula of L without quantifiers and for every term t in A, v(t) = (t), then (S, v)(A) = (, )(A).

Lemma A.5 (of substitution) Let S be a solution in D, v an assignment in D, t a term of L without free variables, and A a formula of L.

(1) If is not a fleeing term that depends on i, then

(2) If in A there is no fleeing term that depends on i, then

Lemma A.6 Let (S, v) be an interpretation for L in D and A a formula of L_D without quantifiers. If for every term occurring in

A,

then

Proposition A.7 Let A be a formula of L and S a solution in a domain D. If no fleeing term depending on i occurs in A, then there exists an assignment v such that (S, v) = 1 iff there exists an assignment v0 such that (S, )(A) = 1.

A.4 THE LÖWENHEIM NORMAL FORM

We say that a formula is in Löwenheim normal form if it has the form , where and II represent (possibly empty) strings of existential and universal quantifiers, respectively, and F is a quantifier-free formula. In other words, a formula is in Löwenheim normal form if it is in prenex form and no existential quantifier occurs in the scope of a universal quantifier.

If A is a formula without fleeing indices, we can transform A into a formula in Löwenheim normal form by following these steps:

1. Introduce in A the alphabetical changes required to ensure that no variable is quantified more than once and no variable is both free and quantified.

2. Obtain a formula in prenex form logically equivalent to the formula that results from the above transformation.

3. Remove each existential quantifier occurring in the scope of a universal quantifier and replace the variable k by k_i1..._in, where i₁,...,i_n are all the universally quantified variables that preceded taken in any order.⁶

An example will help to clarify the last step. Let us suppose that the formula resulting from the two first transformations is

The normal form of this formula is the result of removing the existential quantifiers and and substituting ji for j and lik for l:

As this example shows, each time the last transformation in the procedure is applied, a fleeing term is introduced. Thus, although the original formula A may not have any, whenever this transformation is applied more than once, all the applications after the second one will be performed on formulas that already have fleeing indices.

Proposition A.8 Let A be a formula of L and S a solution in a domain D: If the variable k does not occur in the fleeing terms of A, there exists an assignment v in D such that (S, v)(II_i1,...,_inkA) = 1 iff there exists an assignment such that (S, ) = 1.

Proof. We prove the lemma just for n = 1 (i.e., for the case of only one universal quantifier), as the argument is easily generalizable,. Let A be any formula (with or without fleeing indices, and in prenex form or not), and S a solution in a domain D: We assume that the variable k does not occur in the fleeing terms of A; this assumption will allow us to apply Lemma A.5.

(a) Suppose that there exists an assignment v in D such that

For every a D, we define the set X_a in the following way:

By (A.2), for every a D, X_a . Let f be a choice function for {X_a | a D}. We now define an assignment in D by

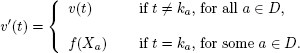
Since f(X_a) X_a, for every a D,

The assignments v and differ at most in the values assigned to the terms of the form k_a, but for every a D, k_a does not occur in thus, by the lemma of coincidence, for every a D,

Now, for every a D

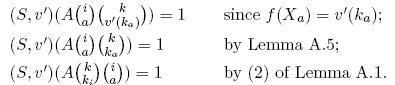
This shows that

(b) Suppose that there exists an assignment v in D such that

Thus, for every a D,

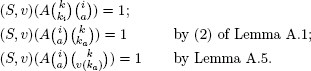
This proves that

Corollary A.8.1 Let A be a formula in prenex form without fleeing terms and a formula in Löwenheim normal form obtained from A by applying the transformation described in the third step of the method sketched above. For every domain D and every solution S for L in D, there exists an assignment v such that (S, v)(A) = 1 iff there exists an assignment such that (S, ) =1.

Proof. is the result of applying the mentioned transformation a finite number of times. Thus, it suffices to observe that Proposition A.8 can be applied each time this transformation is used.

Proposition A.9 Let A be any sentence of L without fleeing indices and a formula in Löwenheim normal form obtained from A by applying the method sketched above. For every domain D and every solution S for L in D, S(A) = 1 iff there exists an assignment v such that (S, v)() = 1.

Proof. We consider proven that every sentence is logically equivalent to its alphabetical variants and to a sentence in prenex form. Thus, we only have to show that the proposition holds for the transformation described in the third step, but this is an immediate consequence of Corollary A.8.1.

Remarks

(1) I have not followed Löwenheim's procedure for obtaining the normal form because, as I explained in chapter 4, it is incorrect.

(2) Observe that (A.1) allows us to prove that ) is logically equivalent to ). The proof is a straightforward variant of the above.

A.5 LÖWENHEIM'S THEOREM

A.5.1 Löwenheim's sequence

Let II_i1...i_nF be a formula of L, where F(i₁,...,i_n) is a quantifier-free formula whose fleeing terms, if any, do not depend on variables other than i₁,...,i_n (although all the terms do not necessarily depend on all of these variables). To simplify our references, we will call this formula IIF. Fix an enumeration j1, j2,... of all individual variables that do not occur in IIF or, if they occur, are free in IIF. The free variables of IIF, if there are any, are an initial segmentof the enumeration. In this way, if IIF is a sentence, the variables j1, j2,... do not occur in IIF.

Let us now define simultaneously and recursively two sequences of formulas (F_x, P_x, x ≥ 1), one of sets of individual variables (J_x, x ≥ 1) and one of sequences of terms (T_x, x ≥ 1), as follows:

(1) If IIF is a sentence, J₀ = {j₁}. If IIF is not a sentence, J₀ is the set of its free variables. Suppose that J₀ = {j₁,...,i_m}. Let F₁ be the product of all the formulas that are obtained when the universally quantified variables of IIF range over the elements of J₀. That is, if {s₁,...,s_h} is the set of all functions from {i₁,...,i_n} into J₀, then

If IIF does not have fleeing indices, then for every n, P_n = F₁ and J₁ = J₀. If m is the number of elements of J₀, let T₁ = (t_m+1,...,t_p) be an enumeration starting at m+1 of the fleeing indices of F₁. Let P₁ be the result of replacing the term t_z by j_z in F₁ and J₁ the set of free variables of P₁, that is, J₁ = f₁, j₂,...,j_m,...,j_p}.

(2) Assume that P_x is defined. Let J_x be the set of individual variables that occur in P_x and {s₁,...,s_d} the set of functions from {i₁,...,i_n} into J_x. As before, let F_x+1 be the product of all the formulas obtained when the quantified variables of IIF range over the elements of J_x, that is,

Notice that the fleeing indices of F_x are also fleeing terms of F_x+1. Let us now suppose that T_x+1 = (t_m+1,...,t_q) is an enumeration of the fleeing indices of F_x+1 that conserve and expand the numeration T_x. That is, if a fleeing term already occurs in F_x and according to T_x is the nth term, in the new enumeration it will still be the nth term. Let P_x+1 be the result of replacing the term t_z by j_z ) in F_x+1. Finally, J_x+1 is the set of the free variables of P_x+1, that is, J_x+1 = {j₁, j₂,...,j_q}.

We will say that the sequence P₁, P₂, P₃,.... is Löwenheim's sequence for IIF.

Example

Let us suppose that

IIF = IIi₁i₂F(i₁, i₂, j₁, h_i1, k_i1i2)

and let j₂, j₃,... be a fixed enumeration of the variables that do not occur in IIF. We will obtain the two first formulas of Löwenheim'ssequence for IIF.

Since j₁ is the unique free variable of IIF, J₀ = {j₁}. If in order to simplify the notation, instead of j₁,j₂,..., we write only the corresponding subscript, then

If the fleeing indices of F₁ (h₁ and k₁₁) are enumerated from 2 onwards in the order in which they occur in F₁ and are replaced by the variables j₂ and j₃, respectively, then

F₂ is the product of the formulas obtained when the quantified variables of IIF range over the elements of J₁. Thus,

If we now suppose that the new fleeing indices of F₂ (i.e. those that do not occur in F₁) are enumerated from 4 onwards in the order in which they occur in the formula and the nth term is replaced by j_n,

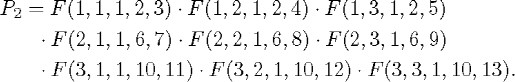
To obtain P₃ we would first form the product obtained when the quantified variables of IIF range over the elements of J₂ (= {j₁, j₂,...,j₁₃}). We would then enumerate the new fleeing terms beginning with 14, and, finally, we would replace them by the corresponding variables of the enumeration j₂, j₃,... .

Remark

If the universal quantifiers of IIF are removed according to any order that is preserved and expanded in each case (as in the example), then for every x > 0, F_x+1 = F_x · A, and, therefore, P_x+1 = P_x · A.

A.5.2 Löwenheim's theorem

Before proving the theorem I would like to note, first that, for the reasons stated in section 6.3 of chapter 6, I will not use Löwenheim's sequence in the proof of the theorem, and, second, that in this case I prefer to include the comments that relate my proof to Löwenheim's as footnotes. There is nothing in the proof that depends on what is said in the notes.

Theorem A.10 (of Löwenheim) If A is a sentence of L without fleeing indices which is not satisfiable in any finite domain, and S is a solution in an infinite domain D such that S(A) = 1, then there is a denumerable D such that the restriction of S to satisfies A.

Proof. Let A be a sentence of L without fleeing indices which is not satisfiable in any finite domain but is satisfied by the solution S in an infinite domain D. Let be a formula in Löwenheim normal form obtained from A by applying the method sketched in section A.4. We can suppose, without loss of generality, that IIF (the result of removing the existential quantifiers of IIF) has the characteristics mentioned at the beginning of subsection A.5.1. By Propositions A.7 and A.9, IIF is not satisfiable in any finite domain and there exists an assignment v in D that such that (S, v)(IIF) = 1.

If f is a function, let ran(f) and dom(f) be the range and the domain of f; respectively. If f is a function and X is a set, is the restriction of f to X (i.e., . I will introduce a new definition of the notion of a term generated by a fleeing index that is more suitable for this proof than the one presented in A.3.1. If k_r1..._rn is a fleeing term and X is a subset of D, then {k_a1...a_n | a₁,...,a_n X} is the set of terms generated by k_r1...r_n in X, and G_X is the set of terms generated by the fleeing indices of IIF in X.

Let d be a fixed element of D and J₀ the set of free variables of IIF.

We define by recursion a sequence of sets as follows:

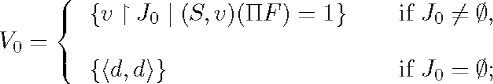
I will call the functions in V_n partial assignments of level n. (Recall that d is also a term of L_D; therefore {(d, d)} can also be seen as a partial assignment.) The range of a partial assignment determines a set of terms: the one generated by the fleeing indices of II F when the universally quantified variables take values over the elements of therange. If IIF is not finitely satisfiable, a partial assignment g of level n does not assign values to all the terms generated by its range, but it has an extension of level n + 1 that determines those values in the appropriate way.

Every partial assignment of level n has an extension of level n + 1. For assume that g V_n. There exist then a partial assignment A_n–1 and an assignment v such that

The function is a partial assignment of level n + 1 that extends g.

If H is a choice function for the class of all non-empty sets of partial assignments, we define by recursion a sequence of functions f2... as follows:

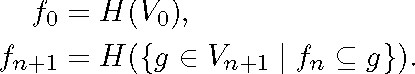
Observe that the axiom of choice is used correctly, since V₀ (as IIF is satisfiable) and every partial assignment of level n has an extension of level n + 1.⁷

Let f and let be the range of f and the restriction of S to . We claim that the function f determines the values of all terms required to evaluate the truth of IIF under the solution in . In order to prove this, we define an assignment for L in that extends the function f.