If a₀ is a fixed element of and t is a term of L, then

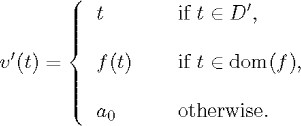
Let a₁,...,a_n be any elements of . We will show that

(recall that F (a₁,...,a_n) = and IIF = IIi₁ ... i_nF).⁸ Since for every m N, f_m fm+1, and for every a , there exists m such that a ran(f_m), it is evident that there exists m such that a₁,...,a_n ran(f_m). Suppose that m is the least number such that a₁,...,a_n ran(f_m). We now observe that the terms of F (a₁,...,a_n) are a₁,...,a_n, the free variables of IIF (i.e., the elements of J₀) and the terms generated by the fleeing indices of IIF when i₁,...,i_n take the values a₁,...,a_n, respectively. Thus, with the exception of a₁,....,a_n, all the terms of F (a₁,....,a_n) belong to dom(f_m+1).

Let v₀ be an assignment in D such that

(the construction of the sequence f₀, f₁,... guarantees the existence of V₀). Clearly,

It easy to see that the assignments v₀ and agree on the terms of F (a₁,...,a_n). Let t be a term of F (a₁,...,a_n). If t ,

if t dom(f_m+1),

By Lemma A.4,

This show that

In order to conclude the proof, it remains only to show that is denumerable. Obviously, is countable because it is the union of a denumerable sequence of finite sets. If were finite, IIF would be finitely satisfiable, contradicting the hypothesis of the theorem. Thus, is denumerable.

¹If the variables on which the fleeing term depends are existentially quantified, as is the case for example in ΣiA(i, K_i), the problem of correctness does not arise, because this type of formula is the result of putting the universal quantifiers in front of the existential quantifiers:

²Rv(t₁) ... v(t_n) is the sentence that results from replacing in Rt₁ ...t_n each m (1 ≤ m ≤ n) with V(t_m).

³Observe that if A is a quantifier-free formula, then

⁴Recall that (3.11) states the following:

ΣkiIIiA(i, k_i) is true with S in D iff there is an indexed family (K_a | a D) of elements of D such that for all a D, A[a, k_a] is true with S in D.

⁵In fact, when in the previous chapters I speak of terms generated by a fleeing index K_i1..._in, I mean the terms of this set. I have introduced a more general definition than is required by the proof of Löwenheim's theorem for the sake of the lemmas in the next subsection.

⁶The existential quantifiers occurring in the scope of a universal quantifier are removed because quantification on fleeing terms is not allowed in L.

⁷The sequence f₀, f₁, f₂,... corresponds to the sequence of formulas Q₁,Q₂,Q₃,... constructed by Löwenheim, but my proof of the existence of the sequence is different from Löwenheim's. If the levels were finite (as is the case in Löwenheim's proof), it would be enough to prove that for every n, V_n , in order to be sure that at each level there must exist a partial assignment having infinitely many extensions. This fact would enable us to show (reproducing the proof of the infinity lemma) the existence of a sequence f₀, f₁, f₂,... such that for every n, f_n V_n and fn f_n+1. Essentially, this is how Löwenheim proceeds in his construction of the sequence of formulas.

It can be proven that for every n N, f_n f_n+1, and perhaps it would be closer to Löwenheim's argument to do so, but then my proof would become a little repetitive. Rather schematically, to show that for every n N, f_n f_n+1, we have to begin by observing that if there exists n such that f_n = f_n+1, then for every m > n, f_m = f_n. This means that ran(f_n) is a closed finite subdomain, i.e., a subdomain of D such that the terms generated by the fleeing indices of IIF in ran( f_n) takes values in ran(f_n). We would prove then that IIF is satisfiable in ran(g), contradicting the hypothesis of the theorem. This fact is proven in the same way in which I will show that IIF is satisfiable in .

⁸The assignment may not treat the fleeing terms of L functionally. In addition, the formulas of Löwenheim's sequence may not be true under (, ). However, if j₁,...,j_m are the free variables of IIF and t_x is the fleeing index replaced by the variable j_x in the construction of Löwenheim's sequence, the assignment for L in defined by|

is such that (, v₂) satisfies all the formulas of Löwenheim's sequence. This proves that if IIF is satisfiable, then for every n N, P_n is satisfiable.