The simplest possible frame is the identity frame. If we take coordinate labels for points on S³ to be (w, x, y, z)—standing for the Euler-eigenvector rotation parameterization q = (cos(θ/2), sin(θ/2))—the 3D identity frame can be represented by either of the two possible quaternions, q = (1, 0, 0, 0) and q = (–1, 0, 0, 0).

Figure 11.1a represents the standard positive hemisphere of the vector part of the quaternions, and the black dot at the origin is the quaternion identity q = (1, 0, 0, 0). We cannot see q = (–1, 0, 0, 0) in this visualization because we can only draw one hemisphere of S³ at a time projected to this coordinate system. On the other hand, if we switch from the standard (x, y, z) projection to the (x, y, w) projection (shown in Figure 11.1b), we can see both alternative signs of the identity quaternion, with the black dot showing q = (1, 0, 0, 0) and the white dot showing q = (–1, 0, 0, 0).

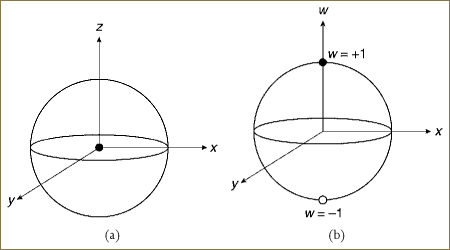
Figure 11.1. (a) The identity frame, q = (1, 0, 0, 0), is a point at the origin in our standard “vector-only” projection. (b) Looked at from the side, we see that this quaternion is of unit length, with the only nonzero component w = 1, as we can infer from the fact that all quaternion frames must have unit length.

If we wish to examine two isolated frames q₁ and q₂ and their relationship, the first thing we need to do is to remember that we should always simplify our lives in this situation by making a good “anchor” for our visualization. We can accomplish this by simply translating q₁ back to the identity frame using

Equation 11.1. 

and applying the same transformation to q₂ to produce a new quaternion p that has the same relation to the identity as q₂ does to q₁:

Equation 11.2. 

Then, as shown in Figure 11.2, we can simply plot (p_x, p_y, p_z) in the standard eigenvector coordinate system. The relationship to the identity transform (the origin of the coordinate system) is immediate: If we denote the vector part of the quaternion by p = (p_x, p_y, p_z), then q₁ and q₂ are related by a rotation about the fixed axis in the direction of

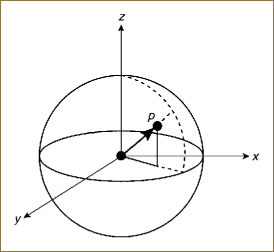
Figure 11.2. The relationship between two arbitrary quaternions, simplified by transforming q₁ back to the identity, leaving the relationship defined completely by .

and with a total angle of rotation about given by

The simplest example of a rotating frame is a parameterized sequence of rotation matrices. For example, this might be a rotation about the axis by an angle ranging from 0 (the identity frame) to θ using intermediate angles tθ with 0 ≤ t ≤ 1:

The corresponding family of quaternions is simply the line segment given by

In the standard coordinate system, the visualization of this family of frames is the straight line on the axis, shown in Figure 11.3a. Viewing this curve from the side to show the (redundant) w coordinate explicitly yields Figure 11.3b.

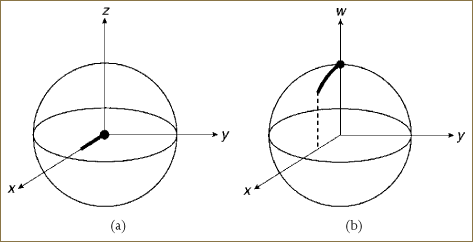
Figure 11.3. A sequence of frames formed by rotating about the axis. (a) Usual projection. (b) w projection.

To replace the rotation about the axis by a rotation about an arbitrary axis , we simply reorient the straight line on the axis (Figure 11.3a) to point in the direction . Figures 11.4a and 11.4b show the corresponding general cases for a sequence of frames generated by a rotation about the axis.

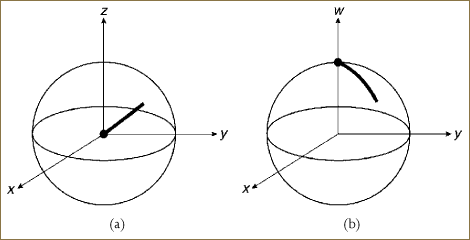
Figure 11.4. A sequence of frames formed by rotating about the axis. (a) Usual projection. (b) w projection.

Using the axis as a reference frame: In conclusion, it is important to note that for the case of the simple rotation about the axis we really do not need to consider anything but the -axis rotation! Just as we understood the relationship between q₁ and q₂ more clearly by translating q₁ back to the identity frame, there is a direct construction that transforms a rotation about the axis back to a “standard” equivalent rotation about the axis, which one can adopt as the “reference origin” for studying these simple rotations. The explicit transformation is achieved by rotating the direction back to the direction using the fixed rotation axis and angle φ derived from

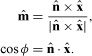
Quaternion frames are points in space with clearly visualizable relationships. By creating plots relying on a variety of display strategies, we not only see the relationships between isolated frames but clearly understand the essential properties of continuous families of orientation frames (e.g., resulting from the application of smooth rotations). In the next chapter, we will exploit this concept of a connected family of rotations to see one way in which everyday 3D space itself gives unmistakable evidence for the existence of quaternions. The ability to make smooth deformations of quaternion paths will also play an essential role in advancing our understanding.