The calculus of quaternions involves studying infinitesimal forms and rates of change. These infinitesimal transformations of quaternions are closely related to their logarithms and exponentials, and we will begin by exploring the relationships among quaternionic logarithms, their exponentials, and quaternion calculus. As is now our custom, we will begin to study these objects and their visualizable properties starting from complex numbers, from which we will see that the polar form of a complex number has particularly useful properties that we will be able to exploit in assisting our intuitions.
Infinitesimal transformations of quaternions are closely related to their logarithms, and the relationship between quaternionic logarithms and their exponentials provides another visualization viewpoint. We introduce the subject here by using, once again, unit-length complex numbers. The quaternion formulas will be very similar, with the important exception that the order of multiplication is not arbitrary.
The logarithm is of course simply the object that when exponentiated produces the argument of the logarithm. In the case of unit-length complex numbers,
log(eiθ) = iθ, |
up to an arbitrary additive factor of 2nπi, since
ei(θ + 2nπ) ≡ eiθ |
for an integer n. However, the real essence of this mathematical tool, which ultimately allows us to work with the order-dependent quaternion algebra instead of just the order-independent complex algebra, is the relation among the logarithm, infinitesimal quantities, and the power series expansion for the exponential. (The power series ultimately gives us a way of handling order dependence.) To begin, the formula for the exponential series is
where by definition
log et = t. |
We are interested in unit-length complex numbers and their derivatives. One way of studying them is to replace t with itθ, converting the exponential into a unit-length complex number due to Euler’s formula. This is represented as
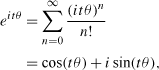
which can be proven in a number of elegant ways, e.g., from the power series for the trigonometric functions.
However, the most striking properties of this expression are found by exploiting the power series to investigate small changes in t, leading to derivative formulas and a sense of the nature of calculus for unit-length complex numbers—ultimately leading to quaternions. For example, if we take a unit-length complex number eiθ to a power we find
(eiθ)t = eitθ. |
Since det/dt = et, the derivative with respect to t is
Similarly, because d if log x = dx/x we have
What is more interesting for us is this: Imagine a picture (see Figure 9.1) in which we think of the logarithm as living “upstairs” in the exponential and the result of the entire power series as living “downstairs” on the bottom line of the equation. Then we can start to see the following.
The exponential is linear upstairs: The logarithm is a pure imaginary nonperiodic number whose magnitude has no bound and whose imaginary part therefore looks like the real line.
The exponential is curved, possibly periodic downstairs: There is a direct correspondence between the flat-space appearance of the logarithm values and the image as each point is mapped to S1 by the exponential function. In particular, because i(θ + 2nπ) produces the same point on the circle as iθ for any integer n, the same point on the circle may correspond to an infinite number of distinct points in the logarithm.
Figure 9.1. A straight, purely imaginary, line “upstairs” in the argument of the exponential function becomes a periodic circle “downstairs” in the complex plane.
In summary:
The Exponential Map
We may therefore visualize the logarithms and their correspondence to points on the circle S1 directly by watching the map from a point on a straight line to a possibly periodically repeated point on a circle, as illustrated in Figure 9.2.
Figure 9.2. Visualizing the exponentiation of a complex logarithm, which is in an unbounded 1D flat space, to produce a result that follows a periodic path on the circle S1.
† Mathematical note: “Upstairs” is essentially where the Lie algebra of a group lives, and “downstairs” is where we see the Lie group itself. For example, if we look at the coefficient of i in the exponential form of a unit-length imaginary number it can take any value on the real line. Once we look at the value of the exponential, however, it must lie on a unit circle in the complex plane, and this circle is precisely the topological group U(1).
Quaternion logarithms follow almost exact parallels to unit-modulus complex numbers. In fact, for any quaternion with 
contained completely in one Cartesian axis, for example, = (1, 0, 0), we recover a unit-modulus complex number. Thus, knowing that
and knowing that the quaternion p = (a, b, 0, 0) obeys exactly the same algebra as complex numbers,
p1 * p2 = (a1a2 – b1b2, a1b2 + a2b1), |
we can deduce that
implies
We are quickly led to attempt to expand the power series of a pure-vector quaternion of the form 
. Substituting into the exponential power series and using the quaternion algebra of Equation 7.5, we find by direct computation that
Therefore, because by definition p = exp(log p),
Standard operations such as taking derivatives proceed in the usual way. Because 
appears in every term of the exponential power series
where the products are quaternion products, we can pull out a factor of logq at either the beginning or the end and obtain the same result. Using the power series to compute the derivative terms, we may resume with the factor of logq at either end, yielding the derivative formula
Polar (logarithmic) version of the multiplication rule: Just as the complex-number multiplication rule exhibits some simplification in polar form, we can use quaternion logarithms to seek a similar quaternion expression. Just as we could rewrite the complex multiplication algebra suggestively as (r1, θ1) * (r2 θ2) = (r1r2, θ1 + θ2), we can do the same for quaternions in a polar form in which the “angle” is a pure quaternion vector:
Here,
and cos(θ12/2) = p0q0 – p · q. Noncommutativity makes this form much less useful than the complex case, but because ‖ (r, θ)‖ ≡ r and (r1)(r2) = (r1r2) it does show that the norm-preserving algebra holds directly.