In this chapter we complete our set of fundamental visualization methods by studying interpolation in the context of spheres, and eventually in the context of quaternion points. The interpolation from one quaternion to another has profound analogies with standard polynomial interpolation methods in Euclidean space. We will see that geodesic curves on spheres provide the starting point for a rich family of interpolation methods and their graphical depiction.
We will begin with the most fundamental object—the interpolation that creates a great circle on a sphere of any dimension. This interpolation is in fact slightly nontrivial to derive even for S1. The derivation we present is the classic method used throughout the mathematical and group theory literature but less often seen in the computer graphics literature.
In Euclidean space, linear interpolation (sometimes abbreviated LERP) takes the form
x(t)= x0 + t(x1 – x0) = (1 – t)x0 + tx1, |
where—with x(0) ≡ x0 and x(1) ≡ x1—taking 0 ≤ t ≤ 1 restricts the parametric curve to the straight line segment between x0 and x1. The LERP is shown in Figure 10.1. However, it would be silly to apply the LERP to points q on a sphere, because even if ‖q0‖ = ‖q1‖ = 1 the linearly interpolated point
p(t)= (1 – t)q0 + tq1 |
will not have the desired properties. We can see easily from Figure 10.2 and the direct computation
p(t) · p(t) = 1–2t + 2t2 + 2t (1 – t)cos φ, |
Figure 10.2. A linear interpolant between the two points q0 and q1 on a circle in any dimension is not on the circle in general.
where q0 · q1 = cosφ, that ‖p(t)‖ can be anywhere from 0 to 1 and thus will not describe a point on the same circle as q0 and q1. Figure 10.3, in contrast, shows the more desirable circular arc interpolation.
Note: Of course it is possible to renormalize a linearly interpolated p(t) at every point to give it unit length and therefore force it to lie on the sphere. However, this neglects the fact that one of the goals of a linear interpolator is the enforcement of constant velocity in the parameter t. Therefore, the correct analog for the spherical linear interpolator is the enforcement of constant angular velocity. Renormalizing p(t) cannot achieve this goal. Examining the projection of equally spaced portions of the straight line from q0 to q1 in Figure 10.4 to the circle, we see that the resulting circular arc segments are never equally spaced. The subtle but important differences between the angular velocity properties of the normalized LERP and the spherical linear interpolation (SLERP) are illustrated explicitly in Figures 10.4 and 10.5.
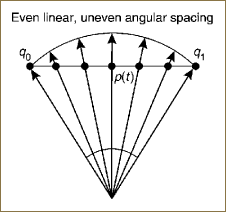
Figure 10.4. A linear interpolant between the two points q0 and q1 on a circle in any dimension is not on the circle in general.
The SLERP has the goal of automatically adjusting the value of the interpolated vector so that it is guaranteed to lie on the circle and to maintain constant angular velocity. We have already seen something similar to this, in our circle-preserving algebra visualization (Figure 7.1). The method for meeting the requirements of the SLERP, which extends trivially to any dimension once we have worked it out for the circle S1 in 2D, is based on the classic Gram–Schmidt procedure. We begin as before by taking two points q0 and q1 on the circle, or any sphere, obeying ‖q0‖ = ‖q1 ‖ = 1. We impose one restriction, namely, that the angle φ describing the angle between the two vectors, where
cos φ = q0 · q1, |
satisfies 0 ≤ φ < π. These conditions can be relaxed if care is taken, but this range turns out to be all that is needed for most quaternion applications.
To find an interpolated unit vector that is guaranteed to remain on the sphere, and thus preserve its length of unity, we first assume that one vector, say q0, is the starting point of the interpolation. To apply a standard rotation formula using a rigid length-preserving orthogonal transformation in the plane of q0 and q1, we need a unit vector orthogonal to q0 that contains some portion of the direction q1. Defining
we see that by construction
where we of course continue to require q0 · q0 = 1. The denominator of this expression has the curious property that
‖q1 – q0(q0 · q1)‖2 | = | 1 – 2cos2 φ + cos2 φ |
= | sin2φ, |
where we recall that cosφ = q0 · q1 Note that because we have imposed 0 ≤ φ < π, the sine is always nonnegative, and we can replace |sinφ| with sinφ, which we will find convenient in the following. When φ = 0, there is no interpolation to be done in any event.
Referring to the graphical construction shown in Figure 10.6, we next rephrase the unit-length-preserving rotation using the angle tφ, where 0 ≤ t ≤ 1 takes us from a unit vector aligned with q0 at t = 0 to one aligned with q1 at t = 1. Using our new orthonormal basis, we thus have
Figure 10.6. The length-preserving spherical interpolation framework, showing the construction of a new orthonormal basis (q0, 
) that allows us simply to rotate the unit vector rigidly using sines and cosines.
This is the SLERP formula, which guarantees that
q(t) · q(t) ≡ 1 |
by construction. The fact that q(0) = q0 is obvious, whereas the fact that q(1) = q1 is slightly more subtle, recognition of which depends on our observing in Figure 10.6 that cosφ is the component of q1 projected onto the q0 axis (remember again the definition of cos φ), and sin φ can only be the remaining component in the orthogonal direction. In summary:
SLERP Properties
Another way of understanding the SLERP is directly in terms of a linear algebra problem (e.g., see Eberly [41]). Let q be a unit vector on a sphere (we will be thinking of quaternions, but it does not matter what dimension the sphere is). We assume that q is located partway between two other unit vectors q0 and q1, with the location defined by some constants c0 and c1 as
As shown in Figure 10.7, q must partition the angle φ between q0 and q1, where cos φ = q0 · q1, into two subangles, φ0 and φ1, where cosφ0 = q · q1 and cosφ1 = q · q0 and φ = φ0 + φ0. The apparently backward labeling is in fact intentional: it is chosen so that φ0 = φ makes q = q0 and φ1 = φ makes q = q1. No matter what the dimension of the unit-length qs, taking two dot products reduces this to a solvable linear system, as follows:
q · q0 | = | cosφ1 | = | c0 + c1 cos φ, |
q · q1 | = | cosφ0 | = | c0 cos φ + c1. |
Figure 10.7. Alternate length-preserving spherical interpolation framework, applying linear algebra to a partition of the angles with φ = φ0 + φ1.
Using Cramer’s rule, we immediately find c0 and c1:
When we replace φ by substituting φ = φ0 + φ1, after a little trigonometry we see that
where we have defined t0 = φ0/φ and t1 = φ1/φ to obtain a partition of unity, t0 + t1 = 1. Choosing, for example, t0 = 1 – t and t1 = t, we recover the standard SLERP formula (Equation 10.1).
Because the SLERP formula (Equation 10.1), applies to any sphere in any dimension, we can use the same formula for simple quaternion interpolation along a geodesic or great circle arc between two quaternion points q0 and q1 with cosφ = q0 · q1.
However, there are several special tricks that we will mention here, and apply in detail later on. In particular, comparing quaternion interpolation operations to ordinary linear interpolations reveals that even the simple ideas of the identity, addition, subtraction, and multiplication need to be handled in a new way, as specified by the following.
Identity: In linear interpolation, x = 0 is the identity. In quaternion interpolation, it is important to remember that quaternion multiplication forms a group and thus has an identity. The quaternion identity is not zero but is analogous to the complex identity value (1, 0):
qIdentity = (1, 0, 0, 0).
Addition: Addition is replaced by quaternion multiplication. In this way, we preserve such properties as the need to get back the same value if we add something to the identity. We thus transform addition in quaternion space as follows.
x1 + x2
⇒
q1 * q2
All of the basic properties are then preserved, and membership in the unit three-sphere is intact as well.
Subtraction: In linear interpolation, we often subtract two objects to get an incremental form of the interpolation—as in, for example, t(x1 – x0). Subtraction has no meaning for quaternion rotation representations, but in most cases where a difference would be used in a linear interpolation we can replace subtraction by a quaternion inverse displacement. The idea is that if x0 = 0 the difference must reduce to the object itself, but there must be a way of getting smoothly from one quaternion point to another. The technique is to premultiply by the inverse of the object you would subtract in ordinary arithmetic. Thus,
(x1 – x0)
⇒
(q0)–1*q1.
Multiplication: Just as subtraction is mapped into multiplication, multiplication is mapped into exponentiation. The quaternion analog of an expression such as t(x1 – x0) uses the factor t as a power, so that t = 0 is the null operation and t = 1 reaches the end via
where quaternion logarithms are treated in the preceding section.
Iteration: Iterative procedures such as the de Casteljau construction can be converted into Bezier splines and B-splines just as is done for linear splines by substituting different control points. For almost any case of this sort, following the quaternion substitution rules for the linear interpolation arithmetic analogies just given works straightforwardly.
We may, in fact, write the SLERP equation now with a completely alternative derivation based on the arithmetic analogies just presented. Following these rules, we would convert the Euclidean expression
x(t) = x0 + t(x1 – x0) |
to the analogous quaternion expression
To see the equivalence of this notation to the others presented, we first note that the scalar component of the quaternion product 
is in fact
Second, we see that we can isolate all essential features of the interpolation by looking at the special case q0 = identity = (1, 0, 0, 0). Then we can simply replace 
with an equivalent q1 whose scalar component agrees with Equation 10.4 and whose vector component is in the direction 
. Thus, q1 = (cosφ, sinφ). Then, we find
where we used log(q1) = (0, tφ). Displacing this to start the interpolation at any arbitrary q0 and using the value of computed from immediately gives the standard SLERP formula (Equation 10.3).
Although it is often claimed that the smooth orientation interpolations desired for computer graphics applications can only be obtained using quaternions, this is not strictly correct. Although the quaternion hypersphere S3 provides us with many capabilities that are most naturally described in terms of quaternions, and in particular quaternion distances for measuring the closeness of families of orientation frames, many individual tasks support alternative approaches that are equivalent to a quaternion approach.
The SLERP and the nested SLERP used to describe higher-order quaternion interpolations do in fact have a completely equivalent formulation that follows from the treatment in the previous section. All we need to do is replace the quaternions in the previous section by ordinary 3 × 3 rotation matrices.
† The logarithm of a 3 × 3 matrix is defined in a group-theoretic context as the associated 3 × 3 antisymmetric matrix (an element of the so(3) Lie algebra) that when exponentiated generates the desired SO(3) matrix corresponding to R(θ,
be a basis for the set of antisymmetric matrices, one can show that
Assuming that we can compute the necessary logarithms and axis-angle components of the chosen 3 × 3 rotation matrices R0, R1, and their products, the entire set of arguments follows through in exactly the same formal way, so that we may write
where we have explicitly denoted the 3 × 3 matrix multiplication by a dot (·) to indicate how matrix multiplication replaces quaternion multiplication in this context. With this formalism, we may replace any iterated SLERP operations on quaternions by iterated 3D matrix interpolations. However, in general it will be easier technically to implement the algebra using quaternion notation and use Equation 6.8 to compute R(t).