Quaternions are related in a fundamental way to 3D rotations, which can represent orientation frames and can act to produce changes in orientation frames. In this chapter, we begin by presenting the relationships among 2D rotation operations, 2D rotation matrices, and complex numbers. We then move on to 3D rotation matrices, examine an interesting idea that looks like the square root of a rotation, and finally relate all of this to 3D rotations and quaternions.
Rotations of 2D vectors are implemented by the action of 2D orthogonal matrices R2 with determinant one, and thus
The 2 × 2 matrix R2, written in the form
obeys by definition the constraints
det R2 = A2 + B2 = + 1 |
and
We have already seen the algebra of complex numbers, (x1 + iy1)(x2 + iy2) = (x1x2 – y1y2) + i(x1y2 + x2y1), in Chapter 3. The 2D rotations can be represented using unit-length complex numbers very simply as
which reproduces exactly the matrix results of Equation 6.1.
With some foreknowledge of where we are going, we now examine an apparently trivial way of rewriting 2D rotations. What we shall see is that although the exact parallels to quaternions do not appear in the standard 2D form of the rotation matrix or its complex equivalents they begin to reveal themselves when we make a half-angle transformation on the 2D rotation framework. If we simply let
A = a2 – b2, | B = 2ab, |
then we can see that with a = cos(θ/2) and b = sin(θ/2) we recover the original matrix, in that
A | = | cos2(θ/2) – sin2(θ/2) |
= | cosθ, | |
B | = | 2cos(θ/2)sin(θ/2) |
= | sinθ, |
and the rotation matrix is unchanged:
Note also that whereas det R2 = A2 + B2 = 1 when we compute the determinant using the variables (a, b) we find the curious property
We will see very soon that the pair (a, b) is interpretable as the simplest special case of a quaternion.
The complex version follows from the half-angle exponential
eiθ/2 | = | cos(θ/2) + i sin(θ/2) |
= | a + ib, |
where eiθ/2eiθ/2 = eiθ. Thus, via Equation 6.2 we see that eiθ/2 is literally the square root of the original complex number representing 2D rotations.
Like R2, the standard 3D rotation matrix R3 is also orthonormal:
However, the following two new features appear in 3D.
Order dependence: The product of two R3 matrices S and T may depend on the order in which the multiplication occurs. That is, except in special cases, we find that
S · T ≠ T · S.
Single real eigenvector: R3 has a single real eigenvector (Euler’s theorem), and thus all 3D rotation matrices (and their products) can be written as follows in terms of one single final rotation matrix R3(θ,
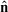) that leaves a particular 3D direction fixed: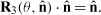
In addition to leaving
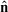fixed, R3(θ, 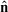) expresses all possible 3D rotations as a spinning by an angle θ about the direction .
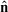We now drop the subscript, write R3 = R for simplicity, and introduce the conventional set of three 3D rotation matrices that are simply rotations in the 2D plane of each pair of orthogonal axes.
These produce right-handed rotations fixing the basis vectors 
= (1, 0, 0), 
= (0, 1, 0), 
= (0, 0, 1), respectively. Rx rotates the yz plane about its origin, Ry the zx plane, and Rz the xy plane. We can explicitly construct R(θ, ) as follows.
Let
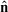= (cos α sin β, sin α sin β, cos β), with 0 
α < 2π and 0 β π, denote the fixed axis of the eigenvector about which we wish to rotate, as shown in Figure 6.1.Define
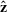as the column vector (0, 0, 1)T, and note that 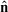= Rz(α) · Ry(β) · 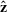.To construct the rotation matrix that spins about
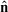, transform 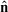to 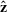by inverting the previously cited transformation, spin about 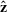by θ using the elementary matrix Rz(θ), and tilt 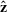back to the direction 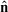(where it started):
Writing out all components of this product of matrices, and rewriting all appearances of α and β in terms of
|
we find finally that the desired rotation matrix fixing the direction is
where c = cosθ, s = sinθ, and · = 1 by construction. The manner in which the eigenvector emerges can be seen directly with the brief computation
Finally, we return to our half-angle form of the 2D rotation and observe that in each 2D subplane there must be a 3D rotation that corresponds to the half-angle form. For example, with n1 = n2 = 0 we must have n3 = 1, and thus
where a = cosθ/2, b = sinθ/2. It would seem highly probable that the general eigenvector form of the matrix can be expressed in terms of half angles as well, not just the Cartesian special cases. Thus, we are tempted to rewrite the entire matrix in terms of θ/2 using a = cos(θ/2) and b = sin(θ/2) for notational convenience. The factor (1 – c) in Equation 6.5 does not immediately take the same form as the expected 2D limit in Equation 6.6 until we have the insight that in fact a2 + b2 = 1. Then, motivated to make the substitution 1 – c = (a2 + b2) – (a2 – b2) = 2b2 we find the remarkable expression
Here we exploited the relation (n1)2 + (n2)2 + (n3)2 = 1 to make the expression even more symmetric by making the substitution
and its cyclic permutations.
This is a quadratic form that can now be written solely in terms of points on the hypersphere S3, and thus in terms of quaternions! To make this explicit, we choose the following parameterization for the set of quaternion variables on the hypersphere, an explicit choice that guarantees that q · q = 1 (see Equation 4.4) is satisfied.
With this substitution, we find the final result
Equations 6.5 and 6.8 are seen to be identical, R(θ, ) ≡ R (q), when we substitute Equation 6.7 into 6.8. In summary:
Relation of Quaternions to 3D Rotations
The quaternion equation 6.7, 
, when substituted into Equation 6.8, produces the standard matrix R(θ, ) of Equation 6.5 for a rotation by θ in the plane perpendicular to , where · = 1 is a unit three-vector lying on an ordinary sphere (the two-sphere S2) and θ is an angle obeying 0 θ < 4π rather than 0 θ < 2π. This extension of the range of θ allows the values of q to reach all points of the hypersphere S3.
† We now can verify various properties of Equation 6.8 that are important in linear algebra. For example, whereas the determinant of R2 in Equation 6.3 is a square of a sum of squares, for R3 it is a cube because there is one additional power in a determinant of a matrix that is one dimension larger:
det R3 = (q · q)3 = 1.
In addition, although it is complicated to verify, each row (or column) of Equation 6.8 has unit magnitude, as in, for example,
where we have used q · q = 1. In addition, each row (or column) is orthogonal to its neighbor, as in, for example,
and so on. These properties (each column or row has unit length and is orthogonal to its neighbors) define R as an orthogonal matrix.
Because the quaternion values appear only quadratically in the rotation matrix Equation 6.8, the matrix obeys
R(q) = R(–q), |
and thus:
Quaternions Double Rotations
Given an arbitrary rotation matrix M, one may recover the Euler-theorem eigenvector and the value of θ using an efficient direct calculation, avoiding the complexity of a general linear-algebra approach. The steps are as follows.
Axis computation: As long as sinθ is nonzero and large enough to avoid numerical errors,
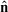may be computed by subtracting the transpose and using Equation 6.5 to find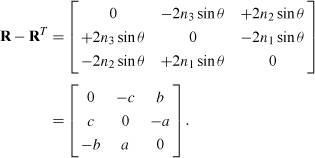
Numerically, we simply compute
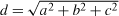and normalize to yield the result
Angle computation: Again, we return to Equation 6.5 and next examine its trace to find that
t = Trace R = 1 + 2cosθ.
Thus, the calculation is completed by taking
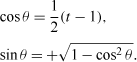
Because
, the sign of sinθ may be taken as positive in the square root without loss of generality.
† There are some cases for which this basic approach requires further (sophisticated) modifications. For example, if sinθ
There are many common ways to parameterize the standard 3 × 3 rotation matrices. So far, we have focused on the standard axis-angle version R(θ, ) of Equation 6.5 and its corresponding quaternion
where the eigenvector of R may itself be parameterized as the S2 point
|
This form has no degenerate variable states (due essentially to the explicit appearance of the eigenvector) and hence avoids gimbal-lock anomalies.
Many applications, however, treat rotations as sequences of axis-angle rotations, and this is one source of the gimbal-lock anomalies we will work through in Chapter 14. Triple sequences of axis-angle rotations are usually called Euler-angle representations, and we can easily relate these representations to corresponding quaternion parameterizations. The following are the two most common forms.
XYZ: Because this sequence of rotations involves all three independent Cartesian rotation axes, it is sometimes mistakenly thought to be singularity-free. The explicit matrix is typically written as
The corresponding quaternion is given by
One can see from the quaternion coordinates that at β = ±π/2, this is a function only at α + γ or α – γ, respectively,
ZYZ: The following sequence corresponds to a coordinate system used traditionally in classical and quantum physics to parameterize the motion of a spinning physical object.
where ĉ = (cos α sin β, sin α sin β, cos β) and
= (– sin α, cos α, 0). The corresponding quaternion is given byOne can see that at β = 0, this is a function only of (α + γ), and that at β = π this is a function only of (α – γ).
The fact that quaternion multiplication preserves membership in S3 leads to the observation that unit quaternions are a realization of the actual group manifold of the group SU(2), whereas ordinary 3D rotations belong to the group SO(3). Because the quaternion is a point q on the three-sphere S3, and because ordinary rotations identify each pair (q, –q) as the same point in their own manifold, ordinary 3D rotation matrices correspond not to the geometry of S3 but to S3/Z2, which is RP3, the real three-dimensional projective space. (For an extensive treatment of the properties of this space, we refer the reader to Weeks [167].)
Many treatments of quaternion rotations begin from a quaternion with a vanishing q0 component and derive Equation 6.8 directly by bracketing the “pure quaternion” υ = (0, v) between a pair of unspecified conjugate quaternions. In fact, when we carry out the computation as follows, we do find exactly the set of matrix components in Equation 6.8.
However, the interpretation of v = (0, v) as a 3D vector in the usual sense in this derivation is a subject of some controversy, eloquently discussed by Altmann [5]. It can be argued that, although Hamilton himself believed strongly in this interpretation, in fact (0, v) only coincidentally obeys the same transformation law as a pure vector. The alternative viewpoint is that, to be precise, v = (0, v) should be considered instead as a rotation by θ = π. Whichever viewpoint one takes, Equation 6.13 does in fact serve as a convenient alternative derivation of Equation 6.8.
In parallel with the complex exponential, an exponential approach using quaternions can be found. We will explore this in detail in a subsequent section. What we will see is that we can write the following exponential and expand it in a power series to find a quaternion expression corresponding exactly in apparent form to the complex expression for 2D rotations.
where the three components of i = (i, j, k) are the quaternion “imaginaries” of Hamilton’s original notation (Chapter 1), obeying i2 = j2 = k2 = ijk = –1. As a consequence, for each component (e.g., just the i component with q2 = q3 = 0) we recover precisely eiθ/2, which is literally the square root of the complex representation of this 2D subset of the 3D rotations. More details and related approaches are presented in Chapter 15.
We now know all of the basic properties of the relationship between complex variables and 2D rotations, and the remarkable ways in which they extend to the more complicated structures relating quaternions to 3D rotations. From this basis, we will build an elaborate framework for the analysis of the orientation properties of many different structures, ranging from curves in space to the properties of the human shoulder.