CHAPTER 10
Excitation, Inhibition, and Competition
Chapters 2 and 3 outline the defining operations of experimental extinction in the procedures of classical and instrumental conditioning. Other chapters, such as chapter 7, illustrate the use of extinction in particular experiments. The defining operations of secondary reward in chapter 7, for example, require measurement under conditions of extinction for primary reward. Extinction is an interesting and important phenomenon in its own right, however, and this chapter concentrates on the problems that the phenomenon of extinction presents for contingent reinforcement theory and cognitive expectancy theory, and also offers an alternative in terms of feed forward contiguity.
Figure 10.1 represents a typical experiment. In acquisition on Monday, S* always follows each correct response. In extinction on Tuesday, S* never follows any response. The third panel of Fig. 10.1 shows two alternative ways of treating the subject on Wednesday after extinction on Tuesday. The lower curve, labeled “Extinction 2,” shows a second session of extinction without S*. The upper curve, labeled “Reacquisition,” shows a session with S* again as on Monday. In a second session of extinction, the response tends to fall faster than in the first session and to fall to a lower level. In reacquisition, the response tends to rise faster than in the initial phase of acquisition, and to rise to a higher level.
In traditional theories, rewards strengthen and punishments weaken responses, but why should responding weaken during extinction? Why should something as neutral as nothing at all have a weakening effect? The only possibility within a reinforcement theory is some inhibitory process arising from nonreward.
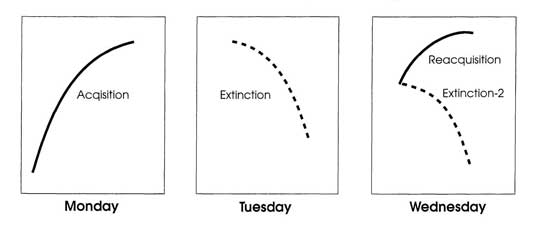
FIG. 10.1. Acquisition, extinction, reacquisition, and extinction 2. Copyright © 1997 by R. Allen Gardner.
A theory that attributes conditioning to a positive process of reinforcement must also include a negative process of inhibition. Otherwise, all learning would be permanent. The negative effect of aversive consequences is a source of inhibition that could weaken a learned response. That would be punishment. In reinforcement theories, the effect of an aversive S* is the reverse of the effect of an appetitive S*. But, extinction by the absence of any consequences requires still another source of inhibition.
In cognitive expectancy theories, the solution seems easier, at first. If the animals increase responding during acquisition because they expect S*, then they must decrease responding during extinction because they cease to expect S*. By this time readers should see that this is an empty explanation, because it is only a different way of saying that responses go up during acquisition and go down during extinction. The problem with expectancy theory becomes even more obvious in spontaneous recovery.
Spontaneous recovery is the most significant and least expected phenomenon shown in the third panel of Fig. 10.1. At the beginning of Wednesday’s session, there is less responding than there was at the beginning of extinction on Tuesday, but at the same time more responding than there was at the end of extinction on Tuesday. This increase in responding after a day of rest without any intervening experience in the experimental apparatus is called spontaneous recovery. Virtually all other experimenters since Pavlov replicated his discovery of spontaneous recovery. Can either reinforcement theory or expectancy theory cope with this finding?
According to reinforcement theory, the response went up on Monday because it was reinforced and down on Tuesday because of it was not reinforced. What happened to the inhibition of nonreinforcement overnight between the end of Tuesday’s extinction and the beginning of extinction 2 or reacquisition on Wednesday? Why is the recovery incomplete? In expectancy theory, the response went up on Monday because the animal learned to expect S* and down on Tuesday because the animal learned not to expect S*. In that case, what happened to the negative expectancy overnight? Why did only part of the positive expectancy recover? Spontaneous recovery seems to defy common sense. Yet, it is one of the most well documented phenomena in all of psychology.
HULL’S EXCITATION AND INHIBITION
Hull’s (1952) book is still the most complete and successful theory of reinforcement that we have at this writing, which is really not very high praise. The reinforcement mechanism in Hull’s theory is the drive reduction that results when a hungry animal eats or a thirsty animal drinks. Drive reduction builds up habit strength, the association between a stimulus and a response that leads to drive reduction. Hull’s symbol for habit strength is sHr and its value depends on a complex set of contributing variables that we can ignore here. Habit strength, in conjunction with a few more variables that need not concern us here, determines excitatory potential or sEr, the effective strength of the response that determines actual performance. In Hull’s system of symbols, a term with both s and r subscripts represents the relation between a particular stimulus and a particular response. Thus, sHr represents the habit strength or positive conditioned effect of drive reduction on the association between a particular S and a particular R while sEr represents the effective strength after factoring several other variablies into the equation. Effective strength is the actual result measured in a particular experiment.
Two Kinds of Inhibition
The inhibitory effect of nonreward enters Hull’s equation in two forms. First, the theory assumes that every response produces an inhibitory reaction that opposes immediate repetition of that response. Immediate repetition is, indeed, difficult for human and nonhuman animals. As well practiced as you may be in signing your name a particular way, you will find it hard to write your signature the same way over and over again without pausing for rest. Almost any habit breaks down with enough immediate repetition. Living systems seem to have a built-in resistance to exact repetition that ensures response variability.
There is an easy way to demonstrate this resistance. Roll up a sheet of paper and, choosing a suitably friendly and cooperative subject, pretend to strike someone across the eyes with the rolled-up paper. Come as close as you can without actually striking the person. Most people will blink the first time you do this. Repeat the pretend strike a few times. Most people will soon stop blinking even when the paper almost hits them in the eyes. Let your subject rest for 20 or 30 seconds and then repeat. Most people will blink again after this short rest indicating that the inhibition was transitory.
In Hull’s system reactive inhibition is the mechanism that prevents immediate repetition; its symbol is Ir, and it specifically inhibits the particular response that was just made. During conditioning, Hull’s Ir grows with each repetition. As long as there is positive drive reduction (e.g., from food or water reward) to build up more sHr with each response, the net effect on sEr is an increase. Hull’s Ir dissipates with rest (like fatigue), which raises sEr, but it also has drive properties that are reduced by rest. That is, the presence of Ir is aversive and the reduction of Ir is rewarding (like the reduction of thirst or hunger). This drive reduction reinforces the habit of not making response r to stimulus s, which produces a negative habit called conditioned inhibition and its symbol is sIr. Conditioned inhibition is like habit strength (or conditioned excitation) in that it is relatively permanent.
The following formula expresses this part of Hull’s theory.
sEr = sEr – Ir – sIr
The theory assumes (a) that Ir builds up with repetition and dissipates with rest, and (b) that Ir has drive properties. Rest reduces Ir, which reinforces rest or nonresponding. This reinforces the habit of not making this response, sIr. The formula is straightforward and consistent with the rest of the theory. It says that the effective strength of the response r to the stimulus s equals habit strength minus temporary reactive inhibition minus relatively permanent conditioned inhibition.
Returning to Fig. 10.1, Hull’s equation describes acquisition, extinction, and spontaneous recovery in the following way. During acquisition on Monday, both sHr and Ir increase, but sHr builds up faster than Ir, so responding increases. On Tuesday, S* stops, which stops the increase of sHr, but Ir continues to increase every time the subject repeats response r to stimulus s. When Ir builds up enough, responding stops momentarily, which dissipates Ir. This reduces reactive inhibition and reinforces the subject for not making response r to stimulus s, thus adding to conditioned inhibition, sIr.
This description agrees with the usual record of individual performance during extinction. Both in acquisition and extinction, individual records show bursts of responding punctuated by pauses. In acquisition, the pauses get shorter and the bursts get longer. In extinction, the pauses get longer and the bursts get shorter. Complete extinction is one long pause. The average curves of responding for a group of subjects show smooth increases and decreases, because the bursts and pauses occur at different times for different subjects.
As for spontaneous recovery, all of the reactive inhibition dissipates during the overnight rest between Tuesday and Wednesday. The sIr cannot increase, however, because the subject only experiences the stimulus situation s in the experimental apparatus. So, the subject cannot receive any reward for not responding to s. Consequently, there is a big increase in responding between the end of Tuesday’s session and the beginning of Wednesday’s session because all of the Ir is gone. Recovery is incomplete, however, because the relatively permanent conditioned inhibition that developed during extinction on Tuesday depresses responding. If the procedure on Wednesday is another session of extinction, then more sIr will build up so that there will be less spontaneous recovery on Thursday, and so on, until extinction is complete.
Hull’s reactive inhibition and conditioned inhibition are straightforwardly consistent with the rest of the theory, and the result does account for all of the facts of the usual experiment. Unfortunately, the theory requires as many principles as there are facts to account for. Habit strength, reactive inhibition, and conditioned inhibition account for acquisition, extinction, and spontaneous recovery, but a theory that is as complex as the phenomena it describes is hardly an improvement over a list of the phenomena. One way to remedy this situation is to apply the principles to predict new phenomena. By predicting new phenomena, a theory proves its value because it tells us something more than we knew without the theory.
Massed and Distributed Practice
Hull’s reactive inhibition and conditioned inhibition apply directly to perceptual-motor learning of all kinds. During World War II, and for decades afterward, learning theorists actively engaged in applied research on training both in military and civilian situations. It was a practical and profitable application of experimental psychology and occupied a great deal of the graduate curriculum. Psychologists studied the development of skills such as gunnery and machine operation and also devised tracking tasks and precise motor tasks such as picking up small pins with a forceps and placing them into small holes. This period corresponded with the period of Hull’s greatest influence.
The principle of massed versus distributed practice emerged from research on perceptual-motor skills. In massed practice, for example, a trainee might practice for 45 minutes and rest for 15 minutes. In distributed practice, the trainee might divide the same hour into three periods of 15 minutes of practice and 5 minutes of rest. In task after task, distributed practice proved superior to massed practice in perceptual-motor learning. This is precisely what should happen if Hull was correct about reactive inhibition. That is, frequent rests should allow Ir to dissipate without developing sIr. With distributed practice, skill, or sHr, should develop faster because so little Ir can accumulate. With massed practice, on the other hand, Ir should accumulate and skill should develop slower. With more Ir there should be more pauses, leading to more of the relatively permanent conditioned inhibition, sIr, and relatively permanent impairment of skill.
Experimenters discovered that performance often declined during massed practice and then improved after a rest. They called the improvement in skilled performance that comes from rest, alone, reminiscence. After a series of highly massed periods of practice, reminiscence produces the paradoxical finding that losses in performance appear during practice and gains appear after rest without practice. This is precisely what should happen if there is a process such as reactive inhibition that grows during practice and dissipates during rest. And, of course, reminiscence looks just like spontaneous recovery. In spite of this agreement, permanent effects of Hull’s hypothetical sIr on perceptual-motor skills have been difficult (perhaps impossible) to demonstrate (Irion, 1969, pp. 5–9).
There are many ways of distributing practice in different tasks. A good theory should provide a set of rules that predict the best way to distribute practice on each new task in each new applied setting—or at least, the best distribution in many new tasks in many new settings. There have been many attempts to set up such rules, but up to the time of writing this book all have failed. The best, or even a relatively more favorable, way to distribute practice must always be determined separately for each new task. Common sense about the similarity between a new task and other, better known, tasks remains more effective than any direct application of existing theory. Nevertheless, the finding of a robust phenomenon that resembles reactive inhibition in entirely new types of behavior supports Hull’s basic concept. Perhaps, by expanding the basic concepts to accommodate competition among incompatible responses, future theorists will apply Hull’s principles more successfully.
RESISTANCE TO EXTINCTION
Just as the level of responding never starts at absolute zero at the beginning of acquisition, it never returns to absolute zero at the end of extinction. Fortunately, long before absolute zero, relative measures of resistance to extinction are quite sensitive to different conditions of acquisition.
Virtually all experimenters measure resistance to extinction in terms of some arbitrary criterion. In Skinner boxes, experimenters have measured frequency of lever-presses in a fixed amount of time under extinction conditions, and number of lever-presses before a criterion period of time, say 10 minutes without a response. In straight alleys, experimenters have measured running speed during a fixed number of extinction trials and number of trials before the first trial in which a rat took longer than a fixed amount of time, say 2 minutes, to run a short distance.
In many situations, measures of response in acquisition reach a limit so that groups that acquired the same response under different conditions appear to be equal. Late in acquisition, rats may be running as fast as they can so that there is no room left for improvement in speed. In two-choice situations, such as a T-maze, the best that a subject can do is to choose the rewarded alternative on every trial. In these cases, resistance to extinction provides a sensitive measure of differences that cannot appear during acquisition. Experimenters have rarely questioned the widely held belief that resistance to extinction measures the strength of conditioning, which for many is the same as strength of reinforcement. Overtraining and partial reward, however, are two well-documented situations in which resistance to extinction actually decreases with increases in reward. Resistance to extinction after overtraining is the subject of the next section of this chapter. Resistance to extinction after partial reward is the subject of chapter 11.
OVERTRAINING
If some reward reinforces a response, then more rewards should have more reinforcing effect. After many trials of rewarded running in a straight alley, however, both the running speed maintained by reward and the resistance to extinction decrease with further rewarded trials (Birch, Ison, & Sperling, 1960; Prokasy, 1960). If both running speed in acquisition and resistance to extinction measure strength of association, how could additional rewarded trials produce lowered speed and faster extinction?
To his credit, Hull’s reinforcement theory actually predicted this paradoxical result. A central principle of the theory assumes that there is a limit to habit strength, sHr. According to this principle, the negatively accelerated learning curve (largest gains early in conditioning and decreasingly smaller gains later in conditioning as in Fig. 1.1) that appears in most experiments arises from the fact that gains in habit strength are proportional to the difference between the current level and the maximum level possible. There are large gains early in acquisition because there is so much room for improvement; smaller and smaller gains late in acquisition because there is much less room left for improvement.
As sHr increases, responding increases and this produces more reactive inhibition, Ir. As Ir increases, the subject takes more rests to dissipate Ir, and this produces more conditioned inhibition, sIr. Early in conditioning, sHr builds up faster than sIr because the strength of conditioning is far from the maximum; but late in conditioning, sHr grows more slowly because it is closer to the maximum. Eventually, sIr builds up faster than sHr and subtracts more and more from effective performance leading to actual decreases late in acquisition. That Hull’s theory of excitation and inhibition predicted this unexpected, even paradoxical, effect of increased reward before it was discovered is a very strong point in favor of the theory.
SUMMARY
Hull’s theory is the reinforcement theory that comes closest to accommodating the paradoxical effects of nonreward in extinction and spontaneous recovery. Unfortunately, Hull’s theory only accomplishes this by adding several layers of complexity, which makes it less parsimonious and less intuitive than more popular treatments such as Skinner’s. To Hull’s credit, his principles predicted some unexpected findings in both animal conditioning and human perceptual-motor learning.
COMPETING RESPONSES
Much of the difficulty with traditional theories, such as Hull’s, arises from the practice of recording a single index, such as lever-pressing or salivation. All that can happen in such a record is that the index goes up or it goes down. With only two outcomes, the only possible theoretical factors are opposing forces of excitation and inhibition.
Considering More Than One Response
When experimenters actually look at their learning subjects, they see a population of responses. A criterion response Rc such as lever-pressing must be one of the responses in this population, otherwise conditioning is impossible. Figure 10.2 is a diagram of the usual observation. The broad, relatively flat curve represents a population of responses before conditioning, R1, R2, … Rn, which includes Rc. The tall, relatively steep curve about Rc represents the distribution of this same population of responses after conditioning. During conditioning, the experimenter presents S* and then Rc increases together with a relatively few other responses. This increase in a small set of responses depresses the rest of the responses in the original population because competing responses are mutually exclusive—that is, the subject can make only one of these responses at any given time.
Traditional reinforcement theories treat the strength of each response in the population as an independent function of excitatory factors and inhibitory factors. This is a necessary characteristic of any theory that describes conditioning and learning as the building up of association between response and stimulus. In that case, the only way that a conditioned response can decline is by some process of weakening. Otherwise, all conditioning would be permanent. The actual strength of response, then, must be some positive function of excitation minus some negative function of inhibition as in Hull’s sEr that equals sHr minus sIr and Ir. Furthermore, each competing stimulus-response pair must have its own equation balancing its own sHr against its own sIr and Ir. In such a system, the response that appears at any moment would be some complex result of all of these separate equations. This a very cumbersome way to describe the situation. It would also be a very cumbersome way for a nervous system to deal with the situation, because it would demand needlessly expensive use of limited nervous tissue; first to keep track of all of the positive and negative values, and then to compute the result.
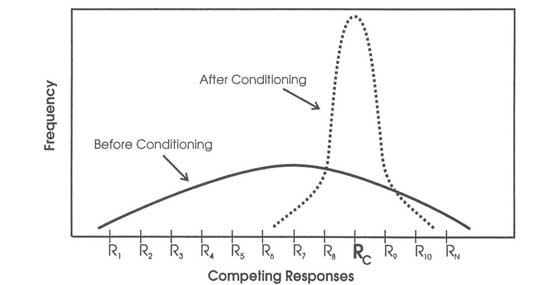
FIG. 10.2. Competing responses before and after conditioning. Copyright © 1997 by R. Allen Gardner.
At any given time, all mutually exclusive responses in a population must compete with each other. Even though many experimenters measure the frequency of only one criterion response, such as lever-pressing, they are necessarily measuring the relative frequency of all other responses, indirectly. Saying that pauses in lever-pressing measure the response of not lever-pressing only dodges the question of what rats actually do when they are not lever-pressing.
Food evokes feeding. One of the feeding responses that food evokes in the Skinner box is lever-pressing. In a sense, the mechanism that evokes feeding responses inhibits nonfeeding responses, but it is simpler to describe the mechanism as one of switching among a set of alternatives. When someone switches channels on a television set, we could say that they are exciting one channel and inhibiting each of the others, but that is a cumbersome way to describe the situation. If the television set tunes in only one channel at a time, then a positive description of the position of the switch is a complete description of the situation.
During acquisition, rats press levers in bursts and pauses. Even when animals are very hungry and very well trained and every press is rewarded with food, they often pause to do other things. During pauses in lever-pressing, rats in a Skinner box groom their whiskers, scratch themselves, sniff the air, rear up on their hind legs, explore the box, and so on.
At the start of extinction, when food stops rats continue to press the lever as before. Indeed, they press at a higher rate without the interference of food to eat. Since nothing about the stimulus situation changes and there is a built-in biological resistance to immediate repetition, the rat eventually varies its response. This built-in tendency to vary responses when the stimulus situation remains the same is also the basis for Hull’s reactive inhibition. In a feed forward analysis, the effect of variability is to get the rat to make some other response to the lever. The rat makes this other response, but without an Sd for the next response in the chain (as in Fig. 7.4), that new response gives way to still another new response, and so on. Eventually, the rat moves away from the lever, and that becomes the last response in that stimulus situation. When the rat returns to the lever, he does the last thing he did when he last approached the lever. If he pressed the lever last time, he presses it again. During extinction, successive bouts of lever-pressing give way to other responses sooner and sooner, without food to evoke feeding behavior. Thus, bursts of lever-pressing become shorter and pauses filled with other responses become longer.
Acquisition on Monday looks the way it does in Fig. 10.1 because there is a shift from the broad, flat curve to the narrow, steep curve of Fig. 10.2. That is, in acquisition on Monday the range of responses narrows to the criterion response, Rc, and a few similar responses. Extinction on Tuesday looks the way it does in Fig. 10.1 because there is a shift from the narrow, steep curve back to the broad, flat curve of Fig. 10.2. That is, there is a shift from concentration on a few responses in acquisition to a broad range of responses. But, what happens on Wednesday? A feed forward system copes with these findings without invoking either excitation or inhibition—and also without invoking either positive or negative expectancies. The stimulus situation at the start of Wednesday’s session is more like the stimulus situation at the start of Tuesday’s session than at the end of Tuesday’s session. So, the rat starts off responding more like it did at the start of Tuesday’s session, but there is some effect of Tuesday’s extinction and the rat responds at a somewhat lower level.
If extinction continues, then the stimulus situation gets more like the end of Tuesday’s session and lever-pressing goes down while other responses go up. Thursday, the stimulus situation at the start is even less like the start and more like the end of Wednesday so lever-pressing falls off further and more quickly in favor of other responses. If instead of more extinction, Wednesday is a day of reacquisition, then the stimulus situation is much more like the situation on Monday and the rat behaves more and more like it did on Monday. Remember also, that part of the stimulus situation in acquisition is the stimulus of actual food, which we know evokes lever-pressing without any contingency at all. Food stimuli are absent in extinction and present in acquisition and reacquisition.
Two-Choice Situations
The difference between feed forward contiguity and feed backward contingency appears more clearly when there are two or more alternative responses. In a Skinner box with two levers, A and B, the experimenter can reward all responses to lever A and never reward any response to lever B. Rats quickly come to press A almost all of the time and hardly ever press B. In a reinforcement theory, this is because positive reinforcement builds up for pressing A and negative inhibition builds up for pressing B. In a feed forward theory, an Sd, such as the click of the food magazine, always follows pressing lever A, which makes pressing the last response to lever A. Pressing B never changes the stimulus situation so the rat makes other responses to B and these become the last responses to that lever (chap. 8).
Suppose that during extinction, the experimenter stops rewarding for A presses and starts rewarding for B presses. In a reinforcement theory, the rat would have to press A without reward repeatedly until enough inhibition developed to overcome the excitation of all of the reward previously received for pressing A. Enough inhibition would have to develop to weaken A presses to the already weakened level of B presses before the animal could make the first B press. Then, the rat would have to make enough rewarded B presses to overcome the inhibition generated by the earlier period of nonreward and build up enough reinforcement to press lever B most of the time.
In a feed forward theory, on the other hand, nonreward for pressing A means that there is no click Sd for making the next response in the chain. Consequently, the rat continues to press A until the built-in tendency to vary results in different responses to lever A. Eventually, one of these responses will be turning away from A and that will become the last response to A. The rat only has to make one rewarded B press to make that the last response to lever B before the click Sd evokes the next response in the chain. The switch from pressing A to pressing B should be fairly quick and there should be little or no spontaneous recovery. In fact, the classical extinction curves shown in Fig. 10.1 are only found in experiments with only one lever or key or only one criterion response, such as salivation or galvanic skin response. With rewarded alternatives, extinction is very rapid and spontaneous recovery is negligible.
Perhaps the following example can make this more clear. Our family lived in the same house in Reno for 13 years before we sold the old place and moved to a new home. The first leg of the drive home from the university where we both worked was the same for both places until we came to a critical intersection. At that point, the driver should turn right to head toward the old place or continue straight through the intersection to head for the new place. For 13 years we had turned right at that intersection. As you would expect, we made the old right turn several times during the first few weeks after moving to the new place. But, we made very few of these perseverative errors considering the thousands of times that we had practiced that right turn at exactly that intersection for 13 years. The number of errors we made and the number of trials that it took to learn to drive straight through the intersection every time without turning right required nothing remotely related to 13 years of reward for getting home after turning right.
Competition and Contingency
In Fig. 10.2, the curve labeled “before conditioning” represents a population of responses under stable conditions. Changes in conditions change the distribution. If, for example, the experimenter attaches a running wheel to the Skinner box, then the frequencies of all responses from grooming whiskers to drinking water will decrease. This decrease in other frequencies must occur because it takes time for a rat to run in a running wheel and this subtracts from the time that the rat can spend on other responses. Removing the running wheel, or blocking its movement with a bolt, will have the opposite effect. The time that the rat spent running in the wheel will now be distributed among the other possible responses. This is a result of basic physics and arithmetic.
Ignoring the problem of response competition, Premack (1965) proposed the results of a new type of experimental operation as evidence for the strengthening effect of response contingent reinforcement. Premack’s proposal fails precisely because it fails to control for response competition, but it is an instructive failure.
Premack (1959) tested first-grade children (average age 6.7 years) one at a time in a room that contained a pinball machine and a candy dispenser. The candy dispenser only dispensed a new piece of candy after a child ate the previous piece. Premack first measured the amount of time that each child spent at each of the two competing activities during a 15-minute sample. In a second 15-minute sample taken several days later, Premack divided the children into two groups. For half of the children, the pinball machine was locked until a child ate a piece of candy. After a bout of pinball, the machine was locked again until the child ate another piece of candy, and so on. For the other half, the candy dispenser was locked until a child played pinball, and locked again until the child played pinball again, and so on.
As expected from Fig. 10.2, eating candy increased when Premack blocked pinball playing, and playing pinball increased when Premack blocked candy eating. As Fig. 10.2 also indicates, the more time the children had spent at an activity during the first sampling period the greater the effect when Premack restricted that activity during the second sampling period. That is, if they had spent more time eating candy than playing pinball in the first period, then restricting candy in the second period increased pinball more than restricting pinball increased eating. Premack amplified the effect of blocking by measuring time spent rather than frequency. Restricting the higher probability activity frees more time for the lower probability activity and thus has a greater effect on the result.
Premack (1962) went on to demonstrate a similar result with rats drinking and running in a Skinner box. He manipulated the relative amount of time spent at each activity in a sampling period by earlier depriving the rats of water and giving them free access to running or depriving them of running and giving them free access to water. In a second sampling period, restricting access to the activity that consumed more time in the first period had a greater effect than restricting access to the activity that consumed less time in the first period.
On the basis of this type of experiment, Premack proposed the following as a principle of reinforcement: Making access to a higher frequency activity contingent on performance of a lower frequency activity reinforces the lower frequency activity. Thus, drinking can reinforce running and running can reinforce drinking depending on which one is more frequent under prevailing conditions.
In these experiments, however, one activity is made contingent on another by blocking the contingent activity until the subject performs the target activity. Obviously, blocking one activity frees time for other activities apart from any hypothetical effect of contingency. The direct effect of competition is more than hypothetical; Dunham (1972), Harrison and Schaeffer (1975), and Premack (1965) all demonstrated in experiments that blocking either competing activity increases the other activity without any contingency whatsoever. Indeed, the effect of noncontingent blocking in these experiments leaves very little room for any additional effect of contingency. If there is any residual effect of contingency apart from the effect of competition, it must be very small, too small to justify any major principle of reinforcement.
The detective must show that a prime suspect could be responsible for the crime. A good detective must also eliminate other prime suspects. In the case of Premack’s proposal for a new principle of contingent reinforcement, response competition is an obvious, likely, empricially supported, and more parsimonious suspect for the factor that is responsible for the experimental results.
Summary
Contingent reinforcement must describe the strength of each response as the combined effect of positive excitation and negative inhibition. This response by response analysis seems appropriate when experimenters only measure a single response that can only increase or decrease. The weakness of this analysis becomes clear in more complex experiments that measure extinction, spontaneous recovery, or response competition.
