B. A Stroll Through 3D Fields
Is there hope that the average signal integrity engineer can acquire enough understanding about the behavior of electric and magnetic fields to facilitate modeling contemporary digital interfaces without having to go back to school and get that PhD in computational electromagnetics? It is probably a bit much to expect that a few pages at the end of a text book will have the reader solving Maxwell's equations on the back of an envelope the next day. Thankfully, today's computers are very capable of doing that for a broad spectrum of arbitrary structures—if the user knows how to set up the problem and has invested in a rather large amount of random access memory!
Four Poetic Equations
Perhaps a little refresher on electromagnetism may restore to working order some of the conceptual tools the reader needs to start using a 3D field solver to explore how these invisible E- and B-fields can degrade system performance.
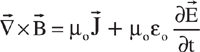
Looking beyond the intimidation factor for a moment, it is truly amazing that these four simple equations describe everything from a child hanging balloons on the wall with static electricity to communication between mission control and a space probe skimming across the edge of the solar system on its way out of the galaxy. Like a well-crafted poem, Maxwell's equations convey a depth of meaning in a small package. They certainly represent one of the crowning achievements of the human race. Consider the civilizations whose contributions to scientific, mathematical, and philosophical thought made this achievement possible: British, German, Muslim, Chinese, Greek, and Egyptian.
Charges at Rest
The first equation expresses the idea that electric field lines spread apart from one another as the distance from a charged body increases. It appears in the first few pages of a text on electrostatics, the study of charges whose positions remain fixed in time, so the concept must be relatively simple. It is possible to derive this equation by applying a little bit of vector calculus to Coulomb's Law, which describes the force between two point charges separated by a distance r.
Translating Maxwell's first equation from the language of mathematics into English, the measure of how much an electric field spreads out around a body of charge is proportional to the charge-per-unit-volume, ρ. Cramming more charge into the same volume causes the density of the electric field lines to increase in a predictable, quantifiable way. What is an electric field anyway? Imagine that the two charges from Coulomb's Law, q1 and q2, are close enough to each other to feel a force repelling them apart. Now imagine that charge q2 disappears, but there is still something surrounding q1 that would exert a force on any other charge that comes near it. That imaginary something is the electric field, simply defined as the force divided by q2. If the body has more than one charge, the aggregate electric field is simply the sum of all the individual electric fields at that point in space.
Incidentally, Coulomb's Law explains why nuclear weapons are so powerful. In the nucleus of a uranium atom, many positively charged protons are confined to a small space. The smaller the radius, the larger the force of repulsion. It takes an awful lot of nuclear binding energy to keep the atom in one piece, and the release of this energy is what gives power to a nuclear explosion.
Steady-State Currents
Maxwell's second equation says that magnetic fields do not diverge radially away from their sources, which are currents of moving charges rather than stationary charges. For magnetic fields, the quantity that measures the spreading of field lines away from their source is equal to zero. The name for this quantity is the divergence, and its mathematical notation is 
. Magnetic fields circle around the current from which they emanate, in contrast to electric fields, which point toward or away from their source. This begs the definition of a magnetic field, and this is where things start to become disturbing to the average student of engineering or science. In fact, the complex nature of magnetic fields is also the reason why there is so much confusion over the inductor, that curly electronic symbol that looks so much like a resistor that it tempts the casual observer to commit the sin of oversimplification.
A short survey of introductory physics textbooks uncovers an unsettling fact: It does not seem possible to define a magnetic field in general terms using more fundamental quantities. The essence of the electric field lies in the more fundamental quantity of force, which in turn appeals to two primary undefined terms: distance and charge. However, discussions of the force on a moving charge in the presence of other moving charges appeal to velocity, charge, and the magnetic field. It seems that in order to define a magnetic field, we must appeal to the notion of a magnetic field! No wonder confusion abounds. Perhaps magnetism is one of those fundamental concepts that are impossible to reduce into simpler components. All is not lost. It is possible to calculate the magnetic field for some simple configurations using the well-established, empirically derived equation of Biot and Savart. The magnitude of the magnetic field surrounding a steady-state current, I, that is confined to a straight line is
where r is the distance from the wire and μo is a fundamental constant of nature. The direction of this field is tangential to a circle of radius r whose plane is perpendicular to the line current and whose center is the line current.
Figure B.1. Magnetic field surrounding a line current
Another structure whose magnetic field is relatively easy to calculate is an inductor formed by wrapping fine copper wire around a cardboard paper-towel tube. Those readers of the ham radio generation may remember constructing a similar component for a crystal radio project. The magnitude of the magnetic field inside such a cylindrical inductor that carries a steady-state current, I, is
where n is the number of turns per unit length along the axis of the cylinder. Notice that the strength of the magnetic field is constant throughout the volume of the cylinder and not a function of radius. The direction of this field is along the axis of the cylinder.
The Non-Intuitive Force
If we have in hand a mathematical expression for magnetic field B, it is possible to calculate the force the magnetic field exerts on a charge q moving through the field with a velocity v.
Here the student of nature begins to feel the force exerted on the mind by the complexity of the physical world. (There may be some small consolation that we are merely discussing electromagnetic theory and not quantum mechanics or the three-dimensional structure of proteins!) There are two vectors on the right-hand side of this equation, v and B, and one scalar, q. The nastiness does not arise from any of these three, but rather from the seemingly insignificant "x" between the v and the B, which represents the vector cross product. Those who have taken a course in electromagnetic theory or vector calculus will probably shudder at the mere mention of this term. The cross product generates a new vector that is perpendicular to the plane formed by the first two vectors. When discussing even the simplest magnetic fields—those that do not vary in time—the cross product is inescapable. The concept of the cross product is not so intimidating, but its mathematical description certainly is. If the two vectors v and B in Cartesian coordinates are given by
then their cross product is given by
where i, j, and k are the unit vectors for the x, y, and z axes, respectively. Six unique terms of two vector components make twelve possibilities for a mistake in a single calculation of this seemingly arbitrary combination of variables. Thankfully, computers are happy to carry out these laborious calculations once the user has understood enough physics to run them. Why mention vector cross products in a text on signal integrity? Although it may be true that a practicing engineer will not spend much time calculating cross products, it is also true that a signal integrity engineer who understands how a 3D field solver works is more likely to get correct results and recognize when it did not solve the problem he thought it was solving. Because 3D field solvers are well on their way to becoming as useful and ubiquitous a tool as SPICE has been, learning how to fly one is likely to become an essential skill in the years ahead.
Returning for a moment to the simple magnetic field of the line current, if an electron is traveling in the same direction as the line current, the force that the magnetic field exerts on the electron will be in a radial direction toward the line current. The right-hand rule is the popular way to determine the direction of the cross-product vector: Point the index finger along v, the middle finger along B, and the thumb points in the direction of the force. Because the electron has a negative charge, the force points toward the line current rather than away from it.
The solenoid is a different story. An electron traveling through a solenoid in the same direction as the axis of the solenoid will experience no force. If the coordinate system is oriented in such a way that the axis of the solenoid and the z-axis are one and the same, then neither the velocity nor the magnetic field has an x or y component. This zeros out every term in the cross product. Of course, the same could be said for an electron traveling in a circular path around the line current or any situation in which the velocity of the charge and the magnetic field point in the same direction.
Enter Time
The preceding examples lay the framework for visualizing these ingenious constructs of the human mind called electric and magnetic fields. Force is the thing that submits itself more readily to measurement, and fields are the means for calculating the force given a known configuration of charges. A configuration of stationary charges generates a sea of three-dimensional electric field vectors that are a function of a three-dimensional position vector in the chosen coordinate system. Likewise, a configuration of steady-state currents generates a sea of three-dimensional magnetic field vectors that are a function of a three-dimensional position vector. Once again, the signal integrity engineer is not terribly interested in charges that just sit there or in currents that remain constant in time. This is where Maxwell's third and fourth equations come in.
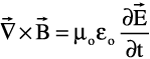
Notice that the variable time appears in these two equations, whereas it did not appear in the first two. Translating these two equations into technical English, the curl of the electric field (a kind of spatial derivative denoted by 
) is proportional to the partial derivative with respect to time of the magnetic field. The curl of the magnetic field is proportional to the partial derivative with respect to time of the electric field. These are first-order, cross-coupled, partial differential equations in dimensions of space and time (nasty beasts to solve analytically), and they express the idea that time-dependent electric and magnetic fields are intertwined with one another. This inter-relationship prompted Albert Einstein to ask the question, "What happens to the magnetic field of a line current if I run alongside it at the same speed the charge is moving? Does it not degenerate into an electric field?" Thus, the Theory of Special Relativity was born. In fact, it turns out that Maxwell's Equations and Einstein's Theory of Special Relativity are physically and mathematically consistent—no coincidence, to be sure.
Waves
In the case of electromagnetic fields in a vacuum where the charge density ρ is zero, a little vector calculus and some physics will decouple Maxwell's third and fourth equations from one another. The price to be paid for decoupling them is that the equations become second-order differential equations.
These two equations follow a form in which the second spatial derivative of a function is proportional to the second time derivative.
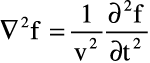
This form is a relative of a more general form that students of differential equations will remember with fondness for its simplicity; namely, a function whose second derivative is proportional to the function itself. The solution to the general differential equation is simply a sinusoidal function, and so is the solution to the more complex equation shown previously, known in physics as the Wave Equation, whose solution is as follows:
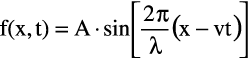
Imagine the Wave Equation and its solution represent the physical system of a wave on a string. Then f(x, t) represents the displacement of the string from its equilibrium position, and it is a function of time and linear location along the string. Imposing the initial conditions introduces the amplitude, A. The two integrations required to solve the equation introduce two constants of integration, the wavelength λ and the velocity v. Now imagine that two separate Wave Equations represent the physical system of electric and magnetic waves traveling through a vacuum.
The initial conditions establish the amplitude of the waves, Eo and Bo, and these waves travel on indefinitely without any attenuation until they encounter something other than a vacuum. There is not much difference between the concept of the wavelength in the wave-on-a-string problem and the fields-in-a-vacuum problem. The biggest difference between these two problems is the things that are doing the oscillating, and they are a bit more complicated than a wave on a string. The electric and magnetic fields are doing the oscillating, and each one is a three-dimensional vector quantity that is a function of a three-dimensional space vector and time. That's a brain-full. Thankfully, when electromagnetic waves travel through a vacuum in a direction along the z-axis, the electric field has only an x-component and the magnetic field has only a y-component. That is, each field vector is perpendicular to the other field vector and to the direction of motion. This is called Transverse Electromagnetic Mode (TEM), and it is a good approximation for transmission lines but does not hold generally for 3D discontinuities.
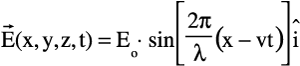
The other big difference is the velocity. A wave on a string travels at a velocity that depends on the mass density of the string and the force of tension. An electromagnetic wave speeding along through empty space travels at the speed of light in a vacuum, c, which is a function of the permittivity and permeability of free space. Note the relationship between the coefficients in front of the electric and magnetic wave equations, which originated in Maxwell's fourth equation, and the coefficient (inverse of velocity squared) in front of the Wave Equation.
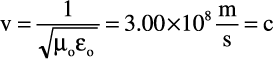
There is one more quantity that is worth talking about because it is a useful indicator of where the energy is flowing. The cross product of the electric and magnetic field vectors defines a new vector, Poynting's vector, which measures the power flux density; that is, integrating this vector over a surface yields the power flowing through that surface.
This one quantity probably provides more insight to the signal integrity engineer than any other. Calculating Poynting's vector for TEM waves is rather boring; it simply "points" in the direction that the wave is traveling, which was along the z-axis in the preceding example. Of course, things get considerably more interesting in the presence of conductors, and Poynting's vector is not the least bit trivial in the vicinity of a 3D discontinuity. It helps the signal integrity engineer visualize how close the discontinuity comes to approximating the conditions on either side of it. Does the energy flow nicely around the discontinuity, or does the variation in geometrical and material properties succeed in directing some of the energy to a less desirable location? These questions are well worth the asking and strike at the heart of the matter more directly than s-parameters or equivalent circuits.
Dropping a Few Dimensions
Everything a signal integrity engineer would care to know about the behavior of electrical interconnect is contained in the four tidy equations of Maxwell. Extracting useful information from them is the real trick. The sheer complexity of the task led engineers to turn to a more simplified representation of the physics that involves currents and voltages—things that are easier to visualize and measure. If we confine the problem to TEM waves, it is possible to derive a set of current-voltage wave equations whose form is mathematically analogous to the equations for electric and magnetic fields.
These equations are still second-order partial differential equations, but voltage and current have replaced the electric and magnetic fields. Compare their mathematical form with the corresponding wave equations for electric and magnetic fields:
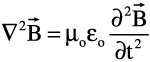
Voltage and current are scalar quantities that are a function of one dimension of space and one dimension of time.
Electric and magnetic fields, on the other hand, are three-dimensional vector quantities that are a function of three dimensions of space and one dimension of time.
What magic occurred that allowed dropping two entire dimensions, both in the vector functions and the arguments of the functions? What were the assumptions, and under what conditions do they apply? It is certainly convenient to solve linear systems of current-voltage relationships using a solver like SPICE, but if you do not know where the models break down, you run the risk of generating entirely bogus results, not to mention intermittently dysfunctional systems.
For starters, the TEM assumption implies that neither the electric field nor the magnetic field has any component in the direction of propagation, assumed to be along the z-axis. Furthermore, the TEM assumption also implies that the electric field has only an x-component, and the magnetic field has only a y-component (or equivalently, the electric field has only a y-component, and the magnetic field has only an x-component). These two statements result in the dropping of four of the six vector components of the electric and magnetic fields, putting them on the same level as the voltage and current, which are scalar functions. That leaves four more dimensions to account for—the x and y arguments of the electric and magnetic field functions on the right-hand side of Equations B.29 and B.30.
In a general 3D electromagnetic field problem, charges are able to move throughout a conductor in whatever trajectory the electric and magnetic fields dictate. Rather than the simple linear current introduced in freshman circuits analysis, it is common to speak of a volume current density vector which points in the direction of flow through a volume element and which is a function of the three-dimensional location of that element, be it on the surface or interior of a conductor. The TEM transmission line problem is much more limited and simple: The charges move along with the wave front in a well-defined trajectory; that is, the velocity of the charges has only a z-component. Although the current may not be uniform across the surface of the conductors, the TEM transmission line model only considers the aggregate of all these surface current elements. The information regarding the distribution of current across the surface of the actual conductor is stored in the inductance and capacitance per unit length, L and C, which are not physical constants as was the case in the electromagnetic wave equation. Inductance and capacitance are a function of geometry and current distribution and therefore store critical information about the fields.
If the classical Wave Equation holds true for the case of current-voltage waves, then the coefficients of Equations B.23 and B.24 must be the inverse of the square of the velocity. Assuming a typical 50 
printed circuit board transmission line with 3 pF per inch of capacitance and 9 nH per inch of inductance, the velocity of propagation should be:
Indeed, this is roughly half the speed of light in a vacuum, which is consistent with material whose dielectric constant is 4.0.
Under what conditions do TEM waves break down and transfer their energy into other modes of propagation? The simplest answer is whenever there is a departure from the uniform two-dimensional cross-sectional geometry of the interconnect medium. A car traveling due north down a Texas interstate will continue traveling north until the driver uses the steering wheel to exert a force against the pavement that redirects the velocity vector of the car. Similarly, the TEM wave will continue propagating until the electric and magnetic fields encounter the charges in the discontinuity and the resulting interaction spawns four new field components from the original electric field component, Ex, and magnetic field component, By. Reality, of course, is always more complicated. The physical size of the discontinuity compared to the shortest wavelength will determine whether or not the conversion from TEM to another mode is large enough to be of interest. It is difficult to visualize this without a lot of experience, which is why a 3D field solver is so useful.