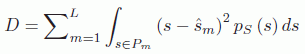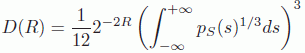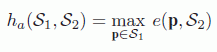Chapter 11

3D Mesh Compression

11.1. Introduction

With technological progress in the domains of digital acquisition, telecommunications and geometric modeling, 3D objects (both static and animated) occupy an increasingly important role. This emerging multimedia content is, for the majority, made up of 3D and 3D+t polygonal meshes, which are generally bulky due to increases in precision and the richness of the data they carry. In parallel, these 3D objects are increasingly used for Internet applications, or as part of online collaborative platforms, where they need to be transmitted rapidly across a network. Thus, the compression of these objects has become an essential scientific concern, involving multiple objectives such as the compact storage of data, interactive time transmission across networks, progressive content visualization and rapid random access.

In this chapter, we begin by considering certain basic points of information theory, the sampling and quantization notions needed to reduce the quantity of data and notions of rate-distortion. We then consider multiresolution analysis. This consists of decomposing a mesh into a series of resolution levels, for example by using wavelet transformations. This method offers an elegant and effective framework for compressing meshes and sequences of meshes, but generally requires the use of a semi-regular mesh, often obtained through an earlier remeshing process. We then present monoresolution coding methods based on highly effective connectivity coders, associating prediction techniques. Other progressive compression techniques, based on iterative simplification processes or guided by geometry, may be used to obtain satisfactory levels of compression with additional functionality. Sequence compression algorithms, fewer in number, will be considered in the following section, before addressing the definition of classic and perceptual metrics which may be used to evaluate the effectiveness of compression techniques.

11.2. Compression basics: rate-distortion trade-off

Compression methods involving information loss enable considerable increases in compression levels, and thus reduce the signal bit rate below the Shannon limit [SHA 48]. Flows of this type are only possible in cases of non-reversible coding, generating degradations of the 3D object. The aim of compression methods with information loss is not only to eliminate signal redundancies, but also to generate losses in non-relevant information and in noise. Coding techniques of this type are required for applications requiring high levels of compression. They are designed to implement effective compression, while “controlling degradation”. In these cases, we speak of rate-distortion optimization.

Quantization is the fundamental operation carried out by a compression system. Its purpose is to select, for a given real input value, the closest neighbor from a finite predetermined set of numerical values. More precisely, a scalar quantifier of size L is an application Q of in a finite set C, also known as a codebook, containing L scalar symbols:

[11.1]

is the quantization of s, where corresponds to the centroid of the quantization interval which includes s. This corresponds to seeking the closest neighbor of s among the elements contained in the dictionary C.

In a general manner, the mean square error (MSE) of a quantizer (power of the quantization noise) is defined by the following relationship:

[11.2]

Here, is the measure of distortion between a source symbol s and its quantization is a quantization cluster to which the source symbol belongs, represented by its centroid ; and is the probability density of the source signal S. For a very high number L of quantization levels (asymptotic hypothesis, or high bit rate), the MSE, expressed as a function of the bit rate R = log₂ L bits/symbol, is bounded asymptotically by [GER 92]:

[11.3]

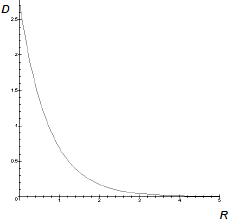
The general behavior of this function is shown in Figure 11.1. It shows that the quantization distortion D is a strictly decreasing function of the bit rate R.

11.3. Multiresolution coding of surface meshes

Meshes constitute a powerful tool for modeling complex 3D objects, thanks to their dual geometric and combinatory nature (positions of vertices and connectivity). While there is a number of alternatives for modeling surface forms, meshes are now omnipresent, and considerable effort has been put into developing methods for the digital processing of their geometry, essentially based on triangular meshes. If a geometry is initially described by a mesh, the mesh is considered to be an instance of the geometry. A certain degree of freedom subsists in the meshing process: we may remesh a geometric form without introducing geometric distortion in order to obtain regularity and sampling properties in the new mesh which may be used for multiresolution representation, processing and compression.

Although multiresolution techniques have long been proved to be effective in the compression of 2D images [ISO 00], their use for 3D meshes is relatively recent. This is due to the fact that it is relatively difficult to design filters for irregular subdivisions [VAL 99], and wavelet theory for meshes with regular or semi-regular subdivisions is a relatively recent idea [LOU 94]. In 1994, Lounsbery introduced a schema for the progressive compression of surfaces using a 3D wavelet transform for triangular surface meshes, obtained by regular subdivision (1:4 subdivision) of an irregular base mesh [LOU 94, LOU 97]. Schröder and Sweldens [SCH 95] and Kovacevic and Swelden [KOV 99] then developed a number of different techniques used to compress the geometry of meshes and to reduce connectivity information as much as possible. For applications where remeshing is not possible, a generalization of Lounsbery’s approach for meshes with irregular subdivisions was proposed in [VAL 99]. The multiresolution approaches obtained in this way are scalable in terms of resolution, precision, quantity and even complexity (see Figure 11.2). The representation of a surface mesh with any connectivity graph (regular or irregular), representing the surface of a 3D object, using geometric wavelets is based on a subdivision inversion problem, and produces an exactly reversible compression method for the connectivity graph and the geometry of the data. Hierarchical transmission, with progressive quality and a binary bit rate, is thus possible. An effective geometrical wavelet decomposition requires prior representation of the geometric signal in a form compatible with a regular structure and uniform sampling. As perfect regularity is impossible to obtain for arbitrary topologies, the mesh is converted into a semi-regular mesh (regular by sections) [GUS 00, LEE 98] where the theory of wavelets using M-channels has been shown to be effective [KAM 12]. Thus, a geometric mesh compression schema is generally made up of three steps (see Figure 11.3):

11.4. Topological and progressive coding

Wavelet-transform coding methods such as those presented above produce excellent performances, but require prior remeshing of the initial object to give a semi-regular structure. This remeshing stage may be undesirable in scenarios where the original connectivity of the object needs to be preserved. Other types of techniques may be used to code arbitrary geometries and connectivities. These may be grouped into two categories of algorithms:

11.4.1. Monoresolution compression

Most monoresolution compression methods follow the same pattern: the geometry and connectivity of the object are coded separately, but not independently. The connectivity is represented by a series of symbols representing a traversal order of the mesh, while the geometry is coded by quantization, then prediction guided by this order.

The first connectivity coding method (only applicable to triangular meshes) was proposed by Deering [DEE 95]. Deering’s method consisted of defining a sequence of vertices such that each vertex of the series forms a triangle with the two previous vertices. The mesh is thus decomposed into triangle strips, producing an efficient coding of connectivity. Working along different lines, Taubin and Rossignac [TAU 98a] proposed a method based on spanning trees. Their method was inspired by theoretical results obtained by [TUR 84], who established that a planar graph may be coded with a constant number of bits per vertex, using two spanning trees, one of faces and the other of vertices.

The majority of recent methods are based on a region growing approach, where a region is extended across the mesh with incremental coding of elements of the mesh and their incidence relationships with the region. This group of methods may be divided into three categories according to the type of element with the dominant role in the coding process: faces [GUM 98, KRO 01, ROS 99, SZY 01], edges [ISE 00] or vertices [ALL 01b, KHO 02, TOU 98].

Geometric information must also be coded in parallel with the connectivity coding. Generally, geometry is coded in three stages: quantization, prediction (using the parallelogram rule, for example) and coding of the difference vector. Recent algorithms propose highly efficient prediction mechanisms [COU 11].

In terms of compression rates, the best monoresolution methods generally require 2–3 bits per vertex for connectivity and 10–16 bits per vertex for geometry (depending on the method and the model in question, for a 12-bit quantization). The methods presented above are based on a connectivity-guided mesh traversal; given the volume of memory occupied by geometry, certain authors have chosen to prioritize this aspect, proposing geometry-guided methods. These include proposals by Kronrod and Gotsman [KRO 02] and Lewiner et al. [LEW 06].

11.4.2. Multiresolution compression

11.4.2.1. Connectivity-driven approaches

The concept of progressive mesh was first introduced by Hoppe [HOP 96]. During the coding process, the mesh is simplified by a series of edge collapsing operations, then refined during the decoding process by the opposite vertex split operator. This method, extended by Popovic and Hoppe [POP 97] for non-manifold arbitrary meshes, has the advantage of presenting fine granularity, but remains costly in terms of complexity and memory requirements (around 16 bits per vertex for connectivity), as the index of the vertices to split is coded explicitly on a one-by-one basis. Thus, Taubin et al. [TAU 98b], then Pajarola and Rossignac [PAJ 00], simplified the mesh by combinations of edge collapses applied to several edges at a time. Thus, for each iteration, a whole region of the object is simplified. The granularity produced is lower than for Hoppe’s algorithm [HOP 96], but the coding cost is reduced (around 10 and 7 bits per vertex respectively for connectivity). Cohen-Or et al. [COH 99] used vertex deletion/insertion operators on sets of independent vertices. Alliez and Desbrun [ALL 01a] proposed an extension of monoresolution compression algorithms [ALL 01b, TOU 98] based on valency. Using their method, a set of independent vertices is removed for each iteration by two decimation conquests. This is followed by retriangulation in order to optimize the quality of the intermediate meshes by preserving regularity and connectivity as far as possible. This method requires, on average, 3.7 bits per vertex for coding connectivity.

The methods presented above are based on connectivity-driven approaches. The geometry of the objects is then coded in a similar way to that used in monoresolution approaches, by quantization then prediction (each new vertex generated by edge separation or vertex insertion may be effectively predicted using neighbors which have already been transmitted).

Several authors [AHN 11, KIM 11, LEE 12] have attempted to optimize the approach put forward by Alliez and Desbrun [ALL 01a], for example by introducing coding using bitplanes, or prediction mechanisms for valency coding.

11.4.2.2. Geometry-driven approaches

As with monoresolution approaches, certain authors consider that it is more efficient to use geometry to guide compression rather than connectivity. Gandoin and Devillers [GAN 02] and Devillers and Gandoin [DEV 00], for example, introduced the first geometry-driven multiresolution algorithm, based on the subdivision of space using a kd-tree. The compression rates obtained using this method are excellent, but the quality of the levels of detail is much lower than for connectivity-driven methods. Peng and Kuo [PEN 05] proposed a similar method based on the subdivision of space using an octree. Through a series of optimizations, they improved compression levels, but the quality of the levels of detail is still low in comparison with that obtained by connectivity-driven approaches.

Finally, several algorithms have been proposed in recent times which can be considered as hybrids of between geometry and connectivity-driven approaches. They notably propose variable quantization mechanisms [LEE 12, PEN 10, VAL 09].

11.5. Mesh sequence compression

Thanks to advances in the domain of camera-based 3D reconstruction, mesh sequences are becoming increasingly widespread. Using short time steps, these are extremely bulky and require particular attention for efficient compression, as in the case of video compression, which makes use of the temporal coherence of successive images. 3D animation is another domain which produces large quantities of mesh sequences. An example of a sequence is shown in Figure 11.4.

11.5.1. Definitions

A mesh sequence is a series of meshes ordered in time. Temporal coherency is required and necessitates temporal sampling at a rate which is sufficiently rapid in relation to the evolution of the object or the scene. We can distinguish at least two different types of sequences:

In the first case, the sequence consists of a geometric evolution of the vertices of the first mesh over time. In the second case, there is no natural link between a vertex at instant t and a vertex at instant t+1. A more precise classification of mesh sequences may be found in a thesis on the subject by R. Arcila [ARC 11].

The interest of compressing sequences with constant connectivity is evident. Connectivity is coded once at the beginning of the sequence. The geometry of each mesh is generally coded by considering the evolution of the position of each vertex over time as a trajectory. In the case of sequences with dynamic connectivity, the complexity of compression problems is considerably increased, and thus has received little attention until now [HAN 07]. In these cases, spatio-temporal redundancies are much harder to exploit without prior mapping.

We may classify sequence compression methods into three categories: methods with spatio-temporal prediction, approaches using prior segmentation and transform-based methods (principal component analysis or wavelets).

11.5.2. Methods using spatio-temporal prediction

These methods exploit the spatio-temporal redundancy of sequences by predicting the position of a vertex from surrounding positions (by interpolation) or from previous positions (by extrapolation). These predictors attempt to minimize the residual error between predicted positions and the real positions of vertices. Errors are then quantified and transmitted to an entropic coder.

Ibarria et al. [IBA 03] present two spatio-temporal predictors: the Extended Lorenzo Predictor (ELP) and Replica. The first extends the parallelogram rule used in the compression of static meshes [TOU 98], taking account of the prediction of the position of the summit at the previous instant. The Replica predictor makes the previous predictor robust to rigid transformations such as rotations and changes of scale, using local reference points and normalization. Ibarria et al. have also proposed another predictor, known as Angle Preserving (AP) [IBA 03].

Methods using this kind of geometric predictors require mapping between the vertices of meshes in the sequence, and cannot, therefore, be applied to sequences with dynamic connectivity. Moreover, they do not exploit potential spatial redundancies in cases where regions are subject to homogeneous movement.

11.5.3. Methods with prior segmentation

In an attempt to improve the performance of compression methods, several authors have proposed partitioning the vertices of a mesh into groups of points with similar movement. In 1999, Lengyel [LEN 99] proposed a method of this type. The basic principle involves estimating the movement of a group of vertices by a rigid transformation, which then acts as a predictor. The segmentation information, the parameters of each transformation and the prediction errors are then coded to allow reconstruction of the sequence. Alignment between successive meshes can be used to improve results, as demonstrated by Gupta et al. [GUP 02].

Without using direct segmentation, Zhang et al. [ZHA 07] placed vertex displacement vectors into a hierarchical tree structure (octree), which allows exploitation of spatio-temporal coherence. Once again, this method requires point-to-point mapping.

In 2007, Han et al. [SEU 07] proposed a first method for compressing sequences with dynamic connectivity, inspired by video compression techniques and using a division of meshes into blocks, mapping and discrete cosine transformation (DCT).

11.5.4. Transform-based methods

Other approaches use transformations applied to the whole of a sequence. Alexa and Muller [ALE 00], for example, propose a mesh alignment, then calculate a principal component analysis using residual errors. This method performs well if the duration of the sequence (number of frames) is long in relation to the number of vertices in the mesh.

Another transformation, the wavelet transform, which has been shown to be effective in compression, may be used on the trajectories of vertices over time. It may be applied directly or be linked to a group of correlated trajectories. After the classification phase, a motion compensation element is introduced for each cluster, and wavelet analysis is applied to their residual errors [BOU 07].

11.6. Quality evaluation: classic and perceptual metrics

The performance of a compression algorithm is evaluated in terms of the rate-distortion compromise. The goal of an algorithm is to produce a high level of compression while preserving the geometry or visual appearance of the object as far as possible. The following sections present the existing metrics used to measure the geometric and/or visual distortion between two 3D objects.

11.6.1. Classic metrics

A classic metric used to evaluate the distortion between two 3D objects is MSE, similar to peak signal-to-noise ratio (PSNR) which is used for images. For two meshes and with the same connectivity, each containing n vertices, this error is defined as follows:

[11.4]

where and are the corresponding 3D vertices between the meshes in question.

We may also consider the square root of this error, the root mean square error (RMSE). Unfortunately, these distances require one-to-one correspondence between vertices of the meshes under comparison, and can therefore only be applied to meshes sharing the same connectivity.

Another widely used metric which, unlike the previous metrics, may be used to compare two objects with different connectivities and/or levels of detail is the Hausdorff distance, defined as follows: we begin by defining e(p, S) the Euclidean distance from a point p in the 3D space to the object S:

[11.5]

where means that the points are sampled in a dense manner across surface (we do not only consider the vertices of ). We may then define the asymmetric Hausdorff distance between two objects and as follows:

[11.6]

Finally, the symmetrical Hausdorff distance is defined as follows:

[11.7]

Definition [11.5] also allows us to define an asymmetric mean square error:

[11.8]

The most widespread measurement is the maximum root mean square error (MRMS):

[11.9]

Metro¹ [CIG 98] is a program providing an efficient implementation of the Hausdorff distance and its derivatives. These geometric distances have equivalents for dynamic meshes [KAR 04].

11.6.2. Perceptual metrics

The drawback of the standard metrics presented above is that they are not correlated with human vision (as with PSNR for images), i.e. they do not reflect the perceived visual distortion between 3D objects. In most applications, visual quality is often more important than pure geometric distortion. More perceptual metrics have been proposed in order to solve this problem; these aim to produce scores predicting the visual impact of the distortion.

To evaluate the quality of 3D meshes compressed using their spectral compression methods, Karni and Gotsman [KAR 00] then Sorkine et al. [SOR 03] used a metric combining the MSE between corresponding vertices and the MSE of their Laplacians (which give an indication of the roughness of the surface). The basic idea involved states that the human eye is more sensitive to high-frequency changes in roughness than to low-frequency geometric changes. Corsini et al. [COR 07] then proposed perceptual metrics based on the global variation in roughness to measure the quality of meshes in the context of a watermarking application. They used two methods to calculate roughness: the variance in geometric differences between a 3D model and its smoothed version and the variance of dihedral angles. More recently, Wang et al. [WAN 12] introduced another metric based on a global difference in roughness, calculated as the Laplacian of the Gaussian curvature. Like roughness, curvature is an important element in the evaluation of perceived quality. Lavoué et al. [LAV 06, LAV 11] have proposed metrics based on differences in curvature statistics between corresponding local windows over the objects to compare; Torkhani et al. [TOR 12] introduced an extension to this method to take account of directions of curvature. Finally, Vasa and Rus [VAS 12] consider the variation in dihedral angles.

We should also cite the work of Pan et al. [PAN 05] and Cheng et al. [CHE 07], who defined a quality metric for textured meshes in the context of bit allocation for transmission. They observed that quality is reduced exponentially in relation to the resolution of the geometry, and in a linear manner in relation to the texture map; from this, they deduced a simple quality estimator, based on these two pieces of resolution information.

For dynamic meshes, only Vasa and Skala [VAS 11] have introduced a perceptual metric.

11.7. Conclusion

3D meshes and mesh sequences are currently used in a number of domains, from entertainment to industry. Their presence on the Internet remains marginal, but is growing. The volume of data associated with these multimedia objects creates a need for efficient compression. In this section, we have discussed the state of the art in the domain of mesh and mesh sequence compression; the moving picture experts group (MPEG) consortium has also been involved in standardization efforts in an attempt to resolve the problem of multiple formats, which limits the acceptation of specific compression methods.

The diffusion of these 3D objects across a variety of networks and to a variety of terminals raises a need for multiresolution methods, allowing both progressive display and adaptation to the visualization terminal. The visual quality of intermediate resolution levels therefore constitutes another important point. The problem of accounting for data associated with meshes such as texture maps remains open, and solutions are needed to enlarge the field of application of compression methods.

11.8. Bibliography

[AHN 11] AHN J.-K., LEE D.-Y., AHN M., et al., “R-D optimized progressive compression of 3D meshes using prioritized gate selection and curvature prediction”, The Visual Computer, vol. 27, no. 6–8, pp. 769–779, April 2011.

[ALE 00] ALEXA M., MÜLLER W., “Representing animations by principal components”, Computer Graphics Forum, vol. 19, pp. 411–418, 2000.

[ALL 01a] ALLIEZ P., DESBRUN M., “Progressive encoding for lossless transmission of triangular meshes”, Proceedings of the 28th annual conference on Computer graphics and interactive techniques (SIGGRAPH ’01) ACM, New York, USA, pp. 195–202, 2001.

[ALL 01b] ALLIEZ P., DESBRUN M., “Valence-driven connectivity encoding of 3D meshes”, Computer Graphics Forum, vol. 20, no. 3, pp. 480–489, 2001.

[ARC 11] ARCILA R., Séquences de maillages: classification et méthodes de segmentation, PhD Thesis, Université Claude Bernard - Lyon I, November 2011.

[BOU 07] BOULFANI-CUISINAUD Y., ANTONINI M., “Motion-based geometry compensation for DWT compression of 3D mesh sequences”, Image Processing, 2007 (ICIP 2007) IEEE International Conference on, IEEE, vol. 1, I-217–I-220, 16 September–19 October 2007.

[CHE 07] CHENG I., YING L., BASU A., “Packet-loss modeling for perceptually optimized 3D transmission”, Advances in Multimedia, vol. 2007, pp. 1–10, 2007.

[CIG 98] CIGNONI P., ROCCHINI C., SCOPIGNO R., “Metro: measuring error on simplified surfaces”, Computer Graphics Forum, IEEE Computer Society Press, vol. 17, no. 2, pp. 167–174, 1998.

[COH 99] COHEN-OR D., LEVIN D., REMEZ O., “Progressive compression of arbitrary triangular meshes”, Proceedings of the conference on Visualization ’99: celebrating ten years (VIS ’99), pp. 67–72, 1999.

[COR 07] CORSINI M., GELASCA E.D., EBRAHIMI T., et al., “Watermarked 3-D mesh quality assessment”, IEEE Transactions on Multimedia, vol. 9, no. 2, pp. 247–256, 2007.

[COU 11] COURBET C., HUDELOT C., “Taylor prediction for mesh geometry compression”, Computer Graphics Forum, vol. 30, no. 1, pp. 139–151, 2011.

[DEE 95] DEERING M., “Geometry compression”, Proceedings of the 22nd annual conference on Computer graphics and interactive techniques (SIGGRAPH’95), ACM Siggraph, pp. 13–20, 1995.

[DEV 00] DEVILLERS O., GANDOIN P.-M., “Geometric compression for interactive transmission”, Proceedings of the conference on Visualization ’00, IEEE Computer Society Press, no. 8, pp. 319–326, 2000.

[GAN 02] GANDOIN P.-M., DEVILLERS O., “Progressive lossless compression of arbitrary simplicial complexes”, Proceedings of the 29th annual conference on Computer graphics and interactive techniques (SIGGRAPH ’02), ACM, no. 8, pp. 372–379, 2002.

[GER 92] GERSHO A., GRAY R., Vector Quantization and Signal Compression, Kluwer Academic Publishers, 1992.

[GUM 98] GUMHOLD S., STRASSER W., “Real time compression of triangle mesh connectivity”, Proceedings of the 25th annual conference on Computer graphics and interactive techniques (SIGGRAPH ’98), ACM, no. 8, pp. 133–140, 1998.

[GUP 02] GUPTA S., SENGUPTA K., KASSIM A., “Compression of dynamic 3D geometry data using iterative closest point algorithm”, Computer Vision and Image Understanding, vol. 87, no. 1, pp. 116–130, 2002.

[GUS 00] GUSKOV I., VIDIMCE K., SWELDENS W., et al., “Normal meshes”, Computer Graphics Proceedings, SIGGRAPH, pp. 95–102, 2000.

[HAN 07] HAN S.-R., YAMASAKI T., AIZAWA K., “Time-varying mesh compression using an extended block matching algorithm.”, IEEE Transactions on Circuits and Systems for Video Technology, vol. 17, no. 11, pp. 1506–1518, 2007.

[HOP 96] HOPPE H., “Progressive meshes”, Proceedings of the 23rd annual conference on Computer graphics and interactive techniques (SIGGRAPH ’96), ACM, pp. 99–108, 1996.

[IBA 03] IBARRIA L., ROSSIGNAC J., “Dynapack: space-time compression of the 3D animations of triangle meshes with fixed connectivity”, Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Eurographics Association, pp. 126–135, 2003.

[ISE 00] ISENBURG M., “Triangle fixer: edge-based connectivity compression”, in Proceedings of 16th European Workshop on Computational Geometry, pp. 18–23, 2000.

[ISO 00] ISO/IEC 15444–1:2000, “Information technology – JPEG 2000 image coding system – Part 1: Core coding system”, 2000.

[KAM 12] KAMMOUN A., PAYAN F., ANTONINI M., “Sparsity-based optimization of two lifting-based wavelet transforms for semi-regular mesh compression”, Elsevier Computers and Graphics, vol. 36, pp. 272–282, 2012.

[KAR 00] KARNI Z., GOTSMAN C., “Spectral compression of mesh geometry”, Proceedings of the 27th annual conference on Computer graphics and interactive techniques (SIGGRAPH ’00), ACM Press/Addison-Wesley Publishing Co., no. 8, pp. 279–286, 2000.

[KAR 04] KARNI Z., GOTSMAN C., “Compression of soft-body animation sequences”, Computers & Graphics, vol. 28, no. 1, pp. 25–34, 2004.

[KHO 02] KHODAKOVSKY A., ALLIEZ P., DESBRUN M., et al., “Near-optimal connectivity encoding of 2-manifold polygon meshes”, Journal of Graphical Models, vol. 64, nos. 3–4, pp. 147–168, 2002.

[KIM 11] KIM J., NAM C., CHOE S., “Bayesian AD coder: mesh-aware valence coding for multiresolution meshes”, Computers & Graphics, vol. 35, pp. 1–6, 2011.

[KOV 99] KOVACEVIC J., SWELDENS W., “Wavelet families of increasing order in arbitrary dimensions”, IEEE Transactions on Image Processing, vol. 9, no. 3, 1999.

[KRO 01] KRONROD B., GOTSMAN C., “Efficient coding of non-triangular mesh connectivity”, Journal of Graphical Models, vol. 63, pp. 263–275, 2001.

[KRO 02] KRONROD B., GOTSMAN C., “Optimized compression of triangle mesh geometry using prediction trees”, International Symposium on 3D Data Processing, Visualization and Transmission, IEEE Computer Society, pp. 602–608, 2002.

[LAV 06] LAVOUÉ G., DRELIE GELASCA E., DUPONT F., et al., “Perceptually driven 3D distance metrics with application to watermarking”, SPIE, vol. 6312, SPIE, pp. 63120L–63120L–12, August 2006.

[LAV 11] LAVOUÉ G., “A multiscale metric for 3D mesh visual quality assessment”, Computer Graphics Forum, vol. 30, no. 5, pp. 1427–1437, 2011.

[LEE 98] LEE A.W.F., SWELDENS W., SCHRÖDER P., et al.., “MAPS: multiresolution adaptive parameterization of surfaces”, Computer Graphics Proceedings (SIGGRAPH 98), ACM Siggraph, pp. 95–104, 1998.

[LEE 12] LEE H., LAVOUÉ G., DUPONT F., “Rate-distortion optimization for progressive compression of 3D mesh with color attributes”, The Visual Computer, vol. 28, no. 2, pp. 137–153, 2012.

[LEN 99] LENGYEL J.E., “Compression of time-dependent geometry”, Proceedings of the 1999 symposium on Interactive 3D Graphics, I3D ’99, ACM, New York, pp. 89–95, 1999.

[LEW 06] LEWINER T., CRAIZER M., LOPES H., “GEncode: geometry-driven compression for general meshes”, Computer Graphics Forum, vol. 25, no. 4, pp. 1–10, 2006.

[LOU 94] LOUNSBERY J., Multiresolution analysis for surfaces of arbitrary topological type, PhD Thesis, University of Washington, Seattle, 1994.

[LOU 97] LOUNSBERY M., DEROSE T., WARREN J., “Multiresolution analysis for surfaces of arbitrary topological type”, ACM Transactions on Graphics, vol. 16, no. 1, pp. 34–73, 1997.

[PAJ 00] PAJAROLA R., ROSSIGNAC J., “Compressed progressive meshes”, IEEE Transactions on Visualization and Computer Graphics, vol. 6, no. 1, pp. 79–93, 2000.

[PAN 05] PAN Y., CHENG I., BASU A., “Quality metric for approximating subjective evaluation of 3-D objects”, IEEE Transactions on Multimedia, vol. 7, no. 2, pp. 269–279, 2005.

[PEN 05] PENG J., KUO C.-C.J., “Geometry-guided progressive lossless 3D mesh coding with octree (OT) decomposition”, ACM Transactions on Graphics (TOG), vol. 24, no. 3, pp. 609–616, 2005.

[PEN 10] PENG J., KUO Y., ECKSTEIN I., et al., “Feature oriented progressive lossless mesh coding”, Computer Graphics Forum, vol. 29, no. 7, pp. 2029–2038, 2010.

[POP 97] POPOVIĆ J., HOPPE H., “Progressive simplicial complexes”, Proceedings of the 24th annual conference on Computer graphics and interactive techniques (SIGGRAPH ’97), ACM Press/Addison-Wesley Publishing Co., no. 8, pp. 217–224, 1997.

[ROS 99] ROSSIGNAC J., “Edgebreaker: connectivity compression for triangle meshes”, IEEE Transactions on Visualization and Computer Graphics, vol. 5, no. 1, pp. 47–61, 1999.

[SCH 95] SCHRÖDER P., SWELDENS W., “Spherical wavelets: efficiently representing functions on the sphere”, Proceedings of SIGGRAPH 95, ACM, pp. 161–172, 1995.

[SEU 07] SEUNG-RYONG HAN., YAMASAKI T., AIZAWA K., “Time-varying mesh compression using an extended block matching algorithm”, IEEE Transactions on Circuits and Systems for Video Technology, vol. 17 , no. 11, pp. 1506–1518, 2007.

[SHA 48] SHANNON C., “A mathematical theory of communication”, Bell System Technical Journal, vol. 27, pp. 379–423, 623–656, 1948.

[SOR 03] SORKINE O., COHEN-OR D., TOLDEO S., “High-pass quantization for mesh encoding”, Proceedings of the 2003 Eurographics/ACM SIGGRAPH symposium on Geometry processing (SGP ’03), Eurographics Association, no. 10, pp. 42–51, 2003.

[SZY 01] SZYMCZAK A., KING D., ROSSIGNAC J., “An edgebreaker-based efficient compression scheme for regular meshes”, Computational Geometry, vol. 20, nos. 1–2, pp. 53–68, 2001.

[TAU 98a] TAUBIN G., ROSSIGNAC J., “Geometric compression through topological surgery”, ACM Transactions on Graphics, vol. 17, no. 2, pp. 84–115, 1998.

[TAU 98b] TAUBIN G., GUÉZIEC A., HORN W., et al., “Progressive forest split compression”, SIGGRAPH, ACM Press, New York, pp. 123–132, 1998.

[TOR 12] TORKHANI F., WANG K., CHASSERY J.-M., “A curvature tensor distance for mesh visual quality assessment”, International Conference on Computer Vision and Graphics, 2012.

[TOU 98] TOUMA C., GOTSMAN C., “Triangle mesh compression”, in DAVIS W.A., BOOTH K.S., FOURNIER A. (eds), Graphics Interface, Canadian Human-Computer Communications Society, pp. 26–34, 1998.

[TUR 84] TURAN G., “Succinct representations of graphs”, Discrete Applied Mathematics, vol. 8, pp. 289–294, 1984.

[VAL 99] VALETTE S., KIM Y., JUNG H., et al., “A multiresolution wavelet scheme for irregularly subdivided 3D triangular mesh”, IEEE International Conference on Image Processing, Kobe, Japon, vol. 1, pp. 171–174, October 1999.

[VAL 09] VALETTE S., CHAINE R., PROST R., “Progressive lossless mesh compression via incremental parametric refinement”, Computer Graphics Forum, vol. 28, no. 5, pp. 1301–1310, 2009.

[VAS 11] VASA L., SKALA V., “A perception correlated comparison method for dynamic meshes”, IEEE Transactions on Visualization and Computer Graphics, vol. 17, no. 2, pp. 220–230, 2011.

[VAS 12] VASA L., RUS J., “Dihedral angle mesh error: a fast perception correlated distortion measure for fixed connectivity triangle meshes”, Computer Graphics Forum, vol. 31, no. 5, pp. 1715–1724, 2012.

[WAN 12] WANG K., TORKHANI F., MONTANVERT A., “A fast roughness-based approach to the assessment of 3D mesh visual quality”, Computers & Graphics, vol. 36, no. 7, pp. 808–818, 2012.

[ZHA 07] ZHANG J., OWEN C.B., “Octree-based animated geometry compression”, Computers and Graphics, vol. 31, no. 3, pp. 463–479, 2007.

¹ http://vcg.isti.cnr.it/activities/surfacegrevis/simplification/metro.html.

Chapter written by Florent DUPONT, Guillaume LAVOUÉ and Marc ANTONINI.