Chapter 9
Reasoning with Rational Functions
IN THIS CHAPTER
![]() Covering the basics of rational functions
Covering the basics of rational functions
![]() Identifying vertical, horizontal, and oblique asymptotes
Identifying vertical, horizontal, and oblique asymptotes
![]() Spotting removable discontinuities in rational graphs
Spotting removable discontinuities in rational graphs
![]() Edging up to rational limits
Edging up to rational limits
![]() Taking rational cues to sketch graphs
Taking rational cues to sketch graphs
The word “rational” has many uses. You say that rational people act reasonably and predictably. You can also say that rational numbers are reasonable and predictable — their decimals either repeat (have a distinctive pattern as they go on forever and ever) or terminate (come to an abrupt end). This chapter gives your rational repertoire another boost — it deals with rational functions.
A rational function may not appear to be reasonable, but it’s definitely predictable. In this chapter, you refer to the intercepts, the asymptotes, any removable discontinuities, and the limits of rational functions to tell where the function values have been, what they’re doing for particular values of the domain, and what they’ll be doing for large values of x. You also need all this information to discuss or graph a rational function.
A nice feature of rational functions is that you can use the intercepts, asymptotes, and removable discontinuities to help you sketch the graphs of the functions. And, by the way, you can throw in a few limits to help you finish the whole thing off with a bow on top.
Whether you’re graphing rational functions by hand (yes, of course, it’s holding a pencil) or with a graphing calculator, you need to be able to recognize their various characteristics (domain, intercepts, asymptotes, and so on). If you don’t know what these characteristics are and how to find them, your calculator is no better than a paperweight to you.
Exploring Rational Functions
You see rational functions written, in general, in the form of a fraction:
where f and g are polynomials (expressions with whole-number exponents; see Chapter 8) and g cannot be equal to 0.
Rational functions (and more specifically their graphs) are distinctive because of what they do and don’t have. The graphs of rational functions do have helpers called asymptotes (lines drawn in to help with the shape and direction of the curve; a new concept that I cover in the “Adding Asymptotes to the Rational Pot” section later in the chapter), and the graphs often don’t have all the real numbers in their domains. Polynomials and exponential functions (which I cover in Chapters 8 and 10, respectively) make use of all the real numbers — their domains aren’t restricted.
Sizing up domain
As I explain in Chapter 6, the domain of a function consists of all the real numbers that you can use in the function equation. Values in the domain have to work in the equation and avoid producing imaginary or nonexistent answers.
The following list illustrates examples of domains of selected rational functions:
- The domain of
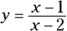 is all real numbers except 2. In interval notation (see Chapter 2), you write the domain as
is all real numbers except 2. In interval notation (see Chapter 2), you write the domain as  . (The symbol
. (The symbol  signifies that the numbers increase without end; and the
signifies that the numbers increase without end; and the  signifies decreasing without end. The
signifies decreasing without end. The 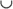 between the two parts of the answer means or.)
between the two parts of the answer means or.) - The domain of
 is all real numbers except 0 and
is all real numbers except 0 and 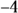 . In interval notation, you write the domain as
. In interval notation, you write the domain as 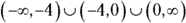 .
. - The domain of
 is all real numbers; no number makes the denominator equal to zero. You can write the domain as
is all real numbers; no number makes the denominator equal to zero. You can write the domain as 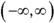 .
.
Introducing intercepts
Functions in algebra can have intercepts. A rational function may have some x - intercepts and/or a y - intercept, but it doesn’t have to have either. You can determine whether a given rational function has intercepts by looking at its equation.
Using zero to find y-intercepts
The coordinate (0, b) represents the y - intercept of a rational function. To find the value of b, you substitute a zero for x and solve for y.
For instance, if you want to find the y - intercept of the rational function ![]() , you replace each x with zero to get
, you replace each x with zero to get ![]() . The y-intercept is
. The y-intercept is ![]() .
.
X marks the spot
The coordinate (a, 0) represents an x-intercept of a rational function. To find the value(s) of a, you let y equal zero and solve for x. (Basically, you just set the numerator of the fraction equal to zero — after you completely reduce the fraction.) You could also multiply each side of the equation by the denominator to get the same equation — it just depends on how you look at it.
To find the x-intercepts of the rational function ![]() , for example, you set
, for example, you set ![]() equal to zero and solve for x. Factoring the numerator, you get
equal to zero and solve for x. Factoring the numerator, you get ![]() . The two solutions of the equation are
. The two solutions of the equation are ![]() and
and ![]() . The two intercepts, therefore, are (0, 0) and (3, 0). Neither
. The two intercepts, therefore, are (0, 0) and (3, 0). Neither ![]() nor
nor ![]() creates a 0 in the denominator.
creates a 0 in the denominator.
Adding Asymptotes to the Rational Pot
The graphs of rational functions take on some distinctive shapes because of asymptotes. An asymptote is a sort of ghost line. Asymptotes are drawn into the graph of a rational function to show the shape and direction of the function. The asymptotes aren’t really part of the graphs, though, because they aren’t made up of function values. Rather, they indicate where the function isn’t (usually). You lightly sketch in the asymptotes when you’re graphing to help you with the final product. The types of asymptotes that you usually find in a rational function include the following:
- Vertical asymptotes
- Horizontal asymptotes
- Oblique (slant) asymptotes
In this section, I explain how you crunch the numbers of rational equations to identify asymptotes and graph them.
Determining the equations of vertical asymptotes
The equations of vertical asymptotes appear in the form ![]() . This equation of a line has only the x variable — no y variable — and the number h. A vertical asymptote occurs in the rational function if f(x) and g(x) have no common factors, and it appears at whatever values the denominator equals zero —
. This equation of a line has only the x variable — no y variable — and the number h. A vertical asymptote occurs in the rational function if f(x) and g(x) have no common factors, and it appears at whatever values the denominator equals zero — ![]() . (In other words, vertical asymptotes occur at values that don’t fall in the domain of the rational function.)
. (In other words, vertical asymptotes occur at values that don’t fall in the domain of the rational function.)
To find the vertical asymptotes of the function ![]() , for example, you first note that there’s no common factor in the numerator and denominator. Then you set the denominator equal to zero. Factoring
, for example, you first note that there’s no common factor in the numerator and denominator. Then you set the denominator equal to zero. Factoring ![]() , you get
, you get ![]() . The solutions are
. The solutions are ![]() and
and ![]() , which are the equations of the vertical asymptotes.
, which are the equations of the vertical asymptotes.
Determining the equations of horizontal asymptotes
The horizontal asymptote of a rational function has an equation that appears in the form ![]() . This linear equation has only the variable y — no x — and the k is some number. A rational function
. This linear equation has only the variable y — no x — and the k is some number. A rational function ![]() has only one horizontal asymptote — if it has one at all (some rational functions have no horizontal asymptotes, others have one, and none of them have more than one). A rational function has a horizontal asymptote when the degree (highest power) of f(x), the polynomial in the numerator, is less than or equal to the degree of g(x), the polynomial in the denominator.
has only one horizontal asymptote — if it has one at all (some rational functions have no horizontal asymptotes, others have one, and none of them have more than one). A rational function has a horizontal asymptote when the degree (highest power) of f(x), the polynomial in the numerator, is less than or equal to the degree of g(x), the polynomial in the denominator.
If you want to find the horizontal asymptote of ![]() , for example, you use the previously stated rules. Because
, for example, you use the previously stated rules. Because ![]() , the horizontal asymptote is
, the horizontal asymptote is ![]() . Now look at what happens when the degree of the denominator is the same as the degree of the numerator. The horizontal asymptote of
. Now look at what happens when the degree of the denominator is the same as the degree of the numerator. The horizontal asymptote of ![]() is
is ![]() (
(![]() over
over ![]() ). The fraction formed by the lead coefficients is
). The fraction formed by the lead coefficients is ![]() .
.
Graphing vertical and horizontal asymptotes
When a rational function has one vertical asymptote and one horizontal asymptote, its graph usually looks like two flattened-out, C-shaped curves that appear diagonally opposite one another from the intersection of the asymptotes. Occasionally, the curves appear side by side, but that’s the exception rather than the rule. Figure 9-1 shows you two examples of the more frequently found graphs in the one horizontal and one vertical classification. Note: The asymptotes are graphed with dashes rather than solid lines to emphasize that they are not really a part of the graph of the function.
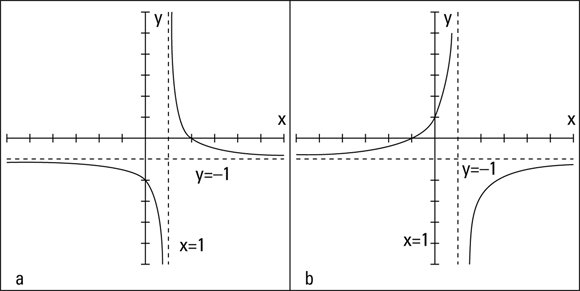
John Wiley & Sons, Inc.
FIGURE 9-1: Rational functions approaching vertical and horizontal asymptotes.
In both graphs, the vertical asymptotes are at ![]() , and the horizontal asymptotes are at
, and the horizontal asymptotes are at ![]() . In Figure 9-1a, the intercepts are
. In Figure 9-1a, the intercepts are ![]() and (2, 0). Figure 9-1b has intercepts of
and (2, 0). Figure 9-1b has intercepts of ![]() and (0, 1).
and (0, 1).
You can have only one horizontal asymptote in a rational function, but you can have more than one vertical asymptote. Typically, the curve to the right of the right-most vertical asymptote and to the left of the left-most vertical asymptote are like flattened-out or slowly turning C’s. They nestle in the corner and follow along the asymptotes. Between the vertical asymptotes is where some graphs get more interesting. Some graphs between vertical asymptotes can be U-shaped, going upward or downward (see Figure 9-2a), or they can cross in the middle, clinging to the vertical asymptotes on one side or the other (see Figure 9-2b). You find out which case you have by calculating a few points — intercepts and a couple more — to give you clues as to the shape. The graphs in Figure 9-2 show you some of the possibilities.

John Wiley & Sons, Inc.
FIGURE 9-2: Rational functions curving between vertical asymptotes.
In Figure 9-2, the vertical asymptotes are at ![]() and
and ![]() . The horizontal asymptotes are at
. The horizontal asymptotes are at ![]() . Figure 9-2a has two x-intercepts lying between the two vertical asymptotes; the y-intercept is there, too. In Figure 9-2b, the y-intercept and one x-intercept lie between the two vertical asymptotes; another x-intercept is to the right of the right-most vertical asymptote.
. Figure 9-2a has two x-intercepts lying between the two vertical asymptotes; the y-intercept is there, too. In Figure 9-2b, the y-intercept and one x-intercept lie between the two vertical asymptotes; another x-intercept is to the right of the right-most vertical asymptote.
Crunching the numbers and graphing oblique asymptotes
An oblique or slant asymptote takes the form ![]() . You may recognize this form as the slope-intercept form for the equation of a line (as seen in Chapter 5). A rational function has a slant asymptote when the degree of the polynomial in the numerator is exactly one value greater than the degree in the denominator (
. You may recognize this form as the slope-intercept form for the equation of a line (as seen in Chapter 5). A rational function has a slant asymptote when the degree of the polynomial in the numerator is exactly one value greater than the degree in the denominator (![]() over
over ![]() , for example).
, for example).
To find the slant asymptote of ![]() , for example, do the long division:
, for example, do the long division:
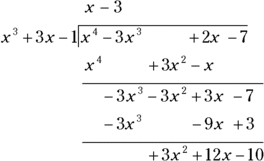
You can ignore the remainder at the bottom. The slant asymptote for this example is ![]() . (For more on long division of polynomials, see Algebra I Workbook For Dummies, written by yours truly and published by Wiley.)
. (For more on long division of polynomials, see Algebra I Workbook For Dummies, written by yours truly and published by Wiley.)
An oblique (or slant) asymptote creates two new possibilities for the graph of a rational function. If a function has an oblique asymptote, its curve tends to be a very-flat C on opposite sides of the intersection of the slant asymptote and a vertical asymptote (see Figure 9-3a), or the curve has U-shapes between the asymptotes (see Figure 9-3b).
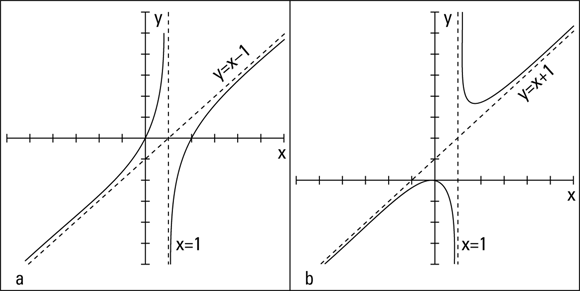
John Wiley & Sons, Inc.
FIGURE 9-3: Graphs between vertical and oblique asymptotes.
Figure 9-3a has a vertical asymptote at ![]() and a slant asymptote at
and a slant asymptote at ![]() ; its intercepts are at (0, 0) and (2, 0). Figure 9-3b has a vertical asymptote at
; its intercepts are at (0, 0) and (2, 0). Figure 9-3b has a vertical asymptote at ![]() and a slant asymptote at
and a slant asymptote at ![]() ; its only intercept is at (0, 0).
; its only intercept is at (0, 0).
Accounting for Removable Discontinuities
Discontinuities at vertical asymptotes (see the “Determining the equations of vertical asymptotes” section earlier in the chapter for a definition) can’t be removed. But rational functions sometimes have removable discontinuities in other places. The removable designation is, however, a bit misleading. The gap in the domain still exists at that “removable” spot, but the function values and graph of the curve tend to behave a little better than at x-values where there’s a nonremovable discontinuity. The function values stay close together — they don’t spread far apart — and the graphs just have tiny holes, not vertical asymptotes where the graphs don’t behave very well (they go infinitely high or infinitely low). Refer to “Going to infinity” later in this chapter for more on this.
You have the option of removing discontinuities by factoring the original function statement — if it does factor. If the numerator and denominator don’t have a common factor, then there isn’t a removable discontinuity.
You can recognize removable discontinuities when you see them graphed on a rational function; they appear as holes in the graph — big dots with spaces in the middle rather than all shaded in. Removable discontinuities aren’t big, obvious discontinuities like vertical asymptotes; you have to look carefully for them. If you just can’t wait to see what these things look like, skip ahead to the “Showing removable discontinuities on a graph” section a bit later in the chapter.
Removal by factoring
Discontinuities are removed when they no longer have an effect on the rational function equation. You know this is the case when you find a factor that’s common to both the numerator and the denominator. You accomplish the removal process by factoring the polynomials in the numerator and denominator of the rational function and then reducing the fraction.
To remove the discontinuity in the rational function ![]() , for example, you first factor the numerator and denominator of the fraction (see Chapter 3):
, for example, you first factor the numerator and denominator of the fraction (see Chapter 3): ![]() .
.
Now you reduce the fraction to the new function statement: 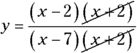 giving you
giving you ![]() .
.
By getting rid of the removable discontinuity, you simplify the equation that you’re graphing. It’s easier to graph a line with a little hole in it than deal with an equation that has a fraction — and all the computations involved.
Evaluating the removal restrictions
The function, which you work with in the previous section, starts out with a quadratic in the denominator (see Chapters 3 and 7). You factor the denominator, and when you set it equal to zero, you find that the solutions ![]() and
and ![]() don’t appear in the domain of the function. Now what?
don’t appear in the domain of the function. Now what?
Numbers excluded from the domain stay excluded even after you remove the discontinuity. The function still isn’t defined for the two values you find. Therefore, you can conclude that the function behaves differently at each of the discontinuities. When ![]() , the graph of the function has a hole; the curve approaches the value, skips it, and goes on. It behaves in a reasonable fashion: The function values skip over the discontinuity, but the values get really close to it. When
, the graph of the function has a hole; the curve approaches the value, skips it, and goes on. It behaves in a reasonable fashion: The function values skip over the discontinuity, but the values get really close to it. When ![]() , however, a vertical asymptote appears; the discontinuity doesn’t go away. The function values go haywire at that x value and don’t settle down at all.
, however, a vertical asymptote appears; the discontinuity doesn’t go away. The function values go haywire at that x value and don’t settle down at all.
Showing removable discontinuities on a graph
A vertical asymptote of a rational function indicates a discontinuity, or a place on its graph where the function isn’t defined. On either side of a vertical asymptote, the graph rises toward positive infinity or falls toward negative infinity. The rational function has no limit wherever you see a vertical asymptote (see the “Pushing the Limits of Rational Functions” section later in the chapter). Some rational functions may have discontinuities at which limits exist. When a function has a removable discontinuity, a limit exists, and its graph shows this by putting a hollow circle in place of a piece of the graph.
Figure 9-4 shows a rational function with a vertical asymptote at ![]() and a removable discontinuity at
and a removable discontinuity at ![]() . The horizontal asymptote is the x-axis (written
. The horizontal asymptote is the x-axis (written ![]() ). Unfortunately, graphing calculators don’t show the little hollow circles indicating removable discontinuities. Oh, sure, they leave a gap there, but the gap is only one pixel wide, so you can’t see it with the naked eye. You just have to know that the discontinuity is there. We’re still better than the calculators!
). Unfortunately, graphing calculators don’t show the little hollow circles indicating removable discontinuities. Oh, sure, they leave a gap there, but the gap is only one pixel wide, so you can’t see it with the naked eye. You just have to know that the discontinuity is there. We’re still better than the calculators!

John Wiley & Sons, Inc.
FIGURE 9-4: A removable discontinuity at the coordinate (3, 0.2).
Pushing the Limits of Rational Functions
The limit of a rational function is something like the speed limit on a road. The speed limit tells you how fast you can go (legally). As you approach the speed limit, you adjust the pressure you put on the gas pedal accordingly, trying to keep close to the limit. Most drivers want to stay at least slightly above or slightly below the limit.
The limit of a rational function acts this way, too — homing in on a specific number, either slightly greater than or slightly less than that number. If a function has a limit at a particular number, as you approach the designated number from the left or from the right (from below or above the value, respectively), you approach the same place or function value. The function doesn’t have to be defined at the number you’re approaching (sometimes they are and sometimes not) — there could be a discontinuity. But, if a limit rests at the number, the values of the function have to be really close together — but not touching.
You read the notation as, “The limit of the function, f(x), as x approaches the number a, is equal to L.” The number a doesn’t have to be in the domain of the function. You can talk about a limit of a function whether a is in the domain or not. And you can approach a, as long as you don’t actually reach it.
Allow me to relate the notation back to following the speed limit. The value a is the exact pressure you need to put on the pedal to achieve the exact speed limit — often impossible to attain.
Look at the function ![]() . Suppose that you want to see what happens on either side of the value
. Suppose that you want to see what happens on either side of the value ![]() . In other words, you want to see what’s happening to the function values as you get close to 1 coming from the left and then coming from the right. Table 9-1 shows you some selected values.
. In other words, you want to see what’s happening to the function values as you get close to 1 coming from the left and then coming from the right. Table 9-1 shows you some selected values.
TABLE 9-1 Approaching ![]() from Both Sides in
from Both Sides in ![]()
x Approaching 1 from the Left |
Corresponding Behavior in |
x Approaching 1 from the Right |
Corresponding Behavior in |
0.0 |
2.0 |
2.0 |
6.0 |
0.5 |
2.25 |
1.5 |
4.25 |
0.9 |
2.81 |
1.1 |
3.21 |
0.999 |
2.998001 |
1.001 |
3.002001 |
0.99999 |
2.9999800001 |
1.00001 |
3.0000200001 |
As you approach ![]() from the left or the right, the value of the function approaches the number 3. The number 3 is the limit. You may wonder why I didn’t just plug the number 1 into the function equation:
from the left or the right, the value of the function approaches the number 3. The number 3 is the limit. You may wonder why I didn’t just plug the number 1 into the function equation: ![]() . My answer is, in this case, you can. I just used the table to illustrate how the concept of a limit works.
. My answer is, in this case, you can. I just used the table to illustrate how the concept of a limit works.
Evaluating limits at discontinuities
The beauty of a limit is that it can also work when a rational function isn’t defined at a particular number. The function ![]() , for example, is discontinuous at
, for example, is discontinuous at ![]() and at
and at ![]() . You find these numbers by factoring the denominator, setting it equal to zero:
. You find these numbers by factoring the denominator, setting it equal to zero: ![]() , and solving for x. This function has no limit when x approaches zero, but it has a limit when x approaches two. Sometimes it’s helpful to actually see the numbers — see what you get from evaluating a function at different values — so I’ve included Table 9-2. It shows what happens as x approaches zero from the left and right, and it illustrates that the function has no limit at that value.
, and solving for x. This function has no limit when x approaches zero, but it has a limit when x approaches two. Sometimes it’s helpful to actually see the numbers — see what you get from evaluating a function at different values — so I’ve included Table 9-2. It shows what happens as x approaches zero from the left and right, and it illustrates that the function has no limit at that value.
TABLE 9-2 Approaching ![]() from Both Sides in
from Both Sides in ![]()
x Approaching 0 from the Left |
Corresponding Behavior of |
x Approaching 0 from the Right |
Corresponding Behavior of |
|
|
1.0 |
1 |
|
|
0.5 |
2 |
|
|
0.1 |
10 |
|
|
0.001 |
1,000 |
|
|
0.00001 |
100,000 |
Table 9-2 shows you that ![]() doesn’t exist. As x approaches from less than zero, the values of the function drop down lower and lower toward negative infinity. Coming from greater than zero, the values of the function raise higher and higher toward positive infinity. The sides will never come to an agreement; no limit exists.
doesn’t exist. As x approaches from less than zero, the values of the function drop down lower and lower toward negative infinity. Coming from greater than zero, the values of the function raise higher and higher toward positive infinity. The sides will never come to an agreement; no limit exists.
Table 9-3 shows you how a function can have a limit even when the function isn’t defined at a particular number. Sticking with the previous example function, you find a limit as x approaches 2.
TABLE 9-3 Approaching ![]() from Both Sides in
from Both Sides in ![]()
x Approaching 2 from the Left |
Corresponding Behavior of |
x Approaching 2 from the Right |
Corresponding Behavior of |
1.0 |
1.0 |
3.0 |
0.3333 … |
1.5 |
0.6666 … |
2.5 |
0.4 |
1.9 |
0.526316 … |
2.1 |
0.476190 … |
1.99 |
0.502512 … |
2.001 |
0.499750 … |
1.999 |
0.500250 … |
2.00001 |
0.4999975 … |
Table 9-3 shows ![]() . The numbers get closer and closer to 0.5 as x gets closer and closer to 2 from both directions. You find a limit at
. The numbers get closer and closer to 0.5 as x gets closer and closer to 2 from both directions. You find a limit at ![]() , even though the function isn’t defined there.
, even though the function isn’t defined there.
Determining an existent limit without tables
If you’ve examined the two tables from the previous section, you may think that the process of finding limits is exhausting. Allow me to tell you that algebra offers a much easier way to find limits — if they exist.
- Factor the rational function equation.
- Reduce the function equation.
- Evaluate the new, revised function equation at the value of x in question.
To solve for the limit when ![]() in the rational function
in the rational function ![]() , an example from the previous section, you first factor and then reduce the fraction:
, an example from the previous section, you first factor and then reduce the fraction:
Now you replace the x with 2 and get ![]() , the limit when
, the limit when ![]() . Wow! How simple! In general, if a rational function factors, then you’ll find a limit at the number excluded from the domain if the factoring makes that exclusion seem to disappear.
. Wow! How simple! In general, if a rational function factors, then you’ll find a limit at the number excluded from the domain if the factoring makes that exclusion seem to disappear.
Determining which functions have limits
- If
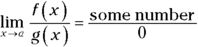 , the function has no limit at a.
, the function has no limit at a. - If
 , the function has a limit at a. You reduce the fraction and evaluate the newly formed function equation at a (as I explain how to do in the preceding section).
, the function has a limit at a. You reduce the fraction and evaluate the newly formed function equation at a (as I explain how to do in the preceding section).
A fraction has no value when a zero sits in the denominator, but a zero divided by a zero does have a form — called an indeterminate form. Take this form as a signal that you can look for a value for the limit.
For example, here’s a function that has no limit when ![]() : You’re looking at what x is approaching in the limit statement, so you’re only concerned about the 1.
: You’re looking at what x is approaching in the limit statement, so you’re only concerned about the 1.
The function has no limit at 1 because the substitution creates a number over zero.
If you try this function at ![]() , you see that the function has a removable discontinuity:
, you see that the function has a removable discontinuity:
The function has a limit at ![]() because the substitution gives you zero over zero. When you factor
because the substitution gives you zero over zero. When you factor ![]() out of the numerator and denominator and then evaluate the new fraction for
out of the numerator and denominator and then evaluate the new fraction for ![]() , you get a limit of 3.
, you get a limit of 3.
Going to infinity
When a rational function doesn’t have a limit at a particular value, the function values and graph have to go somewhere. A particular function may not have the number 3 in its domain, and its graph may have a vertical asymptote when ![]() . Even though the function has no limit, you can still say something about what’s happening to the function as it approaches 3 from the left and the right. The graph has no numerical limit at that point, but you can still tell something about the behavior of the function. The behavior is attributed to one-sided limits.
. Even though the function has no limit, you can still say something about what’s happening to the function as it approaches 3 from the left and the right. The graph has no numerical limit at that point, but you can still tell something about the behavior of the function. The behavior is attributed to one-sided limits.
The notation for indicating one-sided limits from the left or right is shown here:
- The limit as x approaches the value a from the left is
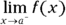 .
. - The limit as x approaches the value a from the right is
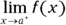 .
.
Do you see the little positive or negative sign after the a? You can think of from the left as coming from the same direction as all the negative numbers on the number line and from the right as coming from the same direction as all the positive numbers.
Table 9-4 shows some values of the function ![]() , which has a vertical asymptote at
, which has a vertical asymptote at ![]() .
.
TABLE 9-4 Approaching ![]() from Both Sides in
from Both Sides in ![]()
x Approaching 3 from the Left |
Corresponding Behavior of |
x Approaching 3 from the Right |
Corresponding Behavior of |
2.0 |
|
4.0 |
1 |
2.5 |
|
3.5 |
2 |
2.9 |
|
3.1 |
10 |
2.999 |
|
3.001 |
1,000 |
2.99999 |
|
3.00001 |
100,000 |
You express the one-sided limits for the function from Table 9-4 as follows:
The function goes down to negative infinity as it approaches 3 from less than the value and up to positive infinity as it approaches 3 from greater than the value. “And nary the twain shall meet.”
Catching rational limits at infinity
The previous section describes how function values can go to positive or negative infinity as x approaches some specific number. This section also talks about infinity, but it focuses on what rational functions do as their x-values become very large or very small (approaching infinity themselves).
A function such as the parabola ![]() opens upward. If you let x be some really big number, y gets very big, too. Also, when x is very small (a “big” negative number), you square the value, making it positive, so y is very big for the small x. In function notation, you describe what’s happening to this function as the x-values approach infinity with
opens upward. If you let x be some really big number, y gets very big, too. Also, when x is very small (a “big” negative number), you square the value, making it positive, so y is very big for the small x. In function notation, you describe what’s happening to this function as the x-values approach infinity with ![]() .
.
For example, the function ![]() approaches negative infinity as x gets very large — think about what
approaches negative infinity as x gets very large — think about what ![]() does to the y value (you’d get
does to the y value (you’d get ![]() ). On the other hand, when
). On the other hand, when ![]() , the y value gets very large, because you have
, the y value gets very large, because you have ![]() , so the function approaches positive infinity.
, so the function approaches positive infinity.
In the case of rational functions, the limits at infinity — as x gets very large or very small — may be specific, finite, describable numbers. In fact, when a rational function has a horizontal asymptote, its limit at infinity is the same value as the number in the equation of the asymptote.
If you’re looking for the horizontal asymptote of the function ![]() , for example, you can use the rules in the section “Determining the equations of horizontal asymptotes” to determine that the horizontal asymptote of the function is
, for example, you can use the rules in the section “Determining the equations of horizontal asymptotes” to determine that the horizontal asymptote of the function is ![]() . Using limit notation, you can write the solution as
. Using limit notation, you can write the solution as ![]() .
.
Here’s how the property works when evaluating the limit of the previous example function, ![]() . The highest power of the variable in the fraction is
. The highest power of the variable in the fraction is ![]() , so every term is divided by
, so every term is divided by ![]() :
:
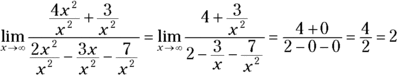
The limit as x approaches infinity is 2. As predicted, the number 2 is the number in the equation of the horizontal asymptote. The quick method for determining horizontal asymptotes is an easier way to find limits at infinity, and this procedure is also the correct mathematical way of doing it — and it shows why the other rule (the quick method) works. You also need this quicker method for more involved limit problems found in calculus and other higher mathematics.
Putting It All Together: Sketching Rational Graphs from Clues
The graphs of rational functions can include intercepts, asymptotes, and removable discontinuities (topics I cover earlier in this chapter). In fact, some graphs include all three. Sketching the graph of a rational function is fairly simple if you prepare carefully. Make use of any and all information you can glean from the function equation, sketch in any intercepts and asymptotes, and then plot a few points to determine the general shape of the curve.
To sketch the graph of the function ![]() , for example, you should first look at the powers of the numerator and denominator. The degrees, or highest powers, are the same, so you find the horizontal asymptote by making a fraction of the lead coefficients. Both coefficients are one, and one divided by one is still one, so the equation of the horizontal asymptote is
, for example, you should first look at the powers of the numerator and denominator. The degrees, or highest powers, are the same, so you find the horizontal asymptote by making a fraction of the lead coefficients. Both coefficients are one, and one divided by one is still one, so the equation of the horizontal asymptote is ![]() .
.
The rest of the necessary information for graphing is more forthcoming if you factor the numerator and denominator:
You factor out a common factor of ![]() from the numerator and denominator. This action tells you two things. First, because
from the numerator and denominator. This action tells you two things. First, because ![]() makes the denominator equal to zero, you know that
makes the denominator equal to zero, you know that ![]() isn’t in the domain of the function. Furthermore, the fact that
isn’t in the domain of the function. Furthermore, the fact that ![]() is removed by the factoring signals a removable discontinuity when
is removed by the factoring signals a removable discontinuity when ![]() . You can plug
. You can plug ![]() into the new equation to find out where to graph the hole or open circle:
into the new equation to find out where to graph the hole or open circle:
The hole is at ![]() . The remaining terms in the denominator tell you that the function has a vertical asymptote at
. The remaining terms in the denominator tell you that the function has a vertical asymptote at ![]() . You find the y-intercept by letting
. You find the y-intercept by letting ![]() , so the y-intercept is
, so the y-intercept is ![]() . You find the x-intercepts by setting the new numerator equal to zero and solving for x. When
. You find the x-intercepts by setting the new numerator equal to zero and solving for x. When ![]() ,
, ![]() , so the x-intercept is (3, 0). You place all this information on a graph, which is shown in Figure 9-5. Figure 9-5a shows how you sketch in the asymptotes, intercepts, and removable discontinuity.
, so the x-intercept is (3, 0). You place all this information on a graph, which is shown in Figure 9-5. Figure 9-5a shows how you sketch in the asymptotes, intercepts, and removable discontinuity.

John Wiley & Sons, Inc.
FIGURE 9-5: Following the steps to graph a rational function.
Figure 9-5a seems to indicate that the curve will have soft-C shapes in the upper left and lower right parts of the graph, opposite one another through the asymptotes. If you plot a few points to confirm this, you see that the graph approaches positive infinity as it approaches ![]() from the left and goes to negative infinity from the right. You can see the completed graph in Figure 9-5b.
from the left and goes to negative infinity from the right. You can see the completed graph in Figure 9-5b.
The graphs of other rational functions, such as ![]() , don’t give you quite as many clues before you have to do the actual graphing. For this example, by factoring the denominator and setting it equal to zero, you get
, don’t give you quite as many clues before you have to do the actual graphing. For this example, by factoring the denominator and setting it equal to zero, you get ![]() ; the vertical asymptotes are at
; the vertical asymptotes are at ![]() and
and ![]() . The horizontal asymptote is at
. The horizontal asymptote is at ![]() , which is the x-axis. The only x-intercept is (1, 0), and a y-intercept is located at
, which is the x-axis. The only x-intercept is (1, 0), and a y-intercept is located at ![]() . Figure 9-6a shows the asymptotes and intercepts on a graph.
. Figure 9-6a shows the asymptotes and intercepts on a graph.

John Wiley & Sons, Inc.
FIGURE 9-6: Graphing a rational function with two vertical asymptotes.
The only place the graph of the function crosses the x-axis is at (1, 0), so the curve must come from the left side of that middle section separated by the vertical asymptotes and continue to the right side. If you try a couple of points — for instance, ![]() and
and ![]() — you get the points
— you get the points ![]() and
and ![]() . These points tell you that the curve is above the x-axis to the left of the x-intercept and below the x-axis to the right of the intercept. You can use this information to sketch a curve that drops down through the whole middle section.
. These points tell you that the curve is above the x-axis to the left of the x-intercept and below the x-axis to the right of the intercept. You can use this information to sketch a curve that drops down through the whole middle section.
Two other random points you may choose are when ![]() and
and ![]() . You choose points such as these to test the extreme left and right sections of the graph.
. You choose points such as these to test the extreme left and right sections of the graph.
From these values, you get the points ![]() and
and ![]() . Plot these points and sketch in the rest of the graph, which is shown in Figure 9-6b.
. Plot these points and sketch in the rest of the graph, which is shown in Figure 9-6b.

 You write the equations of rational functions as fractions — and fractions have denominators. The denominator of a fraction can’t equal zero, so you exclude anything that makes the denominator of a rational function equal to zero from the domain of the function.
You write the equations of rational functions as fractions — and fractions have denominators. The denominator of a fraction can’t equal zero, so you exclude anything that makes the denominator of a rational function equal to zero from the domain of the function. If zero is in the domain of a rational function, you can be sure that the function has at least a y-intercept. A rational function doesn’t have a y-intercept if its denominator equals zero when you substitute zero in the equation for x.
If zero is in the domain of a rational function, you can be sure that the function has at least a y-intercept. A rational function doesn’t have a y-intercept if its denominator equals zero when you substitute zero in the equation for x. Here’s a rule for determining the equation of a horizontal asymptote. The horizontal asymptote of
Here’s a rule for determining the equation of a horizontal asymptote. The horizontal asymptote of