Chapter 16
Making a List: Sequences and Series
IN THIS CHAPTER
![]() Familiarizing yourself with sequence terminology
Familiarizing yourself with sequence terminology
![]() Working with arithmetic and geometric sequences
Working with arithmetic and geometric sequences
![]() Coming to terms with recursively defined functions
Coming to terms with recursively defined functions
![]() Stepping up from sequences to series
Stepping up from sequences to series
![]() Recognizing sequences at work in the real world
Recognizing sequences at work in the real world
![]() Discussing and using special formulas for sequences and series
Discussing and using special formulas for sequences and series
A sequence is a list of items or individuals — and because this is an algebra book, the sequences you see feature lists of numbers. A series is the sum of the numbers in a list. These concepts pop up in many areas of life (outside of top-ten lists). For example, you can make a list of the number of seats in each row at a movie theater. With this list, you can add the numbers to find the total number of seats. You prefer to see situations where the number of items in a list isn’t random; you like it when the number follows a pattern or rule. You can describe the patterns formed by elements in a sequence with mathematical expressions containing mathematical symbols and operations. In this chapter, you discover how to describe the terms in sequences and, when you get lucky, how to add as many of the terms as you want without too much fuss or bother.
Understanding Sequence Terminology
A sequence of events consists of two or more happenings in which one item or event follows another, which follows another, and so on. In mathematics, a sequence is a list of terms, or numbers, created with some sort of mathematical rule. For instance, consider the rule given in the braces; the n represents the counting numbers ![]() . The rule
. The rule ![]() says that the numbers in a particular sequence start with the number 7 and increase by four with each additional term. The numbers in the sequence are
says that the numbers in a particular sequence start with the number 7 and increase by four with each additional term. The numbers in the sequence are ![]()
To get even more specific, here’s the formal definition of a sequence: A function whose domain consists of positive integers ![]() . This is really a nice feature — having to deal with only the positive integers in the domain. The rest of this section has many more useful tidbits about sequences, guaranteed to leave your brain satisfied.
. This is really a nice feature — having to deal with only the positive integers in the domain. The rest of this section has many more useful tidbits about sequences, guaranteed to leave your brain satisfied.
Using sequence notation
One big clue that you’re dealing with a sequence is when you see something like ![]() or
or ![]() . The braces,
. The braces, ![]() , indicate that you have a list of items, called terms; commas usually separate the terms in a list from one another. The term
, indicate that you have a list of items, called terms; commas usually separate the terms in a list from one another. The term ![]() is the notation for the rule that represents a particular sequence. When identifying a sequence, you can list the terms in the sequence, showing enough terms to establish a pattern, or you can give the rule that creates the terms.
is the notation for the rule that represents a particular sequence. When identifying a sequence, you can list the terms in the sequence, showing enough terms to establish a pattern, or you can give the rule that creates the terms.
For instance, if you see the notation ![]() , you know that the sequence consists of the terms
, you know that the sequence consists of the terms ![]() .
. ![]() is the rule that creates the sequence when you insert all the positive integers in place of the n. When
is the rule that creates the sequence when you insert all the positive integers in place of the n. When ![]() ,
, ![]() ; when
; when ![]() ,
, ![]() ; and so on. The domain of a sequence is all positive integers (counting numbers), so the process is easy as 1, 2, 3.
; and so on. The domain of a sequence is all positive integers (counting numbers), so the process is easy as 1, 2, 3.
No-fear factorials in sequences
A mathematical operation you see in many sequences is the factorial. The symbol for factorial is an exclamation mark.
For example, ![]() , and
, and ![]() .
.
So, if ![]() , you write that
, you write that ![]() ,
, ![]() ,
, ![]() , and so on. You write the terms in the sequence as
, and so on. You write the terms in the sequence as ![]() .
.
Alternating sequential patterns
One special type of sequence is an alternating sequence. An alternating sequence has terms that forever alternate back and forth from positive to negative to positive. The terms in an alternating sequence have a multiplier of ![]() , which is raised to some power such as n,
, which is raised to some power such as n, ![]() , or
, or ![]() . Adding the power, which is related to the number of the term, to the
. Adding the power, which is related to the number of the term, to the ![]() causes the terms to alternate because the positive integers alternate between even and odd. Even powers of
causes the terms to alternate because the positive integers alternate between even and odd. Even powers of ![]() are equal to
are equal to ![]() , and odd powers of
, and odd powers of ![]() are equal to
are equal to ![]() .
.
For instance, the alternating sequence ![]() , because
, because
and so on.
Here’s an example of an alternating sequence that has a factorial (see the previous section) and fraction — a little bit of everything. The first four terms of the sequence ![]() are as follows:
are as follows:
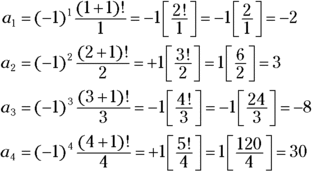
So, the sequence is ![]() .
.
You can see how the absolute value of the terms keeps getting larger while the terms alternate between positive and negative (see Chapter 2 for more on absolute value).
Looking for sequential patterns
The list of terms in a sequence may or may not display an apparent pattern. Of course, if you see the function rule — the rule that tells you how to create all the terms in the sequence — you have a huge hint about the pattern of the terms. You can always list the terms of a sequence if you have the rule, and you can often create the rule when you have enough terms in the sequence to figure out the pattern.
The patterns you can look for range from simple to a bit tricky:
- A single-number difference between each term, such as 4, 9, 14, 19, … , where the difference between each term is 5
- A multiplier separating the terms, such as multiplying by 5 to get 2, 10, 50, 250, …
- A pattern within a pattern, such as with the numbers 2, 5, 9, 14, 20, … , where the differences between the numbers get bigger by one each time
When you have to figure out a pattern and write a rule for a sequence of numbers, you can refer to your list of possibilities — the ones I mention and others — and see which type of rule applies.
Difference between terms
The quickest, easiest pattern to find features a common difference between the terms. A difference between two numbers is the result of subtracting the previous term from the term in question. You can usually tell when you have a sequence of this type by inspecting it — looking at how far apart the numbers sit on the number line.
The following three sequences have something in common: The terms in the sequences have a common first difference, a common second difference, or a common third difference.
FIRST DIFFERENCE
When the first difference of the terms in a sequence is a constant number, the rule determining the terms is usually a linear expression (a linear expression has an exponent of 1 on n; see Chapter 2). For example, the sequence of numbers ![]() consists of terms that have a common difference of 5.
consists of terms that have a common difference of 5.
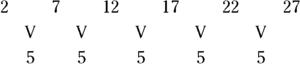
The rule for this example sequence is ![]() . You use the multiplier 5 to make the terms in the sequence each 5 more than the previous term. You subtract the 3 because when you replace n with 1, you get a number too big; you want to start with the number 2, so you subtract 3 from the first multiple. Sequences with a common first difference are called arithmetic sequences (I cover these sequences thoroughly in the section “Taking Note of Arithmetic and Geometric Sequences”).
. You use the multiplier 5 to make the terms in the sequence each 5 more than the previous term. You subtract the 3 because when you replace n with 1, you get a number too big; you want to start with the number 2, so you subtract 3 from the first multiple. Sequences with a common first difference are called arithmetic sequences (I cover these sequences thoroughly in the section “Taking Note of Arithmetic and Geometric Sequences”).
SECOND DIFFERENCE
When the second difference of the terms in a sequence is a constant, like 2, the rule for that sequence is usually quadratic (see Chapter 3) — it contains the term ![]() . The sequence of numbers
. The sequence of numbers ![]() , for example, consists of terms that have a common second difference of 2. The first differences between the terms increase by two for each interval:
, for example, consists of terms that have a common second difference of 2. The first differences between the terms increase by two for each interval:
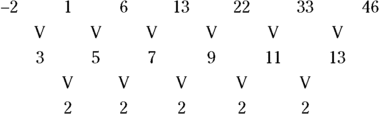
The rule used to create this example sequence is ![]() .
.
THIRD DIFFERENCE
The sequence ![]() features a common third difference of 6. In the following diagram, you see that the row below the sequences shows the first differences; under the first differences are the second differences; and, finally, the third row contains the third differences:
features a common third difference of 6. In the following diagram, you see that the row below the sequences shows the first differences; under the first differences are the second differences; and, finally, the third row contains the third differences:
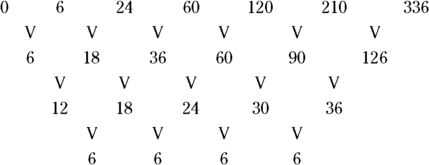
The rule for this example sequence is ![]() , which contains a cubed term.
, which contains a cubed term.
Multiples and powers
Some sequences have fairly apparent rules that generate their terms, because each term is a multiple or a power of some constant number. For instance, the sequence ![]() consists of multiples of 3, and its rule is {3n}.
consists of multiples of 3, and its rule is {3n}.
But what if the sequence starts with 21? What’s the rule for ![]() ? The terms are all multiples of 3, but {3n} doesn’t work because you have to start with
? The terms are all multiples of 3, but {3n} doesn’t work because you have to start with ![]() . Remember, the domain or input of a sequence is made up of positive integers
. Remember, the domain or input of a sequence is made up of positive integers ![]() , so you can’t use anything smaller than 1 for n.
, so you can’t use anything smaller than 1 for n.
The sequence ![]() has two interesting features: The terms alternate signs (see the section “Alternating sequential patterns”), and the fractions have consecutive integers in their denominators. To write the rule for this sequence, consider the two features. The alternating terms suggest a multiplier of
has two interesting features: The terms alternate signs (see the section “Alternating sequential patterns”), and the fractions have consecutive integers in their denominators. To write the rule for this sequence, consider the two features. The alternating terms suggest a multiplier of ![]() . The first, third, fifth, and all other odd terms are positive, so you can create alternating multiples of
. The first, third, fifth, and all other odd terms are positive, so you can create alternating multiples of ![]() that are positive by raising
that are positive by raising ![]() factor to
factor to ![]() . This makes those exponents even when n is odd and all the odd terms positive. For the fractions, you can put n, the term’s number, in the denominator. The rule for this sequence, therefore, is as follows:
. This makes those exponents even when n is odd and all the odd terms positive. For the fractions, you can put n, the term’s number, in the denominator. The rule for this sequence, therefore, is as follows:
Other sequences can have terms that are all powers of the same number. These sequences are called geometric sequences (I discuss them at great length in the section “Taking Note of Arithmetic and Geometric Sequences”). An example of a geometric sequence is ![]() . You can see that these terms are powers of the number 2, and the rule for the terms is
. You can see that these terms are powers of the number 2, and the rule for the terms is ![]() .
.
Taking Note of Arithmetic and Geometric Sequences
Arithmetic and geometric sequences are special types of sequences that have many applications in mathematics. Because you can usually recognize arithmetic or geometric sequences and write their general rules with ease, these sequences have become a mathematician’s best friends. Arithmetic and geometric sequences also have very nice formulas for the sums of their terms, which opens up a whole new branch of mathematical activity.
Finding common ground: Arithmetic sequences
Arithmetic sequences (pronounced air-ith-mat-ick, with the emphasis on mat) are sequences whose terms have the same differences between them, no matter how far down the lists you go (in other words, how many terms the lists include).
One way to describe the general formula for arithmetic sequences is with the following:
The formula says that the nth term of the sequence is equal to the term directly before it (the ![]() term) plus the common difference, d.
term) plus the common difference, d.
Another equation you can use with arithmetic sequences is the following:
This formula says that the nth term of the sequence is equal to the first term, ![]() , plus
, plus ![]() times the common difference, d.
times the common difference, d.
For instance, if you know that the common difference between the terms of an arithmetic sequence is 4 and that the sixth term is 37, you can substitute this information into the equation ![]() , letting
, letting ![]() ,
, ![]() , and
, and ![]() . You get the following:
. You get the following: ![]() , which becomes
, which becomes ![]() . Subtracting 20 from each side of the equation, you get that
. Subtracting 20 from each side of the equation, you get that ![]() . Now, armed with the first term and the difference, you can write the general term using
. Now, armed with the first term and the difference, you can write the general term using ![]() . Replacing
. Replacing ![]() with 17 and d with 4, you have
with 17 and d with 4, you have ![]() . Distributing the 4 and simplifying, you have
. Distributing the 4 and simplifying, you have ![]() .
.
An arithmetic sequence that has a common difference of 4 and whose sixth term is 37 has the general rule ![]() .
.
You use this procedure when you’re given the number values of the terms flat out and when you have to figure them out from some application or story problem. Here’s an example of a story problem for which you need to use an arithmetic sequence.
You and a group of friends have been hired to be ushers at a local theatre performance, and your payment includes free tickets to the show. The theatre allocates the whole last row in the middle section for your group. The first row in the middle section of the theatre has 26 seats, and the number of seats in each row increases by one seat per row as you move backward for a total of 25 rows. How many seats are in the last row?
You can solve this problem quickly with an arithmetic sequence. Using the formula ![]() , you replace
, you replace ![]() with 26, n with 25, and d with 1:
with 26, n with 25, and d with 1:
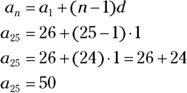
The last row has 50 seats. It looks like your friends can bring their friends, too!
Taking the multiplicative approach: Geometric sequences
A geometric sequence is a sequence in which each term is different from the one that follows it by a common ratio. In other words, the sequence has a constant number that multiplies each term to create the next one. With arithmetic sequences, you add a constant; with geometric sequences, you multiply the constant.
A general formula or rule for a geometric sequence is as follows:
In this equation, r is the constant ratio that multiplies each term. The rule says that, to get the nth term, you multiply the term before it — the ![]() term — by the ratio, r.
term — by the ratio, r.
Another way you can write the general rule for a geometric sequence is as follows:
The second form of the rule involves the first term, ![]() , and applies the ratio as many times as needed. The nth term is equal to the first term multiplied by the ratio
, and applies the ratio as many times as needed. The nth term is equal to the first term multiplied by the ratio ![]() times.
times.
Say that the rule for a particular geometric sequence is ![]() . When
. When ![]() , the power on the fraction is 0, and you have 360 multiplying the number 1. So,
, the power on the fraction is 0, and you have 360 multiplying the number 1. So, ![]() . When
. When ![]() , the exponent is equal to 1, so the fraction multiplies the 360, and you get 120. Here are the first few terms in this sequence:
, the exponent is equal to 1, so the fraction multiplies the 360, and you get 120. Here are the first few terms in this sequence:
You can find each term by multiplying the previous term by ![]() .
.
Here’s another example to familiarize you with geometric formulas … feel free to break it out at parties in the future. An unwise gambler bets a dollar on the flip of a coin and loses. Instead of paying up, he says, “Double or nothing,” meaning that he wants to flip the coin again; he’ll pay two bucks if he loses, and his opponent gets nothing if the gambler wins. Oops! He loses again, and again he says, “Double or nothing!” If he repeats this doubling-and-losing process 20 times, how much will he owe on the 21st try?
Using the formula ![]() (you know the first term — the one dollar — and the multiplier), you replace the first term,
(you know the first term — the one dollar — and the multiplier), you replace the first term, ![]() , with the number 1, r with 2 for the doubling, and n with 21:
, with the number 1, r with 2 for the doubling, and n with 21:
The gambler will owe over one million dollars if he keeps going to 21. If he’s unwilling to part with his first dollar, how’s he going to deal with this number?
Maybe the gambler shouldn’t start with such a big bet at the beginning. What if he starts with a quarter rather than a dollar? Using the same formula, ![]() , the first term is 0.25, and the ratio is still 2. So,
, the first term is 0.25, and the ratio is still 2. So, ![]() . Looks like he’s still in big trouble. And, in two more flips, letting
. Looks like he’s still in big trouble. And, in two more flips, letting ![]() , he reaches the same amount lost in 21 flips with the dollar bill.
, he reaches the same amount lost in 21 flips with the dollar bill.
Recursively Defining Functions
An alternate way to describe the terms of a sequence, in place of giving the general rule for the sequence, is to define the sequence recursively. To do so, you identify the first term, or maybe a few of the initial terms, and describe how to find the rest of the terms by using two or more of the terms that come before them.
Here’s an example of a recursively defined sequence. Let ![]() and
and ![]() . The formula says that, to find a term in the sequence, you look at the previous term
. The formula says that, to find a term in the sequence, you look at the previous term ![]() , double it
, double it ![]() , and add 3. The first term is 6, so the second term is 3 more than the double of 6, or 15. The next term is 3 more than the double of 15, or 33. Here are some of the terms of this sequence listed in order:
, and add 3. The first term is 6, so the second term is 3 more than the double of 6, or 15. The next term is 3 more than the double of 15, or 33. Here are some of the terms of this sequence listed in order: ![]() .
.
You can also define sequences recursively by referring to more than one previous term. For instance, assume that you let ![]() . This rule says that to find the nth term in the sequence (you choose the n you want — the 5th term, the 50th term, and so on), you have to look at the two previous terms [the
. This rule says that to find the nth term in the sequence (you choose the n you want — the 5th term, the 50th term, and so on), you have to look at the two previous terms [the ![]() and the
and the ![]() terms], multiply the term two positions back by 3,
terms], multiply the term two positions back by 3, ![]() , and then add the term one position back,
, and then add the term one position back, ![]() , to that product.
, to that product.
To start writing the terms of this sequence, you need to identify two consecutive terms. To create terms in a particular sequence (let’s name it B) with this rule, you decide to let ![]() and
and ![]() . (Okay, you didn’t get to decide, I did. I just picked random numbers, but, after they’re chosen, they determine what’s going to happen to the rest of the numbers in the sequence — using the given rule.) Here’s how the terms go (note that if you’re looking for the sixth term, you need the
. (Okay, you didn’t get to decide, I did. I just picked random numbers, but, after they’re chosen, they determine what’s going to happen to the rest of the numbers in the sequence — using the given rule.) Here’s how the terms go (note that if you’re looking for the sixth term, you need the ![]() term, which is the fifth term, and the
term, which is the fifth term, and the ![]() term, which is the fourth term):
term, which is the fourth term):
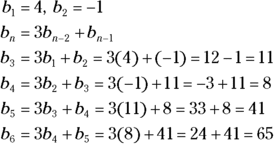
So the terms of this sequence are: ![]() .
.
Recursively formed sequences use earlier terms in the sequences to form later terms. The rules used to write these sequences aren’t as handy as the rules that allow you to find the 50th or 100th term (like arithmetic and geometric sequences) without finding all the terms that come before. But the recursive rule is sometimes easier to write.
For example, if you find out that your salary at a new job would be $20,000 this year, $25,000 next year, and that every year after it will be 80 percent of the salary from 2 years ago plus 40 percent of the salary from the previous year, would you be willing to sign the contract? The rule reads: ![]() . Using the first two terms and this rule, your salary for the first five years would be
. Using the first two terms and this rule, your salary for the first five years would be ![]() .
.
Making a Series of Moves
A series is the sum of a certain number of terms of a sequence. How many terms? That’s part of the problem — either given to you or what you determine in order to answer some question.
Being able to list all the terms in a sequence is a handy tool to have in your algebra tool belt, but you can do much more with sequences. For instance, adding a certain number of terms in a sequence is helpful when the sequence is a list of how much money you’re getting for an allowance during the month or how many seats sit in a theatre.
Finding the sum of the sequence means adding as many terms as you need to figure out your total allowance for the month or to find out how many people are in the first 20 rows of the theatre. This process doesn’t sound like a chore, especially with hand-held calculators, but if the numbers get really big and you want the sum of many terms, the task can be daunting.
For this reason, many sequences used in business and financial applications have formulas for the sum of their terms. These formulas are a big help. In fact, for some geometric series, you can add all the terms — forever — and be able to predict the sum of all those terms.
Introducing summation notation
Mathematicians like to keep formulas and rules neat and concise, so they created a special symbol to indicate that you’re adding the terms of a sequence. The special notation is sigma, ![]() , or summation notation.
, or summation notation.
For instance, if you want the sum ![]() , you need to find the first five terms, letting
, you need to find the first five terms, letting ![]() , and so on; you finish by adding all those terms:
, and so on; you finish by adding all those terms:

You find that the sum is 45.
Summing arithmetically
An arithmetic sequence has a general rule (see the section “Finding common ground: Arithmetic sequences”) that involves the first term and the common difference between consecutive terms: ![]() . An arithmetic series is the sum of the terms that come from an arithmetic sequence. Consider the arithmetic sequence
. An arithmetic series is the sum of the terms that come from an arithmetic sequence. Consider the arithmetic sequence ![]() . The first ten terms in this sequence are 4, 9, 14, 19, 24, 29, 34, 39, 44, and 49. The sum of these ten terms is 265. How did I get that value? Pencil and paper, my friend. Simple addition works just fine for a small list of numbers. However, your algebra teacher may not always bless you with small lists. Consider, now, a formula for the sum of the first n terms of an arithmetic sequence.
. The first ten terms in this sequence are 4, 9, 14, 19, 24, 29, 34, 39, 44, and 49. The sum of these ten terms is 265. How did I get that value? Pencil and paper, my friend. Simple addition works just fine for a small list of numbers. However, your algebra teacher may not always bless you with small lists. Consider, now, a formula for the sum of the first n terms of an arithmetic sequence.
Here, ![]() and d are the first term and difference, respectively, of the arithmetic sequence
and d are the first term and difference, respectively, of the arithmetic sequence ![]() . The n indicates which term in the sequence you get when you put the value of n in the formula.
. The n indicates which term in the sequence you get when you put the value of n in the formula.
To use the formula for the sum of the ten numbers 4, 9, 14, 19, 24, 29, 34, 39, 44, and 49 (previously added to get 265), you insert the known data: ![]() .
.
Now, say you want to add the first 100 numbers in a sequence that starts with 13 and features a common difference of 2 between each of the terms: ![]() , all the way to the 100th number. You find the sum of these 100 numbers by using the first part of the sum formula:
, all the way to the 100th number. You find the sum of these 100 numbers by using the first part of the sum formula:
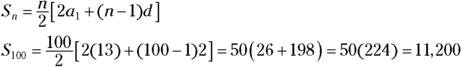
Summing geometrically
A geometric sequence consists of terms that differ from one another by a common ratio. You multiply a term in the sequence by a constant number or ratio to find the next term. You can use two different formulas to find the sum of the terms in a geometric sequence. You use the first formula to find the sum of a certain, finite number of terms of a geometric sequence — any geometric sequence at all. The second formula applies only to geometric sequences that have a ratio whose absolute value lies between zero and one (a proper fraction); you use it when you want to add all the terms in the sequence — forever and ever (for more on geometric sequences, see the section “Taking the multiplicative approach: Geometric sequences”).
Adding the first n terms
The formula you use to add a specific, finite number of terms from a geometric sequence involves a fraction where you subtract the ratio — or a power of the ratio — from one. You can’t reduce the formula, so don’t try. Just use it as it is.
The term ![]() is the first term of the sequence, and r represents the common ratio.
is the first term of the sequence, and r represents the common ratio.
For example, say you want to add the first ten terms of the geometric sequence ![]() . You identify the first term, the 1, and then the ratio by which you multiply, 3. Substitute this information into the formula:
. You identify the first term, the 1, and then the ratio by which you multiply, 3. Substitute this information into the formula:
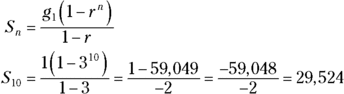
Quite a big number! Isn’t using the formula easier than adding ![]()
![]() ?
?
Adding all the terms to infinity
Geometric sequences have a ratio, or multiplier, that changes one term into the next one in line. If you multiply a number by 4 and the result by 4 and keep going, you create huge numbers in a short amount of time. So, it may sound impossible to add numbers that seem to get infinitely large.
But algebra has a really wonderful property for geometric sequences with ratios between negative one and one. The absolute values of the numbers in these sequences get smaller and smaller, and the sums of the terms in these sequences never exceed set, constant values.
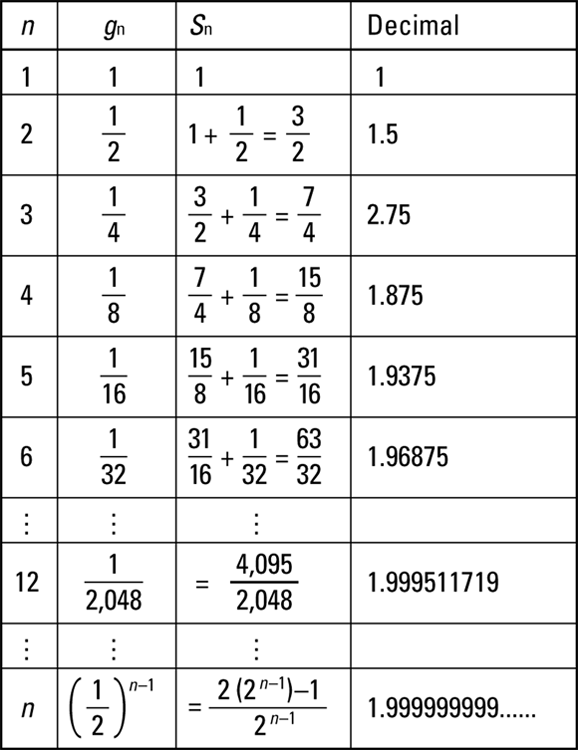
In Figure 16-1, you see the terms in a sequence that starts with 1 and has a ratio of ![]() . You also see the sum of all the terms up to and including that term.
. You also see the sum of all the terms up to and including that term.
John Wiley & Sons, Inc.
FIGURE 16-1: Adding terms in a geometric sequence.
So, you’re really finding powers of ![]() . Here are the first few terms:
. Here are the first few terms:
As you see in Figure 16-1, the sum of the terms is equal to almost two as the number of terms increases. The number in the numerator of the fraction of the sum is always one less than twice the denominator. The sum in Figure 16-1 approaches two but never exactly hits it. The sum gets so very, very close, though, that you can round up to two. This business of approaching a particular value is true of any geometric sequence with a proper fraction (between zero and one) for a ratio.
Algebra also offers a formula for finding the sum of all the terms in a geometric sequence with a ratio between zero and one. You may think this formula should be much more complicated than the formula for finding only a few terms, but that isn’t the case. This formula is actually much simpler.
You can apply this rule to the sum of the sequence whose first term is 1 and whose common ratio is ![]() .
. ![]() .
.
You may be wondering what happens when the ratio is a negative number. Do the positive and negative terms cancel one another out? Not so. First, using the formula, I find the sum of all the terms of the geometric sequence whose first term is 1 and ratio is ![]() :
: 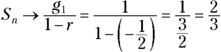 . The sum is smaller than the sequence with a positive ratio, but the positives seem to outweigh the negatives!
. The sum is smaller than the sequence with a positive ratio, but the positives seem to outweigh the negatives!
Applying Sums of Sequences to the Real World
Having the tools to add all the terms in a mathematical sequence is peachy keen from a homework standpoint, but what’s the point outside the classroom? Why would anyone need to be able to find the sum of sequences in the real world? You may be surprised at the possible applications in many walks of life. Hopefully, the three examples I include in this section will give you a hint of how helpful figuring sums can be.
Stacking the blocks
You are teaching your young nephew to stack blocks and show him how to create a flat pyramid where each row has one more block in it than the one preceding it. So the first row has one block, the second has two blocks, and so on. The local toy store is having a sale on block sets, and the biggest set has 210 blocks in it. How many rows of blocks will your nephew have in his pyramid if he uses all the blocks?
You can solve this problem by using the formula for the sum of the terms in an arithmetic sequence. The first row will have 1 block, and the difference in the number of blocks from row to row is 1. Using ![]() , you replace the sum,
, you replace the sum, ![]() with 210, the first term,
with 210, the first term, ![]() with 1, and the difference, d, with 1. Then solve for n, the number of rows.
with 1, and the difference, d, with 1. Then solve for n, the number of rows.

Multiply each side of the equation by 2, and you have ![]() . Distribute the n, and then write the equation as a quadratic set equal to 0. You have
. Distribute the n, and then write the equation as a quadratic set equal to 0. You have ![]() . Factoring,
. Factoring, ![]() . The solutions are
. The solutions are ![]() and 20, but only the 20 works for a number of blocks. Your nephew will have a stack of blocks that has 20 rows!
and 20, but only the 20 works for a number of blocks. Your nephew will have a stack of blocks that has 20 rows!
Negotiating your allowance
You approach your dad about increasing your allowance because $10 per week just doesn’t cut it anymore. He replies, “Absolutely not. Not until you improve your math grade.” You then negotiate a deal with the following proposition: You’ll take 1 cent on the first day of the month, 2 cents on the second day of the month, 4 cents on the third, 8 cents on the fourth, and so on, doubling the amount each day until the end of the month. At that point, your dad can check on your math grade and see if he wants to change the system back and raise your allowance. He knows how crafty you are, so he asks you to explain what you’re up to before he agrees.
How much will you get with your system for the month of January? That month has 31 days of penny-pinching allowance. Using the formula for the sum of a geometric sequence whose first term is 1, common ratio is 2, and number of terms is 31 (see the section “Summing geometrically”), you calculate the following:

Of course, your answer is in pennies, so you move the decimal point over two places. Your allowance comes to a total of $21,474,836.47. What does your dad think of your math ability now? Unfortunately, he wants you to care about your grades as much as your money. No deal.
Bouncing a ball
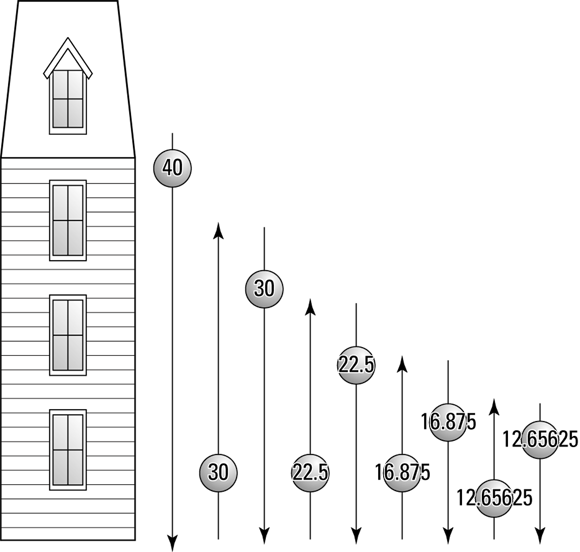
You want to figure the total distance (up and down and up and down …) that a superball travels in n bounces, plus the first drop, if it always bounces back 75 percent of the distance it falls. You drop the superball onto a smooth sidewalk from a window sitting 40 feet off the ground. Look at Figure 16-2 to see what the problem entails.
John Wiley & Sons, Inc.
FIGURE 16-2: The distance the ball rebounds after each drop stays the same on each subsequent nosedive.
As you can see, the first distance is the 40-foot drop. The ball bounces up 75 percent of the distance it fell, or 30 feet, and drops 30 feet again. It then bounces back 75 percent of 30 feet, or 22.5 feet, and repeats the process. Except for the initial 40 feet, all the measures double to account for going upward and then downward.
The question is: How far does the superball travel in 10 bounces, plus that first drop? To figure this out by using a geometric sequence (see the section “Summing geometrically”), you let the first term equal 30, the ratio equal 0.75, and the number of terms equal 10. You double that sum of the sequence to account for the distance the ball travels both up and down, and you add the first 40 feet to get the total distance traveled by the ball.
First, you find the value of the sum of the sequence:

Now you double the sum of the sequence and add 40 feet:
The ball travels over 266 feet in 10 bounces. Well done!
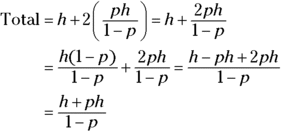
Just fill in the initial height, h, and the percentage, p, as a decimal.
So, if you decide to climb the 897 steps to the top of the Washington Monument and drop a superball that bounces back 60 percent of the dropped height, then how far will the ball travel before stopping, if you’re able to drop it out a window 550 feet off the ground?
Using the formula I just created, you have
The ball travels a total of 2,200 feet.
Highlighting Special Formulas
Algebra offers several special types of sequences and series that you may use frequently in higher mathematics, such as calculus, and in financial and physics applications. For these applications, you have formulas for the sums of the terms in the sequences. Adding consecutive integers is a task made easier because you have formulas at your disposal. Counting tiles to be used in a floor or mosaic, computing the total amount of money in an annuity, and other such applications also use sums of sequences of numbers.
- The sum of the first n positive integers:

- The sum of the first n squares of the positive integers:
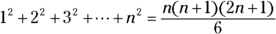
- The sum of the first n cubes of the positive integers:

- The sum of the first n odd positive integers:

For example, if you want the sum of the first 10 squares of positive integers, you use the formula to get the following:

The n is the number of the term, not the term itself.

 You call the three dots following a short list of terms an ellipsis (not to be confused with the ellipse from
You call the three dots following a short list of terms an ellipsis (not to be confused with the ellipse from  Because the terms in a sequence are linked to positive integers, you can refer to them by their positions in the listing of the integers. If the rule for a sequence is
Because the terms in a sequence are linked to positive integers, you can refer to them by their positions in the listing of the integers. If the rule for a sequence is  Here’s the formula for the factorial in a sequence:
Here’s the formula for the factorial in a sequence:  Sometimes, you have to list the numbers in a recursive sequence when given a rule, and, if you’re really lucky, you get to create the rule yourself. You’ll see the “create your own rule” option if you get into discrete mathematics or computer programming — just not here!
Sometimes, you have to list the numbers in a recursive sequence when given a rule, and, if you’re really lucky, you get to create the rule yourself. You’ll see the “create your own rule” option if you get into discrete mathematics or computer programming — just not here!