Chapter 14
Simplifying Complex Numbers in a Complex World
IN THIS CHAPTER
![]() Sparking your math imagination with imaginary numbers
Sparking your math imagination with imaginary numbers
![]() Performing operations with complex numbers
Performing operations with complex numbers
![]() Dividing and conquering complex numbers and radicals
Dividing and conquering complex numbers and radicals
![]() Facing complex solutions in quadratic equations
Facing complex solutions in quadratic equations
![]() Identifying complex roots of polynomials
Identifying complex roots of polynomials
Imaginary numbers are the results of mathematicians’ imaginations. No, imaginary numbers aren’t real — although, is any number real? Can you touch a number (if you don’t count playing with a toddler’s educational toy set)? Can you feel it? Who decided a 9 should be shaped the way it is, and what makes that person right? Does your brain hurt yet?
Mathematicians define real numbers as all the whole numbers, negative and positive numbers, fractions and decimals, radicals — anything you can think of to use in counting, graphing, and comparing amounts. Mathematicians introduced imaginary numbers when they couldn’t finish problems without them. For example, when solving for roots of quadratic equations such as ![]() , you quickly discover that you can find no real answers. Using the quadratic formula (see Chapter 3), the solutions come out to be
, you quickly discover that you can find no real answers. Using the quadratic formula (see Chapter 3), the solutions come out to be
The answers seem sort of final — like you have nowhere to go except to estimate some value for it. But you can’t find the square root of a negative number, because no real number multiplies itself and ends up with a negative result. So, rather than staying stuck there, with no final solution, mathematicians came up with a new rule: They let ![]() .
.
They made up a number to replace ![]() , and they called it i (didn’t take much imagination to come up with that). When you take the square root of each side of
, and they called it i (didn’t take much imagination to come up with that). When you take the square root of each side of ![]() , you get
, you get ![]() or
or ![]() . Using this equivalence, you can complete the problems and write the answers with i’s in them.
. Using this equivalence, you can complete the problems and write the answers with i’s in them.
In this chapter, you find out how to create, work with, and analyze imaginary numbers and the complex expressions they appear in. Just remember to use your imagination!
Using Your Imagination to Simplify Powers of i
The powers of x (representing real numbers) — ![]() , and so on — follow the rules of exponents, such as adding exponents when multiplying the powers of x together or subtracting exponents when dividing them (see Chapter 1). The powers of i (representing imaginary numbers) are rule-followers, too. The powers of i, however, have some neat features that set them apart from other numbers.
, and so on — follow the rules of exponents, such as adding exponents when multiplying the powers of x together or subtracting exponents when dividing them (see Chapter 1). The powers of i (representing imaginary numbers) are rule-followers, too. The powers of i, however, have some neat features that set them apart from other numbers.
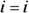 : Just plain old i
: Just plain old i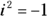 : From the definition of an imaginary number (see the introduction to this chapter)
: From the definition of an imaginary number (see the introduction to this chapter)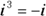 : Use the rule for exponents
: Use the rule for exponents  and then replace
and then replace  with
with 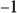 ; so,
; so, 
 : Because
: Because 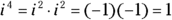
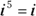 : Because
: Because 
 : Because
: Because 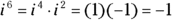
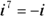 : Because
: Because 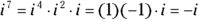
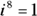 : Because
: Because 
Consider the two powers of i presented in the following list and how you determine the rewritten values; if you want to find a power of i, you make use of the rules for exponents and the first four powers of i:
 : Because
: Because 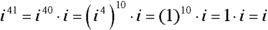
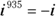 : Because
: Because 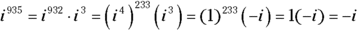
The process of changing the powers of i seems like a lot of work — plus you need to figure out what to multiply four by to get a high power (you want to find a multiple of four — the biggest possible value that’s smaller than the exponent). But you really don’t need to go through all the raising of powers if you recognize a particular pattern in the powers of i.
So, all you need to do to change the powers of i is figure out where a power of i is in relation to some multiple of four. If you need the value of ![]() , for example, you know that 5,000 is a multiple of 4 (because it ends in 00), and 5,001 is 1 value greater than 5,000, so
, for example, you know that 5,000 is a multiple of 4 (because it ends in 00), and 5,001 is 1 value greater than 5,000, so ![]() . It really simplifies expressions when you have a rule that reduces the powers of numbers.
. It really simplifies expressions when you have a rule that reduces the powers of numbers.
Understanding the Complexity of Complex Numbers
An imaginary number, i, is a part of the numbers called complex numbers, which arose after mathematicians established imaginary numbers. The standard form of complex numbers is ![]() , where a and b are real numbers, and
, where a and b are real numbers, and ![]() is
is ![]() . The fact that
. The fact that ![]() is equal to
is equal to ![]() and i is equal to
and i is equal to ![]() is the foundation of the complex numbers. If you didn’t have the imaginary numbers with the i’s, you’d have no need for complex numbers with imaginaries in them.
is the foundation of the complex numbers. If you didn’t have the imaginary numbers with the i’s, you’d have no need for complex numbers with imaginaries in them.
Some examples of complex numbers include ![]() ,
, ![]() , and 7i. In the last number, 7i, the value of a is zero, so the number is pure imaginary. If the value of b is zero as well, you have a complex number that is a real number.
, and 7i. In the last number, 7i, the value of a is zero, so the number is pure imaginary. If the value of b is zero as well, you have a complex number that is a real number.
Complex numbers have many applications, and mathematicians study them extensively. In fact, whole math courses and fields of study are devoted to complex numbers. And, imagine this, you get a glimpse of this ethereal world right here and now in this section.
Operating on complex numbers
You can add, subtract, multiply, and divide complex numbers — in a very careful manner. The rules used to perform operations on complex numbers look very much like the rules used for any algebraic expression, with two big exceptions:
- You simplify the powers of i, change them to their equivalent in the first four powers of i (see the section “Using Your Imagination to Simplify Powers of i” earlier in the chapter), and then combine like terms.
- You don’t really divide complex numbers; you multiply by the conjugate (I tell you all about this in the section “Multiplying by the conjugate to perform division” later in the chapter).
Adding complex numbers
The result of the addition is now in the form of a complex number, where ![]() is the real part and
is the real part and ![]() is the imaginary part.
is the imaginary part.
When you add ![]() , for example, you get
, for example, you get ![]() .
.
Subtracting complex numbers
The result of the subtraction is now in the form of a complex number, where ![]() is the real part and
is the real part and ![]() is the imaginary part.
is the imaginary part.
When you subtract ![]() , for example, you get
, for example, you get ![]() .
.
Multiplying complex numbers
When you multiply complex numbers, the operations get a little more exciting.
The result of the multiplication shown here is in the form of a complex number, with ![]() as the real part and
as the real part and ![]() as the imaginary part. You can see from the following distribution where the values in this rule come from. First, FOILing the binomials, you have
as the imaginary part. You can see from the following distribution where the values in this rule come from. First, FOILing the binomials, you have ![]() . You combine the two middle terms by factoring out the
. You combine the two middle terms by factoring out the ![]() . Replace the
. Replace the ![]() with
with ![]() . And now the first and last terms are both real numbers, and you can write them together:
. And now the first and last terms are both real numbers, and you can write them together: ![]() .
.
To find the product of ![]() , for example, you FOIL to get
, for example, you FOIL to get ![]() . You simplify the last term to
. You simplify the last term to ![]() and combine it with the first term; the two middle terms also combine. Your result is
and combine it with the first term; the two middle terms also combine. Your result is ![]() , a complex number.
, a complex number.
Multiplying by the conjugate to perform division
The complex thing about dividing complex numbers is that you don’t really divide. Do you remember when you first found out how to multiply and divide fractions? You never really divided fractions; you changed the second fraction to its reciprocal, and then you changed the problem to multiplication. You found that the answer to the multiplication problem you created is the same as the answer to the original division problem. You avoid division in much the same way with complex numbers. You do a multiplication problem — one that has the same answer as the division problem. But before you tackle the “division,” you should know more about the conjugate of a complex number.
Defining the conjugate
A complex number and its conjugate have opposite signs between the two terms. The conjugate of the complex number ![]() is
is ![]() , for instance.
, for instance.
Here are a couple numerical examples: The conjugate of ![]() is
is ![]() , and the conjugate of
, and the conjugate of ![]() is
is ![]() . Seems simple enough, because you don’t see the special trait attributed to the conjugate of a complex number until you multiply the complex number and its conjugate together.
. Seems simple enough, because you don’t see the special trait attributed to the conjugate of a complex number until you multiply the complex number and its conjugate together.
Using conjugates to divide complex numbers
When a problem calls for you to divide one complex number by another, you write the problem as a fraction and then multiply by the number one. You don’t actually multiply by one; you multiply by a fraction that has the conjugate of the denominator in both numerator and denominator (because the same value appears in the numerator and denominator, the fraction is equal to one):

To write the result of the division of complex numbers in a strictly real-and-imaginary-parts format, you break up the fraction:
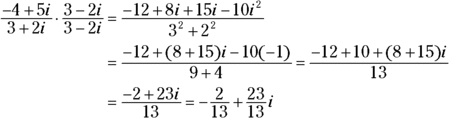
Simplifying radicals
Until mathematicians defined imaginary numbers, many problems had no answers because the answers involved square roots of negative numbers, or radicals. After the definition of an imaginary number, ![]() , came into being, doors opened; windows flung wide; parades were held; children danced in the streets; and problems were solved. Eureka!
, came into being, doors opened; windows flung wide; parades were held; children danced in the streets; and problems were solved. Eureka!
By convention, you write the previous solution as ![]() . This form isn’t at all different in value from the other form. Most mathematicians just want to put the numerical part of the coefficient first, the variables or other letters next (in alphabetical order), and the radicals last. They think it looks better that way.
. This form isn’t at all different in value from the other form. Most mathematicians just want to put the numerical part of the coefficient first, the variables or other letters next (in alphabetical order), and the radicals last. They think it looks better that way.
Solving Quadratic Equations with Complex Solutions
You can always solve quadratic equations with the quadratic formula. It may be easier to solve quadratic equations by factoring, but when you can’t factor, the formula comes in handy. (Refer to Chapter 3 if you need a refresher on the quadratic formula.)
Until mathematicians began recognizing imaginary numbers, however, they couldn’t complete many results of the quadratic formula. Whenever a negative value appeared under a radical, the equation stumped the mathematicians.
The modern world of imaginary numbers, to the rescue! To solve the quadratic equation ![]() , for example, you can use the quadratic formula to get the following:
, for example, you can use the quadratic formula to get the following:
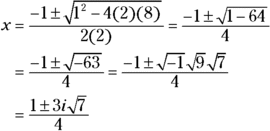
Along with the quadratic formula that produces a complex solution, it helps to look at the curve that corresponds to the equation on a graph (see Chapter 7).
To solve a quadratic function for its x-intercepts, you set the equation equal to zero. When no real solution for the equation exists, you find no x-intercepts. You still have a y-intercept, because all quadratic functions cross the y-axis somewhere, but its graph may stay above or below the x-axis without crossing it.
The quadratic equation ![]() corresponds to the parabola
corresponds to the parabola ![]() . Substituting zero for the y variable allows you to solve for the x-intercepts of the parabola. The fact that you find no real solutions for the equation tells you that the parabola has no x-intercepts. (Figure 14-1 shows you a graph of this situation.)
. Substituting zero for the y variable allows you to solve for the x-intercepts of the parabola. The fact that you find no real solutions for the equation tells you that the parabola has no x-intercepts. (Figure 14-1 shows you a graph of this situation.)

John Wiley & Sons, Inc.
FIGURE 14-1: A parabola with no real solutions for the x-intercepts never crosses the x-axis.
To solve for any y-intercept, you set x equal to zero and then solve the quadratic equation. If the equation has no solution, it has no y-intercepts. Solving the equation ![]() for its y-intercept, for example, you let
for its y-intercept, for example, you let ![]() . The equation doesn’t factor, so you use the quadratic formula:
. The equation doesn’t factor, so you use the quadratic formula:

The parabola ![]() opens to the left and never crosses the y-axis. The graph of this parabola is shown in Figure 14-2.
opens to the left and never crosses the y-axis. The graph of this parabola is shown in Figure 14-2.

John Wiley & Sons, Inc.
FIGURE 14-2: The graph of a quadratic equation whose points stay left of the y-axis.
Working Polynomials with Complex Solutions
Polynomials are functions whose graphs are nice, smooth curves that may or may not cross the x-axis. If the degree (or highest power) of a polynomial is an odd number, its graph must cross the x-axis, and it must have a real root or solution. (In Chapter 8, you discover how to find the real solutions or roots of polynomial equations.) When solving equations formed by setting polynomials equal to zero, you plan ahead as to how many solutions you can expect to find. The highest power tells you the maximum number of solutions you can find. In the case of polynomial equations where the highest powers are even numbers, you may find that the equations have absolutely no real solutions, whereas if the highest powers are odd, you’re guaranteed at least one solution in each equation.
Identifying conjugate pairs
A polynomial of degree (or power) n can have as many as n real zeros (also known as solutions or x-intercepts). If the polynomial doesn’t have n real zeros, it has ![]() zeros,
zeros, ![]() zeros, or some number of zeros decreased two at a time. (Refer to Chapter 8 for how to count the number of zeros by using Descartes’ Rule of Signs.) The reason that the number of zeros decreases by two is that complex zeros always come in conjugate pairs — a complex number and its conjugate.
zeros, or some number of zeros decreased two at a time. (Refer to Chapter 8 for how to count the number of zeros by using Descartes’ Rule of Signs.) The reason that the number of zeros decreases by two is that complex zeros always come in conjugate pairs — a complex number and its conjugate.
The equation ![]() , for example, has three real roots and two complex roots, which you know because you apply the Rational Root Theorem and Descartes’ Rule of Signs (from Chapter 8) and ferret out those real and complex solutions. The equation factors into
, for example, has three real roots and two complex roots, which you know because you apply the Rational Root Theorem and Descartes’ Rule of Signs (from Chapter 8) and ferret out those real and complex solutions. The equation factors into ![]() . The three real zeros are 0, 2, and
. The three real zeros are 0, 2, and ![]() for the solutions of
for the solutions of ![]() ,
, ![]() , and
, and ![]() . The two complex zeros are 4i and
. The two complex zeros are 4i and ![]() . You say that the two complex zeros are a conjugate pair, and you get the roots by solving the equation
. You say that the two complex zeros are a conjugate pair, and you get the roots by solving the equation ![]() .
.
A more typical conjugate pair has both real and imaginary parts to the numbers. For instance, the equation ![]() factors into
factors into ![]()
![]() . The roots are
. The roots are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . You obtain the last two roots by using the quadratic formula on the quadratic factor in the equation (see Chapter 3). The two roots are a conjugate pair.
. You obtain the last two roots by using the quadratic formula on the quadratic factor in the equation (see Chapter 3). The two roots are a conjugate pair.
Interpreting complex zeros
The polynomial function ![]() has two real roots and two complex roots. According to Descartes’ Rule of Signs (see Chapter 8), the function could’ve contained as many as four real roots (you can tell by trying the roots suggested by the Rational Root Theorem; see Chapter 8). You can determine the number of complex roots in two different ways: by factoring the polynomial or by looking at the graph of the function.
has two real roots and two complex roots. According to Descartes’ Rule of Signs (see Chapter 8), the function could’ve contained as many as four real roots (you can tell by trying the roots suggested by the Rational Root Theorem; see Chapter 8). You can determine the number of complex roots in two different ways: by factoring the polynomial or by looking at the graph of the function.
The example function factors into ![]() . The first two factors give you real roots, or x-intercepts. When you set
. The first two factors give you real roots, or x-intercepts. When you set ![]() equal to 0, you get the intercept (2, 0). When you set
equal to 0, you get the intercept (2, 0). When you set ![]() equal to 0, you get the intercept
equal to 0, you get the intercept ![]() . Setting the last factor,
. Setting the last factor, ![]() , equal to 0 doesn’t give you a real root, as you see here when you use the quadratic formula:
, equal to 0 doesn’t give you a real root, as you see here when you use the quadratic formula:
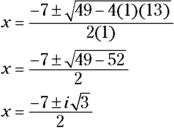
You can also tell that a polynomial function has complex roots by looking at its graph. You can’t tell what the complex roots are, but you can see that the graph has some. If you need the values of the roots, you can resort to using algebra to solve for them. Figure 14-3 shows the graph of the example function, ![]() . You can see the two x-intercepts, which represent the two real zeros. You also see the graph flattening on the left.
. You can see the two x-intercepts, which represent the two real zeros. You also see the graph flattening on the left.

John Wiley & Sons, Inc.
FIGURE 14-3: A flattening curve indicates a complex root.
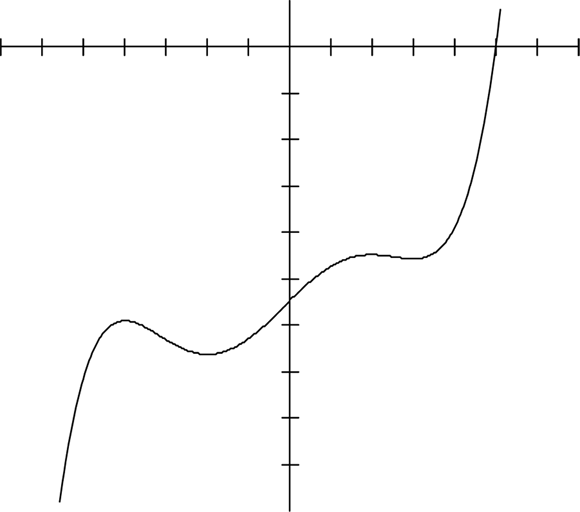
Figure 14-4 can tell you plenty about the number of real zeros and complex zeros the graph of the polynomial has … before you ever see the equation it represents.
John Wiley & Sons, Inc.
FIGURE 14-4: A polynomial with one real zero and several complex zeros.
The polynomial in Figure 14-4 appears to have one real zero and several complex zeros. Do you see how it changes direction all over the place under the x-axis? It goes up, down, up, down, and then up. These changes indicate the presence of complex zeros. The graph represents the polynomial function ![]() . The function has four complex zeros — two complex (conjugate) pairs — and one real zero (when
. The function has four complex zeros — two complex (conjugate) pairs — and one real zero (when ![]() ).
).
You need the efforts and capabilities of good algebra; the Rational Root Theorem and Descartes’ Rule of Signs combined with a graphing calculator or computer; and some luck and common sense to solve these high-order equations. When the zeros are nice integers, life is good. When the zeros are irrational or complex, life is still good, but it’s a bit more complicated. Assume the best, and work through the challenges if they arise.

 You can write all the powers of i as one of four different numbers:
You can write all the powers of i as one of four different numbers:  Every power of i that’s a multiple of four is equal to 1. If the power is one value greater than a multiple of four, the power of i is equal to i. And so the process goes. Here’s the list in full:
Every power of i that’s a multiple of four is equal to 1. If the power is one value greater than a multiple of four, the power of i is equal to i. And so the process goes. Here’s the list in full: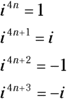
 So, a is the real part of a complex number and the bi is the imaginary part (even though b is a real number). Is that complex enough for you?
So, a is the real part of a complex number and the bi is the imaginary part (even though b is a real number). Is that complex enough for you? Here’s the product of the complex number and its conjugate, all worked out by using FOIL (see
Here’s the product of the complex number and its conjugate, all worked out by using FOIL (see  Technically, in complex form, you write a number with the i at the end, after all the other numbers — even after the radical. That’s the strict
Technically, in complex form, you write a number with the i at the end, after all the other numbers — even after the radical. That’s the strict