3
MOMENTS AND GENERATING FUNCTIONS
3.1 INTRODUCTION
The study of probability distributions of a random variable is essentially the study of some numerical characteristics associated with them. These so-called parameters of the distribution play a key role in mathematical statistics. In Section 3.2 we introduce some of these parameters, namely, moments and order parameters, and investigate their properties. In Section 3.3 the idea of generating functions is introduced. In particular, we study probability generating functions, moment generating functions, and characteristic functions. Section 3.4 deals with some moment inequalities.
3.2 MOMENTS OF A DISTRIBUTION FUNCTION
In this section we investigate some numerical characteristics, called parameters, associated with the distribution of an RV X. These parameters are (a) moments and their functions and (b) order parameters. We will concentrate mainly on moments and their properties.
Let X be a random variable of the discrete type with probability mass function pk = P{X = xk}, k = 1, 2, …. If

we say that the expected value (or the mean or the mathematical expectation) of X exists and write
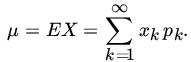
Note that the series ![]() may converge but the series
may converge but the series ![]() may not. In that case we say that EX does not exist.
may not. In that case we say that EX does not exist.
PROBLEMS 3.2
- Find the expected number of throws of a fair die until a 6 is obtained.
- From a box containing N identical tickets numbered 1 through N, n tickets are drawn with replacement. Let X be the largest number drawn. Find EX.
- Let X be an RV with PDFwhere c = Γ(m)/[Γ(1/2)Γ(m−1/2)]. Show that EX2r exists if and only if 2r < 2m −1. What is EX2r if 2r < 2m −1?

- Let X be an RV with PDF

Show that E|X|α < ∞ for α< k. Find the quantile of order p for the RV X.
- Let X be an RV such that E|X| < ∞. Show that E|X −c| is minimized if we choose c equal to the median of the distribution of X.
- Pareto's distribution with parameters α and β (both α and β positive) is defined by the PDF

Show that the moment of order n exists if and only if n < β. Let β > 2 Find the mean and the variance of the distribution.
- For an RV X with PDF

show that moments of all order exist. Find the mean and the variance of X.
- For the PMF of Example 5 show that

and

where 0 ≤ p ≤ 1, q = 1 − p.
- For the Poisson RV X with PMF

Show that
 and
and 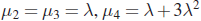
- For any RV X with E|X|4 < ∞ define

Here α3 is known as the coefficient ofskewness and is sometimes used as a measure of asymmetry, and α4 is known as kurtosis and is used to measure the peakedness ("flatness of the top") of a distribution. Compute α3 and α4 for the PMFs of Problems 8 and 9.
- For a positive RV X define the negative moment of order n by EX−n, where n > 0 is an integer. Find
 for the PMFs of Example 5 and Problem 9.
for the PMFs of Example 5 and Problem 9. - Prove Theorem 6.
- Prove Theorem 7.
- In each of the following cases, compute EX, var(X), and EXn (for n > 0, an integer) whenever they exist.
- f(x) = 1, −1/2 ≤ x ≤ 1/2, and 0 elsewhere.
- f(x) = e−x, x ≥ 0, and 0 elsewhere.
- f(x) = (k–1)/xk, x ≥ 1, and 0 elsewhere; k >1 is a constant.
- f(x) = 1/[π(1+x2)], −∞ <x < ∞.
- f(x) = 6x(1−x), 0 < x < 1, and 0 elsewhere.
- f(x) = xe−x, x >0, and 0 elsewhere.
- P(X = x) = p(1−p)x−1, x = 1, 2, …, and 0 elsewhere: 0 <p <1.
- Find the quantile of order p(0 < p < 1) for the following distributions.
- f(x) = 1 /x2, x ≥ 1, and 0 elsewhere.
- f(x) = 2xexp(−x2), x > 0, and 0 otherwise.
- f(x) = 1/θ, 0 ≤ x ≤ θ, and 0 elsewhere.
- P(X = x) = θ(1— θ)x−1, x = 1, 2, …, and 0 otherwise; 0 < θ < 1.
- f(x) = (1/β2)x exp(−x/β), x > 0, and 0 otherwise; β > 0.
- f(x) = (3/b3)(b−x)2,0 < x < b, and 0 elsewhere.
3.3 GENERATING FUNCTIONS
In this section we consider some functions that generate probabilities or moments of an RV. The simplest type of generating function in probability theory is the one associated with integer-valued RVs. Let X be an RV, and let.
with ![]() .
.
PROBLEMS 3.3
- Find the PGF of the; RVs with the following PMFs:
 .
. .
. .
.
- Let X be an integer-valued RV with PGF P(s). Let α and β be nonnegative integers, and write
 . Find the PGF of Y.
. Find the PGF of Y. - Let X be an integer-valued RV with PGF P(s), and suppose that the mgf M(s) exists for
 . How are M(s) and P(s) related? Using
. How are M(s) and P(s) related? Using  for positive integral k, find EXk in terms of the derivatives of P(s) for values of k = 1,2,3,4.
for positive integral k, find EXk in terms of the derivatives of P(s) for values of k = 1,2,3,4. - For the Cauchy PDF

does the MGF exist?
- Let X be an RV with PMF

Set P{X > j} = qj,j = 0, 1, 2, …. Clearly qj= pj+pj+2+…, j ≥ 0. Write
 Then the series for Q(s) converges in |s| < 1. Show that
Then the series for Q(s) converges in |s| < 1. Show that
where P(s) is the PGF of X. Find the mean and the variance of X(when they exist) in terms of Q and its derivatives.
- For the PMF

where
 and
and 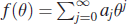 find the PGF and the MGF in terms of f.
find the PGF and the MGF in terms of f. - For the Laplace PDF

show that the MGF exists and equals

- For any integer-valued RV X, show that

where P is the PGF of X.
- Let X be an RV with MGF M(t), which exists for t ∈
 . Show that
. Show that
for any fixed s, 0 < s < t0, and for each integer n ≥ 1. Expanding etx in a power series, show that, for
 ,
,
(Since a power series can be differentiated term by term within the interval of convergence, it follows that for |t| < s,

for each integer k ≥ 1.) (Roy, LePage, and Moore [95])
- Let X be an integer-valued random variable with

Show that X must be degenerate at n.
[Hint: Prove and use the fact that if EXk < ∞ for all k, then
Write P(s) as

- Let p(n, k) = f (n, k) /n! where f (n, k) is given by



Let

be the probability generating function of p(n, k). Show that

(Pn is the generating function of Kendall's τ-statistic.)
- For k = 0, 1, …,
 let un (k) be defined recursively by
let un (k) be defined recursively by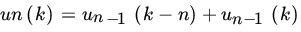
with u0(0) = 1, u0(k) = 0 otherwise, and un(k) = 0 for k < 0. Let
 be the generating function of {un}. Show that
be the generating function of {un}. Show that
If pn(k) = un(k)/2n, find {pn(k)} for n = 2, 3, 4. (Pn is the generating function of one-sample Wilcoxon test statistic.)
3.4 SOME MOMENT INEQUALITIES
In this section we derive some inequalities for moments of an RV. The main result of this section is Theorem 1 (and its corollary), which gives a bound for tail probability in terms of some moment of the random variable.
PROBLEMS 3.4
- For the RV with PDF

where λ ≥ 0 is an integer, show that

- Let X be any RV, and suppose that the MGF of X, M(t) = Eetx, exists for every t > 0. Then for any t > 0

- Construct an example to show that inequalities (4) and (5) cannot be improved.
- Let g(.) be a function satisfying g(x) > 0 for x > 0, g(x) increasing for x > 0, and
 . Show that
. Show that
- Let X be an RV with EX = 0, var(X) = σ2, and EX4 = μ4. Let K be any positive real number. Show that

In other words, show that bound (7) is better than bound (3) if
 and worse if 1 ≤
and worse if 1 ≤  . Construct an example to show that the last inequalities cannot be improved.
. Construct an example to show that the last inequalities cannot be improved. .
. - Use Chebychev's inequality to show that for any k > 1, ek+1 ≥ k2.
- For any RV X, show that

where
 .
. - Let X be an RV such that P(a ≤ X ≤ b) = 1 where –∞ < a < b < ∞. Show that var(X) ≤ (b – a)2/4.
