Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1
PROBABILITY

1.1 INTRODUCTION

The theory of probability had its origin in gambling and games of chance. It owes much to the curiosity of gamblers who pestered their friends in the mathematical world with all sorts of questions. Unfortunately this association with gambling contributed to a very slow and sporadic growth of probability theory as a mathematical discipline. The mathematicians of the day took little or no interest in the development of any theory but looked only at the combinatorial reasoning involved in each problem.

The first attempt at some mathematical rigor is credited to Laplace. In his monumental work, Theorie analytique des probabilités (1812), Laplace gave the classical definition of the probability of an event that can occur only in a finite number of ways as the proportion of the number of favorable outcomes to the total number of all possible outcomes, provided that all the outcomes are equally likely. According to this definition, the computation of the probability of events was reduced to combinatorial counting problems. Even in those days, this definition was found inadequate. In addition to being circular and restrictive, it did not answer the question of what probability is,it only gave a practical method of computing the probabilities of some simple events.

An extension of the classical definition of Laplace was used to evaluate the probabilities of sets of events with infinite outcomes. The notion of equal likelihood of certain events played a key role in this development. According to this extension, if Ω is some region with a well-defined measure (length, area, volume, etc.), the probability that a point chosen atrandom lies in a subregion A of Ω is the ratio measure(A)/measure(Ω). Many problems of geometric probability were solved using this extension. The trouble is that one can define “at random” in any way one pleases, and different definitions therefore lead to different answers. Joseph Bertrand, for example, in his book Calcul des probabilités (Paris, 1889) cited a number of problems in geometric probability where the result depended on the method of solution. In Example 9 we will discuss the famous Bertrand paradox and show that in reality there is nothing paradoxical about Bertrand’s paradoxes; once we define “probability spaces” carefully, the paradox is resolved. Nevertheless difficulties encountered in the field of geometric probability have been largely responsible for the slow growth of probability theory and its tardy acceptance by mathematicians as a mathematical discipline.

The mathematical theory of probability, as we know it today, is of comparatively recent origin. It was A. N. Kolmogorov who axiomatized probability in his fundamental work, Foundations of the Theory of Probability (Berlin), in 1933. According to this development, random events are represented by sets and probability is just a normed measure defined on these sets. This measure-theoretic development not only provided a logically consistent foundation for probability theory but also, at the same time, joined it to the mainstream of modern mathematics.

In this book we follow Kolmogorov’s axiomatic development. In Section 1.2 we introduce the notion of a sample space. In Section 1.3 we state Kolmogorov’s axioms of probability and study some simple consequences of these axioms. Section 1.4 is devoted to the computation of probability on finite sample spaces. Section 1.5 deals with conditional probability and Bayes’s rule while Section 1.6 examines the independence of events.

1.2 SAMPLE SPACE

In most branches of knowledge, experiments are a way of life. In probability and statistics, too, we concern ourselves with special types of experiments. Consider the following examples.

The experiments described above have certain common features. For each experiment, we know in advance all possible outcomes, that is, there are no surprises in store after the performance of any experiment. On any performance of the experiment, however, we do not know what the specific outcome will be, that is, there is uncertainty about the outcome on any performance of the experiment. Moreover, the experiment can be repeated under identical conditions. These features describe a random (or a statistical) experiment.

In probability theory we study this uncertainty of a random experiment. It is convenient to associate with each such experiment a set Ω, the set of all possible outcomes of the experiment. To engage in any meaningful discussion about the experiment, we associate with Ω a σ -field , of subsets of Ω. We recall that a σ -field is a nonempty class of subsets of Ω that is closed under the formation of countable unions and complements and contains the null set Φ.

The elements of Ω are called sample points. Any set A ∈is known as an event. Clearly A is a collection of sample points. We say that an event A happens if the outcome of the experiment corresponds to a point in A. Each one-point set is known as a simple or an elementary event . If the set C contains only a finite number of points, we say that (Ω, ) is a finite sample space . If Ωcontains at most a countable number of points, we call (Ω, ) a discrete sample space. If, however, Ω contains uncountably many points, we say that (Ω, )is an uncountable sample space. In particular, if Ω = _k or some rectangle in _k , we call it a continuous sample space.

Remark 1. The choice of is an important one, and some remarks are in order. If Ω contains at most a countable number of points, we can always take to be the class of all subsets of Ω This is certainly a σ -field. Each one point set is a member of and is the fundamental object of interest. Every subset of Ω is an event. If Ω has uncountably many points, the class of all subsets of Ω is still a σ -field, but it is much too large a class of sets to be of interest. It may not be possible to choose the class of all subsets of Ω as . One of the most important examples of an uncountable sample space is the case in which Ω=or Ω is an interval in . In this case we would like all one-point subsets of Ω and all intervals (closed, open, or semiclosed) to be events. We use our knowledge of analysis to specify . We will not go into details here except to recall that the class of all semiclosed intervals (a,b ] generates a class ₁ which is a σ -field on . This class contains all one-point sets and all intervals (finite or infinite). We take ₁. Since we will be dealing mostly with the one-dimensional case, we will write instead of ₁. There are many subsets of R that are not in ₁, but we will not demonstrate this fact here. We refer the reader to Halmos [42] , Royden [96] , or Kolmogorov and Fomin [54] for further details.

Example 5.

Let us toss a coin. The set Ω is the set of symbols H and T, where H denotes head and T represents tail. Also, is the class of all subsets of Ω, namely, {{H}, {T}, {H, T}, Φ}. If the coin is tossed two times, then

Ω = {(H, H), (H, T), (T, H), (T, T)}, = {∅, {(H, H)},

{(H, T)}, {(T, H)}, {(T, T)}, {(H, H), (H, T)}, {(H, H), (T, H)},

{(H,H), (T,T)}, {(H,T), (T,H)}, {(T,T), (T,H)}, {(T,T),

(H, T)},{(H,H),(H,T), (T,H)},{(H,H),(H,T),(T,T)},

{(H,H), (T,H), (T,T)}, {(H,T), (T,H), (T,T)}, Ω},

where the first element of a pair denotes the outcome of the first toss and the second element, the outcome of the second toss. The event at least one head consists of sample points (H, H), (H, T), (T, H). The event at most one head is the collection of sample points(H, T), (T,H), (T,T).

Example 9.

A rod of length l is thrown onto a flat table, which is ruled with parallel lines at distance 2 l . The experiment consists in noting whether the rod intersects one of the ruled lines.

Let r denote the distance from the center of the rod to the nearest ruled line, and let θ be the angle that the axis of the rod makes with this line (Fig. 1). Every outcome of this experiment corresponds to a point (r , θ)in the plane. As Ω we take the set of all points(r ,) in {(r, θ): 0≤ r ≤ l , 0≤ θ < π}. For we take the Borel σ -field, 2, of subsets of Ω, that is, the smallest σ -field generated by rectangles of the form

{(x , y): a< x ≤ b , c < y ≤ d ,0≤a< b ≤ l ,0 < c < d < π}.

Clearly the rod will intersect a ruled line if and only if the center of the rod lies in the area enclosed by the locus of the center of the rod (while one end touches the nearest line) and the nearest line (shaded area in Fig. 2).

Remark 2. From the discussion above it should be clear that in the discrete case there is really no problem. Every one-point set is also an event, and is the class of all subsets of Ω.

The problem, if there is any, arises only in regard to uncountable sample spaces. The reader has to remember only that in this case not all subsets of Ω are events. The case of most interest is the one in which Ω = _k. In this case, roughly all sets that have a well-defined volume (or area or length) are events. Not every set has the property in question, but sets that lack it are not easy to find and one does not encounter them in practice.

PROBLEMS 1.2

A club has five members A,B, C, D, and E . It is required to select a chairman and a secretary. Assuming that one member cannot occupy both positions, write the sample space associated with these selections. What is the event that member A is an office holder?
In each of the following experiments, what is the sample space?
1. In a survey of families with three children, the sexes of the children are recorded in increasing order of age.
2. The experiment consists of selecting four items from a manufacturer’s output and observing whether or not each item is defective.
3. A given book is opened to any page, and the number of misprints is counted.
4. Two cards are drawn (i) with replacement and (ii) without replacement from an ordinary deck of cards.
Let A, B, C be three arbitrary events on a sample space (Ω, ). What is the event thatonly A occurs? What is the event that at least two of A, B, C occur? What is the event that both A and C , but not B , occur? What is the event that at most one of A,B,C occurs?

1.3 PROBABILITY AXIOMS

Let (Ω, )be the sample space associated with a statistical experiment. In this section we define a probability set function and study some of its properties.

Definition 1.

Let (Ω, ) be a sample space. A set function P defined on is called a probability measure (or simply probability) if it satisfies the following conditions:

P (A) ≥0 for all A .
P (Ω) =1.
Let {A_j}, A_j , j = 1, 2,…,be a disjoint sequence of sets, that is, A_jn ∩ A_k =Φfor j ≠ k where Φ is the null set. Then
(1)
where we have used the notation to denote union of disjoint sets A_j

We call P (A)the probability of event A. If there is no confusion, we will write PA instead of P(A). Property (iii) is called countable additivity. That P Φ = 0 and P is also finitely additive follows from it.

Remark 1. If Ω is discrete and contains at most n (< ∞) points, each single-point set {ω _j} , j= 1, 2,…, n ,is an elementary event, and it is sufficient to assign probability to each {ω _j}. Then, if A , where is the class of all subsets of Ω, One such assignment is the equally likely assignment or the assignment of uniform probabilities. According to this assignment, P{ω_j} = 1 /n, j = 1, 2,…, n. Thus PA = m/n if A contains m elementary events, 1 ≤ m ≤ n.

Remark 2. If Ω is discrete and contains a countable number of points, one cannot make an equally likely assignment of probabilities. It suffices to make the assignment for each elementary event. If A∈ , where is the class of all subsets of Ω, define .

Remark 3. If Ω contains uncountably many points, each one-point set is an elementary event, and again one cannot make an equally likely assignment of probabilities. Indeed, one cannot assign positive probability to each elementary event without violating the axiom P Ω=1. In this case one assigns probabilities to compound events consisting of intervals. For example, if Ω = [0,1] and is the Borel σ -field of all subsets of Ω, the assignment P[I]= length of I , where I is a subinterval of Ω, defines a probability.

In many games of chance, probability is often stated in terms of odds against an event. Thus in horse racing a two dollar bet on a horse to win with odds of 2 to 1 (against) pays approximately six dollars if the horse wins the race. In this case the probability of winningis 1/3.

Theorem 5 (Boole’s Inequality).

For any two events, A and B.

(8)

Corollary 1. , be a countable sequence of events; then

(9)

Proof. Take

In (8).

Corollary 2 (The Implication Rule).

If A, B, C ∈ and A and B imply C , then

(10)

Let {A _n} be a sequence of sets. The set of all points ω ∈ Ω that belong to A_n for infinitely many values of n is known as the limit superior of the sequence and is denoted by

The set of all points that belong to A_n for all but a finite number of values of n is known as the limit inferior of the sequence {A _n} and is denoted by

we say that the limit exists and write for the common set and call it the limit set.

We have

If the sequence {A _n} is such that , it is called nondecreasing; if , it is called nonincreasing. If the sequence A_n is nondecreasing, we write A_n ?? ; if A_n is nonincreasing, we write A_n ??. Clearly, if A_n ??or A_n ?? , the limit exists and we have

and

Theorem 6.

Let {A_n}be a nondecreasing sequence of events in , that is, A_n∈ , n=1,2,…, and

Then

(11)

Proof. Let

Then

By countable additivity we have

and letting , we see that

The second term on the right tends to 0 as since the sum and each summand is nonnegative. The result follows.

Corollary. Let {A_n}be a nonincreasing sequence of events in . Then

(12)

Proof. Consider the nondecreasing sequence of events . Then

It follows from Theorem 6 that

In other words,

as asserted.

Remark 5. Theorem 6 and its corollary will be used quite frequently in subsequent chapters. Property (11) is called the continuity of P from below, and (12) is known as the continuity of P from above. Thus Theorem 6 and its corollary assure us that the set function P is continuous from above and below.

We conclude this section with some remarks concerning the use of the word “random” in this book. In probability theory “random” has essentially three meanings. First, in sampling from a finite population a sample is said to be a random sample if at each draw all members available for selection have the same probability of being included. We will discuss sampling from a finite population in Section 1.4. Second, we speak of a random sample from a probability distribution. This notion is formalized in Section 6.2. The third meaning arises in the context of geometric probability, where statements such as “a point is randomly chosen from the interval (a, b) ”and “a point is picked randomly from a unit square” are frequently encountered. Once we have studied random variables and their distributions, problems involving geometric probabilities may be formulated in terms of problems involving independent uniformly distributed random variables, and these statements can be given appropriate interpretations.

Roughly speaking, these statements involve a certain assignment of probability. The word “random” expresses our desire to assign equal probability to sets of equal lengths, areas, or volumes. Let Ω ⊆_n be a given set, and A be a subset of Ω . We are interested in the probability that a “randomly chosen point” in Ω falls in A . Here “randomly chosen” means that the point may be any point of Ω and that the probability of its falling in some subset A of Ω is proportional to the measure of A (independently of the location and shape of A). Assuming that both A and Ω have well-defined finite measures (length, area, volume, etc.), we define

(In the language of measure theory we are assuming that Ω is a measurable subset of _n that has a finite, positive Lebesque measure. If A is any measurable set, , where μ is the n -dimensional Lebesque measure.) Thus, if a point is chosen at random from the interval (a, b), the probability that it lies in the interval (c, d), a ≤ c <d ≤ b, is (d−c)/(b−a). Moreover, the probability that the randomly selected point lies in any interval of length (d−c) is the same.

We present some examples.

Example 7 (Buffon's Needle Problem).

We return to Example 1.2.9. A needle (rod) of length l is tossed at random on a plane that is ruled with a series of parallel lines at distance 2/ apart. We wish to find the probability that the needle will intersect one of the lines. Denoting by r the distance from the center of the needle to the closest line and by θ the angle that the needle forms with this line, we see that a necessary and sufficient condition for the needle to intersect the line is that r ≤(l /2)sin θ . The needle will intersect the nearest line if and only if its center falls in the shaded region in Fig. 1.2.2. We assign probability to an event A as follows:

Thus the required probability is

Here we have interpreted “at random” to mean that the position of the needle is characterized by a point (r, θ)which lies in the rectangle 0 ≤r≤ l , 0 ≤ θ ≤ π. We have assumed that the probability that the point (r,θ) lies in any arbitrary subset of this rectangle is proportional to the area of this set. Roughly, this means that “all positions of the midpoint of the needle are assigned the same weight and all directions of the needle are assigned the same weight.”

Example 8.

An interval of length 1, say (0, 1), is divided into three intervals by choosing two points at random. What is the probability that the three line segments form a triangle?

It is clear that a necessary and sufficient condition for the three segments to form a triangle is that the length of any one of the segments be less than the sum of the other two. Let x,y be the abscissas of the two points chosen at random. Then we must have either

This is precisely the shaded area in Fig. 4. It follows that the required probability is 1/4.

If it is specified in advance that the point x is chosen at random from (0,1/2), and the point y at random from (1/2,1),we must have

and

y − x < x +1− y or 2(y − x) < 1.

In this case the area bounded by these lines is the shaded area in Fig. 5, and it follows that the required probability is 1/2.

Note the difference in sample spaces in the two computations made above.

Example 9 (Bertrand's Paradox).

A chord is drawn at random in the unit circle. What is the probability that the chord is longer than the side of the equilateral triangle inscribed in the circle?

We present here three solutions to this problem, depending on how we interpret the phrase “at random.” The paradox is resolved once we define the probability spaces carefully.

Solution 1. Since the length of a chord is uniquely determined by the position of its midpoint, choose a point C at random in the circle and draw a line through C and O , the center of the circle (Fig. 6). Draw the chord through C perpendicular to the line OC . If l₁ is the length of the chord with C as midpoint, l ₁ > √3if and only if C lies inside the circle with center O and radius 1/2. Thus PA=(1/2)²/ π = 1/4.

In this case Ω is the circle with center O and radius 1, and the event A is the concentric circle with center O and radius . is the usual Borel σ-field of subsets of Ω.

Solution 2. Because of symmetry, we may fix one end point of the chord at some point P and then choose the other end point P 1 at random. Let the probability that P 1 lies on an arbitrary arc of the circle be proportional to the length of this arc. Now the inscribed equilateral triangle having P as one of its vertices divides the circumference into three equal parts. A chord drawn through P will be longer than the side of the triangle if and only if the other end point P₁ (Fig. 7) of the chord lies on that one third of the circumference that is opposite to P . It follows that the required probability is 1/3. In this case Ω = [0,2π], = ₁Ω and A = [2π/3,4π/3] .

Solution 3. Note that the length of a chord is uniquely determined by the distance of its midpoint from the center of the circle. Due to the symmetry of the circle, we assume that the midpoint of the chord lies on a fixed radius, OM , of the circle (Fig. 8). The probability that the midpoint M lies in a given segment of the radius through M is then proportional to the length of this segment. Clearly, the length of the chord will be longer than the side of the inscribed equilateral triangle if the length of OM is less than radius/2. It follows that the required probability is 1/2.

c1-fig-0003 — **Fig. 2** B = {(x , y):(x - 1 /2)²+ (y - 1 /2)²= 1}.

c1-fig-0004 — **Fig. 3** C = {(x , y) : (x ²+ y ² ≤ 1}

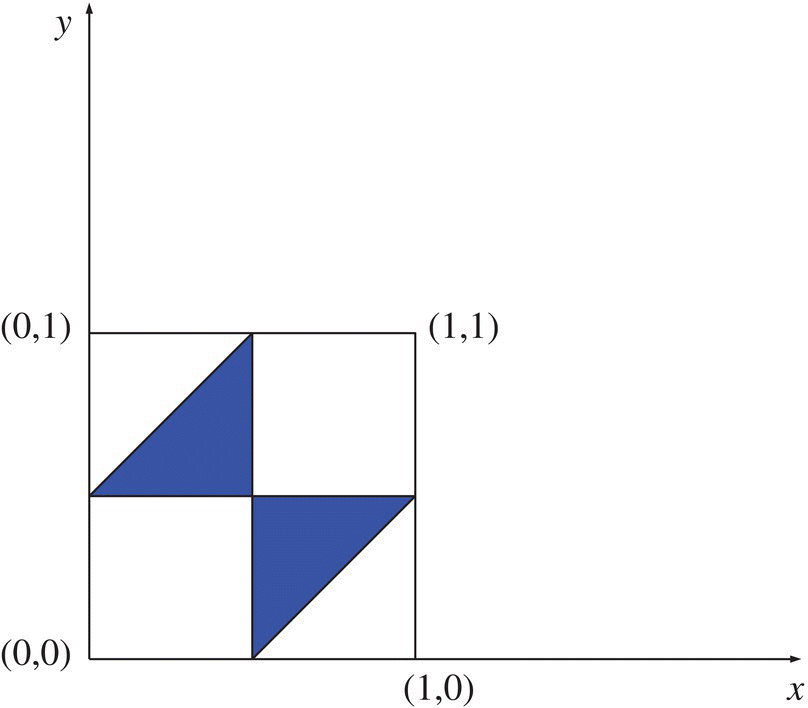
c1-fig-0005 — **Fig. 4** {(x , y) : 0 < x < 1/2 < y < 1, and (y − x) < 1/2 or 0 < y < 1/2 < x < 1, and (x − y) < 1/2}.

c1-fig-0006 — **Fig. 5** {(*x,y*): 0 < x <1/2, 1/2 < y <1and 2 (y -x ) <1}.

PROBLEMS 1.3

Let Ω be the set of all nonnegative integers and S the class of all subsets of Ω. In each of the following cases does P define a probability on (Ω, S)?
1. For A , let
2. For A , let
3. For A ∈ , let PA= 1 if A has a finite number of elements, and PA= 0 otherwise.
Let Ω = and . In each of the following cases does P define a probability on (Ω, S)?
1. For each interval I , let
2. For each interval I , let PI= 1if I is an interval of finite length and PI= 0if I is an infinite interval.
3. For each interval I , let PI= 0if I ⊆ (-∞,1) and PI = ∫_I(1/2) dx if. I ⊆ [1,∞]. (If I = I ₁+ I ₂, where I ₁⊆(-∞,1) and I ₂ ⊆ [1,∞), then PI = PI ₂.)
Let A and B be two events such that B⊇A. What is P (A ∪ B) ? What is P (A ∩ B)? What is P (A - B)?
In Problems 1(a) and (b), let A = {all integers > 2}, B = {all nonnegative integers < 3}, and C = {all integers x , 3 < x < 6}. Find PA , PB , PC , P (A ∩ B), P (A ∪ B), P (B ∪ C), P (A ∩ C), and P (B ∩ C).
In Problem 2(a) let A be the event A = {x: x ≥0}. Find PA . Also find P {x: x >0}.
A box contains 1000 light bulbs. The probability that there is at least 1 defective bulb in the box is 0.1, and the probability that there are at least 2 defective bulbs is 0.05. Find the probability in each of the following cases:
1. The box contains no defective bulbs.
2. The box contains exactly 1 defective bulb.
3. The box contains at most 1 defective bulb.
Two points are chosen at random on a line of unit length. Find the probability that each of the three line segments so formed will have a length > 1/4.
Find the probability that the sum of two randomly chosen positive numbers (both ≤1) will not exceed 1 and that their product will be ≤2/9.
Prove Theorem 3.
Let {A_n} be a sequence of events such that A_n→A as n→∞. Show that PA_n→PA as n→∞.
The base and the altitude of a right triangle are obtained by picking points randomly from [0, a] and [0, b], respectively. Show that the probability that the area of the triangle so formed will be less than ab/4 is (1 + ℓn 2)/2.
A point X is chosen at random on a line segment AB . (i) Show that the probability that the ratio of lengths AX/BX is smaller than a (a > 0) is a/(1 + a). (ii) Show that the probability that the ratio of the length of the shorter segment to that of the larger segment is less than 1/3 is 1/2.

1.4 COMBINATORICS: PROBABILITY ON FINITE SAMPLE SPACES

In this section we restrict attention to sample spaces that have at most a finite number of points. Let Ω = {ω₁, ω₂,…,ω _n}and be the σ-field of all subsets of Ω. For any A∈ ,

In games of chance we usually deal with finite sample spaces where uniform probability is assigned to all simple events. The same is the case in sampling schemes. In such instances the computation of the probability of an event A reduces to a combinatorial counting problem. We therefore consider some rules of counting.

Rule 1. Given a collection of n₁ elements elements and so on, up to n_k elements , it is possible to form n ₁. n ₂..... n _k ordered k -tuples containing one element of each kind, 1 .

Example 3.

Here r distinguishable balls are to be placed in n cells. This amounts to choosing one cell for each ball. The sample space consists of n^rr -tuples (i ₁, i ₂, …, i _r), where i _j is the cell number of the j th ball, .

Consider r tossings with a coin. There are 2^r possible outcomes. The probability that no heads will show up in r throws is (1/2) ^r . Similarly, the probability that no 6 will turn up in r throws of a die is (5/6) ^r .

Rule 2 is concerned with ordered samples. Consider a set of n elements a ₁, a ₂, …, a _n. Any ordered arrangement of r of these n symbols is called an ordered sample of size r . If elements are selected one by one, there are two possibilities:

Sampling with replacement In this case repetitions are permitted, and we can draw samples of an arbitrary size. Clearly there are n^r samples of size r.
Sampling without replacement In this case an element once chosen is not replaced, so that there can be no repetitions. Clearly the sample size cannot exceed n , the size of the population. There are , say, possible samples of size r . Clearly for integers . If , then .

Rule 2. If ordered samples of size r are drawn from a population of n elements, there are n ^r different samples with replacement and _n p _r samples without replacement.

Corollary. The number of permutations of n objects is n !.

Remark 1. We will frequently use the term “random sample” in this book to describe the equal assignment of probability to all possible samples in sampling from a finite population. Thus, when we speak of a random sample of size r from a population of n elements, it means that each of n ^r samples, in sampling with replacement, has the same probability 1 /n^r or that each of nPr samples, in sampling without replacement, is assigned probability

Example 5.

Consider a class of r students. The birthdays of these r students form a sample of size r from the 365 days in the year. Then the probability that all r birthdays are different is ₃₆₅ p _r/(365)^r. One can show that this probability is <1/2 if r = 23.

The following table gives the values of for some selected values of r .

r	20	23	25	30	35	60
qr	0.589	0.493	0.431	0.294	0.186	0.006

Next suppose that each of the r students is asked for his birth date in order, with the instruction that as soon as a student hears his birth date he is to raise his hand. Let us compute the probability that a hand is first raised when the k th student is asked his birth date. Let p_k be the probability that the procedure terminates at the k th student. Then

and

PROBLEMS 1.4

How many different words can be formed by permuting letters of the word “Mississippi”? How many of these start with the letters “Mi”?
An urn contains R red and W white marbles. Marbles are drawn from the urn one after another without replacement. Let A_k be the event that a red marble is drawn for the first time on the kth draw. Show that

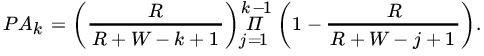
Let p be the proportion of red marbles in the urn before the first draw. Show that as . Is this to be expected?
In a population of N elements, R are red and W=N-R are white. A group of n elements is selected at random. Find the probability that the group so chosen will contain exactly r red elements.
Each permutation of the digits 1, 2, 3, 4, 5, 6 determines a six-digit number. If the numbers corresponding to all possible permutations are listed in increasing order of magnitude, find the 319th number on this list.
The numbers 1, 2 ,…, n are arranged in random order. Find the probability that the digits 1, 2 ,…, k(k<n) appear as neighbors in that order.
A pin table has seven holes through which a ball can drop. Five balls are played. Assuming that at each play a ball is equally likely to go down any one of the seven holes, find the probability that more than one ball goes down at least one of the holes.
If 2n boys are divided into two equal subgroups find the probability that the two tallest boys will be (a) in different subgroups and (b) in the same subgroup.
In a movie theater that can accommodate n + k people, n people are seated. What is the probability that given seats are occupied?
Waiting in line for a Saturday morning movie show are 2 n children. Tickets are priced at a quarter each. Find the probability that nobody will have to wait for change if, before a ticket is sold to the first customer, the cashier has 2 k (k<n) quarters. Assume that it is equally likely that each ticket is paid for with a quarter or a half-dollar coin.
Each box of a certain brand of breakfast cereal contains a small charm, with k distinct charms forming a set. Assuming that the chance of drawing any particular charm is equal to that of drawing any other charm, show that the probability of finding at least one complete set of charms in a random purchase of boxes equals

[ Hint: Use (1.3.6).]
Prove Rules 1-4.
In a five-card poker game, find the probability that a hand will have:
1. A royal flush (ace, king, queen, jack, and 10 of the same suit).
2. A straight flush (five cards in a sequence, all of the same suit; ace is high but A, 2, 3,4, 5 is also a sequence) excluding a royal flush.
3. Four of a kind (four cards of the same face value).
4. A full house (three cards of the same face value x and two cards of the same face value y).
5. A flush (five cards of the same suit excluding cards in a sequence).
6. A straight (five cards in a sequence).
7. Three of a kind (three cards of the same face value and two cards of different face values).
8. Two pairs.
9. A single pair.
1. A married couple and four of their friends enter a row of seats in a concert hall.
  What is the probability that the wife will sit next to her husband if all possible seating arrangements are equally likely?
2. In part (a), suppose the six people go to a restaurant after the concert and sit at a round table. What is the probability that the wife will sit next to her husband?
Consider a town with N people. A person sends two letters to two separate people, each of whom is asked to repeat the procedure. Thus for each letter received, two letters are sent out to separate persons chosen at random (irrespective of what happened in the past). What is the probability that in the first n stages the person who started the chain letter game will not receive a letter?
Consider a town with N people. A person tells a rumor to a second person, who in turn repeats it to a third person, and so on. Suppose that at each stage the recipient of the rumor is chosen at random from the remaining N -1 people. What is the probability that the rumor will be repeated n times
1. Without being repeated to any person.
2. Without being repeated to the originator.
There were four accidents in a town during a seven-day period. Would you be surprised if all four occurred on the same day? Each of the four occurred on a different day?
While Rules 1 and 2 of counting deal with ordered samples with or without replacement, Rule 3 concerns unordered sampling without replacement. The most difficult rule of counting deals with unordered with replacement sampling. Show that there are possible unordered samples of size r from a population of n elementswhen sampled with replacement.

1.5 CONDITIONAL PROBABILITY AND BAYES THEOREM

So far, we have computed probabilities of events on the assumption that no information was available about the experiment other than the sample space. Sometimes, however, it is known that an event H has happened. How do we use this information in making a statement concerning the outcome of another event A? Consider the following examples.

Theorem 1.

Let (Ω,, P)be a probability space, and let H with PH >0. Then (Ω, , P_H)where for all A , is a probability space.

Proof. Clearly for all A . Also, . If A ₁, A ₂, … is a disjoint sequence of sets in , then

Remark 1. What we have done is to consider a new sample space consisting of the basic set H and the σ-field _H = ∩ H, of subsets A ∩ H , A ,of H . On this space we have defined a set function P_H by multiplying the probability of each event by (PH) ^{− 1} . Indeed, (H , _H , P_H)is a probability space.

Let A and B be two events with PA> 0, PB> 0. Then it follows from (1) that

(2)

Equation (2) may be generalized to any number of events. Let A ₁, A ₂,…, A_n n ≥2, and assume that . Since

we see that

It follows that are well defined for k= 2 , 3 , … ,n.

Theorem 3 (Bayes Rule).

Let {H_n}be a disjoint sequence of events such that PH_n > 0, n = 1, 2 …, and . Let B with PB > 0. Then

(5)

Proof . From (2)

and it follows that

The result now follows on using (4).

Remark 2. Suppose that H ₁, H ₂,…are all the “causes” that lead to the outcome of a random experiment. Let Hj be the set of outcomes corresponding to the j th cause. Assume that the probabilities PH_j , j = 1, 2, …, called the prior probabilities, can be assigned. Now suppose that the experiment results in an event B of positive probability. This information leads to a reassessment of the prior probabilities. The conditional probabilities P {H_j|B}are called the posterior probabilities. Formula (5) can be interpreted as a rule giving the probability that observed event B was due to cause or hypothesis H_j.

Let A and B be two events such that PA=p ₁ > 0, PB=p ₂ > 0, and p₁ + p₂ > 1. Show that P {B | A}≥1 − [(1 − p ₂) /p ₁].
Two digits are chosen at random without replacement from the set of integers {1, 2, 3, 4, 5, 6, 7, 8}.
1. Find the probability that both digits are greater than 5.
2. Show that the probability that the sum of the digits will be equal to 5 is the same as the probability that their sum will exceed 13.
The probability of a family chosen at random having exactly k children is ∝p^k ,0 <p< 1. Suppose that the probability that any child has blue eyes is b , 0 <b< 1, independently of others. What is the probability that a family chosen at random has exactly r (r ≥ 0) children with blue eyes?
In Problem 3 let us write p_k = probability of a randomly chosen family having exactly k children = αp^k, k = 1,2,…, Suppose that all sex distributions of k children are equally likely. Find the probability that a family has exactly r boys, r ≥ 1. Find the conditional probability that a family has at least two boys, given that it has at least one boy.
Each of (N + 1) identical urns marked 0, 1, 2,…, N contains N balls. The kth urn contains k black and N –k white balls, k = 0, 1, 2,…, N. An urn is chosen at random, and n random drawings are made from it, the ball drawn being always replaced. If all the n draws result in black balls, find the probability that the (n + 1)th draw will also produce a black ball. How does this probability behave as N →∞?
Each of n urns contains four white and six black balls, while another urn contains five white and five black balls. An urn is chosen at random from the (n + 1) urns, and two balls are drawn from it, both being black. The probability that five white and three black balls remain in the chosen urn is 1/7. Find n .
In answering a question on a multiple choice test, a candidate either knows the answer with probability p (0 ≤ p < 1) or does not know the answer with probability 1 – p. If he knows the answer, he puts down the correct answer with probability 0.99, whereas if he guesses, the probability of his putting down the correct result is 1/ k(k choices to the answer). Find the conditional probability that the candidate knew the answer to a question, given that he has made the correct answer. Show that this probability tends to 1 as k→ ∞.
An urn contains five white and four black balls. Four balls are transferred to a second urn. A ball is then drawn from this urn, and it happens to be black. Find the probability of drawing a white ball from among the remaining three.
Prove Theorem 2.
An urn contains r red and g green marbles. A marble is drawn at random and its color noted. Then the marble drawn, together with c > 0 marbles of the same color, are returned to the urn. Suppose n such draws are made from the urn? Find the probability of selecting a red marble at any draw.
Consider a bicyclist who leaves a point P (see Fig. 1), choosing one of the roads PR₁, PR₂, PR₃ at random. At each subsequent crossroad he again chooses a road at random.
1. What is the probability that he will arrive at point A?
2. What is the conditional probability that he will arrive at A via road PR ₃?
Five percent of patients suffering from a certain disease are selected to undergo a new treatment that is believed to increase the recovery rate from 30 percent to 50 percent. A person is randomly selected from these patients after the completion of the treatment and is found to have recovered. What is the probability that the patient received the new treatment?

Fig. 1 Map for Problem 11.
Four roads lead away from the county jail. A prisoner has escaped from the jail and selects a road at random. If road I is selected, the probability of escaping is 1/8; if road II is selected, the probability of success is 1/6; if road III is selected, the probability of escaping is 1/4; and if road IV is selected, the probability of successis 9/10.
1. What is the probability that the prisoner will succeed in escaping?
2. If the prisoner succeeds, what is the probability that the prisoner escaped by using road IV? Road I?
A diagnostic test for a certain disease is 95 percent accurate; in that if a person has the disease, it will detect it with a probability of 0.95, and if a person does not have the disease, it will give a negative result with a probability of 0.95. Suppose only 0.5 percent of the population has the disease in question. A person is chosen at random from this population. The test indicates that this person has the disease. What is the (conditional) probability that he or she does have the disease?

1.6 INDEPENDENCE OF EVENTS

Let (Ω, , P) be a probability space, and let A, B∈ , with PB> 0. By the multiplication rule we have

In many experiments the information provided by B does not affect the probability of event A, that is, .

We wish to emphasize that independence of events is not to be confused with disjoint or mutually exclusive events. If two events, each with nonzero probability, are mutually exclusive, they are obviously dependent since the occurrence of one will automatically preclude the occurrence of the other. Similarly, if A and B are independent and PA> 0, PB> 0, then A and B cannot be mutually exclusive.

Example 7.

A slip of paper is given to person A , who marks it with either a plus or a minus sign; the probability of her writing a plus sign is 1/3. A passes the slip to B , who may either leave it alone or change the sign before passing it to C . Next , C passes the slip to D after perhaps changing the sign; finally, D passes it to a referee after perhaps changing the sign. The referee sees a plus sign on the slip. It is known that B, C, and D each change the sign with probability 2/3. We shall compute the probability that A originally wrote a plus.

Let N be the event that A wrote a plus sign, and M, the event that she wrote a minus sign. Let E be the event that the referee saw a plus sign on the slip. We have

Now

P{E| N} =P {the plus sign was either not changed or changed exactly twice}

and

P{E | M} = P{the minus sign was changed either once or three times}

It follows that

PROBLEMS 1.6

A biased coin is tossed until a head appears for the first time. Let p be the probability of a head, 0 < p < 1. What is the probability that the number of tosses required is odd? Even?
Let A and B be two independent events defined on some probability space, and let PA= 1/3, PB= 3/4. Find (a) P(A B), (b) P {A | A B}, and (c) P {B | A B}.
Let A 1, A 2, and A 3 be three independent events. Show that A^c₁,A^c₂, and A^c₃ are independent.
A biased coin with probability p,0 < p < 1, of success (heads) is tossed until for the first time the same result occurs three times in succession (i.e., three heads or three tails in succession). Find the probability that the game will end at the seventh throw.
A box contains 20 black and 30 green balls. One ball at a time is drawn at random, its color is noted, and the ball is then replaced in the box for the next draw.
1. Find the probability that the first green ball is drawn on the fourth draw.
2. Find the probability that the third and fourth green balls are drawn on the sixth and ninth draws, respectively.
3. Let N be the trial at which the fifth green ball is drawn. Find the probability that the fifth green ball is drawn on the n th draw. (Note that N take values 5, 6, 7, …)
An urn contains four red and four black balls. A sample of two balls is drawn at random. If both balls drawn are of the same color, these balls are set aside and a new sample is drawn. If the two balls drawn are of different colors, they are returned to the urn and another sample is drawn. Assume that the draws are independent and that the same sampling plan is pursued at each stage until all balls are drawn.
1. Find the probability that at least n samples are drawn before two balls of the same color appear.
2. Find the probability that after the first two samples are drawn four balls are left, two black and two red.
Let A , B , and C be three boxes with three, four, and five cells, respectively. There are three yellow balls numbered 1 to 3, four green balls numbered 1 to 4, and five red balls numbered 1 to 5. The yellow balls are placed at random in box A, the green in B, and the red in C, with no cell receiving more than one ball. Find the probability that only one of the boxes will show no matches.
A pond contains red and golden fish. There are 3000 red and 7000 golden fish, of which 200 and 500, respectively, are tagged. Find the probability that a random sample of 100 red and 200 golden fish will show 15 and 20 tagged fish, respectively.
Let (Ω, , P)be a probability space. Let A, B, C∈ with PB and PC> 0. If B and C are independent show that

Conversely, if this relation holds, P{A I BC} ≠ P{A I B}, and PA> 0, then B and C are independent (Strait [111] ).
Show that the converse of Theorem 2 also holds. Thus A and B are independent if, and only if, A and B^c are independent, and so on.
A lot of five identical batteries is life tested. The probability assignment is assumed to be

for any event A ⊆[0,∞ ), where λ> 0 is a known constant. Thus the probability that a battery fails after time t is given by

If the times to failure of the batteries are independent, what is the probability that at least one battery will be operating after t ₀hours?
On Ω = (a, b) , −∞<a<b< ∞, each subinterval is assigned a probability proportional to the length of the interval. Find a necessary and sufficient condition for two events to be independent.
A game of craps is played with a pair of fair dice as follows. A player rolls the dice. If a sum of 7 or 11 shows up, the player wins; if a sum of 2, 3, or 12 shows up, the player loses. Otherwise the player continues to roll the pair of dice until the sum is either 7 or the first number rolled. In the former case the player loses and in the latter the player wins.
1. Find the probability that the player wins on the n th roll.
2. Find the probability that the player wins the game.
3. What is the probability that the game ends on: (i) the first roll, (ii) second roll, and (iii) third roll?

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.