13.1 INTRODUCTION

In all the problems of statistical inference considered so far, we assumed that the distribution of the random variable being sampled is known except, perhaps, for some parameters. In practice, however, the functional form of the distribution is seldom, if ever, known. It is therefore desirable to devise methods that are free of this assumption concerning distribution. In this chapter we study some procedures that are commonly referred to as distribution-free or nonparametric methods. The term “distribution-free” refers to the fact that no assumptions are made about the underlying distribution except that the distribution function being sampled is absolutely continuous. The term “nonparametric” refers to the fact that there are no parameters involved in the traditional sense of the term “parameter” used thus far. To be sure, there is a parameter which indexes the family of absolutely continuous DFs, but it is not numerical and hence the parameter set cannot be represented as a subset of _n, for any . The restriction to absolutely continuous distribution functions is a simplifying assumption that allows us to use the probability integral transformation (Theorem 5.3.1) and the fact that ties occur with probability 0.

Section 13.2 is devoted to the problem of unbiased (nonparametric) estimation. We develop the theory of U-statistics since many estimators and test statistics may be viewed as U-statistics. Sections 13.3 through 13.5 deal with some common hypotheses testing problems. In Section 13.6 we investigate applications of order statistics in nonparametric methods. Section 13.7 considers underlying assumptions in some common parametric problems and the effect of relaxing these assumptions.

13.2 U-STATISTICS

In Chapter 6 we encountered several nonparametric estimators. For example, the empirical DF defined in Section 6.3 as an estimator of the population DF is distribution-free, and so also are the sample moments as estimators of the population moments. These are examples of what are known as U-statistics which lead to unbiased estimators of population characteristics. In this section we study the general theory of U-statistics. Although the thrust of this investigation is unbiased estimation, many of the U-statistics defined in this section may be used as test statistics.

Let X₁,X₂,…, X_n be iid RVs with common law (X), and let be the class of all possible distributions of X that consists of the absolutely continuous or discrete distributions, or subclasses of these.

We have already encountered many examples of complete statistics or complete families of distributions in Chapter 8.

The following result is stated without proof. For the proof we refer to Fraser [32, pp. 27–30, 139–142].

Clearly, the U-statistic defined in (3) is symmetric in the X_i’s, and

(4)

Moreover, U(X) is a function of the complete sufficient statistic X₍₁₎, X₍₂₎,…,X_(n). It follows from Theorem 8.4.6 that it is UMVUE of its expected value.

For estimating μ³(F), a symmetric kernel is so that the corresponding U-statistic is

For estimating F(x) a symmetric kernel is so the corresponding U-statistic is

and for estimating the U-statistic is

Finally, for estimatin the U-statistic is

Now note that the numerator has factors involving n, while the denominator has m such factors so that for , the ratio involving n goes to 0 as . For , this ratio and

as

Finally we state, without proof, the following result due to Hoeffding [45], which establishes the asymptotic normality of a suitably centered and normed U-statistic. For proof we refer to Lehmann [61, pp. 364–365] or Randles and Wolfe [85, p. 82].

The concept of U-statistics can be extended to multiple random samples. We will restrict ourselves to the case of two samples. Let and be two independent random samples from DFs F and G, respectively.

The statistic T in Definition 8 is called a kernel of g and a symmetrized version of T, T_s is called a symmetric kernel of g. Without loss of generality therefore we assume that the two-sample kernel T in (9) is a symmetric kernel.

Finally we state, without proof, the two-sample analog of Theorem 3 which establishes the asymptotic normality of the two-sample U-statistic defined in (10).

PROBLEMS 13.2

1. Let 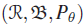be a probability space, and let . Let A be a Borel subset of , and consider the parameter . Is d estimable? If so, what is the degree? Find the UMVUE for d, based on a sample of size n, assuming that is the class of all continuous distributions.
2. Let X₁, X₂,…, X_m and Y₁, Y₂,…, Y_n be independent random samples from two absolutely continuous DFs. Find the UMVUEs of (a) E{XY} and (b) .
3. Let (X₁, Y₁), (X₂, Y₂),…,(X_n, Y_n) be a random sample from an absolutely continuous distribution. Find the UMVUEs of (a) E(XY) and (b) .
4. Let T(X₁, X₂,…, X_n) be a statistic that is symmetric in the observations. Show that T can be written as a function of the order statistic. Conversely, if T (X₁, X₂,…,X_n) can be written as a function of the order statistic, T is symmetric in the observations.
5. Let X₁, X₂, …,X_n be a random sample from an absolutely continuous . Find U-statistics for . Find the corresponding expressions for the variance of the U-statistic in each case.
6. In Example 3, show that μ₂(F) is not estimable with one observation. That is, show that the degree of μ₂(F) where , the class of all distributions with finite second moment, is 2.
7. Show that for .
8. Let X₁, X₂, …,X_n be a random sample from an absolutely continuous . Let
   

   Find the U-statistic estimator of g(F) and its variance.

13.3 SOME SINGLE-SAMPLE PROBLEMS

Let X₁, X₂,…,X_n be a random sample from a DF F. In Section 13.2 we studied properties of U-statistics as nonparametric estimators of parameters g(F). In this section we consider some nonparametric tests of hypotheses. Often the test statistic may be viewed as a function of a U-statistic.

Since F(X_(i)) is the ith-order statistic of a sample from U (0,1) irrespective of what F is, as long as it is continuous, we see that the distribution of is independent of F. Similarly,

and the result follows.

Without loss of generality, therefore, we assume that F is the DF of a U(0,1) RV.

We will not prove this result here. Let D_{n, α} be the upper α-percent point of the distribution of D_n, that is, . The exact distribution of D_n for selected values of n and α has been tabulated by Miller [74], Owen [79], and Birnbaum [9]. The large-sample distribution of D_n was derived by Kolmogorov [53], and we state it without proof.

The statistics and have the same distribution because of symmetry, and their common distribution is given by the following theorem.

Tables for the critical values where , are also available for selected values of n and α; see Birnbaum and Tingey [8]. Table ST7 at the end of this book gives and D_n, α for some selected values of n and α. For large samples Smirnov [108] showed that

(9)

In fact, in view of (9), the statistic has a limiting χ²(2) distribution, for if and only if , and the result follows since

so that

which is the DF of a χ² (2) RV.

It is worthwhile to compare the chi-square test of goodness of fit and the Kolmogorov–Smirnov test. The latter treats individual observations directly, whereas the former discretizes the data and sometimes loses information through grouping. Moreover, the Kolmogorov–Smirnov test is applicable even in the case of very small samples, but the chi-square test is essentially for large samples.

The chi-square test can be applied when the data are discrete or continuous, but the Kolmogorov–Smirnov test assumes continuity of the DF. This means that the latter test provides a more refined analysis of the data. If the distribution is actually discontinuous, the Kolmogorov–Smirnov test is conservative in that it favors H₀.

We next turn our attention to some other uses of the Kolmogorov–Smirnov statistic. Let X₁, X₂,…,X_n be a sample from a DF F, and let be the sample DF. The estimate of F for large n should be close to F. Indeed,

(10)

and, since , we have

(11)

Thus can be made close to F with high probability by choosing λ and large enough n. The Kolmogorov–Smirnov statistic enables us to determine the smallest n such that the error in estimation never exceeds a fixed value ε with a large probability 1 – α. Since

(12)

; and, given ε and α, we can read n from the tables. For large n, we can use the asymptotic distribution of D_n and solve for n.

We can also form confidence bounds for F. Given α and n, we first find D_n,α such that

(13)

which is the same as

Thus

(14)

Define

(15)

And

(16)

Then the region between L_n(x) and U_n(x) can be used as a confidence band for F(x) with associated confidence coefficient 1 – α.

13.3.2 Problem of Location

Let X₁,X₂,…,X_n be a sample of size n from some unknown DF F. Let p be a positive real number, , and let _P (F) denote the quantile of order p for the DF F. In the following analysis we assume that F is absolutely continuous. The problem of location is to test a given number, against one of the alternatives and . The problem of location and symmetry is to test , and F is symmetric against or F is not symmetric.

We consider two tests of location. First, we describe the sign test.

13.3.2.1 The Sign Test

Let X₁,X₂,…,X_n be iid RVs with common PDF f. Consider the hypothesis testing problem

(17)

where _P(f) is the quantile of order p of PDF f, . Let . Then the corresponding U-statistic is given by

the number of positive elements in X₁ – ₀, X₂ – ₀,…,X_n – ₀. Clearly, P(X_i = ₀) = 0. Fraser [32, pp. 167–170] has shown that a UMP test of H₀ against H₁ is given by

(18)

where c and γ are chosen from the size restriction

(19)

Note that, under , so that and . The same test is UMP for against . For the two-sided case, Fraser [32, p. 171] shows that the two-sided sign test is UMP unbiased.

If, in particular, is the median of f, then under H₀. In this case one can also use the sign test to test , F is symmetric.

For large n one can use the normal approximation to binomial to find c and γ in (19).

We have to find c and γ such that

From the table of cumulative binomial distribution (Table ST1) for , , we see that . Then γ is given by

Thus

In our case the number of positive signs, x_i – 195, i = 1,2,..., 12, is 7, so we reject H₀ that the upper quartile is ≤195.

The single-sample sign test described above can easily be modified to apply to sampling from a bivariate population. Let (X₁, Y₁), (X₂, Y₂),…,(X_n, Y_n) be a random sample from a bivariate population. Let , and assume that Z_i has an absolutely continuous DF. Then one can test hypotheses concerning the order parameters of Z by using the sign test. A hypothesis of interest here is that Z has a given median ₀. Without loss of generality let . Then , that is, . Note that med(Z) is not necessarily equal to med(X) – med(Y), so that H₀ is not that but that . The sign test is UMP against one-sided alternatives and UMP unbiased against two-sided alternatives.

Using the two-sided sign test, we cannot reject H₀ at level α = 0.05, since . The RVs Z_i can be considered to be distributed normally, so that under H₀ the common mean of Z_i,'s is 0. Using a paired comparison t-test on the data, we can show that for 9 d.f., so we cannot reject the hypothesis of equality of means of X and Y at level .

Finally, we consider the Wilcoxon signed-ranks test.

13.3.2.2 The Wilcoxon Signed-Ranks Test

The sign test for median and symmetry loses information since it ignores the magnitude of the difference between the observations and the hypothesized median. The Wilcoxon signed-ranks test provides an alternative test of location (and symmetry) that also takes into account the magnitudes of these differences.

Let X₁, X₂,…, X_n be iid RVs with common absolutely continuous DF F, which is symmetric about the median _1/2. The problem is to test against the usual one- or two-sided alternatives. Without loss of generality, we assume that . Then for all . To test or , we first arrange |X₁|, |X₂|,…,|X_n| in increasing order of magnitude, and assign ranks 1, 2,…,n, keeping track of the original signs of X_i. For example, if and , the rank of |X₁| is 3, of |X₂| is 1, of |X₃| is 4, and of |X₄| is 2.

Let

(20)

Then, under H₀, we expect T⁺ and T^- to be the same. Note that

(21)

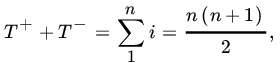
so that T⁺ and T^-are linearly related and offer equivalent criteria. Let us define

(22)

and write for the rank of |X_i| Then and . Also,

(23)

The statistic T⁺ (or T^-) is known as the Wilcoxon statistic. A large value of T⁺ (or, equivalently, a small value of T⁻) means that most of the large deviations from 0 are positive, and therefore we reject H₀ in favor of the alternative, .

A similar analysis applies to the other two alternatives. We record the results as follows:

		Test
H0	H1	Reject H0 if
		or

We now show how the Wilcoxon signed-ranks test statistic is related to the U-statistic estimate of . Recall from Example 13.2.6 that the corresponding U-statistic is

(24)

First note that

(25)

Next note that for if and only if and |X_(i) | |X_(j) | . It follows that is the signed-rank of X_(j). Consequently,

(26)

where U₁ is the U-statistic for .

We next compute the distribution of T⁺ for small samples. The distribution of T⁺ is tabulated by Kraft and Van Eeden [55, pp. 221–223].

Let

Note that if all differences have negative signs, and if all differences have positive signs. Here a difference means a difference between the observations and the postulated value of the median. T⁺ is completely determined by the indicators Z(i), so that the sample space can be considered as a set of 2ⁿ n-tuples (z₁, z₂,…, z_n), where each z_i is 0 or 1. Under and each arrangement is equally likely. Thus

(27)

Note that every assignment has a conjugate assignment with plus and minus signs interchanged so that for this conjugate, T⁺ is given by

(28)

Thus under H₀ the distribution of T⁺ is symmetric about the mean .

Remark 2. If we have n independent pairs of observations (X₁,Y₁),(X₂,Y₂),,…,(X_n,Y_n) from a bivariate DF, we form the differences , . Assuming that Z₁, Z₂,…,Z_n are (independent) observations from a population of differences with absolutely continuous DF F that is symmetric with median _1/2, we can use the Wilcoxon statistic to test .

We present some examples.

From Table ST10, we reject H₀ at if either T⁺ > 46 or T⁺ < 9. Since T⁺ > 9 and < 46, we accept H₀. Note that hypothesis H₀ was also accepted by the sign test.

For large samples we use the normal approximation. In fact, from (26) we see that

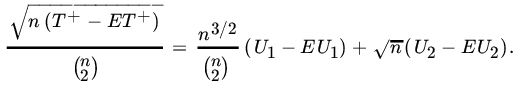
Clearly, and since , the first term →0 in probability as . By Slutsky’s theorem (Theorem 7.2.15) it follows that

have the same limiting distribution. From Theorem 13.2.3 and Example 13.2.7 it follows that , and hence , has a limiting normal distribution with mean 0 and variance

Under H₀, the RVs iZ_(i) are independent b(1,1/2) so

Also, under H₀, F is continuous and symmetric so

and

Thus so that

However,

as n→∞. Consequently, under H₀

Thus, for large enough n we can determine the critical values for a test based on T⁺ by using normal approximation.

As an example, take . From Table ST10 the P-value associated with is 0.10. Using normal approximation

PROBLEMS 13.3

1. Prove Theorem 4.
2. A random sample of size 16 from a continuous DF on [0,1] yields the following data: 0.59,0.72,0.47,0.43,0.31,0.56,0.22,0.90,0.96,0.78,0.66,0.18,0.73,0.43,0.58,0.11. Test the hypothesis that the sample comes from U[0,1].
3. Test the goodness of fit of normality for the data of Problem 10.3.6, using the Kolmogorov–Smirnov test.

   Do not reject H₀.

4. For the data of Problem 10.3.6 find a 0.95 level confidence band for the distribution function.
5. The following data represent a sample of size 20 from U[0,1]: 0.277,0.435,0.130, 0.143, 0.853, 0.889, 0.294, 0.697, 0.940, 0.648, 0.324, 0.482, 0.540, 0.152, 0.477, 0.667, 0.741, 0.882, 0.885, 0.740. Construct a .90 level confidence band for F(x).
6. In Problem 5 test the hypothesis that the distribution is U[0,1]. Take .
7. For the data of Example 2 test, by means of the sign test, the null hypothesis against .

   Reject H₀.

8. For the data of Problem 5 test the hypothesis that the quantile of order is 0.20.
9. For the data of Problem 10.4.8 use the sign test to test the hypothesis of no difference between the two averages.
10. Use the sign test for the data of Problem 10.4.9 to test the hypothesis of no difference in grade-point averages.

    Do not reject H₀ at 0.05 level.

11. For the data of Problem 5 apply the signed-rank test to test against

    , do not reject H₀.

12. For the data of Problems 10.4.8 and 10.4.9 apply the signed-rank test to the differences to test against .

    (Second part) , do not reject H₀ at .

13.4 SOME TWO-SAMPLE PROBLEMS

In this section we consider some two-sample tests. Let X₁,X₂,…,X_m and Y₁,Y₂ ,…,Y_n be independent samples from two absolutely continuous distribution functions F_X and F_Y, respectively. The problem is to test the null hypothesis for all against the usual one- and two-sided alternatives.

Tests of H₀ depend on the type of alternative specified. We state some of the alternatives of interest even though we will not consider all of these in this text.

1. Location alternative: ,
2. Scale alternative: ,
3. Lehmann alternative: , .
4. Stochastic alternative: for all x, and for at least one x.
5. General alternative: for some x.

Some comments are in order. Clearly I through IV are special cases of V. Alternatives I and II show differences in F_X and F_Y in location and scale, respectively. Alternative III states that . In the special case when θ is an integer it states that Y has the same distribution as the smallest of the of X-variables. A similar alternative to test that is sometimes used is for some and all x. When α is an integer, this states that Y is distributed as the largest of the α X-variables. Alternative IV refers to the relative magnitudes of X’s and Y’s. It states that

so that

(1)

for all x. In other words, X’s tend to be larger than the Y’s.

A similar interpretation may be given to the one-sided alternative . In the special case where both X and Y are normal RVs with means μ₁, μ₂ and common variance σ² corresponds to and and corresponds to

In this section we consider some common two-sample tests for location (Case I) and stochastic ordering (Case IV) alternatives. First, note that a test of stochastic ordering may also be used as a test of less restrictive location alternatives since, for example, corresponds to larger Y’s and hence larger location for Y. Second, we note that the chi-square test of homogeneity described in Section 10.3 can be used to test general alternatives (Case V) for some x. Briefly, one partitions the real line into Borel sets A₁,A₂,…,A_k. Let

. Under , , , which is the problem of testing equality of two independent multinomial distributions discussed in Section 10.3.

We first consider a simple test of location. This test, based on the sample median of the combined sample, is a test of the equality of medians of the two DFs. It will tend to accept even if the shapes of F and G are different as long as their medians are equal.

13.4.1 Median Test

The combined sample X₁,X₂,…,X_m, Y₁,Y₂,…,Y_n is ordered and a sample median is found. If is odd, the median is the th value in the ordered arrangement. If is even, the median is any number between the two middle values. Let V be the number of observed values of X that are less than or equal to the sample median for the combined sample. If V is large, it is reasonable to conclude that the actual median of X is smaller than the median of Y. One therefore rejects in favor of for all x and for some x if V is too large, that is, if . If, however, the alternative is for all x and for some x, the median test rejects H₀ if .

For the two-sided alternative that for some x, we use the two-sided test.

We next compute the null distribution of the RV V. If , p a positive integer, then

(2)

Here . If , is an integer, the th value is the median in the combined sample, and

(3)

Remark 1. Under H₀ we expect observations above the median and below the median. One can therefore apply the chi-square test with 1 d.f. to test H₀ against the two-sided alternative.

We now consider two tests of the stochastic alternatives. As mentioned earlier they may also be used as tests of location.

13.4.2 Kolmogorov–Smirnov Test

Let X₁,X₂ ,…,X_m and Y₁,Y₂,…,Y_n be independent random samples from continuous DFs F and G, respectively. Let and , respectively, be the empirical DFs of the X’s and the Y’s. Recall the is the U-statistic for F and , that for G. Under for all x, we expect a reasonable agreement between the two sample DFs. We define

(4)

Then D_{m, n} may be used to test H₀ against the two-sided alternative for some x. The test rejects H₀ at level α if

(5)

where .

Similarly, one can define the one-sided statistics

(6)

and

(7)

to be used against the one-sided alternatives

(8)

and

(9)

respectively.

For small samples tables due to Massey [72] are available. In Table ST9, we give the values of D_m,n,α and for some selected values of m, n, and α. Table ST8 gives the corresponding values for the case.

For large samples we use the limiting result due to Smirnov [107]. Let .

Then

(10)

(11)

Relations (10) and (11) give the distribution of and D_m,n, respectively, under for all .

Let us first apply the Kolmogorov–Smirnov test to test H₀ that the population distribution of length of life for the two brands is the same.

x
30		0
40
45
50
55	1
60	1	1	0

From Table ST8, the critical value for at level is . Since , we accept H₀ that the population distribution for the length of life for the two brands is the same.

Let us next apply the two-sample t-test. We have , , , , . Thus

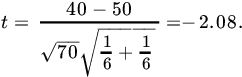
Since , we accept the hypothesis that the two samples come from the same (normal) population.

The second test of stochastic ordering alternatives we consider is the Mann–Whitney–Wilcoxon test which can be viewed as a test based on a U-statistic.

13.4.3 The Mann–Whitney–Wilcoxon Test

Let X₁,X₂,…,X_m and Y₁,Y₂,…,Y_n be independent samples from two continuous DFs, F and G, respectively. As in Example 13.2.10, let

for , . Recall that T(X_i ; Y_j) is an unbiased estimator of and the two sample U-statistic for g is given by . For notational convenience, let us write

(12)

Then U is the number of values of X₁,X₂,…,X_m that are smaller than each of Y₁,Y₂,…,Y_n. The statistic U is called the Mann–Whitney statistic. An alternative equivalent form using Wilcoxon scores is the linear rank statistic given by

(13)

where Q_j = rank of Y_j among the combined observations. Indeed,

Thus

(14)

so that U and W are equivalent test statistics. Hence the name Mann–Whitney–Wilcoxon Test. We will restrict attention to U as the test statistic.

Note that if all the X_i,’s are larger than all the Y_j’s and if all the X_i’s are smaller than all the Y_j’s, because then there are m , , and so on. Thus . If U is large, the values of Y tend to be larger than the values of X (Y is stochastically larger than X), and this supports the alternative for all x and for some x. Similarly, if U is small, the Y values tend to be smaller than the X values, and this supports the alternative for all x and F(x) G(x) for some x. We summarize these results as follows:

H0	H1	Reject H0 if

To compute the critical values we need the null distribution of U. Let

(15)

We will set up a difference equation relating p_{m, n} to p_m–1,_n and p_{m, n–1}. If the observations are arranged in increasing order of magnitude, the largest value can be either an x value or a y value. Under H₀, all values are equally likely, so the probability that the largest value will be an x value is and that it will be a y value is .

Now, if the largest value is an x, it does not contribute to U, and the remaining values of x and n values of y can be arranged to give the observed value with probability p_m–1,_n(u). If the largest value is a Y, this value is larger than all the m x’s. Thus, to get , the remaining values of Y and m values of x contribute . It follows that

(16)

If , then for

(17)

If , , then

(18)

and

(19)

For small values of m and n one can easily compute the null PMF of U. Thus, if , then

If , , then

Tables for critical values are available for small values of m and n, . See, for example, Auble [3] or Mann and Whitney [71]. Table ST11 gives the values of u_α for which for some selected values of m, n, and α.

If m, n are large we can use the asymptotic normality of U. In Example 13.2.11 we showed that, under H₀,

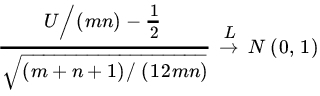
as such that constant. The approximation is fairly good for .

PROBLEMS 13.4

1. For the data of Example 4 apply the median test.
2. Twelve 4-year-old boys and twelve 4-year-old girls were observed during two 15-minute play sessions, and each child’s play during these two periods was scored as follows for incidence and degree of aggression:
   • Boys: 86, 69,72, 65, 113, 65, 118, 45, 141, 104, 41, 50
   • Girls: 55, 40, 22, 58, 16, 7, 9, 16, 26, 36, 20, 15

   Test the hypothesis that there were sex differences in the amount of aggression shown, using (a) the median test and (b) the Mann-Whitney-Wilcoxon test (Siegel [105]).

3. To compare the variability of two brands of tires, the following mileages (1000 miles) were obtained for eight tires of each kind:
   • Brand A:32.1, 20.6, 17.8, 28.4, 19.6, 21.4, 19.9, 30.1
   • Brand B:19.8, 27.6, 30.8, 27.6, 34.1, 18.7, 16.9, 17.9

   Test the null hypothesis that the two samples come from the same population, using the Mann–Whitney–Wilcoxon test.

4. Use the data of Problem 2 to apply the Kolmogorov−Smirnov test.
5. Apply the Kolmogorov−Smirnov test to the data of Problem 3.
6. Yet another test for testing against general alternatives is the so-called runs test. A run is a succession of one or more identical symbols which are preceded and followed by a different symbol (or no symbol). The length of a run is the number of like symbols in a run. The total number of runs, R, in the combined sample of X’s and Y’s when arranged in increasing order can be used as a test of H₀. Under H₀ the X and Y symbols are expected to be well-mixed. A small value of R supports . A test based on R is appropriate only for two-sided (general) alternatives. Tables of critical values are available. For large samples, one uses normal approximation: .
   1. Let of X-runs, -runs, and . Under H₀, show that
      

      Where if if , and .

   2. Show that
      
7. Fifteen 3-year-old boys and 15 3-year-old girls were observed during two sessions of recess in a nursery school. Each child’s play was scored for incidence and degree of aggression as follows:
   • Boys: 96 65 74 78 82 121 68 79 111 48 53 92 81 31 40
   • Girls: 12 47 32 59 83 14 32 15 17 82 21 34 9 15 51

   Is there evidence to suggest that there are sex differences in the incidence and amount of aggression? Use both Mann–Whitney–Wilcoxon and runs tests.

13.5 TESTS OF INDEPENDENCE

Let X and Y be two RVs with joint DF F(x, y), and let F₁ and F₂, respectively, be the marginal DFs of X and Y. In this section we study some tests of the hypothesis of independence, namely,

against the alternative

If the joint distribution function F is bivariate normal, we know that X and Y are independent if and only if the correlation coefficient . In this case, the test of independence is to test .

In the nonparametric situation the most commonly used test of independence is the chi-square test, which we now study.

13.5.1 Chi-square Test of Independence—Contingency Tables

Let X and Y be two RVs, and suppose that we have n observations on (X,Y). Let us divide the space of values assumed by X (the real line) into r mutually exclusive intervals A₁, A₂,…,A_r. Similarly, the space of values of Y is divided into c disjoint intervals B₁, B₂,…,B_c. As a rule of thumb, we choose the length of each interval in such a way that the probability that X(Y) lies in an interval is approximately (1/r)(1/c). Moreover, it is desirable to have n/r and n/c at least equal to 5. Let X_ij denote the number of pairs (X_k, Y_k), , that lie in A_i × B_j, and let

(1)

Where , . If each p_ij is known, the quantity

(2)

has approximately a chi-square distribution with d.f., provided that n is large (see Theorem 10.3.2.). If X and Y are independent, . Let us write and . Then under , , . In practice, p_ij will not be known. We replace p_ij by their estimates. Under H₀, we estimate p_i· by

(3)

and p_·j by

(4)

Since we have estimated only parameters. It follows (see Theorem 10.3.4) that the RV

(5)

is asymptotically distributed as χ² with d.f., under H₀. The null hypothesis is rejected if the computed value of U exceeds χ ²_(r-1)(c-1),_α..

It is frequently convenient to list the observed and expected frequencies of the rc events A_i × Bj in an r × c table, called a contingency table, as follows:

Observed Frequencies, Oij				Expected Frequencies, Eij
	B1	B2…Bc			B1	B2…Bc
A1	X11	X12…X2c		A1	np1.p.1	np1.p.2… np1.p.c	np1
A2	X21	X22…X2c		A2	np2.p.1	np2.p.2… np2.p.c	np2
.	.	....	.	.	.	. ….
.	.	....	.	.	.	. ….
.	.	....	.	.	.	. ….
Ar	Xr1	Xr2…Xrc		Ar	npr.p.1	npr.p.c… npr.p.c	npr
			n		np.1	np.2 np.c	n

Note that the X_ij’s in the table are frequencies. Once the category A_i × B_j is determined for an observation (X, Y), numerical values of X and Y are irrelevant. Next, we need to compute the expected frequency table. This is done quite simply by multiplying the row and column totals for each pair (i, j) and dividing the product by n. Then we compute the quantity

and compare it with the tabulated value. In this form the test can be applied even to qualitative data. A₁, A₂, …,A_r and B₁, B₂,…,B_c represent the two attributes, and the null hypothesis to be tested is that the attributes A and B are independent.

13.5.2 Kendall’s Tau

Let (X₁, Y₁), (X₂, Y₂),…,(X_n, Y_n) be a sample from a bivariate population.

Writing π_c and π_d for the probability of perfect concordance and of perfect discordance, respectively, we have

(8)

and

(9)

and, if the marginal distributions of X and Y are continuous,

(10)

If the marginal distributions of X and Y are continuous, we may rewrite (11), in view of (10), as follows:

(12)

In particular, if X and Y are independent and continuous RVs, then

since then is a symmetric RV. Then

and it follows that for independent continuous RVs.

Note that, in general, does not imply independence. However, for the bivariate normal distribution if and only if the correlation coefficient ρ, between X and Y, is 0, so that if and only if X and Y are independent (Problem 6).

Let

(13)

Then , and we see that is estimable of degree 2, with symmetric kernel ψ defined in (13). The corresponding one-sample U-statistic is given by

(14)

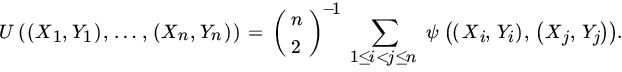
Then the corresponding estimator of Kendall’s tau is

(15)

and is called Kendall’s sample correlation coefficient.

Note that . To test H₀ that X and Y are independent against H₁ : X and Y are dependent, we reject H₀ if |T| is large. Under H₀, , so that the null distribution of T is symmetric about 0. Thus we reject H₀ at level α if the observed value of T, t, satisfies |t| t_α/2, where .

For small values of n the null distribution can be directly evaluated. Values for are tabulated by Kendall [51]. Table ST12 gives the values of S_α for which , where T for selected values of n and α.

For a direct evaluation of the null distribution we note that the numerical value of T is clearly invariant under all order-preserving transformations. It is therefore convenient to order X and Y values and assign them ranks. If we write the pairs from the smallest to the largest according to, say, X values, then the number of pairs of values of for which is the number of concordant pairs, P.

For large n we can use an extension of Theorem 13.3.3 to bivariate case to conclude that , where

Under H₀, it can be shown that

See, for example, Kendall [51], Randles and Wolfe [85], or Gibbons [35]. Approximation is good for .

13.5.3 Spearman’s Rank Correlation Coefficient

Let (X₁, Y₁), (X₂, Y₂),…, (X_n,Y_n) be a sample from a bivariate population. In Section 6.3 we defined the sample correlation coefficient by

(16)

where

If the sample values X₁,X₂,…,X_n and Y₁,Y₂,…,Y_n are each ranked from 1 to n in increasing order of magnitude separately, and if the X’s and Y’s have continuous DFs, we get a unique set of rankings. The data will then reduce to n pairs of rankings. Let us write

then R_i and S_i ∈ {1,2,…,n}. Also

(17)

(18)

and

(19)

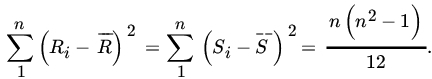
Substituting in (16), we obtain

(20)

Writing , we have

and it follows that

(21)

The statistic R defined in (20) and (21) is called Spearman’s rank correlation coefficient (see also Example 4.5.2).

From (20) we see that

(22)

Under H₀, the RVs X and Y are independent, so that the ranks R_i and S_i are also independent. It follows that

and

(23)

Thus we should reject H₀ if the absolute value of R is large, that is, reject H₀ if

(24)

where . To compute R_α we need the null distribution of R. For this purpose it is convenient to assume, without loss of generality, that . Then , . Under H₀, X and Y being independent, the n! pairs (i,S_i) of ranks are equally likely. It follows that

(25)

Note that , and the extreme values can occur only when either the rankings match, that is, , in which case , or , in which case . Moreover, one need compute only one half of the distribution, since it is symmetric about 0 (Problem 7).

In the following example we will compute the distribution of R for and 4. The exact complete distribution of , and hence R, for has been tabulated by Kendall [51]. Table ST13 gives the values of R_α for some selected values of n and α.

Since , we cannot reject H₀ at or .

For large samples it is possible to use a normal approximation. It can be shown (see, e.g., Fraser [32, pp. 247–248]) that under H₀ the RV

or, equivalently,

has approximately a standard normal distribution. The approximation is good for .

PROBLEMS 13.5

1. A sample of 240 men was classified according to characteristics A and B. Characteristic A was subdivided into four classes A₁, A₂, A₃, and A₄, while B was subdivided into three classes B₁, B₂, and B₃, with the following result:

   	A1	A2	A3	A4
   B1	12	25	32	11	80
   B2	17	18	22	23	80
   B3	21	17	16	26	80
   	50	60	70	60	240

   Is there evidence to support the theory that A and B are independent?

2. The following data represent the blood types and ethnic groups of a sample of Iraqi citizens:

   	Blood Type
   Ethnic Group	O	A	B	AB
   Kurd	531	450	293	226
   Arab	174	150	133	36
   Jew	42	26	26	8
   Turkoman	47	49	22	10
   Ossetian	50	59	26	15

   Is there evidence to conclude that blood type is independent of ethnic group?

3. In a public opinion poll, a random sample of 500 American adults across the country was asked the following question: “Do you believe that there was a concerted effort to cover up the Watergate scandal? Answer yes, no, or no opinion.” The responses according to political beliefs were as follows:

   Political Affiliation	Response
   Yes	No	No Opinion
   Republican	45	75	30	150
   Independent	85	45	20	150
   Democrat	140	30	30	200
   	270	150	80	500

   Test the hypothesis that attitude toward the Watergate cover-up is independent of political party affiliation.

4. A random sample of 100 families in Bowling Green, Ohio, showed the following distribution of home ownership by family income:

   Residential Status	Annual Income (dollars)
   Less than 30,000	30,000-50,000	50,000or Above
   Home Owner	10	15	30
   Renter	8	17	20

   Is home ownership in Bowling Green independent of family income?

5. In a flower show the judges agreed that five exhibits were outstanding, and these were numbered arbitrarily from 1 to 5. Three judges each arranged these five exhibits in order of merit, giving the following rankings:

   Judge A:	5	3	1	2	4
   Judge B:	3	1	5	4	2
   Judge C:	5	2	3	1	4

   Compute the average values of Spearman’s rank correlation coefficient R and Kendall’s sample tau coefficient T from the three possible pairs of rankings.

6. For the bivariate normally distributed RV (X, Y) show that if and only if X and Y are independent. [Hint: Show that , where p is the correlation coefficient between X and Y.]
7. Show that the distribution of Spearman's rank correlation coefficient R is symmetric about 0 under H₀.
8. In Problem 5 test the null hypothesis that rankings of judge A and judge C are independent. Use both Kendall’s tau and Spearman's rank correlation tests.
9. A random sample of 12 couples showed the following distribution of heights:

   Couple	Height (in.)	Couple	Height (in.)
   Husband	Wife	Husband	Wife
   1	80	72	7	74	68
   2	70	60	8	71	71
   3	73	76	9	63	61
   4	72	62	10	64	65
   5	62	63	11	68	66
   6	65	46	12	67	67

   1. Compute T.
   2. Compute R.
   3. Test the hypothesis that the heights of husband and wife are independent, using T as well as R. In each case use the normal approximation.
   1. ;
   2. ;
   3. Reject H₀ in each case.

13.6 SOME APPLICATIONS OF ORDER STATISTICS

In this section we consider some applications of order statistics. We are mainly interested in three applications, namely, tolerance intervals for distributions, coverages, and confidence interval estimates for quantiles and location parameters.

Let X₁, X₂,…,X_n be a sample of size n from F, and let X₍₁₎, X₍₂₎, …,X_(n) be the corresponding set of order statistics. If the end points of the tolerance interval are two-order statistics X_(r), X_(s), r s, we have

(1)

Since F is continuous, F(X) is U(0, 1), and we have

(2)

where U_(r), U_(s) are the order statistics from U(0,1). Thus (1) reduces to

(3)

The statistic , , is called the coverage of the interval (X_(r),X_(s)). More precisely, the differences , for , where and , are called elementary coverages.

Since the joint PDF of U₍₁₎, U₍₂₎,…, U_(n) is given by

the joint PDFofV₁, V₂,…,V_n is easily seen to be

(4)

Note that h is symmetric in its arguments. Consequently, V_i’s are exchangeable RVs and the distribution of every sum of r, r n, of these coverages is the same and, in particular, it is the distribution of namely,

(5)

The common distribution of elementary coverages is

Thus and . This may be interpreted as follows: The order statistics X₍₁₎,X₍₂₎,…,X_(n) partition the area under the PDF in parts such that each part has the same average (expected) area.

The sum of any r successive elementary coverages V_i+1,V_i+1 ,…,V_i+r is called an r-coverage. Clearly

(6)

and, in particular,) . Since V's are exchangeable it follows that

(7)

with PDF

From (3), therefore

(8)

where the last equality follows from (5.3.48). Given n, p, γ it may not always be possible to find s - r to satisfy (8).

In general, given p, 0 < p < 1, it is possible to choose a sufficiently large sample of size n and a corresponding value of such that with probability ≥ γ an interval of the form (X(_r),X(_s)) covers at least 100p percent of the distribution. If is specified as a function of n, one chooses the smallest sample size n.

We next consider the use of order statistics in constructing confidence intervals for population quantiles. Let X be an RV with a continuous DF F,0 < p < 1. Then the quantile of order p satisfies

(9)

Let X₁, X₂,…,X_n be n independent observations on X. Then the number of X_i's < _p is an RV that has a binomial distribution with parameters n and p. Similarly, the number of X_i's that are at least _p has a binomial distribution with parameters n and .

Let X₍₁₎,X₍₂₎,…,X_(n) be the set of order statistics for the sample. Then

(10)

Similarly

(11)

It follows from (10) and (11) that

(12)

It is easy to determine a confidence interval for _p from (12), once the confidence level is given. In practice, one determines r and s such that is as small as possible, subject to the condition that the level is .

Finally we consider applications of order statistics to constructing confidence intervals for a location parameter. For this purpose we will use the method of test inversion discussed in Chapter 11. We first consider confidence estimation based on the sign test of location.

Let X₁,X₂,…,X_n be a random sample from a symmetric, continuous and suppose we wish to find a confidence interval for 6. Let of , be the sign-test statistic for testing against . Clearly, under H₀. The sign-test rejects H₀ if

(13)

for some integer c to be determined from the level of the test. Let . Then any value of θ is acceptable provided it is greater than the rth smallest observation and smaller than the rth largest observation, giving as confidence interval

(14)

If we want level to be associated with (14), we choose c so that the level of test (13) is α.

We next consider the Wilcoxon signed-ranks test of to construct a confidence interval for θ. The test statistic in this case is T⁺ = sum of ranks of positive 's in the ordered |X_t — θ₊|'s. From (13.3.4)

Let , and order the T_ij's in increasing order of magnitude

Then using the argument that converts (13) to (14) we see that a confidence interval for θ is given by

(15)

Critical values c are taken from Table ST10.

1. Find the smallest values of n such that the intervals (a) (X₍₁₎,X_(n)) and (b) (X₍₂₎,X_(n-1)) contain the median with probability 0.90.
   1. 5;
   2. 8.
2. Find the smallest sample size required such that (X₍₁₎, X_(n)) covers at least 90 percent of the distribution with probability > 0.98.
3. Find the relation between n andp such that (X₍₁₎,X_(n)) covers at least 100p percent of the distribution with probability. .

   .

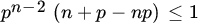4. Given γ, δ, p₀, p₁ with , find the smallest n such that
   

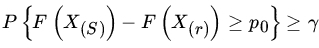
   and

   

   Find also .

   [Hint: Use the normal approximation to the binomial distribution.]

   .

5. In Problem 4 find the smallest n and the associated value of if , , , .
6. Let X₁ , X₂,… , X₇ be a random sample from a continuous DF F. Compute:
   1. .
   2. 
   3. ..
7. Let X₁,X₂,…,X_n be iid with common continuous DF F.
   1. What is the distribution of
      

      for ?

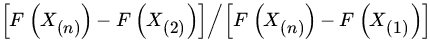   2. What is the distribution of .

13.7 ROBUSTNESS

Most of the statistical inference problems treated in this book are parametric in nature. We have assumed that the functional form of the distribution being sampled is known except for a finite number of parameters. It is to be expected that any estimator or test of hypothesis concerning the unknown parameter constructed on this assumption will perform better than the corresponding nonparametric procedure, provided that the underlying assumptions are satisfied. It is therefore of interest to know how well the parametric optimal tests or estimators constructed for one population perform when the basic assumptions are modified. If we can construct tests or estimators that perform well for a variety of distributions, for example, there would be little point in using the corresponding nonparametric method unless the assumptions are seriously violated.

In practice, one makes many assumptions in parametric inference, and any one or all of these may be violated. Thus one seldom has accurate knowledge about the true underlying distribution. Similarly, the assumption of mutual independence or even identical distribution may not hold. Any test or estimator that performs well under modifications of underlying assumptions is usually referred to as robust.

In this section we will first consider the effect that slight variation in model assumptions have on some common parametric estimators and tests of hypotheses. Next we will consider some corresponding nonparametric competitors and show that they are quite robust.

13.7.1 Effect of Deviations from Model Assumptions on Some Parametric Procedures

Let us first consider the effect of contamination on sample mean as an estimator of the population mean.

The most commonly used estimator of the population mean μ is the sample mean . It has the property of unbiasedness for all populations with finite mean. For many parent populations (normal, Poisson, Bernoulli, gamma, etc.) it is a complete sufficient statistic and hence a UMVUE. Moreover, it is consistent and has asymptotic normal distribution whenever the conditions of the central limit theorem are satisfied. Nevertheless, the sample mean is affected by extreme observations, and a single observation that is either too large or too small may make worthless as an estimator of μ. Suppose, for example, that X₁, X₂,…,X_n is a sample from some normal population. Occasionally something happens to the system, and a wild observation is obtained that is, suppose one is sampling from (μ, σ²), say, 100α percent of the time and from (μ, kσ²), where percent of the time. Here both μ and σ² are unknown, and one wishes to estimate μ. In this case one is really sampling from the density function

(1)

Where f₀ is the PDF of (μ, σ²), and f₁, the PDF of (μ, kσ²). Clearly,

(2)

is still unbiased for μ. If α is nearly 1, there is no problem since the underlying distribution is nearly (μ, σ²), and is nearly the UMVUE of μ with variance σ²/n. If is large (that is, not nearly 0), then, since one is sampling from f, the variance of X₁ is σ² with probability α and is kα ² with probability , and we have

(3)

If is large, is large and we see that even an occasional wild observation makes subject to a sizable error. The presence of an occasional observation from (μ, kσ²) is frequently referred to as contamination. The problem is that we do not know, in practice, the distribution of the wild observations and hence we do not know the PDF f. It is known that the sample median is a much better estimator than the mean in the presence of extreme values. In the contamination model discussed above, if we use Z_1/2, the sample median of the X_i’s, as an estimator of μ (which is the population median), then for large n

(4)

(See Theorem 7.5.2 and Remark 7.5.7.) Since

we have

(5)

As . If there is no contamination, and . Also,

which will be close to 1 if α is close to 1. Thus the estimator Z_1/2 will not be greatly affected by how large k is, that is, how wild the observations are. We have

Indeed, as , whereas as . One can check that, when and , the two variances are (approximately) equal. As k becomes larger than 9 or α smaller than 0.915, Z_1/2 becomes a better estimator of μ than .

There are other flaws as well. Suppose, for example, that X₁, X₂,…,X_n is a sample from . Then both and , where , are unbiased for . Also, , and one can show that . It follows that the efficiency of relative to that of T is

In fact, as , so that in sampling from a uniform parent is much worse than T, even for moderately large values of n.

Let us next turn our attention to the estimation of standard deviation. Let X₁, X₂, …,X_n be a sample from (μ, σ²). Then the MLE of σ is

(6)

Note that the lower bound for the variance of any unbiased estimator for σ is σ²/2n. Although is not unbiased, the estimator

(7)

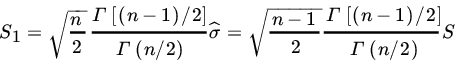
is unbiased for σ Also,

(8)

Thus the efficiency of S₁ (relative to the estimator with least variance = σ²/2n)is

and →1 as n → ∞. For small n, the efficiency of S₁ is considerably smaller than 1. Thus, for , and, for , .

Yet another estimator of σ is the sample mean deviation

(9)

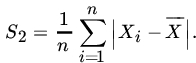
Note that

and

(10)

If n is large enough so that , we see that is nearly unbiased for σ with variance . The efficiency of S₃ is

For large n, the efficiency of S₁ relative to S₃ is

Now suppose that there is some contamination. As before, let us suppose that for a proportion α of the time we sample from (μ, σ²) and for a proportion of the time we get a wild observation from (μ, kσ²), . Assuming that both μ and σ² are unknown, suppose that we wish to estimateσ. In the notation used above, let

Where f₀ is the PDF of (μ, σ²),and f₁, the PDF of us see how even small contamination can make the ma(μ, kσ²). Let us see how even small contamination can make the maximum likelihood estimate of σ quite useless.

If is the MLE of θ, and ϕ is a function of θ, then is the MLE of ϕ(θ). Inview of (7.5.7) we get

(11)

Using Theorem 7.3.5, we see that

(12)

(drooping the other two terms with n² and n³ in the denominator), so that

(13)

For the density f, we see that

(14)

and

(15)

It follows that

(16)

If we are interested in the effect of very small contamination, and . Assuming that , we see that

(17)

In the normal case, and , so that from (11)

Thus we see that the mean square error due to a small contamination is now multiplied by a factor . If, for example, , then . If , then , and so on.

A quick comparison with S₃ shows that, although S₁ (or even a) is a better estimator of σ than S₃ if there is no contamination, S₃ becomes a much better estimator in the presence of contamination as k becomes large.

Next we consider the effect of deviation from model assumptions on tests of hypotheses. One of the most commonly used tests in statistics is Student’s t-test for testing the mean of a normal population when the variance is unknown. Let X₁, X₂,…,X_n be a sample from some population with mean μ and finite variance σ². As usual, let denote the sample mean, and S², the sample variance. If the population being sampled is normal, the t-test rejects against at level α if . If n is large, we replace by the corresponding critical value, z_α/2 under the standard normal law. If the sample does not come from a normal population, the statistic is no longer distributed as a t statistic. If, however, n is sufficiently large, we know that T has an asymptotic normal distribution irrespective of the population being sampled, as long as it has a finite variance. Thus, for large n, the distribution of T is independent of the form of the population, and the t-test is stable. The same considerations apply to testing the difference between two means when the two variances are equal. Although we assumed that n is sufficiently large for Slutsky s result (Theorem 7.2.15) to hold, empirical investigations have shown that the test based on Student s statistic is robust. Thus a significant value of t may not be interpreted to mean a departure from normality of the observations. Let us next consider the effect of departure from independence on the t-distribution. Suppose that the observations X₁, X₂,…,X_n have a multivariate normal distribution with , and ρ as the common correlation coefficient between any X_i and X_j, . Then

(18)

and since X_i’s are exchangeable it follows from Remark 6.3.1 that

(19)

For large n, the statistic will be asymptotically distributed as , instead of (0, 1). Under H₀, and is distributed as . Consider the ratio

(20)

The ratio equals 1 if but is > 0 for and →∞ as ρ→1. It follows that a large value of T is likely to occur when and is large, even though μ₀ is the true value of the mean. Thus a significant value of t may be due to departure from independence, and the effect can be serious.

Next, consider a test of the null hypothesis against . Under the usual normality assumptions on the observations X₁, X₂,…X_n, the test statistic used is

(21)

Which has a distribution under H₀. The usual test is to reject H₀ of

(22)

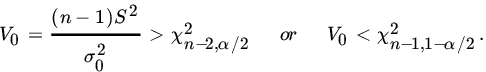
Let us suppose that X₁, X₂,…X_n are not normal. It follows from Corollary 2 of Theorem 7.3.4 that

(23)

so that

(24)

Writing , we have

(25)

When the X_i’s are not normal, and

(26)

when the X_i’s are normal . Now is the sum of n identically distributed but dependent , j = 1, 2,…,n. Using a version of the central limit theorem for dependent RVs (see, e.g., Cramér [17, p. 365]), it follows that

under H₀, is asymptotically , and not (0, 1)as under the normal theory. As a result the size of the test based on the statistic V₀ will be different from the stated level of significance if γ² differs greatly from 0. It is clear that the effect of violation of the normality assumption can be quite serious on inferences about variances, and the chi-square test is not robust.

In the above discussion we have used somewhat crude calculations to investigate the behavior of the most commonly used estimators and test statistics when one or more of the underlying assumptions are violated. Our purpose here was to indicate that some tests or estimators are robust whereas others are not. The moral is clear: One should check carefully to see that the underlying assumptions are satisfied before using parametric procedures.

13.7.2 Some Robust Procedures

Let X₁, X₂,…, X_n be a random sample from a continuous PDF and assume that f is symmetric about θ. We shall be interested in estimation or tests of hypotheses concerning θ. Our objective is to find procedures that perform well for several different types of distributions but do not have to be optimal for any particular distribution. We will call such procedures robust. We first consider estimation of θ.

The estimators fall under one of the following three types:

1. Estimators that are functions of , where R_j is the rank of X_j, are known as R-estimators. Hodges and Lehmann [44] devised a method of deriving such estimators from rank tests. These include the sample median (based on the sign test) and based on the Wilcoxon signed-rank test.
2. Estimators of the form are called L-estimators, being linear combinations of order statistics. This class includes the median, the mean, and the trimmed mean obtained by dropping a prespecified proportion of extreme observations.
3. Maximum likelihood type estimators obtained as solutions to certain equations are called M-estimators. The function gives MLEs.

Two extreme examples of trimmed means are the sample mean and the median when all except the central (n odd) or the two central (n even) observations are excluded.

We will limit this discussion to four estimators of location, namely, the sample median, trimmed mean, sample mean, and Hodges–Lehmann type estimator based on Wilcoxon signed-rank test. In order to compare the performance of two procedures A and B we will use a (large sample) measure of relative efficiency due to Pitman. Pitman’s asymptotic relative efficiency (ARE) of procedure B relative to procedure A is the limit of the ratio of sample sizes n_A/n_B, where n_A, n_B are sample sizes needed for procedures A and B to perform equivalently with respect to a specified criterion. For example, suppose {T_n(B)} and {T_n(A)} are two sequences of estimators for ψ(θ) such that

and

Suppose further that A and B perform equivalently if their asymptotic variances are the same, that is,

Then

Clearly, different performance measures may lead to different measures of ARE.

Similarly if procedures A and B lead to two sequences of tests, then ARE is the limiting ratio of the sample sizes needed by the tests to reach a certain power β₀ against the same alternative and at the same limiting level α.

Accordingly, let e(B,A) denote the ARE of B relative to A. If say, then procedure A requires (approximately) half as many observations as procedure B. We will write e_F(B, A), whenever necessary to indicate the dependence of ARE on the underlying DF F.

For detailed discussion of Pitman efficiency we refer to Lehmann , Lehmann [63, section 5.2], Serfling [102, chapter 10], Randles and Wolfe [85, chapter 5], and Zacks [121]. The expressions for AREs of median and the Hodges-Lehmann estimators of location parameter θ with respect to the sample mean are

(28)

(29)

where f is the PDF corresponding to F. In order to get we use the fact that

(30)

Bickel [5] showed that

(31)

where

(32)

and α is the unique αth percentile of F. It is clear from (32) that no closed form expression for is possible for most DFs F.

In the following table we give the AREs for some selected F.

ARE Computations for Selected F
F
	1/3	1	1/3
(0,1)			2/3
Logistic,		1.10	0.748
Double Exponential,	2	1.5	4/3
(0,1)	∞	∞	4/3

It can be shown that for all symmetric F, so is quite inefficient compared to for . Even for normal f, would require 157 observations to achieve the same accuracy that achieves with 100 observations. For heavier tailed distributions, however, provides more protection that .

The values of , on the other hand, are quite high for most F and, in fact, for all symmetric F. Even for normal F one loses little (4.5%) in using W instead of . Thus W is more robust as an estimator of θ.

A look at the values of shows that is worse than W for distributions with light-tails but does slightly better than W for heavier-tailed F.

Let us now compare the AREs of and W. The following AREs for selected α are due to Bickel [5].

ARE Comparisons
F
Uniform	0.96	1.04	0.83
Normal	0.995	0.96	0.97	0.985
Double Exponential	1.06	1.41	1.21	1.24
Cauchy	∞	6.72	∞	2.67

We note that performs quite well compared to . In fact, for normal distribution the efficiency is quiet close to 1 so there is little loss in using . For heavier-tailed distributions is preferable. For small values of α, it should be noted that does not differ much from . Nevertheless, is more robust; it cannot do much worse than but can do much better. Compared to Hodges–Lehmann estimator, does not perform as well. It (W) provides better protection against outliers (heavy tails) and gives up little in the normal case.

Finally we consider testing against . Recall that X₁, X₂,…, X_n are iid with common continuous symmetric and PDF . Suppose . Let S denotes the sign test based on the statistic, , W denotes the Wilcoxon signed-rank test based on the statistic , M denotes the test based on the Z-statistic , and t denotes the student’s t-test based on the statistic , where S² is the sample variance.

First note that Next we note that so that AREs are the same as given in (28), (29), and (30) and values of ARE given in the table for various F remain the same for corresponding tests.

Similar remarks apply as in the case of estimation of θ. Sign test is not as efficient as the Wilcoxon signed-rank test. But for heavier-tailed distributions such as Cauchy and double exponential sign test does better than the Wilcoxon signed-rank test.

1. Let (X₁, X₂,…, X_n) be jointly normal with and otherwise.
   1. Show that
      

      And

      
   2. Show that the t-statistic is asymptotically normally distributed with mean 0 and variance . Conclude that the significance of t is overestimated for positive values of ρ and underestimated for in large samples.
   3. For finite n, consider the statistic
      

      Compare the expected values of the numerator and the denominator of T² and study the effect of to interpret significant t values (Scheffé [101, p. 338].)

2. Let X₁, X₂,…, X_n be a random sample from :
   1. Show that
      
   2. Show that
      
   3. Show that the large sample distribution of is normal.
   4. Compare the large-sample test of based on the asymptotic normality of with the large-sample test based on the same statistic when the observations are taken from a normal population. In particular, take .
3. Let X₁, X₂,…, X_m and Y₁, Y₂,…, Y_n be two independent random samples from populations with means μ₁ and μ₂ and variances and respectively. Let be the two sample means, and be the two sample variances. Write . The usual normal theory test of is the t-test based on the statistic
   

   where

   

   Under H₀, the statistic T has a t-distribution with d.f., provided that .

   Show that the asymptotic distribution of T in the nonnormal case is for large m and n. Thus, if , T is asymptotically (0,1) as in the normal theory case assuming equal variances, even though the two samples come from nonnormal populations with unequal variances. Conclude that the test is robust in the case of large, equal sample sizes (Scheffé [101, p. 339]).

4. Verify the computations in the table above using the expressions of ARE in (28), (29), and (30).
5. Suppose F is a G(α, β) r.v. Show that
   

   (Note that F is not symmetric.)

6. Suppose F has PDF
   

   for . compute , and . (From Problem 3.2.3, if . .