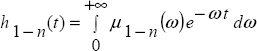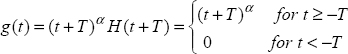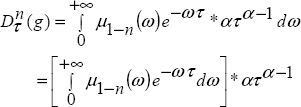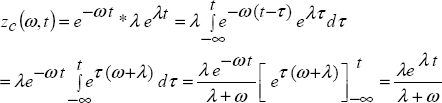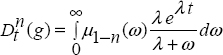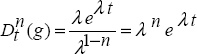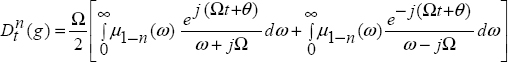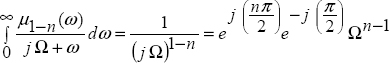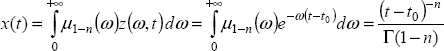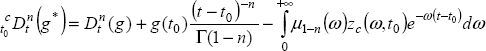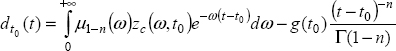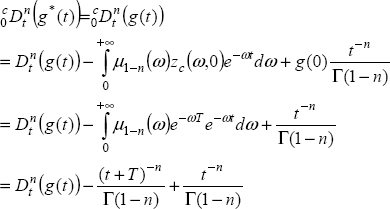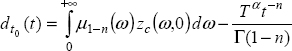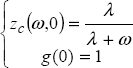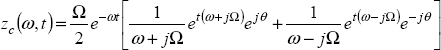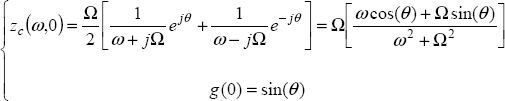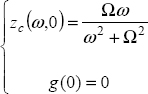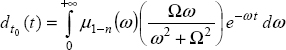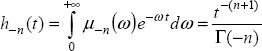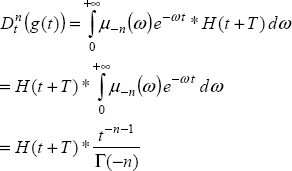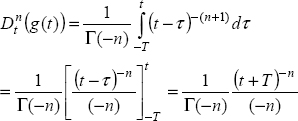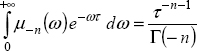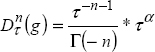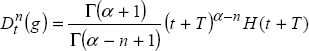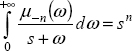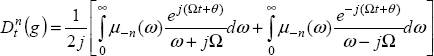10.1. Introduction

Fractional calculus has concerned the calculation of fractional integrals and derivatives for any kind of functions for a long time (see [OLD 72, MIL 93] and the references therein). Of course, integration of FDEs has also been an important issue, stimulated by physical and engineering applications [SAM 87, POD 99].

In the previous chapters, the infinite state approach was applied to the modeling and analysis of FDEs. In fact, this methodology also applies to other domains of fractional calculus, and particularly to the calculation of the fractional derivative of a function g(t), i.e. to . This derivative depends on the differentiation technique used: Riemann–Liouville, Caputo or Grünwald–Letnikov.

Let us consider the calculation of with the Caputo derivative. In the first step, we demonstrate that the calculation of the Caputo derivative on an infinite interval makes it possible to express the fractional derivative of the function g(t). In the second step, we analyze the calculation of the Caputo derivative on a truncated interval and the initial condition problem arising at t = t₀. Thus, we demonstrate that knowledge of these initial conditions makes it possible to correct the calculation on a truncated interval and thus to recover [TRI 11d, TRI 11e]. We consider some generic functions and formulate their fractional derivatives and the corresponding initial conditions.

Moreover, we demonstrate that the implicit derivative is also able to express the fractional derivative . Finally, numerical simulations are used to illustrate previous results for the particular case of the sine function.

10.2. Calculation of the Caputo derivative

Let us consider a function g(t) defined for , and we propose to analytically determine its fractional derivative for 0 < n < 1. Let us recall (Chapter 8) that the Caputo derivative calculated since t = −∞ is equal to the fractional derivative of f(t) because all the possible transients have vanished, so

[10.1]

where is the theoretical fractional derivative of g(t).

Let us recall that the Caputo derivative is defined as:

[10.2]

i.e. the Caputo derivative is the Riemann–Liouville integral, with order 1 – n , of the integer order derivative .

Let z_c(ω, t) be the distributed state variable of the integrator . Thus, z_c(ω, t) and are solutions of the distributed differential system:

[10.3]

[10.4]

[10.5]

Equation [10.3] means that z_c(ω, t) is the convolution of with the impulse response h_ω(t) of a first-order elementary system , where

[10.6]

Therefore

[10.7]

With z_c(ω, t), we finally obtain the fractional derivative as the weighted integral of all the frequency components, using equation [10.4].

Then, we apply this methodology to some generic functions (see [POD 99]).

10.2.1. Fractional derivative of the Heaviside function

Consider the Heaviside function:

[10.8]

We note that

[10.9]

Therefore, using equation [10.3]:

[10.10]

Then, using equation [10.4]:

[10.11]

As

[10.12]

we can write

[10.13]

Let us recall that

[10.14]

Therefore

[10.15]

and

[10.16]

10.2.2. Fractional derivative of the power function

Let us define the power function:

[10.17]

Then

[10.18]

Consider the variable change:

[10.19]

Therefore

[10.20]

Using equation [10.3]

[10.21]

and with equation [10.4]

[10.22]

As

[10.23]

we obtain

[10.24]

Using the convolution lemma (Appendix A.10):

[10.25]

We finally obtain

[10.26]

10.2.3. Fractional derivative of the exponential function

Consider the exponential function:

[10.27]

Then

[10.28]

Using equation [10.3]

[10.29]

Therefore, with equation [10.4]

[10.30]

Let us recall that

[10.31]

Therefore, with s = λ, we obtain

[10.32]

and

[10.33]

10.2.4. Fractional derivative of the sine function

Consider the sine function

[10.34]

and its derivative

[10.35]

As

[10.36]

Equation [10.3] can be written as

[10.37]

Therefore, this equation corresponds to

[10.38]

and using equation [10.40]:

[10.39]

As (equation [10.32]),

[10.40]

we obtain, with x = j Ω:

[10.41]

Finally

[10.42]

which yields:

[10.43]

10.3. Initial conditions of the Caputo derivative

We have previously defined the initial conditions of the Caputo derivative in the context of FDS transients. Our objective is to revisit these definitions, in the context of the calculation of the Caputo derivative applied to a function g(t).

In order to express the fractional derivative , we have calculated the Caputo derivative on an infinite interval . Practically, the derivative is calculated on a truncated interval .

Consequently, the function g(t) is truncated. Let g*(t) be this new function:

[10.44]

Therefore, we calculate

[10.45]

On the other hand

[10.46]

As

[10.47]

We obtain

[10.48]

Then:

[10.49]

REMARK 1.– Let , and define

Then

thus

[10.50]

Therefore, [10.49] is expressed as

[10.51]

We have previously defined [10.1]:

Therefore, using the convolution relation (see Chapter 6), we can write

[10.52]

where is the value of the distributed variable z_c(ω, t) of the integrator at instant t₀ (when the integrator acts since t = –∞).

Note that

so equation [10.51] can be written as

[10.53]

Similarly, [10.52] can be written as

[10.54]

Equaling these two expressions of , we obtain:

[10.55]

The two “initial conditions” are g(t₀) and z_c(ω, t₀).

The distributed variable z_c(ω, t₀) is a true initial condition, corresponding to the distributed variable z_c(ω, t) at t = t₀ of the integrator , acting since t = −∞.

On the contrary, g(t₀) is a pseudo-initial condition [ORT 11]: it corresponds to the jump of the truncated function g*(t) from g*(t) = 0 for t < t₀ to g(t) at t = t₀. The derivative of this jump provides the Dirac g(t₀)δ(t − t₀).

Moreover, note that

[10.56]

and

[10.57]

Therefore

[10.58]

This means that the Caputo derivative, calculated since any instant t₀ , tends asymptotically towards the fractional derivative of g(t), with a long memory transient.

10.4. Transients of fractional derivatives

10.4.1. Introduction

We have demonstrated that the Caputo derivative of the truncated function converges asymptotically towards the exact value with a long memory transient.

This convergence is characterized by a transient depending on the “initial conditions” g(t₀) and z_c(ω,t₀).

This transient is defined as

[10.59]

i.e.

[10.60]

Let us define these “initial conditions” for the previous generic functions; in order to simplify calculations, let t₀ = 0 .

10.4.2. Heaviside function

Consider g(t) = H(t + T) with T > 0 . Then

[10.61]

We have previously calculated

[10.62]

Therefore

[10.63]

and

[10.64]

Then

[10.65]

Thus

[10.66]

10.4.3. Power function

Consider with T > 0 and its truncation

We have previously calculated

[10.67]

and

[10.68]

Therefore

[10.69]

10.4.4. Exponential function

Consider and its truncation

We have previously calculated

[10.70]

Therefore

[10.71]

Consequently

[10.72]

10.4.5. Sine function

Consider and its truncation

We have previously calculated

[10.73]

Therefore

[10.74]

Consider the particular value θ = 0, and then

[10.75]

Therefore

[10.76]

10.5. Calculation of fractional derivatives with the implicit derivative

10.5.1. Introduction

We have demonstrated the interest of the infinite state approach for the calculation of the fractional derivative of a function g(t), i.e. the distributed model z_c(ω,t) of the fractional integrator makes it possible to calculate this fractional derivative using the Caputo derivative definition.

Similarly, we can calculate fractional derivatives with the distributed model associated with the Riemann–Liouville derivative.

More surprisingly, we can also use the implicit derivative. Of course, it is not possible to use the closed-loop formulation of the implicit derivative.

Let us recall that the analytical expression of this derivative (see Chapter 8) corresponds to:

[10.77]

where

[10.78]

As we obtain, for α = −n

[10.79]

Let z_I(ω,t) be the distributed variable associated with the implicit derivative:

[10.80]

10.5.2. Fractional derivative of the Heaviside function

Consider the Heaviside function g(t) = H(t + T).

Then

[10.81]

Therefore

[10.82]

and

[10.83]

Thus

[10.84]

As Γ(x + 1) = xΓ(x) (see Appendix A.1.4), we obtain Γ(1 − n) = −nΓ(−n).

Therefore

[10.85]

10.5.3. Fractional derivative of the power function

Consider the power function g(t) = (t + T)^αH(t + T).

Then

[10.86]

Consider the variable change τ = (t + T)

Therefore

[10.87]

and

[10.88]

Then

[10.89]

As

[10.90]

we obtain

[10.91]

Using the convolution lemma (Appendix A.10):

[10.92]

Finally

[10.93]

10.5.4. Fractional derivative of the exponential function

Consider the exponential function g(t) = e^λt.

Therefore

[10.94]

and

[10.95]

Using the results of section 10.2.3, we obtain

[10.96]

Therefore

[10.97]

As

[10.98]

With s = λ, we obtain

[10.99]

10.5.5. Fractional derivative of the sine function

Consider the sine function .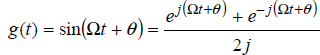

Therefore

[10.100]

and

[10.101]

Then

[10.102]

As

[10.103]

where and , we obtain

[10.104]

Therefore

[10.105]

10.6. Numerical validation of Caputo derivative transients

10.6.1. Introduction

Previous results are essentially theoretical. They do not provide a practical understanding on the computation of the Caputo derivative and particularly of transients caused by initial conditions. Thus, we hereafter illustrate this problem with the sine function.

The objective is to compare the exact fractional derivative and the Caputo derivative computed since t = 0. Thanks to the theoretical values of the corresponding initial conditions, theoretical transients can be computed and compared to the observed ones.

Let us recall:

Sine function: g(t) = sin(Ωt + θ).

Fractional derivative: sin .

Computed Caputo derivative:

Transients:

[10.106]

Let us note that the term related to g(t₀) is a false problem: it represents the amplitude of the jump caused by the truncation of g(t). The corresponding transient can be easily removed by the computation of . Thus, we will only consider the influence of the distributed initial condition z_C(ω,0) .

We have demonstrated: .

The corresponding transient is defined as:

It is compared to

10.6.2. Simulation results

Numerical simulations are performed with:

Riemann–Liouville integration: 1–n = 0.5

Sine function:

Figure 10.1 presents the graphs of and for .

An obvious difference exists between the exact and computed fractional derivatives. It is also obvious that a very long transient is necessary for convergence of the computed derivative.

Figure 10.2 presents the variation of z_C (ω,0) for different values of θ.

These graphs highlight the influence of the lower frequency modes, i.e. the long memory behavior of d(t) .

Figure 10.3 exhibits the graphs of d(t) and d_th(t) for the corresponding values of θ. These graphs are identical: this means that equation [10.106] allows a perfect prediction of transients. The influence of θ is maximum for . On the contrary, fast convergence is provided by θ=0, as the lower frequency modes are close to 0.

A.10. Appendix: convolution lemma

The objective is to express the convolution product

[10.107]

Let

[10.108]

and

[10.109]

Recall that

[10.110]

Then

[10.111]

AS

[10.112]

we obtain

[10.113]