In this book we have referred to causality quite a bit; however, mostly through warnings about interpreting correlation and regression results as reflecting causality. For instance, in Chapter 3 we discussed an example where alcohol drinking and lung cancer rates were correlated with one another, even though alcohol drinking does not cause lung cancer. Here correlation did not imply causality. In fact, it was cigarette smoking that caused lung cancer, but a correlation between cigarette smoking and alcohol drinking produced an apparent relationship between alcohol and lung cancer.

In our discussion of regression, we were on a little firmer ground, since we attempted to use common sense in labeling one variable the dependent variable and the others the explanatory variables. In many cases, because the latter "explained" the former it was reasonable to talk about X "causing" Y. For instance, in our house price example in Chapters 4, 5, 6 and 7, the price of the house was said to be "caused" by the characteristics of the house (e.g. number of bedrooms, number of bathrooms, etc.). However, in our discussion of omitted variable bias in Chapter 6, it became clear that multiple regressions could provide a misleading interpretation of the degree of causality present if important explanatory variables were omitted. Furthermore, there are many regressions in which it is not obvious which variable causes which. For instance, in Chapter 10 (Exercise 10.7), you ran a regression of Y = stock prices in Country A on X = stock prices in Country B. It is possible that stock price movements in Country A cause stock markets to change in Country B (i.e. X causes Y). For instance, if Country A is a big country with an important role in the world economy (e.g. the USA), then a stock market crash in Country A could also cause panic in Country B. However, if Country A and B were neighboring countries (e.g. Thailand and Malaysia) then an event which caused panic in either country could affect both countries. In other words, the causality could run in either direction – or both! Hence, when using the word "cause" with regression or correlation results a great deal of caution has to be taken and common sense has to be used.

However, with time series data we can make slightly stronger statements about causality simply by exploiting the fact that time does not run backward! That is, if event A happens before event B, then it is possible that A is causing B. However, it is not possible that B is causing A. In other words, events in the past can cause events to happen today. Future events cannot.

These intuitive ideas can be investigated through regression models incorporating the notion of Granger causality. The basic idea is that a variable X Granger causes Y if past values of X can help explain Y. Of course, if Granger causality holds this does not guarantee that X causes Y. This is why we say "Granger causality" rather than just "causality". Nevertheless, if past values of X have explanatory power for current values of Y, it at least suggests that X might be causing Y.

Granger causality is only relevant with time series variables. To illustrate the basic concepts we will consider Granger causality between two variables (X and Y) which are both stationary. A nonstationary case, where X and Y have unit roots but are cointegrated, will be mentioned below.

Granger causality in a simple ADL model

Since we have assumed that X and Y are stationary, the discussion of Chapter 10 suggests an ADL model is appropriate. Suppose that the following simple ADL model holds:

This model implies that last period's value of X has explanatory power for the current value of Y. The coefficient β₁ is a measure of the influence of X_t−1 on Y^t. If β₁ = 0, then past values of X have no effect on Y and there is no way that X could Granger cause Y. In other words, if β₁ = 0 then X does not Granger cause Y. An alternative way of expressing this concept is to say that "if β₁ = 0 then past values of X have no explanatory power for Y beyond that provided by past values of Y". Since we know how to estimate the ADL and carry out hypothesis tests, it is simple to test for Granger causality. That is, OLS estimation of the above regression can be conducted using any standard spreadsheet or econometric computer package, and the P-value for the coefficient on X_t−1 examined for significance. If β₁ is statistically significant (e.g. P-value <0.05) then we conclude that X Granger causes Y. Note that the null hypothesis being tested here is H₀: β₁ = 0 which is a hypothesis that Granger causality does not occur. So we should formally refer to the test of β₁ = 0 as a test of Granger non-causality, but we will adopt the more common informal terminology and just refer to this procedure as a Granger causality test.

Granger causality in an ADL model with p and q lags

Of course, the above ADL model is quite restrictive in that it incorporates only one lag of X and Y. In general, we would want to select lag lengths using the methods described in Chapter 10 to work with an ADL(p, q) model of the form:^[74]

Here X Granger causes Y if any or all of β₁,..., β_q are statistically significant. In other words, if X at any time in the past has explanatory power for the current value of Y, then we say that X Granger causes Y. Since we are assuming X and Y do not contain unit roots, OLS regression analysis can be used to estimate this model. The P-values of the individual coefficients can be used to determine whether Granger causality is present. If you were using the 5% level of significance, then if any of the P-values for the coefficients β₁, ..., β_q were less than 0.05, you would conclude that Granger causality is present. If none of the P-values is less than 0.05 then you would conclude that Granger causality is not present.

The strategy outlined above is a useful one that can be carried out quite simply in Excel or any other statistical software package. You are likely to obtain reliable evidence about whether X Granger causes Y by following it. Note, however, that there is formally a more correct – also more complicated – way of carrying out this test. Recall that the null hypothesis tested is formally one of Granger non-causality. That is, X does not Granger cause Y if past values of X have no explanatory power for the current value of Y. Appropriately, then, we want to test the hypothesis H₀: β₁ = β₂ = ... = β_q = 0 and conclude that X Granger causes Y only if the hypothesis is rejected. Note that this test is slightly different from the one proposed in the previous paragraph. That is, a joint test of β₁= β² = ... = β_q = 0 is not exactly the same as q individual tests of β_i = 0 for i = 1, ..., q. We have not discussed how to carry out tests to determine whether several coefficients are jointly equal to zero. For readers interested in such joint tests, Appendix 11.1 offers some practical advice.

However, if you choose to follow the simpler strategy outlined above then you should note the following:

If you find any or all of the coefficients β₁, ..., β_q to be significant using t-statistics or the P-values of individual coefficients, you may safely conclude that X Granger causes Y. If none of these coefficients is significant, it is probably the case that X does not Granger cause Y. However, you are more likely to be wrong if you conclude the latter than if you had used the correct joint test of Granger non-causality.

Example: Do stock price movements in Country A Granger cause stock price movements in Country B?

Monthly data on logged stock prices for Countries A and B is located in data set STOCKPAB.XLS, introduced in Exercise 10.7. If you have done that exercise, you will recall that stock prices in both countries appear to have unit roots, but are not cointegrated. However, the differences of these series are stationary and can be nicely interpreted as stock market returns (exclusive of dividends). We will use these differenced variables to investigate whether stock returns in Country A Granger cause those in Country B.

Table 11.1 contains results from OLS estimation of the regression of ΔY = stock returns in Country A on four lags of itself, four lags of ΔX = stock returns in Country B and a deterministic trend.

Table 11.1. ADL model using stock returns in Country A as the dependent variable.

	Coefficient	Standard error	t-stat	P-value	Lower 95%	Upper 95%
Intercept	−0.751	0.710	−1.058	0.292	−2.156	0.654
ΔYt−1	0.822	0.170	4.850	3.81E – 6	0.486	1.158
ΔYt−2	−0.041	0.186	−0.222	0.825	−0.409	0.326
ΔYt−3	0.142	0.186	0.762	0.448	−0.227	0.511
ΔYt−4	−0.181	0.175	−1.035	0.303	−0.526	0.165
ΔXt−1	−0.016	0.143	−0.114	0.909	−0.299	0.267
ΔXt−2	−0.118	0.143	−0.823	0.412	−0.402	0.166
ΔXt−3	−0.042	0.143	−0.292	0.771	−0.324	0.241
ΔXt−4	0.038	0.142	0.266	0.791	−0.244	0.319
Time	0.030	0.011	2.669	0.009	0.0077	0.052

An examination of the P-values in Table 11.1 indicates that only the deterministic trend and last period's stock returns in Country A have explanatory power for present stock returns in Country A. All of the coefficients on the lags of stock returns in Country B are insignificant. Stock returns in Country B do not seem to Granger cause stock returns in Country A.^[75]

Granger causality with cointegrated variables

Testing for Granger causality among cointegrated variables is very similar to the method outlined above. Remember that, if variables are found to be cointegrated (something which should be investigated using unit root and cointegration tests), then you should work with an error correction model (ECM) involving these variables. In the case where you have two variables, this is given by:

As noted in Chapter 10, this is essentially an ADL model except for the presence of the term λe_t−1. Remember that e_t−1 = Y_t−1 – α – βX_t−1, an estimate of which can be obtained by running a regression of Y on X and saving the residuals. Intuitively, X Granger causes Y if past values of X have explanatory power for current values of Y. Applying this intuition to the ECM, we can see that past values of X appear in the terms ΔX_t−1, ..., ΔX_t-q and e_t−1. This implies that X does not Granger cause Y if ω₁= ... = ω_q = λ = 0. Chapter 10 discussed how we can use two OLS regressions to estimate ECMs, and then use their P-values or confidence intervals to test for causality. Thus, t-statistics and P-values can be used to test for Granger causality in the same way as the stationary case. Also, the F-tests described in Appendix 11.1 can be used to carry out a formal test of H₀: ω₁= ... = ω_q = λ = 0.

In the previous paragraph we described how to test whether X Granger causes Y. Testing whether Y Granger causes X is achieved by reversing the roles that X and Y play in the ECM. One interesting consequence of the Granger Representation Theorem is worth noting here (without the proof). If X and Y are cointegrated then some form of Granger causality must occur. That is, either X must Granger cause Y or Y must Granger cause X (or both).

Exercise 11.3

Use the data on Y = long-term interest rates and X = short term-interest rates in INTERESTRATES.XLS. Assume (perhaps incorrectly in light of Exercise 10.4) that Y and X are cointegrated. Test whether Y Granger causes X. Test whether X Granger causes Y.

Our discussion of Granger causality naturally leads us to an interest in models with several equations and the topic of Vector Autoregressions or VARs. Before discussing their popularity and estimation, we will first define what a VAR is. Initially, we will assume that all variables are stationary. If the original variables have unit roots, then we assume that differences have been taken such that the model includes the changes in the original variables (which do not have unit roots). The end of this section will consider the extension of this case to that of cointegration.

In previous chapters, we used an Excel spreadsheet to produce empirical results. However, even with the single-equation time series models of Chapters 8–10, spreadsheets are somewhat awkward (e.g. creating lagged variables involves extensive copying and pasting of data). When we are working with several equations, it becomes even more difficult. And some of the features introduced (e.g. variance decompositions and impulse responses), are extremely difficult to produce using a spreadsheet. In the following chapter, when considering financial volatility, it becomes yet more difficult to work with a spreadsheet. Accordingly, in the remainder of this book, empirical results will be produced using the computer package Stata. This has good capabilities for working with time series. There are many other good computer packages with similar capabilities (e.g. MicroFit, E-views, etc.). If you plan on working extensively with financial time series, it is a good idea to leave the world of spreadsheets and work with one of these.

When we investigated Granger causality between X and Y, we began with a restricted version of an ADL(p, q) model with Y as the dependent variable. We used it to investigate if X Granger caused Y. We then went on to consider causality in the other direction, which involved switching the roles of X and Y in the ADL; in particular, X became the dependent variable. We can write the two equations as follows:

and

The first of these equations tests whether X Granger causes Y; the second, whether Y Granger causes X. Note that now the coefficients have subscripts indicating which equation they are in. For instance, α₁ is the intercept in the first equation, and α₂ the intercept in the second. Furthermore, the errors now have subscripts to denote the fact that they will be different in the two equations.

These two equations comprise a VAR. A VAR is the extension of the autoregressive (AR) model to the case in which there is more than one variable under study. Remember that the AR model introduced in Chapter 9 involved one dependent variable, Y_t, which depended only on lags of itself (and possibly a deterministic trend). A VAR has more than one dependent variable (e.g. Y and X) and, thus, has more than one equation (e.g. one where Y_t is the dependent variable and one where X_t is). Each equation uses as its explanatory variables lags of all the variables under study (and possibly a deterministic trend).

The two equations above constitute a VAR with two variables. For instance, you can see that in the first equation Y depends on p lags of itself and on q lags of X. The lag lengths, p and q, can be selected using the sequential testing methods discussed in Chapters 8 through 10. However, especially if the VAR has more than two variables, many different lag lengths need to be selected (i.e. one for each variable in each equation). In light of this, it is common to set p = q and use the same lag length for every variable in every equation. The resulting model is known as a VAR(p) model. The following VAR(p) has three variables, Y, X and Z:

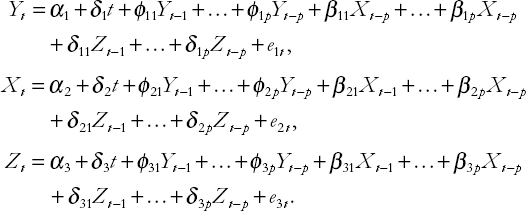
Note that, in addition to an intercept and deterministic trend, each equation contains p lags of all variables in study. VAR(p) models with more than three variables can be obtained in an analogous manner.

Since we assume that all the variables in the VAR(p) are stationary, estimation and testing can be carried out in the standard way. That is, you can obtain estimates of coefficients in each equation using OLS. P-values or t-statistics will then allow you to ascertain whether individual coefficients are significant. You can also use the material covered in Appendix 11.1 to carry out more complicated F-tests. However, as we have stressed above, there are many software packages that allow you to work with VARs in an easier fashion (e.g. Stata, MicroFit or E-views) than any spreadsheet.

VARs are, then, easy to use (especially if you have an appropriate computer software package). However, you may be wondering why we would want to work with such models. One reason has to be Granger causality testing. That is, VARs provide a framework for testing for Granger causality between each set of variables. However, there are many other reasons for why we would want to use them that we should also mention. For instance, a point which we will discuss below is that VARs are often used for forecasting. However, financial researchers also use VARs in many other contexts. This is not a book that discusses financial theory, so exact derivations of the financial theories motivating use of VARs will not be provided. But models involving so-called present value relationships often work with VARs using the (log) dividend-price ratio and dividend growth. VARs have been used to investigate issues relating to the term structure of interest rates (using interest rates of various maturities, interest rate spreads, etc.), intertemporal asset allocation (using returns on various risky assets), the rational valuation formula (using the dividend-price ratio and returns), the interaction of bond and equity markets (using stock and bond return data), etc. Even if you do not understand details of the previous sentences, the point to note is that VARs have been used in a wide variety of financial problems. In the following material, we work through one particularly popular financial VAR.

Forecasting with VARs

We have said relatively little in the book so far about forecasting, despite the fact that this is an important activity of financial researchers. There are two main reasons for omitting the topic. First, the field of forecasting is enormous. Given the huge volume of research and issues to consider, it is impossible to do justice to the field in a book like this.^[78] Second, basic forecasting using the computer is either very easy or very hard, depending on what computer software you have. To be precise, many computer packages (e.g. Stata or MicroFit) have forecasting facilities that are simple to use. Once you have estimated a model (e.g. a VAR or an AR), you can forecast simply by adding an appropriate option to an estimation command. In other words, many computer packages can allow you to undertake basic forecasting without a deep knowledge of the topic. However, spreadsheets such as Excel typically do not have forecasting capabilities for the models used in this book. It is possible to calculate forecasts, but it is awkward, involving extensive typing of formulae.

In light of these issues, we will offer only a brief introduction to some of the practical issues and intuitive ideas relating to forecasting. All our discussion will relate to forecasting with VARs but it is worth noting that the ideas also relate to forecasting with univariate time series models. After all, an AR model is just a VAR with only one equation.

Forecasting is usually done using time series variables. The idea is that you use your observed data to predict what you expect to happen in the future. In more technical terms, you use data for periods t = 1, ..., T to forecast periods T + 1, T + 2, etc.

To provide some intuition for how forecasting is done, consider a VAR(1) involving two variables, Y and X:

and

You cannot observe Y_T+1 but you want to make a guess of what it is likely to be. Using the first equation of the VAR and setting t = T + 1, we obtain an expression for Y_T+1:

This equation cannot be directly used to obtain Y_T+1 since we don't know what e1T+1 is. In words, we don't know what unpredictable shock or surprise will hit the economy next period. Furthermore, we do not know what the coefficients are. However, if we ignore the error term (which cannot be forecast since it is unpredictable) and replace the coefficients by their estimates we obtain a forecast which we denote as Ŷ_T+1:

If you are working in a spreadsheet such as Excel, note that everything in the formula for Ŷ_T+1 can be taken from either the original data or from the output from the regression command. It is conceptually easy just to plug in all the individual numbers (i.e. the estimates of the coefficients and Y_t, X_t and T + 1) into a formula to calculate Ŷ_T+1. A similar strategy can be used to obtain

The previous paragraph described how to forecast one period into the future. We can use the same strategy for two periods, provided that we make one extension. In the one period case, we used X_T Y_T to creat Ŷ_T+1

The above equation can be calculated in a spreadsheet, although somewhat awkwardly.

We can use the general strategy of ignoring the error, replacing coefficients by their estimates and replacing lagged values of variables that are unobserved by forecasts, to obtain forecasts for any number of periods in the future for any VAR(p).

The previous discussion demonstrated how to calculate point estimates of forecasts. Of course, in reality, what actually happens is rarely identical to your forecast. In Chapter 5, we discussed a similar issue. There we pointed out that OLS provides estimates only of coefficients, and that these will not be precisely correct. For this reason, in addition to estimates, we also recommended that you present confidence intervals. These reflect the level of uncertainty about the coefficient estimate. When forecasting, confidence intervals can also be calculated, and these can be quite informative. It is increasingly common for government agencies, for instance, to present confidence intervals for their forecasts. For instance, the Bank of England can be heard on occasion to make statements of the form: "Our forecast of inflation next year is 1.8%. We are 95% confident that it will be between 1.45% and 2.15%". Many computer packages automatically provide confidence intervals and, thus, you do not need to know their precise formula when forecasting. If you are using a spreadsheet, the formula is fairly complicated and it would be awkward to calculate, which is why we do not present it here.

Exercise 11.7

It is recommended that you do this question and others involving forecasting only if you have access to a computer package that is capable of doing forecasts. If you are working with a spreadsheet such as Excel this question will be difficult.

Use the variables er, r, dy, s, dp and rb from VAR.XLS which contains data until February 1987.

1. Using data through December 1986 and a VAR(p) for various values of p (e.g. p = 1, 3, 4) construct forecasts for all variables for January and February 1987. Are these forecasts close to the actual values of these variables in these months?

2. In part (a), data from December 1947 through December 1986 was used to estimate the VAR, which was then used to forecast January and February 1987. Try forecasting for longer and longer periods. For instance, try using data through the end of 1985 to forecast 1986 and 1987 data. Now try using data through the end of 1984 to forecast 1985, 1986 and 1987 data, etc. Discuss your results. Do your results suggest that VARs are better at forecasting a short period ahead than a long period?

Exercise 11.8

Using the data in Exercise 11.6 and the VAR constructed therein, carry out a forecasting exercise for GDP growth for the four included countries. Experiment with various forecast horizons. Does the VAR forecast well?

Vector autoregressions with cointegrated variables

In the preceding discussion of VARs we assumed that all variables are stationary. If some of the original variables have unit roots and are not cointegrated, then the ones with unit roots should be differenced and the resulting stationary variables should be used in the VAR. This covers every case except the one where the variables have unit roots and are cointegrated.

Recall that in this case in the discussion of Granger causality, we recommended that you work with an ECM. The same strategy can be employed here. In particular, instead of working with a vector autoregression (VAR), you should work with a vector error correction model (VECM). Like the VAR, the VECM will have one equation for each variable in the model. In the case of two variables, Y and X, the VECM is:

and

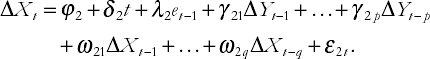
As before, e_t−1 = Y_t−1 – α – βX_t−1. Note that the VECM is the same as a VAR with differenced variables, except for the term e_t−1. An estimate of this error correction variable can be obtained by running an OLS regression of Y on X and saving the residuals. We can then use OLS to estimate ECMs, and P-values and confidence intervals can be obtained. Lag length selection and forecasting can be done in a similar fashion to the VAR, with the slight added complication that forecasts of the error correction term, e_t, must be calculated. However, this is simple using OLS estimates of α and β and replacing the error, e_t, by the residual u_t. Furthermore, many computer packages such as Stata or MicroFit will do estimation, testing and forecasting in VECMs automatically. We have mentioned many financial examples where coin-tegration occurs (see Chapter 10) and will not repeat this material here. However, we will go through an extended example shortly.

Of course, as with any of the models used in this chapter, you should always do unit root tests to see if your variables are stationary or not. If your variables have unit roots, then it is additionally worthwhile to test for cointegration. In the previous chapter, we introduced a test for cointegration based on checking whether there is a unit root in the residuals from the cointegrating regression. However, there is a more popular cointegration test called the Johansen test. To explain this test would require a discussion of concepts beyond the scope of this book. However, if you have a software package (e.g. Stata) which does the Johansen test, then you can use it in practice. Accordingly, we offer a brief intuitive description of this test.

The first thing to note is that it is possible for more than one cointegrating relationship to exist if you are working with several time series variables (all of which you have tested and found to have unit roots). To be precise, if you are working with M variables, then it is possible to have up to M – 1 cointegrating relationships (and, thus, up to M – 1 cointegrating residuals included in the VECM). For instance, in Chapter 10 we mentioned a financial theory arguing that the cay variables (consumption, assets and income) are cointegrated. As we shall see below, there probably is just one cointegrating relationship between these variables. That is, c, a and y all have unit roots, but c_t – α – β₁a_t – β₂Y_t is stationary. However, in theory it would have been possible for there to be two cointegrating relationships (e.g. if c_t – y_t and a_t – y_t were both stationary). Thus, it is often of interest to test, not simply for whether coin-tegrating is present or not, but for the number of cointegrating relationships.

The Johansen test can be used to test for the number of cointegrating relationships using VECMs. For reasons we will not explain, the "number of cointegrating relationships" is referred to as the "cointegrating rank". The details of the Johansen test statistic are quite complicated. However, like any hypothesis test, you can compare the test statistic to a critical value and, if the test statistic is greater than the critical value, you reject the hypothesis being tested. Fortunately, many software packages (e.g. Stata) will calculate all these numbers for you. We will see how this works in the following example.

Before working through this example, note that when you do the Johansen test you have to specify the lag length and the deterministic trend term. The former we have discussed before. That is, lag length can be selected using information criteria as described above. With VECMs it is possible simply to put an intercept and/or deterministic trend in the model (as we have done in the equations above – see the terms with coefficients ϕ and Δ on them). However, it is also possible to put an intercept and/or deterministic trend actually in the cointegrating residual (e.g. if you say c_t – α – β₁a_t – β₂Y_t is the cointegrating residual you are putting an intercept into it). The Johansen test varies slightly depending on the exact configuration of deterministic terms you use, so you will be asked to specify these before doing the Johansen test.

Example: Consumption, aggregate wealth and expected stock returns

In an influential paper in the Journal of Finance in 2001, "Consumption, aggregate wealth and expected stock returns", Lettau and Ludvigson present finan-cial theory arguing that the cay variables should be cointegrated and the cointegrating residual should be able to predict excess stock returns. They then present empirical evidence in favor of their theory. In a subsequent paper ("Understanding trend and cycle in asset values: Reevaluating the wealth effect on consumption" in the American Economic Review in 2004), using the cay data, they build on this argument using VECMs and present variance decompositions which shed light on their theory (we will discuss the variance decomposition in Appendix 11.2).

We will not repeat the theory (nor will we consider the forecasting aspect of their paper). However, we stress that their work uses all the tools we have been developing in this chapter: testing for cointegration, estimation of a VECM and variance decompositions. We will investigate the presence of cointegration here using US data from 1951Q4 through 2003Q1 on c which is consumption (formally it is the log of real per capita expenditures on nondurables and services excluding shoes and clothing); a which is our measure of assets (formally it is the log of a measure of real per capita household net worth including all finan-cial and household wealth as well as consumer durables); and y which is the log of after-tax labor income. This data is available in CAY.XLS.

Unit root tests indicate that all of these variables have unit roots. If we do the Johansen test using a lag length of one and restricting the deterministic term to allow for intercepts only (i.e. no deterministic trends such as those with co-efficients Δ in the previous equations are allowed for), we get the results in Table (using Stata).

Table 11.5. Johansen test for cointegration using cay data.

Rank	Trace statistic	5% Critical value
0	37.27	29.68
1	6.93	15.41
2	0.95	3.76

How should you interpret this table? Note first that "Trace statistic" is the name of the test statistic used in the Johansen test and "Rank" indicates the number of cointegrating relationships with Rank = 0 indicating cointegration is not present. With the Johansen test, the hypothesis being tested is always a certain cointegrating rank with the alternative hypothesis being that cointegrat-ing rank is greater than hypothesis being tested.

If we compare the Trace statistic to its critical value we can see, for Rank = 0, that the test statistic is greater than the 5% critical value. This means we can reject the hypotheses that Rank = 0 at the 5% level of significance (in favor of the hypothesis that Rank ≥ 1). Thus, the Johansen test indicates that cointegra-tion is present. However, if we look at the row with Rank = 1 we see that the test statistic is less than the critical value. Thus, we can accept that hypothesis that Rank = 1 (and are not finding evidence in favor of Rank ≥ 2). Thus, we are finding evidence that Rank = 1 (with this evidence, the information in the last row of the table is not relevant). As expected by Lettau and Ludvigson, we are finding evidence that one cointegrating relationship exists in this data set.

Armed with the information that one cointegrating relationship seems to exist, you can then (following Lettau and Ludvigson) calculate the cointegrat-ing residual and investigate whether this has predictive power for expected stock returns. Alternatively, you could use this information to specify a VECM with one cointegrating relationship (and, thus, one error correction term). Following Lettau and Ludvigson, you could then do a variance decomposition to investigate further issues in financial economics (see Appendix 11.2 for more details).

Exercise 11.9

For this question, use the data on spot and forward exchange rates in FOREX.XLS.

1. Starting with _pmax = 4, select a lag length for the VECM and estimate the VECM.

2. Using the VECM from part (a), carry out a forecasting exercise. Experiment with various forecast horizons. Does the VECM forecast well?

Exercise 11.10

Use the data on Y = long-term interest rates and X = short-term interest rates in INTERESTRATES.XLS.

1. Assume (perhaps incorrectly in light of Exercise 10.4) that Y and X are coin-tegrated. Repeat the steps in Exercise 11.9 to carry out a forecasting exercise.

2. Now assume that Y and X have unit roots but are not cointegrated. Construct a VAR using differenced data (i.e. ΔY and ΔX) and carry out a forecasting exercise.

3. Compare results from part (a) and (b). What effect does assuming (possibly incorrectly) cointegration have on forecasting performance?

Exercise 11.11

Use the data from CAY.XLS.

1. Test for unit roots in all the variables in this data set.

2. Test for cointegration in these variables using the Engle–Granger test from Chapter 10. Does this test yield the same finding as the Johansen test?

3. In Table 11.5, the Johansen test was done with one lag. Does the finding of the Johansen test differ if you use two lags? Three lags? Four lags?

4. Discuss the issue of lag length selection in this data set using information criteria.

In Chapters 5 and 6 we discussed the F-statistic, which was used for testing the hypothesis R₂ = 0 in the multiple regression model:

We discussed how this was equivalent to testing H₀: β₁ = ... = β_k = 0 (i.e. whether all the regression coefficients are jointly equal to zero). We also discussed testing the significance of individual coefficients using t-statistics or P-values.

However, we have no tools for testing intermediate cases (e.g. in the case k = 4, we might be interested in testing H₀: β₁ = β₂ = 0). Such cases arose in our discussion of Granger causality (e.g. we had a regression model with four lags of stock returns in Country A, four lags of stock returns in Country B and a deterministic trend and we were interested in testing whether the coefficients on the four lags of stock returns in Country B were all zero). The purpose of this appendix is to describe a procedure and a rough rule of thumb for carrying out these kind of tests.

The F-statistic described in Chapter 5 is more properly referred to as an F-statistic since it is only one of an enormous class of test statistics that take their critical values from statistical tables for the F-distribution. In this book, as you know by now, we have provided little statistical theory, and do not describe how to use statistical tables. However, if you plan to do much work in Granger causality testing, you are well-advised to study a basic statistics or econometrics book to learn more about the statistical underpinnings of hypothesis testing.

To understand the basic F-testing procedure we introduce a distinction between unrestricted and restricted regression models. That is, most hypotheses you would want to test place restrictions on the model. Hence, we can distinguish between the regression with the restrictions imposed and the regression without. For instance, if the unrestricted regression model is:

and you wish to test the hypothesis H₀: β₂ = β₄ = 0, then the restricted regression model is:

The general strategy of hypothesis testing is that a test statistic is first calculated and then compared to a critical value. If the test statistic is greater than the critical value then you reject the hypothesis; otherwise, you accept the hypothesis. In short, there are always two components to a hypothesis testing procedure: a test statistic and a critical value.

Here the test statistic is usually called the F-statistic and is given by:

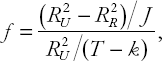
where R²_U are the R²_R from the unrestricted and restricted regression models, respectively. J is the number of restrictions (e.g. J = 2 in our example since β₂ = 0 and β₄ = 0 are two restrictions). T is the number of observations and k is the number of explanatory variables in the unrestricted regression (including the intercept).

Note that the F-statistic can be obtained by running the unrestricted and restricted regressions (e.g. regress Y on X₁, X₂, X₃ and X₄ to get R_U, then regress Y on X₁ and X₃ to get R²_R) and then calculating the above formula using a spreadsheet or calculator. Many specialist statistics packages (e.g. Stata or MicroFit) will calculate the F-statistic for you automatically if you specify the hypothesis being tested.

Obtaining the critical value with which to compare the F-statistic is a more problematic procedure (although some software packages will provide a P-value automatically). Formally, the critical value depends on T – k and J. Most econometrics or statistics textbooks will contain statistical tables for the F-distribution which will provide the relevant critical values. Table 11.6 contains critical values which you may use as a rough rule of thumb if T – k is large.

For instance, if you have a large number of observations, are testing J = 2 restrictions (i.e. β₂ = 0 and β₄ = 0), and you want to use the 5% level of significance, then you will use a critical value of 3.00 with which to compare the F-statistic.

To aid in interpretation, note that the case J = 1 has not been included since testing only one restriction is something that the t-statistic already does. Note also that the critical values always get smaller as the number of restrictions increases. This fact can be used to approximate critical values for values of J that are not included in Table 11.6.

For instance, the critical value for testing J = 7 restrictions will lie somewhere between the critical values for the restrictions J = 5 and J = 10 given in Table 11.6. In many cases, knowing that the correct critical value lies between two numbers will be enough for you to decide whether to accept or reject the hypothesis. Consequently, even though Table 11.6 does not include every possible value for J, you may be able to use it if J differs from those above.

Formally, the critical values in the previous table are correct if T – k is equal to infinity. The correct critical values for T – k > 100 are quite close to these. To give you an idea of how bad an error may be made if T – k < 100, examine Table 11.7, which gives the correct critical values if T – k = 40.

As you can see, these critical values are all somewhat larger than those given in the table for T – k equal to infinity. You may want to use these if your value for T – k is about 40. However, we also report them here to get some idea of the error that may result if you use the large sample critical values. For instance, if J = 2, T – k = 40 and you obtain an F-statistic of 4 then using either table is fine: both state that the hypothesis should be rejected at the 5% level of significance. However, if the F-statistic were 3.1 you would incorrectly reject it using the large sample table.

In summary, you can safely use the methods and tables given in this appendix in the following cases:

Generally speaking, so long as you have either a large number of data points or your data does not fall into one of these "borderline" cases, you should not be led astray by using the methods outlined in this appendix.

Example: Do stock returns in Country A Granger cause stock returns in Country B? (continued from page 187)

In the body of this chapter, we carried out Granger causality tests using stock returns in two countries. We found that stock returns in Country B did not Granger cause stock returns in Country A, but that stock returns in Country A did Granger cause stock returns in Country B. Here, we will investigate whether these conclusions still hold by carrying out the correct F-tests for Granger causality.

Consider first whether stock returns in Country B Granger cause stock returns in Country A. In the body of the chapter we use the following unrestricted model where Y = stock returns in Country A and X = stock returns in Country B:

T = 128^[79] and k = 10 (i.e p = q = 4 plus we have the deterministic trend in the model). OLS estimation of this model yields R²_U = 0.616.

The hypothesis that Granger causality does not occur is H₀: β₁ = ... = β₄ = 0 which involves 4 restrictions; hence J = 4. The restricted regression model is:

OLS estimation of this model yields R²_R = 0.613.

Using these numbers we calculate that the F-statistic is 0.145. Since T – k = 118 and is large, we can compare 0.145 to a critical value of 2.37. Since 0.145 < 2.37 we cannot reject the hypothesis at the 5% level of significance. Accordingly, we accept the hypothesis that stock returns in Country B do not Granger cause stock returns in Country A.

To test whether stock returns in Country A Granger cause stock returns in Country B we repeat the steps above except that now the dependent variable refers to Country B and the explanatory variable refers to Country A. If we use OLS to estimate the restricted and unrestricted regressions, we obtain R²_U = 0.605 and R²_R = 0.532. Note that the other elements in the formula for the F-statistic do not change. Plugging these numbers into the equation for the F-statistic yields f = 33.412, which is much larger than either the 1% or 5% critical values. In this case, we can safely reject the hypothesis that β₁ = ... = β₄ = 0 and conclude that stock returns in Country A do Granger cause stock returns in Country B.

Note that the findings that stock returns in Country B do not Granger cause stock returns in Country A but that stock returns in Country A do Granger cause stock returns in Country B, are exactly the same as given in the body of the chapter. In general, however, the results from joint hypothesis testing may differ from individually testing each hypothesis.

As the examples in this chapter have shown, variance decompositions are popular in finance. To fully understand what they are would require concepts beyond the scope of this book (e.g. matrix algebra). However, some statistical software packages allow you to calculate variance decompositions in a fairly straightforward manner. Accordingly, with a good software package, some intuition and a thorough understanding of the financial problem you are working on, it should be possible for you to do variance decompositions in practice even without matrix algebra. Furthermore, some intuition should help you to read and understand empirical results presented in many papers in finance. The purpose of this appendix is to provide such intuition about variance decompositions.

In the example "What moves the stock and bond markets?" discussed in the body of the chapter, recall that the underlying paper developed a model where unexpected movements in excess stock returns should depend on changes in expectations about future dividend flows and future excess stock returns (among other things). A key question was which of these various factors is most important in driving the stock markets. The authors' model is much more sophisticated, but a simplified version could be written as:

uer = newsd + newser

where uer is the component capturing unexpected movements in expected returns, newsd is the component reflecting future news about dividends and newser is the component reflecting future news about expected returns. Do not worry where these components come from other than to note that they can be calculated using the data and the VAR coefficients.

Financial researchers are interested in the relative roles played by newsd and newser in explaining uer. One way of measuring this is through variances. Remember (see Chapter 2) that, as its name suggests, the variance is a measure of the variability in a variable. We motivated the regression R² (see Chapter 4) as measuring the proportion of the variability in the dependent variable that could be explained by the explanatory variables. Here we can do something similar. That is, we can measure the proportion of the variability of uer that can be explained by newsd (or newser) and use this as a measure of the role played by newsd (or newser) in explaining uer. This is a simple example of a variance decomposition.

Formally, if newsd and newser are independent of one another^[80] we have:

var(uer) = var(newsd) + var(newser).

If we divide both side of this equation by var(uer) then we get:

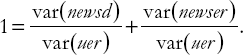
The two terms on the right-hand side of this equation can be interpreted as measures of the relative roles of news about dividends and news about excess returns. For instance, the first of them can be interpreted as: "The proportion of the variability in unexpected excess returns that can be explained by news about future dividends is var(newsd)/var(uer)" and it can be calculated using the VAR.

The Lettau and Ludgvigson example using the cay data allows us to describe another common sort of variance decomposition. The empirical puzzle this paper is investigating is why the huge swings in stock markets over the last decade (e.g. the dot.com boom followed by the bust) did not have larger effects on consumption. The VECM they estimate, along with a variance decomposition, indicates a sensible story: that many fluctuations in the stock market were treated by households as being transitory and these did not have large effects on their consumption. Only permanent changes in wealth affected consumption. This kind of variance decomposition is a so-called "permanent-transitory decomposition".

Remember (see Chapter 9) that unit root variables have a long memory property. Errors in unit root variables tend to have permanent effects. However, the cointegrating error is, by definition, stationary. This can be interpreted as implying the cointegrating error will have only a transitory effect on any of the variables. In a VECM, our variables have unit roots in them, but the cointegrating error is stationary. Thus, it has some errors which have permanent effects and others which have transitory effects. Using the VECM, you can figure out these permanent and transitory components and do a variance decomposition in the same way as described above.

That is, a simplified version of such a model would imply:

a = permanent + transitory,

where permanent and transitory are the permanent and transitory components of assets (denoted by a, which includes stock market investments). As before we can take variances of both sides of the equation, divide by the variance of assets to get:

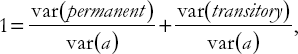
and then use var(permanent)/var(a) as a measure of the role of permanent shocks in driving fluctuations in assets.

These two examples are meant to give you an intuition about what variance decompositions are all about and how they are used in practice. To develop a deeper understanding, you will have to do additional reading in a textbook which uses more sophisticated mathematics than this one. For instance, Quantitative Financial Economics (Second edition) by Cuthbertson and Nitzsche (published by John Wiley & Sons, Ltd) has a discussion of variance decompositions on pages 296–302.