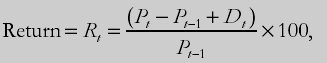Most applications in finance are concerned with the analysis of time series data. However, most of the examples in Chapters 3 to 7 used cross-sectional data. This allowed us to build up the basic ideas underlying regression, including statistical concepts such as hypothesis testing and confidence intervals, in a simple manner. When working with time series variables, knowledge of such ideas is essential. However, some additional issues arise when working with time series data. The purpose of this chapter is to offer an introduction to these issues and to familiarize the reader with some concepts and notation used with time series models. After this introductory material, we take one step away in the direction of developing the models and methods that are used with financial time series.
The goal of the researcher working with time series data does not differ too much from that of the researcher working with cross-sectional data: both aim to develop a regression relating a dependent variable to some explanatory variables. However, the analyst using time series data will face two problems that the analyst using cross-sectional data will not encounter: (1) one time series variable can influence another with a time lag; and (2) if the variables are nonstationary, a problem known as spurious regression may arise.
At this stage, you are not expected to understand the second of these problems. The terms nonstationary, stationary and spurious regression will be discussed in detail in subsequent chapters of this book. But keep in mind this general rule: If you have nonstationary time series variables then you should not include them in a regression model. The appropriate route is to transform the variables before running a regression in order to make them stationary. There is one exception to this general rule, which we shall discuss later, and which occurs where the variables in a regression model are cointegrated. We will elaborate on what we mean by these terms later. If you find it confusing for them to be introduced now without definitions, just think in the following terms: Some problems arise with time series data that do not arise with cross-sectional data. These problems make it risky to naively use multiple regression in the manner of Chapters 4 to 7. The purpose of this and the following chapters is to show you how to correctly modify regression techniques with time series data.
In this chapter, we will assume all variables in the regression are stationary. The next chapter explains what this means. At this point, note only that the second problem will not occur and that we can therefore focus on the first problem.
The first problem can be understood intuitively with some simple examples. When we estimate a regression model we are interested in measuring the effect of one or more explanatory variables on the dependent variable. In the case of time series data we have to be very careful in our choice of explanatory variables since their effect on the dependent variable may take time to manifest itself.
For instance, in previous chapters we worked with cross-sectional regressions involving company data. In one example, our dependent variable was market capitalization and explanatory variables were company characteristics (e.g. income, assets, sales, etc.). In another, our dependent variable was executive compensation which we sought to explain using variables like profits and debt. However, all our dependent and explanatory variables referred to the same year. In practice, this may not be reasonable. The value that the stock market places on a firm might depend not only on current income, but on historical income as well. After all, current income could be affected by short-term factors and may not be a totally reliable guide to long-run performance. For instance, an ice cream company might suffer a short-term fall in income due to an unusually cold summer. Looking at data based on this one unusual event could give an unreliable view of the long-run potential of this company. Similar considerations hold for our executive compensation example where compensation might be determined not only on current profits, but also on past profits. In short, there are good reasons to include not only current values of explanatory variables, but also past values.
To put this concept in the language of regression, we say that the value of the dependent variable at a given point in time should depend not only on the value of the explanatory variable at that time period, but also on values of the explanatory variable in the past. A simple model to incorporate such dynamic effects has the form:[40]
This is precisely the same as the multiple regression model in Chapter 6, with the exception that the "explanatory variables" are not entirely different (e.g. lot size, number of bathrooms, number of bedrooms, etc.) but are just one explanatory variable that is observed at different time periods. In this model, the right-hand side variables are referred to as lagged variables and q, the lag order or lag length. We will focus on the case where the dependent variable depends on one explanatory variable and its lags. However, everything we say can be generalized in a straightforward fashion to several explanatory variables, all having time lags. Since the effect of the explanatory variable on the dependent variable does not happen all at once, but rather is distributed over several time periods, this model is sometimes referred to as a distributed lag model.
Since the regression model with time lags is a regression model, everything we said in Chapters 4 to 6 about regression is relevant here. For instance, computer packages like Excel can provide OLS estimates of coefficients, confidence intervals and P-values for testing whether coefficients are equal to zero. Coefficients can be interpreted as measures of the influence of the explanatory variable on the dependent variable. In this case, we have to be careful with timing. For instance, we interpret results as: "β2 measures the effect of the explanatory variable two periods ago on the dependent variable, ceteris paribus". Other than these minor differences, both the statistical methods and interpretation are very similar to the tools we described previously. Nevertheless, it is worth discussing this class of models separately, as it will help us to develop some time series terminology and introduce ideas that we will build on in subsequent chapters.
Before turning to an illustrative example of how to work with regression models with lagged variables, we will make two brief detours. One of these describes what lagged variables are and how to calculate them in a spreadsheet software package. The other clarifies the notation that will be used in this and subsequent chapters.
The concept of a lagged variable is fundamental to time series data, so we will describe in some detail what it means and how to construct and work with lagged variables on a computer spreadsheet. We do this mostly because it really helps to understand what lagged variables are by seeing how they are constructed. However, we partly work with a spreadsheet to begin to show you that it is awkward to work with spreadsheets when you have time series variables. It is possible to do almost everything in this book (with the exception of models involving volatility which we will discuss later) with a spreadsheet such as Excel. However, it is much more convenient to use a specialized computer package for financial econometrics such as E-views, MicroFit or Stata.
Suppose we have time series data for t = 1, ..., T periods on a variable X. As before, we denote individual observations by Xt for t = 1, ..., T. Consider creating a new variable W which has observations Wt = Xt for t = 2, ..., T and a new variable Z which has observations Zt = Xt−1 for t = 2, ..., T. Why do we write t = 2, ..., T instead of t = 1, ..., T ? If we had written t = 1, ..., T then the first observation of the variable Z, Z1, would be set equal to X0. Yet we do not know what X0 is since variable X is observed only from t = 1, ..., T. In other words, W and Z have only T – 1 observations. Note also that had we written Zt = Xt−2 then the new variable Z would have observations from t = 3, ..., T and only T – 2 observations.
The new variables W and Z both have T – 1 observations. If we imagine W and Z as two columns containing T – 1 numbers each (as in an Excel spreadsheet), we can see that the first element of W will be X2 and the first element of Z will be X1. The second element of W and Z will be X3 and X2, etc. In words, we say that W contains X and Z contains X one period ago or lagged one period. In general, we can create variables "X lagged one period – or "lagged X" for short – "X lagged two periods" – or, in general, "X lagged j periods".
You can think of "X ", "X lagged one period", "X lagged two periods", etc. as different explanatory variables in the same way as you can of "house price", "lot size", or "number of bedrooms" as different explanatory variables.
Note, however, that if you want to include several explanatory variables in a multiple regression model, all variables must have the same number of observations. Let us consider the implication of this statement, in the present context. Suppose a regression includes X = the interest rate lagged j periods as an explanatory variable. If you began with t = 1, ..., T observations on the interest rate, then X lagged j periods will contain only T – j observations. Since this variable contains only T – j observations you must make sure that all the other variables in the model also contain exactly T – j observations. In words, each variable in a time series regression must contain the number of observations equal to T minus the maximum number of lags that any variable has.
Many of the more sophisticated statistical software packages (e.g. E-views, Stata or MicroFit,) will create lagged variables automatically with a simple command, but not most spreadsheet packages like Excel. This is a key reason why, when working with time series data, you might want to learn such a software package and not work with a spreadsheet such as Excel. When working with a spreadsheet you will have to create lagged variables yourself before running a regression involving them. A brief explanation of how to do this will be both useful when you work with spreadsheets and will provide a practical way to illustrate the material above.
As an example, suppose we have 10 observations on variables Y and X (i.e. t = 1, ..., 10) and we wish to run a regression model that includes X, lagged X, X lagged two periods and X lagged 3 periods. That is, we wish to estimate the regression model:
Table 8.1 shows how the data would look in a spreadsheet format.
Note that spreadsheets label each observation by row and column, as in Table 8.1. Each column contains a variable (e.g. Column C contains the variable X lagged one period) and each row contains observations. Note that each of the variables contains 7 observations, which is T minus maximum number of lags (i.e. 10 − 3 = 7). Looking across any row (e.g. Row 4) you can see that: (a) Y and X contain data at a particular point in time (e.g. Y7 and X7 or t = 7); (b) X lagged will contain the observation from one period previously (e.g. X6); (c) X lagged two periods will contain the observation from two periods previously (e.g. X5); and (d) X lagged three periods will contain the observation from three periods previously (e.g. X4).
Table 8.1. Creating lagged variables.
Column A Y | Column B X | Column B X lagged one period | Column D X lagged two periods | Column E X lagged three periods | |
|---|---|---|---|---|---|
Row 1 | Y4 | X4 | X3 | X2 | X1 |
Row 2 | Y5 | X5 | X4 | X3 | X2 |
Row 3 | Y6 | X6 | X5 | X4 | X3 |
Row 4 | Y7 | X7 | X6 | X5 | X4 |
Row 5 | Y8 | X8 | X7 | X6 | X5 |
Row 6 | Y9 | X9 | X8 | X7 | X6 |
Row 7 | Y10 | X10 | X9 | X8 | X7 |
You can create this table in Excel. First use the Cut/Paste commands in the spreadsheet containing the original data on Y and X (i.e. the one that contained the 10 original observations on the two variables) to create a spreadsheet that looks like Table 8.1. Then run the regression by using the Excel regression menu in the standard way and specifying A1:A7 in the box labeled "Input Y-range", and B1:E7 in the box labeled "Input X-range".
This section on lagged variables may seem of little direct relevance for understanding and interpreting results. However, it is important not to forget this material if you are at the computer, working with a spreadsheet.
It is also important to make sure that our notation is clear. Consider a variable, X(e.g. executive compensation). After collecting data on X we will have observations Xi for i = 1, ..., N for cross-sectional data and Xt for t = 1, ..., T for time series data (see Chapter 2).
In other words, X is a generic notation for the variable and Xi or Xt indicates a particular observation of the variable (e.g. Xi = executive compensation in the ith company or Xt = executive compensation in the tth time period). In our discussion of regression in Chapters 4 to 7 we often wrote equations of the form:
Expressed in words, the above implies that "the dependent variable Y depends on the explanatory variable X in a linear fashion". When we have actual data we can write,
Expressed in words, "observation i of Y depends on observation i of X." For instance, "executive compensation in company i depends on profits in company i". Both of these equations are perfectly correct. But, since the subscript i in the latter equation is a little obvious (e.g. it is obvious that executive compensation in Company A depends on profits in Company A — it certainly will not depend on profits in Company B), you often see the i subscript dropped out from the latter equation for simplicity's sake.
We complicated our notation even more in Chapter 6 in our discussion of multiple regression, in which X1, X2, ..., Xk were k different explanatory variables. Here the subscript on X indicated which explanatory variable we were referring to, not which observation. In the rare cases when we wanted to be more explicit we wrote, for example, X2i, to indicate the ith observation of the second explanatory variable. However, since it is usually obvious in the multiple regression case that Yi (e.g. executive compensation in company i) depends on X1i(e.g. profits in company i) and on X2i(e.g. change in sales in company i), the i subscript was often dropped from the equation.
In short, throughout this book our subscript notation, which distinguishes between a variable and a particular observation of a variable, has been a little loose. This is okay (and common in textbooks), since the meaning is fairly obvious from the context and the alternative is to clutter up equations with numerous subscripts. In the time series chapters of this book, we will show similar informality, using the notation Xt-j to indicate both a particular observation (e.g. if t = 1968 and j = 3, then Xt-j is the value of variable X in 1965) and the variable X lagged j periods. It will be obvious from the context which is which. Quite frankly, in virtually any equation in this book it will not matter which way you interpret it.
Example: Long-run prediction of a stock market price index
The issue of whether stock market returns are predictable is a very important one in finance. After all, if an investor could predict stock market behavior, she could make a lot of money. Of course, in practice, predicting which stocks will increase in value tomorrow is extremely difficult. We will return to the issue of short-run prediction of stock prices in the next chapter, when we discuss random walk behavior. In this example, we focus on long-run prediction of the stock market.
This is not a book on financial theory and, hence, we will not describe the theoretical model which motivates the regressions we will run in any detail. In general, many researchers have studied the relationship between stock prices, dividends and returns. The basic equation relating these three concepts was given in Chapter 2 as:
where Rt is the return on holding a share from period t – 1 through t, Pt is the price of the stock at the end of period t and Dt is the dividend earned between period t – 1 and t. This basic relationship, along with various assumptions about how these variables might evolve in the future, can be used to develop various theoretical financial models.[41] A particularly useful such model implies that the ratio of dividends to stock price should have some predictive power for future returns, particularly at long horizons.
How does such a theory relate to our regression model with lagged explanatory variables? It implies a model where the dependent variable (Y) is the total return on the stock market index over a future period (let us say h months, where h denotes the forecasting horizon) but the explanatory variable (X) is the current dividend-price ratio. Thus, we have a regression model of the form:
where the dependent variable, Yt+b, is calculated using the returns Rt+1, Rt+2, ..., Rt+b. Or, equivalently, we can write this regression as:
This is a specialized version of our general regression with lagged explanatory variables described above.
The theory developed by financial researchers suggests that the explanatory power for this regression should be poor at short horizons (e.g. b = 1 or 2) but improve at longer horizons. The file LONGRUN.XLS contains monthly data for a hundred years on Y = 12 month returns (i.e. b = 12) from a stock market along with X the dividend-price ratio (12 months ago).
Table 8.2 contains results from the regression. Since the P-value for the coefficient on Xt−12 is less than 0.05, the coefficient is significant. We can conclude that the dividend-price ratio does have explanatory power for 12 month returns. This supports the theory that the dividend-price ratio does have some predictive power for long-run returns. However, we also find R2 = 0.019 indicating that this predictive power is weak (although it is statistically significant). Only 1.9% of the variation in 12 month returns can be explained by the dividend-price ratio.
Example: The effect of bad news on market capitalization
The share price of a company can be sensitive to bad news. Suppose that Company B is in an industry which is particularly sensitive to the price of oil. If the price of oil goes up, then the profits of Company B will tend to go down and some investors, anticipating this, will sell their shares in Company B driving its price (and market capitalization) down. However, this effect might not happen immediately. For instance, if Company B holds large inventories produced with cheap oil, it can sell these and maintain its profits for a while. But when new production is required, the higher oil price will lower profits. Furthermore, the effect of the oil price might not last forever, since Company B also has some flexibility in its production process and can gradually adjust to higher oil prices. Hence, news about the oil price should affect the market capitalization of Company B, but the effect might not happen immediately and might not last too long.
The file BADNEWS.XLS contains data collected on a monthly basis over five years (i.e. 60 months) on the following variables:
Y = market capitalization of Company B ($000)
X = the price of oil (dollars per barrel).[42]
Since this is time series data[43] and it is likely that previous months' news about the oil price will affect current market capitalization, it is necessary to include lags of X in the regression. Table 8.3 contains OLS estimates of the coefficients in a distributed lag model in which market capitalization is allowed to depend on present news about the oil price and news up to four months ago. That is,
What can we conclude about the effect of news about the oil price on Company B's market capitalization? Increasing the oil price by one dollar per barrel in a given month is associated with:
Table 8.3. Regression results for the effect of news on market capitalization example.
Coefficient | Standard error | t-stat | P-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
Intercept | 92001.51 | 2001.71 | 45.96 | 5.86E – 42 | 87978.91 | 96024.11 |
Xt | −145.00 | 47.62 | −3.04 | 0.0037 | −240.70 | −49.30 |
Xt-1 | −462.14 | 47.66 | −9.70 | 5.52E – 13 | −557.91 | −366.38 |
Xt-2 | −424.47 | 46.21 | −9.19 | 3.12E – 12 | −517.33 | −331.62 |
Xt-3 | −199.55 | 47.76 | −4.18 | 0.00012 | −295.52 | −103.58 |
Xt−4 | −36.90 | 47.45 | −0.78 | 0.44 | −132.25 | 58.45 |
An immediate reduction in market capitalization of $145,000, ceteris paribus.
A reduction in market capitalization of $462,140 one month later, ceteris paribus.
A reduction in market capitalization of $424,470 two onths later, ceteris paribus.
A reduction in market capitalization of $199,550 three months later, ceteris paribus.
A reduction of market capitalization of $36,900 four months later, ceteris paribus.
Confidence intervals can be interpreted in the standard way. For instance, we are 95% confident that the immediate reduction in market capitalization is at least $49,300 and at most $240,700, ceteris paribus.
To provide some intuition about what the ceteris paribus condition implies in this context note that, for example, we can also express the second of these statements as: "Increasing the oil price by one dollar in a given month will tend to reduce market capitalization in the following month by $462,120, assuming that no other change in the oil price occurs."
If we examine the statistical results in the preceding table, we can see that all of the coefficients are statistically significant, except for β4. The P-value for this last coefficient is 0.44 which is not less than 0.05. Also we note that the confidence interval for β4 includes zero. Hence we cannot reject the hypothesis that β4 = 0. In words, we cannot reject the hypothesis that changes in the oil price four months ago have no effect on current market capitalization.
In general the effect of changes in the oil price on market capitalization exhibits a hump-shaped pattern over time: the immediate effect is fairly small ($145,000). The effect then increases to over $400,000 for each of the two subsequent months, falls to roughly $200,000 three months later, and then drops to about zero four months later. If we add up the effects of an increase of one dollar in the oil price in each period (i.e. $145,000 + $462,140 + $424,470 + $199,550 + $36,900 = $1,268,060)[44] we receive a measure of the total effect of this increase on market capitalization. In other words, we can say that: "After four months, the effect of adding one dollar to the price of oil is to decrease market capitalization by $1,268,060".
By calculating this total effect and examining the pattern of the coefficients over time, the company and the investor gain important information. Such results, however, assume that the distributed lag model is not missing any explanatory variables. For instance, we are implicitly assuming that Xt−5 has no effect on current market capitalization. If this assumption is incorrect, our estimates of the total effect of a change in oil prices may be incorrect. This issue relates closely to the problem of omitted variables bias discussed in Chapter 6, and emphasizes the importance of correct choice of lag length (i.e. q in the distributed lag model), a topic to which we now turn.
When working with distributed lag models, we rarely know a priori exactly how many lags we should include. In the previous example, why did we assume that market capitalization depends on movements in the oil price up to four months ago? Why not three or six or even eight? That is, unlike most of the regression models considered in Chapters 4 to 7, we don't know which explanatory variables in a distributed lag model belong in the regression before we actually sit down at the computer and start working with the data. Appropriately, the issue of lag length selection becomes a databased one where we use statistical means to decide how many lags to include.
There are many different approaches to lag length selection in the econometrics literature. Here we outline a common one that does not require any new statistical techniques beyond those developed in Chapter 5. This method uses t-tests for whether β q = 0 to decide lag length. A common strategy is to: (a) Begin with a fairly large lag length, [45] qmax, and test whether the coefficient on the maximum lag is equal to zero (i.e. test whether βq max = 0). (b) If it is, drop the highest lag and re-estimate the model with maximum lag equal to qmax – 1. (c) If you find βqmax−1 = 0 in this new regression, then lower the lag order by one and re-estimate the model. (d) Keep on dropping the lag order by one and re-estimating the model until you reject the hypothesis that the coefficient on the longest lag is equal to zero.
This informal description of lag length selection can be formalized in the following series of steps:
Step 1. Choose the maximum possible lag length, qmax, that seems reasonable to you.
Step 2. Estimate the distributed lag model:
If the P-value for testing βqmax = 0 is less than the significance level you choose (e.g. 0.05) then go no further. Use qmax as lag length. Otherwise go on to the next step.
Step 3. Estimate the distributed lag model:
If the P-value for testing βqmax−2 = 0 is less than the significance level you chose choose (e.g. 0.05) then go no further. Use qmax – 1 as lag length. Otherwise go on to the next step.
Step 4. Estimate the distributed lag model:
If the P-value for testing βqmax−2 = 0 is less than the significance level you choose (e.g. 0.05) then go no further. Use qmax – 2 as lag length. Otherwise go on to the next step, etc.
As an aside of practical relevance to note when you are working with a spreadsheet, the number of observations used in a distributed lag model is equal to the original number of observations, T, minus the maximum lag length. This means that, in Step 2, we are working with T – qmax observations; in Step 3, with T – qmax + 1 observations; in Step 4 with T – qmax + 2, observations; etc. Each step will require some cutting and pasting in the spreadsheet to create variables with the appropriate number of observations. Alternatively, some researchers simply use T – qmax observations for all regressions. This has the advantage that, at each step, the researcher uses the same observations. However, this strategy may mean using a smaller data set than necessary. Remember from Chapter 5 that having more observations increases the accuracy of OLS estimates.
Regressions with time series variables involve two issues we have not dealt with in the past. First, one variable can influence another with a time lag. Second, if the variables are non-stationary, the spurious regressions problem can result. The latter issue will be dealt with in Chapter 10.
Distributed lag models have the dependent variable depending on an explanatory variable and time lags of the explanatory variable.
If the variables in the distributed lag model are stationary, then OLS estimates are reliable and the statistical techniques of multiple regression (e.g. looking at P-values or confidence intervals) can be used in a straightforward manner.
The lag length in a distributed lag model can be selected by sequentially using t-tests beginning with a reasonably large lag length.
[40] We can, of course, label our coefficients using any convention we want. The convention chosen here relates the subscript on β to the number of periods ago to which the explanatory variables refers. For instance, β1 is the coefficient on Xt-1, which is the value of the explanatory variable one period ago.
[41] The interested reader is referred to Chapter 7 of Campbell, Lo and MacKinlay, The Econometrics of Financial Markets, for details.
[42] Formally, this is a price relative to a benchmark price which accounts for the zeros in the data set.
[43] Note that we are assuming this data to be stationary. In a real empirical exercise involving market capitalization, this may be a poor assumption. However, this data set is a fictitious one, created so as to be stationary, so we will not worry about this issue here.
[44] The value $1,268,060 is the estimate of the total effect. It is possible to calculate a confidence interval as well, but this would require a more complicated formula and is beyond the scope of this book.
[45] Although not too large! Remember that each variable in a distributed lag model will have number of observations equal to T minus the maximum number of lags. If you set the maximum number of lags too large, you will be left with very few observations.