Many other econometric models have been proposed in the literature to describe the evolution of the conditional variance 
in Eq. (3.2). We mention the conditional heteroscedastic ARMA (CHARMA) model that uses random coefficients to produce conditional heteroscedasticity; see Tsay (1987). The CHARMA model is not the same as the ARCH model, but the two models have similar second-order conditional properties. A CHARMA model is defined as
where {ηt} is a Gaussian white noise series with mean zero and variance 
, {δt} = {(δ1t, … , δmt)′} is a sequence of iid random vectors with mean zero and nonnegative definite covariance matrix Ω, and {δt} is independent of {ηt}. In this section, we use some basic properties of vector and matrix operations to simplify the presentation. Readers may consult Appendix A of Chapter 8 for a brief review of these properties. For m > 0, the model can be written as
where at−1 = (at−1, … , at−m)′ is a vector of lagged values of at and is available at time t − 1. The conditional variance of at of the CHARMA model in Eq. (3.36) is then
Denote the (i, j)th element of Ω by ωij. Because the matrix is symmetric, we have ωij = ωji. If m = 1, then Eq. (3.37) reduces to 
, which is an ARCH(1) model. If m = 2, then Eq. (3.37) reduces to
which differs from an ARCH(2) model by the cross-product term at−1at−2. In general, the conditional variance of a CHARMA(m) model is equivalent to that of an ARCH(m) model if Ω is a diagonal matrix. Because Ω is a covariance matrix, which is nonnegative definite, and 
is a variance, which is positive, we have 
for all t. In other words, the positiveness of 
is automatically satisfied under a CHARMA model.
An obvious difference between ARCH and CHARMA models is that the latter use cross products of the lagged values of at in the volatility equation. The cross-product terms might be useful in some applications. For example, in modeling an asset return series, cross-product terms denote interactions between previous returns. It is conceivable that stock volatility may depend on such interactions. However, the number of cross-product terms increases rapidly with the order m, and some constraints are needed to keep the model simple. A possible constraint is to use a small number of cross-product terms in a CHARMA model. Another difference between the two models is that higher order properties of CHARMA models are harder to obtain than those of ARCH models because it is in general harder to handle multiple random variables.
For illustration, we employ the CHARMA model
for the monthly excess returns of the S&P 500 index used before in GARCH modeling. The fitted model is
where
where the numbers in parentheses are standard errors. The cross-product term of 
has a t ratio of − 1.63, which is marginally significant at the 10% level. If we refine the model to
but assume that δ3t is uncorrelated with (δ1t, δ2t), then we obtain the fitted model
where the elements of 
and their standard errors, shown in parentheses, are
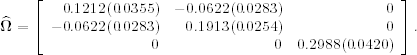
All of the estimates are now statistically significant at the 5% level. From the model, at = rt − 0.0068 is the deviation of the monthly excess return from its average. The fitted CHARMA model shows that there is some interaction effect between the first two lagged deviations. Indeed, the volatility equation can be written approximately as
The conditional variance is slightly larger when at−1at−2 is negative.
3.10.1 Effects of Explanatory Variables
The CHARMA model can easily be generalized so that the volatility of rt may depend on some explanatory variables. Let 
be m explanatory variables available at time t. Consider the model
(3.38) 
where δt = (δ1t, … , δmt)′ and ηt are random vector and variable defined in Eq. (3.36). Then the conditional variance of at is
In application, the explanatory variables may include some lagged values of at.