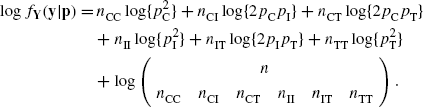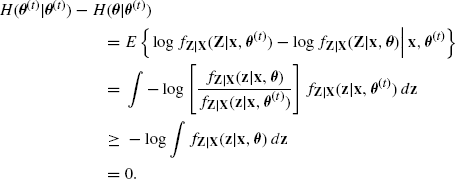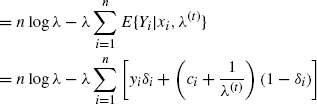Chapter 4
EM Optimization Methods
The expectation–maximization (EM) algorithm is an iterative optimization strategy motivated by a notion of missingness and by consideration of the conditional distribution of what is missing given what is observed. The strategy's statistical foundations and effectiveness in a variety of statistical problems were shown in a seminal paper by Dempster, Laird, and Rubin [150]. Other references on EM and related methods include [409, 413, 449, 456, 625]. The popularity of the EM algorithm stems from how simple it can be to implement and how reliably it can find the global optimum through stable, uphill steps.
In a frequentist setting, we may conceive of observed data generated from random variables X along with missing or unobserved data from random variables Z. We envision complete data generated from Y = (X, Z). Given observed data x, we wish to maximize a likelihood L(θ|x). Often it will be difficult to work with this likelihood and easier to work with the densities of Y|θ and Z|(x, θ). The EM algorithm sidesteps direct consideration of L(θ|x) by working with these easier densities.
In a Bayesian application, interest often focuses on estimating the mode of a posterior distribution f(θ|x). Again, optimization can sometimes be simplified by consideration of unobserved random variables ψ in addition to the parameters of interest, θ.
The missing data may not truly be missing: They may be only a conceptual ploy that simplifies the problem. In this case, Z is often referred to as latent. It may seem counterintuitive that optimization sometimes can be simplified by introducing this new element into the problem. However, examples in this chapter and its references illustrate the potential benefit of this approach. In some cases, the analyst must draw upon his or her creativity and cleverness to invent effective latent variables; in other cases, there is a natural choice.
4.1 Missing Data, Marginalization, and Notation
Whether Z is considered latent or missing, it may be viewed as having been removed from the complete Y through the application of some many-to-fewer mapping, X = M(Y). Let fX(x|θ) and fY(y|θ) denote the densities of the observed data and the complete data, respectively. The latent-or missing-data assumption amounts to a marginalization model in which we observe X having density fX(x|θ) = ∫ {y:M(y)=x}fY(y|θ) dy. Note that the conditional density of the missing data given the observed data is fZ|X(z|x, θ) = fY(y|θ)/fX(x|θ).
In Bayesian applications focusing on the posterior density for parameters of interest, θ, there are two manners in which we may consider the posterior to represent a marginalization of a broader problem. First, it may be sensible to view the likelihood L(θ|x) as a marginalization of the complete-data likelihood L(θ|y) = L(θ|x, z). In this case the missing data are z, and we use the same sort of notation as above. Second, we may consider there to be missing parameters ψ, whose inclusion simplifies Bayesian calculations even though ψ is of no interest itself. Fortunately, under the Bayesian paradigm there is no practical distinction between these two cases. Since Z and ψ are both missing random quantities, it matters little whether we use notation that suggests the missing variables to be unobserved data or parameters. In cases where we adopt the frequentist notation, the reader may replace the likelihood and Z by the posterior and ψ, respectively, to consider the Bayesian point of view.
In the literature about EM, it is traditional to adopt notation that reverses the roles of X and Y compared to our usage. We diverge from tradition, using X = x to represent observed data as everywhere else in this book.
4.2 The EM Algorithm
The EM algorithm iteratively seeks to maximize L(θ|x) with respect to θ. Let θ(t) denote the estimated maximizer at iteration t, for t = 0, 1, . . . . Define Q(θ|θ(t)) to be the expectation of the joint log likelihood for the complete data, conditional on the observed data X = x. Namely,
(4.1) ![]()
(4.2) ![]()
where (4.3) emphasizes that Z is the only random part of Y once we are given X = x.
EM is initiated from θ(0) then alternates between two steps: E for expectation and M for maximization. The algorithm is summarized as:
Stopping criteria for optimization problems are discussed in Chapter 2. In the present case, such criteria are usually built upon (θ(t+1) − θ(t))T(θ(t+1) − θ(t)) or |Q(θ(t+1)|θ(t)) − Q(θ(t)|θ(t))|.
Example 4.1 (Simple Exponential Density) To understand the EM notation, consider a trivial example where Y1, Y2 ~ i.i.d. Exp (θ). Suppose y1 = 5 is observed but the value y2 is missing. The complete-data log likelihood function is log L(θ|y) = log fY(y|θ) = 2 log {θ} − θy1 − θy2. Taking the conditional expectation of log L(θ|Y) yields Q(θ|θ(t)) = 2 log {θ} − 5θ − θ/θ(t), since E{Y2|y1, θ(t)} = E{Y2|θ(t)} = 1/θ(t) follows from independence. The maximizer of Q(θ|θ(t)) with respect to θ is easily found to be the root of 2/θ − 5 − 1/θ(t) = 0. Solving for θ provides the updating equation θ(t+1) = 2θ(t)/(5θ(t) + 1). Note here that the E step and M step do not need to be rederived at each iteration: Iterative application of the updating formula starting from some initial value provides estimates that converge to ![]() .
.
This example is not realistic. The maximum likelihood estimate of θ from the observed data can be determined from elementary analytic methods without reliance on any fancy numerical optimization strategy like EM. More importantly, we will learn that taking the required expectation is tricker in real applications, because one needs to know the conditional distribution of the complete data given the missing data. ![]()
Example 4.2 (Peppered Moths) The peppered moth, Biston betularia, presents a fascinating story of evolution and industrial pollution [276]. The coloring of these moths is believed to be determined by a single gene with three possible alleles, which we denote C, I, and T. Of these, C is dominant to I, and T is recessive to I. Thus the genotypes CC, CI, and CT result in the carbonaria phenotype, which exhibits solid black coloring. The genotype TT results in the typica phenotype, which exhibits light-colored patterned wings. The genotypes II and IT produce an intermediate phenotype called insularia, which varies widely in appearance but is generally mottled with intermediate color. Thus, there are six possible genotypes, but only three phenotypes are measurable in field work.
In the United Kingdom and North America, the carbonaria phenotype nearly replaced the paler phenotypes in areas affected by coal-fired industries. This change in allele frequencies in the population is cited as an instance where we may observe microevolution occurring on a human time scale. The theory (supported by experiments) is that “differential predation by birds on moths that are variously conspicuous against backgrounds of different reflectance” (p. 88) induces selectivity that favors the carbonaria phenotype in times and regions where sooty, polluted conditions reduce the reflectance of the surface of tree bark on which the moths rest [276]. Not surprisingly, when improved environmental standards reduced pollution, the prevalence of the lighter-colored phenotypes increased and that of carbonaria plummeted.
Thus, it is of interest to monitor the allele frequencies of C, I, and T over time to provide insight on microevolutionary processes. Further, trends in these frequencies also provide an interesting biological marker to monitor air quality. Within a sufficiently short time period, an approximate model for allele frequencies can be built from the Hardy–Weinberg principle that each genotype frequency in a population in Hardy–Weinberg equilibrium should equal the product of the corresponding allele frequencies, or double that amount when the two alleles differ (to account for uncertainty in the parental source) [15, 316]. Thus, if the allele frequencies in the population are ![]() ,
, ![]() and
and ![]() , then the genotype frequencies should be
, then the genotype frequencies should be ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() for genotypes CC, CI, CT, II, IT, and TT, respectively. Note that
for genotypes CC, CI, CT, II, IT, and TT, respectively. Note that ![]() .
.
Suppose we capture n moths, of which there are ![]() ,
, ![]() , and
, and ![]() of the carbonaria, insularia, and typica phenotypes, respectively. Thus,
of the carbonaria, insularia, and typica phenotypes, respectively. Thus, ![]() . Since each moth has two alleles in the gene in question, there are 2n total alleles in the sample. If we knew the genotype of each moth rather than merely its phenotype, we could generate genotype counts
. Since each moth has two alleles in the gene in question, there are 2n total alleles in the sample. If we knew the genotype of each moth rather than merely its phenotype, we could generate genotype counts ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , from which allele frequencies could easily be tabulated. For example, each moth with genotype CI contributes one C allele and one I allele, whereas a II moth contributes two I alleles. Such allele counts would immediately provide estimates of
, from which allele frequencies could easily be tabulated. For example, each moth with genotype CI contributes one C allele and one I allele, whereas a II moth contributes two I alleles. Such allele counts would immediately provide estimates of ![]() ,
, ![]() , and
, and ![]() . It is far less clear how to estimate the allele frequencies from the phenotype counts alone.
. It is far less clear how to estimate the allele frequencies from the phenotype counts alone.
In the EM notation, the observed data are ![]() and the complete data are
and the complete data are ![]() . The mapping from the complete data to the observed data is
. The mapping from the complete data to the observed data is ![]() . We wish to estimate the allele probabilities,
. We wish to estimate the allele probabilities, ![]() ,
, ![]() , and
, and ![]() . Since
. Since ![]() , the parameter vector for this problem is
, the parameter vector for this problem is ![]() , but for notational brevity we often refer to
, but for notational brevity we often refer to ![]() in what follows.
in what follows.
The complete data log likelihood function is multinomial:
The complete data are not all observed. Let ![]() , since we know
, since we know ![]() but the other frequencies are not directly observed. To calculate Q(p|p(t)), notice that conditional on
but the other frequencies are not directly observed. To calculate Q(p|p(t)), notice that conditional on ![]() and a parameter vector
and a parameter vector ![]() , the latent counts for the three carbonaria genotypes have a three-cell multinomial distribution with count parameter
, the latent counts for the three carbonaria genotypes have a three-cell multinomial distribution with count parameter ![]() and cell probabilities proportional to
and cell probabilities proportional to ![]() ,
, ![]() , and
, and ![]() . A similar result holds for the two insularia cells. Thus the expected values of the first five random parts of (4.4) are
. A similar result holds for the two insularia cells. Thus the expected values of the first five random parts of (4.4) are
(4.6) ![]()
(4.7) ![]()
(4.8) ![]()
Finally, we know ![]() , where
, where ![]() is observed. The multinomial coefficient in the likelihood has a conditional expectation, say
is observed. The multinomial coefficient in the likelihood has a conditional expectation, say ![]() , that does not depend on p. Thus, we have found
, that does not depend on p. Thus, we have found
(4.10) 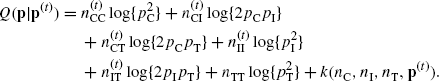
Recalling ![]() and differentiating with respect to
and differentiating with respect to ![]() and
and ![]() yields
yields
(4.11) ![]()
(4.12) ![]()
Setting these derivatives equal to zero and solving for ![]() and
and ![]() completes the M step, yielding
completes the M step, yielding
(4.14) ![]()
(4.15) ![]()
where the final expression is derived from the constraint that the probabilities sum to one. If the tth latent counts were true, the number of carbonaria alleles in the sample would be ![]() . There are 2n total alleles in the sample. Thus, the EM update consists of setting the elements of p(t+1) equal to the phenotypic frequencies that would result from the tth latent genotype counts.
. There are 2n total alleles in the sample. Thus, the EM update consists of setting the elements of p(t+1) equal to the phenotypic frequencies that would result from the tth latent genotype counts.
Suppose the observed phenotype counts are ![]() ,
, ![]() , and
, and ![]() . Table 4.1 shows how the EM algorithm converges to the MLEs, roughly
. Table 4.1 shows how the EM algorithm converges to the MLEs, roughly ![]() ,
, ![]() , and
, and ![]() . Finding a precise estimate of
. Finding a precise estimate of ![]() is slower than for
is slower than for ![]() , since the likelihood is flatter along the
, since the likelihood is flatter along the ![]() coordinate.
coordinate.
Table 4.1 EM results for peppered moth example. The diagnostic quantities R(t), ![]() , and
, and ![]() are defined in the text.
are defined in the text.
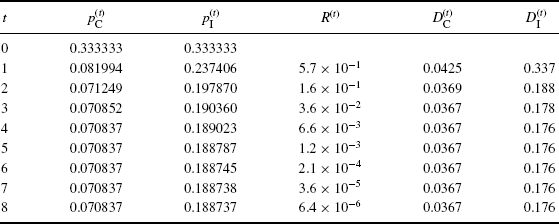
The last three columns of Table 4.1 show convergence diagnostics. A relative convergence criterion,
(4.16) ![]()
summarizes the total amount of relative change in p(t) from one iteration to the next, where ||z|| = (zTz)1/2. For illustrative purposes, we also include ![]() and the analogous quantity
and the analogous quantity ![]() . These ratios quickly converge to constants, confirming that the EM rate of convergence is linear as defined by (2.19).
. These ratios quickly converge to constants, confirming that the EM rate of convergence is linear as defined by (2.19). ![]()
Example 4.3 (Bayesian Posterior Mode) Consider a Bayesian problem with likelihood L(θ|x), prior f(θ), and missing data or parameters Z. To find the posterior mode, the E step requires
where the final term in (4.17) is a normalizing constant that can be ignored because Q is to be maximized with respect to θ. This function Q is obtained by simply adding the log prior to the Q function that would be used in a maximum likelihood setting. Unfortunately, the addition of the log prior often makes it more difficult to maximize Q during the M step. Section 4.3.2 describes a variety of methods for facilitating the M step in difficult situations. ![]()
4.2.1 Convergence
To investigate the convergence properties of the EM algorithm, we begin by showing that each maximization step increases the observed-data log likelihood, l(θ|x). First, note that the log of the observed-data density can be reexpressed as
(4.18) ![]()
Therefore,
![]()
where the expectations are taken with respect to the distribution of Z|(x, θ(t)). Thus,
where
(4.20) ![]()
The importance of (4.19) becomes apparent after we show that H(θ|θ(t)) is maximized with respect to θ when θ = θ(t). To see this, write
Equation (4.21) follows from an application of Jensen's inequality, since − log u is strictly convex in u.
Thus, any θ ≠ θ(t) makes H(θ|θ(t)) smaller than H(θ(t)|θ(t)). In particular, if we choose θ(t+1) to maximize Q(θ|θ(t)) with respect to θ, then
(4.22) ![]()
since Q increases and H decreases, with strict inequality when Q(θ(t+1)|θ(t)) > Q(θ(t)|θ(t)).
Choosing θ(t+1) at each iteration to maximize Q(θ|θ(t)) with respect to θ constitutes the standard EM algorithm. If instead we simply select any θ(t+1) for which Q(θ(t+1)|θ(t)) > Q(θ(t)|θ(t)), then the resulting algorithm is called generalized EM, or GEM. In either case, a step that increases Q increases the log likelihood. Conditions under which this guaranteed ascent ensures convergence to an MLE are explored in [60, 676].
Having established this result, we next consider the order of convergence for the method. The EM algorithm defines a mapping θ(t+1) = Ψ(θ(t)) where the function Ψ(θ) = (Ψ1(θ), . . ., Ψp(θ)) and θ = (θ1, . . ., θp). When EM converges, it converges to a fixed point of this mapping, so ![]() . Let Ψ′(θ) denote the Jacobian matrix whose (i, j)th element is dΨi(θ)/dθj. Taylor series expansion of Ψ yields
. Let Ψ′(θ) denote the Jacobian matrix whose (i, j)th element is dΨi(θ)/dθj. Taylor series expansion of Ψ yields
(4.23) ![]()
since ![]() . Comparing this result with (2.19), we see that the EM algorithm has linear convergence when p = 1. For p > 1, convergence is still linear provided that the observed information,
. Comparing this result with (2.19), we see that the EM algorithm has linear convergence when p = 1. For p > 1, convergence is still linear provided that the observed information, ![]() , is positive definite. More precise details regarding convergence are given in [150, 449, 452, 455].
, is positive definite. More precise details regarding convergence are given in [150, 449, 452, 455].
The global rate of EM convergence is defined as
(4.24) ![]()
It can be shown that ρ equals the largest eigenvalue of ![]() when
when ![]() is positive definite. In Sections 4.2.3.1 and 4.2.3.2 we will examine how
is positive definite. In Sections 4.2.3.1 and 4.2.3.2 we will examine how ![]() is a matrix of the fractions of missing information. Therefore, ρ effectively serves as a scalar summary of the overall proportion of missing information. Conceptually, the proportion of missing information equals one minus the ratio of the observed information to the information that would be contained in the complete data. Thus, EM suffers slower convergence when the proportion of missing information is larger. The linear convergence of EM can be extremely slow compared to the quadratic convergence of, say, Newton's method, particularly when the fraction of missing information is large. However, the ease of implementation and the stable ascent of EM are often very attractive despite its slow convergence. Section 4.3.3 discusses methods for accelerating EM convergence.
is a matrix of the fractions of missing information. Therefore, ρ effectively serves as a scalar summary of the overall proportion of missing information. Conceptually, the proportion of missing information equals one minus the ratio of the observed information to the information that would be contained in the complete data. Thus, EM suffers slower convergence when the proportion of missing information is larger. The linear convergence of EM can be extremely slow compared to the quadratic convergence of, say, Newton's method, particularly when the fraction of missing information is large. However, the ease of implementation and the stable ascent of EM are often very attractive despite its slow convergence. Section 4.3.3 discusses methods for accelerating EM convergence.
To further understand how EM works, note from (4.21) that
(4.25) ![]()
Since the last two terms in G(θ|θ(t)) are independent of θ, the functions Q and G are maximized at the same θ. Further, G is tangent to l at θ(t) and lies everywhere below l. We say that G is a minorizing function for l. The EM strategy transfers optimization from l to the surrogate function G (effectively to Q), which is more convenient to maximize. The maximizer of G provides an increase in l. This idea is illustrated in Figure 4.1. Each E step amounts to forming the minorizing function G, and each M step amounts to maximizing it to provide an uphill step.
Figure 4.1 One-dimensional illustration of EM algorithm as a minorization or optimization transfer strategy.
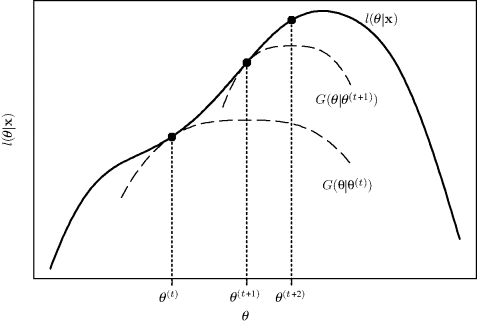
Temporarily replacing l by a minorizing function is an example of a more general strategy known as optimization transfer. Links to the EM algorithm and other statistical applications of optimization transfer are surveyed in [410]. In mathematical applications where it is standard to pose optimizations as minimizations, one typically refers to majorization, as one could achieve by majorizing the negative log likelihood using −G(θ|θ(t)).
4.2.2 Usage in Exponential Families
When the complete data are modeled to have a distribution in the exponential family, the density of the data can be written as f(y|θ) = c1(y)c2(θ) exp {θTs(y)}, where θ is a vector of natural parameters and s(y) is a vector of sufficient statistics. In this case, the E step finds
where k is a quantity that does not depend on θ. To carry out the M step, set the gradient of Q(θ|θ(t)) with respect to θ equal to zero. This yields
after rearranging terms and adopting the obvious notational shortcut to vectorize the integral of a vector. It is straightforward to show that ![]() . Therefore, (4.27) implies that the M step is completed by setting θ(t+1) equal to the θ that solves
. Therefore, (4.27) implies that the M step is completed by setting θ(t+1) equal to the θ that solves
(4.28) ![]()
Aside from replacing θ(t) with θ(t+1), the form of Q(θ|θ(t)) is unchanged for the next E step, and the next M step solves the same optimization problem. Therefore, the EM algorithm for exponential families consists of:
Example 4.4 (Peppered Moths, Continued) The complete data in Example 4.2 arise from a multinomial distribution, which is in the exponential family. The sufficient statistics are, say, the first five genotype counts (with the sixth derived from the constraint that the counts total n), and the natural parameters are the corresponding log probabilities seen in (4.4). The first three conditional expectations for the E step are ![]() ,
, ![]() , and
, and ![]() , borrowing notation from (4.5)-(4.9) and indexing the components of s(t) in the obvious way. The unconditional expectations of the first three sufficient statistics are
, borrowing notation from (4.5)-(4.9) and indexing the components of s(t) in the obvious way. The unconditional expectations of the first three sufficient statistics are ![]() ,
, ![]() , and
, and ![]() . Equating these three expressions with the conditional expectations given above and solving for
. Equating these three expressions with the conditional expectations given above and solving for ![]() constitutes the M step for
constitutes the M step for ![]() . Summing the three equations gives
. Summing the three equations gives ![]() , which reduces to the update given in (4.13). EM updates for
, which reduces to the update given in (4.13). EM updates for ![]() and
and ![]() are found analogously, on noting the constraint that the three probabilities sum to 1.
are found analogously, on noting the constraint that the three probabilities sum to 1. ![]()
4.2.3 Variance Estimation
In a maximum likelihood setting, the EM algorithm is used to find an MLE but does not automatically produce an estimate of the covariance matrix of the MLEs. Typically, we would use the asymptotic normality of the MLEs to justify seeking an estimate of the Fisher information matrix. One way to estimate the covariance matrix, therefore, is to compute the observed information, ![]() , where l′′ is the Hessian matrix of second derivatives of log L(θ|x).
, where l′′ is the Hessian matrix of second derivatives of log L(θ|x).
In a Bayesian setting, an estimate of the posterior covariance matrix for θ can be motivated by noting the asymptotic normality of the posterior [221]. This requires the Hessian of the log posterior density.
In some cases, the Hessian may be computed analytically. In other cases, the Hessian may be difficult to derive or code. In these instances, a variety of other methods are available to simplify the estimation of the covariance matrix.
Of the options described below, the SEM (supplemented EM) algorithm is easy to implement while generally providing fast, reliable results. Even easier is bootstrapping, although for very complex problems the computational burden of nested looping may be prohibitive. These two approaches are recommended, yet the other alternatives can also be useful in some settings.
4.2.3.1 Louis's Method
Taking second partial derivatives of (4.19) and negating both sides yields
where the primes on Q′′ and H′′ denote derivatives with respect to the first argument, namely θ.
Equation (4.29) can be rewritten as
where ![]() is the observed information, and
is the observed information, and ![]() and
and ![]() will be called the complete information and the missing information, respectively. Interchanging integration and differentiation (when possible), we have
will be called the complete information and the missing information, respectively. Interchanging integration and differentiation (when possible), we have
which is reminiscent of the Fisher information defined in (1.28). This motivates calling ![]() the complete information. A similar argument holds for −H′′. Equation (4.30), stating that the observed information equals the complete information minus the missing information, is a result termed the missing-information principle [424, 673].
the complete information. A similar argument holds for −H′′. Equation (4.30), stating that the observed information equals the complete information minus the missing information, is a result termed the missing-information principle [424, 673].
The missing-information principle can be used to obtain an estimated covariance matrix for ![]() . It can be shown that
. It can be shown that
where the variance is taken with respect to fZ|X. Further, since the expected score is zero at ![]() ,
,
(4.33) ![]()
where
![]()
The missing-information principle enables us to express ![]() in terms of the complete-data likelihood and the conditional density of the missing data given the observed data, while avoiding calculations involving the presumably complicated marginal likelihood of the observed data. This approach can be easier to derive and code in some instances, but it is not always significantly simpler than direct calculation of
in terms of the complete-data likelihood and the conditional density of the missing data given the observed data, while avoiding calculations involving the presumably complicated marginal likelihood of the observed data. This approach can be easier to derive and code in some instances, but it is not always significantly simpler than direct calculation of ![]() .
.
If ![]() or
or ![]() is difficult to compute analytically, it may be estimated via the Monte Carlo method (see Chapter 6). For example, the simplest Monte Carlo estimate of
is difficult to compute analytically, it may be estimated via the Monte Carlo method (see Chapter 6). For example, the simplest Monte Carlo estimate of ![]() is
is
(4.34) ![]()
where for i = 1, . . ., m, the yi = (x, zi) are simulated complete datasets consisting of the observed data and i.i.d. imputed missing-data values zi drawn from fZ|X. Similarly, a simple Monte Carlo estimate of ![]() is the sample variance of the values of
is the sample variance of the values of
![]()
obtained from such a collection of zi.
Example 4.5 (Censored Exponential Data) Suppose we attempt to observed complete data under the model Y1, . . ., Yn ~ i.i.d. Exp (λ), but some cases are right-censored. Thus, the observed data are x = (x1, . . ., xn) where xi = (min (yi, ci), δi), the ci are the censoring levels, and δi = 1 if yi ≤ ci and δi = 0 otherwise.
The complete-data log likelihood is ![]() . Thus,
. Thus,
(4.35) ![]()
where ![]() denotes the number of censored cases. Note that (4.36) follows from the memoryless property of the exponential distribution. Therefore, −Q′′(λ|λ(t)) = n/λ2.
denotes the number of censored cases. Note that (4.36) follows from the memoryless property of the exponential distribution. Therefore, −Q′′(λ|λ(t)) = n/λ2.
The unobserved outcome for a censored case, Zi, has density ![]() . Calculating
. Calculating ![]() as in (4.32), we find
as in (4.32), we find
(4.38) ![]()
The variance of this expression with respect to ![]() is
is
(4.39) ![]()
since Zi − ci has an Exp(λ) distribution.
Thus, applying Louis's method,
(4.40) ![]()
where ![]() denotes the number of uncensored cases. For this elementary example, it is easy to confirm by direct analysis that −l′′(λ|x) = U/λ2.
denotes the number of uncensored cases. For this elementary example, it is easy to confirm by direct analysis that −l′′(λ|x) = U/λ2. ![]()
4.2.3.2 SEM Algorithm
Recall that Ψ denotes the EM mapping, having fixed point ![]() and Jacobian matrix Ψ′(θ) with (i, j)th element equaling dΨi(θ)/dθj. Dempster et al. [150] show that
and Jacobian matrix Ψ′(θ) with (i, j)th element equaling dΨi(θ)/dθj. Dempster et al. [150] show that
in the terminology of (4.30).
If we reexpress the missing information principle in (4.30) as
where I is an identity matrix, and substitute (4.41) into (4.42), then inverting ![]() provides the estimate
provides the estimate
This result is appealing in that it expresses the desired covariance matrix as the complete-data covariance matrix plus an incremental matrix that takes account of the uncertainty attributable to the missing data. When coupled with the following numerical differentiation strategy to estimate the increment, Meng and Rubin have termed this approach the supplemented EM (SEM) algorithm [453]. Since numerical imprecisions in the differentiation approach affect only the estimated increment, estimation of the covariance matrix is typically more stable than the generic numerical differentiation approach described in Section 4.2.3.5.
Estimation of ![]() proceeds as follows. The first step of SEM is to run the EM algorithm to convergence, finding the maximizer
proceeds as follows. The first step of SEM is to run the EM algorithm to convergence, finding the maximizer ![]() . The second step is to restart the algorithm from, say, θ(0). Although one may restart from the original starting point, it is preferable to choose θ(0) to be closer to
. The second step is to restart the algorithm from, say, θ(0). Although one may restart from the original starting point, it is preferable to choose θ(0) to be closer to ![]() .
.
Having thus initialized SEM, we begin SEM iterations for t = 0, 1, 2, . . . . The (t + 1)th SEM iteration begins by taking a standard E step and M step to produce θ(t+1) from θ(t). Next, for j = 1, . . ., p, define ![]() and
and
(4.44) ![]()
for i = 1, . . ., p, recalling that ![]() . This ends one SEM iteration. The Ψi(θ(t)(j)) values are the estimates produced by applying one EM cycle to θ(t)(j) for j = 1, . . ., p.
. This ends one SEM iteration. The Ψi(θ(t)(j)) values are the estimates produced by applying one EM cycle to θ(t)(j) for j = 1, . . ., p.
Notice that the (i, j)th element of ![]() equals
equals ![]() . We may consider each element of this matrix to be precisely estimated when the sequence of
. We may consider each element of this matrix to be precisely estimated when the sequence of ![]() values stabilizes for
values stabilizes for ![]() . Note that different numbers of iterations may be needed for precise estimation of different elements of
. Note that different numbers of iterations may be needed for precise estimation of different elements of ![]() . When all elements have stabilized, SEM iterations stop and the resulting estimate of
. When all elements have stabilized, SEM iterations stop and the resulting estimate of ![]() is used to determine
is used to determine ![]() as given in (4.43).
as given in (4.43).
Numerical imprecision can cause the resulting covariance matrix to be slightly asymmetric. Such asymmetry can be used to diagnose whether the original EM procedure was run to sufficient precision and to assess how many digits are trustworthy in entries of the estimated covariance matrix. Difficulties also arise if ![]() is not positive semidefinite or cannot be inverted numerically; see [453]. It has been suggested that transforming θ to achieve an approximately normal likelihood can lead to faster convergence and increased accuracy of the final solution.
is not positive semidefinite or cannot be inverted numerically; see [453]. It has been suggested that transforming θ to achieve an approximately normal likelihood can lead to faster convergence and increased accuracy of the final solution.
Example 4.6 (Peppered Moths, Continued) The results from Example 4.2 can be supplemented using the approach of Meng and Rubin [453]. Stable, precise results are obtained within a few SEM iterations, starting from ![]() and
and ![]() . Standard errors for
. Standard errors for ![]() ,
, ![]() , and
, and ![]() are 0.0074, 0.0119, and 0.0132, respectively. Pairwise correlations are
are 0.0074, 0.0119, and 0.0132, respectively. Pairwise correlations are ![]() ,
, ![]() , and
, and ![]() . Here, SEM was used to obtain results for
. Here, SEM was used to obtain results for ![]() and
and ![]() , and elementary relationships among variances, covariances, and correlations were used to extend these results for
, and elementary relationships among variances, covariances, and correlations were used to extend these results for ![]() since the estimated probabilities sum to 1.
since the estimated probabilities sum to 1. ![]()
It may seem inefficient not to begin SEM iterations until EM iterations have ceased. An alternative would be to attempt to estimate the components of ![]() as EM iterations progress, using
as EM iterations progress, using
(4.45) 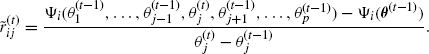
However, Meng and Rubin [453] argue that this approach will not require fewer iterations overall, that the extra steps required to find ![]() first can be offset by starting SEM closer to
first can be offset by starting SEM closer to ![]() , and that the alternative is numerically less stable. Jamshidian and Jennrich survey a variety of methods for numerically differentiating Ψ or l′ itself, including some they consider superior to SEM [345].
, and that the alternative is numerically less stable. Jamshidian and Jennrich survey a variety of methods for numerically differentiating Ψ or l′ itself, including some they consider superior to SEM [345].
4.2.3.3 Bootstrapping
Thorough discussion of bootstrapping is given in Chapter 9. In its simplest implementation, bootstrapping to obtain an estimated covariance matrix for EM would proceed as follows for i.i.d. observed data x1, . . ., xn:
For most problems, a few thousand iterations will suffice. At the end of the process, we have generated a collection of parameter estimates, ![]() , where B denotes the total number of iterations used. Then the sample variance of these B estimates is the estimated variance of
, where B denotes the total number of iterations used. Then the sample variance of these B estimates is the estimated variance of ![]() . Conveniently, other aspects of the sampling distribution of
. Conveniently, other aspects of the sampling distribution of ![]() , such as correlations and quantiles, can be estimated using the corresponding sample estimates based on
, such as correlations and quantiles, can be estimated using the corresponding sample estimates based on ![]() . Note that bootstrapping embeds the EM loop in a second loop of B iterations. This nested looping can be computationally burdensome when the solution of each EM problem is slow because of a high proportion of missing data or high dimensionality.
. Note that bootstrapping embeds the EM loop in a second loop of B iterations. This nested looping can be computationally burdensome when the solution of each EM problem is slow because of a high proportion of missing data or high dimensionality.
4.2.3.4 Empirical Information
When the data are i.i.d., note that the score function is the sum of individual scores for each observation:
(4.46) ![]()
where we write the observed dataset as x = (x1, . . ., xn). Since the Fisher information matrix is defined to be the variance of the score function, this suggests estimating the information using the sample variance of the individual scores. The empirical information is defined as
This estimate has been discussed in the EM context in [450, 530]. The appeal of this approach is that all the terms in (4.47) are by-products of the M step: No additional analysis is required. To see this, note that θ(t) maximizes Q(θ|θ(t)) − l(θ|x) with respect to θ. Therefore, taking derivatives with respect to θ,
(4.48) ![]()
Since Q′ is ordinarily calculated at each M step, the individual terms in (4.47) are available.
4.2.3.5 Numerical Differentiation
To estimate the Hessian, consider computing the numerical derivative of l′ at ![]() , one coordinate at a time, using (1.10). The first row of the estimated Hessian can be obtained by adding a small perturbation to the first coordinate of
, one coordinate at a time, using (1.10). The first row of the estimated Hessian can be obtained by adding a small perturbation to the first coordinate of ![]() , then computing the ratio of the difference between l′(θ) at
, then computing the ratio of the difference between l′(θ) at ![]() and at the perturbed value, relative to the magnitude of the perturbation. The remaining rows of the Hessian are approximated similarly. If a perturbation is too small, estimated partial derivatives may be inaccurate due to roundoff error; if a perturbation is too big, the estimates may also be inaccurate. Such numerical differentiation can be tricky to automate, especially when the components of
and at the perturbed value, relative to the magnitude of the perturbation. The remaining rows of the Hessian are approximated similarly. If a perturbation is too small, estimated partial derivatives may be inaccurate due to roundoff error; if a perturbation is too big, the estimates may also be inaccurate. Such numerical differentiation can be tricky to automate, especially when the components of ![]() have different scales. More sophisticated numerical differentiation strategies are surveyed in [345].
have different scales. More sophisticated numerical differentiation strategies are surveyed in [345].
4.3 EM Variants
4.3.1 Improving the E Step
The E step requires finding the expected log likelihood of the complete data conditional on the observed data. We have denoted this expectation as Q(θ|θ(t)). When this expectation is difficult to compute analytically, it can be approximated via Monte Carlo (see Chapter 6).
4.3.1.1 Monte Carlo EM
Wei and Tanner [656] propose that the tth E step can be replaced with the following two steps:
Then ![]() is a Monte Carlo estimate of Q(θ|θ(t)). The M step is modified to maximize
is a Monte Carlo estimate of Q(θ|θ(t)). The M step is modified to maximize ![]() .
.
The recommended strategy is to let m(t) be small during early EM iterations and to increase m(t) as iterations progress to reduce the Monte Carlo variability introduced in ![]() . Nevertheless, this Monte Carlo EM algorithm (MCEM) will not converge in the same sense as ordinary EM. As iterations proceed, values of θ(t) will eventually bounce around the true maximum, with a precision that depends on m(t). Discussion of the asymptotic convergence properties of MCEM is provided in [102]. A stochastic alternative to MCEM is discussed in [149].
. Nevertheless, this Monte Carlo EM algorithm (MCEM) will not converge in the same sense as ordinary EM. As iterations proceed, values of θ(t) will eventually bounce around the true maximum, with a precision that depends on m(t). Discussion of the asymptotic convergence properties of MCEM is provided in [102]. A stochastic alternative to MCEM is discussed in [149].
Example 4.7 (Censored Exponential Data, Continued) In Example 4.5, it was easy to compute the conditional expectation of ![]() given the observed data. The result, given in (4.37), can be maximized to provide the ordinary EM update,
given the observed data. The result, given in (4.37), can be maximized to provide the ordinary EM update,
(4.49) ![]()
Application of MCEM is also easy. In this case,
(4.50) 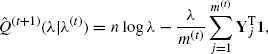
where 1 is a vector of ones and Yj is the jth completed dataset comprising the uncensored data and simulated data Zj = (Zj1, . . ., ZjC) with Zjk − ck ~ i.i.d. Exp (λ(t)) for k = 1, . . ., C to replace the censored values. Setting ![]() and solving for λ yields
and solving for λ yields
(4.51) ![]()
as the MCEM update.
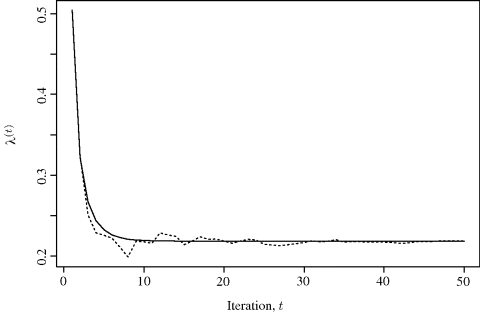
The website for this book provides n = 30 observations, including C = 17 censored observations. Figure 4.2 compares the performance of MCEM and ordinary EM for estimating λ with these data. Both methods easily find the MLE ![]() . For MCEM, we used m(t) = 51+
. For MCEM, we used m(t) = 51+![]() t/10
t/10![]() , where
, where ![]() z
z![]() denotes the integer part of z. Fifty iterations were used altogether. Both algorithms were initiated from λ(0) = 0.5042, which is the mean of all 30 data values disregarding censoring.
denotes the integer part of z. Fifty iterations were used altogether. Both algorithms were initiated from λ(0) = 0.5042, which is the mean of all 30 data values disregarding censoring. ![]()
Figure 4.2 Comparison of iterations for EM (solid) and MCEM (dotted) for the censored exponential data discussed in Example 4.7.
4.3.2 Improving the M Step
One of the appeals of the EM algorithm is that the derivation and maximization of Q(θ|θ(t)) is often simpler than incomplete-data maximum likelihood calculations, since Q(θ|θ(t)) relates to the complete-data likelihood. In some cases, however, the M step cannot be carried out easily even though the E step yielding Q(θ|θ(t)) is straightforward. Several strategies have been proposed to facilitate the M step in such cases.
4.3.2.1 ECM Algorithm
Meng and Rubin's ECM algorithm replaces the M step with a series of computationally simpler conditional maximization (CM) steps [454]. Each conditional maximization is designed to be a simple optimization problem that constrains θ to a particular subspace and permits either an analytical solution or a very elementary numerical solution.
We call the collection of simpler CM steps after the tth E step a CM cycle. Thus, the tth iteration of ECM is composed of the tth E step and the tth CM cycle. Let S denote the total number of CM steps in each CM cycle. For s = 1, . . ., S, the sth CM step in the tth cycle requires the maximization of Q(θ|θ(t)) subject to (or conditional on) a constraint, say
(4.52) ![]()
where θ(t+(s−1)/S) is the maximizer found in the (s − 1)th CM step of the current cycle. When the entire cycle of S steps of CM has been completed, we set θ(t+1) = θ(t+S/S) and proceed to the E step for the (t + 1)th iteration.
Clearly any ECM is a GEM algorithm (Section 4.2.1), since each CM step increases Q. In order for ECM to be convergent, we need to ensure that each CM cycle permits search in any direction for a maximizer of Q(θ|θ(t)), so that ECM effectively maximizes over the original parameter space for θ and not over some subspace. Precise conditions are discussed in [452, 454]; extensions of this method include [415, 456].
The art of constructing an effective ECM algorithm lies in choosing the constraints cleverly. Usually, it is natural to partition θ into S subvectors, θ = (θ1, . . ., θS). Then in the sth CM step, one might seek to maximize Q with respect to θs while holding all other components of θ fixed. This amounts to the constraint induced by the function gs(θ) = (θ1, . . ., θs−1, θs+1, . . ., θS). A maximization strategy of this type has previously been termed iterated conditional modes [36]. If the conditional maximizations are obtained by finding the roots of score functions, the CM cycle can also be viewed as a Gauss–Seidel iteration (see Section 2.2.5).
Alternatively, the sth CM step might seek to maximize Q with respect to all other components of θ while holding θs fixed. In this case, gs(θ) = θs. Additional systems of constraints can be imagined, depending on the particular problem context. A variant of ECM inserts an E step between each pair of CM steps, thereby updating Q at every stage of the CM cycle.
Example 4.8 (Multivariate Regression with Missing Values) A particularly illuminating example given by Meng and Rubin [454] involves multivariate regression with missing values. Let U1, . . ., Un be n independent d-dimensional vectors observed from the d-variate normal model given by
(4.53) ![]()
for Ui = (Ui1, . . ., Uid) and μi = Viβ, where the Vi are known d × p design matrices, β is a vector of p unknown parameters, and Σ is a d × d unknown variance–covariance matrix. There are many cases where Σ has some meaningful structure, but we consider Σ to be unstructured for simplicity. Suppose that some elements of some Ui are missing.
Begin by reordering the elements of Ui, μi, and the rows of Vi so that for each i, the observed components of Ui are first and any missing components are last. For each Ui, denote by βi and Σi the corresponding reorganizations of the parameters. Thus, βi and Σi are completely determined by β, Σ, and the pattern of missing data: They do not represent an expansion of the parameter space.
This notational reorganization allows us to write Ui = (Uobs,i, Umiss,i), μi = (μobs,i, μmiss,i), and
(4.54) 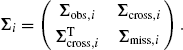
The full set of observed data can be denoted Uobs = (Uobs,1, . . ., Uobs,n).
The observed-data log likelihood function is
![]()
up to an additive constant. This likelihood is quite tedious to work with or to maximize. Note, however, that the complete-data sufficient statistics are given by ![]() for j = 1, . . ., d and
for j = 1, . . ., d and ![]() for j, k = 1, . . ., d. Thus, the E step amounts to finding the expected values of these sufficient statistics conditional on the observed data and current parameter values β(t) and Σ(t).
for j, k = 1, . . ., d. Thus, the E step amounts to finding the expected values of these sufficient statistics conditional on the observed data and current parameter values β(t) and Σ(t).
Now for j = 1, . . ., d
(4.55) 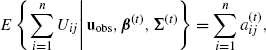
where
(4.56) 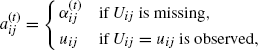
and ![]() . Similarly, for j, k = 1, . . ., d,
. Similarly, for j, k = 1, . . ., d,
(4.57) 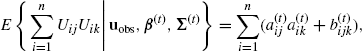
where
(4.58) 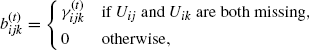
and ![]() .
.
Fortunately, the derivation of the ![]() and
and ![]() is fairly straightforward. The conditional distribution of
is fairly straightforward. The conditional distribution of ![]() is
is
![]()
The values for ![]() and
and ![]() can be read from the mean vector and variance–covariance matrix of this distribution, respectively. Knowing these, Q(β, Σ|β(t), Σ(t)) can be formed following (4.26).
can be read from the mean vector and variance–covariance matrix of this distribution, respectively. Knowing these, Q(β, Σ|β(t), Σ(t)) can be formed following (4.26).
Having thus achieved the E step, we turn now to the M step. The high dimensionality of the parameter space and the complexity of the observed-data likelihood renders difficult any direct implementation of the M step, whether by direct maximization or by reference to the exponential family setup. However, implementing an ECM strategy is straightforward using S = 2 conditional maximization steps in each CM cycle.
Treating β and Σ separately allows easy constrained optimizations of Q. First, if we impose the constraint that Σ = Σ(t), then we can maximize the constrained version of Q(β, Σ|β(t), Σ(t)) with respect to β by using the weighted least squares estimate
(4.59) 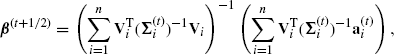
where ![]() and
and ![]() is treated as a known variance–covariance matrix. This ensures that Q(β(t+1/2), Σ(t)|β(t), Σ(t)) ≥ Q(β(t), Σ(t)|β(t), Σ(t)). This constitutes the first of two CM steps.
is treated as a known variance–covariance matrix. This ensures that Q(β(t+1/2), Σ(t)|β(t), Σ(t)) ≥ Q(β(t), Σ(t)|β(t), Σ(t)). This constitutes the first of two CM steps.
The second CM step follows from the fact that setting Σ(t+2/2) equal to
(4.60) 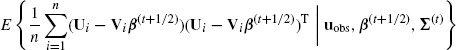
maximizes Q(β, Σ|β(t), Σ(t)) with respect to Σ subject to the constraint that β = β(t+1/2), because this amounts to plugging in ![]() and
and ![]() values where necessary and computing the sample covariance matrix of the completed data. This update guarantees
values where necessary and computing the sample covariance matrix of the completed data. This update guarantees
(4.61) ![]()
Together, the two CM steps yield (β(t+1), Σ(t+1)) = (β(t+1/2), Σ(t+2/2)) and ensure an increase in the Q function.
The E step and the CM cycle described here can each be implemented using familiar closed-form analytic results; no numerical integration or maximization is required. After updating the parameters with the CM cycle described above, we return to another E step, and so forth. In summary, ECM alternates between (i) creating updated complete datasets and (ii) sequentially estimating β and Σ in turn by fixing the other at its current value and using the current completed-data component. ![]()
4.3.2.2 EM Gradient Algorithm
If maximization cannot be accomplished analytically, then one might consider carrying out each M step using an iterative numerical optimization approach like those discussed in Chapter 2. This would yield an algorithm that had nested iterative loops. The ECM algorithm inserts S conditional maximization steps within each iteration of the EM algorithm, also yielding nested iteration.
To avoid the computational burden of nested looping, Lange proposed replacing the M step with a single step of Newton's method, thereby approximating the maximum without actually solving for it exactly [407]. The M step is replaced with the update given by
(4.62) ![]()
where l′(θ(t)|x) is the evaluation of the score function at the current iterate. Note that (4.63) follows from the observation in Section 4.2.3.4 that θ(t) maximizes Q(θ|θ(t)) − l(θ|x). This EM gradient algorithm has the same rate of convergence to ![]() as the full EM algorithm. Lange discusses conditions under which ascent can be ensured, and scalings of the update increment to speed convergence [407]. In particular, when Y has an exponential family distribution with canonical parameter θ, ascent is ensured and the method matches that of Titterington [634]. In other cases, the step can be scaled down to ensure ascent (as discussed in Section 2.2.2.1), but inflating steps speeds convergence. For problems with a high proportion of missing information, Lange suggests considering doubling the step length [407].
as the full EM algorithm. Lange discusses conditions under which ascent can be ensured, and scalings of the update increment to speed convergence [407]. In particular, when Y has an exponential family distribution with canonical parameter θ, ascent is ensured and the method matches that of Titterington [634]. In other cases, the step can be scaled down to ensure ascent (as discussed in Section 2.2.2.1), but inflating steps speeds convergence. For problems with a high proportion of missing information, Lange suggests considering doubling the step length [407].
Example 4.9 (Peppered Moths, Continued) Continuing Example 4.2, we apply the EM gradient algorithm to these data. It is straightforward to show
(4.65) ![]()
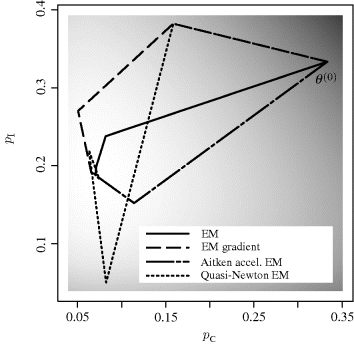
Figure 4.3 shows the steps taken by the resulting EM gradient algorithm, starting from ![]() . Step halving was implemented to ensure ascent. The first step heads somewhat in the wrong direction, but in subsequent iterations the gradient steps progress quite directly uphill. The ordinary EM steps are shown for comparison in this figure.
. Step halving was implemented to ensure ascent. The first step heads somewhat in the wrong direction, but in subsequent iterations the gradient steps progress quite directly uphill. The ordinary EM steps are shown for comparison in this figure. ![]()
Figure 4.3 Steps taken by the EM gradient algorithm (long dashes). Ordinary EM steps are shown with the solid line. Steps from two methods from later sections (Aitken and quasi-Newton acceleration) are also shown, as indicated in the key. The observed-data log likelihood is shown with the gray scale, with light shading corresponding to high likelihood. All algorithms were started from ![]() .
.
4.3.3 Acceleration Methods
The slow convergence of the EM algorithm is a notable drawback. Several techniques have been suggested for using the relatively simple analytic setup from EM to motivate particular forms for Newton-like steps. In addition to the two approaches described below, approaches that cleverly expand the parameter space in manners that speed convergence without affecting the marginal inference about θ are topics of recent interest [421, 456].
4.3.3.1 Aitken Acceleration
Let ![]() be the next iterate obtained by the standard EM algorithm from θ(t). Recall that the Newton update to maximize the log likelihood would be
be the next iterate obtained by the standard EM algorithm from θ(t). Recall that the Newton update to maximize the log likelihood would be
The EM framework suggests a replacement for l′(θ(t)|x). In Section 4.2.3.4 we noted that ![]() . Expanding Q′ around θ(t), evaluated at
. Expanding Q′ around θ(t), evaluated at ![]() , yields
, yields
where ![]() is defined in (4.31). Since
is defined in (4.31). Since ![]() maximizes Q(θ|θ(t)) with respect to θ, the left-hand side of (4.68) equals zero. Therefore
maximizes Q(θ|θ(t)) with respect to θ, the left-hand side of (4.68) equals zero. Therefore
Thus, from (4.67) we arrive at
This update—relying on the approximation in (4.69)—is an example of a general strategy known as Aitken acceleration and was proposed for EM by Louis [424]. Aitken acceleration of EM is precisely the same as applying the Newton–Raphson method to find a zero of Ψ(θ) − θ, where Ψ is the mapping defined by the ordinary EM algorithm producing θ(t+1) = Ψ(θ(t)) [343].
Example 4.10 (Peppered Moths, Continued) This acceleration approach can be applied to Example 4.2. Obtaining l′′ is analytically more tedious than the simpler derivations employed for other EM approaches to this problem. Figure 4.3 shows the Aitken accelerated steps, which converge quickly to the solution. The procedure was started from ![]() , and step halving was used to ensure ascent.
, and step halving was used to ensure ascent. ![]()
Aitken acceleration is sometimes criticized for potential numerical instabilities and convergence failures [153, 344]. Further, when l′′(θ|x) is difficult to compute, this approach cannot be applied without overcoming the difficulty [20, 345, 450].
Section 4.2.1 noted that the EM algorithm converges at a linear rate that depends on the fraction of missing information. The updating increment given in (4.70) is, loosely speaking, scaled by the ratio of the complete information to the observed information. Thus, when a greater proportion of the information is missing, the nominal EM steps are inflated more.
Newton's method converges quadratically, but (4.69) only becomes a precise approximation as θ(t) nears ![]() . Therefore, we should only expect this acceleration approach to enhance convergence only as preliminary iterations hone θ sufficiently. The acceleration should not be employed without having taken some initial iterations of ordinary EM so that (4.69) holds.
. Therefore, we should only expect this acceleration approach to enhance convergence only as preliminary iterations hone θ sufficiently. The acceleration should not be employed without having taken some initial iterations of ordinary EM so that (4.69) holds.
4.3.3.2 Quasi-Newton Acceleration
The quasi-Newton optimization method discussed in Section 2.2.2.3 produces updates according to
for maximizing l(θ|x) with respect to θ, where M(t) is an approximation to l′′(θ(t)|x). Within the EM framework, one can decompose l′′(θ(t)|x) into a part computed during EM and a remainder. By taking two derivatives of (4.19), we obtain
at iteration t. The remainder is the last term in (4.72); suppose we approximate it by B(t). Then by using
(4.73) ![]()
in (4.71) we obtain a quasi-Newton EM acceleration.
A key feature of the approach is how B(t) approximates H′′(θ(t)|θ(t)). The idea is to start with B(0) = 0 and gradually accumulate information about H′′ as iterations progress. The information is accumulated using a sequence of secant conditions, as is done in ordinary quasi-Newton approaches (Section 2.2.2.3).
Specifically, we can require that B(t) satisfy the secant condition
(4.74) ![]()
where
(4.75) ![]()
and
(4.76) ![]()
Recalling the update (2.49), we can satisfy the secant condition by setting
(4.77) ![]()
where v(t) = b(t) − B(t)a(t) and c(t) = 1/[(v(t))Ta(t)].
Lange proposed this quasi-Newton EM algorithm, along with several suggested strategies for improving its performance [408]. First, he suggested starting with B(0) = 0. Note that this implies that the first increment will equal the EM gradient increment. Indeed, the EM gradient approach is exact Newton–Raphson for maximizing Q(θ|θ(t)), whereas the approach described here evolves into approximate Newton–Raphson for maximizing l(θ|x).
Second, Davidon's [134] update is troublesome if (v(t))Ta(t) = 0 or is small compared to ||v(t)|| · ||a(t)||. In such cases, we may simply set B(t+1) = B(t).
Third, there is no guarantee that ![]() will be negative definite, which would ensure ascent at the tth step. Therefore, we may scale B(t) and use
will be negative definite, which would ensure ascent at the tth step. Therefore, we may scale B(t) and use ![]() where, for example, α(t) = 2−m for the smallest positive integer that makes M(t) negative definite.
where, for example, α(t) = 2−m for the smallest positive integer that makes M(t) negative definite.
Finally, note that b(t) may be expressed entirely in terms of Q′ functions since
(4.78) ![]()
Equation (4.79) follows from (4.19) and the fact that l(θ|x) − Q(θ|θ(t)) has its minimum at θ = θ(t). The derivative at this minimum must be zero, forcing ![]() , which allows (4.80).
, which allows (4.80).
Example 4.11 (Peppered Moths, Continued) We can apply quasi-Newton acceleration to Example 4.2, using the expressions for Q′′ given in (4.64)–(4.66) and obtaining b(t) from (4.80). The procedure was started from ![]() and B(0) = 0, with step halving to ensure ascent.
and B(0) = 0, with step halving to ensure ascent.
The results are shown in Figure 4.3. Note that B(0) = 0 means that the first quasi-Newton EM step will match the first EM gradient step. The second quasi-Newton EM step completely overshoots the ridge of highest likelihood, resulting in a step that is just barely uphill. In general, the quasi-Newton EM procedure behaves like other quasi-Newton methods: There can be a tendency to step beyond the solution or to converge to a local maximum rather than a local minimum. With suitable safeguards, the procedure is fast and effective in this example. ![]()
The quasi-Newton EM requires the inversion of M(t) at step t. Lange et al. describe a quasi-Newton approach based on the approximation of −l′′(θ(t)|x) by some M(t) that relies on an inverse-secant update [409, 410]. In addition to avoiding computationally burdensome matrix inversions, such updates to θ(t) and B(t) can be expressed entirely in terms of l′(θ(t)|x) and ordinary EM increments when the M step is solvable.
Jamshidian and Jennrich elaborate on inverse-secant updating and discuss the more complex BFGS approach [344]. These authors also provide a useful survey of a variety of EM acceleration approaches and a comparison of effectiveness. Some of their approaches converge faster on examples than does the approach described above. In a related paper, they present a conjugate gradient acceleration of EM [343].
Problems
4.1. Recall the peppered moth analysis introduced in Example 4.2. In the field, it is quite difficult to distinguish the insularia and typica phenotypes due to variations in wing color and mottle. In addition to the 622 moths mentioned in the example, suppose the sample collected by the researchers actually included nU = 578 more moths that were known to be insularia or typical but whose exact phenotypes could not be determined.
4.2. Epidemiologists are interested in studying the sexual behavior of individuals at risk for HIV infection. Suppose 1500 gay men were surveyed and each was asked how many risky sexual encounters he had in the previous 30 days. Let ni denote the number of respondents reporting i encounters, for i = 1, . . ., 16. Table 4.2 summarizes the responses.
Table 4.2 Frequencies of respondents reporting numbers of risky sexual encounters; see Problem 4.2.

These data are poorly fitted by a Poisson model. It is more realistic to assume that the respondents comprise three groups. First, there is a group of people who, for whatever reason, report zero risky encounters even if this is not true. Suppose a respondent has probability α of belonging to this group.
With probability β, a respondent belongs to a second group representing typical behavior. Such people respond truthfully, and their numbers of risky encounters are assumed to follow a Poisson(μ) distribution.
Finally, with probability 1 − α − β, a respondent belongs to a high-risk group. Such people respond truthfully, and their numbers of risky encounters are assumed to follow a Poisson(λ) distribution.
The parameters in the model are α, β, μ, and λ. At the tth iteration of EM, we use θ(t) = (α(t), β(t), μ(t), λ(t)) to denote the current parameter values. The likelihood of the observed data is given by
(4.81) ![]()
where
for i = 1, . . ., 16.
The observed data are n0, . . ., n16. The complete data may be construed to be nz,0, nt,0, . . ., nt,16, and np,0, . . ., np,16, where nk,i denotes the number of respondents in group k reporting i risky encounters and k = z, t, and p correspond to the zero, typical, and promiscuous groups, respectively. Thus, n0 = nz,0 + nt,0 + np,0 and ni = nt,i + np,i for i = 1, . . ., 16. Let ![]() .
.
Define
for i = 0, . . ., 16. These correspond to probabilities that respondents with i risky encounters belong to the various groups.
4.3. The website for this book contains 50 trivariate data points drawn from the N3(μ, Σ) distribution. Some data points have missing values in one or more coordinates. Only 27 of the 50 observations are complete.
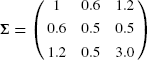
![]()
4.4. Suppose we observe lifetimes for 14 gear couplings in certain mining equipment, as given in Table 4.3 (in years). Some of these data are right censored because the equipment was replaced before the gear coupling failed. The censored data are in parentheses; the actual lifetimes for these components may be viewed as missing.
Table 4.3 Fourteen lifetimes for mining equipment gear couplings, in years. Right-censored values are in parenthesis. In these cases, we know only that the lifetime was at least as long as the given value.

Model these data with the Weibull distribution, having density function f(x) = abxb−1 exp { − axb} for x > 0 and parameters a and b. Recall that Problem 2.3 in Chapter 2 provides more details about such models. Construct an EM algorithm to estimate a and b. Since the Q function involves expectations that are analytically unavailable, adopt the MCEM strategy where necessary. Also, optimization of Q cannot be completed analytically. Therefore, incorporate the ECM strategy of conditionally maximizing with respect to each parameter separately, applying a one-dimensional
Newton-like optimizer where needed. Past observations suggest (a, b) = (0.003, 2.5) may be a suitable starting point. Discuss the convergence properties of the procedure you develop, and the results you obtain. What are the advantages and disadvantages of your technique compared to direct maximization of the observed-data likelihood using, say, a two-dimensional quasi-Newton approach?
4.5. A hidden Markov model (HMM) can be used to describe the joint probability of a sequence of unobserved (hidden) discrete-state variables, H = (H0, . . ., Hn), and a sequence of corresponding observed variables O = (O0, . . ., On) for which Oi is dependent on Hi for each i. We say that Hi emits Oi; consideration here is limited to discrete emission variables. Let the state spaces for elements of H and O be ![]() and
and ![]() respectively.
respectively.
Let O≤j and O>j denote the portions of O with indices not exceeding j and exceeding j, respectively, and define the analogous partial sequences for H. Under an HMM, the Hi have the Markov property
and the emissions are conditionally independent, so
Time-homogeneous transitions of the hidden states are governed by transition probabilities p(h, h∗) = P[Hi+1 = h∗|Hi = h] for ![]() . The distribution for H0 is parameterized by π(h) = P[H0 = h] for
. The distribution for H0 is parameterized by π(h) = P[H0 = h] for ![]() . Finally, define emission probabilities e(h, o) = P[Oi = o|Hi = h] for
. Finally, define emission probabilities e(h, o) = P[Oi = o|Hi = h] for ![]() and
and ![]() . Then the parameter set θ = (π, P, E) completely parameterizes the model, where π is a vector of initial-state probabilities, P is a matrix of transition probabilities, and E is a matrix of emission probabilities.
. Then the parameter set θ = (π, P, E) completely parameterizes the model, where π is a vector of initial-state probabilities, P is a matrix of transition probabilities, and E is a matrix of emission probabilities.
For an observed sequence o, define the forward variables to be
and the backward variables to be
for i = 1, . . ., n and each ![]() . Our notation suppresses the dependence of the forward and backward variables on θ. Note that
. Our notation suppresses the dependence of the forward and backward variables on θ. Note that
The forward and backward variables are also useful for computing the probability that state h occurred at the ith position of the sequence given O = o according to P[Hi = h|O = o, θ] = ∑ h![]() Hα(i, h)β(i, h)/P[O = o|θ], and expectations of functions of the states with respect to these probabilities.
Hα(i, h)β(i, h)/P[O = o|θ], and expectations of functions of the states with respect to these probabilities.
- Initialize α(0, h) = π(h)e(h, o0).
- For i = 0, . . ., n − 1, let
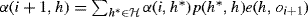 .
.
- Initialize β(n, h) = 1.
- For i = n, . . ., 1, let
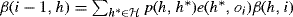 .
.
In addition to considering multiple sequences, HMMs and the Baum–Welch algorithm can be generalized for estimation based on more general emission variables and emission and transition probabilities that have more complex parameterizations, including time inhomogeneity.