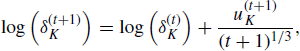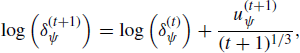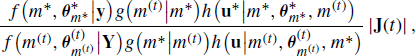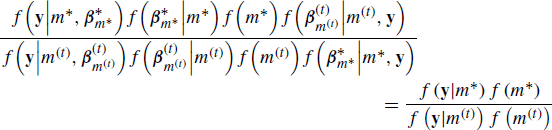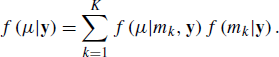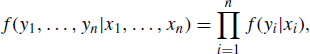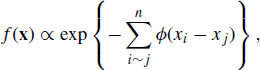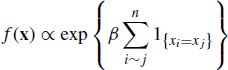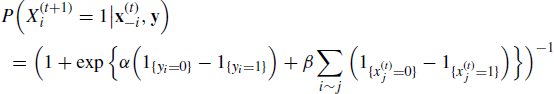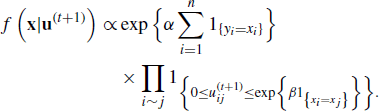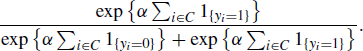Chapter 8
Advanced Topics in MCMC
The theory and practice of Markov chain Monte Carlo continues to advance at a rapid pace. Two particularly notable innovations are the dimension shifting reversible jump MCMC method and approaches for adapting proposal distributions while the algorithm is running. Also, applications for Bayesian inference continue to be of broad interest. In this chapter we survey a variety of higher level MCMC methods and explore some of the possible uses of MCMC to solve challenging statistical problems.
Sections 8.1–8.5 introduce a wide variety of advanced MCMC topics, including adaptive, reversible jump, and auxiliary variable MCMC, additional Metropolis–Hasting methods, and perfect sampling methods. In Section 8.6 we discuss an application of MCMC to maximum likelihood estimation. We conclude the chapter in Section 8.7 with an example where several of these methods are applied to facilitate Bayesian inference for spatial or image data.
8.1 Adaptive MCMC
One challenge with MCMC algorithms is that they often require tuning to improve convergence behavior. For example, in a Metropolis–Hastings algorithm with a normally distributed proposal distribution, some trial and error is usually required to tune the variance of the proposal distribution to achieve an optimal acceptance rate (see Section 7.3.1.3). Tuning the proposal distribution becomes even more challenging when the number of parameters is large. Adaptive MCMC (AMCMC) algorithms allow for automatic tuning of the proposal distribution as iterations progress.
Markov chain Monte Carlo algorithms that are adaptive have been considered for some time but formidable theory was typically required to prove stationarity of the resulting Markov chains. More recently, the development of simplified criteria for confirming theoretical convergence of proposed algorithms has led to an explosion of new adaptive MCMC algorithms [12, 16, 550]. Before describing these algorithms it is imperative to stress that care must be taken when developing and applying adaptive algorithms to ensure that the chain produced by the algorithm has the correct stationary distribution. Without such care, the adaptive algorithm will not produce a Markov chain because the entire path up to present time will be required to determine the present state. Another risk of adaptive algorithms is that they may depend too heavily on previous iterations, thus impeding the algorithm from fully exploring the state space. The best adaptive MCMC algorithms solve these problems by progressively reducing the amount of tuning as the number of iterations increases.
An MCMC algorithm with adaptive proposals is ergodic with respect to the target stationary distribution if it satisfies two conditions: diminishing adaptation and bounded convergence. Informally, diminishing (or vanishing) adaptation says that as t→ ∞, the parameters in the proposal distribution will depend less and less on earlier states of the chain. The diminishing adaptation condition can be met either by modifying the parameters in the proposal distribution by smaller amounts or by making the adaptations less frequently as t increases. The bounded convergence (containment) condition considers the time until near convergence. Let D(t) denote the total variation distance between the stationary distribution of the transition kernel employed by the AMCMC algorithm at time t and the target stationary distribution. (The total variation distance can be informally described as the largest possible distance between two probability distributions.) Let M(t)(
) be the smallest t such that D(t) < . The bounded convergence condition states that the stochastic process M(t)() is bounded in probability for any > 0. The technical specifications of the diminishing adaptation and the bounded convergence conditions are beyond the scope of this book; see [550] for further discussion. However, in practice these conditions lead to simpler, verifiable conditions that are sufficient to guarantee ergodicity of the resulting chain with respect to the target stationary distribution and are easier to check. We describe these conditions for applications of specific AMCMC algorithms in the sections below.
8.1.1 Adaptive Random Walk Metropolis-Within-Gibbs Algorithm
The method discussed in this section is a special case of the algorithm in Section 8.1.3, but we prefer to begin here at a simpler level. Consider a Gibbs sampler where the univariate conditional density for the ith element of 
is not available in closed form. In this case, we might use a random walk Metropolis algorithm to simulate draws from the ith univariate conditional density (Section 7.1.2). The goal of the AMCMC algorithm is to tune the variance of the proposal distribution so that the acceptance rate is optimal (i.e., the variance is neither too large nor too small). While many variants of the adaptive Metropolis-within-Gibbs algorithm are possible, we first consider an adaptive normal random walk Metropolis–Hastings algorithm [551].
In the algorithm below, the adaptation step is performed only at specific times, for example, iterations t 
{50, 100, 150, . . . }. We denote these as batch times Tb where b = 0, 1, . . ., the proposal variance is first tuned at iteration T1 = 50 and the next at iteration T2 = 100. The proposal distribution variance 
will be changed at these times. Performing the adaptation step every 50 iterations is a common choice; other updating intervals are reasonable depending on the total number of MCMC iterations for a particular problem and the mixing performance of the chain.
We present the adaptive random walk Metropolis-within-Gibbs algorithm as if the parameters were arranged so that the univariate conditional density for the first element of X is not available in closed form. An adaptive Metropolis-within-Gibbs update is used for this element. We assume that the univariate conditional densities for the remaining elements of X permit standard Gibbs updates. The adaptive random walk Metropolis-within-Gibbs proceeds as follows.
.
using a random walk update using the following steps:
by drawing 
and then set 
.(8.1) 
according to the following:
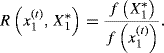
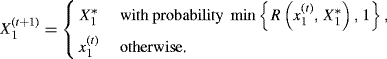
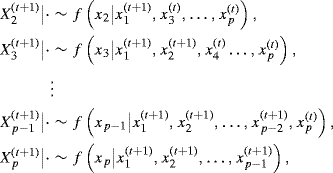
, where 0.01 is an arbitrary constant that initially limits the magnitude of adaptation.In the adaptation step, the variance of the proposal distribution is usually tuned with the goal of obtaining a proposal acceptance rate of about 0.44 (so, 44% of proposals are accepted) when X1 is univariate. This rate has been shown to be optimal for univariate normally distributed target and proposal distributions (see Section 7.3.1.3).
As for any AMCMC implementation, we need to check the convergence criteria. For the Metropolis-within-Gibbs algorithm, the diminishing adaptation condition is satisfied when δ(b) → 0 as b→ ∞. The bounded convergence condition is satisfied if log (σb) [− M, M] where M< ∞ is some finite bound. Less stringent—but perhaps less intuitive—requirements also satisfy the bounded convergence condition; see [554].
The adaptive algorithm above can be generalized to other random walk distributions. Generally, in step 2(a), generate 
by drawing ~ h() for some density h. With this change, note that in step 2(b), the Metropolis–Hastings ratio will need to be adapted to include the proposal distribution as in (7.1) if h is not symmetric.
The adaptive Metropolis-within-Gibbs algorithm is particularly useful when there are many parameters, each with its own variance to be tuned. For example, AMCMC methods have been used successfully for genetic data where the number of parameters can grow very quickly [637]. In that case, the algorithm above will need to be modified so that each element of X will have its own adaptation step and adaptive variance. We demonstrate a similar situation in Example 8.1. Alternatively, the proposal variance can be adapted jointly by accounting for the var{X}. This is discussed further in Section 8.1.3.
8.1.2 General Adaptive Metropolis-Within-Gibbs Algorithm
The adaptive random walk Metropolis-within-Gibbs algorithm is a modification of the random walk algorithm (Section 7.1.2). Other adaptive forms of the Metropolis-within-Gibbs algorithm can be applied as long as the diminishing adaptation and the bounded convergence conditions are met. In the example below we develop one such algorithm for a realistic example.
Example 8.1 (Whale Population Dynamics) Population dynamics models describe changes in animal abundance over time. Natural mortality, reproduction, and human-based removals (e.g., catch) usually drive abundance trends. Another important concept in many such models is carrying capacity, which represents the number of animals that can be sustained in equilibrium with the amount of resources available within the limited range inhabited by the population. As animal abundance increases toward (and potentially beyond) carrying capacity, there is greater competition for limited resources, which reduces net population growth or even reverses it when abundance exceeds carrying capacity. This dependence of the population growth rate on how near the current abundance is to carrying capacity is called density dependence.
A simple discrete-time density-dependent population dynamics model is
where Ny and Cy, respectively, represent abundance and catch in year y, r denotes the intrinsic growth rate, which encompasses both productivity and natural mortality, and K represents carrying capacity. This model is known as the Pella–Tomlinson model [504].
In application, this model should not be taken too literally. Abundances may be rounded to integers, but allowing fractional animals is also reasonable. Carrying capacity can be considered an abstraction, allowing the model to exhibit density-dependent dynamics rather than imposing an abrupt and absolute ceiling for abundance or allowing unlimited growth. Our implementation of (8.2) assumes that abundance is measured on the first day of the year and whales are harvested on the last day.
Consider estimating the parameters in model (8.2) when one knows Cy in every year and has observed estimates of Ny for at least some years over the modeling period. When the population is believed to have been in equilibrium before the modeling period, it is natural to assume N0 = K, and we do so hereafter. In this case, the model contains two parameters: K and r.
Let the observed estimates of Ny be denoted 
. For whales, abundance surveys are logistically challenging and usually require considerable expenditures of time, effort, and money, so 
may be obtained only rarely. Thus, in this example based on artificial data there are only six observed abundance estimates, denoted 
.
The website for this book provides catch data for 101 years, along with survey abundance estimates 
for y {14, 21, 63, 93, 100}. Each abundance estimate includes an estimated coefficient of variation 
. Conditionally on the 
, let us assume that each abundance estimate 
is lognormally distributed as follows:
(8.3) 
where 
. Figure 8.1 shows the available data and the estimated population trajectory using the maximum a posteriori estimate of r and K discussed later. For the purposes of this example, let us assume that 
for all y and incorporate ψ as a third parameter in the model. The overall likelihood is written 
.
Figure 8.1 Six abundance estimates and the maximum a posteriori population trajectory estimate for the whale dynamics model in Example 8.1.
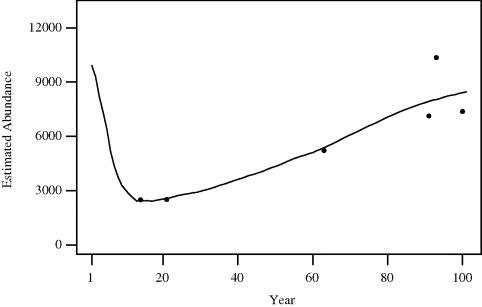
This setup conceals a serious challenge for analysis that is induced by two aspects of the data. First, the catches were huge in a brief early period, causing severe population decline, with subsequent small catches allowing substantial recovery. Second, most of the available abundance estimates correspond either to the near present or to years that are near the population nadir that occurred many years ago. Together, these facts require that any population trajectory reasonably consistent with the observed data must “thread the needle” by using parameter values for which the trajectory passes through appropriately small abundances in the distant past and recovers to observed levels in the present. This situation forces a strong nonlinear dependence between K and r: for any K only a very narrow range of r values can produce acceptable population trajectories, especially when K is at the lower end of its feasible values.
We adopt a Bayesian approach for estimating the model parameters using the independent priors
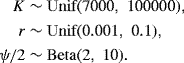
These choices are based on research for other whale species and basic biological limitations such as gestation and reproduction limits. Denote the resultant joint prior distribution as p(K, r, ψ).
For posterior inference we will use a hybrid Gibbs approach (Section 7.2.5) since the univariate conditional distributions are not available in closed form. We update each parameter using a Metropolis–Hastings update.
Let Gibbs cycles be indexed by t. The proposals for each parameter at cycle t + 1 are taken to be random Markov steps from their previous values. Specifically,
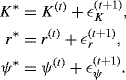
The proposal distributions for the parameters, which we will denote gK, gr, and gψ, are determined by the conditional distributions of 
, 
, and 
. We denote those distributions as 
, 
, and 
. For this example, we use
where the support regions of these densities are
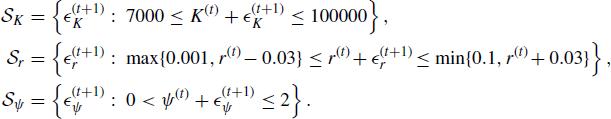
Lastly, 
if 
and zero otherwise, and ϕ(z; a, b) represents the normal distribution density for Z with mean a and standard deviation b. Note that 
is simply a uniform distribution over 
.
These proposal distributions (8.4)–(8.6) are sufficient to specify gK, gr and gψ. Note that proposals are not symmetric in the sense that the probability density for proposing θ∗ from θ(t) is not the same as for proposing θ(t) from θ∗ for θ {K, r, ψ}. This fact holds because in each case the truncation of the distribution of the proposed increment depends on the previous parameter value. Hence when calculating transition probabilities one cannot ignore the direction of transition. Moreover, the setup described above is not a random walk because the Markov increments in (8.4)–(8.6) are not independent of the parameter values at the previous time.
Before we consider an adaptive MCMC approach, let us review a standard implementation. At iteration t, a nonadaptive MCMC algorithm to sample from the posterior is given by:
, 
, and 
as (8.4), (8.5), and (8.6). This step, which doesn't depend on t, is included here nevertheless because when we switch to an adaptive method these definitions will change at each iteration.
, 
, and 
from the distributions specified in step 1.
.
.
.
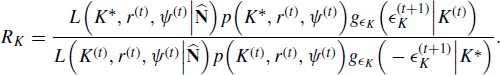
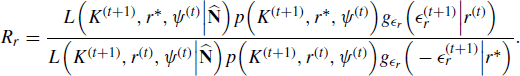
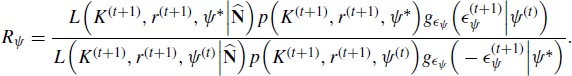
Applying this algorithm for a chain length of 45,000 with a burn-in of 10,000 shows that the mixing properties of this chain are poor. For example, after burn-in the proposal acceptance rates are 81, 27, and 68% for K, r, and ψ, respectively. It would be more desirable to achieve acceptance rates near 44% (see Section 7.3.1.3).
Now we try to improve MCMC performance using an adaptive approach. Redefine the proposal distributions from (8.4)–(8.6) as follows:
(8.8) 
where
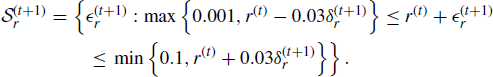
Here, 
, 
, and 
are adaptation factors that vary as t increases. Thus, these equations allow the standard deviations of the normally distributed increments and the range of the uniformly distributed increment to decrease or increase over time.
For this example, we adjust 
, 
, and 
every 1500th iteration. The expressions for rescaling the adaptation factors are
(8.11) 
where 
, 
, and 
are explained below. Thus by controlling {uK, ur, uψ} we control how the proposal distributions adapt.
Each adaptation depends on an acceptance rate, that is, the percentage of iterations within a specified period for which the proposal is accepted. At a specific adaptation step ta we set 
if the acceptance rate for θ during the previous 1500 iterations was less than 44% and 
otherwise, separately for the three parameters indexed as θ {K, r, ψ}. Thus before generating the (ta + 1)th proposals we observe the separate acceptance rates arising from steps 3c, 4c, and 55.3 above during {t : ta − 1500 < t ≤ ta}. Then 
, 
, and 
are individually set to reflect the algorithm performance for each of the parameters during that time period. The u values may have different signs at any adaptation step, so the multiplicative factors 
, 
, and 
will increase and decrease separately as simulations progress.
Using this approach, the adaptive MCMC algorithm for this example will follow the same six steps as above for advancing from t to t + 1 except that step 1 is replaced with
{1500, 3000, . . . 42000}, then
, 
, and 
.
, 
, and 
as in 
, 
, and 
be updated as in 
, 
, and 
remain unchanged from the previous iteration.The diminishing adaptation condition holds since u(t+1)/(t + 1)1/3 → 0 in (8.10)–(8.12). The bounded convergence condition holds because these adaptations are restricted to a finite interval. Actually, we did not state this explicitly in our presentation of the approach because in our example the adaptations settled down nicely without the need to impose bounds.
Figure 8.2 shows how the acceptance rates for each parameter change as iterations progress. In this figure, we see that the initial proposal distributions for K and ψ are too concentrated, yielding insufficient exploration of the posterior distribution and acceptance rates that are too high. In contrast, the original proposal distribution for r is too broad, yielding acceptance rates that are too low. For all three parameters, as iterations progress the proposal distributions are adjusted to provide acceptance rates near 0.44. The evolution of these proposal distributions by means of adjusting 
, 
, and 
is not monotonic and is subject to some Monte Carlo variation. Indeed, the 
, 
, and 
change sign occasionally—but not necessarily simultaneously—as acceptance rates vary randomly for each block of iterations between adaptation steps. Nevertheless, the trends in 
, 
, and 
are in the correct directions.
Figure 8.2 Trends in acceptance rate (top row) and the adapting proposal dispersion parameters (bottom row) for the whale dynamics model in Example 8.1. The range of the horizontal axes is 0–45,000 and adaptations are made every 1500 iterations.
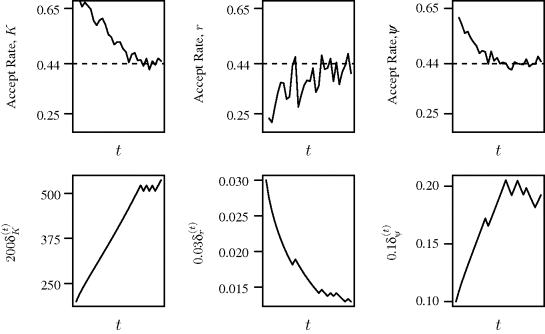
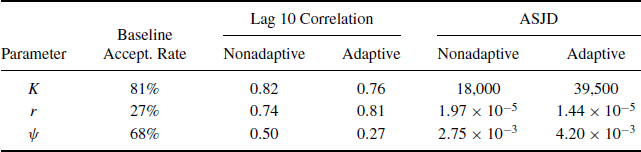
Table 8.1 compares some results from the nonadaptive and adaptive approaches. The results in Table 8.1 are compiled over only the last 7500 iterations of the simulation. For each of the three parameters, the table provides the lag 10 correlation within each chain. For K and r, these correlations are extremely high because—as noted above—the version of the model we use here forces K and r to lie within a very narrow nonlinear band of the joint parameter space. This makes it very difficult for the chain using independent steps for K and r to travel along this narrow high posterior probability ridge. Therefore it is difficult for univariate sample paths of K and r to travel quickly around the full extent of their marginal posterior distributions. The table also reports the average squared jumping distance (ASJD) for each parameter. The ASJD is the sum of the squared distances between proposed values and chosen values weighted by the acceptance probabilities. The adaptive method provided increased ASJDs and decreased lag correlations when acceptance rates were initially too high, but decreased ASJDs and increased lag correlations when acceptances were initially too rare. 
Table 8.1 Comparison of mixing behavior for standard and adaptive Metropolis within Gibbs chains for Example 8.1. The ‘Baseline’ column shows the acceptance rate for the nonadaptive approach. The ASJD columns report average squared jumping distance, as discussed in the text.
While the adaptive Metropolis-within-Gibbs algorithm is simple to understand and to apply, it ignores the correlations between the parameters. More sophisticated adaptive algorithms can have better convergence properties. The adaptive Metropolis algorithm incorporates this correlation into the adaptation.
8.1.3 Adaptive Metropolis Algorithm
In this chapter and the previous chapter, we have stressed that a good proposal distribution produces candidate values that cover the support of the stationary distribution in a reasonable number of iterations and produces candidate values that are not accepted or rejected too frequently. The goal of the adaptive Metropolis algorithm is to estimate the variance of the proposal distribution during the algorithm, adapting it in pursuit of the the optimal acceptance rate. In particular, the adaptive Metropolis algorithm is a one-step random walk Metropolis algorithm (Section 7.1.2) with a normal proposal distribution whose variance is calibrated using previous iterations of the chain.
Consider a normal random walk update for a p-dimensional X via the Metropolis algorithm [12]. At each iteration of the chain, a candidate value X∗ is sampled from a proposal distribution N(X(t), λΣ(t)). The goal is to adapt the covariance matrix Σ(t) of the proposal distribution during the algorithm. For a d-dimensional spherical multivariate normal target distribution where Σπ is the true covariance matrix of the target distribution, the proposal distribution (2.382/p)Σπ has been shown to be optimal with a corresponding acceptance rate of 44% when p = 1, which decreases to 23% as p increases [223]. Thus, in one version of the adaptive Metropolis algorithm, λ is set to (2.382/p) [288]. Since Σπ is unknown, it is estimated based on previous iterations of the chain. An adaptation parameter γ(t) is used to blend Σ(t) and Σ(t+1) in such a way that the diminishing adaptation condition will be upheld. A parameter μ(t) is also introduced and estimated adaptively. This is used to estimate the covariance matrix Σ(t), since var
.
This adaptive Metropolis algorithm begins at t = 0 with the selection of X(0) = x(0) drawn at random from some starting distribution g, with the requirement that 
where f is the target distribution. Similarly, initialize μ(0) and Σ(0); common choices are μ(0) = 0 and Σ(0) = I. Given X(t) = x(t), μ(t), and Σ(t), the algorithm generates X(t+1) as follows:
is the Metropolis-Hastings ratio given in (7.1).
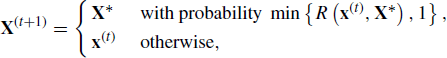
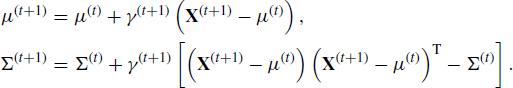
The updating formula for Σ(t) is constructed so that it is computationally quick to calculate and so that the adaptation diminishes as the number of iterations increases. To uphold the diminishing adaptation condition, it is required that limt→∞ γ(t) = 0. The additional condition that 
allows the sequence Σ(t) to move an infinite distance from its initial value [16].
Adapting both the mean and the variance of the proposal distribution in the adaptation step may be overkill, but it can have some advantages [12]. Specifically, the strategy can result in a more conservative sampler in the sense the sampler may resist large moves to poor regions of the parameter space.
Several enhancements to the adaptive Metropolis algorithm may improve performance. It may make sense to adapt λ as well as adapt Σ(t) during the algorithm. In this enhancement λ is replaced by λ(t), and then λ(t) and Σ(t) are updated independently. Specifically, in step 3 of the adaptive Metropolis algorithm λ(t+1) is also updated using
where a denotes the target acceptance rate (e.g., 0.234 for higher-dimensional problems).
One drawback with the adaptive Metropolis algorithm above is that all components are accepted or rejected simultaneously. This is not efficient when the problem is high dimensional (i.e., large p). An alternative is to develop a componentwise hybrid Gibbs adaptive Metropolis algorithm where each component is given its own scaling parameter λ(t+1) and is accepted/rejected separately in step 2. In this case, the constant a in (8.13) is usually set to a higher value, for example, a = 0.44, since now components are updated individually (see Section 7.3.1.3). In addition, the components could be updated in random order; see random scan Gibbs sampling in Section 7.2.3.
Another variation is to carry out the adaptation in batches instead of every iteration. With the batching strategy, the adaptation (step 3 in the adaptive Metropolis algorithm) is only implemented at predetermined times {Tb} for b = 0, 1, 2, . . . . For example, the adaptation step could occur at a fixed interval, such as t {50, 100, 150, . . . }. Alternatively, the batching scheduling could be designed with an increasing number of iterations between adaptations, for example, t {50, 150, 300, 500, . . . }. A batch approach was used in Example 8.1.
The batchwise adaptive Metropolis algorithm is described below.
.
is given in (7.1).
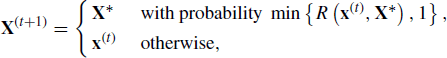
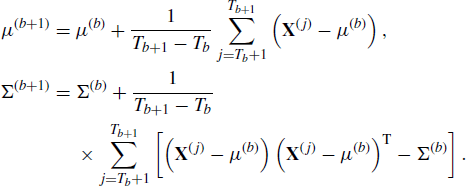
Note that in this algorithm, the diminishing adaptation condition is upheld when limb→∞(Tb+1− Tb) = ∞. It has also been suggested that adaptation times could be selected randomly. For example, one could carry out the adaptation with probability p(t) where limt→∞p(t) = 0 ensures diminishing adaptation [550].
The AMCMC algorithms described here all share the property that they are time inhomogeneous, that is, the proposal distributions change over time. Other time-inhomogeneous MCMC algorithms are described in Section 8.4.
A wide variety of other AMCMC algorithms have been suggested. This area will likely continue to develop rapidly [12, 16, 288, 551].
8.2 Reversible Jump MCMC
In Chapter 7 we considered MCMC methods for simulating X(t) for t = 1, 2, . . . from a Markov chain with stationary distribution f. The methods described in Chapter 7 required that the dimensionality of X(t) (i.e., of its state space) and the interpretation of the elements of X(t) do not change with t. In many applications, it may be of interest to develop a chain that allows for changes in the dimension of the parameter space from one iteration to the next. Green's reversible jump Markov chain Monte Carlo (RJMCMC) method permits transdimensional Markov chain Monte Carlo simulation [278]. We discuss this approach below in the context of Bayesian model uncertainty. The full generality of RJMCMC is described in many of the references cited here.
Consider constructing a Markov chain to explore a space of candidate models, each of which might be used to fit observed data y. Let 
denote a countable collection of models under consideration. A parameter vector θm denotes the parameters in the mth model. Different models may have different numbers of parameters, so we let pm denote the number of parameters in the mth model. In the Bayesian paradigm, we may envision random variables X = (M, θM) which together index the model and parameterize inference for that model. We may assign prior distributions to these parameters, then seek to simulate from their posterior distribution using an MCMC method for which the tth random draw is 
. Here 
, which denotes the parameters drawn for the model indexed by M(t), has dimension 
that can vary with t.
Thus, the goal of RJMCMC is to generate samples with joint posterior density 
. This posterior arises from Bayes' theorem via
(8.14) 
where 
denotes the density of the observed data under the mth model and its parameters, 
denotes the prior density for the parameters in the mth model, and f(m) denotes the prior density of the mth model. A prior weight of f(m) is assigned to the mth model so 
.
The posterior factorization
suggests two important types of inference. First, 
can be interpreted as the posterior probability for the mth model, normalized over all models under consideration. Second, 
is the posterior density of the parameters in the mth model.
RJMCMC enables the construction of an appropriate Markov chain for X that jumps between models with parameter spaces of different dimensions. Like simpler MCMC methods, RJMCMC proceeds with the generation of a proposed step from the current value x(t) to X∗, and then a decision whether to accept the proposal or to keep another copy of x(t). The stationary distribution for our chain will be the posterior in (8.15) if the chain is constructed so that
for all m1 and m2, where a(x2|x1, Y) denotes the density for the chain moving to state 
at time t + 1, given that it was in state 
at time t. Chains that meet this detailed balance condition are termed reversible because the direction of time does not matter in the dynamics of the chain.
The key to the RJMCMC algorithm is the introduction of auxiliary random variables at times t and t + 1 with dimensions chosen so that the augmented variables (namely X and the auxiliary variables) at times t and t + 1 have equal dimensions. We can then construct a Markov transition for the augmented variable at time t that maintains dimensionality. This dimension-matching strategy enables the time-reversibility condition to be met by using a suitable acceptance probability, thereby ensuring that the Markov chain converges to the joint posterior for X. Details of the limiting theory for these chains are given in [278, 279].
To understand dimension matching, it is simplest to begin by considering how one might propose parameters θ2 corresponding to a proposed move from a model 
with p1 parameters to a model 
with p2 parameters when p2 > p1. A simple approach is to generate θ2 from an invertible deterministic function of both θ1 and an independent random component U1. We can write θ2 = q1,2(θ1, U1). Proposing parameters for the reverse move can be carried out via the inverse transformation, 
. Note that q2,1 is an entirely deterministic way to propose θ1 from a given θ2.
Now generalize this idea to generate an augmented candidate parameter vector 
and auxiliary variables U∗), given a proposed move to M∗ from the current model, m(t). We can apply an invertible deterministic function qt,∗ to θ(t) and some auxiliary random variables U to generate
where U is generated from proposal density h(·|m(t), θ(t), m∗). The auxiliary variables U∗ and U are used so that qt,∗ maintains dimensionality during the Markov chain transition at time t, but are discarded subsequently.
When 
, the approach in (8.16) allows familiar proposal strategies. For example, a random walk could be obtained using 
with U ~ N(0, σ2I) having dimension 
. Alternatively, a Metropolis–Hastings chain can be constructed by using 
when 
, for an appropriate functional form of qt,∗ and suitable U. No U∗ would be required to equalize dimensions. When 
, the U can be used to expand parameter dimensionality; U∗ may or may not be necessary to equalize dimensions, depending on the strategy employed. When 
, both U and U∗ may be unnecessary: for example, the simplest dimension reduction is deterministically to reassign some elements of θ(t) to U∗ and retain the rest for 
. In all these cases, the reverse proposal is again obtained from the inverse of qt,∗.
Assume that the chain is currently visiting model m(t), so the chain is in the state 
. The next iteration of the RJMCMC algorithm can be summarized as follows:
of dimension 
.
from a proposal distribution with density 
. Let
to 
and the auxiliary variables have dimensions satisfying 
.
, compute the Metropolis–Hastings ratio given by
(8.18) 
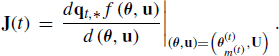
. Otherwise, reject the candidate draw and set X(t+1) = x(t).The last term in (8.17) is the absolute value of the determinant of the Jacobian matrix arising from the change of variables from 
to 
. If 
, then (8.17) simplifies to the standard Metropolis–Hastings ratio (7.1). Note that it is implicitly assumed here that the transformation qt,∗ is differentiable.
Example 8.2 (Jumping between Two Simple Models) An elementary example illustrates some of the details described above [278]. Consider a problem with K = 2 possible models: The model 
has a one-dimensional parameter space θ1 = α, and the model 
has a two-dimensional parameter space θ2 = (β, γ). Thus p1 = 1 and p2 = 2. Let m1 = 1 and m2 = 2.
If the chain is currently in state 
and the model 
is proposed, then a random variable U ~ h(u|1, θ1, 2) is generated from some proposal density h. Let β = α − U and γ = α + U, so 
and
If the chain is currently in state 
and 
is proposed, then 
is the inverse mapping. Therefore
and U∗ is not required to match dimensions. This transition is entirely deterministic, so we replace h(u∗|2, θ2, 1) in (4.17) with 1.
Thus for a proposed move from 
to 
, the Metropolis–Hasting ratio (8.17) is equal to
The Metropolis–Hastings ratio equals the reciprocal of (8.19) for a proposed move from 
to 
.
There are several significant challenges to implementing RJMCMC. Since the number of dimensions can be enormous, it can be critical to select an appropriate proposal distribution h and to construct efficient moves between the different dimensions of the model space. Another challenge is the diagnosis of convergence for RJMCMC algorithms. Research in these areas is ongoing [72–74, 427, 604].
RJMCMC is a very general method, and reversible jump methods have been developed for a myriad of application areas, including model selection and parameter estimation for linear regression [148], variable and link selection for generalized linear models [487], selection of the number of components in a mixture distribution [74, 536, 570], knot selection and other applications in nonparametric regression [48, 162, 334], and model determination for graphical models [147, 248]. There are many other areas for potential application of RJMCMC. Genetic mapping was an early area of exploration for RJMCMC implementation; [122, 645, 648] there are claims that up to 20% of citations related to RJMCMC involve genetics applications [603].
RJMCMC unifies earlier MCMC methods to compare models with different numbers of parameters. For example, earlier methods for Bayesian model selection and model averaging for linear regression analysis, such as stochastic search variable selection [229] and MCMC model composition [527], can be shown to be special cases of RJMCMC [119].
8.2.1 RJMCMC for Variable Selection in Regression
Consider a multiple linear regression problem with p potential predictor variables in addition to the intercept. A fundamental problem in regression is selection of a suitable model. Let mk denote model k, which is defined by its inclusion of the i1th through idth predictors, where the indices {i1, . . ., id} are a subset of {1, . . ., p}. For the consideration of all possible subsets of p predictor variables, there are therefore K = 2p models under consideration. Using standard regression notation, let Y denote the vector of n independent responses. For any model mk, arrange the corresponding predictors in a design matrix 
, where 
is the n vector of observations of the ijth predictor. The predictor data are assumed fixed. We seek the best ordinary least squares model of the form
among all mk, where 
is a parameter vector corresponding to the design matrix for mk and the error variance is σ2. In the remainder of this section, conditioning on the predictor data is assumed.
The notion of what model is best may have any of several meanings. In Example 3.2 the goal was to use the Akaike information criterion (AIC) to select the best model [7, 86]. Here, we adopt a Bayesian approach for variable selection with priors on the regression coefficients and σ2, and with the prior for the coefficients depending on σ2. The immediate goal is to select the most promising subset of predictor variables, but we will also show how the output of an RJMCMC algorithm can be used to estimate a whole array of quantities of interest such as posterior model probabilities, the posterior distribution of the parameters of each model under consideration, and model-averaged estimates of various quantities of interest.
In our RJMCMC implementation, based on [119, 527], each iteration begins at a model m(t), which is described by a specific subset of predictor variables. To advance one iteration, the model M∗ is proposed from among those models having either one predictor variable more or one predictor variable fewer than the current model. Thus the model proposal distribution is given by 
, where
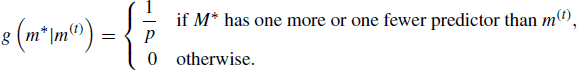
Given a proposed model M∗ = m∗, step 2 of the RJMCMC algorithm requires us to sample 
. A simplifying approach is to let U become the next value for the parameter vector, in which case we may set the proposal distribution h equal to the posterior for βm|(m, y), namely f(βm|m, y). For appropriate conjugate priors, 
has a noncentral t distribution [58]. We draw U from this proposal and set 
and 
. Thus 
, yielding a Jacobian of 1. Since 
, the Metropolis–Hastings ratio in (8.17) can be written as
after simplification. Here 
is the marginal likelihood, and 
is the prior density, for the model m∗. Observe that this ratio does not depend on 
or 
. Therefore, when implementing this approach with conjugate priors, one can treat the proposal and acceptance of β as a purely conceptual construct useful for placing the algorithm in the RJMCMC framework. In other words, we don't need to simulate β(t)|m(t), because 
is available in closed form. The posterior model probabilities and 
fully determine the joint posterior.
After running the RJMCMC algorithm, inference about many quantities of interest is possible. For example, from (8.15) the posterior model probabilities f(mk|y) can be approximated by the ratio of the number of times the chain visited the kth model to the number of iterations of the chain. These estimated posterior model probabilities can be used to select models. In addition, the output from the RJMCMC algorithm can be used to implement Bayesian model averaging. For example, if μ is some quantity of interest such as a future observable, the utility of a course of action, or an effect size, then the posterior distribution of μ given the data is given by
This is the average of the posterior distribution for μ under each model, weighted by the posterior model probability. It has been shown that taking account of uncertainty about the form of the model can protect against underestimation of uncertainty [331].
Example 8.3 (Baseball Salaries, Continued) Recall Example 3.3, where we sought the best subset among 27 possible predictors to use in linear regression modeling of baseball players' salaries. Previously, the objective was to find the best subset as measured by the minimal AIC value. Here, we seek the best subset as measured by the model with the highest posterior model probability.
We adopt a uniform prior over model space, assigning f(mk) = 2−p for each model. For the remaining parameters, we use a normal-gamma conjugate class of priors with 
and 
. For this construction, 
in (8.21) can be shown to be the noncentral t density (Problem 8.1). For the baseball data, the hyperparameters are set as follows. First, let ν = 2.58 and λ = 0.28. Next, 
is a vector of length 
whose first element equals the least squares estimated intercept from the full model. Finally, 
is a diagonal matrix with entries 
, where 
is the sample variance of y, 
is the sample variance of the ith predictor, and c = 2.58. Additional details are given in [527].
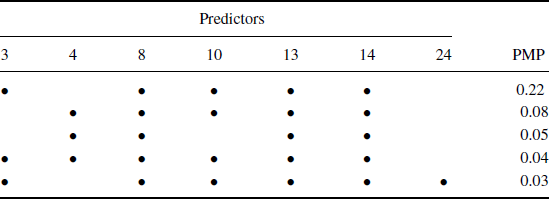
We ran 200,000 RJMCMC iterations. Table 8.2 shows the five models with the highest estimated posterior model probabilities. If the goal is to select the best model, then the model with the predictors 3, 8, 10, 13, and 14 should be chosen, where the predictor indices correspond to those in Table 3.2.
Table 8.2 RJMCMC model selection results for baseball example: the five models with the highest posterior model probability (PMP). The bullets indicate inclusion of the corresponding predictor in the given model, using the predictor indices given in Table 3.2.
The posterior effect probabilities, P(βi ≠ 0|y), for those predictors with probabilities greater than 0.10 are given in Table 8.3. Each entry is a weighted average of an indicator variable that equals 1 only when the coefficient is in the model, where the weights correspond to the posterior model probabilities as in Equation (8.22). These results indicate that free agency, arbitration status, and the number of runs batted in are strongly associated with baseball players' salaries.
Table 8.3 RJMCMC results for baseball example: the estimated posterior effect probabilities P(βi ≠ 0|y) exceeding 0.10. The predictor indices and labels correspond to those given in Table 3.2.
| Index | Predictor | P(βi ≠ 0|y) |
| 13 | FA | 1.00 |
| 14 | Arb | 1.00 |
| 8 | RBIs | 0.97 |
| 10 | SOs | 0.78 |
| 3 | Runs | 0.55 |
| 4 | Hits | 0.52 |
| 25 | SBs×OBP | 0.13 |
| 24 | SOs×errors | 0.12 |
| 9 | Walks | 0.11 |
Other quantities of interest based on variants of Equation (8.22) can be computed, such as the model-averaged posterior expectation and variance for each regression parameter, or various posterior salary predictions.
Alternative approaches to transdimensional Markov chain simulation have been proposed. One method is based on the construction of a continuous-time Markov birth-and-death process [89, 613]. In this approach, the parameters are modeled via a point process. A general form of RJMCMC has been proposed that unifies many of the existing methods for assessing uncertainty about the dimension of the parameter space [261]. Continued useful development in these areas is likely [318, 428, 603]. One area of promise is to combine RJMCMC and AMCMC.
8.3 Auxiliary Variable Methods
An important area of development in MCMC methods concerns auxiliary variable strategies. In many cases, such as Bayesian spatial lattice models, standard MCMC methods can take too long to mix properly to be of practical use. In such cases, one potential remedy is to augment the state space of the variable of interest. This approach can lead to chains that mix faster and require less tuning than the standard MCMC methods described in Chapter 7.
Continuing with the notation introduced in Chapter 7, we let X denote a random variable on whose state space we will simulate a Markov chain, usually for the purpose of estimating the expectation of a function of X ~ f(x). In Bayesian applications, it is important to remember that the random variables X(t) simulated in an MCMC procedure are typically parameter vectors whose posterior distribution is of primary interest. Consider a target distribution f which can be evaluated but not easily sampled. To construct an auxiliary variable algorithm, the state space of X is augmented by the state space of a vector of auxiliary variables, U. Then one constructs a Markov chain over the joint state space of (X, U) having stationary distribution (X, U) ~ f(x, u) that marginalizes to the target f(x). When simulation has been completed, inference is based only on the marginal distribution of X. For example, a Monte Carlo estimator of μ = ∫ h(x)f(x)dx is 
where (X(t), U(t)) are simulated in the augmented chain, but the U(t) are discarded.
Auxiliary variable MCMC methods were introduced in the statistical physics literature [174, 621]. Besag and Green noted the potential usefulness of this strategy, and a variety of refinements have subsequently been developed [41, 132, 328]. Augmenting the variables of interest to solve challenging statistical problems is effective in other areas, such as the EM algorithm described in Chapter 4 and the reversible jump algorithms described in Section 8.2. The links between EM and auxiliary variable methods for MCMC algorithms are further explored in [640].
Below we describe simulated tempering as an example of an auxiliary variable strategy. Another important example is slice sampling, which is discussed in the next subsection. In Section 8.7.2 we present another application of auxiliary variable methods for the analysis of spatial or image data.
8.3.1 Simulated Tempering
In problems with high numbers of dimensions, multimodality, or slow MCMC mixing, extremely long chains may be required to obtain reliable estimates of the quantities of interest. The approach of simulated tempering provides a potential remedy [235, 438]. Simulations are based on a sequence of unnormalized densities fi for i = 1, . . ., m, on a common sample space. These densities are viewed as ranging from cold (i = 1) to hot (i = m). Typically only the cold density is desired for inference, with the other densities being exploited to improve mixing. Indeed, the warmer densities should be designed so that MCMC mixing is faster for them than it is for f1.
Consider the augmented variable (X, I) where the temperature I is now viewed as random with prior I ~ p(i). From a starting value, (x(0), i(0)), we may construct a Metropolis–Hastings sampler in the augmented space as follows:
.
. A simple option is
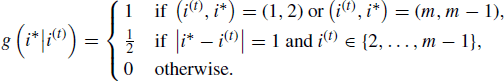
The simplest way to estimate an expectation under the cold distribution is to average realizations generated from it, throwing away realizations generated from other fi. To use more of the data, note that a state (x, i) drawn from the stationary distribution of the augmented chain has density proportional to fi(x)p(i). Therefore, importance weights 
can be used to estimate expectations with respect to a target density 
; see Chapter 6.
The prior p is set by the user and ideally should be chosen so that the m tempering distributions (i.e., the m states for i) are visited roughly equally. In order for all the tempering distributions to be visited in a tolerable running time, m must be fairly small. On the other hand, each pair of adjacent tempering distributions must have sufficient overlap for the augmented chain to move easily between them. This requires a large m. To balance these competing concerns, choices for m that provide acceptance rates roughly in the range suggested in Section 7.3.1.3 are recommended. Improvements, extensions, and related techniques are discussed in [232, 235, 339, 417, 480]. Relationships between simulated tempering and other MCMC and importance sampling methods are explored in [433, 682].
Simulated tempering is reminiscent of the simulated annealing optimization algorithm described in Chapter 3. Suppose we run simulated tempering on the state space for θ. Let L(θ) and q(θ) be a likelihood and prior for θ, respectively. If we let 
for τi = i and i = 1, 2, . . ., then i = 1 makes the cold distribution match the posterior for θ, and i > 1 generates heated distributions that are increasingly flattened to improve mixing. Equation (8.23) then evokes step 2 of the simulated annealing algorithm described in Section 3.3 to minimize the negative log posterior. We have previously noted that simulated annealing produces a time-inhomogeneous Markov chain in its quest to find an optimum (Section 3.3.1.2). The output of simulated tempering is also a Markov chain, but simulated tempering does not systematically cool in the same sense as simulated annealing. The two procedures share the idea of using warmer distributions to facilitate exploration of the state space.
8.3.2 Slice Sampler
An important auxiliary variable MCMC technique is called the slice sampler [132, 328, 481]. Consider MCMC for a univariate variable X ~ f(x), and suppose that it is impossible to sample directly from f. Introducing any univariate auxiliary variable U would allow us to consider a target density for (X, U) ~ f(x, u). Writing f(x, u) = f(x)f(u|x) suggests an auxiliary variable Gibbs sampling strategy that alternates between updates for X and U [328]. The trick is to choose a U variable that speeds MCMC mixing for X. At iteration t + 1 of the slice sampler we alternately generate X(t+1) and U(t+1) according to
(8.24) 
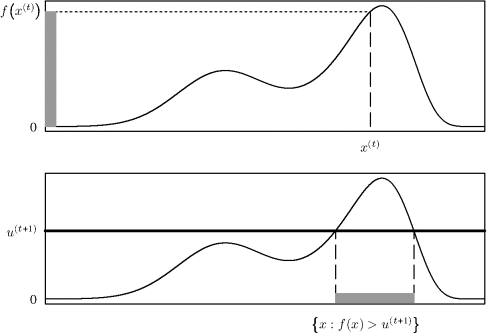
Figure 8.3 illustrates the approach. At iteration t + 1, the algorithm starts at x(t) shown in the upper panel. Then U(t+1) is drawn from Unif
. In the top panel this corresponds to sampling along the vertical shaded strip. Now X(t+1)|(U(t+1) = u(t+1)) is drawn uniformly from the set of x values for which f(x) ≥ u(t+1). In the lower panel this corresponds to sampling along the horizontal shaded strip.
Figure 8.3 Two steps of a univariate slice sampler for target distribution f.
While simulating from (8.25) is straightforward for this example, in other settings the set 
may be more complicated. In particular, sampling X(t+1)|(U(t+1) = u(t+1)) in (8.25) can be challenging if f is not invertible. One approach to implementing Equation (8.25) is to adopt a rejection sampling approach; see Section 6.2.3.
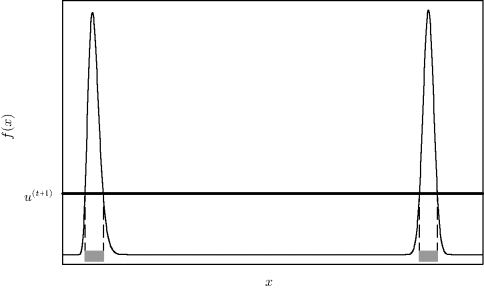
Example 8.4 (Moving between Distant Modes) When the target distribution is multimodal, one advantage of a slice sampler becomes more apparent. Figure 8.4 shows a univariate multimodal target distribution. If a standard Metropolis–Hastings algorithm is used togenerate samples from the target distribution, then the algorithm may find one mode of the distribution, but it may take many iterations to find the other mode unless the proposal distribution is very well tuned. Even if it finds both modes, it will almost never jump from one to the other. This problem will be exacerbated when the number of dimensions increases. In contrast, consider a slice sampler constructed to sample from the density shown in Figure 8.4. The horizontal shaded areas indicate the set defined in (8.25) from which X(t+1)|u(t+1) is uniformly drawn. Hence the slice sampler will have about a 50% chance of switching modes each iteration. Therefore the slice sampler will mix much better with many fewer iterations required.
Figure 8.4 The slice sampler for this multimodal target distribution draws X(t+1)|u(t+1) uniformly from the set indicated by the two horizontal shaded strips.
Slice samplers have been shown to have attractive theoretical properties [467, 543] but can be challenging to implement in practice [481, 543]. The basic slice sampler described above can be generalized to include multiple auxiliary variables U1, . . ., Uk and to accommodate multidimensional X [132, 328, 467, 543]. It is also possible to construct a slice sampler such that the algorithm is guaranteed to sample from the stationary distribution of the Markov chain [98, 466]. This is a variant of perfect sampling, which is discussed in Section 8.5.
8.4 Other Metropolis–Hastings Algorithms
8.4.1 Hit-and-Run Algorithm
The Metropolis–Hastings algorithm presented in Section 7.1 is time homogeneous in the sense that the proposal distribution does not change as t increases. It is possible to construct MCMC approaches that rely on time-varying proposal distributions, 
. Such methods can be very effective, but their convergence properties are generally more difficult to ascertain due to the time inhomogeneity [462]. The adaptive MCMC algorithms of Section 8.1 are examples of time-inhomogeneous algorithms.
One such strategy that resembles a random walk chain is known as the hit-and-run algorithm [105]. In this approach, the proposed move away from x(t) is generated in two stages: by choosing a direction to move and then a distance to move in the chosen direction. After initialization at x(0), the chain proceeds from t = 0 with the following steps.
, where the density 
is defined over Λ(t). The proposal distribution may differ from one iteration to the next only through a dependence on Λ(t).
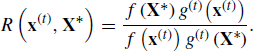
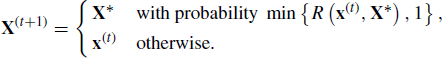
The above algorithm is one variant of several general hit-and-run approaches [105].
The direction distribution h is frequently taken to be uniform over the surface of the unit sphere. In p dimensions, a random variable may be drawn from this distribution by sampling a p-dimensional standard normal variable Y ~ N(0, I) and making the transformation 
.
The performance of this approach has been compared with that of other simple MCMC methods [104]. It has been noted that the hit-and-run algorithm can offer particular advantage when the state space of X is sharply constrained [29], thereby making it difficult to explore all regions of the space effectively with other methods. The choice of h has a strong effect on the performance and convergence rate of the algorithm, with the best choice often depending on the shape of f and the geometry of the state space (including constraints and the chosen units for the coordinates of X) [366].
8.4.2 Multiple-Try Metropolis–Hastings Algorithm
If a Metropolis–Hastings algorithm is not successful in some problem, it is probably because the chain is slow to converge or trapped in a local mode of f. To overcome such difficulties, it may pay to expand the region of likely proposals characterized by g(· |x(t)). However, this strategy often leads to very small Metropolis–Hastings ratios and therefore to poor mixing. Liu, Liang, and Wong proposed an alternative strategy known as multiple-try Metropolis–Hastings sampling for effectively expanding the proposal region to improve performance without impeding mixing [420].
The approach is to generate a larger number of candidates, thereby improving exploration of f near x(t). One of these proposals is then selected in a manner that ensures that the chain retains the correct limiting stationary distribution. We still use a proposal distribution g, along with optional nonnegative weights λ(x(t), x∗), where the symmetric function λ is discussed further below. To ensure the correct limiting stationary distribution, it is necessary to require that g(x∗|x(t)) > 0 if and only if g(x(t)|x∗) > 0, and that λ(x(t), x∗) > 0 whenever g(x∗|x(t)) > 0.
Let x(0) denote the starting value, and define
(8.26) 
Then, for t = 0, 1, . . ., the algorithm proceeds as follows:
i.i.d. from g(· |x(t)).
from the set of proposals, with probability proportional to 
for j = 1, . . ., k.
, sample k − 1 random variables 
i.i.d. from the proposal density 
. Set 
.(8.27)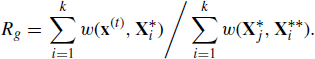 
(8.28) 
It is straightforward to show that this algorithm yields a reversible Markov chain with limiting stationary distribution equal to f. The efficiency of this approach depends on k, the shape of f, and the spread of g relative to f. It has been suggested that an acceptance rate of 40–50% be a target [420]. In practice, using the multiple-try Metropolis–Hastings algorithm to select from one of many proposals at each iteration can lead to chains with lower serial correlation. This leads to better mixing in the sense that larger steps can be made to find other local modes or to promote movement in certain advantageous directions when we are unable to encourage such steps through other means.
The weighting function λ can be used to further encourage certain types of proposals. The simplest choice is λ(x(t), x∗) = 1. An “orientational-biased” method with 
was suggested in [203]. Another interesting choice is 
, defined on the region where g(x∗|x(t)) > 0. When α = 1, the weight 
corresponds to the importance weight 
assigned to x∗ when attempting to sample from f using g and the importance sampling envelope (see Section 6.4.1).
8.4.3 Langevin Metropolis–Hastings Algorithm
In Section 7.1.2 we discussed random walk chains, a type of Markov chain produced by a simple variant of the Metropolis–Hastings algorithm. A more sophisticated version, namely a random walk with drift, can be generated using the proposal
where
and (t) is a p-dimensional standard normal random variable. The scalar σ is a tuning parameter whose fixed value is chosen by the user to control the magnitude of proposed steps. The standard Metropolis–Hastings ratio is used to decide whether to accept this proposal, using
Theoretical results indicate that the parameter σ should be selected so that the acceptance rate for the Metropolis–Hastings ratio computed using (8.31) should be 0.574 [548].
The proposal distribution for this method is motivated by a stochastic differential equation that produces a diffusion (i.e., a continuous-time stochastic process) with f as its stationary distribution [283, 508]. To ensure that the discretization of this process given by the discrete-time Markov chain described here shares the correct stationary distribution, Besag overlaid the Metropolis–Hastings acceptance strategy [37].
The requirement to know the gradient of the target (8.30) is not as burdensome as it may seem. Any unknown multiplicative constant in f drops out when the derivative is taken. Also, when exact derivatives are difficult to obtain, they can be replaced with numerical approximations.
Unlike a random walk, this algorithm introduces a drift that favors proposals that move toward modes of the target distribution. Ordinary Metropolis–Hastings algorithms—including the random walk chain and the independence chain—generally are driven by proposals that are made independently of the shape of f, thereby being easy to implement but sometimes slow to approach stationarity or adequately explore the support region of f. When performance of a generic algorithm is poor, problem-specific Metropolis–Hastings algorithms are frequently employed with specialized proposal distributions crafted in ways that are believed to exploit features of the target. Langevin Metropolis–Hastings algorithms also provide proposal distributions motivated by the shape of f, but the self-targeting is done generically through the use of the gradient. These methods can provide better exploration of the target distribution and faster convergence.
In some applications, the update given by (8.29) can yield Markov chains that fail to approach convergence in runs of reasonable length, and fail to explore more than one mode of f. Stramer and Tweedie [618] generalize (8.29) somewhat with different drift and scaling terms that yield improved performance. Further study of Langevin methods is given in [547, 548, 617, 618].
8.5 Perfect Sampling
MCMC is useful because at the tth iteration it generates a random draw X(t) whose distribution approximates the target distribution f as t → ∞. Since run lengths are finite in practice, much of the discussion in Chapter 7 pertained to assessing when the approximation becomes sufficiently good. For example, Section 7.3 presents methods to determine the run length and the number of iterations to discard (i.e., the burn-in). However, these convergence diagnostics all have various drawbacks. Perfect sampling algorithms avoid all these concerns by generating a chain that has exactly reached the stationary distribution. This sounds wonderful, but there are challenges in implementation.
8.5.1 Coupling from the Past
Propp and Wilson introduced a perfect sampling MCMC algorithm called coupling from the past (CFTP) [520]. Other expositions of the CFTP algorithm include [96, 165, 519]. The website maintained by Wilson surveys much of the early literature on CFTP and related methods [667].
CFTP is often motivated by saying that the chain is started at t = −∞ and run forward to time t = 0. While this is true, convergence does not suddenly occur in the step from t = − 1 to t = 0, and you are not required to somehow set t = −∞ on your computer. Instead, we will identify a window of time from t = τ < 0 to t = 0 for which whatever happens before τ is irrelevant, and the infinitely long progression of the chain prior to τ means that the chain is in its stationary distribution by time 0.
While this strategy might sound reasonable at the outset, in practice it is impossible to know what state the chain is in at time τ. Therefore, we must consider multiple chains: in fact, one chain started in every possible state at time τ. Each chain can be run forward from t = τ to t = 0. Because of the Markov nature of these chains, the chain outcomes at time τ + 1 depend only on their status at time τ. Therefore, this collection of chains completely represents every possible chain that could have been run from infinitely long ago in the past.
The next problem is that we no longer have a single chain, and it seems that chain states at time 0 will differ. To remedy this multiplicity, we rely on the idea of coupling. Two chains on the same state space with the same transition probabilities have coupled (or coalesced) at time t if they share the same state at time t. At this point, the two chains will have identical probabilistic properties, due to the Markov property and the equal transition probabilities. A third such chain could couple with these two at time t or any time thereafter. Thus, to eliminate the multiple chains introduced above, we use an algorithm that ensures that once chains have coupled, they follow the same sample path thereafter. Further, we insist that all chains must have coalesced by time 0. This algorithm will therefore yield one chain from t = 0 onwards which is in the desired stationary distribution.
To simplify presentation, we assume that X is unidimensional and has finite state space with K states. Neither assumption is necessary for CFTP strategies more general than the one we describe below.
We consider an ergodic Markov chain with a deterministic transition rule q that updates the current state of the chain, x(t), as a function of some random variable U(t+1). Thus,
For example, a Metropolis–Hastings proposal from a distribution with cumulative distribution function F can be generated using q(x, u) = F−1(u), and a random walk proposal can be generated using q(x, u) = x + u. In (8.32) we used a univariate U(t+1), but, more generally, chain transitions may be governed by a multivariate vector U(t+1). We adopt the general case hereafter.
CFTP starts one chain from each state in the state space at some time τ < 0 and transitions each chain forward using proposals generated by q. Proposals are accepted using the standard Metropolis–Hastings ratio. The goal is to find a starting time τ such that the chains have all coalesced by time t = 0 when run forwards in time from t = τ. This approach provides X(0), which is a draw from the desired stationary distribution f.
The algorithm to find τ and thereby produce the desired chain is as follows. Let 
be the random state at time t of the Markov chain started in state k, with k = 1, . . ., K.
, and run each chain forward to time 0 via the update 
for k = 1, . . ., K. If all K chains are in the same state at time 0, then the chains have coalesced and X(0) is a draw from f; the algorithm stops.
. Next, you must reuse the U(0) generated in step 1, so 
. If all K chains are in the same state at time 0, then the chains have coalesced and X(0) is a draw from f; the algorithm stops.Propp and Wilson show that the value of X(0) returned from the CFTP algorithm for a suitable q is a realization of a random variable distributed according to the stationary distribution of the Markov chain and that this coalescent value will be produced in finite time [520]. Even if all chains coalesce before time 0, you must use X(0) as the perfect sampling draw; otherwise sampling bias is introduced.
Obtaining the perfect sampling draw X(0) from f is not sufficient for most uses. Typically we desire an i.i.d. n-sample from f, either for simulation or to use in a Monte Carlo estimate of some expectation, μ = ∫ h(x)f(x)dx. A perfect i.i.d. sample from f can be obtained by running the CFTP algorithm n times to generate n individual values for X(0). If you only want to ensure that the algorithm is, indeed, sampling from f, but independence is not required, you can run CFTP once and continue to run the chain forward from its state at time t = 0. While the first option is probably preferable, the second option may be more reasonable in practice, especially for cases where the CFTP algorithm requires many iterations before coalescence is achieved. These are only the two simplest strategies available for using the output of a perfect sampling algorithm; see also [474] and the references in [667].
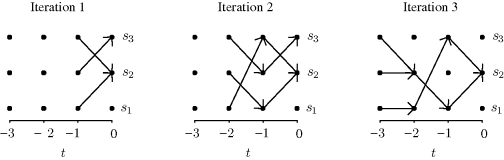
Example 8.5 (Sample Paths in a Small State Space) In the example shown in Figure 8.5, there are three possible states, s1, s2, s3. At iteration 1, a sample path is started from each of the three states at time τ = − 1. A random update U(0) is selected, and 
for k = 1, 2, 3. The paths have not all coalesced at time t = 0, so the algorithm moves to iteration 2. In iteration 2, the algorithm begins at time τ = − 2. The transition rule for the moves from t = − 2 to t = − 1 is based on a newly sampled update variable, U(−1). The transition rule for the moves from t = − 1 to t = 0 relies on the same U(0) value obtained previously in iteration 1. The paths have not all coalesced at time t = 0, so the algorithm moves to iteration 3. Here, the previous draws for U(0) and U(−1) are reused and a new U(−2) is selected. In iteration 3, all three sample paths visit state s2 at time t = 0, thus the paths have coalesced, and X(0) = s2 is a draw from the stationary distribution f.
Figure 8.5 Example of perfect sampling sample paths. See Example 8.5 for details.
Several finer details of CFTP implementation merit mention. First, note that CFTP requires reuse of previously generated variables U(t) and the shared use of the same U(t) realization to update all chains at time t. If the U(t) are not reused, the samples will be biased. Propp and Wilson show an example where the regeneration of the U(t) at each time biases the chain toward the extreme states in an ordered state space [520]. The reuse and sharing of past U(t) ensures that all chains coalesce by t = 0 when started at any time τ′ ≤ τ, where τ is the starting time chosen by CFTP. Moreover, this practice ensures that the coalescent state at time 0 is the same for all such chains in a given run, which enables the proof that CFTP produces an exact draw from f.
Second, CFTP introduces a dependence between the τ and X(0) it chooses. Therefore, bias can be induced if a CFTP run is stopped prematurely before the coupling time has been determined. Suppose a CFTP algorithm is run for a long time during which coupling does not occur. If the computer crashes or an impatient user stops and then restarts the algorithm to find a coupling time, this will generally bias the sample toward those states in which coupling is easier. An alternative perfect sampling method known as Fill's algorithm was designed to avoid this problem [193].
Third, our description of the CFTP algorithm uses the sequence of starting times τ =− 1, − 2, . . . for successive CFTP iterations. For many problems, this will be inefficient. It may be more efficient to use the sequence τ =− 1, − 2, − 4, − 8, − 16, . . ., which minimizes the worst case number of simulation steps required and nearly minimizes the expected number of required steps [520].
Finally, it may seem that this coupling strategy should work if the chains were run forwards from time t = 0 instead of backwards; but that is not the case. To understand why, consider a Markov chain for which some state x′ has a unique predecessor. It is impossible for x′ to occur at the random time of first coalescence. If x′ occurred, the chain must have already coalesced at the previous time, since all chains must have been in the predecessor state. Therefore the marginal distribution of the chain at the first coalescence time must assign zero probability to x′ and hence cannot be the stationary distribution. Although this forward coupling approach fails, there is a clever way to modify the CFTP construct to produce a perfect sampling algorithm for a Markov chain that only runs forward in time [666].
8.5.1.1 Stochastic Monotonicity and Sandwiching
When applying CFTP to a chain with a vast finite state space or an infinite (e.g., continuous) state space, it can be challenging to monitor whether sample paths started from all possible elements in the state space have coalesced by time zero. However, if the state space can be ordered in some way such that the deterministic transition rule q preserves the state space ordering, then only the sample paths started from the minimum state and maximum state in the ordering need to be monitored.
Let 
denote any two possible states of a Markov chain exploring a possibly huge state space 
. Formally, 
is said to admit the natural componentwise partial ordering, x ≤ y, if xi ≤ yi for i = 1, . . ., n and 
. The transition rule q is monotone with respect to this partial ordering if 
for all u when x ≤ y. Now, if there exist a minimum and a maximum element of the state space 
, so xmin ≤ x ≤ xmax for all 
and the transition rule q is monotone, then an MCMC procedure that uses this q preserves the ordering of the states at each time step. Therefore, CFTP using a monotone transition rule can be carried out by simulating only two chains: one started at xmin and the other at xmax. Sample paths for chains started at all other states will be sandwiched between the paths started in the maximum and minimum states. When the sample paths started in the minimum and maximum states have coalesced at time zero, coalescence of all the intermediate chains is also guaranteed. Therefore, CFTP samples from the stationary distribution at t = 0. Many problems satisfy these monotonicity properties; one example is given in Section 8.7.3.
In problems where this form of monotonicity isn't possible, other related strategies can be devised [468, 473, 666]. Considerable effort has been focused on developing methods to apply perfect sampling for specific problem classes, such as perfect Metropolis–Hastings independence chains [123], perfect slice samplers [466], and perfect sampling algorithms for Bayesian model selection [337, 575].
Perfect sampling is currently an area of active research, and many extensions of the ideas presented here have been proposed. While this idea is quite promising, perfect sampling algorithms have not been widely implemented for problems of realistic size. Challenges in implementation and long coalescence times have sometimes discouraged large-scale realistic applications. Nonetheless, the attractive properties of perfect sampling algorithms and continued research in this area will likely motivate new and innovative MCMC algorithms for practical problems.
8.6 Markov Chain Maximum Likelihood
We have presented Markov chain Monte Carlo in the context of Monte Carlo integration, with many Bayesian examples. However, MCMC techniques can also be useful for maximum likelihood estimation, particularly in exponential families [234, 505]. Consider data generated from an exponential family model X ~ f(· |θ) where
(8.33) 
Here θ = (θ1, . . ., θp) and s(x) = (s1(x), . . ., sp(x)) are vectors of canonical parameters and sufficient statistics, respectively. For many problems, c2(θ) cannot be determined analytically, so the likelihood cannot be directly maximized.
Suppose that we generate X(1), . . ., X(n) from an MCMC approach having f(· |ψ) as the stationary density, where ψ is any particular choice for θ and f(· |ψ) is in the same exponential family as the data density. Then it is easy to show that
(8.34) 
Although the MCMC draws are dependent and not exactly from f(· |ψ),
(8.35)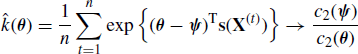 
as n → ∞ by the strong law of large numbers (1.46). Therefore, a Monte Carlo estimator of the log likelihood given data x is
up to an additive constant. The maximizer of 
converges to the maximizer of the true log likelihood as n→ ∞. Therefore, we take the Monte Carlo maximum likelihood estimate of θ to be the maximizer of (8.36), which we denote 
.
Hence we can approximate the MLE 
using simulations from f(· |ψ) generated via MCMC. Of course, the quality of will depend greatly on ψ. Analogously to importance sampling, 
is best. In practice, however, we must choose one or more values wisely, perhaps through adaptation or empirical estimation [234].
8.7 Example: MCMC for Markov Random Fields
We offer here an introduction to Bayesian analysis of Markov random field models with emphasis on the analysis of spatial or image data. This topic provides interesting examples of many of the methods discussed in this chapter.
A Markov random field specifies a probability distribution for spatially referenced random variables. Markov random fields are quite general and can be used for many lattice-type structures such as regular rectangular, hexagonal, and irregular grid structures [128, 635]. There are a number of complex issues with Markov random field construction that we do not attempt to resolve here. Besag has published a number of key papers on Markov random fields for spatial statistics and image analysis, including his seminal 1974 paper [35, 36, 40–43]. Additional comprehensive coverage of Markov random fields is given in [128, 377, 412, 668].
For simplicity, we focus here on the application of Markov random fields to a regular rectangular lattice. For example, we might overlay a rectangular grid on a map or image and label each pixel or cell in the lattice. The value for the ith pixel in the lattice is denoted by xi for i = 1, . . ., n, where n is finite. We will focus on binary random fields where xi can take on only two values, 0 and 1, for i = 1, . . ., n. It is generally straightforward to extend methods to the case where xi is continuous or takes on more than two discrete values [128].
Let 
define the set of x values for the pixels that are near pixel i. The pixels that define δi are called the neighborhood of pixel i. The pixel xi is not in δi. A proper neighborhood definition must meet the condition that if pixel i is a neighbor of pixel j then pixel j is a neighbor of pixel i. In a rectangular lattice, a first-order neighborhood is the set of pixels that are vertically and horizontally adjacent to the pixel of interest (see Figure 8.6). A second-order neighborhood also includes the pixels diagonally adjacent from the pixel of interest.
Figure 8.6 Shaded pixels indicate a first-order and a second-order neighborhood of pixel i for a rectangular lattice.
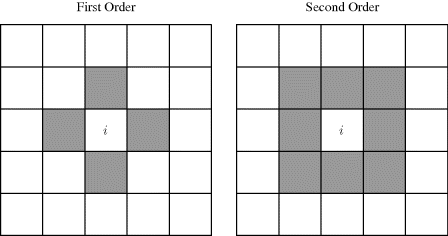
Imagine that the value xi for the ith pixel is a realization of a random variable Xi. A locally dependent Markov random field specifies that the distribution of Xi given the remaining pixels, X−i, is dependent only on the neighboring pixels. Therefore, for X−i = x−i,
for i = 1, . . ., n. Assuming each pixel has a nonzero probability of equaling 0 or 1 means that the so-called positivity condition is satisfied: that the minimal state space of X equals the Cartesian product of the state spaces of its components. The positivity condition ensures that the conditional distributions considered later in this section are well defined.
The Hammersley–Clifford theorem shows that the conditional distributions in (8.37) together specify the joint distribution of X up to a normalizing constant [35]. For our discrete binary state space, this normalizing constant is the sum of 
over all x in the state space. This sum is not usually available by direct calculation, because the number of terms is enormous. Even for an unrealistically small 40 × 40 pixel image where the pixels take on binary values, there are 21600 = 4.4 × 10481 terms in the summation. Bayesian MCMC methods provide a Monte Carlo basis for inference about images, despite such difficulties. We describe below several approaches for MCMC analysis of Markov random field models.
8.7.1 Gibbs Sampling for Markov Random Fields
We begin by adopting a Bayesian model for analysis of a binary Markov random field. In the introduction to Markov random fields above, we used xi to denote the value of the ith pixel. Here we let Xi denote the unknown true value of the ith pixel, where Xi is treated as a random variable in the Bayesian paradigm. Let yi denote the observed value for the ith pixel. Thus X is a parameter vector and y is the data. In an image analysis application, y is the degraded image and X is the unknown true image. In a spatial statistics application of mapping of plant or animal species distributions, yi = 0 might indicate that the species was not observed in pixel i during the sampling period and Xi might denote the true (unobserved) presence or absence of the species in pixel i.
Three assumptions are fundamental to the formulation of this model. First, we assume that observations are mutually independent given true pixel values. So the joint conditional density of Y given X = x is
where f(yi|xi) is the density of the observed data in pixel i given the true value. Thus, viewed as a function of x, (8.38) is the likelihood function. Second, we adopt a locally dependent Markov random field (8.37) to model the true image. Finally, we assume the positivity condition, defined above.
The parameters of the model are x1, . . ., xn, and the goal of the analysis is to estimate these true values. To do this we adopt a Gibbs sampling approach. Assume the prior X ~ f(x) for the parameters. The goal in the Gibbs sampler, then, is to obtain a sample from the posterior density of X,
One class of prior densities for X is given by
where i ~ j denotes all pairs such that pixel i is a neighbor of pixel j, and ϕ is some function that is symmetric about 0 with ϕ(z) increasing as |z| increases. Equation (8.40) is called a pairwise difference prior. Adopting this prior distribution based on pairwise interactions simplifies computations but may not be realistic. Extensions to allow for higher-order interactions have been proposed [635].
The Gibbs sampler requires the derivation of the univariate conditional distributions whose form follows from (8.37) to (8.39). The Gibbs update at iteration t is therefore
(8.41) 
A common strategy is to update each Xi in turn, but it can be more computationally efficient to update the pixels in independent blocks. The blocks are determined by the neighborhoods defined for a particular problem [40]. Other approaches to block updating for Markov random field models are given in [382, 563].
Example 8.6 (Utah Serviceberry Distribution Map) An important problem in ecology is the mapping of species distributions over a landscape [286, 584]. These maps have a variety of uses, ranging from local land-use planning aimed at minimizing human development impacts on rare species to worldwide climate modeling. Here we consider the distribution of a deciduous small tree or shrub called the Utah serviceberry Amelanchier utahensis in the state of Colorado [414].
We consider only the westernmost region of Colorado (west of approximately 104°W longitude), a region that includes the Rocky Mountains. We binned the presence–absence information into pixels that are approximately 8 × 8 km. This grid consists of a lattice of 46 × 54 pixels, giving a total of n = 2484 pixels. The left panel in Figure 8.7 shows presence and absence, where each black pixel indicates that the species was observed in that pixel.
Figure 8.7 Distribution of Utah serviceberry in western Colorado. The left panel is the true species distribution, and the right panel is the observed species distribution used in Example 8.6. Black pixels indicate presence.
In typical applications of this model, the true image is not available. However, knowing the true image allows us to investigate various aspects of modeling binary spatially referenced data in what follows. Therefore, for purposes of illustration, we will use these pixelwise presence–absence data as a true image and consider estimating this truth from a degraded version of the image. A degraded image is shown in the right panel of Figure 8.7. We seek a map that reconstructs the true distribution of this species using this degraded image, which is treated as the observed data y. The observed data were generated by randomly selecting 30% of the pixels and switching their colors. Such errors might arise in satellite images or other error-prone approaches to species mapping.
Let xi = 1 indicate that the species is truly present in pixel i. In a species mapping problem such as this one, such simple coding may not be completely appropriate. For example, a species may be present only in a portion of pixel i, or several sites may be included in one pixel, and thus we might consider modeling the proportion of sites in each pixel where the species was observed to be present. For simplicity, we assume that this application of Markov random fields is more akin to an image analysis problem where xi = 1 indicates that the pixel is black.
We consider the simple likelihood function arising from the data density
for xi {0, 1}. The parameter α can be specified as a user-selected constant or estimated by adopting a prior for it. We adopt the former approach here, setting α = 1.
We assume the pairwise difference prior density for X given by
for 
. We consider a first-order neighborhood, so summation over i ~ j in (8.43) indicates summation over the horizontally and vertically adjacent pixels of pixel i, for i = 1, . . ., n. Equation (8.43) introduces the hyperparameter β, which can be assigned a hyperprior or specified as a constant. Usually β is restricted to be positive to encourage clustering of similar-colored pixels. Here we set β = 0.8. Sensitivity analysis to determine the effect of chosen values for α and β is recommended.
Assuming (8.42) and (8.43), the univariate conditional distribution for Xi|x−i, y is Bernoulli. Thus during the (t + 1)th cycle of the Gibbs sampler, the ith pixel is set to 1 with probability
for i = 1, . . ., n. Recall that
so neighbors are always assigned their most recent values as soon as they become available within the Gibbs cycle.
Figure 8.8 gives the posterior mean probability of presence for the Utah serviceberry in western Colorado as estimated using the Gibbs sampler described above. Figure 8.9 shows that the mean posterior estimates from the Gibbs sampler successfully discriminate between true presence and absence. Indeed, if pixels with posterior mean of 0.5 or larger are converted to black and pixels with posterior mean smaller than 0.5 are converted to white, then 86% of the pixels are labeled correctly.
Figure 8.8 Estimated posterior mean of X for the Gibbs sampler analysis in Example 8.6.
Figure 8.9 Boxplots of posterior mean estimates of P[Xi = 1] for Example 8.6. Averaging pixel-specific sample paths from the Gibbs sampler provides an estimate of P[Xi = 1] for each i. The boxplots show these estimates split into two groups corresponding to pixels where the serviceberry was truly present and pixels where it wasn't.
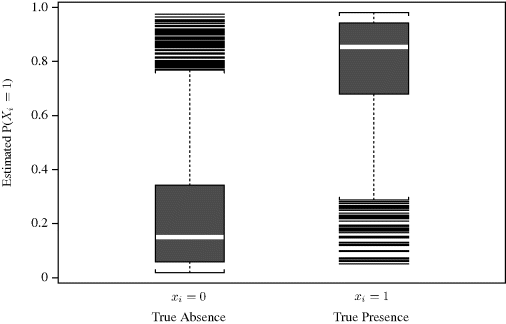
The model used in Example 8.6 is elementary, ignoring many of the important issues that may arise in the analysis of such spatial lattice data. For example, when the pixels are created by binning spatially referenced data, it is unclear how to code the observed response for pixel i if the species was observed to be present in some portions of it and not in other portions.
A model that addresses this problem uses a latent binary spatial process over the region of interest [128, 217]. Let λ(s) denote a binary process over the image region, where s denotes coordinates. Then the proportion of pixel i that is occupied by the species of interest is given by
(8.45) 
where |Ai| denotes the area of pixel i. The Yi|xi are assumed to be conditionally independent Bernoulli trials with probability of detecting presence given by pi, so P[Yi = 1|Xi = 1] = pi. This formalization allows for direct modeling when pixels may contain a number of sites that were sampled. A more complex form of this model is described in [217]. We may also wish to incorporate covariate data to improve our estimates of species distributions. For example, the Bernoulli trials may be modeled as having parameters pi for which
(8.46) 
where wi is a vector of covariates for the ith pixel, β is the vector of coefficients associated with the covariates, and γi is a spatially dependent random effect. These models are popular in the field of spatial epidemiology; see [44, 45, 411, 503].
8.7.2 Auxiliary Variable Methods for Markov Random Fields
Although convenient, the Gibbs sampler implemented as described in Section 8.7.1 can have poor convergence properties. In Section 8.3 we introduced the idea of incorporating auxiliary variables to improve convergence and mixing of Markov chain algorithms. For binary Markov random field models, the improvement can be profound.
One notable auxiliary variable technique is the Swendsen–Wang algorithm [174, 621]. As applied to binary Markov random fields, this approach creates a coarser version of an image by clustering neighboring pixels that are colored similarly. Each cluster is then updated with an appropriate Metropolis–Hastings step. This coarsening of the image allows for faster exploration of the parameter space in some applications [328].
In the Swendsen–Wang algorithm, clusters are created via the introduction of bond variables, Uij, for each adjacency i ~ j in the image. Clusters consist of bonded pixels. Adjacent like-colored pixels may or may not be bonded, depending on Uij. Let Uij = 1 indicate that pixels i and j are bonded, and Uij = 0 indicate that they are not bonded. The bond variables Uij are assumed to be conditionally independent given X = x. Let U denote the vector of all the Uij.
Loosely speaking, the Swendsen–Wang algorithm alternates between growing clusters and coloring them. Figure 8.10 shows one cycle of the algorithm applied to a 4 × 4 pixel image. The left panel in Figure 8.10 shows the current image and the set of all possible bonds for a 4 × 4 image. The middle panel shows the bonds that were generated at the start of the next iteration of the Swendsen–Wang algorithm. We will see below that bonds between like-colored pixels are generated with probability 1 − exp{−β}, so like-colored neighbors are not forced to be bonded. Connected sets of bonded pixels form clusters. We've drawn boxes around the five clusters in the middle panel of Figure 8.10. This shows the coarsening of the image allowed by the Swendsen–Wang algorithm. At the end of each iteration, the color of each cluster is updated: Clusters are randomly recolored in a way that depends upon the posterior distribution for the image. The updating produces the new image in the right panel in Figure 8.10. The observed data y are not shown here.
Figure 8.10 Illustration of the Swendsen–Wang algorithm.
Formally, the Swendsen–Wang algorithm is a special case of a Gibbs sampler that alternates between updates to X|u and U|x. It proceeds as follows:
can exceed 1 only if 
, and in this case 
with probability 1 − exp{−β}. When 
, we declare the ith and jth pixels to be bonded for iteration t + 1.
, where
Thus for our simple model, pixel pairs with the same color are bonded with probability 1 − exp{−β}. The bond variables define clusters of pixels, with each cluster consisting of a set of pixels that are interlinked with at least one bond. Each cluster is updated independently with all pixels in the cluster taking on the same color. Updates in (8.47) are implemented by simulating from a Bernoulli distribution where the probability of coloring a cluster of pixels, C, black is
The local dependence structure of the Markov random field is decoupled from the coloring decision given in (8.48), thereby potentially enabling faster mixing.
Example 8.7 (Utah Serviceberry Distributions, Continued) To compare the performance of the Gibbs sampler and the Swendsen–Wang algorithm, we return to Example 8.6. For this problem the likelihood has a dominant influence on the posterior. Thus to highlight the differences between the algorithms, we set α = 0 to understand what sort of mixing can be enabled by the Swendsen–Wang algorithm. In Figure 8.11, both algorithms were started in the same image in iteration 1, and the three subsequent iterations are shown. The Swendsen–Wang algorithm produces images that vary greatly over iterations, while the Gibbs sampler produces images that are quite similar. In the Swendsen–Wang iterations, large clusters of pixels switch colors abruptly, thereby providing faster mixing.
Figure 8.11 Comparison between Gibbs sampling and the Swendsen–Wang algorithm simulating a Markov random field. Iteration 1 is the same for both algorithms. See Example 8.7 for details.
When the likelihood is included, there are fewer advantages to the Swendsen–Wang algorithm when analyzing the data from Example 8.6. For the chosen α and β, clusters grow large and change less frequently than in Figure 8.11. In this application, sequential images from a Swendsen–Wang algorithm look quite similar to those for a Gibbs sampler, and the differences between results produced by the Swendsen–Wang algorithm and the Gibbs sampler are small.
Exploiting a property called decoupling, the Swendsen–Wang algorithm grows clusters without regard to the likelihood, conditional on X(t). The likelihood and image prior terms are separated in steps 1 and 2 of the algorithm. This feature is appealing because it can improve mixing rates in MCMC algorithms. Unless α and β are carefully chosen, however, decoupling may not be helpful. If clusters tend to grow large but change color very infrequently, the sample path will consist of rare drastic image changes. This constitutes poor mixing. Further, when the posterior distribution is highly multimodal, both the Gibbs sampler and the Swendsen–Wang algorithm can miss potential modes if the chain is not run long enough. A partial decoupling method has been proposed to address such problems, and offers some potential advantages for challenging imaging problems [327, 328].
8.7.3 Perfect Sampling for Markov Random Fields
Implementing standard perfect sampling for a binary image problem would require monitoring sample paths that start from all possible images. This is clearly impossible even in a binary image problem of moderate size. In Section 8.5.1.1 we introduced the idea of stochastic monotonicity to cope with large state spaces. We can apply this strategy to implement perfect sampling for the Bayesian analysis of Markov random fields.
To exploit the stochastic monotonicity strategy, the states must be partially ordered, so x ≤ y if xi ≤ yi for i = 1, . . ., n and for 
. In the binary image problem, such an ordering is straightforward. If 
, define x ≤ y if yi = 1 whenever xi = 1 for all i = 1, . . ., n. If the deterministic transition rule q maintains this partial ordering of states, then only the sample paths that start from all-black and all-white images need to be monitored for coalescence.
Example 8.8 (Sandwiching Binary Images) Figure 8.12 shows five iterations of a Gibbs sampler CFTP algorithm for a 4 × 4 binary image with order-preserving pixelwise updates. The sample path in the top row starts at iteration τ = − 1000, where the image is all black. In other words, 
for i = 1, . . ., 16. The sample path in the bottom row starts at all white. The path starting from all black is the upper bound and the path starting from all white is the lower bound used for sandwiching.
Figure 8.12 Sequence of images from a perfect sampling algorithm for a binary image problem. See Example 8.8 for details.
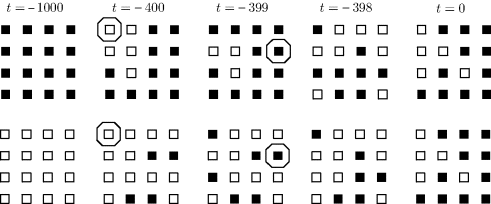
After some initial iterations, we examine the paths around t = − 400. In the lower sample path, the circled pixel at iteration t = − 400 changed from white to black at t = − 399. Monotonicity requires that this pixel change to black in the upper path too. This requirement is implemented directly via the monotone update function q. Note, however, that changes from white to black in the upper image do not compel the same change in the lower image; see, for example, the pixel to the right of the circled pixel.
Changes from black to white in the upper image compel the same change in the lower image. For example, the circled pixel in the upper sample path at t = − 399 has changed from black to white at t = − 398, thereby forcing the corresponding pixel in the lower sample path to change to white. A pixel change from black to white in the lower image does not necessitate a like change to the upper image.
Examination of the pixels in these sequences of images shows that pixelwise image ordering is maintained over the simulation. At iteration t = 0, the two sample paths have coalesced. Therefore a chain started at any image at τ = − 1000 must also have coalesced to the same image by iteration t = 0. The image shown at t = 0 is a realization from the stationary distribution of the chain.
Example 8.9 (Utah Serviceberry Distribution, Continued) The setup for the CFTP algorithm for the species distribution mapping problem closely follows the development of the Gibbs sampler described in Example 8.6. To update the ith pixel at iteration t + 1, generate U(t+1) from Unif(0, 1). Then the update is given by
(8.49)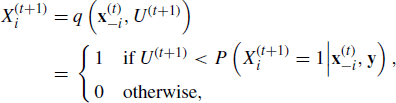 
where 
is given in (8.44). Such updates maintain the partial ordering of the state space. Therefore, the CFTP algorithm can be implemented by starting at two initial images: all black and all white. These images are monitored, and the CFTP algorithm proceeds until they coalesce by iteration t = 0. The CFTP algorithm has been implemented for similar binary image problems in [165, 166].
Problems
8.1. One approach to Bayesian variable selection for linear regression models is described in Section 8.2.1 and further examined in Example 8.3. For a Bayesian analysis for the model in Equation (8.20), we might adopt the normal–gamma conjugate class of priors 
and 
. Show that the marginal density of Y|mk is given by
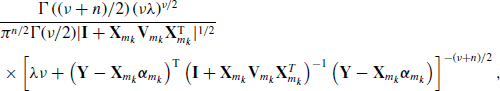
where 
is the design matrix, 
is the mean vector, and 
is the covariance matrix for 
for the model mk.
8.2. Consider the CFTP algorithm described in Section 8.5.
8.3. Suppose we desire a draw from the marginal distribution of X that is determined by the assumptions that θ ~ Beta(α, β) and X|θ ~ Bin(n, θ) [96].
is the inverse cumulative distribution function of the distribution d with parameters μ1 and μ2, evaluated at p. Implement the CFTP algorithm from Section 8.5.1, using the transition rule given in (8.54), to draw a perfect sample for this problem. Decrement τ by one unit each time the sample paths do not coalesce by time 0. Run the function 100 times to produce 100 draws from the stationary distribution for α = 10, β = 5, and n = 10. Make a histogram of the 100 starting times (the finishing times are all t = 0, by construction). Make a histogram of the 100 realizations of X(0). Discuss your results.8.4. Consider the one-dimensional black-and-white image represented by a vector of zeros and ones. The data (observed image) are
for the 35 pixels y = (y1, . . ., y35). Suppose the posterior density for the true image x is given by
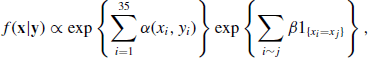
where
Consider the Swendsen–Wang algorithm for this problem where the bond variable is drawn according to 
.
for i = 1, . . ., 17 and 
for i = 18, . . ., 35. Compare the results of these trials with the results from part (a).Figure 8.13 Forty Gibbs sampler iterates for Problem 8.4, with β = 1.
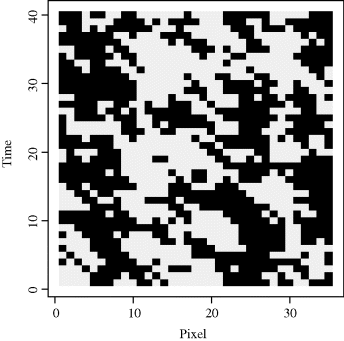
8.5. Data corresponding to the true image and observed images given in Figure 8.14 are available on the website for this book. The true image is a binary 20 × 20 pixel image with prior density given by
for i = 1, . . ., n, where νi is the number of neighbors in the neighborhood δi of xi and 
is the mean value of the neighbors of the ith pixel. This density promotes local dependence. The observed image is a gray scale degraded version of the true image with noise that can be modeled via a normal distribution. Suppose the likelihood is given by
for i = 1, . . ., n.
Figure 8.14 Images for Problem 8.5. The left panel is the true image, and the right panel is an observed image.
- Dealing with the edges is tricky because the neighborhood size varies. You may find it convenient to create a matrix with 22 rows and 22 columns consisting of the observed data surrounded on each of the four sides by a row or column of zeros. If you use this strategy, be sure that this margin area does not affect the analysis.
- Plot X(t) at the end of each full cycle so that you can better understand the behavior of your chain.
- Neighborhood structure chosen to be (i) first-order neighborhoods or (ii) second-order neighborhoods.
- Pixelwise error chosen to have variability given by (i) σ =2, (ii) σ =5, or (iii) σ =15.