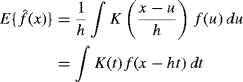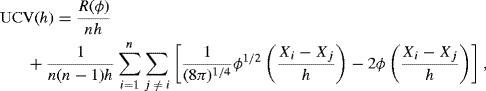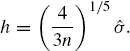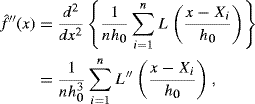Chapter 10
Nonparametric Density Estimation
This chapter concerns estimation of a density function f using observations of random variables X1, . . ., Xn sampled independently from f. Initially, this chapter focuses on univariate density estimation. Section 10.4 introduces some methods for estimating a multivariate density function.
In exploratory data analysis, an estimate of the density function can be used to assess multimodality, skew, tail behavior, and so forth. For inference, density estimates are useful for decision making, classification, and summarizing Bayesian posteriors. Density estimation is also a useful presentational tool since it provides a simple, attractive summary of a distribution. Finally, density estimation can serve as a tool in other computational methods, including some simulation algorithms and Markov chain Monte Carlo approaches. Comprehensive monographs on density estimation include [581, 598, 651].
The parametric solution to a density estimation problem begins by assuming a parametric model, X1, . . ., Xn ~ i.i.d. fX|θ, where θ is a very low-dimensional para-meter vector. Parameter estimates ![]() are found using some estimation paradigm, such as maximum likelihood, Bayesian, or method-of-moments estimation. The resulting density estimate at x is
are found using some estimation paradigm, such as maximum likelihood, Bayesian, or method-of-moments estimation. The resulting density estimate at x is ![]() . The danger with this approach lies at the start: Relying on an incorrect model fX|θ can lead to serious inferential errors, regardless of the estimation strategy used to generate
. The danger with this approach lies at the start: Relying on an incorrect model fX|θ can lead to serious inferential errors, regardless of the estimation strategy used to generate ![]() from the chosen model.
from the chosen model.
In this chapter, we focus on nonparametric approaches to density estimation that assume very little about the form of f. These approaches use predominantly local information to estimate f at a point x. More precise viewpoints on what makes an estimator nonparametric are offered in [581, 628].
One familiar nonparametric density estimator is a histogram, which is a piecewise constant density estimator. Histograms are produced automatically by most software packages and are used so routinely that one rarely considers their underlying complexity. Optimal choice of the locations, widths, and number of bins is based on sophisticated theoretical analysis.
Another elementary density estimator can be motivated by considering how density functions assign probability to intervals. If we observe a data point Xi = xi, we assume that f assigns some density not only at xi but also in a region around xi, if f is smooth enough. Therefore, to estimate f from X1, . . ., Xn ~ i.i.d. f, it makes sense to accumulate localized probability density contributions in regions around each Xi.
Specifically, to estimate the density at a point x, suppose we consider a region of width dx = 2h, centered at x, where h is some fixed number. Then the proportion of the observations that fall in the interval γ = [x − h, x + h] gives an indication of the density at x. More precisely, we may take ![]() , that is,
, that is,
where 1{A} = 1 if A is true, and 0 otherwise.
Let ![]() denote the number of sample points falling in the interval γ. Then Nγ is a Bin(n, p(γ)) random variable, where
denote the number of sample points falling in the interval γ. Then Nγ is a Bin(n, p(γ)) random variable, where ![]() . Thus E{Nγ/n} = p(γ) and var{Nγ/n} = p(γ)(1 − p(γ))/n. Clearly nh must increase as Nγ increases in order for (10.1) to provide a reasonable estimator, yet we can be more precise about separate requirements for n and h. The proportion of points falling in the interval γ estimates the probability assigned to γ by f. In order to approximate the density at x, we must shrink γ by letting h → 0. Then
. Thus E{Nγ/n} = p(γ) and var{Nγ/n} = p(γ)(1 − p(γ))/n. Clearly nh must increase as Nγ increases in order for (10.1) to provide a reasonable estimator, yet we can be more precise about separate requirements for n and h. The proportion of points falling in the interval γ estimates the probability assigned to γ by f. In order to approximate the density at x, we must shrink γ by letting h → 0. Then ![]() . Simultaneously, however, we want to increase the total sample size since var
. Simultaneously, however, we want to increase the total sample size since var![]() as n→ ∞. Thus, a fundamental requirement for the pointwise consistency of the estimator
as n→ ∞. Thus, a fundamental requirement for the pointwise consistency of the estimator ![]() in (10.1) is that nh→ ∞ and h → 0 as n→ ∞. We will see later that these requirements hold in far greater generality.
in (10.1) is that nh→ ∞ and h → 0 as n→ ∞. We will see later that these requirements hold in far greater generality.
10.1 Measures of Performance
To better understand what makes a density estimator perform well, we must first consider how to assess the quality of a density estimator. Let ![]() denote an estimator of f that is based on some fixed number h that controls how localized the probability density contributions used to construct
denote an estimator of f that is based on some fixed number h that controls how localized the probability density contributions used to construct ![]() should be. A small h will indicate that
should be. A small h will indicate that ![]() should depend more heavily on data points observed near x, whereas a larger h will indicate that distant data should be weighted nearly equally to observations near x.
should depend more heavily on data points observed near x, whereas a larger h will indicate that distant data should be weighted nearly equally to observations near x.
To evaluate ![]() as an estimator of f over the entire range of support, one could use the integrated squared error (ISE),
as an estimator of f over the entire range of support, one could use the integrated squared error (ISE),
(10.2) ![]()
Note that ISE (h) is a function of the observed data, through its dependence on ![]() . Thus it summarizes the performance of
. Thus it summarizes the performance of ![]() conditional on the observed sample. If we want to discuss the generic properties of an estimator without reference to a particular observed sample, it seems more sensible to further average ISE (h) over all samples that might be observed. The mean integrated squared error (MISE) is
conditional on the observed sample. If we want to discuss the generic properties of an estimator without reference to a particular observed sample, it seems more sensible to further average ISE (h) over all samples that might be observed. The mean integrated squared error (MISE) is
(10.3) ![]()
where the expectation is taken with respect to the distribution f. Thus MISE (h) may be viewed as the average value of a global measure of error [namely ISE (h)] with respect to the sampling density. Moreover, with an interchange of expectation and integration,
where
and ![]() . Equation (10.4) suggests that MISE (h) can also be viewed as accumulating the local mean squared error at every x.
. Equation (10.4) suggests that MISE (h) can also be viewed as accumulating the local mean squared error at every x.
For multivariate density estimation, ISE (h) and MISE (h) are defined analogously. Specifically, ![]() and MISE (h) = E{ ISE (h)}.
and MISE (h) = E{ ISE (h)}.
MISE (h) and ISE (h) both measure the quality of the estimator ![]() , and each can be used to develop criteria for selecting a good value for h. Preference between these two measures is a topic of some debate [284, 299, 357]. The distinction is essentially one between the statistical concepts of loss and risk. Using ISE (h) is conceptually appealing because it assesses the estimator's performance with the observed data. However, focusing on MISE (h) is an effective way to approximate ISE-based evaluation while reflecting the sensible goal of seeking optimal performance on average over many data sets. We will encounter both measures in the following sections.
, and each can be used to develop criteria for selecting a good value for h. Preference between these two measures is a topic of some debate [284, 299, 357]. The distinction is essentially one between the statistical concepts of loss and risk. Using ISE (h) is conceptually appealing because it assesses the estimator's performance with the observed data. However, focusing on MISE (h) is an effective way to approximate ISE-based evaluation while reflecting the sensible goal of seeking optimal performance on average over many data sets. We will encounter both measures in the following sections.
Although we limit attention to performance criteria based on squared error for the sake of simplicity and familiarity, squared error is not the only reasonable option. For example, there are several potentially appealing reasons to replace integrated squared error with the L1 norm ![]() , and MISE (h) with the corresponding expectation. Notably among these, the L1 norm is unchanged under any monotone continuous change of scale. This dimensionless character of L1 makes it a sort of universal measure of how near
, and MISE (h) with the corresponding expectation. Notably among these, the L1 norm is unchanged under any monotone continuous change of scale. This dimensionless character of L1 makes it a sort of universal measure of how near ![]() is to f. Devroye and Györfi study the theory of density estimation using L1 and present other advantages of this approach [159, 160]. In principle, the optimality of an estimator depends on the metric by which performance is assessed, so the adoption of different metrics may favor different types of estimators. In practice, however, many other factors generally affect the quality of a density estimator more than the metric that might have been used to motivate it.
is to f. Devroye and Györfi study the theory of density estimation using L1 and present other advantages of this approach [159, 160]. In principle, the optimality of an estimator depends on the metric by which performance is assessed, so the adoption of different metrics may favor different types of estimators. In practice, however, many other factors generally affect the quality of a density estimator more than the metric that might have been used to motivate it.
10.2 Kernel Density Estimation
The density estimator given in Equation (10.1) weights all points within h of x equally. A univariate kernel density estimator allows a more flexible weighting scheme, fitting
where K is a kernel function and h is a fixed number usually termed the bandwidth.
A kernel function assigns weights to the contributions given by each Xi to the kernel density estimator ![]() , depending on the proximity of Xi to x. Typically, kernel functions are positive everywhere and symmetric about zero. K is usually a density, such as a normal or Student's t density. Other popular choices include the triweight and Epanechnikov kernels (see Section 10.2.2), which don't correspond to familiar densities. Note that the univariate uniform kernel, namely
, depending on the proximity of Xi to x. Typically, kernel functions are positive everywhere and symmetric about zero. K is usually a density, such as a normal or Student's t density. Other popular choices include the triweight and Epanechnikov kernels (see Section 10.2.2), which don't correspond to familiar densities. Note that the univariate uniform kernel, namely ![]() , yields the estimator given by (10.1). Constraining K so that ∫z2K(z)dz = 1 allows h to play the role of the scale parameter of the density K, but is not required.
, yields the estimator given by (10.1). Constraining K so that ∫z2K(z)dz = 1 allows h to play the role of the scale parameter of the density K, but is not required.
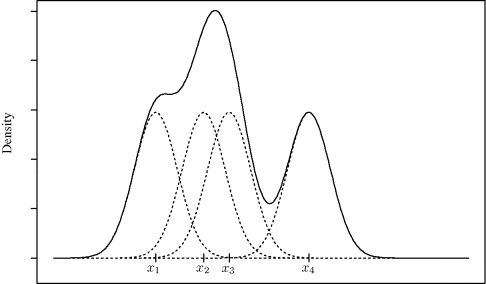
Figure 10.1 illustrates how a kernel density estimate is constructed from a sample of four univariate observations, x1, . . ., x4. Centered at each observed data point is a scaled kernel: in this case, a normal density function divided by 4. These contributions are shown with the dotted lines. Summing the contributions yields the estimate ![]() shown with the solid line.
shown with the solid line.
Figure 10.1 Normal kernel density estimate (solid) and kernel contributions (dotted) for the sample x1, . . ., x4. The kernel density estimate at any x is the sum of the kernel contributions centered at each xi.
The estimator in (10.6) is more precisely termed a fixed-bandwidth kernel density estimator because h is constant. The value chosen for the bandwidth exerts a strong influence on the estimator ![]() . If h is too small, the density estimator will tend to assign probability density too locally near observed data, resulting in a very wiggly estimated density function with many false modes. When h is too large, the density estimator will spread probability density contributions too diffusely. Averaging over neighborhoods that are too large smooths away important features of f.
. If h is too small, the density estimator will tend to assign probability density too locally near observed data, resulting in a very wiggly estimated density function with many false modes. When h is too large, the density estimator will spread probability density contributions too diffusely. Averaging over neighborhoods that are too large smooths away important features of f.
Notice that computing a kernel density estimate at every observed sample point based on a sample of size n requires n(n − 1) evaluations of K. Thus, the computational burden of calculating ![]() grows quickly with n. However, for most practical purposes such as graphing the density, the estimate need not be computed at each Xi. A practical strategy is to calculate
grows quickly with n. However, for most practical purposes such as graphing the density, the estimate need not be computed at each Xi. A practical strategy is to calculate ![]() over a grid of values for x, then linearly interpolate between grid points. A grid of a few hundred values is usually sufficient to provide a graph of
over a grid of values for x, then linearly interpolate between grid points. A grid of a few hundred values is usually sufficient to provide a graph of ![]() that appears smooth. An even faster, approximate method of calculating the kernel density estimate relies on binning the data and rounding each value to the nearest bin center [315]. Then, the kernel need only be evaluated at each nonempty bin center, with density contributions weighted by bin counts. Drastic reductions in computing time can thereby be obtained in situations where n is so large as to prevent calculating individual contributions to
that appears smooth. An even faster, approximate method of calculating the kernel density estimate relies on binning the data and rounding each value to the nearest bin center [315]. Then, the kernel need only be evaluated at each nonempty bin center, with density contributions weighted by bin counts. Drastic reductions in computing time can thereby be obtained in situations where n is so large as to prevent calculating individual contributions to ![]() centered at every Xi.
centered at every Xi.
10.2.1 Choice of Bandwidth
The bandwidth parameter controls the smoothness of the density estimate. Recall from (10.4) and (10.5) that MISE (h) equals the integrated mean squared error. This emphasizes that the bandwidth determines the trade-off between the bias and variance of ![]() . Such a trade-off is a pervasive theme in nearly all kinds of model selection, including regression, density estimation, and smoothing (see Chapters 11 and 12). A small bandwidth produces a density estimator with wiggles indicative of high variability caused by undersmoothing. A large bandwidth causes important features of f to be smoothed away, thereby causing bias.
. Such a trade-off is a pervasive theme in nearly all kinds of model selection, including regression, density estimation, and smoothing (see Chapters 11 and 12). A small bandwidth produces a density estimator with wiggles indicative of high variability caused by undersmoothing. A large bandwidth causes important features of f to be smoothed away, thereby causing bias.
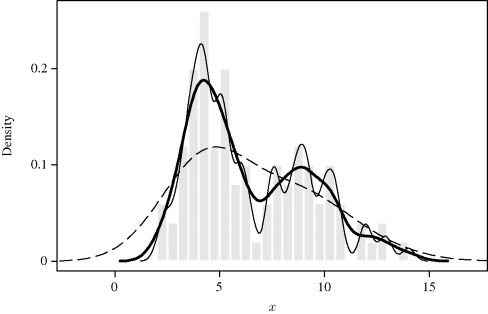
Example 10.1 (Bimodal Density) The effect of bandwidth is shown in Figure 10.2. This histogram shows a sample of 100 points from an equally weighted mixture of N(4, 12) and N(9, 22) densities. Three density estimates that use a standard normal kernel are superimposed, with h = 1.875 (dashed), h = 0.625 (heavy), and h = 0.3 (solid). The bandwidth h = 1.875 is clearly too large because it leads to an oversmooth density estimate that fails to reveal the bimodality of f. On the other hand, h = 0.3 is too small a bandwidth, leading to undersmoothing. The density estimate is too wiggly, exhibiting many false modes. The bandwidth h = 0.625 is adequate, correctly representing the main features of f while suppressing most effects of sampling variability. ![]()
Figure 10.2 Histogram of 100 data points drawn from the bimodal distribution in Example 10.1, and three normal kernel density estimates. The estimates correspond to bandwidths h = 1.875 (dashed line), h = 0.625 (heavy), and h = 0.3 (solid).
In the following subsections we discuss a variety of ways to choose h. When density estimation is used mainly for exploratory data analysis, span choice based on visual inspection is defensible, and the trial-and-error process leading to your choice might itself provide useful insight into the stability of features observed in the density estimate. In practice, one may simply try a sequence of values for h, and choose a value that is large enough to avoid the threshold where smaller bandwidths cause features of the density estimate to become unstable or the density estimate exhibits obvious wiggles so localized that they are unlikely to represent modes of f. Although the density estimate is sensitive to the choice of bandwidth, we stress that there is no single correct choice in any application. Indeed, bandwidths within 10–20% of each other will often produce qualitatively similar results.
There are situations when a more formal bandwidth selection procedure might be desired: for use in automatic algorithms, for use by a novice data analyst, or for use when a greater degree of objectivity or formalism is desired. A comprehensive review of approaches is given in [360]; other good reviews include [32, 88, 359, 500, 581, 592, 598].
To understand bandwidth selection, it is necessary to further analyze MISE (h). Suppose that K is a symmetric, continuous probability density function with mean zero and variance ![]() . Let R(g) denote a measure of the roughness of a given function g, defined by
. Let R(g) denote a measure of the roughness of a given function g, defined by
(10.7) ![]()
Assume hereafter that R(K)< ∞ and that f is sufficiently smooth. In this section, this means that f must have two bounded continuous derivatives and R(f′′)< ∞; higher-order smooth derivatives are required for some methods discussed later. Recall that
We further analyze this expression, allowing h → 0 and nh→ ∞ as n→ ∞.
To compute the bias term in (10.8), note that
by applying a change of variable. Next, substituting the Taylor series expansion
(10.10) ![]()
in (10.9) and noting that K is symmetric about zero leads to
(10.11) ![]()
where ![]() is a quantity that converges to zero faster than h2 does as h → 0.Thus,
is a quantity that converges to zero faster than h2 does as h → 0.Thus,
(10.12) ![]()
and integrating the square of this quantity over x gives
(10.13) ![]()
To compute the variance term in (10.8), a similar strategy is employed:
(10.14) 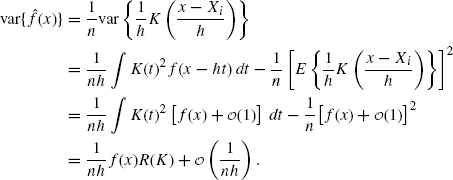
Integrating this quantity over x gives
(10.15) ![]()
Thus,
where
is termed the asymptotic mean integrated squared error. If nh→ ∞ and h → 0 as n→ ∞, then MISE (h) → 0, confirming our intuition from the uniform kernel estimator discussed in the chapter introduction. The error term in (10.16) can be shown to equal ![]() with a more delicate analysis of the squared bias as in [580], but it is the AMISE that interests us most.
with a more delicate analysis of the squared bias as in [580], but it is the AMISE that interests us most.
To minimize AMISE (h) with respect to h, we must set h at an intermediate value that avoids excessive bias and excessive variability in ![]() . Minimizing AMISE (h) with respect to h shows that exactly balancing the orders of the bias and variance terms in (10.17) is best. The optimal bandwidth is
. Minimizing AMISE (h) with respect to h shows that exactly balancing the orders of the bias and variance terms in (10.17) is best. The optimal bandwidth is
but this result is not immediately helpful since it depends on the unknown density f.
Note that optimal bandwidths have ![]() , in which case
, in which case ![]() . This result reveals how quickly the bandwidth should shrink with increasing sample size, but it says little about what bandwidth would be appropriate for density estimation with a given dataset. A variety of automated bandwidth selection strategies have been proposed; see the following subsections. Their relative performance in real applications varies with the nature of f and the observed data. There is no universally best way to proceed.
. This result reveals how quickly the bandwidth should shrink with increasing sample size, but it says little about what bandwidth would be appropriate for density estimation with a given dataset. A variety of automated bandwidth selection strategies have been proposed; see the following subsections. Their relative performance in real applications varies with the nature of f and the observed data. There is no universally best way to proceed.
Many bandwidth selection methods rely on optimizing or finding the root of a function of h—for example, minimizing an approximation to AMISE (h). In these cases, a search may be conducted over a logarithmic-spaced grid of 50 or more values, linearly interpolating between grid points. When there are multiple roots or local minima, a grid search permits a better understanding of the bandwidth selection problem than would an automated optimization or root-finding algorithm.
10.2.1.1 Cross-Validation
Many bandwidth selection strategies begin by relating h to some measure of the quality of ![]() as an estimator of f. The quality is quantified by some Q(h), whose estimate,
as an estimator of f. The quality is quantified by some Q(h), whose estimate, ![]() , is optimized to find h.
, is optimized to find h.
If ![]() evaluates the quality of
evaluates the quality of ![]() based on how well it fits the observed data in some sense, then the observed data are being used twice: once to calculate
based on how well it fits the observed data in some sense, then the observed data are being used twice: once to calculate ![]() from the data and a second time to evaluate the quality of
from the data and a second time to evaluate the quality of ![]() as an estimator of f. Such double use of the data provides an overoptimistic view of the quality of the estimator. When misled in this way, the chosen estimator tends to be overfitted (i.e., undersmoothed), with too many wiggles or false modes.
as an estimator of f. Such double use of the data provides an overoptimistic view of the quality of the estimator. When misled in this way, the chosen estimator tends to be overfitted (i.e., undersmoothed), with too many wiggles or false modes.
Cross-validation provides a remedy to this problem. To evaluate the quality of ![]() at the ith data point, the model is fitted using all the data except the ith point. Let
at the ith data point, the model is fitted using all the data except the ith point. Let
(10.19) ![]()
denote the estimated density at Xi using a kernel density estimator with all the observations except Xi. Choosing ![]() to be a function of the
to be a function of the ![]() separates the tasks of fitting and evaluating
separates the tasks of fitting and evaluating ![]() to select h.
to select h.
Although cross-validation enjoys great success as a span selection strategy for scatterplot smoothing (see Chapter 11), it is not always effective for bandwidth selection in density estimation. The h estimated by cross-validation approaches can be highly sensitive to sampling variability. Despite the persistence of these methods in general practice and in some software, a sophisticated plug-in method like the Sheather–Jones approach (Section 10.2.1.2) is a much more reliable choice. Nevertheless, cross-validation methods introduce some ideas that are useful in a variety of contexts.
One easy cross-validation option is to let ![]() be the pseudo-likelihood (PL)
be the pseudo-likelihood (PL)
(10.20) ![]()
as proposed in [171, 289]. The bandwidth is chosen to maximize the pseudo-likelihood. Although simple and intuitively appealing, this approach frequently produces kernel density estimates that are too wiggly and too sensitive to outliers [582]. The theoretical limiting performance of kernel density estimators with span chosen to minimize PL (h) is also poor: In many cases the estimator is not consistent [578].
Another approach is motivated by reexpressing the integrated squared error as
(10.21) 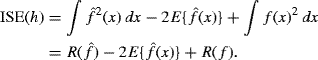
The final term in this expression is constant, and the middle term can be estimated by ![]() . Thus, minimizing
. Thus, minimizing
with respect to h should provide a good bandwidth [56, 561]. UCV (h) is called the unbiased cross-validation criterion because E{ UCV (h) + R(f)} = MISE (h). The approach is also called least squares cross-validation because choosing h to minimize UCV (h) minimizes the integrated squared error between ![]() and f.
and f.
If analytic evaluation of ![]() is not possible, the best way to evaluate (10.22) is probably to use a different kernel that permits an analytic simplification. For a normal kernel ϕ it can be shown that
is not possible, the best way to evaluate (10.22) is probably to use a different kernel that permits an analytic simplification. For a normal kernel ϕ it can be shown that
following the steps outlined in Problem 10.3. This expression can be computed efficiently without numerical approximation.
Although the bandwidth identified by minimizing UCV (h) with respect to h is asymptotically as good as the best possible bandwidth [293, 614], its convergence to the optimum is extremely slow [298, 583]. In practical settings, using unbiased cross-validation is risky because the resulting bandwidth tends to exhibit a strong dependence on the observed data. In other words, when applied to different datasets drawn from the same distribution, unbiased cross-validation can yield very different answers. Its performance is erratic in application, and undersmoothing is frequently seen.
The high sampling variability of unbiased cross-validation is mainly attributable to the fact that the target performance criterion, Q(h) = ISE (h), is itself random, unlike MISE (h). Scott and Terrell have proposed a biased cross-validation criterion [BCV (h)] that seeks to minimize an estimate of AMISE (h) [583]. In practice, this approach is generally outperformed by the best plug-in methods (Section 10.2.1.2) and can yield excessively large bandwidths and oversmooth density estimates.
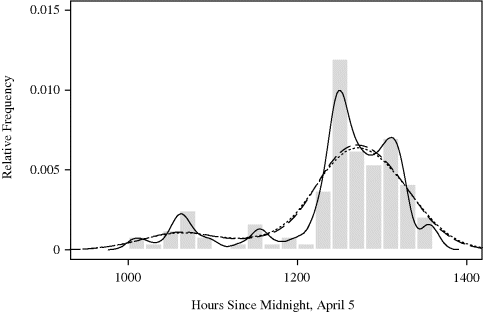
Example 10.2 (Whale Migration) Figure 10.3 shows a histogram of times of 121 bowhead whale calf sightings during the spring 2001 visual census conducted at the ice edge near Point Barrow, Alaska. This census is the central component of international efforts to manage this endangered whale population while allowing a small traditional subsistence hunt by coastal Inupiat communities [156, 249, 528].
Figure 10.3 Histogram of the times of 121 bowhead whale calf sightings during the 2001 spring migration discussed in Example 10.2. The date of each sighting is expressed as the number of hours since midnight, April 5, when the first adult whale was sighted.
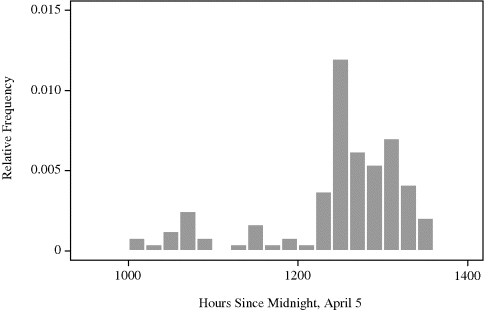
The timing of the northeasterly spring migration is surprisingly regular, and it is important to characterize the migration pattern for planning of future scientific efforts to study these animals. There is speculation that the migration may occur in loosely defined pulses. If so, this is important to discover because it may lead to new insights about bowhead whale biology and stock structure.
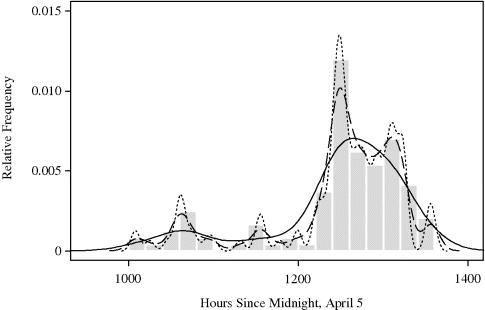
Figure 10.4 shows the results of kernel density estimates for these data using the normal kernel. Three different cross-validation criteria were used to select h. Maximizing cross-validated PL (h) with respect to h yields h = 9.75 and the density estimate shown with the dashed curve. This density estimate is barely adequate, exhibiting likely false modes in several regions. The result from minimizing UCV (h) with respect to h is even worse in this application, giving h = 5.08 and the density estimate shown with the dotted curve. This bandwidth is clearly too small. Finally, minimizing BCV (h) with respect to h yields h = 26.52 and the density estimate shown with the solid line. Clearly the best of the three options, this density estimate emphasizes only the most prominent features of the data distribution but may seem oversmooth. Perhaps a bandwidth between 10 and 26 would be preferable. ![]()
Figure 10.4 Kernel density estimates for the whale calf migration data in Example 10.2 using normal kernels and bandwidths chosen by three different cross-validation criteria. The bandwidths are 9.75 using PL (h) (dashed), 5.08 using UCV (h) (dotted), and 26.52 using BCV (h) (solid).
10.2.1.2 Plug-in Methods
Plug-in methods apply a pilot bandwidth to estimate one or more important features of f. The bandwidth for estimating f itself is then estimated at a second stage using a criterion that depends on the estimated features. The best plug-in methods have proven to be very effective in diverse applications and are more popular than cross-validation approaches. However, Loader offers arguments against the uncritical rejection of cross-validation approaches [422].
For unidimensional kernel density estimation, recall that the bandwidth that minimizes AMISE is given by
where ![]() is the variance of K, viewing K as a density. At first glance, (10.24) seems unhelpful because the optimal bandwidth depends on the unknown density f through the roughness of its second derivative. A variety of methods have been proposed to estimate R(f′′).
is the variance of K, viewing K as a density. At first glance, (10.24) seems unhelpful because the optimal bandwidth depends on the unknown density f through the roughness of its second derivative. A variety of methods have been proposed to estimate R(f′′).
Silverman suggests an elementary approach: replacing f by a normal density with variance set to match the sample variance [598]. This amounts to estimating R(f′′) by ![]() , where ϕ is the standard normal density function. Silverman's rule of thumb therefore gives
, where ϕ is the standard normal density function. Silverman's rule of thumb therefore gives
If f is multimodal, the ratio of R(f′′) to ![]() may be larger than it would be for normally distributed data. This would result in oversmoothing. A better bandwidth can be obtained by considering the interquartile range (IQR), which is a more robust measure of spread than is
may be larger than it would be for normally distributed data. This would result in oversmoothing. A better bandwidth can be obtained by considering the interquartile range (IQR), which is a more robust measure of spread than is ![]() . Thus, Silverman suggests replacing
. Thus, Silverman suggests replacing ![]() in (10.25) by
in (10.25) by ![]() , where Φ is the standard normal cumulative distribution function. Although simple, this approach cannot be recommended for general use because it has a strong tendency to oversmooth. Silverman's rule of thumb is valuable, however, as a method for producing approximate bandwidths effective for pilot estimation of quantities used in sophisticated plug-in methods.
, where Φ is the standard normal cumulative distribution function. Although simple, this approach cannot be recommended for general use because it has a strong tendency to oversmooth. Silverman's rule of thumb is valuable, however, as a method for producing approximate bandwidths effective for pilot estimation of quantities used in sophisticated plug-in methods.
Empirical estimation of R(f′′) in (10.24) is a better option than Silverman's rule of thumb. The kernel-based estimator is
where h0 is the bandwidth and L is a sufficiently differentiable kernel used to estimate f′′. Estimation of R(f′′) follows from (10.26).
It is important to recognize, however, that the best bandwidth for estimating f will differ from the best bandwidth for estimating f′′ or R(f′′). This is because ![]() contributes a proportionally greater share to the mean squared error for estimating f′′ than var
contributes a proportionally greater share to the mean squared error for estimating f′′ than var![]() does for estimating f. Therefore, a larger bandwidth is required for estimating f′′. We therefore anticipate h0 > h.
does for estimating f. Therefore, a larger bandwidth is required for estimating f′′. We therefore anticipate h0 > h.
Suppose we use bandwidth h0 with kernel L to estimate R(f′′), and bandwidth h with kernel K to estimate f. Then the asymptotic mean squared error for estimation of R(f′′) using kernel L is minimized when h0 ∝ n−1/7. To determine how h0 should be related to h, recall that optimal bandwidths for estimating f have h ∝ n−1/5. Solving this expression for n and replacing n in the equation h0 ∝ n−1/7, one can show that
where C1 and C2 are functionals that depend on derivatives of f and on the kernel L, respectively. Equation (10.27) still depends on the unknown f, but the quality of the estimate of R(f′′) produced using h0 and L is not excessively deteriorated if h0 is set using relatively simple estimates to find C1 and C2. In fact, we may estimate C1 and C2 using a bandwidth chosen by Silverman's rule of thumb.
The result is a two-stage process for finding the bandwidth, known as the Sheather–Jones method [359, 593]. At the first stage, a simple rule of thumb is used to calculate the bandwidth h0. This bandwidth is used to estimate R(f′′), which is the only unknown in expression (10.24) for the optimal bandwidth. Then the bandwidth h is computed via (10.24) and is used to produce the final kernel density estimate.
For univariate kernel density estimation with pilot kernel L = ϕ, the Sheather–Jones bandwidth is the value of h that solves the equation
where
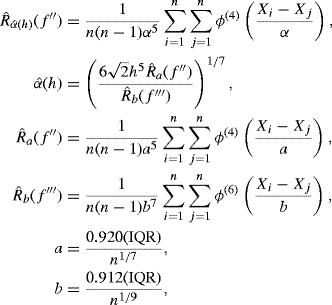
where ϕ(i) is the ith derivative of the normal density function, and IQR is the interquartile range of the data. The solution to (10.28) can be found using grid search or a root-finding technique from Chapter 2, such as Newton's method.
The Sheather–Jones method generally performs extremely well [359, 360, 501, 592]. There are a variety of other good methods based on carefully chosen approximations to MISE (h) or its minimizer [88, 300, 301, 358, 500]. In each case, careful pilot estimation of various quantities plays a critical role in ensuring that the final bandwidth performs well. Some of these approaches give bandwidths that asymptotically converge more quickly to the optimal bandwidth than does the Sheather–Jones method; all can be useful options in some circumstances. However, none of these offer substantially easier practical implementation or broadly better performance than the Sheather–Jones approach.
Example 10.3 (Whale Migration, Continued) Figure 10.5 illustrates the use of Silverman's rule of thumb and the Sheather–Jones method on the bowhead whale migration data introduced in Example 10.2. The bandwidth given by the Sheather–Jones approach is 10.22, yielding the density estimate shown with the solid line. This bandwidth seems a bit too narrow, yielding a density estimate that is too wiggly. Silverman's rule of thumb gives a bandwidth of 32.96, larger than the bandwidth given by any previous method. The resulting density estimate is probably too smooth, hiding important features of the distribution. ![]()
Figure 10.5 Kernel density estimates for the whale calf migration data using normal kernels with bandwidths chosen by three different criteria. The bandwidths are 10.22 using the Sheather–Jones approach (solid), 32.96 using Silverman's rule of thumb (dashed), and 35.60 using the maximal smoothing span of Terrell (dotted).
10.2.1.3 Maximal Smoothing Principle
Recall again that the minimal AMISE is obtained when
but f is unknown. Silverman's rule of thumb replaces R(f′′) by R(ϕ′′). The Sheather–Jones method estimates R(f′′). Terrell's maximal smoothing approach replaces R(f′′) with the most conservative (i.e., smallest) possible value [627].
Specifically, Terrell considered the collection of all h that would minimize (10.29) for various f and recommended that the largest such bandwidth be chosen. In other words, the right-hand side of (10.29) should be maximized with respect to f. This will bias bandwidth selection against undersmoothing. Since R(f′′) vanishes as the variance of f shrinks, the maximization is carried out subject to the constraint that the variance of f matches the sample variance ![]() .
.
Constrained maximization of (10.29) with respect to f is an exercise in the calculus of variations. The f that maximizes (10.29) is a polynomial. Substituting its roughness for R(f′′) in (10.29) yields
(10.30) ![]()
as the chosen bandwidth. Table 10.1 provides the values of R(K) for some common kernels.
Table 10.1 Some kernel choices and related quantities discussed in the text. The kernels are listed in increasing order of roughness, R(K). K(z) should be multiplied by 1{|z|<1} in all cases except the normal kernel, which has positive support over the entire real line. RE is the asymptotic relative efficiency, as described in Section 10.2.2.1.

Terrell proposed the maximal smoothing principle to motivate this choice of bandwidth. When interpreting a density estimate, the analyst's eye is naturally drawn to modes. Further, modes usually have important scientific implications. Therefore, the bandwidth should be selected to discourage false modes, producing an estimate that shows modes only where the data indisputably require them.
The maximal smoothing approach is appealing because it is quick and simple to calculate. In practice, the resulting kernel density estimate is often too smooth. We would be reluctant to use a maximal smoothing bandwidth when the density estimate is being used for inference. For exploratory analyses, the maximal smoothing bandwidth can be quite helpful, allowing the analyst to focus on the dominant features of the density without being misled by highly variable indications of possibly false modes.
Example 10.4 (Whale Migration, Continued) The dotted line in Figure 10.5 shows the density estimate obtained using the maximal smoothing bandwidth of 35.60. Even larger than Silverman's bandwidth, this choice appears too large for the whale data. Generally, both Silverman's rule of thumb and Terrell's maximal smoothing principle tend to produce oversmoothed density estimates. ![]()
10.2.2 Choice of Kernel
Kernel density estimation requires specification of two components: the kernel and the bandwidth. It turns out that the shape of the kernel has much less influence on the results than does the bandwidth. Table 10.1 lists a few choices for kernel functions.
10.2.2.1 Epanechnikov Kernel
Suppose K is limited to bounded, symmetric densities with finite moments and variance equal to 1. Then Epanechnikov showed that minimizing AMISE with respect to K amounts to minimizing R(K) with respect to K subject to these constraints [186]. The solution to this variational calculus problem is the kernel assigning density ![]() , where K∗ is the Epanechnikov kernel
, where K∗ is the Epanechnikov kernel
(10.31) ![]()
This is a symmetric quadratic function, centered at zero, where its mode is reached, and decreasing to zero at the limits of its support.
From (10.17) and (10.18) we see that the minimal AMISE for a kernel density estimator with positive kernel K is ![]() . Switching to a K that doubles σKR(K) therefore requires doubling n to maintain the same minimal AMISE. Thus,
. Switching to a K that doubles σKR(K) therefore requires doubling n to maintain the same minimal AMISE. Thus, ![]() measures the asymptotic relative efficiency of K2 compared to K1. The relative efficiencies of a variety of kernels compared to the Epanechnikov kernel are given in Table 10.1. Notice that the relative efficiencies are all quite close to 1, reinforcing the point that kernel choice is fairly unimportant.
measures the asymptotic relative efficiency of K2 compared to K1. The relative efficiencies of a variety of kernels compared to the Epanechnikov kernel are given in Table 10.1. Notice that the relative efficiencies are all quite close to 1, reinforcing the point that kernel choice is fairly unimportant.
10.2.2.2 Canonical Kernels and Rescalings
Unfortunately, a particular value of h corresponds to a different amount of smoothing depending on which kernel is being used. For example, h = 1 corresponds to a kernel standard deviation nine times larger for the normal kernel than for the triweight kernel.
Let hK and hL denote the bandwidths that minimize AMISE (h) when using symmetric kernel densities K and L, respectively, which have mean zero and finite positive variance. Then from (10.29) it is clear that
where for any kernel we have ![]() . Thus, to change from bandwidth h for kernel K to a bandwidth that gives an equivalent amount of smoothing for kernel L, use the bandwidth hδ(L)/δ(K). Table 10.1 lists values for δ(K) for some common kernels.
. Thus, to change from bandwidth h for kernel K to a bandwidth that gives an equivalent amount of smoothing for kernel L, use the bandwidth hδ(L)/δ(K). Table 10.1 lists values for δ(K) for some common kernels.
Suppose further that we rescale each kernel shape in Table 10.1 so that h = 1 corresponds to a bandwidth of δ(K). The kernel density estimator can then be written as
![]()
where
![]()
and K represents one of the original kernel shapes and scalings shown in Table 10.1. Scaling kernels in this way provides a canonical kernelKδ(K) of each shape [440]. A key benefit of this viewpoint is that a single value of h can be used interchangeably for each canonical kernel without affecting the amount of smoothing in the density estimate.
Note that
(10.33) ![]()
for an estimator using a canonical kernel with bandwidth h [i.e., a kernel from Table 10.1 with bandwidth hδ(K)] and with C(Kδ(K)) = (σKR(K))4/5. This means that the balance between variance and squared bias determined by the factor (nh)−1 + h4R(f′′)/4 is no longer confounded with the chosen kernel. It also means that the contributions made by the kernel to the variance and squared bias terms in AMISE (h) are equal. It follows that the optimal kernel shape does not depend on the bandwidth: The Epanechnikov kernel shape is optimal for any desired degree of smoothing [440].
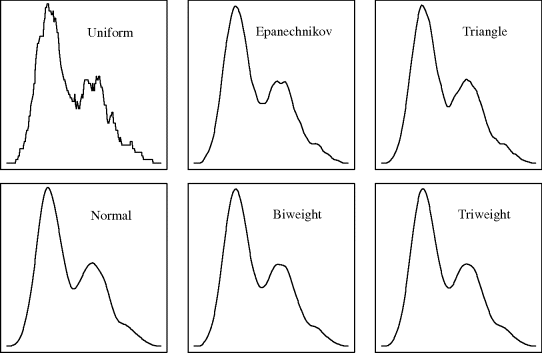
Example 10.5 (Bimodal Density, Continued) Figure 10.6 shows kernel density estimates for the data from Example 10.1, which originated from the equally weighted mixture of N(4, 12) and N(9, 22) densities. All the bandwidths were set at 0.69 for the canonical kernels of each shape, that being the Sheather–Jones bandwidth for the normal kernel. The uniform kernel produces a noticeably rougher result due to its discontinuity. The Epanechnikov and uniform kernels provide a slight (false) suggestion that the lower mode contains two small local modes. Aside from these small differences, the results for all the kernels are qualitatively the same. This example illustrates that even quite different kernels can be scaled to produce such similar results that the choice of kernel is unimportant. ![]()
Figure 10.6 Kernel density estimates for the data in Example 10.1 using the canonical version of each of the six kernels from Table 10.1, with h = 0.69 (dotted).
10.3 Nonkernel Methods
10.3.1 Logspline
A cubic spline is a piecewise cubic function that is everywhere twice continuously differentiable but whose third derivative may be discontinuous at a finite number of prespecified knots. One may view a cubic spline as a function created from cubic polynomials on each between-knot interval by pasting them together twice continuously differentiably at the knots. Kooperberg and Stone's logspline density estimation approach estimates the log of f by a cubic spline of a certain form [389, 615].
This method provides univariate density estimation on an interval (L, U), where each endpoint may be infinite. Suppose there are M ≥ 3 knots, tj for j = 1, . . ., M, with L < t1 < t2 < . . . < tM < U. Knot selection will be discussed later.
Let ![]() denote the M-dimensional space consisting of cubic splines with knots at t1, . . ., tM and that are linear on (L, t1] and [tM, U). Let a basis for
denote the M-dimensional space consisting of cubic splines with knots at t1, . . ., tM and that are linear on (L, t1] and [tM, U). Let a basis for ![]() be denoted by the functions {1, B1, . . ., BM−1}. There are numerical advantages to certain types of bases; books on splines and the other references in this section provide additional detail [144, 577]. It is possible to choose the basis functions so that on (L, t1] the function B1 is linear with a negative slope and all other Bi are constant, and so that on [tM, U) the function BM−1 is linear with a positive slope and all other Bi are constant.
be denoted by the functions {1, B1, . . ., BM−1}. There are numerical advantages to certain types of bases; books on splines and the other references in this section provide additional detail [144, 577]. It is possible to choose the basis functions so that on (L, t1] the function B1 is linear with a negative slope and all other Bi are constant, and so that on [tM, U) the function BM−1 is linear with a positive slope and all other Bi are constant.
Now consider modeling f with a parameterized density, fX|θ, defined by
(10.34) ![]()
where
(10.35) ![]()
and θ = (θ1, . . ., θM−1). For this to be a reasonable model for a density, we require c(θ) to be finite, which is ensured if (i) L> − ∞ or θ1 < 0 and (ii) U< ∞ or θM−1 < 0. Under this model, the log likelihood of θ is
given observed data values x1, . . ., xn. As long as the knots are positioned so that each interval contains sufficiently many observations for estimation, maximizing (10.36) subject to the constraint that c(θ) is finite provides the maximum likelihood estimate, ![]() . This estimate is unique because l(θ|x1, . . ., xn) is concave. Having estimated the model parameters, take
. This estimate is unique because l(θ|x1, . . ., xn) is concave. Having estimated the model parameters, take
(10.37) ![]()
as the maximum likelihood logspline density estimate of f(x).
The maximum likelihood estimation of θ is conditional on the number of knots and their placement. Kooperberg and Stone suggest an automated strategy for placement of a prespecified number of knots [390]. Their strategy places knots at the smallest and largest observed data point and at other positions symmetrically distributed about the median but not equally spaced.
To place a prespecified number of knots, let x(i) denote the ith order statistic of the data, for i = 1, . . ., n, so x(1) is the minimum observed value. Define an approximate quantile function
![]()
for 1 ≤ i ≤ n, where the value of q is obtained by linear interpolation for noninteger i.
The M knots will be placed at x(1), at x(n), and at the positions of the order statistics indexed by ![]() for a sequence of numbers
for a sequence of numbers ![]() .
.
When (L, U) = (− ∞, ∞), placement of the interior knots is governed by the following constraint on between-knot distances:
![]()
for 1 ≤ i ≤ M/2, where r1 = 0 and ![]() is chosen to satisfy
is chosen to satisfy ![]() if M is odd, or
if M is odd, or ![]() if M is even. The remaining knots are placed to maintain quantile symmetry, so that
if M is even. The remaining knots are placed to maintain quantile symmetry, so that
(10.38) ![]()
for M/2 ≤ i < M − 1, where ![]() .
.
When (L, U) is not a doubly infinite interval, similar knot placement rules have been suggested. In particular, if (L, U) is a interval of finite length, then ![]() are chosen equally spaced, so ri = (i − 1)/(M − 1).
are chosen equally spaced, so ri = (i − 1)/(M − 1).
The preceding paragraphs assumed that M, the number of knots, was prespecified. A variety of methods for choosing M are possible, but methods for choosing the number of knots have evolved to the point where a complete description of the recommended strategy is beyond the scope of our discussion. Roughly, the process is as follows. Begin by placing a small number of knots in the positions given above. The suggested minimum number is the first integer exceeding min {2.5n1/5, n/4, n∗, 25}, where n∗ is the number of distinct data points. Additional knots are then added to the existing set, one at time. At each iteration, a single knot is added in a position that gives the largest value of the Rao statistic for testing that the model without that knot suffices [391, 615]. Without examining significance levels, this process continues until the total number of knots reaches min {4n1/5, n/4, n∗, 30}, or until no new candidate knots can be placed due to constraints on the positions or nearness of knots.
Next, single knots are sequentially deleted. The deletion of a single knot corresponds to the removal of one basis function. Let ![]() denote the maximum likelihood estimate of the parameters of the current model. Then the Wald statistic for testing the significance of the contribution of the ith basis function is
denote the maximum likelihood estimate of the parameters of the current model. Then the Wald statistic for testing the significance of the contribution of the ith basis function is ![]() , where
, where ![]() is the square root of the ith diagonal entry of
is the square root of the ith diagonal entry of ![]() , the inverted observed information matrix [391, 615]. The knot whose removal would yield the smallest Wald statistic value is deleted. Sequential deletion is continued until only about three knots remain.
, the inverted observed information matrix [391, 615]. The knot whose removal would yield the smallest Wald statistic value is deleted. Sequential deletion is continued until only about three knots remain.
Sequential knot addition followed by sequential knot deletion generates a sequence of S models, with varying numbers of knots. Denote the number of knots in the sth model by ms, for s = 1, . . ., S. To choose the best model in the sequence, let
(10.39) ![]()
measure the quality of the sth model having corresponding MLE parameter vector ![]() . The quantity BIC (s) is a Bayes information criterion for model comparison [365, 579]; other measures of model quality can also be motivated. Selection of the model with the minimal value of BIC (s) among those in the model sequence provides the chosen number of knots.
. The quantity BIC (s) is a Bayes information criterion for model comparison [365, 579]; other measures of model quality can also be motivated. Selection of the model with the minimal value of BIC (s) among those in the model sequence provides the chosen number of knots.
Additional details of the knot selection process are given in [391, 615]. Software to carry out logspline density estimation in the R language is available in [388]. Stepwise addition and deletion of knots is a greedy search strategy that is not guaranteed to find the best collection of knots. Other search strategies are also effective, including MCMC strategies [305, 615].
The logspline approach is one of several effective methods for density estimation based on spline approximation; another is given in [285].
Example 10.6 (Whale Migration, Continued) Figure 10.7 shows the logspline density estimate (solid line) for the whale calf migration data from Example 10.2. Using the procedure outlined above, a model with seven knots was selected. The locations of these seven knots are shown with the solid dots in the figure. During initial knot placement, stepwise knot addition, and stepwise knot deletion, four other knots were considered at various stages but not used in the model finally selected according to the BIC criterion. These discarded knots are shown with hollow dots in the figure. The degree of smoothness seen in Figure 10.7 is typical of logspline estimates since splines are piecewise cubic and twice continuously differentiable.
Figure 10.7 Logspline density estimate (solid line) from bowhead whale calf migration data in Example 10.6. Below the histogram are dots indicating where knots were used (solid) and where knots were considered but rejected (hollow). Two other logspline density estimates for other knot choices are shown with the dotted and dashed lines; see the text for details.
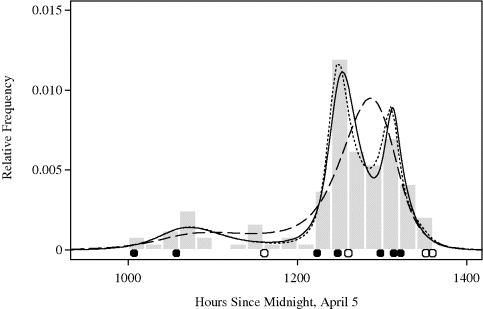
Estimation of local modes can sometimes be a problem if the knots are insufficient in number or poorly placed. The other lines in Figure 10.7 show the logspline density estimates with two other choices for the knots. The very poor estimate (dashed line) was obtained using 6 knots. The other estimate (dotted line) was obtained using all 11 knots shown in the figure with either hollow or solid dots. ![]()
10.4 Multivariate Methods
Multivariate density estimation of a density function f is based on i.i.d. random variables sampled from f. A p-dimensional variable is denoted Xi = (Xi1, . . ., Xip).
10.4.1 The Nature of the Problem
Multivariate density estimation is a significantly different task than univariate density estimation. It is very difficult to visualize any resulting density estimate when the region of support spans more than two or three dimensions. As an exploratory data analysis tool, multivariate density estimation therefore has diminishing usefulness unless some dimension-reduction strategy is employed. However, multivariate density estimation is a useful component in many more elaborate statistical computing algorithms, where visualization of the estimate is not required.
Multivariate density estimation is also hindered by the curse of dimensionality. High-dimensional space is very different than 1, 2, or 3-dimensional space. Loosely speaking, high-dimensional space is vast, and points lying in such a space have very few near neighbors. To illustrate, Scott defined the tail region of a standard p-dimensional normal density to comprise all points at which the probability density is less than one percent of the density at the mode [581]. While only 0.2% of the probability density falls in this tail region when p = 1, more than half the density falls in it when p = 10, and 98% falls in it when p = 20.
The curse of dimensionality has important implications for density estimation. For example, consider a kernel density estimator based on a random sample of n points whose distribution is p-dimensional standard normal. Below we mention several ways to construct such an estimator; our choice here is the so-called product kernel approach with normal kernels sharing a common bandwidth, but it is not necessary to understand this technique yet to follow our argument. Define the optimal relative root mean squared error (ORRMSE) at the origin to be
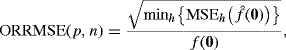
where ![]() estimates f from a sample of n points using the best possible bandwidth. This quantity measures the quality of the multivariate density estimator at the true mode. When p = 1 and n = 30, ORRMSE (1, 30) = 0.1701. Table 10.2 shows the sample sizes required to achieve as low a value of ORRMSE (p, n) for different values of p. The sample sizes are shown to about three significant digits. A different bandwidth minimizes ORRMSE (p, n) for each different p and n, so the table entries were computed by fixing p and searching over n, with each trial value of n requiring an optimization over h. This table confirms that desirable sample sizes grow very rapidly with p. In practice, things are not as hopeless as Table 10.2 might suggest. Adequate estimates can be sometimes obtained with a variety of techniques, especially those that attempt to simplify the problem via dimension reduction.
estimates f from a sample of n points using the best possible bandwidth. This quantity measures the quality of the multivariate density estimator at the true mode. When p = 1 and n = 30, ORRMSE (1, 30) = 0.1701. Table 10.2 shows the sample sizes required to achieve as low a value of ORRMSE (p, n) for different values of p. The sample sizes are shown to about three significant digits. A different bandwidth minimizes ORRMSE (p, n) for each different p and n, so the table entries were computed by fixing p and searching over n, with each trial value of n requiring an optimization over h. This table confirms that desirable sample sizes grow very rapidly with p. In practice, things are not as hopeless as Table 10.2 might suggest. Adequate estimates can be sometimes obtained with a variety of techniques, especially those that attempt to simplify the problem via dimension reduction.
Table 10.2 Sample sizes required to match the optimal relative root mean squared error at the origin achieved for one-dimensional data when n = 30. These results pertain to estimation of a p-variate normal density using a normal product kernel density estimator with bandwidths that minimize the relative root mean squared error at the origin in each instance.
| p | n |
| 1 | 30 |
| 2 | 180 |
| 3 | 806 |
| 5 | 17,400 |
| 10 | 112,000,000 |
| 15 | 2,190,000,000,000 |
| 30 | 806,000,000,000,000,000,000,000,000 |
10.4.2 Multivariate Kernel Estimators
The most literal generalization of the univariate kernel density estimator in (10.6) to the case of p-dimensional density estimation is the general multivariate kernel estimator
where H is a p × p nonsingular matrix of constants, whose absolute determinant is denoted |H|. The function K is a real-valued multivariate kernel function for which ∫K(z)dz = 1, ∫zK(z)dz = 0, and ∫zzTK(z)dz = Ip, where Ip is the p × p identity matrix.
This estimator is quite a bit more flexible than usually is required. It allows both a p-dimensional kernel of arbitrary shape and an arbitrary linear rotation and scaling via H. It can be quite inconvenient to try to specify the large number of bandwidth parameters contained in H and to specify a kernel shape over p-dimensional space. It is more practical to resort to more specialized forms of H and K that have far fewer parameters.
The product kernel approach provides a great deal of simplification. The density estimator is
where K(z) is a univariate kernel function, x = (x1, . . ., xp), Xi = (Xi1, . . ., Xip), and the hj are fixed bandwidths for each coordinate, j = 1, . . ., p.
Another simplifying approach would be to allow K to be a radially symmetric, unimodal density function in p dimensions, and to set
In this case, the multivariate Epanechnikov kernel shape
(10.43) 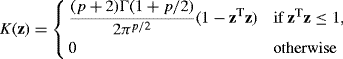
is optimal with respect to the asymptotic mean integrated squared error. However, as with univariate kernel density estimation, many other kernels provide nearly equivalent results.
The single fixed bandwidth in (10.42) means that probability contributions associated with each observed data point will diffuse in all directions equally. When the data have very different variability in different directions, or when the data nearly lie on a lower-dimensional manifold, treating all dimensions as if they were on the same scale can lead to poor estimates. Fukunaga [211] suggested linearly transforming the data so that they have identity covariance matrix, then estimating the density of the transformed data using (10.42) with a radially symmetric kernel, and then back-transforming to obtain the final estimate. To carry out the transformation, compute an eigenvalue–eigenvector decomposition of the sample covariance matrix so ![]() , where Λ is a p × p diagonal matrix with the eigenvalues in descending order and P is an orthonormal p × p matrix whose columns consist of the eigenvectors corresponding to the eigenvalues in Λ. Let
, where Λ is a p × p diagonal matrix with the eigenvalues in descending order and P is an orthonormal p × p matrix whose columns consist of the eigenvectors corresponding to the eigenvalues in Λ. Let ![]() be the sample mean. Then setting
be the sample mean. Then setting ![]() for i = 1, . . ., n provides the transformed data. This process is commonly called whitening or sphering the data. Using the kernel density estimator in (10.42) on the transformed data is equivalent to using the density estimator
for i = 1, . . ., n provides the transformed data. This process is commonly called whitening or sphering the data. Using the kernel density estimator in (10.42) on the transformed data is equivalent to using the density estimator
on the original data, for a symmetric kernel K.
Within the range of complexity presented by the choices above, the product kernel approach in (10.41) is usually preferred to (10.42) and (10.44), in view of its performance and flexibility. Using a product kernel also simplifies the numerical calculation and scaling of kernels.
As with the univariate case, it is possible to derive an expression for the asymptotic mean integrated squared error for a product kernel density estimator. The minimizing bandwidths h1, . . ., hp are the solutions to a set of p nonlinear equations. The optimal hi are all ![]() , and AMISE
, and AMISE![]() for these optimal hi. Bandwidth selection for product kernel density estimators and other multivariate approaches is far less well studied than in the univariate case.
for these optimal hi. Bandwidth selection for product kernel density estimators and other multivariate approaches is far less well studied than in the univariate case.
Perhaps the simplest approach to bandwidth selection in this case is to assume that f is normal, thereby simplifying the minimization of AMISE(h1, . . ., hp) with respect to h1, . . ., hp. This provides a bandwidth selection rationale akin to Silverman's rule of thumb in the univariate case. The resulting bandwidths for the normal product kernel approach are
for i = 1, . . ., p, where ![]() is an estimate of the standard deviation along the ith coordinate. As with the univariate case, using a robust scale estimator can improve performance. When nonnormal kernels are being used, the bandwidth for the normal kernel can be rescaled using (10.32) and Table 10.1 to provide an analogous bandwidth for the chosen kernel.
is an estimate of the standard deviation along the ith coordinate. As with the univariate case, using a robust scale estimator can improve performance. When nonnormal kernels are being used, the bandwidth for the normal kernel can be rescaled using (10.32) and Table 10.1 to provide an analogous bandwidth for the chosen kernel.
Terrell's maximal smoothing principle can also be applied to p-dimensional problems. Suppose we apply the general kernel density estimator given by (10.40) with a kernel function that is a density with identity covariance matrix. Then the maximal smoothing principle indicates choosing a bandwidth matrix H that satisfies
(10.46) 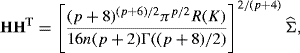
where ![]() is the sample covariance matrix. One could apply this result to find the maximal smoothing bandwidths for a normal product kernel, then rescale the coordinatewise bandwidths using (10.32) and Table 10.1 if another product kernel shape was desired.
is the sample covariance matrix. One could apply this result to find the maximal smoothing bandwidths for a normal product kernel, then rescale the coordinatewise bandwidths using (10.32) and Table 10.1 if another product kernel shape was desired.
Cross-validation methods can also be generalized to the multivariate case, as can some other automatic bandwidth selection procedures. However, the overall performance of such methods in general p-dimensional problems is not thoroughly documented.
10.4.3 Adaptive Kernels and Nearest Neighbors
With ordinary fixed-kernel density estimation, the shape of K and the bandwidth are fixed. These determine an unchanging notion of proximity. Weighted contributions from nearby Xi determine ![]() , where the weights are based on the proximity of Xi to x. For example, with a uniform kernel, the estimate is based on variable numbers of observations within a sliding window of fixed shape.
, where the weights are based on the proximity of Xi to x. For example, with a uniform kernel, the estimate is based on variable numbers of observations within a sliding window of fixed shape.
It is worthwhile to consider the opposite viewpoint: allowing regions to vary in size, but requiring them (in some sense) to have a fixed number of observations falling in them. Then regions of larger size correspond to areas of low density, and regions of small size correspond to areas of high density.
It turns out that estimators derived from this principle can be written as kernel estimators with a changing bandwidth that adapts to the local density of observed data points. Such approaches are variously termed adaptive kernel estimators, variable-bandwidth kernel estimators, or variable-kernel estimators. Three particular strategies are reviewed below.
The motivation for adaptive methods is that a fixed bandwidth may not be equally suitable everywhere. In regions where data are sparse, wider bandwidths can help prevent excessive local sensitivity to outliers. Conversely, where data are abundant, narrower bandwidths can prevent bias introduced by oversmoothing. Consider again the kernel density estimate of bowhead whale calf migration times given in Figure 10.5 using the fixed Sheather–Jones bandwidth. For migration times below 1200 and above 1270 hours, the estimate exhibits a number of modes, yet it is unclear how many of these are true and how many are artifacts of sampling variability. It is not possible to increase the bandwidth sufficiently to smooth away some of the small local modes in the tails without also smoothing away the prominent bimodality between 1200 and 1270. Only local changes to the bandwidth will permit such improvements.
In theory, when p = 1 there is little to recommend adaptive methods over simpler approaches, but in practice some adaptive methods have been demonstrated to be quite effective in some examples. For moderate or large p, theoretical analysis suggests that the performance of adaptive methods can be excellent compared to standard kernel estimators, but the practical performance of adaptive approaches in such cases is not thoroughly understood. Some performance comparisons for adaptive methods can be found in [356, 581, 628].
10.4.3.1 Nearest Neighbor Approaches
The kthnearest neighbor density estimator,
was the first approach to explicitly adopt a variable-bandwidth viewpoint [423]. For this estimator, dk(x) is the Euclidean distance from x to the kth nearest observed data point, and Vp is the volume of the unit sphere in p dimensions, where p is the dimensionality of the data. Since Vp = πp/2/Γ(p/2 + 1), note that dk(x) is the only random quantity in (10.47), as it depends on X1, . . ., Xn. Conceptually, the kth nearest neighbor estimate of the density at x is k/n divided by the volume of the smallest sphere centered at x that contains k of the n observed data values. The number of nearest neighbors, k, plays a role analogous to that of bandwidth: Large values of k yield smooth estimates, and small values of k yield wiggly estimates.
The estimator (10.47) may be viewed as a kernel estimator with a bandwidth that varies with x and a kernel equal to the density function that is uniform on the unit sphere in p dimensions. For an arbitrary kernel, the nearest neighbor estimator can be written as
If dk(x) is replaced with an arbitrary function hk(x), which may not explicitly represent distance, the name balloon estimator has been suggested because the bandwidth inflates or deflates through a function that depends on x [628]. The nearest neighbor estimator is asymptotically of this type: For example, using dk(x) as the bandwidth for the uniform-kernel nearest neighbor estimator is asymptotically equivalent to using a balloon estimator bandwidth of hk(x) = [k/(nVpf(x))]1/p, since
![]()
as n→ ∞, k→ ∞, and k/n → 0.
Nearest neighbor and balloon estimators exhibit a number of surprising attributes. First, choosing K to be a density does not ensure that ![]() is a density; for instance, the estimator in (10.47) does not have a finite integral. Second, when p = 1 and K is a density with zero mean and unit variance, choosing hk(x) = k/[2nf(x)] does not offer any asymptotic improvement relative to a standard kernel estimator, regardless of the choice of k [581]. Finally, one can show that the pointwise asymptotic mean squared error of a univariate balloon estimator is minimized when
is a density; for instance, the estimator in (10.47) does not have a finite integral. Second, when p = 1 and K is a density with zero mean and unit variance, choosing hk(x) = k/[2nf(x)] does not offer any asymptotic improvement relative to a standard kernel estimator, regardless of the choice of k [581]. Finally, one can show that the pointwise asymptotic mean squared error of a univariate balloon estimator is minimized when
![]()
Even with this optimal pointwise adaptive bandwidth, however, the asymptotic efficiency of univariate balloon estimators does not greatly exceed that of ordinary fixed-bandwidth kernel estimators when f is roughly symmetric and unimodal [628]. Thus, nearest neighbor and balloon estimators seem a poor choice when p = 1.
On the other hand, for multivariate data, balloon estimators offer much more promise. The asymptotic efficiency of the balloon estimator can greatly surpass that of a standard multivariate kernel estimator, even for fairly small p and symmetric, unimodal data [628]. If we further generalize (10.48) to
where H(x) is a bandwidth matrix that varies with x, then we have effectively allowed the shape of kernel contributions to vary with x. When H(x) = hk(x)I, the general form reverts to the balloon estimator. Further, setting hk(x) = dk(x) yields the nearest neighbor estimator in (10.48). More general choices for H(x) are mentioned in [628].
10.4.3.2 Variable-Kernel Approaches and Transformations
A variable-kernel or sample point adaptive estimator can be written as
where K is a multivariate kernel and hi is a bandwidth individualized for the kernel contribution centered at Xi [66]. For example, hi might be set equal to the distance from Xi to the kth nearest other observed data point, so hi = dk(Xi). A more general variable kernel estimator with bandwidth matrix Hi that depends on the ith sampled point is also possible [cf. Equation (10.49)], but we focus on the simpler form here.
The variable-kernel estimator in (10.50) is a mixture of kernels with identical shape but different scales, centered at each observation. Letting the bandwidth vary as a function of Xi rather than of x guarantees that ![]() is a density whenever K is a density.
is a density whenever K is a density.
Optimal bandwidths for variable-kernel approaches depend on f. Pilot estimation of f can be used to guide bandwidth adaptation. Consider the following general strategy:
The parameter α affects the degree of local adaptation by controlling how quickly the bandwidth changes in response to suspected changes in f. Asymptotic arguments and practical experience support setting ![]() , which yields the approach of Abramson [3]. Several investigators have found this approach to perform well in practice [598, 674].
, which yields the approach of Abramson [3]. Several investigators have found this approach to perform well in practice [598, 674].
An alternative proposal is α = 1/p, which yields an approach that is asymptotically equivalent to the adaptive kernel estimator of Breiman, Meisel, and Purcell [66]. This choice ensures that the number of observed data points captured by the scaled kernel will be roughly equal everywhere [598]. In their algorithm, these authors used a nearest neighbor approach for ![]() and set hi = hdk(Xi) for a smoothness parameter h that may depend on k.
and set hi = hdk(Xi) for a smoothness parameter h that may depend on k.
Example 10.7 (Bivariate t Distribution) To illustrate the potential benefit of adaptive approaches, consider estimating the bivariate t distribution (with two degrees of freedom) from a sample of size n = 500. In the nonadaptive approach, we use a normal product kernel with individual bandwidths chosen using the Sheather–Jones approach. As an adaptive alternative, we use Abramson's variable-kernel approach (![]() ) with a normal product kernel, the pilot estimate taken to be the result of the nonadaptive approach,
) with a normal product kernel, the pilot estimate taken to be the result of the nonadaptive approach, ![]() = 0.005, and h set equal to the mean of the coordinatewise bandwidths used in the nonadaptive approach times the geometric mean of the
= 0.005, and h set equal to the mean of the coordinatewise bandwidths used in the nonadaptive approach times the geometric mean of the ![]() .
.
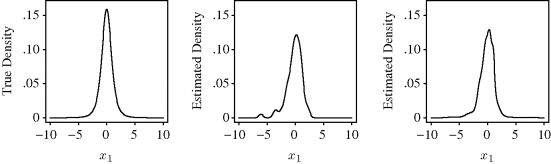
The left panel of Figure 10.8 shows the true values of the bivariate t distribution with two degrees of freedom, f, along the line x2 = 0. In other words, this shows a slice from the true density. The center panel of Figure 10.8 shows the result of the nonadaptive approach. The tails of the estimate exhibit undesirable wiggliness caused by an inappropriately narrow bandwidth in the tail regions, where a few outliers fall. The right panel of Figure 10.8 shows the result from Abramson's approach. Bandwidths are substantially wider in the tail areas, thereby producing smoother estimates in these regions than were obtained from the fixed-bandwidth approach. Abramson's method also uses much narrower bandwidths near the estimated mode. There is a slight indication of this for our random sample, but the effect can sometimes be pronounced. ![]()
Figure 10.8 Results from Example 10.7. From left to right, the three panels show the bivariate density value along the one-dimensional slice for which x2 = 0 for: the true bivariate t distribution with two degrees of freedom, the bivariate estimate using a fixed-bandwidth product kernel approach, and the bivariate estimate using Abramson's adaptive approach as described in the text.
Having discussed the variable-kernel approach, emphasizing its application in higher dimensions, we next consider a related approach primarily used for univariate data. This method illustrates the potential advantage of data transformation for density estimation.
Wand, Marron, and Ruppert noted that conducting fixed-bandwidth kernel density estimation on data that have been nonlinearly transformed is equivalent to using a variable-bandwidth kernel estimator on the original data [652]. The transformation induces separate bandwidths hi at each data point.
Suppose univariate data X1, . . ., Xn are observed from a density fX. Let
denote a transformation, where ![]() is a monotonic increasing mapping of the support of f to the real line parameterized by λ, and
is a monotonic increasing mapping of the support of f to the real line parameterized by λ, and ![]() and
and ![]() are the variances of X and
are the variances of X and ![]() , respectively. Then tλ is a scale-preserving transformation that maps the random variable X ~ fX to Y having density
, respectively. Then tλ is a scale-preserving transformation that maps the random variable X ~ fX to Y having density
(10.52) ![]()
For example, if X is a standard normal random variable and ![]() , then Y has the same variance as X. However, a window of fixed width 0.3 on the Y scale centered at any value y has variable width when back-transformed to the X scale: The width is roughly 2.76 when x = − 1 but only 0.24 when x = 1. In practice, sample standard deviations or robust measures of spread may be used in tλ to preserve scale.
, then Y has the same variance as X. However, a window of fixed width 0.3 on the Y scale centered at any value y has variable width when back-transformed to the X scale: The width is roughly 2.76 when x = − 1 but only 0.24 when x = 1. In practice, sample standard deviations or robust measures of spread may be used in tλ to preserve scale.
Suppose we transform the data using tλ to obtain Y1, . . ., Yn, then construct a fixed-bandwidth kernel density estimate for these transformed data, and then back-transform the resulting estimate to the original scale to produce an estimate of fX. From (10.18) we know that the bandwidth that minimizes AMISE (h) for a kernel estimate of gλ is
(10.53) ![]()
for a given choice of λ.
Since hλ depends on the unknown density gλ, a plug-in method is suggested to estimate ![]() by
by ![]() , where
, where ![]() is a kernel estimator using pilot bandwidth h0. Wand, Marron, and Ruppert suggest using a normal kernel with Silverman's rule of thumb to determine h0, thereby yielding the estimator
is a kernel estimator using pilot bandwidth h0. Wand, Marron, and Ruppert suggest using a normal kernel with Silverman's rule of thumb to determine h0, thereby yielding the estimator
(10.54) ![]()
where ![]() and ϕ(4) is the fourth derivative of the standard normal density [652]. Since tλ is scale-preserving, the sample standard deviation of X1, . . ., Xn, say
and ϕ(4) is the fourth derivative of the standard normal density [652]. Since tλ is scale-preserving, the sample standard deviation of X1, . . ., Xn, say ![]() , provides an estimate of the standard deviation of Y to use in the expression for h0. Related derivative estimation ideas are discussed in [298, 581].
, provides an estimate of the standard deviation of Y to use in the expression for h0. Related derivative estimation ideas are discussed in [298, 581].
The familiar Box–Cox transformation [57],
(10.55) ![]()
is among the parameterized transformation families available for (10.51). When any good transformation will suffice, or in multivariate settings, it can be useful to rely upon the notion that the transformation should make the data more nearly symmetric and unimodal because fixed-bandwidth kernel density estimation is known to perform well in this case.
This transformation approach to variable-kernel density estimation can work well for univariate skewed unimodal densities. Extensions to multivariate data are challenging, and applications to multimodal data can result in poor estimates. Without all the formalism outlined above, data analysts routinely transform variables to convenient scales using functions such as the log, often retaining this transformation thereafter for displaying results and even making inferences. When inferences on the original scale are preferred, one could pursue a transformation strategy based on graphical or quantitative assessments of the symmetry and unimodality achieved, rather than optimizing the transformation within a class of functions as described above.
10.4.4 Exploratory Projection Pursuit
Exploratory projection pursuit focuses on discovering low-dimensional structure in a high-dimensional density. The final density estimate is constructed by modifying a standard multivariate normal distribution to reflect the structure found. The approach described below follows Friedman [206], which extends previous work [210, 338].
In this subsection, reference will be made to a variety of density functions with assorted arguments. For notational clarity, we therefore assign a subscript to the density function to identify the random variable whose density is being discussed.
Let the data consist of n observations of p-dimensional variables, X1, . . ., Xn ~ i.i.d. fX. Before beginning exploratory projection pursuit, the data are transformed to have mean 0 and variance–covariance matrix Ip. This is accomplished using the whitening or sphering transformation described in Section 10.4.2. Let fZ denote the density corresponding to the transformed variables, Z1, . . ., Zn. Both fZ and fX are unknown. To estimate fX it suffices to estimate fZ and then reverse the transformation to obtain an estimate of fX. Thus our primary concern will be the estimation of fZ.
Several steps in the process rely on another density estimation technique, based on Legendre polynomial expansion. The Legendre polynomials are a sequence of orthogonal polynomials on [− 1, 1] defined by P0(u) = 1, P1(u) = u, and Pj(u) = [(2j − 1)uPj−1(u) − (j − 1)Pj−2(u)]/j for j ≥ 2, having the property that the L2 norm ![]() for all j [2, 568]. These polynomials can be used as a basis for representing functions on [− 1, 1]. In particular, we can represent a univariate density f that has support only on [− 1, 1] by its Legendre polynomial expansion
for all j [2, 568]. These polynomials can be used as a basis for representing functions on [− 1, 1]. In particular, we can represent a univariate density f that has support only on [− 1, 1] by its Legendre polynomial expansion
where
and the expectation in (10.57) is taken with respect to f. Equation (10.57) can be confirmed by noting the orthogonality and L2 norm of the Pj. If we observe X1, . . ., Xn ~ i.i.d. f, then ![]() is an estimator of E{Pj(X)}. Therefore
is an estimator of E{Pj(X)}. Therefore
(10.58) ![]()
may be used as estimates of the coefficients in the Legendre expansion of f. Truncating the sum in (10.56) after J + 1 terms suggests the estimator
(10.59) 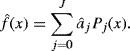
Having described this Legendre expansion approach, we can now move on to study exploratory projection pursuit.
The first step of exploratory projection pursuit is a projection step. If Yi = αTZi, then we say that Yi is the one-dimensional projection of Zi in the direction α. The goal of the first step is to project the multivariate observations onto the one-dimensional line for which the distribution of the projected data has the most structure.
The degree of structure in the projected data is measured as the amount of departure from normality. Let U(y) = 2Φ(y) − 1, where Φ is the standard normal cumulative distribution function. If Y ~ N(0, 1), then U(Y) ~ Unif (− 1, 1). To measure the structure in the distribution of Y it suffices to measure the degree to which the density of U(Y) differs from Unif (− 1, 1).
Define a structure index as
where fU is the probability density function of U(αTZ) when Z ~ fZ. When S(α) is large, a large amount of nonnormal structure is present in the projected data. When S(α) is nearly zero, the projected data are nearly normal. Note that S(α) depends on fU, which must be estimated.
To estimate S(α) from the observed data, use the Legendre expansion for fU to reexpress R(fU) in (10.60) as
where the expectations are taken with respect to fU. Since U(αTZ1), . . ., U(αTZn) represent draws from fU, the expectations in (10.61) can be estimated by sample moments. If we also truncate the sum in (10.61) at J + 1 terms, we obtain
(10.62) 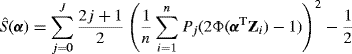
as an estimator of S(α).
Thus, to estimate the projection direction yielding the greatest nonnormal structure, we maximize ![]() with respect to α, subject to the constraint that αTα = 1. Denote the resulting direction by
with respect to α, subject to the constraint that αTα = 1. Denote the resulting direction by ![]() . Although
. Although ![]() is estimated from the data, we treat it as a fixed quantity when discussing distributions of projections of random vectors onto it. For example, let
is estimated from the data, we treat it as a fixed quantity when discussing distributions of projections of random vectors onto it. For example, let ![]() denote the univariate marginal density of
denote the univariate marginal density of ![]() when Z ~ fZ, treating Z as random and
when Z ~ fZ, treating Z as random and ![]() as fixed.
as fixed.
The second step of exploratory projection pursuit is a structure removal step. The goal is to apply a transformation to Z1, . . ., Zn which makes the density of the projection of fZ on ![]() a standard normal density, while leaving the distribution of a projection along any orthogonal direction unchanged. To do this, let A1 be an orthonormal matrix with first row equal to
a standard normal density, while leaving the distribution of a projection along any orthogonal direction unchanged. To do this, let A1 be an orthonormal matrix with first row equal to ![]() . Also, for observations from a random vector V = (V1, . . ., Vp), define the vector transformation
. Also, for observations from a random vector V = (V1, . . ., Vp), define the vector transformation ![]() , where
, where ![]() is the cumulative distribution function of the first element of V. Then letting
is the cumulative distribution function of the first element of V. Then letting
for i = 1, . . ., n would achieve the desired transformation. The transformation in (10.63) cannot be used directly to achieve the structure removal goal because it depends on the cumulative distribution function corresponding to ![]() . To get around this problem, simply replace the cumulative distribution function with the corresponding empirical distribution function of
. To get around this problem, simply replace the cumulative distribution function with the corresponding empirical distribution function of ![]() . An alternative replacement is suggested in [340].
. An alternative replacement is suggested in [340].
The ![]() for i = 1, . . ., n may be viewed as a new dataset consisting of the observed values of random variables
for i = 1, . . ., n may be viewed as a new dataset consisting of the observed values of random variables ![]() whose unknown distribution
whose unknown distribution ![]() depends on fZ. There is an important relationship between the conditionals determined by
depends on fZ. There is an important relationship between the conditionals determined by ![]() and fZ given a projection onto
and fZ given a projection onto ![]() . Specifically, the conditional distribution of
. Specifically, the conditional distribution of ![]() given
given ![]() equals the conditional distribution of Zi given
equals the conditional distribution of Zi given ![]() because the structure removal step creating
because the structure removal step creating ![]() leaves all coordinates of Zi except the first unchanged. Therefore
leaves all coordinates of Zi except the first unchanged. Therefore
Equation (10.64) provides no immediate way to estimate fZ, but iterating the entire process described above will eventually prove fruitful.
Suppose a second projection step is conducted. A new direction to project the working variables ![]() is sought to isolate the greatest amount of one-dimensional structure. Finding this direction requires the calculation of a new structure index based on the transformed sample
is sought to isolate the greatest amount of one-dimensional structure. Finding this direction requires the calculation of a new structure index based on the transformed sample ![]() , leading to the estimation of
, leading to the estimation of ![]() as the projection direction revealing greatest structure.
as the projection direction revealing greatest structure.
Taking a second structure removal step requires the reapplication of equation (10.63) with a suitable matrix A2, yielding new working variables ![]() .
.
Iterating the same conditional distribution argument as expressed in (10.64) allows us to write the density from which the new working data arise as
where ![]() is the marginal density of
is the marginal density of ![]() when
when ![]() .
.
Suppose the projection and structure removal steps are iterated several additional times. At some point, the identification and removal of structure will lead to new variables whose distribution has little or no remaining structure. In other words, their distribution will be approximately normal along any possible univariate projection. At this point, iterations are stopped. Suppose that a total of M iterations were taken. Then (10.65) extends to give
where ![]() is the marginal density of
is the marginal density of ![]() when
when ![]() , and Z(0) ~ fZ.
, and Z(0) ~ fZ.
Now, Equation (10.66) can be used to estimate fZ because—having eliminated all structure from the distribution of our working variables ![]() —we may set
—we may set ![]() equal to a p-dimensional multivariate normal density, denoted ϕp. Solving for fZ gives
equal to a p-dimensional multivariate normal density, denoted ϕp. Solving for fZ gives
Although this equation still depends on the unknown densities ![]() , these can be estimated using the Legendre approximation strategy. Note that if
, these can be estimated using the Legendre approximation strategy. Note that if ![]() for
for ![]() , then
, then
Use the Legendre expansion of ![]() and sample moments to estimate
and sample moments to estimate
(10.69) 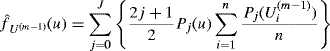
from ![]() derived from
derived from ![]() . After substituting
. After substituting ![]() for
for ![]() in (10.68) and isolating
in (10.68) and isolating ![]() , we obtain
, we obtain
(10.70) ![]()
Thus, from (10.67) the estimate for fZ(z) is
where the
(10.72) ![]()
are estimated using the working variables accumulated during the structure removal process, and ![]() . Reversing the sphering by applying the change of variable
. Reversing the sphering by applying the change of variable ![]() to
to ![]() provides the estimate
provides the estimate ![]() .
.
The estimate ![]() is most strongly influenced by the central portion of the data because the transformation U compresses information about the tails of fZ into the extreme portions of the interval [− 1, 1]. Low-degree Legendre polynomial expansion has only limited capacity to capture substantial features of fU in these narrow margins of the interval. Furthermore, the structure index driving the choice of each
is most strongly influenced by the central portion of the data because the transformation U compresses information about the tails of fZ into the extreme portions of the interval [− 1, 1]. Low-degree Legendre polynomial expansion has only limited capacity to capture substantial features of fU in these narrow margins of the interval. Furthermore, the structure index driving the choice of each ![]() will not assign high structure to directions for which only the tail behavior of the projection is nonnormal. Therefore, exploratory projection pursuit should be viewed foremost as a way to extract key low-dimensional features of the density which are exhibited by the bulk of the data, and to reconstruct a density estimate that reflects these key features.
will not assign high structure to directions for which only the tail behavior of the projection is nonnormal. Therefore, exploratory projection pursuit should be viewed foremost as a way to extract key low-dimensional features of the density which are exhibited by the bulk of the data, and to reconstruct a density estimate that reflects these key features.
Example 10.8 (Bivariate Rotation) To illustrate exploratory projection pursuit, we will attempt to reconstruct the density of some bivariate data. Let W = (W1, W2), where W1 ~ Gamma (4, 2) and W2 ~ N(0, 1) independently. Then E{W} = (2, 0) and var{W} = I. Use
![]()
to rotate W to produce data via X = RW. Let fX denote the density of X, which we will try to estimate from a sample of n = 500 points drawn from fX. Since var{X} = RRT = I, the whitening transformation is nearly just a translation (aside from the fact that the theoretical and sample variance–covariance matrices differ slightly).
The whitened data values, z1, . . ., z500, are plotted in the top left panel of Figure 10.9. The underlying gamma structure is detectable in this graph as an abruptly declining frequency of points in the top right region of the plot: Z and X are rotated about 135 degrees counterclockwise with respect to W.
Figure 10.9 First two projection and structure removal steps for Example 10.8, as described in the text.
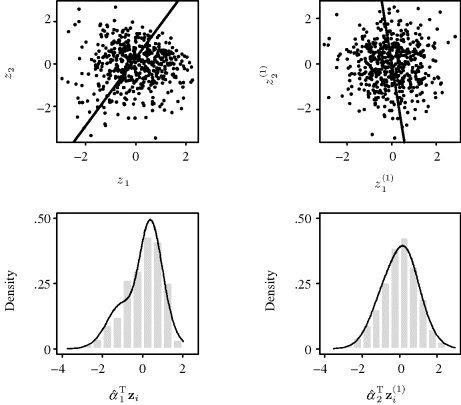
The direction ![]() that reveals the most univariate projected structure is shown with the line in the top left panel of Figure 10.9. Clearly this direction corresponds roughly to the original gamma-distributed coordinate. The bottom left panel of Figure 10.9 shows a histogram of the zi values projected onto
that reveals the most univariate projected structure is shown with the line in the top left panel of Figure 10.9. Clearly this direction corresponds roughly to the original gamma-distributed coordinate. The bottom left panel of Figure 10.9 shows a histogram of the zi values projected onto ![]() , revealing a rather nonnormal distribution. The curve superimposed on this histogram is the univariate density estimate for
, revealing a rather nonnormal distribution. The curve superimposed on this histogram is the univariate density estimate for ![]() obtained using the Legendre expansion strategy. Throughout this example, the number of Legendre polynomials was set to J + 1 = 4.
obtained using the Legendre expansion strategy. Throughout this example, the number of Legendre polynomials was set to J + 1 = 4.
Removing the structure revealed by the projection on ![]() yields new working data values,
yields new working data values, ![]() , graphed in the top right panel of Figure 10.9. The projection direction,
, graphed in the top right panel of Figure 10.9. The projection direction, ![]() , showing the most nonnormal structure is again shown with a line. The bottom right panel shows a histogram of
, showing the most nonnormal structure is again shown with a line. The bottom right panel shows a histogram of ![]() values and the corresponding Legendre density estimate.
values and the corresponding Legendre density estimate.
At this point, there is little need to proceed with additional projection and structure removal steps: The working data are already nearly multivariate normal. Employing (10.71) to reconstruct an estimate of fZ yields the density estimate shown in Figure 10.10. The rotated gamma–normal structure is clearly seen in the figure, with the heavier gamma tail extending leftward and the abrupt tail terminating on the right. The final step in application would be to reexpress this result in terms of a density for X rather than Z. ![]()
Figure 10.10 Exploratory projection pursuit density estimate ![]() for Example 10.8.
for Example 10.8.
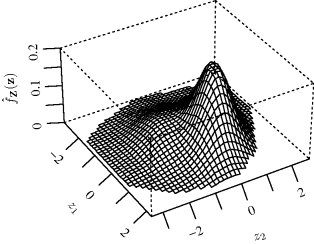
Problems
10.1. Sanders et al. provide a comprehensive dataset of infrared emissions and other characteristics of objects beyond our galaxy [567]. These data are available from the website for our book. Let X denote the log of the variable labeled F12, which is the total 12-μm-band flux measurement on each object.
10.2. This problem continues using the infrared data on extragalactic objects and the variable X (the log of the 12-μm-band flux measurement) from Problem 10.1. The dataset also includes F100 data: the total 100-μm-band flux measurements for each object. Denote the log of this variable by Y. Construct bivariate density estimates for the joint density of X and Y using the following approaches.
10.3. Starting from Equation (10.22), derive a simplification for UCV (h) when ![]() , pursuing the following steps:
, pursuing the following steps:
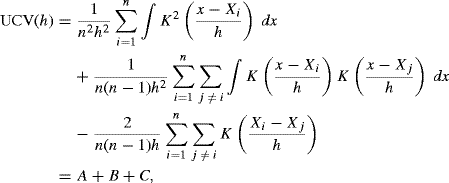
![]()
(10.73) ![]()
10.4. Replicate the first four rows of Table 10.2. Assume ![]() is a product kernel estimator. You may find it helpful to begin with the expression
is a product kernel estimator. You may find it helpful to begin with the expression ![]() , and to use the result
, and to use the result
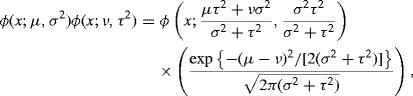
where ϕ(x; α, β2) denotes a univariate normal density function with mean α and variance β2.
10.5. Available from the website for this book are some manifold data exhibiting some strong structure. Specifically, these four-dimensional data come from a mixture distribution, with a low weighting of a density that lies nearly on a three-dimensional manifold and a high weighting of a heavy-tailed density that fills four-dimensional space.