5
DATA REPRESENTATION
Contents
- Number system
- Decimal number system
- Binary number system
- Octal number system
- Hexadecimal number system
- Conversion from decimal to binary, octal, hexadecimal
- Converting decimal integer to binary, octal, hexadecimal
- Converting decimal fraction to binary, octal, hexadecimal
- Converting decimal integer.fraction to binary, octal, hexadecimal
- Conversion of binary, octal, hexadecimal to decimal
- Conversion of binary to octal, hexadecimal
- Conversion of octal, hexadecimal to binary
- Binary arithmetic—Binary addition, binary subtraction
- Signed and unsigned numbers—Complement of binary numbers
- Binary data representation—Fixed point number representation, floating point number representation
- Binary coding schemes—EBCDIC, ASCII, unicode
- Logic gates
Why this chapter
We use computer to process the data and get the desired output. The data input can be in the form of alphabets, digits, symbols, audio, video, magnetic cards, finger prints, etc. Since computer can only understand 0 and 1, the data must be represented in the computer in 0s and 1s. The purpose of this chapter is to introduce you to the data representation in the computer.
5.1 INTRODUCTION
The data stored in the computer may be of different kinds, as follows—
- Numeric data (0, 1, 2, …, 9)
- Alphabetic data (A, B, C, …, Z)
- Alphanumeric data—Combination of any of the symbols—(A, B, C… Z), (0, 1… 9), or special characters (+,−, Blank), etc.
All kinds of data, be it alphabets, numbers, symbols, sound data or video data, is represented in terms of 0s and 1s, in the computer. Each symbol is represented as a unique combination of 0s and 1s.
This chapter discusses the number systems that are commonly used in the computer. The number systems discussed in this chapter are—(1) Decimal number system, (2) Binary number system, (3) Octal number system, and (4) Hexadecimal number system. The number conversions described in this chapter are—
- Decimal (Integer, Fraction, Integer.Fraction) to Binary, Octal, Hexadecimal
- Binary, Octal, Hexadecimal (Integer, Fraction, Integer.Fraction) to Decimal
- Binary to Octal, Hexadecimal
- Octal, Hexadecimal to Binary
The chapter also discusses the binary arithmetic operations and the representation of signed and unsigned numbers in the computer. The representation of numbers using binary coding schemes and the logic gates used for the manipulation of data are also discussed.
5.2 NUMBER SYSTEM
A number system in base r or radix r uses unique symbols for r digits. One or more digits are combined to get a number. The base of the number decides the valid digits that are used to make a number. In a number, the position of digit starts from the right-hand side of the number. The rightmost digit has position 0, the next digit on its left has position 1, and so on. The digits of a number have two kinds of values—
- Face value, and
- Position value.
The face value of a digit is the digit located at that position. For example, in decimal number 52, face value at position 0 is 2 and face value at position 1 is 5.
The position value of a digit is (baseposition). For example, in decimal number 52, the position value of digit 2 is 100 and the position value of digit 5 is 101. Decimal numbers have a base of 10.
The number is calculated as the sum of, face value * baseposition, of each of the digits. For decimal number 52, the number is 5*101 + 2*100 = 50 + 2 = 52
In computers, we are concerned with four kinds of number systems, as follows—
- Decimal Number System —Base 10
- Binary Number System —Base 2
- Octal Number System —Base 8
- Hexadecimal Number System—Base 16
The numbers given as input to computer and the numbers given as output from the computer, are generally in decimal number system, and are most easily understood by humans. However, computer understands the binary number system, i.e., numbers in terms of 0s and 1s. The binary data is also represented, internally, as octal numbers and hexadecimal numbers due to their ease of use.
A number in a particular base is written as (number)base of number For example, (23)10 means that the number 23 is a decimal number, and (345)8 shows that 345 is an octal number.
5.2.1 Decimal Number System
- It consists of 10 digits—0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
- All numbers in this number system are represented as combination of digits 0—9. For example, 34, 5965 and 867321.
- The position value and quantity of a digit at different positions in a number are as follows—
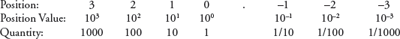
5.2.2 Binary Number System
- The binary number system consists of two digits—0 and 1.
- All binary numbers are formed using combination of 0 and 1. For example, 1001, 11000011 and 10110101.
- The position value and quantity of a digit at different positions in a number are as follows—
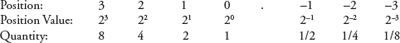
5.2.3 Octal Number System
- The octal number system consists of eight digits—0 to 7.
- All octal numbers are represented using these eight digits. For example, 273, 103, 2375, etc.
- The position value and quantity of a digit at different positions in a number are as follows—

5.2.4 Hexadecimal Number System
- The hexadecimal number system consists of sixteen digits—0 to 9, A, B, C, D, E, F, where (A is for 10, B is for 11, C-12, D-13, E-14, F-15).
- All hexadecimal numbers are represented using these 16 digits. For example, 3FA, 87B, 113, etc.
- The position value and quantity of a digit at different positions in a number are as follows—
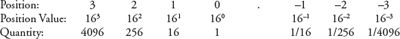
Table 5.1 summarizes the base, digits and largest digit for the above discussed number systems. Table 5.2 shows the binary, octal and hexadecimal equivalents of the decimal numbers 0–16.

Table 5.1 Summary of number system
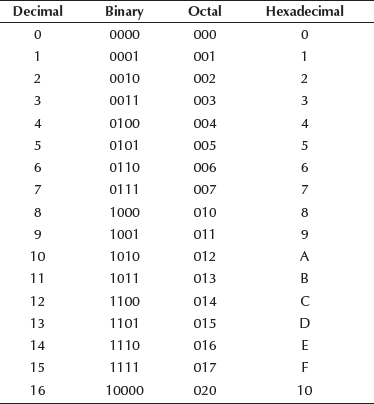
Table 5.2 Decimal, binary, octal and hexadecimal equivalents
5.3 CONVERSION FROM DECIMAL TO BINARY, OCTAL, HEXADECIMAL
A decimal number has two parts—integer part and fraction part. For example, in the decimal number 23.0786, 23 is the integer part and .0786 is the fraction part. The method used for the conversion of the integer part of a decimal number is different from the one used for the fraction part. In the following subsections, we shall discuss the conversion of decimal integer, decimal fraction and decimal integer.fraction number into binary, octal and hexadecimal number.
5.3.1 Converting Decimal Integer to Binary, Octal, Hexadecimal
A decimal integer is converted to any other base, by using the division operation.
To convert a decimal integer to—
- binary-divide by 2,
- octal-divide by 8, and,
- hexadecimal-divide by 16.
Let us now understand this conversion with the help of some examples.
Example 1: Convert 25 from Base 10 to Base 2.
- Make a table as shown below. Write the number in centre and toBase on the left side.
to Base Number
(Quotient)Remainder 225 - Divide the number with toBase. After each division, write the remainder on right-side column and quotient in the next line in the middle column. Continue dividing till the quotient is 0.
to Base Number
(Quotient)Remainder 225212126023021101 - Write the digits in remainder column starting from downwards to upwards,
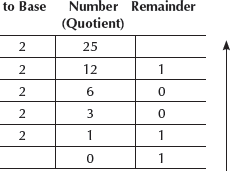
The binary equivalent of number (25)10 is (11001)2
The steps shown above are followed to convert a decimal integer to a number in any other base.
Example 2: Convert 23 from Base 10 to Base 2, 8, 16.

Example 3: Convert 147 from Base 10 to Base 2, 8 and 16.
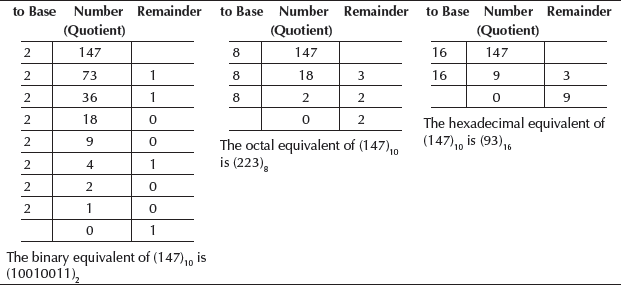
Example 4: Convert 94 from Base 10 to Base 2, 8 and 16.
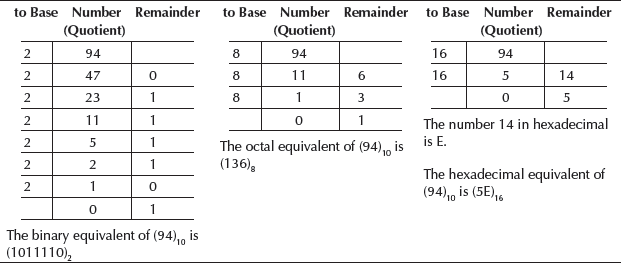
5.3.2 Converting Decimal Fraction to Binary, Octal, Hexadecimal
A fractional number is a number less than 1. It may be .5, .00453, .564, etc. We use the multiplication operation to convert decimal fraction to any other base.
To convert a decimal fraction to—
- binary-multiply by 2,
- octal-multiply by 8, and,
- hexadecimal-multiply by 16.
Steps for conversion of a decimal fraction to any other base are—
- Multiply the fractional number with the to Base, to get a resulting number.
- The resulting number has two parts, non-fractional part and fractional part.
- Record the non-fractional part of the resulting number.
- Repeat the above steps at least four times.
- Write the digits in the non-fractional part starting from upwards to downwards.
Example 5: Convert 0.2345 from Base 10 to Base 2.

The binary equivalent of (0.2345)10 is (0.001111)2
Example 5a: Convert 0.865 from Base 10 to Base 2,8 and 16.

5.3.3 Converting Decimal Integer.Fraction to Binary, Octal, Hexadecimal
A decimal integer.fraction number has both integer part and fraction part. The steps for conversion of a decimal integer.fraction to any other base are—
- Convert decimal integer part to the desired base following the steps shown in section 5.3.1.
- Convert decimal fraction part to the desired base following the steps shown in section 5.3.2.
- The integer and fraction part in the desired base is combined to get integer.fraction.
Example 6: Convert 34.4674 from Base 10 to Base 2.

Example 7: Convert 34.4674 from Base 10 to Base 8.

Example 8: Convert 34.4674 from Base 10 to Base 16.

5.4 CONVERSION OF BINARY, OCTAL, HEXADECIMAL TO DECIMAL
A binary, octal or hexadecimal number has two parts—integer part and fraction part. For example, a binary number could be 10011, 0.011001 or 10011.0111. The numbers 45, .362 or 245.362 are octal numbers. A hexadecimal number could be A2, .4C2 or A1.34.
The method used for the conversion of integer part and fraction part of binary, octal or hexadecimal number to decimal number is the same; multiplication operation is used for the conversion. The conversion mechanism uses the face value and position value of digits. The steps for conversion are as follows—
- Find the sum of the Face Value * (fromBase)positio for each digit in the number.
- In a non-fractional number, the rightmost digit has position 0 and the position increases as we go towards the left.
- In a fractional number, the first digit to the left of decimal point has position 0 and the position increases as we go towards the left. The first digit to the right of the decimal point has position –1 and it decreases as we go towards the right (−2, −3, etc.)
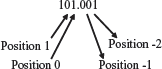
Example 9: Convert 1011 from Base 2 to Base 10.
Convert 62 from Base 8 to Base 10.
Convert C15 from Base 16 to Base 10.

Example 10: Convert .1101 from Base 2 to Base 10.
Convert .345 from Base 8 to Base 10.
Convert .15 from Base 16 to Base 10.

Example 11: Convert 1011.1001 from Base 2 to Base 10.
Convert 24.36 from Base 8 to Base 10.
Convert 4D.21 from Base 16 to Base 10.

5.5 CONVERSION OF BINARY TO OCTAL, HEXADECIMAL
A binary number can be converted into octal or hexadecimal number using a shortcut method. The shortcut method is based on the following information—
- An octal digit from 0 to 7 can be represented as a combination of 3 bits, since 23 = 8.
- A hexadecimal digit from 0 to 15 can be represented as a combination of 4 bits, since 24 = 16.
The Steps for Binary to Octal Conversion are—
- Partition the binary number in groups of three bits, starting from the right-most side.
- For each group of three bits, find its octal number.
- The result is the number formed by the combination of the octal numbers.
The Steps for Binary to Hexadecimal Conversion are—
- Partition the binary number in groups of four bits, starting from the right-most side.
- For each group of four bits, find its hexadecimal number.
- The result is the number formed by the combination of the hexadecimal numbers.
Example 12: Convert the binary number 1110101100110 to octal.
Given binary number |
1110101100110 |
- Partition binary number in groups of three bits, starting from the right-most side.

- For each group find its octal number.

- The octal number is 16546.
Example 13: Convert the binary number 1110101100110 to hexadecimal
Given binary number |
1110101100110 |
- Partition binary number in groups of four bits, starting from the right-most side.
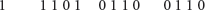
- For each group find its hexadecimal number.
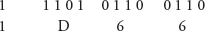
- The hexadecimal number is 1D66.
5.6 CONVERSION OF OCTAL, HEXADECIMAL TO BINARY
The conversion of a number from octal and hexadecimal to binary uses the inverse of the steps defined for the conversion of binary to octal and hexadecimal.
The Steps for Octal to Binary Conversion are—
- Convert each octal number into a three-digit binary number.
- The result is the number formed by the combination of all the bits.
The Steps for Hexadecimal to Binary Conversion are—
- Convert each hexadecimal number into a four-digit binary number.
- The result is the number formed by the combination of all the bits.
Example 14: Convert the hexadecimal number 2BA3 to binary.
- Given number is 2BA3
- Convert each hexadecimal digit into four digit binary number.
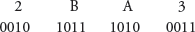
- Combine all the bits to get the result 0010101110100011.
Example 15: Convert the octal number 473 to binary.
- Given number is 473
- Convert each octal digit into three digit binary number.
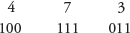
- Combine all the bits to get the result 100111011.
5.7 BINARY ARITHMETIC
The arithmetic operations—addition, subtraction, multiplication and division, performed on the binary numbers is called binary arithmetic. In computer, the basic arithmetic operations performed on the binary numbers is—
- Binary addition, and
- Binary subtraction.
In the following subsections, we discuss the binary addition and the binary subtraction operations.
5.7.1 Binary Addition
Binary addition involves addition of two or more binary numbers. The binary addition rules are used while performing the binary addition. Table 5.3 shows the binary addition rules.
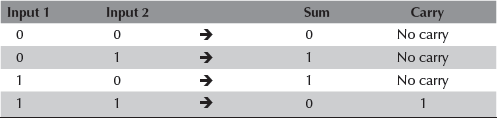
Table 5.3 Binary addition rules
Binary addition of three inputs follows the rule shown in Table 5.4.
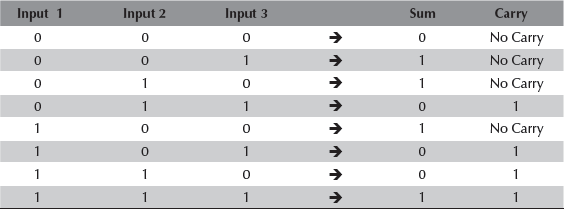
Table 5.4 Binary addition of three inputs
Addition of the binary numbers involves the following steps—
- Start addition by adding the bits in unit column (the right-most column). Use the rules of binary addition.
- The result of adding bits of a column is a sum with or without a carry.
- Write the sum in the result of that column.
- If a carry is present, the carry is carried-over to the addition of the next left column.
- Repeat steps 2–4 for each column, i.e., the tens column, hundreds column and so on.
Let us now understand binary addition with the help of some examples.
Example 1: Add 10 and 01. Verify the answer with the help of decimal addition.
When we add 0 and 1 in the unit column, sum is 1 and there is no carry. The sum 1 is written in the unit column of the result. In the tens column, we add 1 and 0 to get the sum 1. There is no carry. The sum 1 is written in the tens column of the result.

Example 2: Add 01 and 11. Verify the answer with the help of decimal addition.
When we add 1 and 1 in the unit column, sum is 0 and carry is 1. The sum 0 is written in the unit column of the result. The carry is carried-over to the next column, i.e., the tens column. In the tens column, we add 0, 1 and the carried-over 1, to get sum 0 and carry 1. The sum 0 is written in the tens column of the result. The carry 1 is carried-over to the hundreds column. In the hundreds column, the result is 1.

Example 3: Add 11 and 11. Verify the answer with the help of decimal addition.

Example 4: Add 1101 and 1111. Verify the answer with the help of decimal addition.

Example 5: Add 10111, 11100 and 11. Verify theanswer with the help of decimal addition.

5.7.2 Binary Subtraction
Binary subtraction involves subtracting of two binary numbers. The binary subtraction rules are used while performing the binary subtraction. The binary subtraction rules are shown in Table 5.5, where “Input 2” is subtracted from “Input 1.”

Table 5.5 Binary subtraction rules
The steps for performing subtraction of the binary numbers are as follows—
- Start subtraction by subtracting the bit in the lower row from the upper row, in the unit column.
- Use the binary subtraction rules. If the bit in the upper row is less than lower row, borrow 1 from the upper row of the next column (on the left side). The result of subtracting two bits is the difference.
- Write the difference in the result of that column.
- Repeat steps 2 and 3 for each column, i.e., the tens column, hundreds column and so on.
Let us now understand binary subtraction with the help of some examples.
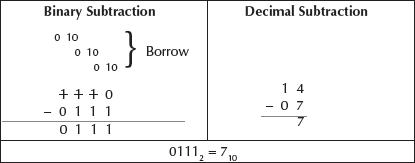
Example 1: Subtract 01 from 11. Verify the answer with the help of decimal subtraction.
When we subtract 1 from 1 in the unit column, the difference is 0. Write the difference in the unit column of the result. In the tens column, subtract 0 from 1 to get the difference 1. Write the difference in the tens column of the result.

Example 2: Subtract 01 from 10. Verify the answer with the help of decimal subtraction.
When we subtract 1 from 0 in the unit column, we have to borrow 1 from the left column since 0 is less than 1. After borrowing from the left column, 0 in the unit column becomes 10, and, 1 in the left column becomes 0. We perform 10-1 to get the difference 1. We write the difference in the unit column of the result. In the tens column, subtract 0 from 0 to get the difference 0. We write the difference 0 in the tens column of the result.

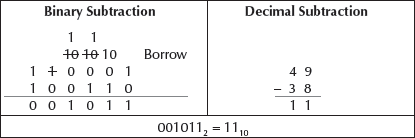
Example 3: Subtract 0111 from 1110. Verify the answer with the help of decimal subtraction.
When we do 0–1 in the unit column, we have to borrow 1 from the left column since 0 is less than 1. After borrowing from the left column, 0 in the unit column becomes 10, and, 1 in the left column becomes 0. We perform 10-1 to get the difference 1. We write the difference in the unit column of the result. In the tens column, when we do 0-1, we again borrow 1 from the left column. We perform 10-1 to get the difference 1. We write the difference in the tens column of the result. In the hundreds column, when we do 0-1, we again borrow 1 from the left column. We perform 10-1 to get the difference 1. We write the difference in the hundreds column of the result. In the thousands column, 0–0 is 0. We write the difference 0 in the thousands column of the result.
Example 4: Subtract 100110 from 110001. Verify the answer with the help of decimal subtraction.
5.8 SIGNED AND UNSIGNED NUMBERS
A binary number may be positive or negative. Generally, we use the symbol “+” and “−” to represent positive and negative numbers, respectively. The sign of a binary number has to be represented using 0 and 1, in the computer. An n-bit signed binary number consists of two parts—sign bit and magnitude. The left most bit, also called the Most Significant Bit (MSB) is the sign bit. The remaining n-1 bits denote the magnitude of the number.
In signed binary numbers, the sign bit is 0 for a positive number and 1 for a negative number. For example, 01100011 is a positive number since its sign bit is 0, and, 11001011 is a negative number since its sign bit is 1. An 8–bit signed number can represent data in the range −128 to +127 (–27to +27−1). The left-most bit is the sign bit.

In an n-bit unsigned binary number, the magnitude of the number n is stored in n bits. An 8–bit unsigned number can represent data in the range 0 to 255 (28 = 256).
5.8.1 Complement of Binary Numbers
Complements are used in computer for the simplification of the subtraction operation. For any number in base r, there exist two complements—(1) r’s complement and (2) r-1 ’s complement.
| Number System | Base | Complements possible |
|---|---|---|
Binary |
2 |
1’s complement and 2’s complement |
Octal |
8 |
7’s complement and 8’s complement |
Decimal |
10 |
9’s complement and 10’s complement |
Hexadecimal |
16 |
15’s complement and 16’s complement |
Let us now see how to find the complement of a binary number. There are two types of complements for the binary number system—1’s complement and 2’s complement.
- 1’s Complement of Binary Number is computed by changing the bits 1 to 0 and the bits 0 to 1. For example,
1’s complement of 101 is 010
1’s complement of 1011 is 0100
1’s complement of 1101100 is 0010011
- 2’s Complement of Binary Number is computed by adding 1 to the 1’s complement of the binary number. For example,
2’s complement of 101 is 010 + 1 = 011
2’s complement of 1011 is 0100 + 1 = 0101
2’s complement of 1101100 is 0010011 + 1 = 0010100
The rule to find the complement of any number N in base r having n digits is
(r − 1)’s complement—(rn − 1) − N
(r’s) complement2—(rn − 1) − N + 1 = (rn − N)
5.9 BINARY DATA REPRESENTATION
A binary number may also have a binary point, in addition to the sign. The binary point is used for representing fractions, integers and integer-fraction numbers. Registers are high-speed storage areas within the Central Processing Unit (CPU) of the computer. All data are brought into a register before it can be processed. For example, if two numbers are to be added, both the numbers are brought in registers, added, and the result is also placed in a register. There are two ways of representing the position of the binary point in the register—fixed point number representation and floating point number representation.
The fixed point number representation assumes that the binary point is fixed at one position either at the extreme left to make the number a fraction, or at the extreme right to make the number an integer. In both cases, the binary point is not stored in the register, but the number is treated as a fraction or integer. For example, if the binary point is assumed to be at extreme left, the number 1100 is actually treated as 0.1100.
The floatingpoint number representation uses two registers. The first register stores the number without the binary point. The second register stores a number that indicates the position of the binary point in the first register.
We shall now discuss representation of data in the fixed point number representation and floating point number representation.
5.9.1 Fixed Point Number Representation
The integer binary signed number is represented as follows—
- For a positive integer binary number, the sign bit is 0 and the magnitude is a positive binary number.
- For a negative integer binary number, the sign bit is 1. The magnitude is represented in any one of the three ways—
- Signed Magnitude Representation—The magnitude is the positive binary number itself.
- Signed 1 ’s Complement Representation—The magnitude is the 1’s complement of the positive binary number.
- Signed 2’s Complement Representation—The magnitude is the 2’s complement of the positive binary number.
Table 5.6 shows the representation of the signed number 18.

Table 5.6 Fixed point representation of the signed number 18
Signed magnitude and signed 1’s complement representation are seldom used in computer arithmetic.
Let us now perform arithmetic operations on the signed binary numbers. We use the signed ’s complement representation to represent the negative numbers.
- Addition of Signed Binary Numbers—The addition of any two signed binary numbers is performed as follows—
- Represent the positive number in binary form.(For example, +5 is 0000 0101 and +10 is 0000 1010)
- Represent the negative number in ’s complement form. (For example, —5 is 1111 1011 and –10 is 1111 0110)
- Add the bits of the two signed binary numbers.
- Ignore any carry out from the sign bit position.
Please note that the negative output is automatically in the ’s complement form.
We get the decimal equivalent of the negative output number, by finding its 2’s complement, and attaching a negative sign to the obtained result.
Let us understand the addition of two signed binary numbers with the help of some examples.
Example 1: Add +5 and +10.
+5 in binary form, i.e., 0000 0101. +10 in binary form, i.e., 0000 1010.

Example 2: Add −5 and +10.
−5 in ’s complement form is 1111 1011. +10 in binary form is 0000 1010.

Example 3: Add +5 and −10.
+5 in binary form is 0000 0101. −10 in ’s complement form is 1111 0110. 1111 1011.

The result is in 2’s complement form. To find its decimal equivalent—
Find the 2’s complement of 1111 1011, i.e., 0000 0100 + 1 = 0000 0101. This is binary equivalent of + 5. Attaching a negative sign to the obtained result gives us −5.
Example 4: Add −5 and −10.
−5 in ’s complement form is 1111 1011. −10 in 2’s complement form is 1111 0110.

The result is in 2’s complement form. To find its decimal equivalent—
Find the ’s complement of 1111 0001, i.e., 0000 1110 + 1 = 0000 1111. This is binary equivalent of +15. Attaching a negative sign to the obtained result gives us −15.
- Subtraction of Signed Binary Numbers—The subtraction of signed binary numbers is changed to the addition of two signed numbers. For this, the sign of the second number is changed before performing the addition operation.
(−A) − (+B) = (−A) + (−B)
(+B in subtraction is changed to −B in addition)
(+A) − (+B) = (+A) + (−B)
(+B in subtraction is changed to −B in addition)
(−A) − (−B) = (−A) + (+B)
(−B in subtraction is changed to +B in addition)
(+A) − (−B) = (+A) + (+B)
(−B in subtraction is changed to +B in addition)
We see that the subtraction of signed binary numbers is performed using the addition operation.
The hardware logic for the fixed point number representation is simple, when we use ’s complement for addition and subtraction of the signed binary numbers. When two large numbers having the same sign are added, then an overflow may occur, which has to be handled.
5.9.2 Floating Point Number Representation
The floating point representation of a number has two parts—mantissa and exponent. The mantissa is a signed fixed point number. The exponent shows the position of the binary point in the mantissa.
For example, the binary number +11001.11 with an 8−bit mantissa and 6−bit exponent is represented as follows—
- Mantissa is 01100111. The left most 0 indicates that the number is positive.
- Exponent is 000101. This is the binary equivalent of decimal number + 5.
- The floating point number is Mantissa x 2exponent, i.e., + (.1100111) x 2+5.
The arithmetic operation with the floating point numbers is complicated, and uses complex hardware as compared to the fixed point representation. However, floating point calculations are required in scientific calculations, so, computers have a built−in hardware for performing floating point arithmetic operations.
5.10 BINARY CODING SCHEMES
The alphabetic data, numeric data, alphanumeric data, symbols, sound data and video data, are represented as combination of bits in the computer. The bits are grouped in a fixed size, such as 8 bits, 6 bits or 4 bits. A code is made by combining bits of definite size. Binary Coding schemes represent the data such as alphabets, digits 0−9, and symbols in a standard code. A combination of bits represents a unique symbol in the data. The standard code enables any programmer to use the same combination of bits to represent a symbol in the data.
The binary coding schemes that are most commonly used are—
- Extended Binary Coded Decimal Interchange Code (EBCDIC),
- American Standard Code for Information Interchange (ASCII), and
- Unicode
In the following subsections, we discuss the EBCDIC, ASCII and Unicode coding schemes.
5.10.1 EBCDIC
- The Extended Binary Coded Decimal Interchange Code (EBCDIC) uses 8 bits (4 bits for zone, 4 bits for digit) to represent a symbol in the data.
- EBCDIC allows 28 = 256 combinations of bits.
- 256 unique symbols are represented using EBCDIC code. It represents decimal numbers (0−9), lower case letters (a−z), uppercase letters (A−Z), Special characters, and Control characters (printable and non−printable, e.g., for cursor movement, printer vertical spacing, etc.).
- EBCDIC codes are mainly used in the mainframe computers.
5.10.2 ASCII
- The American Standard Code for Information Interchange (ASCII) is widely used in computers of all types.
- ASCII codes are of two types—ASCII−7 and ASCII−8.
- ASCII-7 is a 7-bit standard ASCII code. In ASCII-7, the first 3 bits are the zone bits and the next 4 bits are for the digits. ASCII-7 allows 27 = 128 combinations. 128 unique symbols are represented using ASCII-7. ASCII-7 has been modified by IBM to ASCII-8.
- ASCII-8 is an extended version of ASCII-7. ASCII-8 is an 8-bit code having 4 bits for zone and 4 bits for the digit. ASCII-8 allows 28 = 256 combinations. ASCII-8 represents 256 unique symbols. ASCII is used widely to represent data in computers.
- The ASCII-8 code represents 256 symbols.
- Codes 0 to 31 represent control characters (non−printable), because they are used for actions like, Carriage return (CR), Bell (BEL), etc.
- Codes 48 to 57 stand for numeric 0−9.
- Codes 65 to 90 stand for uppercase letters A−Z.
- Codes 97 to 122 stand for lowercase letters a−z.
- Codes 128 to 255 are the extended ASCII codes.
5.10.3 Unicode
- Unicode is a universal character encoding standard for the representation of text which includes letters, numbers and symbols in multi−lingual environments. The Unicode Consortium based in California developed the Unicode standard.
- Unicode uses 32 bits to represent a symbol in the data.
- Unicode allows 232 = 4164895296 (~ 4 billion) combinations.
- Unicode can uniquely represent any character or symbol present in any language like Chinese, Japanese, etc. In addition to the letters; mathematical and scientific symbols are also represented in Unicode codes.
- An advantage of Unicode is that it is compatible with the ASCII−8 codes. The first 256 codes in Unicode are identical to the ASCII-8 codes.
- Unicode is implemented by different character encodings. UTF-8 is the most commonly used encoding scheme. UTF stands for Unicode Transformation Format. UTF-8 uses 8 bits to 32 bits per code.
If you wish to see the Unicode character encoding in MS−Word 2007, do as follows—
<Insert> <Symbol>. A Symbol dialog box will appear which displays the symbols, and the character codes in a coding scheme, as shown in Figure 5.1.
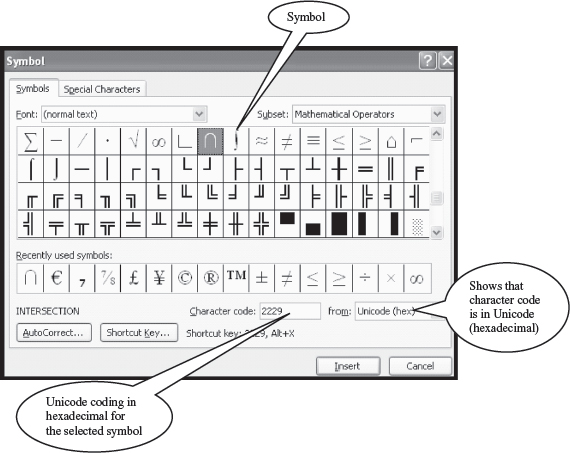
Figure 5.1 Unicode coding
5.11 LOGIC GATES
The information is represented in the computer in binary form. Binary information is represented using signals in two states off or on which correspond to 0 or 1, respectively. The manipulation of the binary information is done using logic gates. Logic gates are the hardware electronic circuits which operate on the input signals to produce the output signals. Each logic gate has a unique symbol and its operation is described using algebraic expression. For each gate, the truth table shows the output that will be outputted for the different possible combinations of the input signal. The AND, OR and NOT are the basic logic gates. Some of the basic combination of gates that are widely used are—NAND, NOR, XOR and XNOR.
Table 5.7 shows the different logic gates, their symbols, their algebraic function and the truth table for each logic gate. The comments list the features of each logic gate.
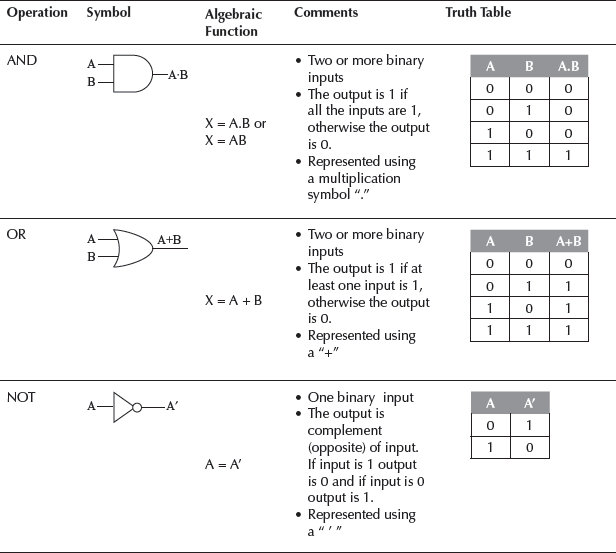
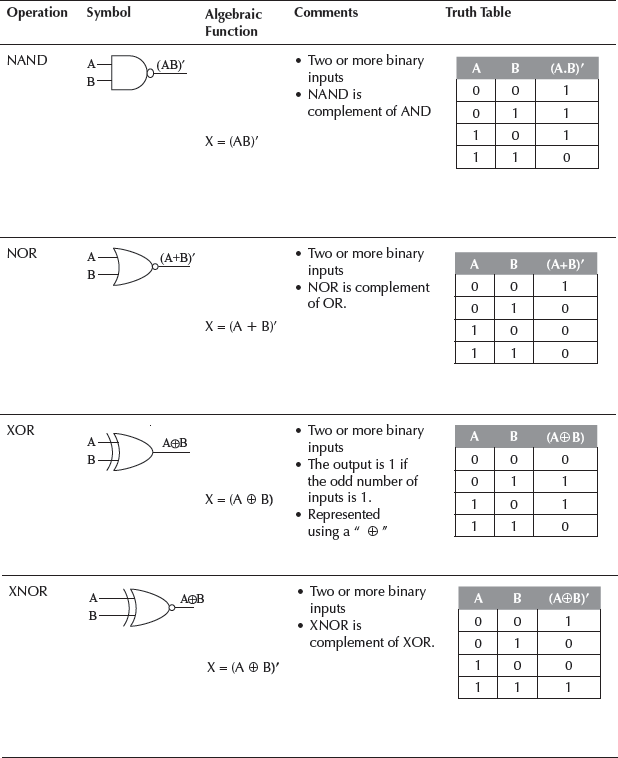
Table 5.7 Logic gates
SUMMARY
- Face value of a digit is the digit located at that place. The position value of digit is (baseposition). The number is the sum of (face value * baseposition) of all the digits.
- In computer science, decimal number system (base 10), binary number system (base 2), octal number system (base 8), and hexadecimal number system (base 16) concern us.
- Decimal number system has 10 digits—0 to 9, the maximum digit being 9.
- Binary number system has two digits—0 and 1.
- Octal number system consists of eight digits—0 to 7, the maximum digit being 7.
- Hexadecimal number system has sixteen digits—0 to 9, A, B, C, D, E, F, where (A is for 10, B is for 11, C—12, D—13, E—14, F—15). The maximum digit is F, i.e., 15.
- Conversion of octal or hexadecimal number to binary or vice−versa uses the shortcut method. Three and four bits of a binary number correspond to an octal digit and hexadecimal digit, respectively.
- Binary arithmetic operations are the binary addition, subtraction, multiplication and division operations performed on the binary numbers.
- For any number in base r, there is r’s complement and r—1’s complement. For example, binary numbers can be represented in 1’s complement and 2’s complement.
- Sign bit is the most significant bit. The sign bit is 1 and 0 for a positive number and negative number, respectively.
- Position of binary point in a binary number is represented using Fixed Point Number Representation and Floating Point Number Representation.
- In fixed point representation, the positive integer binary number is represented with sign bit 0 and magnitude as positive binary number. The negative integer is represented in signed magnitude representation, signed 1 ’s complement representation and signed ’s complement representation.
- Addition of two signed binary numbers requires the positive number to be represented as binary number and negative number to be represented in ’s complement form.
- Floating point representation has two parts—Mantissa and Exponent. Mantissa is a signed fixed point number and exponent shows the position of the binary point in the mantissa.
- Binary Coding schemes represent data in a binary form in the computer. ASCII, EBCDIC, and Unicode are the most commonly used binary coding scheme.
- EBCDIC is a 8-bit code with 256 different representations of characters. It is mainly used in mainframe computers.
- ASCII-8 is a 8-bit code and allows 256 characters to be represented. ASCII is widely to represent data in computers, internally.
- Unicode is a universal character encoding standard for the representation of text in multi-lingual environments. UTF-8 is the most commonly used encoding.
- Logic gate is the hardware electronic circuit that operates on input signals to produce output signal. AND, OR, NOT, NAND, NOR, XOR and XNOR are some of the logic gates.
KEYWORDS
1’s Complement |
ASCII-7 |
Binary Subtraction |
2’s Complement |
ASCII-8 |
Conversions |
Alphabetic Data |
Base or Radix |
Decimal Number |
Alphanumeric Data |
Binary Addition |
Digit Bits |
American Standard Code for |
Binary Arithmetic |
Exponent |
Information Interchange |
Binary Coding Schemes |
Extended Binary Coded |
(ASCII) |
Binary Number |
Decimal Interchange Code |
AND Gate |
Binary Point |
(EBCDIC) |
Face Value |
Number |
Signed Magnitude |
Fixed Point Number |
Number System |
Representation |
Representation |
Numeric Data |
Signed Number |
Floating Point Number |
Octal Number |
Truth Table |
Representation |
OR Gate |
Unicode |
Fraction |
Position |
Unicode Transformation |
Hexadecimal Number |
Position Value |
Format (UTF) |
Integer |
r−1’s Complement |
Unsigned Number |
Logic Gates |
r’s Complement |
UTF-8 |
Mantissa |
Signed 1’s Complement |
XNOR Gate |
Most Significant Bit (MSB) |
Representation |
XOR Gate |
NAND Gate |
Signed 2’s Complement |
Zone Bits |
NOR Gate |
Representation |
|
NOT Gate |
|
|
QUESTIONS
Section 5.2–5.3.3
1. What is the significance of the base of the number?
2. Explain the significance of the face value and position value of a number. Give an example.
3. What is the position value of a digit?
4. The decimal number system is in base _____.
5. The binary number system is in base _____.
6. The octal number system is in base _____.
7. The hexadecimal number system is in base _____.
8. Give the valid digits in the number systems—(a) decimal, (b) binary, (c) octal, and (d) hexadecimal.
9. Write the largest digit in the number systems—(a) decimal, (b) binary, (c) octal, and (d) hexadecimal.
10. How many valid digits are there in the number systems—(a) decimal, (b) binary, (c) octal, and (d) hexadecimal?
11. Show the octal, binary and hexadecimal equivalent of the decimal number 11.
12. Convert the following decimal numbers into binary, octal and hexadecimal.
- 24
- 47
- 675
- 89
- 34.24
- 150.64
- .98
- .29
- 24.14
- 16.1
- 22.33
Section 5.4
13. Convert the following binary numbers into decimal numbers.
- 110000111
- 110011
- 1001111
- 11000001
- 1100110.1110
- 11110.0000
- 01001.0101
- 1010.10101
- 11000011.111
- 11001.1101
- 100.111
- 101.0111
14. Convert the following octal numbers into decimal numbers.
- 234
- 36
- 456
- 217
- 25.33
- 65.34
- 34.56
- 267.12
15. Convert the following hexadecimal numbers into decimal numbers.
- E16
- 389
- 2AB
- FF
- E4.16
- 2A.1B
- 23.89
- AC.BD
Section 5.5
16. Convert the following binary into octal.
- 1100011
- 110011001100
- 100111100
- 110000011
- 110011011
- 1111000
- 0010101
- 101010101
17. Convert the following binary into hexadecimal.
- 11000011111
- 1100110011
- 100111100
- 1100000100
- 11001101110
- 111100000
- 010010101
- 101010101
Section 5.6
18. Convert the following octal into binary
- 25
- 65
- 34
- 267
- 45
- 71
- 150
- 111
19. Convert the following hexadecimal into binary.
- A1
- 2AB
- 239
- CCD
- 45C
- 71D
- 150
- AAA
Section 5.7
20. Perform binary addition on the following binary numbers.
- 111100, 011011
- 1001, 1111
- 0110, 1100
- 1100, 1010
21. Perform binary subtraction on the following binary numbers.
- 111000, 011010
- 1111, 1001
- 0110, 0010
- 1100, 1010
Section 5.7.1
22. Find 1’s complement of the following binary numbers.
- 11000011111
- 1100110011
- 100111100
- 1100000100
23. Find ’s complement of the following binary numbers.
- 11000011111
- 1100110011
- 100111100
- 1100000100
24. What is the relation between the 1’s complement and ’s complement of a binary number?
Section 5.8–5.8.2
25. In addition to the digits, a number may contain a _____ and _____.
26. What is a sign bit?
27. Which bit is considered as a sign bit when representing a number?
28. What is the value of sign bit for a positive number?
29. What is the value of sign bit for a negative number?
30. What is the range of data that can be represented using an 8−bit signed number?
31. What is the range of data that can be represented using an 8−bit unsigned number?
32. _____ representation and _____ representation are the two ways of representing the position of the binary point in the register.
33. Represent the following as 8−bit numbers in (a) Signed Magnitude representation, (b) Signed 1’s complement representation, and (c) Signed ’s complement representation
- −22
- −55
- −34
- −67
34. Represent the following as 8-bit numbers in Fixed Point number representation.
- +22
- +55
- +34
- +67
35. Perform binary addition of the following numbers.
- (+7) + (−9)
- (+3) + (+15)
- (−12) + (+15)
- (−14) + (+25)
- (−7) + (−7)
- (−9) + (−23)
- (−2) + (+4)
- (+34) + (−2)
36. Perform binary subtraction of the following numbers
- (+7) − (−19)
- (+13) − (+15)
- (−12) − (+15)
- (−14) − (+25)
- (−7) − (−7)
- (−9) − (−23)
- (−2) − (+4)
- (+34) − (−2)
37. Represent the following binary numbers in Floating Point number representation.
- 1100.011
- 110.001
- 11.110
- 1010.011
Section 5.9
38. Why are binary coding schemes needed?
39. List any four commonly used binary coding schemes.
40. What number of bits is used to represent the following codes—(a) EBCDIC, (b) ASCII-7, and (c) ASCII−8?
41. How many characters can be represented in the following codes—(a) EBCDIC, (b) ASCII-7, and (c) ASCII-8?
42. How is Unicode different from the other Binary coding schemes? (Hint: multilingual, no. of characters)
43. What is UTF-8 character encoding?
Section 5.10
44. Name the basic logic gates.
45. Draw the symbols of the following logic gates—(a) AND, (b) OR, (c) NOT, (d) NAND, (e) NOR, (f) XOR, and (g) XNOR.
46. Write the truth table of the following logic gates—(a) AND, (b) OR, (c) NOT, (d) NAND, (e) NOR, (f) XOR, and (g) XNOR.
47. Write the algebraic function of the following logic gates− (a) AND, (b) OR, (c) NOT, (d) NAND, (e) NOR, (f) XOR, and (g) XNOR.
Extra Questions
48. Give full form of the following abbreviations
- EBCDIC
- MSB
- UTF
- ASCII
49. Write short notes on
- Decimal Number System
- Binary Number System
- Octal Number System
- Hexadecimal Number System
- Binary arithmetic operations
- 1’s complement of Binary number
- 2’s complement of Binary number
- Fixed Point Number Representation
- Floating Point Number Representation
- Addition of signed binary numbers
- Subtraction of signed binary numbers
- Binary Coding schemes
- Logic Gates
- ASCII coding scheme
- EBCDIC coding scheme
- Unicode character encoding
50. Give differences between the following
- 1’s complement and 2’s complement of Binary number
- ASCII coding scheme and EBCDIC coding scheme
- Decimal Number System and Binary Number System
- Octal Number System and Hexadecimal Number System
- Fixed Point Number Representation and Floating Point Number Representation
ANSWERS
12.
- (24)10 = (11000)2 = (30)8 = (18)16
- (47)10 = (101111)2 = (57)8 = (2F)16
- (675)10 = (1010100011)2 = (1243)8 = (2A3)16
- (89)10 = (10110001)2 = (131)8 = (59)16
- (34.24)10 = (100010.00111)2 = (42.1727)8 = (22.3D7100)16
- (150.64)10 = (10010110.1010)2 = (226.5075)8 = (96.A70A)16
- (.98)10 = (.1111)2 = (.7656)8 = (FAE1)16
- (.29)10 = (.0100)2 = (.2243)8 = (.4A3D)16
- (24.14)10 = (11000.0010)2 = (30.1075)8 = (18.231D)16
- (16.1)10 = (10000.0001)2 = (20.063)8 = (10.199)16
- (22.33)10 = (10110.0101)2 = (26.250)8 = (16.547)16
- (24.14)10 = (11000.0010)2 = (30.1075)8 = (18.231D)16
13.
- (110000111)2 = (391)10
- (110011)2 = (51)10
- (1001111)2 = (79)10
- (11000001)2 = (193)10
- (1100110.1110)2 = (102.087)10
- (11110.0000)2 = (30.0)10
- (01001.0101)2 = (9.312)10
- (1010.10101)2 = (10.65)10
- (11000011.111)2 = (195.875)10
- (11001.1101)2 = (25.8125)10
- (100.111)2 = (4.875)10
- (101.0111)2 = (5.4375)10
14.
- (234)8 = (156)10
- (36)8 = (30)10
- (456)8 = (302)10
- (217)8 = (143)10
- (25.33)8 = (21.4218)10
- (65.34)8 = (53.4375)10
- (34.56)8 = (28.7187)10
- (267.12)8 = (183.1562)10
15.
- (E16)16 = (3606)10
- (389)16 = (905)10
- (2AB)16 = (683)10
- (FF)16 = (255)10
- (E4.16)16 = (228.0859)10
- (2A.1B)16 = (42.1054)10
- (23.89)16 = (35.5351)10
- (AC.BD)16 = (172.7382)10
16.
- (1100011)2 = (143)8
- (110011001100)2 = (6314)8
- (100111100)2 = (474)8
- (110000011)2 = (603)8
- (110011011)2 = (633)8
- (1111000)2 = (170)8
- (0010101)2 = (025)8
- (101010101)2 = (525)8
17.
- (11000011111)2 = (61F)16
- (1100110011)2 = (333)16
- (100111100)2 = (13C)16
- (1100000100)2 = (304)16
- (11001101110)2 = (66E)16
- (111100000)2 = (1E0)16
- (010010101)2 = (095)16
- (101010101)2 = (155) 16
18.
- (25)8 = (010101)2
- (65)8 = (110101)2
- (34)8 = (011100)2
- (267)8 = (010110111)2
- (45)8 = (100101)2
- (71)8 = (111001)2
- (150)8 = (001101000)2
- (111)8 = (001001001)2
19.
- (A1)16= (10100001)2
- (2AB)16= (001010101011)2
- (239)16 = (001000111001)2
- (CCD)16= (110011001101)2
- (45C)16 = (010001011100)2
- (71D)16 = (011100011101)2
- (150)16 = (000101010000)2
- (AAA)16 = (101010101010)2
20.
- 1919111
- 11000
- 10010
- 10110
21.
- 11110
- 0110
- 0100
- 0010
22.
- 00111100000
- 0011001100
- 011000011
- 0011111011
23
- 00111100001
- 0011001101
- 011000100
- 0011111100
33(a)
- 10010110
- 10110111
- 10100010
- 11000011
33(b)
- 01101001
- 01001000
- 01011101
- 00111100
33(c)
- 01101010
- 01001001
- 01011110
- 00111101
34.
- 00010110
- 00110111
- 00100010
- 01000011
35.
- −2 = (11111110)2
- +18 = (00010010)2
- +3= (00000011)2
- +11 = (00001011)2
- −14 = (11110010)2
- −32 = (11100000)2
- +2 = (00000010)2
- +32 = (00100000)2
36.
- +26 = (00011010)2
- −2 = (11111110)2
- −27 = (11100101)2
- −39 = (11011001)2
- 0 = (00000000)2
- +14 = (00001110)2
- −6 = (11111010)2
- +36 = (00100100)2
37.
- .1100011x2+4
- .110001x2+3
- .11110x2+2
- .1010011x2+4
