Chapter 16
The time value of money and net present value
A bird in the hand is worth two in the bush
For economic progress to be possible, there must be a universally applicable time value of money, even in a risk-free environment. This fundamental concept gives rise to the techniques of capitalisation, discounting and net present value, described below.
These are more than just tools, but actual reflexes that must be studied and acquired.
Section 16.1 Capitalisation
Consider an example of a businessman who invests €100 000 in his business at the end of 2004 and then sells it 10 years later for €1 800 000. In the meantime, he receives no income from his business, nor does he invest any additional funds into it. Here is a simple problem: given an initial outlay of €100 000 that becomes €1 800 000 in 10 years, and without any outside funds being invested in the business, what is the return on the businessman's investment?
His profit after 10 years was € 1 700 000 (€ 1 800 000 – € 100 000) on an initial outlay of € 100 000. Hence, his return was (1 700 000/100 000) or 1700% over a period of 10 years.
Is this a good result or not?
Actually, the return is not quite as impressive as it first looks. To find the annual return, our first thought might be to divide the total return (1700%) by number of years (10) and say that the average return is 170% per year.
While this may look like a reasonable approach, it is in fact far from accurate. The value 170% has nothing to do with an annual return, which compares the funds invested and the funds recovered after one year. In the case above, there is no income for 10 years. Usually, calculating interest assumes a flow of revenue each year, which can then be reinvested, and which in turn begins producing additional interest.
To calculate returns over a period greater than one year, we cannot simply compare the end return to the initial outlay and divide by the number of years. This is incorrect reasoning.
There is only one sensible way to calculate the return on the above investment. First, it is necessary to seek the rate of return on a hypothetical investment that would generate income at the end of each year. After 10 years, the rate of return on the initial investment will have to have transformed €100 000 into €1 800 000. Further, the income generated must not be paid out, but rather it has to be reinvested (in which case the income is said to be capitalised).
Capitalising income means foregoing receipt of it. It then becomes capital and itself begins to produce interest during the following periods.
Therefore, we are now trying to calculate the annual return on an investment that grows from €100 000 into €1 800 000 after 10 years, with all annual income to be reinvested each year.
An initial attempt to solve this problem can be made using a rate of return equal to 10%. If, at the end of 2004, € 100 000 is invested at that rate, it will produce 10% × € 100 000, or € 10 000 in interest in 2005.
This € 10 000 will then be added to the initial capital outlay and begin, in turn, to produce interest. (Hence the term “to capitalise,” which means to add to capital.) The capital thus becomes € 110 000 and produces 10% × € 110 000 in interest in 2004, i.e. € 10 000 on the initial outlay plus € 1000 on the interest from 10 000 (10% × € 10 000). As the interest is reinvested, the capital becomes € 110 000 + € 11 000, or € 121 000, which will produce € 12 100 in interest in 2007, and so on.
If we keep doing this until 2014, we obtain a final sum of € 259 374, as shown in the table.
| Year | Capital at the beginning of the period (€ ) (1) | Income (€ ) (2) = 10% × (1) | Capital at the end of the period (€ ) = (1) + (2) |
| 2005 | 100 000 | 10 000 | 110 000 |
| 2006 | 110 000 | 11 000 | 121 000 |
| 2007 | 121 000 | 12 100 | 133 100 |
| 2008 | 133 100 | 13 310 | 146 410 |
| 2009 | 146 410 | 14 641 | 161 051 |
| 2010 | 161 051 | 16 105 | 177 156 |
| 2011 | 177 156 | 17 716 | 194 872 |
| 2012 | 194 872 | 19 487 | 214 359 |
| 2013 | 214 359 | 21 436 | 235 795 |
| 2014 | 235 795 | 23 579 | 259 374 |
Each year, interest is capitalised and itself produces interest. This is called compound interest. This is easy to express in a formula:
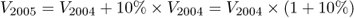
Which can be generalised into the following:
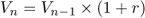
where V is a sum and r the rate of return.
Hence, V2005 = V2004 × (1 + 10%), but the same principle can also yield:
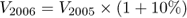
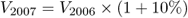

All these equations can be consolidated into the following:

Or, more generally:
Capitalisation formula
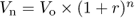
where V0 is the initial value of the investment, r is the rate of return and n is the duration of the investment in years.
This is a simple equation that gets us from the initial capital to the terminal capital. Terminal capital is a function of the rate, r, and the duration, n.
Now it is possible to determine the annual return. In the example, the annual rate of return is not 170%, but 33.5%1 (which is not bad, all the same!). Therefore, 33.5% is the rate on an investment that transforms € 100 000 into € 1 800 000 in 10 years, with annual income assumed to be reinvested every year at the same rate.
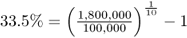
To calculate the return on an investment that does not distribute income, it is possible to reason by analogy. This is done using an investment that, over the same duration, transforms the same initial capital into the same terminal capital and produces annual income reinvested at the same rate of return. At 33.5%, annual income of € 33 500 for 10 years (plus the initial investment of € 100 000 paid back after the tenth year) is exactly the same as not receiving any income for 10 years and then receiving € 1 800 000 in the tenth year.

When no income is paid out, the terminal value rises considerably, quadrupling, for example, over 10 years at 15%, but rising 16.4-fold over 20 years at the same rate, as illustrated in this graph.
Over a long period of time, the impact of a change in the capitalisation rate on the terminal value looks as follows:
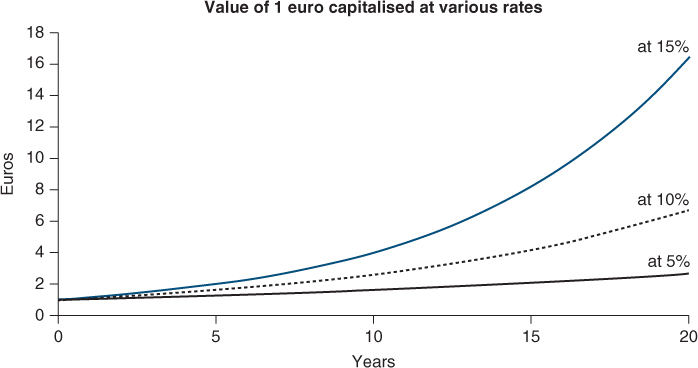
After 20 years, a sum capitalised at 15% is six times higher than a sum capitalised at one-third the rate (i.e. 5%).
This increase in terminal value is especially important in equity valuations. The example we gave earlier of the businessman selling his company after 10 years is typical. The lower the income he has received on his investment, the more he would expect to receive when selling it. Only a high valuation would give him a return that makes economic sense.
The lack of intermediate income must be offset by a high terminal valuation. The same line of reasoning applies to an industrial investment that does not produce any income during the first few years. The longer it takes it to produce its first income, the greater that income must be in order to produce a satisfactory return.
Tripling one's capital in 16 years, doubling it in 10 years or simply asking for a 7.177% annual return all amount to the same thing, since the rate of return is the same.
No distinction has been made in this chapter between income, reimbursement and actual cash flow. Regardless of whether income is paid out or reinvested, it has been shown that the slightest change in the timing of income modifies the rate of return.
To simplify, consider an investment of 100, which must be paid off at the end of year 1, with an interest accrued of 10. Suppose, however, that the borrower is negligent and the lender absent-minded, and the borrower repays the principal and the interest one year later than he should. The return on a well-managed investment that is equivalent to the so-called 10% on our absent-minded investor's loan can be expressed as:
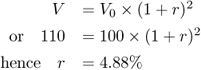
This return is less than half of the initially expected return!
It is not accounting and legal appearances that matter, but rather actual cash flows.
Any precise financial calculation must account for cash flow exactly at the moment when it is received and not just when it is due.
Section 16.2 Discounting
1/ What does it mean to discount a sum?
To discount means to calculate the present value of a future cash flow.
Discounting into today's euros helps us compare a sum that will not be produced until later. Technically speaking, what is discounting?
To discount is to “depreciate” the future. It is to be more rigorous with future cash flows than present cash flows, because future cash flows cannot be spent or invested immediately. First, take tomorrow's cash flow and then apply to it a multiplier coefficient below 1, which is called a discounting factor. The discounting factor is used to express a future value as a present value, thus reflecting the depreciation brought on by time.
Consider an offer whereby someone will give you € 1000 in five years. As you will not receive this sum for another five years, you can apply a discounting factor to it, for example, 0.6. The present, or today's, value of this future sum is then 600. Having discounted the future value to a present value, we can then compare it to other values. For example, it is preferable to receive 650 today rather than 1000 in five years, as the present value of 1000 five years out is 600, and that is below 650.
Discounting makes it possible to compare sums received or paid out at different dates.
Discounting is based on the time value of money. After all, “time is money”. Any sum received later is worth less than the same sum received today.
Remember that investors discount because they demand a certain rate of return. If a security pays you 110 in one year and you wish to see a return of 10% on your investment, the most you would pay today for the security (i.e. its present value) is 100. At this price (100) and for the amount you know you will receive in one year (110), you will get a return of 10% on your investment of 100. However, if a return of 11% is required on the investment, then the price you are willing to pay changes. In this case, you would be willing to pay no more than 99.1 for the security because the gain would have been 10.9 (or 11% of 99.1), which will still give you a final payment of 110.
Discounting is calculated with the required return of the investor. If the investment does not meet or exceed the investor's expectations, he will forego it and seek a better opportunity elsewhere.
Discounting converts a future value into a present value. This is the opposite result of capitalisation.
Discounting converts future values into present values, while capitalisation converts present values into future ones. Hence, to return to the example above, € 1 800 000 in 10 years discounted at 33.5% is today worth € 100 000. € 100 000 today will be worth € 1 800 000 when capitalised at 33.5%. over 10 years.
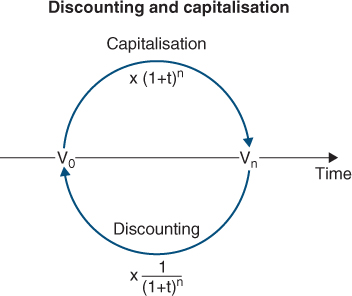
Discounting and capitalisation are thus two ways of expressing the same phenomenon: the time value of money.
2/ Discounting and capitalisation factors
To discount a sum, the same mathematical formulas are used as those for capitalising a sum. Discounting calculates the sum in the opposite direction to capitalising.
To get from € 100 000 today to € 1 800 000 in 10 years, we multiply 100 000 by (1 + 0.335) 10, or 18. The number 18 is the capitalisation factor.
To get from € 1 800 000 in 10 years to its present value today, we would have to multiply € 1 800 000 by (1/+0.335) 10, or 0.056. 0.056 is the discounting factor, which is the inverse of the coefficient of capitalisation. The present value of € 1 800 000 in 10 years at a 33.5% rate is € 100 000.
More generally:
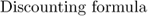

Which is the exact opposite of the capitalisation formula.
1/(1+r) n is the discounting factor, which depreciates Vn and converts it into a present value V0. It remains below 1 as discounting rates are always positive.
Section 16.3 Present value and net present value of a financial security
In the introductory chapter of this book, it was explained that a financial security is no more than a stream of future cash flows, to which we can then apply the notion of discounting. So, without being aware of it, you already knew how to calculate the value of a security!
1/ From the present value of a security …
The present value (PV) of a security is the sum of its discounted cash flows; i.e.:
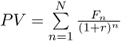
where Fn are the cash flows generated by the security, r is the applied discounting rate and n is the number of years for which the security is discounted.
All securities also have a market value, particularly on the secondary market. Market value is the price at which a security can be bought or sold.
Net present value (NPV) is the difference between present value and market value (V0) :
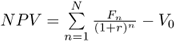
If the net present value of a security is greater than its market value, then it will be worth more in the future than the market has presently valued it. Therefore you will probably want to invest in it, i.e. to invest in the upside potential of its value.
If, however, the security's present value is below its market value, you should sell it at once, for its market value is sure to diminish.
2/ … to its fair value
If an imbalance occurs between a security's market value and its present value, efficient markets will seek to re-establish balance and reduce net present value to zero. Investors acting on efficient markets seek out investments offering positive net present value, in order to realise that value. When they do so, they push net present value towards zero, ultimately arriving at the fair value of the security.
In efficient, fairly valued markets, net present values are zero, i.e. market value is equal to present value.
3/ Applying the concept of net present value to other investments
Up to this point, the discussion has been limited to financial securities. However, the concepts of present value and net present value can easily be applied to any investment, such as the construction of a new factory, the launch of a new product, the takeover of a competing company or any other asset that will generate positive and/or negative cash flows.
The concept of net present value can be interpreted in three different ways:
- the value created by an investment–for example, if the investment requires an outlay of €100 and the present value of its future cash flow is €110, then the investor has become €10 wealthier;
- the maximum additional amount that the investor is willing to pay to make the investment–if the investor pays up to €10 more, he has not necessarily made a bad deal, as he is paying up to €110 for an asset that is worth €110;
- the difference between the present value of the investment (€110) and its market value (€100).
Section 16.4 What does net present value depend on?
While net present value is obviously based on the amount and timing of cash flows, it is worth examining how it varies with the discounting rate.
The higher the discounting rate, the more future cash flow is depreciated and, therefore, the lower is the present value. Net present value declines in inverse proportion to the discounting rate, thus reflecting investor demand for a greater return (i.e. greater value attributed to time).
Take the following example of an asset (e.g. a financial security or a capital investment) with a market value of 2 and with cash flows as follows:
| Year | 1 | 2 | 3 | 4 | 5 |
| Cash flow | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
A 20% discounting rate would produce the following discounting factors:
| Year | 1 | 2 | 3 | 4 | 5 |
| Discounting factor | 0.833 | 0.694 | 0.579 | 0.482 | 0.402 |
| Present value of cash flow | 0.67 | 0.56 | 0.46 | 0.39 | 0.32 |
As a result, the present value of this investment is about 2.4. As its market value is 2, its net present value is approximately 0.4.
If the discounting rate changes, the following values are obtained:
| Discounting rate | 0% | 10% | 20% | 25% | 30% | 35% |
| Present value of the investment | 4 | 3.03 | 2.39 | 2.15 | 1.95 | 1.78 |
| Market value | 2 | 2 | 2 | 2 | 2 | 2 |
| Net present value | 2 | 1.03 | 0.39 | 0.15 | −0.05 | −0.22 |
Which would then look like this graphically:
The present value and net present value of an asset vary in inverse proportion to the discounting rate.

The higher the discounting rate (i.e. the higher the return demanded), the lower the net present value.
Section 16.5 Some examples of simplification of present value calculations
For those occasions when you are without your favourite spreadsheet program, you may find the following formulas handy in calculating present value.
1/ The value of an annuity F over n years, beginning in year 1
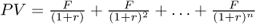
or:

For the two formulas above, the sum of the geometric series can be expressed more simply as:
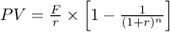
So, if F = 0.8, r = 20% and n = 5, then the present value is indeed 2.4.
Further is ![]() equal to the sum of the first n discounting factors.
equal to the sum of the first n discounting factors.
2/ The value of a perpetuity
A perpetuity is a constant stream of cash flows without end. By adding this feature to the previous case, the formula then looks like this:
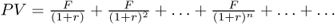
As n approaches infinity, this can be shortened to the following:
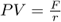
The present value of a € 100 perpetuity discounted back at 10% per year is thus:
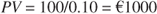
A € 100 perpetuity discounted at 10% is worth € 1000 in today's euros. If the investor demands a 20% return, the same perpetuity is worth € 500.
3/ The value of an annuity that grows at rate g for n years
In this case, the F0 cash flow rises annually by g for n years.
Thus:
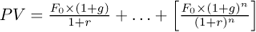
or:

Note: the first cash flow actually paid out is F0 × (1+g)
Thus, a security that has just paid out 0.8, and with this 0.8 growing by 10% each year for the four following years has – at a discounting rate of 20% – a present value of:
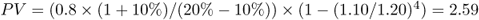
4/ The value of a perpetuity that grows at rate g (growing perpetuity)
As n approaches infinity, the previous formula can be expressed as follows:
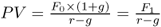
As long as r > g.
The present value is thus equal to the next year's cash flow divided by the difference between the discounting rate and the annual growth rate.
For example, a security with an annual return of 0.8, growing by 10% annually to infinity has, at a rate of 20%, a PV = 0.8 / (0.2 – 0.1) = 8.0.
Summary
The summary of this chapter can be downloaded from www.vernimmen.com.
Capitalisation involves foregoing immediate spending of a given sum of money. By using the interest rate at which the money will be invested, the future amounts can be calculated. Thus, the future value of a sum of money can be determined by way of capitalisation.
Discounting involves calculating today's value of a future cash flow, what is known as the present value, on the basis of rates of return required by investors. By calculating the present value of a future sum, discounting can be used for comparing future cash flows that will not be received on the same date.
Discounting and capitalisation are two ways of expressing the same phenomenon: the time value of money.
Capitalisation is based on compound interest. Vn = V0 × (1 + r) n
where V0 is the initial value of the investment, r is the rate of return, n is the duration of the investment in years, (1+r) n is the capitalisation factor and Vn is the terminal value.
Discounting is the inverse of capitalisation. It is important to note that any precise financial calculation must account for cash flows at the moment when they are received or paid, and not when they are due.
Net present value (NPV) is the difference between present value and the value at which the security or share can be bought. Net present value measures the creation or destruction of value that could result from the purchase of a security or making an investment. When markets are in equilibrium, net present values are usually nil.
Changes in present value and net present value move in the opposite direction from changes in discount rates. The higher the discount rate, the lower the present value and net present value, and vice versa.
In many cases, calculating present value and net present value can be made a lot simpler through ad hoc formulas.
Questions
1/ Why should we discount?
2/ What is the discount factor equal to?
3/ On what should you base a choice between two equal discounted values?
4/ What is the simple link between the discount factor and the capitalisation factor?
5/ Why are capitalisation factors always greater than 1?
6/ Why are discount factors always less than 1?
7/ Should you discount even if there is no inflation and no risk? Why?
8/ Why does the graph on capitalisation show curves and not lines?
9/ Belgacom pays out big dividends. Should its share price rise faster or slower than the share price of Google which doesn't pay out any dividends? Why? Would it be better to have Belgacom stock options or Google stock options? Why?
10/ What is net present value equal to?
11/ The higher the rates of return, the larger present values will be. True or false?
12/ What mechanism pushes market value towards present value?
13/ Can net present value be negative? What does this mean?
14/ What does the discount rate correspond to in formulas for calculating present value and net present value?
15/ Are initial flows on an investment more often positive or negative? What about for final cash flows?
16/ A market is in equilibrium when present values are nil and net present values are positive. True or false?
17/ For the investment in Section 16.2, what is the maximum discount rate above which it would not be worthwhile for the investor?
18/ Can the growth rate to infinity of a cash flow be higher than the discount rate? Why?
19/ Could an investment made at a negative net present value result in the creation of value?
20/ Would you be more likely to find investments with positive net present value on financial markets or on industrial markets? Why?
21/ Which of the formulas in Section 16.6 is more appropriate for valuing a rented building, the Belgacom share price, a bond?
More questions are waiting for you at www.vernimmen.com.
Exercises
1/ What is the present value of €100 received in 3 years at 5%, 10% and 20%?
2/ What is the present value at 10% of €100 received in three years, five years and 10 years? What are the discount factors?
3/ How much would €1000 be worth in five years, invested at 5%, 10% and 20%? Why is the sum invested at 20% not double that invested at 10%?
4/ How much would €1000 be worth in five years, 10 years and 20 years if invested at 8%? Why is the sum invested for 20 years not double that invested for 10 years?
5/ You are keen to obtain a helicopter pilot's licence. A club offers you lessons over two years, with a choice between the following payment terms:
you can either pay the full fees (€10 000) immediately with a 5% discount; or
you can make two equal annual payments, the first one due immediately.
At what interest rate would these two options work out at the same cost?
6/ What is the present value at 8% of €100 to be received in three years, five months and 17 days?
7/ How much would you have to invest today to have 100 in eight years if the interest rate was 5%? What is the capitalisation factor?
8/ At 7%, would you rather have €100 today or €131.1 in four years' time? Why?
9/ Show that in order to double your money in one year, the interest rate would have to be around 75%/year.
10/ Show that in order to treble your money in N years, the interest rate would have to be around 125%/N.
11/ You are only prepared to forego immediate spending if you get a 9% return on your investment. What would be the top price you would be prepared to pay for a security today that would pay you 121 in two years? If other investors were asking for 8%, what would happen?
12/ If instead of throwing his 30 pieces of silver away in 33 AD, Judas had invested them at 3% per annum, how much would his descendants get in 2014? And at 1%? Explain your views.
13/ You have the choice between buying a Francis Bacon painting for €100 000 which will be worth €125 000 in four years, and investing in government bonds at 6%. What would your choice be? Why?
14/ Given the level of risk, you require an 12% return on shares in Google. No dividends will be paid out for five years. What is the lowest price you could sell them at in four years' time, if you bought them for $635 a share today?
15/ Assume that a share in Le Furibard has a market value of 897, with the following cash flow schedule:
| Year | 1 | 2 | 3 | 4 | 5 |
| Cash flow | 300 | 300 | 300 | 300 | 300 |
Calculate the NPV of the share at 5%, 10%, 20% and 25%. Plot your answers on a graph.
16/ What is the present value at 10% of a perpetual income of 100? And a perpetual income of 100 rising by 3% every year from the following year?
17/ What is the present value at 10% of €100 paid annually for three years? Same question for a perpetual income.
18/ An investment promises four annual payments of €52 over the next four years. You require an 8% return. How much would you be prepared to pay for this asset? The share is currently trading at €165. Would you be prepared to buy or to sell? Why? If you buy at that price, how much will you have gained? Will the rate of return on your investment be greater or less than 8%? Why? If you buy at €172, what will your return on this investment be? Why?
19/ Show that at 8% there is little difference between the value of a perpetual income and that of a security that offers a constant annual income equal to that of the perpetual income for only 40 years. Show that this will be even more correct if the rate of return is 15%.
20/ You have the opportunity to buy the right to park in a given parking place for 75 years, at a price of €300 000. You could also rent a parking place for €2000 a year, revised upwards by 2% every year. If the opportunity cost is 5%, which would you choose?
21/ You are the proud owner of the TV screening rights for the film Singing in the Rain. You sell the rights to screen the film on TV once every two years for €0.8m. What is the value of your asset? The film has just been screened. You make the assumption that screenings will be possible for 30 years or in perpetuity. The discount rate is 6%.
22/ You have found your dream house and you have the choice between renting it with a lease in perpetuity for €12 000 or buying it. At what purchase price would you be better off renting, if the loan you needed to buy the house costs you 7%, and the rent increases by 3% per year?
23/ Your current after-tax annual income is €50 000, which should increase by 4% per year until you retire. You believe that if you interrupt your professional career for two years to do an MBA, you could earn €65 000 after tax per year, with an annual increase of 5% until you retire. What is your present value if you retire in 40 years' time, and the discount rate is 4%? If the total cost of the MBA is €50 000 payable immediately, what is the net present value of this investment? Is it worth doing an MBA?
24/ Every year you invest €1 200 for your pension. You started at age 25. How much will you own at 65 if your investment has yielded 4% p.a? If you wanted to have €200 000, how much would you need to save each year?
25/ At what price should you sell Mondass shares in 10 years' if the share pays a €1 dividend each year and you require a 6.67% return, knowing that Mondass' current share price is €15? The solution can be found without any calculation.
Answers
Questions
1/ So as to be able to compare a future value and a present value of a future inflow.
2/ 1/(1 + t)n.
3/ If the present values are equal, it makes no difference.
4/ One is the reverse of the other.
5/ Because interest rates are positive.
6/ Because interest rates are positive.
7/ Yes, because discounting is used to factor in an interest rate which remunerates the foregoing of immediate spending. Discounting is thus unrelated to inflation or risk.
8/ Because of capitalisation, which every year adds interest earned over the past year to the principal, and interest is earned on this interest in the future. This is called compound interest.
9/ The Google share price will have to rise more than that of Belgacom in order to make up for the lack of dividends. As stock options are options to buy shares at a fixed exercise price, their value will increase if the share price rises. So it would be better to have Google's stock options.
10/ To the difference between the present value and the market value of an asset.
11/ False, the opposite is true as the future is more depreciated.
12/ Arbitrage.
13/ Yes. The asset has been overvalued.
14/ To the required return on this asset.
15/ Negative, as we first invest to get positive cash flows in the future; positive.
16/ False, the opposite is true. NPV = 0 and PV > 0.
17/ Around 28%.
18/ No, because growth is not a process that can continue endlessly!
19/ No, unless you've made an error in your calculations of the cash flows or underestimated them.
20/ In industrial markets because arbitrage operations take longer to execute than in financial markets (building a factory takes longer than buying a share) and, therefore, disequilibrium is more frequent.
21/ The perpetuity for the rented building, the growing perpetuity for Belgacom, the value of an annuity for N years for the coupons of the bond.
Exercises
A detailed Excel version of the solutions is available at www.vernimmen.com.
1/ 100/1.053 = €86.4; 100/1.13 = €75.1; 100/1.23 = €57.9.
2/ €75.1; €62.1; €38.6; 0.751; 0.621; 0.386.
3/ €1276, €1611, €2488. Because the principal (€1000) remains the same and interest more than doubles as a result of the process of compound interest.
4/ €1469, €2159 and €4661. Because the principal (€1000) remains the same and interest more than doubles as a result of the process of compound interest.
5/ 11.1% per year.
6/ €76.6 as three years, five months and 17 days equals 3.463 years and 100/1.083.463 =76.6.
7/ €67.7; €1.48.
8/ It makes absolutely no difference, because €100 capitalised at 7% a year would be worth €131.1 in four years.
9/ This is a good estimate. Over five years, a sum doubles at 14.87%, and 75%/5 = 15%.
10/ This is a good estimate. Over five years, a sum trebles at 24.57%, and 125%/5 = 25%.
11/ At 101.8 other investors are prepared to pay 103.7 and you cannot buy this security.
12/ 8.08 × 1026 pieces of silver (808 million billion billion pieces of silver!). Although mathematically possible, Judas's descendants would be unlikely to get anything at all, given the wars, revolutions, periods of inflation, state bankruptcies, etc. that have occurred since 33 AD! It would be “only” at 10.9 billion at a 1% interest rate. Over a very long period a small change in return creates huge differences.
13/ €100 000 at 6% will be worth €126 248 in four years, which is more than €125 000, but if you're an art lover, it might be worth foregoing €1248 for the pleasure of admiring a Francis Bacon in the comfort of your own home for four years. There's more to life than money!
14/ 635 × 1.124 = €999.
15/ 402; 240; 109; 0; −90.
16/ 1000; 1429.
17/ €248.7; €1000.
18/ €172. Buy, because its present value is higher than its market value. €7. Greater than 8%, because at 8% it is worth €172, so if I buy at €165, I'll earn more. 8%.
19/ With income of 100, you get: 1250 and 1192, a difference of 5%. At 15%: 666.7 and 664.2, a difference of 0.4%. Barring other factors, income over a period exceeding 40 years no longer has a significant impact on present value.
20/ €2000 over 75 years growing at 2% would be worth €59 086, so it would be better to buy.
21/ €5.34m, €6.47m.
22/ €300 000.
23/ €1 923 077, €662 470, yes.
24/ €119 791, 6.04%, €2003 p.a.
25/ €15 (the current price) as a €1 dividend per year provides the required rate of return of 6.67% (1/15). To get the return no need for capital gain.
Bibliography
The pioneering works on the net present value rule are:
- I. Fisher, The Theory of Interest, Augustus M. Kelley Publishers, 1965. Reprinted from the 1930 edition.
- J. Hirshleifer, On the theory of optimal investment decision, Journal of Political Economy, 66(4), 329– 352, August 1958.
- F. Lutz, V. Lutz, The Theory of the Investment of the Firm, Princeton University Press, 1951.
- J. Tobin, Liquidity preference as behaviour towards risk, Review of Economic Studies, 25(1), 65– 86, February 1958.
There are a number of financial calculation workbooks available which will help you get to grips with discounting calculations. For example W. Makgwale, Financial Mathematics Made Easy, TNL Publishers, 2012You could also consult:
- E. Fama, M. Miller, The Theory of Finance, Holt, Rinehart and Winston, 1972.
