Chapter 4
Stacks and Queues
This chapter examines three data storage structures widely used in all kinds of applications: the stack, the queue, and the priority queue. We describe how these structures differ from arrays, examining each one in turn. In the last section, we look at an operation in which the stack plays a significant role: parsing arithmetic expressions.
Different Structures for Different Use Cases
You choose data structures to use in programs based on their suitability for particular tasks. The structures in this chapter differ from what you’ve already seen in previous chapters in several ways. Those differences guide the decision on when to apply them to a new task.
Storage and Retrieval Pattern
Arrays—the data storage structure examined thus far—as well as many other structures you encounter later in this book (linked lists, trees, and so on) are appropriate for all kinds of data storage. They are sometimes referred to as low-level data structures because they are used in implementing many other data structures. The organization of the data dictates what it takes to retrieve a particular record or object that is stored inside them. Arrays are especially good for applications where the items can be indexed by an integer because the retrieval is fast and independent of the number of items stored. If the index isn’t known, the array still can be searched to find the object. As you’ve seen, sorting the objects made the search faster at the expense of other operations. Insertion and deletion operations can either be constant time or have the same Big O behavior as the search operation.
The structures and algorithms we examine in this chapter, on the other hand, are used in situations where you are unlikely to need to search for a particular object or item that is stored but rather where you want to process those objects in a particular order.
Restricted Access
In an array, any item can be accessed, either immediately—if its index number is known—or by searching through a sequence of cells until it’s found. In the data structures in this chapter, however, access is restricted: only one item can be read or removed at a time.
The interface of these structures is designed to enforce this restricted access. Access to other items is (in theory) not allowed.
More Abstract
Stacks, queues, and priority queues are more abstract structures than arrays and many other data storage structures. They’re defined primarily by their interface—the permissible operations that can be carried out on them. The underlying mechanism used to implement them is typically not visible to their user.
The underlying mechanism for a stack, for example, can be an array, as shown in this chapter, or it can be a linked list. The underlying mechanism for a priority queue can be an array or a special kind of tree called a heap. When one data structure is used to implement a more abstract one, we often say that it is a lower-level data structure by picturing the more abstract structure being layered on top of it. We return to the topic of one data structure being implemented by another when we discuss abstract data types (ADTs) in Chapter 5, “Linked Lists.”
Stacks
A stack data structure allows access to only one data item in the collection: the last item inserted. If you remove this item, you can access the next-to-last item inserted, and so on. Although that constraint seems to be quite limiting, this behavior occurs in many programming situations. In this section we show how a stack can be used to check whether parentheses, braces, and brackets are balanced in a computer program source file. At the end of this chapter, a stack plays a vital role in parsing (analyzing) arithmetic expressions such as 3×(4+5).
A stack is also a handy aid for algorithms applied to certain complex data structures. In Chapter 8, “Binary Trees,” you will see it used to help traverse the nodes of a tree. In Chapter 14, “Graphs,” you will apply it to searching the vertices of a graph (a technique that can be used to find your way out of a maze).
Nearly all computers use a stack-based architecture. When a function or method is called, the return address for where to resume execution and the function arguments are pushed (inserted) onto a stack in a particular order. When the function returns, they’re popped off. The stack operations are often accelerated by the computer hardware.
The idea of having all the function arguments pushed on a stack makes very clear what the operands are for a particular function or operator. This scheme is used in some older pocket calculators and formal languages such as PostScript and PDF content streams. Instead of entering arithmetic expressions using parentheses to group operands, you insert (or push) those values onto a stack. The operator comes after the operands and pops them off, leaving the (intermediate) result on the stack. You will learn more about this approach when we discuss parsing arithmetic expressions in the last section in this chapter.
The Postal Analogy
To understand the idea of a stack, consider an analogy provided by postal, and to a lesser extent, some email and messaging systems, especially ones where you can see only one message at a time. Many people, when they get their mail, toss it onto a stack on a table. If they’ve been away awhile, the stack might be quite large. If they don’t open the mail, the following day, they may add more messages on top of the stack. In messaging systems, a large number of messages can accumulate since the last time people viewed them. Then, when they have a spare moment, they start to process the accumulated mail or messages from the top down, one at a time. First, they open the letter on the top of the stack and take appropriate action—paying the bill, reading the holiday newsletter, considering an advertisement, throwing it away, or whatever. After disposing of the first message, they examine the next one down, which is now the top of the stack, and deal with that. The idea is to start with the most recently delivered letter or message first. Eventually, they work their way down to the message on the bottom of the stack (which is now the topmost one). Figure 4-1 shows a stack of mail.

FIGURE 4-1 A stack of letters
This “do the top one first” approach works all right as long as people can easily process all the items in a reasonable time. If they can’t, there’s the danger that messages on the bottom of the stack won’t be examined for months, and the bills or other important requests for action are not handled soon enough. By reviewing the most recent one first, however, they’re at least guaranteed to find any updates to bills or messages that occurred after the earlier deliveries.
Of course, many people don’t rigorously follow this top-to-bottom approach. They may, for example, take the mail off the bottom of the stack, to process the oldest letter first. That way, they see the messages in chronological order of arrival. Or they might shuffle through the messages before they begin processing them and put higher-priority messages on top. In these cases, their processing system is no longer a stack in the computer-science sense of the word. If they take mail off the bottom, it’s a queue; and if they prioritize it, it’s a priority queue. We’ll look at these possibilities later.
The tasks you perform every day can be seen as a stack. You typically have a set of goals, often with different priorities. They might include things like these: be happy, be with my family, or live a long life. Each of those goals can have sub-goals. For instance, to be happy, you may have a sub-goal: to be financially stable. A sub-goal of that could be: to have a job that pays enough. The tasks that you perform each day are organized around these goals. So, if “be with my family” is a main goal, you go to work to satisfy your other goal of being financially stable. When work is done, you return to your main goal by returning home. While at work, you might start the day by working on a long-term project. When the manager asks you to handle some new task that just popped up, you set aside the project and work the pop-up task. If a more critical problem comes up, you set aside the pop-up task and solve the problem. When each higher-priority activity is finished, you return to the next lower-priority activity on your stack of tasks.
In data structures, placing a data item on the top of the stack is called pushing it. Removing it from the top of the stack is called popping it. Looking at the top item without popping it is called peeking. These are the primary stack operations. A stack is said to be a last-in, first-out (LIFO) storage mechanism because the last item inserted is the first one to be removed.
The Stack Visualization Tool
Let’s use the Stack Visualization tool to get an idea how stacks work. When you launch this tool by following the guide in Appendix A, “Running the Visualizations,” you see an empty stack with operations for Push, New, Pop, Peek, and the animation controls shown in Figure 4-2.

FIGURE 4-2 The Stack Visualization tool
The Stack Visualization tool is based on an array, so you see an array of data items, this time arranged in a column. Although it’s based on an array, a stack restricts access, so you can’t access elements using an index (even though they appear next to the cells in the visualization). In fact, the concept of a stack and the underlying data structure used to implement it are quite separate. As we noted earlier, stacks can also be implemented by other kinds of storage structures, such as linked lists.
The Push Button
To insert a data item on the stack, use the button labeled Push. The item can be any text string, and you simply type it in the text entry box next to Push. The tool limits the number of characters in the string, so they fit in the array cells.
To the left of the stack is a reddish-brown arrow labeled “__top.” This is part of the data structure, an attribute that tracks the last item inserted. Initially, nothing has been inserted, so it points below the first array cell, the one labeled with a small 0. When you push an item, it moves up to cell 0, and the item is inserted in that cell. Notice that the top arrow is incremented before the item is inserted. That’s important because copying the data before incrementing could either cause an error by writing outside of the array bounds or overwriting the last element in the array when there are multiple items.
Try pushing several items on the stack. The tool notes the last operation you chose when typing an argument, so if you press Return or Enter while typing the next one, it will run the push operation again. If the stack is full and you try to push another item, you’ll get the Error! Stack is already full message. (Theoretically, an ADT stack doesn’t become full, but any practical implementation does.)
The New Button
As with all data structures, you create (and remove) stacks as needed for an algorithm. Because this implementation is based on an array, it needs to know how big the array should be. The Stack Visualization tool starts off with eight cells allocated and none of them filled. To make a new, empty stack, type the number of cells it should have in the text entry box and then select New. The tool adjusts the height of the cells to fit them within the display window. If you ask for a size that won’t fit, you’ll get an error message.
The Pop Button
To remove a data item from the top of the stack, use the Pop button. The value popped is moved to the right as it is being copied to a variable named top. It is stored there temporarily as the pop() method finishes its work.
Again, notice the steps involved. First, the item is copied from the cell pointed to by __top. Then the cell is cleared, and then __top is decremented to point to the highest occupied cell. The order of copying and changing the index pointer is the reverse of the sequence used in the push operation.
The tool’s Pop operation shows the item actually being removed from the array and the cell becoming empty. This is not strictly necessary because the value could be left in the array and simply ignored. In programming languages like Python, however, references to items left in an array like this can consume memory. It’s important to remove those references so that the memory can be reclaimed and reused. We show this in detail when looking at the code. Note that you still have a reference to the item in the top variable so that it won’t be lost.
After the topmost item is removed, the __top index decrements to the next lower cell. After you pop the last item off the stack, it points to −1, below the lowest cell. This position indicates that the stack is empty. If the stack is empty and you try to pop an item, you’ll get the Error! Stack is empty message.
The Peek Button
Push and pop are the two primary stack operations. It’s sometimes useful, however, to be able to read the value from the top of the stack without removing it. The peek operation does this. By selecting the Peek button a few times, you see the value of the item at the __top index copied to the output box on the right, but the item is not removed from the stack, which remains unchanged.
Notice that you can peek only at the top item. By design, all the other items are invisible to the stack user. If the stack is empty in the visualization tool when you select Peek, the output box is not created. We show how to implement the empty test later in the code.
Stack Size
Stacks come in all sizes and are typically capped in size so that they can be allocated in a single block of memory. The application allocates some initial size based on the maximum number of items expected to be stacked. If the application tries to push items beyond what the stack can hold, then either the stack needs to increase in size, or an exception must occur. The visualization tool limits the size to what fits conveniently on the screen, but stacks in many applications can have thousands or millions of cells.
Python Code for a Stack
The Python list type is a natural choice for implementing stacks. As you saw in Chapter 2, “Arrays,” the list type can act like an array (as opposed to a linked list, as shown in Chapter 5, “Linked Lists”). Instead of using Python slicing to get the last element in the list, we continue to use the list as a basic array and keep a separate __top pointer for the topmost item, as shown in Listing 4-1.
LISTING 4-1 The SimpleStack.py Module
# Implement a Stack data structure using a Python list class Stack(object): def __init__(self, max): # Constructor self.__stackList = [None] * max # The stack stored as a list self.__top = -1 # No items initially def push(self, item): # Insert item at top of stack self.__top += 1 # Advance the pointer self.__stackList[self.__top] = item # Store item def pop(self): # Remove top item from stack top = self.__stackList[self.__top] # Top item self.__stackList[self.__top] = None # Remove item reference self.__top -= 1 # Decrease the pointer return top # Return top item def peek(self): # Return top item if not self.isEmpty(): # If stack is not empty return self.__stackList[self.__top] # Return the top item def isEmpty(self): # Check if stack is empty return self.__top < 0 def isFull(self): # Check if stack is full return self.__top >= len(self.__stackList) - 1 def __len__(self): # Return # of items on stack return self.__top + 1 def __str__(self): # Convert stack to string ans = "[" # Start with left bracket for i in range(self.__top + 1): # Loop through current items if len(ans) > 1: # Except next to left bracket, ans += ", " # separate items with comma ans += str(self.__stackList[i]) # Add string form of item ans += "]" # Close with right bracket return ans
The SimpleStack.py implementation has just the basic features needed for a stack. Like the Array class you saw in Chapter 2, the constructor allocates an array of known size, called __stackList, to hold the items with the __top pointer as an index to the topmost item in the stack. Unlike the Array class, __top points to the topmost item and not the next array cell to be filled. Instead of insert(), it has a push() method that puts a new item on top of the stack. The pop() method returns the top item on the stack, clears the array cell that held it, and decreases the stack size. The peek() method returns the top item without decreasing the stack size.
In this simple implementation, there is very little error checking. It does include isEmpty() and isFull() methods that return Boolean values indicating whether the stack has no items or is at capacity. The peek() method checks for an empty stack and returns the top value only if there is one. To avoid errors, a client program would need to use isEmpty() before calling pop(). The class also includes methods to measure the stack depth and a string conversion method for convenience in displaying stack contents.
To exercise this class, you can use the SimpleStackClient.py program shown in Listing 4-2.
LISTING 4-2 The SimpleStackClient.py Program
from SimpleStack import * stack = Stack(10) for word in ['May', 'the', 'force', 'be', 'with', 'you']: stack.push(word) print('After pushing', len(stack), 'words on the stack, it contains: ', stack) print('Is stack full?', stack.isFull()) print('Popping items off the stack:') while not stack.isEmpty(): print(stack.pop(), end=' ') print()
The client creates a small stack, pushes some strings onto the stack, displays the contents, then pops them off, printing them left to right separated by spaces. The transcript of running the program shows the following:
$ python3 SimpleStackClient.py
After pushing 6 words on the stack, it contains:
[May, the, force, be, with, you]
Is stack full? False
Popping items off the stack:
you with be force the MayNotice how the program reverses the order of the data items. Because the last item pushed is the first one popped, the you appears first in the output. Figure 4-3 shows how the data gets placed in the array cells of the stack and then returned for push and pop operations. The array cells shown as empty in the illustration still have the value None in them, but because only the values from the bottom up through the __top pointer are occupied, the ones beyond __top can be considered unfilled. The visualization tool uses the same pop() method as in Listing 4-1, setting the popped cell to None.

FIGURE 4-3 Operation of the Stack class push() and pop() methods
Error Handling
There are different philosophies about how to handle stack errors. What should happen if you try to push an item onto a stack that’s already full or pop an item from a stack that’s empty?
In this implementation, the responsibility for avoiding or handling such errors has been left up to the program using the class. That program should always check to be sure the stack is not full before inserting an item, as in
if not stack.isFull(): stack.push(item) else: print("Can't insert, stack is full")
The client program in Listing 4-2 checks for an empty stack before it calls pop(). It does not, however, check for a full stack before calling push(). Alternatively, many stack classes check for these conditions internally, in the push() and pop() methods. Typically, a stack class that discovers such conditions either throws an exception, which can then be caught and processed by the program using the class, or takes some predefined action, such as returning None. By providing both the ability for users to query the internal state and the possibility of raising exceptions when constraints are violated, the data structure enables both proactive and reactive approaches.
Stack Example 1: Reversing a Word
For this first example of using a stack, we examine a simple task: reversing a word. When you run the program, you type in a word or phrase, and the program displays the reversed version.
A stack is used to reverse the letters. First, the characters are extracted one by one from the input string and pushed onto the stack. Then they’re popped off the stack and displayed. Because of its last-in, first-out characteristic, the stack reverses the order of the characters. Listing 4-3 shows the code for the ReverseWord.py program.
LISTING 4-3 The ReverseWord.py Program
# A program to reverse the letters of a word from SimpleStack import * stack = Stack(100) # Create a stack to hold letters word = input("Word to reverse: ") for letter in word: # Loop over letters in word if not stack.isFull(): # Push letters on stack if not full stack.push(letter) reverse = '' # Build the reversed version while not stack.isEmpty(): # by popping the stack until empty reverse += stack.pop() print('The reverse of', word, 'is', reverse)
The program makes use of Python’s input() function, which prints a prompt string and then waits for a user to type a response string. The program constructs a stack instance, gets the word to be reversed from the user, loops over the letters in the word, and pushes them on the stack. Here the program avoids pushing letters if the stack is already full. After all the letters are pushed on the stack, the program creates the reversed version, starting with an empty string and appending each character popped from the stack. The results look like this:
$ python3 ReverseWord.py Word to reverse: draw The reverse of draw is ward $ python3 ReverseWord.py Word to reverse: racecar The reverse of racecar is racecar $ python3 ReverseWord.py Word to reverse: bolton The reverse of bolton is notlob $ python3 ReverseWord.py Word to reverse: A man a plan a canal Panama The reverse of A man a plan a canal Panama is amanaP lanac a nalp a nam A
The results show that single-word palindromes come out the same as the input. If the input “word” has spaces, as in the last example, the spaces are treated just as any other letter in the string.
Stack Example 2: Delimiter Matching
One common use for stacks is to parse certain kinds of text strings. Typically, the strings are lines of code in a computer language, and the programs parsing them are compilers or interpreters.
To give the flavor of what’s involved, let’s look at a program that checks the delimiters in an expression. The text expression doesn’t need to be a line of real code (although it could be), but it should use delimiters the same way most programming languages do. The delimiters are the curly braces { and }, square brackets [ and ], and parentheses ( and ). Each opening, or left, delimiter should be matched by a closing, or right, delimiter; that is, every { should be followed by a matching } and so on. Also, opening delimiters that occur later in the string should be closed before those occurring earlier. Here are some examples:
c[d] # correct
a{b[c]d}e # correct
a{b(c]d}e # not correct; ] doesn't match (
a[b{c}d]e} # not correct; nothing matches final }
a{b(c) # not correct; nothing matches opening {Opening Delimiters on the Stack
This delimiter-matching program works by reading characters from the string one at a time and placing opening delimiters, when it finds them, on a stack. When it reads a closing delimiter from the input, it pops the opening delimiter from the top of the stack and attempts to match it with the closing delimiter. If they’re not the same type (there’s an opening brace but a closing parenthesis, for example), an error occurs. Also, if there is no opening delimiter on the stack to match a closing one, or if a delimiter has not been matched, an error occurs. It discovers unmatched delimiters because they remain on the stack after all the characters in the string have been read.
Let’s see what happens on the stack for a typical correct string:
a{b(c[d]e)f}Table 4-1 shows how the stack looks as each character is read from this string. The entries in the second column show the stack contents, reading from the bottom of the stack on the left to the top on the right.
Table 4-1 Stack Contents in Delimiter Matching the Expression a{b(c[d]e)f}
Character Read | Stack Contents |
|---|---|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As the string is read, each opening delimiter is placed on the stack. Each closing delimiter read from the input is matched with the opening delimiter popped from the top of the stack. If they form a pair, all is well. Nondelimiter characters are not inserted on the stack; they’re ignored.
This approach works because pairs of delimiters that are opened last should be closed first. This matches the last-in, first-out property of the stack.
Python Code for DelimiterChecker.py
Listing 4-4 shows the code for the parsing program, DelimiterChecker.py. Like ReverseWord.py, the program accepts an expression after prompting the user using input() and prints out any errors found or a message saying the delimiters are balanced.
LISTING 4-4 The DelimiterChecker.py Program
# A program to check that delimiters are balanced in an expression from SimpleStack import * stack = Stack(100) # Create a stack to hold delimiter tokens expr = input("Expression to check: ") errors = 0 # Assume no errors in expression for pos, letter in enumerate(expr): # Loop over letters in expression if letter in "{[(": # Look for starting delimiter if stack.isFull(): # A full stack means we can't continue raise Exception('Stack overflow on expression') else: stack.push(letter) # Put left delimiter on stack elif letter in "}])": # Look for closing delimiter if stack.isEmpty(): # If stack is empty, no left delimiter print("Error:", letter, "at position", pos, "has no matching left delimiter") errors += 1 else: left = stack.pop() # Get left delimiter from stack if not (left == "{" and letter == "}" or # Do delimiters left == "[" and letter == "]" or # match? left == "(" and letter == ")"): print("Error:", letter, "at position", pos, "does not match left delimiter", left) errors += 1 # After going through entire expression, check if stack empty if stack.isEmpty() and errors == 0: print("Delimiters balance in expression", expr) elif not stack.isEmpty(): # Any delimiters on stack weren't matched print("Expression missing right delimiters for", stack)
The program doesn’t define any functions; it processes one expression from the user and exits. It creates a Stack object to hold the delimiters as they are found. The errors variable is used to track the number of errors found in parsing the expression. It loops over the characters in the expression using Python’s enumerate() sequencer, which gets both the index and the value of the string at that index. As it finds starting (or left) delimiters, it pushes them on the stack, avoiding overflowing the stack. When it finds ending (or closing or right) delimiters, it checks whether there is a matching delimiter on the top of the stack. If not, it prints the error and continues. Some sample outputs are
$ python3 DelimiterChecker.py Expression to check: a() Delimiters balance in expression a() $ python3 DelimiterChecker.py Expression to check: a( b[4]d ) Delimiters balance in expression a( b[4]d ) $ python3 DelimiterChecker.py Expression to check: a( b]4[d ) Error: ] at position 4 does not match left delimiter ( Error: ) at position 9 does not match left delimiter [ $ python3 DelimiterChecker.py Expression to check: {{a( b]4[d ) Error: ] at position 6 does not match left delimiter ( Error: ) at position 11 does not match left delimiter [ Expression missing right delimiters for [{, {]
The messages printed by DelimiterChecker.py show the position and value of significant characters (delimiters) in the expression. After processing all the characters, any remaining delimiters on the stack are unmatched. The program prints an error for that using the Stack's string conversion method, which surrounds the list in square brackets, possibly leading to some confusion with the input string delimiters.
The Stack as a Conceptual Aid
Notice how convenient the stack is in the DelimiterChecker.py program. You could have set up an array to do what the stack does, but you would have had to worry about keeping track of an index to the most recently added character, as well as other bookkeeping tasks. The stack is conceptually easier to use. By providing limited access to its contents, using the push() and pop() methods, the stack has made the delimiter-checking program easier to understand and less error prone. (As carpenters will tell you, it’s safer and faster to use the right tool for the job.)
Efficiency of Stacks
Items can be both pushed and popped from the stack implemented in the Stack class in constant O(1) time. That is, the time is not dependent on how many items are in the stack and is therefore very quick. No comparisons or moves within the stack are necessary.
Queues
In computer science, a queue is a data structure that is somewhat like a stack, except that in a queue the first item inserted is the first to be removed (first-in, first-out, or FIFO). In stacks, as you’ve seen, the last item inserted is the first to be removed (LIFO). A queue models the way people wait for something, such as tickets being sold at a window or a chance to greet the bride and groom at a big wedding. The first person to arrive goes first, the next goes second, and so forth. Americans call it a waiting line, whereas the British call it a queue. The key aspect is that the first items to arrive are the first to be processed.
Queues are used as a programmer’s tool just like stacks are. They are found everywhere in computer systems: the jobs waiting to run, the messages to be passed over a network, the sequence of characters waiting to be printed on a terminal. They’re used to model real-world situations such as people waiting in line for tickets, airplanes waiting to take off, or students waiting to see whether they get into a particular course. This ordering is sometimes called arrival ordering because the time of arrival in the queue determines the order.
Various queues are quietly doing their job in your computer’s (or the network’s) operating system. There’s a printer queue where print jobs wait for the printer to be available. Queues also store user input events like keystrokes, mouse clicks, touchscreen touches, and microphone inputs. They are really important in multiprocessing systems so that each event can be processed in the correct order even when the processor is busy doing something else when the event occurs.
The two basic operations on the queue are called insert and remove. Insert corresponds to a person inserting themself at the rear of a ticket line. When that person makes their purchase, they remove themself from the front of the line.
The terms for insertion and removal in a stack are fairly standard; everyone says push and pop. The terminology for queues is not quite as standardized. Insert is also called put or add or enqueue, whereas remove may be called delete or get or dequeue. The rear of the queue, where items are inserted, is also called the back or tail or end. The front, where items are removed, may also be called the head. In this book, we use the terms insert, remove, front, and rear.
A Shifty Problem
In thinking about how to implement a queue using arrays, the first option would be to handle inserts like a push on a stack. The first item goes at the last position (first empty cell) of the array. Then when it’s time to remove an item from the queue, you would take the first filled cell of the array. To avoid hunting for the position of those cells, you could keep two indices, front and rear, to track where the filled cells begin and end, as shown in Figure 4-4. When Ken arrives, he’s placed in the cell indexed by rear. When you remove the first item in the queue, you get Raj from the cell indexed by front.
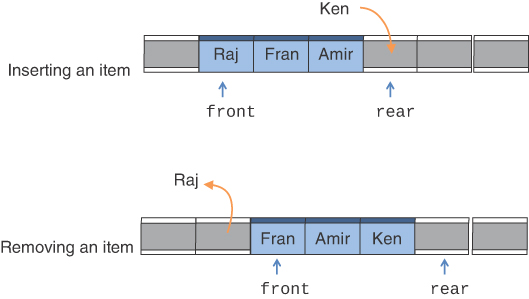
FIGURE 4-4 Queue operations in a linear array
This operation works nicely because both insert and remove simply copy an item and update an index pointer. It’s just as fast as the push and pop operations of the stack and takes only one more variable to manage.
What happens when you get to the end of the array? If the rear index reaches the end of the array, there’s no space to insert new items. That might be acceptable because it’s no worse than when a stack runs out of room. If the front index has moved past the beginning of the array, however, free cells could be used for item storage. It seems wasteful not to take advantage of them.
One way to reclaim that unused storage space would be to shift all the items in the array when an insertion would go past the end. Shifting is similar to what happens with people standing in a line/queue; they all step forward as people leave the front of the queue. In the array, you would move the item indexed by front to cell 0 and move all the items up to rear the same number of cells; then you would set front to 0 and rear to rear − front. Shifting items, however, takes time, and doing so would make some insert operations take O(N) time instead of O(1). Is there a way to avoid the shifts?
A Circular Queue
To avoid the problem of not being able to insert more items into a queue when it’s not full, you let the front and rear pointers wrap around to the beginning of the array. The result is a circular queue (sometimes called a ring buffer). This is easy to visualize if you take a row of cells and bend them around in the form of a circle so that the last cell and first cell are adjacent, as shown in Figure 4-5. The array has N cells in it, and they are numbered 0, 1, 2, …, N−2, N−1. When one of the pointers is at N−1 and needs to be incremented, you simply set it to 0. You still need to be careful not to let the wraparound go too far and start writing over cells that have valid items in them. To see how, let’s look first at the Queue Visualization tool and then the code that implements it.
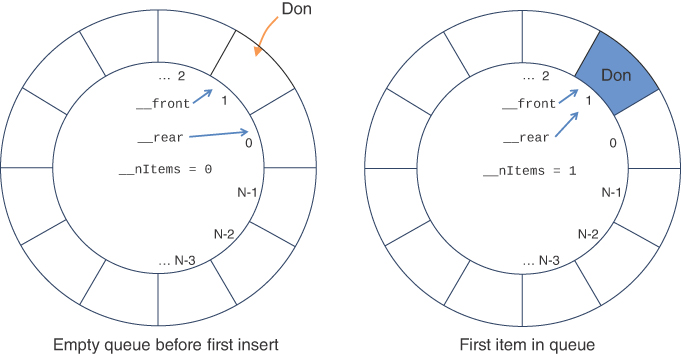
FIGURE 4-5 Operation of the Queue.insert() method on an empty queue
The Queue Visualization Tool
Let’s use the Queue Visualization tool to get an idea how queues and circular arrays work. When you start the Queue tool, you see an empty queue that can hold 10 items, as shown in Figure 4-6. The array cells are numbered from 0 to 9 starting from the right edge. (The indices increase in the counterclockwise direction to match the convention in trigonometry where angles increase from the horizontal, X-axis.)
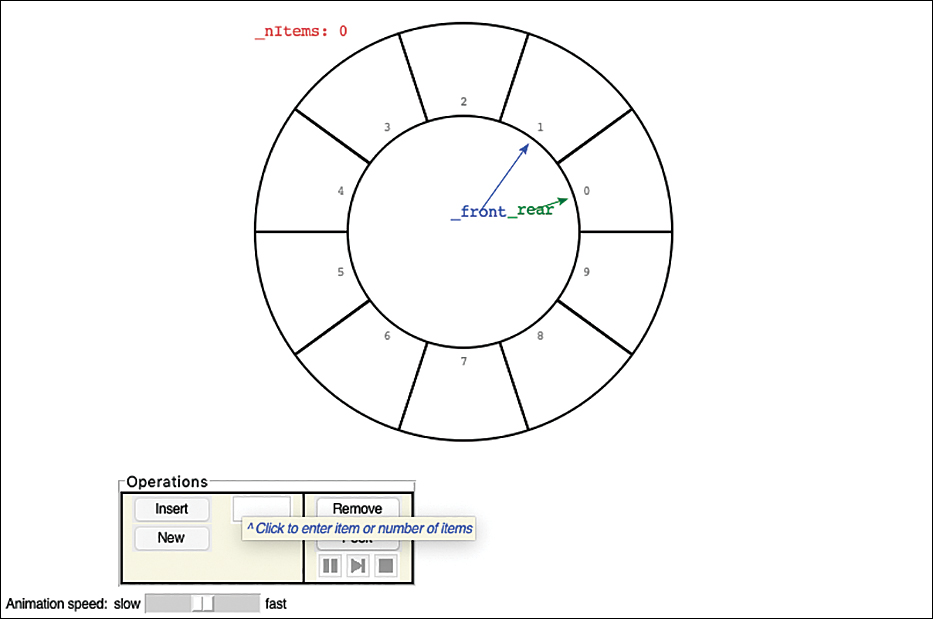
FIGURE 4-6 The Queue Visualization tool
The _front and _rear indices are shown in the center (with underscore prefixes to be somewhat like the attributes named in the code). There’s also an _nItems counter at the top left. It might seem a little odd to have front point to 1 and rear point to 0, but the reason will become clearer shortly.
The Insert Button
After typing some text in the text entry box, select the Insert button. The tool responds by incrementing the _rear index and copying the value to cell 1. As with the stack, you can insert string values of limited length. Typing another string followed by pressing Return advances _rear to cell 2 and copies the value into it.
The Remove Button
When the queue has one or more items in it, selecting the Remove button copies the item at the _front cell to a variable named front. The _front cell is cleared and the index advances by one. The front variable holds the value returned by the operation.
Note that the _front and _rear indices can appear in any order. In the initial, empty queue, _rear was one less than _front. When the first item was inserted, both _rear and_front pointed to the same cell. Additional inserts advance _rear past _front. The remove operations advance _front past _rear.
Keep inserting values until all the cells are filled. Note how the _rear index wraps around from 9 to 0. When all the cells are filled, _rear is one less than _front. That’s the same relationship as when the queue was empty, but now the _nItems counter is 10, not 0.
The Peek Button
The peek operation returns the value of the item at the front of the queue without removing the item. (Like insert and remove, peek, when applied to a queue, is also called by a variety of other names.) If you select the Peek button, you see the value at _front copied to an output box. The queue remains unchanged.
Some queue implementations have a rearPeek() and a frontPeek() method, but usually you want to know what you’re about to remove, not what you just inserted.
The New Button
If you want to start with an empty queue, you can use the New button to create one. Because it’s based on an array, the size of the array is the argument that’s required. The Queue Visualization tool lets you choose a range of queue sizes up to a limit that allows for values to be easily displayed. The animation shows the steps taken in the call to the object constructor.
Empty and Full
If you try to remove an item when there are no items in the queue, you’ll get the Queue is empty! message. You’ll also see that the code is highlighted in a different color because this operation has raised an exception. Similarly, if you try to insert an item when all the cells are already occupied, you’ll get the Queue is full! message from a Queue overflow exception. These operations are shown in detail in the next section.
Python Code for a Queue
Let’s look at how to implement a queue in Python using a circular array. Listing 4-5 shows the code for the Queue class. The constructor is a bit more complex than that of the stack because it must manage two index pointers for the front and rear of the queue. We choose to maintain an explicit count of the number of items, as explained later.
LISTING 4-5 The Queue.py Module
# Implement a Queue data structure using a Python list class Queue(object): def __init__(self, size): # Constructor self.__maxSize = size # Size of [circular] array self.__que = [None] * size # Queue stored as a list self.__front = 1 # Empty Queue has front 1 self.__rear = 0 # after rear and self.__nItems = 0 # No items in queue def insert(self, item): # Insert item at rear of queue if self.isFull(): # if not full raise Exception("Queue overflow") self.__rear += 1 # Rear moves one to the right if self.__rear == self.__maxSize: # Wrap around circular array self.__rear = 0 self.__que[self.__rear] = item # Store item at rear self.__nItems += 1 return True def remove(self): # Remove front item of queue if self.isEmpty(): # and return it, if not empty raise Exception("Queue underflow") front = self.__que[self.__front] # get the value at front self.__que[self.__front] = None # Remove item reference self.__front += 1 # front moves one to the right if self.__front == self.__maxSize: # Wrap around circular arr. self.__front = 0 self.__nItems -= 1 return front def peek(self): # Return frontmost item return None if self.isEmpty() else self.__que[self.__front] def isEmpty(self): return self.__nItems == 0 def isFull(self): return self.__nItems == self.__maxSize def __len__(self): return self.__nItems def __str__(self): # Convert queue to string ans = "[" # Start with left bracket for i in range(self.__nItems): # Loop through current items if len(ans) > 1: # Except next to left bracket, ans += ", " # separate items with comma j = i + self.__front # Offset from front if j >= self.__maxSize: # Wrap around circular array j -= self.__maxSize ans += str(self.__que[j]) # Add string form of item ans += "]" # Close with right bracket return ans
The __front and __rear pointers point at the first and last items in the queue, respectively. These and other attributes are named with double underscore prefixes to indicate they are private. They should not be changed directly by the object user.
When the queue is empty, where should __front and __rear point? We typically set one of them to 0, and we choose to do that for __rear. If we also set __front to be 0, we will have a problem inserting the first element. We set __front to 1 initially, as shown in the empty queue of Figure 4-5, so that when the first element is inserted and __rear is incremented, they both are 1. That’s desirable because the first and last items in the queue are one and the same. So __rear and __front are 1 for the first item, and __rear is increased for the insertions that follow. That means the frontmost items in the queue are at lower indices, and the rearmost are at higher indices, in general.
The insert() method adds a new item to the rear of the queue. It first checks whether the queue is full. If it is, insert() raises an exception. This is the preferred way to implement data structures: provide tests so that callers can check the status in advance, but if they don’t, raise an exception for invalid operations. Python’s most general-purpose Exception class is used here with a custom reason string, ”Queue overflow”. Many data structures define their own exception classes so that they can be easily distinguished from exception conditions like ValueError and IndexError.
You can avoid shifting items in the array during inserts by verifying that space is available before incrementing the __rear pointer and placing the new item at that empty cell of the array. The increment takes an extra step to handle the circular array logic when the pointer would go beyond the maximum size of the array by setting __rear back to 0. Finally, insert() increases the item count to reflect the inserted item at the rear.
The remove() method is similar in operation but acts on the __front of the queue. First, it checks whether the queue is empty and raises an “underflow” exception if it is. Then it makes a copy of the first item, clears the array cell, and increments the __front pointer to point at the next cell. The __front pointer must wrap around, just like __rear did, returning to 0 when it gets to the end of the array. The item count decreases because the front item was removed from the array, and the copy of the item is returned.
The peek() method looks at the frontmost item of the queue. You could create peekfront() and peekrear() methods to look at either end of the queue, but it’s rare to need both in practice. The peek() method returns None when the queue is empty, although it might be more consistent to use the same underflow exception produced by remove().
The isEmpty() and isFull() methods are simple tests on the number of items in the queue. Note that a slightly different Python syntax is used here. The whole body of the method is a single return statement. In that case, Python allows the statement to be placed after the colon ending the method signature. The __len__() method also uses the shortened syntax. Note also that these tests look at the __nItems value of the attribute rather than the __front and __rear indices. That’s needed to distinguish the empty and full queues. We look at how wrapping the indices around makes that choice harder in Figure 4-9.
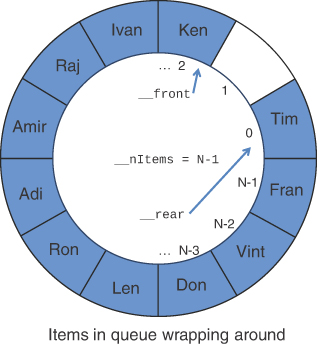
FIGURE 4-9 The __rear pointer wraps around
The last method for Queue is __str__(), which creates a string showing the contents of the queue enclosed in brackets and separated by commas for display. This method illustrates how circular array indices work. The beginning of the string has the front of the queue, and the end of the string is the rearmost item. The for loop uses the variable i to index all current items in the queue. A separate variable, j, starts at the __front and increments toward the __rear wrapping around if it passes the maximum size of the array.
Some simple tests of the Queue class are shown in Listing 4-6 and demonstrate the basic operations. The program creates a queue and inserts some names in it. The initial queue is empty, and Figure 4-5 shows how the first name, 'Don', is inserted. After that first insertion, both __front and __rear point at array cell 1 and the number of items is 1.
LISTING 4-6 The QueueClient.py Program
from Queue import * queue = Queue(10) for person in ['Don', 'Ken', 'Ivan', 'Raj', 'Amir', 'Adi']: queue.insert(person) print('After inserting', len(queue), 'persons on the queue, it contains: ', queue) print('Is queue full?', queue.isFull()) print('Removing items from the queue:') while not queue.isEmpty(): print(queue.remove(), end=' ') print()
The person names inserted into the queue keep advancing the __rear pointer and increasing the __nItems count, as shown in Figure 4-7. After inserting all the names, the QueueClient.py program uses the __str__() method (implicitly) and prints the contents of the queue along with the status of whether the queue is full or not. After that’s complete, the program removes items one at a time from the queue until the queue is empty. The items are printed separated by spaces (which is different from the way the __str__() method displays them). The result looks like this:
$ python3 QueueClient.py
After inserting 6 persons on the queue, it contains:
[Don, Ken, Ivan, Raj, Amir, Adi]
Is queue full? False
Removing items from the queue:
Don Ken Ivan Raj Amir Adi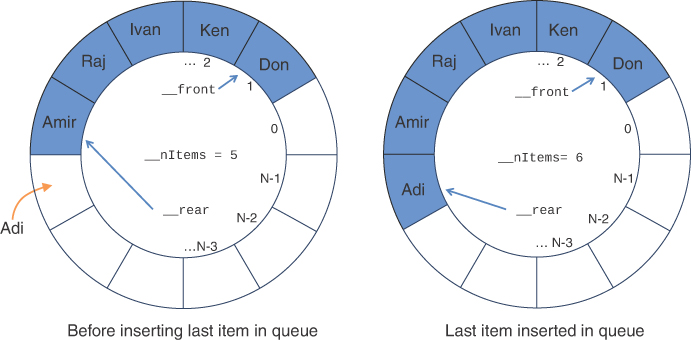
FIGURE 4-7 Inserting an item into a partially full queue
The printed result shows that items are deleted from the queue in the same order they were inserted in the queue. The first step of the deletion process is shown in Figure 4-8. When the first item, 'Don', is deleted from the front of the queue, the __front pointer is advanced to 2, and the number of items decreases to 5. The __rear pointer stays the same.
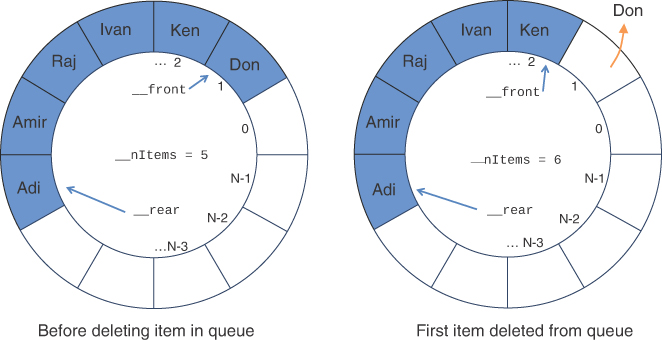
FIGURE 4-8 Deleting an item from the queue
Let’s look at what happens when the queue wraps around the circular array. If you remove only one name and then insert more names into the queue, you’ll eventually get to the situation shown in Figure 4-9. The __rear pointer keeps increasing with each insertion. After it gets to __maxSize − 1, the next insertion forces __rear to point at cell 0.
The last item inserted, 'Tim', is really placed at the beginning of the underlying array. This behavior can be somewhat counterintuitive because the sequence of items in the queue is no longer in one continuous array sequence [__front, __rear]. The front of the queue starts at index 2 and goes up to the max, and the rear is the single cell sequence [0, 0]. We say that these items are in broken sequences, or noncontiguous sequences. It may seem backward that __rear is now less than __front, but that’s how circular arrays work. The design is to always start at __front and increment until you reach __rear, wrapping around to 0 as you pass the maximum size.
Now consider what happens when one more item is inserted in the queue of Figure 4-9. The item would go at cell 1, and __rear would point at an index 1 less than __front (which is 2). That is almost the same condition in which you started the empty queue, except that you’ve increased both __rear and __front by 1. To distinguish that condition from an empty queue, you need to know the count of items it contains. If __rear were always greater than __front, you could get the number of items from __rear - __front + 1. In the case of broken sequences, you could simply add the length of the two broken sequences, but you still need some information to distinguish an empty from a full queue when __rear + 1 == __front. That’s why an explicit count of the items in the queue in the data structure simplifies the implementation.
Efficiency of Queues
As with a stack, items can be inserted and removed from a queue in O(1) time. This is based on avoiding shifts using a circular array.
Deques
There are several variations of a basic queue that you might find useful. A deque is a double-ended queue. You can insert items at either end and delete them from either end. The methods might be called insertLeft() and insertRight(), and removeLeft() and removeRight(). You may also find this structure called a dequeue, but that can be a problem because some implementations like to call insert() as enqueue() and remove() as dequeue(). The shorter deque is preferred and is pronounced “deck” to help distinguish it from “dee cue.”
If you restrict yourself to insertLeft() and removeLeft() (or their equivalents on the right), the deque acts like a stack. If you restrict yourself to insertLeft() and removeRight() (or the opposite pair), it acts like a queue.
A deque provides a more versatile data structure than either a stack or a queue and is sometimes used in container class libraries to serve both purposes. It’s not used as often as stacks and queues, however, so we don’t explore it further here.
Priority Queues
A priority queue is a more specialized data structure than a stack or a queue. Despite being more specialized, it’s a useful tool in a surprising number of situations. Like an ordinary queue, a priority queue has a front and a rear, and items are removed from the front. In a priority queue, however, items are ordered by a priority value so that the item with the highest priority (which in many implementations is the lowest value of a key) is always at the front. When multiple items have the same priority, they follow the queue ordering, FIFO, so that the oldest inserted item comes first. As with both stacks and queues, no access is provided to arbitrary items in the middle of a priority queue.
Priority queues are useful for processing mail or messages. Faced with a big inbox, a reader might choose to put the messages into piles based on priority. All the messages requiring some kind of immediate action come first. There might be piles for immediate response, near-term response, long-term response, and no response. It might make sense to process some or all those piles in the order they arrived. If the messages are correspondence from a friend, going through the communications in chronological order would make the most sense, especially if they refer to things the friend said in previous messages. If the messages are purchase requests for tickets or some other scarce item, typically the first requests are processed before later requests, possibly with some different priority piles (for example, season ticket holders getting higher priority than others for playoff tickets).
Like stacks and queues, priority queues are often used as programmer’s tools. In nearly every computer operating system, the programs are placed in a priority queue to be run. Many low-level operating system tasks get highest priority, especially those that need to determine what job needs to run next and how to respond to important input events. The operating system then takes the frontmost job from the priority queue to run next for a certain slice of time. When the time expires, the system puts that item back in the priority queue, waiting behind other jobs of the same priority. It might also put the job back in the priority queue after some delay in order to leave time open for other, lower-priority jobs to run. Jobs that complete normally—not because their time slice expired—do not get put back in the queue. We show another example of the use of a priority queue in programming techniques when we describe how to build a structure called a minimum spanning tree for a graph in Chapter 15, “Weighted Graphs.”
Priority queues share aspects related to other data structures. They have the FIFO ordering behavior of queues, along with the sorting behavior needed for the different priority levels. As you saw in Chapter 3, “Simple Sorting,” you can implement the sort algorithms in various ways that lead to different time performance. The stacks and queues you’ve seen have O(1) time performance for insert and removal. We will see whether that can be preserved as we add the prioritization behavior.
The PriorityQueue Visualization Tool
The PriorityQueue Visualization tool implements a priority queue with an array, in which the items are kept in sorted order. It’s an ascending-priority queue, in which the item with the smallest key has the highest priority and is accessed with remove(). (If the highest-key item has highest priority, then the sequence of keys during removals decreases, and it would be a descending-priority queue.)
The minimum-key item is always at the right (highest index) in the array, and the largest item is always at index 0. Figure 4-10 shows the arrangement when the tool is started. Initially, there are no items in the 12-element queue, as indicated by the nItems index pointing to cell 0.

FIGURE 4-10 The PriorityQueue Visualization tool
The Insert Button
Try inserting an item by typing a number in the text entry box and selecting Insert. You use numbers for the item key because priorities are often numeric, and this approach makes it easy to draw the height of the item as proportional to the key. The first item is inserted in the leftmost cell, and the nItems index is advanced to 1.
Now try inserting another item. Because the priority queue must keep the items ordered, it behaves like the OrderedArray you saw in Chapter 2. If the item you insert has a lower key than the first, it will go to the right. If you insert a higher key, the items with lower keys will be shifted to the right to make room for the new item. The new item’s key is compared with each item in the priority queue, starting with the one on the right. Items are shifted right until a cell becomes available where the new item can be inserted while preserving the key order.
Notice that there’s no wraparound in this implementation of the priority queue. Insertion is slow out of necessity because the proper in-order position must be found, but deletion is fast. A wraparound implementation wouldn’t improve the situation. Because there’s no wraparound, all the items are in the leftmost, lower index, cells of the array. There’s no need for two indices; all that’s needed is an nItems index.
Try inserting the same key multiple times and observe the behavior. The visualization tool gives the new item a different color to make it easier to distinguish them. You can think of the colors as different data associated with the numeric keys. Where does it insert the new key? It always goes to the left of the other equal-valued keys. Putting it to the left preserves the FIFO queue order of those items.
The Remove Button
When you use the Remove button, the item to be removed is always at the right of the array, in the cell to the left of the nItems index, so removal is quick and easy. The item is copied to a front variable, and the nItems index is decremented, just like in a stack. No shifting or comparisons are necessary.
The Peek Button
You can peek at the minimum item (find its value without removing it) with the Peek button. The value is copied to an output box like the stack and queue.
The New Button
You can create a new, empty, priority queue with the New button. Like the other data structures, the size of the underlying array is the required argument and is limited to what fits easily on the display. The visualization tool animates the steps of recording the size, allocating the array, and setting the nItems index to 0. There’s also a __pri attribute that we discuss later with the code.
Implementation Possibilities
The visualization program uses a particular implementation of priority queue that uses a single array for all the queued items. There are other possibilities, such as using separate queues for each priority or using a heap instead of an array (as discussed in Chapter 13, “Heaps”). Each one of these choices has different advantages.
The single array implementation has the advantage of simplicity at the cost of slowing down the insert or remove time. If you keep the array of items sorted by priority and arrival order, then time is needed to move items in the array during insertions to preserve that order. If you leave the array of items unsorted (but maintain the arrival order), then insertion can still be fast, but removal is slow as you search for the highest-priority item to remove. After you remove an item from the unsorted list, you must shift items within the array to close the gap created by the removal. The movement of items in the array is expected to move half of the items, on average. That happens for either insertion or deletion, depending on whether you keep the array contents sorted. Knowing the number of moves means that either insertion or removal will be an O(N) operation. We examine a specific implementation to see how that works out.
Python Code for a Priority Queue
Listing 4-7 shows an implementation of a PriorityQueue class in Python that uses a single, sorted array (Python list). The choice of maintaining the internal array as sorted means that it won’t need to manage the front and rear pointers of a circular array for the Queue as shown in Figure 4-5. Instead, it keeps a single array where the front of the queue is the last element, in order to quickly remove it. That means the rear of the queue is always at index 0, and it only manages an __nItems attribute somewhat like the Stack class.
LISTING 4-7 The PriorityQueue.py Program
# Implement a Priority Queue data structure using a Python list def identity(x): return x # Identity function class PriorityQueue(object): def __init__(self, size, pri=identity): # Constructor self.__maxSize = size # Size of array self.__que = [None] * size # Queue stored as a list self.__pri = pri # Func. to get item priority self.__nItems = 0 # no items in queue def insert(self, item): # Insert item at rear of if self.isFull(): # priority queue if not full raise Exception("Queue overflow") j = self.__nItems - 1 # Start at front while j >= 0 and ( # Look for place by priority self.__pri(item) >= self.__pri(self.__que[j])): self.__que[j+1] = self.__que[j] # Shift items to front j -= 1 # Step towards rear self.__que[j+1] = item # Insert new item at rear self.__nItems += 1 return True def remove(self): # Return front item of priority if self.isEmpty(): # queue, if not empty, & remove raise Exception("Queue underflow") self.__nItems -= 1 # One fewer item in queue front = self.__que[self.__nItems] # Store frontmost item self.__que[self.__nItems] = None # Remove item reference return front def peek(self): # Return frontmost item return None if self.isEmpty() else self.__que[self.__nItems-1] def isEmpty(self): return self.__nItems == 0 def isFull(self): return self.__nItems == self.__maxSize def __len__(self): return self.__nItems def __str__(self): # Convert pri. queue to string ans = "[" # Start with left bracket for i in range(self.__nItems - 1, -1, -1): # Loop from front if len(ans) > 1: # Except next to left bracket, ans += ", " # separate items with comma ans += str(self.__que[i]) # Add string form of item ans += "]" # Close with right bracket return ans
This class keeps another attribute, __pri, that stores a function, which can be called on any item in the queue to determine its priority. In the default case, __pri is the identity() function, which merely returns the record element itself. This is analogous to the key function used to get the keys of records stored in the OrderedRecordArray structure of Chapter 2. Typically, the client uses a particular field or set of fields to determine the priority among record structures, as explained in Chapter 2.
The insert() method of the PriorityQueue verifies that the queue isn’t full and then searches where the new item should go within the queue based on its priority. It starts at the front of the queue and works toward the rear, by setting index j to point at the last filled cell and decrementing it. The loop compares the priority of the new item with that of item j. If item j has a higher or equal priority (lower value) than that of the new item, it shifts item j one cell to the right, like the InsertionSort algorithm in Chapter 3. After it finds an item that’s lower in priority (a higher key) or the end of the queue, it can place the new item in the gap created by the shifts.
You might wonder why the PriorityQueue doesn’t use binary search, especially after seeing how much it sped up finding items in ordered arrays in Chapter 2. We have chosen not to make that optimization here because it still requires a linear search among equal priority items in the priority queue to preserve FIFO order. The binary search could end on any of the equal priority items. The resulting code for insert() is shorter at the expense of having to do more key comparisons.
The remove() method verifies that the queue isn’t empty, decrements the count of items in the queue, stores the frontmost item, clears the cell in the array, and then returns the noted item. The peek() method is even simpler because it doesn’t have to remove the item before returning it.
The empty and full tests and length methods are based on the __nItems attribute (just like the Queue class). The __str__() method for converting the queue contents to a string also walks through the array from the front (index __nItems - 1) to the rear (index 0) to show the items in the same order used for the Queue class, which had the front of the queue on the left.
The PriorityQueueClient.py program in Listing 4-8 performs some basic tests on the priority queue implementation. It inserts tuples of the form (priority, name) into the PriorityQueue object, defining the first element of those tuples to be the priority.
LISTING 4-8 The PriorityQueueClient.py Program
from PriorityQueue import * def first(x): return x[0] # Use first element of item as priority queue = PriorityQueue(10, first) for record in [(0, 'Ada'), (1, 'Don'), (2, 'Tim'), (0, 'Joe'), (1, 'Len'), (2, 'Sam'), (0, 'Meg'), (0, 'Eva'), (1, 'Kai')]: queue.insert(record) print('After inserting', len(queue), 'persons on the queue, it contains: ', queue) print('Is queue full?', queue.isFull()) print('Removing items from the queue:') while not queue.isEmpty(): print(queue.remove(), end=' ') print()
Like the client program for queues, after inserting the items, it shows the queue contents and then removes them one at a time, printing the results separated by spaces. The output follows:
$ python3 PriorityQueueClient.py
After inserting 9 persons on the queue, it contains:
[(0, 'Ada'), (0, 'Joe'), (0, 'Meg'), (0, 'Eva'), (1, 'Don'),
(1, 'Len'), (1, 'Kai'), (2, 'Tim'), (2, 'Sam')]
Is queue full? False
Removing items from the queue:
(0, 'Ada') (0, 'Joe') (0, 'Meg') (0, 'Eva') (1, 'Don') (1, 'Len')
(1, 'Kai') (2, 'Tim') (2, 'Sam')Note that the PriorityQueueClient.py program inserted the items in a different order than the way they came out. All the items with priority 0 came out first, followed by the priority 1 and priority 2 items. Within each priority, the items are ordered by their insertion/arrival order (for example, 'Joe' moved ahead of 'Don' and 'Tim' in the queue, because its priority was 0 as compared to 1 and 2, but remained after 'Ada' because 'Joe' arrived later).
Efficiency of Priority Queues
In the priority queue implementation we show here, insertion runs in O(N) time, whereas deletion takes O(1) time. That’s a big performance difference. Can you think of ways to implement it that would take only O(log N) or O(1) time? We show how to improve insertion time with heaps in Chapter 13. In the special case where the set of priority values is known in advance, separate queues could be built for each one. Then the complexity of the overall priority queue would depend only on the time it takes to decide on which queue to apply the insert or remove method.
What About Search and Traversal?
We’ve discussed how to insert, remove, and look at one item in stacks, queues, and priority queues. For arrays and many of the data structures described later, the main concern is how they perform for the search operation. Shouldn’t we examine how search and traversal work on stacks, queues, and priority queues?
The answer is: these structures are specifically designed for insertion and removal only. If an application needs to search for an item within the structure, then it’s likely that some other data structure is a better choice. Stacks and (priority) queues serve to make specific orderings of items possible. At a minimum, you could use an array or an ordered array if you needed search and traversal operations. When you do use a stack or a queue and remove items until it is empty, then the algorithm effectively performs a destructive traversal, and the order of those items typically matches some requirement for the program. We look at such algorithms in the next section.
Parsing Arithmetic Expressions
We’ve introduced three different data storage structures and examined their characteristics. Let’s shift gears now and focus on an important application that uses them. The application is parsing (that is, analyzing) arithmetic expressions such as 2+3 or 2×(3+4) or (2+4)×7+3×(9−5). The main storage structure you use is the stack. The DelimiterChecker.py program (Listing 4-4) shows how a stack could be used to check whether delimiters were formatted correctly. Stacks are used in a similar, although more complicated, way for parsing arithmetic expressions.
In some sense, this section should be considered optional. It’s not a prerequisite to the rest of the book, and writing code to parse arithmetic expressions is probably not something you need to do every day, unless you are a compiler writer or are designing domain-specific languages. Also, the coding details are more complex than any you’ve seen so far. Seeing this important use of stacks is educational, however, and raises interesting issues.
It’s fairly difficult, at least for a computer algorithm, to evaluate an arithmetic expression in one pass through the string. It’s easier for the algorithm to use a two-step process:
Transform the arithmetic expression into a different format, called postfix notation.
Evaluate the postfix expression.
Step 1 is a bit involved, but step 2 is easy. In any case, this two-step approach results in a simpler algorithm than trying to parse the arithmetic expression directly. For most humans, of course, it’s easier to parse the ordinary arithmetic expression. We return to the difference between the human and computer approaches in a moment.
Before we delve into the details of steps 1 and 2, we introduce the new notation.
Postfix Notation
Everyday arithmetic expressions are written with an operator (+, −, ×, or /) placed between two operands (numbers, or symbols that stand for numbers). This is called infix notation because the operator is written in-between the operands. Typical arithmetic expressions are things like 2+2 and 4/7, or, using letters to stand for numbers, A+B and A/B.
In postfix notation (which is also called Reverse Polish Notation, or RPN, because it was invented by a Polish mathematician), the operator follows the two operands. Thus, A+B becomes AB+, and A/B becomes AB/. More complex infix expressions can likewise be translated into postfix notation, as shown in Table 4-2. One thing that might stand out in these translations is that there are no parentheses in the postfix expressions. We explain how the postfix expressions are generated in a moment.
Table 4-2 Infix and Postfix Expressions
Infix | Postfix |
|---|---|
A+B−C | AB+C− |
A×B/C | AB×C/ |
A+B×C | ABC×+ |
A×B+C | AB×C+ |
A×(B+C) | ABC+× |
A×B+C×D | AB×CD×+ |
(A+B)×(C−D) | AB+CD−× |
((A+B)×C)−D | AB+C×D− |
A+B×(C−D/(E+F)) | ABCDEF+/−×+ |
Besides infix and postfix, there’s also a prefix notation, in which the operator is written before the operands: +AB instead of AB+. Also known as Polish notation, it is functionally like postfix but seldom used. The lambda calculus (λ calculus) and the Lisp programming language use prefix notation and are very important historically. For functional programming languages, prefix notation is very convenient. The lambda calculus is also the origin of the lambda keyword used for anonymous functions in Python.
Translating Infix to Postfix
The next several pages are devoted to explaining how to translate an expression from infix notation into postfix. This algorithm is fairly involved, so don’t worry if every detail isn’t clear at first. If you get bogged down, you may want to skip ahead to the sections “The InfixCalculator Tool” and “Evaluating Postfix Expressions”
To understand how to create a postfix expression, you might find it helpful to see how a postfix expression is evaluated; for example, how the value 14 is computed from the expression 234+×, which is the postfix equivalent of 2×(3+4). Notice that in this discussion, for ease of writing, we restrict ourselves to expressions with single-digit numbers (and sometimes variable names) for inputs. Later, we look at code to handle expressions with multidigit numbers and multicharacter variable names.
How Humans Evaluate Infix
How do you translate infix to postfix? Let’s examine a slightly easier question first: How does a human evaluate a normal infix expression? Although, as we stated earlier, such evaluation is difficult for a computer, we humans do it fairly easily because of countless hours looking at similar expressions in math class. It’s not hard to find the answer to 3+ 4+5, or 3×(4+5). By analyzing how you evaluate this expression, you can achieve some insight into the translation of such expressions into postfix.
Roughly speaking, when you “solve” an arithmetic expression, you follow rules something like this:
You read from left to right. (At least, we assume this is true. Sometimes people skip ahead, but for purposes of this discussion, you should assume you must read methodically, starting at the left.)
When you’ve read enough to evaluate two operands and an operator, you do the calculation and substitute the answer for these two operands and operator. (You may also need to solve other pending operations on the left, as we see later.)
You continue this process—going from left to right and evaluating when possible—until the end of the expression.
Table 4-3, Table 4-4, and Table 4-5 show three examples of how simple infix expressions are evaluated. Later, Tables 4-6, 4-7, and 4-8 show how closely these evaluations mirror the process of translating infix to postfix.
Table 4-3 Evaluating 3+4−5
Item Read | Expression Parsed So Far | Comments |
|---|---|---|
3 | 3 | |
+ | 3+ | |
4 | 3+4 | |
− | 7 | When you see the −, you can evaluate 3+4. |
7− | ||
5 | 7−5 | |
End | 2 | When you reach the end of the expression, you can evaluate 7−5. |
Table 4-4 Evaluating 3+4×5
Item Read | Expression Parsed So Far | Comments |
|---|---|---|
3 | 3 | |
+ | 3+ | |
4 | 3+4 | |
× | 3+4× | You can't evaluate 3+4 because × is higher precedence than +. |
5 | 3+4×5 | Because you don't know if there is some higher-precedence expression that follows, you simply put the 5 at the end. |
End | 3+20 | When you see there are no more expressions, you can evaluate 4×5. |
23 | Because there are still operators, you now evaluate 3+20. |
Table 4-5 Evaluating 3×(4+5)
Item Read | Expression Parsed So Far | Comments |
|---|---|---|
3 | 3 | |
× | 3× | |
( | 3×( | |
4 | 3×(4 | You can't evaluate 3×4 because of the parenthesis. |
+ | 3×(4+ | |
5 | 3×(4+5 | You can't evaluate 4+5 yet. |
) | 3×(4+5) | When you see the ), you can evaluate 4+5. |
3×9 | After replacing the parenthesized expression, you need to know if there's more to come with a higher precedence. | |
End | 27 | There isn't, so now you evaluate 3×9. |
Table 4-6 Translating A+B−C into Postfix
Character Read from Infix Expression | Infix Expression Parsed So Far | Postfix Expression Written So Far | Comments |
|---|---|---|---|
A | A | A | |
+ | A+ | A | |
B | A+B | AB | |
− | A+B- | AB+ | When you see the −, you can copy the + to the postfix string. |
C | A+B−C | AB+C | |
End | A+B−C | AB+C− | When you reach the end of the expression, you can copy the −. |
Table 4-7 Translating A+B×C into Postfix
Character Read from Infix Expression | Infix Expression Parsed So Far | Postfix Expression Written So Far | Comments |
|---|---|---|---|
A | A | A | |
+ | A+ | A | |
B | A+B | AB | |
C | A+B×C | ABC | When you see the C, you can copy the ×. |
A+B×C | ABC× | ||
End | A+B×C | ABC×+ | When you see the end of the expression, you can copy the +. |
Table 4-8 Translating A×(B+C) into Postfix
Character Read from Infix Expression | Infix Expression Parsed so Far | Postfix Expression Written So Far | Comments |
|---|---|---|---|
A | A | A | |
× | A× | A | |
( | A×( | A | |
B | A×(B | AB | You can't copy × because of the parenthesis. |
+ | A×(B+ | AB | |
C | A×(B+C | ABC | You can't copy the + yet. |
) | A×(B+C) | ABC+ | When you see the ), you can copy the +. |
A×(B+C) | ABC+× | After you've copied the +, you can copy the ×. | |
End | A×(B+C) | ABC+× | Nothing left to copy. |
To evaluate 3+4−5, you would carry out the steps shown in Table 4-3.
You can’t evaluate the 3+4 until you see whether an operator follows the 4 and what operator it is. If it’s × or /, you need to wait before applying the + sign until you’ve evaluated the × or /. In this example, however, the operator following the 4 is a −, which has the same precedence (priority among operators) as a +, so when you see the −, you know you can evaluate 3+4, which is 7. The 7 then replaces the 3+4. You can evaluate the 7−5 when you arrive at the end of the expression, knowing that there are no more operators.
Because of precedence relationships, evaluating 3+4×5 is a bit more complicated, as shown in Table 4-4.
Here, you can’t add the 3 until you know the result of 4×5. Why not? Because multiplication has a higher precedence than addition. In fact, both × and / have a higher precedence than + and −, so all multiplications and divisions must be carried out before any additions or subtractions (unless parentheses dictate otherwise; see the next example).
Often, you can evaluate as you go from left to right, as in the preceding example. You need to be sure, when you come to an operand-operator-operand combination such as A+B, however, that the operator on the right side of the B isn’t one with a higher precedence than the +. If it does have a higher precedence, as in this example, you can’t do the addition yet. After you’ve read the 5 and found nothing after it, however, you know the multiplication can be carried out. Note that because multiplication has the highest priority among the four operators in this sample language, it doesn’t matter whether a × or / follows the 5, and the multiplication could proceed without looking at the next input. You can’t do the addition, however, until you’ve found out what’s beyond the 5. When you find there’s nothing more to read, you can go ahead and perform any remaining operations, knowing the highest precedence operators are on the right.
Parentheses are used to override the normal precedence of operators. Table 4-5 shows how you would evaluate 3×(4+5). Without the parentheses, you would do the multiplication first; with them, you do the addition first.
Here, you can’t evaluate anything until you’ve reached the closing parenthesis. Multiplication has a higher or equal precedence compared to the other operators, so ordinarily you could carry out 3×4 as soon as you see the 4. Parentheses, however, have an even higher precedence than × and /. Accordingly, you must evaluate anything in parentheses before using the result as an operand in any other calculation. The closing parenthesis tells you that you can go ahead and do the addition. You find that 4+5 is 9 and substitute it. Finding that there are no more higher-precedence operators afterward, you can evaluate 3×9 to obtain 27.
As you’ve seen in evaluating an infix arithmetic expression, you go both forward and backward through the expression. You go forward (left to right) reading operands and operators. When you have enough information to apply an operator, you go backward, recalling two operands and an operator and carrying out the arithmetic.
Sometimes, you must defer applying operators if they’re followed by higher-precedence operators or by parentheses. When this happens, you must apply the later, higher-precedence, operator first; then go backward (to the left) and apply earlier operators.
You could write an algorithm to carry out this kind of evaluation directly. As we noted, however, it’s easier to translate into postfix notation first.
How Humans Translate Infix to Postfix
To translate infix to postfix notation, you follow a similar set of rules to those for evaluating infix. There are, however, a few small changes. You don’t do any arithmetic. The idea is not to evaluate the infix expression, but to rearrange the operators and operands into a different format: postfix notation. The resulting postfix expression will be evaluated later.
As before, you read the infix from left to right, looking at each character in turn. As you go along, you copy these operands and operators to the postfix output string. The trick is knowing when to copy what.
If the character in the infix string is an operand, you copy it immediately to the postfix string. That is, if you see an A in the infix, you write an A to the postfix. There’s never any delay: you copy the operands as you get to them, no matter how long you must wait to copy their associated operators.
Knowing when to copy an operator is more complicated, but it’s the same as the rule for evaluating infix expressions. Whenever you could have used the operator to evaluate part of the infix expression (if you were evaluating instead of translating to postfix), you instead copy it to the postfix string.
Table 4-6 shows how A+B−C is translated into postfix notation.
Notice the similarity of this table to Table 4-3, which showed the evaluation of the infix expression 3+4−5. At each point where you would have done an evaluation in the earlier table, you instead simply write an operator to the postfix output.
Table 4-7 shows the translation of A+B×C to postfix. This translation parallels that of Table 4-4, which covered the evaluation of 3+4×5.
As the final example, Table 4-8 shows how A×(B+C) is translated to postfix. This process is similar to evaluating 3×(4+5) in Table 4-5. You can’t write any postfix operators until you see the closing parenthesis in the input.
As in the numerical evaluation process, you go both forward and backward through the infix expression to complete the translation to postfix. You can’t write an operator to the output (postfix) string if it’s followed by a higher-precedence operator or a left parenthesis. If it is, the higher-precedence operator or the operator in parentheses must be written to the postfix before the lower-priority operator.
Saving Operators on a Stack
You’ll notice in both Table 4-7 and Table 4-8 that the order of the operators is reversed going from infix to postfix. Because the first operator can’t be copied to the output until the second one has been copied, the operators were output to the postfix string in the opposite order they were read from the infix string. That suggests a stack might be useful for handling the operators. A longer example helps illustrate how that could work. Table 4-9 shows the translation to postfix of the infix expression A+B×(C−D).
Table 4-9 Translating A+B×(C−D) into Postfix
Character Read from Infix Expression | Infix Expression Parsed So Far | Postfix Expression Written So Far | Stack Contents |
|---|---|---|---|
A | A | A | |
+ | A+ | A | + |
B | A+B | AB | + |
× | A+B× | AB | +× |
( | A+B×( | AB | +×( |
C | A+B×(C | ABC | +×( |
− | A+B×(C− | ABC | +×(− |
D | A+B×(C−D | ABCD | +×(− |
) | A+B×(C−D) | ABCD− | +×( |
A+B×(C−D) | ABCD− | +×( | |
A+B×(C−D) | ABCD− | +× | |
A+B×(C−D) | ABCD−× | + | |
A+B×(C−D) | ABCD−×+ |
Here you see the order of the operands is +×− in the original infix expression, but the reverse order, −×+, in the final postfix expression. This happens because × has higher precedence than +, and −, because it’s in parentheses, has higher precedence than ×. We need to track operators with lower precedence on the stack to be able to process them later. The last column in Table 4-9 shows the stack contents at various stages in the translation process.
Popping items from the stack allows you to, in a sense, go backward (right to left) through the input string. You’re not really examining the entire input string, only the operators and parentheses. They were pushed on the stack when reading the input, so now you can recall them in reverse order by popping them off the stack.
The operands (A, B, and so on) appear in the same order in infix and postfix, so you can write each one to the output as soon as you encounter it; they don’t need to be stored on a stack or reversed. Changing their order would also cause issues with operators that lack the commutative property like subtraction and division; A − B ≠ B − A.
Translation Rules
Let’s make the rules for infix-to-postfix translation more explicit. You read items from the infix input string and take the actions shown in Table 4-10. These actions are described in pseudocode, a blend of programming syntax and English.
Table 4-10 Infix to Postfix Translation Rules
Item Read from Input | Action (Infix) |
|---|---|
Operand | Write operand to postfix output string. |
Open parenthesis ( | Push parenthesis on stack. |
Close parenthesis ) | While stack is not empty: top = pop item from stack. If top is (, then break out of loop. Else write top to postfix output. |
Operator (inputOp) | While stack is not empty: top = pop item from stack. If top is (, then push ( back on stack and break. Else if top is an operator: If prec(top) >= prec(inputOp), output top. Else push top and break loop. Push inputOp on stack. |
End of input | While stack is not empty: Pop stack and output item. |
In this table, the < and >= symbols are applied to the operator precedence, not numerical values. The inputOp operator has just been read from the infix input, while the top operator is popped off the stack. We use prec(inputOp) and prec(top) to mean the operator precedence of inputOp and top, respectively.
Convincing yourself that these rules work may take some effort. Tables 4-11, 4-12, and 4-13 show how the rules apply to the three sample infix expressions, similar to Tables 4-6, 4-7, and 4-8, except that the relevant rules for each step have been added. Try creating similar tables by starting with other simple infix expressions and using the rules to translate some of them to postfix.
Table 4-11 Translation Rules Applied to A+B−C
Character Read from Infix | Infix Parsed So Far | Postfix Written So Far | Stack Contents | Rule |
|---|---|---|---|---|
A | A | A | Write operand to output. | |
+ | A+ | A | + | While stack not empty: (null loop) Push inputOp on stack. |
B | A+B | AB | + | Write operand to output. |
− | A+B− | AB | Stack not empty, so pop item +. | |
A+B− | AB+ | inputOp is −, top is +, prec(top) >= prec(inputOp), so output top. | ||
A+B− | AB+ | − | Then push inputOp. | |
C | A+B−C | AB+C | − | Write operand to output. |
End | A+B−C | AB+C− | Pop leftover item, output it. |
Table 4-12 Translation Rules Applied to A+B×C
Character Read from Infix | Infix Parsed So Far | Postfix Written So Far | Stack Contents | Rule |
|---|---|---|---|---|
A | A | A | Write operand to postfix. | |
+ | A+ | A | + | If stack empty, push inputOp. |
B | A+B | AB | + | Write operand to output. |
× | A+B× | AB | Stack not empty, so pop top +. | |
A+B× | AB | + | inputOp is ×, top is +, prec(top) < prec(inputOp), so push top. | |
A+B× | AB | +× | Then push inputOp. | |
C | A+B×C | ABC | +× | Write operand to output. |
End | A+B×C | ABC× | + | Pop leftover item, output it. |
A+B×C | ABC×+ | Pop leftover item, output it. |
Table 4-13 Translation Rules Applied to A×(B+C)
Character Read from Infix | Infix Parsed So Far | Postfix Written So Far | Stack Contents | Rule |
|---|---|---|---|---|
A | A | A | Write operand to postfix. | |
× | A× | A | × | If stack empty, push inputOp. |
( | A×( | A | ×( | Push ( on stack. |
B | A×(B | AB | ×( | Write operand to postfix. |
+ | A×(B+ | AB | × | Stack not empty, so pop item (. |
A×(B+ | AB | ×( | top is (, so push it and break. | |
A×(B+ | AB | ×(+ | Then push inputOp. | |
C | A×(B+C | ABC | ×(+ | Write operand to postfix. |
) | A×(B+C) | ABC+ | ×( | Pop item, write to output. |
A×(B+C) | ABC+ | × | Quit popping if (. | |
End | A×(B+C) | ABC+× | Pop leftover item, output it. |
The InfixCalculator Tool
Before we look at the code, let’s put these words into action and watch the process of converting infix expressions to postfix using a visualization tool. Follow the instructions in Appendix A to launch the InfixCalculator tool. The interface is simple: select the text entry box in the Operations area, type a numeric expression using infix, and select the Evaluate button. The animation of parsing the expression begins and looks something like Figure 4-11.
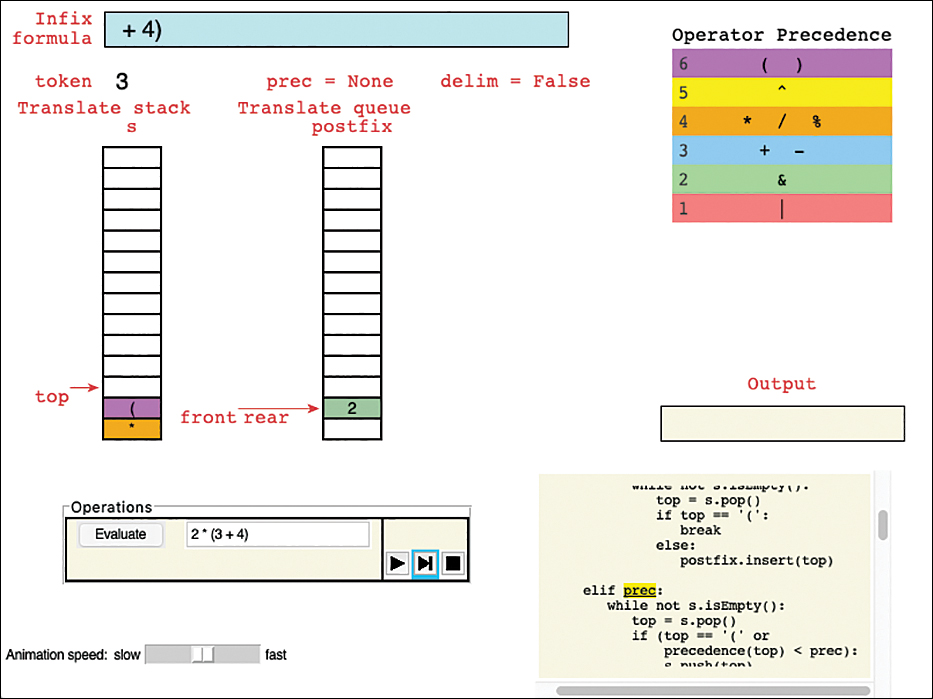
FIGURE 4-11 The InfixCalculator tool
The expression being parsed in the figure, 2 * (3 + 4), is copied in the box at the top of the tool and then reduced as the characters are processed. (The full expression still appears in the text entry box below.) The figure shows that the first operand, 2, the multiplication operator, *, and the open parenthesis have already been pulled out of the expression and placed in the stack or queue. Each one of those strings is called a token. Looking at the “3” token corresponds to the fourth step detailed in Table 4-13 when the B operand is examined.
Because the current token “3” is a number, it’s not an operator or a delimiter like those shown in the Operator Precedence table at the upper right. When the tool looks in that table, it finds that numbers have no precedence and writes prec = None and delim = False to indicate its status as an operand. The next (nonblank) character in the expression is a plus (+). It does have a precedence in the table, 4, and that means it’s an operator.
As the animation runs, the stack contents build up in the stack on the left. Tokens that can be output as the postfix expression go in the queue to its right. The contents of this queue are used to make the postfix string later in the animation. Watch the stack grow as each operator is taken from the front of the expression. Pause the infix calculator and see whether you can predict what will happen next.
The InfixCalculator shows the translation into posftfix, followed by the evaluation of the postfix. Before we look at how the evaluation works, let’s look at the code for the parsing and translation. The visualization tool shows this code during the processing.
Python Code to Convert Infix to Postfix
Listing 4-9 shows the beginning of the PostfixTranslate.py program, which uses the rules from Table 4-10 to translate an infix expression to a postfix expression. This is a long program file, so we show it in two parts. The first part provides the processing of the input string, finding the individual tokens in the expression and determining the precedence of operators.
LISTING 4-9 Processing Tokens in PostfixTranslate.py
from SimpleStack import Stack from Queue import Queue # Define operators and their precedence # We group single character operators of equal precedence in strings # Lowest precedence is on the left; highest on the right # Parentheses are treated as high precedence operators operators = ["|", "&", "+-", "*/%", "^", "()"] def precedence(operator): # Get the precedence of an operator for p, ops in enumerate(operators): # Loop through operators if operator in ops: # If found, return p + 1 # return precedence (low = 1) # else not an operator, return None def delimiter(character): # Determine if character is delimiter return precedence(character) == len(operators) def nextToken(s): # Parse next token from input string token = "" # Token is operator or operand s = s.strip() # Remove any leading & trailing space if len(s) > 0: # If not end of input if precedence(s[0]): # Check if first char. is operator token = s[0] # Token is a single char. operator s = s[1:] else: # its an operand, so take characters up while len(s) > 0 and not ( # to next operator or space precedence(s[0]) or s[0].isspace()): token += s[0] s = s[1:] return token, s # Return the token, and remaining input string
After importing the previous definitions of stacks and queues, the first statement of PostfixTranslate.py defines the operators that the program can process. We have expanded the number of operators that can be used. So far, we’ve only shown examples using the four most common operators, +−×/. This program adds several others available in Python. By putting these operator characters into an array of strings, we have grouped together operators with the same precedence and ordered the groups. Each array cell corresponds to a precedence level. You can look up the precedence of an operator by stepping through the array until you find the character in the string and returning the string’s position in the array. Note that we used the asterisk * for the multiplication symbol ×, to be consistent with Python and other programming languages.
The precedence() function does the lookup, returning a number for the precedence or None if the character is not an operator. The operators are all the single-character operators that Python allows. Parentheses are included in the array of operators for convenience. They act like operators when breaking an expression up into tokens. A separate delimiter() function tests whether its argument is one of these highest-precedence characters.
A function breaks the input string into tokens. A token is a substring that corresponds to exactly one operator, operand, or delimiter in the input expression.
The nextToken() function goes through the input string, skipping over any whitespace, and finding the first token at the beginning of the string. It returns that token along with the rest of the string after the token, which is used for the subsequent call to nextToken(). The function checks whether a character is an operator or a delimiter by checking whether the precedence function returns a number for it (or None for operands). All the operators and delimiters in this example are single characters.
For operands, this program allows multicharacter (multidigit) tokens. The while loop steps through the input string, s, checking whether the first character is an operator or whitespace. If it is not, the first character is added to the output token and removed from the input string. After the loop finds either an operator, delimiter, whitespace, or the end of the input string, the token is complete.
The PostfixTranslate() function appears in Listing 4-10 and does the main work by allocating a stack to hold the operators (and left parentheses) and a queue to hold the postfix output. As you saw with the InfixCalculator Visualization tool, the operators build up in the stack and are then popped and moved to the queue. The queue holds the output postfix string with each operand or operator in its own cell. That enables the program to add some whitespace between elements in the output to make it more legible, especially for operands with more than one digit or character.
PostfixTranslate() loops over the input expression/formula using a fencepost loop—a loop that performs some work on the initial item before entering the main loop body to perform work on all the remaining loop items. In this case, it extracts the first token and then loops until there are no more tokens in the input expression/formula.
After determining whether the current token is an operand, operator, or delimiter, the PostfixTranslate() function applies the rules in Table 4-10. The if delim … elif prec … else statement separates the processing of the three types. The Python statements are very close to the pseudocode used to describe the rules. This is the heart of the algorithm, so study it closely. The if delim: … block handles the parentheses, pushing open parentheses on the stack and then popping off operators between the opening and closing parentheses after they are found.
LISTING 4-10 The PostfixTranslate() Function
def PostfixTranslate(formula): # Translate infix to Postfix postfix = Queue(100) # Store postfix in queue temporarily s = Stack(100) # Parser stack for operators # For each token in the formula (fencepost loop) token, formula = nextToken(formula) while token: prec = precedence(token) # Is it an operator? delim = delimiter(token) # Is it a delimiter? if delim: if token == '(': # Open parenthesis s.push(token) # Push parenthesis on stack else: # Closing parenthesis while not s.isEmpty(): # Pop items off stack top = s.pop() if top == '(': # Until open paren found break else: # and put rest in output postfix.insert(top) elif prec: # Input token is an operator while not s.isEmpty(): # Check top of stack top = s.pop() if (top == '(' or # If open parenthesis, or a lower precedence(top) < prec): # precedence operator s.push(top) # push it back on stack and break # stop loop else: # Else top is higher precedence postfix.insert(top) # operator, so output it s.push(token) # Push input token (op) on stack else: # Input token is an operand postfix.insert(token) # and goes straight to output token, formula = nextToken(formula) # Fencepost loop while not s.isEmpty(): # At end of input, pop stack postfix.insert(s.pop()) # operators and move to output ans = "" while not postfix.isEmpty(): # Move postfix items to string if len(ans) > 0: ans += " " # Separate tokens with space ans += postfix.remove() return ans if __name__ == '__main__': infix_expr = input("Infix expression to translate: ") print("The postfix representation of", infix_expr, "is:", PostfixTranslate(infix_expr))
In the elif prec: … block, new operators from the input string are processed. It uses a loop to walk back through the stack looking for open parentheses or lower-precedence operators. The code shows a bit of an optimization from the loop’s pseudocode for new operators:
While stack is not empty:
top = pop item from stack
If top is (, then push ( back on stack and break
Else if top is an operator:
If prec(top) >= prec(inputOp), output top
Else push top and break loop
The two highlighted phrases in the pseudocode perform the same operation because the open parenthesis is stored in the top variable. In the program, the two conditions are checked in the if (top == '(' or precedence(top) < prec): … statement. When top does not satisfy that condition, it must be an operator whose precedence is greater than or equal to that of the input operator in token. That’s the only condition where the top operator is output by inserting it into the postfix queue.
After all the tokens have been processed in the first while loop, any remaining operators on the stack are popped and output to the postfix queue, reversing their order. That work happens in the final while not s.isEmpty() loop.
At the end, the while not postfix.isEmpty() loop creates the ans string, by concatenating the operands and operators in the postfix output queue separated by spaces. The spaces don’t change the value of the expression but do make the string more readable.
After the function body of PostfixTranslate() is defined, the last section of the program is an if statement that is used to detect whether this file is being used as a program or as a module inside a bigger program. By testing whether the special variable, __name__, is set to the string ‘__main__’, the Python interpreter can determine whether this file is being loaded as the main file to be executed or as part of an import statement inside another file. When __name__ is ‘__main__’ it’s the main file to be executed, and this program prompts for an input infix expression to translate. It then prints that expression along with its postfix translation. The output looks like this:
$ python3 PostfixTranslate.py Infix expression to translate: A+B-C The postfix representation of A+B-C is: A B + C - $ python3 PostfixTranslate.py Infix expression to translate: A+B*C The postfix representation of A+B*C is: A B C * + $ python3 PostfixTranslate.py Infix expression to translate: A*(B+C) The postfix representation of A*(B+C) is: A B C + * $ python3 PostfixTranslate.py Infix expression to translate: A | B*C^D % E - F/G + H & J The postfix representation of A | B*C^D % E - F/G + H & J is: A B C D ^ * E % F G / - H + J & |
The last example uses all the operators the program knows about and shows how it interprets their precedence and ignores whitespace. The PostfixTranslate.py program doesn’t check the input for errors. If you type an incorrect infix expression, such as one with consecutive operators or unbalanced parentheses, the program will provide erroneous output.
Experiment with this program. Start with some simple infix expressions and see whether you can predict what the postfix will be. Then run the program to verify your answer. Pretty soon, “a postfix Jedi, you will become.” Note that you can also use the InfixCalculator tool to practice these transformations, but you won’t be able to use letters as variable names.
Evaluating Postfix Expressions
As you can see, converting infix expressions to postfix expressions is not trivial. Is all this trouble really necessary? Yes, the payoff comes when you evaluate a postfix expression. Before we show how simple the algorithm is, let’s examine how a human might carry out such an evaluation.
How Humans Evaluate Postfix
Figure 4-12 shows how a human can evaluate a postfix expression using visual inspection along with a pencil and paper. The postfix expression, 345+×612+/−, is shown in the gray rectangle. In this simplified example, operands can be only single-digit integers.
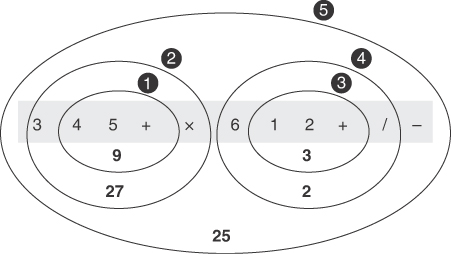
FIGURE 4-12 Visual approach to postfix evaluation of 345+×612+/−
Start with the first operator on the left and draw an oval around it plus the two operands to its immediate left. This is marked as step ➊ in the figure. Then apply the operator to these two operands—performing the actual arithmetic—and write down the result inside the oval. In the figure, evaluating 4+5 gives 9, which will be used in step ➋.
Now go to the next operator to the right and draw an oval around it, the oval you already drew, and the operand to the left of that. Apply the operator to the previous oval and the new operand and write the result in the new oval, labeled ➋. Here 3×9 gives 27. Continue this process until all the operators have been applied: 1+2 evaluates to 3 in step ➌, and 6/3 is 2, in step ➍. The answer is the result in the largest oval at step ➎: 27−2 is 25.
Rules for Postfix Evaluation
How do you write a program to reproduce this evaluation process? As you can see, each time you come to an operator, you apply it to the last two operands you’ve seen. Remembering what the PostfixTranslate.py program does (Listing 4-10) suggests that it might be appropriate to store the operands on a stack. The approach for postfix evaluation, however, differs from the infix-to-postfix translation algorithm, where operators were stored on the stack. You can use the rules shown in Table 4-14 to evaluate postfix expressions.
Table 4-14 Evaluating a Postfix Expression
Item Read from Postfix | Action Expression |
|---|---|
Operand | Push it onto the stack. |
Operator | Pop the top two operands from the stack and apply the operator to them. Push the result. |
When you’re done, pop the stack to obtain the answer. That’s all there is to it. This process is the computer equivalent of the human oval-drawing approach of Figure 4-12.
Python Code to Evaluate Postfix Expressions
In the infix-to-postfix translation, symbols (A, B, and so on) were allowed to stand for numbers. This approach worked because you weren’t performing arithmetic operations on the operands but merely rewriting them in a different format. Now say you want to evaluate a postfix expression, which means carrying out the arithmetic and obtaining an answer. The input must consist of actual numbers mixed with operators.
As shown in Listing 4-11, the PostfixEvaluate.py program imports the PostfixTranslate module and uses its functions to translate an infix expression to postfix before evaluating it. It makes use of the same nextToken() function from that module, but this time it’s applied to the translated postfix string. The fencepost loop goes through each of the tokens in the postfix string. For operators, the left and right operands are popped off the stack, the operation is performed, and the result is pushed back on the stack. For operands, the string version of the operand is converted to an integer and pushed on the stack.
LISTING 4-11 The PostfixEvaluate.py Program
from PostfixTranslate import * from SimpleStack import * def PostfixEvaluate(formula): # Translate infix to Postfix and # evaluate the result postfix = PostfixTranslate(formula) # Postfix string s = Stack(100) # Operand stack token, postfix = nextToken(postfix) while token: prec = precedence(token) # Is it an operator? if prec: # If input token is an operator right = s.pop() # Get left and right operands left = s.pop() # from stack if token == '|': # Perform operation and push s.push(left | right) elif token == '&': s.push(left & right) elif token == '+': s.push(left + right) elif token == '-': s.push(left - right) elif token == '*': s.push(left * right) elif token == '/': s.push(left / right) elif token == '%': s.push(left % right) elif token == '^': s.push(left ^ right) else: # Else token is operand s.push(int(token)) # Convert to integer and push print('After processing', token, 'stack holds:', s) token, postfix = nextToken(postfix) # Fencepost loop print('Final result =', s.pop()) # At end of input, print result if __name__ == '__main__': infix_expr = input("Infix expression to evaluate: ") print("The postfix representation of", infix_expr, "is", PostfixTranslate(infix_expr)) PostfixEvaluate(infix_expr)
The PostfixEvaluate() method includes a print statement that shows the stack contents after each token is processed, plus a final print statement showing the answer. The “main” part of the program (when __name__ == '__main__') prompts the user for an infix expression, prints its postfix representation, and then evaluates it. Running the program produces a result like this:
$ python3 PostfixEvaluate.py Infix expression to evaluate: 3*(4+5)-6/(1+2) The postfix representation of 3*(4+5)-6/(1+2) is 3 4 5 + * 6 1 2 + / - After processing 3 stack holds: [3] After processing 4 stack holds: [3, 4] After processing 5 stack holds: [3, 4, 5] After processing + stack holds: [3, 9] After processing * stack holds: [27] After processing 6 stack holds: [27, 6] After processing 1 stack holds: [27, 6, 1] After processing 2 stack holds: [27, 6, 1, 2] After processing + stack holds: [27, 6, 3] After processing / stack holds: [27, 2.0] After processing - stack holds: [25.0] Final result = 25.0
Note this is the same calculation as shown in Figure 4-12, although the Python interpreter produced a floating-point number when it performed the division operation. The PostfixEvaluate.py program has not added any error checking on the input, so if you give it invalid expressions or expressions that contain names instead of numbers, the results will be wrong.
Experiment with the program and with the InfixCalculator tool. Try different expressions and check to see that they translate into postfix as you expect and verify the evaluation process. Use the animation controls to slow down or pause the calculator to see how the steps are carried out. Trying out different experiments can give you an understanding of the process faster than reading about it. One difference between the code and the InfixCalculator tool is that the tool creates floating-point numbers when division is used and pushes it on the stack. If that floating-point number creates an error, however, the tool will convert it to an integer and try again.
Summary
 Stacks, queues, and priority queues are data structures usually used to simplify common programming operations.
Stacks, queues, and priority queues are data structures usually used to simplify common programming operations. In these data structures, only one data item can be accessed. They are designed to work for specific patterns in the order of access to the items.
In these data structures, only one data item can be accessed. They are designed to work for specific patterns in the order of access to the items. A stack allows access to the last item inserted: last-in, first-out (LIFO).
A stack allows access to the last item inserted: last-in, first-out (LIFO). The important stack operations are pushing (inserting) an item onto the top of the stack and popping (removing) the item that’s on the top.
The important stack operations are pushing (inserting) an item onto the top of the stack and popping (removing) the item that’s on the top. A queue allows access to the first (oldest) item that was inserted: first-in, first-out (FIFO).
A queue allows access to the first (oldest) item that was inserted: first-in, first-out (FIFO). The important queue operations are inserting an item at the rear of the queue and removing the item from the front of the queue.
The important queue operations are inserting an item at the rear of the queue and removing the item from the front of the queue. Stacks and queues typically do not have search or traverse operations because they are not databases.
Stacks and queues typically do not have search or traverse operations because they are not databases. Stacks and queues typically do support a peek operation to examine the next item to be removed.
Stacks and queues typically do support a peek operation to examine the next item to be removed. A queue can be implemented using a circular array, which is based on a linear array in which the indices wrap around from the end of the array to the beginning.
A queue can be implemented using a circular array, which is based on a linear array in which the indices wrap around from the end of the array to the beginning. A deque is a two-ended queue that allows insertion and removal operations at both ends.
A deque is a two-ended queue that allows insertion and removal operations at both ends. The frontmost item in a priority queue is always the highest in priority and is the oldest in the queue of that priority.
The frontmost item in a priority queue is always the highest in priority and is the oldest in the queue of that priority. The important priority queue operations are inserting an item in sorted order based on priority and removing the oldest item within the highest-priority items.
The important priority queue operations are inserting an item in sorted order based on priority and removing the oldest item within the highest-priority items. These data structures can be implemented with arrays or with other mechanisms such as linked lists.
These data structures can be implemented with arrays or with other mechanisms such as linked lists. Ordinary arithmetic expressions are written in infix notation, so-called because the operator is written between the two operands.
Ordinary arithmetic expressions are written in infix notation, so-called because the operator is written between the two operands. In postfix notation, the operator follows the two operands.
In postfix notation, the operator follows the two operands. Arithmetic expressions can be evaluated by translating them to postfix notation and then evaluating the postfix expression.
Arithmetic expressions can be evaluated by translating them to postfix notation and then evaluating the postfix expression. A stack is a useful tool both for translating an infix to a postfix expression and for evaluating a postfix expression.
A stack is a useful tool both for translating an infix to a postfix expression and for evaluating a postfix expression.
Questions
These questions are intended as a self-test for readers. Answers may be found in Appendix C.
1. Suppose you push the numbers 10, 20, 30, and 40 onto the stack in that order. Then you pop three items. Which one is left on the stack?
2. Which of the following is true?
a. The Pop operation on a stack is considerably simpler than the Remove operation on a queue.
b. The contents of a queue can wrap around, while those of a stack cannot.
c. The top of a stack corresponds to the rear of a queue.
d. In both the stack and the queue, items removed in sequence are taken from increasingly higher index cells in the array.
3. What do LIFO and FIFO mean?
4. True or False: A stack or a queue often serves as the underlying mechanism on which an array data type is based.
5. As other items are inserted and removed, does a particular item in a queue move along the array from lower to higher indices, or higher to lower?
6. Suppose you insert 15, 25, 35, and 45 into a queue. Then you remove three items. Which one is left?
7. True or False: Pushing and popping items on a stack and inserting and removing items in a queue all take O(N) time.
8. A queue might be used appropriately to hold
a. the items to be sorted in an insertion sort.
b. reports of a variety of imminent attacks on the star ship Enterprise.
c. keystrokes made by a computer user writing a message.
d. delimiters in an algebraic expression being matched.
9. Inserting an item into a priority queue takes what Big O time, on average?
10. The term priority in a priority queue means that
a. the highest-priority items are inserted first.
b. the programmer must prioritize access to the underlying array.
c. the underlying array is ordered by the priority of the items.
d. the lowest-priority items are deleted first.
11. True or False: At least one of the methods in the PriorityQueue.py program in Listing 4-7 uses a linear search.
12. One difference between a priority queue and an ordered array is that
a. the lowest-keyed item cannot be removed as easily from the array as the lowest-priority item can from the priority queue.
b. the array must be ordered while the priority queue need not be.
c. the highest-priority item can be removed easily from the priority queue but the highest-keyed item in the array takes much more work to remove.
d. All the above.
13. Suppose a priority queue class is based on the OrderedRecordArray class from Chapter 2. This allows treating the priority as the key and provides a binary search capability. Would you need to modify the OrderedRecordArray class to maintain removals as an O(1) operation?
14. A priority queue might be used appropriately to hold
a. patients to be picked up by an ambulance from different parts of the city.
b. keystrokes made at a computer keyboard.
c. squares on a chessboard in a game program.
d. planets in a solar system simulation.
15. When parsing arithmetic expressions, it’s convenient to use
a. a stack for operators and a queue for operands and to evaluate postfix using another stack.
b. a priority queue for the operators and operands and to evaluate postfix using a stack.
c. a stack to transform infix expressions into prefix expressions that are then evaluated with a queue.
d. a queue to transform the operators into postfix and then evaluate them using a priority queue.
Experiments
Carrying out these experiments will help to provide insights into the topics covered in the chapter. No programming is involved.
4-A Start with the initial configuration of the Queue Visualization tool. Alternately insert and remove items. Notice how the front and rear indices rotate around in the queue. Does the inserted item ever get stored in the same cell twice?
4-B Think about how you remember the events in your life. Are there times when they seem to be stored in your brain like a stack? Like a queue? Like a priority queue?
4-C Consider various processing activities and decide which of the data structures discussed in this chapter would be best to represent the process. Some activities are
 Handling order requests on an e-commerce website
Handling order requests on an e-commerce website Dealing with interruptions to the task you’re working on (like this homework)
Dealing with interruptions to the task you’re working on (like this homework) Folding and putting away clothes to be worn next week
Folding and putting away clothes to be worn next week Folding rags to be used in cleaning
Folding rags to be used in cleaning Triaging patients that arrive at hospitals or clinics during a disaster with a limited number of treatment rooms and doctors
Triaging patients that arrive at hospitals or clinics during a disaster with a limited number of treatment rooms and doctors Following the different paths in a maze at each decision point
Following the different paths in a maze at each decision point
4-D Using the InfixCalculator Visualization tool, try entering some valid numeric expressions and some with errors. Try putting in unbalanced parentheses and operators with missing operands. The tool doesn’t try to find your errors, but if you were going to change it to report errors, how would you do it? At what point in the processing are the errors discoverable?
Programming Projects
Writing programs to solve the Programming Projects helps to solidify your understanding of the material and demonstrates how the chapter’s concepts are applied. (As noted in the Introduction, qualified instructors may obtain completed solutions to the Programming Projects on the publisher’s website.)
4.1 Revise the Stack class in SimpleStack.py shown in Listing 4-1 to throw exceptions if something is pushed on to a full stack, or popped off an empty stack. Write a test program that demonstrates that the revised class properly accepts items up to the original stack size and then throws an exception when another item is pushed.
4.2 Create a program that determines whether an input string is a palindrome or not, ignoring whitespace, digits, punctuation, and the case of letters. Palindromes are words or phrases that have the same letter sequence forward and backward. Show the output of your program on “A man, a plan, a canal, Panama.” You should use a Stack as part of the implementation as was shown in the ReverseWord.py program in Listing 4-3.
4.3 Create a Deque class based on the discussion of deques (double-ended queues) in this chapter. It should include insertLeft(), insertRight(), removeLeft(), removeRight(), peekLeft(), peekRight(), isEmpty(), and isFull() methods. It needs to support wraparound at the end of the array, as queues do.
4.4 Write a program that implements a stack class that is based on the Deque class in Programming Project 4.3. This stack class should have the same methods and capabilities as the Stack class in the SimpleStack.py module (Listing 4-1).
4.5 The priority queue shown in Listing 4-7 features fast removal of the highest-priority item but slow insertion of new items. Write a program with a revised PriorityQueue class that has fast, O(1), insertion time but slower removal of the highest-priority item. Write a test program that exercises all the methods of the PriorityQueue class. Include the method that shows the PriorityQueue contents as a string and use it to show the contents of some test examples that include cases where the insertions do not occur in priority order.
4.6 Queues are often used to simulate the flow of people, cars, airplanes, transactions, and so on. Write a program that models checkout lines/queues at a store, using the Queue class (Listing 4-5). The system should model four checkout lines that initially start empty, labeled A, B, C, and D. Use a string to model the arrival and checkout completion events by using a lowercase letter to indicate a new customer arriving in one of the lines, and an uppercase letter to indicate a customer completing checkout from the named line. For example, the string ”aababbAbA” shows three people going into the A checkout line with two being processed, while four people enter the B checkout line and none are processed. When a customer is added, put a “person” in the queue by adding a string like ”C1” to the queue where the number increases for each new person. Any nonalphabetic character in the string (such as a space or comma) signals that the current content of each of the queues should be printed. Use an OrderedRecordArray from Chapter 2 to store the Queues and their labels. Print error messages for queues that overflow or underflow. Show the output of your program on these strings:
aaaa,AAbcd, abababcabc,Adb,Adb,Ca, dcbadcbaDCBA-dddAcccBbbbCaaaD-
4.7 Extend the capabilities of PostfixTranslate.py in Listing 4-9 and PostfixEvaluate.py in Listing 4-11 to include the infix assignment operator, A = B. When evaluating expressions on the stack that reference variables, look up the assigned variable values before performing numeric operations. The assignment operator has the lowest precedence of any of the other operators. Unlike Python, the assignment operator itself should return the right-hand side value as its result. In other words, A=3*2 should return a value of 6 (in Python, it returns None) with the side effect of binding A to 6. In this extended evaluator, references to variables must occur after they have been set (in some higher-precedence expression to the left of the reference). Your program should print an error message if the expression references variables that are not set. Variable values should be retrieved when an operator is trying to use the value for a calculation (not when they are pushed on the stack). Your program should display the contents of the stack as it processes each token. For example:
$ python3 project_4_7_solution.py Infix expression to evaluate: (A = 3 * 2) * A The postfix representation of (A = 3 * 2) * A is: A 3 2 * = A * After processing A stack holds: [A] After processing 3 stack holds: [A, 3] After processing 2 stack holds: [A, 3, 2] After processing * stack holds: [A, 6] After processing = stack holds: [6] After processing A stack holds: [6, A] After processing * stack holds: [36] Final result = 36
The first appearance of A defines the value for A as 6, and the second appearance references that value. Use the OrderedRecordArray class from Chapter 2 to store and retrieve records containing a variable name and value to implement this. Show the result of running your program on '(A = 3 + 4 * 5) + (B = 7 * 6) + B/A'.
